A mathematical model to quantify RYR Ca²⁺ leak and associated heat production in resting human skeletal muscle fibers

Barclay and Launikonis developed a mathematical model to quantify the cycling of Ca²⁺ within muscle cells and the heat produced by that process. That heat contributes to the resting heat production of muscles and thus to the maintenance of body temperature.

Abstract

Cycling of Ca²⁺ between the sarcoplasmic reticulum (SR) and myoplasm is an important component of skeletal muscle resting metabolism. As part of this cycle, Ca²⁺ leaks from the SR into the myoplasm and is pumped back into the SR using ATP, which leads to the consumption of O₂ and generation of heat. Ca²⁺ may leak through release channels or ryanodine receptors (RYRs). RYR Ca²⁺ leak can be monitored in a skinned fiber preparation in which leaked Ca²⁺ is pumped into the t-system and measured with a fluorescent dye. However, accurate quantification faces a number of hurdles. To overcome them, we developed a mathematical model of Ca²⁺ movement in these preparations. The model incorporated Ca²⁺ pumps that move Ca²⁺ from the myoplasm to the SR and from the junctional space (JS) to the t-system, Ca²⁺ buffering by EGTA in the JS and myoplasm and by buffers in the SR, and Ca²⁺ leaks from the SR into the JS and myoplasm and from the t-system into the myoplasm. The model accurately simulated Ca²⁺ uptake into the t-system, the relationship between myoplasmic [Ca²⁺] and steady-state t-system [Ca²⁺], and the effect of blocking RYR Ca²⁺ leak on t-system Ca²⁺ uptake. The magnitude of the leak through the RYRs would contribute ∼5% of the resting heat production of human muscle. In normal resting fibers, RYR Ca²⁺ leak makes a small contribution to resting metabolism. RYR-focused pathologies have the potential to increase RYR Ca²⁺ leak and the RYR leak component of resting metabolism.

Introduction

Cycling of calcium ions (Ca²⁺) between the sarcoplasmic reticulum (SR) and the myoplasm is central to excitation–contraction coupling in muscle: release of Ca²⁺ into the myoplasm and its subsequent binding to sites on troponin C (TnC) initiate and maintain contraction, and removal of Ca²⁺ from the myoplasm initiates relaxation. However, Ca²⁺ cycling is important even in unstimulated or resting muscle and contributes to resting metabolism. In resting muscle, there appears to be a steady leak of Ca²⁺ from the SR into the myoplasm that is balanced by removal of Ca²⁺ from the myoplasm into the SR via the SR Ca²⁺ pump (Chinet et al., 1992). The concentration of free, or unbound, Ca²⁺ in the myoplasm is steady in resting muscle (Konishi and Watanabe, 1995), indicating that the rate at which Ca²⁺ leaks into the myoplasm is equal to the rate at which it is pumped into the SR. The SR Ca²⁺ pump (SERCA) is powered by ATP and, in a metabolic steady state, ATP is replenished by mitochondrial oxidative phosphorylation at the same rate at which it is used. The ATP regenerating processes produce heat, and the heat associated with SERCA activity accounts for about one-quarter of the heat produced by resting mouse skeletal muscles (Chinet et al., 1992).

Two Ca²⁺ leak processes, that are not mutually exclusive, have been proposed. First, Ca²⁺ can leak from the SR through the Ca²⁺ release channels or ryanodine receptors (RYRs; Cully et al., 2016). The importance of this pathway is that the leakiness of RYRs has been shown to vary across a range of naturally occurring variants of RYRs, perhaps most strikingly in the highly modified heater muscles of some fish (Morrissette et al., 2003), and to be associated with pathological conditions, such as malignant hyperthermia (Cully et al., 2018). Second, Ca²⁺ can leak from the SR into the myoplasm via a mechanism independent of RYRs but that involves SERCA (Simonides and Van Hardeveld, 1988; Macdonald and Stephenson, 2001; Lamboley et al., 2014). The focus of the current study is the first of these mechanisms, Ca²⁺ leak through the RYRs.

Launikonis and colleagues have developed a method to measure the rate of Ca²⁺ leak through the RYRs in unstimulated or resting muscle fibers (Cully et al., 2016; Cully et al., 2017; Cully et al., 2018). A skinned muscle fiber preparation is used in which at least some of the Ca²⁺ that leaks through the RYRs is pumped into the t-tubules, which are sealed from the extracellular space in this particular preparation and are loaded with a Ca²⁺-sensitive dye. The inside of the fiber preparation is heavily buffered against changes in [Ca²⁺] by the presence of EGTA. In the junctional space (JS) adjacent to the RYRs, the presence of EGTA attenuates changes in Ca²⁺ concentration due to RYR leaks so that the variation in the concentration of unbound Ca²⁺ in the JS (Ca_JS) due to leaks is within the working range of the Ca²⁺ pump in the neighboring t-tubule membrane. In this way, the rate at which the pump (a plasma membrane Ca²⁺ ATPase [PMCA]) moves Ca²⁺ into the t-tubule reflects Ca_JS and thus the rate at which Ca²⁺ leaks through the RYRs. If Ca²⁺ leaks through the RYRs rapidly enough to raise Ca_JS, then the rate and extent of Ca²⁺ accumulation in the t-system will be increased. A key aspect of these experiments is that the RYR Ca²⁺ flux can be inhibited pharmacologically, using tetracaine. The magnitude of trans-RYR Ca²⁺ leak can then be inferred from the difference in the rate and extent of t-tubule Ca²⁺ accumulation before and after the inhibition (Cully et al., 2018). Those experiments indicate that there is a continual leak of Ca²⁺ through the RYR in unstimulated fibers of human skeletal muscle. However, the complexity of the experimental preparation makes it difficult to determine the magnitude of the RYR Ca²⁺ leak.

Specific aspects of the preparation and the experimental methods that complicate the relationship between RYR Ca²⁺ leak and t-tubule Ca²⁺ uptake are as follows: (1) the skinned fiber contains a high concentration of EGTA, which is used to control the myoplasmic Ca²⁺ concentration (Ca_M) to match the range over which the PMCA functions. However, the buffering action of EGTA must also attenuate the increase in Ca_JS that occurs when Ca²⁺ leaks into the JS. (2) It is likely that there is a leak of Ca²⁺ from the t-system into the myoplasm (Cully et al., 2018; Meizoso-Huesca and Launikonis, 2021). In that case, the empirical relationship between the concentration of unbound Ca²⁺ in the t-system (Ca_T) and Ca_JS reflects the combined characteristics of Ca²⁺ uptake by the PMCA and Ca²⁺ leak from the t-system. (3) JS volume (V_JS) is small compared to that of the SR (V_SR; V_JS < 0.1% V_SR; Eisenberg, 1983), so a leak of Ca²⁺ through the RYRs that makes only a small change in Ca_SR will produce a large change in the total Ca²⁺ concentration (i.e., free + bound to EGTA) in the JS. (4) The experimental protocol starts with emptying Ca²⁺ from the t-tubules and SR. It is not known whether the subsequent time course of SR filling, which in turn is likely to affect RYR leak, influences the time course of t-system Ca²⁺ accumulation.

One way of assessing how these aspects of the preparation and protocol influence the experimental results is to use a mathematical model of the preparation. The purpose of the current study was to develop a model that could be used to quantify the leak of Ca²⁺ from the SR through the RYRs, to identify factors that influence t-tubule Ca²⁺ accumulation, and to estimate the contribution of trans-RYR Ca²⁺ flux to the metabolism of resting muscle.

Materials and methods

Overview of the model

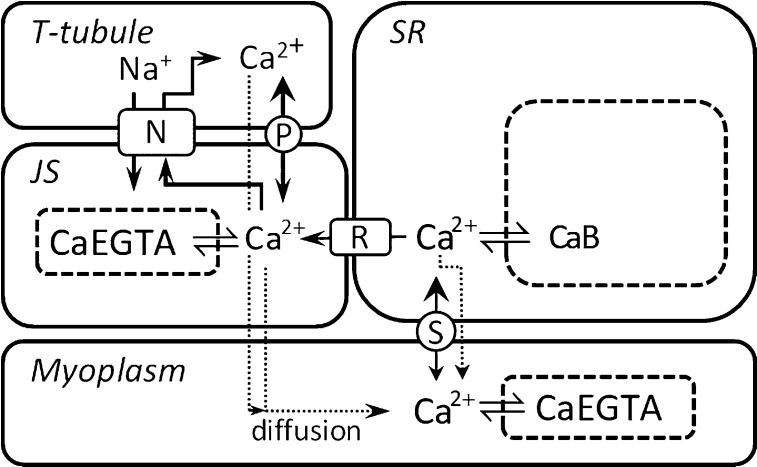
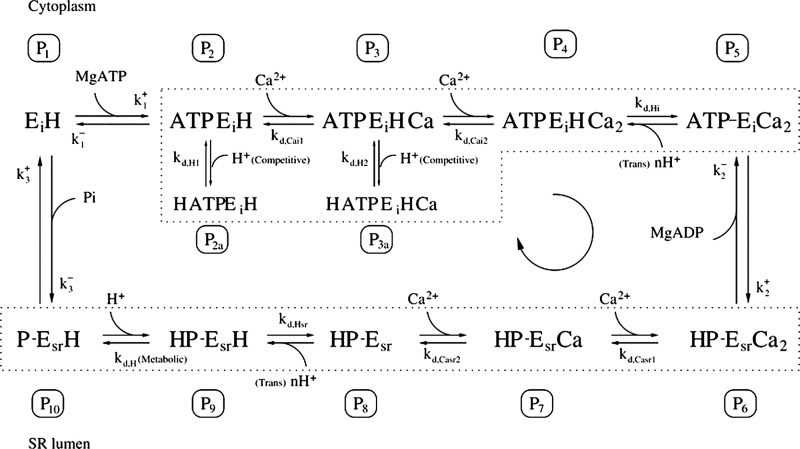
The model describes the movements of Ca²⁺ among the SR, t-tubule, JS, and myoplasm and is illustrated in Fig. 1. The subcellular system that was modeled included seven compartments that Ca²⁺ can occupy, four of which are physically discrete spaces and three of which are molecular compartments (i.e., Ca²⁺ in equilibrium with buffer molecules). The compartments are (1) t-tubules, (2) SR, (3) JS (i.e., region between t-tubule and SR Ca²⁺ release channels), (4) myoplasm, (5) EGTA in the myoplasm, (6) EGTA in the JS, and (7) Ca²⁺ buffers, including calsequestrin (Csq), in the SR.

Figure 1.

Schematic of experimental fiber model. The model includes four physical spaces, the myoplasm, SR, JS, and t-tubule. In the SR, Ca²⁺ is in equilibrium with buffers (B), which includes Csq. In the myoplasm and JS, Ca²⁺ is in equilibrium with EGTA. Ca²⁺ movements were constrained as follows: (1) Ca²⁺ enters the SR only from the myoplasm via SERCA (labeled S); (2) Ca²⁺ enters the t-tubule only from the JS and via PMCA (P) and NCX (N); (3) Ca²⁺ enters the JS by leak from the SR (through the RYR [R]), potentially from NCX working in reverse and from dissociation of Ca²⁺ bound to EGTA; (4) Ca²⁺ can enter the myoplasm by leaking from the SR or the t-system and by diffusive exchange with the JS. The relative sizes of the spaces in the diagram do not reflect the actual relative volumes in a fiber.

Mathematical description of the model

The rates of change in concentration of Ca²⁺ in each of the compartments, taking into account the constraints on Ca²⁺ movements described in the legend of Fig. 1 and the relative volumes of the physical compartments, were described by ordinary differential equations. The equations incorporated Ca²⁺ movements due to (1) ATP-dependent pumping of Ca²⁺ from the myoplasm into the SR via SERCA, (2) ATP-dependent pumping of Ca²⁺ from the JS into the t-tubules via PMCA, (3) exchange of Na⁺ and Ca²⁺ between the JS and t-tubule via the sodium/calcium exchanger (NCX), and (4) diffusive exchange of Ca²⁺ between the JS and myoplasm. The concentrations of unbound Ca²⁺ in the myoplasm and JS were determined from the equilibrium between Ca²⁺ and EGTA, and that in the SR from the equilibrium between Ca²⁺ and the SR buffers. The equation formulation ensured that total Ca²⁺ in the system remained constant.

To provide the model with the complexity and responsiveness to local conditions that is evident in physiological systems, where possible mechanistic descriptions of model components were used. Models for SERCA and PMCA were taken from models described and validated in the literature. Cully et al. (2018) showed that t-system Ca²⁺ accumulation in human fibers was unaffected by pharmacological inhibition of NCX. Therefore, NCX was not incorporated into the final model. Temperature-sensitive model parameters obtained from the literature were adjusted to values appropriate for a temperature of 25°C, similar to that used for the muscle fiber experiments, assuming a Q₁₀ (change in rate for a 10°C change in temperature) of 2.

Model components

SR Ca²⁺ pump (SERCA)

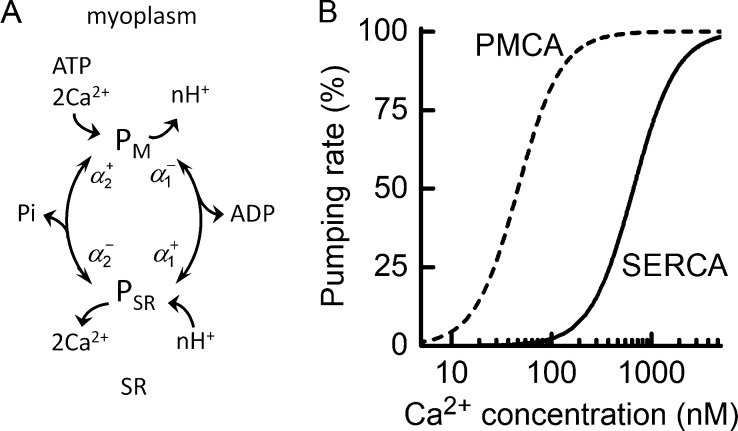
In each pump cycle, SERCA moves two Ca²⁺ from the myoplasm up a concentration gradient into the SR at the expense of one ATP (Weber et al., 1966; Makinose and Hasselbach, 1971). The pump was modeled as described by Tran et al. (2009). Those authors derived a 2-state model (Fig. 2 A) from a 12-state biochemical model. In reducing the model to 2 states, the relevant complexity of the 12-state model was maintained in that the apparent rate constants describing the forward and reverse transitions between the 2 states depend on pH, the concentrations of ATP and its hydrolysis products, and [Ca²⁺] on both sides of the SR membrane (see Appendix 1). The model is thermodynamically constrained; that is, the rate of Ca²⁺ pumping depends on the difference in free energy produced by ATP hydrolysis (ΔG_ATP) and the free energy generated by the Ca²⁺ concentration gradient (ΔG_Ca). The equations describing the pumping rate are given in Appendix 1.

Figure 2.

Characteristics of Ca²⁺ pumps used in model. (A) Schematic of the two-state Ca²⁺ pump model used for SERCA and PMCA. The model consists of two states, one on the myoplasmic side of the membrane (labeled P_M), where Ca²⁺ is collected, and one on the luminal side of the SR membrane for SERCA or t-tubular membrane for PMCA (P_SR), where Ca²⁺ is released. The diagram illustrates the forward and reverse rate constants for transitions between the states (α), Ca²⁺ transport, H⁺ countertransport, and hydrolysis of ATP to provide energy. The rate constants are functions of [ATP] and its metabolites and pH. (B) Dependence on [Ca²⁺] of Ca²⁺ pumping rate of SERCA and PMCA. Curves constructed using the model showing relationship between relative rate of Ca²⁺ pumping (% maximum rate) and [Ca²⁺] using the K_d values for Ca²⁺ dissociation on the myoplasmic side as applied in the current analysis. The maximal rates of pumping (with concentrations expressed relative to myoplasmic water volume; see Table 3) were SERCA, 711 μM s⁻¹; and PMCA, 0.15 μM s⁻¹. Note that expressed relative to JS volume, PMCA maximal Ca²⁺ pumping rate was 705 μM s⁻¹. The Ca₅₀ values were SERCA, 700 nM; and PMCA, 46 nM.

To align the SERCA model with human skeletal muscle, appropriate values for the pump’s concentration and Ca²⁺ sensitivity were determined. Sensitivity of the pump to Ca²⁺ is quantified by its Ca₅₀ value (the Ca_M at which the pump rate is 50% of its maximum). A constraint on the sensitivity is that the rate of Ca²⁺ pumping when Ca_M is at resting levels should not result in SERCA producing heat from oxidative regeneration of ATP consumed by the pump at a rate greater than the experimentally determined Ca²⁺-related heat output in resting muscles. SERCA has been reported to account for ∼25% of the resting metabolism of mouse slow-twitch muscle (Chinet et al., 1992) and 20% of rat fast-twitch muscle (Simonides and Van Hardeveld, 1988), but there are also much lower estimates (e.g., 3–5%; Clausen et al., 1991; Rolfe and Brown, 1997). The rate of heat output from noncontracting human forearm muscles is 0.6 W kg⁻¹ (Table 1), or 600 mW kg⁻¹, so if it is assumed that 25% of this is due to Ca²⁺ cycling via SERCA, then ATP use by the pump would produce heat at 0.25 × 600 = 150 mW kg⁻¹.

Table 1.

Rate of heat output from resting human skeletal muscle

Forearm resting VO2 at 35°C	2.2	ml (liter muscle)−1 min−1	Zurlo et al. (1990)
Rate of muscle heat production at 35°C	46	J (liter muscle)−1 min−1	Assuming 20.9 kJ (liter O2)−1
Express in W (kg muscle)−1	0.73	W (kg muscle)−1	Muscle density, 1.06 kg liter−1
Express in W (kg myoplasmic water)−1	1.2	W (kg myoplasmic H2O)−1	Whole muscle volume = 1.45 × myoplasmic H2O volume (Table 3)
Rate of muscle heat production at 25°C	0.60	W (kg myoplasmic H2O)−1	Q10 = 2 (Barclay et al., 2009)

A Ca₅₀ value that is consistent with this rate of heat production can be calculated as follows. In resting skeletal muscle, Ca_M is in the range 0.05–0.1 μM (for a review, see Konishi, 1998). At 25°C, the maximum rate of ATP breakdown by SERCA in human type 2 fibers is 355 μM s⁻¹ (Table 2). The heat associated with Ca²⁺ cycling in resting muscle arises from oxidative regeneration of ATP; if glucose is the substrate (molar enthalpy change, 2,802 mJ μmol⁻¹; Kabo et al., 2013) and 38 ATP are generated per glucose (for a review, see Barclay and Loiselle, 2020), then the heat produced is 2,802/38 = 74 mJ (μmol ATP)⁻¹. Assuming a sigmoidal dependence of rate of Ca²⁺ pumping on Ca_M with a slope of 2 (Fig. 2 B), Ca_M of 0.05 μM in resting fast-twitch muscle and muscle density of 1.06 kg liter⁻¹, then the Ca²⁺-related rate of heat production (Q; mW kg⁻¹) is given by

$$Q=\frac{{0.05}^2}{{0.05}^2+\mathrm{C}{\mathrm{a}}_{50}^2}\cdot \frac{355.74}{1.06}.$$ (1)

Table 2.

Estimate of maximum rate of SR Ca²⁺ pumping in intact fast-twitch human muscle fibers

Variable	Value
Isometric ATP turnovera	2,333 μM s−1
Fraction of ATP turnover by Ca pumpb	0.35
ATP turnover for Ca pumping at 37°C	817 μM s−1
ATP turnover for Ca pumping at 25°Cc	355 μM s−1
Maximum rate of Ca uptake at 25°Cd	711 μM s−1

^aExpressed relative to myoplasmic H₂O volume; converted from 140 mM min⁻¹ in sustained maximal contraction at 37°C (for details, see Barclay, 2017).

^bFrom data for type 2A human fibers (Szentesi et al., 2001) and other mammalian muscles (Barclay et al., 2007).

^cAssumed Q₁₀ = 2 (Barclay, 2012).

^dTwo Ca²⁺ translocated for each ATP-splitting cycle (Weber et al., 1966).

Setting Q to 150 mW kg⁻¹ and solving for $\mathrm{C}{\mathrm{a}}_{50}$ gives 0.66 μM. This is probably a lower limit, because $\mathrm{C}{\mathrm{a}}_{50}$ would be greater if resting Ca_M was >50 nM. For the current study, $\mathrm{C}{\mathrm{a}}_{50}^{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}$ was set to 0.7 μM, which satisfies Eq. 1 and is comparable to estimates for other mammalian fast-twitch muscles (0.3 μM, Vilsen and Andersen, 1992; 0.62 μM, Cantilina et al., 1993).

The concentration of SERCA in human skeletal muscle was estimated using the maximal turnover rate for individual pumps under cellular conditions applicable to the current experimental preparation, and an estimate of the absolute maximum rate of Ca²⁺ pumping $\left({\mathrm{M}}_{\mathrm{Max}}^{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}\right)$ was calculated using measurements of energy turnover in human muscle fibers (Table 2). At the fiber level, the maximum rate of Ca²⁺ pumping ${\mathrm{M}}_{\mathrm{Max}}^{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}$ (μM s⁻¹) is the product of the turnover rate of individual pumps (γ, s⁻¹), the Ca²⁺/ATP stoichiometry (n_SERCA), and pump concentration (c_SERCA, μM):

$$M_{\mathrm{Max}}^{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}=c_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}\cdot n_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}\cdot \gamma \text{.}$$ (2)

For SERCA, γ is ∼6 s⁻¹ at 25°C (calculated from data in Lytton et al., 1992; Cantilina et al., 1993; Fortea et al., 2001). $M_{\mathrm{Max}}^{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}$ was taken to be 711 μM s⁻¹ (Table 2). Setting n_SERCA = 2 and rearranging Eq. 2, c_SERCA = 711 μM s⁻¹ / (2 × 6 s⁻¹) = 59 μM (expressed relative to myoplasmic water volume). This compares favorably with values for fast-twitch muscles of other mammalian species. Baylor et al. (1983) calculated a pump concentration of 69 μM for rabbit fast-twitch muscle, and the data presented by Ferguson and Franzini-Armstrong (1988) (their Table 2) can be used to calculate a value of 68 μM for guinea pig fast-twitch muscle.

Ca²⁺-cycling component of resting metabolism constrains the magnitude of SR Ca²⁺ leak

There is evidence that Ca²⁺ leaks into the myoplasm from the SR via mechanisms in addition to RYR Ca²⁺ leak. Ca²⁺ leaks from the SR, even with the RYRs blocked, and at least part of this leak involves SERCA itself (Simonides and Van Hardeveld, 1988; Macdonald and Stephenson, 2001). A passive, concentration gradient–driven leak from the SR into the myoplasm, with a rate constant $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{S}\mathrm{R}},$ was incorporated into the model. The magnitude of Ca²⁺ leak, by all mechanisms, from the SR into the myoplasm of resting muscle can be estimated from the energy expenditure of SERCA in resting muscle. Assuming that Ca²⁺ cycling accounts for a heat production of 150 mW kg⁻¹, as calculated above, and that the energy equivalent of ATP turnover is 74 mJ μmol⁻¹ (see above), then SERCA-related ATP turnover would be 150 mJ s⁻¹ kg⁻¹ / 74 mJ μmol⁻¹ ≈ 2.0 μmol kg⁻¹ s^−1, and the rate of Ca²⁺ pumping would be 4 μmol kg⁻¹ s⁻¹. Taking into account of the relative volumes of the myoplasm and SR (Table 3), this uptake rate corresponds to Ca²⁺ exiting the SR at 69 / 3.8 × 4 = 73 μM s⁻¹ with respect to SR volume. If Ca_SR at rest is 400 μM (Sztretye et al., 2011b; Manno et al., 2013), this rate of loss is consistent with a rate constant of 73 μM s⁻¹ / 400 μM = 0.18 s⁻¹. This represents the total SR Ca²⁺ cycling, including leaks via RYRs and any other sources. $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{S}\mathrm{R}}$ will, therefore, be 0.18 − $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ s⁻¹, where $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ is the rate constant for Ca²⁺ efflux from the SR through the RYRs.

Table 3.

Volumes of muscle components and concentration conversion factors for human muscle

Component	Relative volume (% fiber volume)	Comments
SR	3.8	Eisenberg (1983)
Mitochondria	5	Eisenberg (1983)
t-system	0.28	Eisenberg (1983)
JS	0.014	Estimated to be 5% of t-system volume (see text)
Myoplasmic water	69	Fraction of water in whole tissue that is inside fibers, excluding volumes occupied by SR, t-system, and JS
Concentration conversion factors
Whole muscle (kg−1) → fiber (liter−1)	1.18
Whole muscle (kg−1) → myoplasmic water (liter−1)	1.45
Fiber (liter−1) → myoplasmic water (liter−1)	1.23

Other values required for calculations: whole muscle density, 1.05 kg liter⁻¹ (Segal et al., 1986) and protein density, 1.37 kg liter⁻¹ (Fischer et al., 2004; these values give ratio of wet mass/dry mass of whole muscle = 5); extracellular water, 12.5% of total muscle water (Sjogaard et al., 1985).

Plasma membrane Ca²⁺ pump (PMCA)

It was assumed that the pump responsible for moving Ca²⁺ into the t-tubule system is of the PMCA family (Cully et al., 2012). PMCA has a molecular structure similar to SERCA, with the addition of a region enabling kinetic modulation in vivo by calmodulin (Carafoli, 1991), and is localized to the junctional region of skeletal muscle (Sacchetto et al., 1996). The slope of the relationship between Ca²⁺ pumping rate and [Ca²⁺] for PMCA is ∼2 (Kosk-Kosicka and Inesi, 1985), indicative of the cooperative binding of 2 Ca²⁺ in each pump cycle, which is consistent with direct measurements of the pump stoichiometry (Akyempon and Roufogalis, 1982; Valant and Haynes, 1993). It was therefore assumed that the mechanism of PMCA involves the binding and transport of 2 Ca²⁺ in each ATP-splitting cycle. The sensitivity of PMCA to Ca²⁺ depends on calmodulin. In the absence of calmodulin, the pump’s Ca₅₀ $\left(\mathrm{C}{\mathrm{a}}_{50}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}\right)$ is 5–10 μM, but this is reduced to <0.5 μM in the presence of calmodulin (Enyedi et al., 1993). EGTA, which was in the solutions used for the fiber studies on which the current analysis is based, also lowers $\mathrm{C}{\mathrm{a}}_{50}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ and to about the same extent as calmodulin (Schatzmann, 1973). The maximum pump turnover is similar for SERCA and PMCA. For instance, the maximum rates of ATP splitting by PMCA purified from human erythrocytes (Kosk-Kosicka and Inesi, 1985; Kosk-Kosicka and Bzdega, 1988; Enyedi et al., 1993), measured in the presence of calmodulin, are between 5 and 7 s⁻¹ at 25°C (assuming a Q₁₀ of 2). Therefore, as for SERCA, a maximum turnover of 6 s⁻¹ was used.

Given the structural and biochemical similarities between SERCA and PMCA, the same scheme (Fig. 2 A) was used to model both pumps (Sneyd, 2005; Croisier et al., 2013). Support for this approach can be seen in that reported relationships between the rate of ATP breakdown by PMCA and [Ca²⁺] can be described well using the model. For example, two empirical relationships between rate of ATP splitting and [Ca²⁺] are shown in Fig. 3, and both have been fitted with a curve calculated using the PMCA model equations, adjusting only the pump’s Ca²⁺ affinity. The form of the model predictions matches the data well, further supporting the idea that PMCA behaves in a manner consistent with cooperative binding of 2 Ca²⁺ in each cycle. The dashed line in Fig. 3 shows the ATPase–Ca²⁺ relationship produced when the model parameters were optimized to the human muscle fiber PMCA Ca²⁺ accumulation data of Cully et al. (2018).

Figure 3.

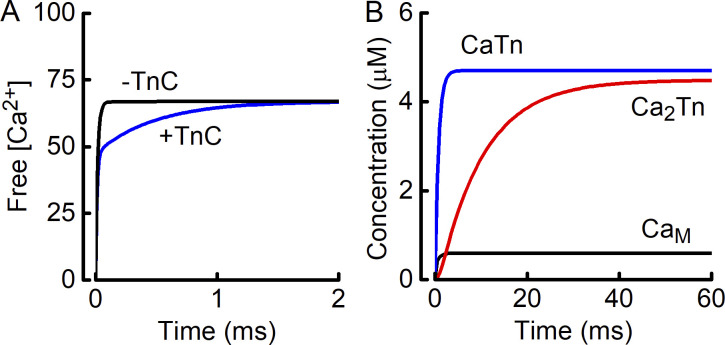
Comparison of experimental and model-derived dependence of rate of PMCA Ca²⁺ pumping on [Ca²⁺]. The PMCA model can replicate published ATPase data. The symbols are experimental data relating the rate of ATP splitting by PMCA as a function of [Ca²⁺] for different preparations of PMCA. Kosk-Kosicka and Inesi (1985; Fig. 3; used with permission from FEBS Letters). Filled circle, solubilized, purified PMCA from human erythrocytes, Ca₅₀, 38 nM (Enyedi et al., 1993; Fig. 5); open circle, microsomal vesicles containing a human PMCA-derived construct, Ca₅₀, 332 nM. The curves (a [blue] and b [red]) drawn through the data are the least-squares fit of the PMCA model used in the current study to the experimental data, adjusting only the value of PMCA Ca²⁺ affinity. The dashed black line (c) shows the relationship used for analysis of Ca²⁺ leak in the skinned fiber preparation.

Determinants of steady-state Ca_T: thermodynamics or leak of Ca²⁺ from t-system?

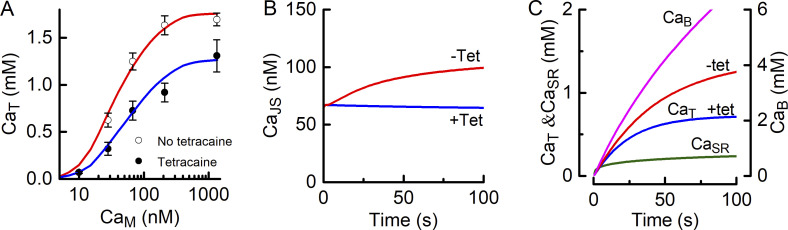
When the t-system fills with Ca²⁺, Ca_T reaches a plateau after ∼60–100 s (Cully et al., 2018). There are two potential causes of this phenomenon. First, the PMCA may reach its thermodynamic limit; that is, the plateau occurs when ΔG_Ca rises sufficiently, as the concentration gradient increases, to match ΔG_ATP. An alternative, and not necessarily mutually exclusive, explanation is that there is passive leak of Ca²⁺ out of the t-system, the rate of which depends on the [Ca²⁺] gradient between the t-tubule and the myoplasm. Each of these concepts is assessed in the following paragraphs. Predictions of the two models for limiting Ca_M are compared to experimental data obtained in the presence of tetracaine (Fig. 4, circles); this is the appropriate comparison because in the absence of a Ca²⁺ leak into the JS, Ca_JS, which drives the pump, is determined by the Ca²⁺–EGTA equilibrium; thus, Ca_JS ≈ Ca_M and can be estimated with some confidence.

Figure 4.

Models to account for steady-state Ca_T. (A) Ca²⁺ accumulation in the t-system limited by pump thermodynamics. The dashed curves show steady-state Ca_T–Ca_JS relationships for different ΔG_ATP values. The curves show what steady-state Ca_T would be if it was determined only by the ability of the pump to generate a gradient (Eq. 5). The symbols are experimental data (mean ± SEM) determined in the presence of tetracaine; the independent variable for the experimental data was Ca_M, but with RYRs blocked by tetracaine, Ca_M ≈ Ca_JS, which drives the pump, both determined by the Ca²⁺–EGTA equilibrium. (B) Steady-state Ca_T determined by balance between pumping Ca²⁺ into the t-system and a concentration gradient–dependent leak of Ca²⁺ out of t-system. The model used is given by Eqs. 6 and 7. Fitted parameters: c_PMCA, 60 μM; $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ 0.023 s⁻¹; and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ 223 μM.

To address the possibility that the thermodynamic limit of the pump determines steady-state Ca_T, an expression was derived that relates maximum Ca_T to Ca_JS and ΔG_ATP. As described by Smith et al. (2005), transport of Ca²⁺ into the t-system, assuming that the Ca²⁺/ATP ratio is 2, occurs only when

$${\Delta G}_{\mathrm{A}\mathrm{T}\mathrm{P}}+{2\Delta G}_{\mathrm{C}\mathrm{a}}<0\text{,}$$ (3)

where ΔG_Ca depends on the ratio of Ca_T to Ca_JS and

$$\Delta G_{\mathrm{C}\mathrm{a}}=RT\ln \left[\frac{{\mathrm{C}\mathrm{a}}_{\mathrm{T}}}{{\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}}\right]\text{,}$$ (4)

where R is the universal gas constant (8.314 J mol⁻¹ K⁻¹) and T is the absolute temperate (298 K). Substituting Eq. 4 into Eq. 3 and rearranging to give an expression for the maximum Ca_T that could be achieved by the pump if the thermodynamics were the only factor limiting Ca²⁺ accumulation (hereafter called the limit Ca_T):

$$\mathrm{L}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}{\mathrm{C}\mathrm{a}}_{\mathrm{T}}={\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}\cdot {\mathrm{e}}^{\frac{{-\Delta G}_{\mathrm{A}\mathrm{T}\mathrm{P}}}{2\cdot R\cdot T}.}$$ (5)

Eq. 5 was used to calculate the relationship between the limit Ca_T and Ca_JS for a series of values of ΔG_ATP; these are shown by the curves in Fig. 4 A. The range of ΔG_ATP values used for the calculations (40–55 kJ mol⁻¹) span the likely values in the skinned human muscle fibers. In intact skeletal muscle fibers, ΔG_ATP is typically ∼60 kJ mol⁻¹ (Barclay, 2015), but lower values are likely for skinned fibers, primarily owing to elevated inorganic phosphate concentration (Park-Holohan et al., 2010). The curves in Fig. 4 A can be used to estimate a lower limit for ΔG_ATP in the skinned fibers. Even if PMCA thermodynamics did not limit Ca²⁺ accumulation, the pump must be capable of generating the observed Ca²⁺ gradients. From Fig. 4 A, if ΔG_ATP was 40 kJ mol⁻¹, then the measured Ca_T values for Ca_JS of 28 and 67 nM were approximately fivefold higher than the pump could generate; therefore, ΔG_ATP cannot have been that low. The curve for ΔG_ATP of 45 kJ mol⁻¹ is close to the measured data points for Ca_JS of 28 and 67 nM. This indicates that ΔG_ATP in the fibers must have been ≥45 kJ mol⁻¹. However, the experimental Ca_T values for Ca_JS of 10, 210, and 1,340 nM lie substantially below the limit Ca_T, so for those values, at least, some other mechanism must limit Ca²⁺ accumulation in the t-system. In fact, the difference between the forms of the limit Ca_T–Ca_JS curves (increasing monotonically) and the experimental data (sigmoidal) precludes a thermodynamic pumping limit determining all the observed Ca_T values.

The second idea is that there is passive leak of Ca²⁺ out of the t-system, the rate of which depends on the [Ca²⁺] gradient between the t-tubule and the myoplasm. If it is assumed that the leak is a single process with a rate constant $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ then when Ca_T increases enough that the rate of leak, = $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}\times \left(\mathrm{C}{\mathrm{a}}_{\mathrm{T}}–\mathrm{C}{\mathrm{a}}_{\mathrm{JS}}\right),$ matches the rate of uptake of Ca²⁺ into the system (determined by Ca_JS), then Ca_T will be constant. To see whether a scheme in which Ca²⁺ pumping into the t-system is opposed by a leak can give a realistic Ca_T–Ca_JS relationship, a simple model was designed. For this proof-of-concept, it was assumed that (1) the rate of Ca²⁺ pumping was described by the model developed by Tran et al. (2009) (Fig. 2 A); (2) the volume of the t-system was 20 times greater than the JS volume (Table 3); and (3) the Ca²⁺ leaking out of the t-tubule did not alter the concentration of Ca²⁺ driving the pump. These ideas are expressed in the differential equations

$$\frac{{\mathrm{d}\mathrm{C}\mathrm{a}}_{\mathrm{T}}}{\mathrm{d}t}=\frac{1}{20}\cdot M_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}\left({\mathrm{C}\mathrm{a}}_{\mathrm{J}}{,\mathrm{C}\mathrm{a}}_{\mathrm{T}}{,K}_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}{,c}_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}\right)-k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}\cdot {\mathrm{C}\mathrm{a}}_{\mathrm{T}}\left(\mathrm{t}\right)\text{,}$$ (6)

and

$$\frac{{\mathrm{d}\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}}{\mathrm{d}t}=0\text{,}$$ (7)

where $M_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ is the rate of Ca²⁺ transfer between the JS and t-system by the PMCA, which is a function of [Ca²⁺] on both sides of the t-tubule membrane, the pump’s dissociation constant on the JS side of the membrane $\left(K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}\right),$ and the concentration of the pump (c_PMCA; for details, see Appendix 1). $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ and c_PMCA were adjusted to give the least-squares fit between the model output and the experimental data. This model captures the characteristics of the observed data well (Fig. 4 B), matching the dependence of Ca_T on Ca_JS across the full Ca_JS range used in the experiments. In the remainder of the analysis, it was assumed that there was a Ca²⁺ leak from the t-tubule that, when a steady Ca_T was achieved, balanced the rate of uptake of Ca²⁺ into the t-system. Note, however, that PMCA model used ensures that, regardless of the other aspects of the overall model, the model pump will operate within its thermodynamic constraints.

To incorporate the t-system Ca²⁺ leak into the fiber model, it was important to decide the destination of the Ca²⁺ leaked from the t-system. The leaked Ca²⁺ could enter either the JS or the myoplasmic space. In trials, it was found that if the Ca²⁺ leaked into the JS then when Ca_M was <50 nM, the leak caused a marked increase in Ca_JS and, consequently, predicted Ca_T values were higher than those observed. In contrast, when the leak was directed into the myoplasm, there was sufficient buffering to prevent changes in Ca_M, and the predicted Ca_T matched the observed Ca_T–Ca_M relationship. Therefore, it was assumed that Ca²⁺ that leaked from the t-system entered the myoplasmic space.

Estimating PMCA concentration

If the rate at which Ca²⁺ accumulates in the t-system depends on the balance between the rates of Ca²⁺ uptake into and leak out of the t-system, then three parameters determine t-system Ca²⁺ accumulation: c_PMCA, $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}.$ Values are not known for any of these parameters. Parameter optimization algorithms can be used to find a combination of values that will allow the model to match experimental data, but in this case such solutions are not unique because c_PMCA and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ are not independent. Therefore, a value for one of the three parameters is required.

c_PMCA could be estimated using Eq. 2, with the reported maximum rate of t-system Ca²⁺ accumulation (using Lagrange’s notation, Ca_T'′). Cully et al. (2018) reported a mean maximum Ca_T′ of 170 μM s⁻¹ (with the concentration referring to t-system volume). However, this rate is too high to be consistent with the overall time course of t-system Ca²⁺ accumulation. For example, when Ca_M is 67 nM and tetracaine is present, Ca_T increases with a half-time (t_½) between 15 and 20 s, and >60 s is required to reach a final steady Ca_T (e.g., Fig. 5 A). If the maximum rate of Ca²⁺ pumping is 170 μM s⁻¹, then by Eq. 2, c_PMCA would be 280 μM, with concentration expressed relative to JS volume. Using that concentration, the model predicts that Ca_T will reach a steady value in ∼15 s, regardless of the value of $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}.$ This suggests that the reported maximum Ca_T′ is not representative of the overall uptake of Ca²⁺ into the t-system.

Figure 5.

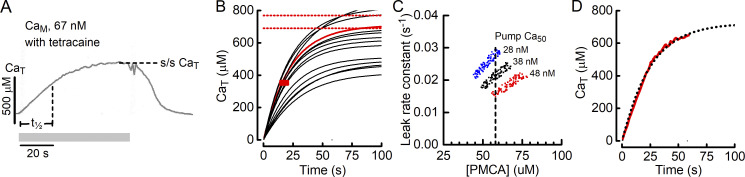
Estimating the concentration of PMCA in the JS. (A) An example of the time course of Ca²⁺ accumulation in the t-system. The t-system was initially depleted of Ca²⁺, and Ca²⁺ (Ca_M, 67 nM) was returned to the fiber for the period indicated by the gray bar. Tetracaine was included in the bathing solution to inhibit RYR Ca²⁺ leak. In that case, Ca_JS, which drives PMCA, can be considered to equal Ca_M. Steady-state Ca_T, steady-state [Ca²⁺]; t_½, time to reach 50% of steady-state Ca_T. (B) Model-generated time courses of Ca²⁺ accumulation in the t-system using different combinations of PMCA concentration and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}.$ The example shows 15 records; the complete analysis used 5,000 records. Parameter combinations that produced records with realistic values of t_½ and steady-state Ca_T were those that passed through the red rectangle (correct t_½) and reached a final Ca_T value between the horizontal red lines. The one record in the sample meeting these criteria is shown in red. (C) Combinations of c_PMCA and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ that are consistent with observed time course of t-system filling. The analysis was performed for three $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ values (150, 200, and 250 μM) that span the range of likely values; these correspond to pump Ca₅₀ values of 28, 38, and 48 nM under the conditions in the skinned fibers. Vertical dashed line, the value chosen for c_PMCA that can fulfill the requirement of producing realistic time course of t-system Ca²⁺ accumulation across the range of likely $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ values. (D) Comparison of measured (solid red line) and calculated (dotted black line) time courses of Ca²⁺ accumulation in the t-system. The measured record is a digitized version of the record in A, and the calculated record was generated using the fiber model with parameter values: c_PMCA, 58 μM; $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ 0.018 s⁻¹; and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ 210 μM (Ca₅₀, 40 nM).

As an alternative, a modeling-based method was used to estimate c_PMCA. The simple PMCA/leak model described above (Eqs. 6 and 7) was used to find combinations of c_PMCA and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ that produce records of t-system Ca²⁺ accumulation consistent with the observed rate of increase in Ca_T and its final magnitude. Using the best-fit parameters from the preliminary analysis of the pump/leak model (Fig. 4 B) as a starting point, a detailed Monte Carlo analysis was performed in which the time course of increase in Ca_T was calculated using the model for 5,000 combinations of c_PMCA and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ each selected at random from a range of ±50% of the preliminary values (Fig. 5 B). The criteria set for a record to be considered consistent with observed data were that t_½ was between 15 and 20 s and the maximum Ca_T was between 690 and 770 μM (±5% of the reported mean value; Cully et al., 2018). Records meeting the criteria were identified (i.e., those that passed through the red rectangle and finished between the horizontal red lines in Fig. 5 B), and the combinations of c_PMCA and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ giving rise to such records were plotted (Fig. 5 C). To determine the effect of the third influential parameter, $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ the analysis was performed for three values of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ that span the range of likely values; $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ is constrained by the range of [Ca²⁺] corresponding to the sloping section of the Ca_T–Ca_M relationship (Fig. 4 B). The results of this analysis are shown in Fig. 5 C.

For each value of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ ∼200 records were identified as being consistent with the observed time course and magnitude of t-system Ca²⁺ accumulation; the combinations of c_PMCA and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ that gave those records are plotted in Fig. 5 C. For each value of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ the range of pump concentrations that can give a time course consistent with those observed is ∼15 μM. As a best estimate of c_PMCA, the value in the middle of the complete range was taken; this was 58 μM. This value, with selection of an appropriate $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ is able to accurately simulate the Ca_T time course across the full range of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ values tested. c_PMCA is expressed relative to the JS volume (Table 3), which is appropriate because the rate of Ca²⁺ pumping is set by Ca_JS and the c_PMCA in that volume. Note that although c_PMCA is numerically similar to c_SERCA, when the difference in volume between the JS and myoplasm (Table 3), and in the surface area of the t-system and SR (Eisenberg, 1983), are taken into account, the current analysis suggests that the density of Ca²⁺ pumps in the t-system membrane is <1% of that for the SR membrane.

In Fig. 5 D, a comparison is shown of the measured record of the time course of Ca_T from Fig. 5 A and that calculated using the PMCA/leak model with c_PMCA of 58 μM, $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ of 0.02 s⁻¹, and $K_{\mathrm{d}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ of 200 μM (corresponding to pump Ca₅₀ = 40 nM). The time courses match well, although the model indicates that the experimental protocol did not allow sufficient time for Ca_T to reach a complete plateau. Overall, the analysis presented in this section shows that a model of t-system Ca²⁺ accumulation consisting of PMCA, driven by a constant [Ca²⁺], and a concentration gradient-dependent Ca²⁺ leak from the t-system can accurately describe both the steady-state Ca_T–Ca_M relationship measured in the presence of tetracaine (Fig. 4 B) and the time course with which Ca²⁺ accumulates in the t-system (Fig. 5 D).

Buffering of Ca²⁺ by EGTA in JS and myoplasm

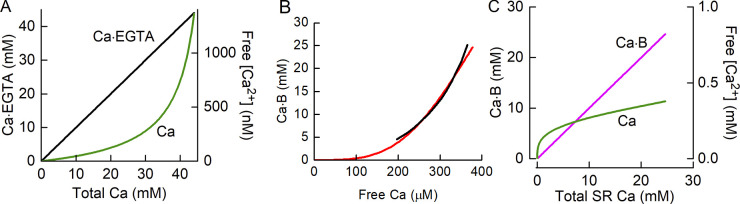
Ca²⁺ was buffered by exogenous EGTA (50 mM) in the myoplasm and JS. Binding of Ca²⁺ by EGTA was assumed to be a second-order reaction (Eq. 8) with a dissociation constant of 0.18 μM under the conditions used for the experiments and an off-rate of 0.3 s⁻¹ (Smith et al., 1984). The on-rate constant was then 0.3 s⁻¹/0.18 μM = 1.67 μM⁻¹ s⁻¹. The variations of bound and free Ca²⁺ with total [Ca²⁺] are shown in Fig. 5 A.

$${\mathrm{C}\mathrm{a}}^{2+}+\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}\stackrel{k_{\mathrm{o}\mathrm{n}}}{\underset{k_{\mathrm{o}\mathrm{f}\mathrm{f}}}{\rightleftharpoons }}\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}\text{.}$$ (8)

Buffering of Ca²⁺ in the SR

In resting muscle fibers, most of the Ca²⁺ is in the SR, and most of that is bound to Csq and, probably, to other unidentified buffers (Manno et al., 2013). The buffering of Ca²⁺ in the SR is an important component of the model, as it was assumed that the rate of Ca²⁺ leak through the RYRs depended on the Ca²⁺ concentration gradient between the SR and JS. In the protocols used in the fiber experiments, Ca_JS was maintained in the submicromolar range by its equilibrium with EGTA; in that case, the rate of leak is primarily determined by Ca_SR (typically 400–1,000 μM) and is thus influenced by the features of Ca²⁺ buffering in the SR. Additionally, the protocol for measuring RYR Ca²⁺ leak starts with the SR depleted of Ca²⁺; therefore, the magnitude of the leak will, at least initially, be time dependent, reflecting the time course with which Ca_SR increases, and so is likely to be influenced by Ca²⁺-buffering kinetics.

The mechanism of Ca²⁺ buffering in the SR is not is not well understood, but the buffering profile has been mapped by Manno et al. (2013), and this was used as a benchmark for the model. Following Lee and Keener (2008), the SR Ca²⁺ buffer molecules (B) were assumed to have an average of n binding sites, all of which are either simultaneously occupied by Ca²⁺ or simultaneously empty; this scheme provides the cooperative binding apparent in the observed Ca²⁺ buffering in the SR (Pape et al., 2007; Manno et al., 2013). The reaction scheme and the associated differential equation are

$$\mathrm{n}\mathrm{C}{\mathrm{a}}^{2+}+B\stackrel{k_{\mathrm{o}\mathrm{n}}}{\underset{k_{\mathrm{o}\mathrm{f}\mathrm{f}}}{\rightleftharpoons }}\mathrm{n}\mathrm{C}\mathrm{a}\mathrm{B}$$ (9)

and

$$\frac{\mathrm{d}\mathrm{C}\mathrm{a}\mathrm{B}}{\mathrm{d}t}=k_{\mathrm{o}\mathrm{n}}\cdot \mathrm{C}{\mathrm{a}}_{\mathrm{S}\mathrm{R}}{\left(t\right)}^n\cdot \left(B_{\mathrm{T}\mathrm{o}\mathrm{t}}-\mathrm{C}\mathrm{a}\mathrm{B}\right)-k_{\mathrm{o}\mathrm{f}\mathrm{f}}\cdot \mathrm{C}\mathrm{a}\mathrm{B}.$$ (10)

In Eq. 9, B is buffer, CaB is Ca²⁺ bound to the buffer molecule, and k_on and k_off are the rate constants for association and dissociation, respectively. In Eq. 10, B_Tot is the total concentration of buffer sites, Ca_B is the concentration of buffer sites with Ca²⁺ bound, B_Tot − Ca_B is the concentration of available buffer sites, and n is the cooperativity coefficient. Manno et al. (2013) estimated that the concentration of Ca²⁺ buffer sites was ∼70 mM (with respect to SR volume), and this value was used in the model. The rate constants are related to the dissociation constant by $K_{\mathrm{D}}^{\mathrm{B}}={\left(k_{\mathrm{o}\mathrm{f}\mathrm{f}}/k_{\mathrm{o}\mathrm{n}}\right)}^{\frac{1}{n}}.$ Dissociation of the Ca²⁺-buffer complex is rapid (Baylor and Hollingworth, 2003; Sztretye et al., 2011a), so k_off was set to 3,000 s⁻¹. The SR Ca²⁺ buffering properties of mouse muscle are well described by a sigmoidal relationship, with $K_{\mathrm{D}}^{\mathrm{B}}$ = 460 μM and n = 3.5 (Manno et al., 2013). With only a slight adjustment to $K_{\mathrm{D}}^{\mathrm{B}}$ (450 μM), using these values in the current model (solid line, Fig. 6 B) provided a close match to the empirical SR Ca²⁺ buffering curve described by Manno et al. (2013) (Fig. 6 B, black line). Using these values, $k_{\mathrm{o}\mathrm{n}}=k_{\mathrm{o}\mathrm{f}\mathrm{f}}/{\mathrm{e}}^{n\cdot \ln \left(K_{\mathrm{D}}^{\mathrm{B}}\right)}$ = 3,000/e^3.5ln(450) = 1.55 × 10⁻⁶ μM⁻¹ s⁻¹. Fig. 6 C shows the variation in bound and unbound [Ca²⁺] as a function of total SR content. A notable feature is that when the SR Ca²⁺ content is low, the Ca²⁺ buffering power is low. Consequently, during the initial stages of SR filling (after prior Ca²⁺ depletion), Ca_SR will increase with little increase in Ca_B.

Figure 6.

Characteristics of Ca²⁺ buffers. (A) Ca²⁺–EGTA dissociation curve. Variation of concentrations of bound Ca²⁺ (Ca·EGTA; black line, left y axis) and unbound or free Ca²⁺ (Ca; green line, right y axis) with total Ca²⁺. Note the 10⁶-fold difference in the scales of the y axes. (B) Equilibrium binding curve for SR Ca²⁺ buffers (including Csq). Solid red curve, relationship for the model used in the current study determined from equilibrium solution of Eq. 10 with total buffer Ca²⁺ binding site concentration = 70 mM, $K_{\mathrm{D}}^{\mathrm{B}}$ = 450 μM, and n = 3.5. Black curve, the empirical relationship determined by Manno et al. (2013; from their Fig. 7 A). (C) SR–Ca²⁺ buffer dissociation curve showing variations in bound Ca²⁺ (Ca·B; magenta line, left x axis) and unbound, or free, Ca²⁺ (green line, right x axis) with total SR Ca²⁺ content.

Buffering of Ca²⁺ by TnC in the myoplasm

TnC binds Ca²⁺ in its role of linking the contractile response to the release of Ca²⁺ into the myoplasm. Fast-twitch mammalian muscle myoplasm contains ∼200 μM of TnC Ca²⁺ binding sites, and at rest, ∼30% of the sites have Ca²⁺ bound. The question of relevance to the current model is, can TnC can bind sufficient Ca²⁺ so that the free Ca²⁺ is not simply that expected from the total Ca²⁺ in the fiber and the kinetics of Ca²⁺ binding by EGTA? To address this question, a model was developed of Ca²⁺ binding by TnC and EGTA. The model is described in detail in Appendix 2. The modeling illustrated that Ca²⁺ binding by TnC would have a negligible effect on the free Ca²⁺ calculated from just the Ca²⁺–EGTA reaction. For example, when the free Ca²⁺ is intended to be 1 μM, the presence of TnC would reduce the actual free [Ca²⁺] by 0.1%; the effect is even smaller for lower free [Ca²⁺]. Consequently, it was not necessary to include Ca²⁺ binding by TnC in the model.

Diffusive exchange of Ca²⁺ between JS and myoplasm

In the absence of a leak of Ca²⁺ into the JS, there is little difference between Ca_JS and Ca_M because both are controlled by the equilibrium with EGTA. In the presence of a leak, it would be expected that Ca_JS increases as Ca²⁺ is added to the JS, despite the buffering by EGTA. The observation that a steady, submaximal Ca_T is achieved when Ca_M is at levels too low to achieve maximal pumping by PMCA indicates that there is a mechanism that limits the increase in Ca_JS. We assumed that this was diffusion of Ca²⁺ between the JS and myoplasm. The diffusion rate was adjusted so that the model steady-state Ca_T matched the experimentally determined values. That is, in the steady state, the sum of the leak of Ca²⁺ from the t-system into the myoplasm and the diffusive movement from the JS to the myoplasm equaled the rate at which Ca²⁺ was added to the JS via the RYRs. The diffusive exchange was modeled as a simple movement of Ca²⁺ depending on the difference (Ca_JS − Ca_M).

Relative volumes of physical compartments

The physiologically relevant Ca²⁺ concentrations (e.g., for stimulating pumps or driving diffusive exchanges) are those expressed with respect to the volume of water within individual compartments rather than to fiber water volume. Therefore, the relative volumes of the different compartments were taken into account when determining the concentration changes resulting from exchanges between compartments. For example, in human vastus lateralis muscle, the relative volume of the SR is ∼100 times that of the JS (Eisenberg, 1983), so that movement of Ca²⁺ from the SR to the JS results in an increase in [Ca²⁺]_JS that is 100-fold greater than the corresponding decrease in [Ca²⁺]_SR. The proportions of fiber volume accounted for by each physical compartment are shown in Table 3.

The JS is a conceptual rather than physical space, and its volume is difficult to both define and estimate; it is a region between the RYRs and the adjacent t-tubule. We estimated V_JS, relative to that of the t-tubule (V_TT), on the basis that (1) t-tubule diameter is 85 nm (Jayasinghe and Launikonis, 2013), (2) the distance between the SR and t-tubules is 12 nm (Mitchell et al., 1983; Franzini-Armstrong et al., 1999), (3) the RYRs are 30 nm in diameter and the spacing between the centers of closest adjacent units is 100 nm (Franzini-Armstrong et al., 1999), and (4) the RYRs are arranged in a double layer, with one layer on either side of the t-tubule (Jayasinghe et al., 2014). The volume of a space with the same diameter as the RYR and the t-tubule was calculated, and it corresponded to ∼4% V_TT if the t-tubule cross-section is circular and 5% if elliptical (Jayasinghe and Launikonis, 2013), with the major axis length twice that of the minor axis. This range of values is consistent with the 4.5% calculated by Dulhunty et al. (1992). In the simulations, V_JS was set to 5% V_TT.

Unless otherwise specified, concentrations are expressed relative to the compartment in which the relevant molecular species is contained. For example, concentrations in the myoplasm are expressed with respect to myoplasmic water volume. The data used to calculate myoplasmic water volume and the concentration conversion values are presented in Table 3.

Composition of myoplasmic and JSs

The rates of Ca²⁺ movement by SERCA and PMCA depend on the concentrations of ATP and its metabolites and on pH. These values are largely determined by the composition of the solutions used with the skinned fiber preparation (Cully et al., 2018). Assumed concentrations (in mM) were as follows: myoplasm/JS: 8 ATP, 0.05 ADP, and 1 Pi; t-tubule: Ca²⁺, time dependent and calculated using the model. pH in all spaces was taken to be 7.1. The rate of Ca²⁺ pumping by SERCA and PMCA is strongly influenced by ADP concentration and pH (Inesi and Hill, 1983; Tran et al., 2009). It was assumed that [ADP] and pH were constant during an experiment, with pH buffered by HEPES in the bathing solution and ATP, and hence ADP, buffered by endogenous creatine kinase, presumably bound to intracellular structures (Dzeja and Terzic, 2003).

Experimental data

The experimental data used in this study are those referred to in Cully et al. (2018) that describe the uptake of Ca²⁺ into the t-system of fibers from human vastus lateralis muscle. The data are from the control group in that study and as such had no apparent abnormalities in Ca²⁺ handling. Briefly, the experimental protocol involved first depleting the SR and t-system of Ca²⁺ by exposing the fibers to caffeine, which kept the RYRs and store-operated Ca²⁺ channels on the t-system open. The caffeine was removed, and the fibers were placed in a solution with a known Ca²⁺ concentration. The time course with which Ca²⁺ entered the t-system was monitored using the Ca²⁺-sensitive compound rhod-5N trapped inside the t-tubules.

Implementing the model

The modeling was carried out using Maple (v2016.1) and MapleSim (v2016) software (Maplesoft). The model equations were deployed, and parameter values were entered in the general mathematics environment provided by Maple. The system of differential equations was solved numerically using the Rosenbrock method (Rosenbrock, 1963). To be consistent with the experimental protocol (Cully et al., 2018), simulations commenced with the SR and T systems depleted of Ca²⁺ so that all the Ca²⁺ was in the myoplasm and JS and in equilibrium with EGTA. The total Ca²⁺ was set to give the desired myoplasmic free [Ca²⁺], as determined by the EGTA–Ca²⁺ equilibrium (Fig. 6 A). The differential equations are shown in Appendix 1. Once the model was developed, the equations were imported into MapleSim to create a fast, compiled version of the model, which was used for subsequent analysis using Maple. Using a computer with a 2.2-GHz processor and 8 GB of memory, the compiled version simulated 120 s of t-system Ca²⁺ accumulation in 8 ms.

To quantify the rate of Ca²⁺ leak from RYRs, c_PMCA was fixed at 58 μM, and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ were treated as variables whose values were those that provided the least-squares fit of the model to the empirical Ca_T–Ca_M relationship determined in the presence of tetracaine (see Results). This was done by creating a function that returned the model-calculated maximum Ca_T for specified values of Ca_M, $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ and using that function in a nonlinear regression fitting routine implemented using Maple software.

Results

Identifying parameters that influence t-system Ca²⁺ accumulation

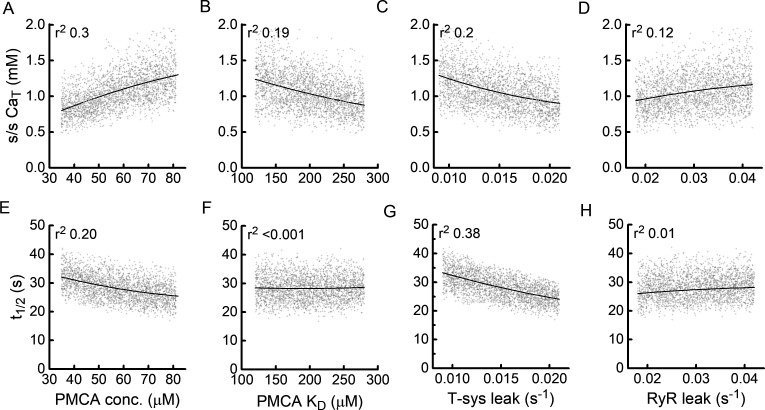
Parameters that influenced t-system Ca²⁺ accumulation were identified using a Monte Carlo analysis in which the model was solved for many random combinations of parameter values. The analysis was performed using nine parameters selected on the basis that their location in the model might allow them to influence t-system Ca²⁺ accumulation. The results of the analysis are summarized in Table 4 and Fig. 7. In Fig. 7, influences of four parameters are illustrated graphically: the cloud of light gray symbols are the Ca_T (Fig. 7, A–D) and t_½ (Fig. 7, E–H) values calculated from 4,000 Ca_T versus time curves with random combinations of the nine parameters, and the solid lines show the variation in Ca_T or t_½ as a function of only the parameter of interest. To quantify the influence of each parameter, the square of the correlation coefficient (r²) was calculated from the least-squares fit of a second-order polynomial through the data cloud, with the parameter of interest as the independent variable. r² is the fraction of the total variance, arising from all the parameters assessed, that can be attributed to the parameter of interest. The r² values for all the parameters assessed are shown in Table 4, which includes analyses for Ca_M of both 67 and 1,340 nM.

Table 4.

r² values for dependence of steady-state Ca_T and t_½ on selected model parameters

CaM		c PMCA		${\mathit{k}}_{\mathbf{Leak}}^{\mathbf{T}}$		${\mathit{K}}_{\mathbf{D}}^{\mathbf{PMCA}}$		V JS		${\mathit{k}}_{\mathbf{Leak}}^{\mathbf{RyR}}$		k Diff		${\mathit{K}}_{\mathbf{D}}^{\mathbf{SERCA}}$		c SERCA		${\mathit{k}}_{\mathbf{Leak}}^{\mathbf{SR}}$
67
Max. CaT		0.3		0.2		0.19		0.15		0.12		0.03		0.015		0.002		0.001
t ½		0.2		0.38		<0.001		0.34		0.01		0.04		0.007		<0.001		0.001
1,340
Max. CaT		0.41		0.2		0.001		0.41		<0.001		0.001		<0.006		<0.003		<0.001
t ½		0.184		0.62		<0.001		0.19		<0.001		<0.001		<0.001		<0.001		<0.001

Figure 7.

Sensitivity of t-system Ca²⁺ accumulation to most influential parameters. (A–H) Each graph shows the variation with one parameter of steady-state Ca_T (A–D) and rate of accumulation of Ca²⁺ in the t-system as quantified by the time taken for Ca_T to reach 50% of its final value (t_½, E–H). Gray points are individual values determined using a Monte Carlo analysis (i.e., 4,000 random combinations of nine parameters). The solid lines are values calculated, using the model, for variation in just the parameter of interest with all other parameter values held constant. The analyses were performed for a Ca_M of 67 nM; the random parameter values were chosen from a range of values spanning ±40% around typical values. A larger span (±60%) was used for RYR leak rate constant. The vertical scatter of the data points reflects the variance from the influences of all the parameters included in the analysis, and the vertical displacement of the solid lines reflects the variance attributable to that parameter. The r² value quantifies the ratio of these two variances.

The four parameters with the greatest influence on Ca²⁺ accumulation in the t-system were those directly involved in the t-system—PMCA concentration and Ca²⁺ sensitivity (quantified by $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}})$ and the magnitude of the Ca²⁺ leak from the t-system—and the Ca²⁺ leak through the RYRs. These parameters accounted for ∼75% of the total variance in steady-state Ca_T and t_½. The extent of t-system filling was mainly determined by c_PMCA (Fig. 7 A) and t-system leak rate (Fig. 7 C); this is consistent with the notion that the level of filling reflects the balance between rate of Ca²⁺ uptake into the t-system, which depends on c_PMCA, and the leak of Ca²⁺ from the t-system. The size of the RYR leak rate constant also influences the magnitude of Ca_T, which is desirable given that the purpose of the protocol was to use changes in Ca_T to estimate RYR leak. It should be noted, however, that although $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ influenced the extent of Ca²⁺ accumulation when Ca_M is lower than that required to fully activate PMCA (e.g., 67 nM), it had no influence when Ca_M is high (1,340 nM). In the latter case, the pump is operating maximally even in the absence of RYR leak, so any further addition of Ca²⁺ to the JS by the leak would not affect the rate at which Ca²⁺ is pumped into the t-system.

It is apparent from Table 4 that parameters associated with the SR Ca²⁺ pump (the right three columns of Table 4) had little influence on Ca²⁺ accumulation in the t-system. This indicates that the time course of increase in Ca_SR, and any effect that has on RYR Ca²⁺ leak and thus Ca_JS, does not limit the pumping of Ca²⁺ from the JS into the t-system.

Steady-state Ca_T–Ca_M relationship

Uptake of Ca²⁺ into the t-system has been characterized by the relationship between the ultimate extent of Ca²⁺ accumulation and the concentration of Ca²⁺ in the myoplasmic solution (i.e., the Ca_T–Ca_M relationship; Fig. 4 B). From Fig. 7, it is apparent that steady-state Ca_T depends on c_PMCA, $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ and the rate constants for the Ca²⁺ leaks from the t-system and through the RYRs. The value of c_PMCA was fixed (see Materials and methods) but the values of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ are not known. Those values were determined using the model by finding the parameter values that gave the least-squares fit of the model to the experimental Ca_T–Ca_M data. There were two steps to this analysis. First, $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ were determined using data obtained in the presence of tetracaine, because in that case it was assumed there was no RYR Ca²⁺ flux, so $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ = 0. It was then assumed that $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ was unaffected by tetracaine but that, as preliminary analysis revealed, $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ did depend on whether the RYRs were functional. Therefore, the second part of the analysis was to use data obtained without tetracaine to determine $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ (in the absence of tetracaine) and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}.$ The results of the fitting procedure are shown in Fig. 8 A, and the parameter values are given in Table 5.

Figure 8.

Model predictions. (A) Comparison of experimental data and model. Symbols represent mean (± SEM) Ca_T data with (filled circles) and without (open circles) tetracaine. The curves are the best fits of the model to the data points. For the tetracaine case (blue line), the model was fitted by adjusting the values of the t-system Ca²⁺ leak and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}.$ For the non-tetracaine case (red line), $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ was assumed to be the same as in the presence of tetracaine, and the parameters adjusted to obtain the best fit were the rate constants for the t-system leak and RYR leak. The parameter values are given in Table 5. (B) Model-derived time courses of Ca_JS in the presence (+Tet, blue line) and absence (−Tet, red line) of a leak of Ca²⁺ through the RYRs. When there is no RYR Ca²⁺ leak, Ca_JS is maintained by the equilibrium with EGTA and diffusion of Ca²⁺ from the myoplasm. In the presence of a RYR Ca²⁺ leak into the JS (red line), sufficient Ca²⁺ enters the JS to increase the unbound [Ca²⁺]. (C) Model-derived time courses of [Ca²⁺] in the SR and t-system in the presence of RYR Ca²⁺ leak. Most Ca²⁺ entering the SR binds to SR Ca²⁺ buffers (Ca_B, right-hand y scale).

Table 5.

Parameter values determined from fitting model to Ca_T versus Ca_M data

Parameter	With tetracaine	Without tetracaine
$k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ (s−1)	0.022 (0.017–0.030)	0.013 (0.009–0.016)
$K_{\mathrm{d}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ (μM)	179.9 (129–349)
$\mathrm{C}{\mathrm{a}}_{50}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ (nM)	66.5	42.1
$k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ (s−1)	Assumed 0	0.035 (0.007–0.041)

Data are expressed as mean (95% CI). See Fig. 10 B.

The shape of the Ca_T–Ca_M relationship predicted by the model matches the experimental data well (Fig. 8 A), indicating that the model included sufficient detail to describe t-system Ca²⁺ accumulation in the experimental preparation. In the absence of RYR Ca²⁺ leak, the calculated $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ values (Table 5) give rise to a Ca_T–Ca_M relationship with a $\mathrm{C}{\mathrm{a}}_{50}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ of ∼67 nM. Withdrawal of tetracaine had two clear effects. (1) The leak of Ca²⁺ from the t-system was reduced, which increased steady-state Ca_T values. $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ in the absence of tetracaine was 60% of that in the presence of tetracaine. (2) Ca²⁺ leak through the RYRs was apparent $(k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ = 0.035 s⁻¹), which shifted the Ca_T–Ca_M curve to the left of that determined with tetracaine; $\mathrm{C}{\mathrm{a}}_{50}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ was reduced to 42 nM. It is difficult to distinguish these two effects—increased RYR leak and decreased t-system leak—by inspection, but they were readily revealed and quantified using the model curve-fitting procedure.

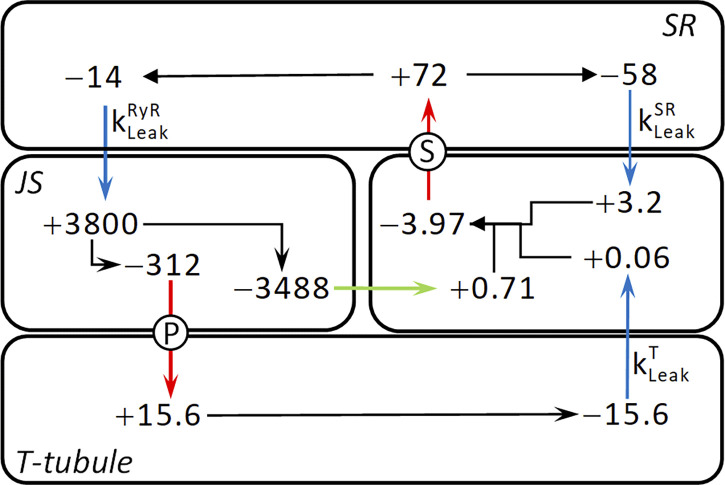
The rate constants for the two Ca²⁺ leaks (Table 5) were combined with known values for Ca_SR and Ca_T to calculate the rates of Ca²⁺ exchanges among fiber compartments. These calculations were done using steady-state data corresponding to Ca_M of 67 nM, this being approximately the free [Ca²⁺] in unstimulated, intact muscle fibers, and assuming that RYR leak was as determined in the skinned fiber preparation in the absence of tetracaine. The steady-state movements of Ca²⁺ in the skinned fiber preparation are summarized in Fig. 9. The flows were calculated using concentrations of Ca²⁺ in the SR and t-system and the rate constants for leaks from those compartments (Table 5). For example, the rate of Ca²⁺ leak from the t-system can be calculated: $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ × steady-state Ca_T = 0.013 s⁻¹ × 1,200 μM = 15.6 μM s⁻¹, and this is the same as the rate of uptake of Ca²⁺ into the t-system by PMCA in the steady state. This sets the rate at which Ca²⁺ is removed from the JS, and so on. In Fig. 9, the flows are quantified according to the volumes of both the origin and destination compartments (Table 3). For example, an outflow (indicated by −) of 14 μM s⁻¹ from the SR produces an influx (+) into the JS, in terms of JS volume, of 14 × (3.8 / 0.014) = 3,800 μM s⁻¹. Note that in a steady state, the amount of Ca²⁺ bound to EGTA will be constant and thus does not need to be considered in this analysis.

Figure 9.

Summary of steady-state Ca²⁺ flows. Flows of Ca²⁺ between compartments of the model fiber are indicated by arrows and quantified by flow rates in μM s⁻¹. Arrow colors: blue, passive leaks; red, active pumps; green, diffusion; black, division of flows within compartments. Pumps: P, PMCA; S, SERCA. Leaks are identified by adjacent leak rate constant symbols. Rates in each compartment are expressed with concentrations relative to that compartment’s volume; −, efflux from a compartment; +, influx into a compartment. Differences in rates between the ends of arrows that span compartment boundaries reflect the difference in volumes of the two compartments. The following values were used to construct the diagram: Ca_SR, 400 μM; Ca_T, 1,200 μM; $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ 0.013 s⁻¹; $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}},$ 0.035 s⁻¹; and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{S}\mathrm{R}},$ 0.145 s⁻¹.

A notable feature of the Ca²⁺ flows is that only a small fraction of the Ca²⁺ calculated to leak into the JS is pumped into the t-system: of the influx of 3,800 μM s⁻¹, 312 μM s⁻¹, or 8%, is pumped into the t-system, and the remainder must diffuse into the myoplasmic space. This is, at least in part, a consequence of the low density of PMCA in the JS, as calculated in Materials and methods. A second notable aspect is that ∼20% of the Ca²⁺ pumped into the SR leaks into the JS, and the remainder leaks into the myoplasm. Therefore, under resting conditions in the skinned fiber, most of the cycling Ca²⁺ leaked from the SR into the myoplasm, presumably via a SERCA-related mechanism; one-fifth leaked into the JS via RYRs; and only a small fraction of that passed through the PMCA.

Time course of Ca²⁺ movements during t-system Ca²⁺ accumulation

The model provides a means of estimating the time course of Ca²⁺ movements during the protocol used to determine Ca²⁺ t-system accumulation. In Fig. 8 B, the time courses of Ca²⁺ concentration in the myoplasm and JS are shown for a RYR leak of the magnitude given in Table 5. In the absence of a leak of Ca²⁺ into the JS through the RYRs, Ca_JS stayed close to its initial value of 67 nM throughout the period over which the t-system accumulated Ca²⁺ (blue line, Fig. 8 B). That constancy reflected the buffering of Ca²⁺ by EGTA and diffusion of Ca²⁺ into the JS from the myoplasm. In the presence of a leak of Ca²⁺ into the JS, Ca_JS increased toward ∼100 nM (red line, Fig. 8 B). In Fig. 8 C, the time courses are shown of Ca²⁺ entering the SR and t-system and binding to buffers in the SR. Note that when Ca_M is 67 nM, the rate at which SERCA operates is ∼1% of its maximum, so the filling of the SR is relatively slow. In the SR, most Ca²⁺ binds rapidly to the SR buffers (magenta curve, Fig. 8 C). The buffer characteristics allow Ca_SR to increase rapidly at the start of filling (green curve, Fig. 8 C), thus stimulating the RYR Ca²⁺ leak when tetracaine is not present. The t-system begins to fill immediately, fueled initially by the free Ca²⁺ in equilibrium with EGTA in the JS when the protocol begins. In the absence of tetracaine, t-system filling is enhanced by the rise in Ca_JS due to the RYR leak (compare with tetracaine [blue curve] to without tetracaine [red curve]; Fig. 8 C).

How precisely can the RYR Ca²⁺ leak be quantified?

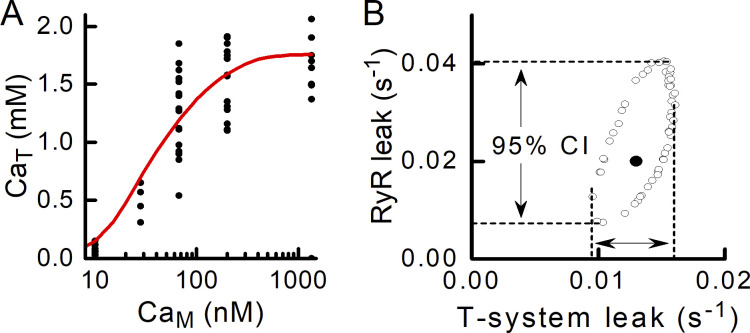
A benefit of using the curve-fitting approach to quantifying the RYR leak is that the parameters derived from the fitting procedure can be used to calculate confidence intervals (CIs) for the model parameters whose values were determined from the fitting procedure. Taking the data obtained in the absence of tetracaine as an example and using the raw data points when fitting the model to the data (Fig. 10 A), a confidence contour can be calculated (Motulsky and Christopoulos, 2004). The confidence contour is an ellipse (outlined by open circles, Fig. 10 B) that encompasses combinations of parameter values that would give rise to a curve that would not differ significantly, at the 5% level in this case, from the best-fit curve. The parameter combination that gave the best fit is indicated by the solid symbol in the middle of the ellipse (Fig. 10 B, filled circle). The extent of the excursion of the ellipse gives the 95% CI for each parameter, indicated by the dashed lines.

Figure 10.

Confidence interval for RYR leak. (A) The raw data (filled circles; 63 data points from 17 fibers) obtained without tetracaine present were fitted with a model-derived curve (solid line) from which the best-fit values of $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ were determined. Knowing the minimum sum of squared residuals (from the best fit), a larger sum of squared residuals can be calculated that would reflect a parameter combination that would give a significantly different curve from the best fit curve (Motulsky and Christopoulos, 2004). (B) The ellipse delimited by open circles is the 95% confidence contour: combinations of the two parameters $(k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}})$ that lie within the ellipse produce Ca_T–Ca_M curves that do not differ significantly (i.e., P > 0.05) from the best-fit curve. The filled circle is the $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ and $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ combination that gave the best fit of the model to the data. The 95% CIs for each parameter are indicated by the arrows. CIs: RYR leak rate constant, 0.007–0.041 s⁻¹; and t-system leak rate constant, 0.009–0.016 s⁻¹.

The 95% CI for the RYR leak rate constant is 0.007–0.041 s⁻¹. The interval excludes 0, which indicates that the method used to quantify the RYR leak was sufficiently sensitive to detect the leak that occurred in the human skinned fibers. The 95% CI would likely be narrowed if data points were obtained at additional Ca_M values on the sloping part of the Ca_T–Ca_M curve.

The 95% CIs for $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ can be determined in the same way (Fig. 10 B and Table 4). In this case, the 95% CIs for the data with and without tetracaine do not overlap, so it can be concluded that the t-system Ca²⁺ leak rate differed significantly depending on whether the RYRs were functional. That is, when Ca²⁺ entered the JS through the RYRs, the leak of Ca²⁺ from the t-system was reduced compared with that occurring when Ca_JS was held constant by the EGTA buffering.

Plotting Ca_T versus Ca_M or Ca_JS?

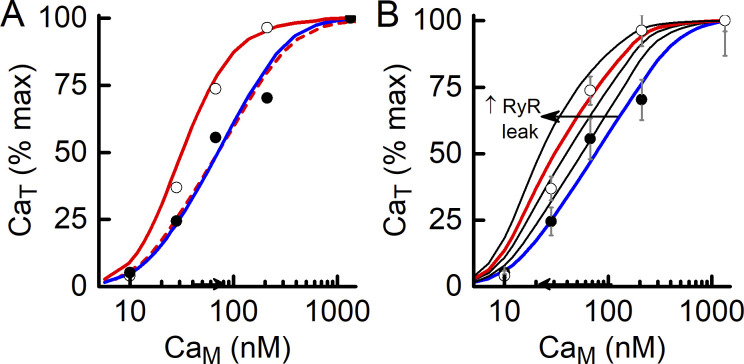
The convention adopted by Launikonis and colleagues (Cully et al., 2016; Cully et al., 2018) is to plot the extent of t-system Ca²⁺ accumulation as a function of Ca_M. The t-system filling is driven by the PMCA and so must reflect Ca_JS rather than Ca_M. However, Ca_JS is unknown; hence the practice of using Ca_M as the independent variable. The model provides the means to estimate Ca_JS, and in Fig. 11 A, a comparison is shown of steady-state Ca_T values plotted against Ca_M and the model-derived Ca_JS. For this comparison, the effect of the change in $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ has been removed from the comparison by normalizing steady-state Ca_T values obtained with and without tetracaine data by their respective maxima (i.e., values at Ca_M of 1,340 nM). When plotted as a function of Ca_M, the effect of withdrawing tetracaine, thus allowing the RYR Ca²⁺ leak, is to shift the normalized Ca_T–Ca_M relationship to the left. This effect is eliminated when Ca_T is plotted against Ca_JS; in that case, the two curves (solid blue and dashed red lines, Fig. 11 A) superimpose. Remembering that changes in $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ have been excluded from this analysis, the observation that the Ca_T–Ca_JS curve overlies the Ca_T–Ca_M curve in the presence of tetracaine is important because it confirms (1) that the PMCA properties are unaffected by the presence of tetracaine, (2) that t-system filling simply reflects the combined properties of PMCA and the t-tubule Ca²⁺ leak, and (3) that the shift of the Ca_T–Ca_M curve to the left when tetracaine is removed from the fibers reflects the increase in Ca_JS in the presence of RYR Ca²⁺ leak. The last point highlights the benefit of using Ca_M as the independent variable: the size of the horizontal difference between the normalized curves reflects the magnitude of the Ca²⁺ leak into the JS, as illustrated in Fig. 11 B.

Figure 11.

Effect of RYR Ca²⁺ leak on Ca_T–Ca_M relationship. (A) Comparison of curves relating Ca_T to Ca_M or Ca_JS. Symbols show experimental data in the presence (filled circles) and absence (open circles) of tetracaine. The curves are the best fits of the model to the data (blue, with tetracaine; red, without tetracaine). In the presence of a leak of Ca²⁺ through the RYRs into the JS (i.e., no tetracaine), the plot of Ca_T–Ca_M is shifted to the left (red solid line) of the case with no RYR leak (blue line). If the curve in the presence of a leak is plotted against the model-derived steady-state Ca_JS, the curve (red dashed line) superimposes on that for no RYR leak. (B) Effect of magnitude of the rate constant for RYR Ca²⁺ leak on the relationship between steady-state Ca_T and Ca_M. The blue curve is that for no RYR Ca²⁺ leak (e.g., in the presence of tetracaine), and the other curves are for leak rate constants of (from right to left) 0.01, 0.02, 0.03 (red), and 0.04 s⁻¹. The horizontal separation between the curves with and without RYR Ca²⁺ leak increases as leak rate increases (direction indicated by arrow).

Applying the model to data from fibers with malignant hyperthermia (MH)-causative RYR mutation

Cully et al. (2018) measured Ca_T–Ca_M curves for human muscle fibers exhibiting a MH-causative RYR mutation. The model was used to quantify RYR Ca²⁺ leak for these fibers. For this analysis, it was recognized that the steady-state Ca_T value measured without tetracaine at the highest Ca_M (indicated by * in Fig. 12) is much lower than the point at the next lowest Ca_M. Cully et al. (2018) suggested that this reflected activation of store-operated calcium entry (SOCE), which occurred only at the highest Ca_M used. No SOCE mechanism was included in the model, so the unusual data point was excluded from the curve-fitting procedure. The model analysis indicated that $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ was twofold higher in the MH fibers (385 μM, corresponding to $\mathrm{C}{\mathrm{a}}_{50}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}$ = 72 nM) than in the control fibers (Table 5) and that $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ was 0.08 s⁻¹, more than twice as great as that for fibers without the MH pathology (Table 5). If SR function is otherwise unaltered by the RYR mutation, then the model indicates that Ca_SR would be little affected by the greater RYR leak (i.e., SR Ca²⁺ is well buffered). The absolute Ca²⁺ leak, assuming Ca_SR is 400 μM, would be ∼32 μM s⁻¹. Thus, RYR Ca²⁺ fluxes in resting muscle fibers are not fixed but rather can be modulated by functional alterations to the RYRs.

Figure 12.

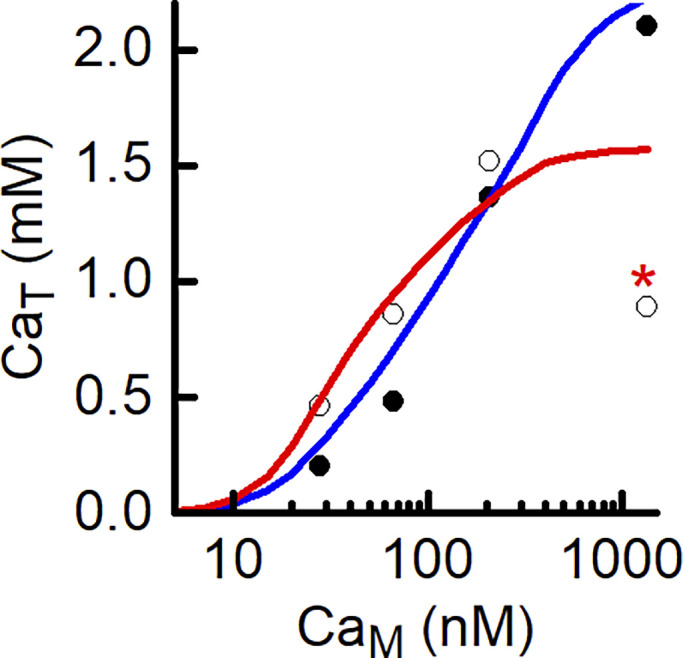
Modeling MH-susceptible fibers. Experimental data (symbols: filled circles, with tetracaine; open circles, without tetracaine) from human muscle fibers containing an MH causative mutation of the RYRs. Curves (blue, with tetracaine; red, without tetracaine) show the best fit of the model to the experimental data. Note, point marked with an asterisk was omitted from the analysis (for explanation, see Results). The best-fit value of $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ was 0.08 s⁻¹.

Discussion

The model accurately predicted Ca²⁺ accumulation by the t-system in the skinned fiber preparation. It predicted the form of the Ca_T–Ca_M relationship (Figs. 4 B and 8 A), the effect of tetracaine on that relationship (Fig. 8 A), and the time course with which Ca²⁺ accumulates in the t-system (Fig. 5 D). This was achieved with most parameter values determined from information in the literature. The only parameters that required fine-tuning to align the model to the experimental data were the rate constants for Ca²⁺ leaks from the t-system into the myoplasm and from the SR into the JS and the Ca²⁺ sensitivity of the PMCA, for which values were unknown. The experimental design used by Cully et al. (2018) sought to identify the presence of a Ca²⁺ leak through the SR Ca²⁺ release channels by comparing the steady-state Ca_T–Ca_M relationships obtained in the presence and absence of the RYR inhibitor tetracaine. From simple observation of the Ca_T–Ca_M curves with and without tetracaine, it was difficult to clearly establish whether the relationship altered as would be expected if there was a flow of Ca²⁺ through the RYRs, because a decrease in the t-system Ca²⁺ leak alone would also shift the relationship to the left. However, with the available experimental data, the statistical sensitivity of the model-based determination of the RYR leak was adequate to establish that there was a leak through the RYRs in the absence of the RYR blocker, and its magnitude was calculated. Furthermore, use of the model enabled the rate of Ca²⁺ leak from the t-system to be quantified, in both the presence and absence of RYR leak.

It was important to ensure that the calculated magnitude of the leak was not dependent on the choice of parameter values. The sensitivity analysis indicated that the parameters with most influence on t-system Ca²⁺ accumulation were, perhaps not surprisingly, those directly associated with the t-system. The value of only one of those, PMCA concentration, was set at a predetermined value. If the pump concentration was different from that assumed, fitting the model to the data would give different values for $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ and $K_{\mathrm{d}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}},$ but the value of $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ would be unaltered.

JS volume influences the estimated value of $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}},$ as indicated by the sensitivity analysis (Table 4). JS volume is difficult to quantify because the region is a conceptual, rather than physically defined, space. Its assumed volume is important in the model in that it determines how much Ca_JS increases for a given RYR Ca²⁺ leak. If a larger JS volume is assumed, then a faster RYR Ca²⁺ leak is required to produce the observed steady-state Ca_T. The magnitude of the effect, however, is not great: if JS volume was 50% greater than the value used, then $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ determined from the curve fitting would be increased by ∼12%. Overall, our estimate of $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ seems fairly robust.

A framework for interpretation of experimental data

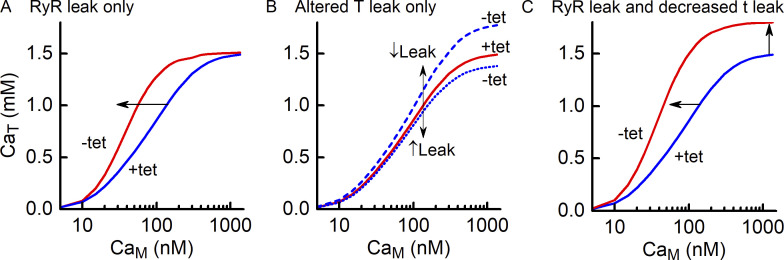
The analysis presented in Results provides a framework for interpreting the Ca_T–Ca_M relationship. In Fig. 13, the effects of a RYR leak, a change in t-system Ca²⁺ leak and the combined effects are illustrated. The presence of a RYR Ca²⁺ leak is evident through a pure leftward shift of the relationship determined in the absence of tetracaine compared with that in the presence of tetracaine (Fig. 13 A). Changes in the rate of leak of Ca²⁺ from the t-system upon the removal of tetracaine are evident as a vertical shift in steady-state Ca_T values (Fig. 13 B). If $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ decreases, steady-state Ca_T values increase, and conversely, if $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ increases, Ca_T values will decrease. When there is both an RYR leak and a change in t-system Ca²⁺ leak, the two effects can be difficult to distinguish by observation alone (Fig. 13 C). The model curve-fitting procedure described here allows the RYR and t-system Ca²⁺ leaks to be identified and quantified.

Figure 13.

A framework for interpreting tetracaine-dependent changes in Ca_T–Ca_M curves. (A) If withdrawal of tetracaine is accompanied by onset of a Ca²⁺ leak through the RYRs, the steady state Ca_T–Ca_M curve is shifted leftward, as indicated by the arrow. (B) If withdrawal of tetracaine is accompanied by a decrease in $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ and no RYR leak, then the Ca_T–Ca_M curve shifts upward if $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ decreases (blue dashed curve) or downward if $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ increases (blue dotted curve). (C) If withdrawal of tetracaine results in onset of an RYR Ca²⁺ leak and a decrease in $k_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ then the Ca_T–Ca_M curve is shifted leftward and upward.

Measurements of t-system filling with Ca_M set to 1,340 nM provide important information. That Ca²⁺ concentration exceeds that required to fully activate PMCA. As shown in Fig. 3 B (curve c), the rate of Ca²⁺ pumping by PMCA reaches its maximum at ∼400 nM. Therefore, if Ca_M is >400 nM, any increase in Ca_JS due to RYR leak will have no effect on the rate of Ca²⁺ pumping by PMCA or on steady-state Ca_T. This is evident from the absence of correlation between $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ and steady-state Ca_T when Ca_M is 1,340 (Table 4). Thus, the tetracaine dependence of steady-state Ca_T measured at 1,340 nM reflects changes in only $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ unsullied by $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}:$ an increase in Ca_T shows that $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ has decreased, whereas a decrease shows that $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ has increased. This is important because, as described earlier (see Fig. 12), Cully et al. (2018) showed that in fibers from people with a susceptibility to MH, steady-state Ca_T at Ca_M of 1,340 nM was markedly reduced when measured in the absence of tetracaine compared with that when measured in the presence of tetracaine. This is consistent with a substantial increase in $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}},$ most likely via activation of SOCE, independent of any changes in RYR leak, at least when Ca_JS is high.

How much could RYR Ca²⁺ leak contribute to resting metabolism?

The cycling of Ca²⁺ between the SR and myoplasm requires SERCA to move the Ca²⁺ into the SR. SERCA consumes ATP, which will be regenerated by oxidative phosphorylation in the mitochondria. In a resting muscle in a metabolic steady state, the net heat production arises from the oxidative regeneration of ATP used by SERCA. The SERCA-related heat production associated with the calculated Ca²⁺ fluxes shown in Fig. 9 can be calculated on the basis of a Ca²⁺:ATP stoichiometry of 2 and the production of 74 mJ (μmol ATP)⁻¹ (see Introduction). If resting Ca_M is stable (Carroll et al., 1995) in the face of a continual flux of Ca²⁺ from the SR into the myoplasm, then Ca²⁺ must be removed from the myoplasm at the same rate that it enters. From Fig. 9, the RYR efflux of Ca²⁺ from the SR was 14 μM s⁻¹. To balance that flow, taking account of the relative volumes, this would require SERCA to remove Ca²⁺ from the myoplasm at 0.77 μM s⁻¹, using ATP at half that rate, 0.39 μM s⁻¹. The associated rate of heat production would be 74 mJ μmol⁻¹ × 0.39 μmol liter⁻¹ s⁻¹ = 29 mW kg⁻¹. With the scheme shown in Fig. 9, 8% of the RYR Ca²⁺ leak is pumped into the t-system before leaking into the myoplasm and being returned to the SR via SERCA; that is, this component is pumped twice in each Ca²⁺ leak/uptake cycle. This would increase the heat production associated with the RYR Ca²⁺ leak by 8%, to 31 mW kg⁻¹.

In comparison, the estimated resting heat production in human forearm muscle is 600 mW kg⁻¹ (Table 1), so the RYR Ca²⁺ leak component is 100 × 31/600 = 5% of muscle resting heat production. The magnitude of this value is consistent with an experimental determination. Chinet et al. (1992) determined the contribution of PMCA to resting heat production of mouse slow-twitch muscle by measuring the decrease in muscle heat production when PMCA was blocked by pharmacological inhibition of calmodulin. It can be difficult to interpret the results of experiments involving blocking part of the Ca²⁺ cycling process, but their results were similar to the current analysis: PMCA accounted for 3.2% of resting heat production. Together with the current estimate, this supports the idea that under normal physiological conditions and in the absence of pathological alterations in Ca²⁺ handling, RYR Ca²⁺ leak makes only a small contribution to skeletal muscle resting metabolism. However, it is clear that RYR Ca²⁺ flux can vary across a huge range. The Ca²⁺ leak calculated in Results for MH fibers was 2.3 times greater than that for fibers with no RYR pathology and thus could be expected to produce ≥60 mW kg⁻¹, which could increase muscle resting metabolism by 5%. At the other extreme to the leak in resting fibers, in response to stimulation, SR [Ca²⁺] decreases at rates of up to 50 mM s⁻¹ (Sztretye et al., 2011a), >3,000 times greater than the leak measured in resting fibers.

Non-RYR Ca²⁺ leak from the SR

The experimental evidence presented by Chinet et al. (1992) indicated that ∼25% of resting metabolism is related to SERCA activity. The simplest interpretation of this observation is that there is a continual leak of Ca ²⁺ from the SR into the myoplasm or JS that is pumped back into the SR with the metabolic cost (as either heat production or O₂ consumption) reflecting the mitochondrial activity required to support SERCA-related ATP turnover. The current analysis shows that RYR Ca²⁺ leak is only one-quarter of the total leak required to account for the SERCA-dependent Ca²⁺ leak (Fig. 9). If this is correct, what accounts for the majority of the leak? Ca²⁺ leaks from the SR of resting fibers (Macdonald and Stephenson, 2001; Lamboley et al., 2014) and from SR vesicles (e.g., Simonides and Van Hardeveld, 1988) via a mechanism directly involving SERCA. These leaks were not associated with the normal pump cycle and thus are not related to pump reversal or uncoupling (both unlikely under physiological conditions of low myoplasmic Ca²⁺ and SR free [Ca²⁺] of ∼500 μM). In fact, a leak mechanism, independent of the ATP-splitting pump cycle, seems to be a characteristic of SERCA (Jilka et al., 1975); Berman (2001) has described this as “channel-like behavior.”

Lamboley et al. (2014) reported that the SERCA-related Ca²⁺ leak in skinned human fibers was 6–8 μM s⁻¹ (recalculated from the original data to express concentrations with respect to myoplasmic volume, allowing direct comparison with values in Fig. 9). That was measured at pH 8.5, which those authors suggested would increase the leak compared with that at physiological pH. In that case, those values are probably in reasonable agreement with the 3.2 μM s⁻¹ from the current analysis (Fig. 9) that arises from the assumption that 25% of resting metabolism arises from Ca²⁺ cycling. Therefore, it would appear that assumption is not unreasonable, and given the relative magnitudes of the RYR and SERCA Ca ²⁺ leaks, a comprehensive investigation of the role of Ca²⁺ cycling in resting metabolism of skeletal muscle should include both leak pathways.

Conclusion

The model developed for this study can accurately predict the characteristics of t-system Ca²⁺ accumulation and can be used to quantify the Ca²⁺ leak through the RYRs. The main analysis used data from human muscle fibers with no Ca²⁺ handling–related pathology. In these fibers, there is only a small flux of Ca²⁺ through the RYRs when the fibers are unstimulated. However, RYR Ca²⁺ fluxes can potentially vary greatly. For example, in resting fibers, larger RYR fluxes occur in pathological states, such as MH (Cully et al., 2018), and in muscle from mice developed to study variations in RYR function (Lamboley et al., 2021). It is apparent from the Ca_T–Ca_M relationships published in those papers that there are changes with genotype in not only $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}$ but also $k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}$ and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}.$ The current model provides a means by which these changes can be distinguished and quantified.

The heat generated, mostly by SERCA, in balancing the small RYR leak is only a small fraction of the resting metabolic rate of skeletal muscle. Although Ca²⁺ pumped into the t-system by PMCA is used by Launikonis and colleagues as a biosensor, it is unlikely that PMCA contributes greatly to muscle heat production. As illustrated in Fig. 9, because of the relatively small amount of PMCA compared with SERCA, the majority of Ca²⁺ that leaks into the JS will be removed from the myoplasm into the SR via SERCA, and that will be the source of most of the heat production. In the current context, the discrete localization of PMCA in the JS, allied with the protocol of comparing t-system Ca²⁺ accumulation in the presence and absence of an RYR inhibitor and a quantitative model, makes for an extremely sensitive sensor of Ca²⁺ movement through the RYR in resting muscle.

The current model was a development of a previous one that was used to predict Ca²⁺ movements and heat production in intact muscle fibers in response to stimulation (Bakker et al., 2017; Barclay and Launikonis, 2021). The improvements in the current model include an enhanced spatial representation of the fiber, a more physiological model of SERCA, and the inclusion of PMCA. There are more sophisticated models of cellular Ca²⁺ handling (e.g., Baylor and Hollingworth, 2007), but a strength of the current approach is the extension from the microscopic Ca²⁺ movements within a cell to the macroscopic consequence of those events in terms of heat production. Incorporation of heat production in the model is useful both for comparison with observed values and as a constraint on the parameters of SERCA. Some models of Ca²⁺ movements incorporate diffusion of mobile Ca²⁺ entities within the fiber (Cannell and Allen, 1984; Baylor and Hollingworth, 1998). This was deemed unnecessary in the current model because the measured variable, the time course of t-system filling, occurs on a scale of tens of seconds, whereas diffusion on an intrafiber scale (i.e., over micrometer distances) occurs on a millisecond time scale. Any effects of diffusion would be obscured by the slow removal of Ca²⁺ from the JS by PMCA.

Ultimately, it is the function of intact muscle fibers that is of interest in relation to the heat produced by resting and contracting muscle fibers. Integrating the current skinned fiber model of Ca²⁺ movements in resting fibers with our previous model of Ca²⁺ movements in intact fibers in response to stimulus-induced Ca²⁺ release would be a valuable step on the path to integrate data from skinned fibers into a model that can relate intracellular Ca²⁺ movements to the metabolism of resting and active intact muscle fibers.

Appendix 1

Model equations and parameter values

The skinned fiber model depicted in Fig. 1 was described mathematically as a set of ordinary differential equations. The equations are listed in Table A1. They are categorized as buffering reactions, those involving EGTA or buffers in the SR, leaks, and combined equations. The latter incorporate all movements in or out of a physical compartment and include corrections for the change in volume moving from one compartment to another. Details of the model used for Ca²⁺ pumping by SERCA and PMCA are given in the following section.

Table A1.

Model equations

Buffering
SR	$\frac{\mathrm{d}\mathrm{C}\mathrm{a}\mathrm{B}}{\mathrm{d}t}{=k}_{\mathrm{o}\mathrm{n}}^{\mathrm{B}}\cdot {\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}{\left(t\right)}^n\cdot \left(B_{\mathrm{T}\mathrm{o}\mathrm{t}}-\mathrm{C}\mathrm{a}\mathrm{B}\right)-k_{\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{B}}\cdot \mathrm{C}\mathrm{a}\mathrm{B}$
Myoplasm	$\frac{{\mathrm{d}\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{M}}}{\mathrm{d}t}=k_{\mathrm{o}\mathrm{n}}^{\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}\cdot {\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\cdot \left({\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{T}\mathrm{o}\mathrm{t}}{-\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{M}}\right)-k_{\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}\cdot {\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{M}}$
JS	$\frac{{\mathrm{d}\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{J}\mathrm{S}}}{\mathrm{d}t}=k_{\mathrm{o}\mathrm{n}}^{\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}\cdot {\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}\left(t\right)\cdot \left({\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{T}\mathrm{o}\mathrm{t}}-{\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{J}\mathrm{S}}\right)-k_{\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}\cdot {\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{J}\mathrm{S}}$
Leaks
From t-system	$k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{T}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)$
From SR, via RYR	$k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}\left(t\right)\right)$
From SR, non-RYR	$k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{S}\mathrm{R}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)$
Diffusion	$k_{\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)$
Combined differential equations
$\frac{{\mathrm{d}\mathrm{C}\mathrm{a}}_{\mathrm{T}}}{\mathrm{d}t}=\frac{V_{\mathrm{J}\mathrm{S}}}{V_{\mathrm{T}}}\cdot M_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}\left({\mathrm{C}\mathrm{a}}_{\mathrm{J}}{,\mathrm{C}\mathrm{a}}_{\mathrm{T}}{,K}_{\mathrm{D}}^{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}{,c}_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{A}}\right)-k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{T}}{\left(t\right)-\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)$
$\frac{dC{a}_{SR}}{\mathrm{d}t}=\frac{V_{\mathrm{M}}}{V_{SR}}\cdot M_{SERCA}\left(C{a}_{\mathrm{M}},C{a}_{SR},K_{\mathrm{D}}^{SERCA},c_{SERCA}\right)-k_{Leak}^{RyR}\cdot \left(C{a}_{SR}\left(t\right)-C{a}_{JS}\left(t\right)\right)-k_{Leak}^{SR}\cdot \left(C{a}_{SR}\left(t\right)-C{a}_{\mathrm{M}}\left(t\right)\right)-\frac{dCaB}{\mathrm{d}t}$
$\frac{{\mathrm{d}\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}}{\mathrm{d}t}=\frac{V_{\mathrm{S}\mathrm{R}}}{V_{\mathrm{J}\mathrm{S}}}\cdot k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{R}\mathrm{y}\mathrm{R}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}\left(t\right)\right)-\frac{{\mathrm{d}\mathrm{C}\mathrm{a}}_{\mathrm{T}}}{\mathrm{d}t}-\frac{{\mathrm{d}\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{J}\mathrm{S}}}{\mathrm{d}t}-k_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)$
$\begin{array}{l}\frac{{\mathrm{d}\mathrm{C}\mathrm{a}}_{\mathrm{M}}}{\mathrm{d}t}=\frac{V_{\mathrm{S}\mathrm{R}}}{V_{\mathrm{M}}}\cdot k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{S}\mathrm{R}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)+\frac{V_{\mathrm{T}}}{V_{\mathrm{M}}}\cdot k_{\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}}^{\mathrm{T}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{T}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)+\frac{V_{\mathrm{J}\mathrm{S}}}{V_{\mathrm{M}}}\cdot k_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}}\cdot \left({\mathrm{C}\mathrm{a}}_{\mathrm{J}\mathrm{S}}\left(t\right)-{\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\right)-\\ M_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}\left({\mathrm{C}\mathrm{a}}_{\mathrm{M}}{,\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}{,K}_{\mathrm{D}}^{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}{,c}_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}\right)-\frac{{\mathrm{d}\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{M}}}{\mathrm{d}t}\\ \end{array}$

Model parameter values

The model used for SERCA and PMCA was a two-state model (Fig. 2 A) developed by Tran et al. (2009). That was based on an eight-state biochemical model (Fig. A1). The apparent rate constants in the two-state model are functions of the rate constants and dissociation constants in the eight-state scheme as indicated in Fig. A1. In normal operation, the reactions proceed in the clockwise direction with fully cooperative binding of two Ca²⁺ from the cytoplasm (from state P₂ to P₄) that are transported across the membrane (P₅ to P₆) and released into the SR (P₆ to P₈). Each cycle involves the binding and hydrolysis of ATP, with products ADP and Pi being released at the steps indicated. The model involves H⁺ both as part of Ca²⁺/H⁺ countertransport and in competition with Ca²⁺ binding. The parameter values for the Ca²⁺ pump used in the current model are mostly those derived by Tran et al. (2009), with the exception of the Ca²⁺ dissociation constant on the myoplasmic side of the pump (K_d,Cai in Fig. A1), which was adjusted to match the empirical Ca₅₀ values for SERCA and PMCA (see Materials and methods), and $k_3^{+},$ which was adjusted to match the maximum turnover of the pump to that determined empirically (see Materials and methods). Values of all the parameters for the Ca²⁺ pumps, buffer reactions, and concentrations of cellular constituents are given in Table A2.

Figure A1.

Schematic of biochemical model of SERCA. The eight-state model of Ca²⁺ transport by SERCA described by Tran et al. (2009). This was a simplification of a 12-state model and underlies their 2-state model, as used in the current study. Rate constants are indicated by $k_x^{+}$ or $k_x^{-}$ for forward and reverse reactions, respectively, and x can be 1, 2, or 3, as shown in the figure). Dissociation constants are depicted by $k_d.$ The figure is reproduced from Tran et al. (2009).

Table A2.

Parameter values

Parameter values for Ca2+ pumps				Rate constants for buffers and diffusion		Concentrations		Rate constants for leaks
Parameter	SERCA	PMCA	Units
$k_1^{+}$	25.9		μM−1 s−1	$k_{on}^B/k_{off}^B$	1.55 × 10−6 μM−1 s−1/3,000 s−1
$k_2^{+}$	2,540		μM−1 s−1	$k_{on}^{EGTA}/k_{on}^{EGTA}$	1.67 μM−1 s−1/0.31 s−1
$k_3^{+}$	23.6		μM−1 s−1	$k_{diff}$	2.8 × 104 s−1
$k_1^{-}$	51.8		s−1
$k_2^{-}$	67.2		s−1			[ATP]	8 × 103 μM
$k_3^{-}$	0.149		s−1			[ADP]	5 μM
$K_{d,Cai}$ *	3,540	180	μM			[Pi]	1 × 103 μM
$K_{{d,Ca}_{SR}}$	2,240		μM			pH/[H+]	7.1/0.0794
$K_{d,H1}$	0.0109		μM
$K_{{d,H}_i}$	3,540		μM					$k_{Leak}^T$	Values determined as described in text
$K_{{d,H}_{SR}}$	0.0105		μM					$k_{Leak}^{RYR}$
$K_{d,H}$	0.0724		μM					$k_{Leak}^{SR}$
[pump]	59	58	μM
n Ca	2

^*$K_{{d,Ca}_i}$ in Fig. A1 corresponds to $K_D^{SERCA}$ and $K_D^{PMCA}$ for SERCA and PMCA, respectively. $k_3^{+}$ was adjusted to match experimentally determined pump turnover (6 s⁻¹); $K_{{d,Ca}_i}$ was adjusted to match the observed Ca₅₀ values; other parameter values for Ca²⁺ pumps were as determined by Tran et al. (2009).

In terms of the two-state model (see Fig. 2 A), the rate of Ca²⁺ translocation by SERCA is

$$M_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}=n_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}\cdot c_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}}\cdot \frac{{\alpha }_1^{+}\cdot {\alpha }_2^{+}-{\alpha }_1^{-}\cdot {\alpha }_2^{-}}{{\alpha }_1^{+}+{\alpha }_2^{+}+{\alpha }_1^{-}+{\alpha }_2^{-}},$$

where ${\alpha }_1^{+}$ and ${\alpha }_2^{+}$ are the apparent rate constants for the forward transitions between states P_M and P_SR, and ${\alpha }_1^{-}$ and ${\alpha }_2^{-}$ are the apparent rate constants for the reverse reactions. The apparent rate constants are functions of the rate constants from the eight-state scheme, the concentrations of ATP and its hydrolysis products, Ca²⁺ (on both sides of the SR membrane), H (on both sides of the membrane), and the dissociation constants for the reactions involving those molecules, as indicated in Fig. A1. The formulae for calculating the apparent rate constants are given in Table A3. For further details of the model, see Tran et al. (2009).

Table A3.

Calculation of apparent rate constants for two-state model of Ca²⁺ pumps

${\alpha }_1^{+}=\frac{k_2^{+}\cdot N_{\mathrm{A}\mathrm{T}\mathrm{P}}\cdot N_{{\mathrm{C}\mathrm{a}}_{\mathrm{i}}}^2}{N_{\mathrm{A}\mathrm{T}\mathrm{P}}\cdot {\left(N_{{\mathrm{C}\mathrm{a}}_{\mathrm{i}}}\right)}^2{+N}_{{\mathrm{H}}_{\mathrm{i}}}\cdot \left({1+N}_{\mathrm{A}\mathrm{T}\mathrm{P}}\cdot \left({1+N}_{{\mathrm{H}}_1}+N_{{\mathrm{C}\mathrm{a}}_{\mathrm{i}}}^2\right)\right)}$	$N_{\mathrm{A}\mathrm{T}\mathrm{P}}{=\left[\mathrm{A}\mathrm{T}\mathrm{P}\right]/K}_{\mathrm{d},\mathrm{A}\mathrm{T}\mathrm{P}}$
	$N_{{\mathrm{Ca}}_{\mathrm{i}}}={\mathrm{Ca}}_{\mathrm{i}}/K_{\mathrm{d},{\mathrm{Ca}}_{\mathrm{i}}}$
	$N_{{\mathrm{H}}_{\mathrm{i}}}{=[\mathrm{H}}^{+}{]}_{\mathrm{i}}/K_{\mathrm{d},{\mathrm{H}}_{\mathrm{i}}}$
	$N_{{\mathrm{H}}_1}{=[\mathrm{H}}^{+}{]}_1{K}_{\mathrm{d},{\mathrm{H}}_1}$
${\alpha }_2^{+}=\frac{k_3^{+}\cdot N_{{\mathrm{H}}_{\mathrm{S}\mathrm{R}}}}{N_{{\mathrm{H}}_{\mathrm{S}\mathrm{R}}}\cdot \left({1+N}_{\mathrm{H}}\right){+N}_{\mathrm{H}}\cdot \left(1+N_{{\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}}^2\right)}$	$N_{{\mathrm{H}}_{\mathrm{S}\mathrm{R}}}{=[\mathrm{H}}^{+}{]}_{\mathrm{S}\mathrm{R}}{/K}_{{\mathrm{d},\mathrm{H}}_{\mathrm{S}\mathrm{R}}}$
	$N_{{\mathrm{Ca}}_{\mathrm{SR}}}={\mathrm{Ca}}_{\mathrm{SR}}/K_{\mathrm{d},{\mathrm{Ca}}_{\mathrm{SR}}}$
	$N_{\mathrm{H}}{=[\mathrm{H}}^{+}{]/K}_{\mathrm{d},\mathrm{H}}$
${\alpha }_1^{-}=\frac{k_2^{-}\cdot \left[\mathrm{A}\mathrm{D}\mathrm{P}\right]\cdot N_{{\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}}^2\cdot N_{\mathrm{H}}}{N_{{\mathrm{H}}_{\mathrm{S}\mathrm{R}}}\cdot \left({1+N}_{\mathrm{H}}\right){+N}_{\mathrm{H}}\cdot \left(1+N_{{\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}}^2\right)}$	$K_{\mathrm{d},\mathrm{A}\mathrm{T}\mathrm{P}}=\frac{k_1^{-}}{k_1^{+}}=\frac{k_2^{+}\cdot k_3^{+}\cdot K_{{\mathrm{d},\mathrm{C}\mathrm{a}}_{\mathrm{S}\mathrm{R}}}^2\cdot K_{{\mathrm{d},\mathrm{H}}_{\mathrm{i}}}\cdot K_{\mathrm{d},\mathrm{H}}}{k_2^{-}\cdot k_3^{-}\cdot K_{{\mathrm{d},\mathrm{C}\mathrm{a}}_{\mathrm{i}}}^2\cdot K_{{\mathrm{d},\mathrm{H}}_{\mathrm{S}\mathrm{R}}}\cdot {\mathrm{e}}^{{\Delta G}_{\mathrm{A}\mathrm{T}\mathrm{P}}/R\cdot T}}$
${\alpha }_2^{-}=\frac{k_3^{-}\cdot \left[\mathrm{P}\mathrm{i}\right]\cdot N_{{\mathrm{H}}_{\mathrm{i}}}}{N_{\mathrm{A}\mathrm{T}\mathrm{P}}\cdot N_{{\mathrm{C}\mathrm{a}}_{\mathrm{i}}}^2{+N}_{{\mathrm{H}}_{\mathrm{i}}}\cdot \left({1+N}_{\mathrm{A}\mathrm{T}\mathrm{P}}\left({1+N}_{{\mathrm{H}}_1}+N_{{\mathrm{C}\mathrm{a}}_{\mathrm{i}}}^2\right)\right)}$

Appendix 2

Ca²⁺ binding by EGTA and TnC

An analysis was carried out to see whether Ca²⁺ binding by TnC would affect Ca²⁺–EGTA buffering to the extent that free Ca²⁺ calculated from considering Ca²⁺–EGTA without taking account of TnC will be inaccurate.

The binding of Ca²⁺ by EGTA was treated as a reversible second-order reaction:

$${\mathrm{C}\mathrm{a}}^{2+}+\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}\stackrel{k_{1+}}{\underset{k_{1-}}{\rightleftharpoons }}\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}\text{.}$$ (11)

The rate of the reaction is given by the differential equation:

$$\frac{\mathrm{d}\left[\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}\right]}{\mathrm{d}t}=k_{1+}\cdot {\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\cdot \left({\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}}_{\mathrm{T}\mathrm{o}\mathrm{t}}-\mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}\left(t\right)\right)-k_{1-}\cdot \mathrm{C}\mathrm{a}\mathrm{E}\mathrm{G}\mathrm{T}\mathrm{A}\left(t\right)\text{,}$$

where EGTA_Tot is the concentration of EGTA, CaEGTA is the concentration of the product of reaction Eq. 11, Ca_M is the concentration of unbound Ca²⁺ in the myoplasm, and k₁₊ and k₁₋ are the rate constants for the forward and backward reactions, respectively.

In fast-twitch mammalian muscle, each TnC molecule binds 2 Ca²⁺ in succession.

$${\mathrm{C}\mathrm{a}}^{2+}+\mathrm{T}\mathrm{n}\stackrel{k_{2+}}{\underset{k_{2-}}{\rightleftharpoons }}\mathrm{C}\mathrm{a}\mathrm{T}\mathrm{n}$$ (12)

$${\mathrm{C}\mathrm{a}}^{2+}+\mathrm{C}\mathrm{a}\mathrm{T}\mathrm{n}\stackrel{k_{3+}}{\underset{k_{3-}}{\rightleftharpoons }}{\mathrm{C}\mathrm{a}}_2\mathrm{T}\mathrm{n}\text{,}$$ (13)

where Tn is TnC, and the rate constants are as shown in the equations. The corresponding differential equations are

$$\frac{\mathrm{d}\mathrm{C}\mathrm{a}\mathrm{T}\mathrm{n}}{\mathrm{d}t}=k_{2+}\cdot {\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\cdot \left({\mathrm{T}\mathrm{n}}_{\mathrm{T}\mathrm{o}\mathrm{t}}-\mathrm{C}\mathrm{a}\mathrm{T}\mathrm{n}\left(t\right)\right)+k_{3-}\cdot {\mathrm{C}\mathrm{a}}_2\mathrm{T}\mathrm{n}\left(t\right)-k_{2-}\cdot \mathrm{C}\mathrm{a}\mathrm{T}\mathrm{n}\left(t\right)\text{,}$$

$$\frac{{\mathrm{d}\mathrm{C}\mathrm{a}}_2\mathrm{T}\mathrm{n}}{\mathrm{d}t}=k_{3+}\cdot {\mathrm{C}\mathrm{a}}_{\mathrm{M}}\left(t\right)\cdot \left(\mathrm{C}\mathrm{a}\mathrm{T}\mathrm{n}\left(t\right)–{\mathrm{C}\mathrm{a}}_2\mathrm{T}\mathrm{n}\left(t\right)\right)-k_{3-}\cdot {\mathrm{C}\mathrm{a}}_2\mathrm{T}\mathrm{n}\left(t\right)\text{,}$$

where Tn_Tot is the concentration of TnC, CaTn is the concentration of TnC with one Ca²⁺ bound, and Ca₂Tn is the concentration of TnC with 2 Ca²⁺ bound. The values of the parameters are given in Table A4. The system of equations was solved, starting with all the Ca²⁺ bound to EGTA. The analysis involved tracking the temporal evolution of Ca_M.

Table A4.

Parameter values used for assessing effect of TnC on Ca²⁺–EGTA equilibrium

Parameter	Value	Comments
EGTA	50,000 μM
k 1+	1.67 M−1 s−1	From Kd of 0.18 μM (Smith et al., 1984) and k1−
k 1−	0.31 s−1	Smith et al. (1984)
Tn	100 μM	2 Ca2+ binding sites/molecule (i.e., binding sites, 200 μM)
k 2+	240 M−1 s−1	Baylor et al. (1983) for rabbit TnC, adjusted from 16°C to 25°C assuming a Q10 of 2.0
k 2−	2,900 s−1
k 3+	4.7 M−1 s−1
k3-	165 s−1

In Fig. A2 A, the calculated time course of the (theoretical) increase of Ca_M as Ca²⁺ dissociates from EGTA is shown. The time taken for this to occur is affected by TnC, being slower (on a millisecond scale) when TnC is present. The important result is that the final concentration of unbound Ca²⁺ was not visibly altered by the inclusion of TnC in the model. By comparing the time courses of Ca_M, CaTn, and Ca₂Tn, it can be seen that EGTA effectively buffers Ca_M even while Ca²⁺ is binding to TnC (Fig. A2 B). The reason for this is that the Ca²⁺–EGTA reaction is faster than Ca²⁺ binding by TnC, so free Ca²⁺ that binds to TnC is rapidly replaced by Ca²⁺ dissociating from EGTA.

Figure A2.

Analysis of Ca binding by TnC. (A) Computed time course of establishment of equilibrium between Ca²⁺ and EGTA. At time 0, all Ca²⁺ bound to EGTA. The kinetic model was used to compute the change in unbound Ca²⁺. The effects of including TnC (labeled +TnC) or considering EGTA alone (−TnC) are shown. In the presence of TnC, equilibration of Ca²⁺–EGTA takes longer (~2 ms), but the eventual free [Ca²⁺] level (67 nM) is the same whether TnC is included or not. (B) Calculated time courses of Ca²⁺ binding by TnC. First Ca²⁺ binds rapidly (blue) and second Ca²⁺ (red) more slowly. Unbound [Ca²⁺] attains a steady value (600 nM in this example) more rapidly than CaTn, reflecting the binding kinetics of EGTA. EGTA effectively buffers Ca²⁺ even when Ca²⁺ is being bound by TnC.

Close inspection of calculated steady-state Ca_M values reveals very small differences in Ca_M depending on whether the effects of TnC are considered (Table A5). Ca_M is lower when TnC is considered than when it is ignored. However, the magnitude of the difference is small for the range of Ca_M values used in the current study. For example, when the anticipated Ca_M is 67 nM, the actual Ca_M, taking account of the effects of TnC, would be 0.006% lower. The effect is larger for higher values of Ca_M, reaching 0.1% when Ca_M is 1 μM. For practical purposes, these effects are negligible.

Table A5.

Effect of TnC on Ca²⁺ buffering by EGTA

Unbound [Ca2+] (nM)		Difference
No TnC	With TnC	nM	%
20	19.999	0.001	0.005
67	66.996	0.004	0.006
200	199.97	0.03	0.015
600	599.69	0.29	0.05
1,000	998.85	1.15	0.11