Abstract
MMP-9 is a calcium-dependent zinc endopeptidase that plays a crucial role in various diseases and is a ubiquitous target for many classes of drugs. The availability of MMP-9 crystal structure in combination with aryl sulfonamide anthranilate hydroxamate inhibitor facilitates to accentuate the computer-aided screening of MMP-9 inhibitors with the presumed binding mode. In the current study, ligand-based pharmacophore modeling and 3D-QSAR analysis were performed using 67 reported MMP-9 inhibitors possessing pIC50 in the range of 5.221 to 9.000. The established five-point hypothesis model DDHRR_1 was statistically validated using various parameters R2 (0.9076), Q2 (0.8170), and F value (83.5) at a partial least square of four. Hypothesis validation and enrichment analysis were performed for the generated hypothesis. Further, Y-scrambling and Xternal validation using mean-absolute error-based criteria were performed to evaluate the reliability of the model. Docking in the XP mode and binding free energy was calculated for 67 selected ligands to explore the key binding interactions and binding affinity against the MMP-9 enzyme. Additionally, high-throughput virtual screening was carried out for 2.3 million chemical molecules to explore the potential virtual hits, and their predicted activity was calculated. Thus, the results obtained aid in developing novel MMP-9 inhibitors with significant activity and binding affinity.
MMP-9 is a calcium-dependent zinc endopeptidase that plays a crucial role in various diseases and is a ubiquitous target for many classes of drugs.
Introduction
Matrix metalloproteinase (MMP)-9, one of the widely investigated MMP, belongs to a family of calcium-dependent endopeptidases that contains zinc.1,2 In general, MMP-9 is involved in breaking the extracellular matrix (ECM) components that facilitate connective tissue remodeling, organogenesis, development, and turnover into normal tissue.3 Usually, MMP-9 activity is strongly controlled by the equilibrium between the synthesis of active enzymes and the presence of inhibitors.3,4 However, this balance is lost in numerous pathological conditions, causing chronic inflammation.5 This chronic condition is responsible for abnormal tissue degradation, causing cancers,6,7 atherosclerosis,8 osteoarthritis,9 cardiovascular,10,11 lung,12,13 neurological,14,15 metabolic-related disorders, and delayed wound healing in diabetes.16 Thus, finding novel inhibitors that block the elevated levels of MMP-9 could be an attractive approach in combating the pathogenesis of several diseases.
The crystal structure of MMP-9 consists of a catalytic domain with three α-helices and five stranded β-sheets. The catalytic pocket contains an active site with two zinc and five calcium ions. The zinc ions in the domain are coordinated by three histidine residues (His401, His405, His411) and glutamic acid residue (Glu402).17 All members of the MMP family differ in their S1 selectivity pocket and chain length. The selectivity loop of MMP-9 has no regular secondary structure and is often mobile, undergoing conformational modifications on ligand binding. Therefore, the sequence of the S1 loop, structural variability, and the cocrystal ligand nature contribute to the observed overall shape and size of the selectivity loop pockets in different MMPs.18 Unfortunately, the electron density at the side chain of residue Arg424 is very poor and oriented into the S1 loop, forming a smaller enclosed catalytic pocket in the MMP-9 crystal structure.19 The asymmetric crystal structure (PDB: 5I12) contains a single chain A, with sequence length 157. It contains a bound ligand, arylsulfonamide anthranilate hydroxamate, the resolution is 1.59 Å, and the selectivity pocket of the protein lacks electron density.20
Besides arylsulfonamide anthranilate hydroxamate, various bioactive moieties have been investigated as potent MMP-9 inhibitors. These include hydroxamates,19 hydroxyquinoline,21 curcuminoid pyrazoles,22 4-thiazolidione,23 tetrahydro β-carboline,24 4-phenoxybenzenesulfonyl pyrrolidine,25 5-substituted pyrimidine-2,4,6-triones,26 ethynylthiophene sulfonamido-based hydroxamates,27 amidine-based thiazole,28 caffeic acid amides,5 and anthranilic acid,29–31 based derivatives. Inhibition of MMP-9 activity has been explored for the advancement of novel small molecules, but a potent inhibitor of MMP-9 has not been reported yet. Although MMP-9 inhibitors have achieved promising therapeutic effects in pre-and peri-metastatic settings, in clinical trials (performed on advanced-stage patients), these inhibitors had serious side effects such as musculoskeletal pain and inflammation due to the broad inhibition of MMPs.
The availability of high-resolution crystal structure of MMP-9 investigated experimentally to develop potential inhibitors with fewer side effects32 using computational approaches.20 Amongst various medicinal chemistry approaches, pharmacophore-based drug design was a more efficient technique for identifying hits or designing novel compounds.33 In this article, we combined ligand-based pharmacophore modeling, 3D-QSAR, molecular docking in the extra-precision (XP) mode, binding free energy and molecular dynamic (MD) studies to discover key interactions between the protein and ligands that are accountable for MMP-9 inhibitory activity. Further, the validation of the model displayed significant predictive power for the in vitro activity (pIC50). The highest active molecule was nominated for MD simulation of 100 ns using GROMACS 2018.1 to validate the proposed binding pose. In addition, in silico virtual screening was performed to determine the novel hits against MMP-9 protein.
Computational methods
Data set generation
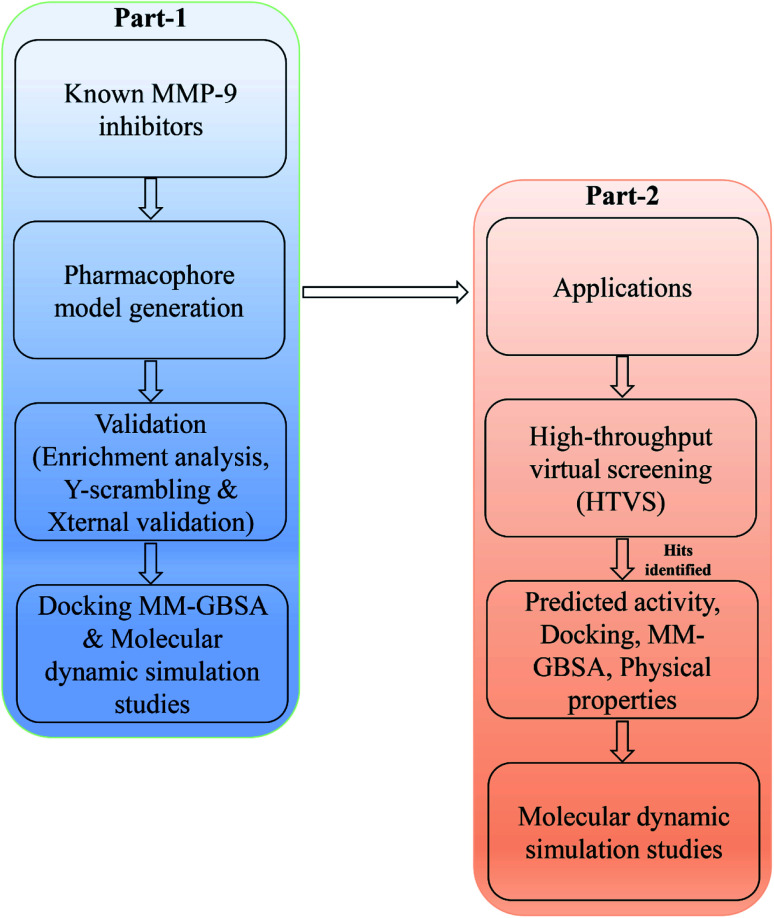
In the current study, a data set comprising of diversified series of 67 molecules possessing 8-hydroxyquinoline, caffeic acid amides, anthranilic acid, and amidine based thiazole scaffolds (ESI, Table S1†) were used.5,21,28,30 Initially, IC50 values (9 to 5.22 μM) of the data set were converted into pIC50. The molecular features of compounds in the test set were used for the internal validation, and those in the training set have been provided as a template for model development. The 3D structures of molecules were created using the Maestro builder panel and optimized using the LigPrep module (Schrödinger suite 2020-3), followed by the generation of possible ionization states by the Propka method.34 Energy optimization was achieved using the OPLS3e forcefield.35 Minimization of energy was carried out for the ligands till it reached the cut-off of 0.1 root-mean-square deviations (RMSD). Then, the prepared ligands were used for further studies. The overall methodology was represented in Fig. 1.
Fig. 1. A workflow methodology of present work.
Pharmacophore hypothesis generation and 3D-QSAR analysis
The phase module (Schrödinger suite 2020-3) was employed to build the pharmacophore hypothesis and 3D-QSAR models for MMP-9 inhibitors. Further, the partial least square (PLS) method was employed to compare the experimental MMP-9 activity with the 3D molecular descriptors. ConfGen was used to generate conformers, and distance-dependent dielectric was applied for the solvation treatment. A data set was assigned with a threshold activity of pIC50 > 8.3 as active and <5.5 as inactive compounds while remaining moderately active.36 The pharmacophoric sites were generated using pharmacophoric features: hydrophobic group (H), hydrogen bond acceptor (A), hydrogen bond donor (D), negative charged group (N), positive charged group (P), and aromatic ring (R) defined in module phase. Amongst 67 ligands, 46 were designated as training sets based on their broad range of activity and diversity. The remaining 21 compounds were selected as test compounds to enable significant comparison with the predicted models. The pharmacophore hypothesis was generated using 10 active compounds, keeping 2 Å for the minimum intersite distance and 1 Å for the pharmacophore-matching tolerance between two pharmacophoric features.
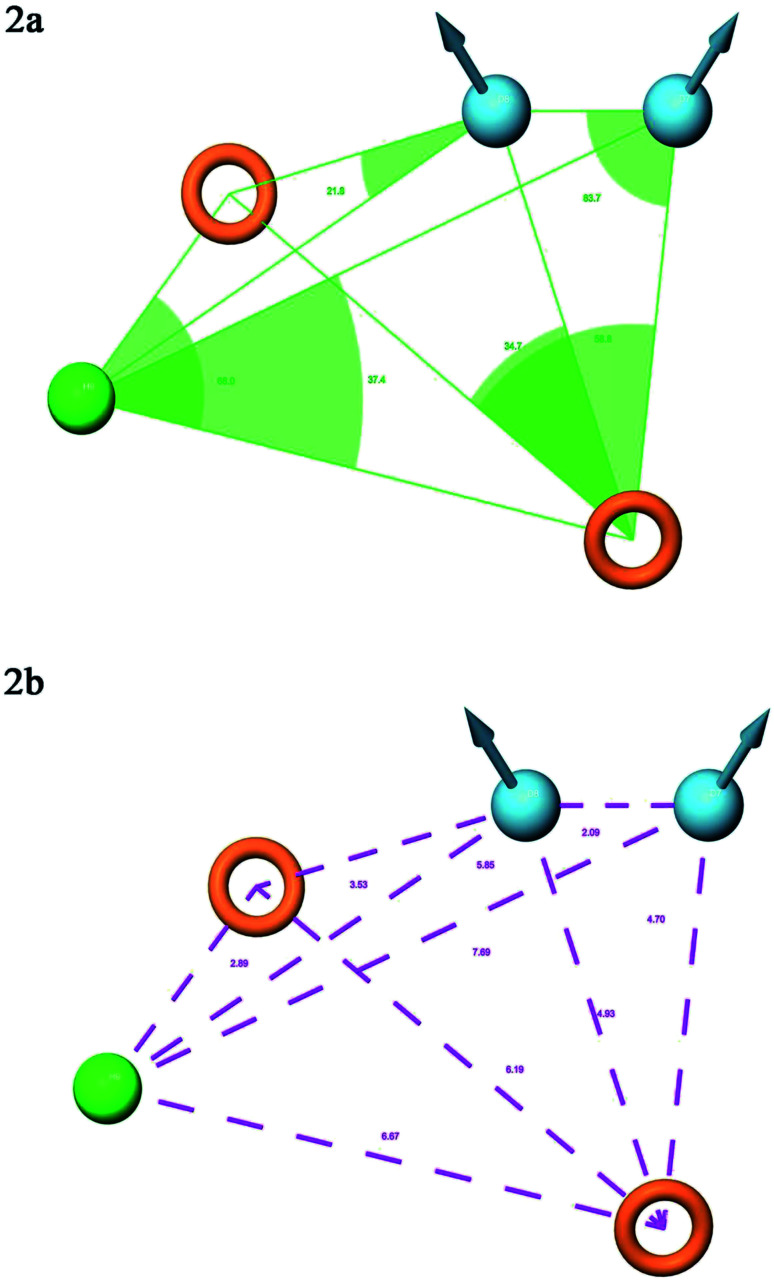
A total of 20 variant hypotheses were developed, keeping five as a maximum number of sites while 50% as actives. Amongst 20 generated hypotheses, the best five were selected based on the survival score, survival inactive, site score, volume, vector, energy terms, and the number of matches (Table 1). The test ligands aligned according to the generated five-point best-fitted hypothesis factor did not affect the model DDHRR_1 model. The angles and distances were calculated among various pharmacophoric features of the selected model and are represented in Fig. 2(a and b) (ESI, Tables S2a and b†). van der Waals model of the aligned training set ligands was employed to generate 3D-QSAR model. A statistically significant model for the DDHRR_1 hypothesis was created based on the 46 training set ligands via PLS regression. The incremental predictivity and statistical significance were detected up to PLS factor four (Table 2). However, further, increase in the PLS statistics and predictive ability. The best-fitted hypothesis model DDHRR_1 was validated by the predicted activity of the test set, which is not included in the model development. Besides, ligands pharmacophoric features arrangement and recognition in space were evaluated using contour plots.
Different parameter scores of the generated hypothesis DDHRR_1a.
| Hypothesis | Survival | Site | Vector | Selectivity | Survival-inactive | Volume | Matches |
|---|---|---|---|---|---|---|---|
| DDHRR_1 | 5.639 | 1 | 0.962 | 2.089 | 1.379 | 0.809 | 7 |
| DDHRR_4 | 5.561 | 0.951 | 0.991 | 2.097 | 1.125 | 0.667 | 7 |
| DHRRR_2 | 5.521 | 0.832 | 0.966 | 2.084 | 1.375 | 0.788 | 7 |
| ADHRR_1 | 5.605 | 1 | 0.958 | 2.005 | 1.356 | 0.797 | 7 |
| ADHRR_2 | 5.523 | 0.956 | 0.958 | 2.005 | 1.476 | 1.387 | 6 |
D: hydrogen bond donor; H: hydrophobic; R: ring aromatic.
Fig. 2. Pharmacophore model DDHRR_1 (a) intersite angles in Å unit (b) intersite distances in Å unit, between the pharmacophoric points.
Phase 3D-QSAR PLS statistical results of the selected pharmacophore model DDHRR_1a.
| PLS | SD | R 2 | F | P | Stability | Q 2 | RMSE | Pearson-R |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.5778 | 0.7216 | 95.9 | 8.07 × 10−12 | 0.854 | 0.6712 | 0.64 | 0.8340 |
| 2 | 0.4696 | 0.8212 | 82.6 | 3.5 × 10−14 | 0.812 | 0.7343 | 0.57 | 0.8744 |
| 3 | 0.4172 | 0.8627 | 73.3 | 3.63 × 10−15 | 0.766 | 0.7650 | 0.54 | 0.9011 |
| 4 | 0.3473 | 0.9076 | 83.5 | 4.27 × 10−17 | 0.709 | 0.8170 | 0.48 | 0.9454 |
PLS: partial least square; SD: standard deviation; R2: regression coefficient; F: test statistic for F-tests; P: level of significance; Q2: cross-validated correlation coefficient; RMSE: root-mean-square error; Pearson-R: Pearson product-moment correlation coefficient.
Hypothesis validation
To validate the utility of the generated model, an enrichment study was conducted by mixing the decoy set retrieved from the Schrödinger database with 10 active molecules (pIC50 > 8.3). Robust initial enhancement (RIE) and enrichment factor of the decoy set molecules were calculated for the accurate ranking of the compounds and to determine the ability to identify actives from inactives.
Moreover, Y-scrambling or randomization test was carried out using a training set to determine the reliability of the generated DDHRR_1 model.37 All independent variables (molecular descriptors) were kept unchanged during the model generation, while the dependent variable (activity data) was randomized throughout the study. After performing 10 Y-scrambling tests, the models with low R2 and Q2 values were considered reliable (ESI, Table S3†).
The prediction quality and systematic errors in the developed hypothesis DDHRR_1 were evaluated by the mean absolute error (MAE)-based criteria method using Xternal Validation plus 1.1 tool recognized by the DTC software lab (https://dtclab.webs.com/sofwafre-tools). All the external validation parameters of the hypothesis were also computed using the MAE-based criterion, which classifies the prediction quality of the model into ‘good’, ‘bad’ and ‘moderate’ based on their evaluation parameters such as standard deviation (SD), MAE, and absolute error (AE). The standard deviation of absolute-error (σAE) is well-defined as follows: (a) bad predictions (MAE + 3 × σAE > 0.25 × training set range and MAE > 0.15 × training set range); (b) good predictions (MAE + 3 × σAE ≤ 0.2 × training set range and MAE ≤ 0.1 × training set range) and moderate predictions are the ones that do not fall under either of the above criteria. Almost 5% of ligands with high AE values were eliminated using the MAE-based criteria method to overwhelm the outlier predictions possibility. About 95% of compounds were employed to determine the external data set of poorly predicted data, whereas, the predictivity of the model was penalized using 100% of MAE-based criteria.38 Besides, to determine the presence of systematic error prediction, absolute value means of the number of negative prediction errors (nNE), negative prediction errors (MNE), the average absolute prediction errors (AAE), the absolute value of average prediction errors (AE), the mean of positive prediction errors (MPE), number of positive prediction errors (nPE) were employed using Xternal validation plus 1.1 tool.39,40 The results obtained using the current method are considered satisfactory if any one or more of the above-mentioned prediction errors obeys the rules demarcated using the MAE-based criterion method (ESI, Table S4†).
Ligand preparation, docking studies, and binding free energy calculation
The X-ray crystal structure of the MMP-9 enzyme conjugation with arylsulfonamide anthranilate hydroxamate inhibitor (PDB: 5I12, resolution 1.80 Å) was retrieved from the RCSB-protein data bank. The optimization of the selected protein was performed by the protein preparation wizard module available in the Schrödinger suite 2020-3.41,42 The addition of hydrogens and refinement were performed using restrained minimization of the OPLS3e force field.35 Side-chain refinement, the building of breaks was carried out using the Prime module.43 Geometric optimization was performed using OPLS3e forcefield (Schrödinger suite 2020-3). Molecular docking was performed for the entire data set ligands against the MMP-9 catalytic domain in (XP) mode using the Glide module (Schrödinger suite 2020-3).44
Minimization of ligands was achieved using the local optimization feature in the Prime module. The continuum solvent model (VSGB), OPLS3e force field, and rotamer search algorithm were used for computing the binding free energies of the ligands.
High-throughput virtual screening (HTVS)
HTVS was performed in the binding pocket of MMP-9 using the Glide docking module of Schrödinger suite 2020-3. The receptor was set as a rigid body, whereas the ligands were set as flexible before subjecting to docking. Before the study, the database library (23 lakh molecules), retrieved from Specs, Timtec, Enamine, and Zinc databases, were filtered based on their physicochemical properties. Three thousand molecules were nominated based on the phase screen-score and fitness to perform clustering using discovery informatics and the 3D-QSAR model available in Maestro 12.5 (Schrödinger suite 2020-3). Volume overlapping matrices were calculated using 1.7 Å fixed radius in the normalized mode by keeping a grid spacing at 1 Å. Clustering was performed using a clustering strain of 1.134 Å and the average linkage method. Almost 20 clusters were generated using duplicate entries to a new group for each cluster formed. The clustering analysis was performed using the Kelley index, dendrogram, and distance matrix.
Virtual screening includes three systematic layers viz., HTVS, standard precision (SP) docking, XP docking. These three precisions of docking were employed to obtain a potential lead molecule with rapid speed. Although HTVS screens a large set of molecules rapidly, the sampling methods were confined, and the outcome could not be interpreted directly. Thus, the ligands screened by HTVS were further docked using SP, which provides a suitable binding pose from a large pool of ligands. Additionally, the best 10% of SP molecules were selected for docking in the XP mode and analyzed using an XP visualizer. The first five molecules were chosen for free energy calculations based on their Glide score, Glide E-model, and Glide energy.
MD simulation
A 100 ns MD simulation was carried out for the 5/5I12 complex using GROMACS 2018.1 software package.45 Energy optimization of the selected complex was performed using the gromos 54a7 force field. The structural topologies of the ligand complex were constructed from the PRODRG web server.46 Simulation of the system was carried out with an SPC water model and in a cubic boundary box. Neutralization of the system was achieved by replacing water molecules with sodium (Na+) and chloride (Cl−) ions that direct periodic boundary conditions. The system was equilibrated at constant 1 atmospheric pressure and 300 K of temperature. As per the report by Duan et al. 2019, it is clear that 300 K is considered as standard and most suitable temperature for MD simulations as it possesses the highest cluster occupancy (cluster analysis), lower free energy state (free energy landscape analysis) and RMSD distribution.47 Energy minimization was performed using the steepest descent algorithm.48
MD analysis
GROMACS 2018.1 software package was used to analyze the MD conformations.45 For analyzing the radius of gyration (RG), root-mean-square deviation (RMSD), command lines g_gyrate and g_cluster were employed. Energy calculation was performed using the g_energy program command line. The commands g_rmsf and g_rmsd were employed for root-mean-square fluctuation (RMSF) of amino acid residues and mean-square displacement. The docked 5/5I12 complex was used to observe the migration over the simulation time.
Molecular Mechanics-Poisson Boltzmann Surface Area (MM-PBSA) calculation
The binding free energy of compound 5/5I12 complex after the MD simulation was calculated using the MM-PBSA.49 This approach calculates the free energies of the end states directly by eliminating the simulation of intermediate states and combines the molecular mechanical energies with the continuum solvent strategies. Explicit water molecules were removed from the snapshots.
The binding free energy (ΔGbind) was calculated as follows:ΔGbind = ΔEgas + ΔGsolv − TΔSconfwhere ΔEgas is the interaction energy between the protein and ligand in the gas phase;ΔEgas = ΔEvdW + ΔEelecwhere ΔEvdW and ΔEelec refer to protein-ligand van der Waals and electrostatic interactions, respectively.
Solvation free energy (ΔGsolv) is the sum of a polar solvation free energy (ΔGNP) and electrostatic solvation free energy (ΔGPB):50ΔGsolv = ΔGNP + ΔGPBTΔSconf, solute entropies were calculated by the module NMODE in GROMACS.
Results and discussion
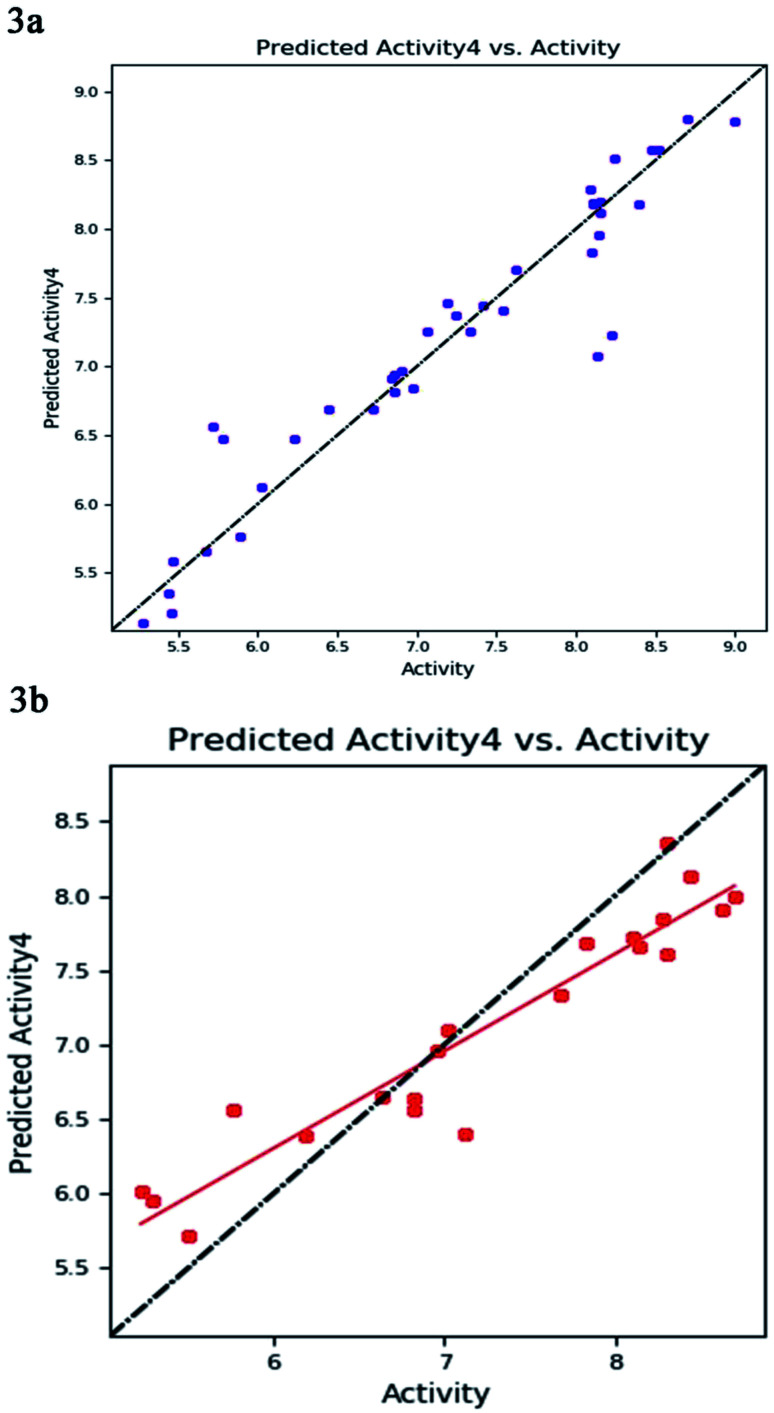
The best five-point model DDHRR_1 hypothesis was created based on 10 active compounds (pIC50 > 8.3). The pharmacophore hypothesis DDHRR_1 was considered as the best model based on the values obtained for cross-validated coefficient (R2) of 0.9076, survival score of 5.639, Pearson-correlation coefficient (r) of 0.9454, regression coefficient of 0.89, smaller significance level of variance ratio (p) of 4.27 × 10−17 and highest variance ratio (F) value of 83.5. The DDHRR_1 model consists of two hydrophobic, two ring features, and a hydrogen bond donor. After the alignment of hypothesis DDHRR_1 over actives (10) and inactives (7) revealed that angles and distances are significant attributes for inhibitory activity of MMP-9. Besides, a higher degree of confidence in the hypothesis model DDHRR_1 was exhibited by the higher value of QSAR model stability 0.709 on a maximum scale of 1 with an SD of 0.3473, root-mean-square-error (RMSE) of 0.48, and Pearson correlation coefficient (r) of 0.9454. In the training set, the high coefficient of determination (R2) of 0.9076 indicated the relevancy of generated model. Further, the validity and ability of the hypothesis model in experimental activity prediction of test compounds were suggested by the higher cross-validated correlation-coefficient (Q2) of 0.8170 PLS-4 (ESI, Table S1†). A comparison between experimental activity and phase-predicted activities of test and training set molecules were calculated, and the results are represented in Fig. 3a and b, respectively. The scatter plots of both training and test indicate the moderate deviation between predicted and experimental activity.
Fig. 3. The correlation plot between the experimental and predicted activity (pIC50) of 8-hydroxyquinoline, caffeic acid amides, anthranilic acid, and amidine based thiazole inhibitors using pharmacophore-based QSAR model of (a) training set (b) test set with best-fit line y = 0.65x + 2.39 (R2 = 0.89).
In enrichment analysis, the hypothesis model DDHRR_1 could determine 100% active compounds on the hit list. The results obtained from the enrichment analysis in terms of the recovered actives from the top 1–20% of decoy set molecules that rank-ordered with respect to fitness score of the generated pharmacophore model (ESI, Tables S7–S9 and Fig. S1†). From the results, it is clear that recovery of the 50% actives is possible from the top 5% of the decoy set with decent enrichment values. RIE was computed for the hypothesis models to evaluate the ranking of active set contribution in the enrichment study. The obtained RIE value 13.07 for the best-fitted model DDHRR_1 directed the superior ranking over random distribution. To estimate the DDHRR_1 performance, the area under the accumulation curve (AUC) of the receiver operating characteristic (ROC) curve was plotted as a reliable metric. The generated DDHRR_1 model achieved a good value of ROC (0.70) and AUC (0.83) (Table 3 and ESI, Fig. S1†).
Results of Enrichment factor (EF) analysis for the generated 3D-QSAR models.
| Pharmacophore model | AUC | RIE | ROC | Phase hypo score | BedROC160.9 |
|---|---|---|---|---|---|
| DDHRR_1 | 0.83 | 13.07 | 0.70 | 1.06 | 0.84 |
| DDHRR_4 | 0.83 | 13.07 | 0.70 | 1.05 | 0.84 |
| DHRRR_2 | 0.83 | 13.07 | 0.70 | 1.05 | 0.83 |
| ADHRR_1 | 0.83 | 13.07 | 0.70 | 1.05 | 0.80 |
| ADHRR_2 | 0.83 | 13.07 | 0.70 | 1.04 | 0.80 |
Further, to determine the reliability and robustness of the predicted model DDHRR_1, the Y-scrambling method was used, which guarantees that the generated hypothesis is reliable and not occurring by chance. Y-scrambling test also validates the training data set sufficiency by comparing the non-randomized score obtained with the scores of non-randomized data. If the similarity persists between the predicted activity of the original model and the randomized model, then the observation set is insufficient to sustenance the generated model. However, the new 3D-QSAR models were reported to have low Q2 and R2 values after numerous repetitions (ESI, Table S3†). The results show that the DDHRR_1 model is noticeably significant and reliable and was in good agreement with the calculated statistical parameters.
A total of 21 external test molecules were found to cover a response range of 2.3332 logarithmic units. The prediction quality of the model generated was found to be ‘good’ in harmony with MAE-based criteria (ESI, Table S4†). The predicted residuals MAE and MAE + 3 × σAE were observed at 0.3734 and 1.1394, respectively, after eliminating 5% test set objects with high residual values. To judge the predictivity of the model, threshold values such as 0.7820 (training set range × 0.1), 1.5639 (training set range × 0.2), 1.1729 (training set range × 0.15), 1.9549 (training set range × 0.25) were used. As per the prediction error of MAE-based criteria, the generated 3D-QSAR model was found to be reliable. Besides, to evaluate the systematic errors in the generated model, it is merely necessary to investigate the prediction errors of test compounds. The prediction errors were calculated and the results obtained are |MPE/MNE| (1.1445), AAE − |AE| (0.2669), nNE/nPE (0.5672), nPE/nNE (1.7632), |MNE/MPE| (0.8738) (ESI, Table S3†). The R2 value was found to be 0.8936 between predicted and observed values (ESI, Table S4†).
Contour plot analysis
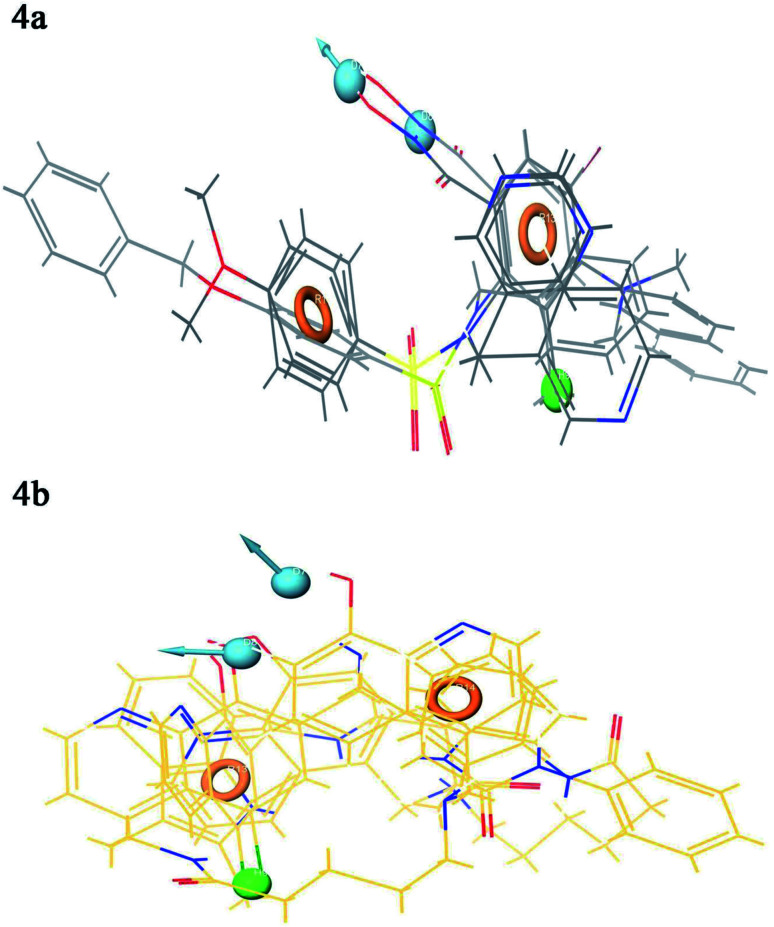
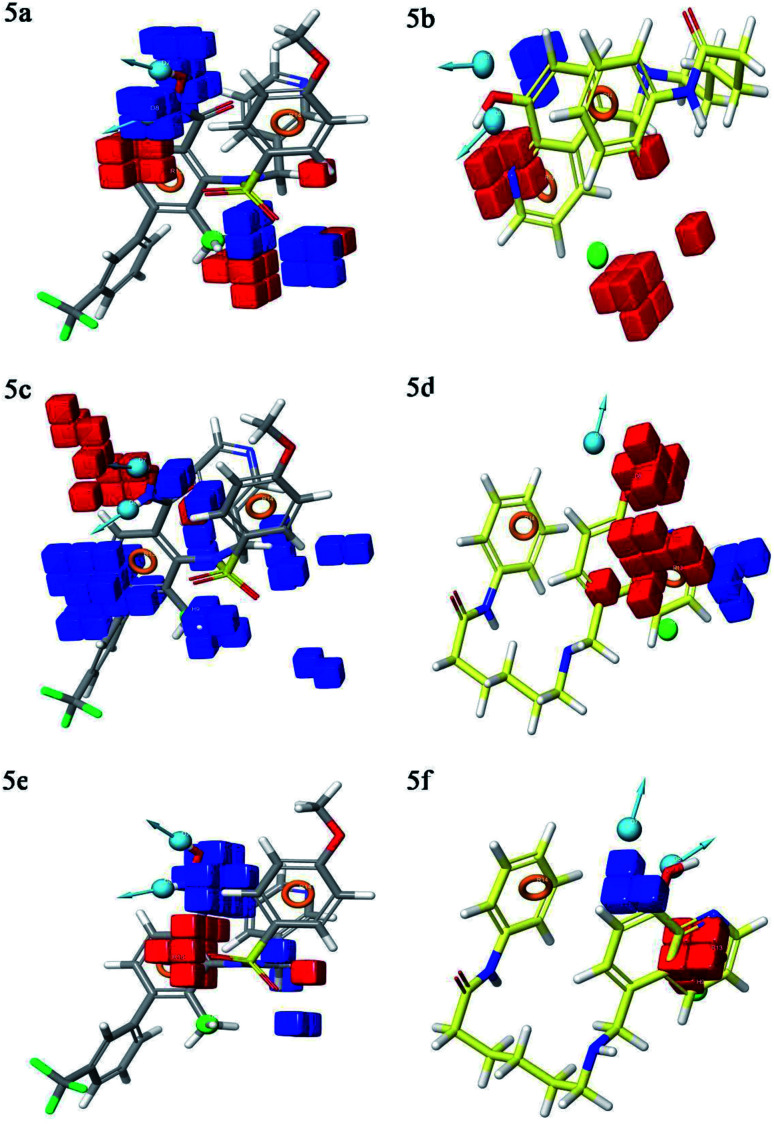
Contour plot analysis was carried out to determine the effects of the spatial arrangement of structural or molecular features of the selected molecules possessing MMP-9 inhibitory activity. The favorable and unfavorable contributions of the ligand inhibitory properties are represented using blue cubes and red cubes, respectively. The best-fitted hypothesis DDHRR_1 of most active ligand 5 (pIC50 = 9.00) and less active ligand 66 (pIC50 = 5.222) were used for a comparison. All the actives and inactives were mapped onto the developed pharmacophore model (Fig. 4(a and b)). The most unfavorable and favorable pharmacophoric sites were nominated in Fig. 5(a–f).
Fig. 4. Mapping of the (a) active compounds (b) inactive compounds onto the pharmacophore. Circle (orange): aromatic rings, dot (blue): donor pharmacophoric feature, dot (green): hydrophobic pharmacophoric feature.
Fig. 5. 3D QSAR contour plot visualization for the generated favorable and unfavorable (a) hydrogen bond effects in the active compound 5 (b) hydrogen bond effects in the inactive compound 66 (c) hydrophobic interactions in the active compound 5 (d) hydrophobic interactions in the inactive compound 66 (e) electron-withdrawing effect in the active compound 5 (f) electron-withdrawing effect in the inactive compound 66. Circle (orange): aromatic rings, dot (blue): donor pharmacophoric feature, dot (green): hydrophobic pharmacophoric feature.
Hydrogen-bond donating pharmacophoric feature was evaluated for active ligands (Fig. 5a) and inactive ligand (Fig. 5b) by visualizing contour plots. The appearance of blue cubes at position four of the biphenyl ring system exhibited favorable contribution of electron-donating groups –OH (D8-pharmacophoric feature) and –NHOH (D7-pharmacophoric feature). In contrast, red cubes on the aromatic ring of the biphenyl system and at position two of the biphenyl ring were unfavorable because of the negative contribution to the MMP-9 inhibitory activity. In the case of inactive 66, the presence of red cubes on the 8-hydroxy quinoline ring demonstrates the non-preference of electron-donating pharmacophoric features with an unfavorable contribution.
The hydrophobic group is a vital pharmacophoric feature that is accountable for the MMP-9 inhibitory activity. The favorable and unfavorable hydrophobic features for active 5 (Fig. 5c) and inactive 66 (Fig. 5d) were analyzed using contour plots. In this hypothesis, hydrophobicity (H9-pharmacophoric feature) was evaluated for both inactive and active compounds. The appearance of blue cubes at positions two and six of the biphenyl ring specifies the preference of hydrophobic feature. Further, the presence of the methyl group at position two is substantially favorable for the inhibitory activity of MMP-9. From this, it is clear that the appearance of blue cubes at these positions is vital for MMP-9 inhibition. However, the appearance of red cubes at position four of the biphenyl ring system was non-crucial for the MMP-9 inhibitory activity. In the case of inactive 66, red cubes around the hydroxy (OH) group of 8-hydroxyquinoline indicate the non-preference of hydrophobic features with an unfavorable contribution. The existence of red cubes on the bridge carbons of the fused ring system (8-hydroxyquinoline) also exemplifies the unfavorable contribution of the hydrophobic feature. Further, the appearance of blue cubes at position two of 8-hydroxyquinoline shows the favorable hydrophobic feature for the inhibitory activity of MMP-9.
Electron withdrawing pharmacophoric feature is another component that potentially impacts inhibitory activity. In the case of active compound 5 (Fig. 5e), the existence of blue cubes around the OH and NHOH at position four of the biphenyl ring system exemplifies the favorable contribution of electron-withdrawing groups at these positions. Moreover, OH and NHOH groups at these positions were observed to be indispensable for the MMP-9 inhibition, as evidenced by the high active compounds (pIC50 range = 8.30103 to 9.000) compared to low active compound 66 (pIC50 = 5.221849). However, the lower activity of compound 66 (Fig. 5f) might be because of the absence of electron-withdrawing features around its nucleus. The explanation was provided by the appearance of red cubes around the pyridine ring of the 8-hydroxyquinoline.
Molecular docking and binding free calculation analyses
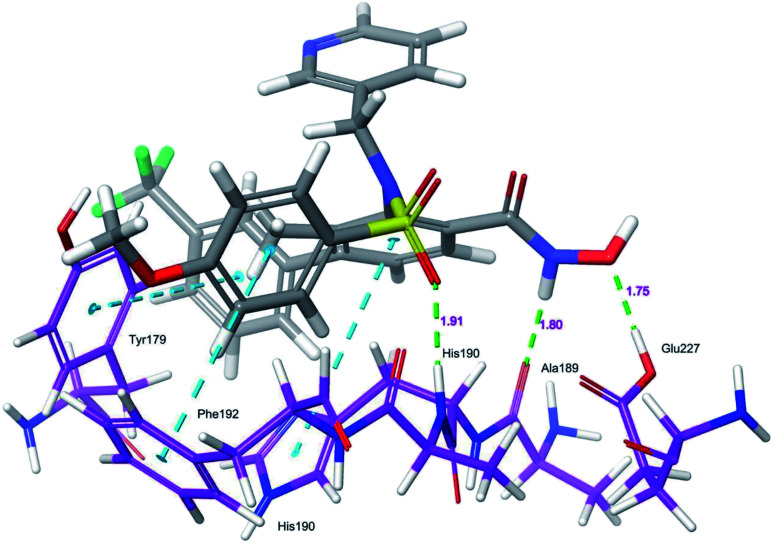
Docking protocol validation was performed by redocking the co-crystallized ligand (PDB: 5I12) into the catalytic domain of the MMP-9 receptor (ESI, Fig. S2†). The conformational orientation similarity between the docked pose and co-crystallized ligand (RMSD = 1.9675 Å) confirms the docking protocol accuracy (ESI, Fig. S3†). The comparative investigation of docking results reported the similarity in the binding poses of the selected ligands (ESI, Table S5†). The hydrogen-bonding interactions and π–π interactions with amino acid residues Tyr179, Leu 188, Ala189, His190, His191, Phe192, and Glu227 played a crucial role in the inhibitory activity of MMP-9. These interactions are in good agreement with the previous study by Kalva et al. 2013.51 Further the occupancy (%) of hydrogen bonding interaction of these residues is detailed in ESI, Table S10.† The binding poses of high active compound 5 were analyzed and compared with the co-crystallized ligand.
The glide score (Gscore) of ligand 5 was found to be −8.414 kcal mol−1 and exhibited good binding affinity with the receptor. From the docked pose of active ligand 5, the –NH present at position four of the biphenyl ring system displayed a hydrogen-bonding interaction with the backbone carbonyl group of Ala189 (–NH O C , 1.80 Å). A second hydrogen-bond interaction was found between the C O of the sulphonyl group attached to the biphenyl ring system at position three and side-chain –NH of His190 ( C O HN–, 1.91 Å). Another hydrogen-bonding interaction was found between the OH of Glu227 and NHOH of ligand 5 (H OH, 1.75 Å). Further, three π–π interactions were observed between the electron cloud of aromatic rings present in the active ligand and electron density residues such as Tyr179, His190, and Phe192 (Fig. 6).
Fig. 6. Glide XP-docked poses of compound 5, in the catalytic pocket of MMP-9 (PDB ID: 5I12). Dotted line (blue): π–π stacking interaction, dotted line (green): hydrogen bonding interaction.
Binding free energy of the selected compounds 1–67/5I12 docked complexes were ranked using Prime, Molecular Mechanics Generalized Born Surface Area (MM-GBSA) approach (ESI, Table S6†). The binding free energy (ΔGbind) values were observed to range from 87.69 to −42.23 kcal mol−1. In addition, the van der Waals energy term (ΔGvdw = −66.300 to −30.350 kcal mol−1) is a major favorable contributor. In comparison, coulombic energy (ΔGcoul = −0.800 to −67.22 kcal mol−1) was a moderately favorable contributor to the MMP-9 inhibitory activity. Covalent energy term (ΔGcov = −2.67 to 14.58 kcal mol−1) strongly disfavors for the inhibitory activity.
Molecular dynamic simulation and analysis
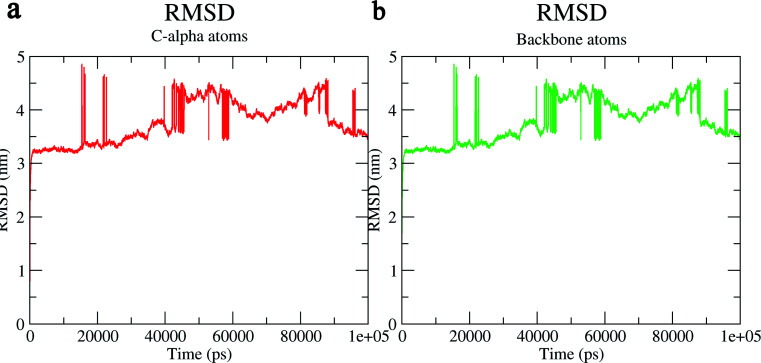
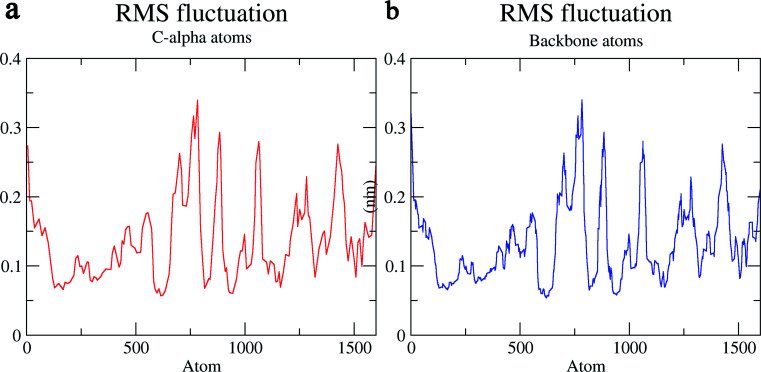
The structural behavior, molecular flexibility, and stability of MMP-9 docked with highly active compound 5 were assessed by 100 ns of MD simulation employing GROMACS 2018.1. RMSD is a measure of the average distance between the backbone residues or atoms of a protein. The RMSD of MMP-9 was calculated against the 5/5I12 complex; a graph was plotted using the three-dimensional Xmgrace plotting tool to compare the stability of the protein backbone and Cα atoms. The protein Cα and backbone residues showed minimal fluctuations before equilibration of the system and were found to be stable throughout the MD simulation study. However, the RMSD of Cα atoms remain stable throughout equilibration but showed minimal fluctuations from 36 to 59 ns (Fig. 7a). While the protein backbone exhibited significant fluctuations between 38 to 60 ns in the MD simulation study (Fig. 7b). RMSF was also calculated for the 5/5I12 complex, and the graph plotted using a three-dimensional Xmgrace plotting tool to compare the flexibility and stability of protein backbone and Cα atoms. The Cα atoms of the RMSF plot exhibited fluctuations at 0.31 and 0.34 nm of 520 and 700 atoms, respectively (Fig. 8a).
Fig. 7. RMSD (Å) of (a) C atoms (b) protein backbone of 5/5I12 complex.
Fig. 8. RMSF (Å) of (a) C atoms (b) protein backbone of 5/5I12 complex.
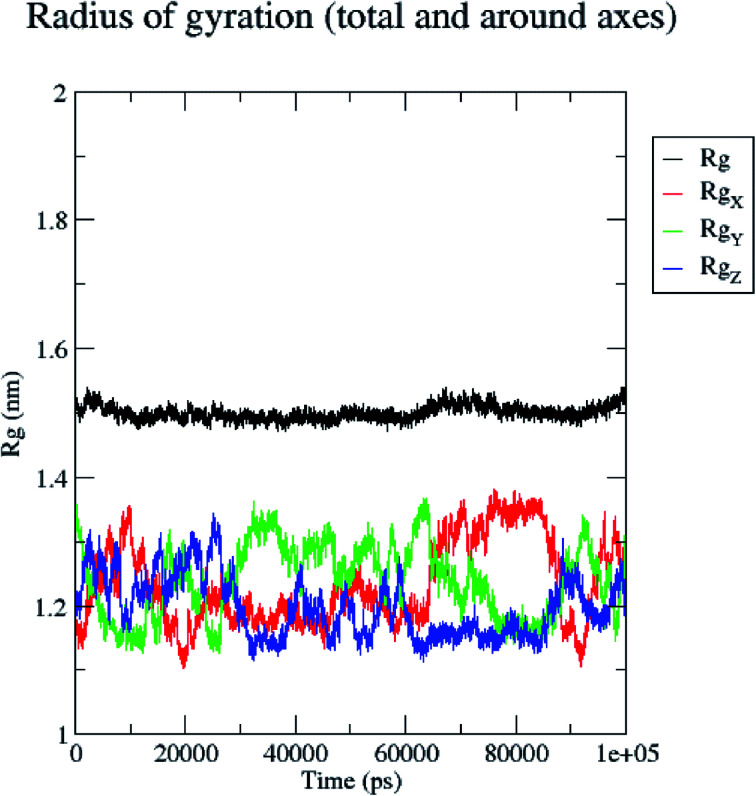
In contrast, the protein backbone showed higher fluctuation at 0.32 and 0.34 nm, which covered almost 500–750 atoms of a receptor (Fig. 8b). Overall, protein residual fluctuations in the 5/5I12 complex were found to be minimal. The radius of gyration (RG) is indicative of the compaction level in the protein structure. The result indicates the constant stability of the 5/5I12 complex throughout the MD simulation study (Fig. 9).
Fig. 9. Radius of gyration of the 5/5I12 complex during 100 ns MD simulation.
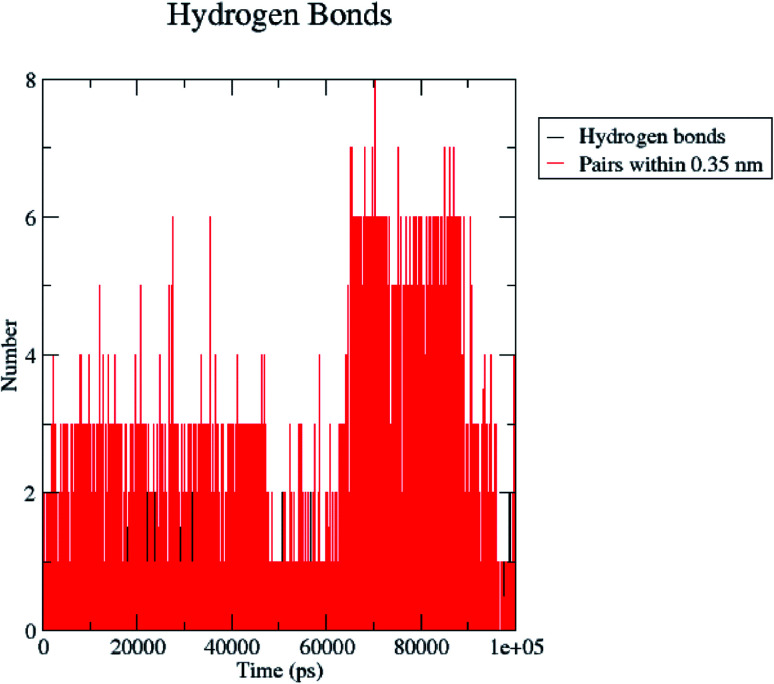
H bond formation/deformation depicts the number of hydrogen bonding interactions formed or broken during the MD simulation study. During 100 ns of study, hydrogen bond number was constant, indicating the molecular or structural stability of compound 5 with MMP-9 (PDB: 5I12). Almost six hydrogen bonds were found to be constant throughout the study. In contrast, extra two hydrogen bonds appeared from 60 to 75 ns (Fig. 10). The binding of the ligand with the protein residues is relatively stable, and electrostatic energy was found to be a key driving force for the binding stability of the 5/5I12 complex.
Fig. 10. Total number of hydrogen bonding interactions exhibited between compound 5 and 5I12 (MMP-9).
Further, the continuous contribution of hydrogen bonding interactions in the binding pose analysis indicates that active compound 5 possesses stable interaction with the MMP-9 protein. The 3D structure of the 5/5I12 complex displayed a key hydrogen bonding interaction with the residues Tyr179, Leu187, His190, Phe192, Pro193. In addition, compound 5 was also stabilized by forming a halogen bond with Leu187 (ESI, Fig. S4†). All these interacting residues exhibited a radius of gyration in the range of 0.16 to 0.28 nm indicating minimal fluctuations and greater stability throughout the MD simulation study (ESI, Fig. S5†).
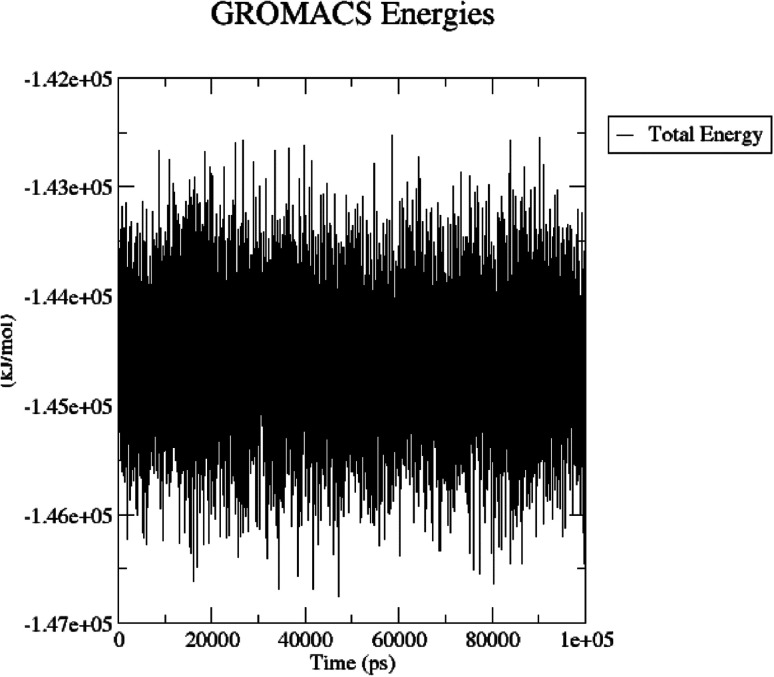
The total energy (potential, kinetic energies) was calculated. The graph was plotted using a three-dimensional Xmgrace plotting tool to know the stability of the 5/5I12 complex after the addition of water molecules and ions. The total energy of the complex should be persistent during the MD simulation study as it is a summation of both the potential and kinetic energy of the residues. Potential energy levels must be increasing or constant to exhibit structural stability. At the same time, the kinetic energy level represents the general confusion of protein structure. The total energy was found to be constant throughout the MD study (Fig. 11).
Fig. 11. Total energy of the 5/5I12 complex during the 100 ns MD simulation.
The 5/5I12 complex was snapshotted at every 20 ns intervals of 100 ns MD simulation trajectory and was superimposed to evaluate the binding stability of compound 5 (ESI, Fig. S6†). It showed that the compound 5 positions bound in MMP-9 are more confined and stable because of the binding pocket accessible volume, which further dictates that ligand interactions inside the catalytic pocket must be stronger and more specific to stabilize the system throughout the study.
Further, RMSD was calculated for conformations obtained through MD, pharmacophore, and docking poses. Similar orientation was observed with compound 5 after XP-docking and MD pose (ESI, Fig. S7†); conformations of compound 5 after MD pose and DDHRR_1 (ESI, Fig. S8†); conformations of compound 5 of XP-docking pose and DDHRR_1 (ESI, Fig. S9†).
MM-PBSA
MM-PBSA analysis allows us to segregate the total free binding energy into van der Waals, electrostatic and solute–solvent interactions, to get insight into the binding modes and the 5/5I12 complex association process. Binding calculation values were represented for every 10 ns intervals of 100 ns after attaining equilibrium. The binding free energy of the complex was found to be −93.698 ± 34.656 kcal mol−1. From Table 4, it is clear that van der Waals interactions (−103.870 ± 41.780 kcal mol−1) play a crucial role in the simulation, contributing significantly more to the total interaction energy than the other energies.
MM-PBSA analysis of compound 5/5I12 complex.
| van der Waal interactions (kcal mol−1) | Electrostatic energy (kcal mol−1) | Polar solvation energy (kcal mol−1) | Solvent accessible surface area energy (kcal mol−1) | Binding energy (kcal mol−1) |
|---|---|---|---|---|
| −103.870 ± 41.78 | −16.633 ± 9.308 | 36.499 ± 23.749 | 9.678 ± 4.00 | −93.698 ± 34.65 |
High-throughput virtual screening (HTVS)
The developed pharmacophore hypothesis DDHRR_1 was utilized as a query model to screen a library of molecules. The clustering analysis was performed using the Kelley index, dendrogram, and distance matrix. The Kelley penalty plot evaluates the balancing of the normalized spread of the ligand clusters generated at a specific level with the total number of clusters developed. The plot shows that all 20 clusters were equally distributed at the specified level (ESI, Fig. S10†). Dendrogram provided information about the 3000 virtual hits merging distance based on their clustering indices (ESI, Fig. S11†). Further, distance matrix or dissimilarity index among the clusters developed for 3000 virtual hits were calculated based on their order of clustering or ranking order (ESI, Fig. S12†). Docking was performed for the 3000 virtual hits against the MMP-9 enzyme (PDB: 5I12) in a standard precision mode. The top 10% of the molecules were selected for the redocking in XP mode based on their glide score and glide model. Further, binding free energy was calculated for these 300 molecules using the MM-GBSA approach. Five virtual hits VH1–VH5 are selected based on their glide score and binding free energy. The activity was predicted for these five virtual hits, and the results obtained are summarized in ESI, Table S11.† In addition, molecular properties were also calculated for virtual hits using the QikProp algorithm. The virtual hit VH1 (CACPD2011a-0002144822) is completely buried within the catalytic pocket of MMP-9, as evident by its glide score (−10.967 kcal mol−1), binding free energy (−68.65 kcal mol−1), and predicted activity (7.963). A hydrogen-bond interaction was formed between the –NH of benzimidazole nucleus and Tyr247, and the other was exhibited between the C O group of the VH1 and Glu227. Further, the molecule was stabilized by π–π interaction between the electron cloud of the aromatic nucleus present in the molecule and His226, His230, His236 (ESI, Fig. S13†). The virtual hit VH2 (CACPD2011a-0000241403) is also embedded within the catalytic pocket of MMP-9, which was supported by its glide score (−9.948 kcal mol−1), binding free energy (−62.97 kcal mol−1), and predicted activity (7.562). VH2 exhibited a single hydrogen bonding interaction with –NH of benzimidazole nucleus and Met247. In addition, VH2 was stabilized by forming a π–π interaction between the electron cloud of the aromatic nucleus present in the molecule and His226 residue (ESI, Fig. S14†).
Further, a 50 ns MD simulation was carried out for the complexes VH1/5I12 and VH2/5I12 to determine the stability of the complex. The RMSD and RMSF were calculated against the complexes (VH1/5I12 and VH2/5I12); graphs were plotted using the three-dimensional Xmgrace plotting tool to compare the stability of protein backbone and Cα atoms. The RMSD for the VH1/5I12 complex, Cα atoms, and the protein backbone atoms remain stable throughout equilibration but showed minimal fluctuations at 20 ns in the MD simulation study (ESI, Fig. S15†). The RMSF plot of complex VH1/5I12 revealed that Cα atoms and protein backbone atoms displayed fluctuations at 0.4 and 0.42 nm, respectively (ESI, Fig. S16†).
The RMSD for the VH2/5I12 complex, Cα atoms, and protein backbone atoms remain stable throughout equilibration but showed minimal fluctuations from 10 to 18 ns in the MD simulation study (ESI, Fig. S17†). The RMSF plot of the complex VH2/5I12 revealed that Cα atoms and protein backbone atoms displayed fluctuations at 0.42 and 0.44 nm, respectively (ESI, Fig. S18†).
Conclusion
In the current study, 8-hydroxyquinoline, caffeic acid amides, anthranilic acid, and amidine-based thiazole scaffolds were subjected to computer-aided drug screening for the potential MMP-9 inhibitors. The generated DDHRR_1 model exhibited cross-validation of coefficient (Q2 = 0.8170) and high-coefficient of determination (R2 = 0.9076) reflecting good predictive power of the models. Further, contour plot visualization exposed a vital pharmacophoric site necessary for MMP-9 inhibition. Molecular docking analysis exposed the hydrogen-bond and hydrophobic interactions with key amino acid residues of enzyme. A 100 ns of MD simulation trajectory of complex 5/5I12 possess greater stability and flexibility as evident from the minimal fluctuations in RMSD and RMSF. The pharmacophore hypotheses and 3D-QSAR predictions retrieved hits with diverse scaffolds and good ADME properties. Virtual hits exhibited significant interactions and binding affinity with the active residues. The MD simulation of 50 ns was carried out for the top-ranked hits (VH1 and VH2) against the MMP-9 enzyme and indicated the significant stability of the binding poses of complexes.
Author contributions
Bharat Kumar Reddy Sanapalli: conceptualization, data curation, writing – original draft preparation, writing – review & editing. Vidyasrilekha Yele: methodology, investigation, visualization, writing – reviewing and editing. Srikanth Jupudi: software, data curation and reviewing. Veera Venkata Satyanarayana Reddy Karri: supervision and validation.
Conflicts of interest
The authors declare that there are no conflicts of interest in this study. The authors alone are responsible for the content and writing of the paper.
Supplementary Material
Acknowledgments
The authors thank Schrödinger for their support in providing the software license for one month. The authors also like to thank the JSS Academy of Higher Education & Research, India, for providing financial support to publish open access.
Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03891e
References
- Yabluchanskiy A. Ma Y. Iyer R. P. Hall M. E. Lindsey M. L. Physiol. J. 2013;28:391–403. doi: 10.1152/physiol.00029.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinhard S. M. Razak K. Ethell I. M. Front. Cell. Neurosci. 2015;9:280. doi: 10.3389/fncel.2015.00280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagase H. Woessner J. F. J. Biol. Chem. 1999;274:21491–21494. doi: 10.1074/jbc.274.31.21491. [DOI] [PubMed] [Google Scholar]
- Mondal S. Adhikari N. Banerjee S. Amin S. A. Jha S. A. T. Eur. J. Med. Chem. 2020;194:112260. doi: 10.1016/j.ejmech.2020.112260. [DOI] [PubMed] [Google Scholar]
- Shi Z. H. Li N. G. Shi Q. P. Tang H. Tang Y. P. Li W. Drug Dev. Res. 2012;73:343–351. doi: 10.1002/ddr.21038. [DOI] [Google Scholar]
- Jian H. Zhao Y. Liu B. Lu S. Tumor Biol. 2014;35:11051–11056. doi: 10.1007/s13277-014-2409-8. [DOI] [PubMed] [Google Scholar]
- Huang H. Sensors. 2018;18:3249. doi: 10.3390/s18103249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y. Waqar A. B. Nishijima K. Ning B. Kitajima S. Matsuhisa F. J. Cell. Mol. Med. 2020;24:4261–4274. doi: 10.1111/jcmm.15087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollmann M. Pinno K. Ehnold L. Märtens N. Märtson A. Pap T. Osteoarthritis Cartilage. 2021;29:280–289. doi: 10.1016/j.joca.2020.10.009. [DOI] [PubMed] [Google Scholar]
- Hassanzadeh-Makoui R. Razi B. Aslani S. Imani D. Tabaee S. S. BMC Cardiovasc. Disord. 2020;20:1–15. doi: 10.1186/s12872-019-01312-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C. Li Q. Yang H. Gao C. Du Q. Zhang C. J. Cell. Physiol. 2020;235:8283–8292. doi: 10.1002/jcp.29485. [DOI] [PubMed] [Google Scholar]
- Duan X. J. Zhang X. Li L. R. Zhang J. Y. Chen Y. P. Exp. Lung Res. 2020;46:321–331. doi: 10.1080/01902148.2020.1778816. [DOI] [PubMed] [Google Scholar]
- Zou F. Zhang J. Xiang G. Jiao H. Gao H. Can Respir. J. 2019;2019:1–10. doi: 10.1155/2019/9260495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu D. Liu F. Meng M. Zhang L. Gordon M. L. Wang Y. Ann. Clin. Transl. Neurol. 2020;7:1681–1691. doi: 10.1002/acn3.51155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X. Zhang L. Yao X. Hu J. Yu L. Jia H. PLoS One. 2013;8:e73777. doi: 10.1371/journal.pone.0073777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jawahar N. Meyyanathan S. Int. J. Res. Health Allied Sci. 2012;1:217. doi: 10.4103/2278-344X.107832. [DOI] [Google Scholar]
- Bode W. Fernandez-Catalan C. Tschesche H. Grams F. Nagase H. Maskos K. Cell. Mol. Life Sci. 1999;55:639–652. doi: 10.1007/s000180050320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovejoy B. Welch A. R. Carr S. Luong C. Broka C. Hendricks R. T. Nat. Struct. Biol. 1999;6:217–221. doi: 10.1038/6657. [DOI] [PubMed] [Google Scholar]
- Rowsell S. Hawtin P. Minshull C. A. Jepson H. Brockbank S. M. Barratt D. G. J. Mol. Biol. 2002;319:173–181. doi: 10.1016/S0022-2836(02)00262-0. [DOI] [PubMed] [Google Scholar]
- Nuti E. Cuffaro D. D'Andrea F. Rosalia L. Tepshi L. Fabbi M. ChemMedChem. 2016;11:1626–1637. doi: 10.1002/cmdc.201600235. [DOI] [PubMed] [Google Scholar]
- Chen C. Yang X. Fang H. Hou X. Eur. J. Med. Chem. 2019;181:111563. doi: 10.1016/j.ejmech.2019.111563. [DOI] [PubMed] [Google Scholar]
- Claramunt R. M. Bouissane L. Cabildo M. P. Cornago M. Elguero J. Radziwon A. Bioorg. Med. Chem. 2009;17:1290–1296. doi: 10.1016/j.bmc.2008.12.029. [DOI] [PubMed] [Google Scholar]
- Incerti M. Crascì L. Vicini P. Aki E. Yalcin I. Ertan-Bolelli T. Molecules. 2018;23:415. doi: 10.3390/molecules23020415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangiatordi G. F. Guzzo T. Rossano E. C. Trisciuzzi D. Alberga D. Fasciglione G. ChemMedChem. 2018;13:1343–1352. doi: 10.1002/cmdc.201800237. [DOI] [PubMed] [Google Scholar]
- Mao J. Zhang H. Wang X. Gao J. Tang J. Zhang J. BioSci. Trends. 2020;14:192–199. doi: 10.5582/bst.2020.01051. [DOI] [PubMed] [Google Scholar]
- Nicolotti O. Catto M. Giangreco I. Barletta M. Leonetti F. Stefanachi A. Eur. J. Med. Chem. 2012;58:368–376. doi: 10.1016/j.ejmech.2012.09.036. [DOI] [PubMed] [Google Scholar]
- Nuti E. Casalini F. Santamaria S. Gabelloni P. Bendinelli S. Da Pozzo E. Eur. J. Med. Chem. 2011;46:2617–2629. doi: 10.1016/j.ejmech.2011.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omar A. M. Bajorath J. Ihmaid S. Mohamed H. M. El-Agrody A. M. Mora A. Bioorg. Chem. 2020;101:103992. doi: 10.1016/j.bioorg.2020.103992. [DOI] [PubMed] [Google Scholar]
- Levin J. I. Du M. T. DiJoseph J. F. Killar L. M. Sung A. Walter T. Bioorg. Med. Chem. Lett. 2001;11:235–238. doi: 10.1016/S0960-894X(00)00642-9. [DOI] [PubMed] [Google Scholar]
- Levin J. Chen J. Du M. Hogan M. Kincaid S. Nelson F. Bioorg. Med. Chem. Lett. 2001;11:2189–2192. doi: 10.1016/S0960-894X(01)00419-X. [DOI] [PubMed] [Google Scholar]
- Levin J. Chen J. Du M. Nelson F. Wehr T. DiJoseph J. Bioorg. Med. Chem. Lett. 2001;11:2975–2978. doi: 10.1016/S0960-894X(01)00601-1. [DOI] [PubMed] [Google Scholar]
- Jana S. Singh S. K. J. Biomol. Struct. Dyn. 2019;37:944–965. doi: 10.1080/07391102.2018.1444510. [DOI] [PubMed] [Google Scholar]
- Rathee D. Lather V. Dureja H. Porto. Biomed. J. 2018;3:1–9. doi: 10.1016/j.pbj.0000000000000001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharadwaj S. Lee K. E. Dwivedi V. D. Yadava U. Kang S. G. J. Cell. Biochem. 2019;120:19064–19075. doi: 10.1002/jcb.29229. [DOI] [PubMed] [Google Scholar]
- Roos K. Wu C. Damm W. Reboul M. Stevenson J. M. Lu C. J. Chem. Theory Comput. 2019;15:1863–1874. doi: 10.1021/acs.jctc.8b01026. [DOI] [PubMed] [Google Scholar]
- Golbraikh A. Tropsha A. Mol. Diversity. 2000;5:231–243. doi: 10.1023/A:1021372108686. [DOI] [PubMed] [Google Scholar]
- Tropsha A. Gramatica P. Gombar V. K. QSAR Comb. Sci. 2003;22:69–77. doi: 10.1002/qsar.200390007. [DOI] [Google Scholar]
- Yele V. Azam M. A. Jupudi S. Chem. Pap. 2020;74:4567–4580. doi: 10.1007/s11696-020-01274-3. [DOI] [Google Scholar]
- Roy K. Ambure P. Aher R. B. Chemom. Intell. Lab. Syst. 2017;162:44–54. doi: 10.1016/j.chemolab.2017.01.010. [DOI] [Google Scholar]
- Zhao M. Wang L. Zheng L. Zhang M. Qiu C. Zhang Y. BioMed Res. Int. 2017;2017:1–11. doi: 10.1155/2017/4649191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidhu J. S. Sharma S. Singh A. Garg N. Kaur N. Singh N. Anal. Methods. 2019;11:4190–4196. doi: 10.1039/C9AY01464K. [DOI] [Google Scholar]
- Sastry G. M. Adzhigirey M. Day T. Annabhimoju R. Sherman W. J. Comput.-Aided Mol. Des. 2013;27:221–234. doi: 10.1007/s10822-013-9644-8. [DOI] [PubMed] [Google Scholar]
- Jacobson M. P. Pincus D. L. Rapp C. S. Day T. J. Honig B. Shaw D. E. Proteins. 2004;55:351–367. doi: 10.1002/prot.10613. [DOI] [PubMed] [Google Scholar]
- Friesner R. A. Murphy R. B. Repasky M. P. Frye L. L. Greenwood R. Halgren T. A. J. Med. Chem. 2006;49:6177–6196. doi: 10.1021/jm051256o. [DOI] [PubMed] [Google Scholar]
- Abraham M. J. Murtola T. Schulz R. Páll S. Smith J. C. Hess B. SoftwareX. 2015;1:19–25. doi: 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Schüttelkopf A. W. Van Aalten D. M. Acta Crystallogr., Sect. D: Struct. Biol. 2004;60:1355–1363. doi: 10.1107/S0907444904011679. [DOI] [PubMed] [Google Scholar]
- Duan L. Guo X. Cong Y. Feng G. Li Y. Zhang J. Z. Front. Chem. 2019;7:1–18. doi: 10.3389/fchem.2019.00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen H. J. Postma Jv. van Gunsteren W. F. DiNola A. Haak J. R. J. Chem. Phys. 1984;81:3684–3690. doi: 10.1063/1.448118. [DOI] [Google Scholar]
- Kollman P. Massova I. Reyes C. Kuhn B. Huo S. Chong L. Donin O. Cieplak P. Srinivasan J. Case D. A. Cheatham R. Acc. Chem. Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Luo R. David L. Gilson M. K. J. Comput. Chem. 2002;23:1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- Kalva S. Vinod D. Saleena L. M. Med. Chem. Res. 2013;22:5303–5313. doi: 10.1007/s00044-013-0479-6. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.