Abstract
This paper provides a comprehensive overview of the applications of game theory in deep learning. Today, deep learning is a fast-evolving area for research in the domain of artificial intelligence. Alternatively, game theory has been showing its multi-dimensional applications in the last few decades. The application of game theory to deep learning includes another dimension in research. Game theory helps to model or solve various deep learning-based problems. Existing research contributions demonstrate that game theory is a potential approach to improve results in deep learning models. The design of deep learning models often involves a game-theoretic approach. Most of the classification problems which popularly employ a deep learning approach can be seen as a Stackelberg game. Generative Adversarial Network (GAN) is a deep learning architecture that has gained popularity in solving complex computer vision problems. GANs have their roots in game theory. The training of the generators and discriminators in GANs is essentially a two-player zero-sum game that allows the model to learn complex functions. This paper will give researchers an extensive account of significant contributions which have taken place in deep learning using game-theoretic concepts thus, giving a clear insight, challenges, and future directions. The current study also details various real-time applications of existing literature, valuable datasets in the field, and the popularity of this research area in recent years of publications and citations.
Keywords: Artificial neural network, Deep learning, GAN, Game theory, Artificial intelligence, CNN, Reinforcement learning
Introduction
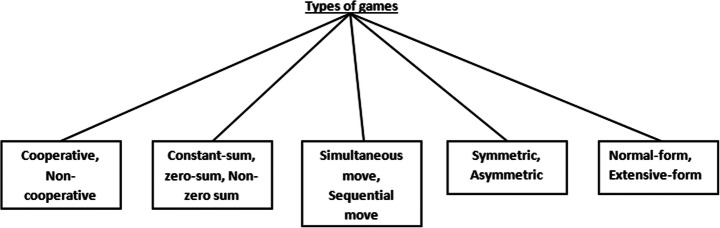
Game theory is an essential field for research, and it helps to choose the suitable strategy of the players in a game. It has several applications in various domains. Game theory has significant applications in technology, especially concerning computer science, electronics, aerospace engineering, etc. [90, 91, 96, 99, 100]. Different types of games are briefed in Fig. 1. Alternatively, Deep Learning is the study of various learning algorithms that uses multiple layers of non-linear processing units. The output of the previous layer is taken as input by each successive layer. Deep learning algorithms are primarily classified into three categories, e.g., supervised, semi-supervised and unsupervised. Deep Learning algorithms implement higher-level features that are extracted from lower-level features. The depth in neural networks plays an essential part in the outcome of the model. The framework of the neural networks can represent dynamic environments, and similarly, dynamic environments can further be presented as games [37, 72].
Fig. 1.
Types of games
Artificial intelligence has adapted the game theory to solve or model various real-time problems, and it is observed that the performance is improved while applying game theory [43, 76, 124, 148]. This paper establishes the connection of deep learning algorithms with game theory. The applications of evolutionary computing and swarm intelligence are discussed in [20]. This paper mainly focuses on applications of game theory to solve GAN models. GAN has received a tremendous response from several research communities because of its complex problem-solving abilities and performance improvement [19, 36, 130].
The multilayer neural network comprises any number of unit neurons and may determine multimodal output functions. The multimodality nature of the output function creates hardships to optimize deep neural network models. Strategic Deep Learning is a defying game task [62, 84, 136, 141, 151]. Table 1 shows research articles in game theory, deep learning, and their collaborative research as per the records obtained from various databases. In a nutshell, the contribution of the paper is as follows:
This paper reviews several significant contributions to applying game theory in deep learning models and achieving performance improvement.
Paper considers a variety of evolutionary algorithms from game-theoretic perspectives.
The paper suggests how the bonding between game theory and deep learning can be strengthened.
Table 1.
A statistics of the number of research articles on game theory, neural/network/deep learning, and applications of game theory in deep learning as per the records of various databases (Data obtained on 20th June 2020)
| Sr No | Database | Total Results | Game theory (From first 25 results) | Neural Network/Deep learning (From the first 25 results) | Both Game theory and Deep Learning (From first 25 results) | Total Citations (From first 25 results) |
|---|---|---|---|---|---|---|
| 1 | Google Scholar | 2270 | 23 | 13 | 8 | 1305 |
| 2 | Sage Journal Database | 8 | 0 | 7 | 0 | (Exact citation metrics is not available) |
| 3 | ProQuest/ABI/Inform (Books, Journal Article, video, Dissertations and thesis/Working Paper) | 18 | 4 | 12 | 0 | 31 |
| 4 | EBSCO | 31, 625 | 7 | 25 | 5 | 1228 |
| 5 | JSTOR | 5 | 0 | 2 | 0 | 23 |
| 6 | ScienceDirect | 51 | 3 | 12 | 2 | 127 |
| 7 | Citeseerx | 1,16,135 | 18 | 21 | 16 | 1443 |
Indexing of this paper is as follows: basics and background of game theory and deep learning are discussed in section 2; game theory in deep learning and artificial intelligence is discussed in section 3; after that, game theory in reinforcement learning (section 4) is followed by game theory in GAN (section 5); section 6 discusses implementation environment of the current study; section 7 outlined challenges and future direction and section 8 summarizes the discussion.
Basics and background
This section discusses fundamentals and rudimentary concepts that are directly or indirectly applied in the existing literature. This section is a platform for the readers to enter into the field and helps readers understand advancements in the field. The objective of this section is to formally introduce important terms in both areas to the readers before elaborating their connections in subsequent sections. This paper discusses various applications of game theory in the domain of deep learning. Thus, this section initially introduces the game theory, followed by an introduction to deep learning architectures and techniques. In the subsequent sections, the scope of the paper is narrowed down, and specific areas of game theory and deep learning are discussed in detail. Section 2.1 explains various game-theoretic concepts, and section 2.2 discusses multiple deep learning architectures and techniques.
Game theory overview
Game theory is a significant area of applied mathematics to model various real-world complex scenarios as games. Thus, game theory is broadly used in multiple fields where strategic interaction among the players plays a vital role.
Game
A game can be defined as a competitive or cooperative interaction among the objects or players [89]. The nature of interactions among players determines the behavior of games. There are several types of games in the game theory: cooperative and non-cooperative, zero and non-zero, sequential and simultaneous, normal-form and extensive-form, finite and infinite, perfect-information and imperfect-information combinatorial, Bayesian, stochastic, etc. In this paper, cooperative and non-cooperative, zero and non-zero, normal-form and extensive-form, perfect-information and imperfect-information, finite and infinite, and stochastic games are addressed, and the games are played between single or multiple players. The basic concepts of the games mentioned above are as follows:
Cooperative and non-cooperative games: The players cooperatively choose their strategies to maximize the overall payoff [23]. Alternatively, the players choose their strategies to maximize their self-payoffs for non-cooperative games [93].
Zero and non-zero games: In zero-games, the value of a game is zero. On the other hand, it can be defined as the summation of payoffs for adversary players for any set of actions must be zero. Alternatively, the value of a non-zero game is non-zero [126].
Normal-form and extensive-form games: Normal-form games are represented by matrices that include possible strategies for players in the topmost row and leftmost column. The payoffs of players are represented as matrix elements separated by commas. Alternatively, extensive-form games are described as trees, where internal nodes represent players’ turns, edges represent players’ actions, and external nodes represent players’ outcomes for a particular set of moves. Figure 2a and b illustrate examples of the normal-form and extensive-form game representations [79].
Perfect-information and imperfect-information games: Perfect information games can be defined as a game where players have the same information. In other words, players are aware of all actions that have occurred in the past. In imperfect information games, players choose their moves simultaneously. So, they are not perfectly informed about the moves of opponents [88].
Finite and infinite games: Finite games/finite strategy games are the games with finite strategies. Alternatively, infinite games are games with infinite strategies [12].
Stochastic games: The game is played in a sequence of time units/stages. In each stage, games enter into a new state. Payoffs of players depend on the present state and chosen action [117].
Fig. 2.
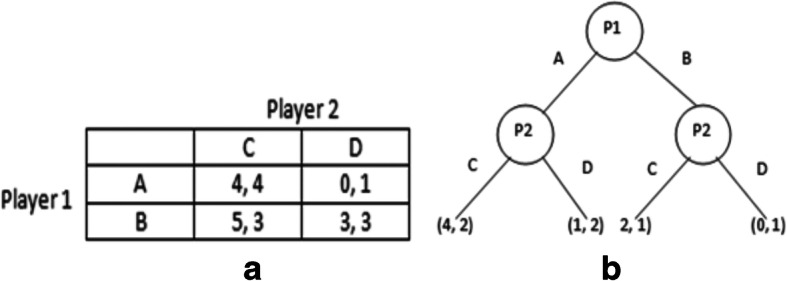
Game representation (a) Normal-form (b) Extensive-form
Players
Players are the critical components of a game. They participate in a game intending to achieve certain goals. The nature of interaction among the players can be primarily classified into two types: cooperative and non-cooperative. Two or more than two players can take part in a game. The players always aim to maximize the overall payoff of the whole group.
Strategies
In a game, strategies are a sequence of actions chosen by the players. The strategies can also be fundamentally classified into two types, cooperative and non-cooperative, based on players’ goals. The paramount of a game is to determine suitable strategies for players.
Payoffs
The payoffs of players represent the rewards or penalties for choosing their respective strategies. In cooperative games, players aim to improve the overall payoffs of a group. In contrast, the players aim to maximize their self-payoff (without considering the overall payoff of the group) in non-cooperative games. The game planners formulate the payoff functions. Let StI represents all possible strategies for player I. If there are m number of players, then, possible combinations of strategies for player I is St1 × St2…Stm. So, the payoff function can be represented as util(St1 × St2…Stm).
Best response
Best response strategies denote the most favorable outcomes for a player considering all the strategies for opponents. The players in a game usually prefer to choose the best response strategies. NE is determined based on the best response strategies for players. Let best response strategy for player I be represented asbrI(.). Thus, considering a set of opponent’s strategiesx−I, brI(x−I) denotes player I’s best response to x−I.
Nash equilibrium
It is a stable state where players cannot earn more profits by unilaterally deviating from their strategies. Players can have a pure or mixed strategy equilibrium in a game.
Let a game with m players be denoted by (St, util), StI represents strategies for player I, St = St1 × … × Stm represents strategy combinations andutil(x) = (util1(x), …, utilm(x)) represents the utility or payoff function, wherexϵSt. xIandx−I are the strategy combination for player I and others except for player I, respectively. When each player Iϵ1, …, mcomputes the strategy xI from the strategy-profilex = x1, …, xm, then, the player I gets a payoffutilI(x). A strategy profile x∗ϵSt is a NE if the following condition is satisfied
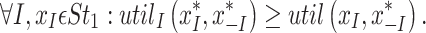 |
Mixed equilibrium is computed for those scenarios, where the players mix their strategies with uncertainties, and the mixed equilibrium is computed based on the expected payoffs of respective players [92].
Shapley function
In cooperative games, the reward of each player is computed by a function called Shapleyfunction. The Shapley value 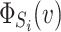 for each player Si, 1 ≤ i ≤ N is computed based on its individual contribution to a coalition, where N represents the player count. The Shapley value [116] for each player is calculated by the equation given below.
for each player Si, 1 ≤ i ≤ N is computed based on its individual contribution to a coalition, where N represents the player count. The Shapley value [116] for each player is calculated by the equation given below.
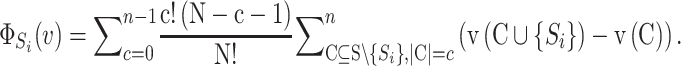 |
In the above equation, S represents a set of N players (|S| = N), C denotes a group (|C| = c) and C is a subset of S\{Si}, 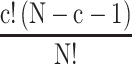 denotes the uncertainty in a permutation, the contributors of C are ahead of the individual player Si and (v(C ∪ {Si}) − v(C)) denotes the individual contribution of a player Si in the group C, where the rewards of all groups are initially determined. In this way, the Shapley function
denotes the uncertainty in a permutation, the contributors of C are ahead of the individual player Si and (v(C ∪ {Si}) − v(C)) denotes the individual contribution of a player Si in the group C, where the rewards of all groups are initially determined. In this way, the Shapley function 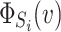 yields the Shapley value of a player Si for a particular group. A player having the highest Shapley value is the most significant contributor in a group.
yields the Shapley value of a player Si for a particular group. A player having the highest Shapley value is the most significant contributor in a group.
Minimax theorem
In 1928, John Von Neumann introduced the Minimax theorem, which opens the door for conventional game theory. For a two-player, zero-sum, simultaneous move finite game, there must be a value and exists an equilibrium point for both the players [126]. The equilibrium point can be determined by applying pure or mixed strategies by either one or both the players. Let’s assume that x and y are strategies of two players and v is the value of the game. Then, the minimax theorem can be formulated as
Deep learning overview
Deep learning is an advanced part of machine learning algorithms based on artificial neural networks and various learning methods, i.e., supervised, unsupervised, and reinforcement. There are well-known deep learning architecture and techniques. Deep learning models use multiple layers in an artificial neural network to extract significant characteristics from the unprocessed data. Graphics Processing Units (GPUs) are required to perform high-power computation on complex deep learning architectures. Deep learning has immense applications in multi-dimensional fields such as speech recognition, computer vision, audio recognition, natural language processing, medical image analysis, games, etc.
Deep learning architecture
In recent times, deep learning has received tremendous responses from various fields. Robust deep learning architectures bring significant improvement in the performance of multiple models. They can solve or model various complex problems because of their robustness. In most cases, it is observed that deep learning architectures outperform other existing models. The most popular deep learning architectures are the convolutional neural network, recurrent neural network, generative adversarial network, deep belief network, autoencoder, residual neural network, etc. This paper primarily studies generative adversarial neural networks because of their architecture, where game-theoretic techniques can be easily applied. In the future, we may explore possibilities of applications of game theory in other deep learning architectures.
Convolutional neural network
The convolutional neural network, a significant type of deep learning architecture, is best known for its vast capabilities when analyzing visual imagery. They comprise regularized versions of complicated multilayer perceptrons (usually fully connected networks). A CNN has three layers, input, hidden, and output. The hidden layers are mainly convolutional layers that convolve with multiplication or other product, and the activation function is commonly a RELU layer. CNNs were inspired by the works [32, 59, 60].
Recurrent neural network
Recurrent Neural Network is a category of advanced artificial neural networks. A directed graph with a temporal sequence is what we get when there is a connection between the nodes. Temporal dynamic behavior is exhibited in RNN. Using internal states, RNNs have capabilities to process inconsistent range sequences of inputs. They are powerful enough because having a distributed hidden state makes them capable of storing huge amounts of information regarding the past and non-linear dynamics, acknowledging them to revise their hidden state in complex ways [39, 111, 146].
Long Short-Term Memory, applied in deep learning, belongs to the family of recurrent neural networks. Its specialty lies in the fact that along with feed-forward neural networks, it has feedback connections too. A general LSTM architecture constitutes a cell, an input gate, an output gate, and a front gate. The utility of a cell is to store values over irregular periods, and all gates examine the flow of data entering into and exiting out of the cell. LSTM networks are best applicable in categorizing, processing, and predicting based on time series data [15, 54].
Generative adversarial network
Generative adversarial network (GAN), a type of deep learning architecture, was invented in 2014 by Ian Goodfellow [36]. Here, two neural networks challenge amongst themselves in a game (initially given a training set). The theory of GAN is to train images that can generate new images that look accurate to human eyes. GANs were originally modeled for unsupervised learning, but they are broadly used in reinforcement learning, semi-supervised learning, and fully supervised learning.
GAN layered architecture is represented in Fig. 3. Let’s introduce the variables and parameters related to the GAN model
- D
Discriminator
- G
Generator
- θd
Parameters of the discriminator
- θg
Parameters of generator
- Pz(z)
Input noise distribution
- Pdata(x)
Original data distribution
- Pg(x)
Generated distribution
Fig. 3.
The layered architecture of GAN
The final loss function for the discriminator can be written as
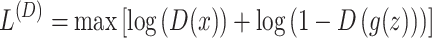 |
Alternatively, the generator is competing with the discriminator. The final loss function for the generator can be written as
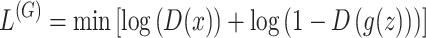 |
Both the equations can be combined and rewritten as
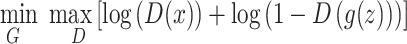 |
The above equation represents a single data point. For an entire dataset, we can write the equation as follows:
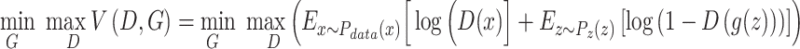 |
Deep belief networks
A deep belief network, a type of deep learning architecture, is a probabilistic generative graphical model. They are constructed from several layers of stochastic, latent variables with binary values called hidden layers or feature identifiers. The two compelling features of deep neural networks are:
A sequential layer-wise, efficient method for learning the top to bottom, generative weights capable of determining how variables on a layer depend upon the variables on its top layer
After learning, values are determined for latent variables in each layer, resulting in the single, bottom-up pass. It starts with a vector of selected data in the bottom layer. It exploits the weights in the opposite direction [48–50].
Autoencoder
Autoencoder, a distinctive category of artificial neural network utilized in learning efficient data coding through unsupervised techniques. Autoencoders target to learn an encoding for a set of given data and to reduce dimensions in data by training the given network to ignore “noise.” They can probably encode a provided input to represent smaller dimensions, being a data-compression model. Later, decoders can then reconstruct the input back from the encoded version [125, 147].
Residual neural network
Residual neural networks, abbreviated as ResNet, are artificial neural networks of a particular type inspired by the pyramidal cells of the animal cerebral cortex. Residual neural networks perform this by applying skip connections or shortcuts to jump through a few layers. ResNet models are achieved using double/triple layer skips consisting of nonlinearities (ReLU) and batch normalization in between [46]. An extra new weight matrix may be used to learn the skip weights. Such architectures are known as HighwayNets [121]. Architecture with several parallel skips is termed as DenseNets [57].
Radial basis function networks (RBFNs)
“The RBF network model is motivated by the locally tuned response observed in biologic neurons. Neurons with a locally tuned response characteristic can be found in several parts of the nervous system, such as cells in the auditory system that are selective to small bands of frequencies [114]”.
Multilayer Perceptrons (MLPs)
“MLPs belong to the class of feedforward neural networks with multiple layers of perceptrons that have activation functions. MLPs consist of an input layer and an output layer that is fully connected. They have the same number of input and output layers but may have multiple hidden layers and can be used to build speech recognition, image recognition, and machine-translation software [8].”
Self-organizing maps (SOMs)
“The SOM algorithm distinguishes two stages: the competitive stage and the cooperative stage. In the first stage, the best matching neuron is selected. In the second stage, neuron weights are not modified independently but as topologically-related subsets on which similar kinds of weight updates are performed [66].”
Deep learning techniques
Dropout
Dropout is adapted as a technique to overcome overfitting problems in a neural network. It addresses both issues – training and testing computations. Effectively, it allows the training of several neural networks without any significant computational overhead. Also, it gives an efficient approximate way of combining exponentially many different neural networks. In the training phase, dropping out refers to dropping out units(neurons) of a certain set of randomly chosen neurons. The dropped out units are not further considered during a forward and backward pass. Temporarily removes a node and all its incoming/outgoing connections, resulting in a thinned network [49, 50].
Rectified linear unit
ReLU is an activation function broadly used in various deep learning architectures. It is a non-linear activation function used for both types of networks, i.e., multiple-layer neural networks and deep neural networks. The function for any negative input returns zero. Alternatively, x is returned by the function for any positive input x. So, the simplified form of the function is f(x) = max(0, x).
In recent times, a sigmoid and hyperbolic tangent is replaced by the ReLU function. The main reason for the popularity of the ReLU function is its ability to make the training speed of deep neural networks faster than other conventional activation functions. A significant feature of ReLU is the derivative of this function is 1 for positive input. Deep neural networks can save additional time for calculating error terms due to a constant during the training phase. The extensive use of ReLU is shown in [34].
Stochastic gradient descent
Stochastic gradient descent is one of the powerful algorithms used in several machine learning and deep learning models. It is the basis of neural networks. It is an essential iterative algorithm. The functionalities of the gradient descent algorithm are as follows: it starts from an arbitrary point on a function. It moves down its slope in several steps/iterations until it reaches the minimum point of the given function. The algorithm is modified by including a random probability, called Stochastic Gradient Descent. In this algorithm, a set of samples is randomly chosen from the whole data set in each iteration. If we consider a large dataset, the programmer may require using many samples in each iteration while using the Gradient Descent algorithm. The task needs to be performed for each iteration until the minima are found, which is the main challenge in the Gradient Descent algorithm. Computational complexity is a significant concern in this algorithm. Stochastic Gradient Descent is introduced as a solution to this problem. SGD reduces the sample size. It takes only a single sample to perform the task for each iteration. Therefore, the sample is randomly mixed and chosen for completing the task for the iteration. The backbone of the SGD is to consider the gradient of the cost function of a single sample for each iteration. Applications of the Gradient Descent method are addressed in [26, 65].
Batch normalization
Batch normalization is an essential technique in artificial neural networks. The advantages of the method are improvement in speed, stability, and performance of neural networks. The input layer can be normalized by scaling and adjusting the activation functions. It is a technique by which the inputs for each layer are normalized to deal with the internal covariate, shift problem, i.e., the problem appears in the intermediate layers because, during training, the distribution of the activation functions is constantly changing. This change slows down the training process because each layer needs to learn a new distribution of activation functions in each training step. This method includes: calculating the variance and mean of the layer inputs, normalizing the layer inputs with the help of batch statistics, scaling, and shifting to find the layer’s output [61].
Application of game theory in deep learning and artificial intelligence
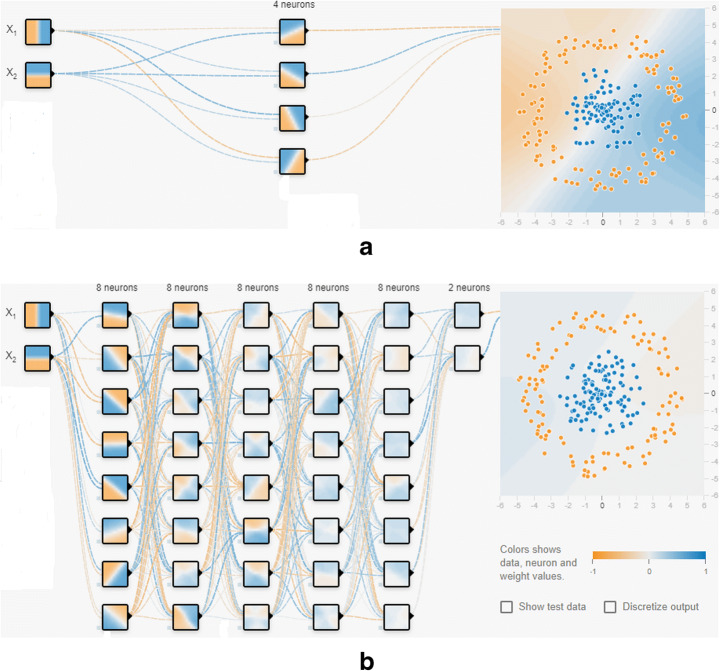
This section addresses some contributions in which game models solve deep learning and artificial intelligence problems. Figure 4 depicts the basic architectures of a simple neural network and deep learning neural network.
Fig. 4.
(a) Simple Neural Network (b) Deep Learning Neural Network
The authors in [112] address a new approach by which game-theoretic techniques can model individual neurons. The authors show that different strategic game-theoretic approaches can be applied to model paired neuron systems. A learning algorithm is developed depending on game theory for neural learning. Artificial neural network has proved its significance in multi-dimensional domains. Selecting an appropriate network is challenging to solve a problem [62, 141, 151]. The authors in [122] show that game-theoretic concepts like the Shapley value help to differentiate significantly from unnecessary elements of an artificial neural network. A cooperative game is designed from a neural network where neurons that form different groups and their contributions to the game are determined with the help of the Shapley value. The experiments prove that the Shapley value concept is better than other heuristics approaches to assess the contribution of neurons.
There are various GAN algorithms. The first is fully connected neural networks for both the generator and discriminator. The second is convolutional GAN, as going from fully connected to convolutional neural networks is a natural extension. The third neural network is conditional GAN. It extends the 2D GAN framework to the conditional setting by making both the generator and the discriminator networks class-conditional [142].
Alternatively, a max-min problem is formulated for adversarial learning with multiplayer stochastic games and two-player sequential games above deep learning networks [17]. The experimental results forecast the efficacy of the used adversarial algorithm. The algorithm can manipulate adversarial features that affect testing results in deep learning models. The work introduces a secure learner who is adaptive to the antagonistic attacks on deep learning. The paper claims that the given framework is more robust than a traditional convolutional neural network (CNN) and a generative adversarial network under adversarial attacks. This paper also highlights the impacts on adversarial payoff functions over randomized strategies while the rules of the games are changed. The offensive scenarios over such strategy spaces find multiplayer games over varied strategies. A reduction of supervised learning to the game is explored in [113]. For convex one-layer problems, an equivalence between Nash equilibria in a simple game and global minimizers of the training problem is shown. It is also demonstrated how the game can be extended to acyclic neural networks using differentiable convex gates. The work in [86] presents a model that integrates the concepts from the field of deep learning and artificial life to reflect their potentiality in various scenarios. The model shows the potentiality of neural networks to simulate population dynamics. The model also shows the applications of evolutionary game theory result in the behavior of the networks.
Modeling humans’ ability to depict the mental state transitions of others is a challenging task for the research community. The authors of [106] train a machine to construct such models. A Theory of Mind neural network (ToMnet) is designed by meta-learning that builds handler models by observing their behavior. The ToMnet model is applied to agents in simple grid environments. This system can autonomously learn modeling other agents, which is a significant contribution to designing multi-agent AI systems. It can be applied to develop technologies for machine-human communication and advance the growth of interpretable artificial intelligence. For large-scale perfect-information games, artificial intelligence is superior to human-level intelligence [124]. On the other hand, it is not easy to find good results in large-scale imperfect-information games (i.e., business strategies, war games, etc.). NFSP is a self-play-based approach without prior information, which helps for effectively learning approximate Nash equilibrium. But, the algorithm depends on Deep Q-Network. In online games, it is not easy to converge by changing opponents’ strategies. Neither in large search scale nor deep search depth games can it find approximate Nash equilibrium. This paper introduces the Monte Carlo Neural Fictitious Self Play (MC-NFSP) algorithm that amalgamates the NFSP and Monte Carlo tree search. For large-scale zero-sum imperfect-information games, the approach improves performance. The asynchronous Neural Fictitious Self Play (ANFSP) model is developed to use a parallel and asynchronous framework to gather the game’s history [145].
The authors in [128] address a reversed reinforcement learning method. After training a deep neural network according to strategies in the payoff table, randomized strategy input is initialized, and the error differentiates the actual output. The required output is propagated back to the initially randomized strategy input in the input layer of the trained deep neural network results in performing a task similar to the human deduction. Detecting imaging biomarkers for autism spectrum disorder (ASD) is challenging to help to explain ASD and predicting or monitoring treatment outcomes. Deep learning classifiers are used to detect ASD from functional magnetic resonance imaging (fMRI) with better correctness than traditional learning strategies. The concept of Shapley value from cooperative game theory is applied to this problem. Cooperative game theory is suitable since it more accurately determines biomarker importance for each instance from deep learning models. The main challenge for using Shapley Value calculation is its computational complexity. The method is validated on the MNIST dataset and compared to human perception. A Random Forest (RF) is modeled is trained to classify ASD or control subjects from fMRI and compare Shapley value outcomes with existing RF-based feature importance [74]. The development of intelligent machine learning applications is studied with expected-long-term profit maximization in multi-agent systems. A learning algorithm for the IPD problem is proposed in [2]. It is shown to outperform the tit-for-tat algorithm and many other adaptive and non-adaptive strategies using numerical analysis. It is also discussed how artificial intelligence and machine learning work closely to provide the agent with a mind-reading capability.
Shin et al. [119] have put forward a model to assign the updating time period to the drones by auctioning. Alternatively, a second-price auction system is applied in which the victorious bidder pays the second-highest bid. In the model, data needed for the dispersal of drones was found from the deep learning algorithm. The shortcoming of the model proposed by Shin and the team was it does not consider two significant criteria; the possibility of increasing the charging station and the uncertainty of charging to the drones at smaller bids. Ren et al. [107] have summarized the representative defenses developed, including adversarial training, randomization-based schemes, de-noising methods, and provable defenses.
Further, to utilize the adversarial training-based intuitive training method, Ren et al. have combined min-max games with deep learning and neural network. Leckie et al. [71] have combined game theory and deep learning to evade jamming attacks in network security. Based on a deep analysis of node behavior characteristics in the opportunistic network, Wang et al. [135] have introduced the evolutionary game theory to traverse the node cooperation mechanism in the opportunistic social network. In the same line, Ranadheera et al. [118] have utilized a deep learning-based deep-Q algorithm with the game theory for fair and efficient resource management in mobile edge computing. To achieve intelligence in the shared environment with multiple agents, Lanctot et al. Further, Lu and Kai [78] have generalized a multi-agent approach using reinforced deep learning and game theory. Dasgupta et al. [21] have combined deep learning and game theory for cybersecurity approaches.
Rudral et al. [108] have used deep learning-based predictive modeling for football games to result in multilayer perception. Wakatsuki et al. (2020) have used multi-player games for decision making. Wang et al. [134] have used the Deep Neural Network (DNN) based deep learning model and the game theory to provide a holistic framework of robot-human interaction. Pinto et al. [104] have used self-supervised deep learning for the robotic adversary. Moreover, they have designed adversarial training as a two-player zero-sum repeated game. Balduzzi [22] has used gradient-based game theory and deep learning to optimize game grammars. Shu et al. [44] have used DNN and game-theoretical approach for developing Multi-granularity Network Representation Learning (MGNRL) framework for the latent representation of nodes in the network. Game theory and deep learning concepts have been widely used in the education field also. Vos et al. [95] have combined game theory and deep learning to understand students’ motivation in education. Urbani [101] has combined game theory and deep learning for music genre classification. Han and Jiequn [63] have concluded that their approach of Deep Learning Approximation for Stochastic Control Problems should apply to broad areas, including dynamic game theory with more than one agent, dynamic resource allocation with several resources and demands, and properties management with large portfolios. Woo [137] has used game-theoretic complex analysis for nuclear security by addressing non-zero-sum algorithms. In the research, Woo has used deep learning for data processing, where the neural network is used for wiretapping. Table 2 summarizes critical game-theoretic models/concepts used to model various deep learning/artificial systems.
Table 2.
A summary of crucial approaches based on game-theoretic models to develop artificial intelligence and deep learning systems
| Deep learning/ Artificial systems | Game-theoretic models/concepts used | References |
|---|---|---|
| Neuronal Networks | Rationality, Simultaneity and equilibrium, Mixed strategies, Nash equilibrium, dynamic games | [112] |
| A cooperative game, Shapley value | [122] | |
| Adversarial deep learning | Stochastic games, Sequential games | [17] |
| Deep learning | Nash equilibria | [113] |
| A cooperative game, Shapley value | [74] | |
| Auctioning | [119] | |
| Minmax game | [107] | |
| Reinforcement learning | Minority game | [118] |
| Self-supervised deep learning | Two-player zero-sum repeated game | [104] |
Application of game theory in deep reinforcement learning
This section addresses several contributions to which game models are used to solve problems in reinforcement learning.
Over the past 4–5 years, reinforcement learning has become an exciting area of research [136]. Reinforcement learning has shown significant applications to develop intelligent opponents in computer games. In such applications, CNN plays a vital role in abstracting important traits from grainy and complex data. Games are modeled for appropriate scenarios to test the reinforcement learning algorithms as they provide an essential overview of how good an algorithm can behave in isolated environments. Real-time strategy games are very complex, and planning for short and long-term strategies is very challenging. The work in [4] addresses the Deep Real-time strategy game for testing advanced artificial intelligence algorithms. It deals with faster learning. It learns at a rate 50,000 times faster than existing real-time strategy games. It is also helpful for moderately observable state spaces and map complexity. Applying Real-time strategy outperforms micro Real-time strategy, StarCraft II, and ELFon advanced system. It is shown that a Deep Q-Network agent outperforms random-play agents most of the time (more than 70%) using the Deep Real-time strategy. In recent times, machine learning is extensively being used for multi-agent systems. [31] discusses the related work on deep multi-agent reinforcement learning, decentralized optimization, hierarchical reinforcement learning, and GANs. Multiple learning agents cause training non-stationary and even lead to non-stable training or unexpected results. A ‘Learning with Opponent-Learning Awareness’ (LOLA) approach is explored in the paper where the agents try to learn by opponents’ learning. The LOLA learning approach considers the effect of one agent’s policy on the other agents’ policy. The results demonstrate that the interaction of two LOLA agents goes for tit-for-tat, and after that, cooperation in the iterated prisoners’ dilemma (IPD). LOLA gains higher payoffs compared to a naïve learner, and it is robust against the application of higher-order gradient-based approaches. On the other hand, LOLA agents move towards the Nash equilibrium for infinitely repeated matching pennies games. The LOLA update scheme can be effectively applied using an advanced likelihood ratio policy gradient estimator and build the scheme suitable for model-free reinforcement learning. Focusing on the learning of the opponent, LOLA agents learn to coordinate out of self-interest.
AlphaGo was the first program to win the game Go against a world champion. AlphaGo computed positions and moves in tree search with the help of deep neural networks. These neural networks are trained using supervised learning depending upon the data of moves of humans and by reinforcement learning achieved from self-play. Algorithms are developed based on reinforcement learning without experimental data of humans, supervision, or level of knowledge of the domain apart from game rules. AlphaGo is considered its own teacher. A neural network is trained to predict the selection of moves forAlphaGo and find the games’ winner. This neural network improves tree search by enhancing quality move selection and better self-play in the next iteration [120]. Tsetlin Automaton is a learning mechanism. A single integer is assumed to be a memory element; the model learns the preferable action in stochastic environments by decrement and increment operations. The Tsetlin is introduced to solve complex pattern identifying problems with simple formulas formed by a set of Tsetlin Automata. The Tsetlin Machine gives satisfying accuracy compared with Logistic Regression, Random Forests, Naive Bayes Classifier, Decision Trees, SVMs, and Neural Networks. The significant features like accuracy, interpretability, and computational complexity make the Tsetlin Machine a prevalent tool [38]. Reinforcement learning is capable of representing psychological and neuro-scientific features of animal behavior [136]. To apply reinforcement learning in complex real-world situations, the agents have a difficult task: they need to properly formulate the actual environment obtained from multi-parameters sensory inputs and apply them to relate the past experience to new instances. A deep Q-network is used for training deep neural networks to build an artificial agent. The agent learns rules from multi-parameters sensory inputs by reinforcement learning. The agent has experimented on classic Atari 2600 games. The performance of the model outperforms other existing algorithms [85]. To achieve intelligence in the shared environment with multiple agents, Lanctot et al. [69] have combined unified game theory with deep reinforced learning. To mitigate societal challenges in learning, education Fang [30] has used deep reinforced learning. Motivated by the urgent need in green security domains such as protecting endangered wildlife from poaching and preventing illegal logging, Yu et al. [144] have proposed game-theoretic and deep reinforced based learning models to optimize patrols conducted by law enforcement agencies. Xiao et al. [139] have used a game-theoretical deep reinforcement-based learning technique to secure mobile crowd-sensing.
Application of game theory in GAN
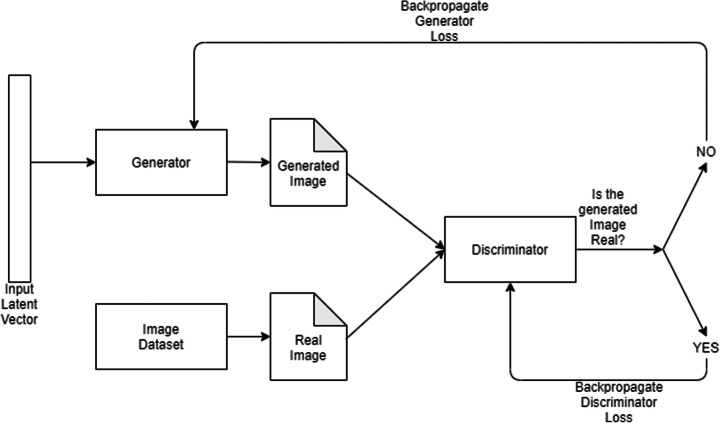
This section addresses some contributions in which game models are used to solve problems in GAN. Figure 5 shows a generalized architecture of GAN.
Fig. 5.
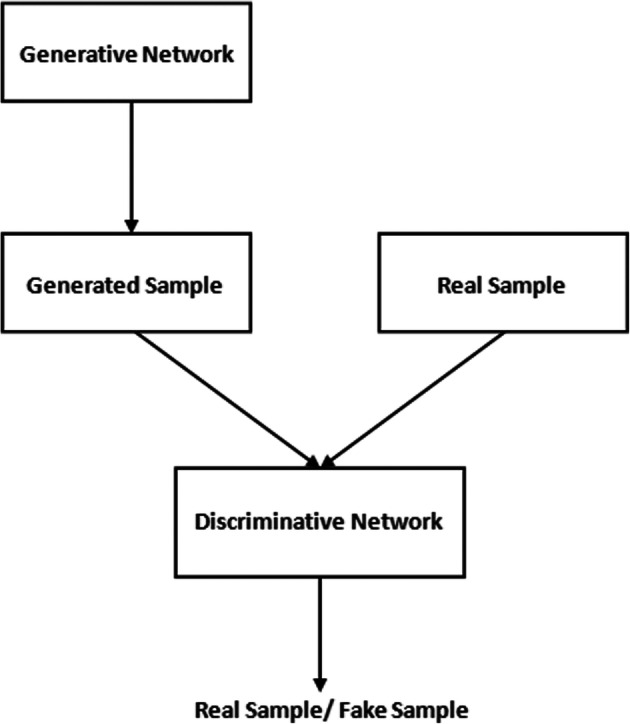
Generalized Generative Adversarial Network Structure
The contribution in [123] sets up a connection amidst a deep learning model and a game-theoretic approach. This work introduces the application of deep learning to solve game-theoretic problems. Some techniques have been addressed to speed up deep learning and gradient-based approaches in actions with continuity for multi-agent adversarial games. On the other hand, multiple GANs are developed as robust distributed games. A Bregman-based strategic deep learning algorithm is introduced for finding robust distributed Nash equilibria, and it is also checked upon in image synthesis and picture classification. GANs are modeled as a min-max game, and a fast learning algorithm using Bregman divergence is explored. A comparative study on the performance of the Bregman-based algorithm with six algorithms is also shown. Table 3 shows a mapping of components of a game with the components of the deep learning network. The work in [16] shows that deep learning is unsafe for changes in data distribution. So, a deep learning network like CNN is dangerous for adversarial scenarios. An adversarial learning model is designed for supervised learning. Adversarial scenarios are modeled by a game-theoretic approach to the conduct of deep learning. A smart antagonist and a deep learning model interact with each other. The interaction is represented as a two-person sequential non-cooperative Stackelberg game, and stochastic payoff functions are formulated.
Table 3.
Deep learning versus game theory terminologies [123]
| Game Theory | Deep Learning |
|---|---|
| Player/Agent | Neuron unit |
| Action/Moves | Weight |
| Objective function | Objective function |
| Sub-goal | Feature/Attribute |
| Measurement | Output |
| Design of game | Design of architecture |
Nash equilibrium is determined for the Stackelberg game. It finds a pair of strategies (genetic operations and weights of learners) by which either learner or antagonist can achieve no better payoff by deviating strategies. The performance of the algorithm is determined under various strategy combinations on the dataset of MNIST handwritten digits. The Nash equilibrium seems to be robust to adversarial environments. The outcomes show that game theory and stochastic optimization methods can be applied to study susceptibilities in performance for deep learning models.
In unsupervised learning, GANs have become one of the most effective techniques for self-learning the given distribution of a specific dataset [36]. In [41], the tragedy is modeled as a two-player zero-sum game between two players: a discriminator D and a generator G. The generator’s objective are to generate fake images from random noise, and the objective of the discriminator is to categorize on fake and real images correctly. The paper addresses applications of generalized zero-sum games or multi-player zero-sum games to formulate and train GANs. The results signify that by applying a multi-player setup, the severity of the mode collapse problem in GANs can be reduced to generate a diverse set of fake images. It is also demonstrated on different fake toy distributions and real-world datasets like MNIST & CIFAR10.
Several real-life scenarios can be represented as large-scale imperfect information games. The Nash equilibria are initially computed to handle such problems. The authors in [47] address a new, without prior knowledge-based, scalable and end-to-end method for learning approximate Nash equilibria effectively. The technique integrates deep learning with fictitious self-play. While implemented on Leduc poker, NFSP finds a Nash equilibrium; alternatively, conventional reinforcement learning approaches diverge. In Limit Texas Hold’em, a large-scale poker game, NFSP learns a strategy that determines the performance, superhuman algorithms with the help of strong domain expertise.
Today, GAN is among the most popular frameworks in Deep Learning [36]. The research on applications of game-theoretic techniques in developing deep learning algorithms has received a great response from the research community. Generative Adversarial Network Games (GANGs) are developed, and they are modeled as a finitely long zero-sum game between a discriminator D and a generator G by applying mixed strategies. Resource-bounded best responses (RBBRs) and source bounded Nash Equilibrium (RB-NE) are defined as a pair of mixed strategies. By using these techniques, neither G nor D can achieve a better RBBR. The RB-NE solution is better than the local Nash equilibria. It detects errors of gradient descent-based escaping local optima and applies them to approximate best response computations. GANGs are solved with the parallel Nash Memory technique that slowly converges to an RB-NE to validate this approach. The results show that it outperforms standard GAN setups and demonstrate that it performs well with typical GAN problems [97].
A mixed Nash equilibrium of GANs is determined in [56] besides finding a pure optimal strategy. The probability distributions over pure strategy are optimized for the network. This paper also discusses well-known prox methods, which are applied to solve two-player games with finite strategies. It can even be drawn out to continuously many strategies. Therefore, it is suitable for training GANs. A proof is given to demonstrate the convergence rates to learning the mixed Nash equilibrium. It is further shown that heuristic approaches significantly reduce memory and computational costs. As a result, they become simple algorithms having complexity per-iteration almost as cheap as SGD. The experimental results prove out that the performance of the algorithms significantly improves, and they are better than popular techniques such as Adam, SGD, and RMSProp.
GANs are used for generating images and learning in a semi-supervised way [19]. In two-player games, a single discriminator plays a vital role in detecting fraudulent specimens and determining labels, and it also guesses the data without the labels. A triple generative adversarial net (Triple-GAN) is developed in [18] to solve the problems. Triple-GAN has three players- a classifier, a generator, and a discriminator. The tasks of the generator and the classifier are to determine the conditional distributions between labels and images. On the other hand, the task of the discriminator is to detect fake image-label pairs. The paper addresses compatible utilities that characterize distributions by the generator and the classifier and converge to the data distribution. The outcomes on different datasets show that Triple-GAN is an improved model that can parallelly perform classification results among deep generative models.
GAN can generate realistic images [19, 36, 130]. The visual presentation of objects is affected by their shape geometry which is crucial information but not considered in existing generative models. The work in [67] addresses the Geometry-Aware Generative Adversarial Networks (GAGAN) that also accounts for geometric information into the image generation technique. In GAGAN, the generator generates latent variables based on the probability distribution of a statistical shape model. By mapping the outcome of the generator with a coordinate table with the help of a differentiable geometric transformation, the geometry of the objects is studied, and the relation from the priorly generated object is determined. The outcomes on face generation show that the GAGAN can generate realistic pictures of faces with random facial traits of superior nature to existing GAN-based models. This approach also enhances the quality of the generated images.
In [129], a minimax game model is formulated for discriminative (classifier) training. In this game, a generator is considered a player that tries to generate training samples. A different player, the discriminator, has to classify the specimens generated by the generator correctly. The generator detects the Bayes decision boundary and only chooses training samples from there. Alternatively, the discriminator only performs random guesses. Rigorous research has been going on GAN for the last few years, but it is still very challenging to conclude which algorithm is most effective [80]. The authors discuss a neutral, multi-faceted large-scale empirical study and also compare the results with existing models. The performances of various models are similar under enough optimization of hyper-parameter and random restarts. Different data sets are used to find the precision and recall to deal with certain limitations. The experimental results show that the GAN research is moving towards more systematic and objective evaluation approaches. The work also highlights that not a single tested algorithm consistently outperforms the other algorithms.
Various training methods and architectural characteristics are developed for GANs. The works in [109] highlight two utilizations of GANs, which are semi-supervised learning and realistic image generation. The techniques discussed in the paper compares the outcomes in semi-supervised classification on various datasets such as CIFAR-10, MNIST, and SVHN. The quality of spawned images is of very superior quality, and the model generates MNIST samples that are very hard to identify for humans. On the other hand, CIFAR-10 samples produce a human inaccuracy rate of nearly 21.3%. The paper also shows that approaches facilitate the model to learn significant features of ImageNet classes.
GANs exploit supervised learning to estimate a cost function. GANs can use a supervised ratio estimation scheme to estimate multiple cost functions such as KL divergence applied for maximum likelihood estimation. Training GANs is to find Nash equilibria in elevated dimensional, continuous, non-convex games [35]. CNNs are helpful to identify objects in an image, but it is tough to find the position of an object relative to others. A novel solution to this problem is trusting “Capsules” – a logistic unit that confirms the object’s existence and orientation. This work also highlights incorporating the Capsule into the Discriminator of the GANs, which can yield a better classification loss and faster convergence. The results are shown both qualitatively and quantitatively [33].
The graph representation learning techniques are divided into a couple of categories: generative models that learn the connectivity relation in the graph and discriminative models that determine the probability of an edge between any two vertices. Graph representation learning aims to store each vertex in a graph into a low-dimensional vector. A new learning framework GraphGAN is introduced in [133]. GraphGAN represents the generative model and discriminative model as a game-theoretical minimax game. The generative model generates accurate connectivity distribution over all vertices and yields forge samples to confuse the discriminative model for a given vertex.
On the other hand, the discriminative model aims to detect whether the sample vertex is real or caused by the generative model. The generative model is implemented using a novel graph softmax. Extensive investigations on real-world datasets confirm that GraphGAN performs well in different applications, e.g., node classification, link prediction, and recommendation.
Lipschitz regularization theory and algorithmic technique for a new Loss-Sensitive Generative Adversarial Network (LS-GAN) are applied in [105]. It instructs a loss function to differentiate original and fake specimens by precise margins, and a generator generates realistic samples by reducing their losses. The LS-GAN regularizes its loss function by incorporating Lipschitz regularity condition on the probability of actual data produces a regularized model, which better generates new data from a fair number of training specimens as compared to conventional GAN. A generalized LS-GAN (GLS-GAN) is discussed. Other GAN models are compared with LS-GAN and GLS-GAN. LS-GAN is elaborated for supervised and semi-supervised learning problems. In [58], a data-driven model is explored, known as generative adversarial privacy (GAP). GAP helps the data holder to study the privacy policy from the data. Determining the optimal privacy policy is modeled as a constrained minimax game between a privatizer and an adversary. GAP offers privacy against robust information-theoretic adversaries. GAP is applied for multi-dimensional Gaussian mixture models and large datasets.
The work in [45] shows an approach for synthesizing a road network by applying GANs. As per the suggested approach, the road network is first converted into a binary image in which pixel intensities represent the presence or absence of streets. Then, the GAN is trained to automatically synthesize the arbitrarily sized street networks, and the generator tries to generate something similar to the original patch. A graph-based representation is extracted from the generated images. The method shows that it can be applicable to synthesize large-scale street networks. Many research articles have already applied recurrent neural networks for music generation. A recent significant contribution, the WaveNet model, was invented by DeepMind. It shows that CNNs can also be used to generate realistic musical waveforms. It has also experimented with that CNNs can generate melody one bar after another in the symbolic representation. GAN is applied in this scenario in which the generator and Discriminator play their roles. A discriminator learns the distributions of melodies. A new conditional approach is exploited based on available prior knowledge. As a result, the model can produce melodies by following a chord sequence or by conditioning on the melody of the preceding, among other capabilities. The proposed MidiNet can also be applied to generate music with multiple MIDI channels. MidiNet and MelodyRNN models are compared, and the results show that MidiNet performs similarly to MelodyRNN models. MidiNet’s melodies are captivating [140].
Story Cloze Test is an intelligent machine comprehension tool to understand natural language problems. The idea behind the device is too many story tests within the dataset that develops common sense assuming capability. The training data is almost unsupervised in this problem in which context documents having a single positive sentence that is understood from the situation. To deal with the problem, GANs are applied to generate fake sentences. The work in [131] also develops Conditional GANs (CGANs) in which the situation influences the generator. The experimental outcomes display the efficacy of the CGANs in the discriminating sentence in practical story reading comprehension tasks. GANs can be modeled by a two-player minimax game [36]. Durugkar et al. [27] presents the Generative Multi-Adversarial Network (GMAN), which uses multiple discriminators. GMAN is trained with the original, untampered objective. Numerous design perspectives are addressed in the paper in which the Discriminator plays various roles ranging from formidable adversary to forgiving teacher. It is shown that GMAN generates higher quality samples in a lesser number of iterations compared to GAN.
Another significant work explores a novel training process, SGAN, in which multiple adversarial local pairs of networks are trained independently to train a global supervising pair of networks against them. The objective of this process is to train the international pair with the corresponding opponent for better performances. This method tries to increase the chances to continue learning for the global pair. It also prevents trapping in an unsatisfactory local minimum and oscillations in results. In the SGAN training process, the global generator and Discriminator are trained using the local discriminators and generators, respectively. Alternatively, the local networks are trained with their fixed local opponents. The experimental results based on a small scale and real-world problems show that this method outperforms existing approaches [14]. Pfau and Vinyals [103] shows that GANs can be modeled as actor-critic frameworks in a scenario wherein the actor cannot influence the payoff. The strategies are formulated for balancing training for each class of models. GANs and reinforcement learning algorithms are analyzed in-depth with more complicated information flow. The contributions in the paper encourage both GAN and reinforcement learning research communities to develop more efficient algorithms for multilevel optimization with deep networks.
Consider a scenario where learning properties from the behavior of an expert are required without interacting with the expert or accessing a reinforcement framework. A solution is to extract the payoff function of the expert with inverse reinforcement learning that leads to extract a property [136]. The work in [53] shows that a specific instantiation of the model relates to imitation learning and GANs from which a model-free imitation learning algorithm is derived. The algorithm outperforms the existing model-free methods in imitating various behaviors in real environments. The Discriminator in GAN works as a classifier with the sigmoid cross-entropy loss function. It is observed that the loss function may struggle from the vanishing gradients problem during the learning process. Least Squares Generative Adversarial Networks (LSGANs) is introduced to solve this problem [82]. LSGANs embrace the least squares loss function for the Discriminator. It is shown that the minimization of the objective function of LSGAN minimizes the Pearson χ2 divergence. It experimented on LSUN and CIFAR-10 datasets and observed that LSGANs could produce superior quality images than GANs. LSGANs are more stabilized during the learning process. It is concluded from two experiments that LSGANs are more stable than GANs.
GAN’s learning dynamics are not still well understood. To deal with GAN’s learning dynamics, a model is explored to demonstrate various problematic convergence behaviors such as vanishing gradient, mode collapse, diverging, or oscillatory behavior [73]. The model also determines the first convergence bounds for parametric GAN dynamics. It is also shown that a GAN with an optimal discriminator may converge while a first order approximation of the discriminator steps becomes unstable GAN dynamics and mode collapse. The model finds a particular challenge in GAN while training that is called discriminator collapse. The work in [9] presents an equilibrium enforcing technique and a loss function by Wasserstein distance for training auto-encoder-based GANs. This technique considers the role of generator and Discriminator while training. It also finds an estimated convergence measure, fast and stable training, and a high-quality sample. It is also controlled the trade-off between sample diversity and quality.
Two information retrieval models: the generative retrieval predicting related documents based on a query and the discriminative retrieval indicating relation based on a query document pair, are addressed in [132]. A minimax game is modeled to optimize both models iteratively. The discriminative model tries to differentiate samples from labeled and unlabelled data. It helps to train the generative model for fitting the distribution of samples based on the query. Alternatively, the generative model generates fake samples for the discriminative model intending to minimize its discrimination objective. (i) the generative model learns to fit the relational distribution of documents with the help of samples from the discriminative model, (ii) the discriminative model can use the unlabelled data chosen by the generative model to perform a better appraisal for document ranking. The experimental outcomes show the efficacy of the model. GAN training may become prosperous, but the trained distribution may not achieve excellent performance for target distribution. Generalization occurs for a weaker metric, neural network length. It is demonstrated that an approximate pure equilibrium is obtained from the Discriminator or generator game. The existence of equilibrium inspires the MIX+GAN protocol [5].
The authors in [94] address a model to deal with the mode collapse problem in GAN. The Kullback-Leibler (KL) and reverse KL divergences are combined into a unified objective function. As a result, it can use various statistical properties from the divergences to properly diversify the approximated density in capturing multi-modes. The contribution in this paper includes dual Discriminators generative adversarial nets (DDGAN) having double discriminators and a single generator. In this model, one of the discriminators pays high scores for samples obtained from data, whereas another discriminator supports data obtained from the generator. Alternatively, the generator yields samples to fool both the discriminators. It is shown that the maximal discriminators optimize the generator of DDGAN, which lessens to minimizing KL and reverse KL divergences between data distribution and the distribution from the data produced by the generator. Extensive experiments are managed on synthetic and real-world large-scale datasets such as MNIST, CIFAR-10, STL-10, ImageNet. The experimental outcomes show the efficacy of the model.
A method is explored in [52] for training GANs with discrete data that exploits the estimated difference from the Discriminator to determine significant weights for generated samples and supplying a policy gradient for training the generator. The significant weights have a robust relationship to the decision boundary of the Discriminator. The name of this method is aptly given boundary-seeking GANs (BGANs). The efficacy of the model is demonstrated with a discrete image and character-based natural language generation. The boundary-seeking objective is also applicable for continuous data shown on Celeba, Large-scale Scene Understanding bedrooms, and Imagenet without conditioning. GANs are best to converge to a local Nash equilibrium. Such a local Nash equilibrium is different from a Nash equilibrium. The work in [98] models GANs as finite games with mixed strategies, and the method ensures that every local Nash equilibrium is a Nash equilibrium. The authors also introduce another way that monotonically converges to a resource-bounded Nash equilibrium in which computational resources are increased to achieve better solutions. The model shows its efficiency concerning typical GANs and MGANs.
For GANs, the data distribution is learned by a two-player zero-sum game, played between a generator and a discriminator, and both of them aim to optimize their payoffs [19, 36]. GANs find Nash equilibrium in which no player can improve payoff by unilaterally deviating its strategy. GANs shows that the training and model distribution difference is the minimum value at an equilibrium point. The divergence has a vital part in the learning process, and each learning step tries to decrease the divergence. We show that this view is overly restrictive. The authors show that GANs can learn distributions when divergence minimization predicts failure [29]. It is also demonstrated that gradient penalties are equally helpful when applied in other cases in which the divergence minimization does not predict they would be beneficial. GAN training may be more helpful in modeling Nash equilibria.
Structure Generative Adversarial Network (SGAN) has been explored for semi-supervised conditional generative modeling to learn from a small set of separate instances to extract the semantics of significant interest from others in the latent space. It is shown that SGAN has improved extraction and controllability compared to primary frameworks. The model is advantageous to apply to various problems. It outruns existing models regarding the inception score and visual quality of controllable image generation [24]. GraphSGAN is proposed for graph-based semi-supervised learning by applying GANs [25]. The scenario is represented as a competitive game between generator and classifier. In the game, the generator generates samples in density gaps at equilibrium. The loss terms cumulatively determine the expected equilibrium. Experiments performed on three standard datasets show the efficacy of the strategy. GraphSGAN model has been thoroughly analyzed. Generated samples minimize the adjacent nodes in density gaps to find decision boundaries prominent. The GraphSGAN is scalable. The experimental results on the DIEL dataset prove the model’s capabilities to execute well on large graphs.
A holistic active learning model by the query synthesis method using GAN is introduced in [149].
Table 4 summarizes critical game-theoretic models/concepts used to model various GAN architectures. The algorithm adaptively synthesizes training samples for querying to enhance learning speed. The queries are generated according to the uncertainty principle, but the model performs well with other active learning principles. The results are obtained from a large number of experiments to show the efficacy of the approach. In a few settings, the algorithm outperforms existing pool-based methods. An approach for modeling the decision-making of players through agents is introduced in [55]. The authors claim that artificial agents have the capabilities to act like a human player’s decision-making processes. Such agents can mimic human decision-making and effectively performing testing tools in the game design process. This claim is proved in a crowdsourced decision-making experiment that shows the decisions of human players in a small-scale dungeon-themed puzzle game. Human choices are correlated to the findings of agents [127]. A decent amount of research has been performed on generative models in computer vision and image classification. These generative models have been made famous in a framework well known as Generative Adversarial Networks. The work in [51] presents the original model proposed by Good fellow et al. and extensions of the original model and compares these models.
Table 4.
A summary of critical approaches based on game-theoretic models to develop Generative Adversarial Network models
| Generative Adversarial Network models | Game-theoretic models/concepts used | References |
|---|---|---|
| Deep learning model | Two-person sequential non-cooperative Stackelberg game, Stochastic payoff functions | [16] |
| GAN | Two-player zero-sum game | [41] |
| Mixed Nash equilibrium | [56] | |
| Minimax game model | [129] | |
| Boundary equilibrium | [9] | |
| Local Nash equilibrium | [98] | |
| Nash equilibrium | [29] | |
| GANG | A finitely long zero-sum game, Resource-bounded best responses (RBBRs), source bounded Nash Equilibrium (RB-NE) | [97] |
| Triple-GAN | Two-player games | [18] |
| GraphGAN | Minimax game | [133] |
| GAP | Minimax game | [58] |
| MIX+GAN | Approximate pure equilibrium | [5] |
| GraphSGAN | Expected equilibrium | [25] |
The theory of mind model is introduced in [143]. The model discusses the intentions and goals of opponents to optimize mutual interactions. Control theory and game theory are applied to model the game theory of mind. The plans are represented as value functions, also known as utility or rewards. The joint value functions are complex since the behaviors of the players are optimized recursively. The joint functions find how player1 determines the value function of player2. Similarly, player2 determines the value function of player1, and so on. If the degree of recursion is bounded, then the players/opponents need to estimate the degree of recursion of the opponent to respond optimally. The contribution shows that it is possible to deduce whether players infer about each other and quantify their value functions based on selections in sequential games. Then, generative models of strategies with and without inference are compared. The comparison is shown using simulated and real data from a ‘stag-hunt.’ It also shows that the same behavior can be found by optimizing the utility function for altruistic agents.
Multiple decision-makers are usually involved in handling real-world problems. They fix their own goals or destinations. Game theory has certain limitations; its applicability is restricted by the intractability of determining equilibrium in large games. Other challenges are that the parameters in the games are sometimes unknown, and the players in real-world scenarios may not be entirely rational. The work in [120] addresses how learning with game theory can solve societal challenges such as security and sustainability.
Table 5 outlines statistics on the number of articles of applications of game theory in deep learning, reinforcement learning, and exclusively in GAN. Machine learning, reinforcement learning, and deep learning have achieved tremendous responses in different fields and can be applied to overcome the limitations of the game-theoretic models [76, 84, 136].
Table 5.
A statistics on applications of game theory in deep learning and artificial intelligence, reinforcement learning, and GAN
| Classification of Articles | Number of Articles | % |
|---|---|---|
| Game theory in deep learning and artificial intelligence | 39 | 41.93 |
| Game theory in reinforcement learning | 10 | 10.75 |
| Game theory in generative adversarial network | 44 | 47.31 |
Table 6 gives statistics of the scientific works discussed in the paper based on the number of articles published, average citations, and maximum citations of applications of game theory in deep learning, reinforcement learning, and exclusively in GAN.
Table 6.
A statistics on the types of articles and citations of applications of game theory in deep learning and artificial intelligence, reinforcement learning, and GAN
| Classification of Articles | Number of journal articles | Number of conference articles | Other articles | Average citations | Maximum citation |
|---|---|---|---|---|---|
| Game theory in deep learning and artificial intelligence | 13 | 15 | 10 | 246 | 4378 |
| Game theory in reinforcement learning | 3 | 5 | 2 | 1461 | 10,058 |
| Game theory in generative adversarial network | 6 | 17 | 18 | 843 | 19,348 |
Figure 6 shows the statistics of Table 6 with the help of a bar chart that will give a clear insight to the readers. Tables 5 and 6, and Fig. 6 individually show that game theory has more applications in GAN over other deep learning models and reinforcement algorithms. GAN has received tremendous responses from the scientific community.
Fig. 6.
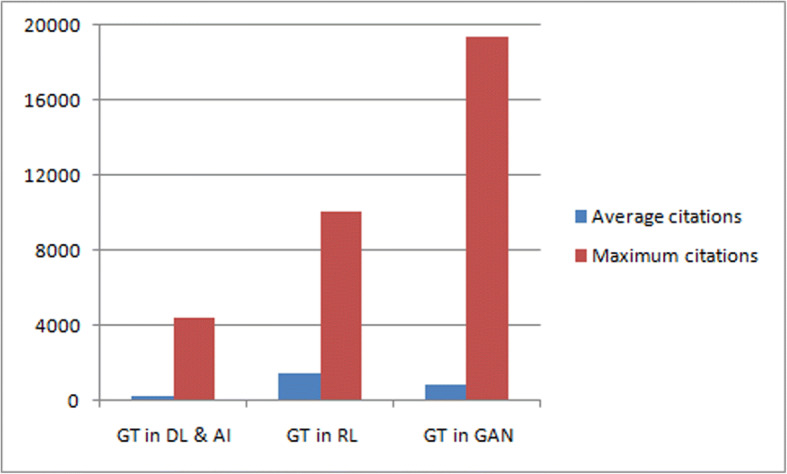
Average citations, maximum citations based on the articles discussed on applications of game theory in deep learning, reinforcement learning, and exclusively in GAN
The datasets used in most of the research articles in this study are as follows: MNIST, CelebA, CIFAR-10, BBBC039, initial dataset, transfer dataset, SVHN, STL-10, ImageNet, DIEL, etc.
Implementation environment
The current study mainly focuses on deep reinforcement learning and GAN models. There are various real-time and business applications of GAN and reinforcement learning. The current study addresses several diverse problems. Some significant implementation environments of GAN and deep reinforcement learning models are described in this section based on the existing literature. GAN is primarily used to generate samples/images for various image datasets. GAN can be used to create images of human faces, which are used for different purposes. GANs also help to create realistic images. The cartoon industry is a popular entertainment industry where GAN is used to generate various cartoon characters. Another critical application of GAN is image to image translation. Text to image translation is another vital application of GAN. GAN can be used to generate new human postures which have security, healthcare, and entertainment applications. Another exciting application is generating emojis from typical images frequently used in various social network platforms, mobile applications for entertainment purposes. Photos are edited using GAN models. Photo blending is also done using GAN models. GAN is used for video prediction and 3D object generation. GAN can be used for improving cybersecurity in various places and improving healthcare sectors. It can create artistic skills; it can generate exact or similar images of a painting. It can even cause fake videos. The quality of an image can also be improved using GAN that serves several purposes. De-noising on images is also done using GAN. Alternatively, deep reinforcement learning has excellent application in real-time systems and industries. It is used for the implementation of a self-driving car and industry automation. Deep reinforcement learning is also used in NLP applications. The Healthcare system has also adopted deep reinforcement learning as a tool. It successfully performs various tasks such as automatic disease prediction etc. It has other robust applications in news recommendation and gaming. It also has applications to build automated robots. It has other significant applications such as resource management in computer clusters, traffic light control, web system configuration, advertisement, etc. Reduction in energy consumption, online recommendation systems are some industrial applications.
The performances of the proposed study can be evaluated through Sensitivity, Specificity, recall. Specificity is defined as the proportion of actual negatives, which got predicted as the negative. Sensitivity is a measure of the balance of real positive cases that got expected as positive. The recall is the measure of our model correctly identifying True Positives [87].
Future research direction and challenges
The previous sections of the present work discuss the linkages and applications of game theory in deep learning. The current section aims to discuss future research challenges related to the application of game theory in deep learning. To narrate and list out all possible future challenges is a complex task as different literature uses different simulation environments, simulation tools, different data sets, and different experimental conditions. Nevertheless, the current section discusses some of the critical representative future research directions. The future research direction is described in Table 7 below. Table 7 also provides hints, literary way, and association of game theory and deep learning to get the breakthrough in solving future research challenges.
Table 7.
Future research challenges and the association of deep learning and game theory
| Sr. no. | Future research challenges | Association of deep learning and game theory |
|---|---|---|
| 1. | Some of the areas of deep learning, like deep games [113], require training heuristics. So far, it has not been investigated how training heuristics for deep games on the recurrent model can be applied. | If the behavioral game theory is used, it may be possible to design training heuristics for deep games [83]. However, experimental results are required to support these claims. |
| 2. | The reward design function plays a crucial role in deep learning, e.g., to improve the Monte-Carlo tree search. Combining more sophisticated deep learning architectures with reinforced learning in Learning Reward-bonus Functions (LRF) [40] remains an important future work | Game theory is widely used for negotiations, bargains, and arbitration [10]. If these concepts are utilized for LRF, a step can be taken to solve future research challenges. |
| 3. | Future work may develop and design algorithms to leverage information-rich, better yet unstructured data in healthcare [28]. | Game theory can be utilized through verbal decision analysis [70] for unstructured problem analysis. If the same approach can experiment with unstructured data, the solution may be achieved for unstructured data in healthcare. Thus, verbal decision analysis may provide a path to solve the challenges. |
| 4. | First, in genomics, the challenge of designing and developing deep learning systems that best represent and complement human experience in making medical diagnosis and decisions (for example, genome representation) is crucial [150]. The second challenge is how to avoid biasing entities in training sets and how to interpret predictions. Robustness and interpretation are two important directions for method development. Lastly, there is a requirement for iterative/recursive experimentation, in which deep learning predictions can be checked and validated by functional laboratory tests, experiments, or formal clinical assessment [150]. The future challenges related to genome data are also described in [11] in detail. | A causal functional contribution analysis based on game theory [81] may help solve the challenges related to a medical decision and bias-less training set. |
| 5. | In deep learning, so far, there is no significant attempt to improve support for distributed computation [102] by providing efficient primitives for data parallelism. | In [1], an attempt has been made to relate distributed computation and game theory. The details of this attempt can be crucial in providing efficient primitives for data parallelism |
| 6. | Deep learning has been widely used for medical imaging tasks. However, major medical imaging tasks are far from solved, and the optimal deep learning method and architecture for each task and application region have not yet been established [42]. | In [42], an algorithm to select feature subsets for hyperspectral image classification using the principle of coalition game theory is discussed. A similar algorithm can be a starting point for research in medical imaging. |
| 7. | Literature suggests that compression dynamics in the information plane are not a common feature of deep learning networks but are critically influenced by the nonlinearities deployed by the network. Research in this direction may reveal new concepts related to deep networks and the information plane [110]. | [75, 138] described how game theory could be associated with the network and related theory. This feature of game theory can be utilized to solve the challenges related to deep networks and the information plane |
| 8 | In the future, there is a possibility of using deep learning for robust meta-analytic estimation—in conjunction with increased transparency and collaboration at the level of the meta-analysis—revives the potential of meta-analysis to function as the platinum standard in scientific debate [13]. | [7, 64] describe that game theory can be helpful in estimation and meta-analysis. It can be a good starting point towards the utilization of deep learning for robust meta-analytic estimation |
| 9 | In the future, the content generation framework requires more than one domain of computational creativity within a game-theoretic context [77]. | Evolutionary game theory has the capability of content generation [115]. |
| 10 | AI-based deep learning applications in COVID-19 research are currently facing several obstacles, such as, scarcity, legislation, unavailability of large-scale training data, large, noisy data and rumors, limited awareness of the intersection between medicine and computer science, security issue, data privacy, and unreliable usability of text data [3]. | Aslan et al. [6] have shown how graph transduction games can be helpful to deal with limited data points. Lamba [68] has shown a game-theoretical model to enhance the awareness of the models. |
In conclusion, researchers and scientists have to do extensive developmental research and efforts in the direction described above to overcome the problems and challenges faced by the future of deep learning, such as genomics and medical imaging. Besides, more techniques and further inspiration are required to develop new deep learning approaches. New methodologies for complex and challenging problems would be necessary as collaborative efforts by various research communities need to be carefully addressed.
Conclusions
Games play a vital role in the advancement of artificial intelligence. Games are frequently used as training mechanisms in learning algorithms, such as reinforcement learning and imitation learning. The paper highlights that AI-enabled and deep learning-enabled multi-agent systems are also developed to compete or cooperate to complete a goal with the help of game theory. In real-time scenarios, deep learning frameworks need to face situations with imperfect information. Paper considers all 31 articles in which game theory and deep learning coincide described in Table 1. It is discussed in the paper that DeepMind’sAlphaGo works with the help of partial knowledge to strategically make superior to the world’s most efficient human in the game of Go.
The paper also puts ample light on the application of game theory to construct adversarial networks. An essential property of an adversarial network is that a closed-form loss function is not needed. Some networks have the capability of finding their loss function. A significant disadvantage of adversarial networks is difficulties in training them. Adversarial learning models find a Nash equilibrium for a two-player non-cooperative game. The paper addresses applications of game theory in artificial neural networks, reinforcement learning, and deep learning. The main focus is to focus on the construction of GAN by applying different game models. The paper’s contribution may help the researchers in game theory, deep learning, and artificial intelligence to acquire a large number of ideas about inter-domain research and contribute holistic works in these domains. The paper also addresses various challenges and future directions of the identified area that will help researchers explore. In the future, behavioral game theory can be applied to model deep learning networks and mimic human neural networks. The combination of the research areas will open several paths for the researchers.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Tanmoy Hazra, Email: tanmoyhazra316@gmail.com.
Kushal Anjaria, Email: kushal.anjaria@gmail.com.
References
- 1.Abraham I, Dolev D, Gonen R, Halpern J (2006) Distributed computing meets game theory: robust mechanisms for rational secret sharing and multiparty computation. In: Proceedings of the twenty-fifth annual ACM symposium on principles of distributed computing, pp 53–62
- 2.Agrawal A, Jaiswal D (1981) When machine learning meets ai and game theory
- 3.Alafif T, Tehame AM, Bajaba S, Barnawi A, Zia S. Machine and deep learning towards COVID-19 diagnosis and treatment: survey, challenges, and future directions. Int J Environ Res Public Health. 2021;18(3):1117. doi: 10.3390/ijerph18031117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Andersen PA, Goodwin M, Granmo OC. 2018 IEEE conference on computational intelligence and games (CIG) IEEE; 2018. Deep RTS: a game environment for deep reinforcement learning in real-time strategy games; pp. 1–8. [Google Scholar]
- 5.Arora S, Ge R, Liang Y, Ma T, Zhang Y. Proceedings of the 34th international conference on machine learning-Volume 70. JMLR.org; 2017. Generalization and equilibrium in generative adversarial nets (gans) pp. 224–232. [Google Scholar]
- 6.Aslan S, Vascon S, Pelillo M. Two sides of the same coin: improved ancient coin classification using graph transduction games. Pattern Recogn Lett. 2020;131:158–165. doi: 10.1016/j.patrec.2019.12.007. [DOI] [Google Scholar]
- 7.Balliet D, Mulder LB, Van Lange PA. Reward, punishment, and cooperation: a meta-analysis. Psychol Bull. 2011;137(4):594–615. doi: 10.1037/a0023489. [DOI] [PubMed] [Google Scholar]
- 8.Baum EB. On the capabilities of multilayer perceptrons. J Complex. 1988;4(3):193–215. doi: 10.1016/0885-064X(88)90020-9. [DOI] [Google Scholar]
- 9.Berthelot D, Schumm T, Metz L (2017) Began: boundary equilibrium generative adversarial networks. arXiv preprint arXiv:1703.10717
- 10.Brams SJ (2003) Negotiation games: applying game theory to bargaining and arbitration, vol 2, Psychology Press
- 11.Caicedo JC, Roth J, Goodman A, Becker T, Karhohs KW, Broisin M, … Carpenter AE (2019) Evaluation of deep learning strategies for nucleus segmentation in fluorescence images. Cytometry Part A 95(9):952–965 [DOI] [PMC free article] [PubMed]
- 12.Carse J. Finite and infinite games. Simon and Schuster; 2011. [Google Scholar]
- 13.Carter E (2019) Deep learning for robust meta-analytic estimation
- 14.Chavdarova T, Fleuret F (2018) Sgan: an alternative training of generative adversarial networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 9407–9415
- 15.Cheng J, Dong L, Lapata M (2016) Long short-term memory-networks for machine reading. arXiv preprint arXiv:1601.06733
- 16.Chivukula AS, Liu W. Adversarial learning games with deep learning models. In: 2017 international joint conference on neural networks (IJCNN) IEEE; 2017. pp. 2758–2767. [Google Scholar]
- 17.Chivukula AS, Liu W. Adversarial deep learning models with multiple adversaries. IEEE Trans Knowl Data Eng. 2018;31(6):1066–1079. doi: 10.1109/TKDE.2018.2851247. [DOI] [Google Scholar]
- 18.Chongxuan LI, Xu T, Zhu J, Zhang B. Triple generative adversarial nets. In: Advances in neural information processing systems. 2017. pp. 4088–4098. [Google Scholar]
- 19.Creswell A, White T, Dumoulin V, Arulkumaran K, Sengupta B, Bharath AA. Generative adversarial networks: an overview. IEEE Signal Process Mag. 2018;35(1):53–65. doi: 10.1109/MSP.2017.2765202. [DOI] [Google Scholar]
- 20.Darwish A, Hassanien AE, Das S (2019) A survey of swarm and evolutionary computing approaches for deep learning. Artificial intelligence review, pp 1–46
- 21.Dasgupta P, Collins JB (2019) A survey of game theoretic approaches for adversarial machine learning in cybersecurity tasks. arXiv preprint arXiv:1912.02258
- 22.David B. Grammars for games: a gradient-based, game-theoretic framework for optimization in deep learning. Front Robot AI. 2016;2:39. [Google Scholar]
- 23.Davis M, Maschler M. The kernel of a cooperative game. Naval Res Logist Q. 1965;12(3):223–259. doi: 10.1002/nav.3800120303. [DOI] [Google Scholar]
- 24.Deng Z, Zhang H, Liang X, Yang L, Xu S, Zhu J, Xing EP. Structured generative adversarial networks. In: Advances in neural information processing systems. 2017. pp. 3899–3909. [Google Scholar]
- 25.Ding M, Tang J, Zhang J. Semi-supervised learning on graphs with generative adversarial nets. In: Proceedings of the 27th ACM international conference on information and knowledge management. ACM; 2018. pp. 913–922. [Google Scholar]
- 26.Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. J Mach Learn Res. 2011;12(Jul):2121–2159. [Google Scholar]
- 27.Durugkar I, Gemp I, Mahadevan S (2016) Generative multi-adversarial networks. arXiv preprint arXiv:1611.01673
- 28.Esteva A, Robicquet A, Ramsundar B, Kuleshov V, DePristo M, Chou K, Dean J. A guide to deep learning in healthcare. Nat Med. 2019;25(1):24–29. doi: 10.1038/s41591-018-0316-z. [DOI] [PubMed] [Google Scholar]
- 29.Fedus W, Rosca M, Lakshminarayanan B, Dai AM, Mohamed S, Goodfellow I (2017) Many paths to equilibrium: GANs do not need to decrease a divergence at every step. arXiv preprint arXiv:1710.08446
- 30.Fei F. Integrate learning with game theory for societal challenges. Proceedings of the 28th International Joint Conference on Artificial Intelligence. AAAI Press; 2019. [Google Scholar]
- 31.Foerster J, Chen RY, Al-Shedivat M, Whiteson S, Abbeel P, Mordatch I. Learning with opponent-learning awareness. In: Proceedings of the 17th international conference on autonomous agents and MultiAgent systems. International Foundation for Autonomous Agents and Multiagent Systems; 2018. pp. 122–130. [Google Scholar]
- 32.Fukushima K. Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol Cybern. 1980;36(4):193–202. doi: 10.1007/BF00344251. [DOI] [PubMed] [Google Scholar]
- 33.Gadirov H (2018) Capsule architecture as a discriminator in generative adversarial networks
- 34.Glorot X, Bordes A, Bengio, Y. (2011) Deep sparse rectifier neural networks. In: Proceedings of the fourteenth international conference on artificial intelligence and statistics, pp 315–323
- 35.Goodfellow I (2016) NIPS 2016 tutorial: generative adversarial networks. arXiv preprint arXiv:1701.00160
- 36.Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y (2014) Generative adversarial nets. In: Advances in neural information processing systems, pp 2672–2680
- 37.Goodfellow I, Bengio Y, Courville A. Deep learning. MIT press; 2016. [Google Scholar]
- 38.Granmo OC (2018) The Tsetlin machine-a game theoretic bandit driven approach to optimal pattern recognition with propositional logic. arXiv preprint arXiv:1804.01508
- 39.Graves A, Mohamed AR, Hinton G. Speech recognition with deep recurrent neural networks. In: 2013 IEEE international conference on acoustics, speech and signal processing. IEEE; 2013. pp. 6645–6649. [Google Scholar]
- 40.Guo X, Singh S, Lewis R, Lee H (2016) Deep learning for reward design to improve Monte Carlo tree search in atari games. arXiv preprint arXiv:1604.07095
- 41.Gupta S. Multi-player generative adversarial networks. In: 2018 international high performance extreme computing conference (HPEC) IEEE; 2018. [Google Scholar]
- 42.Gurram P, Kwon H. Coalition game theory based feature subset selection for hyperspectral image classification. In: 2014 IEEE geoscience and remote sensing symposium. IEEE; 2014. pp. 3446–3449. [Google Scholar]
- 43.Halpern JY (2008) Computer science and game theory. The New Palgrave Dictionary of Economics 1–8:984–994
- 44.Hang S, Liu Q, Xia S. Multi-granularity network representation learning based on game theory. 2018 IEEE international conference on data mining workshops (ICDMW) IEEE; 2018. p. 2018. [Google Scholar]
- 45.Hartmann S, Weinmann M, Wessel R, Klein R (2017) StreetGAN: towards road network synthesis with generative adversarial networks
- 46.He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. pp. 770–778. [Google Scholar]
- 47.Heinrich J, Silver D (2016) Deep reinforcement learning from self-play in imperfect-information games. arXiv preprint arXiv:1603.01121
- 48.Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Comput. 2006;18(7):1527–1554. doi: 10.1162/neco.2006.18.7.1527. [DOI] [PubMed] [Google Scholar]
- 49.Hinton GE, Srivastava N, Krizhevsky A, Sutskever I, Salakhutdinov RR (2012) Improving neural networks by preventing co-adaptation of feature detectors. arXiv preprint arXiv:1207.0580
- 50.Hinton G, Deng L, Yu D, Dahl GE, Mohamed AR, Jaitly N, Senior A, Vanhoucke V, Nguyen P, Sainath TN, Kingsbury B. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups. IEEE Signal Process Mag. 2012;29(6):82–97. doi: 10.1109/MSP.2012.2205597. [DOI] [Google Scholar]
- 51.Hitawala S (2018) Comparative study on generative adversarial networks. arXiv preprint arXiv:1801.04271
- 52.Hjelm RD, Jacob AP, Che T, Trischler A, Cho K, Bengio Y (2017) Boundary-seeking generative adversarial networks. arXiv preprint arXiv:1702.08431
- 53.Ho J, Ermon S (2016) Generative adversarial imitation learning. In: Advances in neural information processing systems, pp 4565–4573
- 54.Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 55.Holmgård C, Liapis A, Togelius J, Yannakakis GN (2014) Generative agents for player decision modeling in games. In: FDG
- 56.Hsieh YP, Liu C, Cevher V (2018) Finding mixed Nash equilibria of generative adversarial networks. arXiv preprint arXiv:1811.02002
- 57.Huang G, Liu Z, Van Der Maaten L, Weinberger KQ (2017) Densely connected convolutional networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 4700–4708
- 58.Huang, C., Kairouz, P., Chen, X., Sankar, L. and Rajagopal, R., 2018. Generative adversarial privacy. arXiv preprint arXiv:1807.05306.
- 59.Hubel DH, Wiesel TN. Receptive fields of single neurones in the cat's striate cortex. J Physiol. 1959;148(3):574–591. doi: 10.1113/jphysiol.1959.sp006308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hubel DH, Wiesel TN. Receptive fields and functional architecture of monkey striate cortex. J Physiol. 1968;195(1):215–243. doi: 10.1113/jphysiol.1968.sp008455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ioffe S, Szegedy C (2015) Batch normalization: accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167
- 62.Jain AK, Mao J, Mohiuddin KM. Artificial neural networks: a tutorial. Computer. 1996;29(3):31–44. doi: 10.1109/2.485891. [DOI] [Google Scholar]
- 63.Jiequn H (2016) Deep learning approximation for stochastic control problems. arXiv preprint arXiv:1611.07422
- 64.Johnson ND, Mislin AA. Trust games: a meta-analysis. J Econ Psychol. 2011;32(5):865–889. doi: 10.1016/j.joep.2011.05.007. [DOI] [Google Scholar]
- 65.Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980
- 66.Kohonen T (1997) Exploration of very large databases by self-organizing maps. In: Proceedings of international conference on neural networks (icnn'97), vol 1). IEEE, pp PL1–PL6
- 67.Kossaifi J, Tran L, Panagakis Y, Pantic M (2018) Gagan: Geometry-aware generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 878–887
- 68.Lamba, A., 2013. Enhancing awareness of cyber-security and cloud computing using principles of game theory. Int J Adv Manag Technol Eng Sci, 3.
- 69.Lanctot M et al (2017) A unified game-theoretic approach to multiagent reinforcement learning. Advances in neural information processing systems
- 70.Larichev OI, Moshkovich HM. Verbal decision analysis for unstructured problems. Springer Science & Business Media; 2013. p. 51. [Google Scholar]
- 71.Leckie C, Peyam P, Jack R. Deep Learning Based Game-Theoretical Approach to Evade Jamming Attacks. Decision and Game Theory for Security: 9th International Conference, GameSec 2018, Seattle, WA, USA, October 29–31, 2018, proceedings. Springer; 2018. [Google Scholar]
- 72.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 73.Li J, Madry A, Peebles J, Schmidt L (2017) Towards understanding the dynamics of generative adversarial networks. arXiv preprint arXiv:1706.09884
- 74.Li X, Dvornek NC, Zhou Y, Zhuang J, Ventola P, Duncan JS. Efficient interpretation of deep learning models using graph structure and cooperative game theory: application to ASD biomarker discovery. In International conference on information processing in medical imaging. Cham: Springer; 2019. pp. 718–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Liang X, Xiao Y. Game theory for network security. IEEE Commun Surv Tutor. 2012;15(1):472–486. doi: 10.1109/SURV.2012.062612.00056. [DOI] [Google Scholar]
- 76.Lippi M. Statistical relational learning for game theory. IEEE Trans Comput Intell AI Games. 2015;8(4):412–425. doi: 10.1109/TCIAIG.2015.2490279. [DOI] [Google Scholar]
- 77.Liu J, Snodgrass S, Khalifa A, Risi S, Yannakakis GN, Togelius J. Deep learning for procedural content generation. Neural Comput & Applic. 2021;33(1):19–37. doi: 10.1007/s00521-020-05383-8. [DOI] [Google Scholar]
- 78.Lu Y, Kai Y (2020) Algorithms in multi-agent systems: a holistic perspective from reinforcement learning and game theory. arXiv preprint arXiv:2001.06487
- 79.Luce RD, Raiffa H. Games and decisions: introduction and critical survey. Courier Corporation; 1989. [Google Scholar]
- 80.Lucic M, Kurach K, Michalski M, Gelly S, Bousquet O (2018) Are gans created equal? A large-scale study. In: advances in neural information processing systems, pp 700–709
- 81.Malherbe C, Umarova RM, Zavaglia M, Kaller CP, Beume L, Thomalla G, Weiller C, Hilgetag CC. Neural correlates of visuospatial bias in patients with left hemisphere stroke: a causal functional contribution analysis based on game theory. Neuropsychologia. 2018;115:142–153. doi: 10.1016/j.neuropsychologia.2017.10.013. [DOI] [PubMed] [Google Scholar]
- 82.Mao X, Li Q, Xie H, Lau RY, Wang Z, Paul Smolley S. Least squares generative adversarial networks. In Proceedings of the IEEE international conference on computer vision. 2017. pp. 2794–2802. [Google Scholar]
- 83.Marchiori D, Nagel R, Schmidt J (2019) Heuristics, thinking about others, and strategic management: insights from behavioral game theory
- 84.Marsland S. Machine learning: an algorithmic perspective. Chapman and Hall/CRC; 2014. [Google Scholar]
- 85.Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A.A., Veness, J., Bellemare, M.G., Graves, A., Riedmiller, M., Fidjeland, A.K., Ostrovski, G. and Petersen, S., 2015. Human-level control through deep reinforcement learning. Nature, 518(7540), p.529. [DOI] [PubMed]
- 86.Moran N, Pollack J (2018) Coevolutionary neural population models. In artificial life, pp 39–46
- 87.Murugan R, Goel T (2021) E-DiCoNet: extreme learning machine based classifier for diagnosis of COVID-19 using deep convolutional network. J Ambient Intell Humaniz Comput:1–12 [DOI] [PMC free article] [PubMed]
- 88.Mycielski J. Games with perfect information. Handbook of game theory with economic applications. 1992;1:41–70. doi: 10.1016/S1574-0005(05)80006-2. [DOI] [Google Scholar]
- 89.Myerson RB. Game theory: analysis of conflict. Harvard university press; 1991. [Google Scholar]
- 90.Myerson RB. Game theory. Harvard university press; 2013. [Google Scholar]
- 91.Narahari Y. Game theory and mechanism design. World Scientific; 2014. [Google Scholar]
- 92.Nash JF. Equilibrium points in n-person games. Proc Natl Acad Sci. 1950;36(1):48–49. doi: 10.1073/pnas.36.1.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Nash J. Non-cooperative games. Ann Math. 1951;54:286–295. doi: 10.2307/1969529. [DOI] [Google Scholar]
- 94.Nguyen T, Le T, Vu H, Phung D (2017) Dual discriminator generative adversarial nets. In: Advances in neural information processing systems, pp 2670–2680
- 95.Nienke V, Van H, Denessen E. Effects of constructing versus playing an educational game on student motivation and deep learning strategy use. Comput Educ. 2011;56(1):127–137. doi: 10.1016/j.compedu.2010.08.013. [DOI] [Google Scholar]
- 96.Nisan N, Roughgarden T, Tardos E, Vazirani VV, editors. Algorithmic game theory. Cambridge university press; 2007. [Google Scholar]
- 97.Oliehoek FA, Savani R, Gallego-Posada J, Van der Pol E, De Jong ED, Groß R (2017) GANGs: generative adversarial network games. arXiv preprint arXiv:1712.00679
- 98.Oliehoek FA, Savani R, Gallego J, van der Pol E, Groß R (2018) Beyond local nashequilibria for adversarial networks. arXiv preprint arXiv:1806.07268
- 99.Osborne MJ (2004) An introduction to game theory, vol 3, no 3. Oxford university press, New York
- 100.Osborne MJ, Rubinstein A. A course in game theory. MIT press; 1994. [Google Scholar]
- 101.Paola U (2018) Combining deep learning and game theory for music genre classification. BS thesis. UniversitàCa'FoscariVenezia
- 102.Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, … Desmaison A (2019) PyTorch: an imperative style, high-performance deep learning library. In Advances in neural information processing systems, pp 8024–8035
- 103.Pfau D, Vinyals O (2016) Connecting generative adversarial networks and actor-critic methods. arXiv preprint arXiv:1610.01945
- 104.Pinto L, James D, Gupta A. Supervision via competition: robot adversaries for learning tasks. 2017 IEEE international conference on robotics and automation (ICRA) IEEE; 2017. p. 2017. [Google Scholar]
- 105.Qi GJ (2017) Loss-sensitive generative adversarial networks on lipschitz densities. arXiv preprint arXiv:1701.06264
- 106.Rabinowitz NC, Perbet F, Song HF, Zhang C., Eslami SM, Botvinick M (2018) Machine theory of mind. arXiv preprint arXiv:1802.07740
- 107.Ren K, Zheng T, Qin Z, Liu X. Adversarial attacks and defenses in deep learning. Engineering. 2020;6:346–360. doi: 10.1016/j.eng.2019.12.012. [DOI] [Google Scholar]
- 108.Rudrapal D, Boro S, Srivastava J, Singh S. A deep learning approach to predict football match result. In: Computational intelligence in data mining. Singapore: Springer; 2020. pp. 93–99. [Google Scholar]
- 109.Salimans T, Goodfellow I, Zaremba W, Cheung V, Radford A, Chen X (2016) Improved techniques for training gans. In: Advances in neural information processing systems, pp 2234–2242
- 110.Saxe AM, Bansal Y, Dapello J, Advani M, Kolchinsky A, Tracey BD, Cox DD. On the information bottleneck theory of deep learning. J Stat Mech Theory Exp. 2019;2019(12):124020. doi: 10.1088/1742-5468/ab3985. [DOI] [Google Scholar]
- 111.Schuster M, Paliwal KK. Bidirectional recurrent neural networks. IEEE Trans Signal Process. 1997;45(11):2673–2681. doi: 10.1109/78.650093. [DOI] [Google Scholar]
- 112.Schuster A, Yamaguchi Y (2010) Application of game theory to neuronal networks. Advances in Artificial Intelligence, 2010
- 113.Schuurmans D, Zinkevich MA (2016) Deep learning games. In: Advances in neural information processing systems, pp 1678–1686
- 114.Schwenker F, Kestler HA, Palm G. Three learning phases for radial-basis-function networks. Neural Netw. 2001;14(4–5):439–458. doi: 10.1016/S0893-6080(01)00027-2. [DOI] [PubMed] [Google Scholar]
- 115.Sengupta N (2021) Information generation in interactions: the link between evolutionary game theory and evolutionary economics
- 116.Shapley LS (1953) A value for n-person games. Contributions to the Theory of Games, 2(28), pp 307–317
- 117.Shapley LS. Stochastic games. Proc Natl Acad Sci. 1953;39(10):1095–1100. doi: 10.1073/pnas.39.10.1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Shermila R, Maghsudi S, Hossain E (2017) Mobile edge computation offloading using game theory and reinforcement learning. arXiv preprint arXiv:1711.09012
- 119.Shin M, Joongheon K, Marco L. Auction-based charging scheduling with deep learning framework for multi-drone networks. IEEE Trans Veh Technol. 2019;68(5):4235–4248. doi: 10.1109/TVT.2019.2903144. [DOI] [Google Scholar]
- 120.Silver D, Schrittwieser J, Simonyan K, Antonoglou I, Huang A, Guez A, Hubert T, Baker L, Lai M, Bolton A, Chen Y. Mastering the game of go without human knowledge. Nature. 2017;550(7676):354. doi: 10.1038/nature24270. [DOI] [PubMed] [Google Scholar]
- 121.Srivastava RK, Greff K, Schmidhuber J (2015) Highway networks. arXiv preprint arXiv:1505.00387
- 122.Stier J, Gianini G, Granitzer M, Ziegler K. Analysing neural network topologies: a game theoretic approach. Procedia Computer Science. 2018;126:234–243. doi: 10.1016/j.procs.2018.07.257. [DOI] [Google Scholar]
- 123.Tembine H (2019) Deep learning meets game theory: Bregman-based algorithms for interactive deep generative adversarial networks. IEEE Trans Cybern [DOI] [PubMed]
- 124.Tennenholtz M. Game theory and artificial intelligence. In Foundations and applications of multi-agent systems. Berlin: Springer; 2002. pp. 49–58. [Google Scholar]
- 125.Vincent P, Larochelle H, Lajoie I, Bengio Y, Manzagol PA. Stacked denoisingautoencoders: learning useful representations in a deep network with a local denoising criterion. J Mach Learn Res. 2010;11(Dec):3371–3408. [Google Scholar]
- 126.Von Neumann J (1959) On the theory of games of strategy. Contributions to the Theory of Games, 4, pp 13–42
- 127.Wakatsuki M, Fujimura M, Nishino T. A decision making method based on society of mind theory in multi-player imperfect information games. In: Deep learning and neural networks: concepts, methodologies, tools, and applications. IGI Global; 2020. pp. 317–329. [Google Scholar]
- 128.Wang B (2018) From deep learning to deep deducing: automatically tracking down Nash equilibrium through autonomous neural agent, a possible missing step toward gneral AI
- 129.Wang Y Discriminative adversarial learning: a general framework for interactive learning
- 130.Wang K, Gou C, Duan Y, Lin Y, Zheng X, Wang FY. Generative adversarial networks: introduction and outlook. IEEE/CAA J Autom Sin. 2017;4(4):588–598. doi: 10.1109/JAS.2017.7510583. [DOI] [Google Scholar]
- 131.Wang B, Liu K, Zhao J (2017) Conditional generative adversarial networks for commonsense machine comprehension. In: IJCAI, pp 4123–4129
- 132.Wang J, Yu L, Zhang W, Gong Y, Xu Y, Wang B, Zhang P, Zhang D. Irgan: a minimax game for unifying generative and discriminative information retrieval models. In: Proceedings of the 40th international ACM SIGIR conference on research and development in information retrieval. ACM; 2017. pp. 515–524. [Google Scholar]
- 133.Wang H, Wang J, Wang J, Zhao M, Zhang W, Zhang F, Xie X, Guo M (2018) Graphgan: graph representation learning with generative adversarial nets. In: Thirty-Second AAAI Conference on Artificial Intelligence.
- 134.Wang RQ et al (2019) Scene recognition based on DNN and game theory with its applications in human-robot interaction. arXiv preprint arXiv:1912.01293
- 135.Wang EK, Chen C-M, Yiu SM, Hassan MM, Alrubaian M, Fortino G. Incentive evolutionary game model for opportunistic social networks. Futur Gener Comput Syst. 2020;102:14–29. doi: 10.1016/j.future.2019.07.034. [DOI] [Google Scholar]
- 136.Wiering M, Van Otterlo M. Reinforcement learning. Adapt Learn Optim. 2012;12:3. [Google Scholar]
- 137.Woo TH. Game theory based complex analysis for nuclear security using non-zero sum algorithm. Ann Nucl Energy. 2019;125:12–17. doi: 10.1016/j.anucene.2018.10.041. [DOI] [Google Scholar]
- 138.Wu TY, Lee WT, Guizani N, Wang TM. Incentive mechanism for P2P file sharing based on social network and game theory. J Netw Comput Appl. 2014;41:47–55. doi: 10.1016/j.jnca.2013.10.006. [DOI] [Google Scholar]
- 139.Xiao L, et al. A secure mobile crowdsensing game with deep reinforcement learning. IEEE Trans Inf Forensics Secur. 2017;13(1):35–47. doi: 10.1109/TIFS.2017.2737968. [DOI] [Google Scholar]
- 140.Yang LC, Chou SY, Yang YH (2017) MidiNet: a convolutional generative adversarial network for symbolic-domain music generation. arXiv preprint arXiv:1703.10847
- 141.Yegnanarayana B. Artificial neural networks. PHI Learning Pvt. Ltd; 2009. [Google Scholar]
- 142.Yoon JH, Lee BK, Kim BW. A study on GAN algorithm for restoration of cultural property (pagoda) J Korea Soc Comput Inf. 2021;26(1):77–84. [Google Scholar]
- 143.Yoshida W, Dolan RJ, Friston KJ. Game theory of mind. PLoS Comput Biol. 2008;4(12):e1000254. doi: 10.1371/journal.pcbi.1000254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Yu L et al (2018) Deep reinforcement learning for green security game with online information. Workshops at the Thirty-Second AAAI Conference on Artificial Intelligence
- 145.Zhang L, Wang W, Li S, Pan G (2019) Monte Carlo neural fictitious self-play: approach to approximate Nash equilibrium of imperfect-information games, arXiv:1903.09569v2
- 146.Zheng S, Jayasumana S, Romera-Paredes B, Vineet V, Su Z, Du D, Huang C, Torr PH (2015) Conditional random fields as recurrent neural networks. In: Proceedings of the IEEE international conference on computer vision, pp 1529–1537
- 147.Zhou C, Paffenroth RC (2017) Anomaly detection with robust deep autoencoders. In: Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pp 665–674
- 148.Zhou Y, Kantarcioglu M, Xi B. A survey of game theoretic approach for adversarial machine learning. Wiley Interdiscip Rev Data Min Knowl Discov. 2019;9(3):e1259. doi: 10.1002/widm.1259. [DOI] [Google Scholar]
- 149.Zhu JJ, Bento J (2017) Generative adversarial active learning. arXiv preprint arXiv:1702.07956
- 150.Zou J, Huss M, Abid A, Mohammadi P, Torkamani A, Telenti A. A primer on deep learning in genomics. Nat Genet. 2019;51(1):12–18. doi: 10.1038/s41588-018-0295-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Zurada JM. Introduction to artificial neural systems. St. Paul: West publishing company; 1992. [Google Scholar]