Abstract
Objective
To determine whether daylight savings time (DST) transitions have an effect on road traffic casualties in Great Britain using causal regression discontinuity design (RDD) analysis. We undertake aggregate and disaggregate spatial and temporal analyses to test the commonly referenced sleep and light hypotheses.
Design
The study takes the form of a natural experiment in which the DST transitions are interventions to be evaluated. Two outcomes are tested: (1) the total number of casualties of all severities and (2) the number of fatalities.
Data
Data were obtained from the UK Department for Transport STATS19 database. Over a period of 14 years between 2005 and 2018, 311 766 total casualties and 5429 fatalities occurred 3 weeks on either side of the Spring DST transition and 367 291 total casualties and 6650 fatalities occurred 3 weeks on either side of the Autumn DST transition.
Primary outcome measure
An RDD method was applied. The presence of a causal effect was determined via the degree of statistical significance and the magnitude of the average treatment effect.
Results
All significant average treatment effects are negative (54 significant models out of 287 estimated), indicating that there are fewer casualties following the transitions. Overall, bootstrapped summary statistics indicate a reduction of 0.75 in the number of fatalities (95% CI −1.61 to –0.04) and a reduction of 4.73 in the number of total casualties (95% CI −6.08 to –3.27) on average per year at both the Spring and Autumn DST transitions combined.
Conclusions
The results indicate minor reductions in the number of fatalities following the DST transitions, and thus, our analysis does not support the most recent UK parliamentary estimate that there would be 30 fewer fatalities in Great Britain if DST was to be abolished. Furthermore, the results do not provide conclusive support for either the sleep or light hypotheses.
Keywords: public health, statistics & research methods, sleep medicine
Strengths and limitations of this study.
We adopt a causal regression discontinuity design method to generate robust estimates of the impact of daylight savings time transitions on road traffic casualties and fatalities in Great Britain.
We undertake both aggregate and disaggregate spatial and temporal analyses to investigate the impacts of sleep and light disruptions at the transitions.
We account for potential confounding through the inclusion of seasonal variables at the level of year, day of week and time of day, and treat heteroscedasticity and autocorrelation to account for unobserved confounders.
Limitations include potential under-reporting of casualties in the Department for Transport STATS19 database, sparse data leading to estimation difficulties in the northernmost regions of Scotland and the presence of potential additional unobserved confounders that could lead to biased estimates.
Introduction
Since its introduction, the implementation of daylight savings time (DST) has been a contentious issue which has regained attention in recent times. In response to a public consultation held in 2018, the European Parliament in 2019 adopted a position to support the elimination of daylight savings in the European Union (EU), with plans for implementation in 2021.1 2 The UK initiated an inquiry to analyse the impact of the EU change to ‘understand what factors should inform [the UK’s] approach’.3 The UK also previously debated and ultimately rejected changes to daylight savings in the Daylight Saving Bill 2010–2011, which proposed to shift UK time forward by 1 hour throughout the year to align with Central European Time (CET).4 A key argument in the elimination or alteration of DST is the impact that clock changes have on road safety. In both the academic literature and government parliamentary debates, two issues are highlighted as having an impact on road safety levels: (1) changes in daylight hours could impact alertness due to the required chronobiological adjustments to the human circadian rhythm,1 5 6 herein referred to as the ‘sleep hypothesis’; and (2) changing of daylight hours could result in detrimental changes to visibility,3 4 7 8 herein referred to as the ‘light hypothesis’.
Evidence on the impact of DST transitions on road traffic casualties is currently inconclusive. In the 2010–2011 Daylight Saving Bill, it was argued that there would be 80 fewer fatalities on UK roads if the UK switched to CET.4 In the more recent UK report on the proposed EU changes, it was stated that abolishing time changes and adopting a permanent move to UK Summer Time could result in 30 fewer fatalities.3 However, it is unclear how these figures were generated and whether robust causal statistical analysis methods were adopted. In the academic literature, there is mixed consensus regarding the impact of DST transitions. Increases in road casualties are reported for studies undertaken in the USA by Smith9 and in New Zealand by Robb and Barnes,10 while reductions in casualties in the USA are reported by Coate and Markowitz11 and Crawley.12 Lindenberger et al13 reports no significant impacts in their analysis of road casualties in Germany.
The aim of this paper is to estimate the causal effect of DST transitions on the number of road traffic casualties and fatalities in Great Britain. This paper contributes to the literature from several perspectives. First, the majority of studies adopt non-causal techniques to quantify the impact of DST transitions, including comparisons of descriptive statistics, linear regression based on ordinary least squares and quasi-Poisson regression.10 11 13–15 Two studies by Carey and Sarma7 and Uttley and Fotios16 adopt a causal regression discontinuity design (RDD) method similar to ours; however, the studies focus on road casualties in the USA and pedestrian casualties in the UK, respectively. We therefore contribute to the literature by adopting a causal RDD method to analyse road traffic casualties in Great Britain, which, to our knowledge, has not been previously undertaken. Second, use of the RDD method with time as the forcing variable requires stringent specification tests to be undertaken to ensure that the models are free from potential confounding factors that can lead to biased estimates. In the literature on RDD methods applied to DST analyses, these specification tests are not typically performed. In our analysis, we follow the recommendations made in Hausman and Rapson17 to test for model robustness. Finally, there are a number of studies in the UK and USA indicating both causal and non-causal relationships between light levels and casualties at DST transitions14–16 18 19; however, we are not aware of causal studies testing the sleep hypothesis at DST transitions. Therefore, in addition to a pooled analysis of Great Britain as a whole, we also undertake disaggregate spatial and temporal analyses to test the sleep and light hypotheses.
Methods
Study area and data
The STATS19 database produced by the Department for Transport is used to obtain records of road traffic accidents that resulted in personal injury in Great Britain between 2005 and 2018 (data set).20 Casualties are defined as personal injuries of any severity as a result of an accident event. As specified by the Department for Transport,21 a single accident event can be associated with more than one casualty. In this analysis, we focus on total casualties (all severities combined) and fatal casualties.
Three week windows on either side of the DST transitions in Spring and Autumn are extracted from the total accident data set. Three weeks is chosen to provide enough data for the optimised local bandwidth to be calculated for each scenario as part of the RDD modelling. It should be noted that after calculation of the optimal bandwidth, the window around the DST transitions is likely to be much shorter than 3 weeks; further details on the optimal bandwidth calculations are given in the RDD framework section. Through data cleaning, less than 0.02% of records have been removed as a result of missing observations in the fields representing latitude and longitude and accident event timestamps as well as records over bank holidays as these observations could potentially represent abnormal out-of-season traffic levels which could confound the baseline time trends before and after the DST transitions. The numbers of casualties and fatalities for all of Great Britain over 3-week windows on either side of the transitions are summarised in table 1. As shown in the table, there are increases in the number of casualties and fatalities after both transitions when considering 3-week windows before and after the transitions. Again, it should be noted that this study considers the impact on casualties in the immediate vicinity of the transition dates, and so the 3-week windows will shrink considerably after calculation of the optimal bandwidth around the transition dates for each model. Therefore, the general trend for the aggregate 3-week windows showing more casualties after the transitions may not be applicable at shorter bandwidths.
Table 1.
Number of casualties, aggregated over great Britain over ±3 week windows from DST transition dates
| Casualty severity | Spring | Autumn | ||
| Before DST | After DST | Before DST | After DST | |
| Total casualties | 153 107 | 158 659 | 175 796 | 191 495 |
| Fatal casualties | 2517 | 2912 | 3211 | 3439 |
DST, daylight savings time.
To investigate whether the DST transitions have different regional effects across Great Britain, National Ordnance Survey data are used to divide Great Britain into distinct bands based on latitude and longitude.22 Using the Ordnance Survey Grid Reference variable within STATS19, we assign each accident event and associated casualties a northings band and an eastings band.
RDD framework
DST is a policy enacted for the entire population of Great Britain and the treatment assignment is deterministic; that is, there is no ambiguity in treated versus untreated observations. Therefore, the DST treatment imposed at the Spring and Autumn transitions is considered as a sharp discontinuity. Further information on RDD frameworks is presented in Imbens and Lemieux23 and in Lee and Lemieux.24
In this analysis, we use spatiotemporal units where refers to a given local area zone within Great Britain; refers to a given time period, where each day is segmented into five time periods; and refers to year. The assignment of the treatment, that is, the imposition of the daylight savings transition, is solely dependent on the value of the forcing variable, time , as follows:
| (1) |
where is the treatment threshold, which is defined as the DST transition date, and is the binary treatment in the sharp RDD. At the Spring transition, the treatment is the imposition of Summer Time, while at the Autumn transition, the treatment is the return to GMT. Observations recorded between 00:00 and 01:00 in March and between 00:00 and 02:00 in October on the day of the transition are designated as non-treated in line with when the transition occurs. Over the analysis time period of 2005–2018, the transition dates for Spring range from 25 to 31 March and those for Autumn range from 25 to 31 October.
The observation of a discontinuity in the average treatment effect on either side of the treatment threshold is evidence of a causal effect of the treatment.23 24 The average treatment effect for a sharp discontinuity in time is defined as
| (2) |
where indicates the potential outcome when treatment is received and indicates the potential outcome when treatment is not received. The second equality holds assuming continuity of expectations in ; that is, .23
Since the forcing variable is time, we follow the recommendations in Hausman and Rapson17 to address potential specification issues. To ensure that there are enough observations in the vicinity of the treatment threshold, we segment daily data into five time periods, and the data are aggregated at a local area zone level which also provides cross-sectional variance at each time point. By segmenting the data to increase the number of observations close to the treatment threshold, we avoid the need to include observations further away from the threshold, which can introduce bias from unobserved confounding variables. We account for potential bias from known confounding variables correlated with time through the inclusion of covariates representing potential seasonal variation in casualties. The covariates are year, day of the week and the time period associated with each observation. Since the daylight savings transitions are universally applied at fixed transition dates, we do not anticipate issues arising from manipulation of treatment status. Further specification tests are undertaken to ensure validity of the design, and these are discussed in the Specification tests section.
The data sets are arranged in a pseudo-panel form with indexes of local area zone and time period per year. The response variable is the sum of the number of casualties per local area zone and time period per year; in cases where no casualties are observed, a value of 0 is designated. For each of the Spring and Autumn transitions, two base regressions are undertaken as follows: (1) the total number of casualties of all severities and (2) the total number of fatalities. The two base regressions are run for three scenarios: (1) for Great Britain overall, (2) for each northing band in each time period and (3) for each easting band in each time period. We adopt a local linear specification for the forcing variable of time. The bandwidth for the models is specified according to the conventional method of minimising the mean squared error (MSE) of the average treatment effect.25–27 This selection procedure selects the shortest (ie, local) bandwidth in the vicinity of the treatment threshold subject to the minimisation of the MSE, thus ensuring that the key assumption of random treatment is upheld. The optimal bandwidth selection process is considered superior to nominating an arbitrary bandwidth as was common in the earliest implementations of RDD as it is objective and data-driven rather than subjective.25 The ‘rdrobust’ package in the R statistical analysis software is used for the optimal bandwidth calculation.27 28
The general equation for the aggregate model of Great Britain is given in equation 3. The regional and time of day analyses enable the investigation of the sleep and light hypotheses. It should be noted that in the disaggregate models, the time of day covariate in equation 3 is not included as the models are presegmented by time of day. All modelling has been undertaken using R statistical analysis software.
| (3) |
where is the total number of casualties per local area zone per time period per year ; is the treatment assignment indicator as previously defined; is the average treatment effect of interest; represents the average long-term trend across the entire bandwidth, that is, ; and is the time trend after the intervention where and . The categorical variables , , condition for year, day of the week and time period, respectively. Year takes a value from 1 to 14 corresponding to the years 2005–2018. As coded in the STATS19 database, the day of the week takes a value of 1–7 with 1 corresponding to Sunday and 7 corresponding to Saturday. The time of the day takes values as follows: overnight=1, AM peak=2, interpeak=3, PM peak=4 and night=5. The peak time periods follow the standards adopted by the Department for Transport: AM peak (07:00–09:59), interpeak (10:00–15:59) and PM peak (16:00–18:59).21 Two additional time bins are added to complete a 24-hour period: overnight (0:00–06:59) and night (19:00–23:59). and are the model constant and model random error term, respectively, where .
It should be noted that the inclusion of group-specific fixed effects for local area zone was trialled to account for potential time-invariant cross-sectional differences. However, using the Bayesian information criterion (BIC) as an indicator of model performance, we found that a majority of models performed better with no local area zone effects compared with those with local area effects, and so these effects are not included in the final model form.
Specification tests
As recommended by Hausman and Rapson,17 we perform the following specification tests:
Specification checks are performed for the bandwidth by varying the bandwidth within the vicinity of the optimal bandwidth and verifying that the magnitude and significance of average treatment effect remains consistent.
Specification checks are performed for the polynomial order of the forcing variable of time. The BIC is used to judge model performance. Polynomials of up to degree 4 are tested, and we verify that the local linear specification performs best in line with the bandwidth selection procedure.
The Breusch-Godfrey test29 30 is performed to test for autocorrelation of the error term for a lag value up to 10 (2 days). If autocorrelation is present, it is treated using Newey-West standard errors,31 which are heteroscedasticity and autocorrelation consistent.
The Breusch-Pagan test32 is performed to test for heteroscedasticity. If heteroscedasticity is present with no error term autocorrelation, it is treated with heteroscedasticity consistent (HC3) errors.33
-
We perform placebo tests as per the recommendations in Imbens and Lemieux23 to verify the model specification. We partition the original data for each model at the DST cut-off to obtain two smaller data sets. We then calculate a placebo cut-off which is equivalent to the mean value of the running variable in each data set. We perform two placebo tests for each original model by undertaking the RDD analysis for the placebo cut-offs before the DST cut-off and after the DST cut-off. The original models pass the placebo test if both placebo models yield an insignificant average treatment effect.
Note: Autoregression of the dependent variable is not considered in this analysis since the majority of casualties per local area zone do not occur in consecutive time periods.
The R code for the generation of the RDD models and all specification tests is provided as online supplemental file.
bmjopen-2021-054678supp001.pdf (53.1KB, pdf)
Patient and public involvement statement
Please note that no patients nor members of the public were involved in this study.
Results
The results for the aggregate Spring and Autumn RDD models are presented in table 2. The results for the disaggregate spatial and temporal RDD analyses are presented in tables 3 and 4. All results tables summarise cases where the RDD models have passed all specification tests as described in the Specification tests section, and the average treatment effect at the DST transition is significant at a minimum significance level of α=0.05 (≥95%). A map of the corresponding northing and eastings bands is given in figure 1. As shown in the figure, higher band numbers represent more northern and more eastern locations. For further information, we have additionally included plots for every significant model including the original observations and fitted values as a online supplemental file. We have generated two plots for each scenario: the first shows all data points including the extent of raw observations, and the second is zoomed in to highlight the time trends.
Table 2.
Aggregate models of Great Britain: RDD results summary
| Transition | Location | Casualty type | BW | % change | ||||
| Spring | Aggregate Great Britain | All casualties | 32 | 173 888 | 32 133 | 27 842 | −0.075 (0.009)*** | 0.003 |
| Fatalities | Not significant | |||||||
| Autumn | Aggregate Great Britain | All casualties | Not significant | |||||
| Fatalities | Not significant | |||||||
Significance notation: p values 0, ‘***’; 0.001, ‘**’; 0.01, ‘*’; 0.05, ‘.’; 0.1, ‘ 1’.
BW in time period units.
SEs in parentheses.
BW, bandwidth; n, total number of observations; RDD, regression discontinuity design; Yafter, total number of casualties or fatalities after the cut-off; Ybefore, total number of casualties or fatalities before the cut-off; τSRD, sharp RDD average treatment effect due to daylight savings time transition.
Table 3.
Spring transition, disaggregate spatial and temporal models: RDD results summary
| Location | Band | Time period | All casualties | Fatalities | ||||||||||
| BW | n | % Change | BW | n | % Change | |||||||||
| Aggregate | 1 | 22 | 27 145 | 1260 | 1507 | −0.110 (0.024)*** | −0.12 | 40 | 12 744 | 133 | 81 | −0.067 (0.022)** | −0.70 | |
| 4 | 38 | 43 472 | 6565 | 6597 | −0.059 (0.020)** | −0.01 | ||||||||
| 5 | 46 | 48 906 | 6918 | 4456 | −0.130 (0.025)*** | −0.03 | ||||||||
| Northing band | 1000–2000 | 1 | 28 | 9925 | 474 | 591 | −0.095 (0.034)** | −0.28 | ||||||
| 3 | 36 | 15 992 | 3880 | 3623 | −0.162 (0.042)*** | −0.06 | ||||||||
| 4 | 38 | 16 008 | 2350 | 2343 | −0.067 (0.029)* | −0.04 | ||||||||
| 5 | 48 | 17 991 | 2606 | 1610 | −0.146 (0.041)*** | −0.08 | ||||||||
| 2000–3000 | 3 | 74 | 19 698 | 3182 | 3346 | −0.137 (0.047)** | −0.06 | |||||||
| 3000–4000 | 1 | 34 | 8365 | 315 | 340 | −0.075 (0.035)* | −0.33 | 44 | 2648 | 25 | 19 | −0.046 (0.021)* | −2.58 | |
| 3 | 64 | 14 496 | 3197 | 3044 | −0.167 (0.063)** | −0.07 | ||||||||
| 5 | 52 | 13 233 | 1342 | 1073 | −0.086 (0.042)* | −0.09 | ||||||||
| Easting band | 3000–4000 | 1 | 28 | 8370 | 324 | 311 | −0.148 (0.056)** | −0.64 | 62 | 4510 | 67 | 34 | −0.139 (0.055)* | −2.89 |
| 4000–5000 | 1 | 30 | 11 814 | 522 | 479 | −0.069 (0.030)* | −0.18 | |||||||
| 3 | 74 | 28 000 | 6172 | 6235 | −0.171 (0.049)*** | −0.04 | ||||||||
| 5 | 50 | 20 000 | 2244 | 1874 | −0.083 (0.038)* | −0.05 | ||||||||
| 5000–6000 | 1 | 28 | 8530 | 428 | 559 | −0.104 (0.039)** | −0.34 | |||||||
| 3 | 70 | 24 066 | 5588 | 5651 | −0.090 (0.037)* | −0.02 | ||||||||
| 4 | 26 | 8565 | 1479 | 848 | −0.110 (0.045)* | −0.10 | ||||||||
| 5 | 44 | 15 453 | 2235 | 1388 | −0.149 (0.045)*** | −0.09 | ||||||||
Significance notation: p values 0, ‘***’; 0.001, ‘**’; 0.01, ‘*’; 0.05, ‘.’; 0.1, ‘1’.
SEs in parentheses.
Time periods are as follows: 1, overnight; 2, AM peak; 3, interpeak; 4, PM peak; 5, night.
BW, bandwidth; n, total number of observations; RDD, regression discontinuity design; Yafter, total number of casualties or fatalities after the cut-off; Ybefore, total number of casualties or fatalities before the cut-off; τSRD, sharp RDD average treatment effect due to daylight savings time transition.
Table 4.
Autumn transition, disaggregate spatial and temporal models: RDD results summary
| Location | Band | Time period | All casualties | Fatalities | ||||||||||
| BW | n | % Change | BW | n | % Change | |||||||||
| Aggregate | 1 | 18 | 16 197 | 1035 | 1043 | −0.096 (0.019)*** | −0.13 | 38 | 13 671 | 104 | 97 | −0.030 (0.012)* | −0.40 | |
| 3 | 72 | 75 642 | 20 645 | 20 684 | −0.101 (0.028)*** | −0.01 | ||||||||
| 4 | 34 | 37 821 | 7728 | 5448 | −0.077 (0.024)** | −0.01 | ||||||||
| 5 | 32 | 37 821 | 7449 | 3851 | −0.231 (0.030)*** | −0.04 | 60 | 24 936 | 285 | 282 | −0.035 (0.016)* | −0.17 | ||
| Northing band | 0–1000 | 1 | 38 | 2534 | 90 | 53 | −0.153 (0.058)** | −2.38 | ||||||
| 5 | 64 | 5044 | 389 | 297 | −0.156 (0.062)* | −0.56 | ||||||||
| 1000–2000 | 1 | 24 | 10 015 | 630 | 572 | −0.158 (0.036)*** | −0.35 | 40 | 4888 | 50 | 19 | −0.052 (0.017)** | −1.45 | |
| 4 | 30 | 12 048 | 1993 | 1837 | −0.129 (0.036)*** | −0.09 | ||||||||
| 2000–3000 | 1 | 32 | 9695 | 408 | 353 | −0.112 (0.035)** | −0.39 | |||||||
| 5 | 48 | 12 708 | 1534 | 891 | −0.190 (0.058)** | −0.17 | ||||||||
| 3000–4000 | 1 | 26 | 6010 | 289 | 265 | −0.152 (0.045)*** | −0.74 | |||||||
| 4 | 40 | 9576 | 1475 | 1540 | −0.118 (0.042)** | −0.11 | ||||||||
| 5000–6000 | 2 | 48 | 3440 | 261 | 309 | −0.076 (0.031)* | −0.41 | |||||||
| 7000–8000 | 5 | 70 | 1470 | 66 | 69 | −0.094 (0.045)* | −1.84 | |||||||
| 8000–9000 | 1 | 56 | 583 | 34 | 27 | −0.280 (0.097)** | −11.53 | |||||||
| 5 | 66 | 793 | 89 | 51 | −0.362 (0.128)** | −5.69 | ||||||||
| Easting band | 1000–2000 | 1 | 64 | 1092 | 30 | 20 | −0.072 (0.036)* | −3.34 | ||||||
| 2000–3000 | 3 | 78 | 3210 | 26 | 37 | −0.056 (0.021)** | −3.00 | |||||||
| 4 | 54 | 7018 | 853 | 678 | −0.091 (0.043)* | −0.15 | ||||||||
| 3000–4000 | 1 | 26 | 8195 | 411 | 352 | −0.136 (0.040)*** | −0.46 | |||||||
| 5 | 44 | 14 985 | 2189 | 1351 | −0.222 (0.050)*** | −0.14 | ||||||||
| 4000–5000 | 1 | 26 | 9825 | 498 | 473 | −0.129 (0.032)*** | −0.36 | |||||||
| 5 | 44 | 17 874 | 2840 | 1663 | −0.252 (0.057)*** | −0.12 | ||||||||
| 5000–6000 | 1 | 22 | 8525 | 566 | 534 | −0.187 (0.037)*** | −0.46 | 44 | 4491 | 34 | 12 | −0.042 (0.014)** | −1.71 | |
| 4 | 34 | 12 033 | 2397 | 1532 | −0.127 (0.039)** | −0.07 | ||||||||
| 5 | 48 | 15 408 | 2853 | 1807 | −0.279 (0.056)*** | −0.14 | ||||||||
| 6000–7000 | 5 | 42 | 2394 | 257 | 106 | −0.191 (0.086)* | −1.04 | |||||||
Significance notation: p values 0, ‘***’; 0.001, ‘**’; 0.01, ‘*’; 0.05, ‘.’; 0.1, ‘1’.
SEs in parentheses.
Time periods are as follows: 1, overnight; 2, AM peak; 3, interpeak; 4, PM peak; 5, night.
BW, bandwidth; n, total number of observations; RDD, regression discontinuity design; Yafter, total number of casualties or fatalities after the cut-off; Ybefore, total number of casualties or fatalities before the cut-off; τSRD, sharp RDD average treatment effect due to daylight savings time transition.
Figure 1.
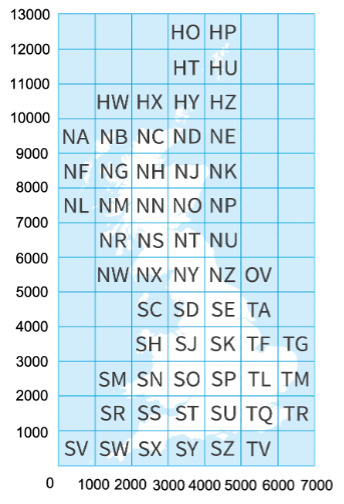
Notes:Values on the x-axis refer to eastings bands, and values on the y-axis refer to northings bands. The two letters in each grid square refer to specific locations on the UK national grid; the exact naming of each square can be found at Ordnance Survey.22
bmjopen-2021-054678supp002.pdf (19.2MB, pdf)
Spring transition
As shown in the tables, all models with significant average treatment effects show a reduction in the number of casualties at the Spring transition. For the whole of Great Britain, approximately 0.075 (-0.003%) fewer total casualties are observed on average per year. The time of day models further indicate reductions in total casualties ranging from 0.06 to 0.13 fewer casualties per year across the overnight, PM peak and night periods (in percentages, −0.01% to −0.03%). In terms of fatalities in isolation, there are 0.07 (−0.7%) fewer fatalities observed in the overnight period.
Latitudinal analysis
In the disaggregate models of northing bands, there are significant reductions in total casualties in 3 out of 12 bands. The reductions range from approximately 0.07 to 0.17 fewer total casualties (−0.04% to −0.33%) per year in all time periods except the morning peak. In terms of fatalities, there are 0.05 fewer fatalities per year (−2.58%) in the overnight time period in band 3000–4000.
Longitudinal analysis
In the disaggregate models of easting bands, there are significant effects in 3 out of 7 bands. There are approximately 0.07–0.17 fewer total casualties (−0.02% to −0.64%) observed in all time periods except the morning peak. For the fatality models, in band 3000–4000, there is a significant reduction of 0.14 fatalities (−2.89%) in the overnight time period.
Autumn transition
As with the Spring transition, in the Autumn transition, all models with significant average treatment effects report a reduction in casualties. Considering Great Britain as a whole, there are no significant effects. However, when splitting by time of day, there are reductions in total casualties in every time period except the morning peak, ranging from 0.08 to 0.23 fewer total casualties on average per year (−0.01% to −0.13%). In terms of fatalities, there are 0.03 fewer fatalities (−0.40%) in the overnight time period and 0.04 fewer fatalities (−0.17%) in the night time period.
Latitudinal analysis
In the disaggregate models of northing bands, there are significant effects in 7 out of 12 bands. The effects range from a 0.08 to 0.36 reduction in the total number of casualties (−0.09% to −11.53%), and all significant effects are observed across all time periods except the interpeak. For fatalities, in band 1000–2000, there are 0.05 fewer fatalities (−1.45%) in the overnight time period.
Longitudinal analysis
In the disaggregate models of easting bands, six out of seven bands report significant effects in the total number of casualties. All significant effects are negative, and they are observed in all time periods except the AM peak and interpeak. The effects range from 0.07 to 0.28 fewer total casualties (−0.07% to −3.34%). For the fatality models, in band 2000–3000, there are 0.06 fewer fatalities (−3.00%) in the interpeak, and in band 5000–6000, there are 0.04 fewer fatalities (−1.71%) in the overnight time period.
Discussion
Pooled analysis of Great Britain
When Great Britain is viewed as a whole regionally and without time segmentation, there is a statistically significant causal effect indicating a very minor reduction of 0.075 (0.003%) in the total number of casualties at the Spring DST transition. The average treatment effects in all other pooled analyses are insignificant at a minimum significance level of ≥95%.
When segmenting the data, there are further geographical zones and time periods with statistically significant average treatment effects. Our analyses therefore indicate that it is important to investigate the impacts of DST transitions at disaggregate spatial and temporal levels, as well as the aggregate effects.
Spring transition
At the Spring transition, clocks are moved forward 1 hour, resulting in an hour less sleep. The reduction in sleep could have an impact on road casualties throughout the day. In the morning, civil twilight sunrise times change from approximately 05:00–5:30 to 06:00–6:30 across Britain. There is an hour less sleep and mornings are darker by an hour before 06:00–6:30. These conditions could result in a compounding effect of the sleep and light hypotheses, likely resulting in an increase in casualties. However, for all models with significant effects in the associated overnight period (from 00:00 to 07:00), there is a reduction in total casualties and fatalities, in opposition to the sleep and light hypotheses.
In terms of regional effects, in the most western locations of Great Britain, the sun rises approximately 23 min later than the most eastern locations. As the civil twilight sunrise times coincide with the beginning of the morning peak in traffic, there could be a possibility of more casualties in the darker western locations compared with the east. Furthermore, sunrise at the most southern locations occurs approximately 20 min after the most northern locations, and so there could be a possibility of more casualties in the south relative to the north. For the northing and easting time of day models, we do not observe a systematic pattern showing progressively more casualties in the west and south; thus, we cannot provide conclusive support for the regional light hypothesis.
At the Spring transition, civil daylight occurs throughout the AM peak (07:00–10:00), interpeak (10:00–16:00) and PM peak (16:00–19:00), and so the light hypothesis is not applicable in these time periods. The sleep hypothesis is applicable, and sleepiness could manifest throughout the day, leading to potential increases in casualties. However, all models with significant effects in these time periods indicate reductions in total casualties, in opposition to the sleep hypothesis.
In the evening, civil twilight sunset times change from approximately 19:00–19:30 to 20:00–20:30 across Great Britain. There is an hour less sleep throughout the day, but evenings are lighter by an hour in the off-peak travel time after 19:00–19:30, therefore resulting in a potential conflict of the sleep and light hypotheses. In all significant models in the associated night time period (19:00–00:00), there is a reduction in the total number of casualties. This result aligns with the light hypothesis but at the same time opposes the sleep hypothesis; however, it is not possible to disentangle the effects. In terms of regional effects of the light hypothesis, the most western locations experience sunset approximately 23 min after the most eastern locations, so there may be potential for increased casualties in the east compared with the west due to the light hypothesis; however, the results do not support this. There is minimal difference (approximately 10 min) between sunset times in the north and south, and so we do not anticipate substantial differences between these locations. In the analysis of northing bands, there are only two models with significant effects in the night time period which show similar reductions in total casualties; however, this does not provide substantial systematic evidence of support for the regional light hypothesis.
Autumn transition
At the Autumn transition, clocks are moved back 1 hour, and this can lead to an hour more sleep. The increase in sleep could have an impact on road casualties throughout the day. In the morning, civil twilight sunrise times change from approximately 07:00–7:30 to 06:00–6:30 across Great Britain. There is an hour more sleep and mornings are lighter by an hour before the morning peak travel time, therefore compounding the sleep and light hypotheses and resulting in the most appropriate conditions for a reduction in casualties. For all models with significant effects in the associated overnight and AM peak periods, there are reductions in total casualties and fatalities. These results therefore support the compounded impact of the sleep and light hypotheses, though it is not possible to disentangle the individual impacts of the two hypotheses. In terms of regional impacts, the most eastern locations experience civil twilight sunrise approximately 23 min before the most western locations, and so eastern locations are expected to report greater reductions in casualties. Furthermore, the most southern locations experience sunrise approximately 21 min before the most northern locations, and so southern locations are expected to report greater reductions in casualties. However, the results show minimal support for a systematic pattern that progressively shows a greater reduction in casualties towards the east and south in the overnight and AM periods; thus, we cannot conclude conclusive support for the regional light hypothesis.
At the Autumn transition, civil daylight occurs throughout the interpeak period (10:00–16:00), and so there are no anticipated effects from the light hypothesis. However, the sleep hypothesis could apply, as there is an extra hour of sleep gained throughout the day, potentially leading to a reduction in casualties. Indeed, for all models with significant effects in the interpeak, there are reductions in total casualties and fatalities, thus supporting the sleep hypothesis.
In the evenings, civil sunset times change from approximately 18:00–18:30 to 17:00–17:30 across Great Britain. There is an hour more sleep throughout the day, but evenings are darker by an hour during the PM peak of traffic. In this situation, there is a potential conflict between the sleep and light hypotheses. All models with significant effects in the PM peak period (16:00–19:00) report reductions in total casualties and fatalities. Therefore, the results support the sleep hypothesis but oppose the light hypothesis; however, it is not possible to disentangle the impacts of the two. In terms of regional effects, sunset in the most eastern locations occurs approximately 24 min before sunset in the most western locations, and so we can expect more casualties in the east. Sunset in the most northern locations occurs approximately 13 min before sunset in the most southern locations. Though it is difficult to ascertain whether it is feasible to expect regional differences, it could be plausible to anticipate more casualties in the north. However, the northing and easting band models do not provide support for a systematic pattern that progressively shows a greater increase in casualties towards the east and north in the night period; thus, the results do not support the regional light hypothesis.
Magnitude of impacts at DST transitions
In the Daylight Savings Bill 2010–2011, it was estimated that there would be 80 fewer fatalities if the UK followed CET time.4 A more recent report on EU DST changes states that there would be 30 fewer fatalities as a result of eliminating DST transitions altogether.3
Overall, our analysis suggests that DST transitions have a minor positive impact rather than a detrimental impact on road traffic casualties and fatalities. All statistically significant models (54 models) report a negative average treatment effect, indicating a reduction in the number of casualties at the DST transitions. Over the 13 northings bands, 7 eastings bands and aggregate models, we attempted to generate a total of 212 models for total casualties and fatalities, respectively. However, due to sparse data in several bands, a number of models were not able to be estimated; 167 were able to be estimated for total casualties; and 120 were able to be estimated for fatalities. Of these, 46 out of 167 estimated models of total casualties have significant average treatment effects, and 8 out of 120 estimated models of fatalities have significant average treatment effects. A potential explanation for why there are fewer fatality models with a significant average treatment effect could be that there are relatively lower numbers of fatalities occurring either side of the DST threshold. Furthermore, we acknowledge that the models with insignificant average treatment effects indicate absence of evidence of a change in casualties/fatalities at the DST threshold rather than evidence of absence of a change in casualties/fatalities at the DST threshold.
We calculate the combined impact of the Spring and Autumn transitions on road casualties, and we generate associated 95% bootstrap CIs using 10 000 iterations as per the bias corrected and accelerated (BCa) bootstrap method.34 35 The statistic of interest that we bootstrap is calculated in two steps: (1) we sum all average treatment effects in the regional time of day models over the Spring and Autumn transitions combined; two estimates are generated: one for easting band segmentation and one for northing band segmentation; and (2) we calculate the mean of the easting and northing band values, and this is taken as the estimated combined number of casualties over the Spring and Autumn transitions. We perform this procedure for fatalities and total casualties separately.
The bootstrapped values indicate a mean reduction of 0.75 in the number of fatalities on average per year with a 95% CI ranging from −1.61 to −0.04 (reduction in fatalities). Our analysis therefore reports minor reductions in fatalities at the DST transitions rather than an increase of 30–80 fatalities as estimated in House of Lords3 and Bennett.4
Similarly, for the total number of casualties of all severities, a mean reduction of 4.73 in the number of total casualties is estimated on average per year with a 95% CI ranging from −6.08 to −3.27 (reduction in the total number of casualties). Therefore, the results for casualties of all severities also question the predictions of DST effects reported in House of Lords3 and Bennett.4
Limitations
One limitation of the RDD methodology is that it is applicable to ex post analyses and not suitable for making ex ante predictions. Therefore, the results reflect the impact of DST transitions on road safety over the study period of 2005–2018, and it is difficult to generalise the results to predict the impact of potential DST changes in the future. However, we have no compelling reason to believe that the average treatment effect will change significantly over time.
The data from the Department for Transport STATS19 database may also pose potential limitations, as the data are compiled from police reports. As a result, there could be potential under-reporting of casualties. One previous study estimated that the number of casualties classified as serious could be under-reported by a factor of two.36 Another data-related limitation is the sparse data in the northernmost regions of Scotland. Due to the limited number of observations, the RDD models reported high standard errors of the average treatment effect estimator and low statistical significance in these regions, and in some cases, estimates were not able to be computed. As such, in future work, either alternate data sources or alternate statistical analysis techniques for small sample data are recommended.
In the interpretation of the results in the Spring transition and the Autumn transition sections, we identified instances of where the sleep and light hypotheses were in conflict, and it was not possible to disentangle and quantify the separate impacts of the two hypotheses on road casualties. We therefore recommend future work to investigate how to disentangle the two effects, with a potential solution involving gathering disaggregate data on sleeping patterns and conditioning for this in the models.
Finally, it should be noted that we have addressed potential sources of bias by conditioning out exogeneous changes in traffic volumes which cannot be attributed to the DST transitions through the inclusion of seasonal year, day of week and time of day variables, along with treatment of heteroscedasticity and autocorrelation of the error term to account for potential unobserved confounders. However, there may be additional unobserved factors that we have not accounted for which may lead to potentially biased estimates. For example, we were not able to obtain a data set that identifies every school holiday in each local area zone nor were we able to obtain weather data at a time period level in each local area zone from 2005 to 2018. We acknowledge that this could lead to potentially biased values of the average treatment effect. However, we would also like to highlight that the bandwidths for each model are narrow around the cut-offs (the mean bandwidth across all models is 4.3 days on either side of the transition), and the narrow windows would minimise the degree of systematic impacts from school holidays and weather effects.
Conclusions
In this paper, we find that DST transitions have only a minor positive impact on road casualties and fatalities. For total casualties, 46 out of 167 models have significant average treatment effects, while for fatalities, 8 out of 120 models have significant effects. All models with a significant average treatment effect (54 models) report a negative effect, indicating a reduction in the number of casualties at the DST transitions.
Considering Great Britain as a whole, we find a significant effect indicating a minor 0.003% reduction in the total number of casualties in the Spring transition into DST. The average treatment effects in all other aggregate models are insignificant at a minimum significance level of ≥95%. When segmenting the data spatially and temporally, there are more models with statistically significant average treatment effects. This highlights the importance of investigating the impacts of DST transitions at a disaggregate level.
The disaggregate spatial and temporal models do not provide clear support or rejection of the sleep and light hypotheses at the transitions. At the Autumn transition, the temporal analyses indicate support for the compounded effect of the sleep and light hypotheses in the overnight and AM peak periods, as well as support for the sleep hypothesis in the interpeak period. For the remaining transitions, there is minimal support for the sleep and light hypotheses in both the temporal and regional analyses, and in some cases, it is difficult to disentangle potential conflicts between the sleep and light hypotheses. In cases where the hypotheses are not supported, other factors such as driver behaviour and other socioeconomic characteristics may be the main cause of the observed estimated changes.
In terms of policy impacts, the Daylight Savings Bill 2010–2011 estimates that 80 lives would be saved per year from transitioning to CET,4 and the report on EU DST changes estimates 30 lives saved per year as a result of abolishing DST altogether.3 Our results question these figures. We apply a BCa bootstrap with 10 000 iterations to estimate the total number of fatalities and casualties on average per year over the Spring and Autumn transitions combined. The bootstrapped values indicate a mean reduction of 0.75 in the number of fatalities (95% CI −1.61 to –0.04) and a mean reduction of 4.73 in the number of total casualties (95% CI −6.08 to –3.27) on average per year at both the Spring and Autumn DST transitions combined. The light hypothesis is the main driver for the Daylight Savings Bill, while both the sleep and light hypotheses are put forward in the recent report on abolishing DST altogether in the EU. However, as mentioned, we do not find definitive evidence to support the sleep and light hypotheses.
A number of areas for future work are recommended. In some cases, modelling was prohibited due to a lack of data in the north of Great Britain, and therefore, it is suggested that alternate data sources or alternate statistical analysis techniques for small sample data be employed to ascertain the impact of DST transitions in these regions. We also recommend further work to disentangle the impacts of the sleep and light hypotheses in cases where the two are in conflict. In regions where the sleep and light hypotheses did not hold, further research to investigate the impact of other potentially influential sociodemographic factors could be undertaken. In this analysis, we considered all casualties across all sociodemographic groups. Further analyses could be undertaken to provide a more disaggregate characterisation of the impact of DST transitions; for example, segmenting casualties by age could assist in testing whether DST transitions impact children walking to school as hypothesised in the Daylight Saving Bill 2010–2011.
Supplementary Material
Footnotes
Contributors: Conceptualisation, supervision and funding acquisition: DJG; data curation: RSo; methodology and writing (original draft, review and editing): RSi, RSo and DJG; formal analysis: RSi and RSo; Study guarantor: RSi and DJG.
Funding: The authors have not declared a specific grant for this research from any funding agency in the public, commercial or not-for-profit sectors.
Competing interests: None declared.
Patient and public involvement: Patients and/or the public were not involved in the design, conduct, reporting or dissemination plans of this research.
Provenance and peer review: Not commissioned; externally peer reviewed.
Supplemental material: This content has been supplied by the author(s). It has not been vetted by BMJ Publishing Group Limited (BMJ) and may not have been peer-reviewed. Any opinions or recommendations discussed are solely those of the author(s) and are not endorsed by BMJ. BMJ disclaims all liability and responsibility arising from any reliance placed on the content. Where the content includes any translated material, BMJ does not warrant the accuracy and reliability of the translations (including but not limited to local regulations, clinical guidelines, terminology, drug names and drug dosages), and is not responsible for any error and/or omissions arising from translation and adaptation or otherwise.
Data availability statement
Data are available in a public, open access repository. The data used in this study are available open-source from the Department for Transport at the following URL: https://www.gov.uk/government/collections/road-accidents-and-safety-statistics.
Ethics statements
Patient consent for publication
Not applicable.
References
- 1.European Commission . Proposal for a Directive of the European Parliament and of the Council discontinuing seasonal changes of time and repealing Directive 2000/84/EC. Technical Report COM(2018)0639 2018.
- 2.European Parliament . European Parliament legislative resolution of 26 March 2019 on the proposal for a directive of the European Parliament and of the Council discontinuing seasonal changes of time and repealing Directive 2000/84/EC (COM(2018)0639 – C8-0408/2018 – 2018/0332(COD)) 2019.
- 3.Lords Hof. Clock changes: is it time for change?. technical report European Union Committee, 5th report of session 2019–21. House of Lords Authority, 2020. [Google Scholar]
- 4.Bennett O. Daylight saving bill 2010-11, 2010. [Google Scholar]
- 5.Meira E Cruz M, Miyazawa M, Manfredini R, et al. Impact of daylight saving time on circadian timing system: an expert statement. Eur J Intern Med 2019;60:1–3. 10.1016/j.ejim.2019.01.001 [DOI] [PubMed] [Google Scholar]
- 6.Varughese J, Allen RP. Fatal accidents following changes in daylight savings time: the American experience. Sleep Med 2001;2:31–6. 10.1016/s1389-9457(00)00032-0 [DOI] [PubMed] [Google Scholar]
- 7.Carey RN, Sarma KM. Impact of daylight saving time on road traffic collision risk: a systematic review. BMJ Open 2017;7:1–14. 10.1136/bmjopen-2016-014319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Plainis S, Murray IJ, Pallikaris IG. Road traffic casualties: understanding the night-time death toll. Inj Prev 2006;12:125–8. 10.1136/ip.2005.011056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Smith AC. Spring forward at your own risk: daylight saving time and fatal vehicle crashes. Am Econ J Appl Econ 2016;8:65–91. 10.1257/app.20140100 [DOI] [Google Scholar]
- 10.Robb D, Barnes T. Accident rates and the impact of daylight saving time transitions. Accid Anal Prev 2018;111:193–201. 10.1016/j.aap.2017.11.029 [DOI] [PubMed] [Google Scholar]
- 11.Coate D, Markowitz S. The effects of daylight and daylight saving time on us pedestrian fatalities and motor vehicle occupant fatalities. Accid Anal Prev 2004;36:351–7. 10.1016/S0001-4575(03)00015-0 [DOI] [PubMed] [Google Scholar]
- 12.Crawley J. Testing for robustness in the relationship between fatal automobile crashes and daylight saving time. PHD thesis. University of California, Berkeley, 2012. [Google Scholar]
- 13.Lindenberger LM, Ackermann H, Parzeller M. The controversial debate about daylight saving time (DST)-results of a retrospective forensic autopsy study in Frankfurt/Main (Germany) over 10 years (2006-2015). Int J Legal Med 2019;133:1259–65. 10.1007/s00414-018-1960-z [DOI] [PubMed] [Google Scholar]
- 14.Adams J, White M, Heywood P. Year-round daylight saving and serious or fatal road traffic injuries in children in the north-east of England. J Public Health 2005;27:316–7. 10.1093/pubmed/fdi047 [DOI] [PubMed] [Google Scholar]
- 15.Sullivan JM, Flannagan MJ. The role of ambient light level in fatal crashes: inferences from daylight saving time transitions. Accid Anal Prev 2002;34:487–98. 10.1016/s0001-4575(01)00046-x [DOI] [PubMed] [Google Scholar]
- 16.Uttley J, Fotios S. The effect of ambient light condition on road traffic collisions involving pedestrians on pedestrian crossings. Accid Anal Prev 2017;108:189–200. 10.1016/j.aap.2017.09.005 [DOI] [PubMed] [Google Scholar]
- 17.Hausman C, Rapson DS. Regression discontinuity in time: considerations for empirical applications. Annu Rev Resour Economics 2018;10:533–52. 10.1146/annurev-resource-121517-033306 [DOI] [Google Scholar]
- 18.Raynham P, Unwin J, Khazova M, et al. The role of lighting in road traffic collisions. Lighting Research & Technology 2020;52:485–94. 10.1177/1477153519870857 [DOI] [Google Scholar]
- 19.Fotios S, Robbins CJ, Uttley J. A comparison of approaches for investigating the impact of ambient light on road traffic collisions. Lighting Research & Technology 2021;53:249–61. 10.1177/1477153520924066 [DOI] [Google Scholar]
- 20.Department for Transport . Data from: road casualty annual statistics. STATS19 database Repository, 2021. Available: www.gov.uk/government/collections/road-accidents-and-safety-statistics
- 21.Department for Transport . Reported road casualties in Great Britain: notes, definitions, symbols and conventions. Department for Transport, 2017: 1–6. [Google Scholar]
- 22.Ordnance Survey . Using the National grid, 2021. Available: getoutside.ordnancesurvey.co.uk/guides
- 23.Imbens GW, Lemieux T. Regression discontinuity designs: a guide to practice. J Econom 2008;142:615–35. 10.1016/j.jeconom.2007.05.001 [DOI] [Google Scholar]
- 24.Lee DS, Lemieux T. Regression discontinuity designs in economics. J Econ Lit 2010;48:281–355. 10.1257/jel.48.2.281 [DOI] [Google Scholar]
- 25.Cattaneo MD, Vazquez-Bare G. The choice of neighborhood in regression discontinuity designs. Observational Studies 2016;2:134–46. [Google Scholar]
- 26.Imbens G, Kalyanaraman K. Optimal bandwidth choice for the regression discontinuity estimator. Rev Econ Stud 2012;79:933–59. 10.1093/restud/rdr043 [DOI] [Google Scholar]
- 27.Calonico S, Cattaneo Matias, D., Titiunik R. Rdrobust: an R package for robust nonparametric inference in regression-discontinuity designs. R J 2015;7:38–51. 10.32614/RJ-2015-004 [DOI] [Google Scholar]
- 28.Thoemmes F, Liao W, Jin Z. The Analysis of the Regression-Discontinuity Design in R. Journal of Educational and Behavioral Statistics 2017;42:341–60. 10.3102/1076998616680587 [DOI] [Google Scholar]
- 29.Breusch TS. Testing for autocorrelation in dynamic linear MODELS*. Aust Econ Pap 1978;17:334–55. 10.1111/j.1467-8454.1978.tb00635.x [DOI] [Google Scholar]
- 30.Godfrey LG. Testing against General autoregressive and moving average error models when the Regressors include Lagged dependent variables. Econometrica 1978;46:1293–301. 10.2307/1913829 [DOI] [Google Scholar]
- 31.Newey WK, West KD. A simple, positive Semi-Definite, Heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 1987;55:703–8. 10.2307/1913610 [DOI] [Google Scholar]
- 32.Breusch TS, Pagan AR. A simple test for heteroscedasticity and random coefficient variation. Econometrica 1979;47:1287–94. 10.2307/1911963 [DOI] [Google Scholar]
- 33.MacKinnon JG, White H. Some heteroskedasticity-consistent covariance matrix estimators with improved finite sample properties. J Econom 1985;29:305–25. 10.1016/0304-4076(85)90158-7 [DOI] [Google Scholar]
- 34.DiCiccio TJ, Efron B. Bootstrap confidence intervals. Statistical Science 1996;11:189–228. 10.1214/ss/1032280214 [DOI] [Google Scholar]
- 35.Efron B. Better bootstrap confidence intervals. J Am Stat Assoc 1987;82:171–85. 10.1080/01621459.1987.10478410 [DOI] [Google Scholar]
- 36.Ward H, Lyons R, Thoreau R. Under-Reporting of road casualties – phase 1. technical report road safety research report, 2006: 69. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
bmjopen-2021-054678supp001.pdf (53.1KB, pdf)
bmjopen-2021-054678supp002.pdf (19.2MB, pdf)
Data Availability Statement
Data are available in a public, open access repository. The data used in this study are available open-source from the Department for Transport at the following URL: https://www.gov.uk/government/collections/road-accidents-and-safety-statistics.


