Abstract
Rapid development of high-throughput technologies has permitted the identification of an increasing number of disease-associated genes (DAGs), which are important for understanding disease initiation and developing precision therapeutics. However, DAGs often contain large amounts of redundant or false positive information, leading to difficulties in quantifying and prioritizing potential relationships between these DAGs and human diseases. In this study, a network-oriented gene entropy approach (NOGEA) is proposed for accurately inferring master genes that contribute to specific diseases by quantitatively calculating their perturbation abilities on directed disease-specific gene networks. In addition, we confirmed that the master genes identified by NOGEA have a high reliability for predicting disease-specific initiation events and progression risk. Master genes may also be used to extract the underlying information of different diseases, thus revealing mechanisms of disease comorbidity. More importantly, approved therapeutic targets are topologically localized in a small neighborhood of master genes in the interactome network, which provides a new way for predicting drug-disease associations. Through this method, 11 old drugs were newly identified and predicted to be effective for treating pancreatic cancer and then validated by in vitro experiments. Collectively, the NOGEA was useful for identifying master genes that control disease initiation and co-occurrence, thus providing a valuable strategy for drug efficacy screening and repositioning. NOGEA codes are publicly available at https://github.com/guozihuaa/NOGEA.
Keywords: Systems pharmacology, Gene entropy, Disease gene network, Disease comorbidity, Drug repositioning
Introduction
The onset and progression of most complex diseases often involve the dysfunction of thousands of genes as well as certain altered interactions among them. High-throughput technologies such as gene expression profiling and whole-genome sequencing have permitted the identification of an increasing number of disease-associated genes (DAGs) [1], which may provide valuable insights into mechanisms of disease initiation and progression. However, as the existing DAGs are usually derived from multiple sources, they often contain large amounts of redundant or false positive information [2] due to collection bias and noise, such that causal relationships among these genes in most cases remain elusive. Therefore, identifying master genes that control disease state transitions from large numbers of DAGs plays a critical role in understanding the mechanisms of disease initiation. In addition, complex diseases show considerable comorbidity [3]. The defects of master genes in one disease may initiate interaction cascades that lead to the co-occurrence of multiple diseases in a given patient. Pharmacological targeting of the DAG module in the human interactome has proven to be a valuable strategy for drug efficacy screening [4]. At present, it is unclear whether the identification of master genes will further facilitate the network-based drug repositioning.
Recent trends in omics technologies and complex biological networks have led to a proliferation of attempts to find the master genes for different diseases. For example, genome-wide association studies (GWAS) have emerged as a powerful tool for detecting sequence variations associated with many human traits and diseases [5]. Due to the low frequency of many mutations, GWAS usually require large cohort size to attain sufficient statistical power. More importantly, GWAS identify only the genetic risk factors associated with the disease rather than the master genes of the disease phenotypes, because patient genomes contain a certain proportion of “passenger mutations” [6] and the initiation of many diseases is often triggered by the interplay between genetic and non-genetic factors. Transcriptome analysis is considered to be an effective complement of GWAS due to its ability to capture non-genetic perturbations to the organism. Yet variations in mRNA expression are sometimes caused by aberrant protein activities of upstream regulators such as transcription factors, making it difficult to directly identify the master gene set using transcriptome profiling [7].
Recently, gene co-expression-based approaches have been proposed to construct context-specific regulatory networks [8], and a local network entropy measure has been developed based on co-expression networks for identifying master genes [9]. While these approaches provide new ways to find master genes, building a highly confident co-expression regulatory network often requires large sample size, which is usually not available for relatively rare diseases. To overcome this limitation, protein–protein interaction (PPI) network-based approaches have been developed to infer master genes that are important for disease-related biological processes, such as predicting therapeutic targets [10] or driver genes [11]. Some topological parameters such as the degree and betweenness centrality of the nodes are usually used as important measures to screen master genes [12]. However, current approaches are based mainly on the constant global undirected interactome, ignoring the fact that disease initiation and therapeutics are frequently context-dependent, depending on specific tissues or pathological microenvironments [13]. Therefore, some genes that exhibit important topological properties on the interaction network, such as the hub genes [14], will be automatically selected as key regulators for disease state initiation and maintenance, leading to a possible increase in false-positive master genes. Conversely, some classes of genes presenting as upstream regulators of a signaling cascade, such as the G protein-coupled receptors [15], may be identified as dispensable genes due to their relatively low degrees in the interactome, thus decreasing the sensitivity for distinguishing core ones from the giant pool of DAGs.
In this study, we developed a network-oriented gene entropy approach (NOGEA) to quantify the perturbation or regulatory ability of each DAG in distinct disease contexts by assembling and interrogating disease-specific regulatory networks. For each disease, genes exhibiting high entropy values by our in silico method were identified as master genes, whose altered expression was considered to be sufficient for disease state transitions; these master genes were further adopted to investigate comorbidity and causal relationships among different diseases. We further confirmed that existing effective drugs are most likely to target the local module of master genes in the interactome, and identified 11 old drugs as potent anti-cancer agents for pancreatic cancer treatment.
Method
Dataset collection
The DAGs for all diseases analyzed in this study were obtained from four publicly available databases, including KEGG Disease [16], Comparative Toxicogenomics Database [17], Therapeutic Target Database [18], and PharmGKB [19]. All disease names and their corresponding IDs were standardized by mapping to Medical Subject Headings (MeSH; https://www.nlm.nih.gov/mesh/), and official gene symbols for these DAGs were retrieved from GeneCards (http://www.genecards.org/). We then conducted a disease filtering process to ensure disease specificity. We first removed diseases with levels < 2 on the MeSH trees, such as “nervous system diseases” and “cardiovascular diseases”, as these disease types are too broad. Tanimoto similarity (ratio of the number of shared DAGs to the number of joined DAGs) was then computed for each disease pair and used to remove diseases showing high similarity (>0.50) with its descendant diseases. The weighted directed PPI network was constructed using data from a previous study [20], which consisted of 13,684 weighted interactions among 6082 proteins. The DAGs were then mapped to corresponding proteins in the PPI network, and those diseases with at least 15 DAGs in the human interactome were retained, because they are likely to induce a module on the network. As a result, we obtained 11,414 disease–gene associations between 274 diseases and 2848 protein-coding genes. For each disease, we manually extracted drug–disease associations from the drug indication information in DrugBank [21]. In addition, we obtained drug–target interactions for all FDA-approved drugs from DrugBank. To construct a disease comorbidity network, we retrieved disease pairs with comorbidity relationships from a previous study [3] of 665 diseases and their corresponding genes extracted from Online Mendelian Inheritance in Man (OMIM) [22].
Construction of NOGEA
Construction of a flux matrix based on the expectation of the Bernoulli distribution
To construct the directed disease-specific gene networks, DAGs are mapped to the directed PPI network. For any given disease D, whose m DAGs can be mapped to the directed PPI network, an initial DAG vector is generated to represent the disease, where is the -th DAG. The directed shortest path between two DAGs of disease D is calculated using the “igraph” package [23] based on the R 3.32 environment (r-porject.org). For a given DAG pair of and , is a random variable that obeys the Bernoulli distribution and represents the interaction or information transferring from to . The distribution function of is defined as.
| (1) |
where or 0, indicating whether signal transduction exists between the paired nodes and , and is a scale parameter to adjust the likelihood for different distances. In addition, is the directed distance between the given paired nodes and , i.e., the number of edges in a directed shortest path connecting them, and is calculated using the “igraph” package based on Dijkstra’s algorithm, reflecting the possibility of the pairwise regulatory relationship from to . The details for determining the optimal scale parameter are presented in File S1 and Figures S1 and S2. Therefore, the space of “possible” values assumed by is , and if , represents the likelihood that there is a signaling flux between the paired nodes. In the field of network communication, it is widely accepted that the success rate of signal propagation decays exponentially with increasing distance [24]. In addition, previous studies have demonstrated that exponential decay is a popular kernel to characterize the network influence between two nodes [25]. Previously, we have used the exponential component to evaluate the association between two nodes in PPI networks [26]. Thus, we believe that the success probability of signal transduction between two proteins decays exponentially with the increase of their distance, and the exponential component is useful for representing the success probability. In this way, the stochastic information flux matrix for a given disease is obtained by a simplified equation.
| (2) |
And, is equal to the expectation of , where.
| (3) |
The expectation is subsequently used to estimate the distribution of signaling flux. For a given disease D with m DAGs, the biological signals may be transmitted between any paired nodes/DAGs and . We then assume that the edge (or the node pair) through which signals are passed is a random variable F, and its event space is.
| (4) |
where represents signals that may be transmitted from to .
Normalization of the flux matrix.
The probability distribution of signal flux is estimated from.
| (5) |
Where is the normalization constant or partition function, and
| (6) |
to ensure that the sum of the probability is 1.
Definition and calculation of disease gene entropy.
Based on the probability distribution of signal flux, we calculate the entropy for a given disease in terms of the weighted Shannon entropy formula, which can be interpreted as the degree of disorder or complexity for the disease-specific context.
| (7) |
where is the out-degree of node in the directed PPI network, which is calculated using the “igraph” package. Interestingly, we find that the disease entropy can be factorized as shown in Equation (8).
| (8) |
where is the gene entropy of DAG , which is obtained by.
| (9) |
Therefore, is a sub-entropy of disease entropy , and is considered as the “disorder contribution” to a disease-specific context.
Gene entropy value normalization
Through the aforementioned procedure, a gene entropy map is established for 274 diseases. For any given disease D, the gene entropy Z-scores are calculated, making the gene entropy values of different diseases comparable.
| (10) |
where and are the estimation of the expectation and standard deviation of for disease D, respectively. In addition, to assess the disturbance capability of a gene in a disease-specific network in a more intuitive manner, the rank scores for all DAGs are calculated according to their entropy values, which range from 0 to 1 and reflect their likelihood as master genes.
Rank score calculation of gene entropy
The gene entropy values for disease D are sorted in an ascending order, and a rank list is generated
| (11) |
where the is the rank score of . Note that those genes that possess equal entropy values have the same rank scores. For example, if there are k genes possessing equal entropy values , their rank scores are determined by Equation (12).
| (12) |
where is the position of in the ascending entropy value list. Based on the rank list, rank score vector is generated by Equation (13).
| (13) |
where and are the maximum and minimum values of , respectively.
Disease–gene classification based on the gene entropy values
To comprehensively explore the biological meaning of the entropy, we divide all DAGs into three (i.e., master, interim, and redundant) groups based on their entropy values using an adaptive approach. Briefly, we create an entropy value curve for each disease, and identify two inflection points in the curve as thresholds. Specifically, for each disease D, we rank each gene entropy value () in ascending order. Then we map each entropy value onto a two-dimensional coordinate system, such that the lowest entropy value () becomes coordinate (1,), the second lowest value becomes (2,), and so on, until the maximum entropy value () is reached. Two inflection points are identified in the entropy value curve from the intervals of 10th–50th percentile and 51st–90th percentile of all entropy values, respectively, which are separately defined as the threshold points of most rapid increase from the low to the medium and from the medium to the high entropy values. The entropy values corresponding to the two inflection points are used as the adaptive disease-specific classification thresholds. Master genes of all diseases are then merged and adopted as the whole master gene set to explore their common biological meanings. Interim and redundant genes from different diseases are treated in the same way to obtain the whole interim and redundant gene sets, respectively. Some genes may belong to all three gene sets (master, interim, and redundant), because they play different roles in distinct disease contexts.
Disease comorbidity relationship evaluation.
We first construct a real human disease comorbidity network (HDCN), where nodes represent diseases and edges represent the reported comorbidity relationships, respectively. Then, five different types of inferred disease comorbidity networks are built to compare with the HDCN: 1) a master gene-based disease network (M−GDN), where edges link two different diseases only if they share at least one high-entropy gene, 2) a redundant gene-based disease network (R-GDN), 3) an interim gene-based disease network (I-GDN), 4) an all DAG-based disease network (A-GDN), and 5) a traditional hereditary disease network (THDN). A Tanimoto coefficient is used to evaluate the similarity between different networks as shown in Equation (14).
| (14) |
where A and B are different networks, represents the edge set of a given network and is the number of edges in the network. To assess the significance of the similarity of different networks, a random gene-based disease network (R-GN) is randomly generated 1000 times and compared with the HDCN using Equation (14). In the R-GN, each disease involves a randomly sampled gene set with the same size as the disease in A-GDN.
Previous research has demonstrated that cellular interaction links result in statistically significant comorbidity patterns [3]. Therefore, we believe that the directed interaction strength from the DAGs of one disease to another in the directed cellular network can reflect the causal relationship between the two diseases. To evaluate whether a causal relationship exists between two diseases, we estimate the significance of the interaction strength between the DAGs of the disease pairs using the Monte Carlo method. We first define a raw causal relationship score (RCRS) for two given diseases D1 and D2.
| (15) |
where is calculated by Equation (1), is the directed distance between a paired master genes and , and is an indicator function. In addition, is calculated as.
| (16) |
where is a threshold, below which the probability is discarded and considered not contributive to the overall interaction, and is determined according to a previous study [27]. We then use a normalized causal relationship score (NCRS) to quantify the risk that disease D1 will induce disease D2. The NCRS is defined in Equation (17).
| (17) |
where and are the estimation of the expectation and standard deviation of RCRS under the same condition, respectively. Then, Monte Carlo simulation was performed 1000 times to estimate and by randomly sampling the same number of genes as and . In each simulation, the values and the mean and standard deviation of RCRS are calculated. To assess whether the causal relationship from disease D1 to D2 is significant, the P value of is further calculated as shown in Equation (18).
| (18) |
where is the total number of simulations, and is the number of random values that are larger than . The significance for RCRS is set to P < 0.01. Finally, for a disease pair D1 and D2, if both and are significant (P < 0.01), the two diseases are considered to be co-occurrent; whereas, if only one is significant (P < 0.01), we determine that a causal relationship exists between the two diseases.
Calculation of drug disturbance entropy
To quantify the effects of a drug on each disease based on the gene network entropy, we apply an ensemble approach, referred to as drug disturbance entropy (DDE), to evaluate the relationship between drug targets and disease-associated proteins (encoded by DAGs) in the interactome. We first evaluate the linkage strength between each DAG and drug target in the interactome, which is then transformed to a probability. The perturbation value for each target and DAG is defined as the product of the strength probability and the DAG entropy.
| (19) |
where represents the strength probability between drug target t and DAG , is the entropy value of DAG , and is the distance between drug target t and DAG . The raw DDE, which represents an estimate of a drug’s therapeutic effects through distinct targets, is defined as.
| (20) |
where is the perturbation entropy between target t and DAG , and is an indicator function as shown in Equation (21).
| (21) |
where is a cut-off threshold of the perturbation values, which is determined by extensive sampling, and relationships with a perturbation value below this threshold are discarded. The remaining values are summed as the raw DDE of the drug to the disease. The advantage of this procedure is that weak relationships are eliminated, which greatly reduces noise and improves the robustness of the measure. By sampling across the range of choices, the threshold that leads to the highest ROC AUC is chosen. We obtain the proper as by evaluating the performance of predictions of drug–disease associations. Detailed information for determining is depicted in File S1.
To avoid possible high DDE that may be caused by a large number of drug targets and DAGs, we convert raw DDE to a size-bias-free value using the mean and standard deviation of raw DDE modeled from sets of random molecules, so that the potential therapeutic effects between distinct drugs and diseases could be evaluated under the same metric. The raw DDE score is transformed to a size-bias-free score under Equation (22).
| (22) |
where and are the drug target set and the DAG set, respectively; and are the estimation of the expectation and standard deviation of DDE under this condition, respectively.
The estimation procedures of and are as follows: for each pair of , we construct 1000 random set pairs with targets and DAGs, preserving the degree distribution of the randomized targets and disease-associated proteins. To avoid repeatedly choosing the same nodes during the degree-preserving random selection, we use a binning approach as described in a previous report [4].
Cell culture and viability assays.
A human pancreatic adenocarcinoma cell line, moderately differentiated BxPC3, was obtained from the American Type Culture Collection (Manassas, VA, USA). Cells were maintained at 37 ℃ under 5% CO2 air atmosphere in Dulbecco’s Modified Eagle Medium supplemented with 10% fetal bovine serum. The BxPC3 cells were plated in 96-well tissue culture microtiter plates at a density of 5 × 103 cells/well and treated with the selected drugs for at least five different concentrations. Cytotoxic effects of drugs on cells were determined by the MTT assay. The absorbance was recorded on a microplate reader (Catalog No. DNM-9602, Beijing Pulang New Technology, Beijing, China) at a wavelength of 490 nm. The maximum drug effects on cell viability were experimentally observed at the endpoint, and the IC50 value was determined after 72 h of treatment. All experiments were performed in quadruplicate and repeated three times.
Results and discussion
Computation and characterization of gene entropy in disease networks
To identify master genes in distinct disease contexts, NOGEA model was developed (Fig. 1A and B). Briefly, Shannon entropy theory was applied to quantify the amount of disorder within intracellular signals in each disease-specific context, which was subsequently factorized as the summation of contribution of each DAG. First, directed disease-specific gene networks for 274 diseases were constructed to reflect the distinct disease contexts by mapping all DAGs (Table S1) to a previously established directed PPI network (Table S2) [20]. A directed network visualizes the hierarchy of intracellular signal transduction between the interacting proteins, and hence clearly reflects the importance of each DAG in a certain physiological and pathological context. The regulation likelihood between each pair of DAGs was then calculated based on the directed distance on the PPI network to generate a probability-based signaling flux matrix (Fig. 1A). Finally, the perturbation ability of each DAG in a disease-specific context was calculated by the network-oriented gene entropy metric (Fig. 1B; see Method). The distribution of entropy values for all DAGs is illustrated as a histogram in Figure S3, and the perturbation ability of each DAG was then ranked based on their entropy values (Table S1).
Fig. 1.
Computation and characterization of gene entropy in disease networks A. Construction of directed disease-specific gene networks by mapping DAGs to the directed PPI network and normalizing the interaction strength. B. Calculation of the perturbation ability (gene entropy) of each gene. C. Venn plot of the DAGs from different classes. Master, interim, and redundant represent master, interim, and redundant genes, respectively. D. and E. Enrichment results of master, interim, and redundant genes in the context of OMIM, cancer, and essential genes (D) and in the context of kinase, MR, and TF (E). F. Comparison of NOGEA performance with other methods for DAG prioritization using AUROC and AUPRC. G.–J. Correlations between gene entropy values and their connective in-degree (G), connective out-degree (H), connective degree (I), and betweenness centrality (J) in the primary directed PPI network. Connective degree, sum of in-degree and out-degree. K. Assessment of the association between gene entropy and four commonly used network topology parameters. DAG, disease-associated gene; PPI, protein–protein interaction; MeSH, Medical Subject Headings; T2DM, type 2 diabetes mellitus; OMIM, Online Mendelian Inheritance in Man; MR, membrane receptor; TF, transcription factor; AUROC, area under the receiver operating characteristic curve; AUPRC, area under the precision-recall curve; AUC, area under the curve.
To efficiently explore the biological features of entropy distribution for each disease, all DAGs were classified as “Master”, “Interim”, and “Redundant” genes which represent high-, medium-, and low-entropy genes, respectively. We created an entropy value curve for each disease and then identified two inflection points as thresholds to separate the low-, medium-, and high-entropy genes, respectively (see Method). We then merged the master genes of all diseases into a whole master gene set. Interim and redundant genes from different diseases were treated in the same way to obtain the whole interim and redundant gene sets, respectively. As a result, 770 master, 1894 interim, and 1332 redundant genes were obtained (Fig. 1C; Table S3).
In order to verify whether the master genes play a key role in disease initiation and development, enrichment analyses were performed using several well-established gene sets (Table S4). We observed that there was an overrepresentation (enrichment Z-score = 22.61) of master genes in the OMIM gene set, which was higher than the enrichment Z-scores of both interim and redundant genes (Fig. 1D). The “essential” genes were demonstrated to play critical roles in human diseases [28], and master genes were enriched in the “essential” gene set, whose Z-score was two times larger than that of the redundant genes (Fig. 1D). More importantly, we found that master genes were highly enriched in the cancer-associated gene set; however, redundant genes showed less enrichment (Fig. 1D). Further KEGG analysis of the master genes showed that these genes were mainly enriched in pathways with close relationships with cancer initiation and progression (Figure S4). For example, PI3K-Akt signaling pathway (has:04151), which is commonly perturbed in cancers, was found among the top 5 enriched pathways (P < 10E − 30). In a recent study, genes in the interactome were classified into different node types, in which “indispensable” nodes were found to be key players in mediating the transition of disease states. As shown in Figure S5A, we found that master genes were highly enriched in the “indispensable” gene set, but redundant genes were enriched in the “dispensable” gene set. Consistent with these observations, master genes were highly enriched in the “critical” gene set that acted as driver nodes in all control configurations (Figure S5B) [26]. Further dissection of all different functional classes within signaling proteins revealed that master genes were most likely enriched in the “kinase” and “membrane receptor (MR)” gene sets (Fig. 1E). In summary, these results indicate that the master genes are preferred key regulators in disease initiation and development, reflecting the reliability of the NOGEA method.
Traditional network topology parameters, such as the connective degree and betweenness centrality, are commonly used as baseline methods for characterizing the importance of nodes in biological networks [29]. To validate the effectiveness of NOGEA, we compared it with four baseline methods (connective degree, connective in-degree, connective out-degree, and betweenness centrality-based methods) and four newly proposed methods (Katz [30], Catapult [30], HANRD [31], and GPS [32]), all of which are network-based methods for prioritizing DAGs. We first compared the area under the receiver operating characteristic curve (AUROC) values between different methods (see Method) and found that NOGEA significantly outperformed both the baseline methods and the newly proposed methods (Fig. 1F). We further evaluated the area under the precision-recall curve (AUPRC) for each method. NOGEA consistently surpassed all other methods, overmatching the second-best method by ∼ 10% (Fig. 1F).
Correlations between gene entropy values and four traditional network topology parameters were assessed using Pearson’s correlation coefficients (PCCs). For most diseases, we observed that the PCCs between gene entropy values and network topology parameters were relatively small (<0.25; Figure S6A). Nonetheless, significant correlation was observed between the connective in-degree (R = 0.2254, P < 1.0E − 15; Fig. 1G), connective out-degree (R = 0.5239, P < 1.0E − 15; Fig. 1H), connective degree (sum of in-degree and out-degree; R = 0.3942, P < 1.0E − 15; Fig. 1I) and betweenness centrality (R = 0.1774, P < 1.0E − 15; Fig. 1J) for genes in the primary directed PPI network versus gene entropy values. Fisher’s exact test was then applied to further determine whether gene entropy is associated with these four traditional network topology parameters. Specifically, we constructed a contingency table to classify the DAGs into different bins based on their entropy values and network parameter values (Fig. 1K). We found that gene entropy was significantly associated with traditional network topology parameters, including connective degree (P < 0.01), connective in-degree (P < 0.01), connective out-degree (P < 0.01), and betweenness centrality (P < 0.01). All these results demonstrate that master genes prefer to possess high topology parameter values, indicating relative consistency between gene entropy and the four network topology parameters.
To investigate variation of the regulatory role of a specific gene in different diseases, we calculated the divergence-degree of gene entropy across diseases using the coefficient of variation (CV) (Table S1; Figure S6B). The results show that up to 60% of the DAGs have a high CV (>0.15), indicating that these DAGs play distinct roles in different disease contexts. We then examined the entropy value variation of the shared DAGs in different diseases, and observed that these DAGs usually exhibited similar entropy values in distinct diseases within the same disease category. For example, corticotropin-releasing hormone receptor 1 (CRHR1) is related to several mental health-associated diseases with similar entropy rank scores (rank > 0.80), including anxiety and depressive disorders (Table S1), which is consistent with its major role in mental disorders [33]. We also observed a low entropy rank score for CRHR1 in pulmonary disease (rank = 0.55), indicating variation in its regulatory role in distinct disease contexts. Further, we found that ∼ 15% of DAGs have approximately equal rank scores in their associated diseases. For instance, among these DAGs, both interleukin 4 receptor (IL4R) and phosphatidylinositol-4,5-bisphosphate 3-kinase catalytic subunit alpha (PIK3CA) have high rank scores in their associated diseases (Table S1), especially for neoplasms, suggesting their crucial roles in these diseases. Taken together, NOGEA provides a new way to explore the regulatory roles of each DAG in distinct disease contexts.
NOGEA for exploring disease comorbidity
Exploration of the underlying mechanisms of comorbidity, which refers to the co-occurrence of multiple diseases or disorders, is difficult due to complex interactions among environmental, lifestyle, and treatment-related factors [34]. In addition, disease comorbidity includes not only the co-occurrence of multiple diseases, but also the potential cause-and-effect relationships among these diseases. Thus, uncovering the underlying mechanisms of disease co-occurrence and causal relationships is of great significance for their prevention and treatment. Using experiment-based approaches or mathematical models, previous studies explored the molecular features of disease comorbidity for several diseases, including from gastritis to gastric cancer [35] and from diabetes to cancer [36]. However, existing experiment-based methods for exploring the underlying mechanisms of co-occurrence and causal relationships remain costly and labor-intensive, and sometimes focus on a small fraction of molecular features. Comparatively, mathematical models provide novel ways to reveal disease comorbidity using multi-omics data; however, these models are difficult to apply in other diseases, due to the lack of multi-scale information for these diseases.
The results discussed above demonstrate that NOGEA-inferred master genes are closely associated with disease initiation and development, prompting us to investigate whether the network entropy-based approach would be capable of uncovering the molecular basis of disease co-occurrence. Therefore, we constructed M−GDN, where an edge would link two different diseases if they share at least one master gene (Table S5). For comparison, we constructed five other disease comorbidity networks: R-GDN, I-GDN, A-GDN, THDN, and R-GN.
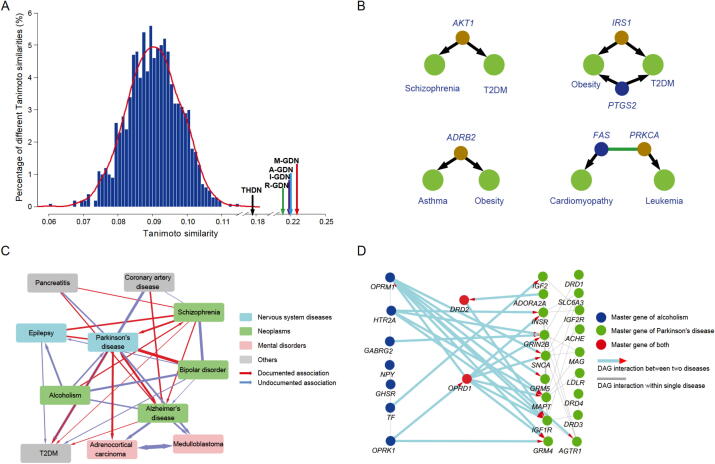
To test whether the M−GDN would provide an accurate picture of disease comorbidity, we evaluated the Tanimoto similarities between these networks and the HDCN, which was extracted from the Medicare Claims Database and constructed in a previous study [3]. The M−GDN showed the highest similarity with the HDCN (higher than that of R-GDN and THDN) and remarkably higher level than the average of random similarity values (Fig. 2A), which indicates that genes most associated with disease comorbidity tend to be master genes with high entropy rather than arbitrary DAGs. In contrast to previous THDN models, M−GDN considers genetic factors as well as genes that respond to environmental, lifestyle, and/or treatment-related factors, thus providing a more comprehensive solution for exploring disease comorbidity. Furthermore, in view of the impact of cellular network interactions on disease comorbidity, we extended our result to a PPI-based M−GDN (Table S6), where two diseases were linked if the master gene of one disease directly interacted with genes of the other disease in the PPI network. Consistent with the aforementioned results, the PPI-based M−GDN demonstrated the best predictive ability in identifying disease comorbidity. We then observed that the inferred underlying molecular mechanisms of disease comorbidity are in accordance with current pathobiological knowledge (Fig. 2B). For example, M−GDN confirmed the conclusion that AKT1 mutations lead to schizophrenia and type 2 diabetes mellitus (T2DM) [37], with entropy rank scores of 0.96 and 0.94 in schizophrenia and T2DM, respectively. We also observed that in the M−GDN, ADRB2 mutations may lead to asthma and obesity with entropy rank scores of 0.95 and 0.97 in asthma and obesity, respectively, which is consistent with a previous study [38]. Previous reports have suggested that mutations in the IRS1 gene are closely related to the comorbidity of T2DM and obesity [39], and PTGS2 influences the inflammatory response and is also closely connected with the comorbidity of T2DM and obesity [40]. Here, M−GDN also revealed that IRS1 and PTGS2 plays a crucial role in the comorbidity of T2DM and obesity. Another example revealed in M−GDN is the comorbidity of leukemia and cardiomyopathy, whose underlying mechanisms remain unclear. Interestingly, FAS is involved in the regulation of cell apoptosis, which affects left ventricular function [41], while PRKCA enhances cell resistance [42], regulates cardiac contractility, and has been implicated in increased risk for heart failure. More importantly, the FAS–PRKCA interaction has been identified as the top connected cross-talk PPI by in situ proximity ligation assays [43]. These results demonstrate that the interaction between FAS and PRKCA may account for the comorbidity of leukemia and cardiomyopathy. Taken together, these results suggest that M−GDN helps bridge the gap between bench-based biological discoveries and bedside clinical solutions, and thus may provide new insights into the mechanisms of disease comorbidity.
Fig. 2.
Exploration of disease comorbidity using NOGEA A. Distribution of Tanimoto similarities between HDCN and other disease comorbidity networks (M−GDN, I-GDN, R-GDN, A-GDN, THDN, and R-GN). B. The inferred molecular basis of disease comorbidity relationships. Brown and blue nodes represent master genes inferred by NOGEA; green nodes represent diseases. C. The comorbidity of Parkinson’s disease with other diseases. The width of the edge represents the likelihood of disease comorbidity; the arrows represent the inferred causative disease–disease associations; the color of the nodes depicts the disease category from MeSH. D. The molecular basis of the comorbidity between Parkinson’s disease and alcoholism. The nodes represent the disease-associated master genes, and the directed links describe the direction from the directed PPI network. HDCN, human disease comorbidity network; M−GDN, master gene-based disease network; I-GDN, interim gene-based disease network; R-GDN, redundant gene-based disease network; A-GDN, all DAG-based disease network; THDN, traditional hereditary disease network; R-GN, random gene-based disease network.
Next, we investigated the molecular basis of disease causal relationships from the perspective of directed biological networks. As an illustration, we constructed a directed comorbidity network (Fig. 2C; Table S7) centered on Parkinson’s disease. We observed high co-occurrence risks between Parkinson’s disease and other diseases including Alzheimer’s disease. Recent research suggests that these diseases are related to the accumulation of common proteins in the brain, such as alpha-synuclein protein [44]. Using alcoholism and Parkinson’s disease as an example, we observed a significant directed interaction from alcoholism to Parkinson’s disease (P < 0.01; see Method), but not vice versa. This result is consistent with recent clinical studies, which suggest that alcoholism may an inducer of Parkinson’s disease [45]. A subsequent network analysis further discovered that the aberration of alcoholism-associated master genes may lead to the modification of most Parkinson’s disease-associated master genes (Fig. 2D). Collectively, NOGEA is potentially useful for investigating mechanisms underlying disease comorbidity as well as their causal relationships.
NOGEA can infer drug–disease associations
Recently, several state-of-the-art network-based methods have been proposed to investigate the relationships between drugs and diseases, such as the network proximity approach (NPA) and network inference algorithm (NIA) [4], [46]. In this study, we assessed relationships between DAGs and drug targets based on the gene network entropy to evaluate the effects of drugs on each disease. For each drug–disease relationship, we calculated the DDE parameter, which represents potential therapeutic effects of the drug (Tables S8–S10; see Method). To further investigate DDE’s effectiveness, we evaluated the correlation between the DDE score and the number of hits for known drug–disease interactions (DDIs), and found that the occurrence number of known DDIs in each bin increased with increasing DDE scores (Fig. 3A). Consistent with previous research [4], a highly significant correlation occurred between the average DDE score of each bin and the enrichment fold of hits for known DDIs (R2 = 0.75, P = 2.2E − 16; Fig. 3B), indicating a high likelihood that a drug will successfully treat a disease if the drug is capable of strongly perturbing the local module of master genes in the interactome.
Fig. 3.
Drug–disease association inference based on NOGEA A. The number of possible drug–disease pairs hitting known DDIs in each bin. All possible drug–disease pairs are ranked by normalized DDE scores, and each bin contains 1000 possible drug–disease pairs. B. The correlation between the average DDE score of each bin and the enrichment fold of hits for known DDIs. C. Comparison of DDE performance with other drug–disease prediction methods by AUROC. D. The interaction between drug targets and pancreatic cancer-associated genes. The thickness of the link, the shade of the pancreatic cancer-associated gene node, and the size of the node describe the interaction strength, entropy value, and degree of each node in the human interactome, respectively. E. The heat map showing the shortest distance between the drug targets and pancreatic cancer-associated genes of four drugs (left) and the entropy value rank plot of pancreatic cancer-associated genes (right). DDI, drug–disease interaction; DDE, drug disturbance entropy; NPA, network proximity approach; NIA, network inference algorithm; NCA, network center approach; NKA, network kernel approach; NSEA, network kernel approach; NSA, network shortest approach.
To validate the utility of DDE for distinguishing known drug–disease pairs from the unknown ones, we compared the AUROC values for different drug–disease association prediction methods (see Method). To obtain a robust AUROC estimation, the drug–disease set was split into a training set and a testing set according to a given fraction coefficient for developing and validating the model, respectively (Figure S7). We compared the DDE’s performance with several other state-of-the-art methods [4], [46], including NIA, NPA, network kernel approach (NKA), network shortest approach (NSA), network center approach (NCA), and network separation approach (NSEA). As shown in Fig. 3C, DDE exhibited the best performance (average AUROC = 0.70) in discriminating known and unknown drug–disease pairs. Interestingly, NIA appeared to be the second-best method (average AUROC = 0.68), which was also able to construct a directed disease-specific gene network and identify master genes before predicting the drug–disease associations. A compressive comparison between the two methods demonstrated their connection and difference (File S1; Figure S8; Tables S11 and S12). Collectively, these results suggest that DDE is effective for predicting drug–disease associations.
Pancreatic cancer is a refractory malignant carcinoma of the digestive tract with a 5-year survival rate of ∼ 4% [47], and it modestly responds to very few existing chemotherapy treatment options. Revisiting the complex interaction pattern between drug targets and pancreatic cancer-associated genes in a systemic manner is essential for developing more effective therapeutic regimens. Therefore, we used pancreatic cancer as an example to explore the utility of NOGEA for drug–disease association inference. By measuring the entropy of each pancreatic cancer-associated gene in the pancreatic cancer-specific network (Fig. 3D and E), we found that those genes with high entropy such as MET, KDR (VEGFR-2), ERBB2, CD44, and EGFR may play more important roles than the lower-entropy genes for pancreatic cancer treatment. As reported in a previous study [48], EGFR-mediated signaling is involved in the tumorigenesis of pancreatic cancer, and the preclinical data support EGFR inhibition as a potential treatment strategy for pancreatic cancer. In addition, c-Met protein, which is encoded by the MET gene, is a marker of pancreatic cancer stem cells and thus a therapeutic target [49]. KDR is known to be crucial for embryonic vasculature development by modulating endothelial cell proliferation and migration [50]. Moreover, CD44 is a potentially interesting prognostic marker and therapeutic target in pancreatic cancer [51].
To investigate differences in the targeting patterns between effective drugs and other less-effective drugs from a network-based perspective, we constructed a gene entropy map for pancreatic cancer. We first calculated the linkage strength between drug targets and pancreatic cancer-associated genes for two FDA-approved drugs: axitinib and erythromycin (Fig. 3D). Axitinib targets FLT4, FLT1, and KDR, among which KDR was identified as a pancreatic cancer master gene by NOGEA. The DDE score of axitinib to pancreatic cancer was 37.6, suggesting that targets of axitinib are more closely related to pancreatic cancer-associated genes than expected by chance. Conversely, the DDE score of erythromycin (whose efficacy remains unknown) to pancreatic cancer was 1.1. Even though this drug inhibits ABCB1, ALB, and KCNH2, they are not closely related to pancreatic cancer-associated genes than expected by randomly selecting gene sets. However, some drugs that do not directly inhibit the pancreatic cancer-associated master genes may still have the potential to be effective drugs. For example, sirolimus, which is currently in phase II clinical trials, targets three proteins (FKBP1A, FGF2, and MTOR) but no known pancreatic cancer-associated genes. Nevertheless, sirolimus had a high DDE score of 12.1 to pancreatic cancer due to the relatively strong perturbation of high-entropy genes such as CD44 and EGFR (Fig. 3E) via FGF2. Drugs (e.g., pravastatin, DDE = − 0.7) were predicted to be ineffective pancreatic cancer drugs due to their weak perturbation of nearly all pancreatic cancer-associated genes (Fig. 3E). Collectively, these results suggest that NOGEA may be capable of identifying the core genes among many DAGs that provide the basis for rational drug discovery.
Screening of potential drugs for pancreatic cancer treatment
Due to the encouraging performance of the DDE metric for accurately inferring drug–disease associations, we screened potentially effective drugs for pancreatic cancer treatment. We first calculated and prioritized DDE scores for all FDA-approved drugs (Tables S13 and S14). From top 10% of these drugs, we selected 19 molecules that were not known to be associated with pancreatic cancer for further experimental validation. The half-maximal inhibitory concentration (IC50) of a molecule, an important metric to measure its response to a certain cancer cell line, has been widely applied in the screening of potential anti-proliferative agents in preclinical cancer pharmacogenomics. The BxPC3 human pancreatic cancer cell line, which has been frequently used in the studies of pancreatic cancer and screening of chemo preventive agents [52], was used in our in vitro study to evaluate its response to the candidate drugs. We identified 11 candidate drugs that inhibited BxPC3 cell line in a dose-dependent manner and exhibited low IC50 values (<100 μM; Fig. 4A–C, Figure S9), demonstrating their efficacies for inhibiting pancreatic cancer cell proliferation and potentials for pancreatic cancer therapy in vivo. One drug for example, vinorelbine, is a drug that has already been approved for non-small-cell lung cancer treatment [53]. In our study, vinorelbine exhibited a low IC50 value of 1.55 nM (Fig. 4A). Interestingly, some non-classical anti-cancer drugs also displayed acceptable suppressive effects on BxPC3. For example, saquinavir (mainly used with other medications for HIV/AIDS treatment or prevention [54]) and celecoxib (mainly used for treatment of pain and inflammation in adults [55]), showed low IC50 values of 22.63 μM (Fig. 4B) and 45.36 μM (Fig. 4C), respectively. These results indicate that our model has the capacity to predict proper drug candidates for disease therapy.
Fig. 4.
Screening of potential drugs for pancreatic cancer treatment A.–C. Cell inhibition rate curves for vinorelbine (A), saquinavir (B), and celecoxib (C) against BxPC3, respectively. D. Venn plot showing the overlap between SAQDEGs and SAQPAGs. E. Venn plot showing the overlap between CELDEGs and CELPAGs. F. Number of potentially efficient pancreatic cancer drugs (the top 10% FDA-approved drugs ranked by DDE scores) in each category. Number in red box indicates the number of drugs significantly associated with pancreatic cancer in literature mining analysis (P < 0.01, hypergeometric test); number in blue box indicates the number of selected drugs not significantly associated with pancreatic cancer in literature mining analysis. IC50, half-maximal inhibitory concentration; SAQDEG, differentially expressed gene after saquinavir treatment; SAQPAG, possibly affected pancreatic cancer-associated master gene after saquinavir treatment; CELDEG, differentially expressed gene after celecoxib treatment; CELPAG, possibly affected pancreatic cancer-associated master gene after celecoxib treatment; AIA, anti-inflammatory agent; AIANS, anti-inflammatory agent (non-steroidal); ANA, antineoplastic agent; ARA, antirheumatic agent; CVA, cardiovascular agent; CNSA, central nervous system agent; ISA, immunosuppressive agent; PNSA, peripheral nervous system agent; SSA, sensory system agent.
Transcriptional expression analysis was conducted to validate our hypothesis that efficient drugs tend to perturb the master genes directly or through their targets. We first identified 1335 differentially expressed genes (DEGs) after saquinavir treatment (referred to as SAQDEGs) (Figure S10A; Table S15). Then, we identified 849 most possibly affected pancreatic cancer-associated master genes after saquinavir treatment (named as SAQPAGs; Table S15), and further incorporated them with their corresponding neighbor genes in the interactome. Finally, a hypergeometric test was used to assess the overlap between SAQDEGs and SAQPAGs. The results showed that the SAQDEGs were significantly enriched for SAQPAGs (P < 0.01, Fig. 4D). Results for celecoxib treatment were similar to those for saquinavir treatment (Fig. 4E, Figure S10B), suggesting a close relationship between genes perturbed by the efficient drugs and the local module of master genes.
Finally, to demonstrate the reliability of the DDE approach for extensive screening of pancreatic cancer candidate drugs, we further conducted a literature mining analysis to evaluate the therapeutic potential of the top 10% FDA-approved drugs ranked by DDE scores (drugs without clear pharmacological category were excluded; n = 108) as described in our previous report [56] (see Method). We observed that 9 of the top 10 selected drugs were antineoplastic agents (ANAs) and showed significant correlation with pancreatic cancer (P < 0.01, Table S16). In addition, most selected drugs belonging to ANAs (27/31, 87.1%) were significantly associated with pancreatic cancer (Fig. 4F; Table S16), suggesting the sensitivity of this model. Interestingly, an analysis of the categories of these candidate drugs revealed that the largest proportion (41/108, 38.0%) was assigned to central nervous system agents (CNSAs) (Fig. 4F). For example, celecoxib, which is sensitive to the BxPC3 cell line as mentioned above (Fig. 4C), also acts as a CNSA. In general, these results indicate that DDE provides a rational strategy for drug repurposing due to its capacity to quantify drug targeting tendency in the interactome.
Conclusion
Disease phenotypes typically result from interactions among multiple complex environmental and genetic factors. The onset, development, and treatment of a disease usually involve hundreds of genes [29]. In this study, we propose NOGEA for accurately inferring master genes that contribute to specific diseases by quantitatively calculating their perturbation abilities on directed disease-specific gene networks. Our results confirm that master genes are enriched in gene sets that account for disease onset and development. This may imply that at a molecular level, master genes with high entropy are the underlying start points of the disease state, impacting those redundant genes with low entropy through a directed disease-specific gene network. Interestingly, the comorbidity prediction model built using the master genes shows the best agreement with the independent clinical dataset compared to the model established using the whole disease gene set. This indicates that our method may decrease the influence of noise and improve the efficiency for extracting more important genes from massive genomic datasets. Finally, through this method, 11 old drugs were newly identified and predicted to be effective for treating pancreatic cancer and then validated by in vitro experiments. However, it remains challenging to simulate the complex contents of the tumor microenvironment in vitro, making it difficult to comprehensively evaluate drug response using IC50. Therefore, despite our encouraging results, future work focusing on in vivo validation before clinical use is needed.
Although the identified master genes may be important for elucidating mechanisms of disease progression and drug screening, we acknowledge that it is difficult to directly evaluate the accuracy of NOGEA for identifying master genes at this stage due to the lack of ‘gold standard’ reference datasets. Nevertheless, the availability of more personal genome data in the future will allow for construction of patient-specific networks, and NOGEA will provide new opportunities to identify patient-specific master genes and promote the development of personalized medicine. Emerging deep learning methods may become powerful techniques for exploring poly-pharmacy side effects [57] and discovering disease–gene associations [58] from massive datasets [59]. Because gene entropy values can be used as novel disease feature data, we expect that integrating deep learning with NOGEA will significantly improve the accuracy for determining disease–drug or disease–disease associations. Extending the systematic approach presented here from signal drugs to multiple drugs may pave the way toward a better understanding of drug combinations.
Code availability
The source code and a detailed usage guide of NOGEA are freely available on GitHub at https://github.com/guozihuaa/NOGEA.
Competing interests
The authors have declared no competing interests.
CRediT authorship contribution statement
Zihu Guo: Methodology, Data curation, Formal analysis, Software, Investigation, Methodology, Writing – original draft, Writing – review & editing. Yingxue Fu: Methodology, Investigation, Writing – original draft. Chao Huang: Methodology, Investigation, Visualization, Writing – original draft. Chunli Zheng: Methodology, Writing – original draft. Ziyin Wu: Validation, Visualization. Xuetong Chen: Data curation. Shuo Gao: Data curation. Yaohua Ma: Data curation. Mohamed Shahen: Writing – original draft. Yan Li: Writing – review & editing. Pengfei Tu: Investigation. Jingbo Zhu: Investigation. Zhenzhong Wang: Resources. Wei Xiao: Conceptualization, Resources, Supervision, Project administration. Yonghua Wang: Conceptualization, Resources, Supervision, Project administration, Funding acquisition.
Acknowledgments
This study was supported by the National Natural Science Foundation of China (Grant Nos. U1603285 and 81803960) and the National Science and Technology Major Project of China (Grant No. 2019ZX09201004-001). We thank TopEdit (www.topeditsci.com) for its linguistic assistance during the preparation of this manuscript.
Handled by Xin Gao
Footnotes
Peer review under responsibility of Beijing Institute of Genomics, Chinese Academy of Sciences / China National Center for Bioinformation and Genetics Society of China.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.gpb.2020.06.023.
Contributor Information
Wei Xiao, Email: xw_kanion@163.com.
Yonghua Wang, Email: yh_wang@nwsuaf.edu.cn, yh_wang@nwafu.edu.cn.
Supplementary material
The following are the Supplementary data to this article:
Additional details of methods, extended results, and extended discussion of this study
Estimation of the scale parameter ω Selecting parameter (ω = 1.1) that showed the highest mean AUROC for further analysis.
Characterization of gene entropy features with different scale parameters ω A. Normalized probability of different distances with scale parameter ω ranging from 0 to 4. B. Coronary disease gene entropy values with different scale parameters, ω = 0 (top) and ω = 10 (bottom). C. Coronary disease gene entropy values with scale parameter ω ranging from 0 to 10.
Distribution of gene entropy values for all DAGs Histogram plots showing the distribution of gene entropy values for all DAGs before (left) and after (right) normalization. The x-axis shows the range of gene entropy values, and the y-axis shows count of genes possessing different entropy values.
KEGG pathway enrichment results X-axis: the top 20 significantly enriched ‘KEGG pathway terms’ of the master genes; y-axis: significance of the enrichment [−log(P-value)].
The disease-gene enrichment analysis for different classifications Enrichment results (Z-score) of master, interim, and redundant genes in the context of gene sets for indispensable (A), dispensable (A), critical (B), and redundant (B) genes.
The property of the disease-gene entropy concept A. The correlation between entropy value and topology property for each disease. In this figure, each point represents a disease. The coordinate of each point represents the Pearson's correlation coefficient (PCC) for the gene entropy values versus the in-degree (x-axis) and the out-degree (y-axis) of DAGs. The size and the color represent PCC for the gene entropy values versus degree (sum of in- and out-degree) and betweenness, respectively. B. The distribution and cumulative probability of CV for the DAGs among different disease contexts.
Performance of the drug-disease relationship predictions using different scale parameters The box plot shows the AUROC for drug-disease predictions using different scale parameters. To account for the heterogeneous degree distribution of the directed interactome, we preserved the degree of randomized targets and disease genes.
Rank scores for the top 20% of high entropy genes for three diseases Bar plots show the rank scores of the top 20% of high entropy genes for systemic lupus (CD4 cells) (top), systemic lupus (B cells) (middle) and rheumatoid arthritis (B cells) (bottom). Red bars represent the rank scores of the core genes retrieved from NIA.
The dose–response curve of the BxPC3 cell of 8 drugs A.–H. The dose–response curve of BxPC3 cells for 8 drugs that have not been associated with pancreatic cancer. X-axis: the concentration of each drug; y-axis: the percent inhibition rate of the BxPC3 cells.
The heat map of microarray experiment results A. Differentially expressed genes between the Saquinavir (saq1, saq2) treated BxPC3 cell group and the control group (con1, con2). Color represent the relative expression of the differentially expressed genes. B. Differentially expressed genes between the Celecoxib (cel1, cel2) treated BxPC3 cell group and the control group (con1, con2)
Disease-gene associations used in this study
The directed protein-protein interactions used in this study
Classification of the disease-associated genes
Gene sets used for enrichment
Inferred comorbidity relationships of disease pairs from the shared genes
Inferred comorbidity relationships of disease pairs from the interacting gene pairs
Inferred causal or co-occurrence relationships between Parkinson’s and other diseases
Information for all FDA-approved drugs that were used in the present study
List of drug-target relationships used in the present study
Drug-disease information
Gene rank list for three diseases
DDE score for each FDA-approved drug associated with three diseases
FDA-approved drugs and their categories
The DDE for each FDA-approved drug associated with pancreatic cancer
Differentially expressed genes and possibly affected pancreatic cancer-associated master genes after treatments with saquinavir or celecoxib.
The results of literature mining analysis for the top 10% potentially efficient drugs.
References
- 1.Jimenez-Sanchez G., Childs B., Valle D. Human disease genes. Nature. 2001;409:853–855. doi: 10.1038/35057050. [DOI] [PubMed] [Google Scholar]
- 2.Debret G., Jung C., Hugot J.P., Pascoe L., Victor J.M., Lesne A. Genetic susceptibility to a complex disease: the key role of functional redundancy. Hist Phil Life Sci. 2011;33:497–514. [PubMed] [Google Scholar]
- 3.Park J., Lee D.S., Christakis N.A., Barabási A.L. The impact of cellular networks on disease comorbidity. Mol Syst Biol. 2009;5:262. doi: 10.1038/msb.2009.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Guney E., Menche J., Vidal M., Barábasi A.L. Network-based in silico drug efficacy screening. Nat Commun. 2016;7:10331. doi: 10.1038/ncomms10331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Todorovic M., Newman J.R.B., Shan J., Bentley S., Wood S.A., Silburn P.A., et al. Comprehensive assessment of genetic sequence variants in the antioxidant 'master regulator' nrf2 in idiopathic Parkinson’s disease. PLoS ONE. 2015;10 doi: 10.1371/journal.pone.0128030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Karn T. High-throughput gene expression and mutation profiling: current methods and future perspectives. Breast Care (Basel) 2013;8:401–406. doi: 10.1159/000357461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Alvarez M.J., Shen Y., Giorgi F.M., Lachmann A., Ding B.B., Ye B.H., et al. Functional characterization of somatic mutations in cancer using network-based inference of protein activity. Nat Genet. 2016;48:838–847. doi: 10.1038/ng.3593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Walsh L.A., Alvarez M.J., Sabio E.Y., Reyngold M., Makarov V., Mukherjee S., et al. An integrated systems biology approach identifies TRIM25 as a key determinant of breast cancer metastasis. Cell Rep. 2017;20:1623–1640. doi: 10.1016/j.celrep.2017.07.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.West J., Bianconi G., Severini S., Teschendorff A.E. Differential network entropy reveals cancer system hallmarks. Sci Rep. 2012;2:802. doi: 10.1038/srep00802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Reilly M.T., Cunningham K.A., Natarajan A. Protein–protein interactions as therapeutic targets in neuropsychopharmacology. Neuropsychopharmacology. 2013;34:247–248. doi: 10.1038/npp.2008.167. [DOI] [PubMed] [Google Scholar]
- 11.Porta-Pardo E., Garcia-Alonso L., Hrabe T., Dopazo J., Godzik A. A Pan-cancer catalogue of cancer driver protein interaction interfaces. PLoS Comput Biol. 2015;11 doi: 10.1371/journal.pcbi.1004518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vidal M., Cusick M.E., Barabási A.L. Interactome networks and human disease. Cell. 2011;144:986–998. doi: 10.1016/j.cell.2011.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Greene C.S., Arjun K., Wong A.K., Ricciotti E., Zelaya R.A., Himmelstein D.S., et al. Understanding multicellular function and disease with human tissue-specific networks. Nat Genet. 2015;47:569–576. doi: 10.1038/ng.3259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Allen J.D., Xie Y., Chen M., Girard L., Xiao G. Comparing statistical methods for constructing large scale gene networks. PLoS ONE. 2012;7 doi: 10.1371/journal.pone.0029348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rozengurt E. Mitogenic signaling pathways induced by G protein-coupled receptors. J Cell Physiol. 2007;213:589–602. doi: 10.1002/jcp.21246. [DOI] [PubMed] [Google Scholar]
- 16.Kanehisa M., Goto S., Sato Y., Kawashima M., Furumichi M., Tanabe M. Data, information, knowledge and principle: back to metabolism in KEGG. Nucleic Acids Res. 2014;42:199–205. doi: 10.1093/nar/gkt1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Davis A.P., Grondin C.J., Johnson R.J., Sciaky D., King B.L., McMorran R., et al. The comparative toxicogenomics database: update 2017. Nucleic Acids Res. 2017;45:D972–D978. doi: 10.1093/nar/gkw838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhu F., Shi Z., Qin C., Tao L., Liu X., Xu F., et al. Therapeutic target database update 2012: a resource for facilitating target-oriented drug discovery. Nucleic Acids Res. 2012;40:D1128–D1136. doi: 10.1093/nar/gkr797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Whirlcarrillo M., Mcdonagh E.M., Hebert J.M., Gong L., Sangkuhl K., Thorn C.F., et al. Pharmacogenomics knowledge for personalized medicine. Clin Pharmacol Ther. 2012;92:414–417. doi: 10.1038/clpt.2012.96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Vinayagam A, Stelzl U, Foulle R, Plassmann S, Zenkner M, Timm J, et al. A directed protein interaction network for investigating intracellular signal transduction. Sci Signal 2011;4:rs8. [DOI] [PubMed]
- 21.Wishart D.S., Feunang Y.D., Guo A.C., Lo E.J., Marcu A., Grant J.R., et al. DrugBank 5.0: a major update to the DrugBank database for 2018. Nucleic Acids Res. 2018;46:D1074–D1082. doi: 10.1093/nar/gkx1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McKusick V.A. Mendelian Inheritance in Man and its online version. OMIM Am J Hum Genet. 2007;80:588–604. doi: 10.1086/514346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Csardi G., Nepusz T. The igraph software package for complex network research. Int J Complex Syst. 2006;1695:1–9. [Google Scholar]
- 24.Takeoka M., Guha S., Wilde M.M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat Commun. 2015;5:5235. doi: 10.1038/ncomms6235. [DOI] [PubMed] [Google Scholar]
- 25.Cohen E, Delling D, Pajor T, Werneck RF. Distance-based influence in networks: computation and maximization. arXiv 2014;1410.6976.
- 26.Li P., Huang C., Fu Y., Wang J., Wu Z., Ru J., et al. Large-scale exploration and analysis of drug combinations. Bioinformatics. 2015;31:2007–2016. doi: 10.1093/bioinformatics/btv080. [DOI] [PubMed] [Google Scholar]
- 27.Keiser M.J., Roth B.L., Armbruster B.N., Ernsberger P., Irwin J.J., Shoichet B.K. Relating protein pharmacology by ligand chemistry. Nat Biotechnol. 2007;25:197–206. doi: 10.1038/nbt1284. [DOI] [PubMed] [Google Scholar]
- 28.Dickerson J.E., Zhu A., Robertson D.L., Hentges K.E. Defining the role of essential genes in human disease. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0027368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Barabási A.L., Gulbahce N., Loscalzo J. Network medicine: a network-based approach to human disease. Nat Rev Genet. 2011;12:56–68. doi: 10.1038/nrg2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Singh-Blom U.M., Natarajan N., Tewari A., Woods J.O., Dhillon I.S., Marcotte E.M. Prediction and validation of gene-disease associations using methods inspired by social network analyses. PLoS ONE. 2013;8 doi: 10.1371/journal.pone.0058977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rao A., Vg S., Joseph T., Kotte S., Sivadasan N., Srinivasan R. Phenotype-driven gene prioritization for rare diseases using graph convolution on heterogeneous networks. BMC Med Genomics. 2018;11:57. doi: 10.1186/s12920-018-0372-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Copps K.D., White M.F. Regulation of insulin sensitivity by serine/threonine phosphorylation of insulin receptor substrate proteins IRS1 and IRS2. Diabetologia. 2012;55:2565–2582. doi: 10.1007/s00125-012-2644-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rogers J., Raveendran M., Fawcett G.L., Fox A.S., Shelton S.E., Oler J.A., et al. CRHR1 genotypes, neural circuits and the diathesis for anxiety and depression. Mol Psychiatry. 2013;18:700–707. doi: 10.1038/mp.2012.152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lee D.S., Park J., Kay K.A., Christakis N.A., Oltvai Z.N., Barabási A.L. The implications of human metabolic network topology for disease comorbidity. Proc Natl Acad Sci U S A. 2008;105:9880–9885. doi: 10.1073/pnas.0802208105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Guo Y., Nie Q., MacLean A.L., Li Y., Lei J., Li S. Multiscale modeling of inflammation-induced tumorigenesis reveals competing oncogenic and oncoprotective roles for inflammation. Cancer Res. 2017;77:6429–6441. doi: 10.1158/0008-5472.CAN-17-1662. [DOI] [PubMed] [Google Scholar]
- 36.Wu D., Hu D., Chen H., Shi G., Fetahu I.S., Wu F., et al. Glucose-regulated phosphorylation of TET2 by AMPK reveals a pathway linking diabetes to cancer. Nature. 2018;559:637–641. doi: 10.1038/s41586-018-0350-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liu Y., Li Z., Zhang M., Deng Y., Yi Z., Shi T. Exploring the pathogenetic association between schizophrenia and type 2 diabetes mellitus diseases based on pathway analysis. BMC Med Genomics. 2013;6:S17. doi: 10.1186/1755-8794-6-S1-S17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Danielewicz H. What the genetic background of individuals with asthma and obesity can reveal: ss β2-adrenergic receptor gene polymorphism important? Pediatr Allergy Immunol Pulmonol. 2014;27:104–110. doi: 10.1089/ped.2014.0360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Schmitz-Peiffer C., Whitehead J.P. IRS-1 regulation in health and disease. IUBMB Life. 2003;55:367–374. doi: 10.1080/1521654031000138569. [DOI] [PubMed] [Google Scholar]
- 40.Bastard J., Maachi M., Lagathu C., Kim M.J., Caron M., Vidal H., et al. Recent advances in the relationship between obesity, inflammation, and insulin resistance. Eur Cytokine Netw. 2006;17:4–12. [PubMed] [Google Scholar]
- 41.Sheppard R., Bedi M., Kubota T., Semigran M.J., Dec W., Holubkov R., et al. Myocardial expression of fas and recovery of left ventricular function in patients with recent-onset cardiomyopathy. J Am Coll Cardiol. 2005;46:1036–1042. doi: 10.1016/j.jacc.2005.05.067. [DOI] [PubMed] [Google Scholar]
- 42.Ruvolo P.P., Deng X., Carr B.K., May W.S. A functional role for mitochondrial protein kinase Cα in Bcl2 phosphorylation and suppression of apoptosis. J Biol Chem. 1998;273:25436–25442. doi: 10.1074/jbc.273.39.25436. [DOI] [PubMed] [Google Scholar]
- 43.Chen T.C., Lin K.T., Chen C.H., Lee S.A., Lee P.Y., Liu Y.W., et al. Using an in situ proximity ligation assay to systematically profile dndogenous protein–protein interactions in a pathway network. J Proteome Res. 2014;13:5339–5346. doi: 10.1021/pr5002737. [DOI] [PubMed] [Google Scholar]
- 44.Guo J.L., Covell D.J., Daniels J.P., Iba M., Stieber A., Zhang B., et al. Distinct α-synuclein strains differentially promote tau inclusions in neurons. Cell. 2013;154:103–117. doi: 10.1016/j.cell.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bettiol S.S., Rose T.C., Hughes C.J., Smith L.A. Alcohol consumption and parkinson’s disease risk: a review of recent findings. J Parkinsons Dis. 2015;5:425–442. doi: 10.3233/JPD-150533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zickenrott S., Angarica V.E., Upadhyaya B.B., del Sol A. Prediction of disease–gene–drug relationships following a differential network analysis. Cell Death Dis. 2016;7 doi: 10.1038/cddis.2015.393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sivakumar S., de Santiago I., Chlon L., Markowetz F. Master regulators of oncogenic KRAS response in pancreatic cancer: an integrative network biology analysis. PLoS Med. 2017;14 doi: 10.1371/journal.pmed.1002223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kelley R.K., Ko A.H. Erlotinib in the treatment of advanced pancreatic cancer. Biologics. 2008;2:83–95. doi: 10.2147/btt.s1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Li C, Wu JJ, Hynes M, Dosch J, Sarkar B, Welling TH, et al. c-Met is a marker of pancreatic cancer stem cells and therapeutic target. Gastroenterology 2011;141:2218–27.e5. [DOI] [PubMed]
- 50.Korc M. Pathways for aberrant angiogenesis in pancreatic cancer. Mol Cancer. 2003;2:8. doi: 10.1186/1476-4598-2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li X., Zhang X., Zheng L., Guo W. Expression of CD44 in pancreatic cancer and its significance. Int J Clin Exp Pathol. 2015;8:6724–6731. [PMC free article] [PubMed] [Google Scholar]
- 52.De Soto J.A., Mullins R. The use of PARP inhibitors as single agents and as chemosensitizers in sporadic pancreatic cancer. J Clin Oncol. 2011;29 [Google Scholar]
- 53.Listed N. Effects of vinorelbine on quality of life and survival of elderly patients with advanced non-small-cell lung cancer. The Elderly Lung Cancer Vinorelbine Italian Study Group. J Natl Cancer Inst. 1999;91:66–72. doi: 10.1093/jnci/91.1.66. [DOI] [PubMed] [Google Scholar]
- 54.Merry C., Barry M.G., Mulcahy F., Tjia J.F., Halifax K.L., Heavey J., et al. Ritonavir pharmacokinetics alone and in combination with saquinavir in HIV-infected patients. AIDS. 1998;12:325–327. [PubMed] [Google Scholar]
- 55.Tindall E. Celecoxib for the treatment of pain and inflammation: the preclinical and clinical results. J Am Osteopath Assoc. 1999;99:S13–S17. doi: 10.7556/jaoa.1999.99.11.S13. [DOI] [PubMed] [Google Scholar]
- 56.Lounkine E., Keiser M.J., Whitebread S., Mikhailov D., Hamon J., Jenkins J.L., et al. Large scale prediction and testing of drug activity on side-effect targets. Nature. 2012;486:361–367. doi: 10.1038/nature11159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Li Y., Huang C., Ding L., Li Z., Gao X. Deep learning in bioinformatics: introduction, application, and perspective in the big data era. Methods. 2019;166:4–21. doi: 10.1016/j.ymeth.2019.04.008. [DOI] [PubMed] [Google Scholar]
- 58.Zitnik M., Agrawal M., Leskovec J. Modeling polypharmacy side effects with graph convolutional networks. Bioinformatics. 2018;34:i457–i466. doi: 10.1093/bioinformatics/bty294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Li Y, Kuwahara H, Yang P, Song L, Gao X. PGCN: disease gene prioritization by disease and gene embedding through graph convolutional neural networks. bioRxiv 2019;532226.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional details of methods, extended results, and extended discussion of this study
Estimation of the scale parameter ω Selecting parameter (ω = 1.1) that showed the highest mean AUROC for further analysis.
Characterization of gene entropy features with different scale parameters ω A. Normalized probability of different distances with scale parameter ω ranging from 0 to 4. B. Coronary disease gene entropy values with different scale parameters, ω = 0 (top) and ω = 10 (bottom). C. Coronary disease gene entropy values with scale parameter ω ranging from 0 to 10.
Distribution of gene entropy values for all DAGs Histogram plots showing the distribution of gene entropy values for all DAGs before (left) and after (right) normalization. The x-axis shows the range of gene entropy values, and the y-axis shows count of genes possessing different entropy values.
KEGG pathway enrichment results X-axis: the top 20 significantly enriched ‘KEGG pathway terms’ of the master genes; y-axis: significance of the enrichment [−log(P-value)].
The disease-gene enrichment analysis for different classifications Enrichment results (Z-score) of master, interim, and redundant genes in the context of gene sets for indispensable (A), dispensable (A), critical (B), and redundant (B) genes.
The property of the disease-gene entropy concept A. The correlation between entropy value and topology property for each disease. In this figure, each point represents a disease. The coordinate of each point represents the Pearson's correlation coefficient (PCC) for the gene entropy values versus the in-degree (x-axis) and the out-degree (y-axis) of DAGs. The size and the color represent PCC for the gene entropy values versus degree (sum of in- and out-degree) and betweenness, respectively. B. The distribution and cumulative probability of CV for the DAGs among different disease contexts.
Performance of the drug-disease relationship predictions using different scale parameters The box plot shows the AUROC for drug-disease predictions using different scale parameters. To account for the heterogeneous degree distribution of the directed interactome, we preserved the degree of randomized targets and disease genes.
Rank scores for the top 20% of high entropy genes for three diseases Bar plots show the rank scores of the top 20% of high entropy genes for systemic lupus (CD4 cells) (top), systemic lupus (B cells) (middle) and rheumatoid arthritis (B cells) (bottom). Red bars represent the rank scores of the core genes retrieved from NIA.
The dose–response curve of the BxPC3 cell of 8 drugs A.–H. The dose–response curve of BxPC3 cells for 8 drugs that have not been associated with pancreatic cancer. X-axis: the concentration of each drug; y-axis: the percent inhibition rate of the BxPC3 cells.
The heat map of microarray experiment results A. Differentially expressed genes between the Saquinavir (saq1, saq2) treated BxPC3 cell group and the control group (con1, con2). Color represent the relative expression of the differentially expressed genes. B. Differentially expressed genes between the Celecoxib (cel1, cel2) treated BxPC3 cell group and the control group (con1, con2)
Disease-gene associations used in this study
The directed protein-protein interactions used in this study
Classification of the disease-associated genes
Gene sets used for enrichment
Inferred comorbidity relationships of disease pairs from the shared genes
Inferred comorbidity relationships of disease pairs from the interacting gene pairs
Inferred causal or co-occurrence relationships between Parkinson’s and other diseases
Information for all FDA-approved drugs that were used in the present study
List of drug-target relationships used in the present study
Drug-disease information
Gene rank list for three diseases
DDE score for each FDA-approved drug associated with three diseases
FDA-approved drugs and their categories
The DDE for each FDA-approved drug associated with pancreatic cancer
Differentially expressed genes and possibly affected pancreatic cancer-associated master genes after treatments with saquinavir or celecoxib.
The results of literature mining analysis for the top 10% potentially efficient drugs.