Incremental Propensity Score Effects for Time-Fixed Exposures

Abstract

When causal inference is of primary interest, a range of target parameters can be chosen to define the causal effect of interest, such as average treatment effects (ATEs). However, ATEs may not always align with the research question at hand. Furthermore, the assumptions needed to interpret estimates as ATEs, such as exchangeability, consistency, and positivity, are often not met. Here, we present the incremental propensity score (incremental PS) approach to quantify the effect of shifting each person’s exposure propensity by some pre-determined amount. Compared to the ATE, incremental PS may better reflect the impact of certain policy interventions, and do not require that positivity hold. Using the Nulliparous Pregnancy Outcomes Study: monitoring mothers-to-be (nuMoM2b), we quantified the relation between total vegetable intake and the risk of preeclampsia, and compared it to average treatment effect estimates. The ATE estimates suggested a reduction of between two and three preeclampsia cases per 100 pregnancies for consuming at least 1/2 a cup of vegetables per 1,000 kcal. However, positivity violations obfuscate the interpretation of these results. In contrast, shifting each woman’s exposure propensity by odds ratios ranging from 0.20 to 5.0 yielded no difference in the risk of preeclampsia. Our analyses show the utility of the incremental propensity score effects in addressing public health questions with fewer assumptions.

Introduction

Applied researchers are increasingly expressing interest in the average treatment effects (ATE) for defining an exposure effect of interest. This effect quantifies an outcome summary of interest (e.g., risk, rate, odds) that would be observed if all individuals in the population were exposed versus unexposed.¹ Methods to quantify ATEs often include inverse-probability weighting,² g computation (a.k.a., the g formula),³ or a range of doubly robust approaches.⁴ The validity of these methods relies on a set of basic assumptions, for example, counterfactual consistency, exchangeability, no interference, correct parametric model specification, and positivity.^5,6 However, in many instances, there are indications that one or more of these assumptions is violated, complicating the interpretation and use of these increasingly common methods.

Epidemiologic studies tend to be complicated by a number of challenges related to the definition, measurement, and the analysis of exposures. At the crossroads of nutritional and reproductive epidemiology, questions of primary importance are often asked with regards to the relation between diet and pregnancy outcomes. However, dietary factors are often strongly correlated with one another.⁷ Such strong relations can lead to violations in the positivity assumption. Positivity is met when there are exposed and unexposed individuals in all strata defined by confounding values. Foods have complex, reciprocal interrelations because of dietary behavioral patterns, meaning that people whose dietary patterns are high in vegetables also tend to consume higher amounts of other healthy foods.⁷ This can lead to problems with positivity.

Additionally, average treatment effects quantify the effect that would be observed under a hypothetical intervention in which all individuals are fully exposed versus fully unexposed to the treatment under study. This property of the average treatment effect has been the source of some recent criticism, largely because public health interventions will rarely result in fully exposed or unexposed populations.^8–11 Incremental propensity score effects are a natural alternative to the ATE. In line with a growing body of literature on the effects of shifts in treatments or exposures based on baseline characteristics of individuals in the sample,^8,27 incremental PS estimands define the effect of shifts in the conditional probability of being exposed. Such shifts represent changes in an individual’s underlying probability of being exposed or unexposed, as a function of their covariate values, rather than their actual exposure status.

Here, we demonstrate how novel incremental propensity score (incremental PS) effects can be estimated via doubly-robust methods,¹² and how they can provide valuable information about the relation between an exposure and outcome of interest, even when positivity is violated. Using an example based on the relation between total vegetable intake and the risk of preeclampsia, we illustrate the causal contrast defined by an incremental PS effect, the reasoning behind its use, and how to interpret results obtained from estimators targeting incremental PS effects.

Methods

Data were obtained from the nuMoM2b Study, a large prospective U.S. pregnancy cohort, previously described elsewhere.¹³ Briefly, nuMoM2b enrolled 10,038 women from eight medical centers across the U.S. between 2010–2013. Women were eligible if they had a viable singleton pregnancy, were between 6 to 13 completed weeks of gestation, and had no previous pregnancy that lasted ≥20 weeks’ gestation. Each site’s local institutional review board approved the study and all women gave written, informed consent. Our analytic sample included 8,259 women who delivered at ≥20 weeks gestation and had complete dietary and birth outcome data.

Usual dietary intake in the 3 months before conception was assessed at 6 to 13 weeks’ gestation using a self-administered modified Block 2005 food frequency questionnaire (FFQ),¹⁴ which was available in English and Spanish. The FFQ methodology was provided in detail previously.¹⁵

The FFQ’s food list was developed from the National Health and Nutrition Examination Survey 1999–2002 dietary recall data, and the nutrient database was developed from the USDA Food and Nutrient Database for Dietary Studies.¹⁶ Food groups were derived from the MyPyramid Equivalents Database, version2.0.¹⁷ For our primary exposure, usual daily vegetable intake was expressed in cup equivalents per 1,000 kcal, reflecting total vegetable density as per the construction of the Healthy Eating Index (HEI)-2010.¹⁸ The usual daily intake of vegetables was expressed relative to energy as cups per 1,000 kcal. Our primary interest was in evaluating whether a hypothetical intervention encouraging women to consume at least $\frac{1}{2}$ a cup of vegetables per 1,000 kcal would be effective at reducing the risk of preeclampsia.

Preeclampsia was defined as the presence of the following symptoms at ≥20 weeks gestation through 14 days: gestational hypertension (≥ 140 mm hg systolic or ≥ 90 mm Hg diastolic on two occasions ≥ 6 hours apart or one occasion with subsequent antihypertensive therapy, excluding blood pressures recorded during the second stage of labor) and proteinuria (≥300mg/24 hour collection or protein/creatinine ration ≥ 0.3 or dincremental PStick ≥ 2+), thrombocytopenia (platelet count <100,000/mm3), or pulmonary edema. Preeclampsia included superimposed preeclampsia or eclampsia, regardless of the timing of onset. We did not distinguish between early and late onset preeclampsia, which may have distinct etiologies.³¹ Cases that presented atypically and were difficult to classify according to study criteria were adjudicated by review of clinical data by the principal investigators and final classification was reached by their consensus judgment.

Confounders of the relationship between vegetable density and preeclampsia included baseline anthropometric and demographic measures, as well as other measures derived from the HEI. HEI confounders included whole grains, dairy products, total protein foods, seafood and plant proteins, fatty acids, refined grains, sodium, and “empty” calories.¹⁸ Other baseline confounders included self-reported highest level of education, self-reported race/ethnicity (indicator of non-Hispanic Black status). Other self-reported confounder information included marital status, smoking before pregnancy, and medical insurance. At the initial visit, women had their weight measured using an electronic or balance scale while wearing only light clothes and no shoes, and height measured using a stadiometer or measuring tape, used to compute body mass index (BMI) in kg/m², which we included as a confounder.

Statistical Analysis

Doubly Robust Estimation of the Average Treatment Effect

We used three different estimators to quantify the relation between total vegetable density and preeclampsia in the nuMoM2b data. We first used two relatively well known doubly robust estimators to quantify the average treatment effect, defined as:

$$\psi \equiv E\left(Y^1-Y^0\right)$$

which, in our setting can be interpreted as the risk difference over all of gestation that would be observed if all women consumed at least 1/2 a cup of vegetables per 1,000 kcal, versus if all women consumed less than or equal to 1/2 a cup per 1,000 kcal.

The average treatment effect can also be quantified with standard approaches (e.g., inverse probability weighting, or g computation). However, as we discuss further below, the incremental propensity score is implemented with machine learning algorithms. In general, inverse probability weighting and g computation methods should not be implemented with machine learning algorithms because of the problems that result from the curse of dimensionality, which include finite-sample bias, high mean squared error, and no general way to obtain valid confidence intervals.¹⁹ Thus, to more fairly compare the results from the doubly-robust estimator of the incremental PS effect and estimators of the ATE, we require estimators that are also doubly robust, such as augmented inverse probability weighting (AIPW) and targeted minimum loss based estimation (TMLE).

The augmented inverse probability weighted estimator we used was defined as:

$${\widehat{\psi }}^{aipw}=\frac{1}{N}\sum _{i=1}^N\left\{\frac{\left(X_i-{\widehat{\pi }}_i\right)}{{\widehat{\pi }}_i\left(1-{\widehat{\pi }}_i\right)}\times \left(Y_i-{\widehat{\mu }}_i(X,\mathbf{C})\right)\right\}+{\widehat{\mu }}_i(X=1,\mathbf{C})-{\widehat{\mu }}_i(X=0,\mathbf{C}).$$ (1)

where X is an indicator of whether total vegetable density is greater than half a cup per 1,000 kcals, Y is an indicator of preeclampsia, C is the vector of confounders defined above, and i indexes each woman in the sample. In the above equation, ${\widehat{\pi }}_i$ represents individual predictions from the propensity score model, which is a model for the exposure regressed against all confounders. Furthermore, ${\widehat{\mu }}_i(X=x,\mathbf{C})$ represents individual predictions from the outcome model if the exposure were set to some value x.

We also used targeted minimum loss-based estimation,^20(p72–3) defined as:

$${\widehat{\psi }}^{tmle}=\frac{1}{N}\sum _{i=1}^N\left\{{\widehat{\mu }}_i^u(X=1,\mathbf{C})-{\widehat{\mu }}_i^u(X=0,\mathbf{C})\right\},$$ (2)

where ${\widehat{\mu }}_i^u(X,\mathbf{C})$ are predictions from an outcome model that is updated using an inverse probability weight, defined as:

$$H(X,\mathbf{C})=\{\begin{array}{c}\frac{1}{{\widehat{\pi }}_i}\text{ if }X=1\\ -\frac{1}{1-{\widehat{\pi }}_i}\text{ otherwise }\end{array}$$

Which is included in a no-intercept logistic regression model for the observed outcome that includes the outcome predictions ${\widehat{\mu }}_i(X,\mathbf{C})$ from the initial model as an offset. The ${\widehat{\mu }}_i^u(X=1,\mathbf{C})$ and ${\widehat{\mu }}_i^u(X=0,\mathbf{C})$ predictions are then generated from this model by first setting X to 1 and then to 0, respectively, for all women in the sample.

Under exchangeability, counterfactual consistency, no interference, and positivity, the average treatment effect is identified, and can be quantified via AIPW and TMLE. Positivity holds when the conditional probability of being exposed or unexposed is bounded away from [0, 1]. Formally, we can define positivity as a function of the propensity score, as:

$$0<\pi (\mathbf{C})\equiv P(X=1\mid \mathbf{C})<1.$$

The positivity assumption can be violated if P(X = 1 | C) ≈ 0 or P(X = 1 | C) ≈ 1 (or equivalently, if P(X = 0 | C) ≈ 1 or P(X = 0 | C) ≈ 0). If positivity is violated, then the average treatment effect is not identified, making the interpretation of ATE estimates more challenging.

Incremental Propensity Score Effects

Instead of targeting the average treatment effect, we might be interested in quantifying the risk of preeclampsia that would be observed if we could shift each women’s propensity for eating at least 1/2 a cup of vegetables per 1,000 kcal by a certain amount.

For example, suppose that the probability that a given woman consumes at least 1/2 a cup of vegetables per 1,000 kcal is 35% (in other words, her propensity score for being exposed is 0.35). We may ask what her preeclampsia risk would be if we were able to shift her propensity for being exposed to 0.45? Such a shift intervention would reflect an odds ratio change in the propensity score of:

$$\frac{0.45/(1-0.45)}{0.35/(1-0.35)}\approx 1.5$$

We can thus define a “shift intervention” for each woman in the sample, such that their propensity score might increase by an odds ratio of, say, 1.5.

Incremental propensity score effects quantify risks under such “shift interventions.”¹² In our setting, we quantify the risk of preeclampsia that would be observed if each women’s propensity for being exposed were shifted by an odds ratio, denoted δ. If we let π_δ = (δπ)/(δπ+1−π) be the propensity score under the shift intervention in which the observed propensity score is increased by the odds ratio δ, then:

$$E\left(Y^{{\pi }_{\delta }}\right)=\sum _{\mathbf{c},{\pi }_{\delta }}E(Y\mid X,\mathbf{C})P_{\delta }(X=1\mid \mathbf{C})p(\mathbf{C}).$$ (3)

One can derive an estimator of E(Y^πδ) as:

$${\xi }_{\delta }^{ips}=\sum _{i=1}^N\frac{\delta {\widehat{\pi }}_i{\widehat{\mu }}_i(X=1\mid \mathbf{C})+\left(1-{\widehat{\pi }}_i\right){\widehat{\mu }}_i(X=0\mid \mathbf{C})}{\delta {\widehat{\pi }}_i+1-{\widehat{\pi }}_i}$$ (4)

where ${\widehat{\pi }}_i$ and ${\widehat{\mu }}_i$ (X = 1 | C) are as defined for the AIPW and TMLE estimators above.

Using the estimator defined in equation 4, one can show why the estimators for incremental PS effects do not require positivity. Consider the scenario where an individual’s propensity score is 0. Under such a positivity violation, equation 4 for this woman becomes:

$$\begin{array}{l}{\xi }_{i,\delta }^{ips}=\frac{\delta \times 0\times {\widehat{\mu }}_i(X=1\mid \mathbf{C})+(1-0)\times {\widehat{\mu }}_i(X=0\mid \mathbf{C})}{\delta \times 0+1-0}\\ ={\widehat{\mu }}_i(X=0\mid \mathbf{C}),\end{array}$$

which is the risk of preeclampsia that would be observed if they were not exposed. For individuals whose propensity score is 1, the above equation yields the risk of preeclampsia that would be observed if they were exposed. In this way, incremental propensity score effects do not require positivity to hold, as the potential outcomes defined above for individuals with extreme propensity scores are identified under exchangeability, no interference, and consistency.¹²

One important feature of incremental PS effects is that shift interventions need not be defined via variables in the propensity score model. For example, confounders in our propensity score model included whole grain consumption, percent empty calories, self-reported race/ethnicity, and BMI. Hypothetical interventions that shift the propensity score need not necessarily occur by changing these variables.

Note that because the AIPW, TMLE, and our estimator for the incremental PS effect are “doubly robust” we can use machine learning methods to quantify the effects of interest.¹⁹ In our study, we used a stacked generalization²¹ that included random forests, generalized additive models, and generalized linear models.

Finally, even though the estimator we used for incremental PS effects is “doubly robust,” the incremental PS estimand is defined as a function of the propensity score. It is therefore important to try to model the propensity score as carefully as possible. In the event that the propensity score model is misspecified, one could still interpret the resulting estimates as quantifying a mathematical projection (or approximation) of the true model, but it may be difficult to interpret what this projection represents.

We used R version 4.0.1 (2020–06-06) for all analyses. The AIPW and estimator for incremental PS effects were implemented via the npcausal package, available on GitHub. TMLE was implemented via the tmle package.²² All the code used to conduct the analyses presented here is also available at https://github.com/ainaimi/numom_IPSI.

Results

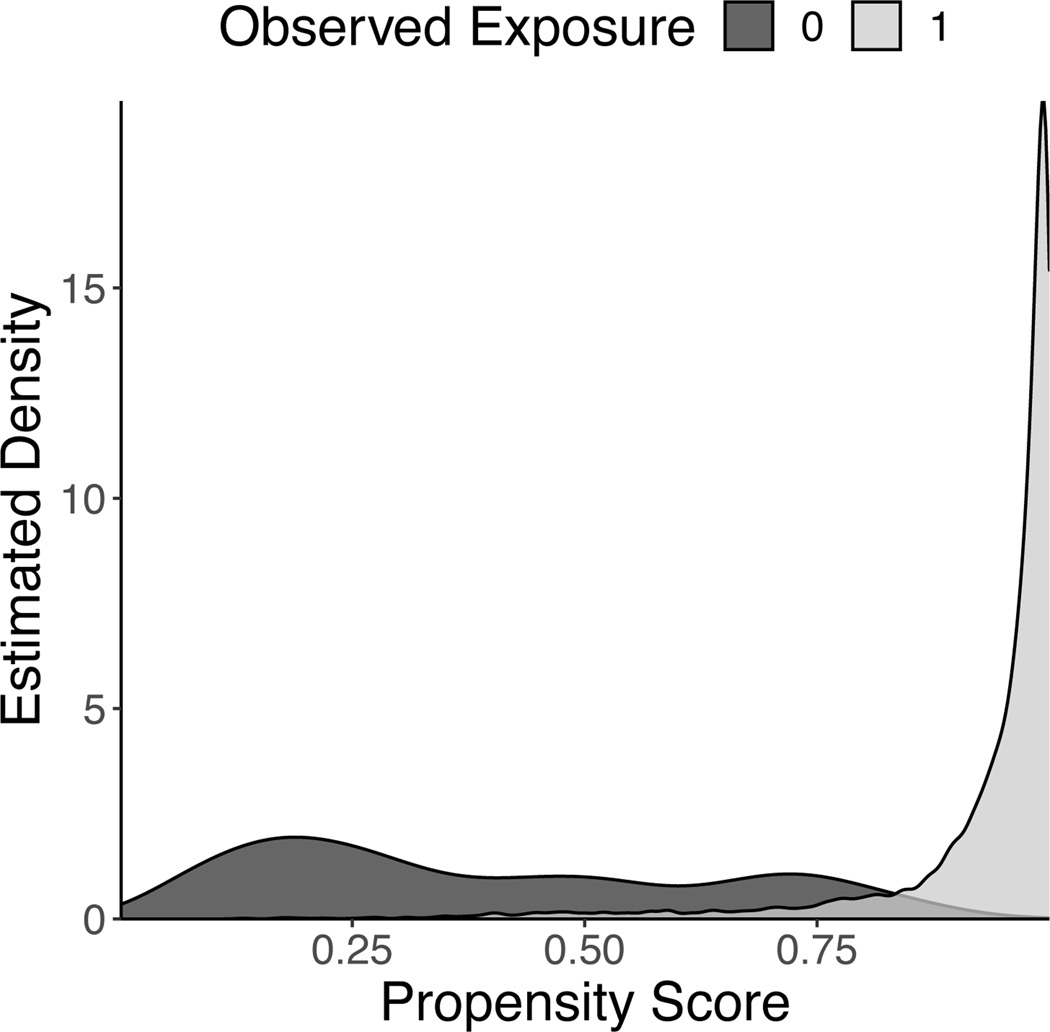
Table 1 shows summary outcome and covariate values within each vegetable density level and overall. There were important confounder differences between exposed and unexposed pregnancies. In particular, large confounder differences were observed for self reported race, marital status, smoking status, public insurance status, as well as several dietary factors (Table 1). These large differences suggest potentially strong relationships between confounders and the exposure. Such strong relations can be suggestive of positivity violations. Indeed, the propensity score overlap plot depicted in Figure 1 confirms that positivity is violated with our exposure. This figure indicates that the average treatment effect is not identified in these data.

Table 1:

Mean confounder values among exposed and unexposed pregnancies and in the overall sample of 8,259 women from the Nulliparous Pregnancy Outcomes Study: monitoring mothers-to-be (nuMoM2b), 2010–2013.

	Vegetable Density1 < 1/2 Cup
	Yes N = 1,370	No N = 6,889	Overall N = 8,259
Preeclampsia, N (%)	151 (11)	531 (7.7)	682 (8.3)
Age in years, mean (SD)	24.8 (5.0)	28.1 (5.2)	27.5 (5.3)
Self Reported Black, N (%)	321 (23)	623 (9)	944 (11)
Married, N (%)	481 (35)	4721 (69)	5202 (63)
Prepregnancy Smoking, N (%)	375 (27)	1019 (15)	1394 (17)
Prepregnancy BMI in kg/m2, mean (SD)	26.2 (7.1)	25.4 (6.0)	25.5 (6.2)
Public Insurance, N (%)	632 (46)	1419 (21)	2051 (25)
Empty Calories as % of energy, mean (SD)	39.3 (9.4)	30.4 (7.6)	31.8 (8.6)
Dairy in cups/1,000 kcal, mean (SD)	0.9 (0.6)	0.9 (0.5)	0.9 (0.5)
Total protein foods in oz/1,000 kcal, mean (SD)	2.1 (0.7)	2.5 (0.8)	2.4 (0.8)
Total fruit in cups/1,000 kcal, mean (SD)	0.7 (0.5)	0.9 (0.5)	0.8 (0.5)
Seafood and plant proteins in oz/1,000 kcal, mean (SD)	0.6 (0.4)	0.8 (0.5)	0.8 (0.5)
Sodium in g/1,000 kcal, mean (SD)	1.4 (0.3)	1.7 (0.2)	1.6 (0.3)
Fatty Acids2, mean (SD)	1.3 (2.0)	1.5 (0.9)	1.4 (1.1)
Refined Grains in oz/1,000 kcal, mean (SD)	2.3 (0.8)	2.2 (0.7)	2.2 (0.7)
Whole Grains in oz/1,000 kcal, mean (SD)	0.5 (0.5)	0.6 (0.4)	0.6 (0.4)

^1.Usual daily vegetable intake, expressed in cups per 1,000 kcal

^2.Ratio of poly- and monounsaturated fatty acids to saturated fatty acids

Figure 1:

Propensity score overlap plot for consuming at least 1/2 a cup of vegetables per 1,000 kcal in the Nulliparous Pregnancy Outcomes Study: monitoring mothers-to-be (nuMoM2b), 2010–2013.

For illustrative purposes, however, we present the average treatment effect estimates from AIPW and TMLE in Table 2. This table shows that both ATE estimators quantified a relatively strong association between total vegetable density and preeclampsia, with between two and three fewer preeclampsia cases per 100 pregnancies among those who consume less than 1/2 a cup of vegetables per 1,000 kcal relative who consume at least 1/2 a cup. Though these results suggest vegetable consumption as a fairly important modality to prevent preeclampsia, the positivity violations observed in Figure 1 raise important questions about the validity of this interpretation.

Table 2:

Average treatment effect estimates on the risk difference scale for the relation between consuming at least 1/2 a cup of vegetables per 1,000 kcal and preeclampsia risk in 8,259 women from the Nulliparous Pregnancy Outcomes Study: monitoring mothers-to-be (nuMoM2b), 2010–2013.

	Risk Difference*	95% CI
Augmented Inverse Probability Weighting	−3.3	−5.1, −1.6
Targeted Minimum Loss-Based Estimation	−2.2	−3.7, −0.7

^*Expressed per 100 pregnancies in the sample.

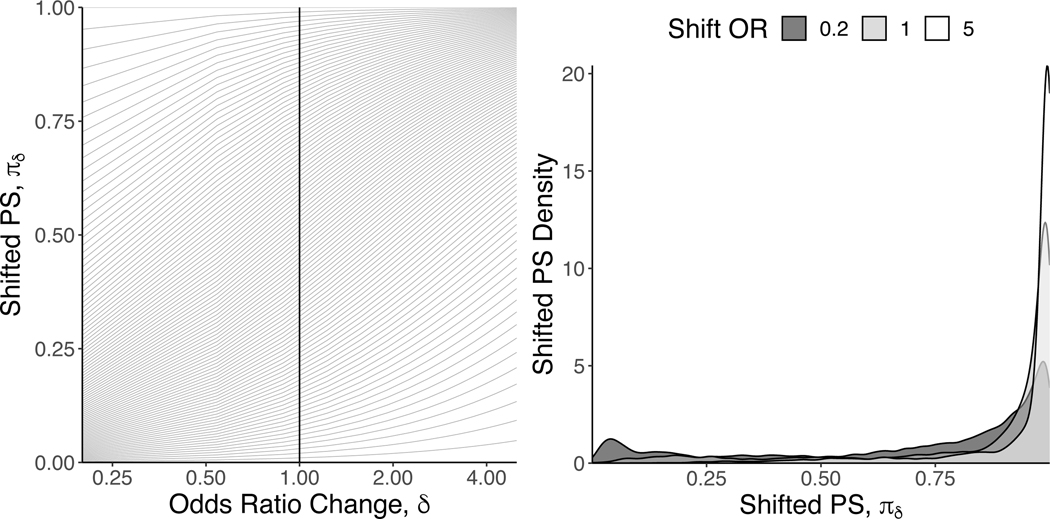
Using incremental propensity scores, we quantified the risk of preeclampsia that would be observed if each woman’s propensity for being exposed were altered by odds ratios ranging between 0.20 and 5.0. The left panel of Figure 2 presents all of the unique propensity score values in the nuMoM2b data as a function of the selected δ values. The vertical line indexes δ = 1, which returns the observed propensity score. This figure shows the extent to which each unique propensity score changes under different δ values. For example, for women whose observed propensity score (rounded to the nearest two digits) was exactly 0.50 (N = 26), their shifted propensity scores range between 0.17 for δ = 0.20 and 0.83 for δ = 5.

Figure 2:

Left Panel: Shifted propensity score values as a function of the δ odds ratio change for all unique propensity score values in 8,259 from the Nulliparous Pregnancy Outcomes Study: monitoring mothers-to-be(nuMoM2b), 2010–2013. Solid vertical line represents point on x-axis with all of the unique observed propensity score values (i.e., no shift intervention). Right Panel: Shifted propensity score distributions for δ values of {0,2, 1, and 5.0} estimated with a kernel density smoother.

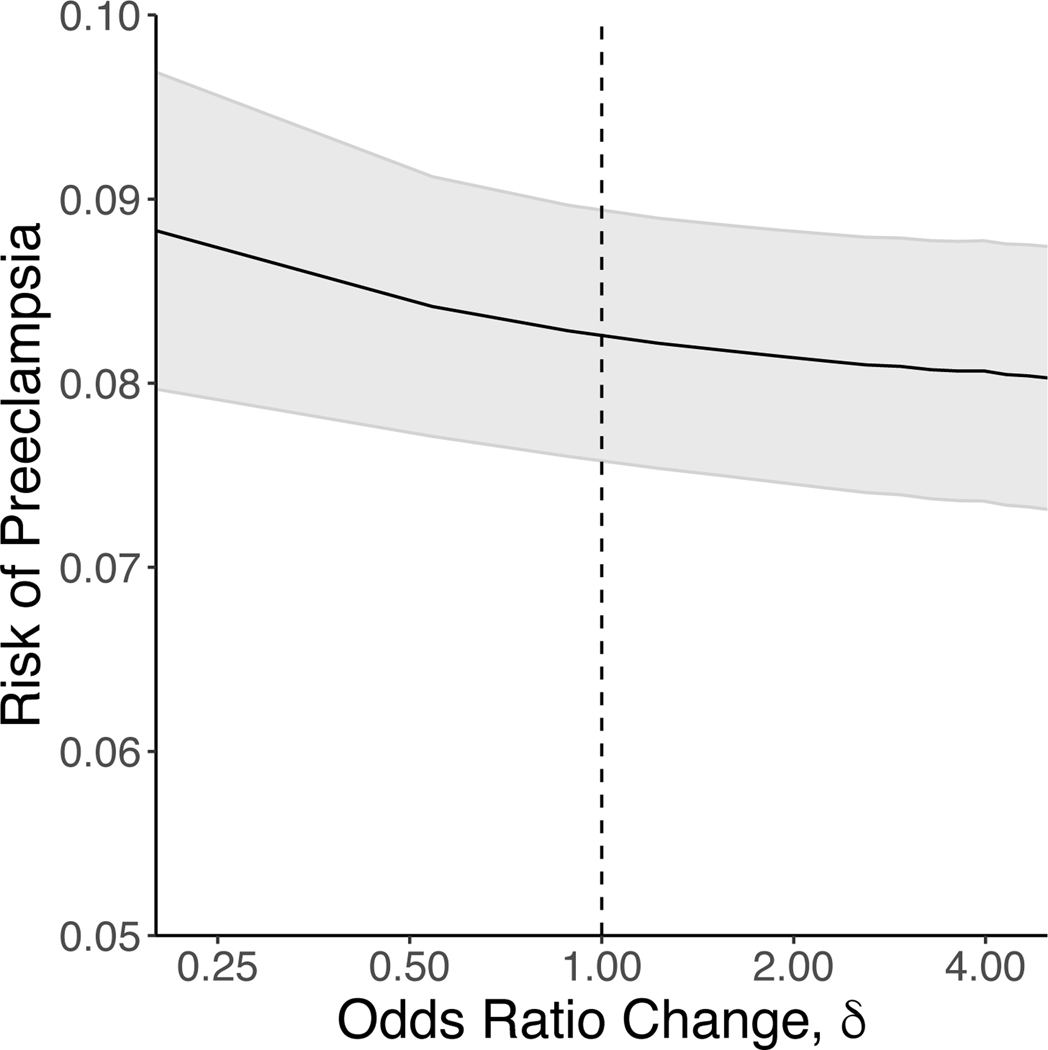
The right panel of Figure 2 demonstrates the overall propensity score distributions under three different shift ORs: 0.2 (minimum δ), 1 (corresponding to the actual propensity scores), and 5 (maximum δ). This left panel shows that, under all three scenarios, a majority of the propensity score density resides in the far right tail of the distribution. This is because the overall probability of consuming at least 1/2 cup of vegetables per 1,000 kcal in our sample was roughly 80%. However, the figure also indicates the extent to which the propensity score distribution changes under the extremes of our selected δ values. For example, under a δ value of 0.2, there is a noticeable shift in the propensity score distribution to the left. Finally, as depicted in Figure 3, changing the propensity for being exposed yielded no meaningful difference in the risk of preeclampsia.

Figure 3:

Risk of preeclampsia as a function of changes in the propensity score (PS) for consuming at least 1/2 a cup of vegetables per 1,000 kcal in 8,259 women from the Nulliparous Pregnancy Outcomes Study: monitoring mothers-to-be (nuMoM2b), 2010–2013.

Discussion

We sought to quantify the causal relation between total dietary vegetable density and the risk of preeclampsia. As is typical, we defined the average treatment effect to capture this relation. Using empirical data to quantify the average treatment effect requires that certain assumptions hold, such as exchangeability, counterfactual consistency, and positivity. We found strong positivity violations for consuming at least 1/2 a cup of vegetables per 1,000 kcal.

Under such conditions, the average treatment effect is not identified. Formally, an effect (defined via potential outcomes) is identified when it can be written as a function of observed data. To do this, we require that certain assumptions (including positivity) hold.⁶ Thus, even though one may obtain a numerical estimate of the average treatment effect, it may not be interpretable as such. Typical strategies to deal with positivity violations include subsetting the sample to those with propensity score overlap,²³ propensity score truncation,²⁴ excluding certain problematic confounders.²⁵ Here, we demonstrated an alternative to these approaches, namely, doubly robust estimation of incremental PS effects.

While we have shown why incremental propensity scores do not require positivity for identifiability, it is important to note that other assumptions are essential. These include exchangeability, no interference, and counterfactual consistency. Exchangeability would be met if there were no information, selection, collider, or confounding bias present in the study. In the context of nutritional epidemiology, collider bias may be of particular concern because we assume reported intake of other dietary components (e.g., total protein consumption, plant protein consumption, percent empty calories) confound the relation between total vegetable consumption and preeclampsia. It is entirely possible that our measures of these other dietary components mediate rather than confound the relation, which could lead to collider bias and blocking of the effect of interest. However, except in certain circumstances (e.g., instrumental variable estimation), the validity of these assumptions do not depend on the which estimator is used. These assumptions are as important when one is targeting average treatment effects via double-robust estimators, or whether incremental PS methods are used.

Similarly, the no interference and counterfactual consistency assumptions do not depend on estimator selection. If one can justify that there is no causal effect between one person’s exposure and another’s outcome, and that the observed outcome is equivalent to the potential outcome under the observed exposure, these assumptions can be justified. Otherwise, identifiability may be jeopardized.

One important feature that differentiates incremental propensity score and other shift intervention effects from, say, the average treatment effect, is the inability to explicitly define a randomized trial, even hypothetically, to evaluate the effect of shift interventions. Because of the inability to conceptualize such shift interventions in terms of a randomized trial, questions may arise about the validity of counterfactual consistency²⁹ or treatment variation irrelevance.³⁰ First, while propensity score shifts may not be easily conceived in terms of an intervention, the same is not necessarily for the exposure used to compute the propensity score. Interventions could be conceptualized for getting women to consume more than 1/2 a cup of vegetables per 1,000 kcal. Second, while shift intervention estimands may not be directly computable in a randomized trial, they can still provide information useful to narrowing down the set of interventions to be studied more in depth via randomization.²⁷

Finally, we did not address the complications that can arise in the presence of loss-to-follow-up or competing risk events.²⁸ Such complications are, in fact, present in the NuMoM study, where, out of the 8,259 women, 45 women experienced a spontaneous pregnancy loss, and 45 women experience a stillbirth over the course of follow-up. Informal ancillary analyses, provided in eAppendix 1, suggested no impact of these competing events on our findings (for both the ATE and incremental PS effects). However, as of the present article, neither the AIPW function, the TMLE function, nor the incremental PS effects function we used include options to compare sub-distribution and cause-specific measures when competing events are present.

Here, we estimated incremental propensity score effects for a time-fixed nutritional exposure and a binary outcome in the absence of censoring. However, incremental propensity score effects can also be used in settings with a time-varying exposure subject to time-dependent confounding,¹² as well as to settings with censored survival outcomes.²⁶

Incremental propensity scores can be useful even when positivity holds. The target estimand for incremental propensity scores effects is closely related to shift interventions that have been studied in various settings.^8–11 Incremental propensity score effects provide a relatively easy approach to quantifying such population relevant effects, as they define interventions that are arguably more likely to align with what might occur in a population health setting: i.e., shifts in the conditional probability of being exposed, instead of setting each person’s exposure to a fixed value. As such, one need not rely on incremental propensity score effects only in situations where positivity is violated. Rather, the approach can prove valuable as one of many tools available for modeling population relevant effects in a public health framework.