Equal-bin-width histogram versus equal-bin-count histogram

Abstract

The histogram has all its bin widths equal to some non-random number arbitrary set by an analyst (EBWH). In the result, particular bin counts are random variables. This paper presents also a histogram that is constructed in a converse manner. Bin counts are all equal to some non-random number arbitrary set by an analyst (EBCH). In the result, particular bin widths are random variables. The first goal of the paper is a choose of constant bin width (of bin numbers k) in the EBWH, which maximize the similarity measure in the Monte Carlo simulation. The second goal is a choose of constant bin count in the EBCH, which maximize the similarity measure in the Monte Carlo simulation. The third goal is to present similarity measures between empirical and theoretical data. The fourth goal is the comparative analysis of two histogram methods by means of the frequency formula. The first additional goal is a tip how to proceed in EBCH when modulo(n,k)≠0. The second additional goal is the software in the form of a Mathcad file with the implementation of EBWH and EBCH.

1. Introduction

Histograms are used extensively as non-parametric density estimators both to visualize data and to obtain summary quantities such as the entropy of the underlying density. The histogram is completely determined by two parameters, the bin width and the bin origin.

An important parameter that needs to be specified when constructing a histogram is the bin width $h$. A major issue with all classifying techniques is how to select the number of bins $k$. There is no “best” number of bins. Different $k$ values can reveal different features of the data. Using wider bins, where the density of the underlying data points is low, reduces noise due to sampling randomness. Whereas using narrower bins, where the signal drowns the noise, gives greater precision to the density estimation. Thus varying the bin width within a histogram can be beneficial. Nonetheless, equal-width bins are widely used.

Several rules of thumb exist for determining the number of bins, such as the belief that between 5 and 20 bins is usually adequate. Mathematical software such as Matlab uses 10 bins as a default. Scott [24,26], Freedman and Diaconis [10], Sturges [31] and many other statisticians derived formulas for bin width and number of bins. The latest publication on this subject is the paper of Knuth [14]. A large set of formulas for calculating the number of bins is presented in [8]. For more information on bin width and number of bins, please see Sections 5 and 6.

Equal-bin-width histograms (EBWHs) are not statistically efficient for two reasons [30]. First, the bins are blindly allocated, not adapting to the data. Second, the normalized frequency may be zero for many bins and there is no guarantee for the consistency of the density estimates. In [18,21], consistency of estimated data-based histogram densities has been proven and general partitioning schemes have been proposed. [29] suggests a variable bin width histogram by inversely transforming an equal bin width histogram obtained on the transformed data. In [15], denoising method based on variable bin width histograms and minimum description length principle is proposed. In [11], a new projective image clustering algorithm by using variable bin width histogram is proposed.

Another equally important parameter when creating a histogram is the bin origin. The investigator must choose the position of the bin origin (very often by using convenient ‘round’ numbers). This subjectivity can result to misleading estimations because a change in the bin origin can change the number of modes in the density estimation [9,26,28]. Another approach to avoid the problem of choosing the bin origin in the histogram is the ‘moving histogram’ as introduced by Rosenblatt [23]. An improved version of the ‘moving histogram’ is the kernel density estimator (KDE) [22]. One drawback presented by the KDEs is the large number of calculations required to compute them. Scott [25] suggested an alternative procedure to eliminate the influence of the chosen origin and proposed the averaged shifted histogram (ASH). Smoothing makes histograms visually appealing and suitable for application, see e.g. [12,30].

An optimally calibrated EBWH with real data often appears rough in the tails due to the paucity of data. This phenomenon is one of several reasons for considering histograms with adaptive meshes. In practice, finding the adaptive mesh is difficult. Thus some authors have proposed (nonoptimal) adaptive meshes that are easier to implement. One of the more intuitively appealing meshes has an equal number (or equal fraction) of points in each bin. Other adaptive histogram algorithms have been proposed in [37,34].

The adaptive histogram with equal bincounts [26] will be called in the rest of the paper as the equal-bin-count histogram (EBCH). In the literature, there are also the terms: the equal area histogram [6] and the dynamic bin-width histogram [38]. According to [6], the EBWH oversmooths in regions of high density and is poor at identifying sharp peaks. The EBCH oversmooths in regions of low density and so does not identify outliers. We agree with [6] that the EBWH did not attract too much attention in statistical literature and therefore we intend to change it.

This paper puts into consideration histogram that has all bin counts equal to some non-random number arbitrary but reasonably set by an analyst. In the result, particular bin widths are random variables. Mainly it results from the will to improve estimation accuracy of skewed histograms.

Scott [26] examines EBWH vs. EBCH for normal data (well Beta(5,5)) with $n=100$ and $n=1000$ using the exact MISE as a function of $h$ for the EBWH and $k$ for the EBCH. He shows the poor performance of the EBCH when compared with EBWH, with the gap increasing with sample size $n$.

In relation to Scott [26], this paper concerns not only the normal distribution but also the other three distributions divided into five groups according to the skewness value. Monte Carlo simulations are carried out for sample sizes $n\le 100$ using an appropriately defined similarity measure.

The first goal of the paper is a choose of bin numbers $k$ (of constant bin width) in the EBWH for analyzed distributions and sample sizes $n$, which maximize the similarity measure in the Monte Carlo simulation. The second goal is a choose of constant bin count (of bin widths) in the EBCH for analyzed distributions and sample sizes, which maximize the similarity measure in the Monte Carlo simulation. The third goal is to present similarity measures between empirical and theoretical data. The fourth goal is the comparative analysis of two histogram methods by means of the frequency formula. The first additional goal is a tip how to proceed in EBCH when $modulo(n,k)\ne 0$. The second additional goal is the software in the form of a Mathcad file (version 14) with the implementation of EBWH and EBCH.

This paper is arranged as follows. Section 2 is devoted to the preliminaries. Here is a tip how to proceed in EBCH when $modulo(n,k)\ne 0$. Section 3 presents distributions selected to the Monte Carlo study. Section 4 presents distance and similarity measures between empirical and theoretical data. Section 5 is devoted to the EBWH whereas Section 6 is devoted to the EBCH. Section 7 compares analyzed histograms. Section 8 presents simulation and real data examples. The paper ends with conclusions. Tables 4–21, due to the size of the paper, are saved in a separate file as additional materials.

2. Preliminaries

The artistry of building the histograms consists in balancing between rough-hewn histogram and waving one. It is exemplified in Figure 1. The sample of n = 30 items on the basis of which the histograms were built was drawn from the Normal N(0,1) general population. The numerator in a histogram formula is the probability for the sample item to fall into particular bin.

Figure 1.

The EBWH, $n=30$, bin count $k=3$ (left), $k=7$ (right), $N(0,1)$.

Let us employ the coefficient of variation (CoV) denoted ${\gamma }_0$ of the binomial distribution as a measure of confidence of ith histogram segment

$${\gamma }_0=\text{standard deviation/expected value}.$$

In the case of the Binomial distribution, we have

$${\gamma }_{0_i}=\sqrt{n{p}_i(1-p_i)}/(n{p}_i)=\sqrt{(1/p_i-1)/n}$$

The coefficient of entire variation (CoEV) is

$${\gamma }_{0ev}=\sum _{i=1}^k{\gamma }_{0_i}=\sum _{i=1}^k\sqrt{(1/p_i-1)/n}$$

Replacing unknown $p_i$ with $n_i\text{/}n$ we get the sample CoV:

$${\hat{\gamma }}_{0_i}=\sqrt{1/n_i-1/n}$$

and the sample CoEV

$${\hat{\gamma }}_{0ev}=\sum _{i=1}^k{\hat{\gamma }}_{0_i}=\sum _{i=1}^k\sqrt{1/n_i-1/n}.$$

The CoEV enables comparing confidences of two or more histograms.

Let us consider the Normal $N(0,1)$ distribution censored from both sides at $-3$ at $+3$ (two areas of cut tiles are negligible) and build non-random histogram of five bins. In histogram of such name particular bin count is a product of sample size and a difference of the normal cumulative distribution functions calculated at bin borders. The results are presented in Table 1.

Table 1. The EBWH, bin width $h=6/5$.

Bin No.	Bin borders		Bin probabilities $p_i$	${\gamma }_{0_i}$
1	−3	−1.8	0.035	0.965
2	−1.8	−0.6	0.238	0.326
3	−0.6	0.6	0.451	0.201
4	0.6	1.8	0.238	0.326
5	1.8	3	0.035	0.965
			${\gamma }_{0ev}$	2.783

What relates to the histogram of equal bin counts, all bin probabilities $p_i$ are, of course, equal to $1/5$. So, all ${\gamma }_{0_i}=0.365$ and ${\gamma }_{0ev}=1.825$. The histogram proposed in this paper has the accuracy of particular bins stabilized and is intended for use mainly on skewed histograms.

Let us consider another example. A sample of $n=70$ items is drawn from general population in which the feature of our interest denoted $x$ follows the lognormal distribution with PDF $f(x)=\text{exp}[-0.5{(\text{ln}(x))}^2]{\left[x\sqrt{2\pi }\right]}^{-1}$. Figure 2 shows the EBWH (left) and the EBCH (right).

Figure 2.

EBWH (left) and EBCH (right), $n=70$, the lognormal distribution.

It is important that the EBCH reveals the mode when the EBWH does not!

At the end of this section, there is a tip how to proceed in EBCH when $modulo(n,k)\ne 0$.

1. Create a $DM[n,2]$ matrix.

2. Locate sample elements in the first column of $DM$.

3. Sort the first column of $DM$ in ascending order.

4. Set $D{M}_{1,2}=1.001$ and $D{M}_{n,2}=1.002$.

5. Generate $n-2$ uniformly distributed random numbers $r_i:i=2,3,\dots ,n-1$.

6. Set $D{M}_{i,2}=r_i;i=2,3,\dots ,n-1$.

7. Order $DM$ according to values of the second column.

8. Calculate $w=modulo(n,k)$.

9. From the whole ordered sample, select a subsample $x_{(i)}^{\ast },i=w+1,w+2,\dots ,n$.

10. Sort the subsample in ascending order.

11. On the basis of the above subsample, determine bin widths.

12. Add remaining sample elements $x_{(i)}^{\ast },i=1,2,\dots ,w$ to bins they belong to.

13. Calculate bin ordinates.

3. Distributions selected to the Monte Carlo study

The lognormal distribution $LOG(m,s)$ is a very good distribution for skewness modeling. The second distribution selected for skewness modeling is the generalized gamma distribution $GGD(a,b,c)$. This distribution includes as special cases a number of well-known distributions in statistics and theory of reliability [32]. Table 2 presents the family of these distributions. A key advantage of $GGD(a,b,c)$ is not that already existing distributions are special cases of $GGD(a,b,c)$, but that it fills the “space” between them. In other words, $GGD(a,b,c)$ allows the parametric description of empirical distributions that are indescribable by the traditional distributions. Parameter values of $GGD(a,b,c)$ were selected to obtain the same levels of skewness as $LOG(m,s).$

Table 2. Groups of distributions selected to the Monte Carlo study.

Group name	Distribution	Skewness value
Zero skewness	$SN$	$0$
	$GGD(1,3.091,5.335)$	$-5.182E-05$
Constant skewness	$EXP(1)$	$2$
Weak skewness	$LOG(0,0.314)$ $GGD(1,1.575,0.978)$	$1$
Medium skewness	$LOG(0,0.716)$ $GGD(1,0.708,1.287)$	$3$
Strong skewness	$LOG(0,0.920)$ $GGD(1,0.618,0.779)$	$5$

Monte Carlo study is carried out based on distributions as follows: standard normal $SN$, exponential $EXP(1),LOG(m,s)$, $GGD(a,b,c)$. These distributions are divided into five groups (see Table 2).

Figure 3 presents PDF of $LOG(m,s)$ and $GGD(a,b,c)$ for selected parameter values and skewness values (in parenthesis).

Figure 3.

PDF of $LOG(m,s)$ and $GGD(a,b,c)$ with parameter values and skewness values (in parenthesis).

4. Distance and similarity measures between empirical and theoretical data

In the literature, there are many definitions of distance and similarly measures between empirical $\hat{f}(x)$ and theoretical $f(x)$ PDFs. These measures are defined for discrete, finite values of $x$ and by the integral for all $x$ in the domain. Discrete measure are reviewed and categorized in both syntactic and semantic relationships [4]. Below we define four integral measures: distance measures $M_1,M_2,M_3$ and similarity measures $M_4,M_5$. $M_1,M_2,M_3$ measure the distance between PDFs and $M_4,M_5$ compare the area under PDFs.

The first popular distance measure is the mean square error (MSE) defined as

$$M_1={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(\hat{f}(x)-f(x){)}^2\text{d}x.$$

If $\hat{f}(x)$ and $f(x)$ are identical, then $M_1=0$. No maximum $M_1$ exists when PDFs are not identical. According to [6], relying on asymptotics of the IMSE leads to inappropriate recommendations.

The second distance measure similar to the Pearson's chi-square statistic is also noteworthy [6]

$$M_2={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{{(\hat{f}(x)-f(x))}^2}{f(x)}\text{d}x$$

If $\hat{f}(x)$ and $f(x)$ are identical, then $M_2=0$. No maximum $M_2$ exists when PDFs are not identical.

The third measure is the Matusita distance [19] given by

$$M_3={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\left(\sqrt{f(x)}-\sqrt{\hat{f}(x)}\right)}^2\text{d}x.$$

If $\hat{f}(x)$ and $f(x)$ are identical, then $M_3=0$. No maximum $M_3$ exists when PDFs are not identical.

The next measure is the Bhattacharyya similarity measure [1] defined as

$$M_4={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sqrt{f(x)}\sqrt{\hat{f}(x)}\text{d}x=1-0.5M_3.$$

Measure $M_4$ takes values in interval $0,1$. If $f(x)$ and $\hat{f}(x)$ are identical, then $M_4=1$. If for any $x$, we have $f(x)=0.48$ and $\hat{f}(x)=0.52$, then $\sqrt{f(x)}\sqrt{\hat{f}(x)}=0.5$. The same value of integral function we obtain for $f(x)=0.985$ and $\hat{f}(x)=0.254$.

We propose a new similarity measure between the actual PDF $f(x)$ and the empirical PDF $\hat{f}(x)$ defined as

$$M_5={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\text{min}\{f(x),\hat{f}(x)\}\text{d}x.$$

The similarity measure $M$ takes values in interval $0,1$. If $f(x)$ and $\hat{f}(x)$ are identical, then $M_5=1$. Figure 4 presents the graphical representation of $M_5$.

Figure 4.

The graphical interpretation of the new similarity measure. The shaded area reflects the measure $M_5$.

Why is the measure $M_5$ better than $M_4$? Figure 5 shows PDFs of $N(0,1)$ and $N(3,1)$. The measure $M_5=0.134$ is more reliable than $M_4=0.325$ and will be used in the simulation study.

Figure 5.

N(0,1) versus N(3,1). Similarity study, $M_4=0.325,M_5=0.134$.

5. Equal-bin-width histogram (EBWH)

Many statisticians have attempted to determine an optimal $k$ value, but these methods generally make strong assumptions about the shape of the distribution. Depending on the actual data distribution and the goals of the analysis, different $h$ values may be appropriate, so experimentation is usually needed to determine an appropriate width. There are, however, various useful guidelines and rules of thumb.

Let us define the set of ordered sample elements as $x_{(1)},x_{(2)},\dots ,x_{(n)}$. Sturges [30] proposed the rule of determining numbers of bins $k$ defined as $k=[3.3lo{g}_{10}n]+1$. In practice, according to Scott [24], Sturges’ rule is applied by dividing the sample range $R=x_{(n)}-x_{(1)}$ into $k$. Technically, Sturges’ rule is a number-of-bins rule rather than a bin-width rule. Much simpler is to adopt the convention that all histograms have an infinite number of bins, only a finite number of which are nonempty. Further, the equal-bin-count histogram (EBCH), which are considered in next section, does not use equal-width bins. Thus focusing on bin width rather than number of bins seems appropriate.

In this section, we compare 17 rules for determining bin width $h=R/k$.

The Scott's normal rule is defined as [24]

$$h_1=3.491\hat{\sigma }{n}^{-1/3},$$

where $\hat{\sigma }$ is the sample standard deviation, is optimal for random samples of normally distributed data as it minimizes the IMSE of the density estimate [23].

The Freedman–Diaconis normal rule, based on the percentiles, is defined by [10]

$$h_2=2(Q_{75}-Q_{25})n^{-1/3}.$$

If the data are in fact normal, the $h_2$ rule is about 77% of the $h_1$ rule as the $2(Q_{75}-Q_{25})\hat{\sigma }=2\ast 1.349\hat{\sigma }=2.698\hat{\sigma }$ in this case.

The third rule, which refers to minimizing cross-validation estimated squared error, is an approach of minimizing IMSE from Scott's normal rule. Using leave-one-out cross validation, it can be generalized beyond normal distribution. The third rule has a form [36]

$$\underset{h_3}{\underset{\sim }{\text{min}}}\hat{J}(h_3)=\underset{h_3}{\underset{\sim }{\text{min}}}\left[\frac{2}{(n-1)h_3}-\frac{n+1}{n^2(n-1)h_3}\sum _k{\eta }_k^2\right],$$

where ${\eta }_k$ is the number of data points in the $k$th bin, and choosing the value of $h_3$ (which minimizes $\hat{J}(h_3)$) will minimize IMSE.

The fourth rule is as follows: the optimal bin width $h_4$ is obtained by minimizing the cost function [27]

$$\underset{h_4}{\underset{\sim }{\text{min}}}{C}_4(h_4)=\underset{h_4}{\underset{\sim }{\text{min}}}\frac{2\overline{\eta }-v}{{(n{h}_4)}^2},$$

where

$$\overline{\eta }=\frac{1}{k}\sum _{i=1}^k{\eta }_i,v=\frac{1}{k}\sum _{i=1}^k({\eta }_i-\overline{\eta }{)}^2.$$

The Doane rule attempts to improve its performance in the case of non-normal data and is given by [7]

$$h_5=\frac{\text{R}}{k_5},k_5=\left[1+\text{lo}{\text{g}}_{2}n+\text{lo}{\text{g}}_2\left(1+{\gamma }_1\sqrt{\frac{(n+1)(n+3)}{6(n-2)}}\right)\right],$$

where ${\gamma }_1$ is the estimated third-moment-skewness.

The Mosteller–Tukey rule [20], used inter alia in Microsoft Excel, is given by

$$h_6=\frac{R}{k_6},k_6=\left[\sqrt{n}\right].$$

The Sturges rule has the form [31]

$$h_7=\frac{R}{k_7},k_7=[\text{lo}{\text{g}}_{2}n]+1.$$

Rules $k_7$ comes from a binomial distribution and implicitly assumes an approximately normal distribution. This formula can perform poorly for $n<30$ and also in case of data that are not normally distributed.

The Rice rule [8], being a simple alternative to $h_7$, is given by

$$h_8=\frac{R}{k_8},k_8=\left[2\sqrt[3]{n}\right].$$

Others rules are as follows [8]:

• Cochran rule [5]: $h_9=\frac{R}{k_9},k_9=\left[\sqrt{n/5}\right]$,

• Cencov rule [3]: $h_{10}=\frac{R}{k_{10}},k_{10}=\left[\sqrt[3]{n}\right]$,

• Bendat and Piersol rule [2]: $h_{11}=\frac{R}{k_{11}},k_{11}=[1.87\ast {(n-1)}^{0.4}]$,

• Larson rule [17]: $h_{12}=\frac{R}{k_{12}},k_{12}=1+[2.2\ast \text{lo}{\text{g}}_2(n)]$,

• Velleman rule [35]: $h_{13}=\frac{R}{k_{13}},k_{13}=\left[2\sqrt{n}\right]I(n\le 100)+[10\text{lo}{\text{g}}_{10}(n)]I(n>100)$,

• Terrel and Scott rule [33]: $h_{14}=\frac{R}{k_{14}},k_{14}=\left[\sqrt[3]{2n}\right]$,

• Ishikawa rule [13]: $h_{15}=\frac{R}{k_{15}},k_{15}=6+[n/50]$,

• Anonymous 1 rule [8]: $h_{16}=\frac{R}{k_{16}},k_{16}=\left[2.5\sqrt[4]{n}\right]$,

• Anonymous 2 rule [8]: $h_{17}=\frac{R}{k_{17}},k_{17}=[lo{g}_2(n)]$.

Rules $k_i(i=6,7,\dots 17)$ are defined using only the sample size $n$ and therefore Table 3 lists number of bins $k$ for these rules and sample sizes used in the simulation study. It can be observed that there is a great diversity of k values obtained.

Table 3. Number of bins $k$ for selected sample size $n$ and rules $k_i(i=6,7,\dots 17)$.

n	$k_6$	$k_7$	$k_8$	$k_9$	$k_{10}$	$k_{11}$	$k_{12}$	$k_{13}$	$k_{14}$	$k_{15}$	$k_{16}$	$k_{17}$
10	3	4	4	1	2	4	3	6	2	6	4	3
15	3	4	4	1	2	5	3	7	3	6	4	3
20	4	5	5	2	2	6	3	8	3	6	5	4
25	5	5	5	2	2	6	4	10	3	6	5	4
30	5	5	6	2	3	7	4	10	3	6	5	4
40	6	6	6	2	3	8	4	12	4	6	6	5
50	7	6	7	3	3	8	4	14	4	7	6	5
60	7	6	7	3	3	9	4	15	4	7	6	5
80	8	7	8	4	4	10	5	17	5	7	7	6
100	10	7	9	4	4	11	5	20	5	8	7	6

The rules $h_i(i=1,\dots ,17)$ determining bin width are compared in the Monte Carlo simulations using the similarity measure. The algorithm calculating values of the similarity measure

$$M={\int }_{x_{(1)}}^{x_{(\text{n})}}\text{min}\{f(x),\hat{f}(x)\}\text{d}x$$ (1)

is as follows:

1. Set sample size n.

2. Repeat the following steps $u={10}^3$ times:

   1. Generate random sample $x_i(i=1,\dots ,n)$ based on distribution with PDF $f(x)$.
   2. Present obtained values in an increasing order, i.e. $x_{(1)},x_{(2)},\dots ,x_{(n)}$.
   3. Calculate bin width $h$ according to an appropriate formula.
   4. Calculate number of bins $k=[(x_{(n)}-x_{(1)})/h]$.
   5. Set bins $U_i=[x_{(1)}+(i-1)h,x_{(1)}+ih),i=1,2\dots .,k$.
   6. Calculate bin counts ${\eta }_k$.
   7. Calculate empirical density function $\hat{f}(x)={\eta }_k/n/h$.
   8. Calculate value of the similarity measure $M$ according to (1)

3. Calculate value of the similarity measure $\overline{M}=\left(\sum _{i=1}^u{M}_i\right)/u$.

Monte Carlo simulations are carried out for five groups of distributions. The similarity measure $\overline{M}$ is calculated for a given sample size $n$ and rules $h_i(i=1,\dots ,17)$ based on the same data. Values $u>{10}^3$ do not significantly affect $\overline{M}$ values. The rules $h_1$ and $h_2$ are calculated, according to the definition, for the SN distribution only. The rules $h_3$ and $h_4$ give bad results for skewness groups of distribution, e.g. for $GGD(1,0.618,0.779)$ and $n=40$ we have $k=25$ ( $h_3$), $k=21$ ( $h_4$). Therefore $h_3$ and $h_4$ are calculated for the zero skewness group only. Tables 4–12 (see additional materials) show $\overline{M}$ values for analyzed distributions. The highest $\overline{M}$ values for a given sample size are in bold. Rules $h_{\text{i}}(i=1,2,\dots ,17)$, which maximizes $\overline{M}$ for a given sample size, will be used in Section 7 (see Tables 22–25).

Table 26. The measure $\overline{M}$ for rules $h_i(i=5,\dots ,17)$ in the EBWH and $\overline{MN}$ for bin count $\eta$ in the EBCH, $CND(8,0.1,2,0.1,0.5)$, $n=100$.

$h_5$	$h_6$	$h_7$	$h_8$	$h_9$	$h_{10}$	$h_{11}$	$h_{12}$	${\mathit{h}}_{13}$	$h_{14}$
0.479	0.575	0.437	0.531	0.275	0.275	0.615	0.531	0.719	0.332
$h_{15}$	$h_{16}$	$h_{17}$	$\eta =2$	$\eta =4$	$\mathit{\eta }=5$	$\eta =10$	$\eta =20$	$\eta =25$	$\eta =50$
0.485	0.437	0.386	0.731	0.760	0.764	0.742	0.652	0.572	0.404

Table 22. Values of the frequency formula $C$. Zero and constant skewness group.

Zero skewness group					Constant skewness group
$n$	$SN$			$GGD(1,3.091,5.335)$			$EXP(1)$
	$r$	$\eta$	$C$	$r$	$\eta$	$C$	$r$	$\eta$	$C$
$10$	${\text{h}}_9$	$5$	0.203	${\text{h}}_9$	$5$	0.193	${\text{h}}_{10}$	$5$	0.499
$15$	${\text{h}}_9$	$5$	0.386	${\text{h}}_{14}$	$5$	0.305	${\text{h}}_{17}$	$5$	0.507
$20$	${\text{h}}_{14}$	$5$	0.292	${\text{h}}_{14}$	$5$	0.267	${\text{h}}_{17}$	$5$	0.433
$25$	${\text{h}}_1$	$5$	0.231	${\text{h}}_{14}$	$5$	0.219	${\text{h}}_{17}$	$5$	0.417
$30$	${\text{h}}_1$	$6$	0.242	${\text{h}}_{17}$	$6$	0.220	${\text{h}}_{16}$	$6$	0.385
$40$	${\text{h}}_{17}$	$8$	0.203	${\text{h}}_{14}$	$8$	0.173	${\text{h}}_{16}$	$8$	0.356
$50$	${\text{h}}_{17}$	$10$	0.142	${\text{h}}_{17}$	$10$	0.125	${\text{h}}_{16}$	$10$	0.306
$60$	${\text{h}}_{17}$	$10$	0.148	${\text{h}}_{17}$	$10$	0.124	${\text{h}}_{15}$	$10$	0.293
$80$	${\text{h}}_{17}$	$10$	0.094	${\text{h}}_{17}$	$10$	0.087	${\text{h}}_{12}$	$10$	0.244
$100$	${\text{h}}_{16}$	$10$	0.049	${\text{h}}_{17}$	$10$	0.058	${\text{h}}_{12}$	$10$	0.181

Table 23. Values of the frequency formula $C$. Weak skewness group.

	$LOG(0,0.314)$			$GGD(1,1.575,0.978)$
$n$	$r$	$\eta$	$C$	$r$	$\eta$	$C$
$10$	$h_{10}$	$5$	0.284	$h_{10}$	$5$	0.303
$15$	$h_{10}$	$5$	0.263	$h_{10}$	$5$	0.210
$20$	$h_{10}$	$5$	0.283	$h_{10}$	$5$	0.150
$25$	$h_{14}$	$5$	0.277	$h_{10}$	$5$	0.166
$30$	$h_{17}$	$6$	0.272	$h_{10}$	$10$	0.192
$40$	$h_{17}$	$8$	0.247	$h_{10}$	$10$	0.154
$50$	$h_{17}$	$10$	0.175	$h_{10}$	$10$	0.140
$60$	$h_{15}$	$10$	0.201	$h_{10}$	$10$	0.151
$80$	$h_{15}$	$10$	0.134	$h_{10}$	$16$	0.091
$100$	$h_{15}$	$10$	0.092	$h_{17}$	$10$	0.092

Table 24. Values of the frequency formula $C$. Medium skewness group.

	$LOG(0,0.716)$			$GGD(1,0.708,1.287)$
$n$	$r$	$\eta$	$C$	$r$	$\eta$	$C$
$10$	$h_{14}$	$5$	0.364	$h_{17}$	$2$	0.57
$15$	$h_{14}$	$5$	0.340	$h_{16}$	$5$	0.679
$20$	$h_{17}$	$5$	0.330	$h_{16}$	$5$	0.713
$25$	$h_{17}$	$5$	0.264	$h_{15}$	$5$	0.725
$30$	$h_{17}$	$6$	0.254	$h_5$	$6$	0.722
$40$	$h_{17}$	$8$	0.230	$h_5$	$8$	0.680
$50$	$h_{17}$	$10$	0.16	$h_5$	$10$	0.676
$60$	$h_{16}$	$10$	0.172	$h_5$	$10$	0.719
$80$	$h_{16}$	$10$	0.230	$h_{13}$	$10$	0.710
$100$	$h_{12}$	$10$	0.187	$h_{13}$	$10$	0.696

Table 25. Values of the frequency formula $C$. Strong skewness group.

	$LOG(0,0.92)$			$GGD(1,0.618,0.779)$
$n$	$r$	$\eta$	$C$	$r$	$\eta$	$C$
$10$	$h_{17}$	$5$	0.433	$h_{11}$	$2$	0.941
$15$	$h_{16}$	$5$	0.495	$h_{15}$	$3$	0.982
$20$	$h_{16}$	$5$	0.45	$h_{13}$	4	0.991
$25$	$h_{16}$	$5$	0.414	$h_{13}$	$5$	0.995
$30$	$h_{12}$	$6$	0.408	$h_{13}$	5	0.997
$40$	$h_{12}$	$5$	0.325	$h_{13}$	5	1
$50$	$h_{11}$	$5$	0.265	$h_{13}$	5	1
$60$	$h_{11}$	$6$	0.229	$h_{13}$	$6$	1
$80$	$h_{11}$	$8$	0.28	$h_{13}$	$8$	1
$100$	$h_{11}$	$10$	0.24	$h_{13}$	$10$	1

6. Equal-bin-count histogram(EBCH)

In the EBWH, all the bins are of equal width that is arbitrary prescribed. Bin counts are random numbers. In the EBCH, the bin counts are arbitrary prescribed to be equal in all the bins. The width of each particular bin is adjusted so that bin counts to be equal. Bin borders are set precisely in the middle between two neighboring observations that have fallen into previous and next bin.

Let us define the set of ordered sample elements as $x_{(1)},x_{(2)},\dots ,x_{(n)}$. If $\eta$ denotes a bin count, then the number of bins is given by $k=n/\eta$. The bin count $\eta$ is $n$ divisor ( $\eta \ne 1,\eta \ne n$). The rules in the EBWH are marked as $h_i(i=1,2,\dots ,17)$, so the bin widths in EBCH are marked as $H_i(i=1,2,\dots ,k)$.

The bin width $H_i(i=1,2,\dots ,k)$ can be calculated as

$$H_1=\frac{x_{(\eta )}+x_{(\eta +1)}}{2}-x_{(1)},H_k=x_{(n)}-\frac{x_{([k-1]\eta )}+x_{([k-1]\eta +1)}}{2},$$ (2a)

$$H_i=\frac{x_{(i\eta )}+x_{(i\eta +1)}}{2}-\frac{x_{([i-1]\eta )}+x_{([i-1]\eta +1)}}{2}(i=2,3,\dots ,k-1).$$ (2b)

A set of bins can be written as

$$U_1=[x_{(1)},x_{(1)}+H_1),U_i=\left[x_{(1)}+\sum _{j=1}^{i-1}{H}_j,x_{(1)}+\sum _{j=1}^i{H}_j\right),i=2,\dots ,k.$$ (2c)

Empirical density function is defined as

$${\hat{f}}_N(x)=\frac{\eta }{n{H}_k},x\in U_k,$$ (3)

where ${\hat{f}}_N(x)\ge 0$ and $\int {\hat{f}}_N(x)\text{d}x=1$ obviously.

The similarity measure related to the EBCH is given by

$$MN={\int }_{x_{(1)}}^{x_{(n)}}\text{min}\{f(x),{\hat{f}}_N(x)\}\text{d}x.$$ (4)

The Monte Carlo simulation is carried out for the optimal constant bin count $\eta$ which maximizes $MN$. Simulation results for a given sample size $n$ and constant bin counts $\eta$ are obtained based on the same data.

The algorithm calculating values of the similarity measure (4) is as follows:

1. Set a sample size n.

2. Set a bin count $\eta$, where $\eta$ is $n$ divisor ( $\eta \ne 1,\eta \ne n$).

3. Calculate the number of bins $k=n/\eta$.

4. Repeat the following steps $u={10}^3$ times:

   1. Generate random sample $x_i(i=1,2,\dots ,n)$ distributed according to distribution.
   2. Present obtained values in an increasing order, i.e. $x_{(1)},x_{(2)},\dots ,x_{(n)}$.
   3. Calculate bin width $H_i(i=1,2\dots ,k)$ according to (2a)–(2b).
   4. Set bins $U_i=\left[x_{(1)}+\sum _{j=1}^{i-1}{H}_j,x_{(1)}+\sum _{j=1}^i{H}_j\right),i=1,2,\dots ,k$.
   5. Calculate empirical density function ${\hat{f}}_N(x)$ (3).
   6. Calculate value of the similarity measure $MN$ (4).

5. Calculate value of the similarity measure $\overline{MN}=\left(\sum _{i=1}^{u}M{N}_i\right)/u$

Tables 13–21 (see additional materials) show the optimally selected bin count $\eta$ determined by the highest value of $\overline{MN}$ for a given distribution and a sample size. The $\overline{MN}$ value increases with a sample size $n$. The optimally selected bin count $\eta$ will be used in Section 7 (Tables 22–25).

7. EBWH vs. EBCH – comparative study

This section is devoted to the comparative study of the EBWH and EBCH by means of the frequency formula. The Monte Carlo study uses the results presented in Sections 5 and 6. These results were calculated to obtain optimal bin widths in the EBWH and optimal constant bin counts in the EBCH.

The rules (r) $h_i(i=1,\dots ,17)$ with the highest value of $\overline{M}$ (Tables 4–12) and the bin counts $\eta$ with the highest value of $\overline{MN}$ (Tables 13–21) are selected for the comparative study. The algorithm describing this study is as follows:

1. Set a counter $win=0$.

2. Repeat the following steps $u={10}^3$ times:

   1. Calculate the similarity measure $\overline{M}$ related to the EBWH with optimally selected rules $h_i(i=1,\dots ,17)$ in Section 5.
   2. Calculate the similarity measure $\overline{MN}$ related to the EBCH with optimally selected η values in Section 6.
   3. If $\overline{MN}>\overline{M}$, then $win=win+1$.

3. Calculate a frequency formula $C=win/u$.

Tables 22–25 present the values of the frequency formula $C$ for five distribution groups. The cases with $C>0.5$ for a given sample size are in bold.

The EBWH is recommended to the zero skewness group (Table 22), the constant skewness group (Table 22) and the weak skewness group of unimodal distributions (Table 23) (see Figure 3).

An advantage of the EBCH over the EBWH (C greater than 0.5) becomes apparent when population distributions are both modeless (see Figure 3) and of medium or great skewness (Tables 24 and 25). The greater the skewness, the greater an advantage of the EBCH over the EBWH. Examples 1–5 confirm this fact.

8. Examples

8.1. Simulation examples

Example 1. Figure 6 compares the EBWH and EBCH for the SN distribution and sample $n=40$. Optimally selected rule is $h_{17}$ (Table 22), optimally selected $\eta =8$ (Table 22). Similarity measure $M=0.846$ for the EBWH is higher than $MN=0.804$ for the EBCH.

Figure 6.

EBWH (left, $h_{17}=0.613,M=0.846$) versus EBCH (right, $\eta =8,MN=0.804$) for SN distribution and $n=40$.

To show an advantage of the EBCH over the EBWH, we will use three distributions. The first one is the generalized gamma distribution $GGD(a,b,c)$ (Example 2), the second one is the compound normal distribution $CND(a_1,b_1,a_2,b_2,\omega )$ (Example 3) and the third one is the lognormal distribution $LOG(m,s)$ (Examples 4 and 5).

Example 2. Figure 7 compares histograms for the $GGD(1,0.618,0.779)$ and $n=60$. Optimally selected rule is $h_{13}$ (Table 24), optimally selected $\eta =6$ (Table 24). Similarity measure $MN=0.843$ for the EBCH is higher than $M=0.626$ for the EBWH.

Figure 7.

EBWH (left, $M=0.626$) versus EBCH (right, $MN=0.843$) for $GGD(1,0.618,0.779)$ distribution and $n=60$.

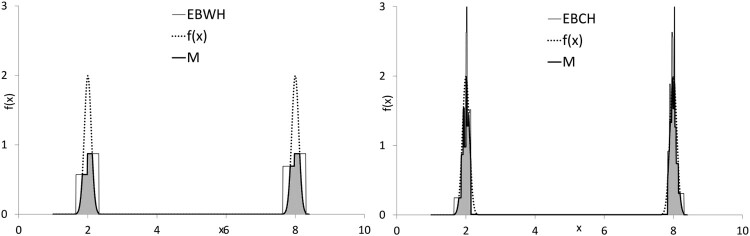
Example 3. Figure 8 compares histograms for the $CND(8,0.1,2,0.1,0.5)$ and $n=100$. Simulation study shows (see Table 26) that optimally selected rule is $h_{13}$ and optimally selected $\eta =5$. Similarity measure $MN=0.782$ for the EBCH is higher than $M=0.586$ for the EBWH.

Figure 8.

EBWH (left, $M=0.586$) versus EBCH (right, $MN=0.782$) for $CND(8,0.1,2,0.1,0.5)$ distribution and $n=100$.

8.2. Resampling from real data examples

Determining histograms is a form of statistical reasoning. Therefore, this paper becomes devoted to assessing a power of statistical reasoning. In order to act properly “assessors” have to know a matter of facts to state whether reasoning is false or true. Assessors’ task causes examples presented in the paper differ from real data examples. The conclusions are drawn on the basis of results of the Monte Carlo experiment that serves to carry out resampling. For this reason, the following requirements must be met before applying the reasoning scheme proposed in this paper:

• Analytical form of a distributions that “holds” in considered general populations has to be known with accuracy to parameter values! Otherwise, actuality remains unknown and results of statistical reasoning are not assessable.

• Data used to determine histograms have to be exact data, i.e. not grouped and not censored. Otherwise, histograms cannot be determined.

The whole histogram competition is performed into eight steps:

1. Dig up a set of real data that seem to come from evidently abnormal population.

2. On the of-chance perform by-eye goodness-of-fit test plotting data on the Gaussian probability paper.

3. Having abnormality confirmed choose such a theoretical probability distribution that fits data in question. Further it will be treated as and called the actual distribution. Like in Step 2 perform appropriate by-eye goodness-of-test.

4. Having correctness of the choice of step 3 confirmed estimate parameters of the actual distribution.

5. Get a sample with the Monte Carlo resampling method from the actual distribution.

6. Determine EBWH and EBCH for optimally selected rule and bin count.

7. Calculate similarity measures of both histograms to the actual distribution.

8. Compare histograms with respect to similarity measure and point out a winner.

Example 4. Lai and Xie [16] present data from a lung cancer study for the treatment of veterans. Data represent survival days for 97 patients with lung cancer from therapy (see Table 27), skewness equals 1.944.

Figure 9.

Gaussian probability paper for survival days from Example 4 (left, $n=97$) and repair times from Example 5 (right, $n=46$).

Figure 10.

Lognormal probability paper for survival days from Example 4 (left, $n=97$) and repair times from Example 5 (right, $n=46$).

Figure 11.

Empirical and theoretical lognormal quantile function for survival days from Example 4 (left, $n=97$) and repair times from Example 5 (right, $n=46$).

Figure 12.

EBWH (left, $M=0.724$) versus EBCH (right, $MN=0.823$) for survival days from Example 4, $Log(4.128,1.217),n=100$.

Figure 13.

EBWH (left, $M=0.83$) versus EBCH (right, $MN=0.864$) for repair times from Example 5, $Log(0.658,1.102)$, $n=50$.

Table 28. The measure $\overline{M}$ for rules $h_i(i=5,\dots ,17)$ in the EBWH and $\overline{MN}$ for bin count $\eta$ in the EBCH, $Log(4.128,1.217)$, $n=100$.

$h_5$	$h_6$	$h_7$	$h_8$	$h_9$	$h_{10}$	$h_{11}$	$h_{12}$	${\mathit{h}}_{13}$	$h_{14}$
0.766	0.749	0.694	0.735	0.587	0.587	0.761	0.735	0.812	0.631
$h_{15}$	$h_{16}$	$h_{17}$	$\eta =2$	$\eta =4$	$\eta =5$	$\mathit{\eta }=10$	$\eta =20$	$\eta =25$	$\eta =50$
0.715	0.694	0.666	0.756	0.801	0.813	0.831	0.798	0.773	0.630

Table 29. The measure $\overline{M}$ for rules $h_i(i=5,\dots ,17)$ in the EBWH and $\overline{MN}$ for bin count $\eta$ in the EBCH, $Log(0.658,1.102)$, $n=50$.

$h_5$	$h_6$	$h_7$	$h_8$	$h_9$	$h_{10}$	$h_{11}$	$h_{12}$	${\mathit{h}}_{13}$	$h_{14}$
0.790	0.763	0.746	0.763	0.631	0.631	0.775	0.763	0.795	0.684
$h_{15}$	$h_{16}$	$h_{17}$	$\eta =2$	$\mathit{\eta }=5$	$\eta =10$	$\eta =25$
0.763	0.746	0.720	0.744	0.794	0.789	0.666

Table 27. Computer implementation of Examples 4 and 5.

Step of above algorithm	Example 4	Example 5
1	Survival days	Repair times
2	A population the data come from is definitely abnormal (Figure 9, left)	A population the data come from is definitely abnormal (Figure 9, right)
3	The data come from the lognormal population (Figure 10, left)	The data come from the lognormal population (Figure 10, right)
4	The actual distribution that holds in the population in question is the $Log(4.128,1.217)$ (Figure 11, left)	The actual distribution that holds in the population in question is the $Log(0.658,1.101)$ (Figure 11, right)
5	$n=100$	$n=50$
6	Optimally selected rules is $h_{13},$ and bin count $\eta =10$(Table 28). Comparison of histograms for analyzed data (Figure 12)	Optimally selected rules is $h_{13},$ and bin count $\eta =5$(Table 29). Comparison of histograms for analyzed data (Figure 13)
7	Similarity measure $MN=0.823$ for the EBCH is higher than $M=0.724$ for the EBWH	Similarity measure $MN=0.864$ for the EBCH is higher than $M=0.83$ for the EBWH

Example 5. Lai and Xie [16] present 46 repair times (in hours) for an airborne communication transceiver (see Table 27), skewness equals 2.987.

What causes that in many cases the EBCH more precisely reflects the actual density function than the EBWH? Because EBWH is insensitive to contents of data set. Notice that EBWH is determined mainly by extreme values of data set. The content is mechanically sliced. In contrast to this in case of EBCH the content is sliced intelligently for equilibrated accuracy of local density estimates.

The software in the form of a Mathcad file (version 14) implementing EBWH and EBCH for sample size n is available at https://sulewski.apsl.edu.pl/index.php/publikacje. This file also contains a tip how to proceed in EBCH when $modulo(n,k)\ne 0$. If you want to compare both histograms, use the theoretical distribution.

9. Conclusion

The EBWH is recommended to symmetric distributions and distributions with constant nonzero skewness (e.g. exponential distribution). The EBCH is recommended to asymmetric distributions, especially in situations when skewness is not weak and empirical PDF is modeless. It has been proved that the greater skewness the greater the advantage of the EBCH over the EBWH. The EBCH should be used for bimodal distributions (see Examples 3 and 4). The greater distance between modes the greater the advantage of the EBCH over the EBWH.

Disclosure statement

No potential conflict of interest was reported by the author(s).