CD-vine model for capturing complex dependence

ABSTRACT

Copula based finite mixture models allow us to capture the dependence between random variables more flexibly. Although bivariate case of finite mixture models has been commonly studied, limited efforts have been spent on finite mixture of vines. Instead of using classical mixture models, it is possible to incorporate C-vines into the D-vine model (CD-vine) to understand both the dependence among the variables over different time points. The aim of this study is to create a CD-vine mixture model expressing the dependencies between variables in temporal order. To achieve this, cumulative distribution function values generated within the time components are tied together with D-vine probabilistically. With this approach, dependence structure between variables at each time point is explained by C-vine and the dependence among the time points is captured by the D-vine model. The performance of the proposed CD-vine model is validated using simulated data and applied on four stock market indices.

1. Introduction

Over the last decades, copulas became a very popular tool to understand the dependence between random variables in different research fields such as finance [1], actuarial science [12], and weather related researches[13]. Under such multi-dimensionality, vine copulas are proposed to detect the complex dependence in multivariate setting by exploiting pair copulas [2,6,7,19,24]. Simply, vine copulas are probabilistic graphical tools, which allow us to overcome the limitations of standard copulas in higher dimensions. It is possible to express a multivariate density function by using both unconditional and conditional bivariate copula pairs. In terms of a large number of possible decompositions for conditional density function, there are numerous ways to generate vines. Among those constructions, two popular types of vine copulas, widely used by researchers, are the Canonical (C) and Drawable (D) vines [23]. For the recent review on vines, interested readers are referred to [10].

The interest in studies based on finite mixture models on copulas is increased to reveal the hidden and complex dependence patterns among the variables in a more flexible manner. In that respect, the fruitful marriage of the finite mixture model and vines is also beneficial for capturing dependence structures in a multivariate setting. Previously, Vrac et al. [24], Cuvelier and Noirhomme-Fraiture [9,17] and [5,23] studied on model-based clustering approach in terms of copulas. Later on, these approaches are extended to higher dimensions with vine copula methodology by [20,29] for clustering and [14] in terms of parameter estimations. On the other hand, the main focus of the above-mentioned studies is on the finite mixture model, constructed by the parametric pair copulas.

This study proposes a novel CD-vine mixture model, to investigate the dependence within and among the components at the same time instead of using a finite mixture scheme. The main inspiration of CD-vine model comes from one of the agricultural problems, capturing the dependence between the growing phases of any crop with respect to weather parameters. For any specific crop, there is a unique requirement for climatic or soil based needs over its growth stages. For feasible agricultural risk management, understanding the dependence among the growth stages for a specific crop yield is very crucial. In that respect, the proposed CD-vine approach can be a useful tool to detect any hidden dependence both within and between growth periods in terms of selected explanatory variables. More clearly, dependence structure between variables during the growing phase is explained by C-vine and the dependence among these time points is captured by D-vine model. This mechanism can be considered to capture the underlying dependence structure on the financial market changing on a yearly basis. Generally, as the most elegant way to consider the dependence as a function of time, time varying copulas appears in the literature [3], [4]. In that respect, CD-vine model can be an aider tool for such kind of financial return studies. By considering the analytically derived joint distributions, the parameter estimations of the CD-vine approach are considered under certain copula families. Since the long term availability of stock market data is common, the proposed model is considered for a financial data set.

The rest of the paper is organized within the following sections. Section 2 summarizes the preliminaries of vine copulas and the analytical derivation for the CD-vine mixture model. Thereafter, Section 3 summarizes the findings of the proposed model using both simulated and real life data sets. Finally, the main conclusion with drawbacks and the further outlook of the study is summarized in Section 4.

2. Materials and methods

2.1. Preliminaries

The notion of copula was first introduced by [28], that aims to derive joint distribution of a random vector in terms of its marginals and the joint dependence structure [16]. For a p-dimensional vector U on the unit hypercube, a copula C is defined as,

$$C(u_1,u_2,\dots ,u_p)=P(U_1\le u_1,U_2\le u_2,\dots ,U_p\le u_p),$$ (1)

where C is associated with p-dimensional distribution function F, having marginals $F_1=F_1(x_1),F_2=F_2(x_2),\dots ,F_p=F_p(x_p)$ satisfies the following [28],

$$F(x_1,x_2,\dots ,x_p)=C(F_1(x_1),F_2(x_2),\dots ,F_p(x_p);\beta ),$$ (2)

where the random variable $X_i$, for $i=1,\dots ,p$ is assumed to be continuous and β is the parameter which measures dependence between the marginals. In particular, C can be interpreted as the distribution function of a p dimensional random variable on $[0,1{]}^p$ with uniform margins. C is unique whenever all $F_1$, $F_2$, …, $F_p$ are continuous marginal distributions. Conversely, if C is a copula and $F_1,\dots ,F_p$ are distribution functions, then the function F defined by Equation (2) is a multivariate distribution function with margins $F_1,\dots ,F_p$. Besides, the corresponding density function for C is given as,

$$f(x_1,x_2,\dots ,x_p)=c_{1\dots p}(F_1(x_1),F_2(x_2),\dots ,F_p(x_p);\beta )\prod _{k=1}^p{f}_k(x_k)$$ (3)

Generally, copula functions can be classified as Elliptical and Archimedean type families that exhibit distinct dependence structures. For example, widely used elliptical copulas are normal and student t-copulas, where the first one represents no tail dependence but the latter exhibits both upper and lower tail dependence [20]. As a member of Archimedean family, Frank copula examines the symmetric dependence structures. On the other hand, Clayton and Gumbel are useful to identify the tail dependencies at lower and upper quantiles, respectively. Even if they are very practical to model the dependence structure in the bivariate case, the use of copulas requires more effort in higher dimensions, where standard multivariate copulas are suffering from inflexible structures. For this reason, vine copula (vines), was proposed to increase the flexibility of multivariate copula models. Vines incorporate unconditional and conditional bivariate copulas to describe a multivariate distribution [7]. A set of linked trees describes the vine copula's factorization of the multivariate density function using pair copulas [7,11]. Historically, Joe [18] gives a probabilistic construction of multivariate distribution functions based on simple building blocks called pair-copulas. This construction method is called Pair Copula Construction (PCC) and it is organized in a graphical way, called regular vines [7].

Therefore, vine construction can be made as a sequence of bivariate unconditional and conditional copulas in a hierarchical manner. By this method, given density in Equation (3) can be decomposed into a product of pair-copulas in an iterative manner, under suitable regularity conditions [2],

$$f(x_k|\mathit{v})=c_{x_k,v_j|{\mathit{v}}_{\mathbf{-}\mathit{j}}}(F(x_k|{\mathit{v}}_{\mathbf{-}\mathit{j}}),F(v_j|{\mathit{v}}_{\mathbf{-}\mathit{j}}))f(x_k|{\mathit{v}}_{\mathbf{-}\mathit{j}})$$ (4)

where $\mathit{v}={\mathit{x}}_{-k}$ is $(p-1)$-dimensional vector excluding $x_k$, $v_j$ is arbitrarily chosen one component from $\mathit{v}$ and ${\mathit{v}}_{\mathbf{-}\mathit{j}}$ is the random vector $\mathit{v}$ excluding $v_j$. In terms of different decompositions, various vine structures can be obtained by using Equation (4). In this study, the main focus is the dependence model construction using both simplified parametric C- and D-vines. For that purpose, the probability density function of C-vine and D-vine for p-dimensional case are defined as,

$$\begin{array}{rl}{f}_{CV}(x_1,\dots ,x_p)& =\prod _{j=1}^{p-1}\prod _{i=1}^{p-j}{c}_{j,j+i|1,\dots ,j-1}^{CV}(F_{j|(1,\dots ,j-1)},F_{j+i|(1,\dots ,j-1)};{\beta }_{j,j+i})\times \prod _{k=1}^p{f}_k(x_k)\end{array}$$ (5)

$$\begin{array}{rl}{f}_{DV}(x_1,\dots ,x_p)& =\prod _{j=1}^{p-1}\prod _{i=1}^{p-j}{c}_{i,i+j|i+1,\dots ,i+j-1}^{DV}(F_{i|(i+1,\dots ,i+j-1)},F_{i+j|(i+1,\dots ,i+j-1)};{\theta }_{i,i+j})\\ & \times \prod _{k=1}^p{f}_k(x_k)\end{array}$$ (6)

2.2. CD-vine model

The main motivation of the proposed method relies on the fact that the dependence pattern of multivariate data can change also with respect to time. For this purpose, C-vines are incorporated into the D-vine copula model with predefined pair copula families and the CD-vine model is proposed. Let $c{v}_t$ for $t=1,\dots ,m$ denote the random vector generated by the distribution functions of the observations belonging to the random vector $X_{k,i}$ where $k=1,\dots ,p$, $i=1,\dots ,N$. The corresponding multivariate density functions, $f_k(x_{k,i})$, for each $c{v}_t$ can be described in terms of C-vine decomposition at a certain value of t. By harmonizing the Equations (5) and (6), CD-vine model can be exemplified for the simplest case (m = 3, p = 4) as follows,

$$\begin{array}{rl}g(\mathit{x};\mathbf{\Gamma })& =c_{12}^{DV}(F(c{v}_1),F(c{v}_2);{\theta }_{12})c_{23}^{DV}(F(c{v}_2),F(c{v}_3);{\theta }_{23})\\ & \times c_{13|2}^{DV}(F(c{v}_1|c{v}_2),F(c{v}_3|c{v}_2);{\theta }_{13|2})\\ & \times \prod _{t=1}^3{f}_{c{v}_t}(x_1,x_2,x_3,x_4;{\varphi }_{C{V}_t})\end{array}$$ (7)

where $c{v}_1$, $c{v}_2$ and $c{v}_3$ are observations specifically extracted from C-vine densities, respectively. $\mathbf{\Gamma }$ denotes the all necessary copula parameters to be estimated for maximizing the log-likelihood of function, $g(\mathit{x};\mathbf{\Gamma })$, based on given sample, where $\mathbf{\Gamma }=({\varphi }_{C{V}_1},{\varphi }_{C{V}_2},{\varphi }_{C{V}_3},{\theta }_{DV})$ and ${\varphi }_{C{V}_t}=({\beta }_{12}^t,{\beta }_{13}^t,{\beta }_{14}^t,{\beta }_{23|1}^t,{\beta }_{24|1}^t,{\beta }_{34|12}^t)$ with $\Vert {\varphi }_{C{V}_t}\Vert =6$ for t = 1, 2, 3 denotes the required set of parameters for the copula pairs of each C-vine part. Under this modeling setup, $f_{c{v}_1}(x_{1:4};{\varphi }_{C{V}_1})$, $f_{c{v}_2}(x_{1:4};{\varphi }_{C{V}_2})$ and $f_{c{v}_3}(x_{1:4};{\varphi }_{C{V}_3})$ denote the multivariate C-vine densities for each of $c{v}_t$. Besides, ${\theta }_{DV}=({\theta }_{12},{\theta }_{23},{\theta }_{13|2})$ represents the necessary parameters for the D-vine modeling. In total, for the considered simplest case of CD-vine model, totally $t\times \Vert {\varphi }_{C{V}_t}\Vert +\Vert {\theta }_{DV}\Vert =21$ parameters are required for the full inference by maximizing the corresponding log-likelihood function with sample size N, which is described as,

$$\begin{array}{rl}L(\mathbf{\Gamma };\mathit{x})& =\log (\prod _{n=1}^{N}g(\mathit{x};\mathbf{\Gamma }))\\ & =\sum _{n=1}^N(\log c_{12}^{DV}(F(c{v}_1),F(c{v}_2);{\theta }_{12})+\log c_{23}^{DV}(F(c{v}_2),F(c{v}_3);{\theta }_{23})\\ & +\log c_{13|2}^{DV}(F(c{v}_1|c{v}_2),F(c{v}_3|c{v}_2);{\theta }_{13|2}))\\ & +(\sum _{t=1}^3\log f_{c{v}_t}(x_1,x_2,x_3,x_4;{\varphi }_{C{V}_t})).\end{array}$$ (8)

Here, the sum of $\log f_{c{v}_t}(x_{1:4};{\varphi }_{C{V}_i})$ for i = 1, 2, 3 in Equation (8) represent the contribution to the log-likelihood function from each C-vine component, and the first three terms denote the contribution to the function $L(\mathbf{\Gamma })$ from D-vine part. For the estimation of parameters, two-stage joint maximization is beneficial to estimate all parameters. For this reason, it is important to first maximize $\log f_{c{v}_t}$ to derive each ${\varphi }_{C{V}_t}$ for t = 1, 2, 3. Afterwards, one can estimate ${\theta }_{DV}$ by considering the first three terms in Equation (8). The ingredients of these functions, $F(c{v}_i)$, are calculated by using the empirical multivariate cumulative distributions function (EMCDF) [27]. These estimated values keep the joint distribution information for the random variables at each time point. Two-stage maximization procedure for CD-vine model can be summarized with the following steps to estimate all parameters:

1. Simulate three different C-vine copula data in 4-dimension having sample size N using different parameter values.

2. For the parameter estimation, first set some initials for the related parameters to maximize each C-vine part (Equation (8)).

3. After deriving the estimates for each component, generate $F(c{v}_t)$ for t = 1, 2, 3 by evaluating (EMCDF) based on approximated parameters.

4. Define pseudo-observations over each column of $F(c{v}_t)$ and use them to maximize the D-vine part of the likelihood function with some predetermined initials.

5. Compare the original and estimated parameters based on different iterations and scenarios.

The derivations are exhibited for Clayton family in Appendix. Further details of the proposed model can be found in [14].

3. Numerical results

For the simulation, 4-dimensional C-vines with M = 3 are investigated. The dependence between the values of EMCDF belonging to each component ( $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$) is the facilitator inter-step for CD-vine modeling. As an optimization routine, derivative free DEoptim function is implemented under two step maximization process [28]. In this proposed model, similar to the widely evaluated Inference For Margins (IFM) method, first, the parameters of each component are estimated. Afterwards, these obtained parameters are used for the construction of $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$ values. EMCDF values store the dependence information within each component. Finally, new 3-dimensional (EMCDF) values are modeled with the help of D-vine. Two special cases are discussed in terms of the parameter estimations. In the first case, truncated D-vine requires an independence copula since the dependence exists only within the components. As a second case, dependence among the components (time points) is studied. All the computations are made by using R programming language [30].

3.1. Simulation study

Suppose each component has Clayton pairs but there is no association between the calculated values of $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$ for D-vine. In this framework, the most suitable copula family for the D-vine modeling part of CD-vine mixture is independence copula. For this reason, CD-vine model having Clayton pairs for C-vine and independence copula pairs for D-vine is studied. The parameters of each component are predefined as $({\beta }_{12}^1=8,{\beta }_{13}^1=7,{\beta }_{14}^1=6,{\beta }_{23|1}^1=9,{\beta }_{24|1}^1=8,{\beta }_{34|12}^1=7)$, $({\beta }_{12}^2=9,{\beta }_{13}^2=6,{\beta }_{14}^2=5,{\beta }_{23|1}^2=9,{\beta }_{24|1}^2=8,{\beta }_{34|12}^2=7)$ and $({\beta }_{12}^3=4,{\beta }_{13}^3=5,{\beta }_{14}^3=7,{\beta }_{23|1}^3=9,{\beta }_{24|1}^3=8,{\beta }_{34|12}^3=7)$.

Simulation results for the case of Clayton-Independence pairs belonging to C- and D-vine parts are presented in Table 1 based on 100 iterations, with varying sample sizes. The parameter estimates are very promising for CD-vine mixture with Clayton-Independence case even for a limited number of iterations. Besides, there is a positive impact of the increase in the sample size over the accuracy of DEoptim method. In this two-step maximization with the case of Clayton-Independence CD-vine mixture model, the parameter estimations for both components are reasonable. When there is no dependence among the components via $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$ values, it is straightforward to exhibit high accuracy for the parameter estimates of such a CD-vine mixture model whose D-vine part is visualized in Figure 1. Here, based on 100 repetitions, the estimated values satisfy the fact that D-vine requires only independence copula (each parameter estimation is very close to zero as given in Figure 1). On the other hand, model identification is not so straightforward in the second scenario for the proposed CD-vine model.

Table 1. Parameter estimations of CD-vine mixture with Clayton-Independence copula pairs ( $max1=100$).

CV1	N	${\hat{\beta }}_{12}^1/{\hat{\beta }}_{13}^1/{\hat{\beta }}_{14}^1/{\hat{\beta }}_{23|1}^1/{\hat{\beta }}_{24|1}^1/{\hat{\beta }}_{34|12}^1$	St. dev. (Bias)
Clayton(8 / 7 / 6 / 9 / 8 / 7)	50	8.17 / 7.13 / 6.12 / 8.91 / 7.95 / 7.64	0.79 / 0.67 / 0.59 / 0.94 / 0.91 / 1.32
			(0.17) / (0.13) / (0.12) / (−0.09) / (−0.05) / (0.64)
	100	8.05 / 7.04 / 6.03 / 9.12 / 8.1 / 7.03	0.58 / 0.52 / 0.46 / 0.68 / 0.61 / 0.78
			(0.05) / (0.04) / (0.03) / (0.12) / (0.1) / (0.03)
	250	8.06 / 7.05 / 6.04 / 8.96 / 7.98 / 7.13	0.34 / 0.3 / 0.26 / 0.54 / 0.5 / 0.62
			(0.06) / (0.05) / (0.04) / (-0.04) / (-0.02) / (0.13)
CV2		${\hat{\beta }}_{12}^2/{\hat{\beta }}_{13}^2/{\hat{\beta }}_{14}^2/{\hat{\beta }}_{23|1}^2/{\hat{\beta }}_{24|1}^2/{\hat{\beta }}_{34|12}^2$	St. dev. (Bias)
Clayton (9 / 6 / 5 / 9 / 8 / 7)	50	9.1 / 6.06 / 5.06 / 9.03 / 8.02 / 7.4	0.7 / 0.51 / 0.45 / 0.92 / 0.78 / 1.26
			(0.1) / (0.06) / (0.06) / (0.03) / (0.02) / (0.4)
	100	9.07 / 6.04 / 5.04 / 8.94 / 7.97 / 7.2	0.59 / 0.41 / 0.36 / 0.72 / 0.66 / 0.84
			(0.07) / (0.04) / (0.04) / (-0.06) / (-0.03) / (0.2)
	250	9.07 / 6.05 / 5.05 / 8.92 / 7.92 / 7.04	0.37 / 0.26 / 0.22 / 0.52 / 0.46 / 0.51
			(0.07) / (0.05) / (0.05) / (-0.08) / (−0.08) / (0.04)
CV3		${\hat{\beta }}_{12}^3/{\hat{\beta }}_{13}^3/{\hat{\beta }}_{14}^3/{\hat{\beta }}_{23|1}^3/{\hat{\beta }}_{24|1}^3/{\hat{\beta }}_{34|12}^3$	St. dev. (Bias)
Clayton (4 / 5 / 7 / 9 / 8 / 7)	50	4.05 / 5.05 / 7.06 / 9.05 / 8.03 / 7.35	0.39 / 0.44 / 0.58 / 1.03 / 0.99 / 1.18
			(0.05) / (0.05) / (0.06) / (0.05) / (0.03) / (0.35)
	100	4.01 / 5 / 7 / 9.13 / 8.14 / 7.15	0.25 / 0.29 / 0.39 / 0.66 / 0.65 / 0.83
			(0.01) / (0) / (0) / (0.13) / (0.14) / (0.15)
	250	4.03 / 5.04 / 7.05 / 9.11 / 8.07 / 7.04	0.17 / 0.2 / 0.26 / 0.49 / 0.45 / 0.57
			(0.03) / (0.04) / (0.05) / (0.11) / (0.07) / (0.04)
DV		${\hat{\theta }}_{12}/{\hat{\theta }}_{23}/{\hat{\theta }}_{13|2}$	St. dev. (Bias)
Independent (0 / 0 / 0)	50	−1.40-07 / −2.39e-07 / −1.16e-07	1.13e-07 / 1.86e-07 / 1.93e-07
			$(-1.40e-07)-(-2.39e-07)-(-1.16e-07)$
	100	−0.0007 / −0.0007 / −0.0006	0.0006 / 0.0006 / 0.0006
			$(-0.0007)-(-0.0007)-(-0.0006)$
	250	−0.0008 / −0.0006 / −0.0006	0.0007 / 0.0005 / 0.0006
			$(-0.0008)-(-0.0006)-(-0.0006)$

Figure 1.

The estimated D-vine parameters (N = 500 and $max1=100$).

Within the context of the CD-vine mixture, nonzero dependence occurs whenever the EMCDF values of each component are calculated at the same levels. In this case, independence copula is not an appropriate choice and it is not possible to identify dependence patterns within the components via $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$ values at the beginning. For this reason, the dependence structure of D-vine part is investigated after finishing the first step, which results in distinct families and parameters.

To illustrate better, consider a 4-dimensional 3-component CD-vine model, generated based on the same parameters, but with Frank (F) copula pairs for C-vine part. The performance of the parameter estimations is similar to the previously studied Clayton case in the C-vine part. After deriving the values of $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$, accordingly the observed dependence pattern requires Gumbel (G) families for each pair in the D-vine part. A small model comparison based on the sample size N = 500 with 250 different realizations is summarized in Table 2. We observe that the best model is (G-G-G) among three ones which matches the base model in terms of lower information criteria values. Furthermore, the parameter estimations are closer to the original parameters, having lower standard deviations and biases rather than (F-F-G) and (F-F-F) models. For the latter models, the parameter estimations of Frank pairs directly attain to the pre-defined upper bounds in DEoptim routine. The zero values of standard deviations with high bias values are attached to this problem, which highlights the importance of initial values under such a multivariate modeling setup. Nevertheless, for the real-life data application, this two step maximization process can be cultivated by capturing the dependence among the components before evaluating D-vine model.

Table 2. CD-vine mixtures with different copulas in D-vine part (N = 500, max1= 250).

	Information criteria vaues	${\theta }_{12},{\theta }_{23},{\theta }_{13|2}$ (16.07 / 10.33 / 1.72)
DV	AIC / BIC / CAIC	Estimates	St. dev. (Bias)
G-G-G	−4470.645 / −4458.001 / −4455.001	12.02 / 8.87 / 2.02	1.72 / 1.25 / 0.34
			(−4.05) / (−1.46) / (0.29)
F-F-G	−3645.486 / −3632.842 / −3629.842	20 / 20 / 2.2	0 / 0 / 0
			(3.93) / (9.67) / (0.48)
F-F-F	−3489.295 / −3476.651 / −3473.651	20 / 20 / 5.41	0 / 0 / 0.01
			(3.93) / (9.67) / (3.68)

3.2. Application to finance: market indices

The proposed CD-vine model is applied to daily closing prices of major indices, DAX, SMI, CAC, FTSE whose descriptive statistics are listed in Table 3. Daily observations of indices between 1991 and 1998, except holidays and weekends, are retrieved from the repository of CRAN data sets package. For the implementation of a 3-component 4-dimensional CD-vine model, only the observations belonging to 1995–1997 are selected as an example and corresponding log return series are plotted in Figure 2.

Table 3. Descriptive statistics for log-return series (1995–1997) and for years CV1: 1995, CV2: 1996 and CV3: 1997.

Index	Min.	Max.	Mean	Variance	Skewness	Kurtosis
DAX	−0.0601	0.0432	0.0013	1.20e−04	−0.2801	2.4429
SMI	−0.0470	0.0497	0.0013	9.53e−05	−0.2046	2.6556
CAC	−0.0437	0.0610	0.0011	1.23e−04	−0.0404	2.0135
FTSE	−0.0310	0.0313	0.0007	6.00e−05	−0.1435	1.3557
$DA{X}_{CV1}$	−0.0318	0.0243	0.0008	5.35e−05	−0.2152	1.6845
$SM{I}_{CV1}$	−0.0255	0.0497	0.0011	5.30e−05	0.8042	7.6202
$CA{C}_{CV1}$	−0.0347	0.0319	0.0005	8.39e−05	0.0393	1.2219
$FTS{E}_{CV1}$	−0.0144	0.0218	0.0004	3.30e−05	0.0716	0.3041
$DA{X}_{CV2}$	−0.0378	0.0327	0.0015	8.20e−05	−0.3177	1.6705
$SM{I}_{CV2}$	−0.0344	0.0310	0.0016	7.14e−05	−0.5082	2.2917
$CA{C}_{CV2}$	−0.0399	0.0295	0.0013	1.07e−04	−0.4599	1.4018
$FTS{E}_{CV2}$	−0.0220	0.0265	0.0009	4.27e−05	−0.2070	1.0154
$DA{X}_{CV3}$	−0.0601	0.0432	0.0017	2.26e−04	−0.2887	0.7929
$SM{I}_{CV3}$	−0.0470	0.0371	0.0013	1.62e−04	−0.2886	0.7565
$CA{C}_{CV3}$	−0.0437	0.0610	0.0014	1.79e−04	0.0811	1.6484
$FTS{E}_{CV3}$	−0.0310	0.0313	0.0009	1.05e−04	−0.1752	0.3311

Figure 2.

Univariate log-returns of selected indices (1 January 1995–31 December 1997).

As a first insight, Table 3 reveals the summary statistics of the total duration 1995–1997 and each year separately. The average returns of DAX, SMI and CAC are closer and show a slight difference in FTSE for 1995–1997. This property is changing year to year, with similar differences in the skewness and kurtosis values. Most of the time log return series at each year represents left-skewed shape, while $SM{I}_{CV1}$, $CA{C}_{CV1}$, $FTS{E}_{CV1}$ in 1995, and only $CA{C}_{CV3}$ in 1997 indicate positive skewness values. It is also depicted that $SM{I}_{CV1}$ in 1995 yields the highest kurtosis.

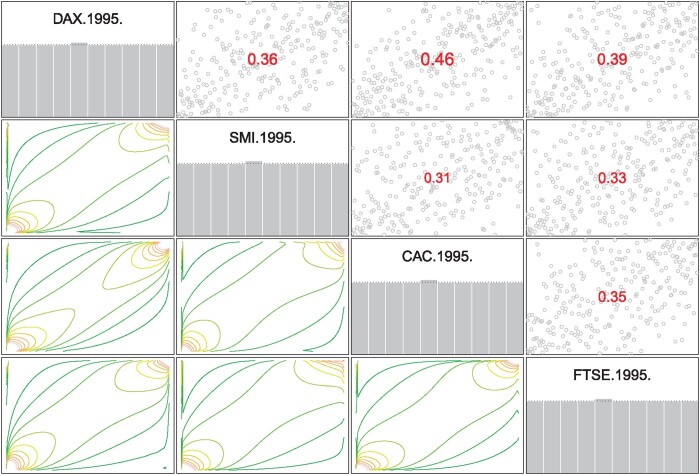
Before employing CD-vine model, each series are modeled after checking the stationarity. Starting with the suitable $ARIMA(p,d,q)$ models, standard $GARCH(1,1)$ models are considered with various distribution assumptions, when necessary. In some cases, we find that there exist ARCH effect, tested by McLeod-Li method. For that purpose, different $GARCH(1,1)$ models have been compared to gain further accuracy in the classical $ARIMA(p,d,q)$ model. Table 4 shows $GARCH(1,1)$ model is quite satisfactory for many log-return series except $DA{X}_{CV2}$, $SM{I}_{CV3}$ and $CA{C}_{CV3}$. On the other hand, modeling residuals with a $GARCH(1,1)$ is still reasonable when the p-values of McLeod-Li test for the original $ARIMA(p,d,q)$ and $GARCH(1,1)$ models are compared. Finally, residuals from two step time series modeling are retrieved for the proposed CD-vine model. To exhibit the dependence information depicted from these models, Kendall τ values for 1995 is visualized in Figure 3. For the upcoming years, the pattern is similar and follows an increasing trend for the Kendall τ values of each pair. These models are studied with built-in functions in rugarch R package [17].

Table 4. ARIMA model selection (LL: Log-likelihood, LB: Ljung-Box, M-Li: McLeod-Li, $GARCH(1,1{)}_k$; k = std: student-t, sstd: skewed student-t, snorm: skewed normal distributions, ${}^{\ast }$: p value <.05).

Index	Model	LL	LB	M-Li
$DA{X}_{CV1}$	ARIMA(1,0,1) $\to GARCH(1,1{)}_{std}$	922.4105	0.485	0.6581
$SM{I}_{CV1}$	ARIMA(1,0,1) $\to GARCH(1,1{)}_{std}$	937.9006	0.6262	0.9997
$CA{C}_{CV1}$	ARIMA(1,0,0) $\to GARCH(1,1{)}_{sstd}$	861.8276	0.8368	0.8005
$FTS{E}_{CV1}$	ARIMA(2,0,2) $\to GARCH(1,1{)}_{std}$	980.7856	0.3024	0.4483
$DA{X}_{CV2}$	ARIMA(4,0,0) $\to GARCH(1,1{)}_{sstd}$	875.944	0.6678	$0^{\ast }$
$SM{I}_{CV2}$	ARIMA(2,1,2) $\to GARCH(1,1{)}_{std}$	890.4312	0.4692	0.3076
$CA{C}_{CV2}$	ARIMA(2,0,0) $\to GARCH(1,1{)}_{sstd}$	835.8359	0.2972	${0.0107}^{\ast }$
$FTS{E}_{CV2}$	ARIMA(0,0,0) $\to GARCH(1,1{)}_{sstd}$	948.8898	0.5206	0.9545
$DA{X}_{CV3}$	ARIMA(9,0,1) $\to GARCH(1,1{)}_{snorm}$	738.8651	0.2092	${0.029}^{\ast }$
$SM{I}_{CV3}$	ARIMA(2,0,0) $\to GARCH(1,1{)}_{snorm}$	779.1635	0.135	$0^{\ast }$
$CA{C}_{CV3}$	ARIMA(5,0,0) $\to GARCH(1,1{)}_{sstd}$	766.9586	0.5108	$0^{\ast }$
$FTS{E}_{CV3}$	ARIMA(0,0,1) $\to GARCH(1,1{)}_{std}$	832.1742	0.3364	0.7369

Figure 3.

Dependence structure among the transformed residuals (1995).

For each year, the dependence structure represents almost symmetric dependence in both tails, that can be visualized by the contour lines in Figure 3. To reduce the overall computational burden, only Frank copula pairs are considered in the first step of the CD-vine model. For the C-vine construction DAX log-return seems to be the best choice for being a root node in terms of Kendall τ values. The CD-vine model flowchart given in Figure 4 represents the structure of the modeling setup briefly. Here, the initial parameter values are borrowed from the parameter estimation of CDVineCopSelect function in CDvine R package [8]. Thereafter, the parameter estimates of each component is obtained by joint maximization for the C-vine part. For D-vine modeling, all available copula functions in the R package are considered to model each pair. The details of the fitted model with their log-likelihood (LL) values, dependence parameters and corresponding Kendall τ values are summarized in Table 5. Furthermore, tree structure of $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$ based on the selected copula family is visualized in Figure 5.

Figure 4.

CD-vine mixture model diagram for the residuals.

Table 5. Comparison of C-vine models for each component.

$CV1$	LL	${\hat{\beta }}_{12}^1/{\hat{\beta }}_{13}^1/{\hat{\beta }}_{14}^1/{\hat{\beta }}_{23|1}^1/{\hat{\beta }}_{24|1}^1/{\hat{\beta }}_{34|12}^1$	Kendall's τ
Frank	176.1582	3.76 / 5.12 / 3.99 / 1.02 / 1.66 / 1.23	0.37 / 0.46 / 0.39 / 0.11 / 0.18 / 0.13
$CV2$		${\hat{\beta }}_{12}^2/{\hat{\beta }}_{13}^2/{\hat{\beta }}_{14}^2/{\hat{\beta }}_{23|1}^2/{\hat{\beta }}_{24|1}^2/{\hat{\beta }}_{34|12}^2$
Frank	268.9389	5.65 / 7.07 / 4.78 / 1.11 / 1.50 / 1.83	0.50 / 0.57 / 0.44 / 0.12 / 0.16 / 0.20
$CV3$		${\hat{\beta }}_{12}^3/{\hat{\beta }}_{13}^3/{\hat{\beta }}_{14}^3/{\hat{\beta }}_{23|1}^3/{\hat{\beta }}_{24|1}^3/{\hat{\beta }}_{34|12}^3$
Frank	386.019	7.28 / 8.20 / 6.22 / 2.65 / 2.56 / 1.72	0.57 / 0.61 / 0.53 / 0.28 / 0.27 / 0.19
DV		${\hat{\theta }}_{12}/{\hat{\theta }}_{23}/{\hat{\theta }}_{13|2}$
G-G-SG	1201.872	13.54 / 16.88 / 1.20	0.93 / 0.94 / 0.17

Figure 5.

D-vine model for $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$.

Based on the results given in Table 5, the stock values exhibit a significant dependence pattern based on Frank family for each year. Especially, for unconditional densities, the dependence parameter values are higher at each year rather than the parameters of conditional ones at higher levels of C-vine. For instance, ordered numbers 7.28−8.20−6.22 for Model $CV1$ express that $DA{X}_{CV3}$ log-return is positively dependent on other stock indices, namely $SM{I}_{CV3}$, $CA{C}_{CV3}$ and $FTS{E}_{CV3}$, in the year 1997 and they behave similarly. This dependence pattern almost similar for the previous years with smaller estimated parameters. For D-vine part, the dependence among the years is described with one-tailed dependence structure. In Figure 5, Gumbel (G) and Survival Gumbel (SG) family with their empirical Kendall τ values are given in parenthesis. For instance, the dependence among years 1995 and 1996 with the values of $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$ is modeled by Gumbel family, which displays the upper tail dependence for these years. On the other hand, the dependence among years 1995 and 1997, conditioned on 1996 exhibits lower tail dependence with small values.

4. Concluding comments

For understanding the complex dependence patterns both within and among the components C-vines are combined via the D-vine model, called as a CD-vine mixture model. After discussing the proposed model with a simulation study, the hidden dependence among log-returns of stock indices and temporal dependence among the years are investigated via the proposed CD-vine model.

For the simulation part, in the case of CD-vine mixture with Clayton-Independence pairs, the parameter estimations are shown to be promising. In the case of no dependence among the components, it is easy to identify correct copula pairs for the D-vine part. On the other hand, when there exists an association between the components, it is not simple to select a copula family for the D-vine part. Besides, this dependence has a varying structure based on the obtained values of $F(c{v}_1)$, $F(c{v}_2)$ and $F(c{v}_3)$. For that reason, in the application part, the copula family and related parameters are initiated by fitting a D-vine model to the obtained data in the first step. Even if only Frank family is considered based on contour plots, this framework can be adapted for the other families for different tail dependence structures.

Further flexibility on the proposed model can be achieved by using different pair copulas. In this study, each component has been modeled by using same copula families, whereas, this methodology can be applied in case of selecting distinct copula functions to model the dependence among the variables. Certainly, this kind of selection increases the flexibility of the proposed mixture models, but the parameter estimation part requires more elegant methods. Additionally, in this study, only the vines with parametric copula families are considered for the sake of simplicity. For further studies, semi-parametric and non-parametric approaches can be adopted for the CD-vine model. Last but not least, the consideration of both C- and D-vines to identify the dependence among the variables and time points jointly rather than the two-step procedure will be the next step. These above-mentioned issues lie on the top of list for future studies.

Appendix. CD-vine model derivations.

The proposed mixture model given in Equation (8) for Clayton pairs is sketched. By following the C-vine definition, each $\log f_{c{v}_t}$ can be written as a product of conditional and unconditional Clayton densities as follows,

$$\begin{array}{rl}& \log f_{c{v}_1}(x_{1:4};{\varphi }_{C{V}_1})=\log [c_{12}(x_1,x_2;{\beta }_{12}^1)c_{13}(x_1,x_3;{\beta }_{13}^1)c_{14}(x_1,x_4;{\beta }_{14}^1)\\ & c_{23|1}(F(x_2|x_1),F(x_3|x_1);{\beta }_{23|1}^1)c_{24|1}(F(x_2|x_1),F(x_4|x_1);{\beta }_{24|1}^1)\\ & c_{34|12}(F(x_3|x_1,x_2),F(x_4|x_1,x_2);{\beta }_{34|12}^1)]\end{array}$$ (A1)

In Equation (A1), the detailed construction is presented for only $\log c_{12}$ as,

$$c_{12}=\frac{{\mathrm{\partial }}^{2}C(x_1,x_2;{\beta }_{12}^1)}{\mathrm{\partial }{x}_1\mathrm{\partial }{x}_2}=({\beta }_{12}^1+1)(x_1{x}_2{)}^{-{\beta }_{12}^1-1}(x_1^{-{\beta }_{12}^1}+x_2^{-{\beta }_{12}^1}-1{)}^{\frac{-1}{{\beta }_{12}^1}-2}$$ (A2)

yielding,

$$\log c_{12}=\log ({\beta }_{12}^1+1)+(-{\beta }_{12}^1-1)\log (x_1{x}_2)+(\frac{-1}{{\beta }_{12}^1}-2)\log (x_1^{-{\beta }_{12}^1}+x_2^{-{\beta }_{12}^1}-1)$$ (A3)

Similarly, one can write the formula for $\log c_{13}$ and $\log c_{14}$ for the first level. Thereafter, it is necessary to use h-functions and derive $F(x_2|x_1)$, $F(x_3|x_1)$ and $F(x_4|x_1)$ for the next level. To illustrate, the computations for the $F(x_l|x_1)$ is given. Let,

$$\begin{array}{rl}{x}_{l1}=F(x_l|x_1)& =\frac{\mathrm{\partial }C(x_1,x_l;{\beta }_{1l}^1)}{\mathrm{\partial }{x}_1}\\ & =x_1^{-{\beta }_{1l}^1-1}(x_1^{-{\beta }_{1l}^1}+x_l^{-{\beta }_{1l}^1}-1{)}^{\frac{-1}{{\beta }_{1l}^1}-1},l=2,3,4\end{array}$$ (A4)

The algorithm of the first corresponding conditional density $c_{23|1}$ is,

$$\begin{array}{rl}\log c_{23|1}& =\log ({\beta }_{23|1}^1+1)+(-{\beta }_{23|1}^1-1)\log (x_{21}{x}_{31})\\ & +(\frac{-1}{{\beta }_{23|1}^1}-2)\log ((x_{21}{)}^{-{\beta }_{23|1}^1}+(x_{31}{)}^{-{\beta }_{23|1}^1}-1)\end{array}$$ (A5)

This recursive process continues until reaching the last conditional density. After deriving each of them, the closed form of the Equation (A1) is identified. The similar mechanism appears for D-vine part after generating pseudo-observations on the values of $c{v}_1$, $c{v}_2$, $c{v}_3$. The final analytical form of the logarithm of D-vine part is given,

$$\begin{array}{rl}& (\log c_{12}^{DV}(F(c{v}_1),F(c{v}_2);{\theta }_{12})+\log c_{23}^{DV}(F(c{v}_2),F(c{v}_3);{\theta }_{23})\\ & +\log c_{13|2}^{DV}(F(c{v}_1|c{v}_2),F(c{v}_3|c{v}_2);{\theta }_{13|2}))\\ & =\log ({\theta }_{12}+1)+(-{\theta }_{12}-1)\log (c{v}_{1}c{v}_2)+(\frac{-1}{{\theta }_{12}}-2)\log (c{v}_1^{-{\theta }_{12}}+c{v}_2^{-{\theta }_{12}}-1)\\ & +\log ({\theta }_{23}+1)+(-{\theta }_{23}-1)\log (c{v}_{2}c{v}_3)+(\frac{-1}{{\theta }_{23}}-2)\log (c{v}_2^{-{\theta }_{23}}+c{v}_3^{-{\theta }_{23}}-1)\\ & +\log ({\theta }_{13|2}+1)+(-{\theta }_{13|2}-1)\log (c{v}_{12}c{v}_{32})\\ & +(\frac{-1}{{\theta }_{13|2}}-2)\log ((c{v}_{12}{)}^{-{\theta }_{13|2}}+(c{v}_{32}{)}^{-{\theta }_{13|2}}-1),\end{array}$$ (A6)

where

$$\begin{array}{rl}c{v}_{12}& =F(c{v}_1|c{v}_2)=c{v}_2^{-{\theta }_{12}-1}(c{v}_1^{-{\theta }_{12}}+c{v}_2^{-{\theta }_{12}}-1{)}^{\frac{-1}{{\theta }_{12}}-1}.\end{array}$$ (A7)

$$\begin{array}{rl}c{v}_{32}& =F(c{v}_3|c{v}_2)=c{v}_2^{-{\theta }_{23}-1}(c{v}_2^{-{\theta }_{23}}+c{v}_3^{-{\theta }_{23}}-1{)}^{\frac{-1}{{\theta }_{23}}-1}.\end{array}$$ (A8)

The further details of the above derivations are available in [14].

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The considered data set in this study is available via https://stat.ethz.ch/R-manual/R-devel/library/datasets/html/EuStockMarkets.html.