ABSTRACT
This paper discusses methods of estimating the reproductive power and the accompanying survival function of communicable events, e.g. infectious disease transmission. The early stage of an outbreak can be described by the infectiousness of the outbreak process, but in later stages of the outbreak, this is complicated by factors such as changing contact patterns and the impact of control measures. It is important to take these factors into account in order to get a good, if approximate, model for an outbreak process. This paper proposes a non-homogeneous birth process and regression model for the reproductive power function, similar to models in discrete survival analysis. A baseline reproductive power function gives a description of the outbreak when covariates are at their baseline values. As an illustration these methods are applied to an avian influenza (H5N1) outbreak among poultry in Thailand.
Keywords: Non-homogeneous birth process, reproductive power function, survival function, discrete survival analysis, avian influenza
2010 Mathematics Subject Classifications: 62M05, 62N02
1. Introduction
On 23 January 2004, the Ministry of Public Health in Thailand informed the World Health Organization of an avian influenza outbreak. This is how the world learned about the H5N1 outbreak in Thailand, an outbreak that lasted more than 3 years. Poultry and wild bird populations in 1417 villages from 60 of the 76 provinces were affected and over 62 million birds died or were culled to prevent further transmission.
An outbreak of an infectious disease like this one does not just involve the dynamics of infectious processes. In the early stages the outbreak process might be dominated by the infectiousness of the disease and might thus be well described by a stochastic differential equation (birth process), but, after a while, this outbreak process includes more than just this infectiousness. At least four other factors are playing a role during the outbreak.
First, the contact process may change during the outbreak, due to changing behaviour of the individuals in the population, or to measures taken. Control measures such as improving hygiene, isolation of infected cases, transport bans and pre-emptive culling, could be taken to reduce the number of contacts but also to limit the reproductive ability of infected individuals, illustrating that a model describing the infectiousness of the pathogen might only be appropriate for the early stages of the break.
Second, it can be very difficult to determine the population at risk at the start of the outbreak. Moreover, during the outbreak the population at risk may change due to measures taken or some other censoring mechanisms. It is therefore very difficult to determine the size of the population at risk. Only when this size is well defined can one calculate certain important characteristics, such as the hazard rate for a disease, i.e. the instantaneous risk of contracting the disease at a certain time point, given the absence of disease before that point in time. This is different with infectious disease outbreaks or other communicable events such as the spread of a rumour or the spread of some kind of behaviour through a population. With events such as these, the number of individuals at risk is not necessary. Of course, in order for the infectious disease to spread, there must be enough individuals without the disease in the population and there must be some kind of contact pattern, but knowing the size of population at risk at each point in time is not necessary. This is due to the communicability of the event. In that case the risk of being infected at a certain point in time is characterized by the ability of current infectious individuals to infect others, the so called reproductive power [10].
A third point is that measurements during an outbreak are often limited to whether an individual was infected in the past, irrespective the precise time point at which this individual was infected. This is similar to current status data.
A fourth point to be observed is that the data are dependent: what happens at a point in time depends on what happened before, due to the contagiousness of the disease.
Usually with outbreak data, the number of infected individuals are measured in discrete time. That is, the number of detected cases per week or per month are registered, not the exact time at which the detected infected case occurred. Kypraios and O'Neill [11] note that in the context of infectious disease data analysis, discrete-time models are often very natural since real-life data are invariably discrete in time.
To deal with the incompleteness of epidemic data, O'Neill and Roberts [15] propose a Bayesian approach to inference for both the Reed-Frost model and the general stochastic epidemic model. They assume that the observed data consist of a set of removal times so the unobserved infection times are treated as parameters in the model.This model can be used for prediction and needs the number of susceptibles at time zero or the assumption of a prior distribution on the initial number of susceptibles as well as assumptions about the other prior distributions. They also assume that the unobserved time of the first infection has an exponential distribution but other distributions might also be taken. They discuss estimating this model with Markov chain Monte-Carlo methods. Kypraios and O'Neill [11] extend this model to a non-parametric Bayesian model using an augmented likelihood (with a thinned homogeneous Poisson process) and a zero mean Gaussian process prior.
For a non-Bayesian approach of the general stochastic epidemic model see [6].
Spatio-temporal models are discussed in [7]. There a point process for the location and time of an event of interest is used. The model is formulated in terms of the conditional intensity for an event at location x and time t. The times at which an event occurs are assumed to be known accurately. Also the number at risk needs to be known. Right censoring is allowed. See also the discussion in [8].
Usually an average quantity, e.g. (the expected number of secondary cases if an infectious individual is introduced in a population of susceptibles), is used to describe aspects of an epidemic outbreak (in the case of : whether or not an outbreak will occur). An estimate of such a quantity can obscure considerable individual variation in infectiousness [13]. These authors showed that the distribution of individual infectiousness around is often highly skewed.
To deal with non-homogeneousness over time, Chowell et al. [4] formulates a SEIR (Susceptible-Exposed-Infectious-Removal) model by their analogous stochastic version. The event times are modelled as a renewal process with exponential distributions for the increments. So the rates at which events occur are fixed over time. The transmission rate however is allowed to change gradually from one value to another, between the time of onset of the intervention to the time of full compliance. The time of onset of the interventions is a parameter in the model. Appropriate initial conditions for the parameters are chosen and the model is fitted using least squares on the cumulative number of cases. This process is repeated 10 times and the best fit is chosen.
Because it is not observed when an individual enters a compartment but only whether or not an individual is a case, the authors of this article use the assumptions of the exponential distributions for increments of the event times and appropriate initial conditions for the event times. They also need an estimate of the population size. Estimates are used that are an upper bound of the effective population size (those at risk of becoming infected). Besides the model assumes mass action or pseudo mass action.
Problems with the basic reproduction number of the SEIR model and (non-homogeneous) generalizations thereof are discussed in [3] and they propose the empirical adjusted reproduction number by considering the expected number of secondary infections produced by a single infected in that population based on the parameters of a spatial SEIR model for the number of new infections or the number of removed individuals. They demonstrate improved ability to detect changes in transmission behaviour not explicitly accounted for by the model. They assign a chain binomial structure to the transmission matrices. The transmission parameters can depend on covariates and they use appropriate prior distributions on the parameters of the intensity process. They further assume a Poisson distribution for the number of contacts within a spatial unit on a certain time point and that individuals travelling to another spatial unit behave according to that unit. They further assume that the contact between spatial locations is proportional to some function.
As said the use of a SEIR model in the situation where it is not determined in what compartment the individuals are but only whether or an individual is infected or removed, needs extra assumptions. In [3] prior distributions are assumed for the chain binomial structure of the transition matrices and further assumptions are used for the contact pattern. The empirically adjusted reproduction number based on the proportion of persons who are infectious at time and spatial unit is estimated additional to the model, so it can detect changes in transmission not detected by the model.
The model proposed in the sequel of this article, models the data as it is observed and uses the expected number of newly infected per existing infected on a certain time point directly with the ability of using covariates for this expected number and thus uses less assumptions.
There are a large number of other approaches. For a discussion of these see [6].
In this paper, it is proposed to address the above five points using a non-homogeneous birth model in discrete time as an approximation for this complicated data-generating process, yielding an approach similar to discrete time survival analysis. The present study is the first – to the best of our knowledge – to formulate this model with important features such as simplicity, ability to deal with current status and dependent data, ability to deal with covariates and similarity with discrete time survival models.
In Section 2 a description of the non-homogeneous birth model Computational Bayesian Statistics is given in continuous and discrete time. In the discrete time case the expected value and variance is given in terms of the reproductive power. The log-likelihood is formulated giving novel expressions for the maximum likelihood estimator of the reproductive power and its standard error and, for the survival function based on this reproductive power and its standard error. In Section 3 a regression model for the reproductive power, similar to discrete time survival models, is formulated with two possible interpretations: a log-odds interpretation and an interpretation of the expected reproduction per existing case. In Section 4 the model is applied to the H5N1 avian influenza outbreak in Thailand and Section 5 contains a discussion.
2. The model
The early stage of the outbreak can be well approximated by a birth process, because then the infectious process dominates the outbreak and there are not many removals or recoveries in that early stage. This model depends on a rate called the reproductive power (the birth rate) [18]. In this paper, this rate is taken to be non-homogeneous in order to deal with developments later on in the outbreak. This is important, because it enables the reproductive power to adapt to other dynamics of the outbreak besides the infectiousness of the disease, such as changing contact patterns, changing population of susceptible individuals and measures taken, as mentioned in the introduction. Furthermore, in the case of a non-homogeneous reproductive power, there is no need for a homogeneous mixing assumption. This is because non-homogeneous mixing – for example if there are periods in which the infected individuals mix well with other individuals and there are periods in which this is less so – can influence the number of infected individuals at specific points in time to which the non-homogeneous reproductive power can adapt.
So instead of describing an outbreak with a single quantity, it might be useful to describe it with a function that takes into account the changing ability of an infected individual to reproduce over time: the reproductive power function. Another argument for making the reproductive power time dependent comes from [2]. They have shown that variation in the susceptibility of individuals can result in an infection rate that declines over time as highly susceptible individuals tend to be infected earlier. A final reason to take reproductive power as a function of time is given below.
The stochastic version of the non-homogeneous birth process has a distribution function as a solution with an expected value equal to the solution of the deterministic version of this process. Moreover it is a Markov model, thus dealing with the dependence of the data mentioned in the fourth point in the introduction.
Suppose is the total number of infected individuals at time t, then the solution of the stochastic non-homogeneous birth process is the shifted negative binomial distribution [18]:
| (1) |
where , is the reproductive power function [10] and is the number of infected at time zero. The reproductive power function is the rate at which all the previous infected individuals generate new ones. It is the rate by which infection occurs due to reproduction. This is another important reason why the reproductive power should be taken as non-homogeneous. Not all infected individuals from the past are still infectious at a specific point in time. As time goes on, the proportion of the total number of infected individuals that spreads the disease decreases. In order to distinguish this reproduction from the reproduction of infectious individuals one might define this as ‘quasi-reproduction’.
The term quasi-reproductive power function is used for this rate (reproductive power as in [10]) to avoid confusion with other quantities that use the word reproduction. The birth process refers to the infected individuals not to the susceptible individuals. The quasi-reproductive power is the rate at which an infected individual is able to produce new infections. The expected value of the total number of infections is
Model (1) gives the probability (likelihood) for the total number of infected individuals at time point t. One can rewrite this in terms of individual probabilities. Looking at the contribution of an individual using the birth process, observation starts with a change of state from susceptible to infected in the past. This change happens with a probability , with the distribution function. So observation starts after an individual has entered the infected compartment. After that the individual remains in that state and contributes a survival probability at every observation point for as long as the outbreak lasts. See Section 3 for more detail on individual probabilities.
Note that a death process [18] gives similar results, although that relates to susceptible individuals. The force of infection is the rate at which susceptible individuals are infected. With the death process, an individual starts in a susceptible state, i.e. an at-risk state, which is observed from the start of the epidemic. It contributes a survival probability at every observation point for as long as it remains in a susceptible state. At the moment that infection is observed, it contributes a probability and the observation ends. So observation starts when an individual is in an at risk,i.e. susceptible, state and ends if there is a change to this state. The non-homogeneous birth model does not need the size of the population at risk, i.e. the size the susceptible population. This constitutes an advantage over the death process, as explained in the second point in the introduction.
Model (1) provides a likelihood that is proportional to the conditional likelihood used for grouped current status data [16]. These data only provide information on whether or not the event occurred before the observation time. As stated above, this is what usually happens during an infectious disease outbreak, because infected individuals are, for various reasons, not observed at the time of infection but are registered by the symptoms of the disease, usually with some delay (the third point in the introduction). This type of outbreak data is similar to current status data in the sense that the likelihood function depends on the survival and distribution function, so the data are interpreted as either left censored or right censored but not both at the same time. This means that if an individual is observed to be infected, the infection happened in the past but it is not clear how far away in the past. Some observations might have a long detection time and some a short one. If an at-risk individual is not observed to be infected, infection may still happen in the future.
To estimate the survival function non-parametrically with current status data, one needs a special algorithm such as pool-adjacent-violators (PAV) to take into account the fact that the survival function is a non-increasing function [5]. Here things are simpler because the model is a Markov model for cumulative data. The maximum likelihood estimate for the survival function in the birth process is (see below for a discussion), the estimated fraction not changing state. It is perhaps more natural to look at the distribution function, since the starting point is on entering the infected state and the number of individuals in that state is measured over time. The maximum likelihood estimate is , the fraction of cases that are new since time zero.
This is a model for the cumulative number . It can be rewritten as a model for new cases :
As observed earlier, the time at which the outbreak is observed is usually discrete [1, p. 108] although the underlying time scale is continuous. This is why the data should be treated as grouped data with discrete observation times . The conditional survival probability is then
| (2) |
where is the discrete quasi-reproductive power probability function hereafter referred to as the reproductive power probability function or shortly as the reproductive power probability. This is the probability that an infection will occur at given that it did not occur before that point in time. The conditional probability of observing new infected individuals at time given infected individuals at the previous time point is:
| (3) |
The expected value is:
| (4) |
the total number of cases in the previous time interval times the odds of the reproductive power probability. The variance of this negative binomial distributed variable is:
which shows that is the over-dispersion parameter relative to the Poisson distribution and that, as time goes on, the process behaves approximately as a Poisson process. Note that this model is a generalized linear model, since one does not have to estimate a dispersion parameter.
Note that, in order to interpret the reproductive power in (3), there are only two kinds of individuals: those who are infected at time point and those who are not, which are those individuals that are already infected in the past. The reproductive power probability shows how many infected are created by the infected already present at time .
Suppose there are T possible time points, then, using (3), the log-likelihood (l) can be written as:
| (5) |
where is the number of new cases at a specific point in time and is the reproductive power probability function at time point j. Maximizing this log-likelihood with respect to gives the maximum likelihood estimator for the reproductive power probability at time point j:
the number of new cases at a time period per total number of infected individuals or the proportion of cases that are new at time interval . As times goes on the reproductive power probability usually becomes smaller since not all the previously infected individuals continue to reproduce.
The standard error of is denoted by and can be determined from the Hessian. It looks very similar to the standard error of a proportion:
Note that, if the reproductive power probability is approximately constant, this standard error decreases over time as the number of previously infected individuals is increasing. This is in contrast to the standard error of the hazard rate or probability in survival analysis, because in that case the population at risk, which is decreasing in number, must be taken into account.
Since the conditional negative binomial log-likelihood with known dispersion parameter (5) is a log-likelihood of a generalized linear model, the parameter estimators are approximately normally distributed for large sample sizes.
An estimate of the survival probability at time can be obtained using with as the observed value of the stochastic variable :
The variance of the reproductive power probability shows that
and thus
and so
3. Regression model for the reproductive power probability
Taking a log link for the expected value of the number of new cases (), at time interval , given the total number of cases in the previous interval as formulated in (4), gives:
One can assume a parametric model for the survival function and use this in (2) to calculate the reproductive power probability function, as was done in [18] with members from the Burr-family. To avoid this parametric assumption, one can model the time effects with a piece wise constant function in discrete time.
The log-odds of the reproductive probability can be modelled linearly in the covariates. If the covariates all have baseline values (usually zero), the model for the log-odds of the base line reproductive probability, , is
so is the log-odds of the reproductive power probability at time , and
The model with covariates is
| (6) |
or
This model for can be plugged into the log-likelihood (5) and then maximized over the parameters and to obtain maximum likelihood estimates and further likelihood results. This model is a generalized linear model with a negative binomial distribution, a dispersion parameter and a log link. If the covariate effect and the parameters do not depend on time, then this model is a proportional odds model. This model can also be written as:
The log-odds of the reproductive power probability at a certain point in time is the same as the log of the expected number of new cases per existing case, at a certain point in time. This model therefore has two interpretations. A piecewise constant linear model with covariates for the log-odds of the reproduction probability at a point in time is the same as a piecewise linear model with covariates for the log of the expected reproduction per existing case at a specific point in time. However, as already noted, not all existing cases reproduce, so the reproduction can be seen as a ‘quasi-reproduction’.
As was mentioned briefly in Section 2, one may reformulate this model in terms of individual contributions. As can be seen from (3), all those individuals that were seen as infected in a time interval contribute and those who were detected as infected before this time point contribute . If one concentrates on individual i then this individual contributes when detected as an infected. After time point this individual contributes from j = i + 1 until the last time point T. Thus the likelihood (L) for n individuals can be written as
with modelled as (6). This formulation makes it easy to incorporate individual (time varying) covariates. This is similar to discrete survival analysis [12].
4. The H5N1 avian influenza outbreak in Thailand (2004–2007)
One can use the model described in Section 3 to learn about the outbreak using covariates and the baseline reproductive power function. This is illustrated here with the transmission data of avian influenza (H5N1) among poultry flocks in Thailand. To study the epidemiology of this viral infection among poultry in Thailand from 2004 through 2007, it was investigated how wild birds play a role in transmission. See [9] for a full description of the research and of the data. The question was: does the joint presence of infected wild birds and poultry increase spread among poultry flocks?
Geographic location and season were recorded for each bird species identified. To study the regional effect on outbreaks of the subtype H5N1 in wild birds, Thailand was divided into four major geographic regions (northern, north-eastern, central, and southern) on the basis of the former administrative regional grouping system used by the Thai Ministry of Interior. Because of the high number of outbreaks in the Central region, this was further divided into six sub-regions: north-west central, north-central, central-central, east-central, south-east central, and south-west central.
The definition of poultry encompasses all farmed avian species in Thailand, including backyard chickens and ducks. Time was measured in months from the first month that infection was detected. There were at most 38 months in the study period.
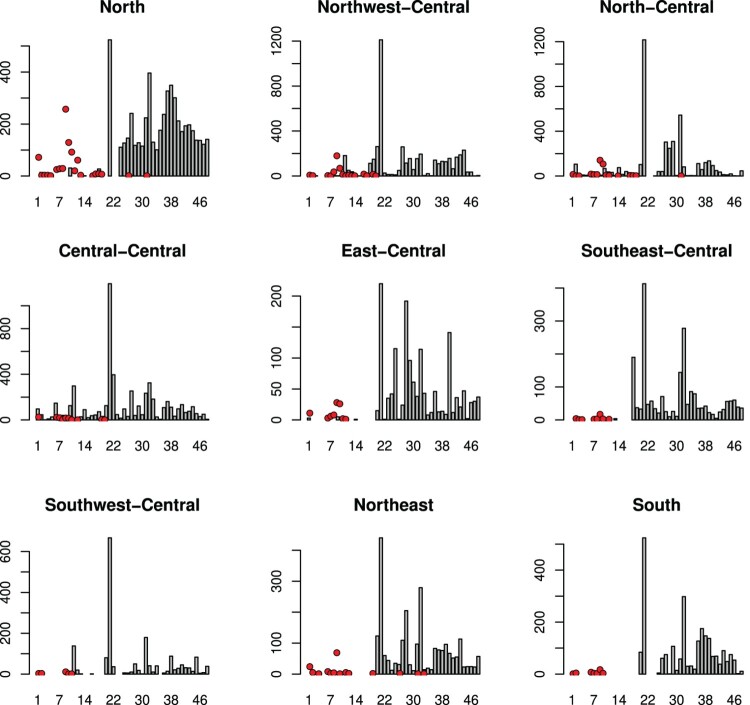
In most regions, sampling among wild birds was only carried out systematically after a poultry outbreak in that region, except in the central-northwest, central-north, and central-central sub-regions, the second, third and fourth regions in Figure 1. This figure shows the numbers of infected (and detected) wild birds (bar) and infected flocks (points).
Figure 1.
The numbers of infected wild birds (bar) and infected flocks (points) in nine regions in Thailand from 2004 through 2007.
We could therefore only use these 3 sub-regions to investigate whether the presence of infected wild birds was related to the poultry outbreak. Within these 3 areas, a wild bird infected month was defined as a month in which infected wild birds were detected or which showed wild bird infection in the preceding month [9]. The idea is that the reproductive power (probability) between poultry flocks might be higher in these months compared to other months because there was ‘help’ from wild birds.
The observations from the regions are assumed to be conditionally independent, given the number of infected birds at time zero in a region, given the total number of infected at the previous time point and given the covariates. This means that it is assumed that the number of contacts between poultry farms in different areas are negligible which seems not unreasonable in this case. This assumption can be relaxed as is mentioned in Section 5. Since time is measured in months, it is viewed as a discrete variable and is therefore modelled with a peacewise constant function. The model used is:
| (7) |
were wb is the indicator of a month with infected wild birds and is the indicator of region .
Figure 2 plots the baseline reproductive probabilities. The blue line shows the baseline reproductive power probabilities of the 38 months. Since after month 13 there are a lot of months with a zero count, time could be grouped more tightly in order to get more stable estimates. A smoothing spline is fitted to the data (the red line) to get an idea of this grouping. With the help of these two lines, a piecewise constant function with more structure is chosen. This is the black line. This piecewise function has five time intervals: month 1 was the first group, months 2, 3, 4 and 5 the second, months 6, 7, 8 and 9 the third, and months 10 and above is the fifth group. The five reproductive probabilities are and 0.003. A reproductive power probability of 0.483, for instance, means that there is a probability of 0.483 in the third interval that existing cases will produce a new case.
Figure 2.
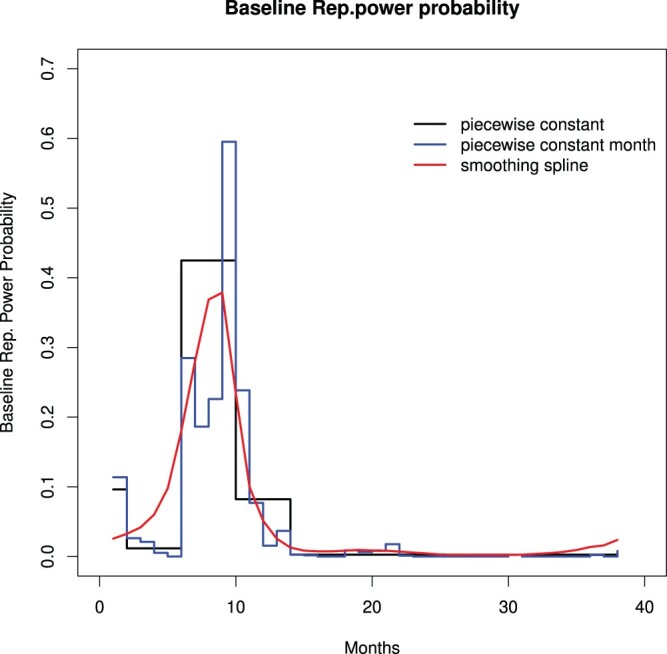
The baseline reproductive power probabilities with 38 months (step line), a smoothing spline (red line) and a piecewise constant function with five time intervals (step line with 5 steps).
The rapid increase of a reproductive power probability to 0.483 in the first 10 months might be seen primarily as a reflection of the infectiousness of the disease. The decrease of the reproductive power function after 10 months can be interpreted as primarily a reflection of the measures taken and, of course, of the fact that not all infected individuals were reproducing during that period of the outbreak.
Figure 3 shows this piecewise constant function for the baseline reproductive probability function (black). To get an impression of the uncertainty of the baseline reproductive power probabilities, 1000 bootstrap samples were obtained, each bootstrap sampling from all nine regions. Model (7) was fitted for each bootstrap sample and the baseline reproductive power probabilities were obtained (gray lines in Figure 3)from the estimates of this fitted model. The blue lines represent the 2.5th and the 97.5th percentiles.
Figure 3.
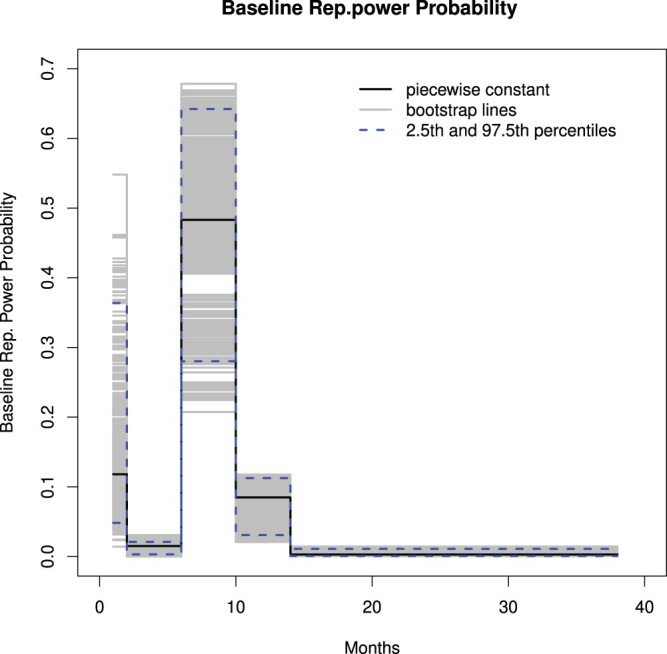
A piecewise constant function for the baseline probability function (black), 1000 bootstrap versions of this function line (gray) and the 0.25th and 0.975th percentile points (dashed) based on the bootstrap samples.
The log-odds ratio for the reproductive power probability (or the log reproductive power ratio) for a month with infected wild birds is estimated as 0.83 with a standard error of 0.0923. The odds ratio is 2.29 and 95% profile log-likelihood confidence interval is . There are two possible interpretations:
The odds of the reproductive power probability are about 2.3 times higher for months with infected wild birds than for months in which no infected wild birds are detected. The reproductive power probability is the proportion of all new infections at a certain point in time.
The reproductive power of a month with infected wild birds is about 2.3 times higher than months in which no infected wild birds are detected. The reproductive power is the number of new infections at a certain time point per existing infection.
Due to the time scale chosen (months), there are time points with a very large number of cases followed by time points with very few or even zero cases. This results in an over-dispersion which is reflected in large deviance residuals. If one concentrates the analysis on the months with the most data, the log-odds ratio for the wild bird infected-month is approximately the same.
5. Discussion
The early stage of an infectious disease outbreak may be approximated by the birth process as then the infectious process dominates the outbreak and there are not many removals or recoveries. The non-homogeneous birth model (negative binomial) for outbreak data proposed here depends on the reproductive power (probability) [18] that can be used in a regression model. This paper takes this reproductive power to be non-homogeneous in order to deal with developments later on in the outbreak. This non-homogeneous is important because, as stated in the introduction, it allows the reproductive power to adapt to other dynamics besides the infectious disease outbreak; dynamics such as changing contact patterns, the changing population of susceptible individuals, and control measures taken. Furthermore, in the case of a non-homogeneous reproductive power, there is no need to include a homogeneous mixing assumption. This is because such non-homogeneous mixing – for example if there are periods in which the infected individuals mix well with other individuals and periods in which this is less the case – can influence the number of infected individuals at certain time points and the non-homogeneous reproductive power can adapt to it. The model has the following features:
The model is a non-homogeneous birth model so it can describe the early phase of the outbreak well and, due to its non-homogeneous nature, can deal with other aspects of the outbreak such as changing behaviour or control measures taken besides.
It does not need the size of an at-risk population; such a population is often hard to determine and can change during the outbreak.
An infection is usually observed as having taken place in the past. This model deals with this in a way similar to current status data.
Because the model is a Markov model, it deals with dependence in the data.
Modelling the log-odds of the reproductive power probabilities (proportion new cases of all the infections at any one time) is the same as modelling the log of the reproductive power (proportion of new cases per existing case).
The model used in the example has (conditionally) independent groups. Given the number of previously infected individuals and given the covariate value, the groups are independent in the sense that the different geographic areas had their own outbreak. The covariate in the example is environmental. Some of the existing cases reproduce and an environmental characteristic (presence of infected wild birds) has a positive influence on such reproduction.
It might also be that the covariates are individual values measured at the time the infected individual was detected. Suppose, for the sake of argument, that the covariate measures the presence or absence of a characteristic. If the covariate is thought to influence the susceptibility for the disease, then one can condition for the total number of previous infections and see whether the reproductive power increases if the characteristic is present by inserting this covariate into the linear part of the model. If the covariate is believed to influence the infectiousness of the disease, then the previous number of infections can be divided in two groups: one with and one without that characteristic. Then, using conditional independence, one can estimate the likelihood, as in the avian influenza example.
One of the possible extensions or modifications of the model is to drop the conditional independence between the areas. If the reproductive power function is thought to be influenced by the number of infected individuals from other areas, one can use the power-law method developed by Meyer and Held [14].
One might also extend the model to one that is dealing with overdispersion. If for instance a lot of zeros are observed a zero inflated distribution could be used. Another possibility is to use the distribution (3) in a hidden Markov model to obtain a Markov-switching model (see [20] Section 10.4.).
The model in this paper uses a non-homogeneous reproductive power function. One reason for this is that after the start of the outbreak not all individuals who are infected still reproduce. This is especially the case when infected individuals are removed quickly for instance in the case of high fatality. The time varying aspect of the reproductive power adapts to this since it might decrease as the number of total infected(which are not all infectious) increase. Another way to deal with this is to include removals by using a non-homogeneous birth-death process [19] or even to use a model with an equal birth and death rate for endemic diseases [17]. In these last cases the distributions are more complicated.
Disclosure statement
No potential conflict of interest was reported by the author.
References
- 1.Becker N.G., Analysis of Infectious Disease Data, Chapman and Hall, London, New York, 1989. [Google Scholar]
- 2.Becker N.G. and Yip P., Analysis of variations in an infection rate, Aust. J. Stat. 31 (1989), pp. 42–52. doi: 10.1111/j.1467-842X.1989.tb00497.x [DOI] [Google Scholar]
- 3.Brown D.B., Oleson J.J., and Porter A.T., An emperically adjusted approach to reproductive number estimation for stochastic compartmental models: A case study of two ebola outbreaks, Biometrics 72 (2016), pp. 335–343. doi: 10.1111/biom.12432 [DOI] [PubMed] [Google Scholar]
- 4.Chowell G., Hengartner N.W., Castillo-Chavez C., Fenimore P.W., and Hyman J.M., The basic reproductive number of Ebola and the effects of public health measures: The cases of Congo and Uganda, J. Theor. Biol. 229 (2004), pp. 119–126. doi: 10.1016/j.jtbi.2004.03.006 [DOI] [PubMed] [Google Scholar]
- 5.De Leeuw J., Hornik K., and Mair P., Optimization in R: Pool-adjacent-violations algorithm (PAVA) and active sets methods, J. Stat. Softw. 32 (2009), pp. 1–24. doi: 10.18637/jss.v032.i05 [DOI] [Google Scholar]
- 6.Diekman O., Heesterbeek H., and Britton T., Mathematical Tools for Understanding Infectious Disease Dynamics, Princeton University Press, Princeton, 2013. [Google Scholar]
- 7.Diggle P.J., Spatio-temporal point processes, partial likelihood, foot and mouth disease, Stat. Methods Med. Res. 15 (2006), pp. 325–336. doi: 10.1191/0962280206sm454oa [DOI] [PubMed] [Google Scholar]
- 8.Diggle P.J., Statistical Analysis of Spatial and Spatio-Temporal Point Patterns, CRC press, Taylor & Francis group, Boca Raton, 2014. [Google Scholar]
- 9.Keawcharoen J., Van den Broek J., Bouma A., Tiensin T., Osterhaus A.D.M.E., and Heesterbeek H., Wild birds and increased transmission of highly pathogenic avian influenza (H5N1) among poultry, Thailand, Emerging Infect. Dis. 17 (2011), pp. 1016–1022. doi: 10.3201/eid/1706.100880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kendall D.G., On the generalized ‘birth-and-death’ process, Ann. Math. Stat. 19 (1948), pp. 1–15. doi: 10.1214/aoms/1177730285 [DOI] [Google Scholar]
- 11.Kypraios T. and O'Neill P.D., Bayesian nonparametrics for stochastic epidemic models, Stat. Sci. 33 (2018), pp. 44–56. doi: 10.1214/17-STS617 [DOI] [Google Scholar]
- 12.Lawless J.F., Statistical Models and Methods for Liftime Data, John Wiley and Sons, Hoboken, NJ, 2003. [Google Scholar]
- 13.Lloyd-Smith J.O., Schreiber S.J., Kopp P.E., and Getz W.M., Superspreading and the effect of individual variation on disease emergence, Nature 438 (2005), pp. 355–359. doi: 10.1038/nature04153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Meyer S. and Held L., Power-law models for infectious disease spread, Ann. Appl. Stat. 8 (2014), pp. 1612–1639. doi: 10.1214/14-AOAS743 [DOI] [Google Scholar]
- 15.O'Neill P.D. and Roberts G.O., Bayesian inference for partially observed stochastic epidemics, J. R. Stat. Soc. A 162 (1999), pp. 121–129. doi: 10.1111/1467-985X.00125 [DOI] [Google Scholar]
- 16.Sun J., The Statistical Analysis of Interval-Censored Data, Springer, New York, 2006. [Google Scholar]
- 17.Van Den Broek J., Modelling volatility using a non-homogeneous martingale model for processes with constant mean on count data, Stat. Modelling 15 (2015), pp. 457–475. doi: 10.1177/1471082X14565358 [DOI] [Google Scholar]
- 18.Van Den Broek J. and Heesterbeek J.A.P., Non-homogeneous birth and death models for epidemic outbreak data, Biostatistics 8 (2007), pp. 453–467. doi: 10.1093/biostatistics/kxl023 [DOI] [PubMed] [Google Scholar]
- 19.Van Den Broek J. and Nishiura H., Using epidemic prevalence data to jointly estimate reproduction and removal, Ann. Appl. Stat. 3 (2009), pp. 1505–1520. doi: 10.1214/09-AOAS270 [DOI] [Google Scholar]
- 20.Zucchini W., Macdonald I.L., and Langrock R., Hidden Markov Models for Time Series. An Introduction Using R, 2nd ed., CRC Press, Boca Raton, 2016. [Google Scholar]