Abstract
In this paper, we propose the MulticlusterKDE algorithm applied to classify elements of a database into categories based on their similarity. MulticlusterKDE is centered on the multiple optimization of the kernel density estimator function with multivariate Gaussian kernel. One of the main features of the proposed algorithm is that the number of clusters is an optional input parameter. Furthermore, it is very simple, easy to implement, well defined and stops at a finite number of steps and it always converges regardless of the data set. We illustrate our findings by implementing the algorithm in R software. The results indicate that the MulticlusterKDE algorithm is competitive when compared to K-means, K-medoids, CLARA, DBSCAN and PdfCluster algorithms. Features such as simplicity and efficiency make the proposed algorithm an attractive and promising research field that can be used as basis for its improvement and also for the development of new density-based clustering algorithms.
Keywords: Kernel density estimation, Gaussian kernel, clustering data, optimization method, multiclusterKDE
1. Introduction
The amount of data generated and also available to users has increased exponentially due to the growth and massive use of technologies. The significant quantity is collected every day from satellite images, biomedicine, security, marketing, searches on networks, among other means [23]. However, ‘large databases’ and ‘knowledge about the phenomenon’ cannot be thought of as synonymous. So, to understand the phenomenon, firstly the data set needs to become a useful knowledge and only after will it be possible to generate applications and simulations.
The process of exploiting large databases in search of patterns, rules or information sequences, in order to detect correlations between variables, is known as data mining. According to [1] and [21], data mining is a branch of computing that started to be widely studied in the 1980s when companies and organizations began to worry about large amounts of data being stored and unusable within companies.
Over the years, many works have been carried out in this area, leading data mining to be subdivided into different research lines, the main ones are regression, sequential analysis, classification, clustering and analysis of outliers.
In this paper, we are interested in clustering whose objective it is to identify patterns or groups of similar objects in a data set. Clustering is a powerful set of exploratory techniques that seek to perform data grouping, automatically, maximizing the homogeneity of observations within each cluster [23].
Several different clustering strategies have been proposed in order to predict, analyze and replicate phenomena. By the way, no consensus has been reached even on the definition of a cluster. According to [40], clustering can be classified into five main classes which are partitioned, hierarchical, grid-based, model-based methods and density-based. In this paper, we propose an alternative approach based on density distribution function.
Partitioning methods are the simplest methods of clustering [1]. The basic idea of these algorithms is to partition the data set into k clusters in such a way that each object is assigned to the nearest cluster using a partitioning criterion as a function of distance-based dissimilarity. Because of this, these approaches are not able to detect non-spherical clusters [36]. Its major challenge is to know the number of cluster a priori, since this information is the question to be answered in many of the problems studied.
The well-known partitioning algorithm is K-means proposed by [28]. It is widely known in literature and its process consists of two stages, the first is to determine a set of k centroids, and the second is the allocation of the observations of these centroids by the criterion of minimum distance. Other partitioning algorithms are K-medoids and CLARA – Clustering Large Applications [20,24]. These algorithms have interesting features, such as less sensibility to noise and outliers, which make them an attractive alternative for clustering. However, they can sometimes be computationally expensive mainly to large data set.
Hierarchical clustering algorithms decompose the data set into several partitioning levels, which are usually represented by a dendrogram, which is a tree that divides the database recursively into subsets until a termination criteria to be satisfied. Each node in the tree represents one cluster. The dendrogram can be created from leaves to root (agglomerative approach) or from root to leaves (divisive approach) by merging or dividing groups at each step [13]. Although hierarchical clustering algorithms can be very effective in pattern discovery, it has a great challenge to determine the termination criteria of the merging or splitting process.
An example of divisive algorithm is DIANA – Divisive Analysis Clustering [24], where initially there is an only cluster consisting of all points of the data set, and at each subsequent step, the largest cluster is split into two new clusters until all clusters contain only a single point. SLINK – Single-Linkage [41] and CLINK – Complete-Linkage [10] are agglomerative methods that start each point in different clusters, and at each subsequent step, two clusters are joined according to the minimum or maximum distance between elements of each cluster.
Grid-based algorithms classify the space of object into a finite number of cells that form a grid structure [21]. The main advantage of this approach is its fast-processing time, which is independent of the number of objects and dependent on the number of cells in each dimension of the quantized space. In the algorithms based on models, a hypothesis is created for the model on each of the clusters and then find the best fit of the data for a given model [40].
Finally, we have the density-based algorithms which are based on the idea that cluster centers are characterized by having a higher density than their neighbors and the elements are incorporated into clusters as long as the density does not exceed a certain limit [40]. Many different density-based algorithms have been proposed in the last years, such as [3,4,7,13,18,23,25,26,30,32,36,45].
In [32], it was proposed the PdfCluster multivariate algorithm as a natural extension of the clustering procedure based on univariate density developed by [4]. It determines clusters that are associated with connected components with an estimated density above a threshold. The detection of connected regions is performed by procedures described in [4], for problems with low dimension and in [32] for larger dimensions. In both cases, after identifying multiple cluster cores with high density, the lowest density data are allocated following an approach similar to the supervised classification. An interesting feature of PdfCluster is that it does not require the information of the number of clusters a priori, which is determined by clustering process. The PdfCluster algorithm is available in R software [3,7,13,23,25,30,36,45].
Another important algorithm based on density is the DBSCAN – Density-Based Spatial Clustering of Applications with Noise proposed by [13]. The key idea of this algorithm is that for each point in a cluster, its neighborhood, bounded by a radius, must contain at least a minimum number of points, so that elements of the same cluster are closely compact and points outside the neighborhood are as far as possible. According to [23], DBSCAN can discover clusters for data sets of different shapes and sizes containing noises or outliers and it has its implementation in R (‘dbscan’ packages). According to the authors, the results obtained by DBSCAN are significantly more effective at discovering clusters than known partition-based algorithms.
Recently, [36] proposed the DPC algorithm which is based on the assumption that cluster centers are surrounded by neighbors with lower local density and that they are at a relatively large distance from any points with a higher local density. However, this algorithm can produce poor clustering, because the density metric depends strongly on the data set dimension and the strategy of assigning the remaining points to an incorrect cluster can cause propagation of errors. To circumvent these problems, it was proposed the FKNN-DPC algorithm that uses two new assignment strategies based on K-nearest neighbors and fuzzy weighted K-nearest neighbors as it can be seen in [45].
In addition to these methods, there are approaches which are fusions from different methods such as density estimation and normal mixture models that have been proposed and studied in the context of clustering, as seen in [15–17,29,39].
It should be noted that all algorithms presented here are focused on clustering of multidimensional data which are stored in an matrix. However, many modern applications such as image and video recognition, text mining, internet search, large-scale telecommunications and social networking records, generate large amounts of data which have multiple aspects and high dimensionality. In these cases, the multi-way arrays can display a natural representation. These applications are beyond the focus of this work, so for more details see [9,11,12,27].
Due to the diversity of applications in data analysis area, we also intend to investigate in the future the viability of our methodology for structured data via tensors, as well as [22,43,44].
In this paper, we propose a new algorithm, named MulticlusterKDE, which has received this denomination because of performing multiple optimizations of Gaussian kernel density applied for clustering of a multidimensional data set. It is divided into two main steps. The first determines the number of clusters and respective centers by minimizing a probability density estimator. The second consists of assigning observations to each cluster obtained by determining smallest distance, that is, the points are being allocated to the centers that are closest to them. At the end of the process, the algorithm has determined the number of clusters which are stored in a matrix.
The new algorithm has the advantage of not requiring, a priori, the number of clusters and the only input data required to run is a parameter used in the bandwidth matrix. If the user, it can provide the number of clusters, but this parameter is not necessary. Numerical experiments were implemented in R software [34] and the proposed algorithm was compared to K-means, K-medoids, CLARA, DBSCAN and PdfCluster algorithms, also available in R.
The paper is organized as follows. In Section 2, we describe the essential elements to develop this paper. In Section 3, we established our algorithm and then we analyze its complexity convergence. Numerical experiments are reported in Section 4. Finally, concluding remarks close our text in Section 5.
2. Kernel density estimation
This section provides background concepts to develop this paper. For further study, we suggest the following readings [5,19,30,32,38,42].
Let be a random variable with probability density function f. The knowledge of this function provides a natural description of the behavior of the variable x and allows the characteristics associated with it to be studied and replicated.
The density function of a given set of observations is not always known, especially when the data set refers to a real phenomenon. This difficulty can be overcome by using non-parametric estimators such as kernel density estimation – KDE. According to [38], the parametric estimators focus is on obtaining the best estimator for a given parameter θ while in the non-parametric case the objective is directly linked to obtaining a good estimate of the density function .
As presented by [19], a general form of the multivariate kernel density estimator is
| (1) |
where
| (2) |
H is a square bandwidth matrix, non-random, symmetric and positive definite, is the determinant of H, is the vector of n-dimensional space of the variables and , , is the set of observations with unknown density function.
The kernel density estimator has a standard normal multivariate density given by
| (3) |
Considering Equations (1) and (3) the Gaussian kernel density estimator is given as
| (4) |
According to [19], the multivariate KDE can be viewed as a weighted sum of density ‘bumps’ that are centered at each data point .
The key to applying the Gaussian kernel density estimator to a data set is to choose the bandwidth matrix. It is an extremely delicate problem, because few changes in H can significantly affect the shape and orientation of KDE.
As reported by [19], the bandwidth matrix is defined by three levels. The simplest case is given by the product of a scalar by the identity matrix of dimension , . The second level of bandwidth matrix complexity occurs when H is a positive definite diagonal matrix, . And finally, the third level and the most complex one occurs when H is a complete matrix, symmetric and positive definite. In this paper, we use the diagonal matrix.
Based on [32,38], a suitable choice for the components of the diagonal matrix H by considering on multivariate normality hypotheses is
| (5) |
where n is the dimension of space, the standard deviation of the components and m the number of observations.
Under the hypothesis of normality and in the one-dimensional space, [30,38,42] define the best choice for h as being
| (6) |
In [30] it was proposed a flexibilization of this value and the authors introduced a variable α as follows
| (7) |
In this paper, we will use an extension of h given by [30] and we will apply the relationship (7) on each component of H, that is
| (8) |
3. MulticlusterKDE algorithm
In this section, we present the main contribution of our paper, that is, the MulticlusterKDE algorithm. Unlike mean-shift [8] and Expectation-Maximization (EM) [31] algorithms, which use the gradient of the Kernel function to determine the cluster centers, our algorithm determines the centers by minimizing the Gaussian kernel using some optimization method, for example BFGS. In addition, we emphasize that other kernel functions can be used instead of Gaussian, what is enough to be differentiable. Another relevant fact of our algorithm is that it does not need to know the cluster number a priori. However, if the user wishes, he can provide this data. Therefore, the algorithm is flexible and, as we will see in the numerical experiments, it is competitive when compared to some of the main clustering algorithms well known in the literature.
Next, we present and explain the steps of the algorithm. For a better understanding of the proposed approach, first we present an example and then the algorithm.
Example 1
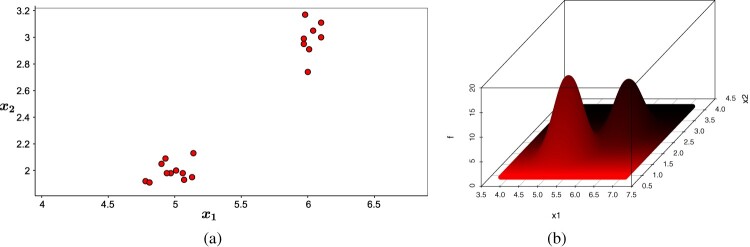
Consider an example with 20 observations of 2 attributes, randomly generated with a structure that defines 2 clusters. The data are in the ‘Attributes’ column of Table 1 and represented in Figure 1(a). For this example, we define as the kernel function's smoothing coefficient.
Table 1. Example data.
| Attributes | |||||
|---|---|---|---|---|---|
| Data | Distance to | Distance to | Minimum distance | ||
| 1 | 4.97 | 1.98 | 0.036 | 1.449 | 0.036 |
| 2 | 4.94 | 1.98 | 0.063 | 1.471 | 0.063 |
| 3 | 5.07 | 1.93 | 0.099 | 1.418 | 0.099 |
| 4 | 4.78 | 1.92 | 0.234 | 1.629 | 0.234 |
| 5 | 5.06 | 1.98 | 0.063 | 1.387 | 0.063 |
| 6 | 5.01 | 2.00 | 0.010 | 1.407 | 0.010 |
| 7 | 4.81 | 1.91 | 0.210 | 1.614 | 0.210 |
| 8 | 4.93 | 2.09 | 0.114 | 1.405 | 0.114 |
| 9 | 4.90 | 2.05 | 0.112 | 1.453 | 0.112 |
| 10 | 5.13 | 1.95 | 0.139 | 1.364 | 0.139 |
| 11 | 5.00 | 2.06 | 0.060 | 1.372 | 0.060 |
| 12 | 5.14 | 2.13 | 0.191 | 1.223 | 0.191 |
| 13 | 5.98 | 3.17 | 1.526 | 0.171 | 0.171 |
| 14 | 6.10 | 3.11 | 1.563 | 0.149 | 0.149 |
| 15 | 6.00 | 2.74 | 1.244 | 0.260 | 0.260 |
| 16 | 5.97 | 2.95 | 1.358 | 0.058 | 0.058 |
| 17 | 6.01 | 2.91 | 1.359 | 0.091 | 0.091 |
| 18 | 6.04 | 3.05 | 1.478 | 0.064 | 0.064 |
| 19 | 5.97 | 2.99 | 1.386 | 0.032 | 0.032 |
| 20 | 6.10 | 3.00 | 1.487 | 0.100 | 0.100 |
Figure 1.
Data set and Gaussian kernel density estimator. (a) Data set. (b) Gaussian kernel.
In the first step of the MulticlusterKDE algorithm, the diagonal elements of the matrix H are determined by equation (8), and then it is built the Gaussian kernel density estimator (Figure 1(b)). An important observation is that H and are constructed only once by the algorithm.
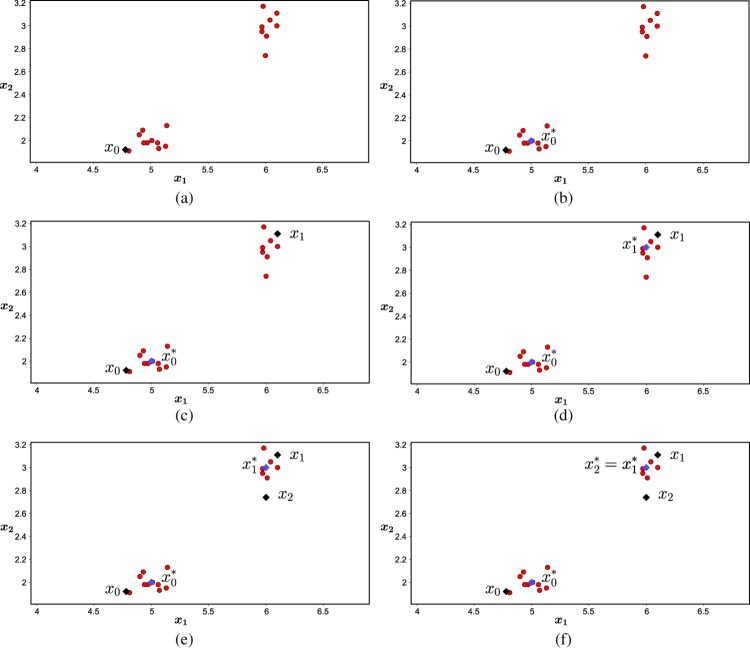
In order to begin the optimization process, the MulticlusterKDE algorithm randomly chooses the point , which is represented by in Figure 2(a). Then the algorithm starts the main loop (while) to find a minimizer point of (Figure 2(b)) and it is assigned to the set as the first center. After this, the algorithm determines the distance from all 20 observations to the centroid , the result is shown in column ‘Distance to ’ of Table 1.
Figure 2.
MulticlusterKDE steps.
Based on the distances of the centroid , the MulticlusterKDE selects the point of the observations set with the longest distance to , that is, it searches in the data set the furthest point of the , which is the point , with an approximate distance 1.5627 to . So, the algorithm uses ( in Figure 2(c)) as the initial point for solve the subproblem and a new iteration begins.
The second iteration begins with as initial point and the MulticlusterKDE determines a minimizer as a solution of the subproblem (Figure 2(d)). Then it checks if belongs to S, if not, it is designated to the set and, otherwise the loop ends.
Giving continuity to the proposed algorithm, it determines the distance of all observations to the centroid , according to column ‘Distance to ’ of Table 1. Since we have 2 centroids in the set S, it follows that each of the 20 observations has 2 distances to the set S. The next step of the algorithm is to determine which of the 20 observations has the furthest distance to both elements of S, i.e. which of the observations presents the highest degree of heterogeneity with S. To determine this element, the algorithm scanned all the 20 observations of the problem, finding the smallest distance between the observation and the two centroids. The results are in the column ‘Minimum distance’ of Table 1. Then the MulticlusterKDE determines , which has the maximum distance between the minimum distances. This point is represented by in Figure 2(e) and it is used as initial point for the new iteration.
The third iteration begins with as initial point and determines as a solution of the subproblem which is represented in Figure 2(f). Since this point already belongs to the set S, the loop ends. The first stage of MulticlusterKDE finishes with , that is, the problem will have two clusters, whose centroids are the elements of S.
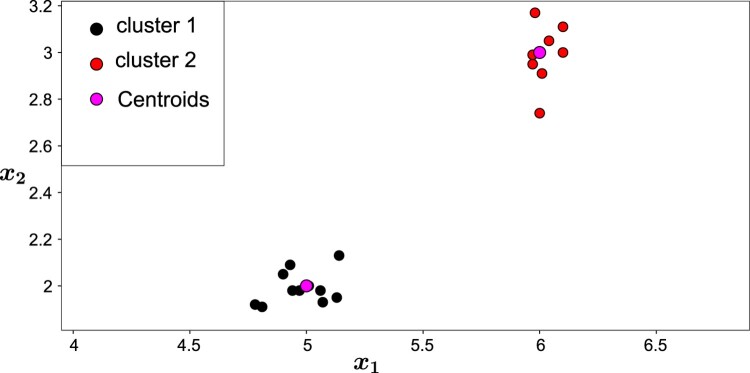
The second stage is extremely simple too. Considering the distances of the twenty observations to the two centroids, as presented by ‘Distance to ’ and ‘Distance to ’, respectively, in Table 1, the proposed algorithm obtains for each observation the nearest centroid and from there the observation is assigned to the respective cluster. For example, the nearest centroid to is , therefore, belongs to cluster 1. By repeating the process for all observations, the MulticlusterKDE is finished. The final result is represented in Figure 3.
Figure 3.
Clustering result for Example 3.1.
After this simple example, we shall describe the MulticlusterKDE algorithm (Algorithm 1).

Firstly, variables and constants are initialized. The matrix contains the problem data, where n and m are the number of attributes (variables) and observations, respectively. The parameter is used in the equation (8) in order to determine the matrix H, which is responsible for the smoothness of the kernel density estimator function; nc is an integer number provided by the user, which is optional, and it limits the number of clusters, and its absence does not disable the algorithm; S is a matrix and F is a vector used to store the centroids and the values of the objective function evaluated on centroids, respectively, and rep = 0 to finish the main loop of the algorithm. Finally, the vector C stores the clustering of data set.
The Algorithm 1 cloops. The first one, represented by the while, has as main task to determine the cluster centers (or centroids). Note that the loop begins by determining a maximizer, , of kernel function . Next, the algorithm checks if this center has already been selected. If it does, the loop ends and otherwise is stored in the matrix S as a new cluster center and the respective value is stored in the vector F. For each iteration k, the value gives the furthest distance of all points to the found centers and becomes the point that is farther from all already determined centers being used as an initial point for the next iteration.
After the end of the first loop, and before starting the second one, the algorithm fixes the number of clusters that can be k or nc. If the user has previously defined it, then the maximum number of the cluster is nc and if nc<k so k−nc points will be eliminated between those already determined by the previous loop (while), that will not be cluster centers.
The second loop, which consists of the commands for j and for i, determines the clusters. The technique used is the one with the smallest distance, that is, the points are being allocated to the centers that are closest to them. At the end of the process, the algorithm has determined k or nc clusters which are stored in the matrix C.
The space complexity of MulticlusterKDE is , where k is the number of clusters obtained and m is the size of data set, which stores the distance matrix. In addition, one matrix and three vectors are used during the algorithm run. The matrix S stores the cluster centers. The vectors F and C store the values of the objective function evaluated on centroids and the clustering result, respectively. Finally, since the matrix H is diagonal, it is stored as a vector.
The time complexity of MulticlusterKDE depends mainly on determining the cluster centers, , which consists of minimizing a function using the BFGS method; the time for computing the distance matrix and to allocate the points in the clusters. In addition, if the user has fixed the maximum number of clusters, it is necessary to perform a classification on the elements in F and S.
In the following theorem, we show that the algorithm is well defined and then that it stops at a finite number of steps.
Theorem 1
Algorithm 1 is well defined and it stops at iteration k, in which the number of cluster is given by min .
Proof.
First, we show that the algorithm is well defined. In fact, in the iteration k of Algorithm 1 we must determine as a minimizer of which is a smooth function and has derivatives of all orders. To solve this subproblem, we use the R software that employs a quasi-Newton method named in optimization as BFGS, which is globally convergent, i.e. the algorithm converges independent of the initial point (see [33], Theorem 8.5, p. 212). Therefore, the subproblem always has a solution. We now show that the number of subproblems that Algorithm 1 needs to solve is finite, in other words, the number of minimizers of this function for a finite value m, of the sample points in matrix X, is finite. If all the points in the sample were isolated, in which case each sample point would be a cluster, we would have at most m clusters and therefore it is finite. In the case where we have p<m minimizers, Algorithm 1 also stops in a finite number of steps. In fact, since p is finite in some iteration k the algorithm will find a point that has already been determined and this is the criterion of stopping the main loop (if this does not happen the amount of sample points will be infinite). Therefore, the maximum number of clusters will be k if the user has not set nc. The case where the user has set nc will be the number of clusters determined by Algorithm 1.
4. Numerical tests
In this section, we present numerical results that evidence and qualify the MulticlusterKDE algorithm. The problems analyzed here are divided into two kinds. The first kind are the problems that grouping structure and the class labels of each observation are known. The objective is to show the ability of the proposed algorithm in grouping the data set in an appropriate way. The second kind are the problems with unknown grouping structure, which requires to get the number of clusters and grouping in order to best fit the data set.
All problems were run by six different algorithms, which are MulticlusterKDE, K-means, PdfCluster, K-medoids, CLARA and DBSCAN. The main reason for choosing these five algorithms is because they are widely used in literature and they are implemented in R software.
In the following, the parameters of each method are exposed, as well as the package and function used in R. MulticlusterKDE requires α which is used to calculate the smoothing matrix, and nc (optional) that corresponds to the number of clusters; we implemented MulticlusterKDE, using only optim() function of stats package for the optimization part, in which we used the method=‘BFGS’ as parameter for this function. For K-means only the number of clusters is given; we used kmeans() function of stats package. PdfCluster has hmult as parameter, which is a shrink factor that multiplies the smoothing parameter to be used in Gaussian kernel density estimation, and bwtype corresponding to a kernel estimator with fixed or adaptive bandwidths; we used PdfCluster() function of PdfCluster package. K-medoids and CLARA, as well as in K-means, require the number of clusters; we used pam() (for K-medoids) and CLARA() (for CLARA) functions of cluster package. For DBSCAN, two parameters are given, eps and minPts, in which a circle of eps radius contains at least minPts points in its neighborhood; dbscan() function of dbscan package was used.
A computer Intel (R) Core i5-7200U CPU @ 2.50 GHz 2.71 GHz processor, Windows 10 home 64-bit operating system, was used to implement the algorithms for all problems. The version 3.6.1(2019-07-05) of R sofware was used with 1.1.463 RStudion version.
4.1. Numerical tests on known class problems
Initially, in this section, seven problems whose grouping structure is known will be addressed. The first one is the classification of Iris species (‘Iris data set’), the second one is the wine production region (‘Wine data set’), the third one is the classification of wheat seeds (‘Seeds data set’), the fourth one is the olive oil production region (‘Olive oil data set’), the fifth one corresponds to the type of Erythema-Squamous Disease and the last two problems refer to waveform classification (‘Waveform Database Generator (Version 1)’ and ‘Waveform Database Generator (Version 2)’).
In order to reduce the standard deviation in obtaining the matrix H, by MulticlusterKDE algorithm, we applied the logarithmic scale to the data set for the problems of this section.
As mentioned before, for all these problems we know the class labels of each observation. According to [35], with the label information you can create validity metrics that are easier to understand and compare between clusters. These metrics are known as external metrics because of their dependency on external class labels. For external metrics, a confusion matrix is created (also called a match matrix) that is a simple table which shows the match between the cluster labels determined by the clustering algorithms and the actual cluster labels of the data. The confusion matrix allows, in a simple way, to visualize an assertive correspondence of the clustering algorithms in relation to real data, that is, it provides the number of hits and misses of the clustering process.
4.1.1. Iris data set
The ‘Iris data set’ contains 150 observations of three plant varieties of the Iris species. The data are equally divided among the varieties of iris, Setosa, Versicolour and Virginica. Each observation consists of four attributes: the length and width of the petal, the length and the width of the sepal.
For this data set, the algorithms were calibrated with some specific input parameters, which are and nc = 3 for MulticlusterKDE algorithm. For K-means, K-medoids and CLARA algorithms the exact number of three clusters were specified like input argument and in PdfCluster the parameter hmult = 0.58 was used. In DBSCAN algorithm the parameters eps = 0.5 and minPts = 14 were used.
In PdfCluster and DBSCAN algorithms the parameters were obtained by numerical tests, it means that the algorithms were running several times and at the end, we chose the parameters based on the best results. In this way, in PdfCluster algorithm we did the hmult parameter to vary from 0.2 to 1.5 with a range of 0.1 and in DBSCAN the minPts parameter varied from 1 to 20 with an interval of 1, and for each of its value , eps varied from 0.1 to 20, with an interval of 0.1. This same strategy was used in all problems of this section. The clustering results are shown in Table 2.
Table 2. Confusion matrix for Iris data set.
| MulticlusterKDE | K-means | PdfCluster | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Variety | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 |
| Setosa | 50 | 0 | 0 | 50 | 0 | 0 | 50 | 0 | 0 |
| Versicolour | 0 | 50 | 0 | 0 | 48 | 2 | 0 | 46 | 4 |
| Virginica | 0 | 7 | 43 | 0 | 14 | 36 | 0 | 13 | 37 |
| K-medoids | CLARA | DBSCAN | |||||||
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | |
| Setosa | 50 | 0 | 0 | 50 | 0 | 0 | 46 | 0 | 4 |
| Versicolour | 0 | 48 | 2 | 0 | 48 | 2 | 0 | 37 | 13 |
| Virginica | 0 | 14 | 36 | 0 | 13 | 37 | 0 | 5 | 45 |
In Table 3 we show the absolute and relative errors and runtime for each algorithm used to classify the Iris species. It should be noted that although several tests were performed with different parameters values, the runtime in this table corresponds to the results printed in Table 2.
Table 3. Comparative results for Iris data set.
| Algorithms | Absolute error | Relative error | time(s) |
|---|---|---|---|
| MulticlusterKDE | 7 | 4,7% | 5.9 |
| K-means | 16 | 10,7% | 0.02 |
| PdfCluster | 17 | 11,3% | 0.141 |
| K-medoids | 16 | 10.7% | 0.016 |
| CLARA | 15 | 10.0% | 0.001 |
| DBSCAN | 22 | 14.7% | 0.001 |
The numerical results indicate that the proposed algorithm spent more computational time, however, it is more efficient to classify Iris data set elements in comparison with the K-means, PdfCluster, K-medoids, CLARA and DBSCAN, because it solved with the lowest error.
4.1.2. Wine data set
The ‘Wine data set’ is a set of 178 wines grown in the same region of Italy, but produced from three different cultivars (Barolo, Grignolino, Barbera). Each cultivar has 28 chemical characteristics, however, according to [32] only 13 are commonly chosen among the 28 originals: Alcohol, Malic acid, Ash, Alcalinity of ash, Magnesium, Total phenols, Flavanoids, Nonflavanoid phenols, Proanthocyanins, Color intensity, Hue, OD280/OD315 of diluted wines e Proline.
As well as done in the previous problem, all algorithms were calibrated with specific input parameters. Thus, and nc = 3 in MulticlusterKDE, 3 is the number of clusters in K-means, K-medoids and CLARA algorithms. In PdfCluster algorithm, the parameters hmult = 1.2 and bwtype=‘adaptive’ were used, while in DBSCAN eps = 13.2 and minPts = 8 were used. The clustering results are shown in Table 4.
Table 4. Confusion matrix for Wine data set.
| MulticlusterKDE | K-means | PdfCluster | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Cultivars | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 |
| Barolo | 59 | 0 | 0 | 46 | 0 | 13 | 59 | 0 | 0 |
| Grignolino | 4 | 66 | 1 | 1 | 50 | 20 | 5 | 62 | 4 |
| Barbera | 0 | 1 | 47 | 0 | 19 | 29 | 0 | 1 | 47 |
| K-medoids | CLARA | DBSCAN | |||||||
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | |
| Barolo | 46 | 0 | 13 | 48 | 0 | 11 | 58 | 1 | 0 |
| Grignolino | 2 | 50 | 19 | 2 | 50 | 19 | 61 | 5 | 5 |
| Barbera | 0 | 18 | 30 | 0 | 18 | 30 | 40 | 2 | 6 |
For all algorithms, the absolute and relative errors and the runtime to cluster the Wine data are presented in Table 5. Despite having a longer runtime followed by PdfCluster algorithm, the results indicate that the MulticlusterKDE algorithm has the advantage of being more efficient than the other ones. Observe that it solved the problem with almost half the absolute error compared to PdfCluster, which was the second best algorithm based on the correct data classifications. According to this evidence, we showed the efficiency and competitiveness of the proposed algorithm.
Table 5. Comparative results for Wine data set.
| Algorithms | Absolute error | Relative error | time(s) |
|---|---|---|---|
| MulticlusterKDE | 6 | 3.4% | 5.51 |
| K-means | 53 | 29.7% | 0.015 |
| PdfCluster | 10 | 5.6% | 2.35 |
| K-medoids | 52 | 29.2% | 0.016 |
| CLARA | 50 | 28.1% | 0.008 |
| DBSCAN | 109 | 61.2% | 0.001 |
4.1.3. Seeds data set
The ‘Seeds data set’ was collected and analyzed by [6] and presented in [2]. The information presented refers to seeds of three wheat varieties: Kama, Rosa and Canadian. This set consists of 210 observations, 70 seeds for each variety. Each observation is composed of 7 geometric parameters of wheat seeds: area (A), perimeter (P), compactness ( ), length of kernel, width of kernel, asymmetry coefficient and length of kernel groove.
In order to execute the MulticlusterKDE algorithm, the parameters α and nc were defined as 1.85 and 3, respectively. Thus, three clusters were considered for the K-means, K-medoids and CLARA algorithms. For the PdfCluster algorithm was assigned, bwtype = ‘adaptive’ and hmult=0.8. Finally, in the DBSCAN, we used eps = 0.9 and minPts = 19. The results are shown in Table 6.
Table 6. Confusion matrix for Seeds data set.
| MulticlusterKDE | K-means | PdfCluster | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Varieties | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 |
| Kama | 60 | 1 | 9 | 60 | 1 | 9 | 59 | 3 | 8 |
| Rosa | 4 | 65 | 1 | 10 | 60 | 0 | 4 | 66 | 0 |
| Canadian | 8 | 0 | 62 | 2 | 0 | 68 | 3 | 0 | 67 |
| K-medoids | CLARA | DBSCAN | |||||||
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | |
| Kama | 57 | 1 | 12 | 60 | 2 | 8 | 69 | 0 | 1 |
| Rosa | 10 | 60 | 0 | 9 | 61 | 0 | 51 | 19 | 0 |
| Canadian | 0 | 0 | 70 | 4 | 0 | 66 | 39 | 0 | 31 |
The numerical results presented in Table 7 indicate that, based on absolute and relative error, the PdfCluster algorithm showed the best performance to solve this problem followed by K-means, MulticlusterKDE/K-medoids/CLARA and lastly DBSCAN. The DBSCAN presented the smallest runtime, however, it had the biggest error in clustering the data set. Thus, it is not enough for an algorithm to guarantee a good runtime, as it is also absolutely necessary to be efficient in classifying data set.
Table 7. Comparative results for Seeds data set.
| Algorithms | Absolute error | Relative error | time(s) |
|---|---|---|---|
| MulticlusterKDE | 23 | 10.9% | 5.28 |
| K-means | 22 | 10.5% | 0.003 |
| PdfCluster | 18 | 8.6% | 3.25 |
| K-medoids | 23 | 10.9% | 0.005 |
| CLARA | 23 | 10.9% | 0.003 |
| DBSCAN | 64 | 30.5% | 0.001 |
4.1.4. Olive oil data set
The ‘Olive Oil data set’ was originally presented by [14] and used by several researchers to validate clustering algorithms, among these [32]. According to [14,32], the data refer to olive oil produced in nine areas of Italy, concentrated into three geographical macro-areas: South, Sardinia Island, Centre-North. In the macro-area of the South, one has the regions of Apulia North, Apulia South, Calabria and Sicily. In the macro-area Sardinia, one has the regions of the coast and the interior of Sardinia and finally in the macro-area center-north one has the regions of Liguria East, Liguria West and Umbria.
According to [32], the data set in its raw form is compositional in nature, totaling 10,000 elements. In their paper, the authors adopted an additive log-ratio (ARL) transformation, which reduces the set of analysis to 572 observations. Each observation consists of eight chemical measurements of the oil (Palmitic, Palmitoleic, Stearic, Oleic, Linoleic, Linolenic, Arachidic, eicosenoic), as well as information about its area and macro-area of origin.
As in [32], we chose to cluster the macro-region, for this in the MulticlusterKDE algorithm we used as input parameters and nc = 3. In K-means, K-medoids and CLARA we used three clusters, in PdfCluster the parameters and hmult = 1.2, while in DBSCAN eps = 12.7 and minPts = 4. The results are shown in Table 8.
Table 8. Confusion matrix for Olive oil data set.
| MulticlusterKDE | K-means | PdfCluster | |||||||
|---|---|---|---|---|---|---|---|---|---|
| macro-area | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 |
| Sul | 323 | 0 | 0 | 190 | 91 | 42 | 296 | 0 | 27 |
| Sardina | 0 | 97 | 1 | 22 | 76 | 0 | 0 | 98 | 0 |
| Centre-North | 0 | 26 | 125 | 0 | 17 | 134 | 0 | 6 | 145 |
| K-medoids | CLARA | DBSCAN | |||||||
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | |
| Sul | 196 | 84 | 43 | 204 | 78 | 41 | 323 | 0 | 0 |
| Sardina | 19 | 79 | 0 | 31 | 67 | 0 | 98 | 0 | 0 |
| Centre-North | 0 | 18 | 133 | 0 | 21 | 130 | 129 | 4 | 18 |
As in the previous cases, Iris and Wine data set, for this problem the proposed algorithm is also more efficient in classifying the data set. Analyzing the results presented in Table 9, we can conclude that MulticlusterKDE has the advantage of being the most accurate in the data classification and with a good runtime. PdfCluster also presented a good performance, however, with the highest runtime. Finally, the other ones showed excellent computational time, however, with a high classification error.
Table 9. Comparative results for Olive oil data set.
| Algorithms | Absolute error | Relative error | time(s) |
|---|---|---|---|
| MulticlusterKDE | 27 | 4.7% | 14.87 |
| K-means | 172 | 29.8% | 0.001 |
| PdfCluster | 33 | 5.7% | 64.12 |
| K-medoids | 164 | 28.7% | 0.04 |
| CLARA | 171 | 29.9% | 0.001 |
| DBSCAN | 231 | 40.4% | 0.001 |
4.1.5. Dermatology data set
The ‘Dermatology data set’ contains 366 observations from patients diagnosed with erythematous-squamous diseases. Altogether, the group presents patients diagnosed with 6 different types of this disease, namely psoriasis, seborrheic dermatitis, lichen planus, pityriasis rosea, chronic dermatitis and pityriasis rubra pilar.
Each of the observations (patients) consists of 34 attributes (variables), 33 of which are integer and 1 nominal, more specifically binary, that specifies if the patient has a family history of the disease or not. Of the 33 integer attributes, 1 is the patient's age, 10 is clinical information that receives the values 0, 1, 2 or 3, where 0 indicates that the characteristic was not present, 3 indicates the largest possible quantity and 1 and 2 indicate the intermediate relative values. Finally, the other 22 attributes are histopathological patient information, which are also graduated by integer values in the range 0 to 3.
The original dermatology data set, available at [2], 8 observations are presented without information about age attribute, so we decided to exclude them resulting in a data set with 358 observations.
For this data set, the algorithms were calibrated with some specific input parameters. In MulticlusterKDE algorithm was used and nc = 6. In PdfCluster was used hmult = 0.7, while in DBSCAN eps = 4.7 and minPts = 12 were considered. In K-means, K-medoids and CLARA algorithms we specified 6 clusters. The clustering results are shown in Tables 10 and 11.
Table 10. Confusion matrix for Dermatology data set.
| MulticlusterKDE | PdfCluster | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diseases | C1 | C2 | C3 | C4 | C5 | C6 | C1 | C2 | C3 | C4 | C5 | C6 |
| psoriasis | 95 | 5 | 0 | 1 | 9 | 1 | 52 | 15 | 0 | 1 | 11 | 32 |
| seboreic dermatitis | 0 | 29 | 0 | 31 | 0 | 0 | 2 | 38 | 15 | 3 | 2 | 0 |
| lichen planus | 0 | 0 | 70 | 1 | 0 | 0 | 31 | 0 | 40 | 0 | 0 | 0 |
| pityriasis rosea | 0 | 0 | 0 | 47 | 1 | 0 | 0 | 13 | 27 | 8 | 0 | 0 |
| cronic dermatitis | 0 | 0 | 0 | 0 | 48 | 0 | 0 | 1 | 1 | 1 | 45 | 0 |
| pityriasis rubra pilaris | 0 | 0 | 0 | 0 | 0 | 20 | 8 | 0 | 10 | 0 | 2 | 0 |
| K-means | K-medoids | |||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C1 | C2 | C3 | C4 | C5 | C6 | |
| psoriasis | 32 | 27 | 0 | 17 | 26 | 9 | 28 | 32 | 15 | 16 | 16 | 4 |
| seboreic dermatitis | 19 | 19 | 0 | 2 | 16 | 4 | 2 | 17 | 17 | 9 | 13 | 2 |
| lichen planus | 17 | 0 | 22 | 4 | 27 | 1 | 6 | 20 | 25 | 14 | 6 | 0 |
| pityriasis rosea | 15 | 15 | 0 | 5 | 8 | 5 | 5 | 14 | 8 | 10 | 10 | 1 |
| cronic dermatitis | 14 | 11 | 0 | 5 | 10 | 5 | 6 | 14 | 9 | 8 | 10 | 1 |
| pityriasis rubra pilaris | 0 | 1 | 0 | 0 | 0 | 19 | 0 | 0 | 0 | 0 | 2 | 18 |
| CLARA | DBSCAN | |||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C1 | C2 | C3 | C4 | C5 | C6 | |
| psoriasis | 29 | 31 | 15 | 20 | 12 | 4 | 111 | 0 | 0 | 0 | 0 | 0 |
| seboreic dermatitis | 6 | 18 | 12 | 10 | 12 | 2 | 11 | 35 | 0 | 13 | 0 | 1 |
| lichen planus | 6 | 20 | 25 | 18 | 2 | 0 | 38 | 0 | 21 | 0 | 12 | 0 |
| pityriasis rosea | 7 | 14 | 6 | 10 | 10 | 1 | 10 | 31 | 0 | 7 | 0 | 0 |
| cronic dermatitis | 8 | 14 | 7 | 8 | 10 | 1 | 27 | 16 | 0 | 4 | 0 | 1 |
| pityriasis rubra pilaris | 0 | 0 | 0 | 0 | 2 | 18 | 3 | 0 | 0 | 0 | 0 | 17 |
Table 11. Comparative results for Dermatology data set.
| Algorithms | Absolute error | Relative error | time(s) |
|---|---|---|---|
| MulticlusterKDE | 49 | 13.9% | 10.5 |
| K-means | 251 | 70.1% | 0.016 |
| PdfCluster | 175 | 48.8% | 28.56 |
| K-medoids | 250 | 69.8% | 0.031 |
| CLARA | 110 | 30.7% | 0.001 |
| DBSCAN | 167 | 46.6% | 0.016 |
The results indicate that all algorithms showed high values for absolute and relative errors, even higher than for the previous problems, however, despite their unsatisfactory performance, the proposed algorithm stands out with the best performance, as we can see in Table 11.
4.1.6. Waveform database generator (Version 1)
The set ‘Waveform database generator (version 1)’ consists of 5000 waveform observations. The set presents 3 classes of waves generated from a combination of 2 or 3 basic waves with noises (with mean 0 and variance 1) added to them, totaling 21 attributes for waveform classification.
For this data set, the algorithms were calibrated with the input parameters. So, in MulticlusterKDE algorithm, and nc = 3 were used. The parameters eps = 4.1 and minPts = 18 were inserted in DBSCAN. In K-means, K-medoids and CLARA algorithms we specified three clusters. The PdfCluster algorithm failed to solve this problem in all tests performed and it stopped with the following message ‘Error: cannot allocate vector of size 2.0 Gb’. The results for this data set are shown in Tables 12 and 13.
Table 12. Confusion matrix for Waveform database (version 1).
| MulticlusterKDE | K-means | PdfCluster | |||||||
| waveform | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 |
| 1 | 1392 | 29 | 236 | 824 | 11 | 822 | – | – | – |
| 2 | 505 | 1085 | 57 | 958 | 689 | 0 | – | – | – |
| 3 | 65 | 277 | 1354 | 0 | 700 | 996 | – | – | – |
| K-medoids | CLARA | DBSCAN | |||||||
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | |
| 1 | 861 | 9 | 787 | 911 | 673 | 73 | 840 | 817 | 0 |
| 2 | 945 | 702 | 0 | 0 | 884 | 763 | 703 | 943 | 1 |
| 3 | 0 | 600 | 1096 | 870 | 0 | 826 | 766 | 925 | 5 |
Table 13. Comparative results for Waveform database (version 1).
| Algorithms | Absolute error | Relative error | time(s) |
|---|---|---|---|
| MulticlusterKDE | 1169 | 23.4% | 3.89 |
| K-means | 2491 | 49.8% | 0.02 |
| PdfCluster | – | – | – |
| K-medoids | 2341 | 46.8% | 7.9 |
| CLARA | 2379 | 47.6% | 0.013 |
| DBSCAN | 3212 | 64.2% | 0.687 |
4.1.7. Waveform database generator (Version 2)
The set ‘Waveform database generator (version 2)’ has the same assignments as its first version, also with 5000 waveform observations, however, each observation consists of 40 attributes.
For this data set, the MulticlusterKDE algorithm was calibrated with and . In DBSCAN, eps = 8.25 and minPts = 1. In K-means, K-medoids and CLARA algorithms were considered three clusters. As in the previous problem (version 1), the PdfCluster algorithm was not able to solve this problem even considering several parameters, because again it had memory allocation error. The results for this data set are shown in Tables 14 and 15.
Table 14. Confusion matrix for Waveform database (version 2).
| MulticlusterKDE | K-means | PdfCluster | |||||||
| waveform | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 |
| 1 | 1002 | 425 | 265 | 880 | 12 | 800 | – | – | – |
| 2 | 139 | 1462 | 52 | 930 | 23 | 0 | – | – | – |
| 3 | 224 | 172 | 1259 | 0 | 685 | 970 | – | – | – |
| K-medoids | CLARA | DBSCAN | |||||||
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | |
| 1 | 677 | 303 | 712 | 878 | 20 | 794 | 1283 | 402 | 7 |
| 2 | 714 | 939 | 0 | 925 | 728 | 0 | 1162 | 491 | 0 |
| 3 | 0 | 646 | 1009 | 0 | 651 | 1004 | 1227 | 420 | 8 |
Table 15. Comparative results for Waveform database (version 2).
| Algorithms | Absolute error | Relative error | time(s) |
|---|---|---|---|
| MulticlusterKDE | 1277 | 25.5% | 5.08 |
| K-means | 2427 | 48.5% | 0.08 |
| PdfCluster | – | – | – |
| K-medoids | 2375 | 47.5% | 3.77 |
| CLARA | 2390 | 47.8% | 0.012 |
| DBSCAN | 3218 | 64.4% | 1.55 |
Such as in Dermatology data set, in Waveform database (versions 1 and 2), all algorithms tested classified several elements in a wrong way, causing a high relative error. However, the smallest error was obtained by the MulticlusterKDE algorithm as it can be seen in Tables 13 and 15.
Further remarks on known class problems
Based on the previous results, we have observed that, according to absolute and relative errors, the MulticlusterKDE algorithm had the best performance in six of seven problems, which in three problems (iris, wine and olive oil) the relative errors did not exceed 5%.
For the iris, wine, olive oil, dermatology, waveform 1 and waveform 2 data set, we compared the MulticlusterKDE algorithm with the second one that obtained the best performance by error criterion, and the results were, respectively, 53.3%, 40%, 18.2%, 55.5%, 50.1% and 46.2% better.
Regarding the runtime, K-means, CLARA and DBSCAN had the best performance in most of the problems, however, the MulticlusterKDE determined the most accurate clustering for almost all data sets.
4.2. Numerical tests on problems with no classes defined
In this section, we consider two kinds of problems with no classes defined. For the first one, we take two real data, USArrests and TripAdvisor [2]. In the second one, eight problems are randomly generated.
In order to compare the algorithms efficiency, we consider the silhouette coefficient as a measure of performance. The coefficient was proposed by [37] and is one of the many indexes to evaluate the clustering structure. It is calculated for each i object in the data set as follows:
| (9) |
where is the average dissimilarity between the i object and all other points in the cluster to which i belongs and is the minimum mean dissimilarity of the objects of each cluster that are different. The silhouette coefficient is the average of all output values and is in the range , such that near 1 means that the object i is well grouped, while near -1 means that it has been misclassified.
The first problem analyzed, consists of the ‘ USArrests data set’, initially presented by McNeil (1977) [2]. This set contains the number of arrests per 100,000 inhabitants for crimes of aggression, murder and rape taking into account the 50 US states in 1973. Besides this information, the sample contains 50 observations that refer to the percentage of the population living in urban areas which are divided in 4.
The second problem consists of user reviews to TripAdvisor.com about 10 categories of East Asian attractions, including art galleries, nightclubs, juice bars, restaurants, museums, resorts, parks, beaches, cinemas and religious institutions. The users evaluate each visited attraction as Excellent (4), Very Good (3), Average (2), Bad (1) or Terrible (0). The average user rating for each type of attraction is attributed to the ‘Travel Reviews data set’, which is available by [2] and consists of 980 numerical records.
In order to improve the analysis of algorithms's performance, besides the two problems already mentioned, we also consider in this section eight random samples, whose procedure adopted to generate them will be described now. Initially, a positive integer was generated, with the objective to determine the number of subgroups or midpoints used in the generation of subgroups with Gaussian distribution. Then, another positive integer was generated, that corresponds to the dimension of the problem and a positive real number that is the standard deviation.
Then, on each of the g accumulation points, it was generated points of dimension n, that is, , with , and . Each component of was obtained by a Gaussian distribution, , with and μ uniformly distributed, . Thus, the following set we will have at the end of the procedure. Due to the random nature of the generation of accumulation points and the standard deviation of the components, the data sets can have several characteristics such as, extremely well-defined groups or even point clouds.
In this section, we tested 10 problems not knowing the ideal number of clusters. To run all problems, some parameters were defined for each algorithm. In MulticlusterKDE, we considered and . In PdfCluster algorithm was used in its default form. As K-means, K-medoids and CLARA require information on the number of clusters, then we performed several tests, varying the number of clusters, from 2 to 10 clusters. For two problems we considered 20 as the maximum number of clusters. So, the best configuration of clustering, according to silhouette coefficient, was considered as the solution and presented in Table 16. Similarly, it was done in DBSCAN algorithm, we varied the parameter eps from 0.1 to 50 and the parameter minPts from 1 to 5. The parameters that returned the best solution were considered.
Table 16. Comparative results for problems with no classes defined.
| USArrests: ( ) | Tripadvisor: ( ) | |||||||
|---|---|---|---|---|---|---|---|---|
| Algorithms | nc | Sil | time(s) | Par | nc | Sil | time(s) | Par |
| MulticlusterKDE | 2 | 0.58 | 0.767 | 6 | 0.52 | 6.193 | ||
| PdfCluster | 1 | – | 0.06 | – | 17 | 0.0353 | 305.94 | – |
| DBSCAN | 8 | 0.43 | 0.001 | 23.7/1 | 8 | 0.54 | 0.001 | 4.6/8 |
| K-means | 2 | 0.59 | 0.01 | 2:10 | 2 | 0.62 | 0.031 | 2:10 |
| K-medoids | 2 | 0.59 | 0.016 | 2:10 | 2 | 0.62 | 0.172 | 2:10 |
| CLARA | 2 | 0.59 | 0.02 | 2:10 | 2 | 0.62 | 0.031 | 2:10 |
| Random 1: ( ) | Random 2: ( ) | |||||||
| MulticlusterKDE | 2 | 0.75 | 5.88 | 7 | 0.79 | 16.145 | ||
| PdfCluster | 2 | 0.75 | 8.77 | – | – | – | – | – |
| DBSCAN | 2 | 0.75 | 0.02 | 1.2/1 | 8 | 0.78 | 0.172 | 2.3/5 |
| K-means | 2 | 0.75 | 0.049 | 2:10 | 6 | 0.76 | 0.74 | 2:10 |
| K-medoids | 2 | 0.75 | 0.31 | 2:10 | 7 | 0.78 | 9.052 | 2:10 |
| CLARA | 2 | 0.75 | 0.045 | 2:10 | 7 | 0.78 | 0.701 | 2:10 |
| Random 3: ( ) | Random 4: ( ) | |||||||
| MulticlusterKDE | 6 | 0.54 | 3.88 | 3 | 0.67 | 2.25 | ||
| PdfCluster | – | – | – | – | 3 | 0.67 | 423.06 | – |
| DBSCAN | 5 | 0.49 | 0.1 | 1.7/5 | 4 | 0.67 | 0.031 | 7.8/5 |
| K-means | 3 | 0.50 | 0.365 | 2:10 | 3 | 0.67 | 0.047 | 2:10 |
| K-medoids | 6 | 0.56 | 11.718 | 2:10 | 3 | 0.67 | 0.225 | 2:10 |
| CLARA | 6 | 0.56 | 0.564 | 2:10 | 3 | 0.67 | 0.048 | 2:10 |
| Random 5: ( ) | Random 6: ( ) | |||||||
| MulticlusterKDE | 14 | 0.83 | 10.1 | 9 | 0.63 | 3.78 | ||
| PdfCluster | – | – | – | – | – | – | – | – |
| DBSCAN | 15 | 0.83 | 0.128 | 5.7/5 | 10 | 0.63 | 0.185 | 10.2/5 |
| K-means | 18 | 0.64 | 2.167 | 2:20 | 8 | 0.57 | 0.373 | 2:20 |
| K-medoids | 14 | 0.83 | 16.72 | 2:20 | 9 | 0.63 | 2.379 | 2:20 |
| CLARA | 14 | 0.83 | 1.20 | 2:20 | 9 | 0.63 | 0.429 | 2:20 |
| Random 7: ( ) | Random 8: ( ) | |||||||
| MulticlusterKDE | 4 | 0.74 | 9.44 | 6 | 0.76 | 159 | ||
| PdfCluster | – | – | – | – | – | – | – | – |
| DBSCAN | 4 | 0.74 | 0.80 | 3.5/5 | 6 | 0.76 | 1.90 | 2/3 |
| K-means | 4 | 0.74 | 0.74 | 2:10 | 6 | 0.76 | 2.95 | 2:10 |
| K-medoids | 4 | 0.74 | 11.02 | 2:10 | 6 | 0.76 | 56.17 | 2:10 |
| CLARA | 4 | 0.74 | 9.88 | 2:10 | 6 | 0.76 | 3.98 | 2:10 |
In Table 16 we show the numerical results obtained by running the algorithms on the set of problems mentioned above, which were implemented in R. To compare the algorithms we selected three performance measures, namely, nc (number of clusters), Sil (silhouette coefficient and times (runtime in seconds). Additionally, it also presents the parameters adopted (Par).
We can notice an equivalent performance of the algorithms analyzed since none of them showed to be effectively superior, except to the PdfCluster algorithm which failed to solve 6 problems.
Taking into account the small variations in algorithms performance, we observe that K-medoids and CLARA obtained the best results for silhouette coefficients, however, we need to carefully observe the analysis because, as well as K-means, they depend on information about the number of clusters a priori. Furthermore, the DBSCAN algorithm was the one that presented the smaller runtime in all tests, however, it requires two specific information of parameters, that can vary from problem to problem.
Finally, although MulticlusterKDE algorithm has presented, in some cases, a slightly higher runtime, it showed a good performance, since the silhouette coefficient was equivalent to other algorithms and besides it, not necessary to give the ideal number of clusters a priori.
For all that, we remark that our algorithm has been shown more suitable for the problems studied by considering both defined and not defined classes.
5. Conclusions
In this paper, we propose a new algorithm for clustering multivariate data, named MulticlusterKDE. This algorithm is based on the multiple optimization of Gaussian multivariate kernel density, with the objective of determining the number of clusters and their respective centroids, with posterior allocation of the observations by the criterion of the minimum Euclidean distance.
MulticlusterKDE was implemented in R software and applied to several clustering problems, being some of them with known label classes. Of the seven problems with the number of clusters defined, according to the error measures, the MulticlusterKDE algorithm was better in six problems, and the second best performance was obtained by PdfCluster algorithm, despite not getting results in two problems. MulticlusterKDE had four of the worst runtime because it uses an optimization function in its process. The surprise was the not good performance of DBSCAN. The other methods had an intermediate performance with better runtimes.
In the problems whose number of clusters is unknown a priori, according to silhouette coefficient, no algorithm stood out in relation to the others. The number of clusters varied considerably, but it is worth mentioning that MulticlusterKDE, without knowing a priori, found exactly the same value as the CLARA and K-medoids algorithms for nine problems.
Another positive aspect of MulticlusterKDE algorithm is that it does not require, a priori, the number of clusters as an input parameter, only as an optional argument. We also show in this paper that the algorithm is well defined and converges independently of the data set. As a negative aspect of the algorithm, we highlight its dependence on the KDE function, which in turn is strictly dependent on the bandwidth matrix. But this occurs in most papers in the literature.
An interesting point about the runtime of MulticlusterKDE is its subdivision between the 2 or 3 steps. The most of its runtime is concentrated in the first step, that is, in the multiple optimizations of Gaussian multivariate kernel density, raising the hypothesis that the MulticlusterKDE has its speed determined by the speed of the optimizer.
In this way, as a proposal to future work, we will focus our efforts on minimizing the influences of the α parameter used as smoothing coefficient in the kernel function. We will also look for alternatives to designate the observations to the centroids. We hope to have some results in this regard in a short period of time.
Acknowledgments
This work was partially supported by CAPES, CNPq, and Fundação Araucária, Brazil.
Funding Statement
This work was partially supported by 10.13039/501100002322(CAPES), 10.13039/501100003593(CNPq), and 10.13039/501100004612, Brazil.
Disclosure statement
No potential conflict of interest was reported by the authors.
References
- 1.Ahuja M. and Bal J., Exploring cluster analysis, Int. J. Comput. Inf. Technol 3 (2014), pp. 594–597. [Google Scholar]
- 2.Asuncion A. and Newman D., Uci machine learning repository (2007).
- 3.Azzalini A. and Menardi G., Clustering via nonparametric density estimation: The r package pdfcluster, arXiv preprint arXiv:1301.6559 (2013).
- 4.Azzalini A. and Torelli N., Clustering via nonparametric density estimation, Stat. Comput. 17 (2007), pp. 71–80. doi: 10.1007/s11222-006-9010-y [DOI] [Google Scholar]
- 5.Chacon J.E. and Duong T., Multivariate Kernel Smoothing and Its Applications, Chapman and Hall/CRC, Boca Raton, FL, 2018. [Google Scholar]
- 6.Charytanowicz M., Niewczas J., Kulczycki P., Kowalski P.A., Łukasik S., and Żak S., Complete gradient clustering algorithm for features analysis of x-ray images, in Information Technologies in Biomedicine, Vol. 69, Springer, 2010, pp. 15–24. doi: 10.1007/978-3-642-13105-9_2 [DOI] [Google Scholar]
- 7.Chen J., Li K., Rong H., Bilal K., Yang N., and Li K., A disease diagnosis and treatment recommendation system based on big data mining and cloud computing, Inf. Sci. (Ny) 435 (2018), pp. 124–149. doi: 10.1016/j.ins.2018.01.001 [DOI] [Google Scholar]
- 8.Cheng Y., Mean shift, mode seeking, and clustering, IEEE. Trans. Pattern. Anal. Mach. Intell. 17 (1995), pp. 790–799. doi: 10.1109/34.400568 [DOI] [Google Scholar]
- 9.Cichocki A., Zdunek R., Phan A.H., and Amari S.i., Nonnegative Matrix and Tensor Factorizations: Applications to ExploratoryMulti-way Data Analysis and Blind Source Separation, John Wiley & Sons, Chichester, WSX, 2009. [Google Scholar]
- 10.Defays D., An efficient algorithm for a complete-link method, Comput. J. 20 (1977), pp. 364–366. doi: 10.1093/comjnl/20.4.364 [DOI] [Google Scholar]
- 11.Duan M., Li K., Liao X., Li K., and Tian Q., Features-enhanced multi-attribute estimation with convolutional tensor correlation fusion network, ACM Trans. Multimed. Comput. Commun. Appl. 15 (2019), pp. 1–23. [Google Scholar]
- 12.Duan M., Li K., and Tian Q., A novel multi-task tensor correlation neural network for facial attribute prediction, arXiv preprint arXiv:1804.02810 (2018).
- 13.Ester M., Kriegel H.P., Sander J., Xu X. et al., A density-based algorithm for discovering clusters in large spatial databases with noise, in Kdd 96 (1996), pp. 226–231. [Google Scholar]
- 14.Forina M., Armanino C., Lanteri S., and Tiscornia E., Classification of olive oils from their fatty acid composition, in Food Research and Data Analysis: proceedings from the IUFoST Symposium, September 20–23, 1982, Oslo, Norway, H. Martens and H. Russwurm Jr., eds., Applied Science Publishers, London, 1983.
- 15.Fraley C.and Raftery A.E., Murphy T.B., and Scrucca L., mclust Version 4 for R: Normal Mixture Modeling for Model-Based Clustering, Classification, and Density Estimation, in Technical Report No. 597, Department of Statistics, University of Washington. 2012.
- 16.Fraley C. and Rafter A.E., Bayesian regularization for normal mixture estimation and model-based clustering, J. Classif. 24 (2007), pp. 155–181. doi: 10.1007/s00357-007-0004-5 [DOI] [Google Scholar]
- 17.Fraley C. and Raftery A.E., Model-based clustering, discriminant analysis and density estimation, J. Am. Stat. Assoc. 97 (2002), pp. 611–631. doi: 10.1198/016214502760047131 [DOI] [Google Scholar]
- 18.Gan J. and Tao Y., Dynamic density based clustering, in Proceedings of the 2017 ACM International Conference on Management of Data, New York, NY, USA, Association for Computing Machinery, 2017, pp. 1493–1507.
- 19.Gramacki A., Nonparametric Kernel Density Estimation and Its Computational Aspects, Springer, Cham, CHE, 2018. [Google Scholar]
- 20.Gupta T. and Panda S.P., A comparison of k-means clustering algorithm and clara clustering algorithm on iris dataset, Int. J. Eng. Technol. 7 (2018), pp. 4766–4768. [Google Scholar]
- 21.Han J., Kamber M., and Pei J., Data Mining Concepts and Techniques Third Edition, Morgan Kaufmann, Burlington, MA, 2011. [Google Scholar]
- 22.Huang H., Ding C., Luo D., and Li T., Simultaneous tensor subspace selection and clustering: the equivalence of high order svd and k-means clustering, in Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data mining, 2008, pp. 327–335.
- 23.Kassambara A., Practical Guide to Cluster Analysis in R: Unsupervised Machine Learning, Vol. 1, STHDA, 2017. Available at http://www.sthda.com/english/download/3-ebooks/. [Google Scholar]
- 24.Kaufman P.J. and Rousseeuw L., Finding Groups in Data: An Introduction to Cluster Analysis, Vol. 344, Wiley-Interscience, Hoboken, NJ, 2009. [Google Scholar]
- 25.Kulczycki P. and Charytanowicz M., A complete gradient clustering algorithm formed with kernel estimators, Int. J. Appl. Math. Comput. Sci. 20 (2010), pp. 123–134. doi: 10.2478/v10006-010-0009-3 [DOI] [Google Scholar]
- 26.Liao L., Li K., Li K., Tian Q., and Yang C., Automatic density clustering with multiple kernels for high-dimension bioinformatics data, in 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), IEEE, 2017, pp. 2105–2112.
- 27.Luo Y., Tao D., Ramamohanarao K., Xu C., and Wen Y., Tensor canonical correlation analysis for multi-view dimension reduction, Transactions on Knowledge and Data Engineering IEEE. Trans. Knowl. Data. Eng. 27 (2015), pp. 3111–3124. doi: 10.1109/TKDE.2015.2445757 [DOI] [Google Scholar]
- 28.MacQueen J. et al., Some methods for classification and analysis of multivariate observations, in Proceedings of the fifth Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1. Oakland, CA, USA, 1967, pp. 281–297.
- 29.Maitra R. and Melnyko V., Simulating data to study performance of nite mixture modeling and clustering algorithms, J. Comput. Graph. Stat. 19 (2010), pp. 354–376. doi: 10.1198/jcgs.2009.08054 [DOI] [Google Scholar]
- 30.Matioli L., Santos S., Kleina M., and Leite E., A new algorithm for clustering based on kernel density estimation, J. Appl. Stat. 45 (2018), pp. 347–366. doi: 10.1080/02664763.2016.1277191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McLachlan G.J. and Krishnan T., The EM Algorithm and Extensions, Vol. 382, Wiley Series in Probability and Mathematical Statistics – John Wiley & Sons, New York, 2007. [Google Scholar]
- 32.Menardi G. and Azzalini A., An advancement in clustering via nonparametric density estimation, Stat. Comput. 24 (2014), pp. 753–767. doi: 10.1007/s11222-013-9400-x [DOI] [Google Scholar]
- 33.Nocedal J. and Wright S., Numerical Optimization. Springer, New York, 1999. [Google Scholar]
- 34.R Core Team , R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2018. Available at https://www.R-project.org/.
- 35.Race S.L., Iterative Consensus Clustering, North Carolina State University, Raleigh, NC, 2014. [Google Scholar]
- 36.Rodrìguez A. and Laio A., Clustering by fast search and find of density peaks, Science 344 (2014), pp. 1492–1496. doi: 10.1126/science.1242072 [DOI] [PubMed] [Google Scholar]
- 37.Rousseeuw P.J., Silhouettes: A graphical aid to the interpretation and validation of cluster analysis, J. Comput. Appl. Math. 20 (1987), pp. 53–65. doi: 10.1016/0377-0427(87)90125-7 [DOI] [Google Scholar]
- 38.Scott D.W., Multivariate Density Estimation: Theory, Practice, and Visualization, John Wiley & Sons, Hoboken, NJ, 2015. [Google Scholar]
- 39.Scrucca L., Fop M., Murphy T.B., and Raftery A.E., mclust 5: Clustering, classification and density estimation using gaussian finite mixture models, R. J. 8 (2016), pp. 205–233. doi: 10.32614/RJ-2016-021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shah G.H., Bhensdadia C., and Ganatra A.P., An empirical evaluation of density-based clustering techniques, Int. J. Soft Comput. Eng. 22312307 (2012), pp. 216–223. [Google Scholar]
- 41.Sibson R., Slink: An optimally efficient algorithm for the single-link cluster method, Comput. J. 16 (1973), pp. 30–34. doi: 10.1093/comjnl/16.1.30 [DOI] [Google Scholar]
- 42.Silverman B.W., Density Estimation for Statistics and Data Analysis, Chapman and Hall, London, 1986. [Google Scholar]
- 43.Sun W.W. and Li L., Dynamic tensor clustering, J. Am. Stat. Assoc. 114 (2019), pp. 1–28. doi: 10.1080/01621459.2019.1660170 [DOI] [Google Scholar]
- 44.Wu J., Lin Z., and Zha H., Essential tensor learning for multi-view spectral clustering, IEEE. Trans. Image. Process. 28 (2019), pp. 5910–5922. doi: 10.1109/TIP.2019.2916740 [DOI] [PubMed] [Google Scholar]
- 45.Xie J., Gao H., Xie W., Lui X., and Grant P.W., Robust clustering by detecting density peaks and assigning points based on fuzzy weighted k-nearest neighbors, Inf. Sci. (Ny) 7 (2016), pp. 10–35. [Google Scholar]