A new flexible generalized family for constructing many families of distributions

Abstract

We propose a new flexible generalized family (NFGF) for constructing many families of distributions. The importance of the NFGF is that any baseline distribution can be chosen and it does not involve any additional parameters. Some useful statistical properties of the NFGF are determined such as a linear representation for the family density, analytical shapes of the density and hazard rate, random variable generation, moments and generating function. Further, the structural properties of a special model named the new flexible Kumaraswamy (NFKw) distribution, are investigated, and the model parameters are estimated by maximum-likelihood method. A simulation study is carried out to assess the performance of the estimates. The usefulness of the NFKw model is proved empirically by means of three real-life data sets. In fact, the two-parameter NFKw model performs better than three-parameter transmuted-Kumaraswamy, three-parameter exponentiated-Kumaraswamy and the well-known two-parameter Kumaraswamy models.

1. Introduction

Both data and model are equally important in applied research. One class of researchers prefer to realize a phenomenon first, and the other is interested in testing models by fitting to real data. We cannot enter into this endless debate but prefer to follow the last option in order to check the suitability of the proposed family, derived sub-families and special models from the generator. This is actually one of the main objectives of the modern distribution theory, where new families and models are proposed and are then adopted or tested to tackle problems encountered in different fields, such as reliability and survival studies, engineering, actuaries, sports sciences, agriculture, etc. This revolution makes the data analyst to cope with data sets available from different phenomenons. In such way: (i) the well-established parent models are extended by adding shape(s) parameters; (ii) the functional forms of the parent models are modified; (iii) inverted and weighted forms are adopted; (iv) generalized (G) classes have been proposed through transformations, mixtures, composition, copulas, convolution and compounding methods; (v)  the special models of generalized classes are investigated, among other methods. All such proposals and their increasing interests led to new and alternative ways for problem solving so that one can reach on a lucid and conclusive end by which the research activity has been kept warm and live. For detailed study and discussion, the reader is referred to [9,13,15].

Alzaatreh et al. [2] introduced a general method for constructing G-families by using the transformed-transformer (T–X) approach. Let $r(t)$ be the probability density function (pdf) and $R(t)$ be the cumulative distribution function (cdf) of a random variable (rv) $T\in [a,b]$ for $-\mathrm{\infty }<a<b<\mathrm{\infty }$ and let $W[G(x)]$ be a function of the cdf $G(x)$ or survival function (sf) $\overline{G}(x)=1-G(x)$ of any baseline rv ( $W(\cdot )$ is known as generator) such that $W[G(x)]$ satisfies three conditions:

1. $W[G(x)]\in [a,b]$,

2. $W[G(x)]$ is differentiable and monotonically non-decreasing, and

3. $\underset{x\to -\mathrm{\infty }}{lim}W[G(x)]=a$ and $\underset{x\to \mathrm{\infty }}{lim}W[G(x)]=b$.

The cdf of the T–X family is

$$F_{TX}(x)={\int }_a^{W[G(x)]}r(t)\mathrm{d}t=R(W[G(x)]),$$ (1)

where $W[G(x)]$ satisfies the conditions (i)–(iii).

The pdf corresponding to Equation (1) is

$$f_{TX}(x)=r(W[G(x)])\frac{\mathrm{d}}{\mathrm{d}x}W[G(x)].$$ (2)

In Table 1, we give an update on pioneer generators $W[G(x)]$ which are natural models of the T–X family. Here T could be $I=(0,1)$, $R^{+}=(0,\mathrm{\infty })$, $R=(-\mathrm{\infty },\mathrm{\infty })$. To the best of our knowledge, we are unable to find any other generator that can be included in Table 1.

Table 1.

Pioneer generators as functions of $G(x)$ (W[G(x)]) from the T–X family.

Range of T	$W[G(x)]$	Models of the T–X family
$\mathbb{I}$	$G(x)$	Beta-G [4]
${\mathbb{R}}^{+}$	$-\log \overline{G}(x)$	ZBgamma-G [17]
${\mathbb{R}}^{+}$	$G(x)/\overline{G}(x)$	Odd log-logistic-G[5]
${\mathbb{R}}^{+}$	$[-\log \overline{G}(x)]/\overline{G}(x)$	Weibull-G[1]
$\mathbb{R}$	$\log [G(x)/\overline{G}(x)]$	Log odd logistic-G[16]
$\mathbb{R}$	$\log [-\log \overline{G}(x)]$	Logistic-X[14]

There exist some G-classes such as Marshall-Olkin-G (MO-G) [11], exponentiated-G (exp-G) which includes the Lehmann alternative of type 1 (LA1) and Lehmann alternative of type 2 (LA2) [7], transmuted-G (Tr-G) [12], cubic rank transmuted-G (CRTr-G) [6] and exponentiated-generalized-G (EG-G) [3]. These six G-classes (MO-G, LA1, LA2, Tr-G, CRTr-G, EG-G) have not been developed from any existing parent model.

The main motivations for the new flexible generalized family (for short, NFGF) of distributions are:

• The NFGF is not developed from any well-known parent model similar to the MO-G, LA1, LA2, Tr-G, CRTr and EG-G classes;

• The NFGF does not include any extra parameter;

• Any baseline model can be chosen for the NFGF;

• The special models generated from the NFGF are free from non-identifiability issue. You may choose either exponentiated or inverted models;

• The new special models based on the NFGF have the ability to compete with existing parent or some other competitive models;

• The new special models based on the NFGF can produce flexible shapes of the density and hazard rate (in some cases) in comparison to existing parent models;

• The new special models of the NFGF can provide consistently better fits than other corresponding models.

We unfold the paper as follows. In Section 2, we propose a new generator called the NFGF. In Section 3, we obtain some of its mathematical properties such as a linear representation for the family density, analytical shapes of the density and hazard rate, random variable generation, moments and generating function. In Section 4, we define a new flexible Kumaraswamy (NFKw) distribution and investigate some structural properties. Its model parameters are estimated by the maximum-likelihood method. In Section 5, a simulation study is carried out to check the precision of the estimates of the NFKw distribution. In Section 6, the potentiality of this model is illustrated by means of three real-life data sets. We show that it performs better than some well-known models. The last section offers some concluding remarks.

2. The proposed flexible G-family

Let T be a baseline rv having cdf $G(x;\xi )$, sf $\overline{G}(x;\xi )$ and pdf $g(x;\xi )$, where ξ is the baseline parameter vector. We define the cdf and pdf of the NFGF by

$$F(x)=F(x;\xi )=1-\overline{G}(x;\xi {)}^{G(x;\xi )}$$ (3)

and

$$f(x)=f(x;\xi )=g(x;\xi )\overline{G}(x;\xi {)}^{G(x;\xi )}[\frac{G(x;\xi )}{\overline{G}(x;\xi )}-\log \overline{G}(x;\xi )],$$ (4)

respectively.

Henceforth, let X be a rv having the density (4). The sf $S(x)$ and hazard rate function (hrf) $h(x)$ of X are, respectively,

$$S(x)=S(x;\xi )=\overline{G}(x;\xi {)}^{G(x;\xi )}$$

and

$$\tau (x)=\tau (x;\xi )=g(x;\xi )[\frac{G(x;\xi )}{\overline{G}(x;\xi )}-\log \overline{G}(x;\xi )].$$ (5)

We consider below some special distributions for different supports of rvs $\{(0,1),(0,\mathrm{\infty }),(-\mathrm{\infty },\mathrm{\infty }),(0,\theta ),(\mu ,0)\}$, namely for Kumaraswamy (Kw), beta, Weibull (W), Burr XII (Br), Gumbel (Gu), logistic (Lo), power function (or generalized uniform) (PF) and Pareto (Pa) models:

1. If $T\sim \mathrm{Kw}(a,b)$ has the cdf $G(x)=1-(1-x^a{)}^b,x\in \mathbb{I}$ and pdf $g(x)=ab{x}^{a-1}(1-x^a{)}^{b-1}$, then the cdf and pdf of the NFKw model are, respectively, given by

   $$F_{\mathrm{NFKw}}(x)=1-{[(1-x^a{)}^b]}^{1-(1-x^a{)}^b},x\in \mathbb{I},a,b>0,$$ (6)

   and

   $$\begin{array}{rl}{f}_{\mathrm{NFKw}}(x)& =ab{x}^{a-1}{(1-x^a)}^{b-1}{[(1-x^a{)}^b]}^{1-(1-x^a{)}^b}\\ & \times \{[(1-x^a{)}^{-b}-1]-b\log (1-x^a)\}.\end{array}$$ (7)
2. If $T\sim \mathrm{Beta}(a,b)$ has the cdf $G(x)=I_x(a,b),x\in \mathbb{I}$ and pdf $g(x)=[B(a,b){]}^{-1}{x}^{a-1}(1-x{)}^{b-1}$, then the cdf and pdf of the new flexible beta (NFB) model are, respectively, given by

   $$F_{\mathrm{NFB}}(x)=1-[1-I_x(a,b){]}^{I_x(a,b)},x\in \mathbb{I},a,b>0,$$

   and

   $$\begin{array}{rl}{f}_{\mathrm{NFB}}(x)& =[B(a,b){]}^{-1}{x}^{a-1}{(1-x)}^{b-1}[1-I_x(a,b){]}^{I_x(a,b)}\\ & \times [\frac{I_x(a,b)}{1-I_x(a,b)}-\log \{1-I_x(a,b)\}],\end{array}$$

   where $B(a,b)={\int }_0^1{t}^{a-1}(1-t{)}^{b-1}\mathrm{d}t$, $B_x(a,b)={\int }_0^x{t}^{a-1}(1-t{)}^{b-1}\mathrm{d}t$ and $I_t(a,b)=\frac{B_x(a,b)}{B(a,b)}=[B(a,b){]}^{-1}{\int }_0^x{t}^{a-1}(1-t{)}^{b-1}\mathrm{d}t$ are the beta function, incomplete beta function and incomplete beta function ratio, respectively.
3. If $T\sim \mathrm{W}(\alpha ,\beta )$ has the cdf $G(x)=1-\exp (-\alpha x^{\beta }),x\in {\mathbb{R}}^{+}$ and pdf $g(x)=\alpha \beta x^{\beta -1}\exp (-\alpha x^{\beta })$, then the cdf and pdf of the new flexible Weibull (NFW) model are, respectively, given by

   $$\begin{array}{rl}{F}_{NFW}(x)& =1-{[\exp (-\alpha x^{\beta })]}^{1-\exp (-\alpha x^{\beta })},x\in {\mathbb{R}}^{+},\alpha ,\beta >0,\end{array}$$

   and

   $$\begin{array}{rl}{f}_{NFW}(x)& =\alpha \beta x^{\beta -1}\exp (-\alpha x^{\beta }){[\exp (-\alpha x^{\beta })]}^{1-\exp (-\alpha x^{\beta })}\\ & \times \{[\exp \left(\alpha x^{\beta }\right)-1]+\alpha x^{\beta }\}.\end{array}$$
4. If $T\sim \mathrm{Br}(c,k)$ has the cdf $G(x)=1-(1+x^c{)}^{-k},x\in {\mathbb{R}}^{+}$ and pdf $g(x)=ck{x}^{c-1}(1+x^c{)}^{-(k+1)}$, then the cdf and pdf of the new flexible Burr XII (NFBr) model are, respectively, given by

   $$F_{\mathrm{NFBr}}(x)=1-{\left[{(1+x^c)}^{-k}\right]}^{1-(1+x^c{)}^{-k}},x\in {\mathbb{R}}^{+},c,k>0,$$

   and

   $$\begin{array}{rl}{f}_{\mathrm{NFBr}}(x)& =ck{x}^{c-1}(1+x^c{)}^{-(k+1)}{\left[{(1+x^c)}^{-k}\right]}^{1-(1+x^c{)}^{-k}}\\ & \times \{[{(1+x^c)}^k-1]+k\log (1+x^c)\}.\end{array}$$
5. If $T\sim \mathrm{Gu}(\mu ,\sigma )$ has the cdf $G(x)=\exp [-\exp \{-(x-\mu )/\sigma \}],x\in \mathbb{R}$ and pdf $g(x)={\sigma }^{-1}\exp \{-(x-\mu )/\sigma \}\exp [-\exp \{-(x-\mu )/\sigma \}]$, then the cdf and pdf of the new flexible Gumbel (NFGu) model are, respectively, given by

   $$F_{\mathrm{NFGu}}(x)=1-{[1-\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })]}^{\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })},x\in \mathbb{R},\mu ,\sigma >0,$$

   and

   $$\begin{array}{rl}{f}_{\mathrm{NFGu}}(x)& =\frac{1}{\sigma }{\mathrm{e}}^{-(x-\mu )/\sigma }\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })\\ & \times {[1-\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })]}^{\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })}\\ & \times \{\frac{\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })}{1-\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })}-\log [1-\exp (-{\mathrm{e}}^{-(x-\mu )/\sigma })]\}.\end{array}$$
6. If $T\sim \mathrm{Lo}(\mu ,\sigma )$ has the cdf $G(x)=[1+\exp \{-(x-\mu )/\sigma \}{]}^{-1},x\in {\mathbb{R}}^{+}$ and pdf $g(x)={\sigma }^{-1}\exp \{-(x-\mu )/\sigma \}[1+\exp \{-(x-\mu )/\sigma \}{]}^{-2}$, then the cdf and pdf of the new flexible logistic (NFLo) model are, respectively, given by

   $$\begin{array}{rl}{F}_{\mathrm{NFLo}}(x)& =1-{\{1-{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}\}}^{{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}},\\ & x\in {\mathbb{R}}^{+},\mu ,\sigma >0,\end{array}$$

   and

   $$\begin{array}{rl}{f}_{\mathrm{NFLo}}(x)& =\frac{\exp \{-(x-\mu )/\sigma \}}{\sigma {[1+\exp \{-(x-\mu )/\sigma \}]}^2}\\ & \times {\{1-{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}\}}^{{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}}\\ & \times \{\frac{{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}}{1-{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}}\\ & \phantom{\frac{{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}}{1-{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}}}-\log [1-{[1+\exp \{-(x-\mu )/\sigma \}]}^{-1}]\}.\end{array}$$
7. If $T\sim \mathrm{PF}(\beta ,\theta )$ has the cdf $G(x)=(\frac{x}{\theta }{)}^{\beta },0<x<\theta$ and pdf $g(x)=\frac{\beta }{{\theta }^{\beta }}{x}^{\beta -1}$, then the cdf and pdf of the new flexible power function (NFPF) model are, respectively, given by

   $$F_{\mathrm{NFPF}}(x)=1-{[1-{\left(\frac{x}{\theta }\right)}^{\beta }]}^{{\left(\frac{x}{\theta }\right)}^{\beta }},0<x<\theta ,\beta ,\theta >0,$$

   and

   $$f_{\mathrm{NFPF}}(x)=\frac{\beta }{{\theta }^{\beta }}{x}^{\beta -1}{[1-{\left(\frac{x}{\theta }\right)}^{\beta }]}^{(\frac{x}{\theta }{)}^{\beta }}\{\frac{{\left(\frac{x}{\theta }\right)}^{\beta }}{1-{\left(\frac{x}{\theta }\right)}^{\beta }}-\log [1-{\left(\frac{x}{\theta }\right)}^{\beta }]\}.$$
8. If $T\sim \mathrm{Pa}(\beta ,\alpha )$ has the cdf $G(x)=1-(\frac{\beta }{x}{)}^{\alpha },x\ge \beta$ and pdf $g(x)=\frac{\alpha {\beta }^{\alpha }}{x^{\alpha +1}}$, then the cdf and pdf of the new flexible Pareto (NFPa) model are, respectively, given by

   $$F_{\mathrm{NFPa}}(x)=1-{\left[{\left(\frac{\beta }{x}\right)}^{\alpha }\right]}^{1-{\left(\frac{\beta }{x}\right)}^{\alpha }},x\ge \beta ,\beta ,\alpha >0,$$

   and

   $$f_{\mathrm{NFPa}}(x)=\frac{\alpha {\beta }^{\alpha }}{x^{\alpha +1}}{\left[{\left(\frac{\beta }{x}\right)}^{\alpha }\right]}^{1-{\left(\frac{\beta }{x}\right)}^{\alpha }}\{[{\left(\frac{\beta }{x}\right)}^{-\alpha }-1]-\alpha \log \left(\frac{\beta }{x}\right)\}.$$

   The density and hazard rate behaviors of the special models NFKw, NFBeta, NFW, NFBr, NFGu, NFLo, NFPF and NFPa are plotted in Figures 1–8.

Figure 2.

Plots for the NFBeta model for some parameter values: (a) density and (b) hazard rate.

Figure 3.

Plots for the NFW model for some parameter values: (a) density and (b) hazard rate.

Figure 4.

Plots for the NFBr model for some parameter values: (a) density and (b) hazard rate.

Figure 5.

Plots for the NFGu model for some parameter values: (a) density and (b) hazard rate.

Figure 6.

Plots for the NFLo model for some parameter values: (a) density and (b) hazard rate.

Figure 7.

Plots for the NFPF model for some parameter values: (a) density and (b) hazard rate.

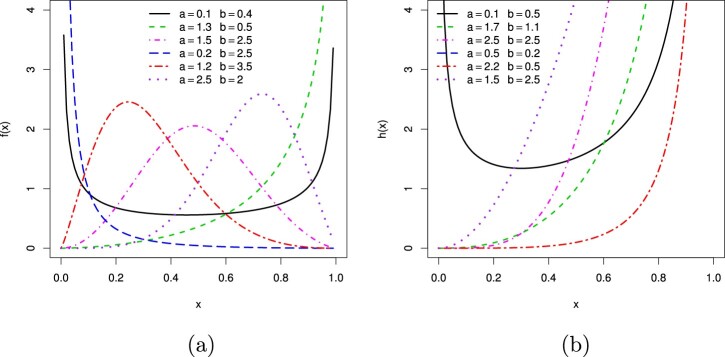
Figure 1.

Plots for the NFKw model for some parameter values: (a) density and (b) hazard rate.

Figure 8.

Plots for the NFPa model for some parameter values: (a) density and (b) hazard rate.

Our proposed generator defined by (3) can extend several well-known G-classes of distributions which can be accessed through SupplementaryDataANFGF.pdf. Secondly, the information regarding the new flexible G-families derived from these G-classes can be accessed through SupplementaryDataBNFGF.pdf.

3. Properties of the NFGF

3.1. Linear representation

For an arbitrary baseline cdf $G(x)$, the exponentiated-G (exp-G) distribution with parameter a>0, has cdf and pdf in the forms $H_a(x)=G(x{)}^a$ and $h_a(x)=ag(x)G(x{)}^{a-1}$, respectively. Re-calling (3) and then using Mathematica, the power series holds

$$F(x)=\sum _{\ell =2}^{\mathrm{\infty }}{\eta }_{\ell }G(x{)}^{\ell },$$ (8)

where ${\eta }_2=1$, ${\eta }_3=1/2$, ${\eta }_4=-1/6$ and ${\eta }_5=-1/4,\dots$, which can be expressed as

$$F(x)=\sum _{\ell =2}^{\mathrm{\infty }}{\eta }_{\ell }{H}_{\ell }(x;\xi ),$$ (9)

where $H_{\ell }(x;\xi )=G(x;\xi {)}^{\ell }$ (for $\ell \ge 2$).

By differentiating (9), the density of X takes the form

$$f(x)=\sum _{\ell =1}^{\mathrm{\infty }}{\eta }_{\ell +1}{h}_{\ell +1}(x;\xi ),$$ (10)

where $h_{\ell +1}$ is the exp-G density with power parameter $\ell +1$. Equation (10) reveals that the NKwG density function is a linear combination of exp-G densities. Thus, some mathematical properties of the NFGF can be determined directly from those of the exp-G distributions, which are known for several baseline distributions.

3.2. Analytical shapes

The shapes of the density and hrf of X can be described analytically. The critical points of the density of X are the roots of the equation:

$$\frac{g^{\prime }(x)}{g(x)}+\frac{g(x)[-{\log }^2(1-G(x))+G(x)(\log (1-G(x))+1{)}^2+2]}{G(x)-(1-G(x))\log (1-G(x))}=0.$$

The critical points of the hrf of X are obtained from the equation:

$$\frac{g^{\prime }(x)}{g(x)}+\frac{g(x)(2-G(x))}{(1-G(x))(G(x)-(1-G(x))\log (1-G(x)))}=0.$$

3.3. Quantile function

The simplest method for generating rvs is based on the inverse cdf. For an arbitrary cdf, the quantile function (qf) is defined as $Q(u)=F^{-1}(u)=\min \{x;F(x)\ge u\}$. The qf of the NFGF can be determined by inverting (3) and solving two nonlinear equations numerically. We can use the following procedure:

1. Set $z=z(u)=1-u$;

2. Find $w=w(u)$ numerically in $w\log (1-w)=\log (z)$ using any Newton-Raphson algorithm;

3. Solving numerically for x in $G(x;\xi )=w$ gives the qf $x=Q(u;\xi )$ of X.

3.4. Moments and generating function

The nth ordinary moment of X, say $\mathbb{E}(X^n)$, can be expressed from Equation (10) as

$$\mathbb{E}(X^n)=\sum _{\ell =1}^{\mathrm{\infty }}{\eta }_{\ell +1}\mathbb{E}(Y_{\ell +1}^n)=\sum _{\ell =1}^{\mathrm{\infty }}(\ell +1){\eta }_{\ell +1}{\tau }_{n,\ell },$$ (11)

where ${\tau }_{n,\ell }={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{x}^{n}G(x;\xi {)}^{\ell }g(x;\xi )\mathrm{d}x={\int }_0^1{Q}_G(u;\xi {)}^n{u}^{\ell }\mathrm{d}u$, and $Q_G(u;\xi )$ is the qf of the baseline G.

The first four moments can be used to describe some characteristics of a distribution. Clearly, the central moments and cumulants of X can be determined from Equation (11) using well-known results.

The nth lower incomplete moment of X, say $m_n(y)={\int }_{-\mathrm{\infty }}^y{x}^{n}f(x)\mathrm{d}x$, is

$$m_n(y)=\sum _{\ell =1}^{\mathrm{\infty }}{\eta }_{\ell +1}{\int }_{-\mathrm{\infty }}^y{x}^n{h}_{\ell +1}(x)\mathrm{d}x=\sum _{\ell =1}^{\mathrm{\infty }}(\ell +1){\eta }_{\ell +1}{\int }_0^{G(y;\xi )}{Q}_G(u;\xi {)}^n{u}^{\ell }\mathrm{d}u.$$ (12)

The last two integrals can be evaluated numerically for most G distributions.

The total deviations from the mean and median are ${\delta }_1=2{\mu }_1^{\mathrm{\prime }}F({\mu }_1^{\mathrm{\prime }})-2m_1({\mu }_1^{\mathrm{\prime }})$ and ${\delta }_2={\mu }_1^{\mathrm{\prime }}-2m_1(M)$, where $F({\mu }_1^{\mathrm{\prime }})$ comes from Equation (3).

The moment generating function (mgf) $M(t)=\mathbb{E}({\mathrm{e}}^{\mathrm{t}\mathrm{X}})$ of X follows from Equation (10) as

$$M(t)=\sum _{\ell =1}^{\mathrm{\infty }}{\eta }_{\ell +1}{M}_{\ell +1}(t)=\sum _{\ell =0}^{\mathrm{\infty }}(\ell +1){\eta }_{\ell +1}{\rho }_{\ell }(t),$$ (13)

where $M_{\ell +1}(t)$ is the mgf of $Y_{\ell +1}$ and ${\rho }_{\ell }(t)={\int }_0^1\exp [t{Q}_G(u;\xi )]u^{\ell }\mathrm{d}u$. Hence, $M(t)$ can be obtained from the exp-G generating function.

3.5. Estimation

Here, we consider the estimation of the unknown parameters of the NFGF family by the maximum-likelihood method. The maximum-likelihood estimates (MLEs) enjoy desirable properties that can be used when constructing confidence intervals and deliver simple approximations that work well in finite samples. The normal approximation for the MLEs in distribution theory can easily be handled either analytically or numerically.

The log-likelihood function $\ell (\theta )$ for the vector of parameters $\theta =(a,b,\xi {)}^{\mathrm{\top }}$ from n observations $x_1,\dots ,x_n$ has the form

$$\begin{array}{rl}\ell =\ell (\theta )& =\sum _{i=1}^n\log g(x_i;\xi )+\sum _{i=1}^{n}G(x_i;\xi )\log [1-G(x_i;\xi )]\\ & +\sum _{i=1}^n\log (\frac{G(x_i;\xi )}{1-G(x_i;\xi )}-\log [1-G(x_i;\xi )]).\end{array}$$ (14)

The MLE $\hat{\theta }$ of θ can be evaluated by maximizing $\ell (\theta )$. There are several routines for numerical maximization of $\ell (\theta )$ in the R program (optim function), SAS (PROC NLMIXED), Ox (sub-routine MaxBFGS), among others. All distributions in the NFGF can also be fitted to data sets using the AdequacyModel package in R (see https://www.r-project.org/). An important advantage of this package is that it is not necessary to define the log-likelihood function and that it computes the MLEs, their standard errors (SEs) and some goodness-of-fit (GoF) statistics. We only need to provide the pdf and cdf of the distribution to be fitted to a data set.

Alternatively, we can differentiate the log-likelihood and solving the resulting nonlinear likelihood equations. Then, the score components with respect to $\mathit{\xi }$ are

$$\begin{array}{rl}\frac{\mathrm{\partial }\ell }{\mathrm{\partial }\xi }& =\sum _{i=1}^n\frac{g_i^{\xi }}{g(x_i;\xi )}-\sum _{i=1}^n\{\frac{G(x_i;\xi )}{1-G(x_i;\xi )}-\log (1-G(x_i;\xi ))\}{G}_i^{\xi }\\ & -\sum _{i=1}^n\frac{G_i^{\xi }[G(x_i;\xi )-2]}{(1-G(x_i;\xi ))[-\log \{1-G(x_i;\xi )\}+G(x_i;\xi )\{1+\log (1-G(x_i;\xi ))\}]},\end{array}$$

where $g_i^{\xi }=\frac{\mathrm{\partial }g(x_i;\xi )}{\mathrm{\partial }\xi }$ and $G_i^{\xi }=\frac{\mathrm{\partial }G(x_i;\xi )}{\mathrm{\partial }\xi }$ are column vectors of the same dimension of ξ.

Setting the score components to zero and solving them simultaneously yields the MLEs of the parameters of the NFGF. The resulting equations cannot be solved analytically, but some statistical softwares can be used to solve them numerically through iterative Newton–Raphson type algorithms.

We can obtain the elements of the $p\times p$ observed information matrix $J(\theta )$ (p is the dimension of ξ) by numerical integration. Further, the approximate multivariate normal ${\mathcal{N}}_{p+2}(\mathbf{0},J(\hat{\theta }{)}^{-1})$ distribution for $\hat{\theta }$, where the observed information matrix $J(\theta )$ is evaluated at $\hat{\theta }$, can be used to construct confidence intervals for the parameters of the NFGF family.

4. The NFKw model and its properties

The sf and hrf of NFKw rv are, respectively, given by

$$S_{\mathrm{NFKw}}(x;a,b)={[(1-x^a{)}^b]}^{1-(1-x^a{)}^b}$$

and

$${\tau }_{\mathrm{NFKw}}(x;a,b)=ab{x}^{a-1}{(1-x^a)}^{b-1}\{[(1-x^a{)}^{-b}-1]-b\log (1-x^a)\}.$$

4.1. Quantile function

The qf of the NFKw distribution cannot be obtained explicitly. However, we can use Newton–Raphson algorithm to generate NFKw variates as follows:

• Step 1:

  Set n, a, b and initial value $x^0$.

• Step 2:

  Generate U∼Uniform $(0,1)$.

• Step 3:
  Update $x^0$ by using the Newton's formula

  $$x\ast =x^0-R(x^0;a,b),$$

  where $R(x^0;a,b)=\frac{F_{\mathrm{NFKw}}(x^0;a,b)}{f_{\mathrm{NFKw}}(x^0;a,b)}$, and $F_{\mathrm{NFKw}}$ and $f_{\mathrm{NFKw}}$ are obtained from Equations (6) and (7), respectively.
• Step 4:

  If $|x^0-x^{\ast }|\le ϵ$, ( $ϵ>0$, very small tolerance limit), then store $x^0=x^{\ast }$ as a variate from the NFKw(a, b) distribution.

• Step 5:

  If $|x^0-x^{\ast }|>ϵ$, then, set $x^0=x^{\ast }$ and go to step 3.

• Step 6:

  Repeat steps (2)–(5) n times to generate $x_1,\dots x_n$.

4.2. Properties

First, the linear representation for cdf of the NFKw model follows from Equation (3) as

$$F_{\mathrm{NFKw}}(x;a,b)=\sum _{\ell =2}^{\mathrm{\infty }}{\eta }_{\ell }[1-(1-x^a{)}^b{]}^{\ell }.$$ (15)

By expanding binomial series and noting that $\sum _{\ell =2}^{\mathrm{\infty }}{\eta }_{\ell }=1$, we can write

$$F_{\mathrm{NFKw}}(x;a,b)=1+\sum _{\ell =2}^{\mathrm{\infty }}{\eta }_{\ell }\sum _{k=1}^{\ell }(-1{)}^k(\genfrac{}{}{0ex}{}{\ell }{k})(1-x^a{)}^{bk}$$

and then by changing k by k + 1

$$F_{\mathrm{NFKw}}(x;a,b)=1+\sum _{\ell =2}^{\mathrm{\infty }}{\eta }_{\ell }\sum _{k=0}^{\ell }(-1{)}^{k+1}(\genfrac{}{}{0ex}{}{\ell }{k+1})(1-x^a{)}^{b(k+1)}.$$

Let ${\delta }_k=2$ for k=0,1,2 and ${\delta }_k=k$ for k ≥ 3. We can change conveniently the double sums

$$F_{\mathrm{NFKw}}(x;a,b)=1+\sum _{\ell ={\delta }_k}^{\mathrm{\infty }}{\eta }_{\ell }\sum _{k=0}^{\mathrm{\infty }}(-1{)}^{k+1}(\genfrac{}{}{0ex}{}{\ell }{k+1})(1-x^a{)}^{b(k+1)}.$$

The last expression can be written as

$$F_{\mathrm{NFKw}}(x;a,b)=1+\sum _{k=0}^{\mathrm{\infty }}(-{\omega }_k)(1-x^a{)}^{b(k+1)},$$

where ${\omega }_k=(-1{)}^k\sum _{\ell ={\delta }_k}^{\mathrm{\infty }}(\genfrac{}{}{0ex}{}{\ell }{k+1}){\eta }_{\ell }$.

By differentiating the last expression, the NFKw density can be written as

$$f_{\mathrm{NFKw}}(x;a,b)=\sum _{k=0}^{\mathrm{\infty }}{\omega }_k\pi (x;a,b(k+1)),$$ (16)

where $\pi (x;a,(k+1)b)$ denotes the Kumaraswamy density with shape parameters a and $(k+1)b$.

It is clear from Equation (16), that the NFKw density is a linear combination of Kumaraswamy densities. So, several of the NFKw properties can be obtained from the Kumaraswamy distribution.

Let $Z_k$ be a rv with density $\pi (x;a,(k+1)b)$. Then, several properties of X can follow from those of $Z_k$. First, the nth ordinary moment of X takes the form

$${\mu }_n^{\mathrm{\prime }}=\sum _{k=0}^{\mathrm{\infty }}{\omega }_{k}b(k+1)B(\frac{n}{a}+1,b(k+1)).$$ (17)

The cumulants ( ${\kappa }_n$) of X can be determined recursively from (17) as ${\kappa }_s={\mu }_s^{\mathrm{\prime }}-\sum _{k=1}^{s-1}(\genfrac{}{}{0ex}{}{s-1}{k-1}){\kappa }_k{\mu }_{s-k}^{\mathrm{\prime }}$, respectively, where ${\kappa }_1={\mu }_1^{\mathrm{\prime }}$.

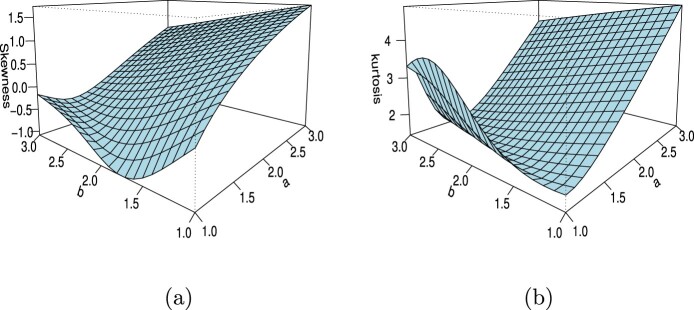
The skewness and kurtosis plots of the NFKw distribution are displayed in Figure 9. These plots reveal that the parameters a and b play a significant role in modeling the skewness and kurtosis behaviors of X.

Figure 9.

Plots for the NFKw model: (a) skewness (b) kurtosis.

The nth incomplete moment of X is $m_n(y)=E(X^n\mid X\le y)={\int }_0^y{x}^n{f}_{\mathrm{NFKw}}(x;a,b)\mathrm{d}x$, which is easily found by changing variables from the lower incomplete beta function $B_t(u,v)={\int }_0^t{t}^{u-1}(1-t{)}^{v-1}\mathrm{d}t$ when calculating the corresponding moment of $Z_k$. Then, we obtain

$$m_n(z)=\sum _{k=0}^{\mathrm{\infty }}{\omega }_{k}b(k+1)B_x(\frac{n}{a}+1,(k+1)b).$$ (18)

The total deviations from the mean ${\mu }_1^{\mathrm{\prime }}$ and median M of X have the forms ${\delta }_1=2{\mu }_1^{\mathrm{\prime }}{F}_{\mathrm{NFKw}}({\mu }_1^{\mathrm{\prime }})-2m_1({\mu }_1^{\mathrm{\prime }})$ and ${\delta }_2={\mu }_1^{\mathrm{\prime }}-2m_1(M)$, where M can be determined from $F_{NKwW}(M)=0.5$.

The first incomplete moment $m_1(y)$ is also used to construct the Bonferroni and Lorenz curves (popular measures in economics, reliability, demography, insurance and medicine). The Bonferroni and Lorenz curves of X for a given probability π are given by $B(\pi )=m_1(q)/(\pi m{u}_1^{\mathrm{\prime }})$ and $L(\pi )=\pi B(\pi )$, respectively, where $q=Q_{(}\pi )$ is the qf of X discussed in Section 4.2.

4.3. Estimation

Let $x_1,\dots ,x_n$ be a sample of size n from the NFKw distribution given in Equation (7). The log-likelihood function for the vector of parameters $\theta =(a,b{)}^{\mathrm{\top }}$ reduces to

$$\begin{array}{rl}\ell (\theta )& =n\log (ab)+(a-1)\sum _{i=1}^n\log (x_i)+(b-1)\sum _{i=1}^n\log (1-x_i^a)+\sum _{i=1}^n[1-{(1-x_i^a)}^b]\\ & \times \log \left[{(1-x_i^a)}^b\right]+\sum _{i=1}^n\log [\frac{1-{(1-x_i^a)}^b}{{(1-x_i^a)}^b}-\log \left({(1-x_i^a)}^b\right)].\end{array}$$

The components of the score vector $U(\theta )$ are

$$\begin{array}{rl}{U}_a& =\frac{n}{a}+\sum _{i=1}^n\log (x_i)-(b-1)\sum _{i=1}^n\frac{x_i^a\log (x_i)}{1-x_i^a}\\ & +\sum _{i=1}^n[b{x}_i^a\log (x_i)(1-x_i^a{)}^{b-1}\log ((1-x_i^a{)}^b)\\ & -\frac{b{x}_i^a\log (x_i)\{1-(1-x_i^a{)}^b\}}{1-x_i^a}]\\ & +\sum _{i=1}^n\frac{b{x}_i^a\log (x_i)\{1-(1-x_i^a{)}^b\}}{(1-x_i^a)[(1-x_i^a{)}^b\{1+\log \left({(1-x_i^a)}^b\right)\}-1]}.\\ U_b& =\frac{n}{b}+\sum _{i=1}^n\log (1-x_i^a)+\sum _{i=1}^n\log (1-x_i^a)\\ & \times [\{1-(1-x_i^a{)}^b\}-(1-x_i^a{)}^b\log ((1-x_i^a{)}^b)]\\ & +\sum _{i=1}^n\frac{\{1-(1-x_i^a{)}^b\}(1-x_i^a{)}^{-b}(-\log (1-x_i^a))-2\log (1-x_i^a)}{(1-x_i^a{)}^{-b}\{1-(1-x_i^a{)}^b\}-\log ((1-x_i^a{)}^b)}.\end{array}$$

Setting these equations to zero and solving them simultaneously yields the MLEs of the model parameters.

5. Simulation study

In this section, we evaluate the accuracy of the MLEs of the NFKw parameters using Monte Carlo simulations. The simulation study is repeated for N= 1,000 times each with given sample size n=50, 100, 200, 300, 400 and parameter scenarios: I: a = 0.5, and b = 1.5, II: a = 1.1, and b = 3.5 and III: $a=2.5$, and b = 1.5. The precision of the MLEs is investigated in terms of the biases and mean square errors (MSEs), namely:

$$Bias(\hat{\theta })=\sum _{i=1}^N\frac{\widehat{{\theta }_i}}{N}-\theta \mathrm{and}MSE(\hat{\theta })=\sum _{i=1}^N\frac{(\widehat{{\theta }_i}-\theta {)}^2}{N}.$$

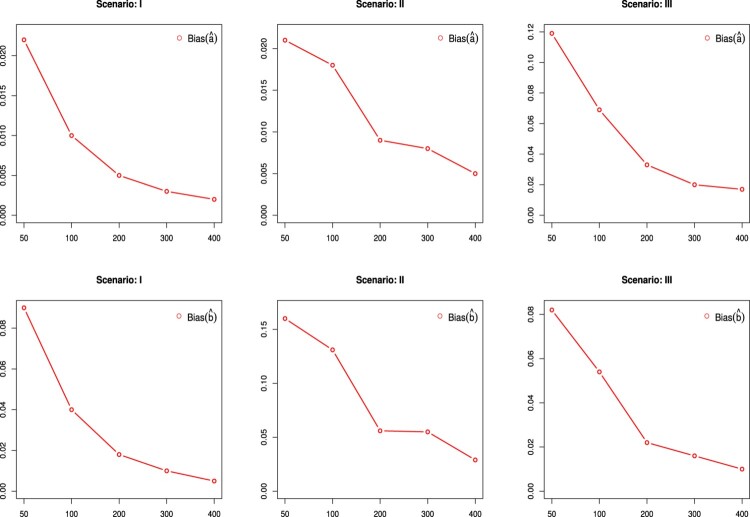
We display plots of the biases and MSEs for the estimates of NFKw parameters a and b in Figures 10 and 11. These plots reveal that the values of biases and MSEs decrease as the sample size n increases. Thus, the MLEs perform well in estimating the parameters of the NFKw distribution.

Figure 10.

Plots of the biases for the estimated values of NFKw parameters.

Figure 11.

Plots of the MSEs for the estimated values of NFKw parameters.

6. Empirical illustration of the NFKw model

We compare the proposed two-parameter NFKw model (a special model of NFGF) with three-parameter transmuted-Kumaraswamy (TrKw) [8], three-parameter exponentiated-Kumaraswamy (EKw) [10] and two-parameter Kumaraswamy (Kw) models to three real-life data sets (Flood data, Leaves data, Glass Fiber data) which can be accessed from SupplementaryDataCNFGF.pdf. The pdfs of these models are, respectively given by:

$$\begin{array}{rl}{f}_{Kw}(x;a,b)& =ab{x}^{a-1}(1-x^a{)}^{b-1},x\in \mathbb{I},a,b>0\\ f_{TrKw}(x;\lambda ,a,b)& =ab{x}^{a-1}(1-x^a{)}^{b-1}[1-\lambda +2\lambda (1-x^a{)}^b],x,\lambda \in \mathbb{I},a,b>0\end{array}$$

and

$$f_{EKw}(x;\alpha ,a,b)=\alpha ab{x}^{a-1}(1-x^a{)}^{b-1}{(1-(1-x^a{)}^b)}^{\alpha -1},x\in \mathbb{I},a,b,\alpha >0.$$

The parameters of the models are estimated by the maximum-likelihood method and the log-likelihood function is evaluated at the MLEs ( $\hat{\ell }$). The well-known goodness-of-fit (GoF) statistics such as Akaike information criterion (AIC), Bayesian Information Criterion (BIC), Hannan–Quinn Information Criterion (HQIC), Anderson-Darling ( $A^{\ast }$), Cramér–von Mises ( $W^{\ast }$) and Kolmogrov-Smirnov (K-S) are used for model comparisons. The lower values of the GoF statistics and higher p-values of K-S indicate good fit.

Tables 2, 4 and 6 give the MLEs and their standard errors for the NFKw model and other competitive models TrKw, EKw and Kw for these data sets. The values of the GoF statistics in Tables 3, 5 and 7 indicate that the NFKw model shows small values of the GoF statistics and hence the proposed model provides best fit as compared to the other models. These plots also support our claim.

Table 2.

MLEs and their SEs (in parentheses) for data set 1.

Distribution	a	b	α	λ
NFKw	2.3455	7.7175	–	–
	(0.4556)	(3.2113)	–	–
TrKw	3.7259	10.9645	–	0.6141
	(0.6490)	(6.0368)	–	(0.3752)
EKw	3.3633	45.8805	0.2570	–
	(0.6021)	(9.4457)	(0.1269)	–
Kw	3.3631	11.7886	–	–
	(0.6033)	(5.3594)	–	–

Table 4.

MLEs and their standard errors (in parentheses) for data set 2.

Distribution	a	b	α	λ
NFKw	1.8585	43.1739	–	–
	(0.1319)	(11.0563)	–	–
TrKw	2.9292	177.1790	–	0.3571
	(0.2128)	(62.1210)	–	(0.3535)
EKw	2.8099	85.9558	2.0498	–
	(0.1940)	(509.7923)	(12.1569)	–
Kw	2.8104	176.3490	–	–
	(0.1941)	(59.9656)	–	–

Table 6.

MLEs and their standard errors (in parentheses) for data set 3.

Distribution	a	b	α	λ
NFKw	1.7263	19.4685	–	–
	(0.2661)	(8.7742)	–	–
TrKw	2.7037	45.8129	–	0.4748
	(0.3944)	(27.9858)	–	(0.3956)
EKw	2.4966	105.2523	0.4157	–
	(0.3691)	(4066.8131)	(16.0628)	–
Kw	2.4998	43.9672	–	–
	(0.3700)	(23.6081)	–	–

Table 3.

The statistics AIC, BIC, HQIC, $A^{\ast }$, $W^{\ast }$, K-S and p-values for data set 1.

								K-S
Distribution	$\hat{\ell }$	AIC	BIC	HQIC	$A^{\ast }$	$W^{\ast }$	K-S	p-value
NFKw	$-14.2378$	$-24.4757$	$-22.4842$	$-24.0869$	0.6966	0.1147	0.1797	0.5380
TrKw	$-13.5209$	$-21.0419$	$-18.0547$	$-20.4588$	0.8409	0.1409	0.1930	0.4455
EKw	$-12.8662$	$-19.7324$	$-16.7452$	$-19.1493$	1.4830	0.2626	0.7960	1.972e−11
Kw	$-12.8662$	$-21.7324$	$-19.7409$	$-21.3436$	0.9722	0.1658	0.2109	0.3360

Table 5.

The statistics AIC, BIC, HQIC, $A^{\ast }$, $W^{\ast }$, K-S and p-values for data set 2.

								K-S
Distribution	$\hat{\ell }$	AIC	BIC	HQIC	$A^{\ast }$	$W^{\ast }$	K-S	p-value
NFKw	$-195.7365$	$-387.4730$	$-381.7689$	$-385.1554$	0.9281	0.1657	0.1005	0.1509
TrKw	$-195.3060$	$-384.6120$	$-376.0559$	$-381.1356$	1.0578	0.1906	0.1098	0.0913
EKw	$-194.8007$	$-383.6015$	$-375.0454$	$-380.1251$	0.9207	0.1670	0.5341	2.2e−16
Kw	$-194.8007$	$-385.6015$	$-379.8974$	$-383.2839$	1.1612	0.2078	0.1181	0.0563

Table 7.

The statistics AIC, BIC, HQIC, $A^{\ast }$, $W^{\ast }$, K-S and p-values for data set 3.

								K-S
Distribution	$\hat{\ell }$	AIC	BIC	HQIC	$A^{\ast }$	$W^{\ast }$	K-S	p-value
NFKw	$-32.0281$	$-60.0563$	$-57.4646$	$-59.2856$	1.1518	0.1835	0.1755	0.3766
TrKw	$-31.1656$	$-56.3312$	$-52.4437$	$-55.1753$	1.3400	0.2187	0.1837	0.3222
Ekw	$-30.6731$	$-55.3462$	$-51.4587$	$-54.1902$	1.7763	0.3018	0.6172	2.325e−09
Kw	$-30.6731$	$-57.3461$	$-54.7545$	$-56.5755$	1.4409	0.2379	0.1915	0.2756

Firstly, it is clear that, the NFKw model provides a better fit than the other tested models, because it has the smallest value among $\hat{\ell }$, AIC, BIC, HQIC, $A^{\ast }$, $W^{\ast }$ and K-S. Figures 12–14 also support our claim about NFKw model.

Figure 13.

Estimated plots (a) density (b) sf (c) hazard rate, and (d) Box-plot for data set 2.

Figure 12.

Estimated plots (a) density (b) sf (c) hazard rate, and (d) Box-plot for data set 1.

Figure 14.

Estimated plots (a) density (b) sf (c) hazard rate, and (d) Box-plot for data set 3.

7. Concluding remarks

We introduce a new cumulative distribution $F(x;\xi )=1-[1-G(x;\xi ){]}^{G(x;\xi )}$ without extra parameters defined from a baseline cumulative distribution $G(x;\xi )$ which serves as a flexible generator of generalized classes of distributions. The function $F(x;\xi )$ defines the new flexible generalized family (NFGF) of distributions. We present many sub-families of the NFGF. We obtain some mathematical properties of the NFGF and also study some properties of the special model called the new flexible Kumaraswamy (NFKw) distribution. We compare this distribution with the transmuted-Kumaraswamy, exponentiated-Kumaraswamy, and Kumaraswamy models by considering six popular GoF statistics. We find that the new distribution provides better estimates and minimum GoF values. The NFKw model outperforms these three models on the basis of numerical and graphical analysis. We expect that this new generator of G-families will be able to attract readers and applied statisticians.

Disclosure statement

No potential conflict of interest was reported by the author(s).