Assessing the impact of the economic crises in 1997 and 2008 on suicides in Hong Kong, Taiwan and South Korea using a strata-bootstrap algorithm

ABSTRACT

The Asian economic crises of 1997 and the 2008 Global Financial Crisis (GFC) had far-reaching impacts on Asian and other global economies. Turmoil in the banking and finance sectors led to downturns in stock markets, resulting in bankruptcies, house repossessions and high unemployment. These crises have been shown to be correlated with a deterioration in mental health and an increase in suicides, and it is important to understand the implication of these impacts and how such recessions affect the health of affected populations. With the benefit of hindsight, did lessons learned from the negative effects of the 1997 Asian economic recession impact the aftermath of the 2008 GFC in Asian countries? Utilising a framework based on a simple strata-bootstrap algorithm using daily data – where available – we investigate the trend in suicide rates over time in three different populations (Hong Kong, Taiwan and South Korea), and examine whether there were any changes in the pattern of suicide rates in each country subsequent to both the 1997 Asian and 2008. We find that each country responded differently to each of the crises and the suicide rates for certain age-gender specific groups in each country were more affected.

1. Introduction and motivation

Economic crises are detrimental to general population well-being. As demonstrated by primary care research in Spain [11] and national surveys in both Greece and England [19], the prevalence of mental disorders increased following the 2008 economic recession. Gili et al. [15] reported that families experiencing job losses and difficulties in meeting mortgage payments were hardest hit, and Katikireddi et al. [19] showed that males were particularly vulnerable. Preliminary analysis from ten European countries by Stuckler et al. [29] showed that all but one country experienced more suicides in 2009 compared to 2007. Two recent studies in England [1] and Italy [10] also recorded a significant rise in suicide between 2008 and 2010. In Greece, which was one of the economies most affected by the GFC, the suicide rate rose 17% in 2009 compared to 2007 [20]. Although these studies serve as valuable references, larger-scale research with an East Asian focus, in particular, remains outstanding. For example, can we determine whether social policies such as active labour market programmes have mitigated some of the more severe impacts of the large economic crisis in Asian countries? These policies are strongly associated with unemployment and indebtedness, both of which are important risk factors for suicides [6,30]. Chen et al. [7] found the escalation in the unemployment rate in Taiwan and Hong Kong to be associated with increases in the population suicide rate, and indebtedness is often found to be a factor in suicides in Asian countries.

The Asian financial crisis occurred in 1997, and in 2008 following the fall of Lehman Brothers and the sub-prime mortgage collapse in the US, the world was plunged into a global financial crisis. The impact of the Asian crisis on suicide trends in east Asian countries including Hong Kong, South Korea, Japan, Singapore, Taiwan and Thailand has been documented [4]. Being the first to document the effects of the Asian crisis on suicides, Chang et al. [4]'s study provides evidence of the impact of economic downturns on suicide rates with more than 10,000 additional suicides in Hong Kong, South Korea and Japan, as well as a reported difference in impacts between genders. Subsequently Chang et al. [5] conducted a global assessment of the impact of the 2008 GFC on suicide rates in 54 countries, including Hong Kong. These results demonstrated that the impact had a greater effect on men in 27 European countries and 18 countries in the Americas, with approximately 5000 additional suicides in 2009 following the GFC. The findings suggested that the impact on suicide rates varies between countries and the variation is particularly associated with the magnitude in the rise in unemployment rates.

The 2008 GFC has had far-reaching impacts on the global economy. Turmoil in the banking sector led to downturns in global stock markets, resulting in bankruptcies, house repossessions and a rise in unemployment world wide. Hong Kong's economy was severely impacted by the 2008 financial tsunami, with four consecutive quarters of economic contractions between the last quarter of 2008 and the third quarter of 2009. The overall GDP growth was 2.3% and −2.6 % in 2008 and 2009, in contrast to the strong economic growth of 6.4 –8.5% in 2004–2007. Hong Kong unemployment rate rose substantially from 3.4% in August 2008 to a high of 5.4% in May–July 2009, with the number of unemployed increasing 52% from 134,000 to 203,000. The Hang Seng stock market index reached a historic high (31,897) in October 2007 but fell dramatically to 10,676 in October 2008. The economic impact of the GFC was obvious, but what impact did this have on the health and mental well-being of the Hong Kong population, particularly on the rates of suicides among various age groups.

Economic indicators show that Hong Kong's neighbouring countries of Taiwan and South Korea were also affected by the 1997 and 2008 economic crises. However, the impact of the two recessions on each of these two countries and the comparison between these regions has not been studied.

Did the experience from the negative impacts of the Asian crisis help to moderate the mental health repercussions following the subsequent financial crisis of 2008?

Lopez Bernal et al. [25] used a segmented regression to study the effects of the 2008 recession on suicide rates in Spain. Coope et al. [8] contrasted the trends in the indicators of the 2008 economic recession and the subsequent trends in suicide rates in England and Wales in men and women of working age using a similar segmented regression analysis. Saurina et al. [28] applied hierarchical mixed models to study the association of suicides and economic crises in England. Harper and Bruckner [18] estimated the number of excess suicides in the USA during the 2000s recession by using an interrupted time-series analysis. Similarly, Corcoran et al. [9] assessed the impact of economic recession in Ireland by an interrupted time series analysis. Milner et al. [27] examined occupational class differences in the increasing number of suicide cases during the global financial crisis in Australia. Chan et al. [3] explored the effects of the 2008 financial crisis among the working-age adults in South Korea, using autoregressive and interrupted time series analyses. In a large-scale study, Garcy and Vågerö [14] used Cox regression to investigate the effects of recessions on suicide rates for Swedish men and women. The common theme in these studies is the fitting of a linear model with a possible jump at a specific time period. However, such methods restrict the fitted models to those with a certain discontinuity at the specific time, and limits the span of the analysis due to the complication made by the types of nonlinearity relation and the locations of the jumps over a long period span.

Chang et al. [4] used age-standardised suicide rates by sex for Japan, Hong Kong, South Korea, Taiwan, Singapore and Thailand to assess the impact of the Asian economic crisis on suicide mortality modelling the location of join points and line segments with a segmented regression. Luo et al. [26] studied the impact of business cycles on US suicide rates using the historical yearly data from 1928 to 2007 which includes 26 expansions and recessions. Blasco-Fontecilla et al. [2] investigated the trends and correlations of gross domestic product (adjusted for purchasing power parity per capita) on suicide rates in 10 WHO regions during 30 years while relaxing the assumption of dependency of data points.

In this article, we will study the age-sex standardised rate of suicide from 1995 to 2011 for the three regions. We show that using the conventional methods to construct confidence intervals for the standardised rate produce confidence intervals with incorrect coverage rates and, consequently, propose a resampling technique to resolve the issue. The results based on the proposed algorithm provide a tool to investigate the jumps of rates over a specific period of time. We use this to gain key insights into the trend of suicide rates during financial crises and measure the impact of the economic downturn on suicide rate changes. The proposed algorithm is a generic method which can be applied in any situation where the rates of events are under the investigation.

The rest of the paper is organised as follows. Section 2 introduces the data and the current methodologies to analyse the data. In this section, a simple algorithm is proposed for constructing confidence intervals for rates, and a simulation study conducted to investigate the performance of the proposed algorithm in practical situations. The theoretical properties of the proposed algorithm are given in the Appendix. Section3 shows the results of applying the proposed algorithm on suicide data. Section 4 concludes our findings and provides some discussion regarding the analysed data sets.

2. Data and methodology

In this article, we use the daily suicide cases to investigate the pattern of the suicide rates during recessions in the three regions and compare the effects of the financial crises on these regions.

The suicide rate is calculated as the number of suicides divided by the population size at a specific time. If $d_t$ denotes the number of suicide cases at time t, the suicide rate at time t is computed as ${\hat{\lambda }}_t=d_t/P_t$ per 100,000 people (i.e. multiplied by 100,000), where $P_t$ is the population size at time t. Assuming that the number of suicide cases at time t has a Poisson distribution, the normal approximation or the exact Poisson distribution can be used to construct a confidence interval for ${\lambda }_t$. For a general population, the suicide rate might not be homogeneous across different age and sex sub-populations. Thus, the suicide rate for each sub-population should be computed separately. If $d_{t,j}$ denotes the number of suicide cases at time t and sub-population j, the suicide rate for this sub-population is computed as ${\hat{\lambda }}_{t,j}=d_{t,j}/P_{t,j}$ per 100,000 people, where $P_{t,j}$ is the number of people at time t for sub-population j.

The suicide rates of two populations are compared by standardising the rates of the two populations by a reference population (usually the world population structure). The standardised rates are the weighted sum of sub-population rates for each population. The weights are obtained from the reference sub-population structure, i.e. ${\hat{\lambda }}_{s,t}=1/P_t^{\prime }\sum _j{P}_{t,j}^{\prime }{\hat{\lambda }}_{t,j}$ (here the subscript s uses to show the standardised rates) where $P_{t,j}^{\prime }$ is the size of the jth sub-population of the reference population and $P_t^{\prime }$ is the size of the reference population at time t. Assuming that the rates in sub-populations are independent, the variance of ${\hat{\lambda }}_{s,t}$ is calculated by adding the variances of each component in the weighted sum. A normal distribution approximation or an exact chi-square distribution (due to the relation between Poisson distribution and chi-square distribution) is used to construct confidence intervals based on ${\hat{\lambda }}_{s,t}$, specifically, a $(1-\alpha )$ confidence interval for ${\lambda }_{s,t}$ is

$$({\hat{\lambda }}_{s,t}-z\sqrt{\mathrm{Var}({\hat{\lambda }}_{s,t})},{\hat{\lambda }}_{s,t}+z\sqrt{\mathrm{Var}({\hat{\lambda }}_{s,t})}),$$

where z is $(1-\alpha /2)$ quantile of the standard normal distribution, and

$$\mathrm{Var}({\hat{\lambda }}_{s,t})={\left(\frac{1}{P_t^{\prime }}\right)}^2\sum _j(P_{t,j}^{\prime }{)}^2\mathrm{Var}({\hat{\lambda }}_{t,j}).$$

The standardised rates for two populations can be compared by comparing the values of ${\hat{\lambda }}_{s,t}$. Specifically, for two independent populations, if the standardised rates are denoted by ${\hat{\lambda }}_{s,t}^{(1)}$ and ${\hat{\lambda }}_{s,t}^{(2)}$ for the first and the second population, respectively, the difference of the two standardised rates is approximately distributed as a normal distribution. The inference on the ratio of ${\hat{\lambda }}_{s,t}^{(1)}$ to ${\hat{\lambda }}_{s,t}^{(2)}$ is based on the log-normal distribution [13], i.e. the $(1-\alpha )$ confidence interval for ${\lambda }_{s,t}^{(1)}/{\lambda }_{s,t}^{(2)}$ is

$$(\frac{{\hat{\lambda }}_{s,t}^{(1)}}{{\hat{\lambda }}_{s,t}^{(2)}}\exp \{-z\sqrt{V_{\log }}\},\frac{{\hat{\lambda }}_{s,t}^{(1)}}{{\hat{\lambda }}_{s,t}^{(2)}}\exp \{z\sqrt{V_{\log }}\}),$$

where z is $(1-\alpha /2)$ quantile of the standard normal distribution and $V_{\log }$ is the variance of $\log (({\hat{\lambda }}_{s,t}^{(1)})/({\hat{\lambda }}_{s,t}^{(2)}))$.

If the independence assumption is violated in sub-populations and/or between two populations, then the standard method of inference based on normal approximation or exact Poisson distribution is not valid. In this case the covariance structure of the sub-populations or between two populations should be taken into account. Although the conventional resampling algorithms may be used in this case for statistical inference, the complex structure of seasonal and non-seasonal dependencies between the yearly and monthly suicide rates in different time periods and/or different sub-populations limits their usage. We propose a simple strata-bootstrap method which automatically corrects the statistical inferences of the rates and standardised rates, and it provides a simple framework for studying the changes in rates at different time periods. We explore the theoretical properties of the proposed method, and conduct a simulation study to gain a better understanding as to how the proposed algorithm works compared to the conventional method in the case of empirical studies.

Our analysis uses the world population as a reference population to study the annual and monthly (or quarterly, when the number of cases is small) standardised suicide rates of Hong Kong, South Korea, and Taiwan. Our aim is to investigate the differences in the impacts of the 1997 and 2008 economic recessions on suicides in Hong Kong in comparison to Taiwan and South Korea.

2.1. Data

Suicide data for Hong Kong was extracted from Coroners, files using the International Classification of Disease, tenth version (‘ICD-10’), codes X64-X80 (suicide) as well as Y10-Y34 code (death of undetermined intent), as previous studies suggest that some deaths in the latter category may be misclassified suicides [5,23]. South Korean suicide data was obtained from the National Statistical Office of Korea using the same ICD-10 codes as those for the Hong Kong data. Taiwan's suicide data was extracted from the national cause-of-death mortality data files.

Each database contains the age, sex, year, month, and the day of suicide for each case. The few missing values for the days of the deaths in the South Korea data sets are replaced by the 15th of the month being the midpoint. Any missing values for ‘the day of the death’ in Hong Kong have been imputed by a uniform random number between 1 and the number of days in the specific month the death occurred. Grouping by 5-year age bands and by gender have been used to construct the sub-populations used in this study. The population sizes for each region are used to compute the suicide rates. Linear interpolation is used if the population size for a specific time interval was needed. The age-groups ‘00–04’, ‘05–09’, and ‘10–14’ are excluded from the analyses. Suicide data available from 1995 to 2011 for all the three regions was used in the study.

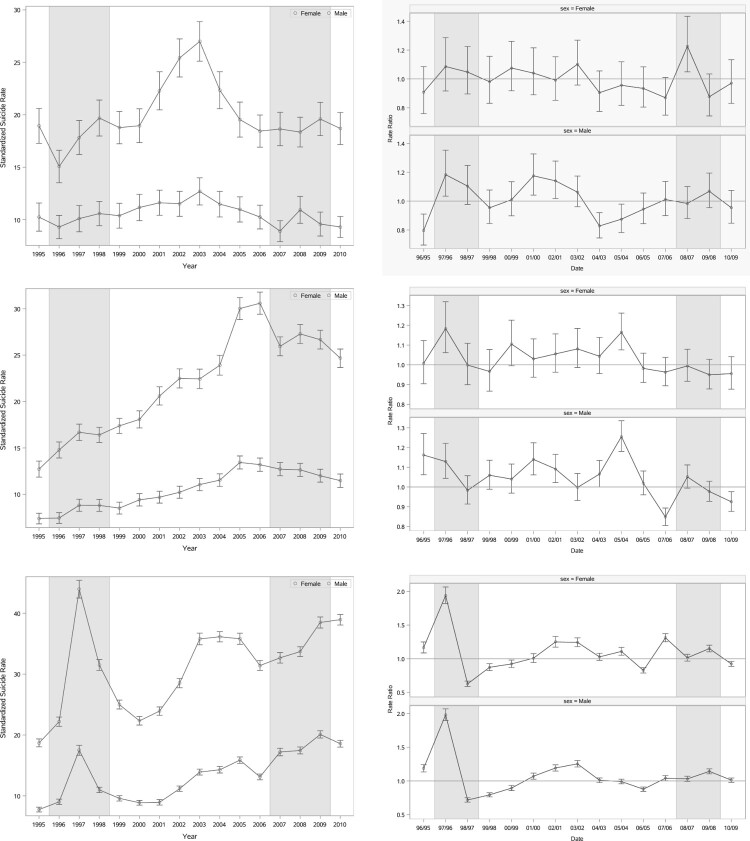
Where daily suicide data are available, we used a simple strata-bootstrap method to calculate the annual standardised rate of suicide cases. Unlike the monthly aggregated data, the daily data do not show a strong autocorrelation in suicide cases during a specific month, and we use this property to develop the strata-bootstrap method. The proposed method corrects the confidence intervals of the rates for each sub-population/population and provides a tool to study the change in rates for different time periods. We calculate the standardised rate (with reference to the world population structure) and its corresponding ratio for two consecutive years for each gender for the three regions. Figure 1 shows those values and their corresponding 95% bootstrap confidence intervals; the details of the computations are given later. The possible range of the effects of the recessions in 1997 and 2008 on suicides is shaded in the graphs. A reference line at 1 on the right panels of Figure 1 provides the guideline for detecting year to year increase or decrease in the standardised suicide rates. Figure 1 illustrates that compared to 1996, suicides increased for all the three regions during 1997. The increased rate for women is similar to males, and in the case of Taiwan, it is even more than men. With the exception of Hong Kong females, the impact of the 2008 recession for all the three regions is less than the 1997 recession.

Figure 1.

The left panels show the plot for the standardised suicide rates for females and males from 1995 to 2010 for Hong Kong, SAR (top), Taiwan (middle), and South Korea (bottom). The right panels show the plot for the corresponding ratios of standardised suicide rates for two consecutive years. The 95% confidence intervals are shown by the error-bars in these graphs.

2.2. Methodology

As suggested earlier, segmented regression models ignore the complex dependency among the monthly/yearly suicide rates, and linear models and classical time series models cannot easily capture the nonlinear trend of the suicide rates. Although the segmented regression and interrupted time series detect the point of discontinuity of the suicide trend, they are unsuitable for detecting the increasing/decreasing pattern of the suicide rates during the economic recessions, and determining the specific time of any jump is not a trivial process in either method. With segmented regression, the common practice is to narrow the time frame of the data in such a way that the trend of suicide rates during the period can be modelled with a piecewise linear fit which may incorporate possible change points. However, narrowing the time frame of the data analysis omits a large amount of historical data and hides the seasonal dependency of suicides. The interrupted time series models can take into account the structural dependency among the data, but it is very challenging to incorporate nonlinear trends into them, and their results are not as interpretable as the results of the segmented regression models. The strata-bootstrap algorithm, which is formally introduced in the following few paragraphs, provides a simple solution for resolving these issues.

Suppose $\{X_{i,m,t,j}\},i=1,\dots ,K,m=1,\dots M,j=1,\dots ,C$ and $t=1,\dots ,T$, denotes the number of cases in sub-population j at time t, where in the case of suicide rates, t indicates the year of study, and i is the day of the incident in month m. In this setup, we assume that the rate is different in each month, m, however, the month period is not part of the strata construction. Here t and j indicate the strata for the bootstrap resampling. We denote by $\{X_{i^{\ast },m,t,j}{\}}_{i^{\ast }=i_1}^{i_K}$ a bootstrap sample from $\{X_{i,m,t,j}\}$, where $i_1\dots i_K$ is a random sample with replacement from integers $\{1,\dots ,K\}$. The values of $\{i^{\ast }\}$ in each stratum are the same and $\{X_{i^{\ast },m,t,j}{\}}_{i^{\ast }=i_{1_{\phantom{0}}}}^{i_K}$ maintains the dependency structure of the observation between each stratum, e.g. Hall et al. [17,21]. For any time frame the number of strata-bootstrap suicide cases is the summation over the corresponding indices, e.g. the monthly numbers of incidents for year t $(t=1,\dots ,T)$, and stratum j $(j=1,\dots ,C)$, are $\{d_{m,t,j}^{\ast }=\sum _{i^{\ast }}{X}_{i^{\ast },m,t,j}{\}}_{m=1}^{12}$.

Similarly, the yearly number of incidents is simply $d_{t,j}^{\ast }=\sum _m{d}_{m,t,j}^{\ast }$. Thus, based on the selected resample, ${\hat{\lambda }}_{t,j}^{\ast }=d_{t,j}^{\ast }/P_{t,j}$ and ${\hat{\lambda }}_{m,t,j}^{\ast }=d_{m,t,j}^{\ast }/P_{t,j}$, $m=1,\dots ,12$ are the yearly and monthly suicide rates, respectively. The standardised rate is ${\hat{\lambda }}_{s,t}^{\ast }=1/P_t^{\prime }\sum _j{P}_{t,j}^{\prime }{\hat{\lambda }}_{t,j}^{\ast }$. The procedure is repeated B times to generate B copies of rates, e.g. in the case of the annual standardised suicide we denotes B copies as ${\hat{\lambda }}_{s,t}^{\ast ,1},\dots ,{\hat{\lambda }}_{s,t}^{\ast ,B}$, and we denote its sample mean and standard deviation with ${\overline{\lambda }}_{s,t}(B)$, $s_{s,t}(B)$, i.e. ${\overline{\lambda }}_{s,t}(B)=1/B\sum _b{\hat{\lambda }}_{s,t}^{\ast ,b}$, and $s_{s,t}^2(B)=1/B\sum _b({\hat{\lambda }}_{s,t}^{\ast ,b}-{\overline{\lambda }}_{s,t}(B){)}^2$, respectively.

On the basis of a strata-bootstrap resample, a ratio of two rates is similarly computed, e.g. the ratio of the annual suicide rates for year $t_1$ and year $t_2$ is ${\hat{r}}_{t_1,t_2,j}^{\ast }=({\hat{\lambda }}_{t_1,j}^{\ast })/({\hat{\lambda }}_{t_2,j}^{\ast })$. We denote the sample mean of ${\hat{r}}_{t_1,t_2,j}^{\ast ,1},\dots ,{\hat{r}}_{t_1,t_2,j}^{\ast ,B}$ with ${\overline{r}}_{t_1,t_2,j}(B)$. If $q_{r,\alpha /2}^{\ast }$ and $q_{r,(1-\alpha /2)}^{\ast }$ denote the $\alpha /2$ and $(1-\alpha /2)$ percentiles of ${\hat{r}}_{t_1,t_2,j}^{\ast ,1},\dots ,{\hat{r}}_{t_1,t_2,j}^{\ast ,B}$, respectively, the $(1-\alpha )$ bootstrap percentile confidence interval for $r_{t_1,t_2,j}$ is $(q_{r,\alpha /2}^{\ast },q_{r,(1-\alpha /2)}^{\ast })$ (see [16], p. 12). Let $p_{r,0}$ denotes the proportion of ${\hat{r}}_{t_1,t_2,j}^{\ast ,1},\dots ,{\hat{r}}_{t_1,t_2,j}^{\ast ,B}$ which is less than or equal to ${\hat{r}}_{t_1,t_2,j}$, $\alpha (lo{)}_{BC}=\mathrm{\Phi }(2{\mathrm{\Phi }}^{-1}(p_{r,0})-z)$ and $\alpha (up{)}_{BC}=\mathrm{\Phi }(2{\mathrm{\Phi }}^{-1}(p_{r,0})+z)$, where z is $(1-\alpha /2)$ quantile of the standard normal distribution and Φ is the normal cumulative distribution function. The bias-corrected percentile confidence interval for $r_{t_1,t_2,j}$ is $(q_{r,\alpha (lo{)}_{BC}}^{\ast },q_{r,(\alpha (up{)}_{BC})}^{\ast })$, see Efron and Hastie [12].

We also construct the confidence intervals by using the normal approximation. Let $s_{t_1,t_2,j}^{\log }(B)$ denotes the sample standard deviation of $\log ({\hat{r}}_{t_1,t_2,j}^{\ast ,1}),\dots ,\log ({\hat{r}}_{t_1,t_2,j}^{\ast ,B})$, when the ratio of rates is under investigation, a $(1-\alpha )$ confidence interval for ratio is

$$(\frac{{\hat{\lambda }}_{t_1,j}}{{\hat{\lambda }}_{t_2,j}}\exp \{-z\times s_{t_1,t_2,j}^{\log }(B)\},\frac{{\hat{\lambda }}_{t_1,j}}{{\hat{\lambda }}_{t_2,j}}\exp \{z\times s_{t_1,t_2,j}^{\log }(B)\}),$$

where z is $(1-\alpha /2)$ quantile of the standard normal distribution. The mathematical properties of the bootstrap estimates of the standard deviations for the standardised rate and the ratio of rates are given in the Appendix.

On the basis of a simulation study we conducted (discussed at the end of this section) the normal approximation method has a more accurate coverage for B as small as 100. In this case, the bootstrap percentile confidence intervals (and bias-corrected intervals) coverage is lower than $(1-\alpha )$, and the confidence intervals are shorter than the confidence intervals constructed based on the normal approximation.

Similarly, the $(1-\alpha )$ confidence interval for ${\lambda }_{s,t}$ based on ${\hat{\lambda }}_{s,t}^{\ast ,1},\dots ,{\hat{\lambda }}_{s,t}^{\ast ,B}$ is

$$({\hat{\lambda }}_{s,t}-z{s}_{s,t}(B),{\hat{\lambda }}_{s,t}+z{s}_{s,t}(B)).$$

The confidence bars on the right panels of Figure 1 are 95% confidence limit for the annual standardised rates of the three regions. Figure 1 shows that the suicide rate in Hong Kong increased sharply during the 2000s, which is related to the emergence of the new method of suicide, charcoal burning [22,24]; Taiwan suicide rates increased steadily from 1998 to 2005, and the magnitude of its impact is similarly felt in 2008. In South Korea, the impact of the financial crisis has some time delay effect. For this region, the impact of the 2008 financial crisis is relatively moderate in comparison to the recession in Asia in 1997. Apparently, in 2008, the GFC had a larger impact on females compared to male counterparts. During the 2008 recession, there were more females in the job market than before, and this might elevate the impact of the economic crisis on the female sub-population. The financial strain on South Korea lasted for about two years which is longer than both Taiwan and Hong Kong. These other two places appear to have ‘learnt’ from the negative impact of the 1997 economic crisis as the social pressure arising from the 2008 crisis had been mitigated through lower suicide rates.

The impact of the financial crises on different age groups is analysed by the ratios of suicide rates over two consecutive years during the recessions periods for each age group. These values and their corresponding confidence intervals are computed for the ratios of suicide rates for different age groups with $t_1=1997$ and $t_2=1996$, and $t_1=2008$ and $t_2=2007$, which represent the recession years of 1997 and 2008 and one year before each recession. Tables 1–3 summarise the output for Hong Kong, Taiwan, and South Korea, respectively. The 1997 recession has a significant impact on all age groups of females and males in South Korea, with the most impact on the older age groups for both sexes. The impact of the 1997 financial crisis is less on the other two regions, Hong Kong and Taiwan. These tables show that the recession in 2008 has less impact compared to the 1997s.

Table 2. The ratios of suicide rates across sex and age groups during 1996–1997 and 2007–2008 in Taiwan.

	Female		Male
Age group	$1997/1996$	$2008/2007$	$1997/1996$	$2008/2007$
15–19	0.947${}_{(0.478,1.877)}$	0.715${}_{(0.363,1.408)}$	1.218${}_{(0.750,1.978)}$	0.938${}_{(0.577,1.523)}$
20–24	1.427${}_{(0.892,2.283)}$	0.830${}_{(0.559,1.233)}$	0.784${}_{(0.553,1.111)}$	0.890${}_{(0.690,1.149)}$
25–29	0.993${}_{(0.694,1.420)}$	1.083${}_{(0.841,1.395)}$	1.059${}_{(0.807,1.388)}$	1.040${}_{(0.870,1.245)}$
30–34	1.069${}_{(0.761,1.500)}$	1.071${}_{(0.849,1.350)}$	1.172${}_{(0.924,1.486)}$	1.063${}_{(0.897,1.261)}$
35–39	1.302${}_{(0.932,1.818)}$	1.057${}_{(0.823,1.357)}$	1.441${}_{(1.149,1.806)}$	1.118${}_{(0.943,1.324)}$
40–44	1.047${}_{(0.739,1.483)}$	1.061${}_{(0.829,1.358)}$	1.207${}_{(0.950,1.535)}$	1.136${}_{(0.975,1.323)}$
45–49	0.968${}_{(0.631,1.483)}$	1.049${}_{(0.835,1.319)}$	1.292${}_{(0.973,1.714)}$	1.076${}_{(0.920,1.259)}$
50–54	1.496${}_{(0.892,2.511)}$	0.890${}_{(0.678,1.170)}$	1.193${}_{(0.848,1.680)}$	1.059${}_{(0.898,1.249)}$
55–59	0.963${}_{(0.620,1.497)}$	0.888${}_{(0.671,1.174)}$	1.195${}_{(0.893,1.600)}$	0.992${}_{(0.833,1.182)}$
60–64	1.558${}_{(0.977,2.484)}$	0.957${}_{(0.699,1.311)}$	1.109${}_{(0.844,1.459)}$	1.074${}_{(0.869,1.328)}$
65–69	1.652${}_{(1.071,2.548)}$	1.131${}_{(0.814,1.571)}$	1.201${}_{(0.921,1.567)}$	1.071${}_{(0.856,1.340)}$
70–74	1.159${}_{(0.799,1.681)}$	1.018${}_{(0.753,1.374)}$	0.822${}_{(0.627,1.076)}$	1.060${}_{(0.846,1.328)}$
75–79	1.409${}_{(0.937,2.117)}$	0.767${}_{(0.555,1.060)}$	1.346${}_{(0.975,1.857)}$	1.099${}_{(0.851,1.420)}$
80–84	1.237${}_{(0.690,2.217)}$	1.010${}_{(0.666,1.531)}$	0.952${}_{(0.661,1.372)}$	0.896${}_{(0.680,1.180)}$
85+	0.700${}_{(0.332,1.477)}$	1.268${}_{(0.736,2.184)}$	0.798${}_{(0.441,1.441)}$	0.765${}_{(0.524,1.118)}$

Note: 95% confidence intervals are provided in parentheses as a subscript.

Table 1. The ratios of suicide rates across sex and age groups during 1996–1997 and 2007–2008 in Hong Kong.

	Female		Male
Age group	$1997/1996$	$2008/2007$	$1997/1996$	$2008/2007$
15–19	0.897${}_{(0.374,2.148)}$	1.828${}_{(0.553,6.047)}$	1.342${}_{(0.552,3.262)}$	1.092${}_{(0.495,2.409)}$
20–24	0.791${}_{(0.398,1.574)}$	1.737${}_{(0.935,3.224)}$	1.358${}_{(0.835,2.207)}$	0.973${}_{(0.587,1.615)}$
25–29	1.331${}_{(0.718,2.469)}$	1.208${}_{(0.683,2.138)}$	1.237${}_{(0.831,1.842)}$	1.038${}_{(0.666,1.619)}$
30–34	0.992${}_{(0.552,1.780)}$	0.781${}_{(0.475,1.284)}$	0.897${}_{(0.579,1.391)}$	1.074${}_{(0.709,1.628)}$
35–39	0.704${}_{(0.375,1.321)}$	1.172${}_{(0.687,2.001)}$	0.841${}_{(0.578,1.222)}$	0.970${}_{(0.666,1.414)}$
40–44	0.850${}_{(0.433,1.670)}$	1.625${}_{(0.976,2.705)}$	0.926${}_{(0.590,1.452)}$	0.958${}_{(0.650,1.412)}$
45–49	1.140${}_{(0.624,2.084)}$	0.890${}_{(0.551,1.438)}$	1.334${}_{(0.850,2.093)}$	1.212${}_{(0.795,1.849)}$
50–54	1.639${}_{(0.728,3.686)}$	1.042${}_{(0.633,1.716)}$	1.025${}_{(0.548,1.916)}$	0.870${}_{(0.600,1.260)}$
55–59	1.986${}_{(0.835,4.724)}$	1.118${}_{(0.651,1.918)}$	1.668${}_{(0.955,2.911)}$	1.531${}_{(0.968,2.423)}$
60–64	1.368${}_{(0.721,2.594)}$	0.923${}_{(0.501,1.699)}$	0.744${}_{(0.452,1.224)}$	0.806${}_{(0.497,1.308)}$
65–69	1.136${}_{(0.635,2.032)}$	1.645${}_{(0.770,3.514)}$	1.595${}_{(0.960,2.651)}$	1.020${}_{(0.664,1.567)}$
70–74	0.782${}_{(0.428,1.428)}$	1.482${}_{(0.770,2.853)}$	1.415${}_{(0.844,2.374)}$	0.953${}_{(0.615,1.478)}$
75–79	0.840${}_{(0.442,1.597)}$	1.501${}_{(0.835,2.697)}$	1.225${}_{(0.738,2.034)}$	0.951${}_{(0.581,1.556)}$
80–84	1.297${}_{(0.574,2.933)}$	1.325${}_{(0.689,2.548)}$	1.789${}_{(0.758,4.224)}$	0.608${}_{(0.380,0.972)}$
85+	1.051${}_{(0.544,2.034)}$	1.957${}_{(0.873,4.391)}$	1.499${}_{(0.519,4.336)}$	0.551${}_{(0.289,1.050)}$

Note: 95% confidence intervals are provided in parentheses as a subscript.

Table 3. The ratios of suicide rates across sex and age groups during 1996–1997 and 2007–2008 in South Korea.

	Female		Male
Age group	$1997/1996$	$2008/2007$	$1997/1996$	$2008/2007$
15–19	1.553${}_{(1.244,1.939)}$	0.973${}_{(0.748,1.265)}$	1.370${}_{(1.143,1.643)}$	1.048${}_{(0.834,1.317)}$
20–24	1.845${}_{(1.522,2.236)}$	0.863${}_{(0.730,1.020)}$	1.904${}_{(1.656,2.189)}$	1.235${}_{(1.044,1.460)}$
25–29	2.094${}_{(1.779,2.465)}$	1.098${}_{(0.963,1.251)}$	1.901${}_{(1.675,2.157)}$	1.119${}_{(0.994,1.261)}$
30–34	2.292${}_{(1.880,2.793)}$	1.025${}_{(0.894,1.175)}$	2.001${}_{(1.744,2.294)}$	0.895${}_{(0.789,1.014)}$
35–39	2.101${}_{(1.745,2.531)}$	1.206${}_{(1.049,1.386)}$	2.070${}_{(1.839,2.329)}$	1.275${}_{(1.148,1.417)}$
40–44	1.509${}_{(1.208,1.885)}$	1.112${}_{(0.965,1.281)}$	1.988${}_{(1.725,2.290)}$	1.017${}_{(0.924,1.119)}$
45–49	2.059${}_{(1.583,2.679)}$	1.136${}_{(0.978,1.320)}$	2.306${}_{(2.001,2.658)}$	1.081${}_{(0.990,1.181)}$
50–54	1.878${}_{(1.416,2.489)}$	1.029${}_{(0.868,1.220)}$	1.881${}_{(1.600,2.211)}$	1.053${}_{(0.959,1.157)}$
55–59	2.467${}_{(1.838,3.311)}$	1.008${}_{(0.829,1.227)}$	2.177${}_{(1.836,2.581)}$	1.069${}_{(0.952,1.200)}$
60–64	1.960${}_{(1.448,2.654)}$	0.919${}_{(0.757,1.117)}$	1.893${}_{(1.585,2.260)}$	0.954${}_{(0.856,1.064)}$
65–69	2.139${}_{(1.588,2.882)}$	0.987${}_{(0.842,1.157)}$	1.859${}_{(1.510,2.288)}$	1.062${}_{(0.954,1.183)}$
70–74	1.649${}_{(1.223,2.222)}$	0.899${}_{(0.768,1.053)}$	2.243${}_{(1.771,2.841)}$	0.949${}_{(0.844,1.067)}$
75–79	2.202${}_{(1.574,3.080)}$	0.913${}_{(0.774,1.077)}$	2.491${}_{(1.860,3.335)}$	0.847${}_{(0.741,0.968)}$
80–84	2.263${}_{(1.517,3.376)}$	0.970${}_{(0.819,1.148)}$	1.524${}_{(0.993,2.338)}$	0.992${}_{(0.827,1.189)}$
85+	1.721${}_{(1.136,2.608)}$	1.010${}_{(0.832,1.227)}$	2.260${}_{(1.338,3.816)}$	0.854${}_{(0.705,1.035)}$

Note: 95% confidence intervals are provided in parentheses as a subscript.

2.3. Simulation study

We conduct a simulation study to investigate the empirical performance of the proposed algorithm compared to the conventional method. For the simulation setup, we fix K=30, M=12, C=5 and T=8, thus the datasets contain 360 observations per year per stratum. In each scenario, we generate a $40\times 40$ correlation matrix which fixes the dependencies between years and strata. The upper triangle of the correlation matrix is filled in such way that those elements which are corresponding to the dependency between years are set to the Toeplitz matrix whose lth entry of its first row is ${\rho }_y^{l-1}$ for a fixed ${\rho }_y$, i.e. without any further restriction, the correlation between years is following an AR(1) model. The values of the correlation matrix which control the dependency between two strata in the same year are set to ${\rho }_s$ and the values corresponding to two strata in time $t_1$ and time $t_2$ are set to ${\rho }_s^{|t_2-t_1|}$. The lower triangle of the correlation matrix is filled in such a way that the matrix is symmetric. The generated matrix is not guaranteed to be a positive definite matrix, thus its eigenvectors and eigenvalues are calculated, and the negative eigenvalues are replaced by small numbers, and the correlation matrix is reconstructed based on the eigenvectors and the new eigenvalues. We use normal copula to generate data from a Poisson distribution with parameter $\lambda =\{9(m-6)/100{\}}^2+1/10,m=1,\dots ,12$ and given correlation matrix. The same setup is used to generate data from a beta-binomial distribution with parameters $\alpha =\{9(m-6)/100{\}}^2+1/10,\beta =6$, and n=5. For each generated data set, we calculate the annual rates and ratios of the first-year rate to all other seven years using the conventional method and the bootstrap method with $B\in \{100,1000\}$, and then the coverage rate of the confidence intervals over 1000 replications is recorded. In this paper, we report the results for four different settings of ${\rho }_y\in \{0.1,0.2,0.3,0.4\}$, four different settings of ${\rho }_s\in \{0.1,0.2,0.3,0.4\}$, and B=1000. The simulation was repeated – but not reported here – for ${\rho }_y\in \{-0.1,-0.2,-0.3,-0.4\}$, ${\rho }_s\in \{-0.1,-0.2,-0.3,-0.4\}$, and ${\rho }_y,$ ${\rho }_s$ selected randomly from a uniform distribution to assure the consistency of the findings.

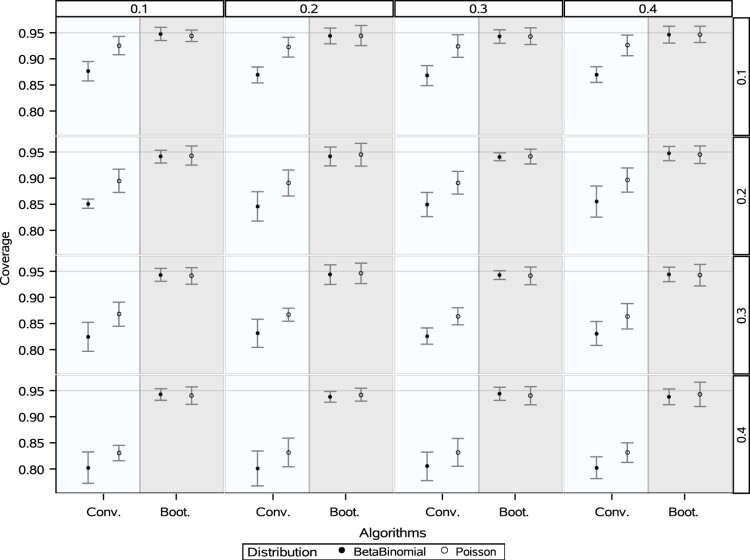
Figure 2 shows the mean coverage of confidence intervals for yearly rates over 8 years across different values of ${\rho }_y$ (columns) and ${\rho }_s$ (rows). One may observe that the proposed method correctly constructs the confidence intervals in each scenario.

Figure 2.

The mean of confidence intervals' coverage of the conventional method and the proposed bootstrap method. The columns' heading shows the value of ${\rho }_y$ and the rows' heading indicates the value of ${\rho }_s$. In this graph, the x-axis indicates the method used to construct the confidence intervals and the y-axis shows the coverage percentage. The error bars show $\pm 2\times$ the standard deviation of coverage of confidence intervals for 8 years.

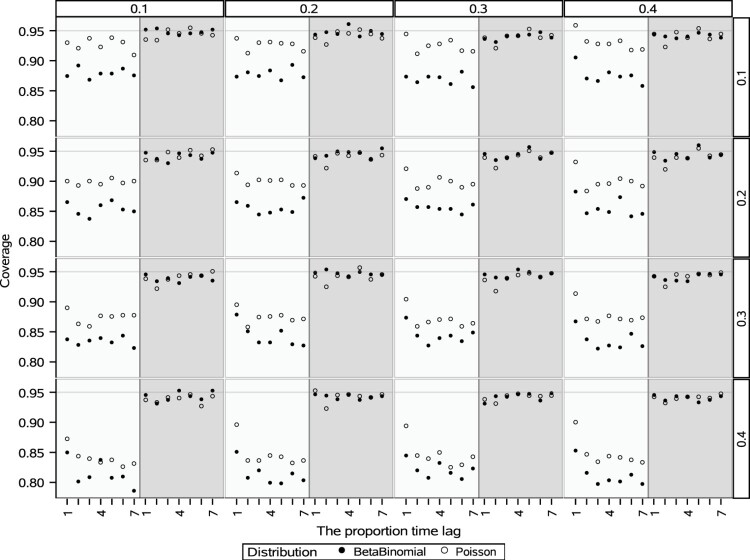
Figure 3 summarises the coverage rate of confidence intervals constructed for the ratios of the first year's rate to rates of subsequent years. The x-axis indicates the time lag between the first year and the year in the denominator of the ratios. Similar to Figure 2, the beta-binomial distribution is more prone to the dependency of data. Nevertheless, the strata-bootstrap method correctly constructs the confidence intervals.

Figure 3.

The coverage of confidence intervals for the ratios of the first year's rate to rates of subsequent years. The columns' heading shows the value of ${\rho }_y$ and the rows' heading indicates the value of ${\rho }_s$. In this graph, the x-axis indicates the index of the subsequent years, and the y-axis shows the coverage values. The shaded area corresponds to the proposed bootstrap method.

3. Results

The confidence interval for the ratio of the standardised rates for two consecutive years in 1996–1997 and 2007–2008 is computed based on ${\hat{\lambda }}_{s,t}^{\ast }$. Table 4 shows the results of the ratios of the standardised rates during the two recessions.

Table 4. Two consecutive year ratio of the standardised suicide rates for the three regions during 1996–1997 and 2007–2008.

	Females			Males
	Estimate	Lower CL	Upper CL	Estimate	Lower CL	Upper CL
Hong Kong
Ratio $1997/1996$	1.08624	0.91004	1.29654	1.18345	1.03279	1.35609
Ratio $2008/2007$	1.22678	1.05620	1.42491	0.98402	0.87373	1.10824
Ratio of Ratios	1.12938	0.89533	1.42462	0.83148	0.69840	0.98994
Taiwan
Ratio $1997/1996$	1.18387	1.05838	1.32425	1.12896	1.04464	1.22009
Ratio $2008/2007$	0.99448	0.91813	1.07718	1.05149	0.99570	1.11041
Ratio of Ratios	0.84002	0.73472	0.96042	0.93138	0.84496	1.02664
South Korea
Ratio $1997/1996$	1.94019	1.82141	2.06671	1.98215	1.89414	2.07425
Ratio $2008/2007$	1.01477	0.96548	1.06657	1.03048	0.99319	1.06917
Ratio of Ratios	0.52302	0.48464	0.56445	0.51988	0.49103	0.55043

Notes: Ratio of ratios compares the effects of the 2008 recession to the 1997 recession. The lower and upper 95% confidence limits are shown by ‘Lower CL’ and ‘Upper CL’, respectively.

Table 4 shows that the Hong Kong female population is the only group which has been affected shortly after the 2008 recession. The rows in this table denoted by ‘Ratio of Ratios’ is the ratio of the ratios of consecutive years of the two financial crises. In Hong Kong, compared to the 1997 financial crisis, the 2008 recession impact has been significantly mitigated for the male population. In Taiwan, although the female population was less hit by the 2008 financial crisis compared to the 1997s, the impact on the male population is at the same level for the two crises. In South Korea, the shock of the 1997 crisis dominates, thus, its suicide rate has remained at a high level since then.

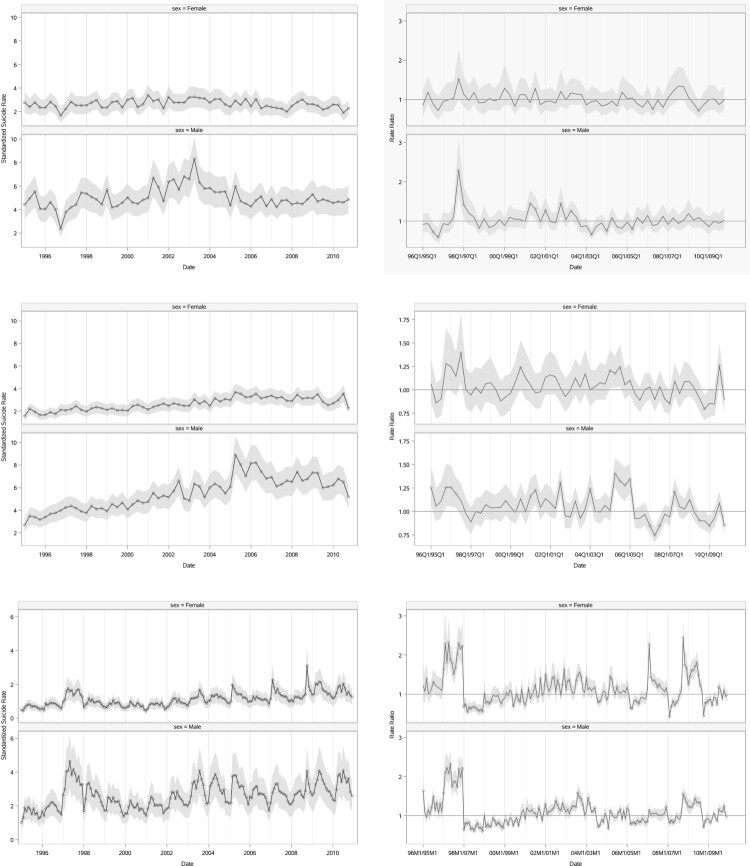
To study the possible start and the duration of the impact of financial crises on suicide rates more precisely, we use South Korea's monthly and Hong Kong and Taiwan's quarterly standardised rates. The reason for using quarterly aggregation in the case of Hong Kong and Taiwan is due to the low number of monthly suicide cases in those two regions. The left panels of Figure 4 show these monthly or quarterly standardised rates. The 95% confidence intervals for ${\hat{\lambda }}_{s,t}$, when the time frame is monthly or quarterly, are shown as a light shaded band in these plots. The ratios of the standardised rates of a month/quarter to the same month/quarter in the previous year are provided on the right panels of Figure 4. A circle above 1 in these graphs means that the ratio of the standardised suicide rate significantly increased compared to the same period in the previous year, and a circle below 1 indicates that the ratio of standardised suicide rate significantly decreased compared to the same period in the previous year. Figure 4 shows how financial crises and/or other factors impact the suicide rates over different periods during 1995–2010. The 1997 economy downturn had a very early impact on Taiwan and a late impact on Hong Kong, and lasted longer in South Korea. Figure 4 shows that the impact of the 2008 economy downturn has a possible six months lag in South Korea, however, the effect lasted for a longer time compared to the other two regions.

Figure 4.

The quarterly standardised suicide rates (left panels) and their corresponding ratios for two consecutive years (right panels) for Hong Kong, SAR are on the top row, and Taiwan in the middle row. The bottom row contains the monthly standardised suicide rates (left panel) and their corresponding ratios for two consecutive years (right panel) for South Korea. The light shaded band shows the 95% confidence interval.

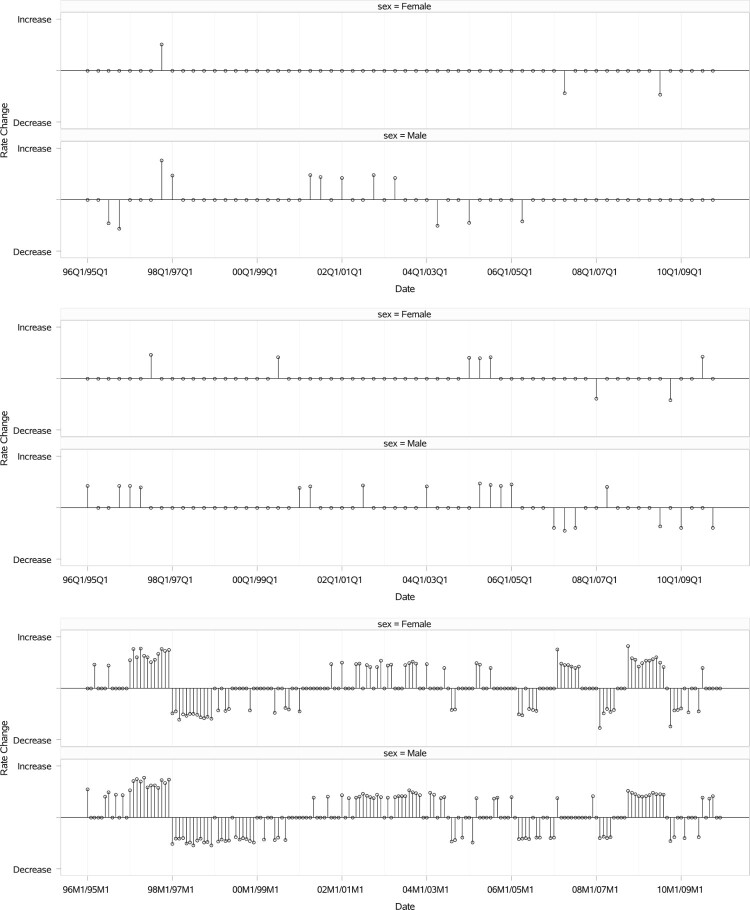
To make the magnitude of the ratios of suicide rates comparable we use needle plots which are shown in Figure 5. This figure can be used to study the changes of suicide rates over time. The middle line in each plot shows that the rate has not changed significantly in a specific time compared to the same period in the previous year. A value above this line means that the rate has significantly increased, and a value below it means that the rate has decreased for a specific time when compared to the same period in the previous year. This figure shows the fluctuation of the changes of suicide rates in South Korea and indicates that a shock impact lasts longer in South Korea, however, as regards the suicide rates, the populations in Hong Kong and Taiwan are becoming less sensitive to the economy downturn. Certainly, suicide is a very complex phenomenon and the risks are usually multi-factorial and interact with one another in socio, economic and biological factors. Economic hardship arising from the financial crisis is negatively correlated to mental well-being. More importantly, it requires multi-layered interventions. The results have provided important observations to implement more targeted population measures for suicide prevention.

Figure 5.

The magnitude of changes on suicide rates year over year for each quarter. The top panel shows the magnitude for Hong Kong, SAR, and the middle for Taiwan. The bottom panel shows the monthly changes for South Korea. The plots have the same vertical scale and they are comparable.

4. Conclusion and discussion

Conventional methods used in studying suicide rates, and standardised suicide rates, ignore the complicated dependency among the sub-populations and restricts the implementation of the methods to compare the rates in different time periods. The common practice in studying the impact of different phenomena on suicide rates is limited to segmented regression and interrupted time series analysis, which, as mentioned, introduces different issues. Although the numerical algorithms such as bootstrap, block bootstrap, and jackknife are able to take into account the dependency of the population, the complex dependency of suicide rates limits their direct usage. The proposed strata-bootstrap algorithm however, uses the daily observations to reduce the complexity of the autocorrelation dependency of the population and provides a simple framework to study suicide rates in a more general context.

Comparing the impact of the two major financial crises provides a new insight into the relation between suicides and economy crises for three high-income and rapidly changing societies. The findings show that in Hong Kong, due to the increasing number of women in the workforce during the period 1997–2007, women experienced a greater impact from the 2008 recession compared to the 1997 economic downturn, reflecting more stress arising from uncertainties in the job market. This scenario should be compared to the findings of [5]. On the positive side, the Hong Kong male population seems to have learnt from the experience of the 1997 crisis, resulting in the impact of the 2008 financial crisis being less severe for men. This also applies to the female population of Taiwan and the female and male populations in South Korea. For the older adults, it seems that the effect of recession is more prominent among the older adults in South Korea.

The commencement and the duration of the impact of each economic recession were different for Hong Kong, Taiwan, and South Korea. Hong Kong was the last region among the three to be affected by the 1997 economy crisis, whereas South Korea was the last affected during the 2008 recession. South Korea was badly hit by the financial crises in 1997 and 2008 and for a longer period. Although the impact of the economic downturn was mitigated, nevertheless, it is important to examine the social support structure available in time of crisis and consider how populations can get through without much impact. For example, the welfare system could be improved, especially during the time of economic crisis to provide enough buffer to protect the vulnerable. In Asia, financial expansion rather than contraction in response to financial crises might be advantageous as government welfare support is relatively less generous than in the west. Thus, it might be more beneficial to inject additional resources into the economy to maintain the financial and economic activities of the societies and so minimise any negative impacts such as increased suicide rates.

Appendix. Properties of the bootstrap estimates of the variances.

In this section, we explore the theoretical properties of the bootstrap estimate of the variance for rates. To simplify the derivation, the value of M is fixed to one, i.e. the monthly rates are considered. Here we derived the properties of the standardised rates, the derivation for the ratio of rates may be done similarly.

The monthly rate for a specific month is

$${\hat{\lambda }}_{s,t}={\sum \sum }_{j,i}{w}_{t,j}{X}_{i,t,j}=K^{-1}{\sum \sum }_{i,j}w(t,j)X_{i,t,j},$$ (A1)

where $w(t,j)$ is the weight function which may depend on t, j, and, K. The $K^{-1}$ factor in Equation (A1) prevents the value of ${\hat{\lambda }}_{s,t}$ from increasing too fast when K is getting larger, and it is not essential in the case of the finite sample size derivations, however, it is helpful for analysing the asymptotic properties.

Let ${\mathcal{B}}_b^{\ast }$ denotes the set of K indices where each index is randomly drawn with replacement from integers $\{1,\dots ,K\}$. Therefore ${\overline{\lambda }}_{s,t}(B)$ is defined as $B^{-1}\sum _b{K}^{-1}\sum _j\sum _{i^{\ast }\in {\mathcal{B}}_b^{\ast }}w(t,j)X_{i^{\ast },t,j}$, and

$$\begin{array}{rl}{s}_{s,t}^2(B)& =B^{-1}{\sum }_b{[K^{-1}{\sum \sum }_{j,i^{\ast }\in {\mathcal{B}}_b^{\ast }}w(t,j)X_{i^{\ast },t,j}]}^2\\ & -{\{B^{-1}{\sum }_b{K}^{-1}{\sum \sum }_{j,i^{\ast }\in {\mathcal{B}}_b^{\ast }}w(t,j)X_{i^{\ast },t,j}\}}^2,\end{array}$$

which reduces to

$$s_{s,t}^2(B)=K^{-2}{\sum }_i{[{\sum }_{j}w(t,j)X_{i,t,j}]}^2-K^{-3}{[{\sum \sum }_{i,j}w(t,j)X_{i,t,j}]}^2,$$

thus,

$$\begin{array}{rl}\mathbb{E}(s_{s,t}^2)& =K^{-2}{\sum }_i\mathbb{E}{[{\sum }_{j}w(t,j)X_{i,t,j}]}^2-K^{-3}\mathbb{E}{[{\sum \sum }_{i,j}w(t,j)X_{i,t,j}]}^2\\ & =K^{-2}{\sum }_i\{\mathrm{Var}[{\sum }_{j}w(t,j)X_{i,t,j}]+{({\sum }_j\mathbb{E}[w(t,j)X_{i,t,j}])}^2\}\\ & -K^{-3}\{\mathrm{Var}[{\sum \sum }_{i,j}w(t,j)X_{i,t,j}]+{({\sum \sum }_{i,j}\mathbb{E}[w(t,j)X_{i,t,j}])}^2\}.\end{array}$$

Since the distribution of the number of incidents within a month is the same, we deduce

$$\mathbb{E}(s_{s,t}^2)=K^{-1}\left\{\mathrm{Var}[{\sum }_{j}w(t,j)X_{i,t,j}]-\mathrm{Var}({\hat{\lambda }}_{s,t})\right\}.$$ (A2)

If ${\mathcal{S}}_i$ denote the set of indices ℓ such that $\mathrm{Cov}(\sum _{j}w(t,j)X_{i,t,j},\sum _{j}w(t,j)X_{\ell ,t,j})\ne 0$ then

$$\mathrm{Var}({\hat{\lambda }}_{s,t})=K^{-1}\mathrm{Var}[{\sum }_{j}w(t,j)X_{i,t,j}]+\gamma ,$$ (A3)

where

$$\gamma =K^{-2}{\sum \sum }_{i,\ell \ne i\wedge \ell \in {\mathcal{S}}_i}\mathrm{Cov}({\sum }_{j}w(t,j)X_{i,t,j},{\sum }_{j}w(t,j)X_{\ell ,t,j}).$$

Equations (A2) and (A3) conclude that

$$\mathbb{E}(s_{t,s}^2)=(1-K^{-1})\mathrm{Var}({\hat{\lambda }}_{s,t})-\gamma .$$

Therefore when γ is zero and K is large, $s_{t,s}^2(B)$ is unbiased.

The variance of $s_{t,s}^2(B)$ may be derived when ${\mathcal{S}}_i$ is empty for all is. In the following few paragraphs we derive its formula under the assumption that the distribution of $X_{i,t,j}$ is the same for all values of i and j. This assumption is only forced to simplify the tedious algebra involved in the derivation. Note that $s_{s,t}^2(B)$ may be written as

$$s_{s,t}^2(B)=K^{-2}(1-K^{-1}){\sum }_i{A}_t^2(i)-K^{-3}{\sum \sum }_{i_1\ne i_2}{A}_t(i_1)A_t(i_2),$$

where $A_t(i)=\sum _{j}w(t,j)X_{i,t,j}$. Thus the variance of $s_{s,t}^2(B)$ involves computing the variances of $\sum _i{A}_t^2(i)$ and $\sum \sum _{i_1\ne i_2}{A}_t(i_1)A_t(i_2)$, and the covariance between them. Observe that $\mathrm{Var}\{\sum _i{A}_t^2(i)\}=\sum _{i_1}\sum _{i_2}\mathrm{Cov}[A_t^2(i_1),A_t^2(i_2)]$, since $\mathrm{Cov}[A_t^2(i_1),A_t^2(i_2)]$ is non-zero whenever $i_1=i_2$, then $\mathrm{Var}\{\sum _i{A}_t^2(i)\}=K{\mathcal{V}}_{x,y}{\mathcal{W}}^2$, where ${\mathcal{V}}_{x,y}=\mathrm{Cov}(X_{i_1,t,j_1}{X}_{i_1,t,j_2},X_{i_1,t,j_1}{X}_{i_1,t,j_2})$, $i_1,i_2=1,\dots ,K$ and $\mathcal{W}=\sum _j{w}^2(t,j)$.

To obtain the formula for variance of $\sum \sum _{i_1\ne i_2}{A}_t(i_1)A_t(i_2)$, note that

$$\mathrm{Var}\{{\sum \sum }_{i_1\ne i_2}{A}_t(i_1)A_t(i_2)\}={\sum \sum }_{i_1\ne l_1}{\sum \sum }_{i_2\ne l_2}\mathrm{Cov}[A_t(i_1)A_t(l_1),A_t(i_2)A_t(l_2)],$$ (A4)

and observe that the covariances in the inner summation on the right-hand side are only non-zero whenever one of the following statements is true: $\{i_1=i_2,l_1=l_2\}$, $\{i_1=i_2,l_1\ne l_2\}$, or $\{i_1\ne i_2,l_1=l_2\}$. In fact, for Equation (A4), the former statement is true for exactly $K(K-1)$ elements, and the latter two statements are true for exactly $2K(K-1)(K-2)$ elements. This implies that $\mathrm{Var}\{\sum \sum _{i_1\ne i_2}{A}_t(i_1)A_t(i_2)\}=2(K-2)(K-1)K{\mathcal{E}}^2\mathcal{V}{\mathcal{W}}^2+K(K-1){\mathcal{V}}_{x,y}{\mathcal{W}}^2$, where $\mathcal{E}=\mathbb{E}(X)$, and $\mathcal{V}=\mathrm{Var}(X)$. Similar calculation shows that

$$\mathrm{Cov}({\sum }_{i_1}{A}_t^2(i_1),{\sum \sum }_{i_1\ne i_2}{A}_t(i_1)A_t(i_2))=K(K-1)\rho \mathcal{E}{\mathcal{W}}^2,$$

where $\rho =\mathbb{E}(X^{2}Y)-\mathbb{E}(XY)\mathbb{E}(X)$ for X and Y in the same strata. Thus

$$\begin{array}{rl}\mathrm{Var}[s_{s,t}^2(B)]& =K^{-3}(1-K^{-1}{)}^2{\mathcal{V}}_{x,y}{\mathcal{W}}^2+K^{-5}2(K-2)(K-1){\mathcal{E}}^2\mathcal{V}{\mathcal{W}}^2\\ & +K^{-5}(K-1){\mathcal{V}}_{x,y}{\mathcal{W}}^2-2K^{-4}(1-K^{-1})(K-1)\rho \mathcal{E}{\mathcal{W}}^2.\end{array}$$ (A5)

Although the equation of the variance of $s_{s,t}^2(B)$ does not seem appealing, its asymptotic behaviour might be used to provide some insights into the strata-bootstrap algorithm. Assuming finite values for ${\mathcal{V}}_{x,y}$, $\mathcal{E}$, $\mathcal{V}$, and ρ, when the value of K is large, the behaviour of the variance of $s_{t,s}^2(B)$ in Equation (A5) relies on $K^{-3}{\mathcal{W}}^2$. Thus, for the simple case where the weights are the same for all strata, the variance of the proposed method converge to zero with rate $K^{-1}$ if $C>K^{1/(4+ϵ)}$, where $ϵ>0$ is an arbitrary number and $P_{t,j}$ is increasing along K. More complicated cases need extra assumptions and are not discussed here.

Funding Statement

The research is supported by a GRF grant (HKU: 17102814).

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Mehdi Soleymani http://orcid.org/0000-0001-7609-964X

Paul S. F. Yip  http://orcid.org/0000-0003-1596-4120