Cause-specific hazard regression estimation for modified Weibull distribution under a class of non-informative priors

ABSTRACT

In time to event analysis, the situation of competing risks arises when the individual (or subject) may experience p mutually exclusive causes of death (failure), where cause-specific hazard function is of great importance in this framework. For instance, in malignancy-related death, colorectal cancer is one of the leading causes of the death in the world and death due to other causes considered as competing causes. We include prognostic variables in the model through parametric Cox proportional hazards model. Mostly, in literature exponential, Weibull, etc. distributions have been used for parametric modelling of cause-specific hazard function but they are incapable to accommodate non-monotone failure rate. Therefore, in this article, we consider a modified Weibull distribution which is capable to model survival data with non-monotonic behaviour of hazard rate. For estimating the cumulative cause-specific hazard function, we utilized maximum likelihood and Bayesian methods. A class of non-informative types of prior (uniform, Jeffrey’s and half-t) is introduced for Bayes estimation under squared error (symmetric) as well as LINEX (asymmetric) loss functions. A simulation study is performed for a comprehensive comparison of Bayes and maximum likelihood estimators of cumulative cause-specific hazard function. Real data on colorectal cancer is used to demonstrate the proposed model.

1. Introduction

The situation of competing risks is commonly encountered in public health, demography, actuarial science and engineering applications. In biomedical sciences, it is commonly seen that an individual may experience p mutually exclusive type of events. For example, in colorectal cancer (CRC) study, death due to CRC may be the event of interest, and death due to other cause(s) may consider as competing event(s). For more details on competing risks, refer to [6,9,15]. In survival analysis, the Kaplan–Meier product-limit method is well known to estimate cumulative survival probability of each event, but it is incapable to consider competing causes of event. Therefore, to overcome this limitation, cumulative incidence function (CIF) is recommended in the literature. CIF is also useful for comparison of different group of patients, for detail discussion in this direction, one may refer to [9,14,20].

The cause-specific hazard function [30] is frequently used for analysing the competing risks data in survival analysis. The triplet $\left(T,C=j,\mathbf{\text{X}}\right);j=1,2,\dots ,p$ represents the standard competing risks setting where T is the survival time, C is the causes of failure and X is the vector of covariates. This process is defined in terms of cause-specific hazard function as

$$h_j\left(t|\mathbf{\text{X}}\right)=\underset{\mathrm{\Delta }t\to 0}{lim}\left\{\frac{P\left(t\le T<t+\mathrm{\Delta }t,C=j|T>t,\mathbf{\text{X}}\right)}{\mathrm{\Delta }t}\right\};j=1,2,\dots ,p.$$ (1)

Cause-specific hazard function simply gives the instantaneous failure rate from the cause j among subjects who are currently event free (i.e. subjects who have not yet experienced any competing events). The CIF is the probability of failure from cause j in the presence of all other risks which is defined as

$$F_j\left(t|\mathbf{\text{X}}\right)=P\left(T\le t,C=j|\mathbf{\text{X}}\right);j=1,2,\dots ,p.$$ (2)

CIF can be obtained in terms of cause-specific hazard function as

$$F_j\left(t|\mathbf{\text{X}}\right)={\int }_0^t{h}_j\left(u|\mathbf{\text{X}}\right)\exp \left(-\sum _{j=1}^p{H}_j\left(u|\mathbf{\text{X}}\right)\right)\text{d}u.$$ (3)

Since

$$H_j\left(t|\mathbf{\text{X}}\right)={\int }_0^t{h}_j\left(u|\mathbf{\text{X}}\right)\text{d}u$$ (4)

and overall survival function is given as

$$S\left(t|\mathbf{\text{X}}\right)=\exp \left(-\sum _{j=1}^p{\int }_0^t{h}_j\left(u|\mathbf{\text{X}}\right)\text{d}u\right).$$ (5)

For interpretation and application of equations (1)–(5), one could refer to [9,29].

A plenty of work on parametric modelling of competing risks are available in the literature under the cause-specific hazard function. Bryant and Dignam [7] considered the constant cause-specific hazard function for the primary event of interest and other mode of hazard estimated non-parametrically. Benichou and Gail [5] estimated the absolute risk by assuming that the cause-specific hazard function follows piecewise exponential as well as exponential distribution. Jeong and Fine [17] considered Weibull cause-specific hazard likelihood estimation and compared with direct likelihood approach by assuming improper Gompertz distribution for CIF and later Jeong and Fine [18] extend this work for parametric regression approach for estimating CIF. Anjana and Sankaran [2] proposed the parametric reverse cause-specific hazard function by assuming inverse Weibull model under left censoring. Lee [22] considered the parametric quantile inference for cause-specific hazard function with adjustment of covariates.

In this paper, we consider parametric competing risks survival analysis through cause-specific hazard approach using the Cox regression model. The commonly used parametric survival models are exponential, Weibull, gamma and log-logistic, etc. in which only monotone shape of the hazard function can be accommodate. A number of work on the generalization of Weibull distribution [21,27] are available in the literature. These distributions have importance due to the flexibility to accommodate various (unimodal and bathtub) shape of the hazard. Which motivate us to analyse the competing risks data using the modified Weibull distribution (MWD) [21] via cause-specific hazard function. The MWD is capable to capture the various behaviour of the hazard depending on shape parameter.

In the literature, most of the work in this direction are focused on classical approach rather than Bayesian approach in estimating the cause-specific hazard function. While dealing with lifetime data, it is obvious that some past information may available in terms of the past record of the subject. For example, in medical science, before examine a patient, investigator may be interested to know his/her history of disease. Classical statistical methods do not have such flexibility to incorporate the prior information in data analysis. Bayesian methods of reasoning well known to incorporate the prior information [24]. Bayesian estimation technique may give some better inference for small sample size and the information about the observation is incomplete. These situations are commonly encountered in reliability and survival analysis. Such facts motivate us to propose Bayesian method of estimation.

However, in the literature, researchers employ Bayesian methods of estimation through semiparametric approach in competing risks survival analysis. Sen et al. [31] estimated the cumulative cause-specific hazard function with masking by considering the Bayes estimate using gamma process prior. Sreedevi and Sankaran [34] proposed the semiparametric Bayesian approach for cause-specific hazard function using gamma process prior for baseline cumulative cause-specific hazard function. Ge and Chen [10] considered the Bayesian analysis for fully specified subdistribution hazard function by considering gamma process prior for cumulative cause-specific hazard function. The aim of this attempt is to employ the Bayesian methods of estimation in competing risks modelling through parametric cause-specific hazard function. Also, we consider a class of non-informative types of prior, namely, uniform, Jeffrey’s and half-t with two different loss functions, viz, squared error (symmetric) and LINEX loss functions (asymmetric).

The rest of the paper is organised as follows: we discuss parametric cause-specific hazard regression analysis in competing risks set-up through MWD in Section 2. The maximum likelihood estimation of cause-specific hazard function is presented in Section 3. The Bayesian analysis is given in Section 4. A simulation study of the proposed methods is presented in Section 5. Application of the proposed model to CRC study is presented in Section 6. Moreover, in Section 6, the fit of the proposed model and proposed methods are compared based on competing causes. Finally, Section 7 presented the brief conclusion.

2. Parametric cause-specific hazard regression model

In practical situation, the population may not be homogenous. Heterogeneity can be represented in terms of covariates or explanatory variables (such as treatment, age, sex, etc.). In survival analysis, the well-known proportional hazards model [8] used to measure the effect of covariates on failure time. Cause-specific hazard function can extend in terms of proportional hazard model as follows:

$$h_j\left(t|\mathbf{\text{X}}\right)=h_{0j}\left(t\right)\exp \left({\mathrm{\text{β}}}_j^{\mathrm{\prime }}\mathbf{\text{X}}\right),j=1,2,\dots ,p,$$ (6)

where X is m×1 vector of covariates and ${\mathrm{\text{β}}}_j$ is a m×1 vector of regression constant attached with covariate X. In Equation (6), $h_j\left(t|\mathbf{\text{X}}\right)$ is the cause-specific hazard function in the presence of covariate X and the effect of the covariates are multiplicative. The baseline hazard rate $h_{0j}\left(t\right)$ is assumed to follow an MWD. The distribution function and hazard function of MWD are given as follows:

$$\begin{array}{rl}F\left(t\right)& =1-\exp \left(-a{t}^{\alpha }{\text{e}}^{\lambda t}\right);t\ge 0,\alpha \ge 0,\lambda >0,a>0,\end{array}$$ (7)

$$\begin{array}{rl}h\left(t\right)& =a\left(\alpha +\lambda t\right)t^{\alpha -1}{\text{e}}^{\lambda t};t\ge 0,\alpha \ge 0,\lambda >0,a>0.\end{array}$$ (8)

The MWD is competent to modelling the failure data set which exhibit bathtub shape of the hazard function, where a is the scale parameter, $\alpha$ and $\lambda$ are the shape parameters. The MWD received considerable attention in lifetime data analysis. Ng [28] discussed the parameter estimation of MWD for progressively type -II censored data. Some extensive study on MWD are available in [19,35]. The MWD is assumed here as a baseline model of the Cox regression analysis due to its flexibility to accommodate various shape of hazard.

The baseline cause-specific hazard function corresponding to MWD is defined as

$$h_{0j}\left(t\right)=a_j\left({\alpha }_j+{\lambda }_{j}t\right)t^{{\alpha }_j-1}{\text{e}}^{{\lambda }_{j}t};t\ge 0,{\alpha }_j\ge 0,{\lambda }_j>0,a_j>0.$$ (9)

The corresponding regression cause-specific hazard function, survival function and cumulative hazard function in the presence of covariate X are given below

$$\begin{array}{rl}{h}_j\left(t|\mathbf{\text{X}}\right)& =a_j\left({\alpha }_j+{\lambda }_{j}t\right)t^{{\alpha }_j-1}{\text{e}}^{{\lambda }_{j}t}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}\mathbf{\text{X}}},\end{array}$$ (10)

$$\begin{array}{rl}S\left(t|\mathbf{\text{X}}\right)& =\exp \left(-\sum _{j=1}^p{H}_j\left(t|\mathbf{\text{X}}\right)\right),\end{array}$$ (11)

$$\begin{array}{rl}{H}_j\left(t|\mathbf{\text{X}}\right)& =a_j{t}^{{\alpha }_j}{\text{e}}^{{\mathrm{\text{λ}}}_{j}t}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}\mathbf{\text{X}}},\end{array}$$ (12)

where

$$t\ge 0,{\alpha }_j\ge 0,{\lambda }_j>0,a_j>0,-\mathrm{\infty }<{\mathrm{\text{β}}}_j<\mathrm{\infty }\text{.}$$

The main interest of this attempt is the parameter estimation of cause-specific hazard function using Bayes and maximum likelihood estimates. Also, based on it make a comprehensive comparative of the estimate of cumulative cause-specific hazard function using (12).

3. Maximum likelihood (ML) estimation under cause-specific approach

According to Prentice et al. [30], we consider $\left(t_i,j_i,c_i,{\mathbf{\text{X}}}_i\right),i=1,2,\dots ,n$ be the observed samples of the ith individual. Where t_i is the observed time, j_i is the observed cause of failure, c_i is a censoring variable and X_i is the vector of m covariate of the ith individual. The likelihood function of n independent observations in the cause-specific hazard framework is given by

$$L=\prod _{i=1}^n\left(\prod _{j=1}^p{h}_j{\left(t_i|{\mathbf{\text{X}}}_i\right)}^{I\left(c_i=j\right)}S\left(t_i|{\mathbf{\text{X}}}_i\right)\right).$$

The cause-specific hazard likelihood function using Equations (10) and (11) is

$$\begin{array}{rl}L\left({\mathbf{\text{t}}}_i,{\mathbf{\text{X}}}_i|a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j\right)& =\prod _{i=1}^n\prod _{j=1}^p{\left(a_j\left({\alpha }_j+{\lambda }_j{t}_i\right)t_i^{{\alpha }_j-1}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)}^{I\left(c_i=j\right)}\\ & \times \exp \left(-\sum _{j=1}^p{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_{\mathbf{\text{i}}}}\right).\end{array}$$ (13)

The log-likelihood function is given as

$$\begin{array}{rl}l& =\sum _{j=1}^p{n}_j\log a_j+\sum _{j=1}^p\sum _{i=1}^{n_j}\log \left({\alpha }_j+{\lambda }_j{t}_i\right)+\sum _{j=1}^p\sum _{i=1}^{n_j}\left({\alpha }_j-1\right)\log t_i+\sum _{j=1}^p{\lambda }_j\sum _{i=1}^{n_j}{t}_i\\ & +\sum _{j=1}^p\sum _{i=}^{n_j}{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i-\sum _{j=1}^p\sum _{i=1}^n{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}.\end{array}$$

The normal equations of likelihood function are given below

$$\begin{array}{rl}\frac{\mathrm{\partial }l}{\mathrm{\partial }{a}_j}& =\frac{n_j}{a_j}-\sum _{i=1}^n{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}=0\end{array}$$ (14)

$$\begin{array}{rl}\frac{\mathrm{\partial }l}{\mathrm{\partial }{\alpha }_j}& =\sum _{i=1}^{n_j}\frac{1}{{\alpha }_j+{\lambda }_j{t}_i}+\sum _{i=1}^{n_j}\log t_i-\sum _{i=1}^n{t}_i^{{\alpha }_j}\log t_i{a}_j{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}=0\end{array}$$ (15)

$$\begin{array}{rl}\frac{\mathrm{\partial }l}{\mathrm{\partial }{\lambda }_j}& =\sum _{i=1}^{n_j}\frac{t_i}{{\alpha }_j+{\lambda }_j{t}_i}+\sum _{i=1}^{n_j}{t}_i-\sum _{i=1}^n{t}_i^{{\alpha }_j+1}{a}_j{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}=0\end{array}$$ (16)

$$\begin{array}{rl}\frac{\mathrm{\partial }l}{\mathrm{\partial }{\mathrm{\text{β}}}_j}& =\sum _{i=1}^{n_j}{\mathbf{\text{X}}}_i-\sum _{i=1}^n{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\mathit{X}}_i{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}=0\end{array}$$ (17)

The likelihood equations (14)–(17) are not in explicit form and cannot be solved analytically. We solve the likelihood equations numerically by using the Newton–Raphson iterative procedure. Under invariance property, the MLE ${\hat{H}}_j\left(t|\mathit{X}\right)$ of cumulative cause-specific hazard function may be obtained by replacing $a_j,{\alpha }_j,{\lambda }_j$ and ${\mathrm{\text{β}}}_j$ by their MLEs ${\hat{a}}_j,{\hat{\alpha }}_j,{\hat{\lambda }}_j$ and ${\widehat{\mathrm{\text{β}}}}_j$, respectively, in (12). Hence, the same, therefore, given by

$${\hat{H}}_j\left(t|\mathit{X}\right)={\hat{a}}_j{t}^{{\widehat{\mathrm{\text{α}}}}_j}{\text{e}}^{{\widehat{\mathrm{\text{λ}}}}_{j}t}{\text{e}}^{{\widehat{\mathrm{\text{β}}}}_j\mathit{X}}.$$

4. Bayes estimate under cause-specific hazard approach

The novelty of Bayesian inference is that it incorporates the prior or past information with the observed information. The Bayesian analysis involves three steps for obtaining the Bayes estimates. First, the assumption of prior information which may be informative, non-informative and weakly informative, i.e. it contains some information between non-informative and informative information. Second is the posterior distribution of the underlying parameter of interest. Third is the selection of appropriate loss function for obtaining the Bayes estimate.

4.1. Assumption of priors

The assumption of priors is fully based on past experiences and expert opinions. The choice of priors is wholly subjective guess or simply depend on mathematical convenient. If the past information is available enough with the evidence of support, one may consider the informative priors. In the case, when information relatively little or vague information (a priori) about the parameter, then non-informative prior may considered. The non-informative prior often leads to a class of improper priors [33].

In this article, we consider a class of non-informative types of prior which consists uniform, Jeffrey’s and half-t distributions for baseline parameters. The normal non-informative prior is assumed for regression parameters.

4.1.1. Uniform prior

We assume that random variables $a_j,{\alpha }_j$ and ${\mathrm{\text{λ}}}_j$ are independently follow a uniform distribution and the random variables ${\mathrm{\text{β}}}_j$ independently follows normal distribution as a non-informative priors, i.e.

$${\pi }_1\left(a_j\right)\propto 1;0<a_j<1,{\pi }_1\left({\alpha }_j\right)\propto 1;0<{\alpha }_j<1,{\pi }_1\left({\lambda }_j\right)\propto 1;0<{\mathrm{\text{λ}}}_j<1$$

and ${\pi }_1\left({\mathrm{\text{β}}}_j\right)\sim N\left(0,1000\right)$. The joint prior distribution of $a_j,{\alpha }_j,{\lambda }_j$ and ${\mathrm{\text{β}}}_j$ is equivalent to

$${\pi }_1\left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j\right)\propto {\text{e}}^{\frac{{\mathbf{-}\mathrm{\text{β}}}_j^2}{2\times 1000}};-\mathrm{\infty }<{\mathrm{\text{β}}}_j<\mathrm{\infty }.$$ (18)

4.1.2. Jeffrey’s prior

We consider the prior according to Jeffrey’s rule (see Sinha [33]) for baseline parameters, i.e. if the domain of parameter is on positive real line then log of parameter is uniformly distributed. The formation of prior is as follows:

$$\begin{array}{rl}& {\pi }_2\left(a_j\right)\propto \frac{1}{a_j};0<a_j<\mathrm{\infty },{\pi }_2\left({\alpha }_j\right)\propto \frac{1}{{\alpha }_j};0<{\alpha }_j<\mathrm{\infty },{\pi }_2\left({\lambda }_j\right)\propto \frac{1}{{\lambda }_j};0<{\mathrm{\text{λ}}}_j<\mathrm{\infty }\text{and}\\ & {\pi }_2\left({\mathrm{\text{β}}}_j\right)\propto N\left(0,1000\right);-\mathrm{\infty }<{\mathrm{\text{β}}}_j<\mathrm{\infty }\text{.}\end{array}$$

The joint prior distribution of $a_j,{\alpha }_j,{\lambda }_j$ and ${\mathrm{\text{β}}}_j$ under independent assumption is equivalent to

$${\pi }_2\left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j\right)\propto \frac{1}{a_j{\alpha }_j{\lambda }_j}{\text{e}}^{\frac{-{\mathrm{\text{β}}}_j^2}{2\times 1000}};a_j,{\alpha }_j{\mathrm{\text{λ}}}_j>0,-\mathrm{\infty }<{\mathrm{\text{β}}}_j<\mathrm{\infty }\text{.}$$ (19)

4.1.3. Half-t prior

Gelman [11] suggested half-t is a default non-informative prior for a large and finite value of the variance (scale parameter) of t distribution. It gives relatively more information compared to uniform/Jeffrey’s priors because half-t prior is not completely flat but nearly flat. In the case when prior distribution contains enough information, numerical approximation algorithm easily explore the target density, i.e. posterior distribution (see Akhtar and Khan [32]). The specification of independent and identically half-t prior for baseline parameters and normal prior for regression parameters are given below

$$\begin{array}{rl}& {\pi }_3\left(a_j\right)\propto {\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{a_j}{\sigma }\right)\right)}^{-\left(\frac{\mathrm{\text{ν}}+1}{2}\right)},{\pi }_3\left({\alpha }_j\right)\propto {\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\alpha }_j}{\sigma }\right)\right)}^{-\left(\frac{\mathrm{\text{ν}}+1}{2}\right)},\\ & {\pi }_3\left({\lambda }_j\right)\propto {\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\lambda }_j}{\sigma }\right)\right)}^{-\left(\frac{\mathrm{\text{ν}}+1}{2}\right)}\end{array}$$

and

$${\pi }_3\left({\mathrm{\text{β}}}_j\right)\propto {\text{e}}^{\frac{\mathbf{-}{\mathrm{\text{β}}}_j^2}{2\times 1000}};a_j,{\alpha }_j,{\mathrm{\text{λ}}}_j,\sigma >0,-\mathrm{\infty }<{\mathrm{\text{β}}}_j<\mathrm{\infty }.$$

The joint prior distribution of $a_j,{\alpha }_j,{\lambda }_j$ and ${\mathrm{\text{β}}}_j$ is given by

$${\pi }_3\left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j\right)\propto {\left(\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{a_j}{\sigma }\right)\right)\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\alpha }_j}{\sigma }\right)\right)\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\lambda }_j}{\sigma }\right)\right)\right)}^{-\left(\frac{\mathrm{\text{ν}}+1}{2}\right)}{\text{e}}^{\frac{-{\mathrm{\text{β}}}_j^2}{2\times 1000}}\text{.}$$ (20)

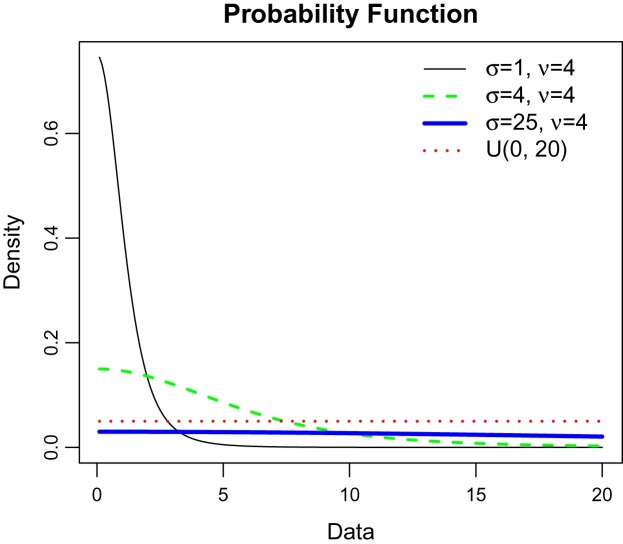
where $\mathrm{\text{ν}}$ denotes the degree of freedom and $\sigma >0$ is the scale parameter of the half-t distribution. Figure 1 shows that at $\alpha =25$ and $\nu =4$ half-t becomes approximate to uniform.

Figure 1.

Half-t density plot.

4.2. Posterior analysis

The posterior probability distribution is obtained by combining the past information with the observed sample through likelihood and prior distribution. The joint posterior probability density function of parameters is directly proportional to the product of likelihood and joint prior density, defined as follows:

$$p\left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j|{\mathbf{\text{t}}}_i,{\mathbf{\text{X}}}_i\right)\propto L\left({\mathbf{\text{t}}}_i,{\mathbf{\text{X}}}_i|a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j\right)\pi \left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j\right)$$

By combining the joint prior densities of $a_j,{\alpha }_j,{\lambda }_j$ and ${\mathrm{\text{β}}}_j$ in (18)–(20) with likelihood in (13), then the joint posterior distributions are obtained as follows:

$$\begin{array}{rl}{p}_1\left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j|{\mathbf{\text{t}}}_i,{\mathbf{\text{X}}}_i\right)& =K_1\prod _{i=1}^n\prod _{j=1}^p{\left(a_j\left({\alpha }_j+{\lambda }_j{t}_i\right)t_i^{{\alpha }_j-1}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)}^{I\left(c_i=j\right)}\\ & \times \exp \left(-\sum _{j=1}^p{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right){\text{e}}^{\frac{\mathbf{-}{\mathrm{\text{β}}}_j^2}{2\times 1000}}\end{array}$$ (21)

$$\begin{array}{rl}{p}_2\left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j|{\mathbf{\text{t}}}_i,{\mathbf{\text{X}}}_i\right)& =K_2\prod _{i=1}^n\prod _{j=1}^p{\left(a_j\left({\alpha }_j+{\lambda }_j{t}_i\right)t_i^{{\alpha }_j-1}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)}^{I\left(c_i=j\right)}\\ & \times \exp \left(-\sum _{j=1}^p{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)\frac{1}{a_j{\alpha }_j{\lambda }_j}{\text{e}}^{\frac{\mathbf{-}{\mathrm{\text{β}}}_j^2}{2\times 1000}}\end{array}$$ (22)

$$\begin{array}{rl}{p}_3\left(a_j,{\alpha }_j,{\lambda }_j,{\mathrm{\text{β}}}_j|{\mathbf{\text{t}}}_i,{\mathbf{\text{X}}}_i\right)& =K_3\prod _{i=1}^n\prod _{j=1}^p{\left(a_j\left({\alpha }_j+{\lambda }_j{t}_i\right)t_i^{{\alpha }_j-1}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)}^{I\left(c_i=j\right)}\\ & \times \exp \left(-\sum _{j=1}^p{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)\\ & \times \left(\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{a_j}{\sigma }\right)\right)\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\alpha }_j}{\sigma }\right)\right)\right.\\ & \times {\left.\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\lambda }_j}{\sigma }\right)\right)\right)}^{-\left(\frac{\mathrm{\text{ν}}+1}{2}\right)}{\text{e}}^{\frac{{\mathbf{-}\mathrm{\text{β}}}_j^2}{2\times 1000}}.\end{array}$$ (23)

where K₁, K₂ and K₃ are the normalizing proportionality constants given by

$$\begin{array}{rl}{K_1}^{-1}& ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\prod _{i=1}^n\prod _{j=1}^p{\left(a_j\left({\alpha }_j+{\lambda }_j{t}_i\right)t_i^{{\alpha }_j-1}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)}^{I\left(c_i=j\right)}\\ & \times \exp \left(-\sum _{j=1}^p{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right){\text{e}}^{\frac{\mathbf{-}{\mathrm{\text{β}}}_j^2}{2\times 1000}}\text{d}{a}_j\text{d}{\alpha }_j\text{d}{\lambda }_j\text{d}{\mathrm{\text{β}}}_j\end{array}$$

$$\begin{array}{rl}{K_2}^{-1}& ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\prod _{i=1}^n\prod _{j=1}^p{\left(a_j\left({\alpha }_j+{\lambda }_j{t}_i\right)t_i^{{\alpha }_j-1}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)}^{I\left(c_i=j\right)}\\ & \times \exp \left(-\sum _{j=1}^p{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)\frac{1}{a_j{\alpha }_j{\lambda }_j}{\text{e}}^{\frac{\mathbf{-}{\mathrm{\text{β}}}_j^2}{2\times 1000}}\text{d}{a}_j\text{d}{\alpha }_j\text{d}{\lambda }_j\text{d}{\mathrm{\text{β}}}_j\end{array}$$

and

$$\begin{array}{rl}{K_3}^{-1}& ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\prod _{i=1}^n\prod _{j=1}^p{\left(a_j\left({\alpha }_j+{\lambda }_j{t}_i\right)t_i^{{\alpha }_j-1}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)}^{I\left(c_i=j\right)}\\ & \times \exp \left(-\sum _{j=1}^p{a}_j{t}_i^{{\alpha }_j}{\text{e}}^{{\lambda }_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}{\mathbf{\text{X}}}_i}\right)\\ & \times {\left(\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{a_j}{\sigma }\right)\right)\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\alpha }_j}{\sigma }\right)\right)\left(1+\frac{1}{\mathrm{\text{ν}}}\left(\frac{{\lambda }_j}{\sigma }\right)\right)\right)}^{-\left(\frac{\mathrm{\text{ν}}+1}{2}\right)}{\text{e}}^{\frac{\mathbf{-}{\mathrm{\text{β}}}_j^2}{2\times 1000}}\text{d}{a}_j\text{d}{\alpha }_j\text{d}{\lambda }_j\text{d}{\mathrm{\text{β}}}_j.\end{array}$$

It seems that under uniform prior, the conditional marginal density up to the proportionality of parameter a_j to be a gamma density with shape parameter n_j and rate parameter ${\sum }_{i=1}^n{t}^{{\alpha }_j}{\text{e}}^{{\mathrm{\text{λ}}}_j{t}_i}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}\mathbf{\text{X}}}$. Therefore, the posterior random samples can be easily generated from the gamma density. However, conditional posterior density functions for other parameters ${\alpha }_j\text{and}{\mathrm{\text{λ}}}_j$ are log concave, then Highly Efficient Derivative Free Adaptive Rejection algorithm [13] can be used for generating the posterior samples. But, for Jeffrey’s and half-t prior, it is difficult to obtain the log concavity property of conditional posterior densities. So, in this situation, Metropolis–Hasting algorithm [25,16] is considered.

4.3. Loss function

The selection of the loss function is vital in Bayesian analysis. In this article, we used two different types of loss function, i.e. symmetric and asymmetric which are squared error loss function (SELF) [33] and LINEX loss function (LLF) [1], respectively. Under SELF, the Bayes estimator of $H_j\left(t|\mathbf{\text{X}}\right)$ is the posterior mean, i.e.

$${\hat{H}}_j^{\text{self}}\left(t|\mathbf{\text{ {X}}}\right)=\frac{1}{N}\sum _{l=1}^N{\left[{\hat{H}}_j\left(t|\mathbf{\text{ {X}}}\right)\right]}_{{\mathrm{\text{α}}}_j={\mathrm{\text{α}}}_l,{\mathrm{\text{λ}}}_j={\mathrm{\text{λ}}}_l,a_j=a_l,{\mathrm{\text{β}}}_j={\mathrm{\text{β}}}_l}$$

and under LLF, the Bayes estimator of $H_j\left(t|\mathbf{\text{X}}\right)$ is defined as

$${\hat{H}}_j^{\text{llf}}\left(t|\mathbf{\text{ X}}\right)=-\frac{1}{p}\log \left(\frac{1}{N}\sum _{l=1}^N{\text{e}}^{-p{\left[{\hat{H}}_j\left(t|\mathbf{\text{ X}}\right)\right]}_{{\mathrm{\text{α}}}_j={\mathrm{\text{α}}}_l,{\mathrm{\text{λ}}}_j={\mathrm{\text{λ}}}_l,a_j=a_l,{\mathrm{\text{β}}}_j={\mathrm{\text{β}}}_l}}\right)$$

where ${\mathrm{\text{α}}}_l,{\mathrm{\text{λ}}}_l,a_l$ and ${\mathrm{\text{β}}}_l$, $l=1,2,\dots ,N$ are the random sample drawn from the posterior distributions of ${\mathrm{\text{α}}}_j,{\mathrm{\text{λ}}}_j,a_j$ and ${\mathrm{\text{β}}}_j$, respectively, through MCMC algorithm and p is the hyper-parameter of LLF which is assumed to be known.

5. Numerical illustration

We conducted a simulation study to observe the behaviour of the maximum likelihood and Bayes estimators of cumulative cause-specific hazard function. We generate the random samples through inverse transformation for four different sample sizes (20, 50, 100, 200). For each sample sizes, we simulated 500 sets of data. In this scenario, we computed average estimates and empirical mean square error (MSE) for each of cumulative cause-specific hazard estimators.

In the simulation study, we assume the two causes of failures (j=1,2) and one single covariate X. We propose MWD baseline hazard function as defined in (9) for (j=1,2) and assume that ${\mathrm{\text{λ}}}_j$ to be known for mathematical convenient. To generate the data sets, the following steps are considered:

Step 1: Let $a_1=0.5,{\alpha }_1=0.7,{\mathrm{\text{λ}}}_1=0.1,{\mathrm{\text{β}}}_1=0.1$ and $a_2=0.4,{\alpha }_2=0.5,{\mathrm{\text{λ}}}_2=0.1,{\mathrm{\text{β}}}_2=0.1$ for cause 1 and cause 2, respectively. The covariate X is generated from standard normal distribution.

Step 2: The inverse transformation method is applied to generate the time variable T, since the expression of the quantile function $a{t}_q^{\alpha }{\text{e}}^{\mathrm{\text{λ}}{t}_q}{\text{e}}^{{\mathrm{\text{β}}}_j^{\mathrm{\prime }}\mathbf{\text{X}}}+\log \left(1-q\right)=0$ of MWD is not in explicit form, so we used the uniroot function, see [6] for solving the following equation:

$$H_1\left(t_q\right)+H_2\left(t_q\right)+\log \left(1-q\right)=0,q\in \left[0,1\right].$$

Step 3: Further, we generate the two causes of failure from the binomial distribution with probability of success p(t) is $h_1\left(t\right)/h\left(t\right)$ for cause 1, where $h\left(t\right)=h_1\left(t\right)+h_2\left(t\right)$ and $(1-(h_1\left(t\right)/h\left(t\right)\left)\right)$ is probability of failure and failure outcome is considered as cause 2.

Step 4: The censoring time C_i is generated from $U(0,c_i)$, where c_i is imposing the percentage of censoring around 20%. The observed failure/censoring time were calculated as $t_i=min\left\{T_i,C_i\right\}$.

It is noticed that the likelihood equations (14)–(17) are not in explicit form and cannot be solved analytically. So, as an alternative, the iterative procedure in R through optim function is used. For obtaining the standard error of the model parameters, we used inverse of the hessian matrix. The Bayes estimators of baseline and regression parameters were calculated for three types of non-informative prior (uniform, Jeffrey’s and half-t) and normal non-informative, respectively, under SELF as well as LINEX loss function. The joint posterior densities in Equations (21)–(23) are not in explicit form and it is difficult to obtain the marginal posterior densities. So, we used MCMC simulation techniques for generating the random samples from the posterior distribution for calculating the Bayes estimates.

We generated 8000 MCMC samples by using BUGS software in R through OpenBUGS interface [23]. The OpenBugs software implements various popular MCMC algorithms such as Gibbs sampling [12] and Metropolis–Hastings algorithm [16], etc., the implementation of algorithm depends on the characteristics of the conditional posterior distribution. Suppose that if the conditional distribution is log concave then BUGS system use the adaptive rejection sampling [13] and if the conditional distribution have unrestricted range, then BUGS system use Metropolis–Hastings algorithm.

For reducing the effect of the initial values, the first half of the samples were used in burn-in period. The effect of the autocorrelation of the chain is observed and it found that the chains are autocorrelated. So, for minimizing the effect of the autocorrelation every second equally spaced outcome is considered, i.e. thin=2. By the visualization of the convergence diagnostics plots, it is realized that chains are converging nicely.

The comparisons of the proposed estimators were carried out through cumulative cause-specific hazard function $H_j\left(t|\mathbf{\text{X}}\right),j=1,2$ at different time points with fixed value of covariate X= −0.3. The findings of simulation study are presented in Tables 1–4 for varying sample sizes n=20, 50, 100, and 200, respectively, with the fixed parameters value $a_1=0.5,{\alpha }_1=0.7,{\mathrm{\text{λ}}}_1=0.1,{\mathrm{\text{β}}}_1=0.1$, and $a_2=0.4,{\alpha }_2=0.5,{\mathrm{\text{λ}}}_2=0.1,{\mathrm{\text{β}}}_2=0.1$ corresponding to cause 1 and cause 2, respectively. The average estimates and MSE of ML and Bayes estimates of cumulative cause-specific hazard function are tabulated in these tables. The simulation results showed that

• for sample size 20, the MSE of the cumulative cause-specific hazard function of both causes is minimum for Bayes estimators with uniform and Jeffrey’s prior under both loss functions when compared with MLE. The Bayes estimators of ${\hat{H}}_j\left(t|\text{X = - 0}\text{.3}\right),j=1,2$ at t=0.5, 0.8 for half-t prior under both loss functions are close to MLE.

• Table 2 shows that the MSE of ML and Bayes estimators for half-t prior are very similar for sample size 50. Moreover, the Bayes estimates for Jeffrey’s and uniform priors under both loss functions are giving more precise results.

• For sample sizes 100 and 200, the magnitude of MSE for Bayes and ML estimates is negligible for both the causes.

• Simulation study shows that the MSE of cumulative cause-specific hazard function is decreasing while increasing the sample size.

Table 1.

ML, Bayes estimates and their MSEs for cumulative cause-specific hazard function.

n=20		Cause 1			Cause 2
Time points		0.5	0.8	1.0	0.5	0.8	1.0
True value		0.314	0.44962	0.53625	0.28856	0.37611	0.429
ML	Estimate	0.31166	0.46562	0.56964	0.28339	0.38589	0.45099
	MSE	2.20604	4.13323	6.00515	2.21305	3.85869	5.26992
Uniform SELF	Estimate	0.33451	0.47848	0.57189	0.29453	0.39727	0.462
	MSE	1.00098	1.9108	2.71769	1.30191	2.28909	3.12379
Jeffrey’s SELF	Estimate	0.31197	0.43964	0.52189	0.26571	0.3514	0.4049
	MSE	1.00382	1.88687	2.65315	1.34578	2.26356	2.98688
Half-t SELF	Estimate	0.32014	0.48209	0.5946	0.29548	0.40765	0.48072
	MSE	2.08172	4.12568	6.37563	2.05055	3.70597	5.19398
Uniform LLF p=1.5	Estimate	0.32597	0.46312	0.55047	0.28569	0.38265	0.44251
	MSE	0.94103	1.77863	2.49443	1.23144	2.10907	2.81362
Jeffrey’s LLF p=1.5	Estimate	0.30335	0.42442	0.5009	0.25726	0.33775	0.38697
	MSE	0.97306	1.85059	2.60594	1.31385	2.1903	2.85998
Half-t LLF p=1.5	Estimate	0.30824	0.45992	0.56242	0.28435	0.38865	0.45486
	MSE	1.88908	3.50911	5.08124	1.85609	3.15865	4.22126
Uniform LLF p=−1.5	Estimate	0.34346	0.49447	0.59423	0.30392	0.41285	0.48291
	MSE	1.07572	2.08256	3.01731	1.39152	2.51823	3.52356
Jeffrey’s LLF p=−1.5	Estimate	0.32108	0.45568	0.54411	0.27476	0.3661	0.42439
	MSE	1.04877	1.95989	2.76975	1.39482	2.37913	3.18899
Half-t LLF p=−1.5	Estimate	0.33345	0.50769	0.63363	0.30792	0.42955	0.51154
	MSE	2.34904	5.05913	8.61909	2.31487	4.51397	6.76714

Table 2.

ML, Bayes estimates and their MSEs for cumulative cause-specific hazard function.

n=50		Cause 1			Cause 2
Time points		0.5	0.8	1.0	0.5	0.8	1.0
True value		0.314	0.44962	0.53625	0.28856	0.37611	0.429
ML	Estimate	0.32066	0.46474	0.55824	0.29061	0.38786	0.44788
	MSE	0.8354	1.55794	2.1983	0.74852	1.26721	1.70019
Uniform SELF	Estimate	0.32794	0.47099	0.56348	0.29274	0.39201	0.45372
	MSE	0.63491	1.2246	1.74489	0.6313	1.10369	1.50926
Jeffrey’s SELF	Estimate	0.31936	0.45555	0.54327	0.28203	0.37407	0.431
	MSE	0.60652	1.14631	1.6161	0.61198	1.03107	1.37589
Half-t SELF	Estimate	0.32141	0.46655	0.56153	0.2933	0.39373	0.45637
	MSE	0.76166	1.43693	2.04978	0.66527	1.16057	1.59296
Uniform LLF p=1.5	Estimate	0.32371	0.46357	0.55326	0.28869	0.38545	0.44508
	MSE	0.60848	1.15968	1.63327	0.60978	1.04355	1.40429
Jeffrey’s LLF p=1.5	Estimate	0.31518	0.44827	0.53328	0.27808	0.36775	0.42274
	MSE	0.58685	1.10334	1.54473	0.59926	0.99546	1.31283
Half-t LLF p=1.5	Estimate	0.31678	0.45853	0.55053	0.28907	0.38689	0.44736
	MSE	0.73123	1.35034	1.89116	0.64019	1.08991	1.46941
Uniform LLF p=−1.5	Estimate	0.33231	0.47868	0.5741	0.29696	0.39886	0.46279
	MSE	0.66571	1.30204	1.88046	0.65722	1.17594	1.63629
Jeffrey’s LLF p=−1.5	Estimate	0.32369	0.4631	0.55366	0.28613	0.38068	0.4397
	MSE	0.6304	1.20124	1.71018	0.62872	1.07744	1.45826
Half-t LLF p=−1.5	Estimate	0.32624	0.47496	0.57317	0.2977	0.4009	0.4659
	MSE	0.79855	1.54436	2.25055	0.69574	1.2468	1.74554

Table 3.

ML, Bayes estimates and their MSEs for cumulative cause-specific hazard function.

n=100		Cause 1			Cause 2
Time points		0.5	0.8	1.0	0.5	0.8	1.0
True value		0.314	0.44962	0.53625	0.28856	0.37611	0.429
ML	Estimate	0.32419	0.46686	0.55869	0.29398	0.38903	0.44713
	MSE	0.45332	0.83328	1.16129	0.41779	0.7092	0.94199
Uniform SELF	Estimate	0.32726	0.47098	0.56369	0.29443	0.39079	0.45
	MSE	0.42371	0.80473	1.13882	0.39568	0.67878	0.90876
Jeffrey’s SELF	Estimate	0.32318	0.4633	0.55347	0.28937	0.38213	0.43897
	MSE	0.40863	0.76046	1.06445	0.38127	0.63975	0.8449
Half-t SELF	Estimate	0.3249	0.46854	0.56141	0.29524	0.39199	0.45146
	MSE	0.43737	0.81556	1.14826	0.39667	0.68198	0.91439
Uniform LLF p=1.5	Estimate	0.325	0.46709	0.55838	0.29235	0.38749	0.44571
	MSE	0.41137	0.77309	1.08443	0.38714	0.65593	0.87036
Jeffrey’s LLF p=1.5	Estimate	0.32095	0.45948	0.54827	0.28733	0.37891	0.43479
	MSE	0.39835	0.73535	1.02193	0.37499	0.62306	0.81686
Half-t LLF p=1.5	Estimate	0.32258	0.46459	0.55605	0.29314	0.38865	0.44711
	MSE	0.42566	0.78442	1.09383	0.38756	0.65773	0.87377
Uniform LLF p=−1.5	Estimate	0.32957	0.47496	0.56913	0.29655	0.39416	0.45441
	MSE	0.43738	0.84031	1.20069	0.40537	0.70469	0.95253
Jeffrey’s LLF p=−1.5	Estimate	0.32546	0.4672	0.5588	0.29145	0.38543	0.44326
	MSE	0.42017	0.78928	1.11403	0.38861	0.65921	0.87776
Half-t LLF p=−1.5	Estimate	0.32727	0.47257	0.56691	0.29737	0.3954	0.45593
	MSE	0.4505	0.85097	1.2108	0.40695	0.7094	0.96062

Table 4.

ML, Bayes estimates and their MSEs for cumulative cause-specific hazard function.

n=200		Cause 1			Cause 2
Time points		0.5	0.8	1.0	0.5	0.8	1.0
True value		0.314	0.44962	0.53625	0.28856	0.37611	0.429
ML	Estimate	0.32798	0.47007	0.56106	0.29778	0.39253	0.45023
	MSE	0.32281	0.6082	0.84975	0.28817	0.48625	0.64169
Uniform SELF	Estimate	0.32679	0.46893	0.56017	0.29625	0.39124	0.44925
	MSE	0.29283	0.55898	0.78692	0.25087	0.42908	0.57145
Jeffrey’s SELF	Estimate	0.32476	0.46509	0.55507	0.29373	0.38692	0.44375
	MSE	0.28547	0.53869	0.75376	0.24404	0.41086	0.54225
Half-t SELF	Estimate	0.32625	0.46811	0.55918	0.29721	0.39245	0.45061
	MSE	0.29017	0.55243	0.777	0.25328	0.43437	0.57918
Uniform LLF p=1.5	Estimate	0.32563	0.46697	0.55753	0.29521	0.3896	0.44713
	MSE	0.28756	0.54564	0.76446	0.24721	0.41965	0.55597
Jeffrey’s LLF p=1.5	Estimate	0.32361	0.46316	0.55246	0.29269	0.3853	0.44165
	MSE	0.28074	0.52701	0.73429	0.24092	0.4029	0.52922
Half-t LLF p=1.5	Estimate	0.32508	0.46615	0.55653	0.29615	0.39079	0.44846
	MSE	0.28505	0.53942	0.75506	0.24943	0.42448	0.56297
Uniform LLF p=−1.5	Estimate	0.32796	0.47091	0.56285	0.2973	0.39289	0.45139
	MSE	0.29843	0.5733	0.81122	0.2548	0.4392	0.58814
Jeffrey’s LLF p=−1.5	Estimate	0.32592	0.46706	0.55773	0.29478	0.38857	0.44588
	MSE	0.29053	0.55132	0.77502	0.24744	0.41951	0.55644
Half-t LLF p=−1.5	Estimate	0.32742	0.4701	0.56187	0.29827	0.39413	0.45279
	MSE	0.29564	0.56644	0.8008	0.25741	0.44499	0.59666

6. Real life application

In this section, we illustrate the proposed estimation procedures of cause-specific hazard analysis with CRC data. A study on CRC data was conducted by Taleghani hospital, Tehran, Iran, from January 2004 to January 2014. A total of 1462 patients with CRC were registered in this study. The patients were followed up, until April 2015 and their survival status were identified. It is observed that 402 patients have incomplete information of non-specific survival time and they are omitted. The demographic variables and clinical features such as age at diagnosis, sex, family history of CRC, body mass index (BMI), tumour size and tumour site were extracted from the hospital records. Death and cause of death were confirmed via telephone contact to patients’ families.

Baghestani et al. [3,4] and Moamer et al.[26] analysed CRC data in competing risks set-up by applying the latent failure time approach with Weibull and generalized Weibull distributions, respectively. But in latent failure time approach, it is difficult to verify the independence assumption in real life. While in cause-specific hazard approach, no need to verify the independence assumption. In this article, we include 1060 CRC patients, in which 380 patients (35.5%) died from CRC and 49 patients (4.6%) died other causes of death such as myocardial infection, stomach cancer, liver cancer, etc. and remaining patients are right censored. The survival time of patients is given in months, but we transform it in years for appropriateness of the model. The CRC data set includes many covariates, such as age, sex, BMI, etc.; in this study, we consider BMI as a covariate.

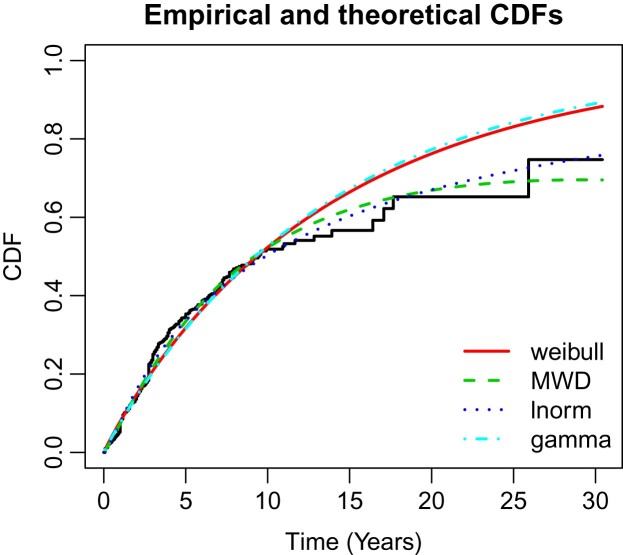
First, we compared the goodness of fit statistics of the model with Weibull, lognormal and gamma distributions based on Akaike information criterion (AIC) and Bayesian information criterion (BIC). The baseline fitting summary of the CRC data are reported in Table 5. The graph of the empirical and fitted models are shown in Figure 2, which clearly shows that MWD gives best fit for CRC when compared with Weibull, lognormal and gamma distributions. It is also clear from the goodness of fit statistics, i.e. MWD have least AIC and BIC (except, lognormal) among the counter distributions.

Table 5.

Baseline parameter estimate and goodness of fit statistics for CRC.

Model	MLE	Log-likelihood	AIC	BIC
MWD	a=0.0785, $\alpha$=1.143, $\lambda$=−0.039	−1351.447	2708.955	2723.853
Weibull	Shape=0.95586, Scale=13.6899	−1361.097	2726.194	2736.126
Lognormal	Meanlog=2.2887, Sdlog=1.6053	−1352.59	2709.179	2719.111
Gamma	Shape=0.97411, Scale=13.84353	−1361.567	2727.135	2737.067

Figure 2.

Fitted and empirical CDFs plot of CRC.

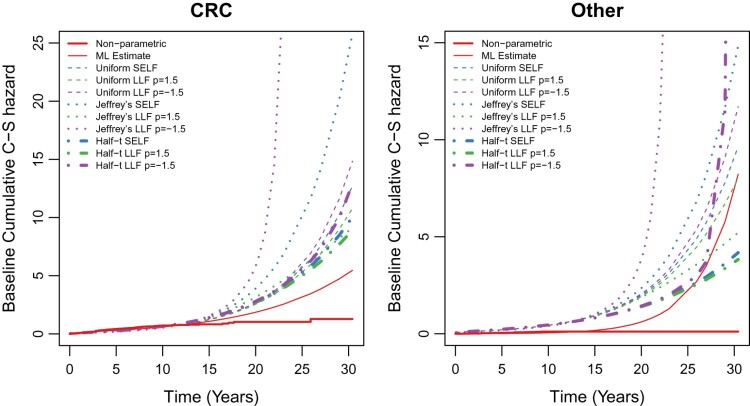
Further, we also fit cause-specific hazard MWD for competing events (i.e. death due to CRC and other cause) by applying both the proposed estimation procedures. The estimates of baseline parameters and regression parameters with their standard error (S.E.) are given in Table 6. Figure 3 shows the estimated cumulative cause-specific hazard function for both the competing events with non-parametric estimates. The non-parametric estimates are obtained without considering the situation of competing risks.

Table 6.

ML and Bayes parameter estimates with standard error for both causes.

	CRC				Other
	$a_1$	${\mathrm{\text{α}}}_1$	${\mathrm{\text{λ}}}_1$	${\mathrm{\text{β}}}_{11}$	$a_2$	${\mathrm{\text{α}}}_2$	${\mathrm{\text{λ}}}_2$	${\mathrm{\text{β}}}_{12}$
ML estimates
Estimate	0.038	0.294	0.097	0.047*	0.049	0.01	0.026	−0.026
S.E.	0.01	0.032	0.008	0.01	0.012	0.01	0.006	0.012
Bayes estimates (uniform prior)
SELF	0.233	0.471	0.205	−0.032	0.5	0.497	0.2	−25.635*
LLF p=1.5	0.203	0.415	0.194	−0.035	0.439	0.436	0.194	−126.374*
LLF p=−1.5	0.273	0.528	0.217	−0.029	0.562	0.558	0.217	−3.28*
SD	0.214	0.277	0.124	0.063	0.289	0.288	0.115	18.723
Bayes estimates (Jeffrey’s prior)
SELF	0.145	0.572	0.211	−0.005	0.975	0.984	0.838	−27.554*
LLF p=1.5	0.123	0.415	0.189	−0.008	0.458	0.465	0.189	−130.474*
LLF p=−1.5	0.18	0.856	0.237	−0.002	6.375	10.038	0.237	−3.614*
SD	0.188	0.527	0.178	0.068	1.341	1.44	1.121	18.562
Bayes estimates (Half-t prior)
SELF	0.271	0.693	0.206	−0.039	24.298	12.214	5.582	−46.925*
LLF p=1.5	0.192	0.527	0.188	−0.042	2.565	2.131	0.188	−141.798*
LLF p=−1.5	1.168	1.074	0.227	−0.036	196.998	69.696	0.227	−8.706*
SD	0.466	0.556	0.161	0.064	22.155	10.119	4.788	19.473

*Significant effect.

${\mathrm{\text{β}}}_{j1}$ = Regression coefficient of BMI for cause j.

Figure 3.

Estimate of baseline cumulative cause-specific hazard for CRC and other causes.

However, to test the significance of BMI effect on CRC, we consider the null hypothesis $H_0:{\mathrm{\text{β}}}_{11}=0$ vs. $H_1:{\mathrm{\text{β}}}_{11}\ne 0$. We use the likelihood ratio test procedure, it gives the p-value $3.09\times {10}^{-7}$ which is much less than 0.01. This indicates that covariate BMI has highly significant effect on death due to CRC.

However, the effect of BMI can measure numerically through hazard ratio (HR). The HR is a descriptive measure which plays a prominent role in survival analysis. Since, BMI is a continuous random variable with median 24.26, therefore, to calculate the HR, we consider two values of BMI as $X_1=21.5$(first quantile) and $X_2=27.00$(third quantile). For CRC, the HR at $X_1$ relative to $X_2$ is obtained as $\text{H}{\text{R}}_{\text{crc}}(t|X_2,X_1)=1.294$. This means that the risk of dying due to CRC in third quantile of BMI increased by approximately $30\mathrm{\%}$ with respect to first quantile. Hence, the patients with higher BMI had lower survival with CRC. In similar fashion, one could observe the effect of other risk factor (age, sex, etc.) on death due to CRC.

7. Conclusion

In this article, we proposed the parametric cause-specific hazard analysis through MWD. Both, maximum likelihood and Bayesian methods, are utilized for the parameter estimation of the model. A class of non-informative types of prior (uniform, Jeffrey’s and half-t) are introduced for Bayesian analysis with two different loss function, namely SELF and LINEX for a comprehensive comparative study.

The conduct of simulation study for cumulative cause-specific hazard function shows that for small sample size Bayes estimates of cause-specific hazard function for Jeffrey’s and uniform priors under both loss functions are dominated over likelihood estimates. Under half-t prior, the Bayes estimates are very close to likelihood estimate except the sample size 20 and ML and Bayes estimates are approximately very close for sample size 200. Also, simulation study showed the convergence and the identifiability of the model. In real data analysis, it is observed that at initial time points, the cumulative cause-specific hazard function for both the causes are close to non-parametric estimate. CRC shows the larger cumulative cause-specific hazard when compared with other causes. BMI have a significant effect on CRC and other causes under MLE and Bayes estimates, respectively.

It is also conjectured that the class of non-informative types of prior gives better inference for cause-specific hazard in competing risks. Further, the problem for informative priors is left for future researchers.

Disclosure statement

No potential conflict of interest was reported by the author(s).