Bayesian hierarchical models for linear networks

Abstract

The purpose of this study is to highlight dangerous motorways via estimating the intensity of accidents and study its pattern across the UK motorway network. Two methods have been developed to achieve this aim. First, the motorway-specific intensity is estimated by using a homogeneous Poisson process. The heterogeneity across motorways is incorporated using two-level hierarchical models. The data structure is multilevel since each motorway consists of junctions that are joined by grouped segments. In the second method, the segment-specific intensity is estimated. The homogeneous Poisson process is used to model accident data within grouped segments but heterogeneity across grouped segments is incorporated using three-level hierarchical models. A Bayesian method via Markov Chain Monte Carlo is used to estimate the unknown parameters in the models and the sensitivity to the choice of priors is assessed. The performance of the proposed models is evaluated by a simulation study and an application to traffic accidents in 2016 on the UK motorway network. The deviance information criterion (DIC) and the widely applicable information criterion (WAIC) are employed to choose between models.

1. Introduction

Traffic crashes have considerable impact on human, economics and the society. To improve road safety, traffic accidents research often seeks to determine prediction methods of traffic accidents. Traditional crash prediction models, such as generalized linear model, are widely used in traffic safety studies. However, multilevel data structure is extensively existed due to technique used to collect or cluster traffic data [21]. Ignoring hierarchical nature of data may produce unreliable estimates of model parameters and statistical inference. Hierarchical modelling is a statistical approach that used to properly take account of multilevel data structure [16,21]. Currently, hierarchical modelling has been employed in many research fields such as sociology, education, political science and public health. Shankar et al. [41] showed that the explanatory power of crash models had been improved when site-specific random effects and time indicator were incorporated into the negative binomial regression model. Jones and Jørgensen [25] expounded and discussed possible applications of hierarchical models in road traffic accidents in Norway. The use of hierarchical modelling technique to represent multilevel data structure in crash prediction has been growing since then. In some research, hierarchical models were used to predict crash frequency [12,18,24,26,31,34,36,39] and in other research, hierarchical models were developed to identify factors affecting crash severity [23,25,29]. In previous studies, models were proposed to account for unobserved heterogeneity at the segment level, for example, hierarchical Bayesian binary probit models [40], binary logit models [15], Bayesian multilevel Poisson-lognormal joint models [2], multivariate hierarchical Poisson-lognormal spatial joint models [1], and grouped latent class ordered probit models with class-probability functions[13]. In general, these models accommodated the unobserved heterogeneity arising from the random effects terms, the possibility of systematic variations of unobserved groups across the highway segments or corridors which consist of intersections and roadway segments. In our study, two-level and three-level Bayesian hierarchical models are proposed to capture the unobserved heterogeneity by varying the accident intensity across the motorways and motorway segments.

The motorway network is considered as a linear network and road accidents as a spatial point pattern involving the spatial locations of accidents. A linear network L is defined as the union $L=\bigcup _{i=1}^n{\ell }_i$ of a finite collection of line segments ${\ell }_1,\dots ,{\ell }_n$ in the plane [4]. The line segment in the plane with endpoints u and v is given by $[u,v]=\{tu+(1-t)v:0\le t\le 1\}$. For a point process on a linear network, an intensity of points along the network is defined as the expected number of points per unit length of network [5].

The novelty of this work is to estimate the intensity function of accidents and study its pattern across the UK motorway network using a Bayesian approach. We proposed hierarchical models to estimate the motorway-specific and segment-specific accidents intensities. In a two-level model, the intensity of accidents was considered homogeneous across segments within each motorway, but was inhomogeneous across motorways. Each motorway consists of junctions that are joined by grouped segments. The intensity of accidents may be inhomogeneous across grouped segments. Thus, ignoring the between grouped segments heterogeneity may underestimate the standard error of the accident intensity. In a three-level model, the intensity of accidents was considered homogeneous within grouped segments, but was inhomogeneous among grouped segments and motorways.

2. Description of data

The accident data are obtained from the Department for Transport in Great Britain [43]. A STATS19 reporting form was used to record accident on the road network by police officers. This form gives details about accident circumstances such as road and weather conditions, time and location of accident, the driver's behaviour and the vehicles involved in a road accident. The traffic accident is registered as the sample point for each link of road in the road network. The road network consists of individual road sections that are segmented in junction to junction link, with different lengths. For this study, the unit of measurement for length is a kilometre. Segments are grouped according to count point locations existing on Great Britain's motorway network. In these count points, traffic estimates are calculated for each link of Great Britain's motorway network, with links' start and end points defined as where the link joins a motorway junction [44,45]. Each link has a uniquely referenced Count Point (CP), where the traffic is usually counted by enumerators [44].

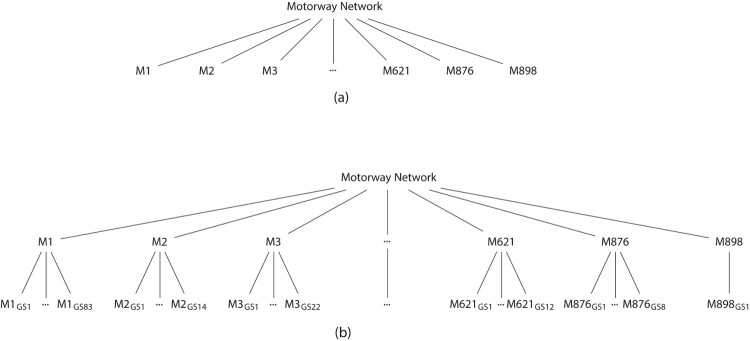
There are 51 motorways in the UK and data are recorded on 49 motorways by STATS19. The hierarchical structure of data in this study is shown in Figure 1.

Figure 1.

The hierarchical structure of UK motorway network in 2016. $\mathrm{Mi}$ denotes motorway $\mathrm{i}$. ${\mathrm{M}1}_{\mathrm{GS}1}$ represents the first grouped segments on M1; ${\mathrm{M}1}_{\mathrm{GS}83}$ represents the eighty third grouped segments on M1 and so on for the rest of the symbols of grouped segments for other motorways. The grouped segments are links joining motorway junctions and they are grouped to incorporate the heterogeneity of the accident intensity across them [44]. (a) Two-level hierarchical model. (b) Three-level hierarchical model.

Table 1 shows the descriptive statistics for the accident data in 2016 for 49 motorways in the UK.

Table 1.

Descriptive statistics for accident data on the UK motorways in 2016.

Motorway	Length of motorway (in kilometres)	Number of accidents	Number of grouped segments
$\mathrm{M}1$	304.50	593	83
$\mathrm{M}2$	39.39	53	14
$\mathrm{M}3$	95.89	188	22
$\mathrm{M}4$	299.84	475	80
$\mathrm{M}5$	256.22	263	52
$\mathrm{M}6$	366.76	637	90
$\mathrm{M}8$	87.85	163	51
$\mathrm{M}9$	52.60	25	18
$\mathrm{M}11$	80.41	130	17
$\mathrm{M}18$	45.25	48	13
$\mathrm{M}20$	79.54	153	18
$\mathrm{M}23$	26.59	34	7
$\mathrm{M}25$	181.52	657	48
$\mathrm{M}26$	15.46	15	2
$\mathrm{M}27$	47.86	151	24
$\mathrm{M}32$	6.87	17	6
$\mathrm{M}40$	140.21	179	33
$\mathrm{M}42$	64.93	88	21
$\mathrm{M}45$	12.39	3	3
$\mathrm{M}48$	19.30	6	5
$\mathrm{M}49$	8.30	1	3
$\mathrm{M}50$	33.19	5	8
$\mathrm{M}53$	32.21	31	17
$\mathrm{M}54$	35.90	12	13
$\mathrm{M}55$	19.90	19	5
$\mathrm{M}56$	57.89	72	30
$\mathrm{M}57$	16.48	22	11
$\mathrm{M}58$	18.95	7	10
$\mathrm{M}60$	56.75	72	40
$\mathrm{M}61$	36.50	50	12
$\mathrm{M}62$	154.90	253	48
$\mathrm{M}65$	41.88	71	19
$\mathrm{M}66$	13.64	15	8
$\mathrm{M}67$	7.53	4	4
$\mathrm{M}69$	26.18	23	5
$\mathrm{M}73$	11.23	10	8
$\mathrm{M}74$	141.30	55	54
$\mathrm{M}77$	28.93	17	22
$\mathrm{M}80$	41.67	38	33
$\mathrm{M}90$	49.32	23	16
$\mathrm{M}180$	39.68	13	6
$\mathrm{M}181$	3.78	2	1
$\mathrm{M}271$	3.74	8	4
$\mathrm{M}275$	3.98	12	5
$\mathrm{M}602$	6.37	7	2
$\mathrm{M}606$	4.03	14	3
$\mathrm{M}621$	15.05	35	12
$\mathrm{M}876$	11.89	11	8
$\mathrm{M}898$	1.38	2	1

Note: The length of motorway is in kilometre.

3. Models

3.1. Two-level Bayesian hierarchical model (Model 1)

3.1.1. Model definition

Let m denote the total number of motorways. The number of accidents $n_i$ on motorway $i(i=1,\dots ,m)$ follows a Poisson distribution with mean ${\lambda }_i{L}_i$, where $L_i$ represents the length of motorway i and ${\lambda }_i$ is the accident intensity on the motorway i per unit length. Here ${\lambda }_i{L}_i$ is the expected number of accidents on motorway i and it can vary from one motorway to another because each motorway could have different conditions and features. Let ${\alpha }_i=\log {\lambda }_i$ denote the log-intensity function and assume it follows a normal distribution $\mathrm{N}(\alpha ,{\tau }^2)$. The two-level hierarchical model for traffic accidents is given below,

$$\begin{array}{rl}{n}_i& \sim \mathrm{Pois}({\lambda }_i{L}_i),i=1,\dots ,m,\\ {\alpha }_i& \sim \mathrm{N}(\alpha ,{\tau }^2).\end{array}$$ (1)

Here α is the overall log-intensity and ${\tau }^2$ is the between-motorway variance. In this model, we assume that each accident's location follows a uniform distribution on interval $(0,L_i)$.

3.1.2. Likelihood function

Let $\mathbf{N}=\{n_i,i=1,\dots ,m\}$ represent the accident count and $\mathrm{\Theta }=\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m;\alpha ;{\tau }^2\}$ the parameters in the two-level hierarchical model. The likelihood for the two-level hierarchical model is given by,

$$L\left(\mathbf{N}|\mathrm{\Theta }\right)\propto \prod _{i=1}^m\exp (n_i{\alpha }_i-L_i\exp \left({\alpha }_i\right))\times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2}).$$ (2)

3.1.3. Prior distribution

The specification of the prior distribution depends on available information about unknown parameters. The strategy for specifying prior distributions for the parameters in the hierarchical model includes conjugate, vague and weakly-informative priors. Where possible, conjugate priors are used to ensure that the conditional distributions are of closed forms to ease the simulation; otherwise, we specify non-conjugate priors. In either cases, we specify the values of parameters to have large variances for vague or non-informative priors, and make use of pre-existing data to construct informative priors. For α, a conjugate normal prior $\mathrm{N}({\mu }_0,{\sigma }_0^2)$ is assigned. We used a conjugate inverse gamma prior with a shape parameter ${\alpha }_0$ and rate parameter ${\beta }_0$ for ${\tau }^2$. Alternatively, we specify a uniform prior $\mathrm{unif}(0,a)$, with a>0, for the between-motorway standard deviation τ [28]. Another choice of prior is a half-normal distribution $\mathrm{HN}(\theta )$ for τ, where $\theta =\frac{\sqrt{\pi }}{\sigma \sqrt{2}}$ and $\sigma >0$ as detailed in [27].

3.1.4. Posterior distribution

Posterior if the prior distribution on ${\tau }^2$ is an inverse gamma distribution

The posterior distribution is the product of the likelihood and the prior distribution. Therefore, the joint posterior density function for the parameters given the observed data is

$$\begin{array}{rl}\pi (\mathrm{\Theta }|\mathbf{N})& =\prod _{i=1}^m\exp (n_i{\alpha }_i-L_i\exp \left({\alpha }_i\right))\times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2})\\ & \times \frac{1}{\sqrt{2\pi {\sigma }_0^2}}\exp (-{\displaystyle \frac{{(\alpha -{\mu }_0)}^2}{2{\sigma }_0^2}})\times \frac{{\beta }_0^{{\alpha }_0}}{\mathrm{\Gamma }({\alpha }_0)}{\left({\displaystyle {\tau }^2}\right)}^{-{\alpha }_0-1}\exp (-{\beta }_0/{\tau }^2).\end{array}$$ (3)

The conditional posterior distribution of ${\alpha }_i$ is given by,

$$\pi ({\alpha }_i|\alpha ,{\tau }^2,\mathbf{N})\propto \exp (n_i{\alpha }_i-L_i\exp \left({\alpha }_i\right))\times \exp (-\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2}).$$ (4)

The conditional posterior distribution of α is a normal distribution $\mathrm{N}({\mu }_{\alpha },{\sigma }_{\alpha }^2)$ with mean and variance respectively given below,

$${\mu }_{\alpha }={\displaystyle \frac{{\displaystyle \frac{\sum _{i=1}^m{\alpha }_i}{{\tau }^2}+{\displaystyle \frac{{\mu }_0}{{\sigma }_0^2}}}}{{\displaystyle \frac{m}{{\tau }^2}+{\displaystyle \frac{1}{{\sigma }_0^2}}}}\mathrm{and}{\sigma }_{\alpha }^2={\displaystyle \frac{1}{{\displaystyle \frac{m}{{\tau }^2}+{\displaystyle \frac{1}{{\sigma }_0^2}}}}.}}$$ (5)

The conditional posterior distribution of ${\tau }^2$ is given by,

$$\pi ({\tau }^2|\alpha ;{\alpha }_1,\dots {\alpha }_m;\mathbf{N})\propto {\left({\tau }^2\right)}^{{\displaystyle -({\alpha }_0+\frac{m}{2})-1}}\exp (-{\displaystyle \frac{{\beta }_0+{\displaystyle \frac{\sum _{i=1}^m{({\alpha }_i-\alpha )}^2}{2}}}{{\tau }^2}}).$$ (6)

Hence, ${\tau }^2$ has an inverse gamma distribution with shape ${\alpha }_0+\frac{m}{2}$ and rate ${\beta }_0+\frac{\sum _{i=1}^m({\alpha }_i-\alpha {)}^2}{2}$.

Posterior if the prior distribution on τ is a uniform distribution

The joint posterior density is

$$\begin{array}{rl}\pi (\mathrm{\Theta }|\mathbf{N})& \propto \prod _{i=1}^m\exp (n_i{\alpha }_i-L_i\exp \left({\alpha }_i\right))\times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2})\\ & \times \frac{1}{\sqrt{2\pi {\sigma }_0^2}}\exp (-{\displaystyle \frac{{(\alpha -{\mu }_0)}^2}{2{\sigma }_0^2}}).\end{array}$$ (7)

The conditional posterior distributions of ${\alpha }_i(i=1,\dots ,m)$  and α are given in (4) and (5). The conditional posterior density of τ is given by,

$$\pi (\tau |\alpha ;{\alpha }_1,\dots ,{\alpha }_m;\mathbf{N})\propto {\left(\frac{1}{\sqrt{2\pi {\tau }^2}}\right)}^m\exp (-\sum _{i=1}^m\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2}).$$ (8)

Posterior if the prior distribution on τ is a half-normal distribution (HN) with parameter θ

The joint posterior distribution is

$$\begin{array}{rl}\pi (\mathrm{\Theta }|\mathbf{N})& =\prod _{i=1}^m\exp (n_i{\alpha }_i-L_i\exp \left({\alpha }_i\right))\times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2})\\ & \times \frac{1}{\sqrt{2\pi {\sigma }_0^2}}\exp (-{\displaystyle \frac{{(\alpha -{\mu }_0)}^2}{2{\sigma }_0^2}})\times \frac{2\theta }{\pi }\exp (-\frac{{\tau }^2{\theta }^2}{\pi }).\end{array}$$ (9)

The conditional posterior distributions of ${\alpha }_i(i=1,\dots ,m)$ and α are the same as in Equations (4) and (5). The conditional posterior distribution of τ is

$$\pi (\tau |\alpha ;{\alpha }_1\cdots ,{\alpha }_m;\mathbf{N})\propto {\tau }^{-m}\exp (-\sum _{i=1}^m\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2}-\frac{{\tau }^2{\theta }^2}{\pi }).$$ (10)

3.1.5. Estimation

In Equations (5) and (6), the conditional posterior distributions of α and ${\tau }^2$ given other parameters have a known form, but the conditional posterior distributions of ${\alpha }_i(i=1,\dots ,m)$ in Equation (4) do not have known forms. Therefore, the Metropolis-Hastings within Gibbs sampler is used to simulate the Markov chains of ${\alpha }_i(i=1,\dots ,m)$, α and ${\tau }^2$. A new value ${\acute{\alpha }}_i$ is simulated from a proposal distribution ${\mathrm{q}}_1({\acute{\alpha }}_i,{\alpha }_i^{(t-1)})$, which is the normal distribution with mean equalling to current value ${\alpha }_i^{(t-1)}$ and the variance is chosen such that an acceptance rate of ${\acute{\alpha }}_i$ is between 0.24 and 0.40 [17]. The proposed value is accepted with the probability

$$r_1({\alpha }_i^{(t-1)},{\acute{\alpha }}_i)=min\left\{{\displaystyle \frac{\pi ({\acute{\alpha }}_i|{\alpha }^{(t-1)},{\tau }^{2(t-1)}){\mathrm{q}}_1({\alpha }_i^{(t-1)},{\acute{\alpha }}_i)}{\pi ({\alpha }_i^{(t-1)}|{\alpha }^{(t-1)},{\tau }^{2(t-1)}){\mathrm{q}}_1({\acute{\alpha }}_i,{\alpha }_i^{(t-1)})},1}\right\}.$$ (11)

If the proposed value is rejected, the current value is taken as the next value in the Markov chain.

The uniform prior distribution on τ leads to the conditional posterior distribution of τ as given in Equation (8). This posterior distribution does not have a closed form, therefore, the Metropolis-Hastings sampler is used. The two steps are defined as follows. Firstly, we draw a proposed value, $\acute{\tau }$, from the proposal distribution ${\mathrm{q}}_2(\acute{\tau },{\tau }^{(t-1)})$, which is a normal distribution with mean equal to the current value ${\tau }^{(t-1)}$. Secondly, the proposed value is accepted with the probability

$$r_2({\tau }^{(t-1)},\acute{\tau })=min\left\{{\displaystyle \frac{\pi (\acute{\tau }|{\alpha }^{(t)},{\alpha }_1^{(t)},\dots ,{\alpha }_m^{(t)}){\mathrm{q}}_2({\tau }^{(t-1)},\acute{\tau })}{\pi ({\tau }^{(t-1)}|{\alpha }^{(t)},{\alpha }_1^{(t)},\dots ,{\alpha }_m^{(t)}){\mathrm{q}}_2(\acute{\tau },{\tau }^{(t-1)})},1}\right\}.$$ (12)

The conditional posterior distribution for τ in Equation (10) is produced by using a half-normal prior distribution and does not have a closed form. Therefore, the Metropolis-Hastings sampler is used to simulate τ. This sampler includes generating the proposed value $\acute{\tau }$ from the proposal distribution ${\mathrm{q}}_2(\acute{\tau },{\tau }^{(t-1)})$ and the proposed value is accepted with the probability $r_2({\tau }^{(t-1)},\acute{\tau })$ described in equation (12). The proposal distribution ${\mathrm{q}}_2(.,{\tau }^{(t-1)}))$ is a normal distribution with current state ${\tau }^{(t-1)}$ as the mean.

3.2. Two-level frequentist hierarchical method (Model 2)

In this section, we describe a two-stage approach to modelling the accident data on the UK motorway network using the frequentist method. In stage one, we used the maximum likelihood method to estimate the log-intensity function ${\mathrm{y}}_i$ and the corresponding standard deviation ${\sigma }_i$. In stage two, the estimated log-intensity functions are combined across motorways to produce an overall estimate. The model can be formulated as follows,

$$\begin{array}{rl}{\mathrm{y}}_i& \sim \mathrm{N}({\alpha }_i,{\sigma }_i^2),\\ {\alpha }_i& \sim \mathrm{N}(\alpha ,{\tau }^2).\end{array}$$ (13)

Here ${\mathrm{y}}_i$ represents the estimated intensity at the log scale for motorway i, ${\alpha }_i$ represents the random effects for the log-intensity and ${\sigma }_i^2$ is the within-motorway variance corresponding to ${\mathrm{y}}_i$;  α is the overall intensity at the log scale and ${\tau }^2$ represents the between-motorway heterogeneity. The marginal distribution of each estimated log-intensity ${\mathrm{y}}_i$ is a normal distribution with mean α and variance $({\sigma }_i^2+{\tau }^2{)}^{-1}$ [19]. Hence, the contribution of motorway i to the likelihood for α and ${\tau }^2$ is given by,

$$L_i(\alpha ,{\tau }^2|{\mathrm{y}}_i,{\sigma }_i^2)=\frac{1}{\sqrt{2\pi ({\sigma }_i^2+{\tau }^2)}}\exp (-\frac{{({\mathrm{y}}_i-\alpha )}^2}{2({\sigma }_i^2+{\tau }^2)}).$$ (14)

For m independent motorways, the likelihood is given by the product of the individual motorway likelihoods as follows,

$$L(\alpha ,{\tau }^2|\mathbf{y},{\sigma }^{\mathbf{2}})=\prod _{i=1}^m\frac{1}{\sqrt{2\pi ({\sigma }_i^2+{\tau }^2)}}\exp (-\frac{{({\mathrm{y}}_i-\alpha )}^2}{2({\sigma }_i^2+{\tau }^2)}).$$ (15)

3.3. Three-level Bayesian hierarchical model (Model 3)

3.3.1. Model definition

In the three-level hierarchical model, the number of accidents within grouped segments follows a homogeneous process but a non-homogeneous process across grouped segments and motorways. Let m denote the total number of motorways and $s_i(i=1,\dots ,m)$ the number of grouped segments for each motorway i. Suppose that the intensity of accidents per kilometre is ${\lambda }_{ij}(i=1,\dots ,m;j=1,\dots ,s_i),$ where i is the index of motorway and j is the index of grouped segments. The number of accidents $n_{ij}$ on each grouped segments follows a Poisson distribution with mean ${\lambda }_{ij}{L}_{ij}$, where $L_{ij}$ represents the length (in kilometre) of the grouped segments j on motorway i. Let ${\alpha }_{ij}=\log {\lambda }_{ij}$ denote the log-intensity function. The three-level hierarchical model is given below,

$$\begin{array}{rl}{n}_{ij}& \sim \mathrm{Pois}\left({\lambda }_{ij}{L}_{ij}\right),i=1,\dots ,m;j=1,..,s_i,\\ {\alpha }_{ij}& \sim \mathrm{N}({\alpha }_i,{\tau }_i^2),\\ {\alpha }_i& \sim \mathrm{N}(\alpha ,{\tau }^2).\end{array}$$ (16)

The second level includes the log-intensity of accidents, ${\alpha }_{ij}$, on each grouped segments and the log-intensity of accidents, ${\alpha }_i$, on each motorway as well as the between grouped segments heterogeneity, ${\tau }_i^2$. The third level includes the overall log-intensity of accidents α and the between-motorway heterogeneity, ${\tau }^2$. The intensity of accidents is constant on grouped segments that have the same mark, but it varies across grouped segments and motorways.

3.3.2. Likelihood function

Let ${\mathrm{\Theta }}_3$ denote model parameters $\{{\alpha }_{11},\dots ,{\alpha }_{m{s}_m};{\alpha }_1,\dots ,{\alpha }_m;{\tau }_1^2,\dots ,{\tau }_m^2;\alpha ;{\tau }^2\}$ in the three-level hierarchical model. Let $\mathit{\gamma }$ denote the log-intensity of accidents on grouped segments $\{{\alpha }_{11},\dots ,{\alpha }_{m{s}_m}\}$, $\mathit{\alpha }=\{{\alpha }_1,\dots ,{\alpha }_m\}$ and ${\mathit{\tau }}^2=\{{\tau }_1^2,\dots ,{\tau }_m^2\}$. It is assumed that the accidents are uniformly distributed within grouped segments.

The likelihood function for the proposed three-level hierarchical model is given by,

$$\begin{array}{rl}L\left(\mathbf{N}|{\mathrm{\Theta }}_3\right)& =P\left(\mathbf{N}|\mathit{\gamma }\right)\times P(\mathit{\gamma }|\mathit{\alpha },{\mathit{\tau }}^2)\times P(\mathit{\alpha }|\alpha ,{\tau }^2)\\ & \propto \prod _{i=1}^m\prod _{j=1}^{s_i}\exp (n_{ij}{\alpha }_{ij}-L_{ij}\exp \left({\alpha }_{ij}\right))\\ & \times \prod _{i=1}^m\prod _{j=1}^{s_i}\frac{1}{\sqrt{2\pi {\tau }_i^2}}\exp (-\frac{{({\alpha }_{ij}-{\alpha }_i)}^2}{2{\tau }_i^2})\times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{{({\alpha }_i-\alpha )}^2}{2{\tau }^2}).\end{array}$$ (17)

3.3.3. Posterior distribution

The same prior distributions for α and ${\tau }^2$ as the ones described in Section 3.1.3 are considered.

Posterior if the prior distribution on ${\tau }^2$ is an inverse gamma distribution with shape $a_0$ and rate $b_0$

A joint posterior distribution for parameters ${\mathrm{\Theta }}_3$ is given by,

$$\begin{array}{rl}\pi \left({\mathrm{\Theta }}_3|\mathbf{N}\right)& \propto \prod _{i=1}^m\prod _{j=1}^{s_i}\exp (n_{ij}{\alpha }_{ij}-L_{ij}\exp \left({\alpha }_{ij}\right))\times \prod _{i=1}^m\prod _{j=1}^{s_i}\frac{1}{\sqrt{2\pi {\tau }_i^2}}\exp (-\frac{{({\alpha }_{ij}-{\alpha }_i)}^2}{2{\tau }_i^2})\\ & \times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{{({\alpha }_i-\alpha )}^2}{2{\tau }^2})\times \prod _{i=1}^m\frac{b_0^{a_0}}{\mathrm{\Gamma }(a_0)}{\displaystyle {\left({\tau }_i^2\right)}^{-a_0-1}\exp \left({\displaystyle \frac{-b_0}{{\tau }_i^2}}\right)}\\ & \times {\displaystyle \frac{1}{\sqrt{2\pi {\sigma }_0^2}}\exp \left({\displaystyle \frac{-{(\alpha -{\mu }_0)}^2}{2{\sigma }_0^2}}\right)\times \frac{{\beta }_0^{{\alpha }_0}}{\mathrm{\Gamma }({\alpha }_0)}{\displaystyle {\left({\tau }^2\right)}^{-{\alpha }_0-1}\exp \left({\displaystyle \frac{-{\beta }_0}{{\tau }^2}}\right).}}\end{array}$$ (18)

The conditional posterior distribution of ${\alpha }_{ij}$ is given by,

$$\pi ({\alpha }_{ij}|\mathit{\alpha },{\mathit{\tau }}^2,\mathbf{N})\propto \exp (n_{ij}{\alpha }_{ij}-L_{ij}\exp \left({\alpha }_{ij}\right))\exp (-\frac{{({\alpha }_{ij}-{\alpha }_i)}^2}{2{\tau }_i^2}).$$ (19)

The conditional posterior distribution of ${\alpha }_i$ is a normal distribution $\mathrm{N}({\mu }_{{\alpha }_i},{\sigma }_{{\alpha }_i}^2)$ with mean and variance:

$${\mu }_{{\alpha }_i}=\frac{{\displaystyle \frac{\sum _{j=1}^{s_i}{\alpha }_{ij}}{{\tau }_i^2}+{\displaystyle \frac{\alpha }{{\tau }^2}}}}{{\displaystyle \frac{s_i}{{\tau }_i^2}+{\displaystyle \frac{1}{{\tau }^2}}}}\mathrm{and}{\sigma }_{{\alpha }_i}^2={\displaystyle \frac{1}{{\displaystyle \frac{s_i}{{\tau }_i^2}+{\displaystyle \frac{1}{{\tau }^2}}}}.}$$ (20)

The conditional posterior distribution of ${\tau }_i^2$ is given by,

$${\tau }_i^2\sim \text{Inv-Gamma}(\frac{s_i}{2}+a_0,\sum _{j=1}^{s_i}\frac{{({\alpha }_{ij}-{\alpha }_i)}^2}{2}+b_0).$$ (21)

The conditional posterior distribution of α is a $\mathrm{N}({\mu }_{\alpha },{\sigma }_{\alpha }^2)$ with mean and variance given below, respectively,

$${\mu }_{\alpha }={\displaystyle \frac{{\displaystyle \frac{\sum _{i=1}^m{\alpha }_i}{{\tau }^2}+{\displaystyle \frac{{\mu }_0}{{\sigma }_0^2}}}}{{\displaystyle \frac{m}{{\tau }^2}+{\displaystyle \frac{1}{{\sigma }_0^2}}}}\mathrm{and}{\sigma }_{\alpha }^2=\frac{1}{{\displaystyle \frac{m}{{\tau }^2}+{\displaystyle \frac{1}{{\sigma }_0^2}}}}.}$$ (22)

The conditional posterior distribution of ${\tau }^2$ is given by,

$${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}\left({\displaystyle \frac{m}{2}+{\alpha }_0,{\displaystyle \frac{\sum _{i=1}^m{({\alpha }_i-\alpha )}^2}{2}+{\beta }_0}}\right).$$ (23)

Posterior if the prior distribution on τ is a uniform distribution

The probability density function of the uniform prior distribution on τ is constant, so it does not appear in the joint posterior distribution. Hence, the joint posterior distribution is given by,

$$\begin{array}{rl}\pi \left({\mathrm{\Theta }}_3|\mathbf{N}\right)& \propto \prod _{i=1}^m\prod _{j=1}^{s_i}\exp (n_{ij}{\alpha }_{ij}-L_{ij}\exp \left({\alpha }_{ij}\right))\times \prod _{i=1}^m\prod _{j=1}^{s_i}\frac{1}{\sqrt{2\pi {\tau }_i^2}}\exp (-\frac{{({\alpha }_{ij}-{\alpha }_i)}^2}{2{\tau }_i^2})\\ & \times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{{({\alpha }_i-\alpha )}^2}{2{\tau }^2})\times \prod _{i=1}^m\frac{b_0^{a_0}}{\mathrm{\Gamma }(a_0)}{\displaystyle {\left({\tau }_i^2\right)}^{-a_0-1}\exp \left({\displaystyle \frac{-b_0}{{\tau }_i^2}}\right)}\\ & \times {\displaystyle \frac{1}{\sqrt{2\pi {\sigma }_0^2}}\exp \left({\displaystyle \frac{-{(\alpha -{\mu }_0)}^2}{2{\sigma }_0^2}}\right).}\end{array}$$ (24)

The conditional posterior distributions of ${\alpha }_{ij}$, ${\alpha }_i$, ${\tau }_i^2(i=1,\dots ,m;j=1,\dots ,s_i)$ and α are the same in Equations (19)–(22). The conditional posterior distribution of τ is given by,

$$\pi (\tau |\mathit{\alpha },\alpha ,\mathbf{N})\propto {\left(\frac{1}{\sqrt{2\pi {\tau }^2}}\right)}^m\exp (-\sum _{i=1}^m\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2}).$$ (25)

Posterior if the prior distribution on τ is a half-normal (HN) distribution with parameter θ

If we use HN(θ) as the prior for τ, the joint posterior distribution is given by,

$$\begin{array}{rl}\pi \left({\mathrm{\Theta }}_3|\mathbf{N}\right)& \propto \prod _{i=1}^m\prod _{j=1}^{s_i}\exp (n_{ij}{\alpha }_{ij}-L_{ij}\exp \left({\alpha }_{ij}\right))\\ & \times \prod _{i=1}^m\prod _{j=1}^{s_i}\frac{1}{\sqrt{2\pi {\tau }_i^2}}\exp (-\frac{{({\alpha }_{ij}-{\alpha }_i)}^2}{2{\tau }_i^2})\times \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp (-\frac{{({\alpha }_i-\alpha )}^2}{2{\tau }^2})\\ & \times \prod _{i=1}^m\frac{b_0^{a_0}}{\mathrm{\Gamma }(a_0)}{\displaystyle {\left({\tau }_i^2\right)}^{-a_0-1}\exp \left({\displaystyle \frac{-b_0}{{\tau }_i^2}}\right)\times {\displaystyle \frac{1}{\sqrt{2\pi {\sigma }_0^2}}\exp \left({\displaystyle \frac{-{(\alpha -{\mu }_0)}^2}{2{\sigma }_0^2}}\right)}}\\ & \times \frac{2\theta }{\pi }\exp (-\frac{{\tau }^2{\theta }^2}{\pi }).\end{array}$$ (26)

The conditional posterior distributions of ${\alpha }_{ij}$, ${\alpha }_i$, ${\tau }_i^2,(i=1,\dots ,m;j=1,\dots ,s_i)$ and α are the same in Equations (19)–(22). The conditional posterior distribution of τ is given by,

$$\pi (\tau |\mathit{\alpha },\alpha ,\mathbf{N})\propto {\tau }^{-m}\exp (-\sum _{i=1}^m\frac{({\alpha }_i-\alpha {)}^2}{2{\tau }^2}-\frac{{\tau }^2{\theta }^2}{\pi }).$$ (27)

3.3.4. Estimation

Bayesian estimation of the three-level hierarchical model is performed using Metropolis-Hastings within Gibbs sampler. We generate random samples from conditional posterior distributions of α, ${\alpha }_i$, ${\tau }^2$ and ${\tau }_i^2(i=1,\dots ,m)$, respectively. Conditional posterior distributions of ${\alpha }_{ij},(i=1,\dots ,m;j=1,\dots ,s_i)$ are not of closed forms. In this case, the Metropolis-Hasting algorithm is used. Normal proposal distributions are specified for ${\alpha }_{ij},(i=1,\dots ,m;j=1,\dots ,s_i)$ with mean ${\alpha }_{ij}^{(t-1)}$ and variance ${\sigma }_{ij}^2$, where $t(t=1,\dots ,M)$ is the iteration index. The variance ${\sigma }_{ij}^2$ is chosen such that an acceptance rate is between 0.24 and 0.40 [17].

A value ${\acute{\alpha }}_{ij}$ generated from the proposal distribution ${\mathrm{q}}_1({\acute{\alpha }}_{ij},{\alpha }_{ij}^{(t-1)})$ is accepted with probability

$$r_1({\alpha }_{ij}^{(t-1)},{\acute{\alpha }}_{ij})=min\left\{{\displaystyle \frac{\pi ({\acute{\alpha }}_{ij}|{\alpha }_i^{(t-1)},{\tau }_i^{2(t-1)}){\mathrm{q}}_1({\alpha }_{ij}^{(t-1)},{\acute{\alpha }}_{ij})}{\pi ({\alpha }_{ij}^{(t-1)}|{\alpha }_i^{(t-1)},{\tau }_i^{2(t-1)}){\mathrm{q}}_1({\acute{\alpha }}_{ij},{\alpha }_{ij}^{(t-1)})},1}\right\}.$$ (28)

A new value $\acute{\tau }$ is generated from a proposal distribution ${\mathrm{q}}_2(\acute{\tau },{\tau }^{(t-1)})$, which is a normal distribution with mean equalling to current value ${\tau }^{(t-1)}$. The new value $\acute{\tau }$ is accepted with probability

$$r_2({\tau }^{(t-1)},\acute{\tau })=min\left\{{\displaystyle \frac{\pi (\acute{\tau }|{\alpha }^{(t)},{\alpha }_1^{(t)},\dots ,{\alpha }_m^{(t)}){\mathrm{q}}_2({\tau }^{(t-1)},\acute{\tau })}{\pi ({\tau }^{(t-1)}|{\alpha }^{(t)},{\alpha }_1^{(t)},\dots ,{\alpha }_m^{(t)}){\mathrm{q}}_2(\acute{\tau },{\tau }^{(t-1)})},1}\right\}.$$ (29)

3.4. Three-level frequentist hierarchical method (Model 4)

The maximum likelihood estimation is used in three stages to estimate the model parameters (16).

In stage one, the log-intensity of accidents ${\alpha }_{ij}$ is estimated for each grouped segment where the relevant part of likelihood function in Equation (17) is used,

$$L_{ij}({\alpha }_{ij};\mathbf{N})=\exp (n_{ij}{\alpha }_{ij}-L_{ij}\exp \left({\alpha }_{ij}\right)).$$ (30)

The log-likelihood function is

$${\ell }_{ij}({\alpha }_{ij};\mathbf{N})=n_{ij}{\alpha }_{ij}-L_{ij}\exp \left({\alpha }_{ij}\right).$$ (31)

The maximum likelihood estimate (M.L.E.) of ${\alpha }_{ij}$ is given by,

$${\hat{\alpha }}_{ij}=\log n_{ij}-\log L_{ij}.$$ (32)

To calculate the standard error of ${\hat{\alpha }}_{ij}$, we use the Fisher information matrix $I({\hat{\alpha }}_{ij})$, which is a scalar containing the entry

$$I({\hat{\alpha }}_{ij})=-E\left[H\left({\hat{\alpha }}_{ij}\right)\right]=-E\left[{\displaystyle \frac{{\mathrm{\partial }}^2{\ell }_{ij}}{\mathrm{\partial }{\alpha }_{ij}^2}}\right]=L_{ij}\exp \left({\alpha }_{ij}\right),$$ (33)

where $H({\hat{\alpha }}_{ij})$ represents the Hessian matrix. The square root of the inverse of the Fisher information scalar is an estimator of the standard error for ${\alpha }_{ij}$

$$SE\left({\hat{\alpha }}_{ij}\right)=\sqrt{I^{-1}({\hat{\alpha }}_{ij})}={\displaystyle {(L_{ij}\exp \left({\alpha }_{ij}\right))}^{-\frac{1}{2}}.}$$ (34)

In stage two, the log-intensity of accidents ${\alpha }_i(i=1,\dots ,m)$ is estimated for each motorway. Here, the point estimates ${\hat{\alpha }}_{ij},(i=1,\dots ,m;j=1,\dots ,n_i)$ are substituted in the likelihood function in Equation (17). The relevant part of the likelihood function is given by,

$$L_i(\mathit{\alpha },{\mathit{\tau }}^2;\hat{\mathit{\gamma }})=\prod _{i=1}^m\prod _{j=1}^{s_i}\frac{1}{\sqrt{2\pi {\tau }_i^2}}\exp (-\frac{{({\hat{\alpha }}_{ij}-{\alpha }_i)}^2}{2{\tau }_i^2}).$$ (35)

The log-likelihood function is

$${\ell }_i(\mathit{\alpha },{\mathit{\tau }}^2;\hat{\mathit{\gamma }})=\sum _{i=1}^m[-{\displaystyle \frac{s_i}{2}\log {\tau }_i^2-\frac{\sum _{j=1}^{s_i}{({\hat{\alpha }}_{ij}-{\alpha }_i)}^2}{2{\tau }_i^2}}].$$ (36)

The maximum likelihood estimates ${\hat{\alpha }}_i$ and ${\hat{\tau }}_i^2$ are, respectively, given by,

$${\hat{\alpha }}_i={\displaystyle \frac{\sum _{j=1}^{s_i}{\hat{\alpha }}_{ij}}{s_i}\mathrm{and}{\hat{\tau }}_i^2={\displaystyle \frac{\sum _{j=1}^{s_i}{({\hat{\alpha }}_{ij}-{\hat{\alpha }}_i)}^2}{s_i}.}}$$ (37)

To obtain the standard errors of ${\hat{\alpha }}_i$ and ${\hat{\tau }}_i^2$, we use the Fisher information matrix as follows,

$$\begin{array}{r}I({\hat{\alpha }}_i,{\hat{\tau }}_i^2)=-E\left[H({\hat{\alpha }}_i,{\hat{\tau }}_i^2)\right]=-E\left[\begin{array}{cc}{\displaystyle \frac{{\mathrm{\partial }}^2{\ell }_i}{\mathrm{\partial }{\alpha }_i^2}}& {\displaystyle \frac{{\mathrm{\partial }}^2{\ell }_i}{\mathrm{\partial }{\alpha }_i\mathrm{\partial }{\tau }_i^2}}\\ {\displaystyle \frac{{\mathrm{\partial }}^2{\ell }_i}{\mathrm{\partial }{\tau }_i^2\mathrm{\partial }{\alpha }_i}}& {\displaystyle \frac{{\mathrm{\partial }}^2{\ell }_i}{\mathrm{\partial }({\tau }_i^2{)}^2}}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{s_i}{{\tau }_i^2}}& 0\\ 0& {\displaystyle \frac{s_i}{2{\tau }_i^4}}\end{array}\right],\end{array}$$ (38)

where $H({\hat{\alpha }}_i,{\hat{\tau }}_i^2)$ represents the Hessian matrix. The inverse of the Fisher information matrix is given by,

$$\begin{array}{r}{I}^{-1}({\hat{\alpha }}_i,{\hat{\tau }}_i^2)=\left[\begin{array}{cc}{\displaystyle \frac{{\tau }_i^2}{s_i}}& 0\\ 0& {\displaystyle \frac{2{\tau }_i^4}{s_i}}\end{array}\right].\end{array}$$ (39)

The standard errors of ${\hat{\alpha }}_i$ and ${\hat{\tau }}_i^2$ are the square root of diagonal elements in (29), and hence are given by,

$$\begin{array}{rl}SE\left({\hat{\alpha }}_i\right)& =\sqrt{{\displaystyle \frac{{\tau }_i^2}{s_i}}}.\end{array}$$ (40)

$$\begin{array}{rl}SE\left({\hat{\tau }}_i^2\right)& =\sqrt{{\displaystyle \frac{2{\tau }_i^4}{s_i}}}.\end{array}$$ (41)

In stage three, α and ${\tau }^2$ are estimated by maximising the following likelihood,

$$L(\alpha ,{\tau }^2;{\hat{\alpha }}_i)=\prod _{i=1}^m\frac{1}{\sqrt{2\pi {\tau }^2}}\exp \{-\frac{{({\hat{\alpha }}_i-\alpha )}^2}{2{\tau }^2}\}.$$ (42)

The estimated values ${\hat{\alpha }}_i$ and $SE({\hat{\alpha }}_i)$ are used as data in (42).

4. Application to UK motorway accident data

Non-informative and weakly informative prior distributions

A non-informative prior distribution reflects the lack of prior information about a parameter [30]. A conjugate prior could be non-informative, such as $\mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$ or weakly-informative, such as $\mathrm{Inv}-\mathrm{Gamma}(0.1,0.1)$ for ${\tau }^2$. As a sensitivity analysis, we use the uniform prior $\mathrm{unif}(0,100)$ and a half-normal prior distribution $\mathrm{HN}(0.14)$ for τ, both are non-informative priors on τ [28,46]. We used $\mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$ as prior for ${\tau }_i^2(i=1,\dots ,m)$. Finally, a non-informative normal prior distribution was used with mean ${\mu }_0=0$ and variance ${\sigma }_0^2=100$ for α.

Informative prior distributions

An informative prior describes specific pre-existing information about parameter [30]. The maximum likelihood estimates of ${\tau }^2$ and α and their standard errors of traffic accident data from an earlier year (e.g. 2015) will be used to specify the informative priors in the Bayesian analysis of accident data in the subsequent year. More specifically, the parameters for inverse gamma prior are calculated from solving the following equation:

$$\begin{array}{rl}E\left({\tau }^2\right)& =\frac{{\alpha }_0}{{\beta }_0}={\hat{\tau }}_{ML}^2,\\ \mathrm{var}\left({\tau }^2\right)& =\frac{{\alpha }_0}{{\beta }_0^2}=\mathrm{var}({\hat{\tau }}_{ML}^2),\end{array}$$ (43)

where ${\hat{\tau }}_{ML}^2$ is the maximum likelihood estimate, 0.3162, and $\mathrm{var}({\hat{\tau }}_{ML}^2)$ is the variance of ${\hat{\tau }}_{ML}^2$, $(0.0738{)}^2$, both are obtained from analysing the UK motorways accident data in 2015. Solving the equations in (43), we obtain ${\alpha }_0=18.36$ and ${\beta }_0=58.06$. Thus, the informative prior for ${\tau }^2$ is $\mathrm{Inv}-\mathrm{Gamma}(18.36,58.06)$. Similarly, ${\mu }_0=-6.65$ and ${\sigma }_0^2={0.09}^2$.

Results

Both two-level and three-level hierarchical models are used to analyse the observed accident data in 2016 for the UK motorways. Model parameters include the overall log-intensity of traffic accidents α, and the between-motorway standard deviation, τ. The MCMC simulation requires specifying starting points for the parameters. The initial values 0 and 0.1 are specified for α and τ, respectively. The MCMC algorithm was run on the two-level hierarchical model for 100,000 iterations with a burn-in period of 10,000 and a thinning interval of 10; and on the three-level hierarchical model, 500,000 iterations with a burn-in period of 50,000 and a thinning interval of 100. The number of iterations of the MCMC is different between the two-level and three-level hierarchical models to ensure convergence to the posterior distributions.

Table 2 shows that the two-level Bayesian hierarchical model with different priors gives similar estimates of both the parameters α and τ and their standard deviations as well as their credible intervals. This indicates that the estimates of the model parameters are robust to the choice of prior. The estimated α and τ using the maximum likelihood estimation are similar to those from two-level Bayesian hierarchical model. Under the three-level Bayesian hierarchical model, the posterior mean, standard deviation and 95% credible interval for α and τ are similar when non-informative and weakly-informative prior distributions are used. The width of the credible interval of α based on the Bayesian method with an informative prior is narrower than the one estimated with non-informative and weakly-informative priors. In addition, the standard deviation for $\hat{\alpha }$ based on the Bayesian method with informative priors is smaller than that based on the Bayesian method with other priors. The estimated α and τ are similar between the frequentist and the Bayesian approaches, although the standard deviations are, in general, slightly smaller in the frequentist approach (see Table 2), as expected.

Table 2.

Results from the two-level Bayesian hierarchical model, three-level Bayesian hierarchical model, two-level frequentist hierarchical model and three-level frequentist hierarchical model of traffic accidents for 2016.The prior of α is $\mathrm{N}(0,100)$. HN represents the half-normal distribution. SD: Standard Deviation and CI: Credible Interval or Confidence Interval.

			Two-level hierarchical model			Three-level hierarchical model
Methods	Prior distribution	Parameter	Point estimate	SD	95% CI	Point estimate	SD	95% CI
Bayesian	${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$	α	−6.82	0.10	(−7.01, −6.64)	−6.93	0.11	(−7.15, −6.71)
		τ	0.60	0.08	(0.47, 0.77)	0.65	0.09	(0.49, 0.85)
	${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(0.1,0.1)$	α	−6.86	0.11	(−7.07, −6.65)	−6.93	0.11	(−7.15, −6.71)
		τ	0.70	0.09	(0.54, 0.88)	0.66	0.09	(0.50, 0.85)
	$\tau \sim \mathrm{unif}(0,100)$	α	−6.86	0.11	(−7.07, −6.64)	−6.93	0.11	(−7.16, −6.71)
		τ	0.70	0.09	(0.55, 0.90)	0.67	0.09	(0.51, 0.87)
	$\tau \sim \mathrm{HN}(0.14)$	α	−6.86	0.11	(−7.07, −6.65)	−6.93	0.11	(−7.16, −6.71)
		τ	0.70	0.09	(0.55, 0.89)	0.67	0.09	(0.51, 0.87)
	$\alpha \sim \mathrm{N}($- $6.65,{0.09}^2)$	α	−6.62	0.09	(−6.79, −6.43)	−6.70	0.08	(−6.86, −6.55)
	${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(18.36,58.06)$	τ	1.40	0.23	(1.14, 2.08)	1.34	0.11	(1.15, 1.57)
Frequentist		α	−6.81	0.10	(−7.00, −6.62)	−6.64	0.08	(−6.80, −6.49)
		τ	0.64	0.10	(0.54, 0.89)	0.51	0.06	(0.41, 0.66)

Notes: The prior of α is $\mathrm{N}(0,100)$. HN represents the half-normal distribution. SD: Standard deviation and CI: credible interval or confidence interval.

Table 3 shows the estimated overall intensity of accidents per one kilometre. It is clear that results for λ from the three-level Bayesian hierarchical model are similar, except for the informative prior where λ is greater but close to the estimate from the frequentist method. The two-level Bayesian hierarchical model produces similar results under non-informative and weakly-informative priors of τ.

Table 3.

Estimates of overall accident intensity λ per one kilometre for UK motorway network in 2016: $\lambda =\exp (\alpha )$.

		Two-level hierarchical model		Three-level hierarchical model
Methods	Prior distribution	Point estimate	95% CI	Point estimate	95% CI
Bayesian	${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$	1.09	(0.90, 1.31)	0.98	(0.79, 1.22)
	${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(0.1,0.1)$	1.05	(0.85, 1.29)	0.98	(0.79, 1.22)
	$\tau \sim \mathrm{unif}(0,100)$	1.05	(0.85, 1.31)	0.98	(0.78, 1.22)
	$\tau \sim \mathrm{HN}(0.14)$	1.05	(0.85, 1.29)	0.98	(0.78, 1.22)
	$\alpha \sim \mathrm{N}($- $6.65,{0.09}^2)$	1.33	(1.12, 1.61)	1.23	(1.05, 1.43)
	${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(18.36,58.06)$
Frequentist		1.10	(0.91, 1.33)	1.31	(1.12, 1.53)

Notes: The prior of α is N(0, 100). CI: credible interval or confidence interval. HN represents the half-normal distribution.

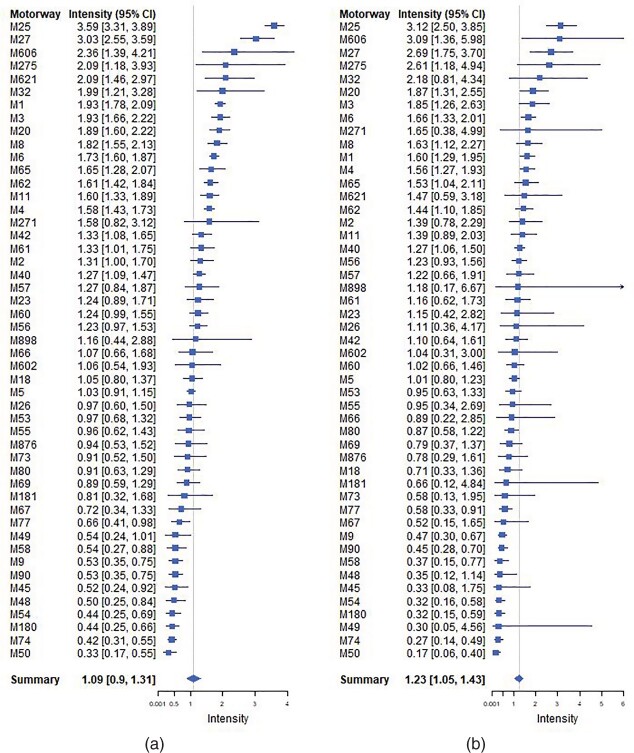
Figure 2 shows 49 motorways with intensities of traffic accidents per one kilometre and their corresponding credible intervals for both two-level and three-level Bayesian hierarchical models.

Figure 2.

Results from the two-level Bayesian hierarchical model and the three-level Bayesian hierarchical model for accident data on the UK motorways in 2016. In the two-level Bayesian hierarchical model, the following prior distributions are used, $\alpha \sim \mathrm{N}(0,100)$ and ${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$. In the three-level Bayesian hierarchical model, the prior distributions are $\alpha \sim \mathrm{N}(-6.65,{0.09}^2)$ and ${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(18.36,58.06)$. Results include the posterior mean and the corresponding 95% credible interval for the intensity of accidents ${\lambda }_i=1000\times \exp ({\alpha }_i)$ per one kilometre on each motorway and the overall intensity of accidents λ per one kilometre. Square boxes represent posterior means of ${\lambda }_i,(i=1,\dots ,m)$. The diamond represents the estimated overall intensity of accident λ and its 95% credible interval. Horizontal lines denote 95% credible intervals and the sold vertical line represents the posterior mean of the overall intensity λ. (a) Two-level Bayesian hierarchical model. (b) Three-level Bayesian hierarchical model.

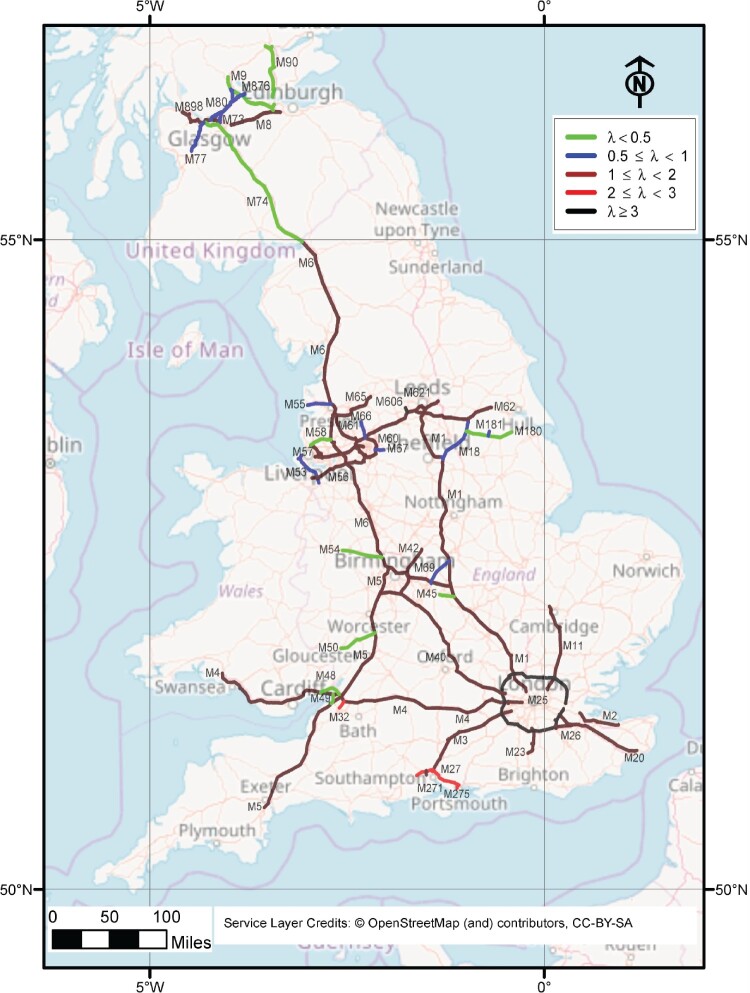
Based on the estimation results from Figure 2 of the Bayesian hierarchical models for the UK motorway data, the estimated intensities of accidents on the UK motorway network are classified into five categories. Category one $(\lambda <0.5)$ is referred to a very low risk; Category two $(0.5\le \lambda <1)$ is referred to a low risk; Category three $(1\le \lambda <2)$ is referred to a moderate risk; Category four $(2\le \lambda <3)$ is referred to a high risk. Finally, category five $(\lambda \ge 3)$ is referred to a very high risk. Based on the results from the Bayeisan three-level hierarchical model, the moderate-risk level represents the general intensity of accidents level of the UK motorway network. Based on the results presented in Figures 2 and 3, motorways: M27, M275 and M32 are at high risk, whereas motorways: M25 and M606 form the highest risk motorways, where the expected number of accidents is above 3 per one kilometre for both motorways. On the other hand, motorways: M9, M90, M58, M45, M48, M49, M180, M54, M74 and M50 have the lowest risk such that the expected number of accidents is lower than 0.5 for these motorways.

Figure 3.

Estimated intensity of traffic accidents per one kilometre on the UK motorway network in 2016. The intensities are estimated using the three-level Bayesian hierarchical model with prior distributions $\alpha \sim \mathrm{N}(-6.65,{0.09}^2)$ and ${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(18.36,58.06)$.

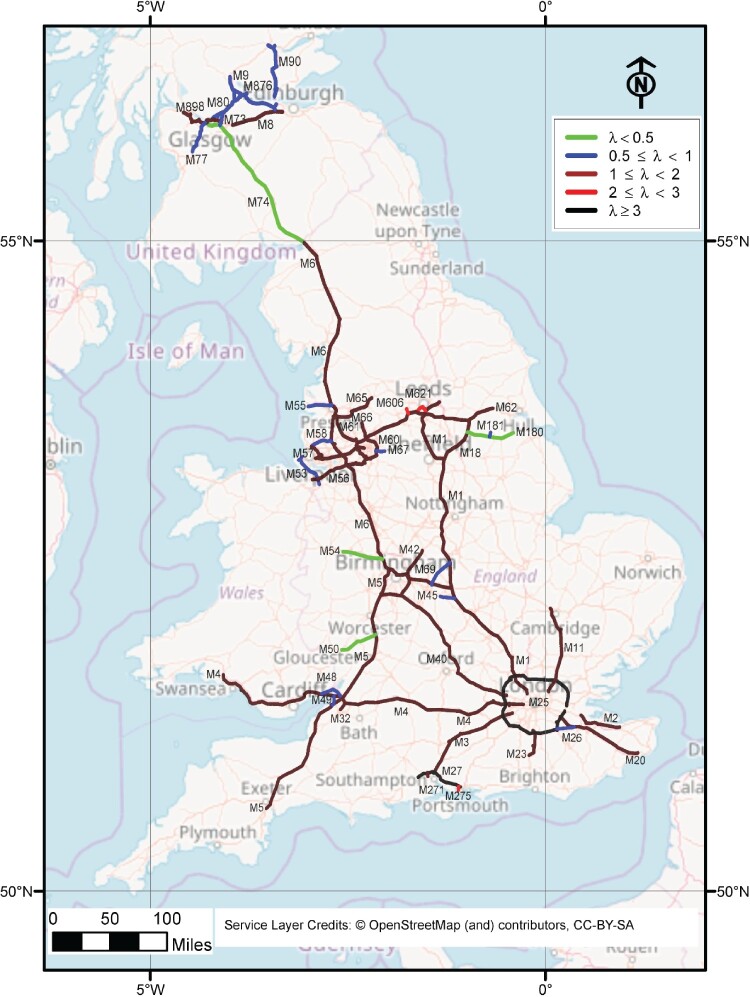
Based on the results of the two-level Bayesian hierarchical model, Figures 2 and 4 shows that a general level of the intensity of accidents on the UK motorway network is of moderate risk where the moderate risk motorways are M32, M1, M3, M20, M8, M6, M65, M62, M11, M4, M271, M42, M61, M2, M40, M57, M23, M60, M56, M898, M66, M602, M18 and M5. Motorways M25 surrounding almost all of Greater London, England, except North Ockendon, in the United Kingdom and M27 in Hampshire, England, starting west-east from Cadnam to Portsmouth, have a very high-risk level. The expected numbers of accidents are 3.59 per one kilometre of M25 and 3.03 per one kilometre of M27. The motorways M54, M180, M74 and M50 form the lowest risk motorways and their estimated intensities are 4.4, 4.4, 4.2, 3.3 per 10 kilometres. Figure 4, moreover, illustrates that the risk intensity level for motorways M606, M621 and M275 is high and the expected number of accidents is 2.36 per one kilometre of M606 and 2.09 per one kilometre for both M621 and M275.

Figure 4.

Estimated intensity of traffic accidents per one kilometre on the UK motorway network in 2016. The intensities are estimated using the two-level Bayesian hierarchical model with prior distributions $\alpha \sim \mathrm{N}(0,100)$ and ${\tau }^2\sim \mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$.

5. Simulation study

We conducted a simulation study to assess the performance of the proposed models.

5.1. Simulation design

For the two-level hierarchical model, we considered six scenarios with different true values of parameters α and τ. The true values of α are set to be -1 and −7. If the overall log-intensity α is chosen to be lower than $-9$, the number of accidents on the motorway will be very close to zero. The between-motorway standard deviation τ is set to be 0.3, 0.8 and 1.5 to reflect the variation between motorways. A magnitude of 0.3 would indicate that there is not much variation in the motorway specific log-intensity while a magnitude of 1.5 would result in much more variation between motorways. These true values are chosen to be close to the results for the observed data set. The log-intensity ${\alpha }_i$ on motorway $i(i=1,\dots ,m)$ is drawn from a normal distribution with mean α and standard deviation τ. For the two-level hierarchical model, the number of accidents $n_i(i=1,\dots ,m)$ on the motorway i is generated from a Poisson distribution with mean $L_i\exp ({\alpha }_i)$, where $L_i$ is the length of the motorway i. We simulated 1,000 data sets for each scenario.

For the three-level hierarchical model, we simulated data according to the following,

$$\begin{array}{rl}{\alpha }_i& \sim \mathrm{N}(\alpha ,{\tau }^2),\\ {\alpha }_{ij}& \sim \mathrm{N}({\alpha }_i,{\tau }_i^2),\\ n_{ij}& \sim \mathrm{Pois}(L_{ij}\exp \left({\alpha }_{ij}\right)),i=1,\dots ,m;j=1,..,s_i.\end{array}$$ (44)

Six different scenarios of simulation are considered with $\alpha =-5,-7$ and $\tau =0.3,0.7,1.5$ for the three-level models.

The performance of the proposed models is evaluated by comparing the simulated results with the true values using the following metrics, bias, mean square error (MSE) and coverage probability (CP) [37]. The bias in the parameter estimate represents the difference between the average of the estimates over all simulation and the true value. The mean square error is the squared bias plus the variance of the estimated parameter, for example $\mathrm{MSE}(\hat{\alpha })=\mathrm{Bias}(\hat{\alpha },\alpha {)}^2+\mathrm{Var}(\hat{\alpha })$. The coverage probability is the percentage of 95% credible intervals across the 1000 simulated data sets that contain the true value.

5.2. Simulation results

Table 4 shows that the performance of the two-level Bayesian hierarchical model is better than the two-level frequentist hierarchical model in terms of the bias, MSE and coverage probability. In Table 4, the bias and MSE in α and τ for the two-level frequentist hierarchical model are larger than those for the two-level Bayesian hierarchical model for scenarios with true value $\alpha =-7$. The bias in τ obtained for the two-level Bayesian hierarchical model is insensitive to the choice of priors.

Table 4.

Simulation results of the two-level Bayesian and frequentist hierarchical models (model 1 and 2) under four prior distributions of ${\tau }^2$ and the prior distribution $\alpha \sim \mathrm{N}(0,{10}^2)$. Time for running the simulation recorded in seconds.

			$\alpha =-1$					$\alpha =-7$
	True τ	Parameters	Mean	Bias	MSE	CP	Time	Mean	Bias	MSE	CP	Time
$\mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$	0.3	α	−0.9982	0.0018	0.0018	94.7%	11,747	−6.9967	0.0033	0.0028	94.8%	11,667
		τ	0.3008	0.0008	0.0009	95.4%		0.2963	−0.0037	0.0021	93.8%
	0.8	α	−0.9929	0.0071	0.0134	95.3%	11,679	−6.9806	0.0194	0.0142	94.7%	11,664
		τ	0.8041	0.0041	0.0066	95.7%		0.7896	−0.0104	0.0083	95.2%
	1.5	α	−0.9923	0.0077	0.0426	96.4%	18,516	−6.9442	0.0558	0.0478	95.0%	11,609
		τ	1.5019	0.0019	0.0238	95.5%		1.4470	−0.0530	0.0270	94.7%
$\mathrm{Inv}-\mathrm{Gamma}(0.1,0.1)$	0.3	α	−0.9982	0.0018	0.0018	95.0%	11,660	−6.9980	0.0020	0.0028	95.6%	11,896
		τ	0.3072	0.0072	0.0009	95.5%		0.3097	0.0097	0.0018	95.5%
	0.8	α	−0.9927	0.0073	0.0134	95.2%	11,593	−6.9807	0.0193	0.0141	95.0%	11,691
		τ	0.8051	0.0051	0.0066	96.0%		0.7910	−0.0090	0.0082	95.6%
	1.5	α	−0.9920	0.0080	0.0426	96.1%	11,903	−6.9441	0.0559	0.0478	94.9%	11,683
		τ	1.5005	0.0005	0.0235	95.4%		1.4454	−0.0546	0.0272	94.7%
$\mathrm{unif}(0,100)$	0.3	α	−0.9983	0.0017	0.0018	94.8%	12,492	−6.9975	0.0025	0.0028	95.8%	12,486
		τ	0.3050	0.0050	0.0010	95.0%		0.3044	0.0044	0.0021	94.5%
	0.8	α	−0.9927	0.0073	0.0134	95.5%	12,707	−6.9816	0.0184	0.0141	95.5%	12,432
		τ	0.8131	0.0131	0.0069	95.6%		0.8007	0.0007	0.0083	95.4%
	1.5	α	−0.9923	0.0077	0.0426	96.6%	12,580	−6.9452	0.0548	0.0478	94.9%	12,465
		τ	1.5181	0.0181	0.0246	95.2%		1.4646	−0.0354	0.0261	95.3%
$\mathrm{HN}(0.14)$	0.3	α	−0.9983	0.0017	0.0018	94.9%	17,933	−6.9974	0.0026	0.0028	95.5%	18,073
		τ	0.3050	0.0050	0.0010	94.9%		0.3046	0.0046	0.0021	94.7%
	0.8	α	−0.9929	0.0071	0.0134	95.3%	17,724	−6.9816	0.0184	0.0141	95.2%	17,807
		τ	0.8129	0.0129	0.0069	95.4%		0.8006	0.0006	0.0083	95.4%
	1.5	α	−0.9924	0.0076	0.0426	96.7%	17,767	−6.9454	0.0546	0.0477	94.5%	17,828
		τ	1.5179	0.0179	0.0245	95.5%		1.4645	−0.0355	0.0261	95.2%
Frequentist method	0.3	α	−0.9982	0.0018	0.0018	94.1%	42	−6.9732	0.0268	0.0034	90.4%	42
		τ	0.2956	−0.0044	0.0009	95.6%		0.2850	−0.0150	0.0021	94.7%
	0.8	α	−0.9928	0.0072	0.0134	94.2%	40	−6.9405	0.0595	0.0166	90.5%	39
		τ	0.7902	−0.0098	0.0065	96.0%		0.7535	−0.0465	0.0096	94.9%
	1.5	α	−0.9925	0.0075	0.0426	95.9%	35	−6.8843	0.1157	0.0551	89.5%	37
		τ	1.4915	−0.0238	0.0234	95.4%		1.3723	−0.1277	0.0386	93.8%

Note: MSE represents mean square error and CP the coverage probability.

Table 5 shows that the three-level Bayesian hierarchical model performs better than the three-level frequentist hierarchical model in terms of the bias, MSE and coverage probability. The three-level frequentist approach produced higher bias for point estimates of α and τ acrosss the six scenarios and a bigger MSE. For scenarios with true value of $\alpha =-5$, the bias of the estimated τ is sensitive to the specification of the prior distribution. For the true value of $\alpha =-7$, the three-level frequentist hierarchical model produced poor coverage probabilities for both the parameters, providing a value of 0 for α. For the true value of $\alpha =-5$, the coverage probabilities are better than those for $\alpha =-7$, but the frequentist approach gave lower coverage probabilities for both parameters. Henderson et al. [20] showed that the separate analysis using the two-stage method is not performing well compared with the one-stage method. Browne and Draper [11] showed that marginal quasi-likelihood method produced the coverage probability as zero for the random effect variance parameter in random-effects logistic regression model. Our simulation results show that Bayesian hierarchical models appeared better than the frequentist hierarchical models in terms of the bias, MSE and coverage probability.

Table 5.

Simulation results of the three-level Bayesian and frequentist hierarchical models (model 3 and 4) under four prior distributions of ${\tau }^2$ and the prior distribution $\alpha \sim \mathrm{N}(0,{10}^2)$.

			$\alpha =-5$					$\alpha =-7$
	True τ	Parameters	Mean	Bias	MSE	CP	Time	Mean	Bias	MSE	CP	Time
$\mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$	0.3	α	−5.0032	−0.0032	0.0026	94.7%	559,000	−6.9940	0.0060	0.0037	93.8%	258,760
		τ	0.3001	0.0001	0.0019	95.0%		0.2937	−0.0063	0.0034	93.5%
	0.7	α	−5.0035	−0.0035	0.0116	95.6%	549,926	−7.0003	−0.0003	0.0132	95.0%	436,154
		τ	0.7004	0.0004	0.0066	96.2%		0.6941	−0.0059	0.0085	94.5%
	1.5	α	−5.0052	−0.0052	0.0500	94.8%	542,032	−7.0198	−0.0198	0.0592	93.1%	263,827
		τ	1.4937	−0.0063	0.0262	95.4%		1.5048	0.0048	0.0336	94.9%
$\mathrm{Inv}-\mathrm{Gamma}(0.1,0.1)$	0.3	α	−5.0037	−0.0037	0.0026	95.2%	584,324	−7.0014	−0.0014	0.0037	95.9%	545,479
		τ	0.3131	0.0131	0.0018	95.8%		0.3164	0.0164	0.0025	96.3%
	0.7	α	−5.0035	−0.0035	0.0116	95.6%	577,621	−6.9944	0.0056	0.0136	94.5%	507,931
		τ	0.7025	0.0025	0.0065	96.1%		0.6946	−0.0054	0.0085	94.2%
	1.5	α	−5.0052	−0.0052	0.0501	94.5%	571,022	−7.0187	−0.0187	0.0536	95.2%	569,115
		τ	1.4920	−0.0080	0.0260	95.2%		1.5032	0.0032	0.0340	94.2%
$\mathrm{unif}(0,100)$	0.3	α	−5.0035	−0.0035	0.0026	95.0%	545,730	−7.0007	−0.0007	0.0037	95.2%	736,853
		τ	0.3082	0.0082	0.0020	94.9%		0.3063	0.0063	0.0033	94.4%
	0.7	α	−5.0041	−0.0041	0.0116	95.6%	533,863	−6.9957	0.0043	0.0137	94.8%	555,450
		τ	0.7111	0.0111	0.0068	96.4%		0.7048	0.0048	0.0089	94.3%
	1.5	α	−5.0062	−0.0062	0.0504	95.5%	580,176	−7.0217	−0.0217	0.0535	95.5%	537,030
		τ	1.5133	0.0133	0.0271	95.8%		1.5287	0.0287	0.0361	93.9%
$\mathrm{HN}(0.14)$	0.3	α	−5.0035	−0.0035	0.0026	95.2%	574,984	−7.0004	−0.0004	0.0037	95.2%	548,584
		τ	0.3082	0.0082	0.0020	95.0%		0.3064	0.0064	0.0033	94.1%
	0.7	α	−5.0041	−0.0041	0.0116	95.6%	584,604	−6.9957	0.0043	0.0136	94.7%	497,680
		τ	0.7111	0.0111	0.0068	96.3%		0.7050	0.0050	0.0089	94.5%
	1.5	α	−5.0061	−0.0061	0.0504	95.5%	546,481	−7.0216	−0.0216	0.0535	95.5%	583,913
		τ	1.5132	0.0132	0.0270	95.7%		1.5286	0.0286	0.0362	93.9%
Frequentist method	0.3	α	−4.9305	0.0695	0.0073	72.4%	537	−6.5961	0.4039	0.1650	0%	479
		τ	0.3082	0.0082	0.0027	81.7%		0.2650	−0.0350	0.0037	89.8%
	0.7	α	−4.9166	0.0834	0.0169	86.0%	528	−6.5297	0.4703	0.2271	0%	547
		τ	0.6602	−0.0398	0.0072	94.1%		0.4942	−0.2058	0.0472	27.1%
	1.5	α	−4.8524	0.1476	0.0593	88.0%	514	−6.3587	0.6413	0.4315	0%	549
		τ	1.3102	−0.1898	0.0532	84.7%		0.9650	−0.5350	0.3012	4.2%

Notes: Time for running the simulation is recorded in seconds. MSE represents mean square error and CP the coverage probability.

6. Model comparisons

6.1. Model comparisons using information criteria

We compare the Bayesian models using the deviance information criterion (DIC) [42] and the Watanabe-Akaike or widely applicable information criterion (WAIC) [47].

Table 6 shows that DIC and WAIC for the three-level Bayesian hierarchical model across different priors are lower than those for two-level Bayesian hierarchical model. This indicates that the three-level Bayesian hierarchical model provides a better fit to the observed data compared with the two-level Bayesian hierarchical model.

Table 6.

DIC and WAIC: 2LBHM represents the two-level Bayesian hierarchical model and 3LBHM represents the three-level Bayesian hierarchical model.

		Prior distribution
Model	Criterion	$\mathrm{Gamma}(0.001,0.001)$	$\mathrm{Gamma}(0.1,0.1)$	$\mathrm{HN}(0.14)$	$\mathrm{unif}(0,100)$	$\mathrm{Gamma}(18.36,58.06)$
2LBHM	DIC	100,408.3	71,999.9	71,825.6	71,950.6	7,1971.7
	WAIC	89,412.6	68,222.7	68,135.6	68,210.9	68,223.2
3LBHM	DIC	85,204.3	71,683.3	71,671.0	71,671.0	71,700.3
	WAIC	1049.9	888.3	895.7	20,271.2	891.3

6.2. Model comparisons using simulation study

Simulation Design

The term ‘misspecification’ means fitting a wrong model to the data [48]. Model misspecification affects estimation and produces biased estimates. To investigate the effects of model misspecification, we fitted a two-level Bayesian hierarchical model (1) to the same data sets that simulated in Section 5.1 via a three-level Bayesian hierarchical model (16). We provide posterior mean, bias, mean square error and coverage probability to investigate whether model (1) is able to analyse data in presence of between grouped segments heterogeneity. The same prior distribution in section 3.1.3 and the same initial values in section 4 are utilized in the Bayesian analysis, and 100,000 iterations were run with a burn-in period of 10,000 and a thinning interval of 10 to obtain posterior samples for α and τ.

Simulation Results

Tables 7 shows that the two-level Bayesian hierarchical model produced biased estimates, with large mean square errors and extremely poor coverage probabilities for both the model parameters. The coverage probabilities were 0 or close to 0 for τ and exactly equal or close to 100% for α when the true value for the between-motorway standard deviation was $\tau =0.3\mathrm{and}0.7$. This indicates that the fitted model, two-level hierarchical Bayesian model, is incorrect, when the underlying model has three levels.

Table 7.

Simulation results from two-level Bayesian hierarchical model under four prior distributions of ${\tau }^2$ and the prior distribution $\alpha \sim \mathrm{N}(0,{10}^2)$. Time for running the simulation is recorded in seconds.

			$\alpha =-5$					$\alpha =-7$
	True τ	Parameters	Mean	Bias	MSE	CP	Time	Mean	Bias	MSE	CP	Time
$\mathrm{Inv}-\mathrm{Gamma}(0.001,0.001)$	0.3	α	−4.8199	0.1801	0.0387	100%	20,147	−6.8121	0.1879	0.0437	99.9%	19,592
		τ	1.6270	1.3270	1.7673	0%		1.6670	1.3670	1.8768	0%
	0.7	α	−4.8165	0.1835	0.0479	99.2%	17,955	−6.8004	0.1996	0.0576	98.7%	21,103
		τ	1.7362	1.0362	1.0868	0%		1.7856	1.0856	1.1946	0%
	1.5	α	−4.8167	0.1833	0.0841	96.6%	19,410	−6.822	0.178	0.0868	97.0%	19,959
		τ	2.188	0.688	0.5142	0.37%		2.2409	0.7409	0.5989	0.34%
$\mathrm{Inv}-\mathrm{Gamma}(0.1,0.1)$	0.3	α	−4.8197	0.1803	0.0387	100%	19,623	−6.8121	0.1879	0.0438	99.9%	20,937
		τ	1.6245	1.3245	1.7607	0%		1.6645	1.3645	1.8699	0%
	0.7	α	−4.8167	0.1833	0.0478	99.6%	18,536	−6.8002	0.1998	0.0577	98.4%	20,114
		τ	1.734	1.034	1.0821	0%		1.7829	1.0829	1.1887	0%
	1.5	α	−4.8163	0.1837	0.084	96.2%	17,885	−6.8219	0.1781	0.0865	97.1%	19,965
		τ	2.1836	0.6836	0.5079	03.7%		2.2368	0.7368	0.5926	0.35%
$\mathrm{unif}(0,100)$	0.3	α	−4.8200	0.1800	0.0388	100%	19,398	−6.8129	0.1871	0.0435	100%	21,003
		τ	1.6452	1.3452	1.816	0%		1.6869	1.3869	1.9318	0%
	0.7	α	−4.8168	0.1832	0.0478	99.4%	19,788	−6.8014	0.1986	0.0573	99.0%	22,654
		τ	1.7562	1.0562	1.1289	0%		1.8075	1.1075	1.2430	0%
	1.5	α	−4.8169	0.1831	0.0837	96.7%	22,420	−6.8243	0.1757	0.086	97.4%	20,769
		τ	2.2136	0.7136	0.5511	0.31%		2.2696	0.7696	0.6437	03.0%
$\mathrm{HN}(0.14)$	0.3	α	−4.8195	0.1805	0.0389	100%	23,911	−6.8129	0.1871	0.0435	100%	24,285
		τ	1.6455	1.3455	1.8169	0%		1.6869	1.3869	1.9319	0%
	0.7	α	−4.8167	0.1833	0.0478	99.5%	24,054	−6.8014	0.1986	0.0573	99.0%	24,808
		τ	1.7561	1.0561	1.1287	0%		1.8075	1.1075	1.2429	0%
	1.5	α	−4.8167	0.1833	0.0839	96.5%	24,214	−6.8243	0.1757	0.0860	97.4%	24,460
		τ	2.2134	0.7134	0.5509	0.32%		2.2697	0.7697	0.6438	3.0%

Note: MSE represents mean square error and CP the coverage probability.

7. Discussion and conclusions

This study focused on Bayesian hierarchical models for analysing road accidents on the UK motorway network. This work helps to identify the most dangerous motorways in the UK network based on the estimated intensity of traffic accidents. These models have not been used for the UK motorway network before. We modelled the accident data at the motorway level by proposing a two-level hierarchical model to take into account the heterogeneity across motorways. We proposed a three-level hierarchical model to incorporate the heterogeneity not only across motorways but also across grouped segments. We assumed accident intensities are homogeneous within grouped segments but heterogeneous across grouped segments. Using the proposed hierarchical models, we identified motorways with highest and lowest intensities of accidents, classified motorway into different risk categories, and estimated the overall intensity of accidents.

We used both Bayesian and frequentist approaches to estimate the model parameters. In the Bayesian approach, a sensitivity analysis with different prior distributions for ${\tau }^2$ has been performed to investigate the effect of the prior choice on the resulting posterior distributions of α and τ. We have used non-informative, weakly informative and informative priors. In the frequentist approach, the maximum likelihood method has been separately used for each level of the model.

We assessed the performance of all proposed models through a simulation study as well as a real application related to the traffic accident data on the UK motorway network in 2016. In the simulation study, different scenarios were explored. We examined three performance criteria, bias, mean square error (MSE) and coverage probability (CP) of parameter estimates. The two parameters α and τ represent the overall accident intensity and between-motorway heterogeneity, respectively. We model all motorways simultaneously using hierarchical models. The performance of different levels of hierarchical models is evaluated through the estimation of these two parameters. The simulation results showed that the performance of the two-level Bayesian hierarchical model is better than the two-level frequentist hierarchical model in terms of the bias and the coverage probability for some simulation scenarios. The performance of both models is similar in terms of mean square errors.

In the real application, the findings from two-level Bayesian hierarchical analysis suggest that three motorways with the highest intensity of traffic accidents are M25, M27 and M606. The M25 has the highest intensity of traffic accidents, where the expected number of accidents is 3.59 per one kilometre. The M27 has the second highest intensity of traffic accidents with the expected number of accidents 3.03 per one kilometre. The M606 is the third most dangerous motorway with the expected number of accidents 2.36 per one kilometre. The three motorways with the lowest intensity of accidents are M50, M74 and M180. The lowest intensity of accidents is the M50 with an expected number of accidents of 3.32 per 10 kilometres. The second lowest intensity of traffic accidents is the M74 with an expected number of accidents of 4.18 per 10 kilometres. The M180 has the third lowest intensity of accidents with an expected number of accidents of 4.35 per 10 kilometres.

The simulation results showed that the three-level Bayesian hierarchical model performed better than the three-level frequentist model in most of the simulation scenarios. The frequentist method failed to attain the required level of actual coverage in some scenarios because of the large bias in the estimates of the overall log-intensity of accidents and the between-motorway standard deviation.

The results of the analysis of the real data using the three-level Bayesian hierarchical model showed that the motorway has the highest intensity of accidents is M25, where the expected number of accidents is 3.12 per one kilometre. The second highest intensity is found on M606 with $\lambda =3.09$ per one kilometre. The third highest intensity is found on M27 with an expected number of accidents of 2.69 per one kilometre. In contrast, M50, M74 and M49 have the lowest intensity of accidents with the expected numbers of accidents being 1.7, 2.7 and 3.0 per 10 kilometres, respectively. Some motorways have the similar intensity of accidents, for example, both M2 and M11 have $\lambda =1.39$ per one kilmeter, both M53 and M55 have $\lambda =9.5$ per 10 kilometres, both M73 and M77 have $\lambda =5.8$ per 10 kilometres and both M54 and M180 have $\lambda =3.2$ per 10 kilometres.

Information criteria (DIC and WAIC) and a simulation study were used to compare between the two-level and three-level Bayesian hierarchical models. The values of DIC and WAIC for the three-level hierarchical model are lower than those for the two-level hierarchical model. This indicates that the three-level Bayesian hierarchical model fits the data better.

Future research can be conducted to investigate the overdispersion of the accident data by employing alternative models, such as negative binomial models [12], zero-inflated Poisson models [33] and Extra-Poisson variation models [10]. The relaxation of the assumption of homogenous accident intensity within grouped segments can be explored to allow for the variation of the accident intensity within grouped segments. The extension could also include incorporating the heterogeneity arising from unobserved factors [3,9,15,38], and spatial correlations at intersections [6,22,32]. In our three-level hierarchical models, we allow parameters of accident intensity to vary across grouped segments. Future research can investigate multivariate random parameters models to account for the spatial correlations [6,8,22,32] and temporal correlations [35], as well as correlations between different types of crash [3]. The incorporation of spatial correlations in crash models has led to improved precision parameter estimates in some data sets [6], and this can be tested for the UK motorway accident data, by taking into account the spatial correlations between grouped segments. The multivariate random parameters models can also be extended to account for the correlations between explanatory variables to further improve the precision of the parameter estimates, due to the possibility of further capturing the underlying unobserved heterogeneity [15]. Variables such as geometric design, traffic conditions, environmental conditions and other variables affecting the accident occurrence in a motorway can be investigated. Models can be developed to include explanatory variables that may attribute to unobserved heterogeneity arising from various sources such as unobserved vehicle characteristics [7], driver characteristics [14,32], roadway attributes, and environmental factors [9].

Funding Statement

This work was supported by the University of Plymouth Collaborative Seed Grant on Big Data Research [Wei, 2017]. The first author was supported by a studentship from the Ministry of Higher Education and Scientific Research, Iraq [Ref: 5672], to undertake a PhD research project at the University of Plymouth.

Disclosure statement

No potential conflict of interest was reported by the author(s).