Extension of biplot methodology to multivariate regression analysis

Abstract

At the core of multivariate statistics is the investigation of relationships between different sets of variables. More precisely, the inter-variable relationships and the causal relationships. The latter is a regression problem, where one set of variables is referred to as the response variables and the other set of variables as the predictor variables. In this situation, the effect of the predictors on the response variables is revealed through the regression coefficients. Results from the resulting regression analysis can be viewed graphically using the biplot. The consequential biplot provides a single graphical representation of the samples together with the predictor variables and response variables. In addition, their effect in terms of the regression coefficients can be visualized, although sub-optimally, in the said biplot.

1. Introduction

Multivariate regression analysis is a statistical tool that is concerned with describing and evaluating the relationship between a given set of responses and a set of predictors [16]. Specifically, regression analysis helps in understanding how a typical value of a response changes when one of the predictors is varied, while the others are kept fixed. It can also be used to predict the outcome of a given response by means of the predictors.

Consider $\text{M}\ge 1$ response variables and $\text{P}\ge 1$ predictors. Let $\mathbf{X}:\text{N}\times \text{P}$ denote the matrix of (centered) predictors while $\mathbf{Y}:\text{N}\times \text{M}$ denote the matrix of (centered) responses. Usually the modeling of one $\text{Y}$-variable by means of $\mathbf{X}$ is given by the equation:

$$\mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{e}$$ (1)

where e: $\text{N}\times 1$ is the error term, $\mathbf{y}$: $\text{N}\times 1$ is the response vector and b: $\text{P}\times 1$ is the unknown (regression) coefficient vector that can be estimated through the least-squares method as

$$\hat{\mathbf{b}}=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y},$$

provided $\mathbf{X}$ is of rank $\text{P}$.

Equation (1) is the general idea in regression analysis, for $\text{M}=1$. However, for $\text{M}>1$ $\text{Y}$-variables, the modeling is done by the multivariate regression model:

$$\mathbf{Y}=\mathbf{X}\mathbf{B}+\in$$

where $\in :\text{N}\times \text{M}$ is the error matrix. The unknown (regression) coefficients matrix B: $\text{P}\times \text{M}$ is then estimated by the least square method as:

$$\hat{\mathbf{B}}=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{Y},$$ (2)

for ${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$ non-singular. Thus, $\mathbf{Y}$ is estimated as

$$\hat{\mathbf{Y}}=\mathbf{X}({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{Y}=\mathbf{X}\hat{\mathbf{B}}.$$ (3)

Equation (3) is referred to as the multivariate regression analysis because $\text{ M}>1$. If $\text{ M}=1$, then equation (3) would be the (ordinary) regression scenario in (1). Moreover, the sign of each coefficient value in $\hat{\mathbf{b}}$ or $\hat{\mathbf{B}}$ gives an indication of the predictors’ effect direction on the response variables.

Since its first introduction by Gabriel [6], biplots have been employed in a number of multivariate methods (such as principal component analysis, correspondence analysis, canonical variate analysis, multidimensional scaling, discriminant analysis and redundancy analysis) as a form of graphical representation of data, as well as pattern and data inspection [3,4,7,10,11,13]. In this paper, the biplot is employed to visualize the effect of the predictors on the response variables graphically and to display results of the regression. It further provides a single graphical representation for displaying results from the regression analysis of a data set. This employment is based on (i) rephrasing the biplot theory in the multivariate regression context, (ii) applying the biplot to real life data, and (iii) developing software for executing these applications. This paper is loosely derived from Oyedele [18].

The remainder of this paper is organized as follows. Section 2 briefly provides the essential concepts behind the biplot before its merging into the multivariate regression framework in Section 3. This is followed by an application with a sensory and composition evaluation data of cocktail juices in Section 4. Finally, some concluding remarks are presented in Section 5 and the developed software.

2. Fundamental idea of the biplot

The biplot extends the idea of a simple scatterplot of two variables to the case of many variables, with the objective of visualizing the maximum possible amount of information in the data [13]. In the first biplots introduced by Gabriel, the rows and columns of a data matrix were represented by vectors, but to differentiate between these two sets of vectors, Gabriel [6] suggested that the rows of the data matrix be represented by points. Gower & Hand [10] went a step further by introducing the idea of representing the columns of the data matrix by axes, rather than vectors, while still representing the rows of the data matrix by points. This was done to support their theory that biplots were the multivariate version of scatter plots. Gower & Hand’s [10] biplot representation is very useful when the data matrix under consideration is a matrix of samples by variables.

By definition, the biplot is a joint graphical display of the rows and columns of a data matrix $\mathbf{K}:\text{N}\times \text{S}$ by means of markers ${\mathbf{g}}_1,{\mathbf{g}}_2,\dots ,{\mathbf{g}}_{\text{N }}$ for its rows and markers ${\mathbf{h}}_1,{\mathbf{h}}_2,\dots ,{\mathbf{h}}_{\text{S }}$ for its columns. Each marker is chosen in such a way that the inner product ${\mathbf{g}}_{\text{i}}^{\text{T}}{\mathbf{h}}_{\text{j }}$represents $k_{\text{ij}}$, the $(\text{i},\text{j}{)}^{\text{th}}$ element of the data matrix $\mathbf{K}$ [2]. In other words, the biplot of $\mathbf{K}$ relies on the decomposition of $\mathbf{K}$ into the product of two matrices, its row markers matrix ( $\mathbf{G}:\text{N}\times \text{r}$)

$$\mathbf{G}=\left[\begin{array}{ccc}{\text{g}}_{11}& {\text{g}}_{12}& \begin{array}{cc}\cdots & {\text{g}}_{1\text{r}}\end{array}\\ {\text{g}}_{21}& {\text{g}}_{22}& \begin{array}{cc}\cdots & {\text{g}}_{2\text{r}}\end{array}\\ \begin{array}{c}⋮\\ {\text{g}}_{\text{N}1}\end{array}& \begin{array}{c}⋮\\ {\text{g}}_{\text{N}2}\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\cdots & {\text{g}}_{\text{Nr}}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}{\mathbf{g}}_{(1)}^{\text{T}}\\ {\mathbf{g}}_{(2)}^{\text{T}}\\ \begin{array}{c}⋮\\ {\mathbf{g}}_{(\text{N})}^{\text{T}}\end{array}\end{array}\right]$$

and its column markers matrix ( $\mathbf{H}:\text{S}\times \text{r}$)

$$\mathbf{H}=\left[\begin{array}{ccc}{\text{h}}_{11}& {\text{h}}_{12}& \begin{array}{cc}\cdots & {\text{h}}_{1\text{r}}\end{array}\\ {\text{h}}_{21}& {\text{h}}_{22}& \begin{array}{cc}\cdots & {\text{h}}_{2\text{r}}\end{array}\\ \begin{array}{c}⋮\\ {\text{h}}_{\text{S}1}\end{array}& \begin{array}{c}⋮\\ {\text{h}}_{\text{S}2}\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\cdots & {\text{h}}_{\text{Sr}}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}{\mathbf{h}}_{(1)}^{\text{T}}\\ {\mathbf{h}}_{(2)}^{\text{T}}\\ \begin{array}{c}⋮\\ {\mathbf{h}}_{(\text{S})}^{\text{T}}\end{array}\end{array}\right].$$

That is,

$$\hat{\mathbf{K}}=\mathbf{G}{\mathbf{H}}^{\text{T}}.$$ (4)

Thus, the approximated rows and columns of a data matrix are represented in biplots. More precisely, for the biplot of a data matrix $\mathbf{K}$, $\text{N}$ rows of $\mathbf{G}$ will serve as the biplot points, while $\text{S}$ rows of $\mathbf{H}$will be used in calculating the directions of the biplot axes [18]. Generally, the number of columns in $\mathbf{G}$ and $\mathbf{H}$ are determined by the low rank approximation of $\mathbf{K}$. In practice, $\text{r}=2$ is usually preferred for a convenient biplot display - i.e. $\mathbf{G}$ and $\mathbf{H}$ have two columns. However, this does not necessarily mean that it is limited to two dimensions, but rather, it is the most convenient biplot display. More in-depth information about the different types of biplot constructions can be found in Gower et al. [11] and Oyedele [18].

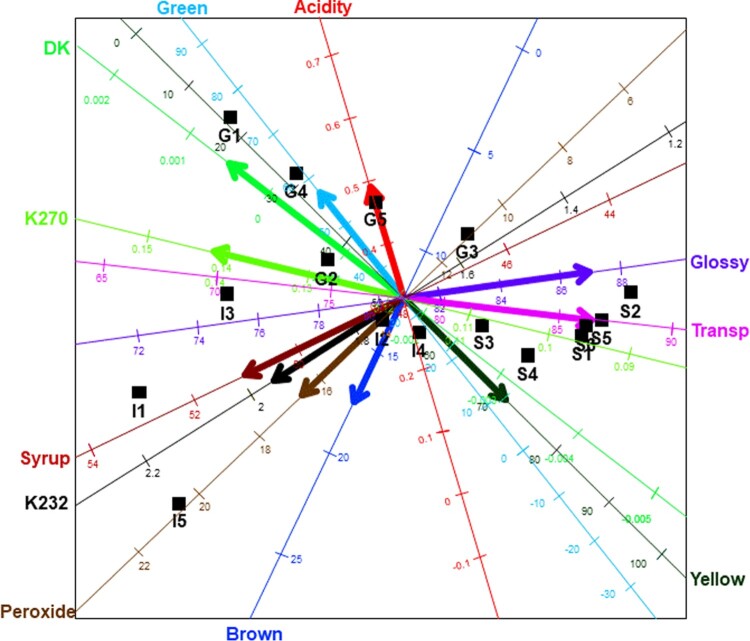
The following example is an illustration of a biplot, using the olive oil data from Mevik & Wehrens [17]. This data shows the sensory and chemical quality evaluations of sixteen olive oil samples. There were five chemical quality measurements (Acidity, Peroxide, K232, K270 and DK) taken, and six sensory panel characteristics (Yellow, Green, Brown, Glossy, Transparent and Syrup) were used in this evaluation. The first five olive oils (G1 to G5) were of Greek origin, while the next five (I1 to I5) were of Italian origin. The last six (S1 to S6) were of Spanish origin. This data can be obtained from the pls package in the $\text{R}$ language [19], downloaded freely from the Comprehensive R Archive Network (CRAN)'s repository, http://cran.rproject.org/. The sixteen olive oils are assigned as samples, while the chemical quality measurements and sensory panel characteristics are the variables. As a result, the olive oil data can be viewed as a $(16\times 11)$ data matrix. To view this data graphically using a single plot, one would require an 11-dimensional display. Currently, no such graphical display exists, thus, the biplot can be used in (graphically) viewing this data. The resulting biplot display is shown in Figure 1 and the row markers $\mathbf{G}$ and the column markers $\mathbf{H}$ are shown in Appendix A1. The low rank approximation of this data was done using the principal component analysis. More details can be found in Oyedele [18].

Figure 1.

The biplot of the olive oil data.

In Figure 1, the samples of the data are represented by the black points, while the variables are represented by the axes. This biplot also shows a representation of the variance of each variable, represented by the thicker arrow (vector) on each axis. From this display, several relationships can be deduced from this biplot, such as a relation between Syrup, K232 and Peroxide. The positions of the biplot axes give an indication of the correlations between the variables. To be precise, axes forming small angles are said to be strongly correlated - either positively or negatively. Axes are positively correlated when they lie in the same direction, while negatively correlated axes lie in opposite directions. In addition, axes that are close to forming right angles are said to be uncorrelated. Another relationships deduction is the relation between K270, Transp and Glossy, and between Green, Yellow and DK.

Since both rows and columns are represented in the biplot display, as per the definition of biplot in Section 2, two out of three aspects can be represented optimally in the biplot display, but not all three at once. These aspects are (1) the distances between the rows of $\mathbf{G}$, (2) the correlations between the rows of $\mathbf{H}$, and, (3) the relationship between the rows and columns in $\mathbf{K}$. Sections 2.6 and 4.3 of Oyedele [18] give more details regarding the types of representation done in a biplot display.

3. Multivariate regression biplot

Since the biplot relies on the decomposition of a data matrix into the product of two matrices, its row markers matrix and its column markers matrix, (as shown in Section 2), the multivariate regression equation (equation (3)) has such a decomposition for its predicted responses $(\hat{\mathbf{Y}})$, with $\hat{\mathbf{Y}}$ serving as the data matrix, $\mathbf{X}$ and $\hat{\mathbf{B}}$ (estimated regression coefficients) serving as the row markers and column markers matrices for $\hat{\mathbf{Y}}$. Since $\text{P}$ is most often larger than $2$, a low rank approximation of $\mathbf{X}$ in equation (3) is needed. If $\text{ P}=2$, then no low rank approximation is needed. Greenacre’s [13] regression biplot displays were based on $\text{ P}=2$. To achieve the low rank approximation of $\mathbf{X}$, the Singular Value Decomposition (SVD) [9] is applied.

By the SVD,

$$\mathbf{X}=\mathbf{U}\mathrm{\Delta }{\mathbf{V}}^{\text{T}}$$ (5)

for $\mathbf{U}:\text{N}\times \text{P}$, $\mathrm{\Delta }:\text{P}\times \text{P}$ and $\mathbf{V}:\text{P}\times \text{P}$. Since ${\mathbf{V}}^{\text{T}}\mathbf{V}={\mathbf{I}}_{\text{P}}$, it is possible to write the matrix product $\mathbf{U}\mathrm{\Delta }:\text{N}\times \text{P}$ as

$$\mathbf{U}\mathrm{\Delta }=\mathbf{U}\mathrm{\Delta }{\mathbf{V}}^{\text{T}}\mathbf{V}=\mathbf{X}\mathbf{V}$$ (6)

Substituting equation (6) into equation (5) approximates $\mathbf{X}$ as $\hat{\mathbf{X}}=\mathbf{X}\mathbf{V}{\mathbf{V}}^{\text{T}}=\mathbf{Z}{\mathbf{V}}^{\text{T}}$, where $\mathbf{Z}=\mathbf{X}\mathbf{V}$. In principal component analysis, $\mathbf{Z}$ can be seen as the matrix containing the principal components of $\mathbf{X}$.

According to Eckart & Young [5], the best $\text{r}$-dimensional approximation of $\mathbf{X}$ is obtained by

$${\hat{\mathbf{X}}}_{[\text{r}]}=\mathbf{X}{\mathbf{V}}_{[\text{r}]}{\mathbf{V}}_{[\text{r}]}^{\text{T}}={\mathbf{Z}}_{[\text{r}]}{\mathbf{V}}_{[\text{r}]}^{\text{T}}$$ (7)

where ${\mathbf{V}}_{[\text{r}]}:\text{P}\times \text{r}$ contains the first $\text{r}$ columns of $\mathbf{V}$ and

$${\mathbf{Z}}_{[\text{r}]}=\mathbf{X}{\mathbf{V}}_{[\text{r}]}.$$ (8)

Matrix ${\mathbf{Z}}_{[\text{r}]}:\text{N}\times \text{r}$ can be considered as the rank $\text{r}$ approximation of $\mathbf{X}$. Replacing $\mathbf{X}$ in equation (3) with its rank $\text{r}$ approximation ${\mathbf{Z}}_{[\text{r}]}$ yields

$${\hat{\mathbf{Y}}}_{[\text{r}]}={\mathbf{Z}}_{[\text{r}]}({\mathbf{Z}}_{[\text{r}]}^{\text{T}}{\mathbf{Z}}_{[\text{r}]}{)}^{-1}{\mathbf{Z}}_{[\text{r}]}^{\text{T}}\mathbf{Y}={\mathbf{Z}}_{[\text{r}]}{\mathbf{Q}}_{+}^{\text{T}}$$ (9)

where ${\mathbf{Q}}_{+}={\mathbf{Y}}^{\text{T}}{\mathbf{Z}}_{[\text{r}]}({\mathbf{Z}}_{[\text{r}]}^{\text{T}}{\mathbf{Z}}_{[\text{r}]}{)}^{-1}$.

Substituting equation (8) into equation (9) yields ${\hat{\mathbf{Y}}}_{[\text{r}]}=\mathbf{X}{\mathbf{V}}_{[\text{r}]}{\mathbf{Q}}_{+}^{\text{T}}=\mathbf{X}{\hat{\mathbf{B}}}_{\text{MVR}}$ where

$${\hat{\mathbf{B}}}_{\text{MVR}}={\mathbf{V}}_{[\text{r}]}{\mathbf{Q}}_{+}^{\text{T}}$$ (10)

is the $(\text{P}\times \text{M})$ multivariate regression coefficients matrix. Several techniques such as principal component analysis and partial least squares can also be used to obtain the rank $\text{r}$ approximation of $\mathbf{X}$ [1,15].

In multivariate regression analysis, the data can be written as an $\text{ N}\times (\text{P}+\text{M})$matrix

$${\mathbf{K}}_{\text{MVR}}=\left[\begin{array}{cc}\mathbf{X}& \mathbf{Y}\end{array}\right]$$

and, from equations (7) and (9), it can be approximated as

$${\hat{\mathbf{K}}}_{\text{MVR}}=[\begin{array}{cc}{\hat{\mathbf{X}}}_{[\text{r}]}& {\hat{\mathbf{Y}}}_{[\text{r}]}\end{array}]=[\begin{array}{cc}{\mathbf{Z}}_{[\text{r}]}{\mathbf{V}}_{[\text{r}]}^{\text{T}}& {\mathbf{Z}}_{[\text{r}]}{\mathbf{Q}}_{+}^{\text{T}}\end{array}]={\mathbf{Z}}_{[\text{r}]}[\begin{array}{cc}{\mathbf{V}}_{[\text{r}]}& {\mathbf{Q}}_{+}\end{array}{]}^{\text{T}}.$$ (11)

Thus, in line with equation (4), the biplot of ${\mathbf{K}}_{\text{MVR }}$ implies that,

$${\hat{\mathbf{K}}}_{\text{MVR}}={\mathbf{Z}}_{[\text{r}]}[\begin{array}{cc}{\mathbf{V}}_{[\text{r}]}& {\mathbf{Q}}_{+}\end{array}{]}^{\text{T}},$$

where ${\mathbf{Z}}_{[\text{r}]}:(\text{N}\times \text{r})$ is the row markers matrix and $\left[\begin{array}{c}{\mathbf{V}}_{[\text{r}]}\\ {\mathbf{Q}}_{+}\end{array}\right]:((\text{P}+\text{M})\times \text{r})$ is the column markers matrix. The resulting (multivariate regression) biplot shall be termed the MVR biplot.

Since the biplot is often constructed in two dimensions due to convenience, ${\mathbf{Z}}_{[\text{r}]}$, ${\mathbf{V}}_{[\text{r}]}$ and ${\mathbf{Q}}_{+}$will have two columns (i.e. $\text{r}=2$). Here, matrix ${\mathbf{Z}}_{[\text{r}]}$contains information about the $N$ samples, while matrices ${\mathbf{V}}_{[\text{r}]}$ and ${\mathbf{Q}}_{+}$ contain information about the $\text{P}$ $\text{ X}$-variables and $\text{M Y}$-variables respectively. Hence, for the MVR biplot, sample points are represented by the $\text{N}$ rows of ${\mathbf{Z}}_{[\text{r}]}$, while the directions of the biplot axes are calculated by the $\text{P}$ and $\text{M}$ rows of ${\mathbf{V}}_{[\text{r}]}$ and ${\mathbf{Q}}_{+}$ respectively. To differentiate between these two sets of axes in the MVR biplot display, the axes defining the predictors will be in purple ink, while the axes defining the response variables will be in black.

3.1. Calibration of the multivariate regression biplot axes

Since the $(\text{P}+\text{M})$ columns of ${\mathbf{K}}_{\text{MVR}}$ are represented by axes in the MVR biplot display, the calibration of these axes is very important. This is because different calibrations are used for adding points to the biplot and for reading off values from the biplot axes. Generally, calibration is done by placing a set of tick marks on each of the biplot axes and then labeling them with any set of markers (not necessarily equally spaced) as desired, e.g. $(0,1,2,3,5,\dots )$.

To construct a calibrated MVR biplot axis, consider the ${\text{k}}^{\text{th}}$ predictor and response variables respectively. From equation (7), ${\mathbf{x}}_{[\text{r}]}^{\text{T}}={\mathbf{z}}_{[\text{r}]}^{\text{T}}{\mathbf{V}}_{[\text{r}]}^{\text{T}}$ for any point $\mathbf{z}$ in the biplot plane. For this reason, the ${\text{k}}^{\text{th}}$ predictor variable value will be given by ${\mathbf{x}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}={\mathbf{z}}_{[\text{r}]}^{\text{T}}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}$, where ${\mathbf{e}}_{\text{k}}$ is the unit vector with zeros except for a one in the ${\text{k}}^{\text{th}}$ position. Let this value be denoted by ${\mu }_{\text{x}}$, then

$${\mu }_{\text{x}}={\mathbf{z}}_{[\text{r}]}^{\text{T}}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}.$$ (12)

Equation (12) defines a line in the two-dimensional biplot plane and for different values, ${\mu }_{\text{x}}\in (-\mathrm{\infty },\mathrm{\infty })$, parallel lines are obtained, as shown below in Figure 2.

Figure 2.

A schematic of the construction of the axis for the ${\text{k}}^{\text{th}}$ predictor variable in the MVR plane $\mathcal{L}$.

To facilitate orthogonal projection onto the biplot axes, similar to the scatterplot, the line through the origin orthogonal to equation (12) is selected as the biplot axis for variable $\text{k}$. Any point on this biplot axis will have the form ${\theta }_{\text{x}}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}$. Thus, the point on the biplot axis predicting the value ${\mu }_{\text{x}}$ for the ${\text{k}}^{\text{th}}$ predictor variable will have

$${\mathbf{z}}_{{\mu }_{\text{x}}}={\theta }_{\text{x}}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}.$$ (13)

Replacing ${\mathbf{z}}_{[\text{r}]}$ in equation (12) with equation (13) yields ${\mu }_{\text{x}}={\theta }_{\text{x}}{\mathbf{e}}_{\text{k}}^{\text{T}}{\mathbf{V}}_{[\text{r}]}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}$. Solving for ${\theta }_{\text{x}}$ then yields

$${\theta }_{\text{x}}=\frac{{\mu }_{\text{x}}}{{\mathbf{e}}_{\text{k}}^{\text{T}}{\mathbf{V}}_{[\text{r}]}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}}.$$ (14)

Moreover, replacing ${\theta }_{\text{x}}$in equation (13) with equation (14) gives the marker ${\mu }_{\text{x}}$ on the ${\text{k}}^{\text{th}}$predictor biplot axis as

$$\frac{{\mu }_{\text{x}}}{{\mathbf{e}}_{\text{k}}^{\text{T}}{\mathbf{V}}_{[\text{r}]}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}}{\mathbf{V}}_{[\text{r}]}^{\text{T}}{\mathbf{e}}_{\text{k}}.$$

Likewise, from equation (9), any point predicting ${\mu }_{\text{y}}\in (-\mathrm{\infty },\mathrm{\infty })$ for the ${\text{k}}^{\text{th}}$ response variable will have ${\mu }_{\text{y}}={\mathbf{z}}_{[\text{r}]}^{\text{T}}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}$, with the biplot axis of the form ${\theta }_{\text{y}}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}$. For this reason, the point on the biplot axis predicting the value ${\mu }_{\text{y}}$ for the ${\text{k}}^{\text{th}}$ response variable will have

$${\mathbf{z}}_{{\mu }_{\text{y}}}={\theta }_{\text{y}}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}.$$ (15)

Substituting equation (15) into ${\mu }_{\text{y}}={\mathbf{z}}_{[\text{r}]}^{\text{T}}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}$ yields ${\mu }_{\text{y}}={\theta }_{\text{y}}{\mathbf{e}}_{\text{k}}^{\text{T}}{\mathbf{Q}}_{+}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}$. Solving for ${\theta }_{\text{y}}$ then yields

$${\theta }_{\text{y}}=\frac{{\mu }_{\text{y}}}{{\mathbf{e}}_{\text{k}}^{\text{T}}{\mathbf{Q}}_{+}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}}.$$ (16)

Moreover, replacing ${\theta }_{\text{y}}$in equation (15) by equation (16) gives the marker ${\mu }_{\text{y}}$ on the ${\text{k}}^{\text{th}}$response biplot axis as

$$\frac{{\mu }_{\text{y}}}{{\mathbf{e}}_{\text{k}}^{\text{T}}{\mathbf{Q}}_{+}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}}{\mathbf{Q}}_{+}^{\text{T}}{\mathbf{e}}_{\text{k}}.$$

Equation (14) is the calibration factor for the ${\text{k}}^{\text{th}}$ predictor axis, while equation (16) is the calibration factor for the ${\text{k}}^{\text{th}}$ response axis.

For the multivariate regression coefficients matrix ${\hat{\mathbf{B}}}_{\text{MVR}}={\mathbf{V}}_{[\text{r}]}{\mathbf{Q}}_{+}^{\text{T}}$ as shown in equation (10), the ${\text{i}}^{\text{th}}$ row of ${\hat{\mathbf{B}}}_{\text{MVR}}$ can be written as ${\hat{\mathbf{b}}}_{(i)}^{\text{T}}=\mathbf{v}{}_{[\text{r}{]}_{(i)}}^{\text{T}}{\mathbf{Q}}_{+}^{\text{T}}$, akin to ${\mathbf{y}}_{[\text{r}]}^{\text{T}}={\mathbf{z}}_{[\text{r}]}^{\text{T}}{\mathbf{Q}}_{+}^{\text{T}}$, so that the regression coefficients are predicted by the biplot axes defining the response variables. Instead of predicting a sample point ${\mathbf{z}}_{[\text{r}]}^{\text{T}}={\mathbf{x}}^{\text{T}}{\mathbf{V}}_{[\text{r}]}$, ${\mathbf{e}}_i^{\text{T}}{\mathbf{V}}_{[\text{r}]}$ are projected onto these axes. That is, projecting each of the rows of ${\mathbf{V}}_{[\text{r}]}$ onto the axes defined by ${\mathbf{Q}}_{+}$ yields the multivariate regression coefficients matrix ${\hat{\mathbf{B}}}_{\text{MVR}}$. Hence, two different sets of marker calibrations are needed on each of the response axes, a set for reading off the predicted response $({\hat{\mathbf{Y}}}_{[\text{r}]})$ values (in black ink) and a set for ${\hat{\mathbf{B}}}_{\text{MVR}}$ (in red ink). The seminal work on the calibration of biplots axes for regression coefficients can be found in Graffelman & Van Eeuwijk [12], although with a different approach of predicting the coefficients.

It would be useful to mention that the use of biplot methodology for the representation of regression coefficients has been previous done by a couple of renowned authors such as Ter Braak & Looman [20] and Graffelman & Van Eeuwijk [12], although using different estimation method to estimate the regression coefficients. Ter Braak & Looman [20] and Graffelman & Van Eeuwijk [12] expressed their biplots of regression coefficients using coefficients derived from redundancy analysis (also known as reduced-rank regression). In their redundancy analysis applications, to get the coefficients, the SVD was applied to the regression model, taking into account both $\mathbf{X}$ and $\mathbf{Y}$ see section 3.4 and equation (11) of Graffelman & Van Eeuwijk [12]. However, this paper proposes a different approach. Here, the SVD is only applied on $\mathbf{X}$, prior to fitting the regression model as shown in equations (5) to (10) of Section 3. In other words, the (estimated) coefficients in Ter Braak & Looman [20] and Graffelman & Van Eeuwijk [12] were derived from the SVDed-regression model, while in this paper, they are derived from the regression model fitted using the SVD-ed $\mathbf{X}$.

3.2. Overall quality of the multivariate regression biplot

Once a biplot has been constructed and calibrated, the next step would be to find out how good the representation in the biplot is. That is, how good is the representation provided by the projections of the biplot points in the biplot [18]? To evaluate how good the MVR biplot representation is, the overall quality of approximation and the axis predictivities are needed. The evaluation of how well the individual biplot axes reproduce the variables of ${\mathbf{K}}_{\text{MVR}}$ can be done by measuring the degree to which the columns of ${\hat{\mathbf{K}}}_{{\text{MVR}}_{[\text{r}]}}$ agree with the corresponding columns of ${\mathbf{K}}_{\text{MVR}}$ [8].

Expressing the sum-of-squares of the approximated values for each variable, given by $\text{diag}({\hat{\mathbf{K}}}_{{\text{MVR}}_{[\text{r}]}}^{\text{T}}{\hat{\mathbf{K}}}_{{\text{MVR}}_{[\text{r}]}})$, as a proportion of their respective total sum-of-squares yields the predictive power of each axis. More precisely,

$$\text{Axis predictivity}=\text{diag}({\hat{\mathbf{K}}}_{{\text{MVR}}_{[\text{r}]}}^{\text{T}}{\hat{\mathbf{K}}}_{{\text{MVR}}_{[\text{r}]}})[\text{diag}({\mathbf{K}}_{\text{MVR}}^{\text{T}}{\mathbf{K}}_{\text{MVR}}){]}^{-1}.$$

The predictivity values lie between 0 and 1. An axis predictivity of 1 means that all values can be read off the axis exactly. The lower the axis predictivity value, the less accurately the axis approximates the observed values under that variable.

Furthermore, the overall quality of approximation by the biplot display can be measured in terms of the percentage of variation in the data matrix ${\mathbf{K}}_{\text{MVR}}$ that is explained by the rank $\text{r}$ approximation ${\mathbf{Z}}_{[\text{r}]}$ (equation (8)). More precisely,

$$\text{Overall quality}=tr({\hat{\mathbf{K}}}_{{\text{MVR}}_{[\text{r}]}}^{\text{T}}{\hat{\mathbf{K}}}_{{\text{MVR}}_{[\text{r}]}})[tr({\mathbf{K}}_{\text{MVR}}^{\text{T}}{\mathbf{K}}_{\text{MVR}}){]}^{-1}.$$

4. A small application

The following example is an illustration of a MVR biplot using the Cocktail data from Husson et al. [14]. This cocktail data can be obtained from the SensoMineR package, downloaded freely from CRAN, http://cran.r-project.org/. This data shows the sensory and composition evaluation of sixteen cocktail juices. The composition of each cocktail was measured using four ingredients (Orange, Banana, Mango and Lemon). There were thirteen sensory panel descriptors (Colour.intensity, Odour.intensity, Odour.orange, Odour.banana, Odour.mango, Odour.lemon, Strongness, Sweet, Acidity, Bitterness, Persistence, Pulp and Thickness) used in this evaluation. The sixteen cocktail juices are assigned as the samples. The ingredients and sensory panel descriptors are the predictor and response variables respectively. As a result, the cocktail data can be viewed as a data matrix $\mathbf{X}:16\times 4$ of predictors and a matrix $\mathbf{Y}:16\times 13$ of responses. To view this data graphically using a single plot, one would require a 17-dimensional display. Currently, no such graphical display exists, thus, the MVR biplot can be used in viewing this data graphically.

Since centering and/or standardization is common in many multivariate analysis methods, this data was later standardized for the MVR analysis. A data matrix is standardized by first centering it and then dividing each variable by their respective standard deviation. An $\text{r}=2$ MVR analysis was performed on the standardized data and the resulting MVR biplot is shown in Figure 3 with an overall quality of 0.5313. In Figure 3, the samples of the data are represented by the blue points, while the red points are for the (multivariate) regression coefficient points. The predictor variables ( $\mathbf{X}$) of the data are represented by the purple axes in the biplot display, while the response variables ( $\mathbf{Y}$) are represented by the black axes. As discussed in Section 3.1, the response (black) axes each has two different sets of tick markers - one set (in black ink) for reading the projected response values and the other set (in red ink) for reading the coefficient values. In addition, in this biplot (Figure 3), the sets of tick markers (purple and black) on the axes have been adjusted for standardization. That is, the calibration markers are fitted using sensible scale values

Figure 3.

The MVR biplot of the cocktail data.

${\mu }_{\text{x}}^{\ast }=({\mu }_{\text{x}}+{\overline{\mathrm{x}}}_{\text{k}}){\text{s}}_{{\text{x}}_{\text{k}}}\text{and}{\mu }_{\text{y}}^{\ast }=({\mu }_{\text{y}}+{\overline{\mathrm{y}}}_{\text{k}}){\text{s}}_{{\text{y}}_{\text{k}}},$

where ${\overline{\mathrm{x}}}_{\text{k}}$, ${\overline{\mathrm{y}}}_{\text{k}}$, ${\text{s}}_{{\text{x}}_{\text{k}}}$ and ${\text{s}}_{{\text{y}}_{\text{k}}}$ are the means and standard deviations of the ${\text{k}}^{\text{th}}$ predictor and response variables respectively. However, for reading the coefficient values, the calibration markers (red) on the response axes are fitted using sensible scale values ${\mu }_{\text{b}}={\mu }_{\text{y}}$ and not ${\mu }_{\text{y}}^{\ast }=({\mu }_{\text{y}}+{\overline{\mathrm{y}}}_{\text{k}}){\text{s}}_{{\text{y}}_{\text{k}}}$.

Moreover, the predictivity of each biplot axis in Figure 3 was estimated and shown in Table 1. Each of these axes represents the original data quite well, with the Orange axis having the highest predictive power of 0.999. However, the Lemon axis has the lowest predictivity power of 0.675. This means that the axis represents the original data, but not quite as well as the other axes.

Table 1. The axis predictivity of the MVA biplot of the cocktail data.

Orange	Banana	Mango	Lemon	Color.intensity
0.999	0.998	0.998	0.675	0.843
Odor.orange	Odor.banana	Odor.mango	Odor.lemon	Strongness
0.991	0.959	0.946	0.973	0.992
Acidity	Bitterness	Persistence	Pulp	Thickness
0.939	0.989	0.996	0.994	0.995
Odor.intensity	Sweet
0.995	0.987

The row markers ${\mathbf{Z}}_{[\text{r}]}$ and the column markers ${\mathbf{V}}_{[\text{r}]}$ and ${\mathbf{Q}}_{+}$ are shown in Appendices A2 and A3 respectively. To illustrate the calibration of the biplot axes (see Section 3.1), consider the Odor.banana variable. The column marker vector for this variable, ${{\mathbf{q}}_{+}}_{(\text{j}=4)}$, is given by the fourth row in ${\mathbf{Q}}_{+}$ in Appendix A3. By the definition of a biplot, ${\mathbf{z}}_{(i)}^{\text{T}}{{\mathbf{q}}_{+}}_{(4)}={\hat{y}}_{i4}$, for $\text{i}=1,2,\dots ,16$ and ${{\mathbf{q}}_{+}}_{(4)}^{\text{T}}=\left(\begin{array}{cc}-0.516& 0.538\end{array}\right)$. This defines the inner product of the samples and the Odor.banana variable. Substituting ${\mu }_{\text{y}}={\hat{y}}_{i4}$ in equation (16) gives the calibration factor for the Odor.banana axis as ${\theta }_{\text{y}}=\text{ (}{\text{y}}_{i4}/-0.278\text{)}$. For values ranging between $1.17$ and $8.17$, ${\theta }_{\text{y}}{{\mathbf{q}}_{+}}_{(4)}^{\text{T}}$ gives the set of tick markers for the Odor.banana axis. More precisely, with the values under the Odor.banana variable given as

$${\text{y}}_4=\left(\begin{array}{c}3.08,5.21,7.54,8.17,1.67,4.92,2.25,3.17,3.50,3.67,\\ 4.42,8.00,1.17,1.62,1.54,3.08\end{array}\right),$$

the set of tick markers for the Odor.banana axis is given by

$${\theta }_{\text{y}}{{\mathbf{q}}_{+}}_{(4)}^{\text{T}}=\left(\begin{array}{c}5.85,9.89,14.31,15.50,3.16,9.33,4.27,6.01,6.64,\\ 6.96,8.38,15.18,2.21,3.08,2.93,5.85\end{array}\right).$$

Rather than using these disproportionate values as the scale markers on the Odor.banana axis, nicer scale markers can be used, such as $(0,1,2,3,\dots )$, as seen in Figure 3.

Furthermore, Figure 3 also shows a representation of the variance of each variable, represented by the thicker arrow (vector) on each axis. These vectors correspond to one unit on the biplot axes. From this display, the standard deviation of Mango is smaller compared to the others. This is evident from the length of the vector on the Mango axis.

Moreover, several variable relationships can be deduced from this biplot, such as the (positive) relation between Mango and Odor.lemon; between Banana and Odor.banana as well as Strongness (positive and negative respectively); between Lemon and Color.intensity, Odor.mango as well as Persistence (negative, negative and negative respectively); between Pulp and Acidity as well as Thickness (negative and positive respectively); and between Bitterness and Odor.intensity, Sweet as well as Odor.orange (negative, negative and positive respectively). All these are done by looking at the position of the biplot axes. Axes are positively related when they lie in the same direction, while negatively related axes lie in opposite directions.

To get the approximated values of the cocktail data from the biplot in Figure 3, each sample point in the MVR biplot is orthogonally projected onto the axes and their respective values are read off. For example, sample point S6 projected onto the Banana, Mango, Odor,lemon and Odor.banana axes yields the values $2.0$, $0.1$, $3.3$ and $6.6$ respectively, as shown in Figure 4. The approximated values of the cocktail data are shown in Appendix A4. Likewise, to get the approximated coefficient values from the biplot, the MVR coefficient points ${\text{b}}_{\text{i}}$, for $\text{ i}=1,2,3,4$, are projected onto the prediction axes representing the sensory panel descriptors. However, the red markers on these axes are used to read off the coefficient values. A zoomed-in display of the coefficient points is shown in Figure 5. For example, points ${\text{b}}_2$, ${\text{b}}_3$ and ${\text{b}}_1$ projected onto the Odor.mango, Odor.lemon and Odor.banana axes gives the value of $-0.25$, $0.45$ and $-0.4$ respectively as shown in Figure 5. The estimated regression coefficient values are shown in Appendix A5.

Figure 4.

Examples of orthogonal projections in the MVA biplot of the cocktail data.

Figure 5.

A zoomed-in display of the coefficient points in the MVR biplot of the cocktail data.

5. Conclusions

The biplot, often referred to as the multivariate version of a scatterplot, allows for the graphical display of rows (samples) as points and each column (variable) by an axis on the same plot. As a result, the structure as well as the revelation of the association between the samples (rows) and/or variables (columns) of a (large) data set can easily be explored.

Results found by the MVR analysis of a data set can be visualized graphically using the biplot, specifically, the MVR biplot. A MVR biplot provides a single graphical representation of the samples together with the predictor variables and response variables. It also provides the inter-variable relationships revelations as well as their causal relationships in the form of the matrix of regression coefficients, although sub-optimally. Even though the developed MVR biplot immensely capitalizes on the representation of the predictor variables, it does not vastly capitalize on the representation of the matrix of regression coefficients. For the cocktail data, the total-sum-of-squares of the matrix of regression coefficients (equation (2)) was 172617.5, while for the fitted regression coefficients (equation (10)) it was 4.0530. Thus, the overall quality of the representation of the variables’ causal relationships in the form of the matrix of regression coefficients can be estimated as $4.0530/172617.5=0.0023\mathrm{\%}$, which is an extremely low quality.

Moreover, for very large numbers of predictors, there is a chance of obtaining an over-estimated regression model. For this reason, a test for the predictive significance of each predictor is necessary and this can be used to determine the appropriate number of predictors to use in the final regression modeling of the responses. Measures such as the Variable Importance in the Projection (VIP) and the Bayesian Information Criterion (BIC) can be used to perform the test. Oyedele [18] discusses, amongst others, the construction of the biplot when dealing with (very) large numbers of predictors in the model.

Software

A collection of functions has been developed in the R language [19] to produce the biplot displays. The collection of functions used to produce the MVR biplots in Figures 3 and 5 is at the final stages of submission for publication on the CRAN's repository. However, these functions are available electronically upon request.

The following R code were used to obtain Figure 1

# Install the PLSbiplot1 package from CRAN at http://cran.r-project.org/.

# Load the PLSbiplot1 package

require(PLSbiplot1)

# Olive oil data

if(require(pls))

data(oliveoil, package=‘pls’)

Kmat = as.matrix(oliveoil)

dimnames(Kmat) = list(paste(c(‘G1’,‘G2’,‘G3’,‘G4’,‘G5’,‘I1’,‘I2’,‘I3’,‘I4’,

‘I5’,‘S1’,‘S2’,‘S3’,‘S4’,‘S5’,‘S6’)), paste(c(‘Acidity’,‘Peroxide’,‘K232’,‘K270’,‘DK’,

‘Yellow’,‘Green’,‘Brown’,‘Glossy’,‘Transp’,‘Syrup’)))

PCA.biplot(D=Kmat, method=mod.PCA, ax.tickvec.D=c(8,5,5,7,6,4,5,5,8,7,7))

Appendix.

Table A1. The row and column markers $\mathbf{G}:16\times 2$ and $\mathbf{H}:11\times 2$ respectively.

	Component 1	Component 2		Component 1	Component 2
S1	−49.037	8.502	Acidity	−0.003	0.002
S2	−43.814	1.303	Peroxide	−0.044	−0.239
S3	−24.975	11.854	K232	−0.004	−0.015
S4	−31.675	5.998	K270	−0.001	−0.001
S5	−1.475	−11.163	DK	0.000	0.000
S6	−18.004	−18.977	Yellow	0.624	−0.016
S7	3.774	−2.816	Green	−0.751	0.253
S8	−41.389	2.696	Brown	−0.024	−0.346
S9	25.581	−4.205	Glossy	0.111	0.540
S10	−4.864	−14.392	Transp	0.168	0.665
S11	31.296	6.335	Syrup	−0.060	−0.159
S12	35.605	9.690
S13	26.283	−8.117
S14	26.605	1.147
S15	32.776	5.985
S16	33.311	6.157

Table A2. The row markers ${\mathbf{Z}}_{[\text{r}]}:16\times 2$.

	Component 1	Component 2
S1	−1.550	−1.150
S2	−1.780	−0.769
S3	−1.550	1.150
S4	−1.660	0.961
S5	−0.222	−1.920
S6	−0.222	1.920
S7	0.000	0.000
S8	0.000	0.000
S9	0.000	0.000
S10	0.000	0.000
S11	0.000	0.000
S12	0.222	1.920
S13	1.780	−0.769
S14	1.550	−1.150
S15	1.780	0.769
S16	1.660	0.961

Table A3. The column markers ${\mathbf{V}}_{[\text{r}]}:4\times 2$ and ${\mathbf{Q}}_{+}:13\times 2$ respectively.

	Component 1	Component 2		Component 1	Component 2
Orange	0.816	0.000	Color.intensity	0.039	−0.134
Banana	−0.408	0.707	Odor.intensity	−0.511	0.091
Mango	−0.408	−0.707	Odor.orange	0.739	−0.200
Lemon	0.000	0.000	Odor.banana	−0.516	0.538
			Odor.mango	0.040	−0.342
			Odor.lemon	−0.198	−0.526
			Strongness	0.171	−0.236
			Sweet	−0.631	0.147
			Acidity	0.415	−0.230
			Bitterness	0.527	−0.140
			Persistence	0.003	−0.247
			Pulp	−0.645	0.278
			Thickness	−0.711	0.319

Table A3. The approximated cocktail values ${\hat{\mathbf{K}}}_{\text{MVR}}:16\times 17$.

	Orange	Banana	Mango	Lemon	Color.intensity
S1	0.837	0.837	2.007	0.219	5.82
S2	0.707	1.097	1.877	0.219	5.67
S3	0.837	2.007	0.837	0.219	5.04
S4	0.772	1.942	0.967	0.219	5.10
S5	1.617	0.057	2.007	0.219	6.22
S6	1.617	2.007	0.057	0.219	4.91
S7	1.747	−0.008	1.942	0.219	6.24
S8	1.747	0.967	0.967	0.219	5.59
S9	1.747	0.967	0.967	0.219	5.59
S10	1.747	0.967	0.967	0.219	5.59
S11	1.747	0.967	0.967	0.219	5.59
S12	1.877	1.877	−0.073	0.219	4.96
S13	2.787	0.057	0.837	0.219	6.03
S14	2.657	−0.073	1.097	0.219	6.13
S15	2.787	0.837	0.057	0.219	5.50
S16	2.722	0.967	−0.008	0.219	5.43
	Odor.intensity	Odor.orange	Odor.banana	Odor.mango	Odor.lemon
S1	5.60	3.69	4.356	4.48	5.33
S2	5.68	3.33	5.094	4.33	5.17
S3	5.71	3.00	7.206	3.60	4.06
S4	5.73	2.94	7.100	3.67	4.19
S5	5.21	5.38	1.826	4.84	5.48
S6	5.39	4.24	6.576	3.36	3.36
S7	5.15	5.63	1.562	4.85	5.43
S8	5.24	5.05	3.937	4.11	4.37
S9	5.24	5.05	3.937	4.11	4.37
S10	5.24	5.05	3.937	4.11	4.37
S11	5.24	5.05	3.937	4.11	4.37
S12	5.28	4.73	6.049	3.38	3.27
S13	4.74	7.24	0.881	4.48	4.43
S14	4.78	7.11	0.669	4.62	4.69
S15	4.81	6.78	2.781	3.89	3.58
S16	4.85	6.60	3.150	3.81	3.50
	Strongness	Sweet	Acidity	Bitterness	Persistence
S1	6.21	7.04	4.96	1.77	6.29
S2	6.13	7.27	4.62	1.72	6.25
S3	5.88	7.44	3.97	1.67	6.05
S4	5.90	7.49	3.97	1.66	6.07
S5	6.46	5.93	6.31	2.00	6.37
S6	5.91	6.59	4.67	1.85	5.98
S7	6.48	5.76	6.48	2.04	6.37
S8	6.21	6.09	5.66	1.96	6.17
S9	6.21	6.09	5.66	1.96	6.17
S10	6.21	6.09	5.66	1.96	6.17
S11	6.21	6.09	5.66	1.96	6.17
S12	5.96	6.26	5.01	1.91	5.98
S13	6.50	4.65	7.35	2.26	6.25
S14	6.53	4.75	7.35	2.24	6.29
S15	6.28	4.91	6.69	2.20	6.1
S16	6.24	5.03	6.53	2.17	6.08
	Pulp	Thickness
S1	2.44	6.24
S2	2.52	6.59
S3	2.66	7.17
S4	2.67	7.19
S5	2.05	4.72
S6	2.43	6.28
S7	2.00	4.52
S8	2.19	5.30
S9	2.19	5.30
S10	2.19	5.30
S11	2.19	5.30
S12	2.33	5.88
S13	1.71	3.39
S14	1.72	3.43
S15	1.86	4.01
S16	1.91	4.19

Table A3. The estimated MVR coefficient values ${\hat{\mathbf{B}}}_{\text{MVR}}:4\times 13$.

	Color.intensity	Odor.intensity	Odor.orange	Odor.banana
b1: Orange	0.032	−0.417	0.604	−0.421
b2: Banana	−0.111	0.273	−0.443	0.591
b3: Mango	0.079	0.144	−0.160	−0.169
b4: Lemon	0.000	0.000	0.000	0.000
	Odor.mango	Odor.lemon	Strongness	Sweet
b1: Orange	0.032	−0.162	0.139	−0.515
b2: Banana	−0.258	−0.291	−0.237	0.361
b3: Mango	0.226	0.453	0.097	0.154
b4: Lemon	0.000	0.000	0.000	0.000
	Acidity	Bitterness	Persistence	Pulp
b1: Orange	0.338	0.430	0.003	−0.526
b2: Banana	−0.332	−0.314	−0.176	0.460
b3: Mango	−0.006	−0.116	0.173	0.067
b4: Lemon	0.000	0.000	0.000	0.000
	Thickness
b1: Orange	−0.581
b2: Banana	0.516
b3: Mango	0.065
b4: Lemon	0.000

Disclosure statement

No potential conflict of interest was reported by the author.