Rapid detection of hot-spots via tensor decomposition with applications to crime rate data

ABSTRACT

In many real-world applications of monitoring multivariate spatio-temporal data that are non-stationary over time, one is often interested in detecting hot-spots with spatial sparsity and temporal consistency, instead of detecting system-wise changes as in traditional statistical process control (SPC) literature. In this paper, we propose an efficient method to detect hot-spots through tensor decomposition, and our method has three steps. First, we fit the observed data into a Smooth Sparse Decomposition Tensor (SSD-Tensor) model that serves as a dimension reduction and de-noising technique: it is an additive model decomposing the original data into: smooth but non-stationary global mean, sparse local anomalies, and random noises. Next, we estimate model parameters by the penalized framework that includes Least Absolute Shrinkage and Selection Operator (LASSO) and fused LASSO penalty. An efficient recursive optimization algorithm is developed based on Fast Iterative Shrinkage Thresholding Algorithm (FISTA). Finally, we apply a Cumulative Sum (CUSUM) Control Chart to monitor model residuals after removing global means, which helps to detect when and where hot-spots occur. To demonstrate the usefulness of our proposed SSD-Tensor method, we compare it with several other methods including scan statistics, LASSO-based, PCA-based, T2-based control chart in extensive numerical simulation studies and a real crime rate dataset.

1. Introduction

In many real-world applications such as biosurveillance, epidemiology, and sociology, multiple data sources are often measured from many spatial locations repeatedly over time, say, daily, monthly, or annually. This is commonly referred as multivariate spatio-temporal data. When such data are non-stationary over time, compared with detecting the global or system-wise changes as in the traditional statistical process control (SPC) or sequential change-point detection literature, we would be more interested in detecting hot-spots with spatial sparsity and temporal consistency. Here, we define hot-spots as the anomalies that can occur in the temporal and spatial domains among the multivariate spatio-temporal data.

The primary objective of this paper is to develop an efficient method for hot-spots detection and localization for multivariate spatio-temporal data. From the viewpoint of monitoring non-stationary multivariate spatial-temporal data, there are two kinds of changes: one is the change on the global-level trend (e.g. the first-order changes), and the other is the local-level hot-spot (e.g. second-order changes). Here we focus on detecting the latter one and assume that local-level hot-spots have the following two properties: (1) spatial sparsity, i.e. the local changes are sparse in the spatial domain; and (2) temporal consistency, i.e. the local changes last for a reasonable period of time.

Little research has been done on the hot-spot detection for multivariate spatio-temporal data, although there are two major related existing research areas for detection in multivariate spatio-temporal data: one is spatio-temporal cluster detection, and the other is change-point detection. In the first area, the famous representative is the scan statistics-based method, which was first developed in the 1960s in [17] and later extended by [11] to detect anomalous clusters in spatio-temporal data. The main idea of scan statistics is to detect the abnormal clusters by utilizing maximal log-likelihood ratio (more mathematical details are provided in Appendix 3). It is worth noting that the scan statistics-based method is a parametric method, in which the parametric families of data distributions are made. For instance, [26] assumes the negative binomial distribution, [11,12,18,19] investigate the Poisson distribution. A limitation of scan statistics is that it assumes that the background is independent and identically distributed (i.i.d.) or follow a rather simple probability distribution, which might not be suitable to handle non-stationary spatio-temporal data.

The second category of existing research is the change-point detection problem for spatio-temporal data. Below we will further review two approaches that are related to our context: the Least Absolute Shrinkage and Selection (LASSO)-based methods and dimension-reduction-based methods. Note that LASSO has been demonstrated to be an effective method for variable selection to address sparsity issues for high-dimensional data in the past decades since its developments in [27], and thus it is natural to apply it to detect sparse changes in high-dimensional data, see [24,32,34,36–38]. While the sparse change of LASSO is similar to the hot-spots, unfortunately, as our extensive simulation studies will demonstrate, the LASSO-based control chart is unable to separate the local hot-spots from the non-stationary global trend mean in the spatio-temporal data.

For the dimension-reduction-based change-point detection method, principal component analysis (PCA) or other dimension-reduction methods are often used to extract the features from the high-dimensional data. More specifically, [14] reduces the dimensionality in spatio-temporal data by constructing $T^2$ and Q charts separately. [22] combines multivariate functional PCA with change-point models to detect the hot-spots. For other dimension reduction methods, please see [1,5,9,16,21,33] for more details. The drawbacks of PCA or other dimension-reduction-based methods are the restriction of the change-point detection problem and the failure to consider the spatial sparsity and temporal consistency of hot-spots.

Our proposed method is essential to the application of the LASSO-based method and dimension-reduction-based method for SPC or change-point detection over a model based on tensor, which is a multi-dimensional array. It is worth noting that the multivariate spatio-temporal data can often be represented in 3-dimensional tensor format as ‘Spatial dimension × Temporal dimension × Attributes dimension’. Therefore, we propose to use tensor to represent the original data and consider the additive model that decomposes this tensor into three components: (1) smooth but non-stationary global trend mean, (2) sparse local hot-spots, and (3) residuals. We term our proposed decomposition model as Smooth Sparse Decomposition-Tensor (SSD-Tensor). Besides, when fitting the raw data to the SSD-Tensor model, we propose to add two penalty functions: the first one is the LASSO type penalty to guarantee the spatial sparsity of hot-spots, and the second one is the fused-LASSO penalty [see, 28] to guarantee the temporal consistency of hot-spots. This allows us to not only detect when the hot-spot happens over the temporal domain (i.e. hot-spot detection problem) but also localize where and which types/attributes of the hot-spots occurs if the change happens (i.e. hot-spot localization problem).

It is useful to highlight the novelty of our proposed method as compared to the existing research on spatio-temporal data. First, our proposed SSD-Tensor method can detect hot-spots when the global trend of the spatio-temporal data is dynamic (i.e. non-stationary or non-i.i.d). That is, our method is robust to the global trend, in the sense that it can detect hot-spots with positive or negative mean shifts on top of the global trend of raw data, no matter whether it is decreasing or increasing. In comparison, existing SPC or change-point detection methods often assume that the background is i.i.d. and focus on detecting the anomalies under the static and i.i.d. background. Second, we should clarify that the primary goal of our proposed method is not the prediction or model fitting. Instead, we focus on hot-spots detection and localization among the dynamic spatio-temporal data. Of course, good fitting or estimation of the global trend will be useful to detect hot-spots accurately. Finally, while our paper focuses only on a 3-dimensional tensor arising from our motivating application in crime rates, our proposed hot-spot method can easily be extended to any d-dimensional tensor ( $d\ge 3$), as we can simply add corresponding dimensions and bases in the tensor analysis. The capability of extending to high-dimensional tensor data is one of the main advantages of our proposed SSD-Tensor method.

The remainder of this paper is as follows. Section 2 introduces and visualizes the crime rate dataset, which will be used as our motivating example. Section 3 presents our proposed SSD-Tensor model and discusses how to estimate model parameters from data. Section 4 describes how to use our proposed SSD-Tensor model to detect and localize hot-spots. Section 5 compares our proposed method with several benchmark methods and demonstrates its usefulness through extensive simulations. Section 6 represents the application of our proposed method in a real crime rate dataset.

2. Motivating example and background

This section gives a detailed description of the crime rate dataset that is available from the US Department of Justice Federal Bureau of Investigation (see https://www.ucrdatatool.gov/Search/Crime/State/StateCrime.cfm). The crime rates are recorded from 1965 to 2014 for 51 states in the United States annually. In each year and for each state, three types of crime crates are reported: (1) Murder and non-negligent manslaughter; (2) Legacy rape; and (3) Revised rape. Table 1 shows the head of the dataset, and the value in the table is the crime rate per 100,000 population in each state.

Table 1.

Head of the crime rate dataset from 1965 to 2014 for 51 states in the United States annually. The dataset is publicly available from https://www.ucrdatatool.gov/Search/Crime/State/StateCrime.cfm.

Year	State	Murder and non-negligent manslaughter	Legacy rape	Revised rape
1965	Alabama	11.4	10.6	28.7
1965	Alaska	6.3	17.8	39.9
1965	Arkansas	5.9	10.4	23.7
⋮	⋮	⋮	⋮	⋮
1965	Wyoming	2.9	11.5	17.9
1966	Alabama	10.9	9.7	32.0
1966	Alaska	12.9	19.5	36.0
⋮	⋮	⋮	⋮	⋮

Notes: The recorded three types of crime rates are murder and non-negligent manslaughter, legacy rape, and revised rape. The value in the table is the crime rate per 100,000 population of each state, and the states are ordered in alphabetical order.

It is worth noting that the crime rate dataset has three dimensions: (1) the temporal dimension (i.e. years), (2) the spatial dimension (i.e. states) and (3) the attribute/category dimension (i.e. three different types of crime rates). For a visual representation, we plot several figures that show the characteristics of each dimension.

To begin with, we first illustrate the temporal dimension (i.e. years), where we plot the time series of the sum of all states' crime rates in the logarithm scale in Figure 1(a). The x-axis is the year ranging from 1965 to 2014, and the y-axis is the sum of all state's crime rates in the logarithm scale. We acknowledge that this summation is different from the actual annual crime rate in the United States, which needs to take into account different population sizes of each state at different years. Here, we use this notation to refer it as the annual crime rate of the United States for simplicity, since our purpose here is only for demonstration of the overall temporal trends. Figure 1(a) suggests that the crime rates are increasing in the first 10 years (1965–1975), then become stationary during 1975–1995, and finally have a decreasing trend during 1995–2014. Furthermore, it is interesting to point out the two peaks around 1980 and 1992, since we are interested in finding out whether they are caused by global trends or local hot-spots.

Figure 1.

(a) Time series of annual crime rates in the United States from1965 to 2014 & (b) Bar plot of three cumulative rates from 1965 to 2014. For Figure (a), the x-axis plot is the year ranging from 1965 to 2014, and the y-axis is the annual crime rate of the United States in the logarithm scale. Because the value of the crime rate is the number of crime cases per 100,000 population, it is reasonable for the annual crime rate to be larger than 100 during some years. For plot (b), different bars represent different types of crime rates, and the height of the bar represents the cumulative crime rate from 1965 to 2014 in the United States in the logarithm scale.

Next, we show the characteristics of the crime rate dataset on the attribute/category dimension (i.e. three types of the crime rates) in Figure 1(b), where different bars represents the different types of the crime rates, and the height of the bar represents the cumulative crime rate from 1965 to 2014 in the United States. It can be seen that these three crime rates overall happen with similar frequencies. This can possibly make it challenging to detect the hot-spots if we analyze the three-dimension data as a whole.

Finally, we illustrate the crime rate data in the spatial dimension (i.e. states) in Figure 2. In Figure 2, each map shows the spatial information of the crime rates in six different years. The selected six years are starting from 1965 with a ten-year interval, and the only exception is the sixth map, which uses the Year 2014 data, as the data in Year 2015 is not available yet as of August 2020. If a state has a very dark color in Figure 2, it has very high crime rates. We can see from the spatial plot in Figure 2 that the spatial patterns of crime rates are generally very smooth.

Figure 2.

Each map shows the spatial information of the crime rates in six different years. The selected six years are (a) 1965, (b) 1975, (c) 1985, (d) 1995, (e) 2005, (f) 2014. A darker color represents a higher crime rate. We can see that, the spatial patterns of crime rates are generally very smooth.

From Figures 1 and 2, there seems to be a brief increasing trend during 1984–1995, but it is difficult to conclude whether this is due to the global trend or local hot-spots without refined analysis. Note that global trend might be caused by the US federal governments' policies or the worldwise economic or political situations that are out of control of any local state or certain government branches. However, it is possible that the issues from local hot-spots can be addressed by borrowing other states' successful strategies or policies.

Below we provide the technical background on tensor through the crime rate dataset. Note that we can store our data set as a tensor of order three, denoted by $\mathcal{Y}=({\mathcal{Y}}_{i,j,t}),$ where an element ${\mathcal{Y}}_{i,j,t}$ represents the jth crime rate of state i in year t, where $i=1,\dots ,51$ for 51 states, j = 1, 2, 3 for three different type of crime rate and $t=1,\dots ,50$ for 50 years from 1965 to 2014.

We are now ready to introduce some basic tensor notation and algebra that are useful in this paper. For the notations throughout the paper, scalars are denoted by lowercase letters (e.g. θ), vectors are denoted by lowercase boldface letters ( $\mathit{\theta }$), matrices are denoted by uppercase boldface letter ( $\mathbf{\Theta }$), and tensors by curlicue letter (ϑ). For example, a tensor of order N is represented by $\vartheta \in {\mathbb{R}}^{I_1\times \dots \times I_N},$ where $I_n$ represent the mode-n dimension of ϑ for $n=1,\dots ,N$.

Next, we introduce the notation of slice, which is a two-dimensional section of a tensor by fixing all but two indices. Let us take tensor ${\mathcal{Y}}^{n_1\times n_2\times n_3}$ as an example, and Figure 3 visualizes its horizontal, lateral, and frontal slides, which are denoted by ${\mathcal{Y}}_{i::}(\mathrm{\forall }i=1,\dots ,n_1),{\mathcal{Y}}_{:j:}(\mathrm{\forall }j=1,\dots ,n_2)$, and ${\mathcal{Y}}_{::t}(\mathrm{\forall }t=1,\dots ,n_3)$, respectively.

Figure 3.

Slices of three-dimension tenor. (a) The original tensor: ${\mathcal{Y}}^{n_1\times n_2\times n_3}$, (b) horizontal slices: ${\mathcal{Y}}_{i::}\mathrm{\forall }i=1,\dots ,n_1$, (c) lateral slices: ${\mathcal{Y}}_{:j:}\mathrm{\forall }j=1,\dots ,n_2$, (d) frontal slices: ${\mathcal{Y}}_{::t}\mathrm{\forall }t=1,\dots ,n_3$.

Moreover, we introduce the mode-n product between tensor and matrix. For a given tensor of order N, i.e. $\vartheta \in {\mathbb{R}}^{I_1\times \dots \times I_N}$ and a given matrix $\mathbf{B}\in {\mathbb{R}}^{J_n\times I_n},$ the mode-n product between ϑ and $\mathbf{B}$, denoted by $\vartheta {\times }_n\mathbf{B},$ is a new tensor of dimension ${\mathbb{R}}^{I_1\times \dots I_{n-1}\times J_n\times I_{n+1}\times \dots I_N}$, where its $(i_1,\dots ,i_{n-1},j_n,i_{n+1},\dots ,i_N)$th entry can be computed as $\sum _{i_n}{\vartheta }_{i_1,\dots ,i_N}{\mathbf{B}}_{j_n,i_n}.$ Here we use the notation ${\mathbf{B}}_{j_n,i_n}$ to refer the $(j_n,i_n)$th entry in matrix $\mathbf{B},$ and ${\vartheta }_{i_1,\dots ,i_N}$ to refer the $(i_1,\dots ,i_N)$th entry tensor ϑ.

Finally, we discuss the Tucker decomposition, which is a useful technique in tensor algebra. Its main idea is to decompose a tensor $\mathcal{Y}\in {\mathbb{R}}^{I_1\times \dots \times I_N}$ into a core tensor multiplied by matrices along each dimension:

$$\mathcal{Y}=\vartheta {\times }_1{\mathbf{B}}^{(1)}{\times }_2{\mathbf{B}}^{(2)}\dots {\times }_N{\mathbf{B}}^{(N)},$$

where ${\mathbf{B}}^{(n)}\in {\mathbb{R}}^{I_n\times I_n}$ is an orthogonal matrix for $n=1,\dots ,N$. The above equation can be equivalently represented by a Kronecker product, i.e.

$$\mathrm{vec}(\mathcal{Y})=({\mathbf{B}}^{(N)}\otimes {\mathbf{B}}^{(N-1)}\dots \otimes {\mathbf{B}}^{(1)})\mathrm{vec}(\mathit{\theta }),$$

where $\mathrm{vec}(\cdot )$ is the vectorized operator. Here the Kronecker product ⊗ is defined as follow: suppose ${\mathbf{B}}_1\in {\mathbb{R}}^{m\times n}$ and ${\mathbf{B}}_2\in {\mathbb{R}}^{p\times q}$ are matrices, the Kronecker product of these matrices is an $mp\times nq$ block matrix defined by

$${\mathbf{B}}_1\otimes {\mathbf{B}}_2=\left[\begin{array}{ccc}{b}_{11}{\mathbf{B}}_2& \dots & b_{1n}{\mathbf{B}}_2\\ ⋮& \ddots & ⋮\\ b_{m1}{\mathbf{B}}_2& \dots & b_{mn}{\mathbf{B}}_2\end{array}\right].$$

The Kronecker product has been shown to have excellent computational efficiency for tensor data, see [10].

3. Our proposed SSD-tensor model

This section presents our proposed SSD-Tensor model and its parameter estimation, whereas the discussion of hot-spot detection and localization will be postponed to the next section. The main advantage of using tensor is not only to characterize the complicated ‘within-dimension’ or ‘between-dimension’ correlations, but also to simplify the computations. The latter is similar to the matrix context where it might be difficult to compute the inverse of a large matrix in general, but it will be straightforward to calculate the inverse of a large block diagonal matrix through the inverse of sub-matrices in the diagonal.

To better present our main ideas, we split this section into three subsections. Section 3.1 presents the mathematical formulation of our proposed SSD-Tensor model, and Section 3.2 develops the optimization algorithm for the parameter estimation problem of the model when fitting the observed data. Since the choice of basis in the tensor decomposition plays an important role in representing spatial or temporal patterns, we devote Section 3.3 to discuss the choice of basis in our context.

3.1. Our proposed model

In this section, we present the mathematical formulation of our proposed SSD-Tensor model. Here let us focus on our motivating data with three-dimension tensor ${\mathcal{Y}}_{n_1\times n_2\times n_3}$, where the $(i,j,t)$th entry indicate the jth crime rate in ith state in year t, with $i=1,\dots ,n_1=51$, $j=1,\dots ,n_2=3$, and $t=1,\dots ,n_3=50$.

At the high level, our proposed SSD-Tensor model is to decompose a raw data ${\mathcal{Y}}_{i,j,t}$ into three components: the smooth global trend mean ${\mathcal{U}}_{i,j,t}$, local hot-spots ${\mathcal{H}}_{i,j,t}$, and residuals ${\mathcal{E}}_{i,j,t}$. Mathematically, it is an additive model with the form

$${\mathcal{Y}}_{i,j,t}={\mathcal{U}}_{i,j,t}+{\mathcal{H}}_{i,j,t}+{\mathcal{E}}_{i,j,t},$$

where the residuals ${\mathcal{E}}_{i,j,t}$ are i.i.d. with $N(0,{\sigma }^2).$ Under the tensor notation, we denote $\mathcal{U},\mathcal{H},\mathcal{E}$ as the corresponding tensors of dimension ${\mathbb{R}}^{n_1\times n_2\times n_3}.$ Then our proposed model can be rewritten as $\mathcal{Y}=\mathcal{U}+\mathcal{H}+\mathcal{E}$.

It remains to discuss two main components of our model in more detail. For the global trend mean $\mathcal{U}$, our main idea is to adopt the basis decomposition framework that allows us to address the complicated within-dimension correlation and between-dimension correlations. To be more specific, we propose to decompose the global trend mean tensor $\mathcal{U}$ as

$$\mathcal{U}={\vartheta }_m{\times }_1{\mathbf{B}}_{m,1}{\times }_2{\mathbf{B}}_{m,2}{\times }_3{\mathbf{B}}_{m,3},$$

where ${\vartheta }_m\in {\mathbb{R}}^{n_1\times n_2\times n_3}$ is an unknown tensor parameter to be estimated, and matrices ${\mathbf{B}}_{m,1}\in {\mathbb{R}}^{n_1\times n_1},{\mathbf{B}}_{m,2}\in {\mathbb{R}}^{n_2\times n_2},{\mathbf{B}}_{m,3}\in {\mathbb{R}}^{n_3\times n_3}$ are pre-specified bases to describe the within-state correlation, within-rate correlation, and within-year correlation in $\mathcal{U}$, respectively. The choices of the base matrices, i,e., ${\mathbf{B}}_{m,1},{\mathbf{B}}_{m,2}$ and ${\mathbf{B}}_{m,3},$ are very important in practice, and we will discuss them in more details in Section 3.3. In our tensor decomposition, the operator ${\times }_1,{\times }_2,{\times }_3$ is the mode-n product reviewed in the previous section, where n = 1, 2, 3. This mode-n product is used to model the between-dimension correlations in $\mathcal{U}$.

Since some readers might not be familiar with the basis decomposition in tensor, let us provide a little more background. Loosely speaking, basis decomposition for tensor is an extension of the matrix decomposition, and is similar to the singular value decomposition (SVD) in the sense of representing a matrix or tensor as the product of several specialized matrices or tensors. The main difference is that the bases ${\mathbf{B}}_{m_1},{\mathbf{B}}_{m,2},{\mathbf{B}}_{m,3}$ are known in the basis decomposition. Figure 4 illustrates the relationship between SVD and basis decomposition.

Figure 4.

The relationship between SVD and basis decomposition. The plot (a) is the SVD of matrix $\mathbb{U}\in {\mathbb{R}}^{n_1\times n_2}$. The plot (b) is the basis decomposition of tensor $\mathcal{U}\in {\mathbb{R}}^{n_1\times n_2\times n_3}$.

Next, for the local hot-spot tensor $\mathcal{H}$, we follow the similar basis decomposition way as $\mathcal{U}$:

$$\mathcal{H}={\vartheta }_h{\times }_1{\mathbf{B}}_{h,1}{\times }_2{\mathbf{B}}_{h,2}{\times }_3{\mathbf{B}}_{h,3},$$

where ${\vartheta }_h\in {\mathbb{R}}^{n_1\times n_2\times n_3}$ is the unknown tensor to be estimated. And matrices ${\mathbf{B}}_{h,1}\in {\mathbb{R}}^{n_1\times n_1},{\mathbf{B}}_{h,2}\in {\mathbb{R}}^{n_2\times n_2},{\mathbf{B}}_{h,3}\in {\mathbb{R}}^{n_3\times n_3}$ are pre-specified bases to describe the within-state correlation, within-rate correlation, and within-year correlation in $\mathcal{H}$, respectively. For the selection of these bases, i,e., ${\mathbf{B}}_{h,1},{\mathbf{B}}_{h,2},{\mathbf{B}}_{h,3}$, a detailed discussion can be found in Section 3.3. The operator ${\times }_1,{\times }_2,{\times }_3$ is the mode- $n(n=1,2,3)$ product (see the definition of mode-n product in the end of Section 2) to model the between-dimension correlations in $\mathcal{H}$.

In summary, our proposed SSD-Tensor model can be written as the following tensor format:

$$\mathcal{Y}={\vartheta }_m{\times }_1{\mathbf{B}}_{m,1}{\times }_2{\mathbf{B}}_{m,2}{\times }_3{\mathbf{B}}_{m,3}+{\vartheta }_h{\times }_1{\mathbf{B}}_{h,1}{\times }_2{\mathbf{B}}_{h,2}{\times }_3{\mathbf{B}}_{h,3}+\mathcal{E}.$$ (1)

This tensor representation above allows us to develop computationally efficient methods for estimation and prediction. For the detailed reason why tensor is more computational efficient can be found in Section 3.2 and Appendix 2. By introducing tensor algebra, the above format of our model can be written in an equivalent way:

$$\mathbf{y}=\underset{{\mathbf{B}}_m}{\underbrace{({\mathbf{B}}_{m,1}\otimes {\mathbf{B}}_{m,2}\otimes {\mathbf{B}}_{m,3})}}{\mathit{\theta }}_m+\underset{{\mathbf{B}}_h}{\underbrace{({\mathbf{B}}_{h,1}\otimes {\mathbf{B}}_{h,2}\otimes {\mathbf{B}}_{h,3})}}{\mathit{\theta }}_h+\mathbf{e},$$ (2)

where vector $\mathbf{y}=\mathrm{vec}(\mathcal{Y})$, vector ${\mathit{\theta }}_m=\mathrm{vec}({\vartheta }_m)$, vector ${\mathit{\theta }}_h=\mathrm{vec}({\vartheta }_h)$, and vector $\mathbf{e}=\mathrm{vec}(\mathcal{E})$. The residual vector $\mathbf{e}$ is assumed to be the Gaussian white noise, i.e. $\mathbf{e}\sim N(0,{\sigma }^2\mathbf{I})$.

In our proposed SSD-Tensor model in (2), it is crucial to estimate the global mean parameter ${\mathit{\theta }}_m$ and the local hot-spots parameter ${\mathit{\theta }}_h$ when fitting to the observed data. Here we propose to estimate them by the penalized likelihood-function framework. To be more concrete, we propose to add two penalties in our parameter estimation. The first one is the LASSO penalty term on ${\mathit{\theta }}_h$ to ensure the sparsity property of hot-spots: $R_1({\mathit{\theta }}_h)={\lambda }_1\Vert {\mathit{\theta }}_h{\Vert }_1.$ The second penalty is the fused LASSO penalty ([28]) on ${\mathit{\theta }}_h$ to encourage the temporal consistency of the hot-spots: $R_2({\mathit{\theta }}_h)={\lambda }_2\sum _{t=2}^{n_3}\Vert {\mathit{\theta }}_{h,t}-{\mathit{\theta }}_{h,t-1}{\Vert }_1,$ where ${\mathit{\theta }}_{h,t}=\mathrm{vec}({\vartheta }_{h,::t})$.

Thus, by combining these two penalties, we propose to estimate the parameters ( ${\mathit{\theta }}_m,{\mathit{\theta }}_h,\mathit{e}$) via the following optimization problem:

$$\begin{array}{cl}\arg & \underset{{\mathit{\theta }}_m,{\mathit{\theta }}_h,\mathit{e}}{min}{\Vert \mathit{e}\Vert }_2^2+{\lambda }_1{\Vert {\mathit{\theta }}_h\Vert }_1+{\lambda }_2\sum _{t=2}^{n_3}{\Vert {\mathit{\theta }}_{h,t}-{\mathit{\theta }}_{h,t-1}\Vert }_1\\ s.t.& \mathit{y}=({\mathbf{B}}_{m,1}\otimes {\mathbf{B}}_{m,2}\otimes {\mathbf{B}}_{m,3}){\mathit{\theta }}_m+({\mathbf{B}}_{h,1}\otimes {\mathbf{B}}_{h,2}\otimes {\mathbf{B}}_{h,3}){\mathit{\theta }}_h+\mathbf{e}.\end{array}$$ (3)

We will discuss how to efficiently solve this optimization problem in the next section.

3.2. Optimization algorithm for estimation

In this section, we develop an efficient computational algorithm for solving the optimization problem in (3). To emphasize the tuning parameters ${\lambda }_1$ and ${\lambda }_2$ in the penalty terms in (3), we rewrite ${\mathit{\theta }}_m$ and ${\mathit{\theta }}_h$ as ${\mathit{\theta }}_{m,{\lambda }_1,{\lambda }_2}$ and ${\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2},$ respectively.

Our proposed optimization algorithm to solve (3) contain two main steps. The first one is to estimate ${\mathit{\theta }}_{m,{\lambda }_1,{\lambda }_2}$ and $\mathit{e}$ for a given ${\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}$. The second step is to estimate ${\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}$ by using the Fast Iterative Shrinkage Thresholding Algorithm (FISTA) in [2] that iteratively updates the estimators. When implementing the FISTA algorithm to our context, at each iteration, we face an optimization problem that involves both LASSO and fused LASSO penalty parameters ${\lambda }_1$ and ${\lambda }_2.$ To make the computation feasible, we apply an useful proposition that establishes the relationship of the optimal solutions between ${\lambda }_1=0$ and general ${\lambda }_1\ne 0.$

Let us first discuss the estimation of ${\mathit{\theta }}_{m,{\lambda }_1,{\lambda }_2}$ and $\mathit{e}$ for a given ${\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}$. It turns out that we have a closed-form solution, as shown in the following proposition.

Proposition 3.1

In the optimization problem in (3), for a given ${\hat{\mathit{\theta }}}_{h,{\lambda }_1,{\lambda }_2}$, the optimal solution of ${\hat{\mathit{\theta }}}_{m,{\lambda }_1,{\lambda }_2}$ is given by:

$${\hat{\mathit{\theta }}}_{m,{\lambda }_1,{\lambda }_2}=({\mathbf{B}}_m^{\mathrm{\top }}{\mathbf{B}}_m{)}^{-1}({\mathbf{B}}_m^{\mathrm{\top }}\mathbf{y}-{\mathbf{B}}_m^{\mathrm{\top }}{\mathbf{B}}_h{\hat{\mathit{\theta }}}_{h,{\lambda }_1,{\lambda }_2}).$$ (4)

The proof of Proposition 3.1 follows the standard argument in the method of least squares in linear regression, and thus omitted. Moreover, since ${\mathbf{B}}_m\in {\mathbb{R}}^{n_1{n}_2{n}_3\times n_1{n}_2{n}_3}$ can have huge dimension when $n_1,n_2,n_3$ is large, it might be computationally expensive to solve the inverse of matrix ${\mathbf{B}}_m^{\mathrm{\top }}{\mathbf{B}}_m$. By using the tensor algebra, we can greatly simplify the computations, see Appendix 2 for the details.

Next, we discuss the estimation of ${\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}$, which is highly non-trivial. By Proposition 3.1, the original optimization problem in (3) becomes

$$\arg \underset{{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}}{min}{\Vert {\mathbf{y}}^{\ast }-\mathbf{X}{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}\Vert }_2^2+{\lambda }_1{\Vert {\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}\Vert }_1+{\lambda }_2{\Vert {\mathit{D}\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}\Vert }_1,$$ (5)

where ${\mathbf{y}}^{\ast }=[\mathbf{I}-{\mathbf{H}}_m]\mathbf{y},\mathbf{X}=[\mathbf{I}-{\mathbf{H}}_m]{\mathbf{B}}_h$ with ${\mathbf{H}}_m={\mathbf{B}}_m({\mathbf{B}}_m^{\mathrm{\top }}{\mathbf{B}}_m{)}^{-1}{\mathbf{B}}_m^{\mathrm{\top }}$ as the projection matrix. Here the matrix $\mathbf{D}$ is defined to make ${\lambda }_2\Vert {\mathit{D}\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}{\Vert }_1$ equivalent to ${\lambda }_2\sum _{t=2}^{n_3}\Vert {\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2,t}-{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2,t-1}{\Vert }_1$ (see Appendix 1 for the explicit definition of $\mathbf{D}$).

It suffices to solve the new optimization problem in (5). Note that (5) is a generalized LASSO problem, and there are many optimization methods available in the literature. For instance, [29] solves a generalized LASSO problem through transformation to a common LASSO problem, but unfortunately, it is computationally heavy. [30] uses the alternating direction methods of multipliers (ADMM) algorithm to solve a generalized LASSO problem, but its convergence rate is of $O(1/k)$ as shown in [8], where k indicating the iterations. Another popular method is iterative shrinkage thresholding algorithms (ISTA) proposed by [4], which also has a convergence rate of $O(1/k).$ Later, researchers in [2] proposed a faster version of the ISTA, called FISTA, and shown that it has a convergence rate $O(1/k^2)$. Thus in our paper, we decide to choose the FISTA algorithm of [2] as the primary tool to solve (5) due to its fast convergence rate.

There is a technical challenge to apply the FISTA algorithm to (5). In FISTA algorithm, each iteration is based on the proximal mapping of the loss function $F({\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2})=\Vert {\mathbf{y}}^{\ast }-\mathbf{X}{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}{\Vert }_2^2.$ To be more concrete, the updating rule from ith FISTA iteration to $(i+1)$th FISTA iteration is given by

$$\begin{array}{rl}{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}^{(i+1)}& =\arg \underset{\mathit{\theta }}{min}F({\mathit{\eta }}^{(i)})+\frac{\mathrm{\partial }F({\mathit{\eta }}^{(i)})}{\mathrm{\partial }{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}}(\mathit{\theta }-{\mathit{\eta }}^{(i)})+\frac{L_{\theta }}{2}\Vert \mathit{\theta }-{\mathit{\eta }}^{(i)}{\Vert }_2^2+{\lambda }_1\Vert \mathit{\theta }{\Vert }_1+{\lambda }_2\Vert \mathbf{D}\mathit{\theta }{\Vert }_1\\ & \triangleq {\pi }_{{\lambda }_2}^{{\lambda }_1}({\mathbf{v}}^{(i)})\end{array}$$

where ${\mathit{\eta }}^{(i)}$ is the auxiliary variable, i.e. ${\mathit{\eta }}^{(i)}={\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}^{(i)}+\frac{t_i-1}{t_{i+1}}({\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}^{(i)}-{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}^{(i-1)})$ with $t_0=1$, $t_{i+1}=\frac{1+\sqrt{1+4t_i^2}}{2}$, ${\mathbf{v}}^{(i)}={\mathit{\eta }}^{(i)}-\frac{\mathrm{\partial }}{L_{\theta }\mathrm{\partial }\mathit{\theta }}F({\mathit{\eta }}^{(i)})$ and $L_{\theta }$ is the stepsize which is fixed as the maximal eigenvalue of matrix ${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}$ (see Appendix 4 for more details).

The challenge of applying the FISTA algorithm is because it is difficult to solve ${\pi }_{{\lambda }_2}^{{\lambda }_1}({\mathbf{v}}^{(i)})$ directly, as it involves two penalties with parameters ${\lambda }_1$ and ${\lambda }_2.$ To overcome this challenge, we propose to combine a nice theoretical result in [13] with an augmented ADMM algorithm in [35]. Specifically, [13] shows that there is a closed-form relationship between ${\pi }_{{\lambda }_2}^{{\lambda }_1}({\mathbf{v}}^{(i)})$ and ${\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)})$. Thus we can easily compute ${\pi }_{{\lambda }_2}^{{\lambda }_1}({\mathbf{v}}^{(i)})$ if we know how to solve ${\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)})$. The latter can be solved by the augmented ADMM algorithm in [35], which is an extension of the regular ADMM method.

Proposition 3.2 summarizes that, in the ith FISTA iteration, how to derive ${\pi }_{{\lambda }_2}^{{\lambda }_1}({\mathbf{v}}^{(i)})$ from ${\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)}),$ whose iterative applications lead to the estimation of ${\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}$ in (5):

Proposition 3.2

Assume that

1. there is a diagonal matrix $\mathbf{Q}\in {\mathbb{R}}^{n_1{n}_2{n}_3\times n_1{n}_2{n}_3}$ satisfying $\mathbf{Q}⪰{\mathbf{D}}^{\mathrm{\top }}\mathbf{D}$, i.e. $\mathbf{Q}-{\mathbf{D}}^{\mathrm{\top }}\mathbf{D}$ is a positive semidefinite matrix;

2. there is a scaler $\rho >0$, which is a positive penalty parameter;

The updating procedure of augmented ADMM algorithm from kth augmented ADMM iteration to the $(k+1)$th augmented ADMM iteration is

$$\begin{array}{rl}{\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)}{)}^{(k+1)}& ={\displaystyle \arg \underset{\mathit{\theta }\in {\mathbb{R}}^{n_1{n}_2{n}_3}}{min}[F(\mathit{\theta })+(2{\mathit{\alpha }}^{(k)}-{\mathit{\alpha }}^{(k-1)}{)}^{\mathrm{\top }}\mathbf{D}\mathit{\theta }}\\ & +\frac{\rho }{2}(\mathit{\theta }-{\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)}{)}^{(k+1)}{)}^{\mathrm{\top }}\mathbf{Q}(\mathit{\theta }-{\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)}{)}^{(k+1)})];\\ {\mathit{\gamma }}^{(k+1)}& ={\displaystyle \arg \underset{\mathit{\theta }\in {\mathbb{R}}^{n_3-1}}{min}[\mathbf{D}\mathit{\gamma }+\frac{\rho }{2}{\Vert \mathbf{D}{\mathit{\theta }}^{(k+1)}-\mathit{\gamma }+\frac{1}{\rho }{\mathit{\alpha }}^{(k)}\Vert }_2^2];}\\ {\mathit{\alpha }}^{(k+1)}& ={\mathit{\alpha }}^{(k)}+\rho (\mathbf{D}{\mathit{\theta }}^{(k+1)}-{\mathit{\gamma }}^{(k+1)}).\end{array}$$ (6)

Suppose the above updating procedure lasts for $M_2$ iterations with $M_2$ as the number of augmented ADMM iterations, then we have can well approximate $\widehat{{\pi }_{{\lambda }_2}^0}({\mathbf{v}}^{(i)})$ as ${\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)}{)}^{(M_2)}$. Then $\widehat{{\pi }_{{\lambda }_2}^{{\lambda }_1}}({\mathbf{v}}^{(i)})$ can be solved as

$$\widehat{{\pi }_{{\lambda }_2}^{{\lambda }_1}}({\mathbf{v}}^{(i)})=\mathrm{sign}(\widehat{{\pi }_{{\lambda }_2}^0}({\mathbf{v}}^{(i)}))\odot max\{|\widehat{{\pi }_{{\lambda }_2}^0}({\mathbf{v}}^{(i)})|-{\lambda }_1,0\},$$ (7)

where ⊙ is an operator, which multiply two vectors in an element-wise fashion. For example, for two vectors $\mathbf{a},\mathbf{b}$, the ith operator of $\mathbf{a}\otimes \mathbf{b}$ is ${\mathbf{a}}_i{\mathbf{b}}_i$.

The proof of Proposition 3.2 is omitted, as the update rule in (6) is an application of the augmented ADMM algorithm of [35], and equation (7) follows directly from Theorem 1 of [13].

Combining the above two propositions together, our optimization algorithm to solve the optimization problem in (3) can be summarized as the pseudocode in Algorithm 1.

3.3. Selection of bases in our context

This section discusses how to choose the bases ${\mathbf{B}}_{m,1}$, ${\mathbf{B}}_{m,2}$, ${\mathbf{B}}_{m,3}$, ${\mathbf{B}}_{h,1}$, ${\mathbf{B}}_{h,2}$, ${\mathbf{B}}_{h,3}$ in our contexts. In general, these bases can be Gaussian kernels, Cosine kernel, etc. depending on the nature or characteristics of the data. When one has little to no prior knowledge of the data structure, a simple choice of bases can be identity matrix.

Let us now discuss our choices of these bases in our simulation studies and case study of the crime rate dataset. For the bases of the global trend mean, it involves the selection of ${\mathbf{B}}_{m,1}$, ${\mathbf{B}}_{m,2}$, ${\mathbf{B}}_{m,3}$, where ${\mathbf{B}}_{m1}$ is the basis in the state dimension of the global trend, ${\mathbf{B}}_{m2}$ is the basis in the crime rate dimension of the global trend, ${\mathbf{B}}_{m3}$ is the basis in the temporal dimension of the global trend. By Figure 2, the data are spatially smooth in the state dimension, and thus we propose to choose ${\mathbf{B}}_{m,1}$ as the Gaussian kernel matrix whose $(i,j)$th element is defined by $\exp \{-d^2/(2c^2)\}$, where d is the distance between the center of ith state and jth state. Here the bandwidth constant c is chosen by Silverman's Rule of thumb of [25]: $c=(4{\hat{\sigma }}^5/(3n_3){)}^{1/5}$, where $\hat{\sigma }$ is the estimated variance of ${\mathbf{y}}_1,\dots ,{\mathbf{y}}_{n_3}$. Meanwhile, we set ${\mathbf{B}}_{m,2}$ and ${\mathbf{B}}_{m,3}$ to be the identity matrix, since we have little prior knowledge in the crime rate dimension and temporal dimension.

For the selection of the hot-spots basis, i.e. ${\mathbf{B}}_{h,1}$, ${\mathbf{B}}_{h,2}$, ${\mathbf{B}}_{h,3}$, we propose to set all of them as the identity matrix, since there is no prior knowledge of the hot-spots. It is informative to mention that while the identify matrix seems to lack the temporal consistency of the hot-spots, our optimization problem adds the fused LASSO penalty that might have already addressed the temporal consistency of the hot-spots.

4. Detection and localization of hot-spots

In this section, we discuss the detection and localization of the hot-spots. For the ease of presentation, we first discuss the detection of the hot-spots, i.e. detect when a hot-spot occurs in Section 4.1. Then, in Section 4.2, we consider the localization of the hot-spot, i.e. determine which states and which crime types are involved for the detected hot-spots.

4.1. Detect when hot spots occur?

To detect when hot-spots occur, we develop a control chart based on the following hypothesis test problem:

$$H_0:{\mathbf{r}}_t({\lambda }_1,{\lambda }_2)=0\mathrm{v}.\mathrm{s}.H_1:{\mathbf{r}}_t({\lambda }_1,{\lambda }_2)=\delta {\hat{\mathbf{h}}}_t({\lambda }_1,{\lambda }_2)(\delta >0),$$ (8)

where

$${\mathbf{r}}_t({\lambda }_1,{\lambda }_2)={\mathbf{y}}_t({\lambda }_1,{\lambda }_2)-{\hat{\mathit{\mu }}}_t({\lambda }_1,{\lambda }_2)$$

is the residual after removing the global trend mean under the penalty parameters ${\lambda }_1,{\lambda }_2,$ and the vector ${\hat{\mathit{\mu }}}_t({\lambda }_1,{\lambda }_2)=\mathrm{vec}({\hat{\mathcal{U}}}_{::t}({\lambda }_1,{\lambda }_2)),{\hat{\mathbf{h}}}_t({\lambda }_1,{\lambda }_2)=\mathrm{vec}({\hat{\mathcal{H}}}_{::t}({\lambda }_1,{\lambda }_2))$ are the estimated global trend men and local hot-spots in tth year. Here, we add $({\lambda }_1,{\lambda }_2)$ to emphasize that, ${\hat{\mathit{\mu }}}_t({\lambda }_1,{\lambda }_2),{\hat{\mathbf{h}}}_t({\lambda }_1,{\lambda }_2)$ are the global trend mean and local hot-spots estimation under penalty parameter ${\lambda }_1,{\lambda }_2$ respectively.

The motivation of the above hypothesis test is as follows. When there are no hot-spots, the residual ${\mathbf{r}}_t({\lambda }_1,{\lambda }_2)$ is exactly the model noises. However, when hot-spots exist, the residual ${\mathbf{r}}_t$ includes both hot-spots and noises. By including the hot-spot information of ${\hat{\mathbf{h}}}_t({\lambda }_1,{\lambda }_2)$ in the alternative hypothesis, we hope to provide a direction in the alternative hypothesis space, which allows one to construct a test with more power, see [36].

Next, we construct the likelihood ratio test in the above-mentioned hypotheses testing problem. By [7], the test statistics monitoring upward shift is

$$P_t^{+}({\lambda }_1,{\lambda }_2)={\hat{\mathbf{h}}}_t^{+}({\lambda }_1,{\lambda }_2)\mathrm{\top }{\mathbf{r}}_t({\lambda }_1,{\lambda }_2)/\sqrt{{\hat{\mathbf{h}}}_t^{+}({\lambda }_1,{\lambda }_2)\mathrm{\top }{\hat{\mathbf{h}}}_t^{+}({\lambda }_1,{\lambda }_2)}$$

where ${\hat{\mathbf{h}}}_t^{+}({\lambda }_1,{\lambda }_2)$ only takes the positive part of ${\hat{\mathbf{h}}}_t({\lambda }_1,{\lambda }_2)$ with other entries as zero, because our objective is to detect positive hot-spots. The superscript ‘+’ emphasizes that we aim at detecting upward shift. In other words, we focus on the hot-spots that have increasing means, partly because increasing crime rates are generally more harmful to the societies and communities. If one is also interested in detecting decreasing mean shifts, one could modify it by using a two-sided test.

It remains to discuss how to choose $({\lambda }_1,{\lambda }_2)$ suitably in our test. We propose to follow [36] to calculate a series of $P_t^{+}({\lambda }_1,{\lambda }_2)$ under different combination of $({\lambda }_1,{\lambda }_2)\in \mathrm{\Gamma }=\{({\lambda }_1^{(1)},{\lambda }_2^{(1)})\dots ({\lambda }_1^{(n_{\lambda })},{\lambda }_2^{(n_{\lambda })})\}$ and then select the combination of $({\lambda }_1,{\lambda }_2)$ with the largest power. The final chosen test statistics, denoted as ${\tilde{P}}_t^{+}({\lambda }_{1,t}^{\ast },{\lambda }_{2,t}^{\ast })$, can be computed by

$${\tilde{P}}_t^{+}({\lambda }_{1,t}^{\ast },{\lambda }_{2,t}^{\ast })=\underset{({\lambda }_1,{\lambda }_2)\in \mathrm{\Gamma }}{max}\frac{P_t^{+}({\lambda }_1,{\lambda }_2)-E(P_t^{+}({\lambda }_1,{\lambda }_2))}{\sqrt{\mathrm{Var}(P_t^{+}({\lambda }_1,{\lambda }_2))}},$$ (9)

where $E(P_t^{+}({\lambda }_1,{\lambda }_2))$, $\mathrm{Var}(P_t^{+}({\lambda }_1,{\lambda }_2))$ respectively are the mean and variance of $P_t^{+}({\lambda }_1,{\lambda }_2)$ under $H_0$ (e.g. for phase-I in-control samples). Here $({\lambda }_{1,t}^{\ast },{\lambda }_{2,t}^{\ast })\in \mathrm{\Gamma }$ is the penalty parameter maximizing the above equation.

With the test statistic available, we detect when hot-spots occur based on the widely used Cumulative Sum (CUSUM) Control Chart, see [15,20]. At each time t, we recursively compute the CUSUM statistics as

$$W_t^{+}=max\{0,W_{t-1}^{+}+{\tilde{P}}_t^{+}({\lambda }_{1,t}^{\ast },{\lambda }_{2,t}^{\ast })-d^{\ast }\},$$ (10)

with the initial value $W_{t=0}^{+}=0$, where $d^{\ast }$ is a constant and can be chosen according to the degree of the shift that we want to detect. Then we declare that a hot-spot might occurs whenever $W_t^{+}>L$ for some pre-specified control limit L.

Note that the CUSUM statistics $W_t^{+}$ leads to the optimal control chart to detecting a mean shift from ${\mu }_0$ to ${\mu }_1=2d^{\ast }-{\mu }_0$ for normally distributed data, see [15]. When the data are not normally distributed, the optimality properties might not hold, but it can still be a reasonable control chart. Also, it is important to choose the control limit L in the CUSUM control chart suitably, and the detailed discussion will be presented in Section 5 for our simulation studies and in Section 6 for our case study.

4.2. Localize where and which the hot spots occur?

In this section, we discuss how to localize the hot-spots if the CUSUM control chart in (10) raises an alarm at year $t^{\ast }.$ In other words, we want to determine where and which crime rates may account for the hot-spots. To do so, we propose to utilize the matrix ${\hat{\mathcal{H}}}_{::t^{\ast }}({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$, which is the hot-spot estimation in $t^{\ast }$th year. If the $(i,j,t^{\ast })$th entry in ${\hat{\mathcal{H}}}_{::t^{\ast }}({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$ is non-zero, then we declare that there is a hot-spot for the jth crime rate type in the ith state at the $t^{\ast }$th year.

The mathematical procedure to derive ${\hat{\mathcal{H}}}_{::t^{\ast }}({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$ is as follows. First, $\hat{\mathcal{H}}({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$ is the tensor format of $\hat{\mathbf{h}}({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})={\mathbf{B}}_h{\hat{\mathit{\theta }}}_h({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$, where ${\hat{\mathit{\theta }}}_h({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$ is the minimizer in (2) with penalty parameter as ${\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }}$. Second, ${\hat{\mathcal{H}}}_{::t^{\ast }}({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$ is the $t^{\ast }$ slices along the temporal dimension of $\hat{\mathcal{H}}({\lambda }_{1,t^{\ast }},{\lambda }_{2,t^{\ast }})$.

As one reviewer points out, this approach might lead to a relatively high false positive rate (FPR), since some non-zero entries might not be statistically significant. Two possible ways to improve our approach are (1) to conduct the significant test, or (2) to set up a pre-specified threshold and only keep the positive entries that are larger than the threshold. It is useful to investigate how to improve our approach, which is an interesting topic for future research. Here we focus on our main ideas of using tensor decomposition for hot-spots, and adopt the simple approach for hot spots localization.

5. Simulation study

In this section, we report the numerical simulation results of our proposed method as well as its comparison with several benchmark methods in the literature. To better present our results, we divide this section into several subsections. Section 5.1 includes the data generation mechanism for our simulation studies, and Section 5.2 presents the benchmark methods for the comparison purpose. The performance of hot-spot detection and localization are reported in Section 5.3, and the fitness of the global trend mean is evaluated in Section 5.4.

5.1. Data generation

In our simulation, we detect the hot-spots on the complete data, i.e. $\mathcal{Y}\in {\mathbb{R}}^{n_1\times n_2\times n_3}$. In order to shed light on the case study, we match the tensor dimension of the crime rate dataset and choose $n_1=51,n_2=3,n_3=250$ in our simulation. To generate the data $\mathcal{Y}$, we generate it by generating its front slices ${\mathcal{Y}}_{::t}$ for $t=1\dots n_3$. Mathematically, we generate ${\mathbf{y}}_t=\mathrm{vec}({\mathcal{Y}}_{::t})$ by

$${\mathbf{y}}_{i,t}=(\mathbf{B}{\mathit{\theta }}_t{)}_i+\delta \mathbb{1}\{t\ge \tau \}\mathbb{1}\{i\in S_h\}+{\mathbf{w}}_{i,t},$$ (11)

where ${\mathbf{y}}_{i,t}$ denotes the ith entry in vector ${\mathbf{y}}_t\in {\mathbb{R}}^{n_1{n}_2}$. The last term on the right hand side of the above equation, i.e. ${\mathbf{w}}_{i,t}$, is the ith entry in the white noise ${\mathbf{w}}_t$. And ${\mathbf{w}}_t$ is a vector whose entries are independent and follow $N(0,{0.1}^2)$ distribution. Note that while we generate the data sequentially over time t, our proposed SSD-Tensor method is actually an off-line method that analyzes the complete tensor.

The first term on the right hand side of the above equation, i.e. $(\mathbf{B}{\mathit{\theta }}_t{)}_i$, is the global mean, where the subscript $(\cdot {)}_i$ denotes the ith entry. Matrix $\mathbf{B}$ is a fixed B-spline basis with the degree of three and fifty knots evenly spacing on interval $[1,50]$. Note that the B-spline basis is only used in the generative model in simulation to generate data, but is not used in our proposed methodologies. Vector ${\mathit{\theta }}_t$ is a constant parameter controlling the trend of the global mean. We set ${\mathit{\theta }}_t$ in two different ways, so we discuss 2 scenarios:

• Scenario 1: The global trend mean is stationary, in which ${\mathit{\theta }}_{t,i}=1+\sin (\frac{2\pi }{470}(106.75+i))$ for $i=1,\dots n_1{n}_2$ and $t=1,\dots ,n_3$. Here ${\mathit{\theta }}_{t,i}$ is the ith entry in ${\mathit{\theta }}_t$.

• Scenario 2: The global trend mean is decreasing over time, in which ${\mathit{\theta }}_t=0.995{\mathit{\theta }}_{t-1}$ for $t=1,2,\dots ,n_3$. And ${\mathit{\theta }}_{0,i}=1+\sin (\frac{2\pi }{470}(106.75+i))$ for $i=1,\dots n_1{n}_2$.

The second term on the right side hand of equation (11), i.e. $\delta \mathbb{1}\{t\ge \tau \}\mathbb{1}\{i\in S_h\}$ is the local hot-spot, where $\mathbb{1}(A)$ is the indicator function, which has the value 1 for all elements of A and the value 0 for all elements not in A. First, $\mathbb{1}\{t\ge \tau \}$ indicates that the hot-spots only occur after the hot-spot τ. This ensures that the simulated hot-spot is temporal consistent. The second indicator function $\mathbb{1}\{i\in S_h\}$ shows that only those entries whose location index belongs set $S_h$ are assigned as local hot-spots. This ensures that the simulated hot-spot is sparse. Here we assume the change happens at $\tau =200$ and the hot-spots index set $S_h=\{3,15,16,19,20,23,31,35,42,48,54,66,67,70,71,72,74,82,86,92,105,118,121,122,$ $125,133,137,140,144,151\}$. The hot-spots only account for around $20\mathrm{\%}$, so it is sparse. Parameter $\delta \in \mathbb{R}$ denotes the change magnitude. In our simulation studies, two change magnitudes are considered, one is $\delta /\sigma =1$ (small shift) and the other is $\delta /\sigma =5$ (large shift). Here we follow the existing research [see, 6,34] to set the variance of the white noise as ${0.1}^2$. Note that the white noise standard deviation $\sigma =0.1$ might seem to be small, but we want to emphasize that the σ value itself is not crucial here, and the signal-to-noise-ratio (SNR), i.e. $\delta /\sigma$, is more fundamental.

Here is the detailed implementation of our proposed SSD-Tensor method. For the selection of basis, we use the the same bases as Section 3.3. For the penalty parameters $({\lambda }_1,{\lambda }_2)\in \mathrm{\Gamma }$, we set $\mathrm{\Gamma }=\{({\lambda }_1,{\lambda }_2):{\lambda }_1\in \{{10}^{-4},{10}^{-3},{10}^{-2},{10}^{-1},1,10\}\mathrm{and}{\lambda }_2\in \{{10}^{-6},{10}^{-5},{10}^{-4},{10}^{-3},{10}^{-2},{10}^{-1}\}\}$. Since our proposed method is an off-line method that uses the complete data, our simulation setting on the average run length under the out-of-control status ( ${\mathrm{ARL}}_1$) is slightly different from the standard SPC literature. In standard SPC literature, ${\mathrm{ARL}}_1$ of a procedure with the stopping time N is defined as $E_{\tau }(N-\tau +1|N\ge \tau )$ when the true change occurs at a given time $\tau =1.$ While in our paper, we choose $\tau =200$ to better illustrate real-world applications. To be more specific, in each Monte Carlo run for ${\mathrm{ARL}}_1$, we simulate a complete tensor data with $n_3=250$ years and the change-time $\tau =200$ years. Next, we focus only those runs that the control chart raises an alarm at $T\ge 200$ (if T<200 it will be counted as false alarm), and then define the detection delay, or ${\mathrm{ARL}}_1$, as ${\mathbf{E}}_{\tau }(T-\tau +1|T\ge \tau )$ with the change time $\tau =200$.

5.2. Benchmark methods

In this section, we present the description and implement of benchmark methods that will be used to compare with our method.

The first benchmark method is the scan statistics method in [19], which is a Bayesian extension of Kulldorff's scan statistic. The reason for us to choose [19] is that it has large power to detect clusters and the fast runtime. In our paper, we use the a R function called scan_bayes_negbin() from the package scanstatistics. To implement this function, the population size is needed. For a fair comparison, we will not give more data to scan-stat, and simply assume that the population is 100, 000 for all states and all years. Because scan_bayes_negbin() can only handle one type of crime rate one time, we apply scan bayes_negbin() to three crime rates separately and set the probability of an outbreak as $0.02/3$. Because scan-statistics-based method does not give the clear calculation of average run length under the in-control status ( ${\mathrm{ARL}}_0$) and ${\mathrm{ARL}}_1$, so we can only use the probability of an outbreak as $0.02/3$ to define the control limit to achieve similar ${\mathrm{ARL}}_0$ with other benchmarks.

The second benchmark method is the LASSO-based method in [36]. The main idea of [36] is to integrate the multivariate Exponentially Weighted Moving Average (EWMA) charting scheme. Under the assumption that the hot-spots are sparse, the LASSO model is applied to the EWMA statistics. If the Mahalanobis distance between the expected response (the LASSO estimator) and observed values is larger than a pre-specified control limit, temporal hot-spots are detected, with non-zero entries of the LASSO estimator are declared as spatial hot-spots. For the control limits and the penalty parameters of the LASSO-based method, we use the same criterion as our proposed SSD-Tensor method.

The third benchmark is the dimension-reduction method of [5] that uses PCA to extract a set of uncorrelated new features that are linear combinations of original variables. Note that [5] fails to localize the spatial hot-spots, and it can only detect the temporal change-point when the PCA-projected Mahalanobis distance is larger than a pre-specified control limit. For this control limit, we set it by using the same criterion as our proposed SSD-Tensor method. In both our simulations and case study, we select three principle components, since they can explain more than $90\mathrm{\%}$ cumulative percentage of variance (CPV).

Finally, the fourth benchmark is the traditional T2 control chart [23] method with the control limit set using the same criterion as our proposed SSD-Tensor method. Since the T2 control chart method is a well-defined method, we skip the detailed description, and more details can be found in [23].

5.3. Performance on hot-spot detection and localization

In this section, we compare our proposed SSD-Tensor method with four benchmark methods with the focus on the performance of hot-spots detection and localization. The four benchmark methods are scan-statistics method proposed by [19] (denoted as ‘scan-stat’), LASSO-based control chart proposed by [36] (denoted as ‘ZQ-LASSO’), PCA-based control chart proposed by [5] (denoted as ‘PCA’), and the traditional Hotelling $T^2$ control chart [23] (denoted as ‘T2’). All simulation results below are based on 1000 Monte Carlo replications.

Let us first compare the performance of hot-spots detection over the time domain, i.e. when the hot-spots occur. The criterion we use to measure the performance of detection is ${\mathrm{ARL}}_1$. Because ${\mathrm{ARL}}_1$ measures the delay after the change occurs, the smaller the ${\mathrm{ARL}}_1$, the better detection performance. The results can be found in Tables 2 and 3. For our proposed SSD-Tensor, it has a small ${\mathrm{ARL}}_1$ under all scenarios, no matter there is a stable or decreasing global trend. This illustrates that our proposed SSD-Tensor method can provide a rapid alarm after the hot-spots occur, even if there are stable or unstable global trends. This good behavior is due to the ability to capture both temporal consistency and spatial sparsity of the hot-spots. For the scan-statistics method, it is hard to estimate the exact ${\mathrm{ARL}}_1$ because it focuses on the hot-spots localization, not sequential change point detection. So we will not report the ${\mathrm{ARL}}_1$ of it. For ZQ-LASSO, it successfully detects the hot-spots when the global trend is stable, but unfortunately it fails to do so when there is a decreasing global trend. The latter is not surprising because ZQ-LASSO is unable to separate the global trend and local hot-spots. For PCA and T2, both of them fail to detect the hot-spots in all scenarios within the entire $n_3=250$ (simulated) years, as their ${\mathrm{ARL}}_1=50$. The reason for the unsatisfying results of PCA and T2 is that, they are designed based on a multivariate hypothesis test on the global mean change, which cannot take into account the non-stationary global mean trend and the sparsity of the hot-spots.

Table 2.

Scenario 1 (stable global trend mean): Comparison of hot-spot detection under small and large hot-spots with four criterions: precision, recall, F-measure and ${\mathrm{ARL}}_1$.

	Large shift $\delta /\sigma =5$				Small shift $\delta /\sigma =1$
Methods	Precision	Recall	F-measure	ARL	Precision	Recall	F-measure	ARL
SSD-Tensor	0.3210	0.9898	0.6554	1.2680	0.3217	0.9890	0.6553	2.0970
	(0.0345)	(0.0893)	(0.0599)	(0.3321)	(0.0362)	(0.0946)	(0.0634)	(0.8979)
Scan-stat	0.3109	0.4664	0.3887	–	0.2242	0.3364	0.2803	–
	(0.0020)	(0.0030)	(0.0025)	(–)	(0.0301)	(0.0451)	(0.0376)	(–)
ZQ-LASSO	0.1961	1.0000	0.5980	1.0000	0.1961	1.0000	0.5980	1.9750
	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(2.1291)
PCA	–	–	–	50.0000	–	–	–	50.0000
	–	–	–	(0.0000)	–	–	–	(0.0000)
T2	–	–	–	50.0000	–	–	–	50.0000
	–	–	–	(0.0000)	–	–	–	(0.0000)

Table 3.

Scenario 2 (decreasing global trend mean): Comparison of hot-spot detection under small and large hot-spots with four criterions: precision, recall, F-measure and ${\mathrm{ARL}}_1$.

	Large shift $\delta /\sigma =5$				Small shift $\delta /\sigma =1$
Methods	Precision	Recall	F-measure	ARL	Precision	Recall	F-measure	${\mathrm{ARL}}_1$
SSD-Tensor	0.3242	0.9978	0.6610	1.3490	0.3245	0.9978	0.6612	3.4120
	(0.0184)	(0.0085)	(0.0105)	(0.4762)	(0.0188 )	(0.0085)	(0.0108)	(0.8217)
Scan-stat	0.3111	0.4666	0.3889	–	0.2567	0.3851	0.3209	–
	(0.0007)	(0.0011)	(0.0009)	(–)	(0.0307)	(0.0460)	(0.0383)	(–)
ZQ-LASSO	0.0000	0.0000	0.0000	50.0000	0.0000	0.0000	0.0000	50.0000
	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)
PCA	–	–	–	50.0000	–	–	–	50.0000
	–	–	–	(0.0000)	–	–	–	(0.0000)
T2	–	–	–	50.0000	–	–	–	50.0000
	–	–	–	(0.0000)	–	–	–	(0.0000)

We visualize the hot-spots detection results in Figure 5, which illustrates the trend of the detection delay, ${\mathrm{ARL}}_1,$ of all methods, as δ changes from 0.1 to 0.5 with the step size of 0.1. Because scan-stat does not represent the ${\mathrm{ARL}}_1$ and PCA, T2 fail to detect hot-spots in all scenarios, we only plot the ${\mathrm{ARL}}_1$ of SSD-Tensor and ZQ-LASSO. From the plot, our proposed SSD-Tensor method, compared with ZQ-LASSO, shares similar detection delays when there is a stable global trend. However, our proposed SSD-Tensor method has much smaller detection delays than ZQ-LASSO, particularly when there is a decreasing global trend mean and the magnitude of the hot-spot is small. Also, it is interesting to note that the detection delays of all methods are decreasing as the magnitude of the hot-spot is increasing, which is consistent with our intuition that it is easier to detect larger changes.

Figure 5.

${\mathrm{ARL}}_1$ plot under different magnitude δ of the hot-spot. (a) ARL₁ under stable global trend, (b) ARL₁ under decreasing global trend.

Next, let us compare the performance on hot-spots localization of these methods, i.e. localize where the hot-spots occur. To evaluate the localization performance of all the methods, we will compute the following four criteria: (1) precision, defined as the proportion of detected hot-spots that are true hot-spots; (2) recall, defined as the proportion of the hot-spots that are correctly identified; (3) F-measure, a single criterion that combines the precision and recall by calculating their harmonic mean. Moreover, we also compare the true positive rate (TPR), true negative rate (TNR), false positive rate (FPR), and false negative rate (FNR). The localization performance measuring in precision, recall, F-measure can be found in Tables 2 and 3, and the localization performance measuring in TPR, TNR, FPR, FNR can be found in Tables 4 and 5. For our proposed SSD-Tensor method, its localization performance is satisfactory no matter there is a stable or unstable global trend. For instance, when there is a decreasing global trend and $\delta =0.5$, our method has $32.42\mathrm{\%}$ precision and $99.78\mathrm{\%}$ recall, which outperforms those of scan-stat and ZQ-LASSO. The only weakness of our proposed SSD-Tensor method is that it has a relatively high FPR: this is consistent with our expectation, since we did not conduct the significance test of the positive entry in ${\hat{\mathcal{H}}}_{::t^{\ast }}$. For scan-stat, it has very similar precision as our proposed SSD-Tensor method (both are around $30\mathrm{\%}$), but its recall is much lower. This is because scan-stat tends to detect clustered hot-spots, which results in detecting fewer hot-spots and missing some true hot-spots. This might also explain why scan-stat has low TPR, but high FNR. It is worth noting that the precision/recall/F-measure might be overestimated for scan-stat: we record all the Monte Carlo runs, even if it is a false alarm, since scan-stat fails to report ${\mathrm{ARL}}_1$. For ZQ-LASSO, it has $19.61\mathrm{\%}$ precision and $100\mathrm{\%}$ recall when the global trend is stable, but it has a very high FPR. This is because ZQ-LASSO fails to detect the significance of the non-zero entries, and declares all non-zero entries as hot-spots. However, when there is a decreasing global trend, ZQ-LASSO fails to detect hot-spots, so we represent its localization performance as 0. This unsatisfactory performance is due to the inability of ZQ-LASSO to separate the global trend and local hot-spots, particularly in Scenario 2 (decreasing global trend mean). For PCA and T2, they cannot localize hot-spots, and thus we do not report the corresponding values on the precision, recall, F-measure, TPR, TFR, FPR and FNR.

Table 4.

Scenario 1 (stable global trend mean): Comparison of hot-spot detection under small and large hot-spots under four criterions: TPR, TNR, FPR, FNR.

	Large shift $\delta /\sigma =5$				Small shift $\delta /\sigma =1$
Methods	TPR	TNR	FPR	FNR	TPR	TNR	FPR	FNR
SSD-Tensor	0.9898	0.4848	0.5072	0.0022	0.9890	0.4865	0.5045	0.0020
	(0.0893)	(0.0616)	(0.0630)	(0.0085)	(0.0946)	(0.0635)	(0.0648)	(0.0080)
Scan-stat	0.4664	0.7479	0.2521	0.5336	0.3364	0.7162	0.2838	0.6636
	(0.0030)	(0.0007)	(0.0007)	(0.0003)	(0.0451)	(0.0110)	(0.0110)	(0.0451)
ZQ-LASSO	1.0000	0.0000	1.0000	0.0000	1.0000	0.0000	1.0000	0.0000
	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)

Table 5.

Scenario 2 (decreasing global trend mean): Comparison of hot-spot detection under small and large hot-spots under four criterions: TPR, TNR, FPR, FNR.

	Large shift $\delta /\sigma =5$				Small shift $\delta /\sigma =1$
Methods	TPR	TNR	FPR	FNR	TPR	TNR	FPR	FNR
SSD-Tensor	0.9978	0.4903	0.5097	0.0022	0.9978	0.4909	0.5091	0.0022
	(0.0085)	(0.0422)	(0.0422)	(0.0085)	(0.0085)	(0.0431)	(0.0431)	(0.0085)
Scan-stat	0.4666	0.7480	0.2520	0.5334	0.3851	0.7281	0.2719	0.6149
	(0.0011)	(0.0003)	(0.0003)	(0.0011)	(0.0460)	(0.0112)	(0.0112)	(0.0460)
ZQ-LASSO	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)	(0.0000)

Moreover, we also visualize the hot-spot localization results in Figure 6. In the first row, the blue states are the true hot-spots (true positive), whereas the white states are the normal states (true negative). In the second row, the red states are the detected hot-spots (true positive + false positive) by scan-stat. In the third row, the red states are the detected hot-spots by our proposed SSD-Tensor method. Different color represents how likely it is hot-spot: the darker red, the more likely it is. From Figure 6, we can see that scan-stat tends to detect clustered hot-spots. Meanwhile, there is no clear pattern for the hot-spots detected by our proposed SSD-Tensor method. We need to acknowledge that while our proposed method is able to detect most of the true hot-spots (the blue states), but there are some false alarms. We should emphasize that this kind of false alarm is reasonable on the hot-spot localization, which is related to the multiple hypothesis testing in the high-dimensional data.

Figure 6.

Hot-spots detection performance by SSD-Tensor and scan-stat in Scenario 2 (decreasing global trend mean) with large hot-spots ( $\delta =0.5$). In the first row, the blue states are the true hot-spots (true positive), whereas the white states are the normal states (true negative). In the second row, the red states are the detected hot-spots (true positive + false positive) by scan-stat. In the third row, the red states are the detected hot-spots by our proposed SSD-Tensor method. Different color represents how likely it is hot-spot: the darker red, the more likely it is. In these figures, $r_1,r_2,r_3$ represent the first, second, third category, respectively. To match the dimension of our motivating data set, we choose three categories to match the three types of crime rates in our motivating crime rate dataset, namely legacy rape rate, murder and non-negligent manslaughter, and revised rape rate.

5.4. Background fitness

In this section, we illustrate that our proposed SSD-Tensor method leads to a reasonably well estimation for the global trend mean. To do this, we compare the Squared-Root of Mean Square Error (SMSE) of the fitness of a global trend mean in Table 6. Here we only show our proposed method, since other baseline methods (scan-stat, ZQ-LASSO, PCA, and T2) cannot model the global trend mean. It is clear from Table 6 that, our proposed SSD-Tensor method performs well in terms of the background fitness, especially in Scenario 2 (decreasing global trend).

Table 6.

SMSE in two scenarios under different $\delta /\sigma$ of the hot-spot.

Methods	$\delta /\sigma =1$	$\delta /\sigma =2$	$\delta /\sigma =3$	$\delta /\sigma =4$	$\delta /\sigma =5$
	Scenario 1 (stationary global trend mean)
SSD-Tensor	0.0075	0.0076	0.0075	0.0077	0.0077
	(7.1331e $-04$)	(3.4049e $-04$)	(8.0032e $-04$)	(1.0799e $-05$)	(6.9222e $-04$)
	Scenario 2 (decreasing global trend mean)
SSD-Tensor	0.0039	0.0039	0.0039	0.0039	0.0039
	(1.2357e $-05$)	(1.2647e $-05$)	(1.1054e $-05$)	(1.1845e $-05$)	(1.2619e $-05$)

6. Case study

In this section, we apply our proposed SSD-Tensor method to detect and localize hot-spots in the crime rate dataset described in Section 2 and compare its performance with other benchmarks.

First, we compare the performance of the detection delay of the hot-spot. For all the methods, we set the control limits so that the average run length to false alarm constraint ${\mathrm{ARL}}_0=50$ via Monte Carlo simulation under the assumption that data from the first 20 years are in control. For the setting of the parameters and the selection of basis, they are the same as that in Section 5. For our proposed SSD-Tensor method, we build a CUSUM control chart utilizing the test statistic in Section 4, which is shown in Figure 7(a). From this figure, we can see that the hot-spots are detected in 2012 by our proposed SSD-Tensor method. For the benchmark methods for comparison, we also apply scan-stat [see, 19], ZQ-LASSO [see, 36], PCA [see, 5] and T2 [see, 23] to the crime rate dataset and summarize the performance of the detection of a hot-spot in Table 7. Note that the value in Table 7 is the first year that raises alarm, i.e. $\underset{t=1986,\dots ,2014}{min}\{t:W_t^{+}>L\}$. Our proposed SSD-Tensor method raises an alarm of hot-spots in year 2012, while other benchmarks fail to detect any hot-spots (we do not represent the hot-spots year of scan-stat, as it does not report the hot-spots). While nobody knows the true hot-spots of the real dataset such as the crime rate data, our numerical simulation experiences suggest that year 2012 is likely a hot-spot.

Figure 7.

(a) Hot-spot detection by SSD-Tensor. Since the CUSUM test statistics of 2012, 2013 and 2014 exceed the threshold (red dashed line), we declare that year 2012 is the first change-points. (b) Fitted global trend mean and the observed annual data points. Each point (blue circle) is an actual observed annual data in logarithm scale, which is fitted by a fitted mean curve (blue line).

Table 7.

Detection of change-point year in crime rate dataset.

Methods	SSD-Tensor	scan-stat	ZQ-LASSO	PCA	T2
Year when an alarm is raised	2012	–	None	None	None

Notes: The label ‘Year when an alarm is raised’ is first year that raises alarm, i.e. $\underset{t=1986,\dots ,2014}{min}\{t:W_t^{+}>L\}$, where $W_t^{+}$ is the CUSUM statistics defined in equation (10), and L is control limits to achieve the average run length to false alarm constraint ${\mathrm{ARL}}_0=50$ via Monte Carlo simulation under the assumption that data from the first 20 years are in control.

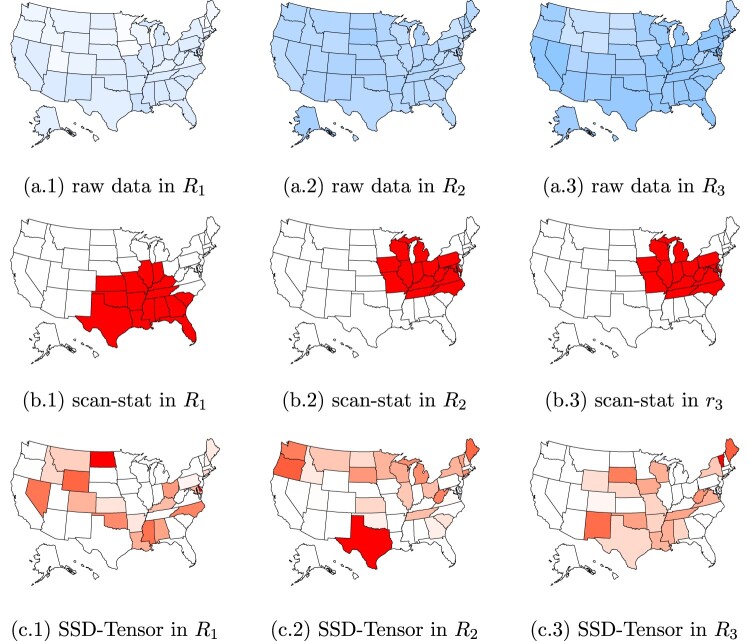
Next, after the detection of hot-spots, we need to further localize the hot-spots in the sense of determining which state and which type of crime rates may lead to the occurrence of a hot-spot. Because the baseline methods, PCA and T2, can only detect when the changes happen and ZQ-LASSO fails to detect any changes, we only show the localization of hot-spot by SSD-Tensor and scan-stat, where the results are visualized in Figure 8. We also represent the raw crime rates in 2012 in the first row of Figure 8, where the darker the blue, the high value of the crime rates. The first row (a.1)–(a.3) in this figure represents the raw data, where we can see that all three types of crime rates share a very smooth background, so it becomes difficult to find out the hot-spots directly from the raw data. The second row (b.1)–(b.3) and third (c.1)–(c.3) in this figure represents the hot-spots (TP + FP) detected by scan-stat [see, 19] and SSD-Tensor, respectively. Scan-stat tends to detect clustered hot-spots, while there is no obvious pattern of the hot-spots detected by our proposed SSD-Tensor method. Thus, as compared to scan-stat, our proposed SSD-Tensor method seems to detect sparse hot-spots, which might be useful in practice when identifying where the sudden increase of crime happens.

Figure 8.

Localization of hot-spot. (a.1)–(a.3): the raw data of the three crime rates in 2012. (b.1)–(b.2): the detected hot-spots by scan-stat. (c.1)–(c.3): the detected hot-spots by SSD-Tensor. The red color of the states means that this is a hot-spot state. And the deeper the color, the larger of the hot-spots size. In these figures, $R_1$ is the legacy rape rate, $R_2$ is the murder and non-negligent manslaughter, and $R_3$ is the revised rape rate.

Finally, we also represent the fitted global trend mean curve in Figure 7(b), where the blue line is the fitted mean curve, and the blue circle is the observed annual data points in logarithm scale. Note that the actual observed data in 2012 is a little bit higher than the fitted mean curve, which may lead to hot-spots detection in 2012. Overall, the fitness of our proposed method works very well, which can help us greatly remove the effect of the global trend.

7. Conclusion

In this paper, we propose the SSD-Tensor method for hot-spot detection and localization in multivariate spatio-temporal data, which is an important problem in many real-world applications. The main idea is to represent the multi-dimension data as tensor, and then to decompose the tensor into the global trend mean, local hot-spots and residuals. The estimation of model parameters and hot-spots is formulated as an optimization that includes the sum of residual squares with both LASSO and fused LASSO penalties, which control the sparsity and the temporal consistency of the hot-spots, respectively. Moreover, we develop an efficient algorithm to solve these optimization problems for parameter estimation by using the FISTA algorithm. In addition, we compare our proposed SSD-Tensor method with other benchmarks through Monte Carlo simulations and the case study of the crime rate dataset.

Clearly, there are many opportunities to improve the algorithms and methodologies. First, it would be interesting to investigate the confounding between the global trend and local hot-spots in future research. In our paper, we assume that they are additive, but it is possible that increasing global trend yields an increased number of hot-spots. Second, the significance test of the non-zero entries of ${\hat{\mathcal{H}}}_{::t^{\ast }}$ can be promising future research, so we can reduce the false positive rate (FPR) in localizing the hot-spots. Third, it will be useful to extend our method to the context of missing or incomplete data. We feel it is straightforward to combine our method with the imputation method when missing is (completely) at random, but it remains an open problem if missing is not at random. Fourth, in this paper, we fix the tensor basis, and it will be useful to investigate the robustness effects of different tensor bases, or better yet, to adopt some data-driven method to learn the bases from the data. Fifth, a promising research direction is to combine our proposed SSD-Tensor method with the spatially adaptive method in [31] for trend filtering. Finally, it will be interesting to derive the theoretical properties of our proposed method including the sufficient or necessary conditions under which our hot-spot estimation properties.

Appendix 1. Construction of matrix $\mathbf{D}$

The main idea to construct matrix $\mathbf{D}$ is to make

$${\lambda }_2{\Vert {\mathit{D}\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2}\Vert }_1={\lambda }_2\sum _{t=2}^{n_3}{\Vert {\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2,t}-{\mathit{\theta }}_{h,{\lambda }_1,{\lambda }_2,t-1}\Vert }_1.$$

Here is more details. Matrix $\mathbf{D}$ can be constructed as:

$$\mathbf{D}={\mathbf{D}}_1\otimes {\mathbf{D}}_2\otimes {\mathbf{D}}_3,$$

where matrix ${\mathbf{D}}_1\in {\mathbb{R}}^{n_1\times n_1},{\mathbf{D}}_2\in {\mathbb{R}}^{n_2\times n_2}$ are the identity matrix. And matrix ${\mathbf{D}}_3\in {\mathbb{R}}^{(n_3-1)\times n_3}$ is defined as

$${\mathbf{D}}_{3,i,j}=\{\begin{array}{ll}-1& \mathrm{if}i=j\\ 1& \mathrm{if}i=j-1\\ 0& \mathrm{otherwise}\end{array},$$

where ${\mathbf{D}}_{3,i,j}$ is the $(i,j)$th entry in matrix ${\mathbf{D}}_3$.

Appendix 2. Proof of fast calculation of ${\mathbf{y}}^{\ast }$ via tensor algebra

Proof.

$$\begin{array}{rl}{\mathbf{y}}^{\ast }& =[\mathbf{I}-{\mathbf{B}}_m({\mathbf{B}}_m^{\mathrm{\top }}{\mathbf{B}}_m{)}^{-1}{\mathbf{B}}_m^{\mathrm{\top }}]\mathbf{y}\\ & =\mathbf{y}-{\mathbf{B}}_m(({\mathbf{B}}_{m,1}^{\mathrm{\top }}\otimes {\mathbf{B}}_{m,2}^{\mathrm{\top }}\otimes {\mathbf{B}}_{m,3}^{\mathrm{\top }})({\mathbf{B}}_{m,1}\otimes {\mathbf{B}}_{m,2}\otimes {\mathbf{B}}_{m,3}){)}^{-1}){\mathbf{B}}_m^{\mathrm{\top }}\mathbf{y}\\ & =\mathbf{y}-{\mathbf{B}}_m(({\mathbf{B}}_{m,1}^{\mathrm{\top }}{\mathbf{B}}_{m,1})\otimes ({\mathbf{B}}_{m,2}^{\mathrm{\top }}{\mathbf{B}}_{m,2})\otimes ({\mathbf{B}}_{m,3}^{\mathrm{\top }}{\mathbf{B}}_{m,3}){)}^{-1}){\mathbf{B}}_m^{\mathrm{\top }}\mathbf{y}\\ & =\mathbf{y}-{\mathbf{B}}_m(({\mathbf{B}}_{m,1}^{\mathrm{\top }}{\mathbf{B}}_{m,1}{)}^{-1}\otimes ({\mathbf{B}}_{m,2}^{\mathrm{\top }}{\mathbf{B}}_{m,2}{)}^{-1}\otimes ({\mathbf{B}}_{m,3}^{\mathrm{\top }}{\mathbf{B}}_{m,3}{)}^{-1}){\mathbf{B}}_m^{\mathrm{\top }}\mathbf{y}\\ & =\mathbf{y}-({\mathbf{B}}_{m,1}({\mathbf{B}}_{m,1}^{\mathrm{\top }}{\mathbf{B}}_{m,1}{)}^{-1}{\mathbf{B}}_{m,1}^{\mathrm{\top }})\otimes ({\mathbf{B}}_{m,2}({\mathbf{B}}_{m,2}^{\mathrm{\top }}{\mathbf{B}}_{m,2}{)}^{-1}{\mathbf{B}}_{m,2}^{\mathrm{\top }})\\ & \otimes ({\mathbf{B}}_{m,3}({\mathbf{B}}_{m,3}^{\mathrm{\top }}{\mathbf{B}}_{m,3}{)}^{-1}{\mathbf{B}}_{m,3}^{\mathrm{\top }})\mathbf{y}\\ & =\mathbf{y}-\mathrm{vec}(\mathcal{Y}{\times }_1({\mathbf{B}}_{m,1}({\mathbf{B}}_{m,1}^{\mathrm{\top }}{\mathbf{B}}_{m,1}{)}^{-1}{\mathbf{B}}_{m,1}^{\mathrm{\top }}){\times }_2({\mathbf{B}}_{m,2}({\mathbf{B}}_{m,2}^{\mathrm{\top }}{\mathbf{B}}_{m,2}{)}^{-1}{\mathbf{B}}_{m,2}^{\mathrm{\top }})\\ & {\times }_3({\mathbf{B}}_{m,3}({\mathbf{B}}_{m,3}^{\mathrm{\top }}{\mathbf{B}}_{m,3}{)}^{-1}{\mathbf{B}}_{m,3}^{\mathrm{\top }}))\end{array}$$

Appendix 3. Review of all benchmarks

For the scan-stat-besed method, we select [19] as the representative. The goal of [19] is to find regions (a collection of location index) which has high posterior probability to be an anomalous cluster. To realize this objective, [19] compare the null hypothesis $H_0$ is no anomalous clusters with a set of alternative $H_1(S)$, each representing a cluster in some region S. The anomalous cluster $S^{\ast }$ is declared as the one with highest posterior probabilities $P(H_1(S)|D)$, i.e.

$$S^{\ast }=\arg \underset{S}{max}\frac{P(D_j|H_1(S))}{P(D_j|H_0)},$$

where dataset $D_j=\{{\mathcal{C}}_{i,j,t}{\}}_{i=1,\dots ,n_1,t=1,\dots ,n_3}$ with $C_{i,j,t}$ as the number of crime counts in index $(i,j,t)$. And ${\mathcal{C}}_{i,j,t}$ is assumed to follow Poisson distribution, i.e. ${\mathcal{C}}_{i,j,t}\sim \mathrm{Poisson}(q{\mathcal{B}}_{i,j,t})$, where ${\mathcal{B}}_{i,j,t}$ represents the (known) population of index $(i,j,t)$ and q is the (unknown) underlying crime rate. To calculate the posterior probability $P(H_1(S)|D_j)$, a hierarchical Bayesian model is used, where q are drawn from Gamma distribution. For selection of prior parameters of the Gamma distribution, please see [19] for the detailed description. For each j in $\{1,\dots ,n_2\}$, the above procedure is repeated to find anomalous regions in all type of rates.

For LASSO-based methods, we select [36] as the representative. In a given time t, [36] build a multivariate Exponentially Weighted Moving Average (EWMA) on data ${\mathbf{x}}_t=({\mathcal{Y}}_{1,1,t},\dots ,{\mathcal{Y}}_{n_1,1,t},{\mathcal{Y}}_{1,2,t},\dots ,{\mathcal{Y}}_{n_1,n_2,t}{)}^{\mathrm{\top }}$: ${\mathbf{u}}_t=\alpha {\mathbf{x}}_t+(1-\alpha ){\mathbf{u}}_{t-1},\mathrm{for}t=1,\dots ,n_3$ where ${\mathbf{u}}_0=\mathbf{0}$ and α is a weighting parameter in $(0,1]$. For each ${\mathbf{u}}_t$, a LASSO estimator $\hat{\mathit{\mu }}$ is derived from the penalized likelihood function $({\mathbf{u}}_t-\mathit{\mu }{)}^{\mathrm{\top }}{\mathbf{\Sigma }}^{-1}({\mathbf{u}}_t-\mathit{\mu })+\lambda \sum _{k=1}^{n_1{n}_2}\frac{|{\mathit{\mu }}_k|}{{\mathbf{u}}_{k,t}},$ where $\mathbf{\Sigma }$ is the covariance matrix of the normal distribution which ${\mathbf{x}}_t$ follows. Temporal change point is detected when

$$\underset{k=1,\dots ,q}{max}\frac{W_{t,{\lambda }^{\ast }}-E(W_{t,{\lambda }^{\ast }})}{\sqrt{\mathrm{Var}(W_{t,{\lambda }^{\ast })}}}>L_{\mathrm{LASSO}},$$

where $L_{\mathrm{LASSO}}>0$ is the control limit chosen to achieve a given in-control average run length. $W_{t,{\lambda }^{\ast }}=\underset{\lambda \in \{{\lambda }_1,\dots ,{\lambda }_q\}}{max}\frac{W_{t,\lambda }-E(W_{t,\lambda })}{\sqrt{\mathrm{Var}(W_{t,\lambda })}}$ and $W_{t,\lambda }=\frac{2-\alpha }{\alpha [1-(1-\lambda {)}^{2t}]}\frac{({\mathbf{u}}_t^{\mathrm{\top }}{\mathbf{\Sigma }}^{-1}\hat{\mathit{\mu }}{)}^2}{{\hat{\mathit{\mu }}}^{\mathrm{\top }}{\mathbf{\Sigma }}^{-1}\hat{\mathit{\mu }}}.$ The spatial hot-spots are localized at non-zero entries of $\hat{\mathit{\mu }}$.

For the dimension-reduction methods, we select [5] as the representative. The main tool of this method is PCA, which defines a linear relationship between the original variables of the data set, mapping them to a set of uncorrelated variables. [5] fails to localize the spatial hot-spots, and it can only realize detecting the temporal change-point when

$$({\mathbf{x}}_t-\overline{\mathbf{x}}{)}^{\mathrm{\top }}{\mathbf{P}}_k{\mathbf{\Lambda }}_k^{-1}{\mathbf{P}}_k^{\mathrm{\top }}({\mathbf{x}}_t-\overline{\mathbf{x}})>L_{\mathrm{pca}},$$

where $L_{\mathrm{pca}}$ is the control limit chosen to achieve a given in-control average run length. Vector $\overline{\mathbf{x}}=\frac{1}{n_1{n}_2}{\mathbf{X}}^{\mathrm{\top }}\mathbf{1}$ with $\mathbf{X}=(x_1,\dots ,x_{n_3})$ and $\mathbf{1}=(1,1,\dots ,1{)}_{n_1{n}_2}^{\mathrm{\top }}$. Matrix ${\mathbf{P}}_k,{\mathbf{\Lambda }}_k$ is derived from the covariance matrix of $\mathbf{X}$, i.e. $\mathbf{S}=\frac{1}{n_1{n}_2-1}(\mathbf{X}-\mathbf{1}{\overline{\mathbf{x}}}^{\mathrm{\top }}{)}^{\mathrm{\top }}(\mathbf{X}-\mathbf{1}{\overline{\mathbf{x}}}^{\mathrm{\top }})=\mathbf{P}\mathbf{\Lambda }{\mathbf{P}}^{\mathrm{\top }}$, where $\mathbf{P}$ is the loading vectors of $\mathbf{S}$ and $\mathbf{\Lambda }=\mathrm{diag}({\lambda }^1,\dots ,{\lambda }^{n_1{n}_2})$ contains the eigenvalues of $\mathbf{S}$ in descending order. The correlation of $\mathbf{P}$ and ${\mathbf{P}}_k$ is that, ${\mathbf{P}}_k$ contains only the first k columns of $\mathbf{P}$, where k is the number of components selected. The selection criterion is cumulative percentage of variance (CPV), and in our case, we select k = 3. The correlation of $\mathbf{\Lambda }$ and ${\mathbf{\Lambda }}_k$ is that, ${\mathbf{\Lambda }}_k=\mathrm{diag}({\lambda }^1,\dots ,{\lambda }^k)$. Also, we select the traditional T2 control chart [23] method as a benchmark. Because T2 control chart method is a very well-defined method, we ignore the detailed description of it in this paper, and the details of it can be found in [23].

Appendix 4. Choice of $L_{\theta },\mathbf{Q},\rho ,$ in Algorithm 1

For the choice of $L_{\theta }$, the theoretical value can set as the Lipschitz constant of $F(\mathit{\theta })=\Vert {\mathbf{y}}^{\ast }-\mathbf{X}\mathit{\theta }{\Vert }_2^2$. In practice, researchers often use the maximal eigenvalue of the Hessian matrix of $F(\mathit{\theta })$ as the fixed $L_{\theta }$ [see, 2], i.e. the maximal eigenvalue of matrix ${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}$, where the definition of matrix $\mathbf{X}$ can be found in Section 3.2. Please note that the value of $L_{\theta }$ is fixed throughout our algorithm, and guarantees the convergence of the algorithm.

For choice of $\mathbf{Q}$, a simple choice to ensure $\mathbf{Q}⪰{\mathbf{D}}^{\mathrm{\top }}\mathbf{D}$ would be $\mathbf{Q}=\delta \mathbf{I}$, where $\mathbf{I}$ is the identity matrix and $\delta \ge \Vert \mathbf{D}{\Vert }_{\mathrm{op}}^2$ with $\Vert \mathbf{D}{\Vert }_{\mathrm{op}}$ denoting the operator norm of matrix $\mathbf{D}$ [see, 35]. The definition of matrix $\mathbf{D}$ can be found in Appendix 1 in our paper. Please note that $\mathbf{Q}$ is fixed throughout our algorithm and guarantees the convergence of the algorithm.

For choice of ρ, it has be theoretically proved that, any choice of ρ will lead to the convergence of the algorithm, but a good choice of ρ would help us realize faster convergence [see, 35]. In practice, a good choice of ρ is to start with an initial value ${\rho }^{(0)}=5$ and then update it in each iteration. The updating rule from ${\rho }^{(k-1)}$ to ${\rho }^{(k)}$ is:

$${\rho }^{(k)}=\{\begin{array}{ll}\tilde{\eta }{\rho }^{(k-1)}& \mathrm{if}\Vert {\mathcal{R}}^{(k)}{\Vert }_2/\ddot{ϵ}\ge \tilde{\mu }\Vert {\mathcal{S}}^{(k+1)}{\Vert }_2/\dot{ϵ}\\ {\tilde{\eta }}^{-1}{\rho }^{(k-1)}& \mathrm{if}\Vert {\mathcal{S}}^{(k)}{\Vert }_2/\dot{ϵ}\ge \tilde{\mu }\Vert {\mathcal{R}}^{(k)}{\Vert }_2/\ddot{ϵ}.\end{array},$$

where ${\mathcal{R}}^{(k)}=\mathbf{D}{\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)}{)}^{(k)}-{\mathit{\gamma }}^{(k)}$ and ${\mathcal{S}}^{(k)}={\rho }^{(k)}{\mathbf{D}}^{\mathrm{\top }}({\mathit{\gamma }}^{(k)}-{\mathit{\gamma }}^{(k-1)}).$ The explicit format of ${\pi }_{{\lambda }_2}^0({\mathbf{v}}^{(i)}{)}^{(k)},{\mathit{\gamma }}^{(k)}$ can be found in (6). Besides, $\dot{ϵ},\ddot{ϵ}$ is the dual and primal feasibility, i.e. $\Vert {\mathcal{R}}^{(k)}{\Vert }_2\le \ddot{ϵ}$ and $\Vert {\mathcal{R}}^{(k)}{\Vert }_2\le \dot{ϵ}$. In practice, $\dot{ϵ},\ddot{ϵ}$ can be set as ${10}^{-2},{10}^{-4},{10}^{-6},{10}^{-8}$, depending on the desired precision. The parameter $\tilde{\eta },\tilde{\mu }$ are set to be 2 and 10 as suggested by [3]. More details about the setting of ρ can be found in Section 2.3 in [35] and [3].

Funding Statement

H. Yan's research was supported in part by NSF grant [grant number DMS-1830363], S. E. Holte's research was supported in part by NSF grant DMS [grant number DMS-1830372], and University of Washington / Fred Hutch Center for AIDS Research, an NIH-funded program under award number [AI027757]. Y. Zhao and Y. Mei's research was supported in part by NSF [grant numbers DMS-1830344 and DMS-2015405], and in part by the National Center for Advancing Translational Sciences of the National Institutes of Health under Award Number UL1TR000454.

Disclosure statement

No potential conflict of interest was reported by the author(s).