A bivariate inverse Weibull distribution and its application in complementary risks model

ABSTRACT

In reliability and survival analysis the inverse Weibull distribution has been used quite extensively as a heavy tailed distribution with a non-monotone hazard function. Recently a bivariate inverse Weibull (BIW) distribution has been introduced in the literature, where the marginals have inverse Weibull distributions and it has a singular component. Due to this reason this model cannot be used when there are no ties in the data. In this paper we have introduced an absolutely continuous bivariate inverse Weibull (ACBIW) distribution omitting the singular component from the BIW distribution. A natural application of this model can be seen in the analysis of dependent complementary risks data. We discuss different properties of this model and also address the inferential issues both from the classical and Bayesian approaches. In the classical approach, the maximum likelihood estimators cannot be obtained explicitly and we propose to use the expectation maximization algorithm based on the missing value principle. In the Bayesian analysis, we use a very flexible prior on the unknown model parameters and obtain the Bayes estimates and the associated credible intervals using importance sampling technique. Simulation experiments are performed to see the effectiveness of the proposed methods and two data sets have been analyzed to see how the proposed methods and the model work in practice.

1. Introduction

The Marshall–Olkin [16] bivariate exponential distribution (MOBE) is one of the popular bivariate exponential distributions. The MOBE is a singular distribution with exponentially distributed marginals. The MOBE distribution can be used quite effectively when there are ties in the data set, but if there are no ties, it cannot be used. Block and Basu [2] introduced an absolutely continuous bivariate exponential (BBBE) distribution by removing the singular component from the MOBE distribution and it can be used to analyze a data set when there are no ties. Similar to the BBBE distribution Block and Basu bivariate Weibull distribution (BBBW) also has been studied in the literature and its properties and inferential procedures have been developed, see for example Kundu and Gupta [12] and Pradhan and Kundu [19] and the references cited therein.

Although the Weibull distribution is a very flexible lifetime distribution, it cannot have non-monotone hazard function. In this respect, the inverse Weibull (IW) distribution can be used quite effectively if the data come from a distribution which has a non-monotone hazard function. It is well known that if $0<\alpha \le 1$, where α is the shape parameter of an IW distribution as defined in (1), then the mean does not exist, and if $1<\alpha \le 2$, then the mean exists but the variance does not exist. Hence, it can be used if the data come from a heavy tailed distribution also with a suitable choice of the shape parameter. Recently, Muhammed [17] and Kundu and Gupta [14] independently introduced a bivariate inverse Weibull (BIW) distribution with the marginals having the IW distributions and discussed different inferential issues of the proposed model. Although, it has been observed that the BIW is a very flexible model, it also has a singular component. Hence, the BIW distribution can be used to analyze a data set if there are ties, similar to the MOBE or Marshall Olkin bivariate Weibull distribution. The main aim of this paper is to introduce an absolutely continuous bivariate inverse Weibull (ACBIW) distribution and use it as a dependent complementary risks model.

In a reliability or in a survival analysis, very often experimental units are exposed to more than one causes of failure and one needs to analyze the effect of one cause in presence of the other causes. In this case one observes the failure time along with the cause of failure. In the statistical literature it is popularly known as the competing risk problem. In a competing risk scenario the failure time T can be written as $T=min(X_1,X_2,\dots ,X_m)$ where $X_i$ denotes the latent failure time due to the i-th risk factor for $i=1,2,\dots ,m$. Here $X_i$'s cannot be observed separately, hence, called latent failure times. An extensive amount of work has been done in developing different competing risks models, analyzing their properties and providing various inferential procedures. Interested readers are referred to the book length treatment of Crowder [4]. Recently, a growing interest is on developing different dependent competing risks models, see for example Feizjavadian and Hashemi [7], Shen and Xu [20] and the references cited therein.

The duality of the competing risk model is known as the complementary risk model and it was originally introduced by Basu and Ghosh [1]. In this case the failure time T can be written as $T=max(X_1,X_2,\dots ,X_m)$, where $X_i$'s are same as defined before. Although an extensive amount of work has been done in the area of competing risks not much work been done in the area of the complementary risks, although survival or reliability data in presence of complementary risks are observed in several areas such as public health, actuarial sciences, biomedical studies, demography and in industrial reliability, see for example Louzada et al. [15] and Han [8]. It is observed that the proposed ACBIW can be used quite effectively as a dependent complementary risks model.

In this paper first we define the ACBIW distribution and obtain its marginals. We provide different properties of the proposed distribution. The distribution has four parameters and the maximum likelihood estimators (MLEs) cannot be obtained in closed form. One has to solve a four dimensional optimization problem to compute the MLEs. To avoid that we have applied the expectation maximization (EM) algorithm, and it is observed that at each ‘E’-step the corresponding ‘M’-step can be performed by solving a one dimensional optimization problem. We have further considered the Bayesian inference of the unknown parameters based on a very general Gamma-Dirichlet (GD) prior on the scale parameters and an independent log-concave prior on the shape parameter. The Bayes estimators and the associated credible intervals of the unknown parameters are obtained based on importance sampling technique. Extensive simulations have been performed to see the effectiveness of the proposed method and one bivariate data set has been analyzed to show how the model can be used in practice.

We further describe how this model can be used as a dependent complementary risks model. We modify both the EM algorithm and the Bayesian algorithm to analyze dependent complementary risks data. We have analyzed one real complementary risks data set to show how the methods can be used in practice.

The rest of the paper is arranged as follows. In Section 2 we describe the model. Different properties of the ACBIW distribution are discussed in Section 3. In Section 4 we propose the EM algorithm to compute the MLEs and in Section 5 the Bayesian procedure has been provided. Simulation experiments and the analysis of a bivariate data set are provided in Section 6. The application of the ACBIW distribution in complementary risk model is discussed in Section 7 along with a real data analysis. Finally, we conclude the paper in Section 8.

2. Model description

A random variable X is said to follow an inverse Weibull distribution with shape parameter α and scale parameter λ, denoted by $X\sim IW(\alpha ,\lambda$) if its cumulative distribution function (CDF) is of the form

$$F_{\mathrm{IW}}(x;\alpha ,\lambda )=\{\begin{array}{ll}{\mathrm{e}}^{-\lambda x^{-\alpha }}& \mathrm{if}x>0,\\ 0& \mathrm{otherwise},\end{array}$$ (1)

and the probability density function (PDF) is as follows

$$f_{\mathrm{IW}}(x;\alpha ,\lambda )=\{\begin{array}{ll}\alpha \lambda x^{-(\alpha +1)}{\mathrm{e}}^{-\lambda x^{-\alpha }}& \mathrm{if}x>0,\\ 0& \mathrm{otherwise}.\end{array}$$

The BIW can be defined as follows. Supposes $U_1,U_2,U_3$ are three independent random variables, where $U_i\sim$ IW($\alpha ,{\lambda }_i$), for i=1, 2, 3. If $Y_1=max(U_1,U_3)$ and $Y_2=max(U_2,U_3)$, then $(Y_1,Y_2)$ is said to follow a BIW distribution with parameters $\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$. The joint CDF of $(Y_1,Y_2)$ where $(Y_1,Y_2)\sim$ BIW($\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$) can be written as

$$F_{Y_1,Y_2}(y_1,y_2)=\{\begin{array}{ll}\frac{{\lambda }_1+{\lambda }_2}{{\lambda }_1+{\lambda }_2+{\lambda }_3}{F}_a(y_1,y_2)+\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2+{\lambda }_3}{F}_s(y_1,y_2)& \mathrm{if}{y}_1,y_2>0,\\ 0& \mathrm{otherwise}.\end{array}$$

Here,

$$\begin{array}{rl}{F}_s(y_1,y_2)& ={\mathrm{e}}^{({\lambda }_1+{\lambda }_2+{\lambda }_3)z^{-\alpha }}\mathrm{and}\\ F_a(y_1,y_2)& =\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-{\lambda }_1{y}_1^{-\alpha }-{\lambda }_2{y}_2^{-\alpha }-{\lambda }_3{z}^{-\alpha }}-\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)z^{-\alpha }},\end{array}$$

where $z=min(y_1,y_2)$.

Therefore $F_{Y_1,Y_2}(\cdot ,\cdot )$ consists of $F_s(\cdot )$ and $F_a(\cdot )$ where $F_s(\cdot )$ is the singular part and $F_a(\cdot )$ is the absolute continuous part. The joint PDF of $(Y_1,Y_2)$ can be written as

$$f_{Y_1,Y_2}(y_1,y_2)=\{\begin{array}{ll}\frac{{\lambda }_1+{\lambda }_2}{{\lambda }_1+{\lambda }_2+{\lambda }_3}{f}_a(y_1,y_2)+\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2+{\lambda }_3}{f}_s(z)& \mathrm{if}{y}_1,y_2>0,\\ 0& \mathrm{otherwise},\end{array}$$

where,

$$f_a(y_1,y_2)=\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}\{\begin{array}{ll}{f}_{\mathrm{IW}}(y_1;\alpha ,{\lambda }_1+{\lambda }_3)f_{IW}(y_2,\alpha ,{\lambda }_2)& \mathrm{if}0<y_1<y_2,\\ f_{\mathrm{IW}}(y_1;\alpha ,{\lambda }_1)f_{IW}(y_2,\alpha ,{\lambda }_2+{\lambda }_3)& \mathrm{if}0<y_2<y_1,\end{array}$$

and

$$f_s(y)=f_{\mathrm{IW}}(y;\alpha ,{\lambda }_1+{\lambda }_2+{\lambda }_3).$$

The ACBIW distribution can be obtained by omitting the singular part of the BIW distribution and it can be defined as follows. $(X_1,X_2)$ is said to follow a ACBIW($\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$), if the joint CDF is of the form

$$F_{\mathrm{ACBIW}}(x_1,x_2)=\{\begin{array}{ll}\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-{\lambda }_1{x}_1^{-\alpha }-{\lambda }_2{x}_2^{-\alpha }-{\lambda }_3{u}^{-\alpha }}-\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)u^{-\alpha }}& \mathrm{if}{x}_1,x_2>0\\ 0& \mathrm{otherwise},\end{array}$$ (2)

where, $u=min(x_1,x_2)$.

Therefore, the joint PDF can be written as

$$f_{\mathrm{ACBIW}}(x_1,x_2)=\{\begin{array}{lll}\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{f}_{\mathrm{IW}}(x_1;\alpha ,{\lambda }_1+{\lambda }_3)f_{IW}(x_2,\alpha ,{\lambda }_2)& \mathrm{if}0<x_1<x_2,\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{f}_{IW}(x_1;\alpha ,{\lambda }_1)f_{IW}(x_2,\alpha ,{\lambda }_2+{\lambda }_3)& \mathrm{if}0<x_2<x_1,\\ 0& \mathrm{otherwise}.\end{array}$$ (3)

Note that ACBIW has been obtained by removing the singular part from a BIW distribution, and then normalizing it to make a proper distribution function. The main advantage of the ACBIW distribution is that it is an absolutely continuous distribution with respect to two dimensional Lebesgue measure, and it can be used quite effectively to analyze bivariate lifetime data when there are no ties.

The following result provides the shape of the joint PDF of ACBIW distribution.

Theorem 2.1

Let $(X_1,X_2)\sim$ ACBIW($\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$). Then

1. If ${\lambda }_1={\lambda }_2$, then $f_{\mathrm{ACBIW}}(x_1,x_2)$ is continuous for $0<x_1,x_2<\mathrm{\infty }$. Moreover, $f_{\mathrm{ACBIW}}(x_1,x_2)$ is unimodal and the mode is at $(x_m,x_m),$ where $x_m=\{\alpha (2{\lambda }_1+{\lambda }_3)/(2(\alpha +1)){\}}^{1/\alpha }$

2. If ${\lambda }_1+{\lambda }_3<{\lambda }_2$, then $f_{\mathrm{ACBIW}}(x_1,x_2)$ is not continuous at $x_1=x_2$. Further, $f_{\mathrm{ACBIW}}(x_1,x_2)$ is unimodal and the mode is at $(x_{1m},x_{2m})$, where $x_{1m}=\{\alpha ({\lambda }_1+{\lambda }_3)/(\alpha +1)){\}}^{1/\alpha }$ and $x_{2m}=\{\alpha {\lambda }_2/(\alpha +1){\}}^{1/\alpha }$.

3. If ${\lambda }_2+{\lambda }_3<{\lambda }_1,$ then $f_{\mathrm{ACBIW}}(x_1,x_2)$ is not continuous at $x_1=x_2$. Further, $f_{\mathrm{ACBIW}}(x_1,x_2)$ is unimodal and the mode is at $(x_{1m},x_{2m})$, where $x_{1m}=\{\alpha {\lambda }_1/(\alpha +1){\}}^{1/\alpha }$ and $x_{2m}=\{\alpha ({\lambda }_2+{\lambda }_3)/(\alpha +1)){\}}^{1/\alpha }$ and.

Proof.

It can be easily obtained, see for example Kundu and Gupta [14].

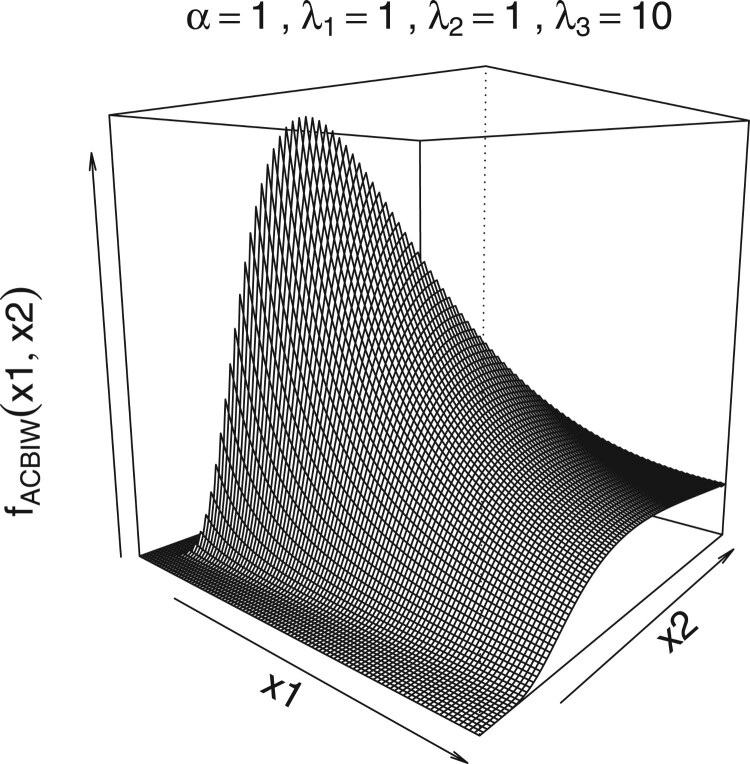
From Theorem 2.1, it is observed that the joint PDF of a ACBIW is unimodal and it can take various shapes. We have provided the surface plots of the joint PDFs of a ACBIW distribution for different parameter values in Figures 1–5. It is observed that it can be heavy tailed also. From the derivation of the ACBIW it is evident that if ($Y_1,Y_2$) ∼ BIW($\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$) and

$$(X_1,X_2)\stackrel{d}{=}(Y_1,Y_2)|Y_1\ne Y_2,$$

then $(X_1,X_2)\sim$ ACBIW$(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)$. Here, $\stackrel{d}{=}$ means equal in distribution. Therefore, the following algorithm can be applied to generate a random sample from the ACBIW distribution.

Figure 2.

Surface plot of the joint PDF of ACBIW distribution.

Figure 3.

Surface plot of the joint PDF of ACBIW distribution.

Figure 4.

Surface plot of the joint PDF of ACBIW distribution.

Figure 1.

Surface plot of the joint PDF of ACBIW distribution.

Figure 5.

Surface plot of the joint PDF of ACBIW distribution.

Algorithm 1

1. Generate $U_1,U_2,U_2$ independently where $U_i\sim$ IW($\alpha ,{\lambda }_i$) for i=1, 2, 3.

2. If $U_3>U_1$ and $U_3>U_2$ go back to Step 1, otherwise set $X_1$=max$(U_1,U_3)$ and $X_2$=max$(U_2,U_3)$.

3. Different properties of the marginals

In this section we provide different properties of the marginals of the ACBIW distribution. The following result gives the marginal distributions of a ACBIW distribution.

Theorem 3.1

If $(X_1,X_2)\sim \mathrm{ACBIW}(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3),$ then the marginal PDFs of $X_1$ and $X_2$ are

$$f_{X_1}(x_1)=\{\begin{array}{ll}\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{f}_{IW}(x_1;\alpha ,{\lambda }_1+{\lambda }_3)-\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2}{f}_{IW}(x_1;\alpha ,{\lambda }_1+{\lambda }_2+{\lambda }_3)& \mathrm{if}{x}_1>0,\\ 0& otherwise,\end{array}$$ (4)

and

$$f_{X_2}(x_2)=\{\begin{array}{ll}\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{f}_{IW}(x_2;\alpha ,{\lambda }_2+{\lambda }_3)-\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2}{f}_{IW}(x_2;\alpha ,{\lambda }_1+{\lambda }_2+{\lambda }_3)& \mathrm{if}{x}_2>0,\\ 0& otherwise,\end{array}$$ (5)

respectively.

Proof.

The marginal PDFs can be derived from (3) using simple integration.

Therefore, the marginal distribution functions can be obtained as

$$\begin{array}{rl}{F}_{X_1}(x_1)& =\{\begin{array}{ll}\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_3)x_1^{-\alpha }}-\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)x_1^{-\alpha }}& \mathrm{if}{x}_1>0,\\ 0& \mathrm{otherwise},\end{array}\end{array}$$ (6)

$$\begin{array}{rl}{F}_{X_2}(x_2)& =\{\begin{array}{ll}\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-({\lambda }_2+{\lambda }_3)x_2^{-\alpha }}-\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)x_2^{-\alpha }}& \mathrm{if}{x}_2>0,\\ 0& \mathrm{otherwise},\end{array}\end{array}$$ (7)

Note that, the marginal distributions are the generalized mixture of the IW distributions. Therefore, k th moment of the marginals will exist only when $\alpha >k$. It is observed that the PDFs of the marginals are unimodal or a decreasing function depending on the values of α. The hazard functions of the marginals are also either unimodal or a decreasing function.

The next result provides the conditional PDFs and CDFs of the marginals of the ACBIW distribution and it will be needed in the application section.

Theorem 3.2

If $(X_1,X_2)\sim \mathrm{ACBIW}(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3),$ then the conditional PDF of $X_1|X_2=x_2$ is given by

$$f_{X_1|X_2=x_2}(x_1)=\{\begin{array}{ll}\frac{{\lambda }_2}{{\mathrm{e}}^{-{\lambda }_3{x}_2^{-\alpha }}({\lambda }_2+{\lambda }_3(1-{\mathrm{e}}^{-{\lambda }_1{x}_2^{-\alpha }}))}{f}_{IW}(x_1;\alpha ,{\lambda }_1+{\lambda }_2)& \mathrm{for}0<x_1<x_2,\frac{{\lambda }_2+{\lambda }_3}{{\lambda }_2+{\lambda }_3(1-{\mathrm{e}}^{-{\lambda }_1{x}_2^{-\alpha }})}{f}_{IW}(x_1;\alpha ,{\lambda }_1)\mathrm{for}0<x_2<x_1,\\ 0& otherwise,\end{array}$$ (8)

and the conditional PDF of $X_2|X_1=x_1$ is given by

$$f_{X_2|X_1=x_1}(x_2)=\{\begin{array}{lll}\frac{{\lambda }_1+{\lambda }_3}{{\lambda }_1+{\lambda }_3(1-{\mathrm{e}}^{{\lambda }_2{x}_1^{-\alpha }})}{f}_{IW}(x_2;\alpha ,{\lambda }_2)& \mathrm{for}0<x_1<x_2,\frac{{\lambda }_1}{{\mathrm{e}}^{-{\lambda }_3{x}_1^{-\alpha }}({\lambda }_1+{\lambda }_3(1-{\mathrm{e}}^{-{\lambda }_2{x}_1^{-\alpha }}))}{f}_{IW}(x_2;\alpha ,{\lambda }_2+{\lambda }_3)& \mathrm{for}0<x_2<x_1,\\ 0& otherwise.\end{array}$$ (9)

Proof.

The results can be derived using (3), (4) and (5).

Some of the following properties will be useful for data analysis purposes and they will be used in Section 6.

Theorem 3.3

If $(X_1,X_2)\sim \mathrm{ACBIW}(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3),$ then

1. $P(X_1<X_2)={\lambda }_2/({\lambda }_1+{\lambda }_2),$

2. $max(X_1,X_2)\sim \mathrm{IW}(\alpha ,{\lambda }_1+{\lambda }_2+{\lambda }_3),$

3. $X_1|X_1>X_2\sim \mathrm{IW}(\alpha ,{\lambda }_1+{\lambda }_2+{\lambda }_3),$

4. $X_2|X_2>X_1\sim \mathrm{IW}(\alpha ,{\lambda }_1+{\lambda }_2+{\lambda }_3).$

Proof.

See in Appendix.

From the above result it is interesting to observe that, though any of the marginals are not IW variables, maximum of the two marginals follows a IW distribution. The marginal distribution of one variable provided it is greater than the other variable follows a IW distribution.

4. Maximum likelihood estimation

In this section we derive the MLEs of the unknown parameters $\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$ of a ACBIW distribution when we have a random sample of size n. The data are of the form $Data=\{(x_{11},x_{21}),\dots ,(x_{1n},x_{2n})\}$. We introduce two sets $I_1,I_2$, where $I_1=\{i:x_{1i}<x_{2i}\}$ and $I_2=\{i:x_{1i}>x_{2i}\}$; $|I_1|=n_1,|I_2|=n_2$. Based on the above data the log-likelihood function can be written as

$$\begin{array}{rl}l(\mathit{\theta }|Data)& =2n\ln \alpha +n\ln ({\lambda }_1+{\lambda }_2+{\lambda }_3)-n\ln ({\lambda }_1+{\lambda }_2)+n_1\ln ({\lambda }_1+{\lambda }_3)\\ & +n_1\ln {\lambda }_2+n_2\ln {\lambda }_1+n_2\ln ({\lambda }_2+{\lambda }_3)-(\alpha +1)\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}(\ln x_{1i}+\ln x_{2i})\\ & -({\lambda }_1+{\lambda }_3)\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{1i}^{-\alpha }-{\lambda }_2\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{2i}^{-\alpha }-{\lambda }_1\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{1i}^{-\alpha }-({\lambda }_2+{\lambda }_3)\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{2i}^{-\alpha }.\end{array}$$ (10)

Here $\mathit{\theta }=(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)$. The MLEs of the unknown parameters can be obtained by maximizing (10) with respect to the unknown parameters. Clearly, they cannot be obtained in explicit forms and they have to be obtained by solving a four dimensional optimization problem. To avoid that we propose to use the EM algorithm using the missing information principle. The basic idea behind the proposed EM algorithm is the following. Let us go back to the basic formulation of the ACBIW distributions based on $U_1,U_2$ and $U_3$. We will show that along with $(X_1,X_2)$ if we had observed the associated $U_1,U_2$ and $U_3$, then the MLEs of the unknown parameters can be obtained by solving a one dimensional optimization problem. Let us assume that along with $(X_1,X_2)$, we observe $({\delta }_1,{\delta }_2)$, where ${\delta }_1=i$ if $X_1=U_i$ and ${\delta }_2=j$ if $X_2=U_j$, for j=1, 2, 3. It is assumed that we have the complete observation as follows: $\{((x_{1i},{\delta }_{1i}),(x_{2i},{\delta }_{2i})):i=1,\dots ,n\}$. Let us use the following notations.

$$\begin{array}{rl}{I}_{312}& =\{i:x_{1i}<x_{2i},{\delta }_{1i}=1,{\delta }_{2i}=2\}\\ I_{132}& =\{i:x_{1i}<x_{2i},{\delta }_{1i}=3,{\delta }_{2i}=2\}\\ I_{321}& =\{i:x_{1i}>x_{2i},{\delta }_{1i}=1,{\delta }_{2i}=2\}\\ I_{231}& =\{i:x_{1i}>x_{2i},{\delta }_{1i}=1,{\delta }_{2i}=3\}.\end{array}$$

We have $I_1=I_{312}\bigcup I_{132}$ and $I_2=I_{321}\bigcup I_{231}$. In the observed data set $I_1$, ${\delta }_{2i}=2$, is known, but ${\delta }_{1i}$ is unknown. Similarly, in $I_2$, ${\delta }_{1i}=1$, is known, but ${\delta }_{2i}$ is unknown. The possible arrangement of the $U_i$'s along with the associated probabilities are provided in Table 1. It will be useful in computing the likelihood function of the complete data set.

Table 1. The possible arrangements of $U_1,U_2$ and $U_3$.

Different arrangements	Probabilities	(${\delta }_1,{\delta }_2$)	$X_1$ and $X_2$	Set
$U_3<U_1<U_2$	$\frac{{\lambda }_1{\lambda }_2}{({\lambda }_1+{\lambda }_3)({\lambda }_1+{\lambda }_2)}$	$(1,2)$	$X_1<X_2$	$I_{312}$
$U_1<U_3<U_2$	$\frac{{\lambda }_2{\lambda }_3}{({\lambda }_1+{\lambda }_3)({\lambda }_1+{\lambda }_2)}$	$(3,2)$	$X_1<X_2$	$I_{132}$
$U_3<U_2<U_1$	$\frac{{\lambda }_1{\lambda }_2}{({\lambda }_2+{\lambda }_3)({\lambda }_1+{\lambda }_2)}$	$(1,2)$	$X_1>X_2$	$I_{321}$
$U_2<U_3<U_1$	$\frac{{\lambda }_1{\lambda }_3}{({\lambda }_2+{\lambda }_3)({\lambda }_1+{\lambda }_2)}$	$(1,3)$	$X_1>X_2$	$I_{231}$

The likelihood contribution of a data point from the complete data, for each set is given below.

1. From the set $I_{312}$ the contribution is $\alpha {\lambda }_1{x}_{1i}^{-(\alpha +1)}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_3)x_{1i}^{-\alpha }}\alpha {\lambda }_2{x}_{2i}^{-(\alpha +1)}{\mathrm{e}}^{-{\lambda }_2{x}_{2i}^{-\alpha }}$,

2. From the set $I_{132}$ the contribution is $\alpha {\lambda }_3{x}_{1i}^{-(\alpha +1)}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_3)x_{1i}^{-\alpha }}\alpha {\lambda }_2{x}_{2i}^{-(\alpha +1)}{\mathrm{e}}^{-{\lambda }_2{x}_{2i}^{-\alpha }}$,

3. From the set $I_{321}$ the contribution is $\alpha {\lambda }_1{\lambda }_2{x}_{1i}^{-(\alpha +1)}{\mathrm{e}}^{-{\lambda }_1{x}_{1i}^{-\alpha }}\alpha x_{2i}^{-(\alpha +1)}{\mathrm{e}}^{-({\lambda }_2+{\lambda }_3)x_{2i}^{-\alpha }}$,

4. From the set $I_{231}$ the contribution is $\alpha {\lambda }_1{\lambda }_3{x}_{1i}^{-(\alpha +1)}{\mathrm{e}}^{-{\lambda }_1{x}_{1i}^{-\alpha }}\alpha x_{2i}^{-(\alpha +1)}{\mathrm{e}}^{-({\lambda }_2+{\lambda }_3)x_{2i}^{-\alpha }}$.

Based on the complete data set $\mathcal{C}=\{((x_{1i},{\delta }_{1i}),(x_{2i},{\delta }_{2i})):i=1,\dots ,n\}$ the log-likelihood function can be obtained as follows.

$$\begin{array}{rl}l(\mathit{\theta }|\mathcal{C})& =\sum _{\begin{array}{c}i\in I_{312}\end{array}}(2\ln \alpha +\ln {\lambda }_1+\ln {\lambda }_2)-({\lambda }_1+{\lambda }_3)\sum _{\begin{array}{c}i\in I_{312}\end{array}}{x}_{1i}^{-\alpha }-{\lambda }_2\sum _{\begin{array}{c}i\in I_{312}\end{array}}{x}_{2i}^{-\alpha }\\ & -(\alpha +1)\sum _{\begin{array}{c}i\in I_{312}\end{array}}(\ln x_{1i}+\ln x_{2i})\\ & +\sum _{\begin{array}{c}i\in I_{132}\end{array}}(2\ln \alpha +\ln {\lambda }_2+\ln {\lambda }_3)-({\lambda }_1+{\lambda }_3)\sum _{\begin{array}{c}i\in I_{132}\end{array}}{x}_{1i}^{-\alpha }-{\lambda }_2\sum _{\begin{array}{c}i\in I_{132}\end{array}}{x}_{2i}^{-\alpha }\\ & -(\alpha +1)\sum _{\begin{array}{c}i\in I_{132}\end{array}}(\ln x_{1i}+\ln x_{2i})\\ & +\sum _{\begin{array}{c}i\in I_{321}\end{array}}(2\ln \alpha +\ln {\lambda }_1+\ln {\lambda }_2)-{\lambda }_1\sum _{\begin{array}{c}i\in I_{321}\end{array}}{x}_{1i}^{-\alpha }-({\lambda }_2+{\lambda }_3)\sum _{\begin{array}{c}i\in I_{321}\end{array}}{x}_{2i}^{-\alpha }\\ & -(\alpha +1)\sum _{\begin{array}{c}i\in I_{321}\end{array}}(\ln x_{1i}+\ln x_{2i})\\ & +\sum _{\begin{array}{c}i\in I_{231}\end{array}}(2\ln \alpha +\ln {\lambda }_1+\ln {\lambda }_3)-{\lambda }_1\sum _{\begin{array}{c}i\in I_{231}\end{array}}{x}_{1i}^{-\alpha }-({\lambda }_2+{\lambda }_3)\sum _{\begin{array}{c}i\in I_{231}\end{array}}{x}_{2i}^{-\alpha }\\ & -(\alpha +1)\sum _{\begin{array}{c}i\in I_{231}\end{array}}(\ln x_{1i}+\ln x_{2i}).\end{array}$$ (11)

It can be easily seen that for a given α, the maximization of (11) can be obtained in explicit forms in terms of ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$, and the maximization with respect to α can be obtained by solving a one dimensional optimization problem with respect to α. This is the main motivation of the proposed EM algorithm. We need the following result for developing the EM algorithm. They can be obtained from Table 1.

RESULT 4 :

$$\begin{array}{rl}P({\delta }_1=1,{\delta }_2=2|X_1<X_2)& =\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_3)}=a,P({\delta }_1=3,{\delta }_2=2|X_1<X_2)\\ & =\frac{{\lambda }_3}{({\lambda }_1+{\lambda }_3)}=1-a,\\ P({\delta }_1=1,{\delta }_2=2|X_1>X_2)& =\frac{{\lambda }_2}{({\lambda }_2+{\lambda }_3)}=b,P({\delta }_1=1,{\delta }_2=3|X_1>X_2)\\ & =\frac{{\lambda }_3}{({\lambda }_2+{\lambda }_3)}=1-b.\end{array}$$

Let us use the following notations. At the r-th stage of the EM algorithm, the estimates of α, ${\lambda }_1$, ${\lambda }_2$ ${\lambda }_3$ will be denoted by ${\alpha }^{(r)}$, ${\lambda }_1^{(r)}$, ${\lambda }_2^{(r)}$, ${\lambda }_3^{(r)}$, respectively. Similarly, ${\lambda }^{(r)}={\lambda }_1^{(r)}+{\lambda }_2^{(r)}+{\lambda }_3^{(r)}$, $a^{(r)}={\lambda }_1^{(r)}/({\lambda }_1^{(r)}+{\lambda }_3^{(r)})$ and $b(r)={\lambda }_2^{(r)}/({\lambda }_2^{(r)}+{\lambda }_3^{(r)})$ are also defined. Now, using the idea of Dinse [6], see also Kundu [10], the ‘pseudo’ log-likelihood function at the r-th stage (‘E’-step) of the EM algorithm can be written as

$$\begin{array}{rl}l(\mathit{\theta }|{\mathit{\theta }}^{(r)},Data)& =(n_1{a}^{(r)}+n_2)\ln {\lambda }_1-{\lambda }_1\sum _{i\in I_1\cup I_2}{x}_{1i}^{-\alpha }+(n_1+n_2{b}^{(r)})\ln {\lambda }_2-{\lambda }_2\sum _{i\in I_1\cup I_2}{x}_{2i}^{-\alpha }\\ & +(n_1(1-a^{(r)})+n_2(1-b^{(r)}))\ln {\lambda }_3-{\lambda }_3[\sum _{i\in I_1}{x}_{1i}^{-\alpha }+\sum _{i\in I_2}{x}_{2i}^{-\alpha }]\\ & +2n\ln \alpha -(\alpha +1)\sum _{i\in I_1\cup I_2}(\ln x_{1i}+\ln x_{2i}).\end{array}$$ (12)

The ‘M’-step can be obtained by maximizing $l(\mathit{\theta }|{\mathit{\theta }}^{(r)},Data)$ with respect to the unknown parameters. For fixed α, the function (12) is maximized at ${\lambda }_1={\lambda }_1^{(r+1)}(\alpha )$, ${\lambda }_2={\lambda }_2^{(r+1)}(\alpha )$, ${\lambda }_3={\lambda }_3^{(r+1)}(\alpha )$, where,

$$\begin{array}{rl}{\lambda }_1^{(r+1)}(\alpha )& =\frac{n_1{a}^{(r)}+n_2}{\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{1i}^{-\alpha }},{\lambda }_2^{(r+1)}(\alpha )=\frac{n_1+n_2{b}^{(r)}}{\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{2i}^{-\alpha }},{\lambda }_3^{(r+1)}(\alpha )\\ & =\frac{n_1(1-a^{(r)})+n_2(1-b^{(r)})}{\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{1i}^{-\alpha }+\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{2i}^{-\alpha }}.\end{array}$$

The corresponding ${\alpha }^{(r+1)}$ can be obtained by maximizing pseudo profile log-likelihood function $l(\alpha ,{\lambda }_1^{(r+1)}(\alpha ),{\lambda }_2^{(r+1)}(\alpha ),{\lambda }_3^{(r+1)}(\alpha )|{\mathit{\theta }}^{(r)},Data)=h^{(r)}(\alpha )$. Without the additive constant,

$$\begin{array}{rl}{h}^{(r)}(\alpha )& =-(n_1{a}^{(r)}+n_2)\ln \left(\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{1i}^{-\alpha }\right)-(n_1+n_2{b}^{(r)})\ln \left(\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{2i}^{-\alpha }\right)\\ & -(n_1(1-a^{(r)})+n_2(1-b^{(r)}))\ln (\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{1i}^{-\alpha }+\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{2i}^{-\alpha })\\ & +2n\ln \alpha -(\alpha +1)\sum _{i\in I_1\cup I_2}(\ln x_{1i}+\ln x_{2i}).\end{array}$$

The following result ensures the existence of a unique maximum of the pseudo profile log-likelihood function at every stage of the iteration.

RESULT 5 :

At the r-th stage the pseudo log-likelihood function $h^{(r)}(\alpha )$ is a unimodal function of α.

Proof.

See in Appendix.

The maximization of the pseudo log-likelihood function which is a one dimensional optimization problem can be done by the Newton Raphson or bisection method. Once ${\alpha }^{(r+1)}$ can be obtained, we can compute ${\lambda }_1^{(r+1)}={\lambda }_1^{(r+1)}({\alpha }^{(r+1)})$, ${\lambda }_2^{(r+1)}={\lambda }_2^{(r+1)}({\alpha }^{(r+1)})$ and ${\lambda }_3^{(r+1)}={\lambda }_3^{(r+1)}({\alpha }^{(r+1)})$. The process will be continued till convergence.

5. Bayesian inference

In this section we provide the Bayesian analysis of the unknown model parameters. The Bayes estimators are derived based on the squared error loss function although any other loss function also can be easily incorporated. The prior assumption and its posterior analysis are discussed below.

5.1. Prior assumption

Following the approach of Pena and Gupta [18] the following prior assumptions are made on the scale parameters. It is assumed that $\lambda ={\lambda }_1+{\lambda }_2+{\lambda }_3$ follows a gamma distribution, say GA$(a_0,b_0)$ with the density

$$f_{GA}(\lambda )=\frac{b_0^{a_0}}{\gamma a_0}{\lambda }^{a_0-1}{\mathrm{e}}^{b_0\lambda };\lambda >0,a_0,b_0>0.$$

To incorporate dependence among ${\lambda }_1,{\lambda }_2,{\lambda }_3$, it is assumed that given λ, $({\lambda }_1/\lambda ,{\lambda }_2/\lambda )$ follows a Dirichlet prior say, $D(a_1,a_2,a_3)$. Note that, a random vector $(X_1,x_2,\dots ,X_{k-1})$ is said to follow a Dirichlet distribution with parameter $a_1,a_2,\dots ,a_k,$ denoted by $(X_1,X_2,\dots ,X_{k-1})\sim D(a_1,a_2,\dots ,a_k),$ with the density of the form

$$\begin{array}{rl}& f(x_1,\dots ,x_{k-1})=\frac{1}{B(a_1,a_2,\dots ,a_k)}\prod _{i=1}^{k-1}{x}_i^{a_i-1}\times {(1-\sum _{i=1}^{k-1}{x}_i)}^{a_k-1};\\ & \mathrm{where},0<x_i<1\mathrm{\forall }i=1,\dots ,k-1,\\ & \mathrm{and}B(a_1,a_2,\dots ,a_k)=\frac{\prod _{i=1}^k\mathrm{\Gamma }(a_i)}{\mathrm{\Gamma }(a)}\mathrm{and}{a}_i>0,\mathrm{\forall }i=1,\dots ,k,a=\sum _{i=1}^k{a}_k.\end{array}$$

The joint prior of $({\lambda }_1,{\lambda }_2,{\lambda }_3)$ can be obtained as

$${\pi }_1({\lambda }_1,{\lambda }_2,{\lambda }_3)\propto {({\lambda }_1+{\lambda }_2+{\lambda }_3)}^{a_0-a_1-a_2-a_3}{\lambda }_1^{a_1-1}{\lambda }_2^{a_2-1}{\lambda }_3^{a_3-1}{\mathrm{e}}^{-b_0({\lambda }_1+{\lambda }_2+{\lambda }_3)}.$$ (13)

The joint prior with hyper parameters $a,b,a_1,a_2,a_3$ is called the Gamma-Dirichlet prior, denoted by GD($a_0,b_0,a_1,a_2,a_3$) and it is a very flexible prior, see Pena and Gupta [18] for details. It is further assumed that the shape parameter α has a log-concave prior ${\pi }_2(\alpha )$ with a positive support on $(0,\mathrm{\infty })$ and ${\pi }_2(\alpha )$ is independent of ${\pi }_1({\lambda }_1,{\lambda }_2,{\lambda }_3)$. Hence the joint prior of $\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$ is obtained as $\pi (\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)={\pi }_2(\alpha ){\pi }_1({\lambda }_1,{\lambda }_2,{\lambda }_3)$.

5.2. Posterior analysis

In this section we provide the Bayes estimators based on the squared error loss function and the associated credible intervals CRI of the unknown parameters. The joint posterior density of $\mathit{\theta }=(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)$ can be obtained as

$$\begin{array}{rl}\pi (\mathit{\theta }|Data)& \propto {\left\{\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}\right\}}^n{\lambda }_1^{n_2+a_1-1}{\lambda }_2^{n_1+a_2-1}{({\lambda }_1+{\lambda }_2)}^{n_1}{({\lambda }_2+{\lambda }_3)}^{n_3}\\ & \times {\mathrm{e}}^{-({\lambda }_1+{\lambda }_3)\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{1i}^{-\alpha }}{\mathrm{e}}^{-{\lambda }_2\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{2i}^{-\alpha }}{\mathrm{e}}^{-{\lambda }_1\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{1i}^{-\alpha }}{\mathrm{e}}^{-({\lambda }_2+{\lambda }_3)\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{2i}^{-\alpha }}\\ & \times {({\lambda }_1+{\lambda }_2+{\lambda }_3)}^{a_0-a_1-a_2-a_3}{\mathrm{e}}^{-b_0({\lambda }_1+{\lambda }_2+{\lambda }_3)}\times {\alpha }^{2n}{\pi }_2(\alpha )\\ & \times \left\{\prod _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{1i}^{-(\alpha +1)}{x}_{2i}^{-(\alpha +1)}\right\}.\end{array}$$

The Bayes estimate of any function of $\mathit{\theta }$ say $g(\mathit{\theta })$ can be obtained as

$$E(g(\mathit{\theta })|Data)={\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}g(\mathit{\theta })\pi (\mathit{\theta }|Data)\mathrm{d}\alpha \mathrm{d}{\lambda }_1\mathrm{d}{\lambda }_2\mathrm{d}{\lambda }_3,$$

provided it exists. The estimator cannot be obtained in closed form. For further development simplify the posterior density as follows.

$$\pi (\mathit{\theta }|Data)\propto h({\lambda }_1,{\lambda }_2,{\lambda }_3){\pi }_{11}^{\ast }({\lambda }_1|\alpha ,data){\pi }_{12}^{\ast }({\lambda }_2|\alpha ,data){\pi }_{13}^{\ast }({\lambda }_3|\alpha ,Data){\pi }_2^{\ast }(\alpha |data)$$

where,

$$\begin{array}{rl}{\pi }_{11}^{\ast }({\lambda }_1|\alpha ,Data)& \equiv \text{GA}(n_2+a_1,b_0+\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{1i}^{-\alpha }),\\ {\pi }_{12}^{\ast }({\lambda }_2|\alpha ,Data)& \equiv \text{GA}(n_1+a_2,b_0+\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{2i,}^{-\alpha }),\\ {\pi }_{13}^{\ast }({\lambda }_3|\alpha ,Data)& \equiv \text{GA}(n+a_3,b_0+\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{1i}^{-\alpha }+\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{2i}^{-\alpha }),\\ {\pi }_2^{\ast }(\alpha |Data)& \propto \frac{\left\{\prod _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{1i}^{-(\alpha +1)}{x}_{2i}^{-(\alpha +1)}\right\}{\alpha }^{2n}{\pi }_2(\alpha )}{\begin{array}{c}{(b_0+\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{1i}^{-\alpha })}^{n_2+a_1}{(b_0+\sum _{\begin{array}{c}i\in I_1\bigcup I_2\end{array}}{x}_{2i}^{-\alpha })}^{n_1+a_2}\\ {(b_0+\sum _{\begin{array}{c}i\in I_1\end{array}}{x}_{1i}^{-\alpha }+\sum _{\begin{array}{c}i\in I_2\end{array}}{x}_{2i}^{-\alpha })}^{n+a_3}\end{array}},\\ h({\lambda }_1,{\lambda }_2,{\lambda }_3)& ={({\lambda }_1+{\lambda }_2+{\lambda }_3)}^{n+a_0-a_1-a_2-a_3}{(1+\frac{{\lambda }_1}{{\lambda }_3})}^{n_1}{(1+\frac{{\lambda }_2}{{\lambda }_3})}^{n_2}{({\lambda }_1+{\lambda }_2)}^{-n}.\end{array}$$

As the posterior cannot be obtained in any standard form we rely on the importance sampling technique to compute the Bayes estimates and the associated credible intervals. The following result is needed for further development.

RESULT 6 :

When ${\pi }_2(\alpha )$ is log-concave, ${\pi }_2^{\ast }(\alpha |data)$ is also log-concave.

Proof.

It can be obtained similarly as in Kundu [11].

To apply the importance sampling technique, it is required to generate $\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_2$ from the posterior density. Based on the method by Devroye [5] α can be generated from the log-concave density function ${\pi }_2^{\ast }(\alpha |data)$. Here we follow the simpler method suggested in Kundu [11] to generate α from its log-concave posterior density. Once α is generated we can generate ${\lambda }_1,{\lambda }_2,{\lambda }_3$ from the respective conditional densities. The following algorithm can be used to compute the Bayes estimate and the associated credible intervals.

Algorithm 2

1. Given data, generate α from ${\pi }_2^{\ast }(\alpha |data)$.

2. For a given α, generate ${\lambda }_1,{\lambda }_2,{\lambda }_3$ from ${\pi }_{11}^{\ast }({\lambda }_1|data)$, ${\pi }_{12}^{\ast }({\lambda }_2|data)$ and ${\pi }_{13}^{\ast }({\lambda }_3|data)$, respectively.

3. Repeat the process say N times to generate $(({\alpha }_1,{\lambda }_{11},{\lambda }_{21},{\lambda }_{31}),\dots ,({\alpha }_N,{\lambda }_{1N},{\lambda }_{2N},{\lambda }_{3N}))$.

4. To compute the Bayes estimate of $g(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)$ compute $(g_1,\dots ,g_N)$ and $(h_1,\dots ,h_N)$ where $g_i=g({\alpha }_i,{\lambda }_{1i},{\lambda }_{2i},{\lambda }_{3i})$ and $h_i=h({\lambda }_{1i},{\lambda }_{2i},{\lambda }_{3i})$ for $i=1,\dots ,N.$

5. The Bayes estimate of $g(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)$ based on the squared error loss function can be computed as $\frac{\sum _{i=1}^N{h}_i{g}_i}{\sum _{j=1}^N{h}_j}=\sum _{i=1}^N{w}_i{g}_i$ where $w_i=\frac{h_i}{\sum _{j=1}^N{h}_j}$.

6. To compute a $100(1-\gamma )\mathrm{\%}$ credible interval of $g(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)$, arrange $g_i$'s in an ascending order to obtain $(g_{(1)},\dots g_{(N)})$ and record the corresponding $w_i$ as $(w_{[1]},\dots ,w_{[N]})$. Here $w_{[i]}$ is not ordered and they are assigned to the corresponding ordered $g_{(i)}$'s. A $100(1-\gamma )\mathrm{\%}$ credible interval can be obtained as $(g_{(j_1)},g_{(j_2)})$ where $j_1,j_2$ such that

   $$j_1<j_2,j_1,j_2\in \{1,\dots ,N\}\mathrm{and}\sum _{i=j_1}^{j_2}{w}_{[i]}\le 1-\gamma <\sum _{i=j_1}^{j_2+1}{w}_{[i]}.$$ (14)

6. Simulation results and data analysis

6.1. Simulation results

In this section we present the results based on the simulation experiments. The experiment is performed to check how the different methods perform for different sample sizes and for different parameter values. We consider n=20, 30, 40 for three different sets of parameter values with $\alpha =0.5,1,2$ and ${\lambda }_1=1$, ${\lambda }_2=1$, ${\lambda }_3=1$. We compute the average estimates (AE) and the corresponding mean squared errors (MSE) of the MLEs derived through EM algorithm as described in Section 4. In Tables 2–4 we provide the AEs and MSEs based on 1000 samples. In the EM algorithm we set the initial guesses as the true parameter values and stop the process until the absolute differences of the estimates from two consecutive iteration is less than ${10}^{-4}$. It may be mentioned that in our simulation experiments we have kept λ's to be constant and we have changed α. In fact we have performed some simulations with different values of λ's also, but we have obtained similar results, hence they have not been reported. The effect of change of α is more evident in the simulation experiments. All the computations are performed using R software, and they are available on request from the authors.

Table 2. AE and MSE of the MLEs and Bayes estimators for different values of n with $\alpha =0.5,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		MLE		Bayes (IP)		Bayes (NIP)
n	Parameter	AE	MSE	AE	MSE	AE	MSE
n=20	α	0.530	0.007	0.516	0.005	0.517	0.005
	${\lambda }_1$	1.162	0.418	0.956	0.095	0.914	0.115
	${\lambda }_2$	1.142	0.378	0.956	0.087	0.928	0.113
	${\lambda }_3$	0.948	0.445	1.165	0.107	1.246	0.163
n=30	α	0.520	0.004	0.507	0.003	0.507	0.003
	${\lambda }_1$	1.096	0.267	0.928	0.058	0.889	0.072
	${\lambda }_2$	1.107	0.288	0.939	0.060	0.900	0.075
	${\lambda }_3$	0.993	0.370	1.181	0.084	1.219	0.117
n=40	α	0.513	0.002	0.503	0.002	0.502	0.002
	${\lambda }_1$	1.065	0.174	0894	0.056	0.896	0.058
	${\lambda }_2$	1.069	0.186	0.846	0.060	0.889	0.063
	${\lambda }_3$	0.978	0.268	1.213	0.091	1.213	0.099
n=80	α	0.508	0.001	0.498	0.001	0.499	0.001
	${\lambda }_1$	1.044	0.098	0.888	0.032	0.874	0.036
	${\lambda }_2$	1.027	0.093	0.895	0.031	0.877	0.036
	${\lambda }_3$	0.985	0.160	1.186	0.055	1.196	0.063

Table 4. AE and MSE of the MLEs and Bayes estimators for different values of n with $\alpha =2,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		MLE		Bayes (IP)		Bayes (NIP)
n	Parameter	AE	MSE	AE	MSE	AE	MSE
n=20	α	2.940	0.097	2.049	0.073	2.053	0.086
	${\lambda }_1$	1.097	0.502	0.964	0.095	0.893	0.112
	${\lambda }_2$	1.118	0.527	0.954	0.094	0.890	0.116
	${\lambda }_3$	1.027	0.705	1.157	0.102	1.240	0.161
n=30	α	2.076	0.064	2.029	0.047	2.026	0.052
	${\lambda }_1$	1.061	0.382	0.940	0.063	0.891	0.069
	${\lambda }_2$	1.065	0.383	0.931	0.062	0.894	0.075
	${\lambda }_3$	1.645	0.594	1.181	0.086	1.221	0.115
n=40	α	2.062	0.044	2.014	0.032	2.022	0.041
	${\lambda }_1$	1.080	0.295	0.879	0.053	0.887	0.056
	${\lambda }_2$	1.084	0.302	0.849	0.058	0.877	0.061
	${\lambda }_3$	0.991	0.465	1.226	0.101	1.233	0.100
n=80	α	2.032	0.023	2.001	0.017	1.998	0.017
	${\lambda }_1$	1.025	0.161	0.899	0.032	0.877	0.035
	${\lambda }_2$	1.035	0.166	0.897	0.031	0.871	0.036
	${\lambda }_3$	0.992	0.277	1.180	0.054	1.195	0.060

Based on the observed information matrix we compute the asymptotic confidence intervals and record the average lengths (AL) and coverage percentages (CP) based on 1000 replications in Tables 5–10. In the Bayesian analysis, for the shape parameter α we choose a gamma prior which is a log-concave, i.e. ${\pi }_2(\alpha )\equiv$ GA$(c,d)$. The Bayes estimates based on the squared error loss function is computed both for an informative prior (IP) and non-informative prior (NIP). In the informative prior we choose the values of the hyper parameters equating the prior mean with the true parameter values. When $\alpha =0.5,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$ the hyper parameters are: $a_0=1,b_0=\frac{1}{3},a_1=1,a_2=1,a_3=1,c=1,d=0.5$. When $\alpha =1,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$ the hyper parameters are: $a_0=1,b_0=\frac{1}{3},a_1=1,a_2=1,a_3=1,c=1,d=1$ and for $\alpha =2,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$, the hyper-parameters are: $a_0=1,b_0=\frac{1}{3},a_1=1,a_2=1,a_3=1,c=2,d=1$. In the non-informative prior following the idea from Congdon [3] in every set of parameters, the hyper-parameters are as $a={10}^{-5},b={10}^{-5},a_1={10}^{-5},a_2={10}^{-5},a_3={10}^{-5},c={10}^{-5},d={10}^{-5}$. We have considered both the informative and non-informative priors to see the effect of priors on the performance of the Bayes estimators.

Table 6. AL and CP of $95\mathrm{\%}$ Asymptotic CI and $95\mathrm{\%}$ Symmetric CRI for different values of n with $\alpha =0.5,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		$95\mathrm{\%}$ Asymptotic CI		$95\mathrm{\%}$ Symmetric CRI (IP)		$50\mathrm{\%}$ Symmetric CRI (NIP)
n	Parameter	AL	CP	AL	CP	AL	CP
n=20	α	0.312	95.7%	0.245	91.2%	0.242	91.3%
	${\lambda }_1$	3.129	98.1%	1.275	95.1%	1.285	93.5%
	${\lambda }_2$	3.186	98.7%	1.257	95.6%	1.280	93.1%
	${\lambda }_3$	3.530	99.8%	1.382	98.6%	1.446	98.1%
n=30	α	0.246	96.1%	0.98	93.1%	0.199	91.8%
	${\lambda }_1$	2.645	98.9%	1.019	94.9%	1.038	93.2%
	${\lambda }_2$	2.650	98.7%	1.030	94.5%	1.036	93.3%
	${\lambda }_3$	2.993	99.2%	1.139	98.9%	1.172	98.4%
n=40	α	0.211	96.4%	0.169	91.4%	0.169	91.0%
	${\lambda }_1$	2.376	99.3%	0.877	94.2%	0.887	91.2%
	${\lambda }_2$	2.356	99.5%	0.894	93.5%	0.889	91.2%
	${\lambda }_3$	2.766	99.7%	0.987	97.4%	1.007	96.9%
n=80	α	0.146	95.0%	0.117	91.2%	0.118	91.1%
	${\lambda }_1$	1.812	99.3%	0.619	89.3%	0.626	88.2%
	${\lambda }_2$	1.811	98.9%	0.628	91.8%	0.623	87.8%
	${\lambda }_3$	2.187	98.9%	0.708	92.7%	0.713	91.9%

Table 7. AL and CP of $90\mathrm{\%}$ Asymptotic CI and $90\mathrm{\%}$ Symmetric CRI for different values of n with $\alpha =1,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		$90\mathrm{\%}$ Asymptotic CI		$90\mathrm{\%}$ Symmetric CRI (IP)		$90\mathrm{\%}$ Symmetric CRI (NIP)
n	Parameter	AL	CP	AL	CP	AL	CP
n=20	α	0.518	91.8%	0.412	86.4%	0.413	84.4%
	${\lambda }_1$	2.709	97.3%	1.092	92.9 %	1.101	88.8%
	${\lambda }_2$	2.701	96.1%	1.114	92.1%	1.121	88.6%
	${\lambda }_3$	3.019	99.7%	1.226	97.0%	1.287	96.3%
n=30	α	0.415	91.3%	0.329	86.9%	0.330	84.6%
	${\lambda }_1$	2.339	97.5%	0.886	90.2%	0.911	88.7%
	${\lambda }_2$	2.360	98.2%	0.898	91.2%	0.908	88.5%
	${\lambda }_3$	2.669	98.2%	1.024	86.6%	1.063	95.%
n=40	α	0.354	91.7%	0.280	85.9%	0.283	85.7%
	${\lambda }_1$	2.113	98.0%	0.772	88.0%	0.777	87.4%
	${\lambda }_2$	2.081	98.2%	0.760	85.3%	0.772	85.7%
	${\lambda }_3$	2.382	98.7%	0.911	93.4%	0.912	92.4%
n=80	α	0.246	91.1%	0.198	86.4%	0.196	84.4%
	${\lambda }_1$	1.561	97.8%	0.542	83.4%	0.549	81.4%
	${\lambda }_2$	1.559	98.1%	0.542	81.4%	0.548	80.7%
	${\lambda }_3$	1.885	99.6%	0.634	86.6%	0.647	86.0%

Table 8. AL and CP of $95\mathrm{\%}$ Asymptotic CI and $95\mathrm{\%}$ Symmetric CRI for different values of n with $\alpha =1,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		$95\mathrm{\%}$ Asymptotic CI		$95\mathrm{\%}$ Symmetric CRI (IP)		$95\mathrm{\%}$ Symmetric CRI (NIP)
n	Parameter	AL	CP	AL	CP	AL	CP
n=20	α	0.618	96.0%	0.490	92.2%	0.498	90.2%
	${\lambda }_1$	3.050	98.2%	1.276	97.4 %	1.306	94.4%
	${\lambda }_2$	3.079	98.7%	1.286	96.3 %	1.291	94.1%
	${\lambda }_3$	3.541	99.7%	1.395	99.3%	1.452	98.2%
n=30	α	0.496	96.2%	0.395	91.6%	0.395	92.8%
	${\lambda }_1$	2.702	99.2%	1.036	96.0%	1.016	94.1%
	${\lambda }_2$	2.641	98.9%	1.034	96.2%	1.027	91.3%
	${\lambda }_3$	3.007	99.1%	1.145	98.4%	1.160	97.4%
n=40	α	0.422	95.1%	0.338	93.3%	0.336	91.4%
	${\lambda }_1$	2.342	98.2%	0.889	93.4%	0.887	91.6%
	${\lambda }_2$	2.336	98.6%	0.886	93.5%	0.889	93.6%
	${\lambda }_3$	2.764	99.2%	0.991	98.1%	1.014	96.8%
n=80	α	0.294	96.2%	0.235	90.3%	0.234	92.1%
	${\lambda }_1$	1.812	99.3%	0.620	88.5%	0.620	87.4%
	${\lambda }_2$	1.811	98.9%	0.628	91.6%	0.617	87.0%
	${\lambda }_3$	2.151	99.2%	0.710	91.3%	0.721	90.2%

Table 9. AL and CP of $90\mathrm{\%}$ Asymptotic CI and $90\mathrm{\%}$ Symmetric CRI for different values of n with $\alpha =2,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		$90\mathrm{\%}$ Asymptotic CI		$90\mathrm{\%}$ Symmetric CRI (IP)		$90\mathrm{\%}$ Symmetric CRI (NIP)
		AL	CP	AL	CP	AL	CP
n=20	α	1.043	90.3%	0.815	85.7%	0.816	85.1%
	${\lambda }_1$	2.747	96.7%	1.097	91.6%	1.113	88.9%
	${\lambda }_2$	2.720	98.3%	1.104	90.6%	1.131	89.3%
	${\lambda }_3$	3.122	98.8%	1.224	96.0%	1.298	95.4%
n=30	α	0.836	90.3%	0.660	86.0%	0.662	84.9%
	${\lambda }_1$	2.314	97.2%	0.898	91.7%	0.918	89.5%
	${\lambda }_2$	2.321	97.8%	0.893	89.8%	0.913	87.8%
	${\lambda }_3$	2.636	98.6%	1.018	95.0%	1.060	94.3%
n=40	α	0.711	91.8%	0.566	87.9%	0.570	83.1%
	${\lambda }_1$	2.075	97.8%	0.767	88.3%	0.787	87.7%
	${\lambda }_2$	2.072	97.6%	0.752	87.8%	0.782	84.8%
	${\lambda }_3$	2.391	99.2%	0.911	92.7%	0.916	92.9%
n=80	α	0.492	91.0%	0.394	86.9%	0.396	84.8%
	${\lambda }_1$	1.546	96.4%	0.549	85.5%	0.545	81.6%
	${\lambda }_2$	1.539	96.1%	0.551	84.5%	0.542	81.7%
	${\lambda }_3$	1.854	98.2%	0.643	87.2%	0.645	86.8%

Table 5. AL and CP of $90\mathrm{\%}$ Asymptotic CI and $90\mathrm{\%}$ Symmetric CRI for different values of n with $\alpha =0.5,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		$90\mathrm{\%}$ Asymptotic CI		$90\mathrm{\%}$ Symmetric CRI (IP)		$90\mathrm{\%}$ Symmetric CRI (NIP)
n	Parameter	AL	CP	AL	CP	AL	CP
n=20	α	0.262	91.3%	0.202	85.2%	0.207	85.3%
	${\lambda }_1$	2.824	98.8%	1.102	92.2%	1.132	89.2%
	${\lambda }_2$	2.855	97.8%	1.109	92.0%	1.116	89.4%
	${\lambda }_3$	3.047	99.8%	1.232	96.9%	1.288	96.2%
n=30	α	0.209	91.0%	0.165	86.2%	0.168	84.2%
	${\lambda }_1$	0.428	98.9%	0.905	90.5%	0.909	89.9%
	${\lambda }_2$	2.420	98.5%	0.886	90.7%	0.903	89.4%
	${\lambda }_3$	2.642	99.0%	1.019	96.6%	1.049	94.5%
n=40	α	0.176	91.9%	0.141	85.6%	0.142	85.5%
	${\lambda }_1$	2.088	98.3%	0.780	88.3%	0.782	86.8%
	${\lambda }_2$	2.089	98.4%	0.755	85.2%	0.768	85.7%
	${\lambda }_3$	2.400	99.8%	0.917	93.0%	0.909	93.7%
n=80	α	0.122	90.4%	0.098	84.4%	0.098	83.2%
	${\lambda }_1$	1.555	98.8%	0.542	84.7%	0.548	81.8%
	${\lambda }_2$	1.556	98.6%	0.543	84.4%	0.550	83.3%
	${\lambda }_3$	1.925	99.8%	0.633	86.7%	0.651	86.4%

Table 10. AL and CP of $95\mathrm{\%}$ Asymptotic CI and $95\mathrm{\%}$ Symmetric CRI for different values of n with $\alpha =2,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		$95\mathrm{\%}$ Asymptotic CI		$95\mathrm{\%}$ Symmetric CRI (IP)		$95\mathrm{\%}$ Symmetric CRI (NIP)
n	Parameter	AL	CP	AL	CP	AL	CP
n=20	α	1.246	96.3%	0.976	92.1%	0.981	89.9%
	${\lambda }_1$	3.098	98.3%	1.269	95.8%	1.275	93.8%
	${\lambda }_2$	3.106	97.8%	1.251	94.9%	1.303	94.1%
	${\lambda }_3$	3.514	99.9%	1.371	99.1%	1.438	98.8%
n=30	α	0.998	96.4%	0.784	91.7%	0.785	90.4%
	${\lambda }_1$	2.648	98.2%	1.028	95.0 %	1.027	92.0%
	${\lambda }_2$	2.645	98.1%	1.019	94.0%	1.037	94.1%
	${\lambda }_3$	3.069	98.6%	1.129	97.7%	1.169	98.0%
n=40	α	0.841	96.3%	0.671	91.9%	0.669	90.3%
	${\lambda }_1$	2.349	98.6%	0.898	94.5%	0.881	91.3%
	${\lambda }_2$	2.357	98.8%	0.886	94.3%	0.903	92.1%
	${\lambda }_3$	2.681	99.2%	0.999	97.8%	1.009	96.2%
n=80	α	0.588	94.7%	0.467	90.7%	0.465	91.9%
	${\lambda }_1$	1.789	98.4%	0.622	89.4%	0.618	88.2%
	${\lambda }_2$	1.794	98.6%	0.614	89.4%	0.623	88.4%
	${\lambda }_3$	2.144	99.9%	0.703	92.3%	0.713	91.7%

Both for the informative and the non-informative priors we compute the AEs and the corresponding MSEs of the Bayes estimators based on 1000 replications are provided in Tables 2, 3 and 4 for different sample sizes and for different sets of parameters. In interval estimation we compute both $90\mathrm{\%}$ and 95% symmetric credible intervals and report the ALs and CPs based on 1000 replications in Tables 5–10.

Table 3. AE and MSE of the MLEs and Bayes estimators for different values of n with $\alpha =1.0,{\lambda }_1=1,{\lambda }_2=1,{\lambda }_3=1$.

		MLE		Bayes (IP)		Bayes (NIP)
n	Parameter	AE	MSE	AE	MSE	AE	MSE
n=20	α	1.060	0.024	1.030	0.021	1.030	0.021
	${\lambda }_1$	1.162	0.496	0.968	0.098	0.925	0.124
	${\lambda }_2$	1.159	0.481	0.946	0.082	0.905	0.111
	${\lambda }_3$	0.957	0.616	1.168	0.096	1.237	0.156
n=30	α	1.039	0.015	1.016	0.012	1.023	0.013
	${\lambda }_1$	1.095	0.333	0.929	0.064	0.894	0.077
	${\lambda }_2$	1.089	0.313	0.929	0.055	0.888	0.080
	${\lambda }_3$	0.998	0.503	1.166	0.076	1.239	0.126
n=40	α	1.026	0.010	1.009	0.008	0.999	0.009
	${\lambda }_1$	1.102	0.246	0.879	0.055	0.890	0.057
	${\lambda }_2$	1.076	0.225	0.856	0.058	0.877	0.064
	${\lambda }_3$	0.953	0.356	1.218	0.095	1.241	0.105
n=80	α	1.014	0.006	0.997	0.004	1.000	0.004
	${\lambda }_1$	1.043	0.138	0.890	0.031	0.878	0.035
	${\lambda }_2$	1.043	0.133	0.886	0.032	0.877	0.036
	${\lambda }_3$	0.968	0.224	1.172	0.051	1.206	0.065

From Tables 2–4, it is clear that as sample size increases the MLEs perform better in terms of average bias and the mean squared error. This result indicates the consistency of the estimators. Also the Bayes estimator of the shape parameter α is consistent estimator. Again we see that as n increases, the Bayes estimates for the scale parameters become more distant from the true values, though the MSEs decrease. This result indicates the Bayes estimators of the scale parameters converge to some values but not the true parameter values. It is also observed that the Bayes estimators based on the informative prior have lower MSEs than the other two estimators. The MLEs over estimate ${\lambda }_1,{\lambda }_2$ and under estimate ${\lambda }_3$, slightly, where as the Bayes estimators under estimate ${\lambda }_1,{\lambda }_2$ and over estimate ${\lambda }_3$.

In interval estimation for small to moderate sample sizes the symmetric credible intervals perform better than the asymptotic intervals in terms of average length and CP. As sample size increases, the CPs of the symmetric credible intervals for the scale parameters go lesser than the nominal level. The asymptotic intervals for the scale parameters perform better than the symmetric credible intervals in terms of CP for large sample.

6.2. Data analysis

In this section we analyze a real data set for illustrative purposes. The data set has been taken from Johnson et al. [9]. This is a bivariate data set ($X_1,X_2$) on 24 children where $X_1$ represents the bone mineral density in ${\mathrm{g}/\mathrm{cm}}^2$ for Dominant Ulna and $X_2$ represents the bone mineral density in $g/c{m}^2$ for Ulna bones. The data are as follows.

(0.869, 0.964), (0.602, 0.689), (0.765, 0.738), (0.761, 0.698), (0.551, 0.619), (0.753, 0.515), (0.708,0.787), (0.687 0.715), (0.844 0.656), (0.869 0.789), (0.654, 0.726), (0.692, 0.526), (0.670, 0.580), (0.823,0.773), (0.746, 0.729), (0.656, 0.506), (0.693, 0.740), (0.883, 0.785), (0.577, 0.627), (0.802, 0.769), (0.540, 0.498), (0.804, 0.779), (0.570, 0.634), (0.585, 0.640).

To check whether a IW distribution can fit the maximum of $X_1$ and $X_2,$ we perform Kolmogorov-Smirnov (K-S) goodness of fit test. The MLEs and the K-S distance between the empirical distribution and the fitted distribution along with the p value are recorded in Table 11. Based on the results in Theorem 3.3 we have fitted also ACBIW distributions both on $X_1|X_1>X_2$ and $X_2|X_2>X_1$ and perform the K-S test for both the cases. The results are also provided in Table 11. Based on the results, it is reasonable to assume that the ACBIW may be used to analyze this data set.

Table 11. Goodness of fitting of real data set.

	MLE
Case	shape parameter	scale parameter	K−S distance	p value
$\max (X_1,X_2)$	7.563	10.961	0.110	0.933
$X_1|X_1>X_2$	6.602	9.355	0.227	0.461
$X_2|X_2>X_1$	9.999	19.067	0.201	0.813

We consider the classical and the Bayes estimations of the parameters α, ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$. In the EM algorithm as the initial guesses of the parameters we consider the MLEs for $max(X_1,X_2).$ Here, in Table 11, the MLE of shape parameter is 7.563 and the MLE of the scale parameter is $\mathrm{10.961.}$ Therefore, we set ${\alpha }^{(0)}=7$ and ${\lambda }_1^{(0)}=3,{\lambda }_2^{(0)}=3,{\lambda }_3^{(0)}=3$. We start the EM algorithm with these initial guesses and continue until the absolute differences of the estimates in two consecutive iterations is less than ${10}^{-4}.$

The MLEs and the percentile bootstrap confidence intervals are recorded in Table 12. The Bayes estimates are derived for the non-informative prior based on the squared error loss function. We compute the $90\mathrm{\%}$ symmetric credible intervals for the unknown model parameters. All these results are provided in Table 12.

Table 12. Maximum likelihood estimate and Bayesian estimates for Real Data set.

Parameter	MLE	$90\mathrm{\%}$ Asymptotic CI	Bayes estimate	$90\mathrm{\%}$ symmetric CRI
α	5.133	(3.331, 6.381)	4.950	(4.745, 5.140)
${\lambda }_1$	2.142	(0.465, 3.819)	2.147	(1.209,, 3.629)
${\lambda }_2$	1.434	(0.587, 2.281)	1.409	(0.606, 2.924)
${\lambda }_3$	3.097	(1.315, 4.879)	2.971	(1.485,, 4.505)

Here we have performed the data analysis considering $(X_1,X_2)$ follows a ACBIW distribution. Now we perform K-S tests to check whether the marginal distributions of the ACBIW can fit $X_1$ and $X_2.$ The p values are $0.647$ and 0.449 for $X_1$ and $X_2$, respectively. Therefore the assumption of ACBIW on the Data set is quite reasonable.

7. Application

In this section we apply the ACBIW distribution as a dependent complementary risks model. It is assumed that n experimental units are put on a life testing experiment and each unit is susceptible to two risk factors with latent failure times $X_1$ and $X_2$. It is further assumed that $(X_1,X_2)\sim$ ACBIW($\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3$). For each experimental unit we observe $T=max(X_1,X_2)$. We define a random variable δ with ${\delta }_i=1$ if i-th failure occurs due to cause 1 and ${\delta }_i=2$ if it is due to cause 2. Therefore we observe the data $\mathcal{D}=\{(t_1,{\delta }_1),\dots ,(t_n,{\delta }_n)\}$. The problem is to estimate the unknown parameters $\mathit{\theta }=(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3)$ based on the observed data.

The likelihood function of the observation can be written as

$$L(\mathit{\theta }|\mathcal{D})={\left(\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{{\lambda }_1+{\lambda }_2}\right)}^n{\lambda }_1^{d_1}{\lambda }_2^{d_2}{\alpha }^n\prod _{i=1}^n{t}_i^{-(\alpha +1)}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)\sum _{i=1}^n{t}_i^{-\alpha }}.$$ (15)

Here $d_1$ = # $\{i:{\delta }_i=1\}$ and $d_2$ = # $\{i:{\delta }_i=2\}$. Now to compute the MLEs of the unknown parameters, we can modify the EM algorithm described in Section 4, very easily. Using the notation in Section 4, note that if ${\delta }_i=1$, then clearly $x_{1i}=t_i$ and $x_{2i}<x_{1i}$, and it is unknown. Moreover, $t_i\in I_2$. Similarly, if ${\delta }_i=2$, then clearly $x_{2i}=t_i$ and $x_{1i}<x_{2i}$, and it is unknown. Here $t_i\in I_1$. Therefore, the EM algorithm as described in Section 4, can be modified as follows. In the set $I_1$, $x_{1i}$'s are replaced by their expectations, similarly, in the set $I_2$, the missing $x_{2i}$'s are replaced by their expectations. These expectations cannot obtained in explicit forms, but they can be obtained in the integration form using Theorem 3.2 as follows:

$$\begin{array}{rl}E(X_1|X_1<X_2=t)& ={\mathrm{e}}^{({\lambda }_1+{\lambda }_3)t^{-\alpha }}({\lambda }_1+{\lambda }_3{)}^{1/\alpha }{\int }_{({\lambda }_1+{\lambda }_3)t^{-\alpha }}^{\mathrm{\infty }}{u}^{-1/\alpha }{\mathrm{e}}^{-u}\mathrm{d}u.\\ E(X_2|X_2<X_1=t)& ={\mathrm{e}}^{({\lambda }_2+{\lambda }_3)t^{-\alpha }}({\lambda }_2+{\lambda }_3{)}^{1/\alpha }{\int }_{({\lambda }_2+{\lambda }_3)t^{-\alpha }}^{\mathrm{\infty }}{u}^{-1/\alpha }{\mathrm{e}}^{-u}\mathrm{d}u.\end{array}$$

In the Bayesian analysis part, we use the same prior as in Section 6. Based on the likelihood in (15), the joint posterior density function can be written as

$$\pi (\mathit{\theta }|\mathcal{D})\propto h({\lambda }_1,{\lambda }_2,{\lambda }_3){\pi }_{11}^{\ast }({\lambda }_1|\alpha ,\mathcal{D}){\pi }_{12}^{\ast }({\lambda }_2|\alpha ,\mathcal{D}){\pi }_{13}^{\ast }({\lambda }_3|\alpha ,\mathcal{D}){\pi }_2^{\ast }(\alpha |\mathcal{D})$$ (16)

where

$$\begin{array}{rl}{\pi }_{11}^{\ast }({\lambda }_1|\alpha ,\mathcal{D})& \equiv \text{GA}(d_1+a_1,b+\sum _{i=1}^n{t}_i^{-\alpha }),\\ {\pi }_{12}^{\ast }({\lambda }_2|\alpha ,\mathcal{D})& \equiv \text{GA}(d_2+a_2,b+\sum _{i=1}^n{t}_i^{-\alpha }),\\ {\pi }_{13}^{\ast }({\lambda }_3|\alpha ,\mathcal{D})& \equiv \text{GA}(a_3+n,b+\sum _{i=1}^n{t}_i^{-\alpha }),\\ {\pi }_2^{\ast }(\alpha |\mathcal{D})& \equiv \frac{{\alpha }^n\prod _{i=1}^n{t}_i^{-(\alpha +1)}{\pi }_2(\alpha )}{{(b+\sum _{i=1}^n{t}_i^{-\alpha })}^{2n+a_1+a_2+a_3}},\\ h({\lambda }_1,{\lambda }_2,{\lambda }_3)& =\frac{{({\lambda }_1+{\lambda }_2+{\lambda }_3)}^{n+a-a_1-a_2-a_3}}{{({\lambda }_1{\lambda }_3+{\lambda }_2{\lambda }_3)}^n}.\end{array}$$

To derive the Bayes estimate of any function $g(\alpha ,{\lambda }_1,{\lambda }_2,{\lambda }_3),$ based on the squared error loss function, provided it exists, as well as associated credible intervals we follow the Algorithm 2 from Section 6.

A real data set under complementary risk is analyzed for illustrative purposes. The data set are originally taken from Han [8]. Here we see a small unmanned aerial vehicle (SUAV) is equipped with dual propulsion systems and the SUAV drops from its flying altitude only when both the propulsion systems fail. Table 13 indicates the failure time of the SUAV as well as which propulsion system fails later.

Table 13. real Data in presence of complementary risks.

Failure Time	Cause of Failure
2.365	1
3.467	2
5.386	2
7.714	2
9.578	1
9.683	2
11.416	1
11.789	1
12.039	2
14.928	1
14.938	2
15.325	2
15.781	2
16.105	1
16.362	2
17.178	2
17.366	1
17.803	1
19.578	2

We ignore the censored data as given in Han [8] and conduct the analysis based on the first n=19 units. To check whether a IW distribution can fit the failure time data (without the cause of failure) we compute the K-S distance between the empirical and the fitted distributions. The MLEs of the shape and scale parameters become 1.427 and 1.991, respectively. The K-S distance and the associated p value become 0.247 and 0.196, respectively. Therefore, based on the p value we say IW distribution can be used to analyze the SUAV failure data. We have calculated the MLEs and the Bayes estimates along with the asymptotic confidence and symmetric credible intervals. The results are presented in Table 14.

Table 14. Maximum likelihood estimate and Bayes estimate for SUAV Data in presence of complementary risks.

Parameter	MLE	$90\mathrm{\%}$ Asymptotic CI	Bayes estimate	$90\mathrm{\%}$ symmetric CRI
α	1.363	(1.119, 1.607)	1.354	(1.320, 1.546)
${\lambda }_1$	0.488	(0.325,0.651)	0.480	(0.315, 0.628)
${\lambda }_2$	0.907	(0.379, 1.435)	0.947	(0.371, 1.065)
${\lambda }_3$	0.755	(0.300, 1.210)	0.759	( 0.563, 1.470)

8. Conclusion

In this paper we have introduced a new absolutely continuous bivariate distribution by omitting the singular part of the BIW distribution introduced by Muhammed [17] and Kundu and Gupta [14]. The proposed ACBIW distribution can be used quite effectively if the marginals have heavy tailed distribution and there are no ties in the data set. We have studied different properties of the model. The MLEs of the unknown parameters cannot be obtained in explicit forms, we have provided a very effective EM algorithm to estimate unknown parameters. It is observed based on extensive simulation studies that the proposed EM algorithm works quite well in practice. We further considered the Bayesian inference of the unknown parameters based on a fairly general set of priors. We have provided a very effective method of generating samples from the joint posterior PDFs, and it can be used to compute Bayes estimates and the associated credible intervals. The model has been used as dependent complementary risks model. In this paper we have mainly concentrated on the bivariate set up, but it can be extended to the multivariate case also. Moreover, in most of the times in reliability and survival analysis, the data are censored. Here, we have considered complete sample only. It will be of interest to study the analysis of this model under different censoring schemes. More work is needed along that direction.

Appendix.

Proof of Theorem 3.3 —

(i)

$$\begin{array}{rl}P(X_1<X_2)& ={\int }_0^{\mathrm{\infty }}{\int }_0^{x_2}{f}_{ACBIW}(x_1,x_2)\mathrm{d}{x}_1{x}_2\\ & ={\int }_0^{\mathrm{\infty }}{\int }_0^{x_2}\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{({\lambda }_1+{\lambda }_2)}{f}_{IW}(x_1;\alpha ,{\lambda }_1+{\lambda }_3)f_{IW}(x_2;\alpha ,{\lambda }_2)\mathrm{d}{x}_1\mathrm{d}{x}_2\\ & =\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{({\lambda }_1+{\lambda }_2)}{\int }_0^{\mathrm{\infty }}{f}_{IW}(x_2;\alpha ,{\lambda }_2){\mathrm{e}}^{-({\lambda }_1+{\lambda }_3)x_2^{-\alpha }}\mathrm{d}{x}_2\\ & =\frac{{\lambda }_2}{{\lambda }_1+{\lambda }_2}.\end{array}$$

(ii)

$$\begin{array}{rl}P(max(X_1,X_2)<x)& =P(X_1<X_2<x)+P(X_2<X_1<x)\\ & =\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{({\lambda }_1+{\lambda }_2)}{\int }_0^x{\int }_0^{x_2}{f}_{IW}(x_1;\alpha ,{\lambda }_1+{\lambda }_3)f_{IW}(x_2;\alpha ,{\lambda }_2)\mathrm{d}{x}_1\mathrm{d}{x}_2\\ & +\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{({\lambda }_1+{\lambda }_2)}{\int }_0^x{\int }_0^{x_1}{f}_{IW}(x_1;\alpha ,{\lambda }_1)f_{IW}(x_2;\alpha ,{\lambda }_2+{\lambda }_3)\mathrm{d}{x}_2\mathrm{d}{x}_1\\ & =\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{({\lambda }_1+{\lambda }_2)}({\int }_0^x{f}_{IW}(x_2;\alpha ,{\lambda }_2)({\mathrm{e}}^{-({\lambda }_1+{\lambda }_3)x^{-\alpha }}\mathrm{d}{x}_2\\ & +{\int }_0^x{f}_{IW}(x_1;\alpha ,{\lambda }_1){\mathrm{e}}^{-({\lambda }_2+{\lambda }_3)x^{-\alpha }}\mathrm{d}{x}_1)\\ & =\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{({\lambda }_1+{\lambda }_2)}(\frac{{\lambda }_2}{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)x^{-\alpha }}\\ & +\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)x^{-\alpha }})\\ & ={\mathrm{e}}^{-({\lambda }_1+{\lambda }_2+{\lambda }_3)x^{-\alpha }}\end{array}$$

(iii) and (iv) can be proved in similar ways.

Proof of Result 5 —

First we will prove that if $y_i>0$ for $i=1,\dots ,n$, then $g(\alpha )=-\ln (\sum _{i=1}^n{y}_i^{\alpha })$ is a concave function. It mainly follows from the fact that $d^2/\mathrm{d}{\alpha }^{2}g(\alpha )<0$ due to Cauchy-Schwartz inequality. It implies that $h^{(r)}(\alpha )$ is a concave function. Now the result follows as $h^{(r)}(\alpha )\to -\mathrm{\infty }$ as $\alpha \to 0$ or $\alpha \to \mathrm{\infty }$

Funding Statement

Part of the work of the second author has been partially funded by the grant from Science and Engineering Research Board (SERB) MTR/2018/000179.

Disclosure statement

No potential conflict of interest was reported by the authors.