Zero-inflated models for adjusting varying exposures: a cautionary note on the pitfalls of using offset

Abstract

Zero-inflated count data are frequently encountered in public health and epidemiology research. Two-parts model is often used to model the excessive zeros, which are a mixture of two components: a point mass at zero and a count distribution, such as a Poisson distribution. When the rate of events per unit exposure is of interest, offset is commonly used to account for the varying extent of exposure, which is essentially a predictor whose regression coefficient is fixed at one. Such an assumption of exposure effect is, however, quite restrictive for many practical problems. Further, for zero-inflated models, offset is often only included in the count component of the model. However, the probability of excessive zero component could also be affected by the amount of ‘exposure’. We, therefore, proposed incorporating the varying exposure as a covariate rather than an offset term in both the probability of excessive zeros and conditional counts components of the zero-inflated model. A real example is used to illustrate the usage of the proposed methods, and simulation studies are conducted to assess the performance of the proposed methods for a broad variety of situations.

1. Introduction

In public health and epidemiology research, count data with a large proportion of zeros are often encountered. For example, in health services utilization study, the number of service utilization often includes a large number of zeros representing the patients with no utilization during the study period. A common feature of this type of data is that the count measure tends to have excessive zeros beyond a common count distribution that can accommodate, such as Poisson or negative binomial (NB).

To overcome the issue with excessive zeros, the so-called zero-inflated (ZI) models [19] can be specified, which are a mixture of two components: a point mass at zero and a count distribution, such as a Poisson or negative binomial distribution. An alternative modeling strategy is hurdle model [17,23], which assumes all zero data are from one ‘structural’ source with one part of the model being a binary model for modeling whether the response variable is zero or positive, and another part using a zero truncated model, such as a zero truncated Poisson or a zero truncated NB distribution for the positive data. Both types of models were rapidly embraced by a large number of areas, from population and epidemiological studies to ecological studies [7,10,11,20,22,24,25,27,34,35].

Despite the widespread application of both types of models in the literature, one question arises of how to address the effect of varying exposure (underlying population or duration at risk) in such models. For example, for geographically distributed disease count data, the number of cases in region i might be larger than that in the region j because region i had a substantially larger population at risk than the region j. As a result, a higher number of disease counts in one region compared to another does not necessarily imply subjects in this region have a higher susceptibility to this disease. Similarly, in longitudinal studies, the number of repeated events may depend on the follow-up time for the patients. Event rates can be calculated as events per unit time, which allows the observation window to vary for each unit. In these examples, exposure is respectively unit area, person–years and unit time.

In literature, a commonly used method for incorporating a population size at risk and/or the amount of exposure time is through the introduction of an offset term, i.e. the log of exposure, as an explanatory variable whose coefficient is fixed at one [1]. For example, for a Poisson log-linear model with expected mean ${\mu }_i$ and covariate ${\mathit{X}}_i$, the model can be written as $\log \left({\mu }_i\right)={\mathit{X}}_i^T\mathit{\alpha }+\log \left(E_i\right)$, where $\log \left(E_i\right)$ is referred to as an offset. This implies

$${\mu }_i={\mathrm{e}}^{{\mathit{X}}_i^T\mathit{\alpha }+\mathrm{l}\mathrm{o}\mathrm{g}\left(E_i\right)},\text{i.e.}{\mu }_i=E_i{\mathrm{e}}^{{\mathit{X}}_i^T\mathit{\alpha }}.$$ (1)

This means that the mean count ${\mu }_i$ has a proportionality constant for $E_i$ that depends on the values of the explanatory variables. However, such proportionality assumption may not be plausible. For example, for modeling the incidence of infectious disease, the heterogeneity of the underlying population may have a varying effect on the likelihood and intensity of disease transmission. As a result, the number of events in the response variable may increase non-proportionally with the population at risk. When such sophisticated exposure effects arise from applications, the assumption embedded in the offset term becomes inadequate. Hence, using offset to adjust the varying extent of exposure as a widely accepted common practice should be carefully examined and used with caution.

For zero-inflated models, offset is often incorporated only in the count component of the model ([13,20,21,32,38], for example). Hall [16] considered relaxing the assumption in offset by setting the coefficient on the logarithm of exposure as an unknown parameter in the count component to be estimated in the model-fitting procedure. However, the probability of observing excessive zeros can also be impacted by varying exposure in many situations; that is, the probability of excessive zeros is expected to decrease with increasing exposure. Baetschmann et al. [4] proposed a modified zero-inflated count model where the probability of extra zero is derived from an underlying duration model with Weibull hazard rate. However, to the best of our knowledge, no attempt has been made to extend the zero-inflated model to adjust for the extent of exposure as a covariate in both excess zeros and the count components, particularly in the context of modeling disease incidence collected over a geographical region. Further, simulation studies to explore the impact of misspecification of modeling the effect of varying exposures are limited and therefore warranted.

The overall goal of this study is to discuss the impact of misspecification of the modeling method for varying exposures for zero-inflated models. We explored two potential types of misspecification:

• The effect of varying exposure may differ from one. In the situation when the mean count is not proportional to the population at risk, imposing the offset term by constraining the effect of the population at risk as one can be very restrictive. Such a constraint may lead to a biased estimation of the parameter estimates and prediction through a biased estimation of the effect of exposure.

• Both excess zero and count components may depend on varying exposures. In literature, the zero-inflated model typically only includes the exposure as an offset in the count component of the zero-inflated model. We show that ignoring varying exposures for the binary part can lead to biased parameter estimates and can be sensitive to the degree of the effect of exposures.

The results for the hurdle models are consistent with zero-inflated models, so for the ease of presentation, we chose to focus on the zero-inflated models. The remainder of the paper is organized as follows. In Section 2, a review of zero-inflated models without and with varying extent of exposure is presented. Section 3 describes the methods for model selection and diagnosis check for zero-inflated models. To demonstrate the pitfalls of using an offset term for zero-inflated models, in Section 4, a real example of a health care utilization study is given. Simulation studies comparing the finite sample performance of the approaches for accounting for varying extent of exposure for zero-inflated models are presented in Section 5. Concluding remarks are given in Section 6.

2. Statistical models

2.1. Zero-inflated model

In a zero-inflated (ZI) model [19], zero observations have two different origins: ‘structural’ and ‘sampling’. The sampling zeros are due to the usual Poisson or negative binomial (NB) distribution, which assumes that those zero observations happened by chance.

Let $Y_i$ denote the response for the ith subject, $i=1,\dots ,n$. The zero-inflated Poisson (ZIP) model is given by:

$$Y_i\sim \left\{\begin{array}{ll}0& \text{with probability }{\pi }_i\\ \text{Poisson}\left({\mu }_i\right)& \text{with probability }1-{\pi }_i\end{array}\right.,$$ (2)

where ${\pi }_i$ denotes the probability of the observation arising from the degenerated distribution at zero and ${\mu }_i$ represents the mean of the Poisson distribution. This formulation allows for more zeros than permitted under the Poisson assumption when ${\pi }_i>0$. The probability distribution function of the ZIP model can be written as

$$P(Y_i=y_i|{\pi }_i,{\mu }_i)=\left\{\begin{array}{ll}{\pi }_i+(1-{\pi }_i){\mathrm{e}}^{-{\mu }_i}& \text{if {y\_i=0}},\\ (1-{\pi }_i)\frac{{\mathrm{e}}^{-{\mu }_i}{\mu }_i^{y_i}}{y_i!}& \text{if {y\_i>0}}\end{array}\right..$$ (3)

ZIP model can include covariates for modeling both ${\mu }_i$ and ${\pi }_i$. Generally, ${\pi }_i$ is modeled with a logistic regression and ${\mu }_i$ is modeled as a log-linear regression. The ZI model can be written as,

$$\begin{array}{rl}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)& ={\mathit{Z}}_i^T\mathrm{\text{β}}\\ \log \left({\mu }_i\right)& ={\mathit{X}}_i^T\mathit{\alpha }\end{array},$$ (4)

where $\mathrm{\text{β}}=({\mathrm{\text{β}}}_0,{\mathrm{\text{β}}}_1,\dots ,{\mathrm{\text{β}}}_{p_1}{)}^T$ is the $(p_1\times 1)$ column vector of parameters associated with the excess zeros and $\mathit{\alpha }=({\alpha }_0,{\alpha }_1,\dots ,{\alpha }_{p_2}{)}^T$ is a ( $p_2\times 1$) column vector of parameters associated with the Poisson process and ${\mathit{Z}}_{i(1\times p_2)}^T$ and ${\mathit{X}}_{i(1\times p_2)}^T$ are the vectors of covariates for the ith study subject for the excess zeros and Poisson processes, respectively. Note that the explanatory variables describing the ${\mu }_i$ do not need to be the same as those describing ${\pi }_i$. To account for the unobserved heterogeneity, one can assume the Poisson process as $\log \left({\mu }_i\right)={\mathit{X}}_i^T\mathit{\alpha }+b_i$, where $b_i$ is a random effect term, which can follow an independent $\text{Normal}(0,{\sigma }_b^2)$. In this article, we consider the common logit and log link functions for the binary and count outcomes. Other choices of link functions are possible, such as probit or complementary log-log link functions for the binary component.

The ZIP model can be regarded as a mixture of Poisson and a degenerate component with all of its mass at zero. As such, this model posits an unobserved and latent binary variable ${\delta }_i$ with ${\delta }_i=1$, $y_i=0$ and ${\delta }_i=0$, $y_i$ is a Poisson $\left({\mu }_i\right)$ variate. The marginal mean of the ZIP model can be then derived as

$$\begin{array}{r}E\left(Y_i\right)=E\left[E\right(Y_i|{\delta }_i\left)\right]=p({\delta }_i=1)E(Y_i|{\delta }_i=1)+p({\delta }_i=0)E(Y_i|{\delta }_i=0)=(1-{\pi }_i){\mu }_i.\end{array}$$ (5)

The second equality holds because ${\delta }_i=1$ implies $y_i=0$. The variance can be derived as

$$\begin{array}{rl}\mathrm{V}\mathrm{a}\mathrm{r}\left(Y_i\right)& =E\left[\mathrm{V}\mathrm{a}\mathrm{r}\right(Y_i|{\delta }_i\left)\right]+\mathrm{V}\mathrm{a}\mathrm{r}\left[E\right(Y_i|{\delta }_i\left)\right]\end{array}$$ (6)

$$\begin{array}{rl}& =\left[{\pi }_i\cdot 0+(1-{\pi }_i){\mu }_i\right]+\left\{{\pi }_i[0-(1-{\pi }_i){\mu }_i{]}^2+(1-{\pi }_i\left)\right[{\mu }_i-(1-{\pi }_i){\mu }_i{]}^2\right\}\end{array}$$ (7)

$$\begin{array}{rl}& =(1-{\pi }_i){\mu }_i[1+{\pi }_i{\mu }_i].\end{array}$$ (8)

As a result, zero-inflated model can accommodate overdispersion relative to a Poisson model, since $\mathrm{V}\mathrm{a}\mathrm{r}\left(Y_i\right)>E\left(Y_i\right)$. This also indicates that model misspecification of either the binary or Poisson component of a ZIP model can lead to biased predicted mean and variance estimations.

2.2. Zero-inflated models with varying exposures

In modeling zero-inflated count data, the population at risk and/or the amount of time of exposure are often heterogeneous among the study subjects. In this article, we refer to the population at risk and/or amount of time of exposure as ‘exposure’. The variable exposure for the positive count process is handled typically through an offset term, as is typically done in a log-linear Poisson regression. For example, let $E_i$ denote the population at risk for the disease of interest. An offset term, $\log \left(E_i\right)$ is often incorporated into the count component of a ZI model to account for variable exposure, so the model can be written as,

$$\begin{array}{rl}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)& ={\mathit{Z}}_i^T\mathrm{\text{β}}\\ \log \left({\mu }_i\right)& ={\mathit{X}}_i^T\mathit{\alpha }+\log \left(E_i\right)\end{array}.$$ (9)

This model implicitly assumes that all subjects who belong to the excessive zero component with the same covariates profiles are at the same risk of experiencing the outcome regardless of the size of the population at risk. This may not be plausible, as the probability of observing excessive zero is likely to decrease as the exposure size increases. Ignoring the differential exposure may result in biased estimates for both the binary and Poisson components of the ZIP model. A direct adaptation of the model ZIP-O ${}^c$ is to introduce an offset term in the binary component of the model as well; that is,

$$\begin{array}{rl}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)& ={\mathit{Z}}_i^T\mathrm{\text{β}}+\log \left(E_i\right)\\ \log \left({\mu }_i\right)& ={\mathit{X}}_i^T\mathit{\alpha }+\log \left(E_i\right)\end{array}.$$ (10)

Nevertheless, this model can be implausible, since zero inflation and the conditional model work in opposite directions. (i.e. a higher expected value for the zero inflation ( ${\pi }_i$) leads to a lower response, but a higher value for the conditional model ( ${\mu }_i$) leads to a higher response). Further, restricting the effect of exposure as one can be inconsistent with the true extent of association between exposure and the outcome.

Therefore, we propose modifying the ZIP model to addresses the variable exposure not only for the count component but also for the binary process by incorporating exposure as a covariate in both binary and count components of the model. The modified ZIP model can be expressed as,

$$\begin{array}{rl}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)& ={\mathit{Z}}_i^T\mathrm{\text{β}}+g_1\left(E_i\right)\\ \log \left({\mu }_i\right)& ={\mathit{X}}_i^T\mathit{\alpha }+g_2\left(E_i\right)\end{array},$$ (11)

where $g_1\left(E_i\right)$ and $g_2\left(E_i\right)$ represent the functional effects of the extent of exposure ( $E_i$) for the binary and count components of a ZIP model, respectively, which can take on any form, such as polynomials or spline functions, or can be modeled as:

$$g_1\left(E_i\right)={\xi }_1\log \left(E_i\right),g_2\left(E_i\right)={\xi }_2\log \left(E_i\right),$$ (12)

where ${\xi }_1$ and ${\xi }_2$ are the regression coefficients for the logarithm transformed $E_i$. This model relaxes the assumption made on the offset term by allowing ${\xi }_1$ and ${\xi }_2$ to deviate from one and also have opposite signs.

2.3. Statistical inference

The log-likelihood function for the proposed ZIP model as presented in Equation (11) is given by:

$$\begin{array}{rl}\log L(\mathrm{\text{β}},\mathit{\alpha })& =\sum _{i=1}^n(I(y_i=0)\log [{\pi }_i+(1-{\pi }_i\left){\mathrm{e}}^{-{\mu }_i}\right]\\ & +I(y_i>0)\left[\log (1-{\pi }_i)-{\mu }_i+y_i\log \left({\mu }_i\right)-\log (y_i!)\right]),\end{array}$$

where ${\pi }_i=\exp [{\mathit{Z}}_i^T\mathrm{\text{β}}+g_1(E_i\left)\right]/\{1+\exp [{\mathit{Z}}_i^T\mathrm{\text{β}}+g_1\left(E_i\right)\left]\right\}$ and ${\mu }_i=\exp [{\mathit{X}}_i^T\mathit{\alpha }+g_2(E_i\left)\right]$. For the model accounting for the unobserved regional variation, the marginal log likelihood function of the ZIP model with random effects can be written as,

$$\log L(\mathrm{\text{β}},\mathit{\alpha },\sigma )=\sum _{i=1}^n\log \left[{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}P(Y_i=y_i|b_i,\mathrm{\text{β}},\mathit{\alpha },\sigma )\mathrm{\Phi }\left(b_i\right)\mathrm{d}{b}_i\right],$$ (13)

where the unobserved heterogeneity is quantified by the random effect $b_i$, which is assumed to be Gaussian on the scale of the linear predictor with mean zero and standard error ${\sigma }_b$. $\mathrm{\Phi }(\cdot )$ is the standard normal density function. Lambert [19] expressed the log-likelihood in terms of latent variables ${\delta }_i$ and used the EM algorithm for maximum likelihood fitting by treating ${\delta }_i$ as missing values. For a model with random effect terms, numerical integration techniques, such as Gauss-Hermite quadrature or Markov chain Monte Carlo (MCMC) can be used. Nevertheless, those methods can be computationally intensive. Alternatively, the models can be fitted using glmmTMB R package [8], which performs maximum likelihood estimation via TMB (Template Model Builder) [18]. To maximize computational efficiency, TMB uses the Laplace approximation to integrate over random effects and automatic differentiation to estimate the first and second derivatives of the log likelihood function [18]. This package is more flexible than other packages available for estimating zero-inflated models via maximum likelihood estimation and is faster than packages that use MCMC sampling for estimation [8].

3. Model selection and diagnostic checks

To inform model selection, we use the Akaike Information Criterion (AIC) [2] and Bayesian information criteria (BIC) [28]. AIC and BIC are defined as $\mathrm{A}\mathrm{I}\mathrm{C}=D+2p$, $\mathrm{B}\mathrm{I}\mathrm{C}=D+m\log \left(n\right)$, where m is the number of parameters in the model, n is number of observations, D is the deviance defined as twice of negative log likelihood in the ZIP model. $D=\sum _{i=1}^n{d}_i$, where

$$d_i=-2\left\{\begin{array}{ll}\log \left[{\pi }_i+(1-{\pi }_i){\mathrm{e}}^{-{\mu }_i}\right]& \text{if {y\_i=0}},\\ \log \left[(1-{\pi }_i)\frac{{\mathrm{e}}^{-{\mu }_i}{\mu }_i^{y_i}}{y_i!}\right]& \text{if {y\_i>0}}\end{array}\right..$$ (14)

The smaller the values of AIC and BIC, the better a model fits the data. Examining residuals is a standard tool for assessing the adequacy of regression models. For discrete response, Pearson or deviance residuals are far from normality; graphical and quantitative inspection of these residuals provides little information for model diagnosis [14]. Hence, the adequacy of the ZIP models is examined on the basis of randomized quantile residuals (RQR), as developed by Dunn and Smyth [14]. RQR can be defined as follows. Suppose $F(y_i;{\pi }_i,{\mu }_i)$ denote the CDF for the response variable $y_i$ following ZIP distribution given the set of covariates ${\mathit{Z}}_i$ and ${\mathit{X}}_i$, for the binary and count component, respectively, where ${\pi }_i=\exp ({\mathit{Z}}_i^T\mathrm{\text{β}}+g_1(E_i\left)\right)/[1+\exp ({\mathit{Z}}_i^T\mathrm{\text{β}}+g_1\left(E_i\right)\left)\right]$ and ${\mu }_i=\exp ({\mathit{X}}_i^T\mathit{\alpha }+g_2(E_i\left)\right)$. Let $d(y_i;{\pi }_i,{\mu }_i)$ be the corresponding probability mass function of $F(y_i;{\pi }_i,{\mu }_i)$. Since F is discrete, it is then randomized into a uniform random number, which is defined as a function with a random number $u_i$ from the uniform distribution on $(0,1]$ as an additional argument,

$$F(y_i;{\hat{\pi }}_i,{\hat{\mu }}_i,u_i)=F(y_i-;{\hat{\pi }}_i,{\hat{\mu }}_i)+u_{i}d(y_i;{\hat{\pi }}_i,{\hat{\mu }}_i),$$ (15)

where $F(y_i-;{\hat{\pi }}_i,{\hat{\mu }}_i)$ is the lower limit of F at $y_i$, i.e. $\underset{y<y_i}{sup}F(y;{\hat{\pi }}_i,{\hat{\mu }}_i)$, the lower limit in the ‘gap’ of $F(\cdot ,{\hat{\pi }}_i,{\hat{\mu }}_i)$ at $y_i$. RQR for $y_i$ is the standard normal quantile corresponding to the random lower tail probability with ${\pi }_i$ and ${\mu }_i$ estimated from the sample,

$$r_i={\mathrm{\Phi }}^{-1}\left[F\right(y_i;{\hat{\pi }}_i,{\hat{\mu }}_i,u_i\left)\right],i=1,\dots ,n,$$ (16)

where ${\mathrm{\Phi }}^{-1}(\cdot )$ is the quantile function of the standard normal distribution, and $u_i$ is a random number uniformly distributed on $(0,1]$. These residuals are expected to approximately follow a standard normal distribution, if the model is correctly specified. Hence, the validity of the model can be assessed by graphing the RQRs versus the predicted response variable. If the model fits the data well, RQRs should be randomly scattered between $-3$ and 3 without a discernible pattern. The normality of the RQRs can be examined using Q-Q plots, which should lie along the straight diagonal line, if the model is correctly specified.

4. Motivating example: respiratory hospital admissions data

The adverse effect of ambient air pollution has drawn considerable attention over the past decade and has been shown to be associated with respiratory morbidity and mortality. In this motivating example, our goal is to study the relationship between nitrogen dioxide ( ${\text{NO}}_2$) and the number of hospital admissions for respiratory causes in Turin province (Italy) in 2004, while accounting for the differential size of the population at risk from the study area. The dataset records the number of observed hospitalizations for respiratory causes and population size at the municipality level as well as the average ${\text{NO}}_2$ for the same period and the same areas. The data were obtained from the data repository of the Spatial and Spatial-temporal Bayesian Models with R-INLA [6].

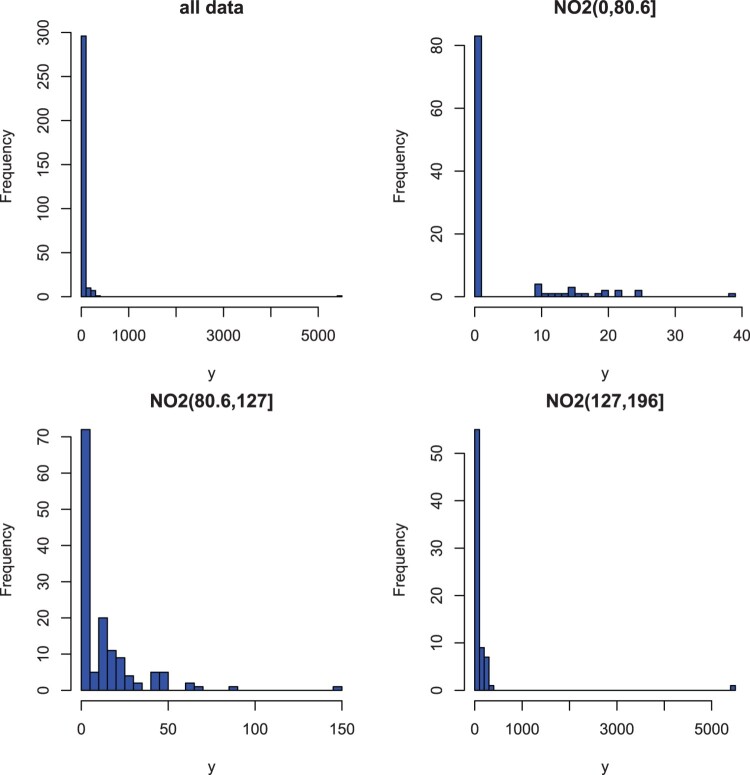
Of the 315 municipalities, 173 (54.9 $\mathrm{\%}$) had zero hospitalizations. We categorize ${\text{NO}}_2$ according to its tertiles, i.e. 80.57 and 126.54 into three levels ${\text{NO}}_2\le 80.57$ (reference category), $80.57<{\text{NO}}_2\le 126.54$ and ${\text{NO}}_2>126.54$. As shown in Figure 1, the distribution of the hospitalization counts is highly positively skewed and the distribution depends on the values of NO ${}_2$ with higher response values occurring at a higher level of NO ${}_2$. Let $Y_i$ and $n_i$ denote the number of observed hospitalizations and size of the population at risk at the ith municipality, respectively. In the context of disease mapping, the expected number is often included as an offset term, which is often expressed as the number of cases defined by an epidemiologic ‘null model’ of incidence, i.e. the product of $n_i$, the number of individuals at risk in region i, and r, a constant ‘baseline’ risk per individual defined as $r=\sum _{i=1}^n{Y}_i/\sum _{i=1}^n{n}_i$, the global observed disease rate. The following four competing models are considered, which are expressed as

$$\begin{array}{rl}& {\text{ZIP-W}}^b\left\{\begin{array}{l}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)={\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{\text{NO}}_{2i}^{\left(1\right)}+{\mathrm{\text{β}}}_2{\text{NO}}_{2i}^{\left(2\right)}+{\xi }_1\log \left(E_i\right)\\ \log \left({\mu }_i\right)={\alpha }_0+{\alpha }_1{\text{NO}}_{2i}^{\left(1\right)}+{\alpha }_2{\text{NO}}_{2i}^{\left(2\right)}+b_i+{\xi }_2\log \left(E_i\right),\end{array}\right.\end{array}$$ (17)

$$\begin{array}{rl}& {\text{ZIP-W}}^c\left\{\begin{array}{l}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)={\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{\text{NO}}_{2i}^{\left(1\right)}+{\mathrm{\text{β}}}_2{\text{NO}}_{2i}^{\left(2\right)}\\ \log \left({\mu }_i\right)={\alpha }_0+{\alpha }_1{\text{NO}}_{2i}^{\left(1\right)}+{\alpha }_2{\text{NO}}_{2i}^{\left(2\right)}+b_i+{\xi }_2\log \left(E_i\right),\end{array}\right.\end{array}$$ (18)

$$\begin{array}{rl}& {\text{ZIP-O}}^b\left\{\begin{array}{l}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)={\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{\text{NO}}_{2i}^{\left(1\right)}+{\mathrm{\text{β}}}_2{\text{NO}}_{2i}^{\left(2\right)}+\log \left(E_i\right)\\ \log \left({\mu }_i\right)={\alpha }_0+{\alpha }_1{\text{NO}}_{2i}^{\left(1\right)}+{\alpha }_2{\text{NO}}_{2i}^{\left(2\right)}+b_i+\log \left(E_i\right),\end{array}\right.\end{array}$$ (19)

$$\begin{array}{rl}& {\text{ZIP-O}}^c\left\{\begin{array}{l}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)={\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{\text{NO}}_{2i}^{\left(1\right)}+{\mathrm{\text{β}}}_2{\text{NO}}_{2i}^{\left(2\right)}\\ \log \left({\mu }_i\right)={\alpha }_0+{\alpha }_1{\text{NO}}_{2i}^{\left(1\right)}+{\alpha }_2{\text{NO}}_{2i}^{\left(2\right)}+b_i+\log \left(E_i\right),\end{array}\right.\end{array}$$ (20)

where ${\pi }_i$ is the probability of no hospital admissions at the ith municipality and ${\mu }_i$ is the expected mean number of hospitalizations of the Poisson distribution; ${\text{NO}}_2^{\left(1\right)}$ and ${\text{NO}}_2^{\left(2\right)}$ denote the dummy variables for $80.57<{\text{NO}}_2\le 126.54$ and ${\text{NO}}_2>126.54$, respectively. To account for unobservable heterogeneity, the area-specific random effect, $b_i\sim \text{Normal}(0,{\sigma }_b^2)$, is included in the model. In the model ${\text{ZIP-W}}^b$, the coefficient on log( $E_i$) is considered as an unknown parameter in both the binary and Poisson processes to be estimated in the model-fitting procedure, where the superscript b refers to ‘both’ components; ${\text{ZIP-W}}^c$ includes $\log \left(E_i\right)$ as an explanatory variable only in the count component, where the superscript c refers to ‘count’ component. In contrast, ${\text{ZIP-O}}^b$ considers the population at risk as an offset term in both the binary and count components of the ZIP model and ${\text{ZIP-O}}^c$ only includes the offset term in the count component. The parameter estimations were carried out in R (R Core Team, 2019) via glmmTMB package [8]. For the binary component of the candidate models, ${\text{NO}}_2^{\left(1\right)}$ and ${\text{NO}}_2^{\left(2\right)}$ are not significantly associated with the probability of excessive zeros and therefore were removed from the binary component of the models.

Figure 1.

Distributions of number of hospital admissions for respiratory causes over 315 municipalities in Turin province (Italy) in 2004. The top left panel is for the whole data and rest of the panels are for the data stratified by three categories of NO ${}_2$.

From Table 1, ZIP-W ${}^b$ gave the smallest values of AIC and BIC, suggesting that they provided the best fit to the data compared to the other competing models. The intercept for the binary component of the ZIP-W ${}^b$ model is significantly different from zero with ${\widehat{\mathrm{\text{β}}}}_0=4.24(p\text{{-}value}<0.001)$ and is positive. Under model ZIP-O ${}^b$, the estimated intercept is negative and significantly different from zero ${\widehat{\mathrm{\text{β}}}}_0=-3.31(p\text{{-}value}<0.001)$. By comparison, the estimated intercept of the binary component is not significantly different from zero under models ZIP-W ${}^c$ and ZIP-O ${}^c$. The opposite signs of the estimated intercept under ZIP-O ${}^b$ compared to ZIP-W ${}^b$ and non-significance under models ZIP-W ${}^c$ and ZIP-O ${}^c$ are due to the model misspecification of the exposure effect in the binary component, so ${\mathrm{\text{β}}}_0$ is trying to recover from this misspecification.

Table 1. Parameter estimates (Est), standard error (SE), p-value, AIC and BIC values for the ZIP-W ${}^b$, ZIP-W ${}^c$, ZIP-O ${}^b$ and ZIP-O ${}^c$ models for modeling the number of hospital admissions for respiratory causes over 315 municipalities in Turin province (Italy) in 2004.

	ZIP-W ${}^b$			ZIP-W ${}^c$			ZIP-O ${}^b$			ZIP-O ${}^c$
	Est	SE	p-value	Est	SE	p-value	Est	SE	p-value	Est	SE	p-value
	Binary component
${\mathrm{\text{β}}}_0$(intercept)	4.24	0.52	0.00	0.03	0.12	0.81	−3.31	0.20	0.00	−0.11	0.13	0.39
${\xi }_1$ $(\log (E\left)\right)$	−2.27	0.27	0.00
	Count component
${\alpha }_0$ (intercept)	1.04	0.13	0.00	0.79	0.14	0.00	−0.55	0.15	0.00	0.21	0.13	0.10
${\alpha }_1$ $\left({\text{NO}}_2^{\left(1\right)}\right)$	0.24	0.12	0.04	0.34	0.12	0.00	0.85	0.17	0.00	0.36	0.14	0.01
${\alpha }_2$ $\left({\text{NO}}_2^{\left(2\right)}\right)$	0.43	0.12	0.00	0.48	0.13	0.00	0.91	0.17	0.00	0.26	0.14	0.07
${\xi }_2$ $(\log (E\left)\right)$	0.73	0.04	0.00	0.78	0.04	0.00
${\sigma }_b^2$	0.15	0.38	0.00	0.15	0.39	0.00	0.48	0.69	0.00	0.23	0.48	0.00
	Model fit
AIC	1358.04			1560.22			1856.33			1585.32
BIC	1384.30			1582.74			1875.10			1604.08

The effect of $\log \left(E_i\right)$ for the binary component of the model ZIP-W ${}^b$ is estimated as ${\xi }_1=-2.27(p\text{{-}value}<0.001)$, which models the fact that the probability of observing an excess zero count decreases as the extent of exposure increases. In other words, odds of observing an excess zero count are inversely proportional to $E_i$. In contrast, the effect of $\log \left(E_i\right)$ for the count component of the ZIP-W ${}^b$ model is estimated as ${\xi }_2=0.73(p\text{{-}value}<0.001)$, which reflects that the conditional mean count increases as the extent of exposure increases. Thus, including the population at risk as an offset term by imposing its effect as one results in an incorrect assumption, particularly for the binary component. This is evident from the model comparison between ZIP-W ${}^b$ ( $\mathrm{A}\mathrm{I}\mathrm{C}=1358.04$, $\mathrm{B}\mathrm{I}\mathrm{C}=1384.30$) and ZIP-O ${}^b$ ( $\mathrm{A}\mathrm{I}\mathrm{C}=1856.33$, $\mathrm{B}\mathrm{I}\mathrm{C}=1875.10$) or ZIP-W ${}^c$ ( $\mathrm{A}\mathrm{I}\mathrm{C}=1560.22$, $\mathrm{B}\mathrm{I}\mathrm{C}=1582.74$) and ZIP-O ${}^c$ ( $\mathrm{A}\mathrm{I}\mathrm{C}=1585.32$, $\mathrm{B}\mathrm{I}\mathrm{C}=1604.08$). For covariates included in the Poisson component of the ZIP models, ${\text{NO}}_2^{\left(1\right)}$ and ${\text{NO}}_2^{\left(2\right)}$ are significantly and positively related to the expected counts of hospital admissions under the best fitting model ZIP-W ${}^b$ with the estimated effects equal to ${\hat{\alpha }}_1=0.24$ for ${\text{NO}}_2^{\left(1\right)}$ and ${\hat{\alpha }}_1=0.43$ for ${\text{NO}}_2^{\left(2\right)}$. The effects of ${\text{NO}}_2^{\left(1\right)}$ and ${\text{NO}}_2^{\left(2\right)}$ are estimated to be slightly larger under model ZIP-W ${}^c$ and much larger under ZIP-O ${}^b$ as compared to ZIP-W ${}^b$. A notable difference between ZIP-W ${}^b$ and ZIP-O ${}^b$ is that the two methods provide estimates of opposite signs for the intercept. Under model ZIP-O ${}^c$, only ${\text{NO}}_2^{\left(1\right)}$ is positively and significantly associated with the conditional mean number of hospitalizations with ${\hat{\alpha }}_1=0.36$, but ${\text{NO}}_2^{\left(2\right)}$ is not significant at the $5\mathrm{\%}$ level of significance. The variances of the random effect ${\sigma }_b^2$ are all estimated significantly different from zero, suggesting the importance of accounting for unobserved regional effect. We also observe that the variance component under the model ZIP-O ${}^b$ ( ${\hat{\sigma }}_b^2=0.48$) is much larger than the model ZIP-O ${}^c$ ( ${\hat{\sigma }}_b^2=0.23$). Models ZIP-W ${}^b$ and ZIP-W ${}^c$ give an almost identical estimate for the variance component ( ${\hat{\sigma }}_b^2=0.15$). These results suggest that including exposure as a covariate in either or both of the binary and count components of the ZIP model can explain the residual variation of the response variable.

We have so far only considered NO ${}_2$ and extent of exposure have an ‘additive’ effect; however, NO ${}_2$ and exposure may have an interaction effect. We, therefore, extended ZIP-W ${}^b$ and ZIP-W ${}^c$ models by including the interactions between $\log \left(E\right)$ and ${\text{NO}}_2^{\left(1\right)}$ and ${\text{NO}}_2^{\left(2\right)}$ in both the binary and count components, named as ZIP-W ${}^{b2}$ and only in the count component, named as ZIP-W ${}^{c2}$. Our model fit shows that ${\text{NO}}_2^{\left(1\right)}$ and ${\text{NO}}_2^{\left(2\right)}$ have no main and interaction effect with $\log \left(E\right)$ for the binary component of the ZIP model and therefore were excluded from the model ZIP-W ${}^{b2}$. Nevertheless, ${\text{NO}}_2^{\left(1\right)}$ and ${\text{NO}}_2^{\left(2\right)}$ have significant interaction effect with exposure for the Poisson component of the ZIP-W ${}^{b2}$ model, but not for ZIP-W ${}^{c2}$, as shown in Table 2. ZIP-W ${}^{b2}$ also gives the best model fit among all the competing models ( $\mathrm{A}\mathrm{I}\mathrm{C}=1325.53$, $\mathrm{B}\mathrm{I}\mathrm{C}=1359.30$). These results indicate that (i) failing to include $\log \left(E\right)$ in the binary component of the model may lead to incorrect inference for the parameters in the count component (ii) covariates and extent of exposure can have a significant interaction effect on the outcome.

Table 2. Parameter estimates (Est), standard error (SE), p-value, AIC and BIC values for the ZIP-W ${}^{b2}$ and ZIP-W ${}^{c2}$ models including the interaction between exposure and NO ${}_2$ for modeling the number of hospital admissions for respiratory causes over 315 municipalities in Turin province (Italy) in 2004.

	ZIP-W ${}^{b2}$			ZIP-W ${}^{c2}$
	Est	SE	p-value	Est	SE	p-value
	Binary component
${\mathrm{\text{β}}}_0$ (Intercept)	4.25	0.52	0.00	0.13	0.15	0.39
${\xi }_1$ $(\log (E\left)\right)$	−2.28	0.27	0.00
	Count component
${\alpha }_0$(Intercept)	2.21	0.26	0.00	1.37	0.72	0.06
${\alpha }_1$ $\left({\text{NO}}_2^{\left(1\right)}\right)$	−0.57	0.31	0.06	0.24	0.73	0.74
${\alpha }_2$ $\left({\text{NO}}_2^{\left(2\right)}\right)$	−1.26	0.31	0.00	−0.44	0.73	0.55
${\alpha }_3$ $({\text{NO}}_2^{\left(1\right)}:\log (E\left)\right)$	0.34	0.12	0.00	0.04	0.28	0.90
${\alpha }_4$ $({\text{NO}}_2^{\left(2\right)}:\log (E\left)\right)$	0.63	0.11	0.00	0.31	0.27	0.25
${\xi }_2$ $(\log (E\left)\right)$	0.25	0.10	0.02	0.57	0.27	0.04
${\sigma }_b^2$	0.11	0.33	0.00	0.12	0.35	0.00
	Model fit
AIC	1325.53			1550.40
BIC	1359.30			1580.42

We also considered fitting Poisson and NB models including the random effect term at the municipality level with and without interactions between ${\text{NO}}_2$ and $\log \left(E\right)$ to examine if a simpler model can adequately describing the data. Our results indicate that Poisson and NB models fit to the data worse than the candidate ZIP models, i.e. for Poisson without interaction ( $\mathrm{A}\mathrm{I}\mathrm{C}=1771.9$, $\mathrm{B}\mathrm{I}\mathrm{C}=1786.9$) and NB without interaction ( $\mathrm{A}\mathrm{I}\mathrm{C}=1720.7$, $\mathrm{B}\mathrm{I}\mathrm{C}=1739.5$) and Poisson with interaction ( $\mathrm{A}\mathrm{I}\mathrm{C}=1710.0$, $\mathrm{B}\mathrm{I}\mathrm{C}=1736.3$) NB with interaction ( $\mathrm{A}\mathrm{I}\mathrm{C}=1711.1$, $\mathrm{B}\mathrm{I}\mathrm{C}=1741.1$). These results suggest the importance of accounting for excess zeros in this application.

In many applications, interest focuses on estimating and predicting marginal means given the explanatory variables. Misspecification of the extent of the population at risk may also have an impact on the marginal mean response, since the marginal means depend on the estimated parameters in both binary and Poisson processes. In this application, we are interested in estimating and predicting the population-level mean counts of the number of hospitalizations over the studied area in association with the NO ${}_2$ and size of the population at risk. For ease of computation without marginalizing and conditioning on the random effects, the population-level predicted values of the response variable are calculated as the predicted unconditional counts at the mode (i.e. area-level effect $b_i=0$), as suggested by Brooks et al. [8]. For example, the predicted response value under model ZIP-W ${}^{b2}$ can be calculated as,

$$\begin{array}{rl}E\left(Y_i\right)& =E\left[E\right(Y_i|{\delta }_i\left)\right]=(1-{\pi }_i){\mu }_i\\ & =\left\{1-{\text{logit}}^{-1}\left[{\widehat{\mathrm{\text{β}}}}_0+{\hat{\xi }}_1\log \left(E_i\right)\right]\right\}\\ & \times \exp \left[{\hat{\alpha }}_0+{\hat{\alpha }}_1{\text{NO}}_{2i}^{\left(1\right)}+{\hat{\alpha }}_2{\text{NO}}_{2i}^{\left(2\right)}+{\hat{\alpha }}_3{\text{NO}}_{2i}^{\left(1\right)}\log \left(E_i\right)\right.\\ & +\left.{\hat{\alpha }}_4{\text{NO}}_{2i}^{\left(2\right)}\log \left(E_i\right)+{\hat{\xi }}_2\log \left(E_i\right)\right].\end{array}$$

For the standard errors of the predicted values, posterior predictive simulations were used by drawing multivariate normal samples from the parameters for the fixed effects, given that the resulting estimators follow asymptotically normal distributions [8].

Figure 2 displays the predicted response value and $95\mathrm{\%}$ point-wise confidence intervals of the respiratory hospitalization counts at the mode (i.e. area-specific random effect $b_i=0$) against $\log \left(E\right)$ by the three categories of NO ${}_2$ for all the considered ZIP models. The results based on models ZIP-W ${}^{b2}$ and ZIP-W ${}^{c2}$ clearly demonstrate the significance of the interaction effect between NO ${}_2$ and $\log \left(E\right)$, with the number of hospitalizations increases more sharply as $\log \left(E\right)$ increases for NO ${}_2$ at the highest category (127, 196] as compared to the other NO ${}_2$ levels. For the models without interaction terms, i.e. ZIP-W ${}^b$, ZIP-W ${}^c$, and ZIP-O ${}^c$, the predicted marginal means did not differ substantially at various levels of NO ${}_2$ and appeared to be averaged out across the levels. ZIP-O ${}^b$ yielded unreasonably low predicted values compared to other models.

Figure 2.

The predicted number of respiratory hospitalization count at the mode, i.e. area-specific random effect $b_i=0$ (labeled as ‘RESP’) and $95\mathrm{\%}$ point-wise confidence intervals against the log of the population at risk, i.e. $\log \left(E\right)$, by the categories of NO ${}_2$.

We also examined the model goodness of fit by comparing the predicted and the observed response variable, as shown in Figure 3. The panels in the left column are for the entire data and the panels in the right column are for displaying the data after excluding the largest observed response value for the ease of visualization. It is evident that the predicted values under models ZIP-W ${}^{b2}$ and ZIP-W ${}^b$ are very close to the observed values. The other competing models result in underestimated response values. The results suggest that the models ZIP-W ${}^{b2}$and ZIP-W ${}^b$ predict the number of hospitalizations better than the other candidate models.

Figure 3.

Fitted vs. observed response variable values based on the models ZIP-W ${}^{b2}$ (panels in row 1), ZIP-W ${}^{c2}$ (panels in row 2), ZIP-W ${}^b$ (panels in row 3), ZIP-W ${}^c$ (panels in row 4), ZIP-O ${}^b$ (panels in row 5) and ZIP-O ${}^c$ (panels in row 6). The panels in the left column are for the full data. For ease of visualization, the panels in the right column display the results after suppressing the largest value of the observed response variable.

Despite the aforementioned numerical comparisons of model fit, a careful residual analysis indicates that model ZIP-W ${}^{b2}$ has the best model fit with RQRs nearly normally distributed and no discernible pattern, as shown in the top panels of Figure 4. The distributions of the RQRs under the models ZIP-W ${}^{c2}$, ZIP-W ${}^c$, ZIP-O ${}^b$ and ZIP-O ${}^c$ exhibit bimodal pattern separated at zeros, which suggest the importance of including exposure as an exploratory variable in the binary component of the ZIP model in this application. Altogether, failure to properly model the effect of exposure in both the binary and count components of the ZIP model can have a serious impact on the marginal parameter estimates. Inevitably, incorrect inferences may follow.

Figure 4.

Scatter plots of RQRs vs. fitted values (first column), histograms of RQRs (second column) and QQ plots of RQRs (third column) based on the models ZIP-W ${}^{b2}$ (panels in row 1), ZIP-W ${}^{c2}$ (panels in row 2), ZIP-W ${}^b$ (panels in row 3), ZIP-W ${}^c$ (panels in row 4), ZIP-O ${}^b$ (panels in row 5) and ZIP-O ${}^c$ (panels in row 6).

5. Simulation studies

Simulations were carried out to investigate the performances of the proposed method relative to the traditional methods specifying the underlying population at risk as an offset term in the model under a wide range of scenarios.

5.1. Data-generating mechanism

In the simulations, zero-inflated counts were generated from ZIP-W ${}^b$ model of sizes n = 250, 500 and 1000, defined as

$${\text{ZIP-W}}^b\left\{\begin{array}{l}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left({\pi }_i\right)={\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{x}_{i1}+{\mathrm{\text{β}}}_2{x}_{i2}+{\xi }_1\log \left(E_i\right)\\ \log \left({\mu }_i\right)={\alpha }_0+{\alpha }_1{x}_{i1}+{\alpha }_2{x}_{i2}+{\xi }_2\log \left(E_i\right),\end{array}\right.$$ (21)

where $({\mathrm{\text{β}}}_0,{\mathrm{\text{β}}}_1,{\mathrm{\text{β}}}_2)=(5,-1,-1)$, $({\alpha }_0,{\alpha }_1,{\alpha }_2)=(1,1,1)$, $x_{1i}\sim \text{Bernoulli}\left(0.3\right)$ and $x_{2i}\sim \text{Normal}(\tau ,{\sigma }^2)$ with $\tau =0$ and ${\sigma }^2=0.25$. We considered ${\xi }_1=-2$ and ${\xi }_2=0.8$, respectively, to reflect the fact that the probability of excessive zeros decreases with increasing extent of exposure and the conditional mean count increases over the increased extent of exposure. The values are chosen to mimic our motivating example presented in Section 4. The intercept for the binary component ${\mathrm{\text{β}}}_0$ is set as 5 to yield about 53 $\mathrm{\%}$ zeros in the simulated datasets. The expected population at risk $E_i$ is simulated from a zero truncated negative binomial distribution with probability mass function $\left[\mathrm{\Gamma }\right(x+r\left)p^r\right(1-p{)}^x\left]/\right[\mathrm{\Gamma }\left(n\right)x!(1-p^r)]$ where r is set as 0.1 and p is set as 0.0005, which gives the mean about 40, median 10 and variance 6000. For simplicity of presentation, we assume $x_{i1}$, $x_{i2}$ and log( $E_i$) do not interact.

For each simulation scenario, we generated 200 random samples from the true model and fitted ZIP-W ${}^c$, ZIP-O ${}^b$ and ZIP-O ${}^{b2}$ to determine the impact of mismodelling the effect of exposure on the parameter estimates in both parts of the ZIP model and the overall model fits. To simulate zero inflated data, we firstly simulate the latent variable ${\delta }_i$ from Bernoulli ( ${\pi }_i$) with ${\pi }_i=\exp [{\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{x}_{i1}+{\mathrm{\text{β}}}_2{x}_{i2}+{\xi }_1\log (E_i\left)\right]/\{1+\text{exp }[{\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{x}_{i1}+{\mathrm{\text{β}}}_2{x}_{i2}+{\xi }_1\log \left(E_i\right)\left]\right\}$. Then, if ${\delta }_i=1$, $y_i=0$; otherwise, simulate $y_i$ from Poisson with mean ${\mu }_i=\exp [{\alpha }_0+{\alpha }_1{x}_{i1}+{\alpha }_2{x}_{i2}+{\xi }_2\log (E_i\left)\right]$.

To assess how biased the parameter estimates can be related to the increased or decreased effect of exposures, additional simulation studies were conducted by setting ${\xi }_1=-2,{\xi }_2=2$ and ${\xi }_1=-0.5,{\xi }_2=0.5$, respectively. We also considered simulating data from ZIP-O ${}^c$, which includes the exposure as an offset term only in the count component of the model, to examine the impact of over parametrization of our proposed model ZIP-W ${}^b$ on statistical inference.

5.2. Performance measures

The goals of the simulation study are to determine how parameter estimates, standard errors, coverage probability and overall model fits are affected by misspecification of the effect of the extent of exposures. To this end, we present the bias (the mean of the estimated parameter minus the true value), mean square error (MSE, the average of the sum of the squared differences between the estimated parameter and the true value), the coverage probabilities (CP) of 95 $\mathrm{\%}$ confidence intervals of the estimated parameters and average values of AIC and BIC over repeated samples.

5.3. Simulation results

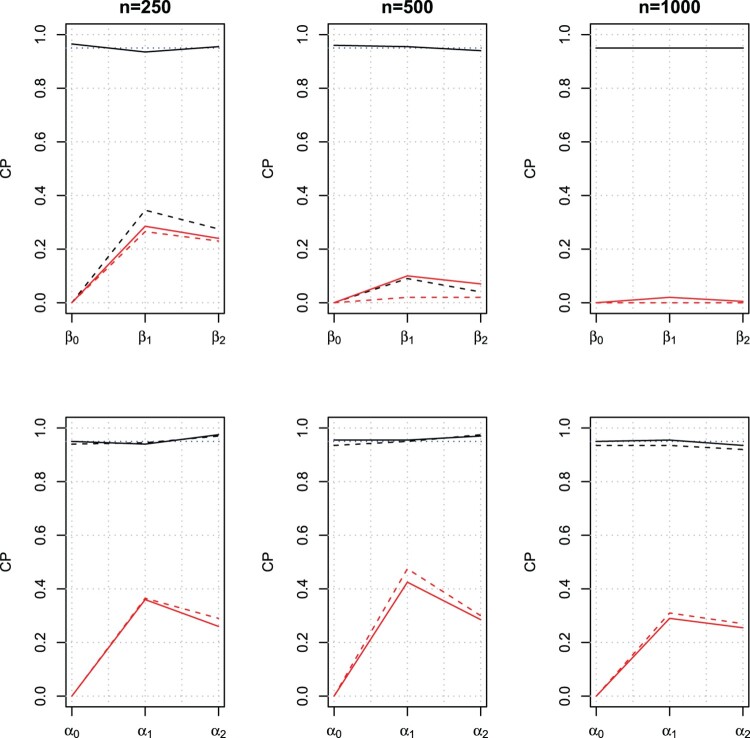
Table 3 reports the bias, MSE, and CP of the $95\mathrm{\%}$ confidence intervals for the parameter estimates from ZIP-W ${}^b$, ZIP-W ${}^c$, ZIP-O ${}^b$ and ZIP-O ${}^c$ fitted to the 200 simulated datasets generated from model ZIP-W ${}^b$ of sample size n = 250, 500 and 1000, respectively. For the binary component, only ZIP-W ${}^b$ results in unbiased estimates with CPs very close to the nominal level of 0.95. In contrast, fitting the misspecified model results in severely biased parameter estimates with CPs far from the nominal level. CP also decreases towards zero as the sample size increases from 250 to 1000. In particular, the intercept ( ${\mathrm{\text{β}}}_0$) is highly affected by model misspecification yielding very large bias and there is also a substantial bias in the estimated regression coefficients ${\mathrm{\text{β}}}_1$ and ${\mathrm{\text{β}}}_2$. The biased parameter estimates of the ZIP-W ${}^c$ model indicates that omitting exposure as a covariate in the binary component of the model results in biased estimates and invalid inference. This result is consistent with the finding from the literature, which showed that if a covariate is removed from a Poisson model, both the estimated regression coefficient and the standard error are the same as the results based on the full model [5]. ZIP-O ${}^b$ gives the worst model fit, yielding the largest bias, MSE, and lowest CP. This result is not surprising, since ZIP-O ${}^b$ constrains the regression coefficients for the exposure in both model components equal to one; nevertheless, both the binary and count processes are influenced by the exposure, but in opposite directions. Hence, the degree of model misspecification is higher compared to other candidate models.

Table 3. Bias, MSE and coverage probability (CP) of the $95\mathrm{\%}$ confidence intervals for the parameter estimates from models ZIP-W ${}^b$, ZIP-W ${}^c$, ZIP-O ${}^b$ and ZIP-O ${}^c$ fitted to the 200 simulated datasets generated from the model ZIP-W ${}^b$ of sample size n = 250, 500 and 1000, respectively.

	Binary component					Count component
		ZIP-W ${}^b$	ZIP-W ${}^c$	ZIP-O ${}^b$	ZIP-O ${}^c$		ZIP-W ${}^b$	ZIP-W ${}^c$	ZIP-O ${}^b$	ZIP-O ${}^c$
		n = 250
Bias	${\mathrm{\text{β}}}_0$	0.229	−4.786	−8.100	−4.944	${\alpha }_0$	−0.005	−0.012	−0.946	−0.938
	${\mathrm{\text{β}}}_1$	−0.033	0.667	1.248	0.778	${\alpha }_1$	0.000	0.001	0.030	0.025
	${\mathrm{\text{β}}}_2$	−0.097	0.674	1.273	0.787	${\alpha }_2$	0.002	0.003	0.039	0.033
MSE	${\mathrm{\text{β}}}_0$	0.583	22.918	65.716	24.464	${\alpha }_0$	0.002	0.002	0.896	0.881
	${\mathrm{\text{β}}}_1$	0.252	0.539	2.246	0.705	${\alpha }_1$	0.000	0.000	0.006	0.005
	${\mathrm{\text{β}}}_2$	0.240	0.524	2.166	0.695	${\alpha }_2$	0.000	0.000	0.008	0.008
CP	${\mathrm{\text{β}}}_0$	0.965	0.000	0.000	0.000	${\alpha }_0$	0.950	0.940	0.000	0.000
	${\mathrm{\text{β}}}_1$	0.935	0.345	0.285	0.265	${\alpha }_1$	0.940	0.945	0.360	0.365
	${\mathrm{\text{β}}}_2$	0.955	0.275	0.240	0.230	${\alpha }_2$	0.975	0.970	0.260	0.290
		n = 500
Bias	${\mathrm{\text{β}}}_0$	0.088	−4.764	−8.437	−4.966	${\alpha }_0$	−0.001	−0.010	−0.958	−0.949
	${\mathrm{\text{β}}}_1$	0.003	0.707	1.528	0.845	${\alpha }_1$	0.000	0.001	0.021	0.015
	${\mathrm{\text{β}}}_2$	−0.024	0.714	1.436	0.845	${\alpha }_2$	0.000	0.001	0.033	0.027
MSE	${\mathrm{\text{β}}}_0$	0.255	22.703	71.240	24.668	${\alpha }_0$	0.001	0.001	0.919	0.900
	${\mathrm{\text{β}}}_1$	0.128	0.542	2.721	0.759	${\alpha }_1$	0.000	0.000	0.002	0.002
	${\mathrm{\text{β}}}_2$	0.121	0.546	2.396	0.754	${\alpha }_2$	0.000	0.000	0.004	0.003
CP	${\mathrm{\text{β}}}_0$	0.960	0.000	0.000	0.000	${\alpha }_0$	0.955	0.935	0.000	0.000
	${\mathrm{\text{β}}}_1$	0.955	0.090	0.100	0.020	${\alpha }_1$	0.955	0.950	0.425	0.475
	${\mathrm{\text{β}}}_2$	0.940	0.040	0.070	0.020	${\alpha }_2$	0.970	0.975	0.285	0.300
		n = 1000
Bias	${\mathrm{\text{β}}}_0$	0.051	−4.811	−8.644	−5.028	${\alpha }_0$	−0.001	−0.009	−0.991	−0.982
	${\mathrm{\text{β}}}_1$	−0.007	0.703	1.494	0.849	${\alpha }_1$	0.000	0.001	0.023	0.018
	${\mathrm{\text{β}}}_2$	−0.027	0.713	1.390	0.848	${\alpha }_2$	−0.001	0.000	0.027	0.022
MSE	${\mathrm{\text{β}}}_0$	0.137	23.146	74.749	25.284	${\alpha }_0$	0.000	0.000	0.982	0.965
	${\mathrm{\text{β}}}_1$	0.057	0.513	2.424	0.741	${\alpha }_1$	0.000	0.000	0.002	0.002
	${\mathrm{\text{β}}}_2$	0.052	0.529	2.129	0.742	${\alpha }_2$	0.000	0.000	0.002	0.002
CP	${\mathrm{\text{β}}}_0$	0.950	0.000	0.000	0.000	${\alpha }_0$	0.950	0.935	0.000	0.000
	${\mathrm{\text{β}}}_1$	0.950	0.000	0.020	0.000	${\alpha }_1$	0.955	0.935	0.290	0.310
	${\mathrm{\text{β}}}_2$	0.950	0.000	0.005	0.000	${\alpha }_2$	0.935	0.920	0.255	0.270

For the count component of the ZIP models, ZIP-W ${}^b$ and ZIP-W ${}^c$ result in nearly unbiased estimates with CPs very close to the nominal level of 0.95. The results based on the ZIP-W ${}^c$ model indicate that omitting exposure as a covariate in the binary component has minimal impact on the parameter estimates for the count component. This result is consistent with the finding from the literature that if a covariate is removed from a Poisson model, both the estimated regression coefficient and the standard error are the same as those of the full model [26]. Nevertheless, under ZIP-O ${}^b$ and ZIP-O ${}^c$ models, the intercept is severely underestimated, the estimated regression coefficients are biased upward and the CPs decline as sample size increases. For the ease of comparison of the results among the considered models, we also graphed the estimated regression coefficients over the 200 simulated samples in Figure 5 and the CPs of the 95 $\mathrm{\%}$ confidence intervals for the regression coefficients in Figure 6. Table 4 presents the average AIC and average BIC over 200 simulated datasets for model comparison. The results indicate that ZIP-W ${}^b$ consistently gives the smallest AIC and BIC compared to other competing models in all scenarios, followed by ZIP-W ${}^c$, ZIP-O ${}^c$ and ZIP-O ${}^b$. Model ZIP-O ${}^b$ gives the worst model fit, since it forces a model fit that is inconsistent with the binary and Poisson processes of the ZIP model.

Table 4. Comparison of model fit of ZIP-W ${}^b$, ZIP-W ${}^c$, ZIP-O ${}^b$ and ZIP-O ${}^c$ in terms of average AIC and BIC across 200 simulated datasets generated from the model ZIP-W ${}^b$.

n	ZIP-W ${}^b$	ZIP-W ${}^c$	ZIP-O ${}^b$	ZIP-O ${}^c$
	AIC
250	976.520	1162.257	2064.654	1732.514
500	1900.825	2288.361	4130.966	3448.865
1000	3887.104	4671.542	8960.393	7597.910
	BIC
250	1004.692	1186.908	2085.782	1753.643
500	1934.542	2317.863	4156.254	3474.153
1000	3926.366	4705.896	8989.840	7627.356

Figure 5.

Estimated regression coefficients for the binomial process for modeling the probability of excess zeros (left panels) and the Poisson process (right panels) over 200 simulated datasets from the model ZI-W ${}^b$ of sample size n1 = 250, n2 = 500 and n3 = 1000.

Figure 6.

Coverage probabilities of the $95\mathrm{\%}$ confidence intervals of the estimated regression coefficients for the binomial process for modeling the probability of excess zeros (top panels) and the Poisson process (bottom panels) over 200 simulated datasets from model ZI-W ${}^b$ of sample size n = 250, 500 and 1000. The black solid and dashed lines are for the models ZI-W ${}^b$ and ZI-W ${}^c$, respectively; the red solid and dashed lines are for the models ZI-O ${}^b$ and ZI-O ${}^c$, respectively.

Additional simulation studies were conducted by increasing or decreasing the values of ${\xi }_1$ and ${\xi }_2$. For the scenario when ${\xi }_1=-2,{\xi }_2=2$, the results are presented in Figures S1 and S2 in the web supplementary materials, which indicate that the results for the binary component remain roughly consistent with the results from the previous simulation setting when ${\xi }_1=-2$ and ${\xi }_2=0.8$. However, for the count component, the performances of ZIP-O ${}^b$ and ZIP-O ${}^c$ become worse with increased bias and much lower CPs as compared to Figures 5 and 6, since models ZIP-O ${}^b$ and ZIP-O ${}^c$ constrain ${\xi }_2=1$ and ${\xi }_2=2$ deviates more from one than ${\xi }_2=0.8$. As a comparison, when ${\xi }_1=-0.5$ and ${\xi }_2=0.5$, as shown in Figures S3 and S4, the parameter estimates of the regression coefficients in the binary component are less biased and CPs are closer to the nominal level compared to the previous setting, since ${\xi }_1=-0.5$ is less deviated from 1 as compared to ${\xi }_1=-2$. The results of the model fit for these additional simulation studies are presented in Tables S1 and S2, with the results being consistent with the previous simulation setting showing model ZIP-W ${}^b$ outperforms the other competing models. In summary, the results based on the model ZIP-W ${}^c$ suggest that ignoring modeling the effect of varying exposure in the binary component of the ZIP model can bias the estimation of the covariate effect in the binary component. Such bias becomes more severe as the effect of varying exposure increases. The results based on the ZIP-O ${}^b$ and ZIP-O ${}^c$ indicate that incorporating the varying exposure as an offset term can lead to biased and inefficient parameter estimates in both the binary and count components of the ZIP model. The simulation results confirmed that the degree of bias and variation of the estimated regression coefficients depend on the effect of the exposure variable.

In another set of the simulation study, we simulate data from ZIP-O ${}^c$ model. Our results (Figures S5 and S6) indicate that both ZIP-W ${}^b$ and ZIP-W ${}^c$ models provide parameter estimates with negligible bias, low MSE and nominal coverage probabilities reasonably close to 95 $\mathrm{\%}$. Only ZIP-O ${}^b$ yielded biased estimates for the binary component but not for the count component, since it imposes unreasonable assumption on the effect of exposure in the binary component. Overall, it appears over parametrization by estimating ${\xi }_1$ and ${\xi }_2$ rather than restricting them equal to one as specified in the offset terms for both binary and count component has negligible effects on inference.

We also run another set of simulations to ascertain whether the percentage of zeros is an important feature in determining the impact of misspecification of the effect of varying exposure. We generated data from the ZIP-W ${}^b$ model with about $30\mathrm{\%}$, $60\mathrm{\%}$, and $90\mathrm{\%}$ of zeros. Our simulation results are comparable to the results presented earlier.

6. Conclusion and future work

In this study, we reviewed zero-inflated regression models with a focus on investigating the extent to which misspecification of modeling underlying population at risk on the estimation of the regression coefficients and overall model fit for the zero-inflated model. We showed that including an offset term could be very restrictive in the sense that it forces the effect of exposure as one, which can be inconsistent with the data, as shown in our motivating example. Therefore, we formulated and developed a framework to understand the nature of zero-inflated models by allowing the extent of exposure to be included in both parts of the binary and count components of the ZI model as a regular covariate.

The evidence provided in this paper serves as a warning not to make strong assumptions about the effect of exposure, like those embodied in using offset in a Poisson distribution. It is wise at least to make a sensitivity check by estimating the effect of the varying exposure. Also, the probability of excessive zero may also depend on the population at risk. The relationship between exposure and the probability of excessive zero component, therefore, needs to be carefully assessed and properly incorporated in the model.

In our motivating example, the ZIP model with varying exposure being included in both the binary and count components as a covariate fits this particular data set well. However, in some situations, after accounting for zero-inflation and adjusting for the effects of the covariates and varying exposure, the data may still suggest additional overdispersions. The proposed modeling approach could then be applied to other zero-inflated models to account for additional overdispersion, such as zero-inflated negative binomial model and zero-inflated generalized Poisson model [12,33]. Score test could be conducted to help determine whether a more complex model is appropriate, without fitting a more complex model [33].

In addition, including varying exposure as a covariate in both the binary and count components of the ZI model leads to an increase in the number of parameters to be estimated. In the situation where many covariates are involved, the variable selection needs to be conducted to address the potential over parametrization problem, especially when the sample size is small. Traditional variable selection procedures, such as the automated variable selection methods, may result in models that are unstable and not reproducible [3]. Penalized regression methods are popular for selecting variables, which keep all the variables in the model but constrain the regression coefficients by shrinking them toward zero. A variety of penalty functions can be considered, such as Least Absolute Shrinkage and Selection Operator (LASSO) [29], Smoothly Clipped Absolute Deviation penalty (SCAD) [15], and minimax concave penalty (MCP) [37]. Penalized regression methods have been extended for selecting parsimonious zero-inflated models [9,30,31,36]. Future studies will be conducted to evaluate the performance of the proposed modeling strategy with these variable selection methods under different ratios of the number of candidate covariates to the sample size.

Note that zero-inflated and hurdle models have been extended to model longitudinal or clustered count measures with excess zeros by linking the binary and count components using a shared subject-specific random effect term or bivariate normal distribution. The linkage of the model components allows the dependence between the binary and count components of the model [24,25]. As a result, the binary and count processes will not act independently; that is, model misspecification for one component may have an impact on the other component passed through the shared random effect terms. Future work will be conducted to investigate the impact of misspecification of the exposure effect on such correlated random effects models.

In our simulations and empirical studies, we considered the linear effect of the log of the exposure variable. However, more flexible modeling of exposure-outcome associations can be applied to avoid constraining a priori functional form of this relationship to a particular parametric family of functions, such as conventionally used linear functions.

Funding Statement

This research was supported by the discovery grant from the Canadian Network for Research and Innovation in Machining Technology, Natural Sciences and Engineering Research Council of Canada [RGPIN 07212-2019].

Disclosure statement

No potential conflict of interest was reported by the author(s).