Some Shrinkage estimators based on median ranked set sampling

Abstract

In this study, some shrinkage estimators using a median ranked set sample in the presence of multicollinearity were studied. Initially, we constructed the multiple regression model using median ranked set sampling. We also adapted the Ridge and Liu-type estimators to these multiple regression model. To investigate the efficiency of these estimators, a simulation study was performed for a different number of explanatory variables, sample sizes, correlation coefficients, and error variances in perfect and imperfect ranking cases. In addition, these estimators were compared with other estimators that are based on ranked set sample using simulation study. It is shown that when the collinearity is moderate, Ridge estimator using median ranked set sample performs better than other estimators and when the collinearity increases, Liu-type estimator using median ranked set sample gets better than all other estimators do. When the collinearity is smaller than 0.95, ridge estimator based on median ranked set sample is more efficient than Liu-type estimator based on same sample. However, this threshold increases as the sample size increases and the number of explanatory variables decreases. In addition, real data example is presented to illustrate how collinearity affects the estimators under median ranked set sampling and ranked set sampling.

1. Introduction

The linear regression model and least squares (LS) method are widely used in many fields of natural and social sciences. In the presence of collinearity, the LS estimator is unstable and often gives misleading information. Ridge regression is the most common method to overcome this problem. One of the estimators under the class of biased estimators is called the shrinkage estimator. Principal components regression, Ridge regression and their variates are parts of this class. Liu [18] suggested a biased estimator as an alternative to the Ridge estimator. Later, this estimator is named as ‘Liu estimator’ by Akdeniz and Kaçıranlar [1]. Ridge regression and Liu estimators, which include a single biasing parameter, specially depend on the LS estimator. Because of the elimination of the effects of multicollinearity on the LS estimator, biased estimators including two biasing parameters have been proposed [19]. Estimating biasing parameters of estimators include two biasing parameters that are usually based on the methods proposed for Ridge and Liu estimators. In case of high collinearity, the biasing parameter selected by the existing methods for Ridge regression may not fully address the ill-conditioning problem. To solve this problem, the two-parameter estimator is proposed by Liu [19]. This two-parameter estimator has two advantages over Ridge regression. One of them is that this estimator has less mean squared error (MSE). The other is that this estimator can fully address the ill-conditioning problem. On the other hand, it is known that statisticians experience the problem of choosing either the LS estimator or a biased estimator, as well as choosing one of the two biased estimators.

Ebegil et al. [10] suggested the test statistics for the Ridge and Liu estimators, which are Shrinkage estimators, and these estimators were compared under different correlation structures among independent variables with a simulation study. Sakallıoglu and Kaçıranlar [27] proposed a new estimator based on the Ridge estimator and compared the performance of their estimator with two other special Liu-type estimators proposed by Liu [19]. Ebegil and Gökpınar [9] obtained necessary and sufficient conditions for comparing the Liu-type biased estimator and the LS estimator by using their MSE matrices. They also showed that Liu-type estimator is better than the Ridge estimators under different value of parameters are when the collinearity is severe by a simulation study.

In the regression analysis, the measurement of the response variable can be quite costly or very difficult in terms of time and labour. Such scenarios may arise especially in certain areas, such as environment, ecology, agriculture and medicine. In such conditions, the ranked set sampling (RSS) increases the efficiency of the estimation according to the simple random sampling (SRS) [20].

The use of RSS in the linear regression model for the first time was introduced by Stokes [28]. Muttlak [21,22] considered the performance of RSS for simple and multiple regression models. Özdemir and Esin [25] obtained the best linear unbiased estimators in the class of linear combinations of the ranked set sample values for multiple linear regression models with replicated observations. Chen [3] suggested an adaptive RSS method in the derivation of the regression estimator of the population mean when more than one concomitant variable is available. However, his proposed method needs a ranking criterion function for using all explanatory variables in the ranking. Ranking of the units by response variable can be done by visual ranking, using one of the explanatory variables or using the external ranking variable, which is cheap and easy to measure. For example, when the age of a fish needs to be determined in animal growth studies, it is usually time consuming and costly. However, the length or weight of a fish which is closely related to the age of a fish can be measured easily and economically [5]. In addition, an external ranking variable can be used for ranking the response variable. For example, in automobile technology, evaporative emissions require controls on both the vehicle and the gasoline. The most effective gasoline control is to reduce the volatility of the gasoline, which is measured by the Reid vapour pressure (RVP). RVP can be measured in the laboratory or at the gas station. Laboratory analysis of RVP is not overly expensive, but it is too expensive to ship the field sample of the gasoline to the laboratory. Therefore, inexpensive field measurement of RVP, which is highly correlated with the laboratory measurement of RVP, can be used for ranking the pumps at the gas stations [4,12]. When we try to investigate the effects of some factors on RVP measurement, we need to construct a regression model of RVP measurement according to these factors. For this kind of model, field measurement of RVP can be used as an external ranking variable for laboratory measurement of RVP. Therefore, due to these advantages mentioned here, an explanatory or external ranking variable can be used to rank the response variable.

Median ranked set sampling (MRSS) is a modification of RSS and it performs better than classical RSS in the estimation of the population mean under symmetrical unimodal distributions [23]. There are many studies about MRSS and its applications [2,13,15,16,26]. However, MRSS cannot perform better than RSS under asymmetrical distributions. Besides, since error terms have a normal distribution in regression models in general, the efficiency of estimators can be increased using MRSS. In this study, the Ridge and Liu-type estimators were investigated using a median ranked set sample to obtain efficient estimators of regression model parameters.

The rest of this study is organized as follows: in Section 2, the procedure of obtaining a Ridge regression estimator using a median ranked set sample was given. In Section 3, the MSE of this estimator against its competitors was compared using Monte Carlo simulation. In Section 4, the real data example was presented to illustrate how collinearity affects the estimators under median ranked set sampling and concluding remarks are summarized in Section 5.

2. Ridge and Liu-type estimator using a median ranked set sample

We consider the following multiple linear regression model:

$$Y=X\beta +\epsilon ,\epsilon \sim N(\underset{\_}{0},{\sigma }^2{I}_n),$$ (1)

where Y is a $(n\times 1)$ dimensional vector of the response variable; $X$ is a $(n\times p)$ dimensional non-stochastic input matrix with $\text{rank}(X_{n\times p})=p\le n$, $\beta$ is a $(p\times 1)$ dimensional unknown coefficient vector and $\epsilon$ is the error vector. We also assume that $E(\epsilon )=0$ and $E(\epsilon {\epsilon }^{\mathrm{\prime }})={\sigma }^2{I}_n$. The most common method to estimate the regression coefficients is the LS method. The LS estimator of parameter $\beta$ is given by

$$\hat{\beta }=(X^{\mathrm{\prime }}X{)}^{-1}{X}^{\mathrm{\prime }}Y.$$ (2)

Multicollinearity is one of the most encountered problems in regression, and the ridge regression is the most common method to overcome this problem. The ridge estimator can be described as

$$\begin{array}{cc}{\tilde{\beta }}_R={(X^{\mathrm{\prime }}X+kI)}^{-1}{X}^{\mathrm{\prime }}Y& (k>0)\end{array},$$ (3)

where k is the ridge parameter and I is a $(n\times n)$ dimensional identity matrix. In the multicollinearity case, the columns of the X matrix are almost linearly dependent. Thus, the matrix $(X^{\mathrm{\prime }}X{)}^{-1}$ is very close to singular. This kind of matrices is called ill-conditioned matrices. Adding k to the diagonal of $X^{\mathrm{\prime }}X$ can fix the ill-conditioned situation.

Liu [19] shows that the small k selected in the Ridge estimator may not be able to improve the ill-conditioning problem. For this reason, Liu [19] defined the Liu-type biased estimator

$${\tilde{\beta }}_{LT}=(X^{\mathrm{\prime }}X+kI{)}^{-1}(X^{\mathrm{\prime }}Y+d{\beta }^{\ast }),$$ (4)

where k>0, $-\mathrm{\infty }$<d< $\mathrm{\infty }$ and ${\beta }^{\ast }$ be any estimator of $\beta$. There are two choices ${\beta }^{\ast }$: ${\tilde{\beta }}_R$ and $\hat{\beta }.$ In this study, we focused on ${\tilde{\beta }}_R$ to obtain the Liu-type estimator.

The canonical form of the model in the Equation (1) can be expressed as

$$Y=XP{P}^{\mathrm{\prime }}\beta +\epsilon =Z\alpha +\epsilon ,$$ (5)

where $Z=XP$ and $\alpha =P^{\mathrm{\prime }}\beta$. Also, $\hat{\alpha }=P^{\mathrm{\prime }}\hat{\beta }$ and $(X^{\mathrm{\prime }}X)$ is a symmetric matrix and such that there is an orthonormal matrix P that diagonalizes $(X^{\mathrm{\prime }}X)$. The elements of $P^{\mathrm{\prime }}{X}^{\mathrm{\prime }}XP=\mathrm{\Lambda }$ are ${\lambda }_1>{\lambda }_2>\cdots {\lambda }_p$ which are the positive eigenvalues of $(X^{\mathrm{\prime }}X)$. $\mathrm{\Lambda }$ is the diagonal matrix with the dimension of $(p\times p)$ [10,8].

In the rest of this section, we present the procedure for obtaining ridge regression and Liu-type estimators using a median ranked set sample. In general, since the errors have normal distribution in regression models, the efficiency of estimators can be increased using MRSS. This selection procedure in MRSS depends on the sample size being even or odd and can be described as in Algorithm 1, which is a modification of Level 1 sampling in Deshpande et al. [6].

Algorithm 1

In the jth selection $(j=1,2,\cdots ,n)$,

Stage 1. A simple random sample of size n is selected from the population.

Stage 2. The sample units are ranked with respect to a variable of interest Y, assuming that there is no ranking error in the sampling.

Stage 3.

1. Sample unit with rank $(n+1)/2$ is selected for actual measurement for odd set size n.

2. Sample unit with rank $n/2$ is selected when

3. $j\le n/2$, and the $(n+2)/2$ is selected when $j>n/2$ for even set size n.

Stages 1–3 are repeated for $j=1,2,\cdots ,n$, to obtain a median ranked set sample of size n.

This sample selection procedure can be applied to the multiple regression model in Equation (1) as given in Algorithm 2.

Algorithm 2

In the jth selection $(j=1,2,\dots ,n)$,

Stage 1. A simple random sample of size n, $(Y_{j1};X_{1(j1)},\dots ,X_{p(j1)})$, … , $(Y_{jn};X_{1(jn)},\dots ,X_{p(jn)}),$ is selected from the population.

Stage 2. The sample units are ranked with respect to the variable Y, assuming that there is no ranking error in the sampling, and $(Y_{(1)}^j;X_{1[1]}^j,\dots ,X_{p[1]}^j)$, … , $(Y_{(n)}^j;X_{1[n]}^j,\dots ,X_{p[n]}^j)$ are obtained.

Stage 3.

1. Sample unit with rank $(n+1)/2$ is selected for actual measurement for odd set size n.

2. Sample unit with rank $n/2$ is selected for actual measurement when $j\le n/2$, and the sample unit with rank $(n+2)/2$,

3. $(Y_{((n/2)+1)}^j;X_{1[(n/2)+1]}^j,\dots ,X_{p[(n/2)+1]}^j)$, is selected for actual measurement when $j>n/2$ for the even set size n.

Sample selection procedure is also presented in Tables 1 and 2 for odd and even set size, respectively.

Table 1.

Sample selection procedure according to the response variable with the odd set size.

Set	Stage 1	Stage 2	Stage 3
$1\{\begin{array}{l}{Y}_{11}={\beta }_1{X}_{1(11)}+\dots +{\beta }_p{X}_{p(11)}+{\epsilon }_{11}\\ \dots \dots \\ Y_{1n}={\beta }_1{X}_{1(1n)}+\dots +{\beta }_p{X}_{p(1n)}+{\epsilon }_{1n}\end{array}\Rightarrow \begin{array}{c}{Y}_{(1)}^1={\beta }_1{X}_{1[1]}^1+\dots +{\beta }_p{X}_{p[1]}^1+{\epsilon }_{[1]}^1\\ \dots \dots \\ Y_{(n)}^1={\beta }_1{X}_{1[n]}^1+\dots +{\beta }_p{X}_{p[n]}^1+{\epsilon }_{[n]}^1\end{array}\Rightarrow \begin{array}{c}\dots \\ Y_{((n+1)/2)}^1={\beta }_1{X}_{1[(n+1)/2]}^1+\dots +{\beta }_p{X}_{p[(n+1)/2]}^1+{\epsilon }_{[(n+1)/2]}^1\\ \dots \end{array}$
$2\{\begin{array}{l}{Y}_{21}={\beta }_1{X}_{1(21)}+\dots +{\beta }_p{X}_{p(21)}+{\epsilon }_{21}\\ \dots \dots \\ Y_{2n}={\beta }_1{X}_{1(2n)}+\dots +{\beta }_p{X}_{p(2n)}+{\epsilon }_{2n}\end{array}\Rightarrow \begin{array}{c}{Y}_{(1)}^2={\beta }_1{X}_{1[1]}^2+\dots +{\beta }_p{X}_{p[1]}^2+{\epsilon }_{[1]}^2\\ \dots \dots \\ Y_{(n)}^2={\beta }_1{X}_{1[n]}^2+\dots +{\beta }_p{X}_{p[n]}^2+{\epsilon }_{[n]}^2\end{array}\Rightarrow \begin{array}{c}\dots \\ Y_{((n+1)/2)}^2={\beta }_1{X}_{1[(n+1)/2]}^2+\dots +{\beta }_p{X}_{p[(n+1)/2]}^2+{\epsilon }_{[(n+1)/2]}^2\\ \dots \end{array}$
…
$n\{\begin{array}{l}{Y}_{n1}={\beta }_1{X}_{1(n1)}+\dots +{\beta }_p{X}_{p(n1)}+{\epsilon }_{n1}\\ \dots \dots \\ Y_{nn}={\beta }_1{X}_{1(nn)}+\dots +{\beta }_p{X}_{p(nn)}+{\epsilon }_{nn}\end{array}\Rightarrow \begin{array}{c}{Y}_{(1)}^n={\beta }_1{X}_{1[1]}^n+\dots +{\beta }_p{X}_{p[1]}^n+{\epsilon }_{[1]}^n\\ \dots \dots \\ Y_{(n)}^n={\beta }_1{X}_{1[n]}^n+\dots +{\beta }_p{X}_{p[n]}^n+{\epsilon }_{[n]}^n\end{array}\Rightarrow \begin{array}{c}\dots \\ Y_{((n+1)/2)}^n={\beta }_1{X}_{1[(n+1)/2]}^n+\dots +{\beta }_p{X}_{p[(n+1)/2]}^n+{\epsilon }_{[(n+1)/2]}^n\\ \dots \end{array}$

Table 2.

Sample selection procedure according to the response variable with the even set size.

Set	Stage 1	Stage 2	Stage 3
$1\{\begin{array}{l}{Y}_{11}={\beta }_1{X}_{1(11)}+\dots +{\beta }_p{X}_{p(11)}+{\epsilon }_{11}\\ \dots \dots \\ Y_{1n}={\beta }_1{X}_{1(1n)}+\dots +{\beta }_p{X}_{p(1n)}+{\epsilon }_{1n}\end{array}\Rightarrow \begin{array}{c}{Y}_{(1)}^1={\beta }_1{X}_{1[1]}^1+\dots +{\beta }_p{X}_{p[1]}^1+{\epsilon }_{[1]}^1\\ \dots \dots .\\ Y_{(n)}^1={\beta }_1{X}_{1[n]}^1+\dots +{\beta }_p{X}_{p[n]}^1+{\epsilon }_{[n]}^1\end{array}\Rightarrow \begin{array}{c}\dots \\ Y_{(n/2)}^1={\beta }_1{X}_{1[n/2]}^1+\dots +{\beta }_p{X}_{p[n/2]}^1+{\epsilon }_{[n/2]}^1\\ \dots \end{array}$
…
$n/2\{\begin{array}{l}{Y}_{21}={\beta }_1{X}_{1(21)}+\dots +{\beta }_p{X}_{p(21)}+{\epsilon }_{21}\\ \dots \dots \\ Y_{2n}={\beta }_1{X}_{1(2n)}+\dots +{\beta }_p{X}_{p(2n)}+{\epsilon }_{2n}\end{array}\Rightarrow \begin{array}{c}{Y}_{(1)}^2={\beta }_1{X}_{1[1]}^2+\dots +{\beta }_p{X}_{p[1]}^2+{\epsilon }_{[1]}^2\\ \dots \dots \\ Y_{(n)}^2={\beta }_1{X}_{1[n]}^2+\dots +{\beta }_p{X}_{p[n]}^2+{\epsilon }_{[n]}^2\end{array}\Rightarrow \begin{array}{c}\dots \\ Y_{(n/2)}^{n/2}={\beta }_1{X}_{1[n/2]}^{n/2}+\dots +{\beta }_p{X}_{p[n/2]}^{n/2}+{\epsilon }_{[n/2]}^{n/2}\\ \dots \end{array}$
$(n/2)+1\{\begin{array}{l}{Y}_{n1}={\beta }_1{X}_{1(n1)}+\dots +{\beta }_p{X}_{p(n1)}+{\epsilon }_{n1}\\ \dots \dots \\ Y_{nn}={\beta }_1{X}_{1(nn)}+\dots +{\beta }_p{X}_{p(nn)}+{\epsilon }_{nn}\end{array}\Rightarrow \begin{array}{c}{Y}_{(1)}^n={\beta }_0+{\beta }_1{X}_{1[1]}^n+\dots +{\beta }_p{X}_{p[1]}^n+{\epsilon }_{[1]}^m\\ \dots \dots \\ Y_{(n)}^n={\beta }_0+{\beta }_1{X}_{1[n]}^n+\dots +{\beta }_p{X}_{p[n]}^n+{\epsilon }_{[n]}^n\end{array}\Rightarrow \begin{array}{c}\dots \\ Y_{((n/2)+1)}^{(n/2)+1}={\beta }_1{X}_{1[(n/2)+1]}^{(n/2)+1}+\dots +{\beta }_p{X}_{p[(n/2)+1]}^{(n/2)+1}+{\epsilon }_{[(n/2)+1]}^{(n/2)+1}\\ \dots \end{array}$
…
$n\{\begin{array}{l}{Y}_{n1}={\beta }_0+{\beta }_1{X}_{1(n1)}+\dots +{\beta }_p{X}_{p(n1)}+{\epsilon }_{n1}\\ \dots \dots \\ Y_{nn}={\beta }_0+{\beta }_1{X}_{1(nn)}+\dots +{\beta }_p{X}_{p(nn)}+{\epsilon }_{nn}\end{array}\Rightarrow \begin{array}{c}{Y}_{(1)}^n={\beta }_0+{\beta }_1{X}_{1[1]}^n+\dots +{\beta }_p{X}_{p[1]}^n+{\epsilon }_{[1]}^n\\ \dots \dots \\ Y_{(n)}^n={\beta }_0+{\beta }_1{X}_{1[n]}^n+\dots +{\beta }_p{X}_{p[n]}^n+{\epsilon }_{[n]}^n\end{array}\Rightarrow \begin{array}{c}\dots \\ Y_{((n/2)+1)}^n={\beta }_1{X}_{1[(n/2)+1]}^n+\dots +{\beta }_p{X}_{p[(n/2)+1]}^n+{\epsilon }_{[(n/2)+1]}^n\\ \dots \end{array}$

Using Tables 1 and 2, the ridge regression and Liu-type estimator can be obtained as follows, respectively:

$$\begin{array}{rl}{\tilde{\beta }}_{R(\text{MRSS})}& =({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}+kI{)}^{-1}{X}_{\text{MRSS}}^{\mathrm{\prime }}{Y}_{\text{MRSS}}\\ & =A_{R(\text{MRSS})}{\hat{\beta }}_{\text{MRSS}},\end{array}$$ (6)

$$\begin{array}{rl}{\tilde{\beta }}_{LT(\text{MRSS})}& =({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}+kI{)}^{-1}({X^{\mathrm{\prime }}}_{\text{MRSS}}{Y}_{\text{MRSS}}+d{\tilde{\beta }}_{R(\text{MRSS})})\\ & =A_{LT(\text{MRSS})}{\hat{\beta }}_{\text{MRSS}}.\end{array}$$ (7)

Here,

$$Y_{\text{MRSS}}=\{\begin{array}{ll}(Y_{(n+1/2)}^1,Y_{(n+1/2)}^2,\dots ,Y_{(n+1/2)}^n{)}^{\mathrm{\prime }},& n\text{ is odd,}\\ (Y_{(n/2)}^1,\dots ,Y_{(n/2)}^{n/2},Y_{((n+2)/2)}^{(n+2)/2},\dots ,Y_{((n+2)/2)}^n{)}^{\mathrm{\prime }},& n\text{ is even,}\end{array}$$

$$X_{\text{MRSS}}=\{\begin{array}{cc}\left[\begin{array}{ccc}{X}_{1[(n+1)/2]}^1& \dots & X_{p[(n+1)/2]}^1\\ \dots & \dots & \dots \\ X_{1[(n+1)/2]}^n& \dots & X_{1[(n+1)/2]}^n\end{array}\right],& n\text{ is odd,}\\ \left[\begin{array}{ccc}{X}_{1[n/2]}^1& \dots & X_{p[n/2]}^1\\ \dots & \dots & \dots \\ X_{1[n/2]}^{n/2}& \dots & X_{p[n/2]}^{n/2}\\ X_{1[(n+2)/2]}^{(n+2)/2}& \dots & X_{p[(n+2)/2]}^{(n+2)/2}\\ \dots & \dots & \dots \\ X_{1[(n+2)/2]}^n& \dots & X_{p[(n+2)/2]}^n\end{array}\right],& n\text{ is even,}\end{array}$$

$${\hat{\beta }}_{\text{MRSS}}=(X_{\text{MRSS}}^{\mathrm{\prime }}{X}_{\text{MRSS}}{)}^{(-1)}{X}_{\text{MRSS}}^{\mathrm{\prime }}{Y}_{\text{MRSS}},$$ (8)

and

$$A_{LT(\text{MRSS})}=({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}+k\mathrm{I}{)}^{-1}(\mathrm{I}+d{({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{MRSS}+k\mathrm{I})}^{-1})X_{\text{MRSS}}^{\mathrm{\prime }}{X}_{\text{MRSS}}.$$

The MSEs of the ridge regression and Liu-type estimators in Equations (6) and (7) are defined, respectively, as follows

$$\begin{array}{rl}\text{MSE}({\tilde{\beta }}_{R(\text{MRSS})})& ={\sigma }_{\text{MRSS}}^2{A}_{R(MRSS)}({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}{)}^{-1}{A^{\mathrm{\prime }}}_{R(\text{MRSS})}\\ & +{\beta }^{\mathrm{\prime }}(I-A_{R(\text{MRSS})}{)}^{\mathrm{\prime }}(I-A_{R(\text{MRSS})})\beta ,\end{array}$$

$$\begin{array}{rl}\text{MSE}({\tilde{\beta }}_{LT(\text{MRSS})})& ={\sigma }^2{A}_{LT(\text{MRSS})}({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{MRSS}{)}^{-1}{A^{\mathrm{\prime }}}_{LT(\text{MRSS})}\\ & +{\beta }^{\mathrm{\prime }}(I-A_{LT(\text{MRSS})}{)}^{\mathrm{\prime }}(I-A_{LT(\text{MRSS})})\beta .\end{array}$$

Here, the unbiased estimator of ${\sigma }^2$ was written as

$${\hat{\sigma }}_{\text{MRSS}}^2=\frac{{Y^{\mathrm{\prime }}}_{\text{MRSS}}{Y}_{\text{MRSS}}-{\hat{\beta }}_{\text{MRSS}}{X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}}{n-(p+1)}.$$

The MSE criterion was used to compare the estimators given in Equations (3) and (4), Equations (6)–(8). The estimators and their MSEs are summarized in Table 3 [11,17].

Table 3.

Regression estimators and their MSEs.

Estimators	MSE
$\hat{\beta }=(X^{\mathrm{\prime }}X{)}^{-1}{X}^{\mathrm{\prime }}Y$	$\text{MSE}(\hat{\beta })={\sigma }^2(X^{\mathrm{\prime }}X{)}^{-1}$
${\hat{\beta }}_{\text{MRSS}}=({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}{)}^{-1}{X}_{\text{MRSS}}^{\mathrm{\prime }}{Y}_{\text{MRSS}}$	$\text{MSE}({\hat{\beta }}_{\text{MRSS}})={\sigma }_{\text{MRSS}}^2({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}{)}^{-1}$
${\tilde{\beta }}_R=(X^{\mathrm{\prime }}X+kI{)}^{-1}{X}^{\mathrm{\prime }}Y=A\hat{\beta }$	$\text{MSE}({\tilde{\beta }}_R)={\sigma }^{2}A(X^{\mathrm{\prime }}X{)}^{-1}{A}^{\mathrm{\prime }}+{\beta }^{\mathrm{\prime }}(I-A{)}^{\mathrm{\prime }}(I-A)\beta$
${\tilde{\beta }}_{R(\text{MRSS})}=({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}+kI{)}^{-1}{X}_{\text{MRSS}}^{\mathrm{\prime }}{Y}_{\text{MRSS}}=A_{R(\text{MRSS})}{\hat{\beta }}_{\text{MRSS}}$	$\text{MSE}({\tilde{\beta }}_{R(\text{MRSS})})={\sigma }_{\text{MRSS}}^2{A}_{R(\text{MRSS})}({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}{)}^{-1}{A}_{R(\text{MRSS})}^{\mathrm{\prime }}+{\beta }^{\mathrm{\prime }}(I-A_{R(\text{MRSS})}{)}^{\mathrm{\prime }}(I-A_{R(\text{MRSS})})\beta$
${\tilde{\beta }}_{LT}=(X^{\mathrm{\prime }}X+kI{)}^{-1}(X^{\mathrm{\prime }}Y+d{\tilde{\beta }}_R)=A_{LT}\hat{\beta }$	$\text{MSE}({\tilde{\beta }}_{LT})={\sigma }^2{A}_{LT}(X^{\mathrm{\prime }}X{)}^{-1}{A}_{LT}^{\mathrm{\prime }}+{\beta }^{\mathrm{\prime }}(I-A_{LT}{)}^{\mathrm{\prime }}(I-A_{LT})\beta$
${\tilde{\beta }}_{LT(\text{MRSS})}=({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}+kI{)}^{-1}({X^{\mathrm{\prime }}}_{\text{MRSS}}{Y}_{\text{MRSS}}+d{\tilde{\beta }}_{R(\text{MRSS})})=A_{LT(\text{MRSS})}{\hat{\beta }}_{\text{MRSS}}$	$\text{MSE}({\tilde{\beta }}_{LT(\text{MRSS})})={\sigma }^2{A}_{LT(\text{MRSS})}({X^{\mathrm{\prime }}}_{\text{MRSS}}{X}_{\text{MRSS}}{)}^{-1}{A}_{LT(\text{MRSS})}^{\mathrm{\prime }}+{\beta }^{\mathrm{\prime }}(I-A_{LT(\text{MRSS})}{)}^{\mathrm{\prime }}(I-A_{LT(\text{MRSS})})\beta$

3. Simulation study

In this section, we conducted a simulation study to calculate the Monte Carlo estimates of MSEs of the estimators given in Table 3. For this simulation study, we used two different sample sizes n = 9, 15 and two different explanatory variable numbers, p = 3, 4. The explanatory variables were generated by

$$x_{ij}=(1-{\kappa }^2{)}^{1/2}{u}_{ij}+\kappa u_{ip+1}\text{,}i=1,2,\dots ,n;j=1,2,\dots ,p,$$

where u_ij is the explanatory standard normal pseudo-random numbers and κ is the theoretical correlation between any two explanatory variables [9]. We chose different correlations κ from 0.90 to 0.999. The response variable was generated from

$$y_i={\beta }_1{x}_{i1}+{\beta }_1{x}_{i2}+\cdots +{\beta }_p{x}_{ip}\text{ + }{\epsilon }_i\text{,}i=1,2,\dots ,n,$$

where ${\epsilon }_i$ is explanatory normal pseudo-numbers with zero mean and standard deviation σ. We chose three different standard deviation of errors, σ = 1, 3, 5. Besides, $\beta =({\beta }_1,{\beta }_2,\dots ,{\beta }_p)$ vector was taken as $(1/p,1/p,\dots ,1/p)$. Although there are many k values in the literature, one of the most popular optimal k values was given by Hoerl, Kennard and Baldwin [14]. This k value is denoted as $k_{HKB}$. Thus, we used this value to obtain the ridge regression estimator, which is estimated as follows:

$${\hat{k}}_{HKB}=p{\hat{\sigma }}^2/{\hat{\beta }}^{\mathrm{\prime }}\hat{\beta }.$$

The Liu-type estimator with the optimum k and d values is given by Liu [19]. These optimum values for the Liu-type estimator are given below

$${\hat{k}}_{LT}=\frac{{\lambda }_1-100{\lambda }_p}{99},{\hat{d}}_{LT}=-\frac{{\sum }_{i=1}^p(({\lambda }_i({\hat{\sigma }}_R^2-{\hat{k}}_{LT}{\hat{\alpha }}_{Ri}^2))/{({\lambda }_i+{\hat{k}}_{LT})}^3)}{{\sum }_{i=1}^p(({\lambda }_i({\lambda }_i{\hat{\alpha }}_{Ri}^2+{\hat{\sigma }}_R^2))/{({\lambda }_i+{\hat{k}}_{LT})}^4)},$$

where ${\hat{\sigma }}_R^2$ is the estimator of ${\sigma }^2$ using Ridge regression and ${\hat{\alpha }}_R=(\mathrm{\Lambda }+kI{)}^{-1}{Z}^{\mathrm{\prime }}Y$ [19]. This ${\hat{k}}_{LT}$ is selected to make the condition number (CN) of $X^{\mathrm{\prime }}X+kI$ reduce to 10 [9].

We generated 10,000 sets of explanatory and response variables for MRSS, RSS and SRS. We use the MSE criteria for the efficiency of the estimators. When MSE of an estimator is smaller than the other estimators, it is said to be more efficient than the other estimators. To estimate MSEs of the estimator of $\beta$, we used the following formula:

$$\widehat{\text{MSE}}=\frac{1}{10,000}\sum _{h=1}^{10,000}({\hat{\beta }}_h-\beta {)}^{\mathrm{\prime }}({\hat{\beta }}_h-\beta ).$$

To compare the performance of the ${\tilde{\beta }}_R$, ${\tilde{\beta }}_{LT}$, ${\hat{\beta }}_{\text{MRSS}}$, ${\tilde{\beta }}_{R(\text{MRSS})}$, ${\tilde{\beta }}_{LT(\text{MRSS})}$ estimators with the $\hat{\beta }$ estimator in detail, we can use the relative efficiency (RE) measurement. The RE of $\hat{\beta }$ against other estimators can be defined as follows:

$$\begin{array}{rl}R{E}_{{\tilde{\beta }}_R}& =\frac{\widehat{\text{MSE}}({\tilde{\beta }}_R)}{\widehat{\text{MSE}}(\hat{\beta })},R{E}_{{\tilde{\beta }}_{LT}}=\frac{\widehat{\text{MSE}}({\tilde{\beta }}_{LT})}{\widehat{\text{MSE}}(\hat{\beta })},R{E}_{{\hat{\beta }}_{\text{MRSS}}}=\frac{\widehat{\text{MSE}}({\hat{\beta }}_{\text{MRSS}})}{\widehat{\text{MSE}}(\hat{\beta })},\\ R{E}_{{\tilde{\beta }}_{R(\text{MRSS})}}& =\frac{\widehat{\text{MSE}}({\tilde{\beta }}_{R(\text{MRSS})})}{\widehat{\text{MSE}}(\hat{\beta })}\text{and}R{E}_{{\tilde{\beta }}_{LT(\text{MRSS})}}=\frac{\widehat{\text{MSE}}({\tilde{\beta }}_{LT(\text{MRSS})})}{\widehat{\text{MSE}}(\hat{\beta })}.\end{array}$$

Thus, it shows how much MSE values of the other estimators are relatively greater than the MSE of the $\hat{\beta }$ estimator.

We also investigated the robustness of the estimators in the imperfect ranking case for different correlations between the external ranking variable and the response variable of the model. The correlation coefficients are ρ = 0.50, 0.60, 0.70, 0.80, 0.90. The external ranking variable z is generated depending on the response variable as follows:

$$z_i=(1-{\rho }^2{)}^{1/2}{v}_i+\rho y_i\text{,}i=1,2,\dots ,n,$$

where $v_i$ is generated from the standard normal distribution.

In addition, we compared the efficiency of the estimators based on MRSS versus the estimators based on RSS $({\hat{\beta }}_{\text{RSS}},{\tilde{\beta }}_{R(\text{RSS})},{\tilde{\beta }}_{LT(\text{RSS})})$.

The results are summarized in Figures 1–21.

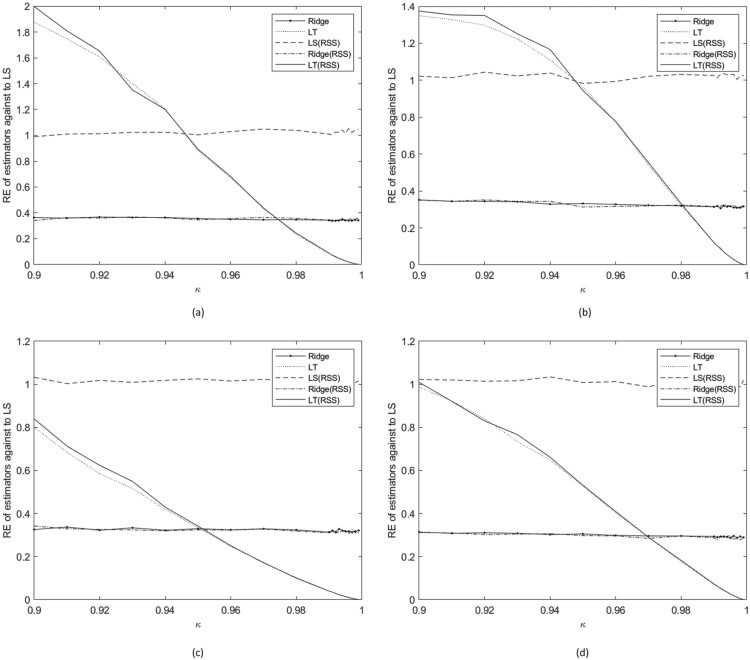
Figure 1.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 1 in the perfect ranking case.

Figure 2.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 1 and ρ = 0.50.

Figure 3.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 1 ρ = 0.60.

Figure 4.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 1 and ρ = 0.70.

Figure 5.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; (d) p = 4 and n = 15 when σ = 1 and ρ = 0.80.

Figure 6.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 1 and ρ = 0.90.

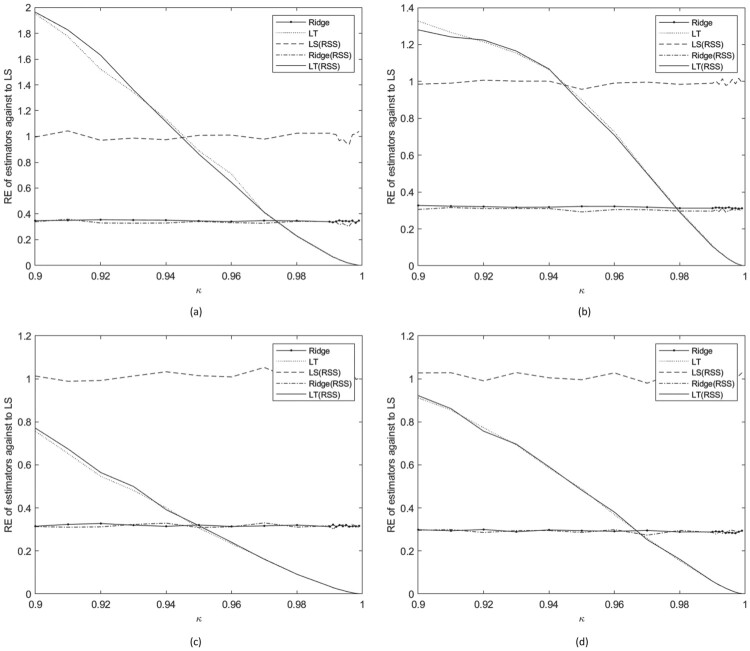
Figure 7.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 3 in perfect ranking case.

Figure 8.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 3 and ρ = 0.50.

Figure 9.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 3 ρ = 0.60.

Figure 10.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 3 and ρ = 0.70.

Figure 11.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 3 and ρ = 0.80.

Figure 12.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 3 and ρ = 0.90.

Figure 13.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 5 in perfect ranking case.

Figure 14.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 5 and ρ = 0.50.

Figure 15.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 5 and ρ = 0.60.

Figure 16.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 5 and ρ = 0.70.

Figure 17.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 5 and ρ = 0.80.

Figure 18.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on MRSS, Ridge estimator based on MRSS, and Liu-type estimator based on MRSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 5 and ρ = 0.90.

Figure 19.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on RSS, Ridge estimator based on RSS, and Liu-type estimator based on RSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 1.

Figure 20.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on RSS, Ridge estimator based on RSS, and Liu-type estimator based on RSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 3.

Figure 21.

Relative efficiency of the Ridge estimator based on SRS, Liu-type estimator based on SRS, LS estimator based on RSS, Ridge estimator based on RSS, and Liu-type estimator based on RSS against LS estimator based on SRS for (a) p = 3 and n = 9; (b) p = 3 and n = 15; (c) p = 4 and n = 9; and (d) p = 4 and n = 15 when σ = 5.

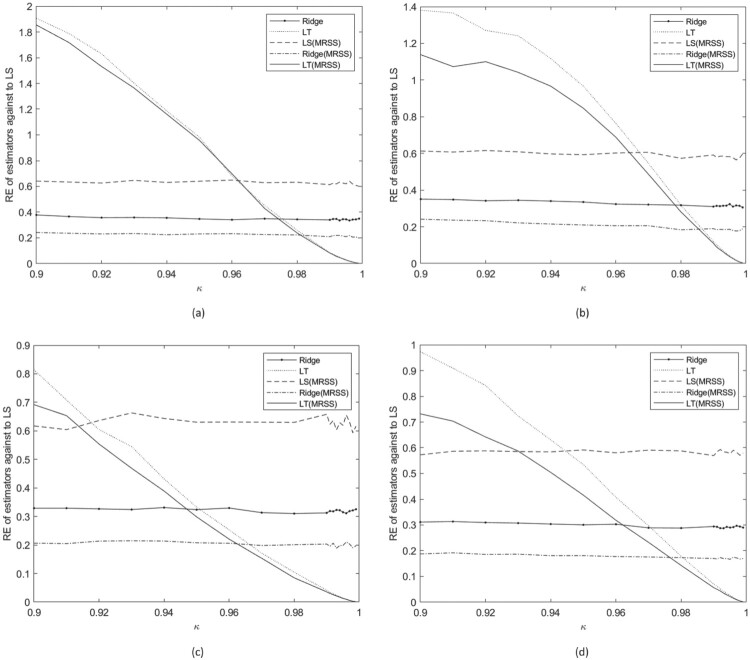
As seen from Figure 1, in the perfect ranking case, $R{E}_{{\tilde{\beta }}_{LT(\text{MRSS})}}$ is smaller than $R{E}_{{\tilde{\beta }}_{LT}}$ and $R{E}_{{\tilde{\beta }}_{R(\text{MRSS})}}$ is smaller than $R{E}_{{\tilde{\beta }}_R}$ for all the considered cases. This shows that the MRSS affects the MSE values of the estimators positively. Although $R{E}_{{\tilde{\beta }}_R}$, $R{E}_{{\hat{\beta }}_{\text{MRSS}}}\text{and}R{E}_{{\tilde{\beta }}_{R(\text{MRSS})}}$ values get smaller over the κ values, these values do not vary too much. However, $R{E}_{{\tilde{\beta }}_{LT}}\text{and}R{E}_{{\tilde{\beta }}_{LT(\text{MRSS})}}$ get smaller over the κ values dramatically. As a result of this, $R{E}_{{\hat{\beta }}_{\text{MRSS}}}$ is the smallest RE value when the κ is smaller than 0.985 for p = 3 and n = 9, as seen in Figure 1(a). As can be seen from Figure 1(b), when n = 15, this threshold value increases and becomes 0.988. Also, $R{E}_{{\hat{\beta }}_{\text{MRSS}}}$ is the smallest RE value when κ is smaller than 0.97 for p = 4 and n = 9 as seen from Figure 1(c). As seen in Figure 1(b), when n = 15, this threshold value increases and becomes 0.98. These results show that when n gets larger, this threshold also gets larger and when p gets larger this threshold value gets smaller.

As seen in Figures 2–6, in the imperfect ranking case, when the correlation coefficient of interested variable and external ranking variable are low and the sample size is n = 9, $R{E}_{{\tilde{\beta }}_{LT(\text{MRSS})}}$ is quite similar to $R{E}_{{\tilde{\beta }}_{LT}}$. As the sample size increases, $R{E}_{{\tilde{\beta }}_{LT(\text{MRSS})}}$ gets smaller than $R{E}_{{\tilde{\beta }}_{LT}}$. When κ gets higher, the difference between $R{E}_{{\tilde{\beta }}_{LT(\text{MRSS})}}$ and $R{E}_{{\tilde{\beta }}_{LT}}$ gets higher. The other results are similar to perfect ranking cases.

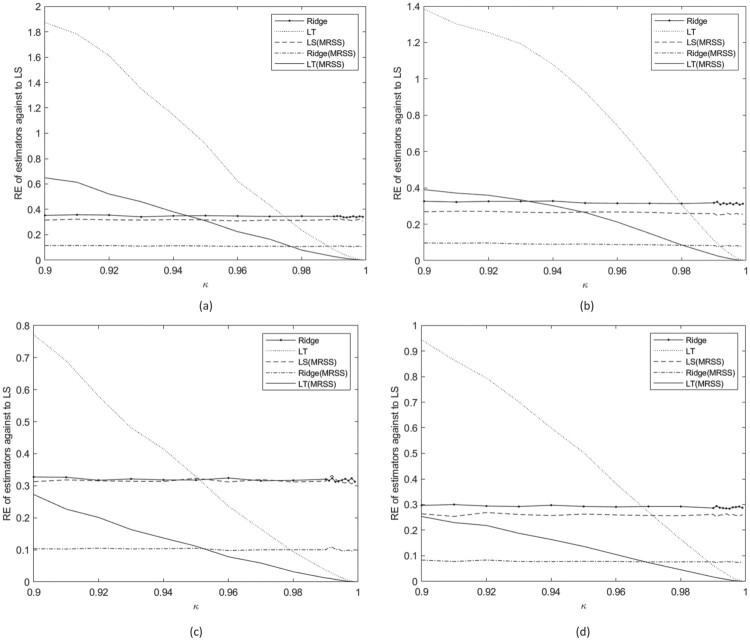
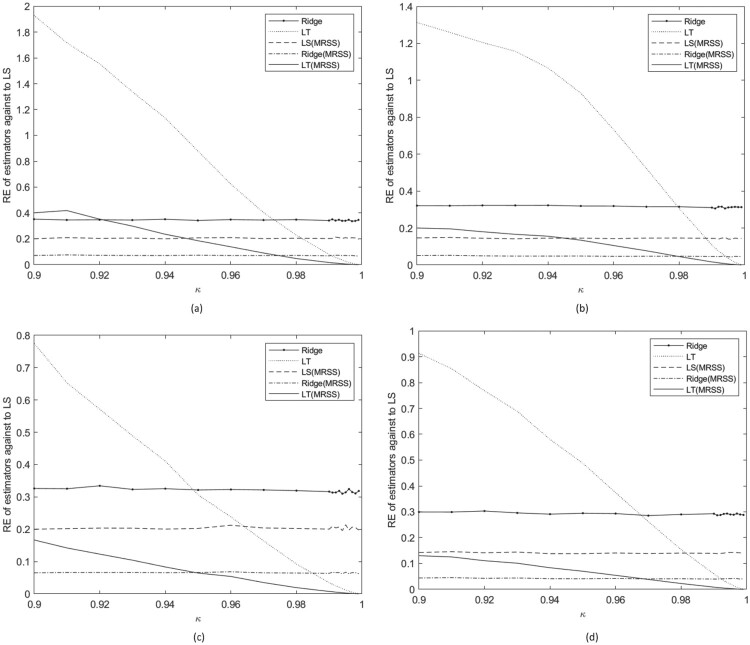
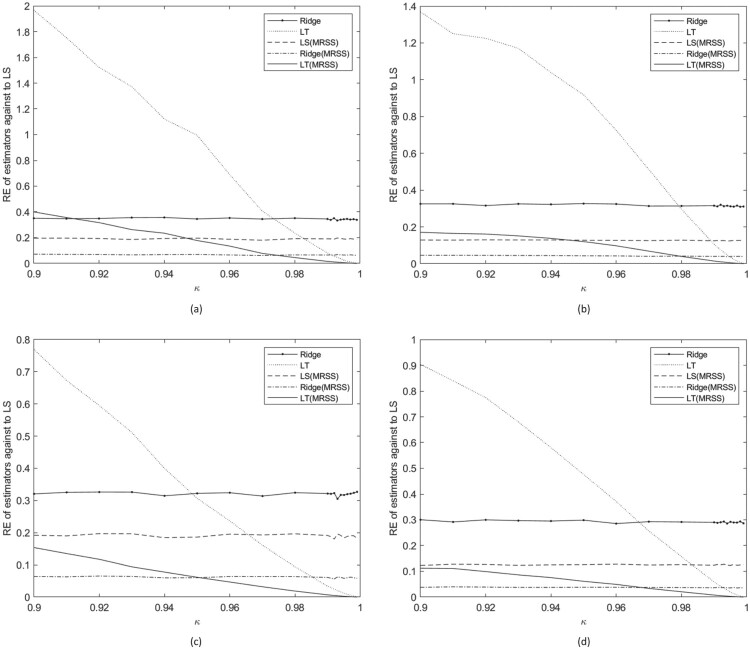
The obtained results in Figures 7–18 are very similar to those in Figures 1–6. Besides these results, the threshold value gets smaller when σ gets larger. This result shows that the LT estimator using MRSS performs better than the other estimators even when κ values are relatively small.

In general, it can be said that the Ridge estimator based on MRSS is better than the other estimators when collinearity is moderate. However, the Liu-type estimator based on MRSS is better than other estimators when collinearity gets severe.

As can be seen in Figures 19–21, when RSS was used in the LT estimator, the results were similar to classical SRS, and using RSS did not have much effect. It would be better to use MRSS instead of RSS as RSS does not have much effect on LT, Ridge and LS estimators.

For the investigation of the bias of the estimators, Table 4 was compiled. As seen in Table 4, for the same ρ, n and κ values, the biases of all considered estimators decrease as the p value increases. However, biases generally increase when the sample size increases. In addition, when the κ value increases, the biases are similar for the same ρ, n and p values. Thus, it can be said that the κ value has no effect on the biases of the estimators. This result can arise from the use of high and close κ values. When p = 3, the biases increase as ρ increases for the same κ value. This is an expected result since the median ranked set sample will be closer to the sample from SRS as ρ decreases.

Table 4.

The biases of the Ridge estimator based on SRS.

			n = 9			n = 15
			κ = 0.9	κ = 0.99	κ = 0.999	κ = 0.9	κ = 0.99	κ = 0.999
p = 3	$\rho$ = 0.6	Ridge	−0.024	0.059	−0.027	−0.016	0.004	−0.060
		LS(MRSS)	−0.079	−0.046	0.006	−0.104	−0.109	−0.223
		Ridge(MRSS)	−0.103	−0.072	−0.059	−0.123	−0.115	−0.183
		LT	−0.001	0.025	−0.007	0.003	−0.001	−0.005
		LT(MRSS)	−0.072	−0.084	−0.093	−0.109	−0.108	−0.109
	$\rho$ = 0.8	Ridge	−0.018	−0.011	0.061	−0.015	−0.004	−0.010
		LS(MRSS)	−0.155	−0.149	−0.183	−0.190	−0.193	−0.069
		Ridge(MRSS)	−0.173	−0.161	−0.182	−0.202	−0.190	−0.102
		LT	0.019	−0.008	−0.002	0.012	−0.002	0.000
		LT(MRSS)	−0.146	−0.164	−0.162	−0.197	−0.189	−0.178
	$\rho$ = 0.9	Ridge	−0.020	−0.022	−0.158	−0.013	−0.013	−0.001
		LS(MRSS)	−0.207	−0.207	−0.318	−0.223	−0.218	−0.277
		Ridge(MRSS)	−0.219	−0.208	−0.283	−0.234	−0.229	−0.272
		LT	0.012	−0.008	−0.007	0.015	0.001	−0.004
		LT(MRSS)	−0.219	−0.205	−0.202	−0.214	−0.224	−0.227
	$\rho$ = 1	Ridge	−0.026	0.080	0.002	−0.015	−0.006	0.089
		LS(MRSS)	−0.241	−0.208	−0.262	−0.271	−0.271	−0.247
		Ridge(MRSS)	−0.251	−0.226	−0.255	−0.280	−0.273	−0.260
		LT	0.018	0.030	−0.007	0.005	0.001	0.000
		LT(MRSS)	−0.241	−0.238	−0.243	−0.273	−0.269	−0.270
p = 4	$\rho$ = 0.6	Ridge	−0.010	0.022	0.065	−0.009	−0.006	−0.023
		LS(MRSS)	−0.073	−0.054	0.010	−0.075	−0.093	−0.123
		Ridge(MRSS)	−0.083	−0.057	−0.053	−0.088	−0.088	−0.079
		LT	0.007	0.014	−0.001	0.014	−0.003	−0.002
		LT(MRSS)	−0.064	−0.066	−0.069	−0.073	−0.080	−0.081
	$\rho$ = 0.8	Ridge	−0.014	0.044	−0.075	−0.021	−0.001	0.060
		LS(MRSS)	−0.109	−0.101	0.207	−0.135	−0.128	−0.076
		Ridge(MRSS)	−0.126	−0.100	−0.008	−0.144	−0.132	−0.116
		LT	−0.002	0.006	−0.005	−0.008	−0.004	0.001
		LT(MRSS)	−0.106	−0.110	−0.115	−0.133	−0.134	−0.134
	$\rho$ = 0.9	Ridge	−0.020	−0.004	−0.066	−0.015	−0.016	0.025
		LS(MRSS)	−0.150	−0.138	−0.169	−0.168	−0.175	−0.157
		Ridge(MRSS)	−0.157	−0.148	−0.119	−0.176	−0.175	−0.174
		LT	−0.001	0.002	−0.003	0.000	−0.006	−0.001
		LT(MRSS)	−0.152	−0.151	−0.149	−0.168	−0.172	−0.169
	$\rho$ = 1	Ridge	−0.014	0.031	−0.154	−0.011	0.003	0.013
		LS(MRSS)	−0.188	−0.182	−0.130	−0.208	−0.221	−0.152
		Ridge(MRSS)	−0.191	−0.171	−0.170	−0.212	−0.214	−0.194
		LT	0.001	0.009	−0.003	0.008	0.004	0.002
		LT(MRSS)	−0.185	−0.184	−0.178	−0.207	−0.209	−0.202

Note: Liu-type estimator based on SRS. The LS estimator based on MRSS. The Ridge estimator based on MRSS. The Liu-type estimator based on MRSS against the LS estimator based on SRS for p = 3 and n = 9 and 15.

4. Real data example

In this section, we use a real data example, which is partially used by Özdemir et al. [24] and presented by Doğan and Şen [7]. Doğan and Şen [7] investigated the relationship between the fish age and the total weight and length of the Capoeta trutta population of the Keban Dam Lake (Elazığ) between November 2011 and December 2012. Fish age is exactly determined by using the otolith bone. However, this process is quite time consuming, costly and results in the death of the fish. For these reasons, we can use other highly correlated variables such as length or weight of the fish for determining the fish age. In these data, the correlation coefficient between the fish age and the total weight was calculated to be approximately 0.80. Thus, we used the total weight as the ranking variable. Therefore, the response variable is fish age (Y) and explanatory variables are total weight (X₁) and total length (X₂). Samples were ranked according to total fish weight and the age of the selected fish was determined by using the otolith bone. The correlation matrix between total weight and length was also calculated as follows:

$$\rho =\left[\begin{array}{cc}1& 0.884\\ 0.884& 1\end{array}\right].$$

CN and variance inflation factor (VIF) values are also given, respectively, as follows:

$$\begin{array}{l}\text{CN}=15.78,\\ \text{VIF}=\mathrm{63.725.}\end{array}$$

As seen in VIF and CN values, there is a moderate multicollinearity between explanatory variables. Thus, ridge regression estimators are more suitable for these data rather than LS and Liu-type estimators.

According to the median ranked set sample, ranked set sample and simple random sample, we obtained the regression coefficients of the model and we used the ridge estimator based on SRS, MRSS and RSS. We also obtained the sum of squared residuals (SSR) of these models. It is known that smaller SSR fits the data of the model more tightly.

As can be seen from Table 5, it can be said that ${\tilde{\beta }}_{R(\text{MRSS})}$ is a more efficient estimator than ${\tilde{\beta }}_R$ and ${\tilde{\beta }}_{R(\text{RSS})}$ for this sample.

Table 5.

Estimations of model parameters.

	Model parameters
Estimators	β1	β1	SSR
${\tilde{\mathit{\beta }}}_{\mathit{R}}$	0.0291	0.0896	2.8372
${\tilde{\mathit{\beta }}}_{\mathit{R}(\text{MRSS})}$	−0.0310	0.5974	0.4587
${\tilde{\mathit{\beta }}}_{\mathit{R}(\text{RSS})}$	−0.0172	0.4894	2.0930

5. Conclusion

In this study, we obtained the Ridge and Liu-type estimators using a median ranked set sample in the presence of multicollinearity. We presented a simulation study to determine the efficiency of the estimators. The simulation study shows that the proposed estimators perform better than the other estimators for all the considered cases do. We also showed our findings on a real data example. These results are also similar to the simulation study. In future studies, the proposed method can be generalized by using different types of ranked set samplings to obtain more efficient results for different cases.

Disclosure statement

No potential conflict of interest was reported by the authors.