A data-driven hybrid ensemble AI model for COVID-19 infection forecast using multiple neural networks and reinforced learning

Abstract

The COVID-19 outbreak poses a huge challenge to international public health. Reliable forecast of the number of cases is of great significance to the planning of health resources and the investigation and evaluation of the epidemic situation. The data-driven machine learning models can adapt to complex changes in the epidemic situation without relying on correct physical dynamics modeling, which are sensitive and accurate in predicting the development of the epidemic. In this paper, an ensemble hybrid model based on Temporal Convolutional Networks (TCN), Gated Recurrent Unit (GRU), Deep Belief Networks (DBN), Q-learning, and Support Vector Machine (SVM) models, namely TCN-GRU-DBN-Q-SVM model, is proposed to achieve the forecasting of COVID-19 infections. Three widely-used predictors, TCN, GRU, and DBN are used as elements of the hybrid model ensembled by the weights provided by reinforcement learning method. Furthermore, an error predictor built by SVM, is trained with validation set, and the final prediction result could be obtained by combining the TCN-GRU-DBN-Q model with the SVM error predictor. In order to investigate the forecasting performance of the proposed hybrid model, several comparison models (TCN-GRU-DBN-Q, LSTM, N-BEATS, ANFIS, VMD-BP, WT-RVFL, and ARIMA models) are selected. The experimental results show that: (1) the prediction effect of the TCN-GRU-DBN-Q-SVM model on COVID-19 infection is satisfactory, which has been verified in three national infection data from the UK, India, and the US, and the proposed model has good generalization ability; (2) in the proposed hybrid model, SVM can efficiently predict the possible error of the predicted series given by TCN-GRU-DBN-Q components; (3) the integrated weights based on Q-learning can be adaptively adjusted according to the characteristics of the data in the forecasting tasks in different countries and multiple situations, which ensures the accuracy, robustness and generalization of the proposed model.

1. Introduction

1.1. Background

With the COVID-19 pandemic, the world's health system is suffering a huge impact. The effective estimation (or prediction, forecasting) of the number of COVID-19 cases will be of great help for each country to plan its own health policies (including vaccination, quarantine, isolation, lockdown, social distancing, etc.) and estimate the economic and social losses of the epidemic [1]. Scholars have been committed to solving the problems of COVID-19 incidence prediction and epidemiological modeling, and proposed epidemiological models (SIR [2], SEIR [3,4], SIRD [5], phenomenology [6], etc.), time series models (autoregressive models [7,8], exponential models [9], regression model [10,11], Prophet model [12], etc.), machine learning model (based on regression tree [13], LSTM [14], polynomial neural network [15], ANFIS [16], SVM [17], etc.) and other types of models [18].

Classical epidemiological studies are mostly deterministic and works with large populations [18]. They are constructed based on correct physical dynamic modeling, which are based on SIR dynamics models and parameter estimation methods in statistics to complete the modeling of the epidemiological pathology and transmission process, and then to predict the process characteristics of the disease epidemic, but the accuracy of such dynamic models depends on a complete and accurate description of the dynamics process and highly dependent on the results of reliable parameter estimation [18]. Therefore, although the SIR dynamics model can give a long-term analysis of transmission characteristics, their reliability is limited by many changing factors including population immunity status of diseases (such as vaccines), public events (such as quarantine, migration, and other policy changes) and so on. For example, in Bhattacharjee et al.’s SAHQD (Susceptible, infected, hospitalized, quarantined, deceased) model, a complex multi-compartment dynamics model, although information on the social distancing measures and diagnostic testing rates are incorporated to characterize the dynamics of the various compartments of their model, the degree of social distance restrictions and the mobility within the population were neglected [19].

Data-driven models, including statistic models and machine-learning models, overcome these shortcomings to a great extent. Statistic models such as Autoregressive Integrated Moving Average (ARIMA), Seasonal Autoregressive Integrated Moving Average (SARIMA) were adopted by previous COVID-19 infection prediction studies. K.E. ArunKumar et al. adopted Autoregressive Integrated Moving Average (ARIMA) and Seasonal Autoregressive Integrated Moving Average (SARIMA) forecasts to predict the future trend (rising or falling) of the COVID-19 epidemic in the top 16 countries [20]. Christopher J Lynch et al. adopted and compared Holt-Winters exponential smoothing (HW), growth rate model (Growth), moving average (MA), autoregressive (AR), autoregressive moving average (ARMA), and autoregressive integrated moving average (ARIMA) models [21]. However, their prediction accuracy remains to be further improved.

Recently, deep learning models have been proved to be a reliable and promising tool in data prediction. Therefore, there are also many studies focusing on the potential of applying deep learning to predict the COVID-19 infection numbers. Most of previous researches were based on single models, such as LSTM, MLP, ELM, etc. Ammar H. Elsheikh et al. applied the LSTM model to predict the total number of confirmed cases and deaths in 6 different countries; Brazil, India, Saudi Arabia, South Africa, Spain and the United States. Their model is only based on a single LSTM model, and the prediction accuracy needs to be improved [22]. Nasrin Talkhi et al. compared nine models including NNETAR, ARIMA, Holt-Winter, BSTS, TBATS, Prophet, MLP and ELM network models by evaluating indicators RMSE, MAE and MAPE%, and they selected the best model that had the lowest value of the performance index [23].

Generally, hybrid models proposed by several scholars has better overall performances in COVID-19 infection number forecasting than single models. For example, Mohammed A.A. Al-qaness et al. proposed a new short-term prediction model, using an enhanced version of the Adaptive Neuro-Fuzzy Inference System (ANFIS). An improved marine predator algorithm (MPA), chaotic MPA (CMPA), is proposed, which improves the ANFIS algorithm [16]. Nanning Zheng proposed a hybrid AI model based on an improved susceptible–infected (ISI) model, the natural language processing (NLP) module and the long short-term memory (LSTM) to predict the cumulative infection numbers in China during February 19, 2020 to February 24, 2020 [24]. Although their research used hybrid models, the accuracy of the single predictor could be further improved, and the weights of their component models were given in a manual or randomized way. Meanwhile, the error compensation was not considered and embedded in their hybrid model systems [25].

1.2. Motivation and our work

We conducted this study based on several considerations: First, most of the current studies carry out prediction of COVID-19 incidence based on dynamics modeling or multivariate data regression, etc., often relying on complex compartment models or extensive but not always available multidimensional data for forecasting, which makes the models less effective and powerful. Meanwhile, due to the unavailability or incompletion of data and factors that interfere with the dynamic state, such as epidemic policies and virus variants, it is difficult to consistently describe the progress of the epidemic or to generalize across regions. Second, current studies of deep learning and reinforcement learning for COVID-19 forecast are relatively few compared to dynamics modeling and classical time series analysis (e.g., ARIMA), whereas they are very likely to have a significant role in COVID-19 morbidity prediction and deserve to be included in researchers' perspectives. Third, the proposed ensemble model can improve the generalizability of existing deep learning sub-models across geographies and time, achieving satisfactory predictions using only a single time series of COVID-19 daily incidence numbers. It also provides an idea of weight training and error compensation based on reinforcement learning framework, which can be used as a reference for subsequent integration of multimodal data and hybrid integration of multiple modeling approaches.

In this work, we present a data-driven TCN-GRU-DBN-Q-SVM ensemble hybrid model. First, three widely used networks, TCN, GRU and DBN, are used as single predictors. Second, three predictors are ensembled by reinforcement learning method (Q-learning) with different weights. Third, an error predictor built by SVM, is trained with validation set, and the final prediction result could be obtained by combining the TCN-GRU-DBN-Q model with the SVM error predictor. The proposed model adopted multiple newly-proposed predictors (TCN, GRU and DBN) with satisfying standalone performance to work collectively, and the integrated weights based on Q learning can be adaptively adjusted according to the characteristics of the data in different countries and multiple situations, which ensures the accuracy and generalization of the proposed model. Meanwhile, an SVM-based error compensation mechanism was utilized to further improve the accuracy of the model. Our study can better improve the generalization ability and accuracy of the model on COVID-19 prediction driven by single time series data through an ensemble way, and the study provides a possible framework for embedding other data modalities or other modeling methods based on reinforcement learning, which can enrich and inspire the methodology of COVID-19 prediction to some extent.

1.3. Structure of this article

In this article, Section 2 (Literature review) further subsumes and summarizes the existing literature on COVID-19 forecast based on a brief summary of basic COVID-19 forecast tools given in Section 1 (Introduction).

Section 3 (Methods) shows the architecture of the model and its training steps (section 3.1), and introduces the three sub-models TCN, GRU, DBN and the basic ideas of Q-learning and SVM error compensation (section 3.2).

Section 4 (Experiment) introduces the datasets used in the experiments and the split of training, validation, and test set (section 4.1), and specifies the metrics to evaluate the models (section 4.2). Section 4.3 gives the parameters for model training and shows the process of determining the number of input neurons (section 4.3.1). It gives the optimized weights derived from Q-learning during the model integration, and compares the performance of the ensemble model and the component models to clarify the effectiveness of model (section 4.3.2).

Section 5 (Results and Discussion) discusses the forecast results of the model and verifies the good generalization ability and prediction accuracy of the integrated model by comparing it with the existing model on three different national datasets.

Section 6 (Limitations and Further Work) gives the application scenario of the model, and suggests some possible directions for improvement and factors to be considered when improving the model.

Section 7 (Conclusion) gives the conclusion of the study.

2. Literature review

Table 1 and Fig. 1 (A) show the prediction models for the number of COVID-19 incidences from the existing literature. It can be seen that the current COVID-19 prediction tools are mainly of the following types:

• 1)Models based on kinetic (or dynamics) modeling, which further clarify the pattern of changes in the number of a specific population by dividing the population into Susceptible (S), Infected (I), Recovered (R) compartments, etc., and defining the transition relationships among them through several differential equations. Since the onset of the COVID-19 epidemic, multi-generational kinetic models have emerged, whose evolution route could be summarized as: SIR→SEIR [26], SLIR [27] (considering close contacts or the latent) → SEI_AIR [28] (considering asymptomatic infected persons), SAHQD [19] (considering quarantine policies) → SEIRMH [29], SEPIAHR [30] (considering medical-related factors) → SCUAQIHMRD [31] (considering COVID-19 hierarchical treatment).
• 2)Time series analysis. The simpler exponential smoothing model arranges the data in chronological order from new to old. The weights are assigned from large to small, and the weight values are exponentially decreasing. In addition to exponential smoothing, which smoothes the data based on exponentially decreasing parameters, there is also the common method of fitting an ARIMA [[32], [33], [34]] model, which consists of three parts: the autoregressive process (AR), the differential part (Integrated) and the moving average process. In addition, there are multivariate time series analysis based on the standard Autoregressive model (AR) [35], including the VAR (Vector Autoregressive model) [36], STAR (smooth transition autoregressive) [35] and their modifications.
• 3)Forecast model based on Grey Theory. Grey prediction model is a prediction method that builds a mathematical model to make a forecast through a small amount of incomplete information. The modifications of the basic GM(1,1) model, such as Fractional Order Accumulation Grey Model (FGM) [37], Hybrid grey exponential smoothing approach [38], and Internally Optimized Grey Prediction Models (IOGMs) [39], have been proposed to be effective tools for COVID-19 forecast.
• 4)Forecast model based on Machine Learning. Models such as LSTM, RF regressions, shown in Table 1 (A), have been widely researched in the COVID-19 forecast. Long short-term memory (LSTM), the most representative one of deep-learning, is a special kind of RNN, which is mainly designed to solve the gradient disappearance and gradient explosion problems during the training of long sequences. LSTM has been proved to be a powerful deep-learning network for the forecast of COVID-19 infections [[40], [41], [42], [43]].

Table 1.

A summary of recent COVID-19 forecast models.

(A) Recent COVID-19 forecast models
Types	Method	Performance				Religion	Ref.
		MAE	RMSE	Pearson	Spearman
Dynamics	SAHQD model (Susceptible, infected, hospitalized, quarantined, deceased)	N.P.	N.P.	N.P.	N.P.	U.S.	[19]
	SCUAQIHMRD model (Susceptible, close contact, uninfected under home quarantine, asymptomatic under home quarantine, mild symptoms under home quarantine, severe symptoms under home quarantine, infectious in Designed Hospitals, infectious in Fangcang Hospitals, Recovered, Death)	N.P.	N.P.	N.P.	N.P.	Wuhan, China	[31]
	SEPIAHR model (Susceptible, exposed, pre-symptomatic infectious, ascertained infectious, unascertained infectious, isolation in hospital and removed	N.P.	N.P.	N.P.	N.P.	Wuhan, China	[30]
	SEIAIR model (Susceptible, incubation, asymptotic infected, recovered)	N.P.	N.P.	N.P.	N.P.	Wuhan, China	[28]
	SEIRMH model (Susceptible, exposed without symptoms, infected with symptoms, with medical care, and removed from the system)	N.P.	N.P.	0.84	N.P.	Belgium	[29]
	Adaptive interacting cluster-based SEIR (AICSEIR) model	N.P.	N.P.	0.84	N.P.	Italy, the U.S., and India	[44]
	modified SEIR model (Including vaccination)	N.P.	N.P.	N.P.	N.P.	NYC, U.S.	[45]
	SEIR model with Bayesian inference	N.P.	N.P.	N.P.	N.P.	Israel	[46]
	SLIR model (Susceptible, latent, infected, recovered	N.P.	N.P.	N.P.	N.P.	China	[27]
	SEIR model	N.P.	N.P.	N.P.	N.P.	Texas, USA	[26]
	Sequential compartmental models	N.P.	N.P.	N.P.	N.P.	Homeless Shelter, Chicago, Illinois, USA	[47]
Time series	smooth transition autoregressive (STAR) model	0.208	0.297	N.P.	N.P.	Africa sub-region	[35]
	Linear AR model	0.251	0.385	N.P.	N.P.	Africa sub-region	[35]
	ARIMA	27.86	35.69	N.P.	N.P.	Malaysia	[32]
	ARIMA	N.P.	N.P.	N.P.	N.P.	France	[33]
	Modified VAR regression	47.43	N.P.	N.P.	N.P.	NYC, U.S.	[36]
	Linear regression	N.P.	7.562	N.P.	N.P.	Iran	[40]
	Poisson count time series model (Disease surveillance and Twitter-based population mobility data)	N.P.	N.P.	N.P.	N.P.	South Carolina	[48]
	ARIMA	50.109	95.322	N.P.	N.P.	India	[34]
Grey forecast	Fractional Order Accumulation Grey Model (FGM)	N.P.	109496/96411/14560/64253/15/1123/106223	N.P.	N.P.	U.S., France, UK, Germany, China, Japan, India	[37]
	Hybrid grey exponential smoothing approach	N.P.	5.05	N.P.	N.P.	Sri Lanka	[38]
	Internally Optimized Grey Prediction Models (IOGMs)	N.P.	N.P.	N.P.	N.P.	Rajasthan, Maharashtra, Delhi	[39]
ML methods	random forest regression algorithm	5.42	9.27	0.89	0.84	215 countries and territories	[49]
	long short-term memory (LSTM) models	N.P.	27.187	N.P.	N.P.	Iran	[40]
	multilayer perceptron (MLP) neural network (n hidden layer)	0.36 (n = 1) 0.40 (n = 2)	0.64 (n = 1) 0.84 (n = 2)	0.36 (n = 1) 0.47 (n = 2)	N.P.	U.S.	[50]
	Pearson correlation test and general linear model	N.P.	N.P.	0.978	N.P.	U.S.	[51]
	a simple random forest statistical model	N.P.	N.P.	0.89	N.P.	Ohio, U.S.	[52]
	WEKA tool	≈1200	≈1000	N.P.	N.P.	Pakistan	[53]
	deep interval type-2 fuzzy LSTM (DIT2FLSTM)	N.P.	N.S.	N.P.	N.P.	USA, Brazil, etc.	[41]
	generalized linear and tree-based machine learning models	0.21	N.P.	0.99	N.P.	Tennessee	[54]
	an ensemble of 10 LSTM-based networks	90.38	N.P.	N.P.	N.P.	The county-level in the US	[42]
	LSTM + Rt method	N.P.	N.P.	0.872	N.P.	West Virginia	[43]
	Least-Square Boosting Classification algorithm	1200	N.P.	N.P.	N.P.	Countries having maximum number >2000 of confirmed cases in a day	[55]

(B) Comparison between different types of COVID-19 forecast models
Types	Strength	Weakness
Dynamics	➢Able to forecast over a wide future time window ➢The physical meaning of the model is very clear	➢Cannot be adapted to situations where the model subject has increased or where model parameters change with specific policies, disease pathogen variability, etc. ➢High requirements for parameter estimation ➢High demands on data sources, some of which are often missing or inaccessible, and their neglect often leads to unrealistic model assumptions
Time series	➢Simple and reproducible steps ➢The required data are easily available ➢Particularly suitable for cases where time series are periodic	➢Application scenarios are limited, e.g. ARMA model can only be applied to stationary situations, etc.
Grey forecast	➢Simple and reproducible steps ➢The required data are easily available	➢Similar to fuzzy mathematical theory, the physical meaning of the model is not clear
Machine learning	➢Higher potential for hybrid integration ➢Satisfactory performance for information mining ➢Satisfactory accuracy if the amount of data permits	➢Features obtained by deep learning methods do not have a clear physical meaning ➢The generalization ability of the model may be insufficient

Notes: N.P. = Not provided. Meanwhile, it is worth noting that although we give specific model performance in above table, it is not generalizable and comparable across datasets due to the different number of infections within different geographic regions.

Fig. 1.

(A) Dynamic modeling of COVID-19 pandemic, SEIR model as an example; (B) Basic idea of forecast with Grey Theory; (C) A neuron net structure in Deep-learning forecast of COVID-19; (D) ARIMA model, a combination of differential operation and ARMA method.

A comparison of the advantages and disadvantages of the four types of prediction approaches is given in Table 1(B). From the literature review, it can be seen that the current research is still less on deep-learning based ensemble models and more focused on broadening the amount of information covered by existing models from multiple data modalities. It is meaningful to investigate how to further optimize the performance of deep learning models on single-input time series through weight optimization and error compensation strategies in the ensemble framework to further improve the accuracy and generalization of COVID-19 forecast models.

3. Methods

3.1. Model architecture

As shown in Fig. 2 , our model includes three sub-predictors TCN, GRU, and DNB. These sub-predictors give prediction results respectively. Under the integrated effect of Q reinforcement learning, these three models are given different weights, and then an integrated model could be built based on TCN, GRU, DNB, and their weightsω ₁, ω ₂, ω ₃. We further trained an error training model based on SVM by comparing the prediction results with the validation set. By integrating the SVM model with the synthetic predictor obtained by Q reinforcement learning, the final hybrid integration model is obtained. The detailed steps of model building are as follows:

• Step 1: Preprocess and normalize time series data.

• Step 2: Train the three neural networks, TCN, GRU and DBN, with the time-series data of the training set respectively, and then input the test set into the network to obtain the test result sequence, denoted as x₁, x_2, and x ₃.

• Step 3: Give a randomized initial weight of each output sequence as ω₁, ω₂, ω₃, and set the output:

$$output={\omega }_1{X}_1+{\omega }_2{X}_2+{\omega }_3{X}_3$$

Fig. 2.

(A) The architecture of the proposed model; (B) The experimental procedures of this study, where the total experiment was divided into four parts: training the component model, training the hybrid model, training the SVM model for error predicting, and calculating the final prediction value by hybrid ensemble model composed of TCN-GRU-DBN-Q hybrid model and error-predicting SVM model.

In order to optimize the weights of three network, reinforce learning method, Q-learning, is used. The optimization goal of Q-learning was to minimize the output RMSE (namely the loss function, or the evaluation function Q in Q-learning training) value:

$$\text{RMSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(y_i-y_i^{\prime }\right)}^2}$$

where $y_i$ is the actual value, and $y_i^{\prime }$ is the forecasting value. The Q-learning is trained with validation set.

• Step 4: Calculate the error between O and the actual sequence (in validation set) and get the error sequence R. Taking R as the training set, SVM is used to model the error sequence, which gives a compensation for the predictive result given by the TCN-GRU-DBN-Q model.

• Step 5: Input the test set into the hybrid ensemble model to get the output. For each output, input it into the error prediction SVM model to get the prediction error error _pred, then the final output O is:

$$O=output+erro{r}_{\text{pred}}$$

3.2. Components of the proposed model

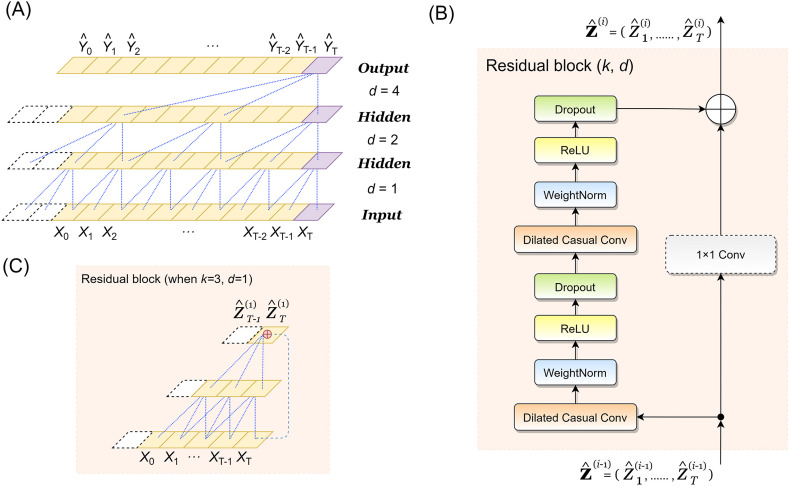
3.2.1. Temporal Convolutional Networks (TCN)

TCN is adopted as a sub-predictor of the proposed ensemble model. In essence, TCN is an integration of fully convolutional networks, causal convolution, dilated convolution, and residual connections [56]. First, generally, TCN combines the 1D FCN and casual convolutions [57]. In FCN architecture, each layer is the same length as the input layer, and a zero padding layer is added to keep subsequent layers the same length as previous ones, which assures that the output produced by the network is of the same length as the input [56]. Second, the casual convolutions, where an output at time t is convolved only with elements from the time t and earlier in the previous layer, are also adopted in TCN to ensure that there is no information leakage. Third, dilated convolutions enable TCN to adapt to forecasting tasks with a longer history, i.e., to expand the receptive field. For each 1-D input sequence $\mathbf{x}\in {ℝ}^n$ and a filter $f:\left\{0,\mathrm{...},k-1\right\}\to ℝ$, the operation F on element s of the sequence is defined as [57]:

$$F\left(s\right)=\left(\mathbf{x}{\ast }_{d}f\right)\left(s\right)=\sum _{i=0}^{k-1}f\left(i\right)\cdot {\mathbf{x}}_{s-d\cdot i}$$

where the dilation factor is d, k denotes the size of the filter $f:\left\{0,\mathrm{...},k-1\right\}\to ℝ$, s-d·i is the direction of the past [57]. Thus, a fixed step is introduced between every two adjacent filter taps, and the larger the dilation is, the wider the input ranges (i.e. an output at the top level) could be, which increase the receptive field to a great extent. Fourth, a residual block (shown in Fig. 3 (B) and (C)) is added to the model to allow layers to adapt to the modifications to the identity mapping. It contains a branch leading out to serial transformations $ℱ\left(\mathbf{x}\right)$:

$$o=\text{Activation}(x+ℱ\left(\mathbf{x}\right))$$

where o accounts for the outputs added to the input x of the residual block.

Fig. 3.

Architecture and elements in a TCN [57]. (A) A dilated casual convolution where the dilation factors d = 1, 2, 4 and filter size is 3; (B) The residual block of TCN, where an unit convolution (1 × 1 conv) is added to adapt the model structure to situations that the residual input is of different dimension with the output; (C) A possible residual connection in a TCN, where the solid purple lines are filters and the dashed purple lines are identity mappings. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

3.2.2. Gated Recurrent Unit (GRU)

GRU is one of the predictors of the ensemble model in this study. The classical LSTM solves the problem of long-term dependencies of Recurrent Neural Networks (RNN). However, its complex structure reduces the efficiency. Therefore, GRU was proposed in 2014 as a simpler design of RNN with the accuracy of original RNN maintained and its efficiency improved [58,59]. There are only two gate structures, reset gate and update gate (a combination of the forgetting gate and the input gate), in a GRU network, which reduces the parameter numbers significantly and improves the model efficiency to a great extent. The ratio between the transmission and retention of information in the past moment is determined by the update gate and the reset gate jointly, and the mathematical expressions of the reset gate and update gate are shown in the following formulas:

The update gate $z_t$ is:

$$z_t=\sigma \left(W^{\left(z\right)}{x}_t+U^{\left(z\right)}{h}_{t-1}\right)$$

The reset gate $r_t$ is:

$$r_t=\sigma \left(W^{\left(r\right)}{x}_t+U^{\left(r\right)}{h}_{t-1}\right)$$

where $x_t$ is the t-th component of the input sequence, $h_{t-1}$ is the information of the previous time step, $W^{\left(z\right)}$, $W^{\left(r\right)}$, $U^{\left(z\right)}$ and are the weight matrices, and the sigmoid function σ(x) is:

$$\sigma \left(x\right)=\frac{1}{1+e^{-x}}$$

Due to the introduction of the sign function, the values of $z_t$ and $r_t$ could only be 0 or 1, which indicates the switch state of the corresponding gate. To put it simply, if $z_t=0$, the update gate is closed and the information in the initial time step can be kept.

Meanwhile, referring to the stored historical data, the reset gate could be calculated as follows:

$$h_t^{\prime }=\tanh \left(W{x}_t+r_t\Theta U{h}_{t-1}\right)$$

where W and U are the weight matrices. The information content could be retained or forgotten, which is determined by calculating the Hadamard product of $r_t$ and $U{h}_{t-1}$.

3.2.3. Deep Belief Networks (DBN)

In this paper, the DBN is one of the predictors of the ensemble model. The essence of DBN is a stacking of a series of well-trained Restricted Boltzmann Machine (RBM). Boltzmann machines are a large class of neural network models, but the most used in practical applications is RBM, a specific type of Markov Random Fields (MRFs). The model of RBM is a two-layer simple neural network, so it cannot be regarded as the category of deep learning in the strict sense. However, as a stack of RBMs, DBM can be regarded as the promotion of RBM. In an RBM, visible variables v are connected to stochastic hidden units h using undirected weighted connections [60]. The aim of RBM training is to get a favored probability distribution P(v, h) described by an energy function E(v, h; θ) where θ=(ω, b, a) denotes a parameter set (where ω _ij denotes the symmetric weight between visible unit i and hidden unit j, b _i is the bias of i-th visible unit v _i, and a _j is the bias of j-th hidden unit h _j) which could be described as (for a binary RBM [61]):

$$-\log P(\mathbf{v},\mathbf{h})\propto E(\mathbf{v},\mathbf{h};\mathbf{\theta })=-\sum _{i=1}^{\left|V\right|}\sum _{j=1}^{\left|H\right|}{\omega }_{ij}{v}_i{h}_j-\sum _{i=1}^{\left|V\right|}{b}_i{v}_i-\sum _{i=1}^{\left|V\right|}{a}_j{h}_j$$

where $\left|V\right|$ and $\left|H\right|$ are the numbers of visible and hidden units, respectively. Thus, supposing the v or h is fixed, the conditional probability distributions of $p(h_j|\mathbf{v};\mathbf{\theta })$ and $p(v_i|\mathbf{h};\mathbf{\theta })$ could be calculated as [61]:

$$p(h_j|\mathbf{v};\mathbf{\theta })=\sigma \left(\sum _{i=1}^{\left|V\right|}{\omega }_{ij}{v}_i+a_j\right)$$

$$p(v_i|\mathbf{h};\mathbf{\theta })=\sigma \left(\sum _{j=1}^{\left|H\right|}{\omega }_{ij}{h}_j+b_i\right)$$

where the sigmoid function σ(x) is defined in previous section, and the parameters θ = (ω, b, a) of each RBM could be learned from training. The training process is based on the contrastive divergence (CD) algorithm raised by G. Hinton [62]. Stacking the obtained RBMs together, we get a DBN. For each RBN, we have a parameter set θ = (ω, b, a) that defines the distribution of possibility p(v, h; θ) and prior possibility p(h; θ) [63]. In this way, the possibility of generating visible variables is:

$$p\left(\mathbf{v}\right)=\sum _{\mathbf{h}}p\left(\mathbf{h}|\mathbf{\theta }\right)p(\mathbf{v}|\mathbf{h},\mathbf{\theta })$$

where the p(v|h, θ) is fixed when parameter set θ is obtained from an RBM, and p(h|θ) could be replaced by a consecutive RBM, where the hidden layer of the previous RBM could be regarded as visible data.

3.2.4. Q-learning

As an online learning approach, reinforcement learning (RL) is different from supervised/unsupervised learning. During the process of interaction with the environment, the model obtains the optimal decision through trial-and-error, and then obtains the optimal result [65] (see Fig. 4 ). As a widely-used RL algorithm in feature selection, driver-less, route planning, and other fields, the Q-learning algorithm was proposed by Watkins et al., in 1989 [64]. Considering its good convergence and strong decision-making ability, the Q-learning method is applied as an ensemble learning method in this study, i.e., the Q-learning method is used to integrate three deep networks.

Fig. 4.

The principle of Q-learning [64].

The steps of the ensemble method based on reinforcement learning are shown as follows:

• Step 1: Build the state matrix S and the action matrix a, where the state matrix S denotes the weights of the three deep networks in the ensemble model, and the action matrix a is the weight adjustment action.

$$S=\left[w_1,w_2,w_3\right]$$

$$a=\left[\Delta w_1,\Delta w_2,\Delta w_3\right]$$

where w ₁ is the weight of the TCN network, w ₂ is the weight of the GRU network, and w ₃ is the weight of the DBN network. Δw _i (i = 1,2,3) in action matrix a represent the weight change of the deep networks.

• Step 2: Construct the Loss function L, the reward R, and the function Q for evaluation. In this study, the optimization goal was to minimize the output RMSE value. Therefore, the evaluation function Q is defined as:

$$Q=\text{RMSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(y_i-y_i^{\prime }\right)}^2}$$

where $y_i$ is the actual value, and $y_i^{\prime }$ is the forecasting value.

• Step 3: Train the agent (namely the ensemble model) based on the training sets of three kinds of deep network. According to the current state S, the agent performs an action a. During this process, the action is selected based on the ԑ-greedy policy as [66]:

$$a_m=\{\begin{array}{l}\text{Based on}{Q}_{\text{max}}(p=1-\epsilon )\\ \text{Random}(p=\epsilon )\end{array}$$

where the parameter $\epsilon \in \left(\mathrm{0,1}\right)$ is the exploration probability.

• Step 4: Calculate the loss function L, get the reward R, and develop the next step strategy.

$$L=\frac{1}{n}\sum _{m=1}^n{(A\left(m\right)-\hat{A}\left(m\right))}^2$$

$$R=\{\begin{array}{l}+1+L_m-L_{m+1}(L_{m+1}<L_m)\\ -1+L_m-L_{m+1}(L_{m+1}>L_m)\end{array}$$

where $A\left(m\right)$ is the measured wind speed data in the training set, $\hat{A}\left(m\right)$ is the forecasted COVID-19 infection data in the training set.

• Step 5: Calculate the evaluation function Q, and update the Q-table [67].

$$Q_{m+1}(S_m,a_m)=Q_m(S_m,a_m)+{\gamma }_m\left(R(S_m,a_m)+\lambda \max Q_m(S_{m+1},a_{m+1})-Q_m(S_m,a_m)\right)$$

where λ is the discount parameter, and γ is the learning rate.

• Step 6: Repeat steps 3 to 5 until the iteration stop condition is satisfied. The state matrix S currently is the optimal weight of three deep networks.

• Step 7: Input the test set into three well-trained deep networks to obtain the final prediction results. Then, the prediction results of the three deep networks are multiplied by the weight, and then they are ensembled together to obtain the final prediction result.

3.2.5. Support Vector Machine (SVM)

In this study, SVM is applied as a tool for error prediction, which further improves generalization ability and the accuracy of the final ensemble hybrid model. As a classical soft computing learning algorithm, SVM is widely-adopted in regression analysis, classification, pattern recognition and forecasting [68]. Based on the theory proposed by Vapnik [68,69], suppose a data series ${\left\{x_i,d_i\right\}}_i^n$ (n is the data size, x _i is the input space vector, d _i represents the target value), SVM estimates the function represented in following equations:

$$f\left(\mathbf{x}\right)=k\phi \left(\mathbf{x}\right)+\mathbf{b}$$

$$R_{\text{SVM}}\left(C\right)=\frac{1}{2}{k}^2+\frac{C}{n}\sum _{i=1}^{n}L(x_i,d_i)$$

where $\phi \left(\mathbf{x}\right)$ denotes the high-dimensional space feature that plots the input space vector x, b represents the scalar, k is a normal vector, and $\frac{C}{n}\sum _{i=1}^{n}L(x_i,d_i)$ denotes the empirical error. The positive slack variables ${\xi }_{\text{i}}$ and ${\xi }_{\text{i}}^{\text{*}}$ denotes the upper and lower excess deviation. By minimalizing the regularized risk $R_{\text{SVM}}\left(C\right)$, the scalar b and the space feature $\phi \left(\mathbf{x}\right)$ could be obtained.

In this way, the object of building an SVM is to:

$$\begin{array}{l}\text{Minimize}{R}_{\text{SVM}}(k,{\xi }^{(\ast )})=\frac{1}{2}{\Vert k\Vert }^2+C\sum _{(i=1)}^n({\xi }_i+{\xi }_i^{\ast })\\ \text{s.t.}\{\begin{array}{l}{d}_i-k\phi \left(x_i\right)+b_i\le \epsilon +{\xi }_i\\ k\phi \left(x_i\right)+b_i-d_i\le \epsilon +{\xi }_i^{\ast }\\ {\xi }_i,{\xi }_i^{\ast }\ge 0,i=1,\mathrm{...},m\end{array}\end{array}$$

Here, $k^2/2$ is the regularization term, the quantity of features in the training dataset is l. In order to control the difference between the empirical error and regularization term, the error penalty factor C is introduced in the object function. ϵ represents the loss function determined by approximation precision of the training set.

Given the optimality constraints, the problem $f\left(\mathbf{x}\right)=k\phi \left(\mathbf{x}\right)+\mathbf{b}$ could be solved by Lagrange multiplier. A generic function could be obtained by following formula:

$$f(x,{\omega }_i,{\omega }_i^{\ast })=\sum _{i=1}^n({\omega }_i-{\omega }_i^{\ast })\cdot K(x,x_i)+b$$

where the K(x _i, x _j) is kernel function and K(x, x _i) = φ(x _i)φ(x _j) is product of x _i and x _j inner vectors in the feature spaces φ(x _i) and φ(x _j), respectively.

4. Experiment

4.1. Dataset

We used a dataset containing a daily situation update on COVID-19 and the global geographical distribution collected and provided by Epidemic Intelligence team of European Centre for Disease Prevention and Control (ECDC). Since the beginning of the COVID-19 pandemic, ECDC's Epidemic Intelligence team has been collecting the number of COVID-19 cases and deaths daily, based on reports from health authorities worldwide. To ensure the accuracy and reliability of the data, this process is being constantly refined. Every day between 6:00 and 10:00 CET, a team of epidemiologists screens up to 500 relevant sources to collect the latest figures. The data screening is followed by ECDC's standard epidemic intelligence process for which every single data entry is validated and documented in an ECDC database. An extract of this database, complete with up-to-date figures and data visualizations, is then shared on the ECDC website, ensuring a maximum level of transparency [70]. This study used 300 daily data of national cumulative infection numbers from India, the United Kingdom (UK), and the United States (US) from February 19, 2020 to December 14, 2020 (the data were accessed at 19:00 CST, January 19, 2021), and divided the data into three at a ratio of 3:1:1, which are training set (2020/2/19–2020/8/16, 180 days), validation set (2020/8/17–2020/10/15, 60 days), and test set (2020/10/16–2020/12/14, 60 days). The specific conditions of each data set are shown in Table 2 (A). The training set is used to train the three neural networks of TCN/GRU/DBN, and the validation set is used to train the integrated model based on Q reinforcement learning and the error correction model based on SVM.

Table 2.

Data information [70].

(A) Content and split of data
Nation	Training set (60%)	Validation set (20%)	Test set (20%)
India	2020/2/19–2020/8/16 (180 days)	2020/8/17–2020/10/15 (60 days)	2020/10/16–2020/12/14 (60 days)
UK
US

(B) Split of data in the day forward-chaining validation
#1 2020/2/19–2020/4/18 (60 days)	#2 2020/4/19–2020/6/17 (60 days)	#3 2020/6/18–2020/8/16 (60 days)	#4 2020/8/17–2020/10/15 (60 days)	#5 2020/10/16–2020/12/14 (60 days)
Training set	Validation set	Test set	/	/
Training set	Training set	Validation set	Test set	/
Training set	Training set	Training set	Validation set	Test set

For the validation of the ensemble model, we adopted the Day Forward-chaining, a nested cross-validation method that is suitable for time-series data [71,72]. Day forward-chaining method is essential to keep the sequence of time-series data and prevent the possible information leakage that will caused by the k-fold cross validation. The concrete split of data is shown in Table 2(B).

4.2. Performance evaluation indices

We adopted four widely-used and well-acknowledged indices to comprehensively evaluate the prediction performance of the proposed model. They were the mean absolute error (MAE), the mean absolute percentage error (MAPE%), the root mean squared error (RMSE), and the Pearson correlation coefficient (PCC).

For the first three indices (MAE, MAPE%, RMSE), the lower the values were, the better the prediction effect of the model was. As for the PCC, it is a commonly-used statistic to reflect the degree of linear correlation between two variables. The value range of PCC is [−1,1], and the closer the absolute value of PCC is to 1, the stronger the linear correlation between the two variables is. In this study, PCCs were calculated to evaluate the correlation between the predicted number and the actual number. The calculation of RMSE is defined before, and the other three indices could be calculated as follows:

$$\text{MAE}=\frac{1}{N}\sum _{i=1}^N\left|y_i-y_i^{\prime }\right|$$

$$\text{MAPE\%}=\frac{1}{N}\sum _{i=1}^N\left|\frac{\left|y_i-y_i^{\prime }\right|}{y_i}\right|\times 100\text{\%}$$

$$\text{PCC}=\frac{\sum _{i=1}^N\left(y_i-{\bar{y}}_i\right)\left(y_i^{\prime }-{\bar{y}}_i^{\prime }\right)}{\sqrt{\sum _{i=1}^N{\left(y_i-{\bar{y}}_i\right)}^2}\cdot \sqrt{\sum _{i=1}^N{\left(y_i^{\prime }-{\bar{y}}_i^{\prime }\right)}^2}}$$

where N is the number of the samples, $y_i$ is the actual value, ${\bar{y}}_i$ is the mean value of the actual value, $y_i^{\prime }$ is the forecasting value, and ${\bar{y}}_i^{\prime }$ is the mean value of the forecasting value.

4.3. Model training

4.3.1. Determine the best input neuron numbers

The number of neurons in the input layer needs to be determined experimentally to ensure its matching with the prediction task. We used the data of the number of infected people in India for experiments and took different numbers of input neurons (3, 5, 7, 9) for experiments to determine an optimal number of input neurons. As for the experimental set-up, the essential parameters used in model training are given in Table 3 .

Table 3.

Essential parameters used in model training.

Name of parameter	Essential parameters
Q-learning
Maximum iteration	50
Learning rate	0.95
Discount parameter	0.5
GRU
Size of input units	3/5/7/9
Size of hidden units	100
Size of output units	1
Number of the Hidden layers	16
Optimizer	Adam
Learning rate	0.01
Training epochs	200
DBN
Size of input units	3/5/7/9
Size of hidden units	20
Size of output units	1
number of the Hidden layer	1
Momentum factor	0
Optimizer	Adam
Learning rate	0.01
Training epochs	200
TCN
Size of input units	3/5/7/9
Size of hidden units	60
Size of output units	1
number of the Hidden layer	6
Learning rate	0.01
Optimizer	Adam
Filter size	2
Training epochs	100
Dropout	0.05
SVM
Size of input units	3/5/7/9
Size of output units	1
Kernel function	RBF
Gamma	10
σ2	20

Fig. 5 shows the prediction results and the corresponding model structures of models with different numbers of input neurons (see Fig. 4). To put it intuitively, we calculated the MAE, MAPE%, RMSE and PCC values of four investigated models with different input neuron numbers (shown in Table 4 ). As can be seen from Table 4, as the number of input neurons increases, the MAPE% value of the model shows a trend of first decreasing and then increasing. According to the four indices, when the number of input neurons is 5, the prediction effect of the model is the best. Therefore, in subsequent experiments, we set the number of input layers of each model as 5, that is, the data of the first 5 days are used to predict the data of the next day.

Fig. 5.

The prediction results (X-1) and the model structure (X-2) (X = A, B, C, D) for different numbers of input neurons: (A) three input neurons; (B) five input neurons; (C) seven input neurons; (D) nine input neurons.

Table 4.

Comparative results of performance indices from models with different input neuron numbers.

4.3.2. Model integration

The model proposed in this paper is mainly composed of three parts: predictor, optimizer, and error correction. The RMSE is used as the error when the model is trained. Fig. 6 (A) shows the error iteration diagram of the model during training, and Fig. 6(B)–(D) gives the prediction results of different components of the model on three data sets. Table 5 shows the weight optimization results of the three predictors of TCU, GRU and DBN optimized by reinforcement learning.

Fig. 6.

(A) Model training processes (object function: RMSE, data: the number of infected people in UK/India/US); (B) to (D) Predictive output of elements (GRU, DBN, TCN) and error output predicted by SVM: (B) UK; (C) India; (D) US.

Table 5.

The weights of ensemble model (TCN, GRU, DBN) determined by Q-learning.

Weights	$w_1$ (TCN)	$w_2$ (GRU)	$w_3$ (DBN)
UK	0.46557	0.16110	0.29218
India	0.32941	0.65251	0.02186
USA	0.08401	0.21992	0.74092

By analyzing Fig. 6 and Table 6 , the following conclusions can be drawn:

• (1)It can be seen from the results in the table that the prediction accuracy of TCN, GRU, and DBN is not much different on the same data set, but there is still a certain difference in the prediction accuracy between each other, and the performance of TCN, GRU, and DBN varies on different data sets, which indicates the deficiency of a single model in the generalization ability. For example, on the UK data set, TCN (MAE: 2266.439) and GRU (MAPE%: 11.988, RMSE: 3022.743, PCC: 0.707) has better performance than DBN, but DBN has the best performance on the Indian dataset (MAE: 3485.223, MAPE%: 8.861, RMSE: 4563.702), which shows that the performance of a single predictor is not stable enough and is related to specific data sets.
• (2)Basically, the proposed hybrid ensemble model obtained by using Q-learning to integrate the TCN, GRU and DBN achieved higher prediction accuracy than a single component on the three data sets, which shows that the integration method proposed in this paper is effective, as can be seen from Table 6. By adjusting the weight of each predictor in the component, the model can adjust the weight adaptively according to the characteristics of the data set, integrate the advantages of each sub-predictor, and achieve the improvement of the overall accuracy. This feature of the model also improves the robustness of the model, which enables the proposed model to achieve high-precision prediction results on various data sets. Additionally, comparing different data sets, we can see that the accuracy change of the integrated model on the three data sets is lower than its single components (TCN, GRU, and DBN), which indicates that the integrated model has a better stability than single model.
• (3)In order to further improve the accuracy of the integrated model, it is feasible to adopt the method of error compensation. As can be seen from the results in the table, the accuracy of the model has been further improved by adding the error correction mechanism based on SVM, and the optimal performance has been achieved on each data set.
• (4)In the ablation study, the weights of three sub-model are 1/3. Namely the effect of Q-learning in weight optimization was cancelled. Compared to TCN-GRU-DBN-Q model that the weights of each output sequence (X ₁, X ₂, X ₃ given by TCN, GRU, DBN, respectively) are determined by Q-learning, the model output O in ablation study could be denoted as:

$$O=\frac{1}{3}\cdot X_1+\frac{1}{3}\cdot X_2+\frac{1}{3}\cdot X_3$$

Table 6.

The performance indices of models in case studies^†.

It can be seen that compared the TCN-GRU-DBN-Q model, the ensemble model constituted by equal weights of TCN, GRU, DBN has a bigger forecast error, where the MAE, MAPE%, RMSE in each task are generally higher, and the PCC is generally lower than the model with Q-learning weight optimization. Meanwhile, it can be seen that in some tasks the model in ablation study performed less well than some sub-models (e.g., UK: MAE_{TCN-GRU-DBN-Q} (2237.399) < MAE _TCN (2266.439) < MAE _Ablation (2274.252) < MAE_GRU (2292.62) < MAE_DBN (2325.047)), which further proved the effectiveness of Q-learning in the optimization of sub-model weights.

• (5)Day Forward-chaining validation results are recorded in Table 6 as well. The MAE, MAPE%, RMSE, and PCC values were calculated as the average value of three models trained with the split of data shown in Table 2(B). It can be seen that the metrics of the model remain largely stable, which proves the generalization ability of the proposed model.

In summary, it can be known that the model integration method proposed in this paper is effective. Each component of the model improves the performance of the model. With their cooperation, the integrated model can provide high-precision COVID-19 prediction results.

5. Results and Discussions

5.1. Case studies

In order to verify the accuracy of the model, as mentioned in the previous section, this paper uses actual case data from three countries, including the United States, India, and the United Kingdom, for experiments. The prediction results of the model are shown in Fig. 7 and Table 7 .

Fig. 7.

Case studies: infection prediction of the UK, India, and the US.

Table 7.

The performance indices in case studies.

Nation	MAE	MAPE%	RMSE	PCC
UK	1952.11	9.95	2779.90	0.76
India	13760.00	10.72	20602.58	0.93
US	2744.22	7.06	3527.82	0.91

As can be seen from Fig. 7 and Table 7, on all data sets, the model proposed in this paper can accurately predict the increase in the number of new crown cases in the data set. It has achieved the highest prediction accuracy in the USA, and its MPAE value has reached 7.06. This shows that the model proposed in this article has a strong practicability and can play a good role in assisting decision-making in the prevention and control of the COVID-19 epidemic. Meanwhile, in order to verify the effectiveness of each component of the integrated model, Table 6 compares the prediction results of each component of the model (TCN, GRU, DBN, TCN-GRU-DBN-Q) with the final hybrid model (TCN-GRU-DBN-Q-SVM), and an ablation study was conducted with model of 0.333*TCN-0.333*GRU-0.333*DBN to verify the effectiveness of Q-learning in weights optimization. The results, as described in Section 4.3.2, demonstrated the effectiveness of ensemble and error compensation strategy.

5.2. Contrast study

In order to prove the advancement and superiority of the proposed TCN-GRU-DBN-Q-SVM algorithm, this paper compares it with two classic models (LSTM [73] and ANFIS [74]), three state-of-the-art models (VMD-BP [75], N-Beats [76], and WT-RVFL [77]), and time series analysis methods (ARIMA). In addition, in order to prove that residual prediction can effectively improve the model's comprehensive prediction and data analysis accuracy, the proposed TCN-GRU-DBN-Q-SVM was compared with TCN-GRU-DBN-Q. Fig. 8 and Table 8 show the comparison results of the models.

Fig. 8.

Contrast studies of different models (TCN-GRU-DBN-Q-SVM, TCN-GRU-DBN-Q, LSTM, N-BEATS, ANFIS, VMD-BP, WT-RVFL, ARIMA) used for infection prediction in the UK, India, and the US.

Table 8.

Comparative results.

Through the contrast study, we can see that model 1 (the proposed hybrid model) has the best accuracy, which shows the superiority of the proposed model. From the results, it can be found that for the number of infections in the UK, India, and the US, model 1 (TCN-GRU-DBN-Q-SVM) has a higher prediction accuracy than model 2 (TCN-GRU-DBN-Q) (MRSE₁＜MRSE₂, MAE₁＜MAE₂, MAPE%₁＜MAPE%₂, ||PCC1|-1|＜||PCC2|-1|), which proves that the establishment of an error prediction model is meaningful for improving the prediction accuracy. Furthermore, in order to verify the high forecast accuracy of the proposed hybrid model quantitatively, we propose the prediction performance indices improvement percentages P _MAPE% (%), P _MAE (%), P _RMSE (%) and P _pcc (%) to compare and analyze the improvement of the prediction accuracy of the proposed model (TCN-GRU-DBN-Q-SVM) compared with the TCN-GRU-DBN-Q (proposed model without SVM error predictor), LSTM [73], ANFIS [74], VMD-BP [75], N-Beats [76], WT-RVFL [77] and ARIMA models (see Table 9 ). The specific calculation method is as follows:

$$\{\begin{array}{l}{P}_{MAPE\%}=\frac{MAPE{\%}_2-MAPE{\%}_1}{MAPE{\%}_2}\times 100\%\\ P_{MAE}=\frac{MA{E}_2-MA{E}_1}{MA{E}_2}\times 100\%\\ P_{RMSE}=\frac{RMS{E}_2-RMS{E}_1}{RMS{E}_2}\times 100\%\\ P_{PCC}=\frac{PC{C}_1-PC{C}_2}{PC{C}_2}\times 100\%\end{array}$$

where MAPE% ₁, MAE ₁, RMSE ₁ and PCC ₁ are forecasting performance indices of the proposed model, while MAPE% ₂, MAE ₂, RMSE ₂ and PCC ₂ are the indices of the comparison model.

• (1)The prediction result of TCN-GRU-DBN-Q-SVM is better than that of TCN-GRU-DBN-Q algorithm, which proves that the residual prediction modeling based on SVM can effectively improve the overall prediction ability of the model. The possible reason is that residual prediction analyzes the deviation information between the predictor and the real data to further correct the prediction results of the model and improve the accuracy comprehensively.
• (2)Although VMD-BP and WT-RVFL algorithms can achieve good prediction results, their prediction performance is difficult to surpass the classic model (ANFIS, LSTM, ARIMA), the recently proposed model (N-Beats) and the model proposed in this paper. The possible reason is that the decomposition algorithm has a certain boundary effect in the modeling process, which affects the model's ability to analyze and identify the original time series to a certain extent.
• (3)The TCN-GRU-DBN-Q-SVM proposed in this paper can achieve satisfactory prediction results in all case studies. Compared with the suboptimal model, the performance improvement of the model on the three data sets is huge. The possible reasons of the performance improvement are: first, the three neural networks (TCN, GRU, DBN) used in this article have their own unique network frameworks, which improves their ability to extract deep features of time series. Second, the integrated learning algorithm based on Q-learning can comprehensively analyze the modeling capabilities of these types of neural networks for different time series to construct a satisfying hybrid ensemble model with improved comprehensive robustness and adaptability (or, generalization). Finally, SVM constructs a residual correction model to further optimize the result of the hybrid model by analyzing the deviation between the real data and the predicted value of the TCN-GRU-DBN-Q network. Therefore, the model proposed in this article has extremely high application value in the field of COVID-19 infection prediction.

Table 9.

The promoting percentages of the proposed model comparing to other experimental models.

INDICES	COMPARISON MODELS	UK	INDIA	US
PMAPE% (%)	Model 1 v.s. Model 2	12.75%	14.09%	11.34%
	Model 1 v.s. Model 3	16.49%	29.78%	22.42%
	Model 1 v.s. Model 4	18.08%	21.29%	14.40%
	Model 1 v.s. Model 5	24.29%	45.80%	26.14%
	Model 1 v.s. Model 6	20.82%	45.57%	29.72%
	Model 1 v.s. Model 7	28.28%	48.17%	21.13%
	Model 1 v.s. Model 8	29.20%	19.23%	18.94%
PMAE (%)	Model 1 v.s. Model 2	15.12%	13.63%	9.62%
	Model 1 v.s. Model 3	18.65%	29.60%	16.76%
	Model 1 v.s. Model 4	15.78%	25.07%	16.11%
	Model 1 v.s. Model 5	27.51%	45.35%	19.07%
	Model 1 v.s. Model 6	23.79%	45.12%	25.45%
	Model 1 v.s. Model 7	31.40%	47.73%	19.03%
	Model 1 v.s. Model 8	28.59%	22.29%	19.53%
PRMSE (%)	Model 1 v.s. Model 2	7.34%	15.09%	9.06%
	Model 1 v.s. Model 3	10.39%	29.93%	11.02%
	Model 1 v.s. Model 4	4.83%	21.66%	7.01%
	Model 1 v.s. Model 5	16.91%	46.62%	14.37%
	Model 1 v.s. Model 6	14.02%	46.57%	27.65%
	Model 1 v.s. Model 7	20.83%	48.67%	19.98%
	Model 1 v.s. Model 8	20.41%	22.82%	19.65%
Ppcc (%)	Model 1 v.s. Model 2	6.79%	3.71%	1.08%
	Model 1 v.s. Model 3	7.16%	3.80%	0.50%
	Model 1 v.s. Model 4	3.32%	6.33%	0.95%
	Model 1 v.s. Model 5	7.18%	8.67%	0.35%
	Model 1 v.s. Model 6	7.30%	8.98%	0.98%
	Model 1 v.s. Model 7	7.27%	9.88%	0.71%
	Model 1 v.s. Model 8	3.58%	4.69%	1.89%

Note: Where Model 1 is TCN-GRU-DBN-Q-SVM (the proposed model), Model 2 is TCN-GRU-DBN-Q, Model 3 is LSTM, Model 4 is N-BEATS, Model 5 is ANFIS, Model 6 is VMD-BP, Model 7 is WT-RVFL, Model 8 is ARIMA.Based on the experimental results, the following conclusions can be drawn.

6. Limitations and further work

The TCN-GRU-DBN-Q-SVM model in this paper has the following points that are still worth improving. First, as an ensemble model, the higher the variability of the sub-model, the higher the accuracy of the integrated model obtained in general. Therefore, a larger integrated model can be explored in the future. Although a larger model will take more time to train and forecast, it is feasible for COVID-19 morbidity prediction, a task that does not require high real-time performance (generally forecast in days). Second, integration with other modeling approaches (e.g., time series models such as ARIMA, STAR models, dynamic models such as SAHQD model [19], SEIAIR model [28], even the SCUAQIHMRD model [31]) can also be performed, where reinforcement learning can still provide an integration framework. Third, the data of other modalities, such as Mobility Report released by Google [78], search interest [51], local weather data, human contact data [33], etc., could also considered as meaningful input into the model [79], although the inaccessibility and incompleteness of some data modalities may limit the power and generalizability of the model with integrated multi-modalities. Additionally, as a deep learning model, there are some inherent drawbacks. First, the “features” decoded by the forecast model are abstract information, which are not sufficiently interpretable. Second, as with all data-driven models, the model relies on the accuracy of the data provided for model training, and the prediction step is not as long as dynamics modeling. However, the corresponding advantages are obvious: deep learning is more adequate for mining the information contained in the time series data, and does not rely on complicated (often multi-compartment, multi-stage, and multi-parameter) dynamic modeling that requires delicate analysis of epidemic situation ranging from the policy changes to the pathogenicity and crowd immunity, and accordingly requires less parameter estimation and manual feature extraction [80].

It must be noted that in the above elaboration, it is easy to see that for the task of forecasting the number of COVID-19 infections, there are various forecasting models, but their respective advantages and disadvantages are also apparent. Researchers need to make trade-offs and choose the appropriate prediction scheme according to the needs of prediction. The TCN-GRU-DBN-Q-SVM model involved in this study can give better case number forecasts than many existing models for scenarios where information such as temperature data, transportation data, and network human behavior is missing but only daily incidence case number information is available, but the forecast step size is limited.

In a word, the forecast models must keep up with a rapidly changing situation [80]. The modeling of COVID-19 pandemic is, in essential, a difficult trade-off (see Fig. 9 ). First, the data-driven models were easier to acquire compared to those dynamic model-based forecasting models. However, how to determine the ensemble strategy can vary when the training time requirements, hardware space, and the amount of training data change, although the ensemble model can achieve higher forecast performance than single ones. Second, the deep-learning models may sacrifice the interpretability of forecast model since the “features” they learn could be abstract and obscure, but the accuracy of deep-learning, if the data quantity permits, is generally higher than interpretable methods ranging from time-series models to regression models where the artificial feature engineering may be performed to acquire the features in data's statistical, spectral, and temporal domain. Last but not least, the modality (or the source) of data should be flexibly and smartly determined since the ease of quantification and the accessibility to data may reduce when the modality and source of data become multiple and extensive.

Fig. 9.

Trade-offs to consider in data-driven and dynamics model-driven COVID-19 prevalence modeling.

7. Conclusion

The COVID-19 pandemic is posing a huge challenge to international public health. Accurate and effective prediction of the number of cases is significant for the health resource planning and the epidemic situation evaluation. Unlike SIR models, the data-driven machine learning model does not rely on accurate physical dynamics modeling and can adapt to complex changes in the epidemic situation (for example, vaccination, quarantine, isolation, lockdown, social distancing, etc.), and can be sensitive and accurate in predicting the development of the epidemic. In this work, a novel TCN-GRU-DBN-Q-SVM ensemble hybrid model is proposed for COVID-19 infection prediction. First, three widely used networks, TCN, GRU, and DBN, are used as single predictors. Second, three predictors are ensembled by reinforcement learning method (Q-learning) with different weights. Third, an error predictor built by SVM, is trained with validation set, and the final prediction result could be obtained by combining the TCN-GRU-DBN-Q model with the SVM error predictor.

The strengths of our model could be concluded as follows. First, we use multiple predictors to work collectively. The integrated weights based on Q reinforcement learning can be adaptively adjusted according to the characteristics of the data, which ensures model's capability of various forecasting work in different countries and multiple situations (such as social-distancing, vaccination, migration, etc.). Therefore, the accuracy, robustness and generalization of the proposed model are ensured. Second, our model uses an SVM-based error compensation mechanism to further improve the accuracy of the model. Third, we use relatively newly-proposed deep learning network to ensure the accuracy of the model. Fourth, the proposed model is data-driven, and the amount of data required is easily met.

In the future, we will further consider whether the proposed integrated model can integrate more information modalities. For example, Wensen Huang et al. evaluated predictive value of regional outbreaks of online medical behavior data, including online medical consultation (OMC), online medical appointment (OMA) and online medical search (OMS) for the 2019 coronavirus disease in Shenzhen, China from January 1, 2020 to March 5, 2020 [81]. If this type of information model can be integrated with data-driven predictive models, and natural language processing (NLP) and other algorithms can be used to extract more information and merge into the model, it will have a certain significance for further improving the predictive effect of COVID-19. The integration with other modeling approaches is also very interesting. Sumit Mohan et al. have proposed a hybrid ARIMA and Prophet model to predict daily confirmed and cumulative confirmed cases in India, which is an inspiring step [82].

However, as we discuss in this paper, the exact modeling approach, data modality, and integration strategy needs to consider a number of different factors, including data sources, model generalization capabilities, model accuracy, and hardware conditions during model training, which is a difficult trade-off [80]. Researchers must put more effort to make machine learning, time series analysis, dynamical modeling, and other data science models more useful for COVID-19 forecasting to provide more accurate and reliable information for the outbreak prevention and control.

Declaration of competing interest

Declare none.

Abbreviations

ANFIS

Adaptive Neuro-Fuzzy Inference System

AR

autoregressive

ARIMA

Autoregressive Integrated Moving Average

ARMA

autoregressive moving average

BP

Back Propagation

CET

Central European Time

CST

Central Standard Time

CMPA

chaotic marine predator algorithm

CD

contrastive divergence

COVID-19

Corona Virus Disease 2019

DBN

Deep Belief Networks

GRU

Gated Recurrent Unit

GRM

growth rate model

HW

Holt-Winters exponential smoothing

MPA

marine predator algorithm

MRFs

Markov Random Fields

MA

moving average

OMA

online medical appointment

OMC

online medical consultation

OMS

online medical search

RL

reinforcement learning

RBM

Restricted Boltzmann Machine

RVFL

random vector functional link

SARIMA

Seasonal Autoregressive Integrated Moving Average

SVM

Support Vector Machine

SEIR

Susceptible-Exposed-Infected-Recovered Model

SIR

Susceptible-Infected-Recovered Model

TNC

Temporal Convolutional Networks

TCN

Temporal Convolutional Networks

MAE

the mean absolute error

MAPE%

the mean absolute percentage error

N-BEATS

Neural basis expansion analysis for interpretable time series forecasting

PCC

the Pearson correlation coefficient

RMSE

the root mean squared error

UK

the United Kingdom

US

the United States

VMD

Variational Mode Decomposition

WT

wavelet transform