Mathematical modeling of radiotherapy and its impact on tumor interactions with the immune system

Abstract

Radiotherapy is a primary therapeutic modality widely utilized with curative intent. Traditionally tumor response was hypothesized to be due to high levels of cell death induced by irreparable DNA damage. However, the immunomodulatory aspect of radiation is now widely accepted. As such, interest into the combination of radiotherapy and immunotherapy is increasing, the synergy of which has the potential to improve tumor regression beyond that observed after either treatment alone. However, questions regarding the timing (sequential vs concurrent) and dose fractionation (hyper-, standard-, or hypo-fractionation) that result in improved anti-tumor immune responses, and thus potentially enhanced tumor inhibition, remain. Here we discuss the biological response to radiotherapy and its immunomodulatory properties before giving an overview of pre-clinical data and clinical trials concerned with answering these questions. Finally, we review published mathematical models of the impact of radiotherapy on tumor-immune interactions. Ranging from considering the impact of properties of the tumor microenvironment on the induction of anti-tumor responses, to the impact of choice of radiation site in the setting of metastatic disease, these models all have an underlying feature in common: the push towards personalized therapy.

Introduction

Mathematical modeling in oncology has a long history, with various theoretical approaches being used to explore and describe biological mechanisms as well as tumor growth and treatment response dynamics [1], [2], [3], [4], [5], [6], [7]. Mathematical oncology may hold the key to bridging experimental, clinical, and data science studies; to test and generate hypotheses and evaluate conceptual models for validity. In radiation oncology specifically, mathematical modeling has a rich history, likely due in part to the field of medical physics. Approximately 50% of cancer patients are prescribed radiotherapy (RT) during their treatment course, either alone as definitive therapy or in combination with surgery, chemotherapy, targeted therapy, or immunotherapy. As our understanding of the complexity of tumor heterogeneity grows, motivation for the tailoring of cancer therapy to individual patients increases, thus driving the push towards precision medicine. While the flood of new available genomic data has thus far affected decisions regarding chemotherapy and certain targeted biological agents, it has yet to impact radiotherapy: the selection of total dose and fractionation is currently based empirically on average clinical outcome data, albeit often from randomized trials.

Historically, the main driver of tumor response to radiotherapy was thought to be cytotoxic DNA damage, however, the immunomodulatory effects of radiation can no longer be ignored, leading to research into potential synergy between radiotherapy and immunotherapies. While the exact mechanisms and relationships between radiation dose, dose fractionation, and immune response have not yet been fully elucidated, ongoing preclinical studies and clinical trials are investigating the combination of RT with various types of immunotherapies such as vaccines, adoptive cell transfers, and checkpoint inhibitors against cytotoxic T-lymphocyte-associated protein 4 (CTLA-4) or programmed cell death protein 1 (PD-1) or the associated PD-1 ligand (PD-L1) [8], [9], [10]. These studies aim to answer important questions regarding combination treatment schedules, such as optimal timing (sequential vs concurrent) and dose fractionation (hyper-, standard-, or hypo-fractionation) to achieve superior tumor inhibition.

Mathematical oncology is well positioned to assist in these investigations, either by elucidating underlying biological mechanisms of radio-immunotherapy synergy, or by predicting which patients may benefit most from these combination treatments. Here we review published pre-clinical data and clinical trials investigating these questions and discuss the contribution of published mathematical models of tumor immune interactions focusing on those that explicitly include radiotherapy simulations.

The biological response to radiotherapy

The administration of total radiation dose as smaller fractionated doses, often over many weeks, creates a therapeutic window for normal tissue to recover from radiation injury. The biological effects of fractionated radiation are often described by the 5 R's, namely radiosensitivity, repair, reoxygenation, reassortment, and repopulation [11,12]. Seminal studies in the 1980s showed that different types of cells exhibit a wide range of inherent radiosensitivity [13]. Indeed, significant variations in radiosensitivity between cancer types, and even between tumors of the same type have recently been reported [14]. Understanding tumor and patient-specific sensitivity to radiation, and particularly to radiation dose fractionation, may help inform the choice of RT schedule, to ultimately control the tumor whilst preventing overtreatment of radiosensitive tumors.

Radiation causes DNA damage primarily in the form of double strand breaks [15], [16], [17]. Cellular attempts to repair such damage between therapeutic radiation fractions may lead to cell cycle arrest, recovery, or death, depending on the degree of DNA damage induced and the cells’ capacity for repair. Dysregulation of DNA repair mechanisms occurs early on in carcinogenesis [18] across many cancer types. By comparison, DNA repair processes are usually intact in normal cells, allowing for repair of radiation induced damage in normal cells which mediates reduced radiation toxicity in normal tissue [19]. The extent of DNA damage induced by radiation is strongly dependent on tissue oxygenation, as radiation energy deposited in the tissue creates reactive oxygen species that in turn damage DNA [20]. Consequently, tumor cells in hypoxic conditions often require approximately three times the radiation dose to exhibit a comparable response to tumor cells in well oxygenated, normoxic conditions. Notably, the discrepant effects of equivalent radiation doses in hypoxic versus normoxic conditions can be quantitatively described by the oxygen enhancement ratio [21]. Several factors determine oxygen availability in the tumor bed, including the varying degree of functional vasculature in the tumor. Radiation-induced cell death may release pressure on obstructed blood vessels in a dense tumor, thereby increasing blood flow and reoxygenation of the tissue and increased sensitivity to subsequent radiation fractions.

Furthermore, cells in different cell cycle phases exhibit differential levels of radiosensitivity and capacity to initiate DNA damage repair [22]. Killing of radiosensitive cells and re-oxygenation of the tumor allows for cells to redistribute into cell cycle phases that confer higher radiosensitivity. Simultaneously, tumors may enter phases of accelerated repopulation. Historically, the repopulation of tumors after fractionated doses was attributed to the gradual proliferation of surviving tumor cells [23,24]. However, factors released by dying malignant cells have recently been implicated as inducers of rapid re-growth and subsequent repopulation [25]. Additionally, dying cells may also release damage associated molecular patterns (DAMPs) which stimulate an immunogenic response, while other forms of cell death may be immunogenically silent [26]. Furthermore, tumors that quickly regenerate after radiation have been reported to exhibit reduced local control under prolonged treatment plans [27]. Thus, the length of radiotherapy treatment schedules may also play an important role in treatment response [28], and therein exist as a crucial factor to consider when making treatment decisions.

The immunomodulatory effects of radiotherapy

Radiation kills cells either directly via induction of double stranded DNA breaks, or indirectly by generating free radicals from water molecules within the cell which react with DNA to cause macromolecular damage [29]. The resulting DNA damage varies in lethality, depending on the severity and pervasiveness of the induced DNA damage and functionality of DNA damage repair pathways. However, loss or disruption of DNA damage repair pathways occurs early in carcinogenesis [18], leaving cancer cells sensitive to DNA damaging agents. Following irradiation cells may undergo various forms of cell death, including immunogenic cell death [26]. Critically, the form of death cancer cells undergo significantly impacts their induction or suppression of immune responses. Apoptotic or other forms of immunogenically silent cell death hinder activation of anti-tumor immune responses whereas immunostimulatory forms of cell death, most notably immunogenic cell death itself, support radiation induced immune activation [30]. Thus, the capacity for radiation to induce immune activation also hinges on the propensity for irradiated tumor cells to undergo different forms of cell death which likely occurs in a tumor type and radiation dose specific manner.

Notably, the context in which DNA is detected significantly impacts the cellular effects. In the context of pro-inflammatory cues, exposure to DNA can stimulate immune activation, whereas exposure to DNA under homeostatic conditions can promote development of immunosuppressive subsets to avert development of auto-immune responses. Release of additional DAMPs via immunogenic cell death during irradiation including heat shock proteins (HSPs), nuclear protein HMGB1, calreticulin and ATP all promote the development of antitumor immune responses upon DNA exposure [31], [32], [33].

Cytosolic DNA-sensing via the cGAS-STING pathway among others and detection of both intra- and extracellular DNA via toll ligand receptors (TLRs) promotes immune activation in response to radiation induced DNA damage. Detection of DNA damage within cancer cells occurs via direct interaction of the cGas protein with cytosolic DNA which has leaked from the nuclei or mitochondria of damaged cells. There cGas associates with STING which undergoes activating phosphorylation and induction of downstream signaling to induce type I interferon production and secretion of inflammatory cytokines. Furthermore, cytosolic DNA can be sensed by intracellular TLR receptors, most notably CpG motif recognizing TLR9 which stimulates subsequent activation of the NFKB transcription factors upon DNA binding. Additional intracellular sensors of cytosolic DNA include AIM2, which stimulates caspase 1 activation; RIG1 and DAI which stimulate downstream STING activation and LRRFIP1. Notably, in the context of transformed cells, activation of each intracellular DNA sensor hinges on intact expression of pathway members and the sequence specific motifs present in cytosolic DNA. Overall, exposure of tumor cells to cytosolic DNA can result in induction of immunogenic cell death via STING-pathways induced NLRP3 activation, AIM2 induced caspase activation, and TLR-mediated induction of mitochondrial pore formation. Collectively induction of tumor cell death in response to cytosolic DNA stimulates production of immunostimulatory cytokines and release of additional DAMPs [34,35].

Similarly, tumor infiltrating immune cells can react to radiation induced release of DNA via several mechanisms. Immune cells may also react to the release of tumor DNA into the extracellular environment or respond to DNA from phagocytosed/endocytosed tumor debris [36]. In immune cells, exposure to DNA triggers cell type specific responses. Exposure of immature dendritic cells to DNA promotes dendritic cell maturation, secretion of immunostimulatory cytokines and expression of costimulatory markers. Exposure of B cells or macrophages to DNA can provoke upregulation of antigen presenting functions and secretion of stimulatory cytokines [37]. Exposure of T cells to tumor DNA can also promote development of anti-tumor effector functions including production of type I interferon; however, prolonged exposure to DNA can activate cell death pathways in T cells [38].

In terms of stimulating tumor specific T cell responses, exposure to DNA directs maturation of antigen presenting cells and promotes uptake of antigen containing tumor debris material released from dying tumor cells following irradiation. Importantly, presentation of tumor antigens alongside costimulatory markers occurs after DNA-induced maturation of antigen presenting cells. Additionally, DNA exposed antigen presenting cells secrete chemotactic factors which promote T cell infiltration into the tumor which further amplifies the anti-tumor potential of radiation induced DNA release [39].

Multiple pre-clinical studies have shown that radiation affects this process, with some reporting immune stimulation, while others have observed immune suppression. For instance, although radiation has been shown to increase dendritic cell maturation [40], it may also impair the antigen presentation ability of mature dendritic cells [41]. Increases in MHCI expression levels on cancer cells following radiation have also been reported [42], leading to an increase in the recognition of tumor cells by activated CD8+ T-cells, although radiation has been shown to be detrimental to vasculature in the tumor bed, thereby inhibiting the trafficking of immune cells [43]. Furthermore, the radiation-induced increase in programmed death-ligand 1 (PD-L1) expression may strengthen the immune-suppressive capacity of tumor cells [44]. A thorough review of the contradictory immunological consequences of radiation can be found elsewhere [45,46]. In the face of so much evidence, a sixth ‘R’ of radiobiology, that of immunological response has been postulated [47].

The radiation-induced immune response can act both locally at the site of irradiation, and systemically, mediating regression of distant tumors [48]. Previously thought to be a rare event, with only 46 cases reported during the 1969-2014 period [49], the abscopal effect has become more common, especially in pre-clinical and clinical trials of radio-immunotherapy combinations [50]. However, the exact relationships between radio-immunotherapy schedules and the induction of the abscopal effect remain to be elucidated. Below we briefly discuss pre-clinical and clinical studies investigating these matters.

Investigating the timing of radiation with concurrent immunotherapy

Dovedi et al. showed survival in a murine colon carcinoma model was significantly higher in mice receiving anti-PD-L1 concurrently with $2Gy\times 5$ radiation as opposed to sequentially [51]. Investigating this result, the authors observed a transient but significant increase in PD-1 expression on both CD4+ T-cells and CD8+ T-cells, which was present 24 hours after the last dose of radiation but not 7 days after. This suggests the existence of an optimal timing for administration of this immunotherapy when in combination with radiation. However, PD-1 failure may interfere with subsequent radiation responses [52]. Young et al. investigated a similar timing schedule in the same murine model as Dovedi et al., but in combination with either an anti-CTLA-4 antibody or an anti-OX40 antibody [53]. OX40 (CD134) is a co-stimulatory molecule transiently expressed on T cells following activation. The antibody binds to and activates the OX40 receptor, inducing the proliferation of T cells [54]. Although the overall survival of mice treated with the radiotherapy and anti-CTLA-4 antibody combination was improved compared to those treated with monotherapies, all mice treated with the inhibitor prior to irradiation had complete tumor clearance. However, the same results were not seen in mice treated with combinations of radiotherapy and the anti-OX40 agonist antibody; in fact, administration of this immunotherapy a day after radiation resulted in the highest overall survival. Similar experiments using a MMTV-PyMT model did not yield the same results, indicating that the optimal timing of the combination therapy may also be cancer type and immunotherapy type specific.

The KEYNOTE 001 trial (NCT01295827), which investigated the PD-1 targeted antibody pembrolizumab for treatment of non-small cell lung cancer (NSCLC), found that patients who received radiotherapy prior to the trial demonstrated higher overall and progression free survival compared to patients who had not received any radiation [55]. In addition, NSCLC patients in the PACIFIC trial (NCT02125461) treated with chemoradiation (CRT) and the PD-L1 inhibitor durvalumab, showed a higher progression free survival when receiving the immunotherapy within 14 days following CRT, compared to patients with longer wait times until durvalumab [56]. Recruitment for NCT02239900 which investigates concurrent vs sequential administration of the anti-CTLA-4 antibody ipilimumab and stereotactic body radiation therapy (SBRT) for both liver and lung cancers has recently been completed, although results are still pending. A similar trial, NCT03223155, is focused on the sequencing of ipilimumab, nivolumab and SBRT for NSCLC with estimated completion in December 2022.

Investigating radiation dose fractionations for immune activation

Dewan et al. investigated the immunological consequences of radio-immunotherapy in a bi-lateral murine mammary adenocarcinoma model [57]. Mice were randomized into cohorts receiving either no treatment to the primary tumor or $20Gy\times 1$, $8Gy\times 3$, or $6Gy\times 5$ on consecutive days with or without an anti-CTLA-4 antibody at various times following radiation. The primary tumors of mice receiving radiation alone exhibited comparable responses regardless of dosing schedule. However, combination therapy resulted in improved primary tumor inhibition, with complete regression of the primary tumor observed in mice treated with either the $8Gy\times 3$ or $6Gy\times 5$ dose schedules. In addition, complete regression of 2 of 5 non-irradiated secondary tumors was reported in mice treated with the $8Gy\times 3$ combination therapy, indicative of systemic anti-tumor immunity and radiation-induced immune-mediated abscopal responses. In contrast, the $6Gy\times 5$ combination exhibited superior responses in a murine colon carcinoma model, lending further support to the notion that optimal dose fractionations may be tumor type specific.

Vanpouille-Box et al. completed a similar investigation using radiotherapy doses of $8Gy,30Gy$ or $8Gy\times 3$and an anti-CTLA-4 antibody [58]. Delayed growth of the irradiated primary tumor was observed, but only the $8Gy\times 3$ combination treatment regimen resulted in complete regression of primary tumors (6 out of 7 tumors). Although significant growth inhibition of the unirradiated secondary tumors was observed in mice that received this combination therapy, tumor volumes at the abscopal site were comparable between all other cohorts.

Immunostimulatory properties effects have also been reported following low dose radiation. In a preclinical study of pancreatic cancer, Klug et al. observed higher levels of infiltration by tumor specific T cells following radiation with $0.5Gy$ compared to more clinically standard doses of $1Gy$, $2Gy$ or $6Gy$. The authors compared infiltration levels of host derived CD8+ T cells following priming of the tumor with either $0.5Gy$, $1Gy$, $2Gy$ or $6Gy$ prior to transfer of tumor specific CD8+ T cells. Priming with $1Gy$ resulted in the highest levels of infiltration of host derived CD8+ T cells, although all treatment groups had significantly higher levels of infiltration than the control group [59].

Multiple clinical trials have investigated optimal radiotherapy dose fractionation schemes to be used in combination with immunotherapies. For instance, NCT02659540 investigated the combination of ipilimumab, nivolumab and RT in the setting of stage IV melanoma. Here radiation was administered in either $3Gy\times 10$ or $9Gy\times 3$ fractions. A limited number of patients completed this trial, only 4 and 2 of the 10 enrolled patients enrolled in each cohort respectively, yet the results suggest that treatment with the lower fractionation exhibits a higher number of partial responses and a lower number of progressive disease occurrences compared to the hypofractionated regimen [60]. NCT02888743 is investigating the combination of monoclonal antibodies that inhibit CTLA-4 and the PD-L1:PD-1 interaction and radiotherapy in high or low dose fractions, focusing on colorectal cancer and non-small cell lung cancer, with an expected completion date of December 2021. A similar trial, NCT03085719, is actively recruiting head and neck squamous cell carcinoma patients to investigate the combination of anti-PD-1 immunotherapy and three high-dose RT fractions, with or without two additional low-dose fractions. Started in 2015, NCT02406183 looked at ipilimumab-SBRT combination for the treatment of metastatic melanoma. Here, radiotherapy was administered in either $8Gy\times 3$, $10Gy\times 3$, or $12Gy\times 3$dose fractionation schemes, no results have yet been posted.

More in-depth discussions of clinical trials investigating the combination of radiotherapy and immunotherapies can be found elsewhere [8], [9], [10]. While these clinical studies provide invaluable insights into selected protocols, to exhaustively evaluate every possible radiation dose and dose fractionation with different sequencing and timing of the various immuno-therapeutics remains infeasible [61]. Integrating mathematical modeling into experimental and clinical research may help analyze the complex, non-linear multifactorial treatment responses [62], [63], [64].

The purpose of mathematical oncology

Interest into mathematical oncology has increased with the growing realization that the translation of in vitro and in vivo results into clinic is hindered by crucial differences between humans and animal models [64,65]. The burgeoning field of mathematical oncology may be uniquely positioned to help bridge the scales from pre-clinical to clinical studies. The type of data at hand and the scale of the system under consideration both inform the type of mathematical model to be developed [66].

Modeling of the temporal evolution of data on the population level is best done using deterministic modelling methods such as ordinary differential equations, or partial differential equations if also accounting for spatial evolution. However, when the available data is of higher granularity and the system is instead focused on interactions between or movement of discrete individuals (or cells), agent-based models (ABMs) are better suited. Individuals within these models follow predetermined sets of rules giving rise to emergent behavior, which may vary with each simulation due to the inherent stochasticity of this model type. Thus, a high number of simulations is required to ensure consistency of model outcomes [67]. Conversely, the behavior of deterministic systems is fully determined by initial conditions and the parameter set used.

The extent to which the underlying biological mechanisms are reflected in a mathematical model may inform its use. For instance, mechanistic models, which include in-depth quantitative descriptions of a system's underlying biological processes, can be used in hypothesis generation to further knowledge [68]. Alternatively, descriptive models, which may include little to no biological mechanism explicitly, can be used in predictive settings [7,[69], [70], [71]]. For predictive modeling, it is paramount to integrate the model with experimental and clinical data [62], [63], [64]. Successful studies calibrate mathematical models with relevant data, validate the model on independent data sets, and test the prediction accuracy on known outcomes before making predictions about novel treatment protocols [72], [73], [74], [75], [76]. Most challenging for such interdisciplinary modeling is to match available data with the right modeling approaches to test specific scientific hypotheses. Often, further abstractions and simplifications have to be made to accommodate and balance lack of data, biological uncertainty, and mathematical modeling complexity. These can most successfully be overcome by a close dialog of interdisciplinary collaborations.

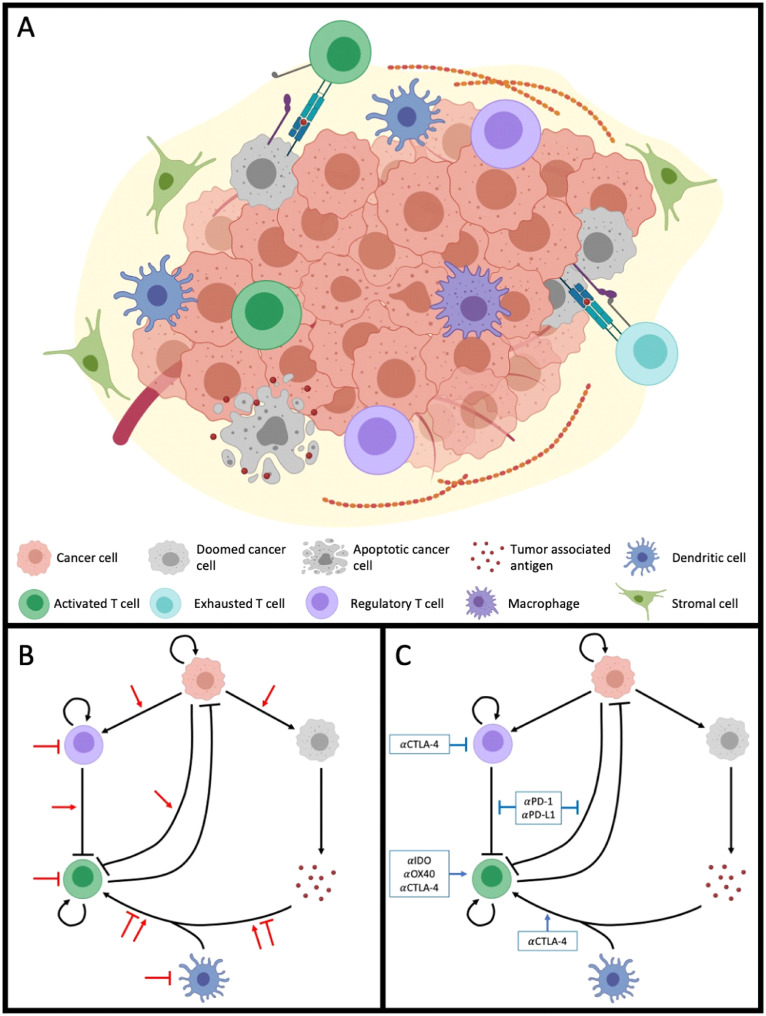
Mathematical models that faithfully include a myriad of tumor-associated cell populations, their interactions, associated biological processes, and underlying mechanisms in the tumor-immune microenvironment under radiotherapy and/or immunotherapies would be incredibly complex (see Fig. 1). However, assumptions regarding the cellular populations can simplify the system sans treatment to a six-compartment model: Cancer cells (C), dying cancer cells (D), tumor associated antigen (A), antigen presenting cells (P), effector immune cells such as CD8+ T cells (E), and regulatory immune cells denoted by (R). A general formulation of such a mathematical model is presented below, where  $\dot{C},\dot{D},\dot{A},\dot{P},\dot{E}$ and  $\dot{R}$ denote the temporal evolution of the respective population. While this formulation may be a relatively faithful representation of the population level of the underlying biological system, the complexity requires large amounts of data for calibration, and limits the possible mathematical analysis and utility of the model [77]. Development of mathematical models must be done with the trade-offs between complexity and simplicity in mind.

Icon	Equation
	$\dot{C}={\overbrace{f\left(C\right)}}^{proliferation}-{\overbrace{g\left(C,E\right)}}^{inactivation}$
	$\dot{D}=g\left(C,E\right)-{\overbrace{aD}}^{removal}$
	$\dot{A}={\overbrace{h\left(D\right)}}^{production}-{\overbrace{j\left(A,P\right)}}^{uptake\&processing}-{\overbrace{bA}}^{decay}$
	$\dot{P}={\overbrace{\Lambda }}^{influx}-{\overbrace{cP}}^{decay}$
	$\dot{E}={\overbrace{k\left(E,P,A\right)}}^{influx\&recruitment}-{\overbrace{m\left(C,E\right)}}^{exhaustion}-{\overbrace{n\left(E,R\right)}}^{regulation\&death}$
	$\dot{R}={\overbrace{n\left(C,D,P,E\right)}}^{influx\&recruitment}-{\overbrace{dR}}^{death}$

Fig. 1.

The tumor immune microenvironment (TIME), and the effects of radiation and immunotherapy thereon.A) The tumor immune microenvironment, consisting of various cell types including cancer and immune subpopulations, some of which are shown. Interactions within the TIME include the uptake and processing of tumor associated antigen (TAA) by professional antigen presentation cells (APC) such as dendritic cells; the influx of TAA specific activated T cells, the recognition and lysis of cancer cells. Additionally, activated T cells can be regulated and suppressed by T-reg cells or tumor cells via the PD-1:PD-L1 axis or CTLA-4, and macrophages can phagocytose cancer cells. B-C) Interactions within the TIME can be generalized as occurring between six compartments: cancer cells, doomed cancer cells, TAA, APCs, effector immune cells, and regulatory immune cells. Black arrows denote these interactions, with inhibitory interactions shown as blocked arrows, and stimulatory interactions indicated by sharp arrows. Administration of (B) radiotherapy and (C) immunotherapy affect these interactions in different ways, detailed reviews of which can be found elsewhere [45,151]. Figures created with BioRender (www.biorender.com).

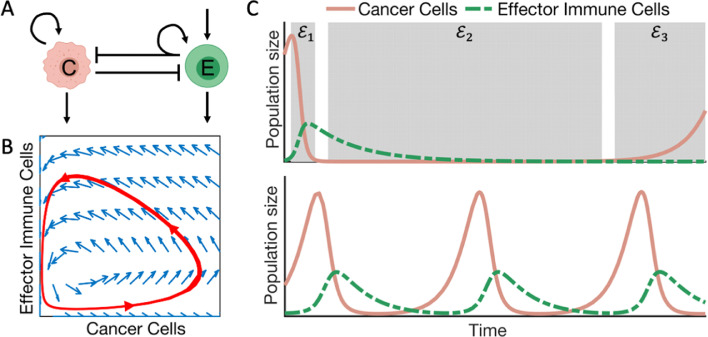
In this system however, additional simplifying assumptions can be made, resulting in a so-called predator-prey or Lotka-Volterra type mathematical model [78,79]. This model describes the proliferation of cancer cells, influx and recruitment of tumor specific effector immune cells, and the interactions between these two populations. A general example of the structure of such a model can be seen below. The oscillatory behavior of this system is dependent on parameter values and recapitulates the immunoediting phase of the three E's as postulated by Dunn et al. [80] (Fig. 2).

$$\dot{C}=\stackrel{proliferation}{\overbrace{f\left(C\right)}}-\stackrel{immune-mediateddeath}{\overbrace{g\left(C,E\right)}}-\stackrel{death}{\overbrace{\mu C}}$$

$$\dot{E}=\stackrel{influx\&recruitment}{\overbrace{k\left(E,C\right)}}-\stackrel{exhaustion}{\overbrace{m\left(C,E\right)}}-\stackrel{death}{\overbrace{dE}}$$

Fig. 2.

The dynamics of a predator-prey type model of cancer-effector immune interactions.A) Model schematic. Cancer cells (C) proliferate, (curved returning arrow), and die (outgoing arrow). Effector cells (E) are recruited (incoming arrow) and die (outgoing arrow). The interactions between cancer cells and effector immune cells are inhibitory, denoted by the blunt arrow. Inhibition of cancer cells by effector cells recruits more immune cells (curved, returning arrow). B) The phase-plane of the model in (A). The red trajectory illustrates how the two populations change with regards to each other. Starting from the bottom left, the cancer cells increase in number while effector cells are recruited. Once the inhibitory effect exerted by effector cells is larger than the replacement of cancer cells, the trajectory moves towards the vertical axis. At this point the effector population is unsustainable by the cancer cell population and experiences a rapid decline, and the trajectory moves towards the horizontal axis. These oscillations continue indefinitely. C) Two solutions of the model in (A). Top panel, this model can recapitulate the three E's of immunoediting postulated by Dunn et al. [80]: elimination (${\epsilon }_1$), equilibrium (${\epsilon }_2$) and escape (${\epsilon }_3$). Bottom panel, solutions showing the explicit oscillatory behavior described in (B).

Thus, assumptions regarding the importance of subpopulations and their contributions yield models of varying simplicity for the same biological system. The Akaike Information Criterion (AIC) [81,82] is one of several measures that report on a model's ability to balance data fitting and complexity, relative to others fitted to the same dataset. Comparison of AIC values can be used in model selection, and hypothesis generation. This is the approach Yamamoto et al. followed in their investigation of the impact of the immune system on transient increases in prostate specific antigen (PSA) levels in prostate cancer patients undergoing interstitial brachytherapy [83]. Comparison of AIC values of two models, one with and one without an immune compartment, suggests the immune compartment is a necessary inclusion to explain the PSA bounces. The authors go on to confirm, at least mathematically, that patients who experience this PSA bounce have significantly higher mean densities of CD8+ T cells and CD3+ T cells pre-treatment, although further validation of this hypothesis is required.

Several mathematical models that predict response to radiation have been developed, but the most widely used is the linear quadratic (LQ) model. The underlying assumptions can be summarized as: radiation-induced cellular death is due to sufficient levels of irreparable double strand DNA breaks created directly by ionizing radiation, or through interactions between non-lethal (single-strand) DNA breaks [84]. The LQ model, $SF\left(d\right)=\exp \left(-\alpha d-\beta d^2\right)$, predicts the surviving fraction of a population following a radiation dose of $dGy$, where $\alpha G{y}^{-1}$ denotes the cellular responses due mainly to `single-hit’ damage, and $\beta G{y}^{-2}$ denotes ‘multi-hit’ damage from independent radiation events [85]. Estimates for these radiosensitivity parameters of various cancer types have been reported [14] and are useful in the calculation of the biological effective dose (BED) [86,87]. BED can be used to compare dose fractionation schemes, and to identify alternative fractionation regimens [88].

Radiobiological response models have been used in more complex models of tumors undergoing treatment with radiotherapy, such as the seminal work by Leder et al. [73]. Here the authors used an approach that iteratively integrates theoretical and experimental methods to develop a mathematical model with which to predict optimal radiotherapy schedules for platelet derived growth factor (PDGF) driven glioblastoma. In this interdisciplinary study, the mathematical model was calibrated with experimental data and used to identify two optimal treatment schedules. The response predicted for these schedules showed improved response over standard, hyper- and hypo-fractionated regimens with equal total dose. These model predictions were subsequently verified in a glioma murine model.

Proliferating cells are more radiosensitive than quiescent cells [89], and thus the proportions in which these cells appear in a tumor may influence response to radiation. This is the basis of Prokopirou et al.’s proliferation saturation index (PSI), which originally used a logistic-type growth model to implicitly link the proliferative fraction of the tumor to radiation sensitivity and response [90]. It has since been shown to be descriptive of tumor data for various growth models [91] and different cancer types including non-small cell lung cancer [92] and head and neck cancers (HNC) [93]. PSI can specifically be used to compare predicted outcomes for various treatment schedules with different BEDs, using only two data points, making it useful for identifying patients who may benefit from alternative radiation schedules. The PSI model is currently being validated in the ongoing clinical trial NCT03656133, using patient-specific PSI to select between a hyperfractionated regimen of $1.2Gy$ doses twice daily or the standard $2Gy$ daily fractionation for oropharyngeal cancer patients. In a recent variation of the PSI model, Zahid et al. simulated the effect of radiation not by linear-quadratic cell survival but by modulation of the tumor microenvironment to prospectively predict patient-specific responses to radiation in head and neck cancer with high accuracy [74]. Of note, the PSI model assumes that the proportion of cells that proliferate decrease as the tumor approaches its carrying capacity, which in turn decreases the overall tumor response to radiation. Routine radiological imaging cannot give sufficient resolution into intra-tumoral composition to validate such assumption. An alternative explanation for growth saturation could be a balance of rapid proliferation and high cell death rates. In such scenario, the tumor would remain radiosensitive even at dormancy. Different mathematical models have explored these alternatives and discuss future data collection suggestions to better decipher the intra-tumoral dynamics during different tumor growth and dormancy phases [94], [95], [96].

A different application of mathematical modeling in radiation oncology was demonstrated in the development of the radiation sensitivity index (RSI), a linear regression model that relates the expression of ten genes to the radiosensitivity of a cell line, specifically for single doses of $2Gy$ [97]. First proposed in 2009, this model has been validated for multiple disease sites, including head and neck, rectal, and esophageal cancers [97], breast cancer [98], and glioblastoma [99]. Building on this work, Scott et al. developed a genome-based model for adjusting radiotherapy dose (GARD) [100]. This model links patient specific RSI values and the LQ model to radiation dose fractionation schedules to evaluate dose-fractionation schemes. This model may enable personalization of treatment schedules according to patient radiosensitivity or inform clinicians as to which patients would benefit from receiving treatments other than radiation. GARD has been retrospectively validated using lung, breast, and pancreas cancer cohorts [100,101].

Treatment types or plans that aim to protect surrounding normal tissue are also on the rise, such as temporally feathered radiotherapy (TFRT). Recently proposed by Alfonso et al. [102], this strategy consists of specific daily treatment plans that result in the sequential administration of high and low doses to each organ at risk (OAR). The underlying logistic-type model for the recovery of normal tissue from sublethal damage takes OAR-specific recovery rates into account and can easily be made patient-specific. The first stage I/IIa trial, NCT03768856, using TFRT was recently completed for head and neck cancer [103]. Further clinical investigation and implementation has recently been rendered more clinically accessible by the publication of a step-by-step technical paper on TFRT utilization [104].

Mathematical models of tumor immune dynamics

Mathematical models of tumor-immune interactions have a long history, and range in complexity. Some focus on the effect of anti-tumor effector immune cells such as CD8+ T cells, natural killer cells, or classically activated macrophages. These models generally have the dynamics of ecological predator-prey systems, with the immune system preying on tumor cells. Other models may include separate compartments for naïve T-cells [105], immunosuppressive cell types [106] and cytokines [107]. Reviews of these models can be found elsewhere [108], [109], [110], [111]. Many of the models we discuss here are based on pioneering work done by Kuznetsov et al., wherein a model of the interaction between cytotoxic lymphocytes and cancer cells is proposed [112,113]. The mathematical model is a good fit to growth data of a murine B-cell lymphoma (BCL₁) model [114], and can predict the observed regrowth in the murine model to which it was calibrated [115]. The steady states of this model are descriptive of tumor immunoediting phases [80,116], namely tumor dormancy due to a tumor-immune equilibrium and tumor escape despite a strong anti-tumor immune response.

Trafficking of activated T-cells between metastatic sites after local therapy

Poleszczuk et al. modeled the activation and movement of activated effector T cells within and between distinct metastases [117] following an unspecified local therapy. The growth dynamics of individual sites are governed by logistic growth with immune predation, as in Kuznetsov et al.’s tumor regrowth model [113]. Here, the immune compartment is extended to include the probability that T cells that are activated at one anatomical site arrive at a tumor in a different location after extravasation out of the circulatory system, dependent on the blood flow fraction to the different organs and tissues. Analysis of a virtual cohort of 40 patients with combinations of lung, breast, liver, and kidney metastases suggests that the strength of the immune response following local therapy is a complex combination of the different tumor volumes and their respective locations. Thus, decisions of which metastases to target with local therapies to induce systemic immune responses may be highly patient-specific.

Systemic consequences of local radiotherapy

Walker et al. extended Poleszczuk et al.’s model to explicitly consider the cytotoxic and immune activating effects of radiotherapy [118], by including a subpopulation of lethally damaged tumor cells that contribute to immune recruitment. The net effect of radiation on immune cells is also included. The model is fit to data from a BCL₁ murine model [114], and used to investigate the systemic immune effects after local radiotherapy. Analysis of model simulations suggest that the order in which metastases emerge, the corresponding growth rates, as well as which site is focally irradiated combine to yield systemic pro- or anti-tumor immune response. These relationships and the underlying mechanisms, whilst intriguing, remain as of yet experimentally unvalidated.

Considering instead the relationship between radiation-induced immune responses, dose sizes and inter-fraction time, Serre et al. proposed the concept of an immunologically effective dose (IED). This metric can be used for comparing radiation dose fractionation schedules to identify those expected to result in higher systemic immune responses [119]. As with most conceptual models, experimental and clinical validation will be necessary before IED can be translated into clinical practice.

Treatment schedules to protect the induced immune response

Sung et al. investigated the relationships between both the radiation schedule length and inter-fraction time, and the recovery period of the immune system of hepatocellular carcinoma patients treated with radiation [120]. This model considers primary tumor cells, radiotherapy-inactivated tumor cells releasing a tumor-specific antigen, metastatic cells, and circulatory lymphocytes (CL). The tumor is assumed to follow exponential growth, and interaction with lymphocytes occurs along the periphery. Radiation effects on the tumor are modelled using the LQ model, but the higher radiosensitivity of lymphocytes motivates a modification by omitting the quadratic term. Thus, in this model the surviving fraction of lymphocytes after a dose $dGy$ is given by $S{F}_L\left(D_L\right)=e^{-{\alpha }_L*D_L}$ where $D_L$ denotes the dose per fraction delivered to a given volume of circulating lymphocytes. The model, calibrated to longitudinal CL data of 17 hepatocellular carcinoma patients, is used to simulate various radiotherapy schedules. Comparisons of the recovery time of CLs reveals that immune recovery time is shortest after treatments with fewer total fractions. However, when treated with a fixed number of fractions, schedules with shorter inter-fraction breaks are ideal for immune recovery. It is conceivable that inter-fraction times are further dependent on several patient-specific factors, including the tumor growth and repopulation rates as well as the radiosensitivity, trafficking and extravasation of cytotoxic immune effector cells, and the immunological composition of the tumor microenvironment.

Possible predictive biomarkers for response to radio-immunotherapy

Byun et al. investigated the relationship between the ratio of PD-1 and PD-L1 expression levels and the tumor size pre- and post-treatment with radio-immunotherapy [121]. The efficacy of both treatments is modelled by exponential decay. After calibration to longitudinal data from a murine mammary carcinoma model [44], a global sensitivity analysis between the parameters and tumor size throughout therapy suggests that the ratio in which PD-1 and PD-L1 are expressed on effector T cells may be informative as to which patients will benefit from radio-immunotherapy.

The relationship between vascularization of tumors and radiotherapy response

Hatzikirou et al. proposed a tumor-immune-vasculature model, which they used to investigate immune- and vasomodulatory combination therapies but not RT [122]. This model assumes a radially symmetric tumor, with an outer vascularized proliferative layer and an inner avascular region composed of a proliferative rim, a hypoxic quiescent section, and a necrotic inner core. Immune cells are recruited by immunogenic signals released by tumor cells and those undergoing immunogenic cell death. Tumor-immune interactions initially occur along the periphery of the tumor, but immune cells rely on the degree of functional vasculature to infiltrate and attack the tumor. This model has subsequently been modified by Montaseri et al. [123] and Alfonso et al. [124] to investigate the impact of vascularity on treatment success following radiotherapy. Montaseri et al. developed a radiotherapy planning framework based on the application of impulse control theory to Hatzikirou's model [123]. This approach was chosen to determine radiation schedules which lead to a tumor-free state. In particular, the authors link tumor growth, radiosensitivity, vascularity and hypoxia, as well as immune response to the required number of fractions with a specific dose to eradicate a tumor. Once calibrated to patient data, and validated, this framework could be used to personalize treatment.

Alfonso et al. modified Hatzikirou's model to investigate the impact of vascularity on radiation response and the efficacy of radiation induced anti-tumor immune responses [124]. Simulation outcomes suggest the existence of a range of tumor sizes for which the efficacy of combination therapy is high. Outside this range, however, tumor reduction by radiation may be too small or too large to generate an immune response of sufficient strength to control the tumor. Comparison of outcomes for in silico tumors treated with schedules of various lengths reveal that a higher number of total fractions, and thus longer schedules, may lead to progressive disease, suggesting the existence of a subset of patients that may benefit from radiation de-escalation. The impact of treatment breaks was investigated via simulation of a standard weekday-only schedule vs. consecutive fractions without breaks. Results suggest that regardless of the degree of functional vasculature and simulated tumor outcome, treatment breaks lead to larger populations of radiation-induced effector cells suggesting that these schedules may be ideal candidates for radio-immunotherapy combinations. Further analysis reveals the existence of ranges of vascularity and effector recruitment for which each type of schedule would be better suited. For instance, treatments with weekend breaks led to control of poor to intermediately vascularized tumors, but not for those with high levels of functional vasculature. Thus, patients may benefit from treatment personalization according to their tumor microenvironments. However, experimental, and clinical validation of the model results are necessary.

Investigating personalization of radio-immunotherapy to patients’ immune responses

Sotolongo-Grau et al. proposed a simple predator-prey like model describing tumor-immune interactions [125]. The effects of radiation on cancer cells are included by the addition of a non-clonogenic tumor cell compartment which has no contribution to tumor growth but retains the ability to induce and suppress the immune response. This suppression is mediated by secreted factors such as interleukins. The LQ model was used to describe the effect of radiation on both the tumor and immune cell populations. The authors identified parameters for which tumor growth isn't controlled by the anti-tumor immune response due tumor-mediated suppression of the immune system. Analysis of a large cohort of virtual patients with characteristics within this region suggests a relationship between the treatment success probability, immune efficiency, and the so-called tissue effects that depend on the radiosensitivity parameters of the tissue. Based on this the authors suggest a method for personalization of dose according to immune efficacy. However, by sampling values for the tissue effects from a Gaussian distribution, rather than clinical or preclinical data, this model requires rigorous validation before being used for predictions.

Investigating the optimal radiation dose fractionation schedules to induce immune responses

Poleszczuk and Enderling investigated the induction of a systemic anti-tumor immune response following treatment with radio-immunotherapy [126]. This model considers two spatially distant tumors, of which only one is irradiated, although activated T-cells are assumed to travel between the two sites. Comparison of simulated post-treatment tumor volumes suggest that the optimal dose fractionation scheme for the clinically relevant dose range of $60-70Gy$ is $5-6$ fractions in the range of $11-13\mathit{Gy}$ as opposed to the clinically used $2Gy\times 30$. While this model was calibrated to murine data, results of recent clinical studies corroborate these findings [127].

Serre et al. reports a model describing the tumor dynamics, antigen, immune effector cells, primary immune response, and secondary immune response [128]. Radiotherapy and two checkpoint inhibitors are included, namely anti-PD-L1 and anti-CTLA-4. The model is calibrated to data from a murine fibrosarcoma model and is able to describe the non-linear relationship between tumor size and rejection probability observed in a preclinical study [129].

Chakwizira et al. adapted the model from Serre et al. to investigate the synergy between radiotherapy and 1-MT (1-methyl tryptophan) [130]. This immunotherapy abrogates tumor-tolerance developed by a variety of immune cells by inhibiting IDO (indoleamine-2,3-dioxygenase) [131]. The immune component is adapted via removal of the anti-PD-1 and anti-CTLA-4 specific terms, and the assumption that the tumor is strongly immunosuppressive on days without immunotherapy but has no immunosuppressive ability on days that 1-MT is administered. From the lack of long-term survivors in the syngeneic rat glioma model to which this mathematical model is calibrated, Chakwizira et al. assume that the effect of the memory immune cells is negligible, and thus omit it from the model completely. In silico simulations suggest the existence of an optimal number of fractions for a range of BED values, which increase the synergy between the treatments leading to increased predicted survival time. However, the model requires validation before it can be used in a non-hypothesis generating manner.

In 2020, Ahlstedt et al. investigated the effect of single- or two-fraction radiotherapy in combination with 1-MT in a syngeneic rat glioma model [132]. The authors adapted the model proposed by Chakwizira et al. [130] to include Gompertzian tumor growth as opposed to exponential tumor growth. The model yields a good visual fit to tumor area measurements, and model simulations suggest that variations in inter-fraction timing may affect tumor regression at day 18, with intervals of between 5 and 7 days resulting in the lowest predicted tumor areas. However, statistical significance remains to be further demonstrated.

Kosinsky et al. presented a tumor growth model [133] with detailed immune components related to the cancer-immune cycle described by Chen and Mellman [134]. These include tumor antigen levels, population levels of mature dendritic cells, differentiated and non-differentiated T cells, and an immune-suppression component related to PD-L1 expression levels. The model was calibrated and validated on data from a CT26 murine colorectal carcinoma model and can recapitulate observed growth dynamics of control tumors and those receiving treatments, including radiation and anti-PD-L1 monotherapies, and combinations of these. After investigation of various combination therapy characteristics including timing and dose size, the authors suggest that administration of the immune checkpoint inhibitor prior to, or concurrently with, radiotherapy results in superior tumor responses compared to administration following radiation.

More recently, Alfonso et al. developed a three-dimensional, spatially explicit, agent-based model to simulate radiation-induced shifts in patient-specific tumor-immune ecosystem composition [135]. Combining molecular and bioinformatics analysis of over 10,000 patient tissue samples across 31 cancer types to map the pan-cancer tumor-immune milieu with dynamic simulation of radiation response revealed that radiation response may be a combination of the direct cytotoxic effects of radiation on cancer cells as well as subsequent stimulation or inhibition of immune cell infiltrates. For selected patients, radiation could potentially be drastically de-escalated while other patients may need significantly larger doses to control the tumor. This work further emphasizes the need to depart from average outcomes of large clinical trials towards more patient-specific response analyses.

Optimal sequencing of radiotherapy and surgery for the induction of an immune response

Poleszczuk et al. [136] and Alfonso et al. [137] focused on comparing adjuvant and neoadjuvant radiotherapy. In a rigorous analysis of more than a quarter of a million female patients in the Surveillance, Epidemiology, and End Results (SEER) database with early-stage breast cancer who received radiation either before or after surgery, Poleszczuk used different statistical approaches including the Wilcoxon rank-sum test with normal approximation to compare continuous factors, Pearson's chi-square test to compare categorical factors, Kaplan-Meier analysis, and multivariate Cox proportional hazards models to estimate hazard ratios of developing second primary tumors after either adjuvant or neoadjuvant radiation. Their analyses showed that neoadjuvant radiotherapy may significantly improve disease-free survival without reducing overall survival, especially for estrogen receptor-positive patients

Alfonso et al. [137] extended this work by statistically analyzing additional SEER data sets of adjuvant or neoadjuvant radiation of early-stage cancers, including cancers of lung and bronchus, esophagus, rectum, cervix uteri, corpus uteri, and breast. Data suggested improved overall survival after neoadjuvant radiation for cancers with low 20-year survival rates and improved disease-free survival for cancers with higher survival (breast: HR = 0.64; P < .001). In addition to the statistical analyses, mechanistic ordinary differential equation mathematical model simulations suggested that neoadjuvant radiation could increase outcomes by creating an immune memory that facilitates tumor elimination for a broader range of model parameters.

The spatial evolution of these interaction dynamics may also be considered using systems of partial differential equations. Lai and Friedman considered six cell populations, four different cytokines, the levels of PD-1, PD-L1 and the PD-1:PD-L1 complex, and an anti-PD-L1 immunotherapy [138]. Simulations suggest combination therapy with concurrent administration results in higher treatment efficacies than sequential schedules. However, the authors caution against drawing conclusions from this model, instead encouraging its use in hypothesis generation.

As previously discussed, preclinical and clinical studies into the optimal timing, and fractionation schedules are ongoing for various cancer sites and immunotherapies. Once optimal schedules have been found, we expect the focus will shift to identifying patients who would benefit from these combinations, and how to truly personalize radiation treatment with and without concurrent immunotherapeutics.

Spatially fractionated radiotherapy

Recently Asperud et al. [139] developed a model for tumor-immune interactions following spatially fractionated radiotherapy (SFRT). In this radiotherapy modality the radiation beam is fractionated, creating areas of high and low dose [140,141]. The model was calibrated to published tumor growth data for syngeneic xenograft models of breast cancer (67NR) and Lewis lung carcinoma, following administration of either full tumor or half-tumor irradiation with singles doses of $10Gy$ or $15Gy$ respectively [142]. Despite acceptable model fits, predictions of 67NR tumor growth following $15\mathit{Gy}$ and $20\mathit{Gy}$ failed to recapitulate the reported regrowth of tumors. The authors comment that these discrepancies may be due to the adoption of parameter values from published data of various cancer models, rather than parameter values specifically calibrated to the experimental data reported by Markovsky et al. [142]. Another possibility is the underlying assumption of a well-mixed tumor-immune model. SFRT induced cell death is concentrated in the irradiated portion of the tumor, although higher than expected death has been reported in the unirradiated portions, suggesting that bystander effects may occur [143]. Thus, incorporation of a spatial aspect may be necessary.

Tools that are useful in the field

Most of the models discussed herein consider tumor-immune interactions on the cell population level, modeled by either ordinary or partial differential equations. These models can be simulated and analyzed using commercial software packages such as MATLAB, Mathematica, and Maple, or a variety of open-source differential equation solver solutions. However, the type and granularity of the available data, including multiplex-immuno-florescence images from patient biopsy samples, may facilitate the use of cell-based approaches, such as agent-based models, cellular automata, or hybrid models [144]. Several freely available tools have been developed for these modeling techniques, including NetLogo [145], CompuCell3D [146], PhysiCell [147], and HAL [148].

Open questions

The combination of radiotherapy and immunotherapy has the potential to induce durable responses and may be more effective than either treatment individually for a subset of patients. However, the underlying mechanisms of such synergy and methods with which to identify eligible patients remain to be determined. Whilst a large selection of mathematical models in oncology have been developed to help answer intriguing questions, a close iterative dialog between mathematics, cancer biology, immunology, radiobiology, and radiation oncology is necessary to advance the rapidly evolving field of radio-immunology.

A current hot topic in the field is the induction of sustained systemic anti-tumor immune responses, especially in the setting of metastatic disease. Reports of such abscopal effects in clinic, which lead to either partial or complete responses are increasing [49,149], yet they remain a rarity. Thus, elucidation of the underlying mechanisms of this process and the identification of responsible treatment schedules as well as time frames to monitor responses may lead to improved tumor regression. The use of mathematical models in this setting could shift the discussion from “do abscopal effects exist” to “how can we best observe and monitor them.” This will pave the way for interdisciplinary identification of radiation and radio-immunotherapy protocols to best harness the patient immune system to achieve systemic tumor clearance.

However, the relatively high radiosensitivity of immune effector cells motivates investigation into radiotherapy modalities with immune sparing potential such as spatially fractionated radiotherapy [142]. Exploration of the immunological consequences of these modalities alone, or in combination with conventional external beam radiation or immunotherapies would be well suited to in silico models with explicit spatial components such as agent-based models or partial differential equations. Future investigations may reveal immune protection in so-called immune reservoirs, opening another avenue for personalization of treatment: according to the patient's tumor immune microenvironment.

Other exciting discoveries in the field are the extreme tissue sparing benefits of irradiation at ultra-high dose rates (FLASH-RT). Recent studies have shown that FLASH-RT, delivered at $\ge 40Gy{s}^{-1}$ compared to conventional dose rates of $\ge 0.01Gy{s}^{-1}$, leads to tumor growth inhibition comparable to conventional RT but has higher tissue sparing effects [150], and may have immune sparing potential due to the short associated on-treatment times. Investigation into possible synergy between FLASH-RT and immunotherapies may elucidate the protective effects and determine for which patients this treatment would be most beneficial for.

Conclusion

Pioneering work in mathematical modeling has both accompanied and accelerated the fields of radiation biology and radiation oncology over many decades. The increasing understanding of the complex dynamic tumor-immune interactions and their perturbation by radiotherapy, in combination with expanding computing capabilities, has enabled mathematical oncology approaches to help investigate the immunological consequences of radiation – alone and in combination with novel immunotherapies. A wealth of preclinical- and clinical trial data are collected while testing variations of radio-immunotherapies, and mathematical modeling approaches may become invaluable tools to complement available techniques to help elucidate the mechanistic underpinnings of observed dynamics and responses. While clearly promising, and truly exciting, we should proceed with caution. Mathematical and computational models developed in isolation without proper calibration and validation may not be positioned to advance the fields [72]. However, iterative integration of mathematical modeling, computer simulation, and quantitative data sciences, including the bourgeoning fields of artificial intelligence and machine learning, in oncology in general, and particularly radiation oncology, could help propel our understanding of the adaptive and ever-evolving dynamics of tumor growth, tumor-immune interactions, and radiation responses. This may allow for reliable prediction of treatment outcomes, leading to the ultimate goal of therapy personalization and optimization.

Funding

This work was supported by the National Institutes of Health U01CA244100 and by support from the Florida Breast Cancer Foundation.

CRediT authorship contribution statement

Rebecca Anne Bekker: Conceptualization, Investigation, Writing – original draft. Sungjune Kim: Writing – review & editing. Shari Pilon-Thomas: Writing – review & editing. Heiko Enderling: Conceptualization, Writing – review & editing, Supervision.

Declaration of Competing Interest

None.