A multi-task Gaussian process self-attention neural network for real-time prediction of the need for mechanical ventilators in COVID-19 patients

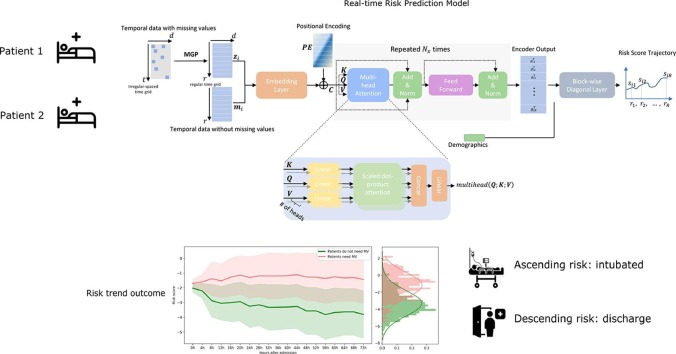
Graphical abstract

Abstract

Objective

The Coronavirus Disease 2019 (COVID-19) pandemic has overwhelmed the capacity of healthcare resources and posed a challenge for worldwide hospitals. The ability to distinguish potentially deteriorating patients from the rest helps facilitate reasonable allocation of medical resources, such as ventilators, hospital beds, and human resources. The real-time accurate prediction of a patient's risk scores could also help physicians to provide earlier respiratory support for the patient and reduce the risk of mortality.

Methods

We propose a robust real-time prediction model for the in-hospital COVID-19 patients' probability of requiring mechanical ventilation (MV). The end-to-end neural network model incorporates the Multi-task Gaussian Process to handle the irregular sampling rate in observational data together with a self-attention neural network for the prediction task.

Results

We evaluate our model on a large database with 9,532 nationwide in-hospital patients with COVID-19. The model demonstrates significant robustness and consistency improvements compared to conventional machine learning models. The proposed prediction model also shows performance improvements in terms of area under the receiver operating characteristic curve (AUROC) and area under the precision-recall curve (AUPRC) compared to various deep learning models, especially at early times after a patient's hospital admission.

Conclusion

The availability of large and real-time clinical data calls for new methods to make the best use of them for real-time patient risk prediction. It is not ideal for simplifying the data for traditional methods or for making unrealistic assumptions that deviate from observation's true dynamics. We demonstrate a pilot effort to harmonize cross-sectional and longitudinal information for mechanical ventilation needing prediction.

1. Introduction

The novel coronavirus disease (COVID-19) is caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). As of October 2021, over two hundred million people have been infected with the virus, which has directly caused more than four million deaths worldwide. Among the patients with COVID-19, people's situations could develop into critical illness and would require respiratory support in their disease course, especially for the elderly patients and the patients who have comorbid health conditions [1], [2]. Mechanical ventilation (MV) is a crucial medical procedure for a patient with respiratory failure that helps the body maintain healthy oxygen and CO₂ level. Therefore, it is usually considered a timely intervention to mitigate a patient's condition deterioration. However, since the beginning of the COVID-19 pandemic, many countries have experienced a critical situation where the demand for ventilators and other intensive treatments far outstrips the supply. This situation also happens when more contagious variants appear and surge across the world, such as the recent Delta (B.1.617.2) variant [3]. Clinicians and researchers have developed different workarounds, such as exploring the possibility of sharing ventilators among multiple patients [4], [5]. To solve this problem fundamentally, a method for accurate and early recognition of those at-risk patients who will need mechanical ventilators in the future is in critical need. Such methodology is not only critical for hospitals to allocate strategically the scarce medical resources during the pandemic outbreak, but also beneficial to these patients with a higher risk of being critically ill, as clinicians could intervene early and apply aggressive treatments to increase the patient's survival rate. This is a difficult task because multiple clinical factors usually intervene in a complicated manner that may directly or indirectly lead to the situation that a patient would require a mechanical ventilator. Therefore, predicting patients' need for mechanical ventilators several days ahead remains an unrealistic task even for experienced clinicians.

To solve this task, Khandelwal et al. proposed a scoring system named “COVID-19 Score” for predicting the likelihood that patients will require tracheal intubation [6]. Burdick et al. use the XGBoost classifier to fit boosted decision trees on the patient's two-hour data after hospital admission to predict respiratory decompensation in patients with COVID-19 within the next 24 h [7]. Several risk factors were identified to be associated with intubation and prolonged intubation in hospitalized patients with COVID-19 [8]. They studied time-to-extubating for in-hospitalized patients using multivariable logistic regression analysis. Roca et al. used the ROX index (defined as the ratio of oxygen saturation, measured by pulse oximetry/FiO2) to predict high-flow nasal cannula (HFNC) outcome, i.e., need or not for intubation [9]. An unsupervised symptom time series clustering model was proposed to predict disease severity or the need for dedicated medical support for COVID-19 positive patients [10]. Su et al. used the patient’s post-intubation trajectory of the sequential organ failure assessment (SOFA) score to identify and characterize distinct sub-phenotypes of COVID-19 critical illness and classified them into mild, intermediate, and severe groups [11]. Liang et al. used a deep-learning-based survival model to predict the risk of patients with COVID-19 developing critical illness. The model used ten clinical characteristics at admission selected by the least absolute shrinkage and selection operator (LASSO) method [12]. The variables considered in their study include X-ray abnormalities, age, dyspnea, chronic obstructive pulmonary disease (COPD), number of comorbidities, cancer history, neutrophil/lymphocytes ratio, lactate dehydrogenase, direct bilirubin, and creatine kinase.

These models successfully achieve the prediction goal but with certain limitations. The majority of the models cannot provide consistent real-time risk predictions over time due to the lack of a temporal attention mechanism and only optimize the model's performance at each time point individually. Some models use temporal features; however, these features are overly simplistic and do not take full advantage of all available patient information. For example, the SOFA score is defined only on six features: partial pressure of oxygen (PaO₂), fraction of inspired oxygen (FiO₂), platelets, bilirubin, mean arterial pressure, creatinine, and the ROX score is defined on only three factors: PaO₂, FiO₂, respiratory rate. The feature-selection-based models (such as LASSO) may induce information loss, especially when the covariates are correlated, which leads to lower accuracy results.

This paper explores the possibility of using data-driven approaches to solve this problem utilizing the high dimensional physiological longitudinal data that is generally available from in-hospital patients nowadays. A challenge we face when leveraging longitudinal electronic health record (EHR) data for neural-network-based models is that the data is often collected irregularly -- lab tests are rarely collected on a fixed routine, and vital sign observations are missing due to the patient leaving, etc., which cause patient records as unstructured.

We propose a model that leverages the Multi-task Gaussian Process (MGP) to impute the missing values in the multivariate longitudinal EHR data combined with an improved self-attention neural network for predicting the real-time need for mechanical ventilation. The proposed MGP self-attention neural network demonstrates significant improvements in the prediction accuracy, robustness, and consistency of the risk trajectories compared to other neural networks and machine learning models. The Gaussian process is built into the self-attention network serving as modeling data uncertainty and screening out noise through resampling from the learned multivariate normal distribution. It is optimized jointly end-to-end with the self-attention neural network. On the other hand, the multi-head self-attention architecture brings twofold benefits. First, the multi-head self-attention shows greater potential to encode multiple relationships and nuances for multivariant longitudinal data and brings significant accuracy gain compared to traditional recurrent neural networks. Second, compared to previous works that used the Gaussian process as add-ons to the recurrent neural network [13], our self-attention network processes the longitudinal data in a parallel manner. This mechanism avoids the long-dependency problem that widely exists in recurrent network architectures, and also significantly improves the speed of training the neural network.

By jointly modeling the physiological time series as a multivariate Gaussian Process with rich kernel functions, we aim to discover the latent correlations among the longitudinal physiological data. In particular, we model the correlation among the variables by a trainable covariance matrix and model the noise in the observational physiological data using a noise variance matrix. Both are trainable parameters and are updated with the neural network in an end-to-end fashion. Given a new patient's observed data and the learned covariance and noise matrix, we impute the missing values on the unobserved time points in this patient's encounter using the Multivariant Gaussian Process, and the post-imputation data will be used as input for the prediction network. Our model is denoted as MGP-MS in the following, and the contributions of this study are highlighted:

• •Real-time prediction. The proposed model predicts a patient's risk score upon hospital admission and updates his/her risk score as more observational data is collected without re-training the model.
• •Robust, and consistent risk trajectory prediction. The model predicts a patient's risk score trajectory which enhances the prediction's robustness and consistency over time, whereas most traditional models make isolated predictions at each time point that are highly fluctuating or conflicting over time.
• •End-to-end model. We build an end-to-end prediction model by integrating the MGP into the self-attention deep neural network and jointly train them using backpropagation, such that the two modules could benefit from each other for finding global optima.

2. Methods

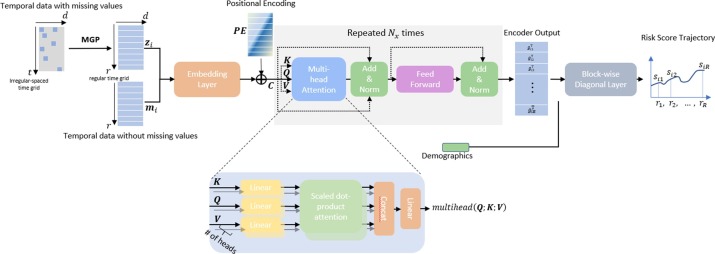
Our proposed model is composed of a missing data imputation network together with a predictive neural network. The two modules are combined seamlessly and trained together in an end-to-end fashion, see Fig. 1 .

Fig. 1.

MGP-MS model overview. The model combines a Multi-task Gaussian Process module with a self-attention neural network for trajectory prediction.

2.1. Multi-task Gaussian process

The Gaussian process is a Bayesian nonparametric statistical model which is flexible and well suited to modeling irregularly sampled time-series data. The core of Gaussian process is the specified kernel function that models the correlations of clinical covariates across time, which defines a covariant matrix that represents the similarities of a random variable's observations at different time points. The Gaussian process assumes a collection of random variables indexed by time or space following a multivariate normal distribution, and it has been widely adopted to model patient physiological time series data [14], [15], [16], [17]. Under this assumption, the Gaussian process is completely specified by a mean and a covariance function. We use the Multi-task Gaussian Process [18] to impute the missing values in multivariate time series data, specifically, the missing values of lab tests and vital signs, where each lab or vital can be viewed as one task. The mean and covariance matrices are our proposed MGP self-attention network parameters and will be learned via back-propagation.

Compared to traditional methods using filling with observed values (fill with zeros/average/majority, forward/backward filling, etc.), and some other complex imputation methods such as multiple imputation [19] which fail to model longitudinal data, the Gaussian process is an advanced modeling technique that estimates the multivariant distribution of longitudinal multivariate data. Compared to the above methods, a critical advantage of the Gaussian process is its ability to model data uncertainties (at the unobserved time points) and prevent over-fitting when trained together with neural networks (through sampling and estimation at the unobserved time points).

The time-lapse between consecutive observations of lab tests and vital signs of hospitalized COVID-19 patients often has irregular property. We denote the number of temporal variables (labs tests, vital signs) as $D$. For the $i$ th patient, we denote all his observed lab and vital values and the time points as $({\mathit{t}}_i,{\mathit{Y}}_i)$, and $T_i=|{\mathit{t}}_i|$ is the number of observational times during patient $i$'s entire hospital stay. The vector ${\mathit{t}}_i=[t_{i1},...t_{i{T}_i}]$ represents all observational time points (not necessarily even-spaced), and ${\mathit{Y}}_i=\left[{\mathit{y}}_{i1},...,{\mathit{y}}_{i{T}_i}\right]$ is a matrix of $T_i\times D$ dimension where ${\mathit{y}}_{\mathit{id}}\in {\mathbb{R}}^D$ is a vector of observed values at those time points. Function $f_{\mathit{id}}(t)$ is used to represent the latent function of time $t$ for patient $i$'s $d$-th feature. In our task, we assume the prior distribution of the Gaussian process has zero mean value, and we have.

$$〈f_{\mathit{id}}\left(t\right),f_{id\prime }\left(t\prime \right)〉={\mathit{K}}_{dd\prime }^D{k}^t\left(t,t\prime \right),$$ (1)

$$y_{\mathit{id}}\left(t\right)~\mathcal{N}\left(f_{\mathit{id}}\left(t\right),{\sigma }_d^2\right),$$ (2)

where $y_{\mathit{id}}(t)$ is the observed value of variable $d$ at time point $t$ of the patient $i$. Similarly, if we denote ${\mathit{y}}_i\triangleq vec({\mathit{Y}}_i)=[y_{i,11},...,y_{i,T_{i}1},y_{i,12},...,y_{i,T_{i}2},...,y_{i,1D},...,y_{i,T_{i}D}]$, then ${\mathit{y}}_i$ follows the distribution.

$${\mathit{y}}_i\mathbf{~}\mathcal{N}\left(0,{\mathrm{\Sigma }}_i\right)$$ (3)

$${\mathrm{\Sigma }}_i~{\mathit{K}}^D\otimes {\mathit{K}}^{T_i}+\mathit{E}\otimes \mathit{I}$$ (4)

where ${\mathit{K}}^D$ is a $D\times D$ matrix representing the inter-task similarities, ${\mathit{K}}^{T_i}$ is a kernel matrix representing the similarities among the observational times, and the diagonal matrix $\mathit{E}$ denotes the noise variances, $\mathit{E}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\sigma }_d^2),d=1,...D$. The kernel functions are usually chosen based on a different set of assumptions on the function to be modeled, for example, the periodic kernel is often chosen to model periodic functions, see [20]. The squared exponential function kernel (radial basis function kernel) $k_{\mathrm{S}\mathrm{E}}(t,t\text{'})=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\left|t-t\text{'}\right|}^2/(2l^2)\right)$ is a kernel function that assumes the local smoothness, where the parameter $l$ is the length scale of the process. The parameter $l$ determines the length scale of the "shape" of the function, such that the extrapolation can only be performed within $l$ units away from the data. This is in accordance with the property of most physiological temporal variables that the missing data can be inferred from nearby observations but is less influenced by early observations that are too further away. Other more complex and powerful kernels such as the rational quadratic kernel can be used to model discontinuous functions which do not fit our application here. An alternative kernel to replace the SE kernel is the OU (Ornstein-Uhlenbeck) Kernel function $k_{\mathrm{O}\mathrm{U}}\left(t,t\prime \right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-|t-t\prime |/l\right).$ Compared to the radial basis function kernel which produces more smooth results, the OU kernel function provides more sharp values on the results since the covariance decrease exponentially for an increasing distance. In our experiments, we notice the SE kernel provides slightly better performance on our prediction task.

In practice, each patient encounter has its unique observational time points ${\mathit{t}}_i=[t_{i1},...t_{i{T}_i}]$ and often the $T_i$ and $T_{i^{\text{'}}}$ are different for different encounters $i$ and $i^{\prime }$. The MGP not only plays the role of imputing missing values but also serves the role of transferring the irregularly spaced data at ${\mathit{t}}_i$ to a regularly spaced (for example, every 4 h) grid $\mathit{r}$ which is commonly shared across all patients. Hence, the downstream prediction neural network has regularly structured data as input.

We denote the regularly spaced time grid $\mathit{r}=\left\{r_1,r_2,...,r_R\right\}$, where $\left|\mathit{r}\right|=R$ is the same for all patients. The patient $i$'s imputed values on the grid $\mathit{r}$ are denoted as a matrix ${\mathit{Z}}_i$ of dimension $R\times D$ . The goal of MGP is to estimate the posterior distribution $P({\mathit{z}}_i\left|{\mathit{y}}_i,{\mathit{t}}_i,\mathit{r};\mathit{\theta }\right))$, where $\mathit{\theta }$ is the parameter(s) of the multi-task Gaussian process. Let vector ${\mathit{z}}_i$ denote the flattened matrix ${\mathit{Z}}_i$, that is, ${\mathit{z}}_i\triangleq vec({\mathit{Z}}_i)=[z_{i,11},...,z_{i,R1},z_{i,12},...,z_{i,R2},...,z_{i,1D},...,z_{i,RD}]$, then ${\mathit{z}}_i$ have the following distribution.

$${\mathit{z}}_i\mathbf{~}\mathcal{N}\left(\mathit{\mu }\left({\mathit{z}}_i\right),\mathrm{\Sigma }\left({\mathit{z}}_i\right);\mathit{\theta }\right),$$ (5)

$$\mathit{\mu }\left({\mathit{z}}_i\right)=\left({\mathit{K}}^D\otimes {\mathit{K}}^{{\mathit{RT}}_i}\right){\mathrm{\Sigma }}_i^{-1}{\mathit{y}}_i,$$ (6)

$$\mathrm{\Sigma }\left({\mathit{z}}_i\right)=\left({\mathit{K}}^D\otimes {\mathit{K}}^R\right)-\left({\mathit{K}}^D\otimes {\mathit{K}}^{{\mathit{RT}}_i}\right){\mathrm{\Sigma }}_i^{-1}\left({\mathit{K}}^D\otimes {\mathit{K}}^{R{X}_i}\right),$$ (7)

where ${\mathit{K}}^{R{T}_i}$ is the kernel matrix among all observational time points ${\mathit{t}}_i$ and the regularly spaced time grids $\mathit{r}$. ${\mathit{K}}^R$ is the kernel matrix denoting the similarity among regularly spaced times r. The ⊗ denotes the Kronecker product, which is, for an $m\times n$ matrix $\mathit{A}$ with $r,s$-th element $a_{\mathit{rs}}$ $(r=1,\cdots ,m,s=1,\cdots ,n)$ and a $p\times q$ matrix $\mathit{B}$ with $v,w$-th element $a_{\mathit{vw}}$($v=1,\cdots ,p,w=1,\cdots ,q)$, their Kronecker product is a $\mathit{pm}\times qn$ matrix, ${\left(\mathit{A}\otimes \mathit{B}\right)}_{\mathit{pr}+v,qs+w}=a_{\mathit{rs}}{b}_{\mathit{vw}}$. The parameter $\mathit{\theta }$ denotes all parameters of the Gaussian process to be learned, i.e., $\mathit{\theta }=\left\{{\mathit{K}}^D,\mathit{E},l\right\}$. The multi-task Gaussian process outputs an $R\times D$ matrix ${\mathit{Z}}_i$, where each row is the observational values of the $D$ physiological variables (lab tests and vital signs) on the regular spaced time grid $\mathit{r}$.

2.2. Self-attention neural network

The post-imputation sequential data (labs and vitals) ${\mathit{Z}}_i$ will be concatenated with the temporal data without missing values ${\mathit{M}}_i$ and feed into the predictive neural network. The matrix ${\mathit{M}}_i$ is an $R\times M$ one-hot (0/1) matrix encoding the information of whether a medication is administrated at each time window. The $M$ is the total number of medications and $R$ is the length of the regular time grid. The matrix ${\mathit{M}}_i$ denotes the medication administration data in our experiment, and it is important since it contains decisions of physiologists that incorporate information about patients' status from the expert. We treat the medication administration data as missing-value-free temporal data since i) medication administration that has been performed is usually recorded in our dataset, ii) contrary to the physiological information such as labs and vitals, whose values are objective, continuous, where missing values are easy to model and impute, medication administration information involves physician decisions which is difficult to model.

The concatenated matrix $({\mathit{Z}}_i,{\mathit{M}}_i)$ of dimension $R\times \left(D+M\right)$ is fed into the prediction neural network. We leverage the self-attention neural network (the Transformer) proposed in [21]. First, each row of the matrix $({\mathit{Z}}_i,{\mathit{M}}_i)$ is encoded to an embedding space of dimension $d_{\mathit{embed}}$ using an input embedding layer. Second, the embedding vector is fed into the transformer-encoder network. In the end, the output of the transformer-encoder will go through a prediction network to realize the task of predicting the risk of performing mechanical ventilation.

The transformer-encoder network consists of 3 modules: the positional encoder, the multi-head attention module, and the position-wise feed-forward network, see Fig. 1. In the positional encoder module, we adopt the sine and cosine functions and construct a matrix $\mathit{P}\mathit{E}$,

$${\mathit{P}\mathit{E}}_{\left(r,2e\right)}=\mathrm{s}\mathrm{i}\mathrm{n}(m/{10000}^{2e/d_{\mathit{model}}})$$ (8)

$${\mathit{P}\mathit{E}}_{\left(r,2e+1\right)}=\mathrm{c}\mathrm{o}\mathrm{s}(m/{10000}^{2e/d_{\mathit{model}}}),$$ (9)

where $r\in 1,\cdots ,R$ is the position index of the regularly spaced time axis $\mathit{r}=\left\{r_1,r_2,...,r_R\right\}$, $e\in 1,..,d_{\mathit{embed}}$ refers to the position along the embedding vector dimension, and $d_{\mathit{model}}$ is a hyperparameter. The function of the positional encoder module is to make use of the temporal information in the input matrix. Compared to the conventional recurrence or convolution function, it not only speeds up the training process by parallelization but also helps avoid the challenge of long-range dependency problems.

The embedding matrix is summed with the position encoding matrix $\mathit{P}\mathit{E}$ to produce a position-encoded embedding matrix $\mathit{C}$ (with dimension $R\times d_{\mathit{embed}}$) to be fed into the self-attention module. The self-attention module consists of multiple ($h$) attention heads where each head is composed of four attention matrices to be trained, the query matrix ${\mathit{W}}^Q$(of dimension $d_{\mathit{model}}\times d_k$), the key matrix ${\mathit{W}}^K$(of dimension $d_{\mathit{model}}\times d_k$), the value matrix $W^V$(of dimension $d_{\mathit{model}}\times d_v$) and the output matrix ${\mathit{W}}^O$(of dimension ${\mathit{hd}}_v\times d_{\mathit{model}}$). In the general transformer model, there are three matrices $Q,K,V$ that is multiplied with the ${\mathit{W}}^Q,{\mathit{W}}^K,{\mathit{W}}^V$, respectively, see equation (12). In the transformer-encoder network itself, the above three matrices are simply identical copies of the matrix $\mathit{C}$ itself. The network performs dot product on all resultant queries with all keys, divide by $\sqrt{d_k}$, and apply a SoftMax function to calculate weights on resultant value vectors,

$$attention\left(\mathit{Q};\mathit{K};\mathit{V}\right)=softmax\left(\frac{\mathit{Q}{\mathit{K}}^T}{\sqrt{d_k}}\right)\mathit{V}.$$ (10)

In the multi-head attention module, the results of all attention heads are concatenated together, and a weight matrix is applied to obtain the final output of the encoder,

$$multihead\left(\mathit{Q};\mathit{K};\mathit{V}\right)=concat\left(hea{d}_1,\cdots ,hea{d}_h\right){\mathit{W}}^O,$$ (11)

$${\mathit{head}}_l=attention\left(\mathit{Q}{\mathit{W}}_l^Q;\mathit{K}{\mathit{W}}_l^K;\mathit{V}{\mathit{W}}_l^V\right).$$ (12)

Note that in equations (10–12),$\mathit{Q}=\mathit{K}=\mathit{V}=\mathit{C}$.

The output of the attention layers $multihead\left(\mathit{Q};\mathit{K};\mathit{V}\right)$ is a matrix of size $R\times d_{\mathit{model}}$, and a feed-forward network is applied on each row of this matrix separately,

$$FFN\left(u\right)=\max \left(0;\mathit{u}{W}_1+{\mathit{b}}_1\right){\mathit{W}}_2+{\mathit{b}}_2,$$ (13)

where $u$ refers to each row of the matrix $multihead\left(\mathit{Q};\mathit{K};\mathit{V}\right)$, ${\mathit{W}}_1$ has dimension $d_{\mathit{model}}\times d_{\mathit{ff}}$ and ${\mathit{W}}_2$ has dimension $d_{\mathit{ff}}\times d_{\mathit{model}}$. We denote the final output of the multi-head self-attention model's output as ${\mathit{G}}_i$ (of dimension $R\times d_{\mathit{model}}$), where $i$ denotes the $i$-th patient.

The multi-head attention module and the feed-forward modules are repeated $N_x$ times, this helps to increase the model's generalizability and to capture richer interpretation of the input sequence. The output of both modules has the dimension of $R\times d_{\mathit{model}}$ to ensure dimension consistency for repeated computation.

2.3. Risk score trend prediction

We introduce a block-wise upper-triangular layer to make the model capable of producing risk scores on the regularly spaced time points for a patient, forming a risk score trajectory. The final encoder's output ${\mathit{G}}_i$ will be flattened row-wisely to a vector and then concatenated with the vector of static variables ${\mathit{w}}_i$ (patient's baseline covariates such as demographics) of dimension $F$ before fed into the block-wise upper-triangular network. The final risk score output will be a length $R$ vector of real values, representing the score of risk at each time,

$$\left(flatten\left({\mathit{G}}_i\right),{\mathit{w}}_i^T\right)=\left({\mathit{g}}_{i1}^T,...,{\mathit{g}}_{\mathit{iR}}^T,{\mathit{w}}_i^T\right)\bullet \left(\begin{array}{ccc}\begin{array}{cc}{\mathit{B}}_1& {\mathit{B}}_1\\ 0& {\mathit{B}}_2\\ 0& 0\end{array}& \begin{array}{c}\cdots \\ \cdots \\ \cdots \end{array}& \begin{array}{c}{\mathit{B}}_1\\ {\mathit{B}}_2\\ {\mathit{B}}_3\end{array}\\ \begin{array}{cc}⋮& ⋮\end{array}& \ddots & ⋮\\ \begin{array}{cc}0& 0\\ \mathit{P}& \mathit{P}\end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}& \begin{array}{c}{\mathit{B}}_R\\ \mathit{P}\end{array}\end{array}\right)=(s_{i1},...,s_{\mathit{iR}})$$ (14)

where each $\mathit{g}$ is a row of the matrix ${\mathit{G}}_i$, matrix ${\mathit{B}}_r,r=1,...,R$ is a column vector of dimension $d_{\mathit{model}}$, and $\mathit{P}$ is a column vector of dimension $F$. The proposed model outputs a sequence of risk scores $(s_{i1},...,s_{\mathit{iR}})$ at the regular spaced time points $\mathit{r}$. The design of such structure of the block-wise upper-triangular network is to ensure each risk score $s_r$ is only using patient temporal information ${\mathit{G}}_i$ before the time point $r$, and the static information ${\mathit{w}}_i^T$.

The MGP together with the self-attention neural network can be viewed as an implicit function $h({\mathit{t}}_i,{\mathit{y}}_i,\mathit{r},{\mathit{m}}_i,{\mathit{w}}_i;\mathit{\theta },\mathit{\omega })$, where $\mathit{\theta },\mathit{\omega }$ are the MGP parameters and weights in the neural network, respectively. The loss function of the proposed model is defined as.

$${\mathit{\theta }}^{\mathbf{\ast }},{\mathit{\omega }}^{\mathbf{\ast }}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_{\mathit{\theta },\mathit{\omega }}\sum _{i=1}^N\sum _{r=1}^R{\mathrm{E}}_{{\mathit{z}}_{\mathit{i}}\mathcal{N}~(\mathit{\mu }({\mathit{z}}_i),\mathrm{\Sigma }({\mathit{z}}_i);\mathit{\theta })}l(s_{\mathit{ir}},o_{\mathit{ir}}),$$ (15)

where $N$ is the total number of patients in the training dataset and $l$ is the loss function for which we choose the binary cross-entropy function. The true label $o_i$ of a patient $i$ is replicated $R$ times to form the above optimization problem, i.e., $o_i=o_{\mathit{ir}},\forall r$.

The multiple objective design let the model foresee the outcome at each previous time point ahead of the event (needing mechanical ventilation) occurring. Therefore, the model is encouraged to predict correctly at all time points rather than being correct only at the end of the observational trajectory. On the other hand, the block-wise upper-triangular module also brings the benefit of promoting the network to make consistent and robust predictions over time for each individual, such that the predicted risk score for a truly intubated patient ($Y_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}=1$)'s will be continually increasing over time as the network sees more information about this patient after hospital admission (t = 0), and vice versa for a negative patient. This can be explained by the nature of the binary cross-entropy (BCE) loss function $\mathrm{L}\mathrm{o}\mathrm{s}{\mathrm{s}}_{\mathrm{B}\mathrm{C}\mathrm{E}}=-({\mathrm{Y}}_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}\mathrm{l}\mathrm{o}\mathrm{g}(Y_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}})+(1-Y_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}})\mathrm{l}\mathrm{o}\mathrm{g}(1-Y_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}))$. For a positive patient, even though both $Y_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}=0.60$ and $Y_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}=0.99$ yield correct predictions (suppose 0.5 is used as the cut-off threshold for risk score probability), the latter induces a smaller loss than the former. This design ensures the prediction at a certain time point only leverages data information before this time point, and when the neural network connects more patient data over time, the information-gain will facilitate the network to make more confident and accurate predictions over time.

The loss function in (15) is calculated over the expectation of the random samplings of ${\mathit{z}}_{\mathit{i}}$, and we use Monte Carlo sampling to approximate this loss function. The number of Monte Carlo samples is a hyperparameter to be tuned. Given a well-trained model and a new patient $i$'s time-series data (with missing values), the post-imputation data ${\mathit{z}}_{\mathit{i}}$ is drawn multiple times from the learned model parameters $\mathit{\mu }({\mathit{z}}_i)$ and $\mathbf{\Sigma }({\mathit{z}}_i)$, which are referred to as the Monte Carlo samples. The prediction risk value of this patient is thus the average over the predictions of the Monte Carlo samples.

2.4. Evaluation metrics

Based on the goal of the prediction task, we evaluate the model's performance from two perspectives: the individual level and the population level.

Individual-level: The model should be able to provide consistent and robust risk score predictions over time for each individual. We propose two performance evaluation metrics, i.e., consistency and robustness, to measure the predicted risk score trajectory. We fit the risk score trend using a linear function and use the function slope to measure consistency and measure robustness according to the Mean Squared Error (MSE) between the linear fitting function and the real risk score. Specifically, we fit the risk score trend of a patient $i$, ${\mathit{s}}_i=(s_{i1},...,s_{\mathit{iR}})$ at time points $\mathit{r}=\left\{r_1,r_2,...,r_R\right\}$ using linear regression. Denote the fitted function as $h_i(\mathit{r})$, an individual $i$'s risk score trend consistency and robustness are defined as.

$${\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}}_i\triangleq \left|\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\left(h_i\left(\mathit{r}\right)\right)\right|,$$ (16)

$${\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}}_i\triangleq \frac{1-\frac{1}{R}{\sum }_{r=1}^R{\left(h_i\left(r_r\right)-s_{\mathit{ir}}\right)}^2}{1+\frac{1}{R}{\sum }_{r=1}^R{\left(h_i\left(r_r\right)-s_{\mathit{ir}}\right)}^2},$$ (17)

Intuitively, a patient's risk score trajectory should demonstrate an overall upward tendency for those patients who would need mechanical ventilation and a downward tendency for those who would not. The consistency measures the slope where a higher absolute value of the slope corresponds to larger consistency, that is, a more obvious development tendency (positive or negative) and a clearer trend. Also, the risk score trend should be robust and avoid fluctuating frequently or significantly over time, and the definition of robustness captures the fluctuation by measuring the mean squared error between the linearly fitted line and the real predictions.

Population-level: The model should be able to distinguish the patients on the whole population who would need mechanical ventilation from those who would not need it. We use AUROC (area under the receiver operating characteristic curve) and AUPRC (area under the precision-recall curve) to evaluate the binary classification task's overall accuracy on the entire population at each time point.

3. Results

3.1. Data

Our model is trained on a dataset of patients with COVID-19, and the patient information is derived from the Optum® de-identified COVID-19 Electronic Health Record dataset (2007–2020). The information we use includes the patient's lab tests history, vital sign observations, medication administrations, and demographic information.

We performed screening and select patients whose COVID-19 tests are positive and hospitalized since the pandemic outbreak during the year 2020 and selected a final cohort of 9,532 patients. After an initial data cleansing to remove the features that have too few observations, we selected 16 lab tests and 9 vital signs (we chose labs and vital signs that are measured at least once by more than half of all patients), shown in Table 2 . For medication administration data, there are over 3,000 different medication names, and the same medication has a variety of different names across different patients. For example, the medication "Lidocaine" has over 60 different names (including "Lidocaine HCL 10 mg/mL (1%)", "Lidocaine HCL 100 mg/10 mL (1%) injection syringe", "Lidocaine HCL 5 mg/mL (0.5%) injection solution", "Lidocaine HCL 1% (10 mg/mL) injection solution", "Lidocaine HCL 1% injection solution'', etc.) in the database, and different names are used in different hospital systems. Including all the variations of the same medication not only makes the medication administration matrix very high dimensional and very sparse but also decreases model performance by introducing a large heterogeneity of variables names that represent the same medication. Therefore, we decided to use the more general medication category (in total 18 categories) as medication administration variables instead of the specific medication names, see Table 3 . The medication categories are according to the Drugbank standard [22]. In the appendix Table S1, we list the example medications names in each category, and for a complete list of medication names in each category, see [22]. In this way, we also naturally omit the dosage information of each medication. The patient medication administration table would be a binary (0/1) matrix where the entry being 1 denotes certain medication was administrated to this patient at a certain time point.

Table 2.

Lab tests, vital signs (observations) used in the experiment.

Index	Lab tests	Index	Vitals and Observations
1	Blood urea nitrogen (BUN)	1	Diastolic Blood Pressure (DBP)
2	Phosphorus (PO4)	2	Heart Rate (HR)
3	Total serum bilirubin (TSB)	3	Systolic Blood Pressure (SBP)
4	Hematocrit (HCT)	4	Respiratory Rate (RESP)
5	Lactate Dehydrogenase (LDH)	5	Pulse Rate (PULSE)
6	Mean Corpuscular Volume (MCV)	6	Urine Output (UROUT)
7	Partial Thromboplastin Time (PTT)	7	Weight (WT)
8	Ferritin	8	Body Temperature
9	Conjugated (“directed”) Bilirubin	9	Pain Assessment
10	Total Calcium
11	Alkaline Phosphatase (ALP)
12	Alanine Aminotransferase (ALT)
13	Aspartate Aminotransferase (AST)
14	Mean Corpuscular Hemoglobin Concentration (MCHC)
15	Immature granulocytes/100 leukocytes in Blood by Automated count
16	Prothrombin Time (PT)

Table 3.

Medicine administrations.

Index	Medicine Class	Index	Medicine Class
1	Central nervous system agents	10	Nutritional agents
2	Respiratory agents	11	Hormones, synthetic substitutes, & metabolic agents
3	Anti-infective agents	12	Ophthalmic preparations
4	Cardiovascular agents	13	Skin & mucus membrane condition agents
5	Gastrointestinal agents	14	Biologic & immunologic agents
6	Antineoplastic agents	15	Mouth & throat preparations
7	Electrolyte, caloric, water balance agents	16	Otic preparations
8	Blood formation & coagulation agents	17	Compounding products
9	Medical supplies	18	Diagnostic agents
10	Miscellaneous agents

Patient's categorical demographic data, including race (African American, Asian, Caucasian, Other/Unknown), ethnicity (Hispanic, not-Hispanic and Unknown), gender (Male, Female), region (Northeast, South, West, Midwest, Other/Unknown) and census bureau division (West North Central, East South Central, South Atlantic/West South Central, New England, Other/Unknown, East North Central, Pacific, Mountain, Middle Atlantic) are one-hot encoded, and numerical data (age) are kept as it is. Patients' summary statistics are shown in Table 1.

Table 1.

Characteristics of the Study Sample (N = 9,532).

Intubation
Intubated	1,485 (15.58%)
Not intubated	8,047 (84.42%)
Mean age (range)	65.12 (21.23, 89.10)
Gender
Female	4,231 (44.39%)
Male	5,299 (55.59%)
Unknown	2 (0.02%)
Race
Caucasian	5,155 (54.08%)
Other/Unknown	1,803 (18.92%)
African American	2,299 (24.12%)
Asian	275 (2.89%)
Ethnicity
Unknown	1,036 (10.87%)
Not Hispanic	7,287 (76.45%)
Hispanic	1,209 (12.68%)
Region
West	492 (5.16%)
Northeast	4,725 (49.57%)
Midwest	3,532 (37.05%)
Other/Unknown	246 (2.58%)
South	537 (5.63%)
Deceased
No	7,473 (78.40%)
Yes	2,059 (21.60%)

3.2. Experiment setting

Time window setting: The observational window of each patient ($T_i$) of each patient is a hyperparameter to be chosen. Larger observational windows incorporate more patient data which we find will increase the model performance, however, notice from equation (7) that the matrix ${\mathrm{\Sigma }}_i$ is of dimension $D{T}_i\times D{T}_i$, and the matrix inversion's time complexity is $O{\left((D{T}_i\right)}^{2.37}$) [23]. We set $T_i=3$ days (72 h) as the observational window to achieve both good performance and acceptable computation time.

4-hour averaging: We also use the 4-hour average value for each lab test and vital sign observation. The timestamps of patient's lab and vital observations in our EHR data are by seconds, including all observations not only makes the parameter ${\mathrm{\Sigma }}_i$ a high dimensional matrix and increases the computational time, but also being unnecessary as most features stay stable within a reasonable time window.

Model input: In the training phase of our model, we set the observational time window to be from the patient's hospital admission to the 3rd day after admission, that is, ${\mathit{t}}_i$ contains patient $i$'s time stamps of all the $D$ variables (lab tests and vital signs) within the 3 days (72 h) after admission. The ${\mathit{r}}_i$ is set to be a 42-length vector, indicating the 1st 4-hour window, 2nd 4-hour window, etc.

Our model is generic, and the observational time window setting depends on the specific application. In a critical scenario where the hospitals fall short of medical beds and ventilators, it is crucial to predict early (like within the first 24–72 h after hospital admission) about a patient's future condition, see also [24], [25], [26] for similar settings. Another interesting application would be to use a patient's 72 h of data counting backward from the time point of the event of intubation happens. The target is to train a model to predict intubation within 72 h before the intubation event happens. In this study, we target the first task. We also what to highlight that compared to the second application, this is a slightly harder task since many biomarkers show abnormality only within a few hours before intubation happens.

Under the above settings, we exclude all patients from our dataset who stayed in the hospital for less than 72 h and those patients who performed mechanical ventilation in less than 72 h. We will use the first 72-hour observational data after admission to train our model and use the well-trained model to predict the post-admission 72-hour risk score trajectory for an unseen patient. There are in total 9,532 patients selected after preprocessing, and 1,485 (15.58%) patients would need mechanical ventilation 3 days afterward. We deal with the class imbalance in the loss function by using class weighting, another and equivalent way is to leverage data oversampling.

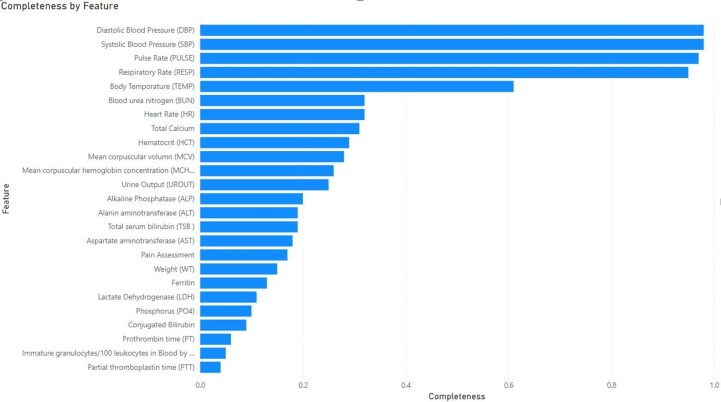
A patient's certain feature may not be observed during a 4-hour window, in this case, we denote has a missing value. We calculate the missingness of all 25 lab tests and vital sign variables in the 72 h observation time of all patients and summarize the data completeness of each variable in Fig. 2 , where 1.0 denotes data no missingness, that is, all patients have at least one observation in each 4-hour window.

Fig. 2.

Data completeness of lab tests and vital signs (100% means a feature's data is fully complete).

Other hyper-parameters: Our model hyperparameters are set to have an embedding size of 512; the feed-forward network dimension is 2048; we use 6 encoder layers and 8 attention heads in the attention module. The L2 regularization and a dropout rate of 0.3 are added to avoid model overfitting. We use the Adam optimizer [27], and a learning rate scheduler is adapted to adjust the learning rate (starting from 0.03) based on the number of epochs, i.e., decaying the learning rate by a multiplicative factor of 0.95 after each epoch. The model is trained for 100 epochs with a batch size of 50 patients. During the joint training of the Multi-task Gaussian Process and the neural network, the MGP generates 50 Monte Carlo Samples (pseudo-patients) for each original patient as the neural network's input, and the predicted risk score at each time point takes the mean of the 50 Monte Carlo Samples. We implemented our pipeline in PyTorch, and the model is trained on Nvidia Tesla V100 GPU.

3.3. Risk score trajectory prediction

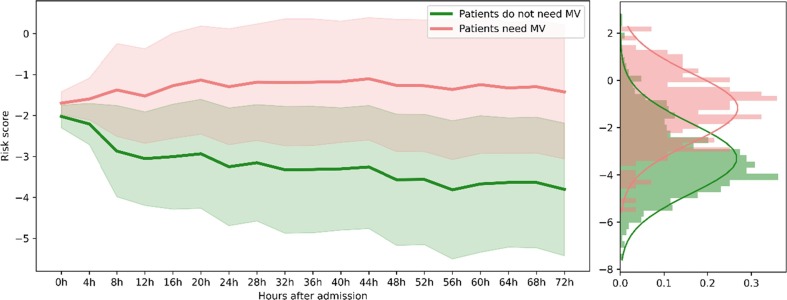
The model is well-trained on the train set (70% of patients) and makes predictions on the test set (30% of patients). For each patient in the test set, the model outputs a 72-hour risk score trajectory. Fig. 3 demonstrates the mean of 3-day risk score pathways of all test set patients that would need MV after 3 days (light red) and the mean of all test set patients that would not (light green), and the shaded area is the +/− one standard deviation. The model successfully distinguishes the two classes of patients, i.e., similar pathways within a class and different between the two classes. The patients who would need MV 3 days afterward have obvious ascending risk score trajectories while those who would not need MV have descending trajectories.

Fig. 3.

The average risk score trajectories of the two classes of patients with the shaded area denote the +/− 1 standard deviation. The right panel shows the two risk score distributions at the 64th hour, and the Wilcoxon rank-sum test yields a p-value of $6.00\times {10}^{-38}$ when assuming the null hypothesis to be two distributions are the same.

3.4. Compare with machine learning approaches

We compare our model with the Cox Proportional-Hazard Model [28] and machine learning models including Logistic Regression and Gradient Boosted Tree Model (using XGBoost) [29]. To make a fair comparison with our model, when making predictions at a time point (for example, at the 20th hour after admission), the model only uses patients' data before this time point. Similar to the input of our model, we take a 4-hour average for each feature. Finally, the time series matrix data (row: number of time indices, column: number of features) will be stacked into one vector and concatenated with the demographic data to form the input vector. For Logistic Regression, the LogisticRegression from python library Scikit-learn was used and the class weights were specified to handle the class imbalance. The Xgboost model was from the library XGBoost [30] and Cox's proportional hazard model is from Lifelines [31]. For missing values, we explored filling with zeros, forward filing (use the next valid observation to fill the missing values), backward filling (propagating the last valid observation forward to the next observation valid, if for certain missing positions there is no previous observation then it is filled using forward filling), and Multiple Imputation and selected the one with the best performance.

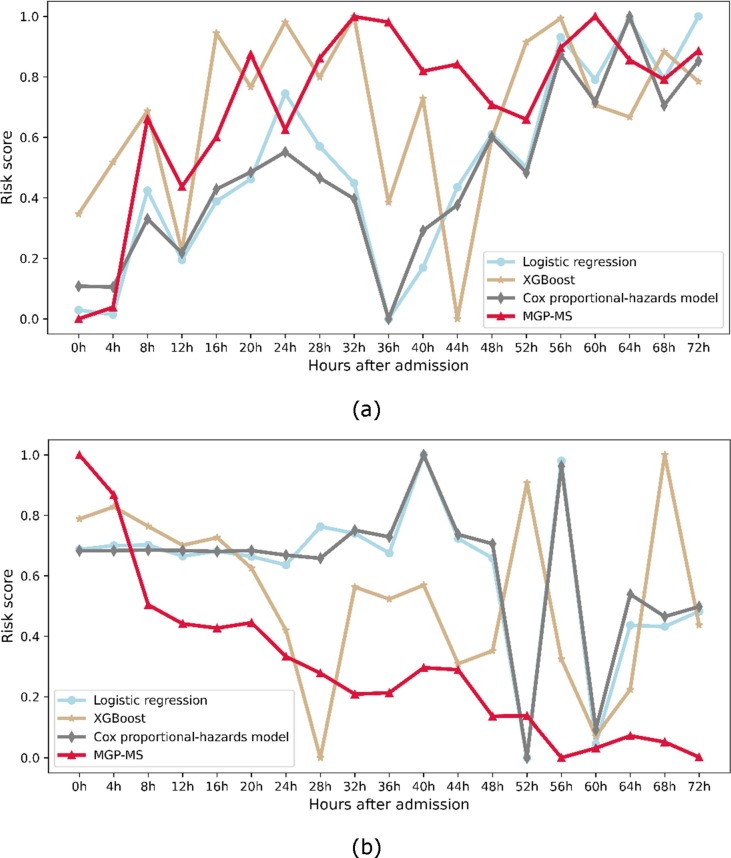
Fig. 4 (a) shows the risk score prediction of a randomly selected patient in the dataset who would need MV after 3 days since being admitted to the hospital, and Fig. 4 (b) shows that of a patient who would not after 3 days. Since the compared models cannot output consistent real-time predictions, each model is trained using the instant physiological data collected during a 4-hour window and makes risk score predictions every 4 h, and form a trajectory. It is worth paying attention that, for a particular patient, the risk scores predicted by different models are not of the same value at the same time point. The risk values produced by different models are not comparable, and here we focus on the tendency of the risk score trajectory rather than the particular values themselves. To this end, we normalize all models' predictions to the range of 0.0–1.0. A smooth and consistent risk score pathway is deemed to be a robust prediction instead of a pathway that highly fluctuates, which indicates inconsistent predictions over time.

Fig. 4.

Two sample patients' risk score trajectory prediction using different models. (a) The risk score pathway of a randomly selected patient with COVID-19 who would need MV after 3 days since admission. (b) The risk score pathway of a randomly selected patient with COVID-19 who would not need MV after 3 days since admission.

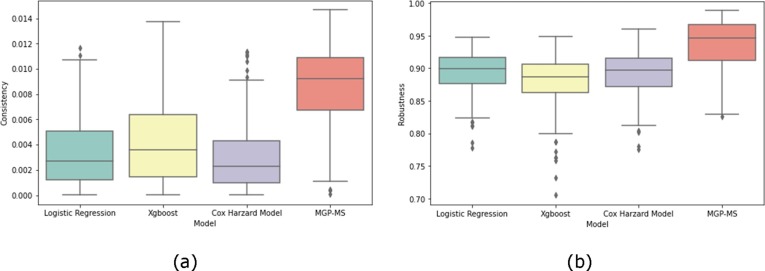
In Fig. 5 , we evaluated the consistency and robustness of the 3-day risk score trajectories of all patients predicted by the four models. It can be seen that our proposed model has significant improvement in consistency and robustness compared to the other three models (consistency improved by around 258.00%, 166.00%, and 343.00%, respectively; robustness improved by around 5.56%, 8.05%, and 6.74%, respectively).

Fig. 5.

Performance evaluation of different models, (a) Consistency (b) Robustness.

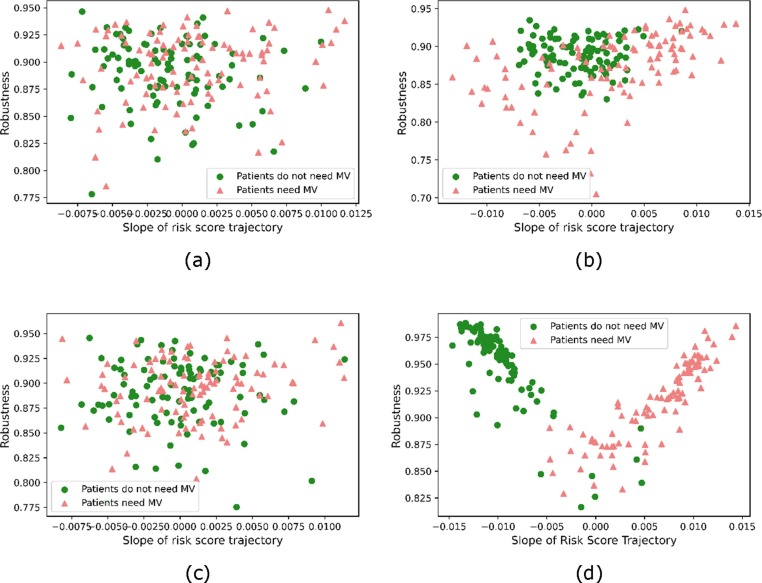
In Fig. 6 , each patient's 3-day risk score trajectory's robustness and consistency are shown as a scatter plot where the robustness and consistency metrics are formed as perpendicular axes. The horizontal axis is the slope of the fitted linear function, and the vertical axis is the robustness. For the two classes of patients, the figure shows the proposed model has more separable slope values for the two categories, where the slope is positive (an increasing risk score trend) for each patient who would need mechanical ventilation and negative (a decreasing risk score trend) for those who would not need it.

Fig. 6.

Scatter plots of 200 sample patients' trajectory robustness and slopes. (a) Logistic Regression, (b) XGBoost, (c) Cox Proportional-Hazard Model, (d) the proposed MGP-MS model.

3.5. Compare with neural-network-based approaches

The proposed model outperforms Neural-network-based models in the prediction accuracy for the whole population.

Several models were previously proposed and showed success on similar prediction tasks that take irregularly sampled data as input, including the time-aware LSTM network (T-LSTM) [32], the GRU-D [33], the Gaussian process temporal convolutional networks (GP-TCN) [34], the Interpolation-prediction networks (IPN) [35] and the multi-task Gaussian process RNN model (MGP-RNN) [13]. This section compares them with our proposed model in terms of the AUROC and AUPRC performance metrics. We also compare MGP-MS with typical RNN models combined with simple data imputation methods, including the standard long short-term memory (LSTM) [36] network and the gated recurrent unit (GRU) [37] network. Similar to the machine learning models, we explored different data imputation techniques including zero-filling, forward (backward)-filling, and selected the forward-filling since it produces slightly better performance. In all the above models, patients' static demographics data are appended to the input vector of the last layer (classification layer) to make the prediction.

In Table 4 , we summarize the population-level performances (AUROC and AUPRC) of our proposed model and several other models for the mechanical ventilation prediction task on the same dataset. To ensure a fair comparison, we tuned the hyper-parameters to ensure the best performance. The predictions at a time point are made using all observations after hospital admission and before this time point. Our model outperforms most of the previous models and gains the largest improvement in the early times after admission.

Table 4.

AUROC and AUPRC Performance Comparison.

Model	Admission		0.5 Day		1 Day		2 Days		3 Days
	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR	AUROC	AUPR
GRU-ffill	0.7378 $\pm$ 0.0487	0.3193 $\pm$ 0.0562	0.7404 $\pm$ 0.0968	0.3348 $\pm$ 0.0626	0.7901 $\pm$ 0.0333	0.3756 $\pm$ 0.0388	0.7754 $\pm$ 0.0760	0.4048 $\pm$ 0.0688	0.8061 $\pm$ 0.0507	0.4447 $\pm$ 0.0176
GRU-D	0.6080 $\pm$ 0.0064	0.2420 $\pm$ 0.0094	0.6062 $\pm$ 0.0077	0.2442 $\pm$ 0.0096	0.6747 $\pm$ 0.0093	0.3031 $\pm$ 0.0072	0.7517 $\pm$ 0.0107	0.4109 $\pm$ 0.0292	0.8099 $\pm$ 0.0055	0.4814$\pm$0.0182
MGP-TCN	0.5972 $\pm$ 0.0152	0.2220 $\pm$ 0.0064	0.5862 $\pm$ 0.0127	0.2135 $\pm$ 0.0084	0.6394 $\pm$ 0.0135	0.3131 $\pm$ 0.0132	0.7602 $\pm$ 0.0037	0.3909 $\pm$ 0.0053	0.7732 $\pm$ 0.0153	0.4632 $\pm$ 0.0125
IPN	0.7034 $\pm$ 0.0136	0.3473 $\pm$ 0.0056	0.7286 $\pm$ 0.084	0.3687 $\pm$ 0.0043	0.7605 $\pm$ 0.0094	0.3904 $\pm$ 0.0148	0.7653 $\pm$ 0.0158	0.4116 $\pm$ 0.0053	0.7770 $\pm$ 0.0198	0.4014 $\pm$ 0.0098
T-LSTM	0.5051 $\pm$ 0.0020	0.1836 $\pm$ 0.0098	0.5132 $\pm$ 0.0066	0.2020 $\pm$ 0.0293	0.5540 $\pm$ 0.0046	0.2642 $\pm$ 0.0099	0.6140 $\pm$ 0.0156	0.3525 $\pm$ 0.0054	0.6910 $\pm$ 0.0045	0.3956 $\pm$ 0.0124
MGP-GRU	0.7048 $\pm$ 0.0036	0.2912 $\pm$ 0.0021	0.7329 $\pm$ 0.0078	0.3176 $\pm$ 0.0100	0.7631 $\pm$ 0.0101	0.3555 $\pm$ 0.0069	0.7859 $\pm$ 0.0023	0.4398 $\pm$ 0.0145	0.7912 $\pm$ 0.0089	0.4712 $\pm$ 0.0120
MGP-MS	0.7920$\pm$0.0063	0.3992$\pm$0.0112	0.8221$\pm$0.0030	0.4507$\pm$0.0043	0.8292$\pm$0.0046	0.4587$\pm$0.0066	0.8420$\pm$0.0052	0.4678$\pm$0.0062	0.8421$\pm$0.0056	0.4813 $\pm$ 0.0096

4. Discussions

We presented a novel data-driven early warning model to predict the COVID-19 patient's risk score and distinguish the patients that will need mechanical ventilation or not soon after admission. The proposed model provides accurate, robust, and real-time risk score predictions. We evaluated our model on a cohort of nearly 10,000 COVID-19 patients and demonstrated high accuracies. We also compared our model with several baseline models and it demonstrated a clear performance improvement, at individual level and population level. The model achieves higher prediction accuracy compared to other deep-learning models, especially in the early times after the patient's hospital admission.

Overall, we address the following challenges in this study. First, typical classification models such as logistic regression, tree-based methods, Cox proportional-hazards model, etc., cannot provide real-time risk predictions despite their high accuracy. Whereas training separate models at different time points often produces a good overall performance on the population level but raises consistency on the individual level. Second, EHRs are usually collected in an unscheduled manner such that traditional frameworks view most patients as having missing data, which deteriorates the model's performance. Third, the EHRs among different patient encounters face the problems of asynchronously sampling (lab tests and vital signs are sampled at different timestamps) and irregularly sampling (the time interval between every two contiguous observations is not always consistent), and EHR data often demonstrates a mixture of both patterns which causes the conventional data imputation methods such multiple imputation methods to fail. Fourth, the need for mechanical ventilation (indicating deterioration of the patient's situation) is determined by a combination of many factors such that complicated interaction pattern is too complex to capture for human beings and simple scoring systems, which limit their performances. Finally, it is difficult to distinguish the patients who would need mechanical ventilation from the others at very early times after admission, since the biochemical indicators only become abnormal after several hours or even a few days for most patients.

We addressed these challenges by the integration of the MGP for data imputation and the deep neural network for prediction. We leverage the self-attention mechanism to handle long-term dependency problems. The model has clinical significance during the circumstances of the ongoing COVID-19 pandemic, especially for the hospitals that are experiencing a shortage of ventilators due to the increasing number of in-hospital patients. The allocation of ventilators to patients of higher risk would significantly increase the overall survival rate.

Several future directions are worth exploring. The Gaussian process involves a large matrix inversion, approximation techniques could be utilized to decrease the computational complexity. The medication administration information in our dataset needs an inspection to make the medication names consistent for all patients. The medication administration dosage would also be an important factor for the prediction task but extracting the dosage information would be a more difficult task on the dataset we use. It would also be interesting to cluster the patients into sub-phenotypes based on their risk trend progression pattern, to analyze how factors such as age, race, and comorbidities would cause disease progression pathways.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

The following are the Supplementary data to this article: