How well can you tailor the charge of lipid vesicles?

Abstract

Knowledge and control of surface potential (or charge) is important for tailoring colloidal interactions. In this work we compare widely used zeta potential measurements of charged lipid vesicle surface potential to direct measurements using the surface force apparatus (SFA). Our measurements show good agreement between the two techniques. On varying the fraction of anionic lipids dimyristoylphosphatidylserine (DMPS) or dimyristoylphosphatidylglycerol (DMPG) mixed with zwitterionic dimyristoylphosphatidylcholine (DMPC) from 0 to 100 mol % we observed a near-linear increase in membrane surface charge/potential up to 20 – 30 mol% charged lipids beyond which charge saturation occurred in physiological salt conditions. Similarly, in low salt concentrations a linear increase in charge/potential was found, but only up to ~ 5 – 10 mol% charged lipids beyond which the surface potential/charge leveled off. While a lower degree of ionization is expected due to the lower dielectric constant (ε ~ 4) of the lipid acyl chain environment, increasing intra-membrane electrostatic repulsions between neighboring lipid head groups at higher charge loading contributes to charge suppression. Measured potentials in physiological (high) salt solutions were consistent with predictions using the Gouy-Chapman-Stern-Grahame (GCSG) model of the electrical double layer with Langmuir binding of counterions, but in low salt conditions, the model significantly overestimated the surface charge/potential. The much lower ionization in low salt (maximum fraction dissociated ~ 1 – 2 % of total lipids) instead was consistent with counterion condensation at the bilayer surface which limited the charge/potential that could be obtained. The strong interplay between membrane composition, lipid head group ionization, solution pH and electrolyte concentration complicates exact prediction and tuning of membrane surface charge or potential for applications. However, the theoretical frameworks used in the work can be used as guidelines to understand this interplay and establish a range of achievable potentials for a system to tune or predict the response to triggers like pH and salt concentration changes.

Graphical Abstract

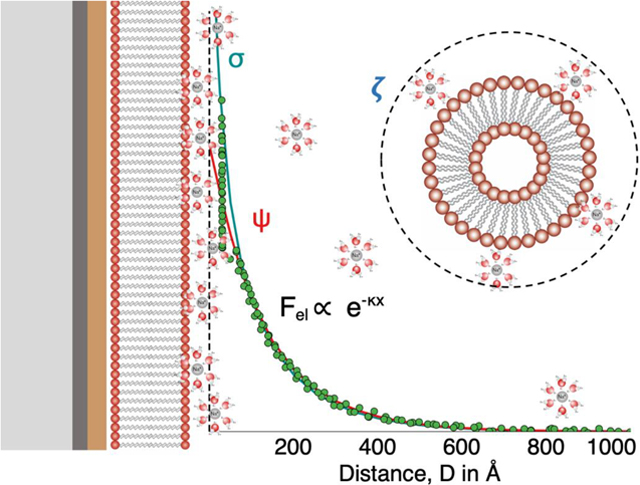
INTRODUCTION

Biological membranes are largely composed of amphiphilic phospholipids which self-assemble to form a stable bilayer-like structure with a hydrophobic core of acyl-chains and a hydrophilic exterior consisting of lipid head groups bearing different moieties- zwitterionic, glycosylated or anionic.^2–3 Given the complexity of cellular biomembranes, simpler biomimetic systems like lipid monolayers, bilayers and vesicles, are commonly used in biophysical studies of membrane properties and the interaction of membranes with soluble species.^4–6 Vesicle or liposomes are also attractive candidates for use in a variety of applications like drug delivery^7–10, cosmetic formulations^11–13, development of novel analytical or biomedical diagnostic tools¹⁴, and for innovations in food technology because they are biocompatible and biodegradable.^15–16 The interior aqueous environment can be loaded with aqueous, polar material while the enclosing bilayer membrane can retain non-polar species.⁷ The size and composition of vesicles are the most commonly varied parameters for modulating vesicle properties to control specific interactions, particle stability, cellular uptake and retention, and their sensitivity to environmental factors or triggers like pH and temperature.⁷ The surface charge on lipid vesicles is an important determinant of colloidal stability as modulating electrostatic interactions can help prevent particle agglomeration.^17–18 In a biological context, surface charge on particles is often correlated with toxicity to cells, retention or removal by the reticuloendothelial system (RES), and cellular uptake/permeability.^{7, 19} It is therefore important to understand how membrane surface charge can be manipulated to suit a particular application.

The most common method used to characterize vesicle charge is by zeta potential measurements.²⁰ This light scattering-based technique uses electrophoretic mobility of particles (U_E) in an electric field to determine potential (ξ) at the hydrodynamic shear/slip plane using Henry’s equation (Eq. 1).

$$U_E=\frac{2{\epsilon }_0{\epsilon }_r\xi f\left(\kappa a\right)}{3\eta }$$ (Eq. 1)

Henry’s equation accounts for solution properties like viscosity (η), dielectric constant (ε) directly, while the like ionic strength (Debye length, κ⁻¹) and particle size (a) are indirectly accounted for using a fitting parameter f(κa) which is varied between 1 and 1.5 based on the value of κa.^21–22 Typically, the Hückel approximation, f(κa) = 1, is used for non-polar solvents and for κa < 1. The Smoluchowski approximation, f(κa) = 1.5, is used for aqueous solutions with κa >> 1. The location of the hydrodynamic shear or slip plane (also known as the zeta plane) with respect to the particle surface (usually assumed to be between 2 – 20 Å) is often hard to define, making conclusive data interpretation difficult.^22–23 In this work vesicle zeta potential measurements are compared to direct measurements of electrostatic forces between similarly composed supported lipid bilayers using the surface force apparatus (SFA). The SFA has been used extensively to study interactions forces between lipid bilayers composed of neutral, zwitterionic lipids (PC, PE), but little work has been done on charged lipid bilayers.^24–30 Further, a direct comparison of measured potential using the two techniques has not been previously reported.

A variety of studies have been conducted on charged vesicles investigating zeta potential variation. For example, the zeta potential of DSPC:cholesterol vesicles linearly increased with the addition of up to 8 mol% anionic (DOPS) or cationic (DOTAP) lipid groups in 10 mM NaCl (pH 7.4 – 7.7).²⁰ Similar studies on cholesterol-containing mixed PS:PC vesicles between 6.6 to 17.6 mol% PS also found a linear potential increase in high salt concentrations (152 mM, pH 5.9), but no potential increase with charged lipid fraction in low salt concentrations (6.6 mM, pH 5.9).³¹ A systematic investigation of the effect of monovalent salt over a concentration range of 10 to 90 mM NaCl (pH 7.4) on zeta potential of charged vesicles composed of 20 or 100 mol% DOPG found greater potential values at low salt concentrations and a larger variation in potential with salt concentration when the vesicles contained 20 mol% compared to 100 mol% DOPG.³² Similarly, the zeta potential of DOPS:DOPC vesicles in ultrapure water saturated at 10 mol% DOPS.³³ In other words, just increasing the concentration of charged lipid in the vesicle did not necessarily result in a higher potential.

In this work, the charge behavior of lipid vesicles and supported bilayers composed of two different anionic lipids DMPS and DMPG mixed with zwitterionic lipid DMPC in monovalent salt solutions was investigated. (Figure 1) The fraction of charged lipids (DMPS or DMPG) was varied from 0 to 100 mol% in solutions of different ionic strength and pH. In general, good agreement was found between vesicle zeta potential and direct force spectroscopy measurements using the SFA. In particular, the SFA enables direct measurements of electrostatic forces between lipid bilayers as a function of exact surface separation. This removes ambiguity associated with Henry’s equation. For measurements in physiological conditions, the interplay of membrane composition, lipid headgroup pKa, solution ionic strength and pH was reasonably well captured by the Gouy-Chapman-Stern-Grahame (GCSG) model of the electrical double layer when counterion binding was taken into account. In low ionic strength solutions, the GCSG model overestimated surface potential, particularly at high surface charge loading (> 20 mol %). Instead, under low ionic strength the measured membrane potential was accurately predicted by Manning’s charge condensation theory which indicates that in dilute salt solutions, there exists a critical surface charge density beyond which counterion condensation is observed. Beyond this limit, the addition of more charged groups to the surface does not further increase the surface charge. Lastly, some rules of thumb for tuning vesicle charge through composition and solution conditions are provided.

Figure 1:

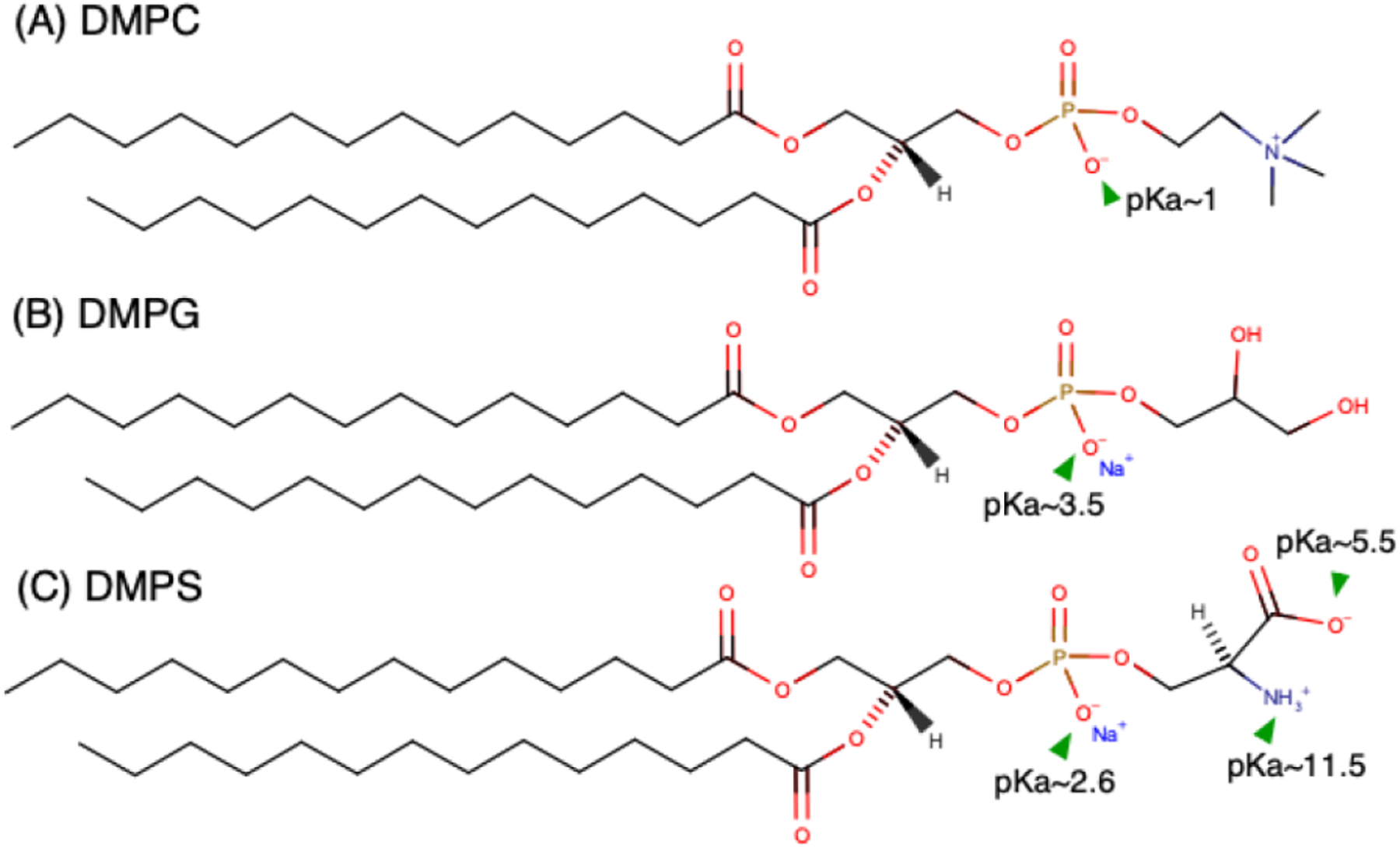
Structure of (A) DMPC, (B) DMPG, and (C) DMPS. Ionization constants (pKa) of different head group moieties are highlighted.¹

MATERIALS AND METHODS

Chemicals

1,2-dimyristoyl-sn-glycero-3-phospho-(1’-rac-glycerol) (sodium salt) (DMPG, T_m= 23°C), 1,2-dimyristoyl-sn-glycero-3-phospho-L-serine (sodium salt) (DMPS, T_m= 35°C), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC, T_m= 24°C) and 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine (DPPE, T_m= 63°C) were purchased in powder form (>99% purity, Avanti Polar Lipids, Inc, Alabaster, AL, USA). Lipid stock solutions of desired concentrations (<5 mg/ml) were prepared by dissolving the powders in 9:1 volume % chloroform: methanol. Sodium nitrate (NaNO₃, 99.995% purity, Sigma, St. Louis, MO, USA) was used to prepare monovalent electrolyte solutions used in surface force measurements and low salt zeta potential measurements. Sodium phosphate dibasic heptahydrate (Na₂HPO₄.7H₂O, >99+% purity, ACROS Organics, NJ, USA), sodium phosphate monobasic monohydrate and sodium chloride (NaH₂PO₄.H₂O, 99.2% purity, NaCl, 99.9% purity, Fisher Scientific, Waltham, MA, USA) were used to prepare the phosphate buffer for zeta potential measurements. Water used in experiments was purified with a MilliQ Gradient water purification system with a resistivity of 18.0 MΩ·cm.

Vesicle preparation

Appropriate volumes of each lipid stock solution were added to an amber glass vial to obtain the desired lipid composition. A gentle stream of nitrogen gas was used to evaporate the solvent from the lipid mixture while rotating the vial to ensure the lipids coated the walls uniformly. The samples were then fully dried by placing them in a vacuum chamber for a minimum of 4 h to ensure complete removal of solvent. The dried lipid samples were rehydrated with 3 mL of 0.5 mM NaNO₃ (to a concentration of 0.4 mg/ml) for measurements in low salt conditions or with a 140 mM phosphate buffer (7.5 mM Na₂HPO₄.7H₂O, 2.5 mM NaH₂PO₄.H₂O, 130mM NaCl, pH 7.4) for measurements in physiological conditions. The solutions were thoroughly vortexed to dissolve the lipids, sonicated in a water bath sonicator (Cole Palmer Ultrasonic cleaner, Model 8891, 42 kHz) for 10 minutes to form vesicles, and finally, homogenized using a probe-tip sonicator (Ultrasonic Homogenizer, Model 150 V/T, Biologics, Inc.) at 30 % power for 1 minute. After probe-tip sonication, vesicle solutions were filtered using a 0.22 μm syringe filter to remove any titanium particles generated during the sonication process. For samples rehydrated with 140 mM phosphate buffer, the samples were heated to approx. 35 °C and extruded through a vesicle extruder with 100 nm polycarbonate filter 15 times to further ensure sample homogeneity. All vesicle samples were characterized for size and surface potential within 2 hours of preparation.

Dynamic light scattering (DLS) and Zeta potential

A Malvern Zetasizer Nano ZS90 instrument (Southborough, MA, USA) was used to perform dynamic light scattering measurements to characterize the vesicle size distribution and measure the zeta potential. Approximately 1 ml of sample was loaded into the cuvette and allowed equilibrate to 25 °C. A minimum of three size measurements (90° scattering angle) were performed per sample with more than 30 runs per measurement. Zeta potential measurements based on the electrophoretic mobility were performed on the same sample to quantify the surface potential at the hydrodynamic slip plane using the Smoluchowski approximation (f(κa) = 1.5). Potential values were obtained from at least 3 independently prepared samples with at least 3 separate measurements per sample (>30 runs per measurement) for each vesicle composition.

Lipid bilayer/vesicles are highly hydrated systems with water molecules and counterions strongly associated with the membrane interface.³ In this work, the Stern or stagnant layer thickness (d_s) was assumed to be 5 Å approximately the size of a hydrated Na⁺ counterion (~ 4 – 4.7 Å).³⁴ That is to say, the zeta-potential value at the hydrodynamic slip plane was assumed to correspond to the potential (ψ) at d_s = 5 Å. This selection is supported by x-ray photoelectron spectroscopy (XPS) studies of silica nanoparticle surfaces, which indicated that the Stern layer thickness of a single hydration shell of water was 1.4 ± 0.6 Å and between 6.2 ± 0.4 to 9.1 ± 0.9 Å for Na⁺ solutions.^34–35 Similarly, x-ray reflectivity measurements of muscovite mica interface in monovalent electrolyte solutions show electron density peaks between 2 and 6 Å from the interface due to layering of hydronium (H₃O⁺) and sodium (Na⁺) ions in electrolyte solutions.³⁶

Monolayer isotherms and bilayer deposition

A Teflon® Langmuir–Blodgett trough (Type 611, Nima Coventry, UK) was used to measure lipid monolayer surface pressure – area (Π–A) isotherms. The trough experiments were carried out at a room temperature of 24.5 ± 1.0 °C on a subphase of milliQ water with a pH of 5.7 ± 0.2. SI figure S1 shows the Π–A isotherms curves for pure DMPC, DMPG, DMPS and lipid mixtures of 10 and 20 mol% charged lipids DMPS or DMPG in DMPC (e.g. 10:90 DMPS: DMPC). The isotherms indicate that while pure DMPC at 35 mN/m is in the fluid state, pure DMPG, pure DMPS and the lipid mixtures were in the gel state. No evidence of phase separation was indicated by the collapse pressure of the mixed monolayers. (SI figure S2).

Lipid bilayers were deposited onto mica surfaces using the Langmuir-Blodgett (LB) deposition technique.^37–38 The inner leaflet in all cases was DPPE deposited at 45mN/m because it is known to produce a robust, defect-free, strongly physisorbed, gel-phase monolayer on mica with minimal lipid exchange with the outer leaflet.^39–40 The outer leaflet comprised of 10:90, 20:80 or 100:0 DMPS:DMPC or DMPG:DMPC was deposited at 35mN/m to mimic the surface pressure of vesicles.^41–42 Fluorescence microscopy images of the various bilayer compositions are shown in SI figure S3. The transfer ratio was 1.00 ± 0.05 for the DPPE inner leaflet and 0.98 ± 0.08 for the various compositions of the outer leaflet. A transfer ratio of 1 indicates that the deposited lipids maintained their packing area during deposition.³⁸ Once the complete bilayer was formed on mica-coated SFA discs, the surfaces were kept submerged under water and mounted in the SFA box.

Surface force apparatus (SFA)

The SFA technique has been used extensively to measure the interaction forces between surfaces.^43–46 In brief, the substrates supporting the LB deposited bilayers were atomically smooth mica substrates (with a 55 nm thick back coating of evaporated silver) glued onto cylindrical glass discs. The silver layer on each disk partially transmits light directed normally through the surfaces, which constructively interferes to produce fringes of equal chromatic order (FECO). The SFA uses multiple-beam interferometry (MBI) to provide a definitive measure of surface separation (± 0.2 nm) and film thickness.⁴³

One of the bilayer-coated mica surfaces was mounted on a fixed stage, and the other was mounted on a double-cantilever spring of known stiffness (~ 2.8 × 10⁵ mN/m) which can be displaced vertically. The distance between the surfaces was measured by observing and tracking the position and displacement of FECO peak wavelengths within a spectrometer. A custom-automated SFA Mark- II was used for data collection and surface displacements via a computer-controlled motor system. A sensitive CCD camera (Princeton SPEC-10:2K Roper Scientific, Trenton, NJ) was interfaced with the spectrometer and computer acquisition system to allow automated FECO wavelength tracking. The water in the SFA box was saturated with a small volume of lipid solution (same composition as the outer leaflet) to minimize lipid desorption from the bilayer during the course of the measurements. After the surfaces were mounted, the SFA box was placed in a temperature-controlled room at 25.0 ± 0.1 °C to equilibrate for a minimum of 2h before measurements. The experiments were completed within 24 h of bilayer deposition. The separation distance was calculated by approximating the system as a symmetric 3-layer interferometer and using analytical solutions for the resulting optical interference, as is typical for lipid bilayers deposited on mica.^29–30 The membrane thickness was determined using the FECO wavelength shift from the membrane contact relative to the bare mica substrates after completing the experiment. Three independent SFA experiments were carried out for each of the membrane compositions. Force profiles shown in the results and discussion section are for one set of experimental measurements but were consistent among the three independent experiments.

Membrane thickness determination and D=0

At the end of each experiment, the surfaces were separated, and the apparatus solution was drained, thereby removing the outer leaflets of the bilayers. The SFA box was connected to a vacuum source for a minimum of 2 h to dry the box completely. The hydrophobic inner DPPE layers were brought into contact to determine the thickness change attributable to the two outer leaflets which includes their hydration. Theoretical thicknesses for anhydrous bilayers (without headgroup hydration) were obtained from previous x-ray scattering studies (D_HH (Å)) performed on gel phase lipid bilayers.^47–50 Area per molecule values obtained from lipid monolayer pressure-area isotherms (SI figure S1) were in good agreement with values reported from x-ray scattering experiments on DMPC (48.1 Ų) and DMPS (40.8 Ų) in the gel phase. No X-ray scattering bilayer measurements of DMPG in the gel phase were found. As DMPG has a similar transition temperature (T_m) as DMPC, similar area per molecule and D_HH (Å) in the fluid phase, the thickness of gel-phase DMPC was used for gel-phase DMPG.^49–50 Zwitterionic lipid bilayers are known to have a 6 – 10 Å thick hydration layer associated with the headgroups (per bilayer).^{3, 50–51} Based on the measured hydrated bilayer thicknesses form SFA and the anhydrous thicknesses based on the lipid molecular structure, we found that bilayers containing DMPS and DMPG had an average hydration thickness of 9 ± 2 Å and 15 ± 2 Å per bilayer respectively. This difference can be attributed to the fact that the glycerol head group on DMPG has a higher tendency to form hydrogen bonds with neighboring water molecules. The SFA measurements are consistent with inter-bilayer water spacing obtained from osmotic pressure measurements performed on DMPG bilayers.⁵² The values for bilayer thickness (from x-ray scattering) and hydrated thickness (from SFA measurements) are summarized in Table 1. In this work, D = 0 was defined as the anhydrous contact of the lipid bilayers. The “charge” plane of origin (outer Helmholtz plane, OHP), was assumed to be located 5 Å from each bilayer surface (surface separation distance, D = 10 Å). This plane is equivalent to the assumed hydrodynamic shear or slip plane for the vesicle zeta potential measurements which corresponds to a Stern layer thickness of one hydrated Na⁺ counterion diameter (ξ = potential at d_s = 5 Å). A schematic of this frame of reference is shown in figure 2. In SI section S5, an analysis of surface charge and potential obtained from assumptions of different charge planes of origin (D = 0, 10, 20 Å for opposing bilayers which is equivalent to d_s = 0, 5, 10 Å respectively for a vesicle) is provided for two different bilayer compositions - 10:90 DMPG:DMPC and 100:0 DMPG:DMPC.

Table 1.

Anhydrous bilayer thickness (D_HH Å) from x-ray scattering experiments.^47–48 Hydrated bilayer thickness from surface force measurements averaged over all compositions, 10:90, 20:80, 100:0 DMPG:DMPC or DMPS:DMPC.

Bilayer composition	Anhydrous bilayer thickness (Å)	Hydrated thickness (Å)
DMPG	40.1	69.9 ± 4.6
DMPS	44.3	62.4 ± 1.6

Figure 2:

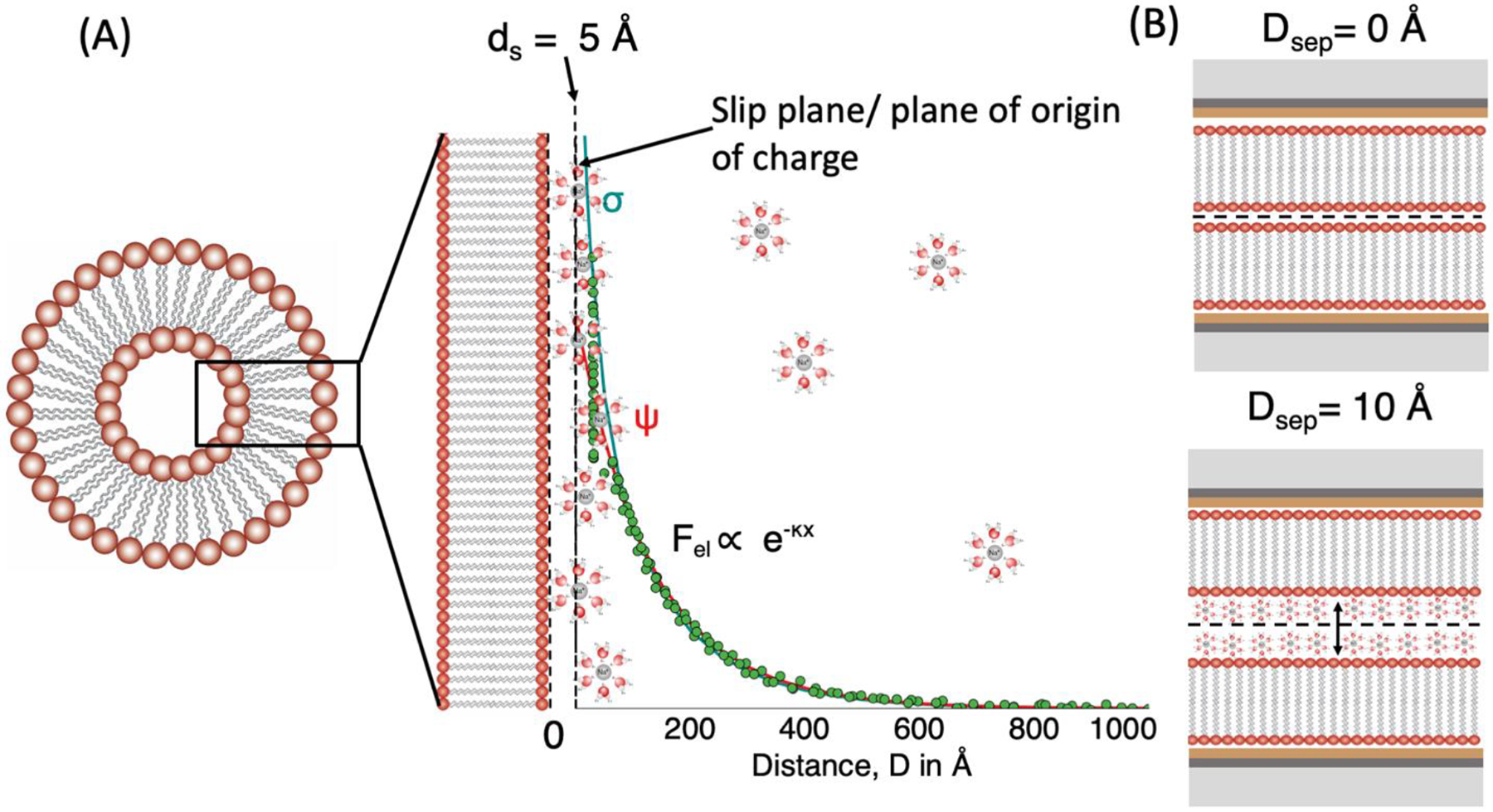
A schematic of the equivalent frame of references used to interpret (A) Zeta potential measurements and (B) SFA measurements.

Electrostatic forces (SFA)

At large separation distances, (D > 100 Å), electrostatic repulsion was the only contributor to the measured force between the bilayers. An exponential curve was fit to the data between 100 to 600 Å to determine the Debye length and effective salt concentration of the system. The surface charge density and potential of the lipid bilayers were then calculated using a numerical iterative solution to the nonlinear Poisson Boltzmann equation (NLPB, Eq. 2) using constant charge and constant potential boundary conditions to fit the experimentally measured electrostatic force.

$$\frac{{\text{d}}^2\text{Y}}{\text{d}{\text{x}}^2}=\text{sinh\hspace{0.17em}Y}$$ (Eq. 2)

where $\text{Y}=\frac{\text{ze}\psi }{\text{kT}}$ and $\text{x}=\frac{\text{D}}{{\kappa }^{-1}}$, z the valency of the ion, e is electronic charge, ψ the electrical double-layer potential, k the Boltzmann constant, T is temperature, κ⁻¹ is the Debye length aD is the separation distance between the surfaces,. The Derjaguin approximation (Eq. 3) was used to convert the NLPB solution which gives double layer electrostatic interaction energy (E) between flat plates to the force (F) between crossed cylinders as used in the SFA normalized by the geometric mean radius of curvature ($R=\sqrt{R_1{R}_2}$).

$$\text{E}\left(\text{D}\right)=\frac{\text{F}\left(\text{D}\right)}{2\pi \text{R}}$$ (Eq. 3)

Gouy-Chapman-Stern-Grahame (GCSG) model

Following the work of Ohki, S., et. al.⁵³ and others^54–56, the GCSG model of the electrical double layer was used to predict the surface charge/potential at the charged bilayer surface. The Gouy Chapman (Eq. 4) solution to the NLPB equation gives the diffuse double layer electrostatic potential distribution from a planar surface of uniform surface charge in a symmetric (z:z) electrolyte.

$$\text{tanh}\left(\frac{ze{\psi }_d}{4kT}\right)=\text{tanh}\left(\frac{ze{\psi }_0}{4kT}\right)\text{exp}\left(-\kappa d\right)$$ (Eq. 4)

where ψ_0,ψ_d are the electrical double-layer potentials at the surface and at a distance d from the surface. For κa ≫ 1, the interacting spherical vesicles can be approximated as flat planes. The use of spherical Gouy Chapman solution resulted in a difference in potential value of less than 5 percent. The Grahame equation (Eq. 5), derived from the Guoy Chapman solution, gives the relationship between the surface charge density and potential at the interface.

$${\sigma }_0={\left(8{\epsilon }_r{\epsilon }_0{N}_{A}kT\left({\left[N{a}^{+}\right]}_{\infty }+{\left[H^{+}\right]}_{\infty }\right)\right)}^{\frac{1}{2}}\text{\hspace{0.17em}sinh}\left(\frac{e{\psi }_0}{2kT}\right)$$ (Eq. 5)

where σ₀ is the surface charge density, N_A is Avogadro’s number, and [Na⁺]_∞ and [H⁺]_∞ are the bulk concentration of the counterions. Bilayer charge originates from the dissociation of PS or PG head groups and can be calculated using ${\sigma }_{max}=\pm \frac{e{\chi }_j}{A_j}$ where χ_j is the mol fraction of charged lipids, and A_j is the area per lipid. Accounting for counterion binding to the head groups at the interface using the Langmuir adsorption model reduces the surface charge to an effective value σ_0,eff :

$${\sigma }_{0,eff}=\frac{{\sigma }_{max}}{1+\left(\frac{{\left[H^{+}\right]}_{\infty }}{K_a}+K_c{\left[N{a}^{+}\right]}_{\infty }\right)\text{\hspace{0.17em}exp}\left(-\frac{e{\psi }_0}{kT}\right)}$$ (Eq. 6)

K_c is the binding constant for Na⁺ counterions and K_a is the dissociation constant for H⁺ ions calculated from the acid dissociation constant for the lipid (pKa). An average area per lipid value of 45 Ų/molecule (corresponding to a surface pressure of 30 – 35 mN/m) was used for these calculations based on isotherms for different bilayers compositions as shown in SI figure S1.

Charge Condensation Model

Manning’s charge condensation theory is often used in the context of linear polyelectrolytes in dilute electrolyte solutions to explain saturation in surface charge density beyond a maximum value (σ_crit).⁵⁷ The condensation refers to the collapse of counterions from the diffuse ion atmosphere onto the charged surface to minimize free energy, thereby keeping the system ≤ σ_crit. For large spheres in dilute solutions following the criteria κa~O(1), counterion condensation occurs above a critical value of surface charge density σ_crit given by Eq. (7):

$${\sigma }_{\mathit{\text{crit}}}=\frac{e\left(1-\kappa a\right)\text{ln}\left(\kappa l_B\right)}{2\pi z{l}_{B}a}$$ (Eq. 7)

where l_B is Bjerrum length (~ 7.01 Å for water at 298K). For a thick cylinder geometry with κa ≫ 1, where a is the radius of the cylinder (a ~ 1 cm for SFA discs), the σ_crit is the same as that for a large plane given by Eq. (8):

$${\sigma }_{\mathit{\text{crit}}}=\frac{e\kappa \text{\hspace{0.17em}ln}\left(\kappa l_B\right)}{2\pi z{l}_B}$$ (Eq. 8)

Both the GCSG and charge condensation models have been used to explain measured vesicle zeta potential under different solution conditions.

RESULTS AND DISCUSSION

Dynamic light scattering (DLS) size measurements

The average size of vesicles produced by extrusion in 140 mM phosphate buffer (pH 7.4 ± 0.1) was 156 ± 39 nm and for vesicles produced by probe tip sonication in 0.5 mM NaNO₃ (pH 5.7 ± 0.1) was 141 ± 65 nm. The average size of vesicles varied between 127 – 193 nm in 140 mM salt solution and 97 – 182 nm in 0.5 mM salt solution but no clear trends in size with varying membrane composition were observed, summarized in SI Table S1. 100 mol% DMPS or DMPG samples were observed to be more prone to aggregation over time and care was taken to carry out size and potential measurement soon after preparation. For some vesicle compositions, upto 10 % of the lipid assemblies were ~20–30 nm in size but the measured zeta potential result was unaffected.

Zeta potential measurements

Figure 3 shows the dependence of zeta potential on the mol% of charged lipid in mixed DMPS:DMPC and DMPG:DMPC vesicles prepared in physiological and in low salt conditions. The error bars indicate one standard deviation. As expected, the zeta potential was negative for vesicles composed of negatively charged lipids. Both DMPG and DMPS, can bear one negative charge per lipid head group for solution pH < 9 −10. In physiological salt condition, a monotonic increase in zeta potential was observed with fraction of charged lipid up to 20 – 30 mol% above which the surface potential saturated at −34 ± 3 mV for 100 mol% DMPS and −32 ± 3 mV for 100 mol% DMPG. In the low salt condition, a more rapid increase in zeta potential was observed but only up to ~ 5–10 mol% charged lipids. Above this concentration the zeta potential saturated at −68 ± 3 mV for 100 mol% DMPS and −69 ± 3 mV for 100 mol% DMPG. Table 2 gives the fraction of charged lipids dissociated (α = σ_0,eff/σ_max) and the effective fraction of total lipids dissociated in the membrane for the different membrane compositions. (calculated using the Eq. 4 and 5 assuming zeta potential value corresponded to ψ_{d=5 Å}). The similarity in surface potential between DMPS and DMPG is somewhat surprising at the low salt condition. Here, the solution pH is 5.7 ± 0.2 but the difference in pKa of the lipids (3.5 vs. 5.5 does not result in a discernable difference in ionization behavior. The importance of pH, ionic strength and lipid pKa will be further discussed after comparison to direct force measurements of bilayer charge/potential.

Figure 3:

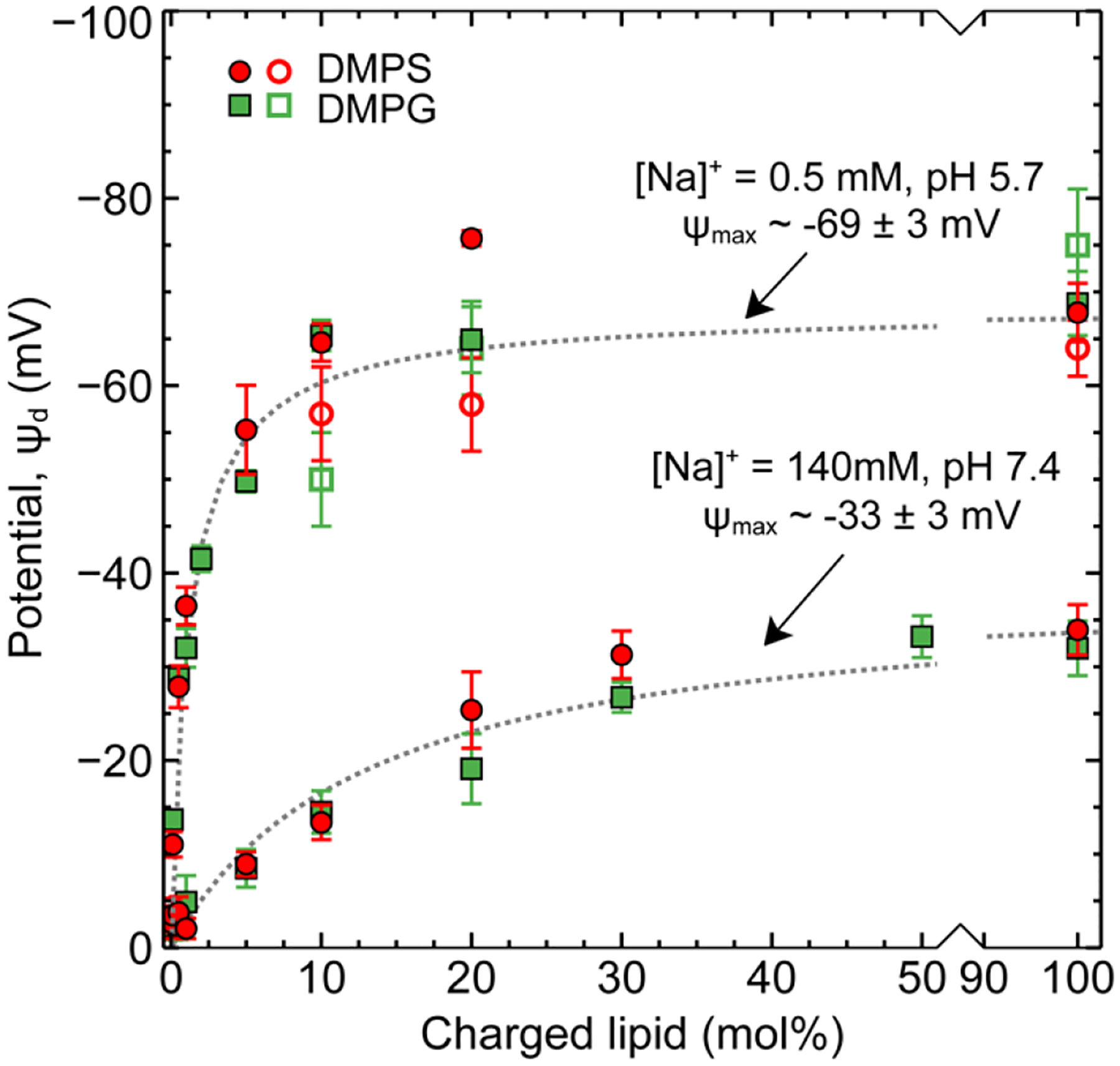
Zeta potential measurements of mixed DMPS:DMPC and DMPG:DMPC vesicles in physiological (140 mM, pH 7.4) and low salt (0.5 mM, pH 5.7) conditions (solid markers). SFA measurements of mixed DMPS:DMPC and DMPG:DMPC lipid bilayers in low salt conditions 0.5 mM, pH 5.7 (hollow markers). Dotted lines are guides to the eye.

Table 2:

Zeta potential measurements. Fraction of charged lipids dissociated was calculated by comparison of surface charge with theoretical maximum surface charge for each composition (based on mole fraction of charged species and area per lipid of 45 Ų/molecule). Given the similarity in potential trends for DMPS and DMPG, only dissociation data for DMPS:DMPC mixtures is reported.

140 mM phosphate buffer, pH 7.4
DMPS:DMPC	Zeta potential ζ, mV	Surface charge σ0, mC/m2	Fraction of charged lipids dissociated (Approx.%)	Overall lipids dissociated (%)
1:99	−2 ± 1	−3 ± 3	91	1
5:95	−9 ± 1	−15 ± 2	82	4
10:90	−13 ± 2	−22 ± 3	63	6
20:80	−25 ± 4	−49 ± 10	69	14
30:70	−31 ± 3	−68 ± 11	64	19
100:0	−34 ± 3	−79 ± 15	22	22 ± 4
0.5 mM NaNO 3 , pH 5.7
DMPS:DMPC	Zeta potential ζ, mV	Surface charge σ0, mC/m2	Fraction of charged lipids dissociated (Approx. %)	Overall lipids Dissociated (%)
0.5: 99.5	−28 ± 2	−1.6 ± 0.1	88	0.4
1:99	−36 ± 3	−2.1 ± 0.2	60	0.6
5:95	−55 ± 5	−3.7 ± 0.4	21	1.0
10:90	−65 ± 3	−4.6 ± 0.2	13	1.3
20:80	−76 ± 2	−6.0 ± 0.3	8	1.7
100:0	−68 ± 3	−5.0 ± 0.4	1.4	1.4 ± 0.2

Surface force measurements

Surface force measurements were performed in low salt conditions of 0.5 mM NaNO₃. At high salt concentrations it is difficult to separate electrostatic for short Debye lengths (~8 Å) from hydration repulsion forces. Figure 4 shows an exemplar force profile for a pure, 100% DMPG supported bilayer in 0.5 mM NaNO_3, pH 5.7 ± 0.2. Similar plots for other membrane compositions are provided in SI figure S4. The data is presented on a semi-logarithmic plot to clearly demonstrate the electrostatic force which decays exponentially according to the Debye length. The experimentally measured Debye length across all experiments was consistent with the solution electrolyte concentration, 137 ± 10 Å. At small surface separations (~ 20 – 30 Å compared to the anhydrous bilayer contact D = 0) a strong repulsive force was measured corresponding to physical contact of opposing, hydrated lipid bilayers. Numerical solutions to the non-linear Poisson Boltzmann equation were used to fit the electrostatic repulsion and determine the surface potential and charge of the membrane. These values are tabulated in Table 3. Figure 3 (open symbols) shows the potential values obtained from surface force measurements for 10:90, 20:80, 100:0 DMPG:DMPC or DMPS:DMPC in 0.5 mM NaNO₃ compared to vesicle zeta potential measurements (closed symbols).

Figure 4:

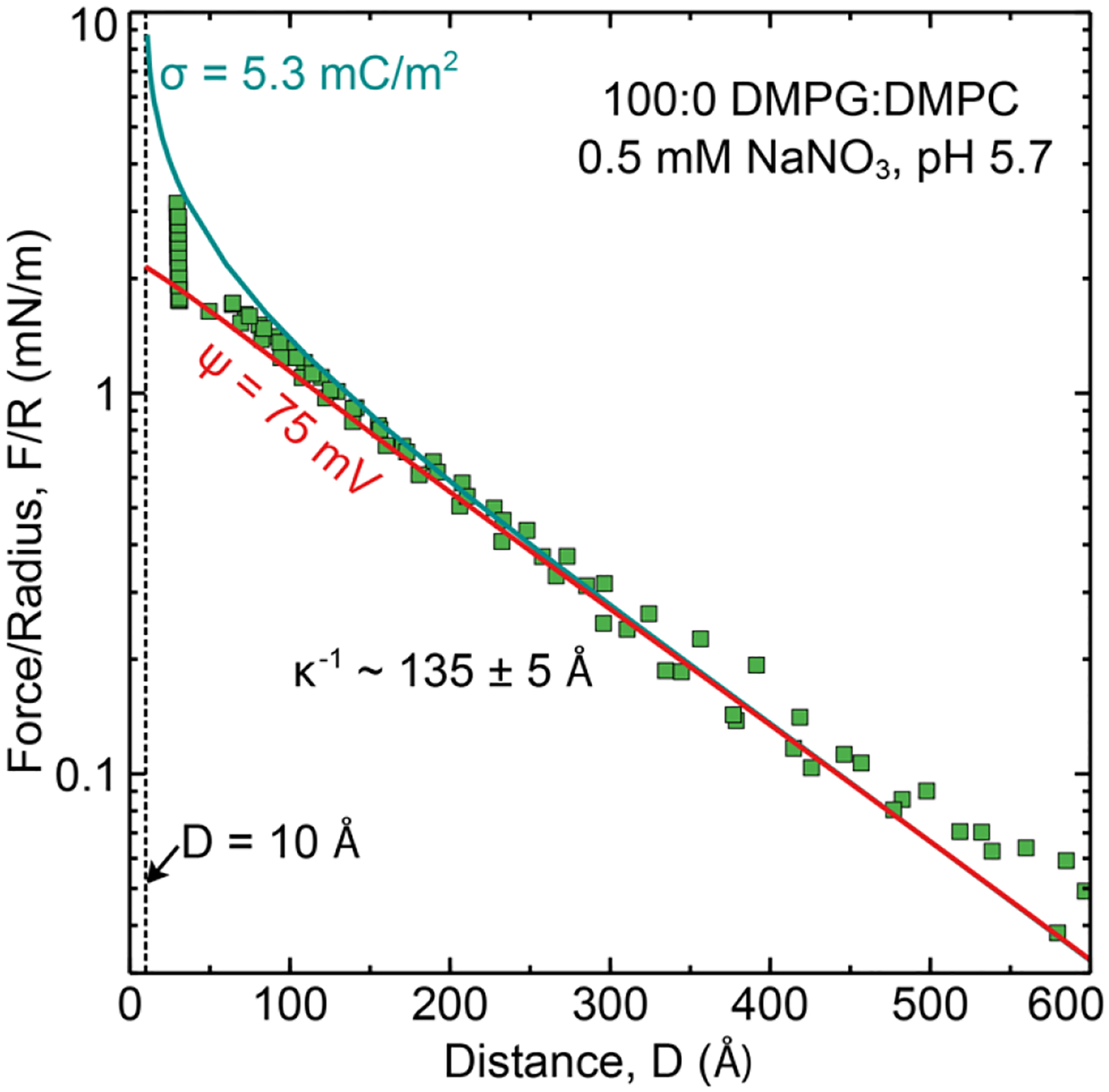
Measured interaction force profile between lipid bilayers composed of 100 mol% DMPG (outer leaflet) deposited on DPPE (inner leaflet) in 0.5mM NaNO₃, pH 5. D = 0 was set to be the anhydrous bilayer contact which corresponds to the location of the phosphate head group plane. D = 10 corresponds to a contact of the OHP planes. This is equivalent to d_s = 5 Å from the opposing membranes 2 d_s = 10 Å).

Table 3.

Surface charge and potential from surface force measurements. Fraction of charged lipids dissociated was calculated as described in Table 2.

Outer leaflet composition (mol%)	σ (mC/m2)	ψ (mV)	Area per charge (nm2 per e−)	Fraction of charged lipids dissociated (Approx.%)	Overall lipids dissociated (%)
10:90 DMPG:DMPC	−2.9 ± 0.6	−50 ± 5	55 ± 10	8	0.8
20:80 DMPG:DMPC	−4.0 ± 0.5	−64 ± 5	40 ± 5	6	1.2
100:0 DMPG:DMPC	−5.3 ± 0.6	−75 ± 6	30 ± 3	1.5	1.5 ± 0.2
10:90 DMPS:DMPC	−3.4 ± 0.6	−57 ± 5	47 ± 7	10	1
20:80 DMPS:DMPC	−3.5 ± 0.5	−58 ± 5	46 ± 6	5	1
100:0 DMPS:DMPC	−4.0 ± 0.3	−64 ± 3	40 ± 3	1.1	1.1 ± 0.1

The experimentally determined potentials were consistent between the two techniques and show similar charge saturation behavior. While there were slight differences (typically < 10 mV) observed between potential values obtained for DMPS and DMPG by SFA and vesicle zeta potential measurements, there were no particular trends that could be attributed to differences in ionization constants (pKa) between the two lipids, which suggests that both DMPS and DMPG have a similar ionization behavior in a bilayer. Although one might expect that the electrostatic repulsion would scale with the fraction of charged lipids, this was far from what was observed. In both measurement conditions, two different regimes were observed – a linear regime wherein the potential increased with added charged lipid followed by a constant potential regime where the potential remained independent of the amount of charged lipid in the membrane. These results are in agreement with previous studies by Smith et. al.²⁰, which investigated zeta potential as a function of 0 to 8 mol% charged anionic lipid DOPS and cationic lipid DOTAP mixed with DSPC and cholesterol in 10 mM NaCl (pH 7.4 – 7.7). Over this small concentration range a linear dependence between potential and mol% charged lipid was found. Crommelin³¹ also observed a near linear dependence (up to −40 mV) with cholesterol-containing mixed PS:PC multilamellar vesicles (6.6, 12.5, and 17.6 mol% PS) in 152 mM salt solution. A saturation at 6.6 mol% (potential ~ −60 mV) was found in 6.6 mM salt (pH 5.9). The vesicle composition at which a linear dependence of potential on the fraction of charged lipid changes to a saturation in potential clearly depends on the ionic strength and pH of the experiments. Together, these studies demonstrate that there is a maximum membrane charge/potential attainable for a given solution condition. As shown in Table 2 and 3, in the case high ionic strength we observe a maximum dissociation fraction of 15–20 % of total lipids on the surface and in low ionic strength solutions a far lower amount 1–2 %. As the fraction of charged lipid in the membrane is increased, intra-membrane repulsion between neighboring “charged” lipid head groups is a significant factor and affects lipid head-group dissociation. In solutions of high ionic strength, the electrostatic repulsion forces decay over a short distance (1/κ ~0.8 nm) allowing for higher fractions of added lipids to be dissociated compared to low ionic strength solutions 1/κ ~ 13.6 nm).

To better understand the interplay of solution conditions and lipid pKa, we first compared our results to predictions of the GCSG model of the electrical double layer. Based on previous studies, a value of 0.6 M⁻¹ was chosen for the binding constant K_c between Na⁺ and DMPG or DMPS head groups.^53–54 ${K_a}^{-1}$, the binding constant for H⁺ with the charged lipid species, was calculated from the pKa of the relevant dissociable group (COO- for DMPS and PO₄⁻ for DMPG). While the intrinsic pKa value for a given dissociable group is constant, the apparent pKa value depends on local environment including dielectric, ionic strength, local charge and electrostatics making it hard to determine. The pKa of primary phosphate groups is thought to be ~ 0 – 2, secondary phosphates ~ 6 – 7, carboxyl groups ~ 3 – 5, and primary amines ~ 9 – 11.¹ A lower degree of ionization is expected for charged lipid head groups containing these dissociable moieties, especially when present in a lipid monolayer/bilayer, due to the lower dielectric constant (ε ~ 4) of the acyl chains that make up the hydrophobic core of a lipid bilayer.⁵⁸ Estimates of 3.5 and 5.5 pKa were used for DMPG and DMPS respectively based on titrations of gel to fluid bilayer phase transition temperature.¹ The magnitudes of $\frac{{[H^{+}]}_0}{K_a}$ and K_c[Na⁺]₀ in Eq. 6 determine whether and which ion binding effects are significant. Since the interfacial concentration of counterions increases exponentially with surface potential, at higher surface charges, ion binding effects become more prominent. To separate the effects of pH and ionic strength, additional complementary experiments were done on 10:90 and 100:0 DMPS:DMPC vesicles in 0.5 mM, pH 7.4 and 140 mM, pH 5.7. The measured vesicle potentials are included in Figure 5 which also shows theoretical predictions of potential at the OHP (ψ_5A). In the physiological salt solution (low H⁺ and high Na⁺), Na⁺ ion binding is the dominant effect and the GCSG model with a pKa ~ 3.5 explains the measured trends of vesicle zeta potential reasonably well for both measured solution pH conditions 5.7 and 7.4. Film expansion studies and titration experiments on PG lipid monolayers at the air-water interface have also shown a strong dependence of pKa on ionic strength, lipid acyl chain length and area per lipid, with higher apparent pKa values in low salt concentration, for longer acyl chain length and smaller area per lipid.⁵⁹ In the low ionic strength solution with solution pH 5.7, an assumption of pKa ~ 3.5 (DMPG) accurately predicts potential up to 2 mol % but significantly overpredicts the potential at high concentration of charged lipid. pKa ~ 5.5 (DMPS) under predicts the potential at low charged lipid concentrations (< 5%) but reasonably fits compositions between 5 – 20 mol %. At 100 mol% DMPS, the deviation between GCSG predictions and theory is quite significant (> 30 mV). Furthermore, the measured potential is the same at pH 5.7 and 7.4 despite theory predicting otherwise. In order to fit the measured potentials at 100 % charged lipid in pH 5.7 and the potentials obtained in pH 7.4 an unphysical pKa value ~ 7 – 8 would be required for both DMPS and DMPG. In summary counterion binding within the GCSG framework is able to predict the charge behavior at high ionic strength but not in low ionic strength.

Figure 5:

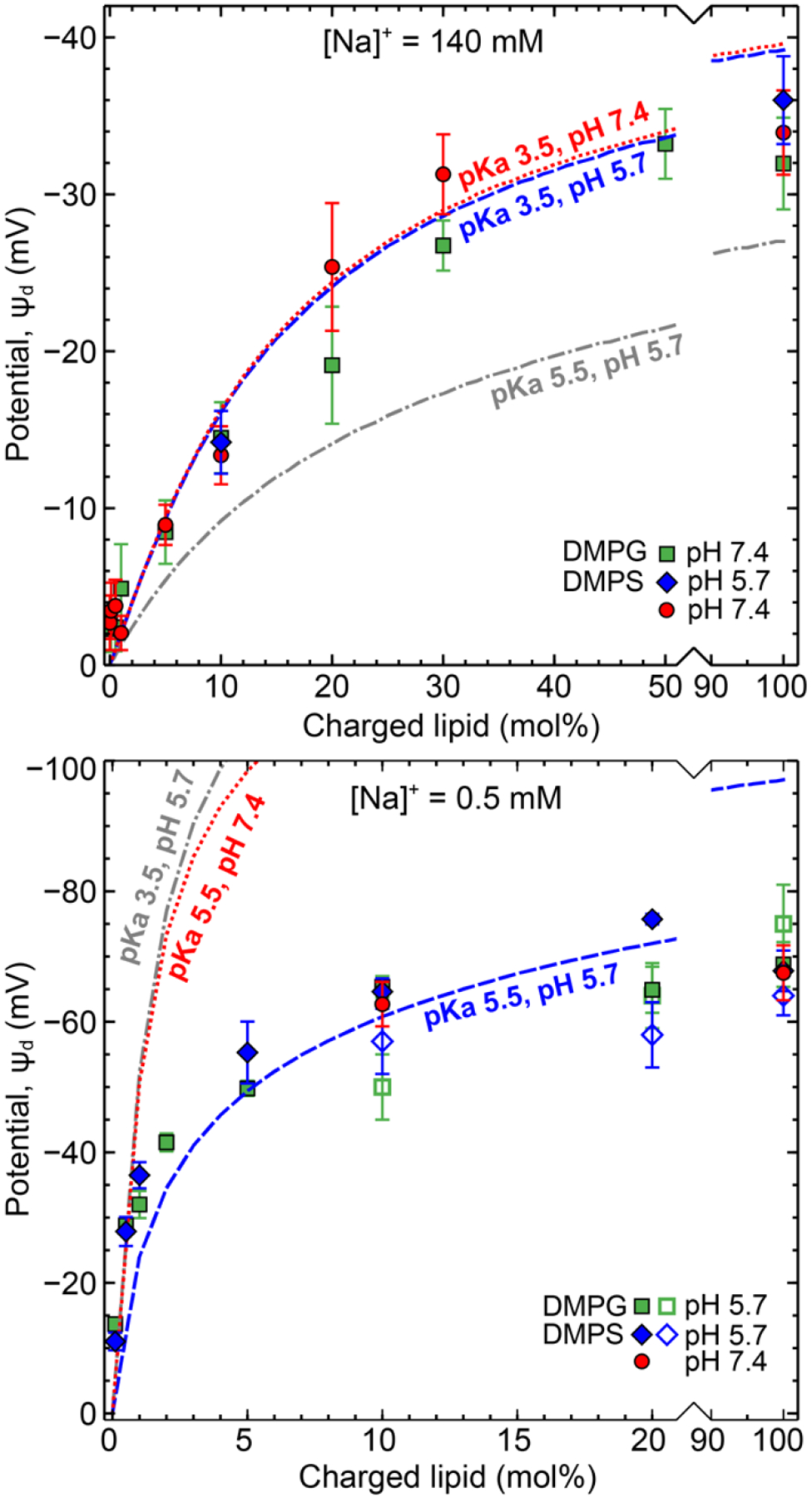
A comparison of predicted potential at the OHP/zeta slip plane (d_s =5 Å or D = 10 Å) from Gouy-Chapman-Stern-Grahame theory after accounting for counterion binding effects with experimental zeta potential results in (A) 140 mM salt and (B) 0.5 mM salt.

At low ionic strength, a charge condensation model is required. Charge condensation phenomena is often observed with highly charged polyelectrolytes in dilute salt solutions wherein beyond a critical surface charge density, counterions collapse on the charged species to minimize the free energy of the system.⁵⁷ For vesicles with an average radius a ~ 80 ± 20 nm the σ_crit value for 0.5 mM salt solution is −5.35 < σ_crit < −5.99 mC/m² and for lipid bilayers deposited on cylindrical SFA discs (a ~1 cm), the σ_crit is ~ 6.94 mC/m². The experimentally measured maximum surface charge for vesicles and bilayers was around 5 ± 1 mC/m² which is in good agreement with charge condensation theory. A similar charge condensation behavior and saturation to a potential of −44 mV (~ 2 mC/m²) was observed by Lütgebaucks. et. al.³³, in their experiements on 0–100 mol% DOPS:DOPC vesicles in ultrapure water. In complementary sum-frequency generation (SFG) spectroscopy studies⁶⁰ of water alignment near mixed anionic and cationic lipid monolayers in 10 mM NaCl, Dreier et. al.⁶⁰ detected a linear increase in water alignment with increase in membrane charge at low surface charge densities. Beyond 20 % excess anionic lipid, a saturation in water alignment was observed attributable to charge condensation as also found in our studies.

Eisenberg et. al.⁶¹ investigated the zeta potential of large (1–20 μm), single component multilamellar anionic vesicles composed of pure – PS, PG, PI and PA in monovalent high salt solutions (100 mM, pH 7.5). They also found similar potential values for PS and PG vesicles. The zeta potential for PA vesicles was ~ 10 mV higher and for PI was 15 – 20 mV lower. In comparison to this work, the higher value zeta potential for PA vesicles could be explained by additional dissociation of the phosphate group (pKa₂ ~ 8). The lower potentials for PI vesicles are likely due to the bulky, hydrated sugar head group shielding charges more effectively or increasing the stern layer thickness. This reiterates the importance of knowing the lipid head group structure, its correlation with ionization properties and plane of potential measurement. Similarly, different counterions have different binding affinities to lipid head groups (e.g. for 1:4 DOPG:DOPC vesicles, Li⁺ > Na⁺ > K⁺ > Rb⁺ > Cs⁺)³², as well as different hydrated ion sizes emphasizing the importance of specific ion effects.^{32, 61}

Finally, biological membranes are soft, fluid interfaces which can often regulate surface charges by reorganization or counterion penetration and binding to minimize the system free energy. Clearly, there is a strong interplay between membrane composition (lipid type and concentration), phase behavior (represented by area per lipid), electrolyte type, concentration, and solution pH. While values of intrinsic and apparent lipid ionization constants are intended to capture this complex interplay they often measured experimentally and therefore dependent on the measurement conditions. This makes it difficult to predict a priori exact surface potential values for a given experimental system. The GCSG model is a good starting point to predict how the interplay of membrane composition and solution conditions can be tailored to obtain a desired surface potential. In general, higher potential values are obtained by decreasing electrolyte concentration though charge condensation limits the surface charge in dilute solutions. A pH-driven response is expected around the apparent pKa of the lipid (|pH – pKa_app| <1). Therefore, to maximize surface dissociation, the pH of the electrolyte solution should be at least 2 units greater than the apparent pKa. Increasing the fraction of charged lipid results in an increase in potential but saturates at high charge loadings. Overall, this understanding can be used to guide the choice and concentration of charged lipids, especially for the development of stimulus-responsive systems that have properties dependent on pH, temperature or environmental salt concentrations.

CONCLUSION

Zeta potential measurements of lipid vesicle surface charge/potential in monovalent salt solutions were in good agreement with direct measurements of supported bilayer surface charge/potential using the surface force apparatus. Given the ubiquitous use of the zeta potential technique, these results are significant as they demonstrate that the zeta potential results provide an accurate measure of lipid membrane charge behavior. The charge/potential of the lipid membrane can be controlled by increasing the concentration of charged lipid. However, depending on the ionic strength charge saturation occurs between 5–30 mol%. Intra-membrane repulsion between neighboring lipid head groups at high charge loading results in a decrease in head group dissociation. In terms of theoretical predictions, the membrane potential values obtained in physiological conditions (140 mM, pH 5.7 – 7.4) could be well fit by the Gouy-Chapman-Stern-Grahame model of the electrical double layer with Langmuir counterion binding. In low ionic strength solutions (0.5 mM, pH 5.7 – 7.4), the model overpredicted surface charge/potential. Instead, at low ionic strength Manning’s charge condensation theory was much more accurate. The theoretical frameworks used in the work can be used to understand how different factors like lipid head group pKa, pH, ionic strength of the solution and counterion binding constants interplay to yield a specific potential value for the system. Though it is important to note that dissociation constants for lipids (apparent pKa) depend on lipid structure and measurement conditions. Values in literature should therefore only be used as starting point guides while designing responsive systems.