Developing end-point methods for absolute binding free energy calculation using the Boltzmann-quasiharmonic model

Abstract

Understanding the physical forces underlying receptor–ligand binding requires robust methods for analyzing the binding thermodynamics. In end-point binding free energy methods the binding free energy is naturally decomposable into physically intuitive contributions such as the solvation free energy and configurational entropy that can provide insights. Here we present a new end-point method called EE-BQH (Effective Energy-Boltzmann-Quasiharmonic) which combines the Boltzmann-Quasiharmonic model for configurational entropy with different solvation free energy methods, such as the continuum solvent PBSA model and the integral equation-based 3D-RISM, to estimate the absolute binding free energy. We compare EE-BQH with other treatments of configurational entropy such as Quasiharmonic models in internal coordinates (QHIC) and in Cartesian coordinates (QHCC), and Normal Mode analysis (NMA), by testing them on the octa acids host–guest complexes from the SAMPL8 blind challenge. The accuracies in the calculated absolute binding free energies strongly depend on the configurational entropy and solvation free energy methods used. QHIC and BQH yield the best agreements with the established potential of mean force (PMF) estimates, with R² of ~0.7 and mean unsigned error of ~1.7 kcal mol⁻¹. These results from the end-point calculations are also in similar agreement with experiments. While 3D-RISM in combination with QHIC or BQH lead to reasonable correlations with the PMF results and experiments, the calculated absolute binding free energies are underestimated by ~5 kcal mol⁻¹. While the binding is accompanied by a significant reduction in the ligand translational/rotational entropy, the change in the torsional entropy in these host–guest systems is slightly positive. Compared with BQH, QHIC underestimates the reduction of configurational entropy because of the non-Gaussian probability distributions in the ligand rotation and a small number of torsions. The study highlights the crucial role of configurational entropy in determining binding and demonstrates the potential of using the new end-point method to provide insights in more complex protein–ligand systems.

Introduction

Molecular recognition plays vital roles in many biological processes such as enzyme catalysis, signal transduction, immune response, and gene regulation. Modeling molecular recognition at an atomistic detail can provide crucial insights for understanding the molecular mechanism underlying these biological phenomena. While many methods are available for computing the absolute and relative binding free energies,^1–8 our understanding of the molecular recognition will remain incomplete without a quantitative knowledge of the balance of various thermodynamic forces underlying binding. For example, DNA groove binders typically exhibit large entropy gain, whereas DNA intercalators generally show entropy loss.⁹ What are the roles of solvent reorganization entropy and solute configurational entropy in these DNA-ligand systems? In another case, HIV-1 antivirals Darunavir (DRV) and Atazanavir (ATV) bind at the same pocket in the protease; however, while the former is driven by enthalpy, the latter is driven entirely by entropy.¹⁰ The physical reasons for these fascinating behaviors have rarely been understood. Reliable computational tools to address such mechanistic questions will help inform ligand design beyond the estimation of binding affinity.

The receptor–ligand binding free energy can be computed using pathway methods such as the widely used alchemical pathway double decoupling method (DDM)^11–13 and physical pathway potential of mean force PMF¹⁴ methods, and the more recently developed implicit ligand theory^15–17 and the alchemical transfer (ATM) method.¹⁸ Alternatively, end-point methods such as MM-PB(GB)/SA,¹⁹ LIE (Linear Interaction Energy),²⁰ and M2 (Mining Minima)²¹ which need only consider the two end macrostates, are also popular in binding free energy calculations. While end-point methods generates a binding free energy estimate from the difference between two large numbers, which can lead to larger statistical error, such methods often allow for the binding free energy to be decomposed into physically intuitive components such as the direct intermolecular interaction, the solvation energy and entropy, and the solute configurational entropy, thus providing more direct insights into the thermodynamic driving forces of binding.²² In contrast, in pathway based binding free energy methods, except for the state functions like the total entropy and enthalpy, the free energy components are dependent on the pathway. Furthermore, in terms of sampling, an end-point binding free energy calculation is not hampered by some of the sampling bottlenecks encountered in the pathway methods, such as the water occlusion problem in the ligand extraction simulations in PMF.

The successful estimation of the binding free energy using end-point methods requires accurate calculations of both the solvation free energy and the configurational entropy.^23–27 While MM-PB(GB)/SA is the most widely used end-point method,^22,27–30 its utility in dissecting the free energy contributions has been limited by the inadequate treatment of configurational entropy using approximate methods such as Normal Mode analysis (NMA). To provide a robust tool for analyze the thermodynamic determinants of binding, here we develop a new end-point method, called EE-BQH (Effective Energy-Boltzmann-Quasiharmonic), by incorporating an improved configurational entropy method Boltzmann-Quasiharmonic (BQH)³¹ with different treatments of solvation free energy such as the continuum solvent PBSA³² and the integral equation based 3D-RISM³³ to more rigorously calculate the absolute binding free energy. While BQH has been validated against theoretical configurational entropy computed using the exact Clausius expression,^31,34 it has yet to be used to compute binding free energy, which is one of the goals of the present study.

For realistic molecular systems, the direct calculation of the configurational entropy contribution ΔS^config using the full probability distribution function (PDF) $p\left(q_1,\dots ,q_N\right)$ is computationally intractable and many approximate methods have been developed.^{24,25,35–40} In the quasiharmonic (QH) analysis,^{35,37,41–43} the PDF is fitted to multivariate Gaussian which leads to overestimation of the calculated entropy when the underlying PDF is non-Gaussian.^36,37 To account for the non-Gaussian behavior, the leading term in the Boltzmann-Quasiharmonic method (BQH)^31,34,44 is the uncorrelated Gibbs entropy $-k_{\text{B}}\sum _i\int p\left(q_i\right)\ln p\left(q_i\right)\text{d}{q}_i$, with the marginal PDF p(q_i) estimated from the simulation data, which do not have to assume Gaussian. In both BQH and QH, the correlation among different degrees of freedom is estimated from the determinant of the normalized covariance matrix $C_{ij}={\sigma }_{ij}/{\left({\sigma }_{ii}{\sigma }_{jj}\right)}^{1/2}$ which can only capture linear pairwise correlations. While more rigorous treatments of the correlation are available in the mutual information expansion approaches MIE²⁴ and MIST,⁴⁵ these methods are computationally more demanding, as they require many two- and higher dimensional PDFs which can be difficult to converge. In contrast, BQH is computationally more feasible for realistic systems since the evaluation of covariance matrix does not involve two- or higher order PDFs. BQH has been tested in several model systems against the theoretically exact entropies from the Clausius equality and appears to strike a good balance between accuracy and computational complexity.^31,34 In this work we apply BQH in end-point absolute binding free energy calculations and compare its performance with other treatments of configurational entropy such as QHIC (Quasiharmonic model in Internal Coordinates), QHCC (Quasiharmonic model in Cartesian Coordinates), and NMA. The results are compared against those from the more accurate potential mean force (PMF) method^14,46,47 using the same force field to provide more meaningful tests of the different approaches.

The calculation of solvation free energy is another essential component in end-point binding free energy approaches. While PB and GB implicit solvent models are most frequently used in end-point binding free energy calculations, these methods treat the solvent as a featureless continuum dielectric medium and are known to introduce errors when the molecular nature of solvent molecules are important for binding.^27,29,30,48 On the other hand, the three-dimensional extension of the reference interaction site model (3D-RISM)^33,49,50 based on the Ornstein–Zernike integral equation theory⁵¹ can capture the inhomogeneous distribution and correlation of the molecular solvent.^52,53 In this study we compare the performance in end-point absolute binding free energies calculations of PBSA and 3D-RISM (the latter with linear partial molar volume corrections^54,55) in combination with the configurational entropy approaches.

Because of their small sizes and simpler intermolecular energy landscapes compared to the more complex protein–ligand systems, host–guest systems allow for more complete sampling of the phase space and serve as useful model systems for validating and comparing binding free energy models.^{21,36,56–59} Using host–guest systems as examples, Chang and Gilson et al. in an early study elucidated the roles of configurational entropy, preorganization, and induced fit effects in binding and observed strong compensation between the configurational entropy and effective energy.²¹ Recently Chang’s group reported the binding thermodynamics and kinetics of host–guest systems obtained using direct sampling of the association/dissociation event in microseconds MD and end-point calculations in explicit solvent.⁶⁰ Henchman and coworkers studied the binding thermodynamics of the CB8 host–guest systems as part of the SAMPL8 challenge using an end-point method in which the total entropy is calculated in a hierarchical manner.⁶¹

In the present study, we validate the EE-BQH end-point method by applying it to compute the absolute binding free energies for the host–guest systems from the recent SAMPL8 (Statistical Assessment of the Modeling of Proteins and Ligands) GDCC Host–Guest Challenge set⁶² and compare the results with other treatments of configurational entropy such as QHIC, QHCC, and NMA. We found that the results obtained using BQH and QHIC show the best correlations with the absolute binding free energies computed using the more accurate pathway-based potential of mean force method (PMF),^{8,46,47,63–65} with R² of 0.69–0.77 and averaged unsigned errors of 1.53–1.88 kcal mol⁻¹. These results from the end-point calculations are also in similar agreement with the experimental measurements. Interestingly, while the binding is opposed by a large reduction in ligand external entropy, these host–guest systems exhibit a small increase in the torsional entropy upon binding. By dissecting the binding free energy into contributions from solute configurational entropy and effective potential energy, the EE-BQH model provides thermodynamic insights for analyzing the driving forces of binding not easily available from pathway methods.

Methods and materials

The end-point formula for absolute binding free energy¹¹ can be derived from the solute chemical potential for dilute solutions⁶⁶

$${\mu }_i=-kT\ln \left(\frac{8{\pi }^2}{C^{\circ }\prod _{j=1}^M{\Lambda }_j^3}\int \text{d}q{\text{e}}^{-\varphi (q)/kT}\right)+kT\ln \frac{C_i}{C^{\text{o}}}$$ (1)

where ${\Lambda }_j$ is the de Broglie thermal wavelength of the atom j in the solute molecule i, $\varphi \left(q\right)$ is the effective potential energy of a solute molecule in solution as a function of the 3M − 6 internal coordinates q of the solute (M is the number of atoms in a solute molecule).

Eqn (1) can be derived in different ways, such as using the grand canonical ensemble,⁶⁷ but the most straightforward way involves using the Widom insertion formula⁶⁸ as shown below:

Consider a binary solution containing N₁ solvent molecules 1 and N₂ solute molecules 2. In the canonical ensemble, the Helmholtz free energy $A=-kT\ln Q_{N1,N2}$ with $Q_{N1,N2}=\frac{1}{N_1!{\Lambda }_1^{3N_1}}\frac{1}{N_2!{\Lambda }_2^{3N_2}}\int e^{-\beta U\left(r^{N_1},R^{N_2}\right)}\text{d}{r}^{N_1}\text{d}{R}^{N_2}$. Standard manipulation yields

$$\begin{gathered} {\mu }_2={\left(\frac{\partial A}{\partial N_2}\right)}_{N_1,V,T}=-kT\ln \frac{Q_{N_1,N_2}}{Q_{N_1,N_2-1}} \\ =kT\ln N_2{\Lambda }_2^3-kT\ln \frac{Z_{N_1,N_2}}{Z_{N_1,N_2-1}} \end{gathered}$$ (2)

where r^N₁ and R^N₂ denote the solvent and solute coordinates, respectively; $Z_{N_1,N_2}=\int {\text{e}}^{-\beta U\left(r^{N_1},R^{N_2}\right)}\text{d}{r}^{N_1}\text{d}{R}^{N_2}$, and $Z_{N_1,N_2-1}=\int {\text{e}}^{-\beta U\left(r^{N_1},R^{N_2-1}\right)}\text{d}{r}^{N_1}\text{d}{R}^{N_2-1}$. Applying the Widom insertion formula, the system potential energy $U\left(r^{N_1},R^{N_2}\right)$ can be written as

$$U\left(r^{N_1},R^{N_2}\right)=U\left(r^{N_1},R^{N_2-1}\right)+u\left(R_{\alpha },r^{N_1},R^{N_2-1}\right)$$ (3)

where R_α denotes the coordinates of an arbitrarily chosen solute molecule α and $u\left(R_{\alpha },r^{N_1},R^{N_2-1}\right)$ is the perturbation energy of inserting the solute α into the solution containing N₁ solvent molecules 1 and N₂ − 1 solute molecules

$$u\left(R_{\alpha },r^{N_1},R^{N_2-1}\right)=U\left(r^{N_1},R^{N_2}\right)-U\left(r^{N_1},R^{N_2-1}\right)$$

Inserting eqn (4) into the expression of $Z_{N_1,N_2}$ and integrating out the six external degrees of freedom of the distinguished molecule $\alpha$ yields

$$Z_{N_1,N_2}=8{\pi }^{2}V\int \text{d}{q}_{\alpha }\int {\text{e}}^{-\beta U\left(r^{N_1},R^{N_2-1}\right)}{\text{e}}^{-\beta u\left(q_{\alpha },r^{N_1},R^{N_2-1}\right)}\text{d}{r}^{N_1}\text{d}{R}^{N_2-1}$$ (4)

It follows from eqn (4) that

$$\begin{array}{l}-kT\ln \frac{Z_{N_1,N_2}}{Z_{N_1,N_2-1}}\\ =-kT\ln 8{\pi }^{2}V\frac{\int \text{d}{q}_{\alpha }\int {\text{e}}^{-\beta U\left(r^{N_1},R^{N_2-1}\right)}{\text{e}}^{-\beta u\left(q_{\alpha },r^{N_1},R^{N_2-1}\right)}\text{d}{r}^{N_1}\text{d}{R}^{N_2-1}}{\int {\text{e}}^{-\beta U\left(r^{N_1},R^{N_2-1}\right)}\text{d}{r}^{N_1}\text{d}{R}^{N_2-1}}\end{array}$$ (5)

For an infinitely dilute solution, N₂ − 1 → 0, and eqn (5) becomes

$$\begin{array}{l}-kT\ln \frac{Z_{N_1,N_2}}{Z_{N_1,N_2-1}}\\ =-kT\ln 8{\pi }^{2}V\int \text{d}{q}_{\alpha }\frac{\int {\text{e}}^{-\beta U\left(r^{N_1}\right)}{\text{e}}^{-\beta u\left(q_{\alpha },r^{N_1}\right)}\text{d}{r}^{N_1}}{\int {\text{e}}^{-\beta U\left(r^{N_1}\right)}\text{d}{r}^{N_1}}\end{array}$$ (6)

Inserting eqn (6) into eqn (2) yields

$${\mu }_2=-kT\ln \frac{8{\pi }^2}{{\Lambda }_2^{3}C}-kT\ln \frac{\int {\text{e}}^{-\beta U\left(r^{N_1}\right)}{\text{e}}^{-\beta u\left(q_{\alpha },r^{N_1}\right)}\text{d}{r}^{N_1}}{\int {\text{e}}^{-\beta U\left(r^{N_1}\right)}\text{d}{r}^{N_1}}$$ (7)

$\left(C=\frac{N_2}{V}\right)$. Define the effective energy ϕ(q) as

$${\text{e}}^{-\varphi \left(q_{\alpha }\right)/kT}=\frac{\int {\text{e}}^{-\beta U\left(r^{N_1}\right)}{\text{e}}^{-\beta u\left(q_{\alpha },r^{N_1}\right)}\text{d}{r}^{N_1}}{\int {\text{e}}^{-\beta U\left(r^{N_1}\right)}\text{d}{r}^{N_1}}$$ (8)

It follows from eqn (7) and (8) that

$${\mu }_2=-kT\ln \frac{8{\pi }^2}{{\Lambda }_2^{3}C}-KT\ln \int \text{d}{q}_{\alpha }{e}^{-\varphi \left(q_{\alpha }\right)/kT},$$

which is eqn (1).

For the binding reaction A + B ⇌ AB, inserting eqn (1) into the equilibrium condition μ_A + μ_B = μ_AB yields

$$\begin{array}{l}\text{Δ}{G}_{\text{bind}}^{\circ }\equiv -kT\ln \left(\frac{C_{\text{AB}}{C}^{\circ }}{C_{\text{A}}{C}_{\text{B}}}\right)\\ =-kT\ln \frac{C^{\circ }}{8{\pi }^2}-kT\ln {\int }_{V_{\text{site}}}\text{d}{q}_{\text{AB}}{\text{e}}^{-\varphi \left(q_{\text{AB}}\right)/kT}\\ +kT\ln \int \text{d}{q}_{\text{A}}{\text{e}}^{-\varphi \left(q_{\text{A}}\right)/kT}+kT\ln \int \text{d}{q}_{\text{B}}{\text{e}}^{-\varphi \left(q_{\text{B}}\right)/kT}\end{array}$$ (9)

Note that the momentum energy terms ${\Lambda }_j^3$ in ${\mu }_{\text{AB}}$, ${\mu }_A$ and ${\mu }_B$ cancel. The phase space integration for the complex AB is limited to the sub-volume V_site which defines the complexed state in the six external dimensions of B relative to A.⁴⁶

Since

$$-kT\ln \int \text{d}q{\text{e}}^{-\varphi (q)/kT}=\int \text{d}qp(q)\varphi (q)+kT\int \text{d}qp(q)\ln p(q)$$ (10)

where p(q) is the probability density of finding solute i in configuration q in solution

$$p(q)=\frac{{\text{e}}^{-\varphi (q)/kT}}{\int \text{d}q{\text{e}}^{-\varphi (q)/kT}},$$

it follows from eqn (10) and (9) that

$$\begin{gathered} \text{Δ}{G}_{\text{bind}}^{\circ }=\text{Δ}\langle \varphi \rangle -T\text{Δ}{S}_{\text{config}}^{\circ } \\ =\left({\langle \varphi \rangle }_{\text{AB}}-{\langle \varphi \rangle }_{\text{A}}-{\langle \varphi \rangle }_{\text{B}}\right) \\ -T\left(S_{\text{config,AB}}-S_{\text{config, A}}-S_{\text{config,B}}+k_{\text{B}}\ln \frac{C^{\circ }}{8{\pi }^2}\right) \end{gathered}$$ (11)

where ${\langle \varphi \rangle }_X=\int \text{d}q\varphi \left(q\right)p\left(q\right)$, $S_{\text{config,X}}=-k\int \text{d}qp\left(q\right)\ln p(q)$ and the total configurational entropy of binding is given by

$$\Delta S_{\text{config}}^{\circ }=S_{\text{config,AB}}-S_{\text{config,A}}-S_{\text{config,B}}+k_{\text{B}}\ln \frac{C^{\circ }}{8{\pi }^2}$$ (11a)

Eqn (11) is the end-point binding free energy formula. Note that the above derivation does not assume the pairwise additivity in the interaction potential and is therefore applicable for both classical additive force fields and polarizable force fields.

In the present study the potential used is pairwise additive, in which case the effective energy $\varphi \left(q\right)$ can be written as the sum of intramolecular energy $u_{\text{intra}}\left(q\right)$ and solvation free energy $w\left(q\right)$, i.e.,

$$\varphi \left(q\right)=u_{\text{intra}}\left(q\right)+w\left(q\right)$$ (11b)

where the solvent potential of mean force w(q) is

$${\text{e}}^{-w\left(q\right)/kT}=\frac{1}{Z_{N,0}}\int \text{d}{r}^{N_1}{\text{e}}^{-\left[u_{uv}\left(q,r^{N_1}\right)+U_{vv}\left(r^{N_1}\right)\right]/kT}$$ (12)

Here $u_{uv}\left(q,r^{N_1}\right)$ is the interaction between one solute with the N₁ solvent molecules, and $U_{\text{vv}}\left(r^{N_1}\right)$ denotes the solvent–solvent interactions. $Z_{N,0}=\int \text{d}{r}^{N_1}{e}^{-U_{\text{vv}}\left(r^{N_1}\right)/kT}$ is the configurational integral of the pure solvent.

To obtain the effective energy $\langle {\varphi }_i\rangle$ requires calculating the solute internal energy $\langle u_{\text{intra}}\left(q\right)\rangle$ and solvation free energy $\langle w\left(q\right)\rangle$. The latter can be computed for the solute in the fixed configuration q as

$$\begin{gathered} w(q)=[\int \text{d}{r}^{N_1}P\left(r^{N_1}\mid q\right)\left(u_{\text{uv}}\left(q,r^{N_1}\right)+U_{\text{vv}}\left(r^{N_1}\right)\right) \\ -\int \text{d}{r}^{N_1}{P}_0\left(r^{N_1}\right)U_{\text{vv}}\left(r^{N_1}\right)] \\ -T[-k\int \text{d}{r}^{N_1}P\left(r^{N_1}|q\right)\ln P\left(r^{N_1}|q\right) \\ +k\int \text{d}{r}^{N_1}{P}_0\left(r^{N_1}\right)\ln P_0\left(r^{N_1}\right)] \end{gathered}$$ (13)

where $P\left(r^{N_1}|q\right)=P\left(q,r^{N_1}\right)/P\left(q\right)$ is the conditional probability density of finding solvent in the $r^{N_1}$ configuration given that the solute configuration is q. $P_0\left(r^{N_1}\right)$ is the probability density in pure solvent. The first and second brackets in the eqn (13) corresponds to the solvation enthalpy $\Delta H_{\text{solv}}\left(q\right)$ and solvation entropy $-T\Delta S_{\text{solv}}\left(q\right)$, respectively. While several methods exist to compute separately the solvation entropy $\Delta H_{\text{solv}}\left(q\right)$ and solvation entropy $-T\Delta S_{\text{solv}}\left(q\right)$,^60,61,69 since the main goal of this study is to improve end-point calculations of absolute binding free energy by using better configurational entropy treatments, here we apply two approximate solvation free energy methods, the continuum solvent based PBSA^29,30 and the integral equation based 3D-RISM,⁷⁰ on the configurations sampled from explicit solvent MD to estimate the solvation free energy $\langle w\left(q\right)\rangle$. The resulting $\langle w\left(q\right)\rangle$ are used in eqn (11b) to estimate the effective energy $\langle \varphi \rangle$ and the absolute binding free energy.

Quasiharmonic model in internal coordinates (QHIC)

In the Quasiharmonic approximation,³⁵ the multidimensional probability density of a molecule with n internal degrees of freedom is assumed to be normalized multivariate Gaussian

$$p(q)=\frac{1}{{(2\pi )}^{n/2}|\sigma {|}^{1/2}}{\text{e}}^{-\frac{1}{2}\left[{(q-\langle q\rangle )}^{\text{T}}{\sigma }^{-1}(q-\langle q\rangle )\right]}$$ (14)

where σ is the covariance matrix, ${\sigma }_{ij}=\langle \left(q_i-\langle q_i\rangle \right)\left(q_j-\langle q_j\rangle \right)\rangle$, of the internal coordinates (including for the complex the six ligand external degrees of freedom $X_{\text{L}}$, $Y_{\text{L}}$, $Z_{\text{L}}$, $\theta$, $\phi$, and $\psi$ relative to the receptor). $\left|\sigma \right|$ is the determinant of σ. Substituting the PDF of eqn (14) into the Gibbs entropy expression yields the configurational entropy of the molecule

$$S^{\text{QHIC}}=-k\int \text{d}qp(q)\ln p(q)=\frac{1}{2}nk+\frac{1}{2}k\ln \left[{(2\pi )}^n\left|\sigma \right|\right]$$ (15)

And the configurational entropy change due to binding is given by

$$\text{Δ}{S}_{\text{config}}^{\circ }=-k\ln 8{\pi }^2{V}^{\circ }+S_{\text{AB}}^{\text{QHIC}}-S_{\text{A}}^{\text{QHIC}}-S_{\text{B}}^{\text{QHIC}}$$ (16)

Note that while $S_{\text{AB}}^{\text{QHIC}}$ includes both the six guest external degrees of freedom and all the torsions in both host and guest molecules, $S_{\text{A}}^{\text{QHIC}}$ and $S_{\text{B}}^{\text{QHIC}}$ only include their torsional degrees of freedom. The determinant $\left|\sigma \right|$ in eqn (15) is calculated using the MATLAB library.

Boltzmann Quasiharmonic model (BQH)

It is well known that fluctuations in certain degrees of freedom such as a torsion with several rotamer states can be strongly non-Gaussian and the application of QHIC approximation eqn (15) in such cases will overestimate the configurational entropy.^36,37 The Boltzmann Quasiharmonic model (BQH) was proposed to better account for the non-Gaussian behavior in estimating entropy.³¹ Note that the determinant $\left|\sigma \right|$ in eqn (15) can be factored into the product of the diagonal elements of σ and the determinant of the normalized fluctuation covariance matrix C

$$\left|\sigma \right|=\prod _i^n{\sigma }_{ii}\left|C\right|$$ (17)

where $C_{ij}={\sigma }_{ij}/{\left({\sigma }_{ii}{\sigma }_{jj}\right)}^{1/2}$. Therefore, eqn (15) can be written as

$$S^{\text{QHIC}}=\left\{\frac{1}{2}nk+\frac{1}{2}k\ln \left[{(2\pi )}^n\prod _i^n{\sigma }_{ii}\right]\right\}+\frac{1}{2}k\ln \left|C\right|$$ (18)

It is easy to see that first term in the right-hand side of eqn (18) is the uncorrelated first order Boltzmann entropy, i.e. $\frac{1}{2}nk+\frac{1}{2}k\ln \left[{(2\pi )}^n\prod _i^n{\sigma }_{ii}\right]=-k_{\text{B}}\sum _i^n\int p\left(q_i\right)\ln p\left(q_i\right)\text{d}{q}_i$, when the distribution along each q_i is Gaussian, i.e. $p\left(q_i\right)=\frac{1}{{\sigma }_{ii}\sqrt{2\pi }}{\text{e}}^{-\frac{{\left(q_i-q_i\right)}^2}{2{\sigma }_{ii}^2}}$. When the distributions $p\left(q_i\right)$ are non-Gaussian, a more accurate treatment is to replace the first term in eqn (18) with the uncorrelated first order Boltzmann entropy $-k_{\text{B}}\sum _i^n\int p\left(q_i\right)\ln p\left(q_i\right)\text{d}{q}_i$, rather than estimating it from the variances ${\sigma }_{ii}$ as in the QHIC approximation. Thus, in BQH, the configurational entropy of a molecule is given by

$$S^{\text{BQH}}=-k_{\text{B}}\sum _i^n\int p\left(q_i\right)\ln p\left(q_i\right)\text{d}{q}_i+\frac{1}{2}k\ln |C|$$ (19)

Note that the treatment of the correlation between degrees of freedom are the same as in QHIC and can only account for linear pairwise correlations.

The configurational entropy of binding from BQH is calculated by substituting eqn (19) into eqn (11a)

$$\text{Δ}{S}_{\text{config}}^{\circ }=-k\ln 8{\pi }^2{V}^{\circ }+S_{\text{AB}}^{\text{BQH}}-S_{\text{A}}^{\text{BQH}}-S_{\text{B}}^{\text{BQH}}$$ (19a)

$\text{Δ}{S}_{\text{config}}^{\circ }$ can be written as the sum of the uncorrelated Boltzmann entropy change $\text{Δ}{S}_1$ and the second order correlated entropy contribution $\text{Δ}{S}_2$

$$\text{Δ}{S}_{\text{config}}^{\circ }\approx \text{Δ}{S}_1+\text{Δ}{S}_2$$ (20)

where

$$\text{Δ}{S}_1=\left(S_{1,\text{AB}}+k_{\text{B}}\ln \frac{C^{\circ }}{8{\pi }^2}\right)-S_{1,\text{A}}-S_{1,\text{B}}$$ (21)

and

$$\text{Δ}{S}_2=S_{2,\text{AB}}-S_{2,\text{A}}-S_{2,\text{B}}$$ (22)

In this study, we focus on the soft degrees of freedom that contribute most to $\text{Δ}{S}_{\text{config}}$, which includes torsion angles and the ligand translational/rotational degrees of freedom, since the contributions from the bond stretching and angle bending are typically much smaller than those from the soft degrees of freedom^31,71 and can be safely ignored. Thus

$$\begin{gathered} \text{Δ}{S}_1=\left(S_{1,\text{AB}}+k_{\text{B}}\ln \frac{C^{\text{o}}}{8{\pi }^2}\right)-S_{1,\text{A}}-S_{1,\text{B}} \\ =\text{Δ}{S}_1^{\text{trans}/\text{rot}}+\text{Δ}{S}_1^{\text{torsion}} \end{gathered}$$ (23)

Here $\text{Δ}{S}_1^{\text{trans}/\text{rot}}$ is the change in the uncorrelated translational/rotational entropy from the complexation and is written in discretized form as

$$\begin{array}{l}\text{Δ}{S}_1^{\text{trans}/\text{rot}}=S_{1,\text{AB}}^{\text{trans/rot}}-k_{\text{B}}\ln \left(\frac{8{\pi }^2{V}^{\circ }}{\prod _q\text{Δ}q}\right),\\ S_{1,\text{AB}}^{\text{trans}/\text{rot}}=-k\sum _q\sum _i^{N_{\text{bin}}}{p}_i^q\ln p_i^q\left(q=X_{\text{L}},Y_{\text{L}},Z_{\text{L}},\theta ,\phi ,\psi \right)\end{array}$$ (24)

where $S_{1,\text{AB}}^{\text{trans}/\text{rot}}$ is the ligand translational and rotational entropies within the complex, as described by the six external degrees of freedom of the bound ligand, i.e., the ligand center of mass $\left(X_{\text{L}},Y_{\text{L}},Z_{\text{L}}\right)$ defined in the reference frame of the receptor, and the three Euler angles $\left(\theta ,\phi ,\psi \right)$ defined by choosing two receptor atoms and three ligand atoms as described previously.^46,47 $-k_{\text{B}}\ln \left(\frac{8{\pi }^2{V}^{\circ }}{\prod _q\text{Δ}q}\right)$ in eqn (18) is the translational/rotational entropy of the reference state for a free ligand in a solution at the standard concentration $C^{\circ }=\frac{1}{V^{\circ }}$, which has a uniform distribution over the N_bin bins along each of the six external degrees of freedom. Here $\text{Δ}$q is the bin width of the corresponding degree of freedom q. In this work, N_bin is set to be 100 for each degree of freedom.

For the uncorrelated torsional entropy change

$$\begin{gathered} \text{Δ}{S}_1^{\text{torsion}}=S_{1,\text{AB}}^{\text{torsion}}-S_{1,\text{A}}^{\text{torsion}}-S_{1,\text{B}}^{\text{torsion}} \\ {S}_{1,\text{X}}^{\text{torsion}}=-k\sum _{\left\{\text{torsions}\right\}}\sum _i^{N_{\text{bin}}}{p}_i^q\ln p_i^q \end{gathered}$$ (25)

where $S_{1,\text{X}}^{\text{torsion}}$ is the torsional entropy of each species in solution.

For the second order correlation contribution to $S_{\text{config}}^{\circ }$, S₂ is calculated using eqn (19), i.e.

$$S_{2,\text{X}}=\frac{1}{2}k\ln \left|C\right|,$$

where $C_{ij}={\sigma }_{ij}/{\left({\sigma }_{ii}{\sigma }_{jj}\right)}^{1/2}$ as defined in eqn (17). Note that while $S_{2,\text{AB}}$ includes the correlations among the ligand translations and rotations within the bound complex and all the torsions in the two molecules, $S_{2,\text{A}}$ and $S_{2,\text{B}}$ only include the correlations among the torsional degrees of freedom within each of the host and guest molecules. To avoid the problem of periodicity in the torsion angles in calculating the covariance matrix ${\sigma }_{ij}$, a torsion angles φ is represented as ${\text{e}}^{i\phi }$,³¹ and the corresponding covariance matrix ${\sigma }_{mn}=\langle \left({\text{e}}^{i\phi m}-\langle {\text{e}}^{i\phi m}\rangle \right)\left({\text{e}}^{-i\phi n}-\langle {\text{e}}^{-i\phi n}\rangle \right)\rangle$ is guaranteed to have real determinant because it is Hermitian.

Quasiharmonic model in Cartesian coordinates (QHCC) and Normal Mode analysis (NMA)

In both QHCC and NMA, the configurational entropy change due to binding is approximated as^42,43,72

$$\text{Δ}{S}_{\text{config}}^{\circ }=\text{Δ}{S}^{\text{trans}}+\text{Δ}{S}^{\text{rot}}+\text{Δ}{S}^{\text{vibr}}$$ (26)

where $\text{Δ}{S}^{\text{trans}}$ and $\text{Δ}{S}^{\text{rot}}$ are estimated using the ideal gas entropy (Sackur–Tetrode) at standard concentration $C^{\circ }$ and the rigid-rotor expressions,⁷³ respectively. In both methods, the $S^{\text{vibr}}$ is calculated using the entropy expression for harmonic oscillators

$$\text{Δ}{S}^{\text{vibr}}=\sum _{i=1}^{3N-6}k\left[\frac{h{v}_i/kT}{{\text{e}}^{-h{v}_i/kT}-1}-\ln \left(1-{\text{e}}^{-\frac{h{v}_i}{kT}}\right)\right]$$ (27)

where v_i is the frequency of the i-th harmonic oscillator. In NMA, v_i is calculated from the eigenvalue of the mass-normalized second derivative matrix for energy minimized structures. In QHCC, after removing the overall translation and rotation of the solute, the eigenvalues of the mass-normalized covariance matrix are solved to obtain v_i. Both QHCC and NMA entropies are calculated using the implementation in the Amber package.⁷⁴

MD Simulation of the host–guest systems

In this work, the MD free energy simulations were performed using the PMEMD program in the AMBER20 package.⁷⁴ The atomic coordinates of the ten bound complexes of the two octa acids hosts, tetramethyl octa acid (TEMOA) and tetraethyl octa acid (TEETOA), and five guest molecules were obtained by manually docking the guests to each host using Maestro (Schrodinger Inc.), see Fig. 1. The TEETOA host differ from TEMOA by the replacement of a methyl at the cavity rim with an ethyl. The Amber GAFF2 parameters set⁷⁵ and the AM1-BCC charge model⁷⁶ are used to describe the solute. The dimension of the solvent box is set up to ensure that the distance between solute atoms from nearest walls of the box is at least 12 Å and Na⁺ ions are added to the solvent box to maintain charge neutrality. The system equilibration involved the following series of minimization and molecular dynamics steps: the structure was first minimized and heated from 0 to 300 K in 200 ps with harmonic restraints on the heavy atoms and a force constant of 10 kcal Å⁻² mol under constant volume conditions, followed by four MD simulations with gradually reduced restraints: (1) 3 ns with k = 5 kcal Å⁻² mol, (2) 3 ns with k = 1 kcal Å⁻² mol, (3) 3 ns with k = 0.25 kcal Å⁻² mol⁻¹, and (4) 3 ns unrestrained MD under constant pressure conditions. Finally, a production MD of 30 ns was performed using the NPT ensemble and Langevin thermostat with isotropic position scaling for constant pressure. The electrostatic interactions were computed using the particle–mesh Ewald (PME)⁷⁷ method with a real space cutoff of 9.0 Å and a grid spacing of 1.0 Å. MD simulations were performed in the NPT ensemble with a time step of 2 fs. For configurational entropy calculation, MD trajectories are saved every 0.1 ps, with a total of 300 000 trajectory frames used for one entropy calculation.

Fig. 1.

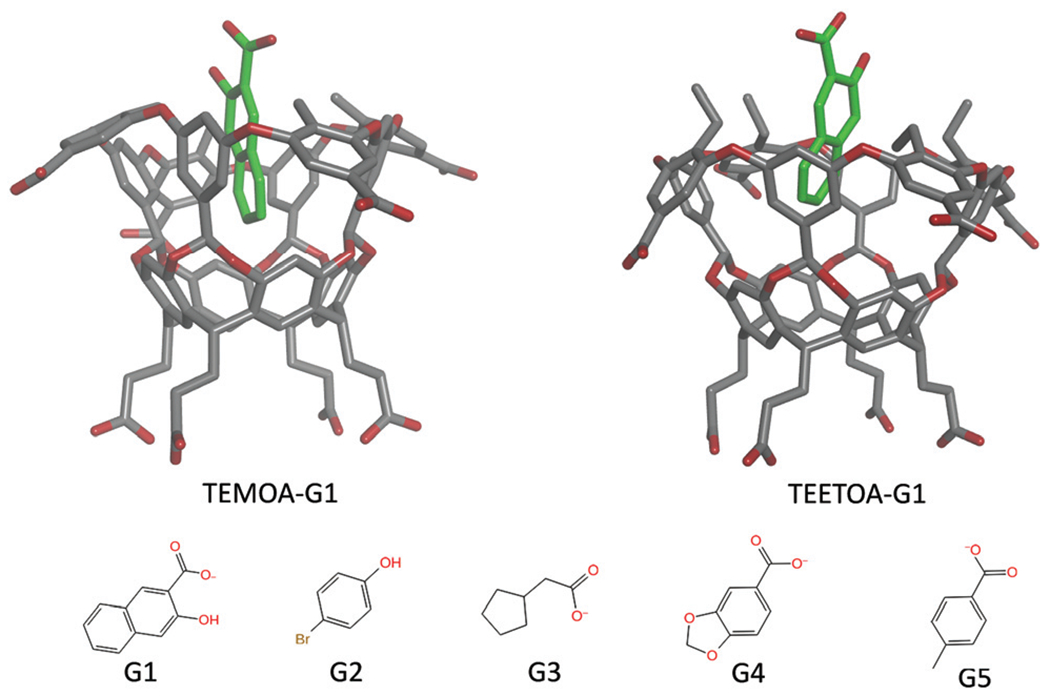
Representative MD structures of TEMOA-G1 and TEETOA-G1 complexes and chemical structures of the guest molecules.

Solvation free energy calculations

The solvation free energy w(q) in eqn (12) is calculated using two approximate methods, the continuum solvent based PBSA^29,30 and the integral equation based 3D-RISM,⁷⁰ on the MD structures sampled from three independent simulations for the three species (complex, host and guest) in explicit solvent. In 3D-RISM, the solvation free energy is calculated using the rism3d.snglpnt program available from the AMBER20 package⁷⁴ on the solute structures extracted from the explicit solvent MD simulations of the three species in binding; the KH closure and the linear partial molar volume correction^54,55 are used in the rism3d.snglpnt calculations. We found that the use of the partial molar volume correction^54,55 leads to substantially improved absolute binding free energies predictions (compare Fig. 3 with Fig. S2, ESI†).

Fig. 3.

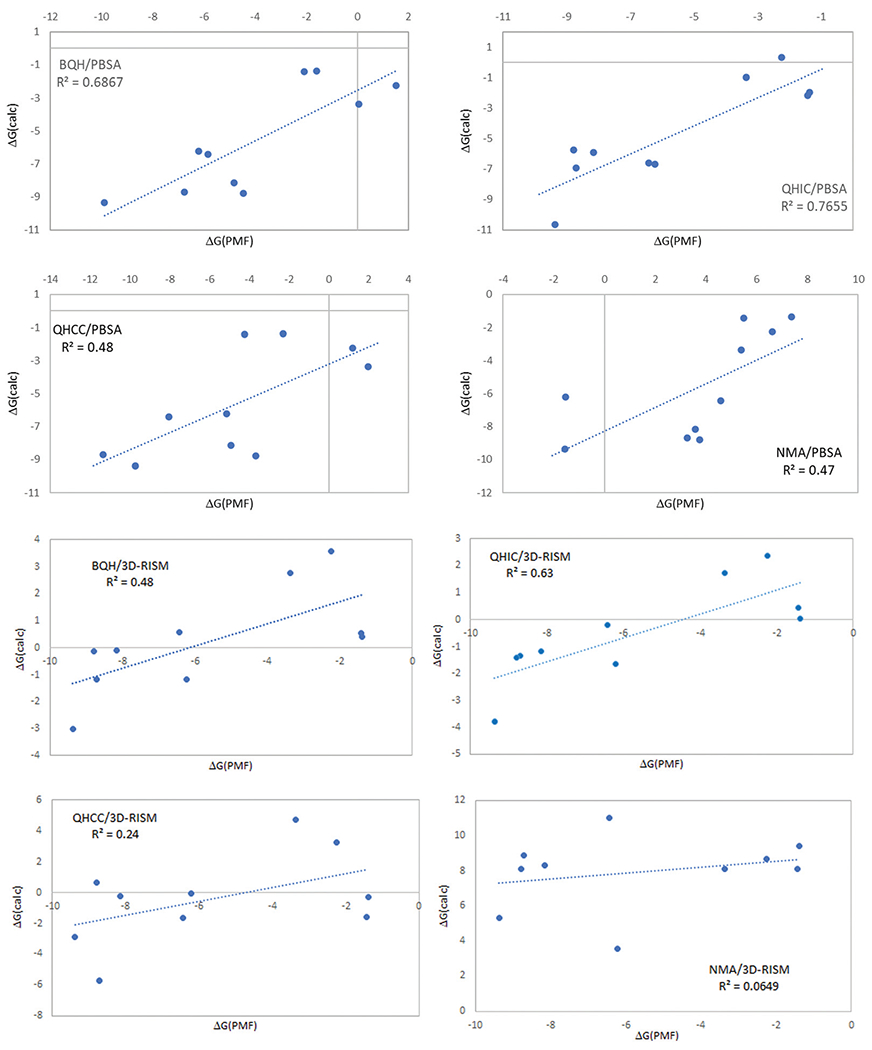
Correlations of the absolute binding free energies from the end-point calculations with the PMF results.

The PBSA solvation free energy calculations were performed using the MMPBSA.py³² tool from the AMBER20⁷⁴ package. The solvation free energies of the complex, host and guest are computed using 600 trajectory frames (i.e., every 50 ps) of solute structures extracted from the corresponding 30 ns MD trajectories in explicit solvent. The ionic concentration was set to 0.1 M for all calculations. Error bars were generated by comparing binding energy components of the first and second half of the MD simulations.

Results

Absolute binding free energies from the different end-point methods

We performed end-point calculations using different combinations of configurational entropy and solvation free energy models to estimate the absolute binding free energy of the ten SAMPL8 host–guest complexes. Since comparing the calculated binding free energies with the experiments can be complicated by the errors from the energy functions, to minimize such complications in evaluating a new method we first compare the end-point results with those obtained using the more well established PMF method in explicit solvent with the same force field, see Table 1 and Fig. 2. The latter were found in excellent agreement with the experimental measurements of the absolute binding free energies.⁶⁵ The comparisons between the end-point calculations with the experimental results are given in the Table S1 and Fig. S1 (ESI†).

Table 1.

R² and averaged unsigned errors (AUE) of the absolute binding free energy estimates from the end-point calculations relative to the results of the PMF method⁶²

	BQH/PBSA	QHIC/PBSA	QHCC/PBSA	NMA/PBSA	BQH/3D-RISM	QHIC/3D-RISM	QHCC/3D-RISM	NMA/3D-RISM
R 2	0.69	0.77	0.48	0.47	0.48	0.63	0.24	0.06
AUEa	1.88	1.53	2.65	9.30	5.84	5.11	5.26	13.5

^aIn kcal mol⁻¹.

Fig. 2.

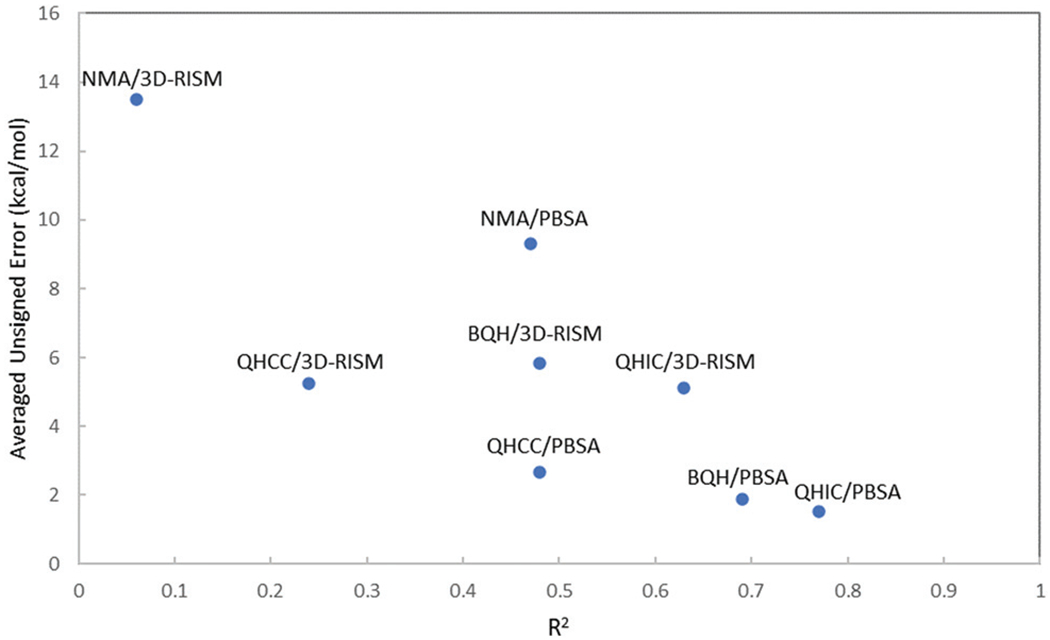
Average deviations and R² between the end-point binding free energy estimates using different combinations of configurational entropy and solvation free energy treatments and the reference PMF results.

Table 1 summarizes the overall results compared with the theoretical benchmark of the absolute binding free energies obtained from the PMF calculations in explicit solvent.⁶⁵ Fig. 2 provides a graphical view of the overall performance of different combinations. QHIC/PBSA and BQH/PBSA are the only endpoint methods that produced absolute binding free energy estimates with an averaged error smaller than 2.0 kcal mol⁻¹ compared with the PMF results. The two methods also resulted in good correlations with the PMF-calculated absolute binding free energies in terms of rank-ordering, with the R² of 0.69 for BQH/PBSA and 0.77 for QHIC/PBSA. Both methods correctly predicted that every guest molecule binds more strongly with TEMOA host than TEETOA host, and that TEMOA-G2 shows the strongest binding affinity. Therefore, despite the use of implicit solvent model for solvation free energy, the results from the end-point methods QHIC/PBSA and BQH/PBSA are in good agreement with those obtained using the pathway based PMF method in explicit solvent simulations. Besides QHIC/PBSA and BQH/PBSA, the results from QHCC/PBSA also shows a reasonable correlation with the PMF calculations, with R² = 0.48 and averaged error 2.65 kcal mol⁻¹.

While the combinations QHIC/3D-RISM and BQH/3D-RISM produced reasonably good correlations with the PMF results with R² of 0.63 and 0.48, respectively, the averaged unsigned errors in the absolute binding free energies obtained by using the 3D-RISM solvation model are significantly larger than those obtained from QHIC/PBSA and BQH/PBSA calculations using the continuum solvent PBSA (Table 1 and Fig. 2). Table 2 reveals that on average the combination of 3D-RISM with the different configurational entropy methods systematically underestimated the absolute binding free energies by ≥ 5.1 kcal mol⁻¹. Unsurprisingly, the calculations using the more approximate NMA for configurational entropy in combination with either of the solvation methods resulted in poor correlations with the theoretical benchmark of the PMF calculations and very large unsigned errors in the calculated absolute binding free energies (Table 2 and Fig. 3). Overall, using the PMF calculated absolute binding free energies as the theoretical benchmark shows that for the host–guest systems tested here, both BQH and QHIC in combination with PBSA lead to more accurate absolute binding free energy estimates than other approaches tested.

Table 2.

Absolute binding free energies in kcal mol⁻¹ for the SAMPL8 GDCC host–guest complexes calculated using the different end-point methods and the PMF method

Host–guest	BQH/PBSA	QHIC/PBSA	QHCC/PBSA	NMA/PBSA	BQH/3D-RISM	QHIC/3D-RISM	QHCC/3D-RISM	NMA/3D-RISM	PMF
TEETOA-G1	−1.60	−1.96	−2.31	7.37	0.42	0.05	−0.30	9.38	−1.38
TEETOA-G2	−6.21	−6.68	−5.14	−1.53	−1.15	−1.62	−0.09	3.53	−6.22
TEETOA-G3	−2.07	−2.18	−4.23	5.49	0.55	0.44	−1.61	8.11	−1.42
TEETOA-G4	1.52	0.32	1.18	6.61	3.57	2.37	3.23	8.66	−2.25
TEETOA-G5	0.05	−0.98	1.98	5.40	2.77	1.74	4.70	8.12	−3.36
TEMOA-G1	−5.85	−6.62	−8.05	4.57	0.57	−0.20	−1.63	10.99	−6.43
TEMOA-G2	−9.89	−10.64	−9.72	−1.57	−3.03	−3.79	−2.86	5.29	−9.37
TEMOA-G3	−6.76	−6.94	−11.34	3.26	−1.15	−1.33	−5.73	8.87	−8.71
TEMOA-G4	−4.47	−5.75	−3.67	3.76	−0.13	−1.41	0.67	8.10	−8.79
TEMOA-G5	−4.83	−5.90	−4.94	3.59	−0.10	−1.18	−0.21	8.32	−8.15

Comparing these results with experiments lead to essentially the same conclusion that BQH and QHIC in combination with PBSA yield reasonably good absolute binding free energy estimates: see Table S1 (ESI†). Both the R² and the averaged unsigned errors obtained using the experimental results as the reference are comparable to those obtained using the PMF results as the reference. We also note that the predictions from BQH/PBSA and QHIC/PBSA also compare favorably to the results reported in the SAMPL8 challenge using other binding free energy methods (Table S2, ESI†). Among the nine sets of results obtained using nonpolarizable force fields (AMOEBA uses a polarizable charge model), the BQH/PBSA and QHIC/PBSA are ranked at top 3 and top 2 places, respectively in terms of R².

Insights into the host–guest binding from the entropic components from BQH

We analyze the components of the solute configurational entropy from BQH to gain insights into the host–guest binding. First, we check the convergence of the BQH calculated configurational entropy change on binding. Fig. 4 shows the time behavior of the $T\text{Δ}{S}_{\text{config}}^{\circ }$ components for the G1 guest molecule in complex with both TEETOA and TEMOA hosts. While the uncorrelated torsional entropies show small drifts of the order of ~0.3 kcal mol⁻¹, the translational/rotational entropy and the second order correlation contributions appear to be more stable starting from t = 15 ns.

Fig. 4.

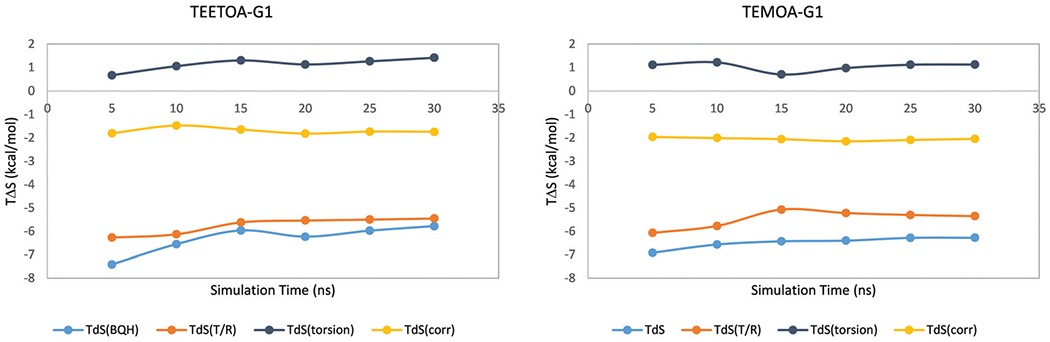
The cumulative BQH entropy and its components during the simulations for the TEETOA-G1 and TEMOA-G1 systems.

Table 3 lists the configurational entropy contributions calculated from BQH for the host–guest complexes. The uncorrelated ligand translation/rotation entropy accounts for the bulk of the configurational entropy loss due to binding. According to Table 3, the bulk of the total solute entropy change $\text{Δ}{S}_{\text{config}}^{\circ }$ comes from the 1st order uncorrelated entropy $\text{Δ}{S}_1$, while the correlation among the different degrees of freedom, i.e., $\text{Δ}{S}_2^{\text{corr}}$ accounts for between 10% and 30% of the total configurational entropy loss upon binding. There is no clear-cut relationship between the uncorrelated entropy ΔS₁ and the 2nd order correlation entropy $\text{Δ}{S}_2^{\text{corr}}$.

Table 3.

The configurational entropy contributions to binding calculated from BQH^ab

System	$T\text{Δ}{S}_1^{\text{trans}}$	$T\text{Δ}{S}_1^{\text{rot}}$	$T\text{Δ}{S}_1^{\text{torsion}}$	TΔS1	$T\text{Δ}{S}_2^{\text{corr}}$	$T\text{Δ}{S}_{\text{config}}^{\circ }$
TEETOA-G1	−3.43	−2.02	1.41	−4.04	−1.43	−5.47
TEETOA-G2	−4.35	−2.05	1.46	−4.94	−1.11	−6.05
TEETOA-G3	−3.43	−2.00	1.67	−3.77	−1.47	−5.24
TEETOA-G4	−4.15	−2.56	0.34	−6.37	−1.85	−8.22
TEETOA-G5	−3.86	−2.11	0.81	−5.16	−1.66	−6.83
TEMOA-G1	−3.51	−1.85	1.13	−4.23	−1.78	−6.01
TEMOA-G2	−4.30	−2.00	1.32	−4.97	−1.50	−6.48
TEMOA-G3	−3.82	−1.55	0.31	−5.07	−0.31	−5.37
TEMOA-G4	−4.71	−2.01	1.18	−5.54	−1.81	−7.35
TEMOA-G5	−4.14	−2.12	1.06	−5.20	−1.65	−6.85

^aT = 300 K. Unit: kcal mol⁻¹.

^b$\text{Δ}{S}_{\text{config}}^{\circ }=\text{Δ}{S}_1+\text{Δ}{S}_2^{\text{corr}}$, $\text{Δ}{S}_1=\text{Δ}{S}_1^{\text{trans}}+\text{Δ}{S}_1^{\text{rot}}+\text{Δ}{S}_1^{\text{torsion}}$.

Some of the configurational entropy values in Table 3 can be intuitively related to the chemical structures. For example, the complexes TEETOA-G3 and TEMOA-G3 both exhibits relatively small configurational entropy losses, which could be explained by the fact that G3 has the smallest and more flexible ring comparing with the other guest molecules (Fig. 1). Interestingly, for both TEETOA and TEMOA hosts, the guest binding is accompanied by a small increase in the uncorrelated torsional entropy $\text{Δ}{S}_1^{\text{torsion}}$, which ranges from 0.31 to 1.67 kcal mol⁻¹ (Table 3). Fig. 5 shows the histograms extracted from MD trajectories of a torsion angle in the unliganded host and in the complex, which illustrates the increase in the torsion entropy upon binding. In this example, the distribution of the torsion in the unliganded host is dominated by a peak centered at 100°, whereas in the complex the distribution is more even (Fig. 5).

Fig. 5.

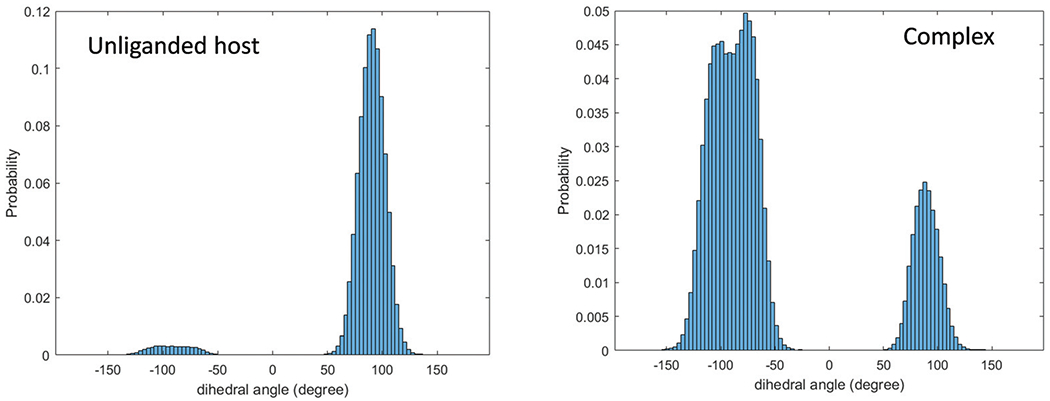
The histograms of the torsion angle distribution for one of the ethyl sidechains in the unliganded TEETOA host and that in the TEETOA-G1 complex sampled during a 30 ns MD in solution.

Comparison of BQH vs. QHIC calculated entropies

As shown in the Methods, BQH and QHIC are two closely related methods. While the configurational entropy changes calculated by these two best performing methods are highly correlated with each other (Fig. 6), QHIC consistently predicts smaller entropy losses upon binding ($T\text{Δ}{S}_{\text{config}}^{\text{QHIC}}$) than BQH does by up to 1.28 kcal mol⁻¹ (Table 4). As will be shown below, the smaller entropy loss predicted by QHIC is the result of its overestimation of the configurational entropy due to the non-Gaussian nature of the PDF along the ligand rotational and a small number of torsional degrees of freedom (Fig. 7 and 8). Even before we delve into the PDFs, there is evidence suggesting that the BQH calculated entropy change $T\text{Δ}{S}_{\text{config}}^{\text{BQH}}$ is more correct. For example, when comparing the TEETOA-G3 and TEETOA-G1 complexes, the smallest and most flexible guest molecule G3 is correctly predicted to experience the smaller entropy loss upon binding by BQH (Table 4). According to the QHIC calculations, however, G3 shows larger entropy loss than G1, which is likely a result of the overestimation of the entropy as shown in detail below.

Fig. 6.

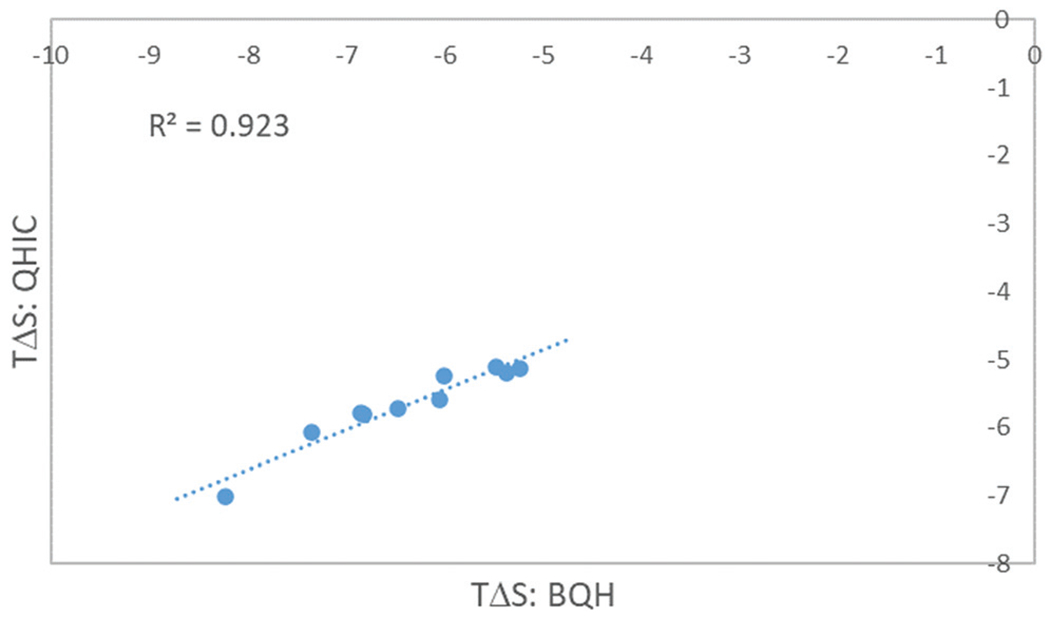
The correlation between the configurational entropy of binding $T\text{Δ}{S}_{\text{config}}^{\circ }$ computed using BQH and QHIC.

Table 4.

Comparisons of the configurational entropy change in binding $T\text{Δ}{S}_{\text{config}}^{\circ }$ calculated using BQH and QHIC (unit: kcal mol⁻¹)

System	$T\text{Δ}{S}_{\text{config}}^{\text{BQH}}$	$T\text{Δ}{S}_{\text{config}}^{\text{QHIC}}$	$T(\text{Δ}{S}_{\text{config}}^{\text{QHIC}}-S_{\text{config}}^{\text{BQH}})$
TEETOA-G1	−5.47	−5.11	0.36
TEETOA-G2	−6.05	−5.58	0.47
TEETOA-G3	−5.24	−5.13	0.11
TEETOA-G4	−8.22	−7.02	1.21
TEETOA-G5	−6.83	−5.80	1.03
TEMOA-G1	−6.01	−5.24	0.78
TEMOA-G2	−6.48	−5.73	0.75
TEMOA-G3	−5.37	−5.19	0.18
TEMOA-G4	−7.35	−6.07	1.28
TEMOA-G5	−6.85	−5.78	1.07

Fig. 7.

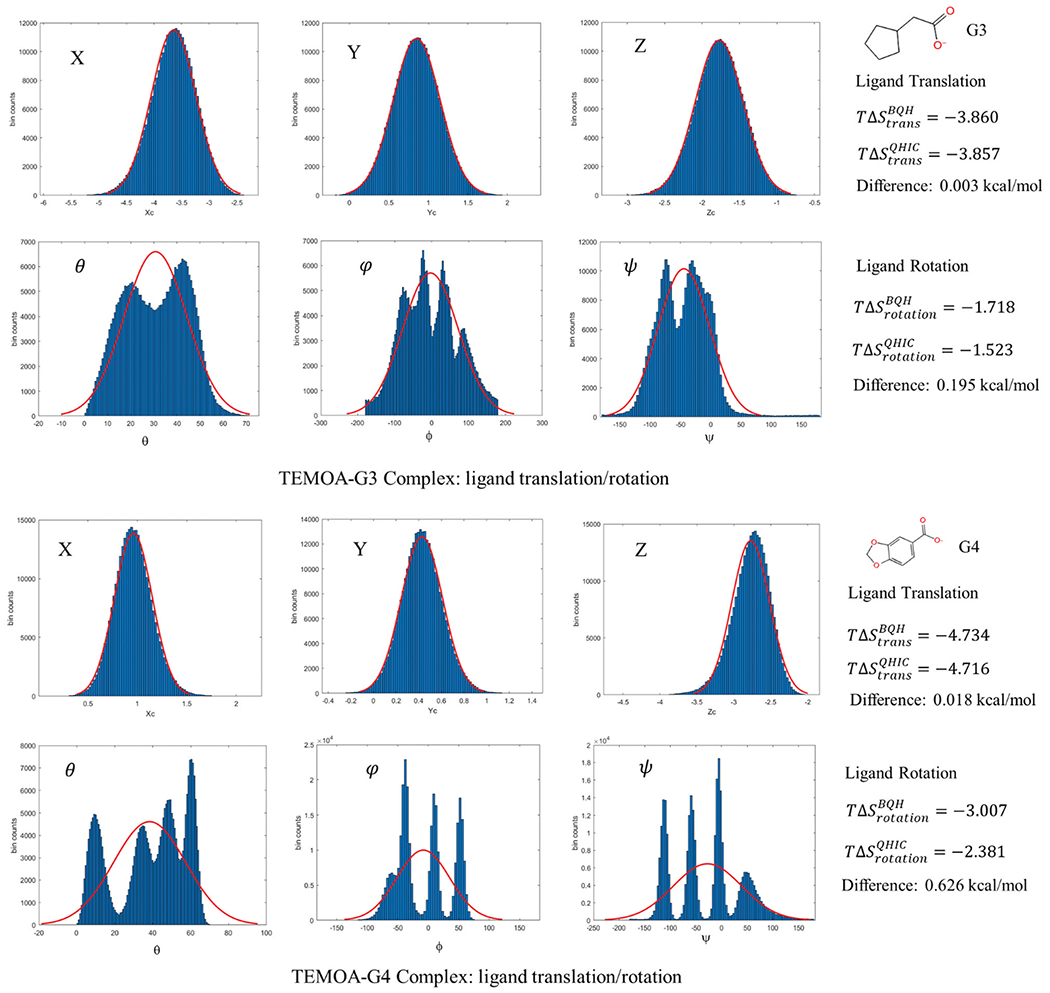
Histograms of the distributions along the three translational and three rotation degrees of freedom (Euler angles θ, φ, and ψ) of the G3 guest molecules in the TEMOA-G3 and TEMOA-G4 complexes. The red curves are the single Gaussian fits. The translational and rotational entropy losses upon binding are calculated as $\text{Δ}{S}_{\text{trans}}=S_{\text{trans}}-k\ln V^{\circ }$ and $\text{Δ}{S}_{\text{rotation}}=S_{\text{rotation}}-k\ln 8{\pi }^2$.

Fig. 8.

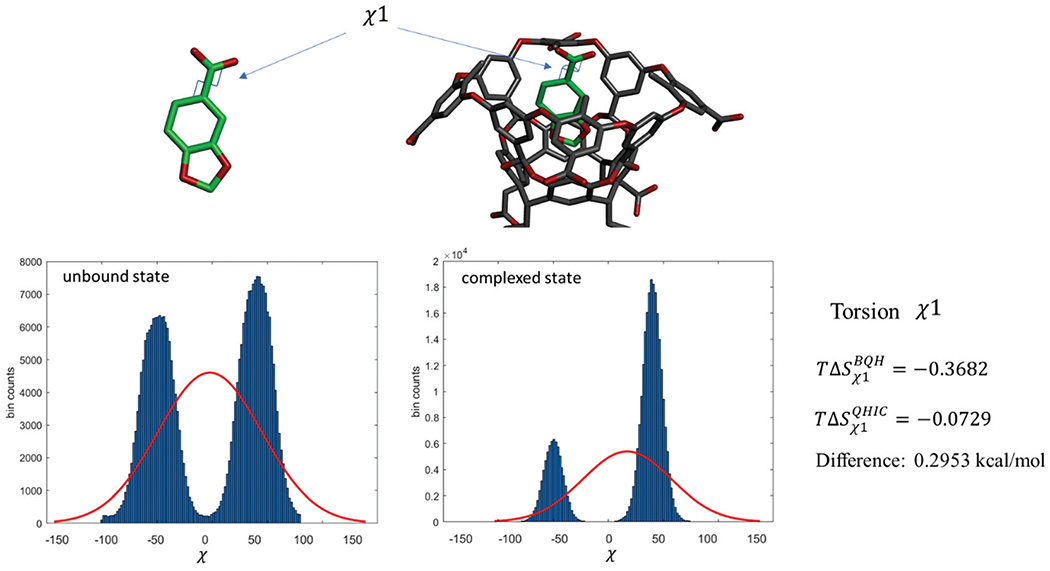
The distributions of the torsion angle χ1 in the guest molecule G3 in the TEMOA-G3 complex and unbound state. The red curves are the single Gaussian fits. The torsional entropy loss ΔS_χ1 = S_χ1 (complexed) − S_χ1 (unbound) calculated by BQH and QHIC are also shown.

Since $\text{Δ}{S}_{\text{config}}^{\circ }$ is largely dominated by the ligand translation and rotation entropy contributions (Table 3), we first examine the marginal PDF along the three translational and three rotational degrees of freedom of the bound ligand to understand the physical reasons for the differences between the entropies calculated using QHIC and BQH. Fig. 7 shows the results for the guest molecules in the TEMOA-G3 and TEMOA-G4 complexes, which are representative for the ten complexes in Table 4, as these two complexes show the smallest and largest differences between the QHIC- and BQH-calculated entropies $\text{Δ}{S}_{\text{config}}^{\text{QHIC}}-\text{Δ}{S}_{\text{config}}^{\text{BQH}}$. As seen from Fig. 7, while the PDFs for the ligand translations inside the complex can be well described by single Gaussian, the ligand rotations can deviate sharply from unimodal Gaussian distribution, especially in the TEMOA-G4 complex. Consequently, while BQH and QHIC predict very similar translational entropy losses upon binding $\text{Δ}{S}_{\text{trans}}^{\text{QHIC}}$ and $\text{Δ}{S}_{\text{trans}}^{\text{BQH}}$ ($\text{Δ}{S}_{\text{trans}}=S_{\text{trans}}-k\ln V^{\circ }$) that differ by <0.02 kcal mol⁻¹, QHIC overestimates the rotational entropy compared those from BQH, resulting in smaller rotational entropy losses given by $\text{Δ}{S}_{\text{rotation}}^{\text{QHIC}}$ ($\text{Δ}{S}_{\text{rotation}}^{\text{QHIC}}=\text{Δ}{S}_{\text{rotation}}^{\text{QHIC}}-k\ln 8{\pi }^2$), see Fig. 7, right panel. For example, in the TEMOA-G3 complex, the ligand rotational PDFs contain multimodal peaks that are not well separated and can still be fitted approximately by a single Gaussian; in this case the overestimation in the calculated rotational entropies by using the QHIC will be relatively small, with $T\left(\text{Δ}{S}_{\text{rotation}}^{\text{QHIC}}-\text{Δ}{S}_{\text{rotation}}^{\text{BQH}}\right)=0.195\mathrm{kcal}{\mathrm{mol}}^{-1}$. In the TEMOA-G4 complex, however, the three ligand rotational PDF contain multiple well-separated peaks; using unimodal Gaussian fitting therefore causes a significantly larger overestimation in entropy,³⁷ in this case $T\left(\text{Δ}{S}_{\text{rotation}}^{\text{QHIC}}-\text{Δ}{S}_{\text{rotation}}^{\text{BQH}}\right)=0.626\mathrm{kcal}{\mathrm{mol}}^{-1}$ (Fig. 7).

In addition to the three ligand rotational degrees of freedom, the non-Gaussian behavior in a small number of torsional degrees of freedom also contributes to the overestimated configurational entropy by QHIC, but to a smaller extent compared with the ligand rotations discussed above. This is because first, only a very small number of torsion angles in these host–guest systems exhibit non-Gaussian, multimodal distributions. Fig. 8 shows one of such torsions that exhibit non-Gaussian multimodal distributions in both complexed and unbound state. Second, for those few torsions that show multimodal distributions, the entropies for bound state and unbound state will both be overestimated by QHIC, and the net effect on binding entropy is small because of error cancellation. For example, the strongly non-Gaussian distribution in the torsion angle χ1 in Fig. 8 leads to just 0.295 kcal mol⁻¹ for the difference between the QHIC- and BQH-calculated entropy changes $T\left(\text{Δ}{S}_{\text{config}}^{\text{QHIC}}-\text{Δ}{S}_{\text{config}}^{\text{BQH}}\right)$.

In summary, the smaller losses of entropy due to binding predicted by QHIC (Table 4) are attributable to the overestimation of the ligand rotational entropy and the torsional entropy by QHIC, which uses single Gaussian to approximate the underlying PDF that can be strongly non-Gaussian. These results show that a histogram approach like the one implemented in BQH is required to more accurately account for non-Gaussian behavior to compute the uncorrelated entropies.

Lastly, we note that although QHIC overestimated the configurational entropies compared with the more accurate BQH method, when combined with PBSA, the QHIC/PBSA actually leads to absolute binding free energies in slightly better agreement with the PMF results (and with experiments) than the BQH/PBSA combination (Table 1). This seemingly puzzling result is because of cancellation of errors in QHIC and implicit solvent PBSA, which is known to introduce error when the molecular nature of solvent is important.⁵⁹ Based our recent study,⁶⁵ water molecules play important but distinct roles in guest binding with the two host molecules TEMOA and TEETOA, with TEMOA undergoing a dehydration transition whereas guest binding to TEETOA resulted in the opening of the binding cavity that remains essentially dry during the process. It will be challenging for a continuum solvent model such as PBSA or the hybrid 3D-RISM to precisely model the molecular nature of the desolvation processes involved and the errors in the solvation free energy calculated by PBSA could be compensated by the errors in the configurational entropy calculated by QHIC, resulting in a slightly better agreement with the more accurate explicit solvent based PMF results. We believe that the real advantage of BQH over QHIC will be realized when combined with superior solvation free energy methods and applied on more flexible receptor–ligand systems.

Discussion and conclusion

End-point binding free energy methods, while widely used for estimating relative binding strengths (e.g. with the widely used MM-PB(GB)/SA), are generally considered less accurate compared with the pathway based methods. As a result, they have rarely been used for estimating absolute binding free energies, except for a few conceptually insightful studies.^{21,41,42,60,78} However, despite this generally correct assessment, such methods do have the advantage of being able to decompose the total binding free energy into the physically appealing terms such as configurational entropy that may be related to structural features of the complexed and unbounded state. In this work, we tested the ability of different combinations of solute configurational entropy and solvation free energy models in the end-point approach, including the new EE-BQH method which incorporates the Boltzmann-Quasiharmonic model for configurational entropy in terms of reproducing the absolute binding free energies of the ten host–guest complexes from the SAMPL8 challenge.⁶⁵ We found that despite the use of implicit solvent model for solvation, the results obtained with the best combinations QHIC-PBSA and BQH-PBSA are well correlated to those obtained from the more accurate PMF method in explicit solvent (Tables 1 and 2). In terms of quantitatively reproducing the absolute values of the binding free energies the averaged errors in these two methods are about 1.5–1.9 kcal mol⁻¹ compared with the theoretical benchmark of the PMF calculation. It is possible that the bulk of the remaining errors in the QHIC-PBSA and BQH-PBSA calculations are to be found in the implicit solvent model PBSA. Compared with BQH, QHIC underestimates the reduction of configurational entropies in binding because of the ligand rotational fluctuations that are non-Gaussian (Table 4 and Fig. 7). However, because of the cancellation of errors in the QHIC entropies and in the PBSA solvation free energies, the QHIC/PBSA calculated absolute binding free energies are in slightly better agreement with experiments compared with those predicted by BQH/PBSA (Table 1 and Fig. 2). More studies are needed to examine this further by comparing with more accurate explicit solvent based solvation free energy methods.^79–82 The main advantage of the EE-BQH approach outlined is that with this method, the different thermodynamic contributions to the free energy of binding can be decomposed into their physical contributions (translational, rotational, and torsional entropies, correlation entropies, etc.). This potentially allows for focusing ligand design efforts by addressing specifically the various contributions to the free energy of binding thereby providing useful guidance for ligand design. Due to the tendency of QHIC to overestimate the first order uncorrelated entropy (Fig. 7 and 8), such information cannot be reliably obtained from QHIC.

Perhaps not unexpectedly, the study shows that the more approximate configurational entropy methods QHCC and NMA lead to significantly poorer correlations with the theoretical benchmark from the PMF calculations and substantially larger errors in the calculated absolute binding free energies (Fig. 3). The results of QHCC and QHIC are consistent with previous studies in which the configurational entropies calculated using QH approximation in the internal coordinates are superior to those using the Cartesian coordinates;^34,36 The main reason is that the degrees of freedom in the Cartesian coordinates are more strongly correlated (e.g. three bonded atoms forming a bond angle are highly correlated) than those in the internal coordinates (e.g. two adjacent torsions can still move somewhat independently from each other). Such strong correlations in the Cartesian space are difficult to be accounted for using the QH approximation which only considers pairwise linear correlation.

The results of end-point calculations also indicate that for the host–guest systems studied here, the use of 3D-RISM with the linear partial molar volume correction^54,55 for solvation free energy in combination with the different configurational entropy methods are generally less accurate compared with the corresponding combinations using the PBSA continuum solvent model (Tables 1 and 2). While 3D-RISM in combination with QHIC and BQH yield reasonably good correlation with the results from the PMF calculations (with R² from 0.48–0.63), the absolute binding free energies are systematically underestimated by 5–6 kcal mol⁻¹, suggesting possible directions for parameter tuning in the 3D-RISM. In summary, the present study highlights the crucial role of both configurational entropy and solvation energy in determining binding free energy and demonstrates the potential of using the new endpoint method to provide insights in more complex protein–ligand systems in combination with more rigorous solvation thermodynamics methods for absolute binding free energy analysis.

Lastly, we note that in recent years, two new configurational entropy methods, Interaction-Entropy method⁸³ and Cumulant Expansion method⁸⁴ that are based on the analysis of fluctuations and higher order expansions of the potential energy respectively, have been developed. These methods are in a sense fundamentally different than the QH type of approaches studied here that are based on approximating PDF of structural fluctuations. Compared with the structure-based approaches such as BQH, the new energy fluctuation-based approaches are not limited to only linear pairwise correlations along the different degrees of freedom. However, it can be difficult to extract the entropy contributions from different degrees of freedom from the energy-fluctuation based methods. It will be interesting to compare the QH types of structure-based entropy approaches with the energy fluctuation-based approaches in future studies.