Workforce planning and production scheduling in a reconfigurable manufacturing system facing the COVID-19 pandemic

Abstract

Due to the outbreak of the COVID-19 pandemic, the manufacturing sector has been experiencing unprecedented issues, including severe fluctuation in demand, restrictions on the availability and utilization of the workforce, and governmental regulations. Adopting conventional manufacturing practices and planning approaches under such circumstances cannot be effective and may jeopardize workers’ health and satisfaction, as well as the continuity of businesses. Reconfigurable Manufacturing System (RMS) as a new manufacturing paradigm has demonstrated a promising performance when facing abrupt market or system changes. This paper investigates a joint workforce planning and production scheduling problem during the COVID-19 pandemic by leveraging the adaptability and flexibility of an RMS. In this regard, workers' COVID-19 health risk arising from their allocation, and workers' preferences for flexible working hours are incorporated into the problem. Accordingly, first, novel Mixed-Integer Linear Programming (MILP) and Constraint Programming (CP) models are developed to formulate the problem. Next, exploiting the problem’s intrinsic characteristics, two properties of an optimal solution are identified. By incorporating these properties, the initial MILP and CP models are considerably improved. Afterward, to benefit from the strengths of both improved models, a novel hybrid MILP-CP solution approach is devised. Finally, comprehensive computational experiments are conducted to evaluate the performance of the proposed models and extract useful managerial insights on the system flexibility.

Graphical Abstract

1. Introduction

Being a long-term crisis, the COVID-19 pandemic has imposed a massive worldwide disruption on the manufacturing sector and supply chains [1], [2]. Accordingly, global manufacturing recorded severe declines of 6%, 11.1%, and 1.1% in the output during the first three quarters of 2020 compared to the same periods in 2019 [3]. In addition to the demand volatilities, several workforce-related issues, such as workers’ absence due to the infection and adhering to health regulations, enforce restrictions on workforce availability and utilization in manufacturing shop floors [4]. Having registered 1438 epidemics between 2011 and 2018, the World Health Organization (WHO) pointed out that besides their death tolls, epidemics can trigger enormous threats to the world’s economies [5]. Thus, it is critical to provide manufacturing systems with the ability to keep running while ensuring their workers’ health and satisfaction in the event of such crises.

Reconfigurable Manufacturing System (RMS) is a new manufacturing paradigm that has been recognized for its efficiency and high adaptability in coping with drastic volatility in demand, mass customization, rapid technological advancements, the introduction of new regulations, and abrupt changes in shop floors’ resources [6], [7]. It can quickly reconfigure its structure, hardware, and software components in a cost-effective manner. Therefore, it is well capable of adjusting to the new functionality and capacity requirements [8], [9]. Reconfiguration in a physical form can be achieved at the system level (e.g., adding or removing a machine, or changing the layout of machines) or at the machine level (e.g., changing or modifying modules of a machine) [10]. Regarding the machine level reconfiguration, a core enabler technology of RMSs is Reconfigurable Machine Tool (RMT). RMTs are novel types of machine tools with modular components (e.g., machining tools, turrets, and spindle heads), whose functionality and speed can be altered by changing their modules [9], [11]. As the COVID-19 pandemic requires fast capacity adjustments under workforce-related restrictions, RMSs have been considered as a promising solution to tackle such a crisis [12], [13].

In this regard, this paper investigates an integrated workforce planning and production scheduling problem in an RMS setting to fulfill demand during the pandemic. The investigated system consists of several non-identical parallel RMTs, which can provide different functionalities due to their various configurations, and heterogeneous workers with different capabilities to operate a set of distinct machines. In this paper, two key issues, including workers’ COVID-19 health risk arising from their allocation (briefly called the COVID-19 risk), and workers’ preferences for flexible working hours (briefly called workers’ preferences), are addressed as explained below.

• •COVID-19 risk: As the risk of the COVID-19 infection cannot be eliminated in workplaces [4], it should be mitigated as much as possible when allocating workers. The COVID-19 risk depends on the vulnerability of workers, as well as the safety risk of workspaces against the COVID-19 [14], [15], [16]. A person’s vulnerability against the COVID-19 is defined as the risk of developing severe illness after infection, which might result in hospitalization or death [17]. Several models (e.g., ALAMA [17]) have been developed to assess the vulnerability of a person based on age, gender, ethnicity, pregnancy, obesity, and pre-existing health conditions [14], [17]. Moreover, the safety risk of a workspace to the COVID-19 can be evaluated by occupational safety and health experts based on its proximity to other workspaces and corridors, the presence of barriers, and the ventilation conditions [18], [19]. Thus, observing the COVID-19 risk, the number of workers is kept as few as possible according to their vulnerability levels and the capabilities required by the demand. Moreover, at the same time, the workers with higher vulnerability levels are tried to be allocated to workspaces with lower safety risk levels if their presence is crucial.
• •Workers’ preferences: Enabling flexibility in working hours has been encouraged during the pandemic. On one hand, it grants workers the flexibility to manage their personal life, e.g., taking care of sick family members or children during school closure, which contributes to workers’ satisfaction. On the other hand, it decreases workers' congestion in public transportation systems, factories' entrances, and exits, which results in the reduction of the infection risk [20]. Hence, the workers’ preferences to enter into the system at different arrival times are also regarded in this problem.

Based on these issues, a new Mixed-Integer Linear Programming (MILP) model is devised, in which multiple decisions are made simultaneously regarding the employment and allocation of workers to machines, reconfigurations of machines, and scheduling of jobs on machines. Due to the promising performance of the Constraint Programming (CP) approach, especially in solving scheduling problems [21], it is also employed to model the problem. Afterward, two intrinsic properties of an optimal solution are identified and incorporated in the proposed MILP and CP models to improve their performances. Furthermore, to find a higher quality solution within a shorter run time, a hybrid model is devised to benefit from the advantages of both improved MILP and CP models. Finally, comprehensive computational experiments are conducted to evaluate the performance of the developed models and provide relevant managerial insights.

The rest of the paper is organized as follows. In the next section, some related studies are reviewed, and the contributions of this study are highlighted. In Section 3, the integrated workforce planning and production scheduling problem is elaborated, and the corresponding MILP model is presented. The CP model is introduced in Section 4. In Section 5, two properties of the problem are theoretically proved, and then, the MILP and CP models are accordingly improved, and finally, a hybrid model is developed. Section 6 concentrates on the computational experiments, and finally, conclusions and future research directions are given in Section 7.

2. Literature review

Two streams of the literature are reviewed in this section. First, the current progress in integrated workforce planning and parallel machine scheduling problems is investigated. Second, the literature on reconfigurable machine scheduling problems is explored. Afterward, the research gaps are identified and the contributions of the papers are stated.

2.1. Integrated workforce planning and parallel machine scheduling problems

Activity scheduling and workforce planning are two critical and highly interrelated problems in many contexts including healthcare, project planning, and more specifically, manufacturing. Ignoring their connection can lead to poor or sub-optimal results [22]. Recently, some studies investigated these problems in an integrated manner. For example, Van Den Eeckhout et al. [23] integrated the project scheduling problem with the personnel staffing problem. Regarding the literature on parallel machine scheduling, the incorporation of the workforce can be classified into three categories that are described here.

2.1.1. Allocation of workers to machines

Studies in this category aim to jointly allocate workers to machines and schedule jobs on the machines so that the workers will not be reallocated during the planning horizon. Thus, the number of workers is equal to or greater than the number of machines. In this regard, Hu [24] studied an identical parallel machine scheduling problem to minimize the total tardiness where the processing time of a job depends on the number of allocated workers to the associated machine. He developed a two-phase heuristic method to solve the problem, in which the first phase is related to job scheduling, and the second phase performs worker allocation. Later, Chaudhry and Drake [25] provided a Genetic Algorithm (GA) for a similar problem. Two meta-heuristic algorithms, namely GA and particle swarm optimization (PSO), were developed by Lee et al. [26] to solve a uniform parallel machine problem with the makespan objective. In their problem, the learning effect was considered, in which the learning rates of workers are different. Zouba et al. [27] investigated a particular case for parallel machine scheduling, where the workers simultaneously supervise a few neighboring machines. They supposed that there are some predefined work modes for worker allocation, and the processing times of the jobs depend on the selected mode. A heuristic method was devised for the problem to determine the work mode in each period and the scheduling of jobs to minimize the makespan.

2.1.2. Allocation of workers to jobs

In this category, besides job scheduling on machines, a worker is determined for each job, and the number of workers is typically less than the number of machines. Thus, a worker can visit another machine after performing his/her current job. Depending on the automation level of the manufacturing system, a worker performs the whole operation of a job or a portion of it (e.g., setting up machines before performing operations, loading or unloading the jobs on machines, and cleaning and testing the jobs). Accordingly, Celano et al. [28] developed a simulation-optimization method for an unrelated parallel machine scheduling, in which a worker is needed to just set up a machine before performing a job. In their study, the workers are homogenous (i.e., their qualification and skill level are the same), and several objective functions were considered, including the total tardiness, makespan, and machine and worker workload. Lee and Jang [29] investigated a uniform parallel scheduling problem with job splitting on dedicated machines and a limited number of homogenous operators for setting up machines. They formulated the problem as an MILP model and provided a constructive heuristic for large-sized problems. Yepes-Borrero et al. [30] provided an MILP and three Greedy Randomized Adaptive Search Procedure (GRASP) algorithms for unrelated parallel machine scheduling to minimize the makespan with sequence and machine-dependent setup times and limited homogenous workers for setting up machines. Later, Yepes-Borrero et al. [31] extended this problem to a bi-objective MILP model that minimizes the makespan and the number of workers and devised an iterated Pareto greedy algorithm to find Pareto solutions. Fang et al. [32] incorporated the limitation on the maximum consecutive working time, total working time, and minimum rest time of workers to an integrated scheduling and workforce allocation problem in an unrelated parallel machine setting. They developed an MILP model and a combinatorial Benders decomposition algorithm to minimize the machines’ deprecation cost, workers-related costs, and the cost associated with the makespan. Recently, Zhang et al. [33] investigated unrelated parallel machine scheduling, in which workers are responsible for setting up machines. The setups are sequence and machine-dependent and the duration of a setup on a machine is influenced by the worker performing the setup and his/her learning procedure on the machine. They provided a combinatorial evolutionary algorithm to solve the problem.

2.1.3. Workforce as a limited additional resource

Other studies have been considered the workforce just as an additional resource with limited capacity. Thus, there is no decision regarding workforce allocation, and only the workers’ requirements for jobs are respected. In this line, Edis and Ozkarahan [34] probed an identical parallel machine scheduling problem with eligibility restriction, in which each job may require an entire worker, half of a worker, or no worker to be processed. They provided two solution methods based on a combination of two different Integer Programming (IP) models, and a combination of IP and CP models, in which the IP model determines the assignment of jobs to machines, then the scheduling of jobs on each machine is specified by either the IP or CP model. Afzalirad and Shafipour [35] also worked on this problem and presented a genetic algorithm (GA) to solve it. Lee et al. [36] and Lee and Kim [37] studied a special type of this problem where a job can be split into multiple parts and processed concurrently on different machines. In their works, workers are assumed as a limited resource to perform setups on machines. Accordingly, they provide MILP models, and heuristic algorithms to obtain decent solutions.

2.2. Reconfigurable machine scheduling problems

Since its introduction, lots of studies have been performed on different aspects of RMSs, including conceptual design, system design, performance evaluation, and production and process planning. In this regard, comprehensive reviews were provided by Bortolini et al. [8], Yelles-Chaouche et al. [9], and Koren et al. [38]. However, a limited number of studies explored scheduling problems in RMSs. Due to the importance of scheduling on operational decisions and consequently on the performance and profitability of RMSs, reconfigurable machine scheduling problems have recently received a lot of attention. Accordingly, Bensmaine et al. [39] presented a heuristic for an integrated process planning and scheduling problem in a shop floor consisting of RMTs. In this problem, each operation of a job can be processed with different machine-configuration combinations and there are precedence constraints among the operations of a job. Dou et al. [40] devised a multi-objective PSO algorithm for a cyclic process planning and scheduling problem in a reconfigurable flow line with the objectives of the total capital and reconfigurable cost, and the total tardiness. In this problem, the configuration of the system (i.e., the number and type of the machines for each stage of the flow line) and RMTs are determined and fixed for the entire planning period. Mahmoodjanloo et al. [41] explored a flexible job shop environment with multiple RMTs in which a reconfiguration on a machine can be implemented between every two consecutive operations. They developed two MILP models and a Self-Adaptive Differential Evolution Algorithm (SADEA) to solve the problem considering the makespan as the objective function. Later, Mahmoodjanloo et al. [42] devised a self-adaptive hybrid Equilibrium Optimizer (EO) algorithm for a dynamic and multi-factory extension of this problem with the objective of the total weighted lateness. Fan et al. [43] also studied the scheduling problem of a reconfigurable flexible job shop with the objective of total weighted tardiness. They developed an MILP model and an improved GA for the problem assuming that the number of auxiliary modules to provide different configurations on RMTs are limited.

2.3. Contribution of the paper

Although integrated workforce planning and production scheduling has widely been investigated, there is a lack of research to assimilate restrictions and health concerns arising from an infectious disease like the COVID-19 into the problem. Thus, the existing approaches in the literature are not applicable during such crises and may jeopardize workers’ health and satisfaction as well as the continuity of businesses. Moreover, despite the substantial impact of the workforce on the performance of all manufacturing systems, to the best of the authors’ knowledge, no study has integrated workforce-related decisions and human factors in RMS scheduling problems.

To address these gaps, this study explores an integrated workforce planning and production scheduling during the COVID-19 pandemic leveraging the adaptability of an RMS. The main contributions of this study can be summarized below:

• •Investigating an integrated workforce planning and production scheduling problem in an RMS consisting of several non-identical parallel RMTs addressing workers’ COVID-19 health risk arising from their allocation and workers’ preferences for flexible working hours.
• •Formulating novel MILP and CP models for the problem, which concurrently makes decisions regarding workforce allocation, reconfigurations of machines, and job scheduling.
• •Identifying two properties of an optimal solution for the problem and incorporating them in the proposed MILP and CP models to enhance their performance.
• •Developing a hybrid MILP-CP model to take advantage of both models’ strengths.
• •Conducting comprehensive computational experiments to evaluate the performance of the proposed solution methods and provide some managerial insights as well.

3. Problem description and mathematical model

In the following subsections, first, the investigated problem is stated, and its characteristics and assumptions are described. Afterward, the notations and corresponding MILP model are provided.

3.1. Problem description

In this paper, the integrated production scheduling and workforce planning in an RMS is investigated. This system consists of a set of non-identical parallel RMTs. Moreover, there is a set of heterogeneous workers (i.e., workers with different capabilities in operating a set of specific machines) to be allocated to the machines. The planning horizon is assumed to be one day, in which a set of jobs must be performed. The main assumptions of the problem are listed below.

• •Each worker is capable of working on a specific subset of machines.
• •At most, one worker is allocated to a machine during the day, and likewise, a worker is allocated to at most one machine.
• •The RMTs are non-identical, and their functionality and speed can be changed through a reconfiguration. The reconfiguration time on a machine depends on the current and new configurations, and the reconfiguration is performed by the allocated worker. Moreover, the triangle inequality holds for the reconfiguration times.
• •Each job can be performed by at least one machine-configuration combination. In other words, some configurations of some machines may be eligible to perform a specific job. On the other hand, each configuration of a machine may be eligible for performing more than one job.
• •The processing time of a job depends on the assigned machine-configuration combination and the related allocated worker.
• •Each machine cannot perform more than one job at any moment, and the processing of a job cannot be preempted.
• •Each machine has a COVID-19-related safety risk level that can be determined by an occupational safety and health expert based on the proximity of a machine to other machines and corridors, the presence of barriers, and the ventilation condition.
• •There is a COVID-19-related vulnerability level associated with each worker. This can be evaluated by the existing measure (like ALAMA), which is a comprehensive web-based tool provided by the Association of Local Authority Medical Advisors [17].
• •Regarding the occupational regulation, a maximum allowed working time is considered for each worker.
• •Complying with the curfew regulation, a maximum allowed end time of the day is respected.
• •Workers’ priorities to enter into the system at different arrival times are regarded (a lower value of worker priority is more favorable).
• •Regarding governmental regulations, a limit on the number of workers entering into the system at the same arrival time is established.
• •Each worker needs to sanitize his/her allocated machine, table, and equipment at the beginning of his/her work.

This problem aims to provide a plan to fulfill the demand, by considering the issues arising from the COVID-19 pandemic. Accordingly, the following decisions are simultaneously made in the problem.

• •Allocation of workers to the machines and determination of their arrival times. It should be noted that considering the reduction of the demand during the COVID-19 pandemic and the vulnerability level of workers, the presence of all workers may not be necessary. Thus, the decision on the presence of each worker is also made in the problem.
• •Assignment of jobs to machines
• •Determination of a configuration to perform each job on its assigned machine.
• •Scheduling of jobs on their assigned machines.

Three objective functions are followed in the problem, which gets normalized and integrated into a single objective. The first objective minimizes the workers’ COVID-19 health risk (briefly COVID-19 risk), which is the total product of the vulnerability level of each worker and the safety risk level of his/her allocated machine. The second objective respects workers’ preferences, which minimizes the total workers’ priorities based on their allocated arrival times. Moreover, the third one is the minimization of the maximum completion time (i.e., makespan).

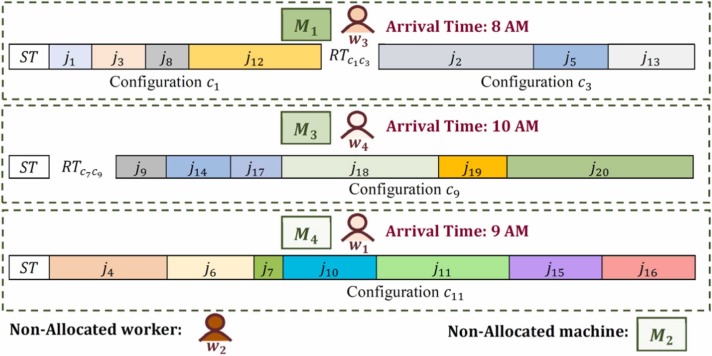
Fig. 1 depicts a schematic of this production system with four workers, four machines, and 20 jobs. In this figure, a worker with a higher vulnerability level is shown with darker orange color and a machine with a lower safety risk level with darker green color. The worker allocation and job sequencing on each machine are also presented in Fig. 1. For instance, worker $w_2$ with the highest vulnerability level is not allocated, and machine 2 with the highest safety risk level is not utilized. Worker $w_3$, who arrived at 8 AM, is allocated to machine $M_1$. After sanitization, jobs $j_1,j_3,j_8$, and $j_{12}$ are processed on machine $M_1$ with configuration $c_1$, then the machine is reconfigured to configuration $c_3$ (with the reconfiguration time equal to ${\mathit{RT}}_{c_1{c}_3}$), and then jobs $j_2,j_5,$ and $j_{13}$ are performed. In Subsections 3.2 and 3.3, the notations and the corresponding MILP model are presented.

Fig. 1.

Schematic of the investigated problem.

3.2. Notations

Sets:

$J$

Set of jobs.

$M$

Set of machines.

$W$

Set of workers.

$C_m$

Set of configurations for machine $m$.

$T$

Set of times.

Indices:

$j,j^{\prime }$

Index of job.

$m$

Index of machine.

$w$

Index of worker.

$c,c^{\prime }$

Index of configuration.

$t$

Index of time.

Parameters:

$P_{\mathit{mc}}^{\mathit{jw}}$

Processing time of job $j$ performed by worker $w$ on machine $m$ with configuration $c$.

${\mathit{CVL}}_w$

Covid-19 vulnerability level associated with worker $w$.

${\mathit{CSL}}_m$

Covid-19 safety risk level associated with machine $m$.

${\mathit{RT}}_{\mathit{mc}{c}^{\prime }}$

Reconfiguration time on machine $m$ from configuration $c$ to $c^{\prime }$.

${\mathit{ME}}_{\mathit{jmc}}$

1 if machine $m$ with configuration $\mathit{c}$ is eligible to process job $j$; 0, otherwise.

${\mathit{WC}}_{\mathit{wm}}$

1 if worker $w$ is capable of operating machine $m$; 0, otherwise.

${\mathit{AT}}_t$

Arrival time $t$ (i.e., the moment that a relevant worker enters into the system).

$\mathit{ST}$

Sanitization time.

$\mathrm{\Psi }$

Maximum portion of the number of workers that are allowed to enter into the system at each arrival time.

$\mathrm{\Phi }$

Maximum allowed end time of the day.

${\mathit{WP}}_{\mathit{wt}}$

Worker $w$’s priority to enter into the system at arrival time $t$; a lower value is more favorable for a worker.

$\mathrm{\Pi }$

Maximum allowed working time of a worker.

$I_m$

Initial configuration on machine $m$ at the beginning of the planning horizon.

${\alpha }_1,{\alpha }_2,{\alpha }_3$

Weight of each term of the objective function, where $0\le \alpha \le 1$ & ${\alpha }_1+{\alpha }_2+{\alpha }_3=1$.

Variables:

$x_{\mathit{jmc}}$

1 if job $j$ is assigned to machine $m$ with configuration $c$; 0, otherwise.

$y_{\mathit{wmt}}$

1 if worker $w$ is allocated to machine $m$ and enter into the system at arrival time $t$; 0, otherwise.

$z_{j{j}^{\prime }}$

1 if job $j$ is scheduled before job $j^{\prime }$; 0, otherwise.

${\mathit{Ct}}_j$

Completion time of job $j$.

$C_{\mathit{max}}$

Maximum completion time of all jobs.

${\mathit{Wt}}_{\mathit{wm}}$

Working time of worker $w$ when allocated to machine $m$.

3.3. MILP model

$$\begin{array}{c}\mathit{Minimize}F=\\ \frac{{\alpha }_1}{\sum _{w\in W}{\mathit{CVL}}_w\cdot {\max }_{m\mathrm{|}{\mathit{WC}}_{\mathit{wm}}=1}\left({\mathit{CSL}}_m\right)}\sum _{w\in W}\sum _{m\in M}\sum _{t\in T}{\mathit{CVL}}_w\cdot {\mathit{CSL}}_m\cdot y_{\mathit{wmt}}\\ +\frac{{\alpha }_2}{{\sum _{w\in W}\max }_t\left({\mathit{WP}}_{\mathit{wt}}\right)}\sum _{w\in W}\sum _{m\in M}\sum _{t\in T}{{\mathit{WP}}_{\mathit{wt}}\cdot y}_{\mathit{wmt}}\\ +\frac{{\alpha }_3}{\mathrm{\Phi }}\cdot C_{\mathit{max}}\end{array}$$ (1)

Subject to:

$$\sum _{m\in M}\sum _{c\in C_m}{x}_{\mathit{jmc}}=1,\forall j\in J$$ (2)

$$x_{\mathit{jmc}}\le {\mathit{ME}}_{\mathit{jmc}},\forall j\in J,\forall m\in M,c\in C_m$$ (3)

$$\sum _{m\in M}\sum _{t\in T}{y}_{\mathit{wmt}}\le 1,\forall w\in W$$ (4)

$$\sum _{t\in T}{y}_{\mathit{wmt}}\le {\mathit{WC}}_{\mathit{wm}},\forall w\in W,\forall m\in M$$ (5)

$$\sum _{w\in W}\sum _{t\in T}{y}_{\mathit{wmt}}\le 1,\forall m\in M$$ (6)

$$\sum _{j\in J}\sum _{c\in C_m}{x}_{\mathit{jmc}}\le \sum _{w\in W}\sum _{t\in T}{\left|J\right|\cdot y}_{\mathit{wmt}},\forall m\in M$$ (7)

$${\mathit{Ct}}_j\ge \sum _{t\in T}{\mathit{AT}}_t\cdot y_{\mathit{wmt}}+\mathit{ST}+{\mathit{RT}}_{m,I_m,c}+P_{\mathit{mc}}^{\mathit{jw}}-\mathrm{\Phi }\cdot \left(2-x_{\mathit{jmc}}-\sum _{t\in T}{y}_{\mathit{wmt}}\right),\forall j\in J,\forall w\in W,\forall m\in M,\forall c\in C_m$$ (8)

$${\mathit{Ct}}_{j^{\prime }}\ge {\mathit{Ct}}_j+{\mathit{RT}}_{\mathit{mc}{c}^{\prime }}+P_{m{c}^{\prime }}^{j^{\prime }w}-\mathrm{\Phi }\cdot \left(4-x_{\mathit{jmc}}-x_{j^{\prime }m{c}^{\prime }}-\sum _{t\in T}{y}_{\mathit{wmt}}-z_{j{j}^{\prime }}\right),\forall j,j^{\prime }\in J\mathrm{|}j\ne j^{\prime },\forall w\in W,\forall m\in M,\forall c,c^{\prime }\in C_m$$ (9)

$$z_{j{j}^{\prime }}+z_{j^{\prime }j}=1,\forall j,j^{\prime }\in J,j\ne j^{\prime }$$ (10)

$$C_{\mathit{max}}\ge {\mathit{Ct}}_j,\forall j\in J$$ (11)

$$C_{\mathit{max}}\le \mathrm{\Phi }$$ (12)

$${\mathit{Wt}}_{\mathit{wm}}\ge {\mathit{Ct}}_j-\sum _{t\in T}{\mathit{AT}}_t{\cdot y}_{\mathit{wmt}}-\mathrm{\Phi }\cdot \left(2-\sum _{c\in C_m}{x}_{\mathit{jmc}}-\sum _{t\in T}{y}_{\mathit{wmt}}\right),\forall w\in W,\forall j\in J,\forall m\in M$$ (13)

$${\mathit{wt}}_{\mathit{wm}}\le \mathrm{\Pi },\forall w\in W,\forall m\in M$$ (14)

$$\sum _{w\in W}\sum _{m\in M}{y}_{\mathit{wmt}}\le \mathrm{\Psi }\cdot \left|W\right|,\forall \mathrm{t}\in \mathrm{T}$$ (15)

$$x_{\mathit{jmc}},y_{\mathit{wmt}},z_{j{j}^{\prime }}\in \left\{0,1\right\},{\mathit{Ct}}_j,{\mathit{Wt}}_{\mathit{wm}}\ge 0$$ (16)

Eq. (1) minimizes the integrated objective function. The first term is related to the COVID-19 risk, the second is related to the workers’ preferences, and the third one is the makespan. The terms are normalized by dividing them to their maximum possible values, and then, they are integrated considering the weight of each term. Constraints (2) and (3) are related to the assignment of jobs to machine-configuration combinations respecting the eligibility restriction. Constraint (4) indicates that a worker can be allocated to at most one machine-arrival time combination. It also means that the model may decide a worker be absent. The restriction for workers’ capability is regarded by Constraint (5). Constraint (6) relates that at most, one worker can be allocated to a machine during the day. It also allows the idleness of a machine. Constraint (7) expresses that jobs can be assigned to a machine only if a worker is allocated to the respected machine. The completion time of a job is calculated by Constraints (8), (9), (10) according to the determined machine-configuration combination, the previous configuration on the machine, the related allocated worker, his/her arrival time, and sanitization time. Constraint (11) specifies the makespan, while Constraint (12) restricts it to the maximum allowed end time of the day. The working time of a worker is determined by Constraint (13), while the maximum allowed working time of a worker is enforced by Constraint (14). Constraint (15) restricts the number of workers that can arrive at each arrival time. Finally, Constraint (16) defines the domains of the decision variables.

4. Constraint programming (CP) approach

CP has been recognized as a powerful solution approach to tackle combinatorial optimization problems. Although it was initially developed to find high-quality feasible solutions within a reasonable time, the current commercial CP solvers can find optimal solutions and prove the optimality [21]. This approach has successfully been applied in various optimization problems, more noticeably in production scheduling and sequencing (e.g., Safarzadeh and Kianfar [44], Mokhtarzadeh et al. [45], Ham [46]). In this paper, IBM ILOG CP Optimizer is used to model and solve the problem.

Two fundamental variables in the CP Optimizer are interval and sequence variables, which are very useful to formulate scheduling problems. An interval represents an activity, task, or operation possessing some characteristics, including startOf, endOf, sizeOf, lengthOf, and presenceOf. The sizeOf an interval is the actual processing time, while the lengthOf indicates the duration between the startOf and endOf an interval. An interval can be optional, which can represent the possible allocations of activity to resources. When an optional interval is present, its presenceOf is equal to true (one). A sequence variable indicates the permutation for a set of preset intervals. In the CP Optimizer, several specific constraints exist, which will be described later in the CP model. The sets, indices, and parameters of the developed CP model are the same as the described MILP model. The decision variables of the CP model are as follows.

4.1. Variables

${job}_j:$ Interval variable representing ${\mathrm{j}\mathrm{o}\mathrm{b}}_j$.

${jobAssign}_{jmc},optional:$ Optional interval variable representing the assignment of job j to machine m with configuration $c$.

${\mathit{W}\mathit{o}\mathit{r}\mathit{ker}}_w,optional:$ Optional interval variable representing worker $w$.

${\mathit{W}\mathit{o}\mathit{r}\mathit{ker}\mathit{A}\mathit{l}\mathit{c}}_{\mathit{w}\mathit{m}\mathit{t}},\mathit{o}\mathit{p}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathit{a}\mathit{l}:$ Optional interval variable representing worker $w$.

${\mathit{S}}_{\mathit{m}}({\mathit{j}\mathit{o}\mathit{b}\mathit{A}\mathit{s}\mathit{s}\mathit{i}\mathit{g}\mathit{n}}_{\mathit{j}\mathit{m}\mathit{c}},\mathit{t}\mathit{y}\mathit{p}\mathit{e}\mathit{s}\mathit{c},\forall \mathit{j},\forall \mathit{c}\in {\mathit{C}}_{\mathit{m}}:{\mathit{M}\mathit{E}}_{\mathit{j}\mathit{m}\mathit{c}}=\mathit{1}):$ Sequence variable representing thesequence of jobs assigned to machine m. Moreover, the configurations of jobs processed by machine $m$ in each position of the sequence are tracked by $typesc$. This will be useful for imposing reconfiguration time between every two consecutive jobs on a machine.

4.2. CP model

$$\begin{array}{c}M\mathit{inimize}F=\\ \frac{{\alpha }_1}{\sum _{w\in W}{\mathit{CVL}}_w\cdot {\max }_{m\mathrm{|}{\mathit{WC}}_{\mathit{wm}}=1}\left({\mathit{CSL}}_m\right)}\sum _{w\in W}\sum _{m\in M}\sum _{t\in T}{\mathit{CVL}}_w\cdot {\mathit{CSL}}_m\cdot \mathit{presenceOf}({\mathit{WorkerAlc}}_{\mathit{wmt}})\\ +\frac{{\alpha }_2}{{\sum _{w\in W}\max }_t\left({\mathit{WP}}_{\mathit{wt}}\right)}\sum _{w\in W}\sum _{m\in M}\sum _{t\in T}{\mathit{WP}}_{\mathit{wt}}\cdot \mathit{presenceOf}\left({\mathit{WorkerAlc}}_{\mathit{wmt}}\right)\\ +\frac{{\alpha }_3}{\mathrm{\Phi }}{\cdot C}_{\mathit{max}}\end{array}$$ (17)

Subject to:

$$\mathit{alternative}\left({\mathit{Job}}_j,{\left[{\mathit{JobAssign}}_{\mathit{jmc}}\right]}_{\forall m\in M,c\in C_m:{\mathit{ME}}_{\mathit{jmc}}=1}\right),\forall j\in J$$ (18)

$$\mathit{alternative}\left({\mathit{Worker}}_w,{\left[{\mathit{WorkerAlc}}_{\mathit{wmt}}\right]}_{\forall m\in M,t\in T:{\mathit{WC}}_{\mathit{wm}}=1}\right),\forall w\in W$$ (19)

$$\sum _{w\in w:{\mathit{WC}}_{\mathit{wm}}=1}\sum _{t\in T}\mathit{presenceOf}({\mathit{WorkerAlc}}_{\mathit{wmt}})\le 1,\forall m\in M$$ (20)

$$\sum _{j\in J}\sum _{c\in C_m:{\mathit{ME}}_{\mathit{jmc}}=1}\mathit{presenceOf}\left({\mathit{JobAssign}}_{\mathit{jmc}}\right)\le \left|J\right|\cdot \underset{w\in W:{\mathit{WC}}_{\mathit{wm}}=1,t\in T}{\max }\mathit{presenceOf}({\mathit{WorkerAlc}}_{\mathit{wmt}}),\forall m\in M$$ (21)

$$\mathit{startBeforeStart}\left({\mathit{WorkerAlc}}_{\mathit{wmt}}{,\mathit{JobAssign}}_{\mathit{jmc}},\mathit{ST}+{\mathit{RT}}_{m,I_m,c}\right),\forall j\in J,\forall m\in M,\forall c\in C_m:{\mathit{ME}}_{\mathit{jmc}=1},\forall w\in W:{\mathit{WC}}_{\mathit{wm}}=1,t\in T$$ (22)

$$\mathit{presenceOf}\left({\mathit{JobAssign}}_{\mathit{jmc}}\right)=1\Rightarrow \mathit{sizeOf}\left({\mathit{JobAssign}}_{\mathit{jmc}}\right)=\sum _{w\in w:{\mathit{WC}}_{\mathit{wm}}=1}\sum _{t\in T}\mathit{presenceOf}\left({\mathit{WorkerAlc}}_{\mathit{wmt}}\right)\cdot P_{\mathit{mc}}^{\mathit{jw}},\forall j\in J,\forall m\in M,\forall c\in C_m:{\mathit{ME}}_{\mathit{jmc}=1}$$ (23)

$$\mathit{noOverlap}\left(S_m,\mathit{RT},\mathit{true}\right),\forall m\in M$$ (24)

$$C_{\mathit{max}}=\underset{j\in J}{\max }\mathit{endOf}({\mathit{Job}}_j)$$ (25)

$$C_{\mathit{max}}\le \mathrm{\Phi }$$ (26)

$$\mathit{presenceOf}\left({\mathit{WorkerAlc}}_{\mathit{wmt}}\right)=1\Rightarrow \mathit{startOf}\left({\mathit{WorkerAlc}}_{\mathit{wmt}}\right)={\mathit{AT}}_t,\forall w\in W,m\in M:{\mathit{WC}}_{\mathit{wm}}=1,t\in T$$ (27)

$$\mathit{presenceOf}\left({\mathit{WorkerAlc}}_{\mathit{wmt}}\right)=1\Rightarrow \mathit{endOf}\left({\mathit{WorkerAlc}}_{\mathit{wmt}}\right)=\underset{j\in J,c\in C_m:{\mathit{ME}}_{\mathit{jmc}=1}}{\max }\mathit{endOf}({\mathit{JobAssign}}_{\mathit{jmc}}),\forall w\in W,m\in M:{\mathit{WC}}_{\mathit{wm}}=1,t\in T$$ (28)

$$\mathit{lenghtOf}\left({\mathit{Worker}}_w\right)\le \mathrm{\Pi },\forall w\in W$$ (29)

$$\sum _{w\in w}\sum _{m\in M:{\mathit{WC}}_{\mathit{wm}}=1}\mathit{presenceOf}({\mathit{WorkerAlc}}_{\mathit{wmt}})\le \mathrm{\Psi }\cdot \mathrm{|}W\mathrm{|},\forall t\in T$$ (30)

Eq. (17) indicates the objective function of the problem, which is similar to Eq. (1); it consists of the three normalized terms, including the COVID-19 risk, workers’ preferences, and makespan, respectively. Through alternative function, Constraint (18) determines the assignment of machine-configuration combination for each job respecting the eligibility restriction, and the start time and end time of the selected interval (${\mathit{JobAssign}}_{\mathit{jmc}}$) are equal to its associated job interval (${\mathit{Job}}_j$). Likewise, in Constraint (19), a worker’s allocated machine and arrival time are determined (if he/she is present) respecting the capability restriction. Constraint (20) expresses that at most, one worker is allocated to a machine. Constraint (21) ensures that a job can only be processed by an eligible machine-configuration combination if a capable worker is allocated to it. Constraints (22), (23), (24) are equivalent to Constraints (8), (9), (10) that determine the start time, size, and sequence of jobs on machines. The $\mathit{noOverlap}$ function in Constraint (24) guarantees that the intervals (jobs) assigned to a machine do not overlap, and the corresponding reconfiguration time between every two consecutive intervals is imposed (if a reconfiguration is needed). Constraint (25) calculates the makespan while Constraint (26) restricts it to the maximum allowed end time of the day. Constraints (27) and (28) specify the start time and end time of a worker, while the maximum allowed working duration of a worker is respected by Constraint (29). Finally, Constraint (30) limits the maximum number of workers who can arrive at each arrival time.

5. Solution approaches

In this section, first, two properties of an optimal solution for the investigated problem are presented. Then, the improved MILP and CP models are developed accordingly. Finally, a hybrid model is devised based on these improved MILP and CP models.

Property 1

There always exists an optimal solution for the investigated problem, in which on each machine all assigned jobs with the same configuration are performed consecutively.

Proof

To prove this property, two cases should be considered:

• a)Machines with completion times equal to$C_{\mathit{max}}$: proceeding with a proof by contradiction, let ${\sigma }^{*}$ indicate an optimal schedule on a machine with the completion time of $C_{\mathit{max}}$, in which Property 1 is not held. As a result, at least one job is performed separately from other jobs with the same configuration on the corresponding machine. Fig. 2(a) represents the schedule, where ${RT}_{[1]}$ denotes the first reconfiguration time, $j_{[1]}$ the job on the first position of ${\sigma }^{*}$, and each color represents a configuration of the machine. The makespan of ${\sigma }^{*}$ is calculated by Eq. (31), where $c_{[1]}$ is the first configuration in the schedule.

$${\mathit{makespan}}_{{\sigma }^{*}}=\mathit{AT}+\mathit{ST}+{\mathit{RT}}_{[1]}+\left(\sum _{j\in \left\{j_{[1]},\dots ,j_{[k]}\right\}}{P}_{m{c}_{[1]}}^{\mathit{jw}}\right)+{\mathit{RT}}_{[2]}+\lambda +{\mathit{RT}}_{[s]}+P_{m{c}_{[1]}}^{j_{[l]}w}$$ (31)

Fig. 2.

Properties of an optimal solution.

Since there is no precedence between jobs, inserting $j_{[l]}$ right after $j_{[k]}$, a feasible solution, namely ${\sigma }^{\prime }$, which is shown in Fig. 2(b), can be achieved. Accordingly, the makespan of the new solution is calculated by:

$${\mathit{makespan}}_{{\sigma }^{\prime }}=\mathit{AT}+\mathit{ST}+{\mathit{RT}}_{[1]}+\left(\sum _{j\in \left\{j_{[1]},\dots ,j_{[k]}\right\}}{P}_{m{c}_{[1]}}^{\mathit{jw}}\right)+P_{m{c}_{[1]}}^{j_{[l]}w}+{\mathit{RT}}_{[2]}+\lambda$$ (32)

Thus, ${\mathit{makespan}}_{{\sigma }^{*}}-{\mathit{makespan}}_{{\sigma }^{\prime }}={\mathit{RT}}_{[s]}>0$. In addition, since this movement has no impact on the allocation of workers to machines and their arrival times, the other two terms of the objective function (the COVID-19 risk, and workers’ preferences) are unchanged. As a result, ${\sigma }^{\prime }$ is better than ${\sigma }^{*}$, which is in contradiction to the assumption. It is worth mentioning that if more than one job does not comply with Property 1, the difference between the makespan of ${\sigma }^{*}$ and ${\sigma }^{\prime }$ can be even widened.

• b)Machines with completion times less than$C_{\mathit{max}}$: suppose that Fig. 2(a) represents an optimal schedule on a machine with a completion time less than $C_{\mathit{max}}$. By performing $j_{[l]}$ right after $j_{[k]}$, the completion time of the machine is improved. However, since it does not worsen $C_{\mathit{max}}$, and the other terms of the objective function are unchanged, Property 1 is held, and it completes the proof.◽

Definition 1

Jobs with the same configuration on a machine can form a group of jobs which is called a block.

Property 2

In an optimal solution for the investigated problem, different permutations of jobs within blocks lead to an equivalent objective value.

Proof

Following Property 1, since there is no reconfiguration time between the jobs with the same configuration on a machine, changing the order of jobs within a block does not change the completion time of the respected machine. Also, the two other terms of the objective function (the COVID-19 risk, and workers’ preferences) remain unchanged. Since instead of sequencing jobs on machines, just sequencing of blocks is required, it can be helpful to reduce the number of relevant binary variables in the mathematical model. Fig. 2(c) presents a schedule (${\sigma }^{\prime \prime }$) where job $j_{[l]}$ in the optimal solution related to ${\sigma }^{\prime }$ (Fig. 2(b)) is swapped with $j_{[k]}$. As can be seen, the makespan does not change. ◽

5.1. Improved MILP model

Following Property 1, Property 2, besides allocating workers to machine-arrival time and assigning jobs to machine-configuration combination, just sequencing the blocks on the relevant machines is required. This considerably improves the model by reducing the number of related constraints and variables. In this regard, the required decision variables and the Improved MILP (I-MILP) model are provided as follows.

5.1.1. Variables

$b_{\mathit{mc}}$

1 if block $\mathit{c}$ on machine $m$ is formed; 0, otherwise.

$z_{\mathit{mc}{c}^{\prime }}$

1 if on machine $m$, block $c$ is scheduled before block $c^{\prime }$; 0, otherwise.

${\mathit{Cb}}_{\mathit{mc}}$

Completion time of block $c$ on machine $m$.

5.1.2. I-MILP model

Eq. (1).

Subject to:

Constraints (2), (3), (4), (5), (6), (12), (14), and (15).

$$b_{\mathit{mc}}\le \sum _{w\in W}\sum _{t\in T}{y}_{\mathit{wmt}},\forall m\in M,\forall c\in C_m$$ (33)

$$\sum _{j\in J}{x}_{\mathit{jmc}}\le \left|J\right|{\cdot b}_{\mathit{mc}},\forall m\in M,\forall c\in C_m$$ (34)

$${\mathit{Cb}}_{\mathit{mc}}\ge \sum _{t\in T}{\mathit{AT}}_{t\cdot }{y}_{\mathit{wmt}}+\mathit{ST}+{\mathit{RT}}_{m,I_m,c}+\sum _{j\in J}{P}_{\mathit{mc}}^{\mathit{jw}}{\cdot x}_{\mathit{jmc}}-\mathrm{\Phi }\cdot \left(2-b_{\mathit{mc}}-\sum _{t\in T}{y}_{\mathit{wmt}}\right),\forall w\in W,\forall m\in M,\forall c\in C_m$$ (35)

$${\mathit{Cb}}_{{\mathit{mc}}^{\prime }}\ge {\mathit{Cb}}_{\mathit{mc}}+{\mathit{RT}}_{\mathit{mc}{c}^{\prime }}+\sum _{j\in J}{P}_{m{c}^{\prime }}^{\mathit{jw}}\cdot x_{\mathit{jm}{c}^{\prime }}-\mathrm{\Phi }\cdot \left(4-b_{\mathit{mc}}-b_{m{c}^{\prime }}-\sum _{t\in T}{y}_{\mathit{wmt}}-z_{\mathit{mc}{c}^{\prime }}\right),\forall w\in W,\forall m\in M,\forall c,c^{\prime }\in C_m\mathrm{|}c\ne c^{\prime }$$ (36)

$$C_{\mathit{max}}\ge {\mathit{Cb}}_{\mathit{mc}},\forall m\in M,\forall c\in C_M$$ (37)

$${\mathit{Wt}}_{\mathit{wm}}\ge {\mathit{Cb}}_{\mathit{mc}}-\sum _{t\in T}{\mathit{AT}}_t\cdot y_{\mathit{wmt}}-\mathrm{\Phi }\cdot \left(2-b_{\mathit{mc}}-\sum _{t\in T}{y}_{\mathit{wmt}}\right),\forall w\in W,\forall m\in M,\forall c\in C_m$$ (38)

$$x_{\mathit{jmc}},y_{\mathit{wmt}},b_{\mathit{mc}},z_{\mathit{mc}{c}^{\prime }}\in \left\{0,1\right\},{\mathit{Cb}}_{\mathit{mc}},{\mathit{Wt}}_{\mathit{wm}}\ge 0$$ (39)

Constraints (33) and (34) ensure that a job can be assigned to a machine-configuration combination if a worker is allocated to the machine and the relevant block is formed. Similar to Constraints (8), (9), (10), Constraints (35) and (36) calculate the completion time of each block on each machine based on its allocated worker, assigned jobs, and previous configuration. The makespan is determined by Constraint (37). Constraint (38) calculates the working time of each worker. Lastly, the domains of the variables are defined in Constraint (39).

5.2. Improved CP model

Similarly, new variables are defined for Improve CP (I-CP), and the modified formulation is presented as follows.

5.2.1. Variables

${Block}_{mc},optional:$ Optional interval variable indicating configuration $c$ is utilized on machine $m$.

$H_{mc}({jobAssign}_{jmc},\forall j:{ME}_{jmc}=1):$ Sequence variable representing the sequence of jobs assigned to machine $m$ with configuration $c$.

$Q_m({Block}_{mc},typesc,{\forall }_c\in C_m):$ Sequence variable representing the sequence of blocks utilized in machine $m$. Also, the configuration in each position of the sequence is tracked by $typesc$ to impose reconfiguration time between every two consecutive configurations on a machine.

5.2.2. I-CP model

Eq. (17).

Subject to:

Constraints (18), (19), (20), (21), (22), (23) and (25), (26), (27), (28), (29), (30).

$$\mathit{noOverlap}\left(H_{\mathit{mc}}\right),\forall m\in M,\forall c\in C_m$$ (40)

$$\mathit{span}\left({\mathit{Block}}_{\mathit{mc}},{\left[{\mathit{JobAssign}}_{\mathit{jmc}}\right]}_{\forall j\in J:{\mathit{ME}}_{\mathit{jmc}=1}}\right),\forall m\in M,\forall c\in C_m$$ (41)

$$\mathit{noOverlap}\left(Q_m,\mathit{RT},\mathit{true}\right),\forall m\in M$$ (42)

Constraint (40) guarantees that there is no overlap among the jobs performed on a machine with the same configuration. Constraint (41) expresses that if ${\mathit{Block}}_{\mathit{mc}}$ is present, it spans all jobs with configuration $c$ on machine $m$ so that it starts with the first job and finishes together with the last job. Constraint (42) indicates that on each machine, there is no overlap among ${\mathit{Block}}_{\mathit{mc}}$ and makes sure the reconfiguration times between the blocks are respected.

5.3. Hybrid model based on the I-MILP and I-CP

Providing an initial solution (starting point) to a CP model as an input may considerably improve its performance to obtain a better solution in a shorter computational time. The starting point is not necessary to be a complete or feasible solution. The CP Optimizer first visits this solution. If it is infeasible or incomplete, the information included in the starting point is utilized as a guideline for the search [21]. This technique, known as warm starting, has been successfully implemented in several studies (e.g., Ham [47], Edis [48], Qin et al. [49]).

A warm start solution can be generated by a heuristic method, an MILP, or even a CP model. To take advantage of the strength of both MILP (in the assignment) and CP (in sequencing) models, in this paper, a combination of the I-MILP and I-CP models is considered. Hereafter, this hybrid model is called I-CP with warm starting (I-CP-WS). The pseudo-code of the I-CP-WS is presented in Algorithm 1. First, the I-MILP solves the problem within a specified time limit (line 1). Then, the obtained assignments of jobs to machine-configuration combination, and allocations of workers to machine-arrival times (i.e., the values of $x_{\mathit{jmc}}$ and $y_{\mathit{wmt}}$) are used to set the present values of the related interval variables in the I-CP (i.e., ${\mathit{JobAssign}}_{\mathit{jmc}}$ and ${\mathit{WorkerAlc}}_{\mathit{wmt}}$) (Lines 2–10). Finally, the CP Optimizer employs this partial solution as a starting point for the I-CP model and then proceeds its procedure to solve the problem within the time limit (Lines 11 and 12). It should be noted that according to our preliminary experiments, ignoring the third term of the objective function (related to $C_{\mathit{max}}$) in the I-MILP leads to more satisfactory results in the I-CP-WS.

Algorithm 1

Pseudo-code of the hybrid model based on the I-MILP and I-CP models (I-CP-WS).

6. Computational experiments

This section provides comprehensive computational experiments to assess the performance of the developed MILP models, CP models, and the hybrid model as well. Furthermore, some relevant managerial insights are extracted through a sensitivity analysis conducted on a few influential parameters of the investigated problem. All the models are implemented in IBM ILOG CPLEX Optimization Studio Version: 20.1.0.0, and executed on a personal computer with Processor Intel (R) Core (TM) i5–7300HQ 2.5 GHz and 12 GB of RAM.

6.1. Random instance generation

Several instances are generated to conduct the computational experiments. Different numbers of jobs (15, 20, 30, 40, 50, 60, 70, 80, 90, 100, and 110), machines/workers (3, 5, 6, 8, 9, 12, 15, and 16), and configurations per machine (3, 5, and 7) are considered. A three-field name is employed to represent each instance. For example, 30j-5m-3c indicates an instance with 30 jobs, 5 machines/workers, and 3 configurations per machine. The instances are categorized into three groups based on their sizes. If the values of $\left|J\right|*\left|M\right|*\mathit{|C|}$ are less than 1200, between 1200 and 4000, and greater than 4000, the instances are considered small, medium, and large sizes, respectively. The following values are utilized to randomly generate the instances: $P_{\mathit{mc}}^{\mathit{jw}}\in \left\{20,21,..,100\mathrm{minutes}\right\}$; ${\mathit{CVL}}_w\in \left\{\mathrm{1,3,5,7}\right\}$; ${\mathit{CSL}}_m\in \left\{1,2,3\right\}$;${\mathit{AT}}_t\in \left\{480,540,600\mathrm{minutes}\right\}$, which equal to 8:00, 9:00, and 10:00 AM; ${\mathit{RT}}_{\mathit{mc}{c}^{\prime }}\in \left\{15,16,\dots ,30\mathrm{minutes}\right\}$; $\mathit{ST}=10\mathrm{minutes}$; $\mathrm{\Psi }=.4$; $\mathrm{\Phi }=1080\mathrm{minutes}$, which equals to 6:00 PM; ${\alpha }_1=0.6,{\alpha }_2=0.2,{\alpha }_3=0.2$; ${\mathit{WP}}_{\mathit{wt}}\in \left\{1,2,3\right\}$; $\mathrm{\Pi }=480\mathrm{minutes}$. Moreover, 20% of machine-configuration combinations are regarded eligible to process a job, and $⌊\frac{\mathit{|W|}}{3}⌋+1$ workers are considered being capable of working on a machine.

6.2. Evaluation of the developed models

To examine the performance of the developed models, 33 instances are solved. Based on the size of an instance, the computational time limits of 100 s, 300 s, and 900 s are applied for small-, medium-, and large-sized instances, respectively. The Relative Percentage Deviation (RPD) is employed as an evaluation metric according to Eq. (43), in which $\mathit{Model}$ is the objective found by a model, and $\mathit{Best}$ is the best objective found among all models.

$$\mathit{RPD}=\frac{\mathit{Model}-\mathit{Best}}{\mathit{Best}}\times 100$$ (43)

Table 1 reports the computational time limits, the best objectives found among all models, the RPD values of each model, and the times when each model reached its best solutions. Based on the results, it can be observed that the MILP cannot find any feasible solution within the time limits for a large portion of the instances, especially for the large-sized instances due to the memory outage (indicated with NS in Table 1). In contrast, implementing the proposed properties in I-MILP leads to a considerable improvement as I-MILP can find proper solutions for all the instances within reasonable computational times. The average RPD for the instances solved by the MILP is 62.51, while the I-MILP reaches the average RPD of 0.59 for these instances. Likewise, comparing the CP and I-CP, incorporating these properties results in about a 21% reduction in the average RPD (from 41.56 to 32.84). Moreover, applying the warm start technique in the I-CP-WS bring about the best results in the majority of instances. Fig. 3 depicts the computational times the I-MILP and I-CP-WS models reach their best solutions. Accordingly, not only the I-CP-WS obtained the best average RPD (0.91) compared to the I-MILP (4.44), but also it managed to reach its solutions in notably shorter computational times. As a result, the I-CP-WS model demonstrated itself as an efficient solution method, especially when a high-quality solution is required within a limited time.

Table 1.

Comparison results for the developed models.

Instance	Time limit (s)	Best objective	MILP		I-MILP		CP		I-CP		I-CP-WS
			RPD	Time (s)	RPD	Time (s)	RPD	Time (s)	RPD	Time (s)	RPD	Time (s)
15j-3 m-3c	100	0.6224	0.00	9	0.00	< 1	0.00	< 1	0.00	< 1	0.00	< 1
15j-3 m-5c	100	0.3409	0.44	81	0.00	4	0.00	1	0.00	2	0.00	< 1
15j-3 m-7c	100	0.3468	0.87	94	0.00	94	0.00	1	0.00	7	0.00	2
20j-3 m-3c	100	0.6324	0.09	94	0.00	< 1	0.00	10	0.00	2	0.00	< 1
20j-3 m-5c	100	0.6259	1.21	95	0.00	13	0.00	4	0.00	2	0.00	3
20j-3 m-7c	100	0.3557	74.67	97	0.34	100	17.37	52	17.37	2	0.00	30
30j-5 m-3c	100	0.3118	38.87	94	0.00	2	34.03	12	34.03	32	0.00	3
30j-5 m-5c	100	0.3088	155.60	99	6.80	100	34.75	70	13.57	99	0.00	52
30j-5 m-7c	100	0.4211	60.32	100	0.14	100	0.33	87	5.37	65	0.00	45
40j-6 m-3c	100	0.3218	135.89	9	0.00	96	29.37	68	23.34	16	0.09	30
40j-6 m-5c	300	0.3951	60.97	300	0.10	296	39.91	170	8.25	167	0.00	99
40j-6 m-7c	300	0.3938	NS	–	4.44	290	9.45	273	5.15	199	0.00	163
50j-8 m-3c	300	0.3095	129.31	289	0.00	146	48.14	261	31.34	202	0.36	270
50j-8 m-5c	300	0.3063	154.42	237	0.26	299	26.05	268	26.05	241	0.00	170
50j-8 m-7c	300	0.3622	NS	–	6.93	294	45.80	299	33.30	271	0.00	234
60j-9 m-3c	300	0.2995	NS	–	0.00	292	38.10	293	22.30	71	7.51	248
60j-9 m-5c	300	0.2951	NS	–	4.03	297	76.38	246	25.08	294	0.00	230
60j-9 m-7c	300	0.2897	NS	–	0.28	199	62.24	204	51.98	147	0.00	210
70j-10 m-3c	300	0.3339	NS	–	0.00	298	61.73	107	35.04	272	2.01	140
70j-10 m-5c	300	0.3212	NS	–	7.25	300	45.67	223	36.39	278	0.00	152
70j-10 m-7c	900	0.316	NS	–	6.39	898	37.94	892	40.51	859	0.00	704
80j-12 m-3c	300	0.3115	NS	–	0.00	300	43.95	249	30.30	253	8.44	198
80j-12 m-5c	900	0.3111	NS	–	6.33	900	50.63	834	73.35	891	0.00	860
80j-12 m-7c	900	0.2809	NS	–	11.21	900	101.39	561	61.02	895	0.00	233
90j-14 m-3c	300	0.3053	NS	–	0.00	298	41.40	218	55.91	281	7.89	160
90j-14 m-5c	900	0.3013	NS	–	16.03	898	89.71	500	44.24	516	0.00	374
90j-14 m-7c	900	0.2835	NS	–	8.36	898	72.91	670	52.98	804	0.00	327
100j-15 m-3c	900	0.2795	NS	–	0.00	888	44.51	827	62.40	669	3.76	581
100j-15 m-5c	900	0.2868	NS	–	5.40	876	50.07	873	46.03	888	0.00	758
100j-15 m-7c	900	0.2809	NS	–	19.01	880	78.60	401	59.74	873	0.00	489
110j-16 m-3c	900	0.3099	NS	–	0.77	900	56.05	894	41.63	827	0.00	269
110j-16 m-5c	900	0.2851	NS	–	19.71	894	69.91	865	70.15	809	0.00	832
110j-16 m-7c	900	0.2851	NS	–	22.69	892	65.03	885	77.03	564	0.00	851
				Average	4.44	413	41.56	343	32.84	348	0.91	264

Fig. 3.

Comparison between the I-MILP and I-CP-WS models based on the times reaching their best solutions.

To statistically evaluate the performance of the developed models, the individual value plot, and Games-Howell simultaneous tests for differences of means with 95% Confidence Intervals (CIs) are employed (using Minitab 18) based on the values of the RPD reported in Table 1.

Fig. 4 indicates the distribution of the obtained RPD for each model. As it is evident, the I-CP-WS is the most reliable model with the lowest variation and average RPDs followed by I-MILP. Furthermore, each pair of the models is compared in Fig. 5. According to the Games-Howell simultaneous test, if an interval does not contain zero, there is a significant difference between the relevant pair of methods, and the method with a better average is superior. Accordingly, the I-CP-WS significantly outperformed the other models. Moreover, the superiority of the I-MILP over the CP and I-CP is evident while there is no statistical difference between the CP and I-CP.

Fig. 4.

Individual value plot regarding the RPD.

Fig. 5.

Games-Howell simultaneous tests for differences of means 95% CIs regarding the RPD.

6.3. Sensitivity analysis and managerial insights

This subsection focuses on analyzing the impact of three influential and controllable factors on the objectives of the problem, including i) worker flexibility to work with different machines, ii) machine flexibility to perform various jobs based on different configurations, and iii) reconfiguration times. In this regard, instance 40j-6 m-3c is considered to conduct the analysis. To obtain more solid results, 10 different sets of parameters are randomly generated for this problem (based on Section 6.1), and in each case, the average changes of the 10 problems are reported. The results are provided in the following subsections, which can provide helpful insights for managers to shape their decisions to be prepared during the COVID-19 pandemic or even similar situations.

6.3.1. Impact of worker flexibility

Fig. 6 illustrates the percentages of changes in the three objectives and the integrated objective based on the number of machines each worker is capable of working with. As depicted, by increasing the number from 1 to 2 (3), the integrated objective (Obj) and the COVID-19 risk are significantly dropped by 22% (27%) and 25% (30%), respectively. However, the further increase does not noticeably impact them. Thus, worker flexibility can be a helpful remedy in such situations. As a result, managers should pay more attention to this fact by implementing some training strategies, like cross-training, to enhance the skillset and flexibility of their workforce up to a reasonable level, respecting their budget limits.

Fig. 6.

Impact of the worker flexibility on the objectives.

6.3.2. Impact of machine flexibility

According to Fig. 7, the positive impact of machine flexibility is evident. Respectively, by increasing the number of eligible machine-configuration combinations for each job from 2 to 4, the integrated objective, COVID-19 risk, and workers’ preferences will be improved by 26%, 48.5%, and 26%. In this regard, this aspect can be appreciated by a reasonable investment in RMTs with higher levels of flexibility and providing more multi-function modules and tools for them. Undoubtedly, making a trade-off between budget and machine flexibility is crucial.

Fig. 7.

Impact of the machine flexibility on the objectives.

6.3.3. Impact of reconfiguration times

Despite the substantial advantages of RMSs, the drawbacks regarding reconfiguration, like reconfiguration times, can be noticeable. For this reason, a sensitivity analysis based on different ranges of reconfiguration times is conducted, and the results are demonstrated in Fig. 8. Accordingly, the negative impact of an increase in reconfiguration times is evident. By doubling the reconfiguration times, the integrated objective, COVID-19 risk, and workers’ preferences will be worsened by19.5%, 59.5%, and 22.5%, respectively. For this reason, the proper design or purchasing of modules and tools for RMTs, as well as adequate training of workers to quickly perform reconfigurations are of great importance.

Fig. 8.

Impact of reconfiguration times on the objectives.

7. Conclusions and future research directions

This paper delved into a novel integrated workforce planning and production scheduling problem, considering issues arising from the COVID-19 pandemic. In this regard, due to the promising capability of RMSs to adapt to sudden changes, a shop floor with multiple non-identical parallel RMTs was studied. Accordingly, MILP and CP models were developed to formulate the problem while taking workers’ COVID-19 health risk and workers’ preferences for flexible working hours into account. Then, two properties of an optimal solution were excavated and incorporated in the developed models, namely I-MILP and I-CP models. Next, to enjoy the advantages of both models, a hybrid model (I-CP-WS) was introduced by warm starting the I-CP model with a partial solution provided by the I-MILP model. According to the computational experiments, the I-CP-WS model significantly outperformed the other models regarding both RPD and computational time criteria. Moreover, regarding the RPD, the superiority of the I-MILP model over the MILP, CP, and I-CP models is evident. Based on the sensitivity analysis, the worker and machine flexibility, and reconfiguration times have sizeable impacts on the objective of the problem, and particularly on the COVID-19 risk. The following recommendations can be applied to strengthen the health risk mitigation and workers’ preferences against situations similar to the COVID-19 pandemic: a) implementing worker training strategies, like cross-training, to enhance the flexibility of workers, b) investing in RMTs with proper levels of flexibility, and modules and tools with wider functionality, respecting the budget limit, and c) careful design and selection of RMTs’ modules as well as adequate training of workers to reduce reconfiguration times.

Although the proposed models were formulated based on the specific conditions during the COVID-19 pandemic, they can be adjusted to other similar situations (e.g., an outbreak of a disease), in which a health risk can influence the allocation of workers. Applying collaborative robots (cobots) can also be fruitful to mitigate the related health risks. As a result, extending the problem to incorporate cobots and providing relevant models can be considered for future research. Moreover, exploring the problem in other manufacturing settings like cellular manufacturing and assembly lines, where the density of workers is high, is valuable. Furthermore, expanding the planning horizon to multi-day planning can lead to more practical results. Therefore, it can be regarded as a promising research direction.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.