NAToRA, a relatedness-pruning method to minimize the loss of dataset size in genetic and omics analyses

Abstract

Genetic and omics analyses frequently require independent observations, which is not guaranteed in real datasets. When relatedness cannot be accounted for, solutions involve removing related individuals (or observations) and, consequently, a reduction of available data. We developed a network-based relatedness-pruning method that minimizes dataset reduction while removing unwanted relationships in a dataset. It uses node degree centrality metric to identify highly connected nodes (or individuals) and implements heuristics that approximate the minimal reduction of a dataset to allow its application to complex datasets. When compared with two other popular population genetics methodologies (PLINK and KING), NAToRA shows the best combination of removing all relatives while keeping the largest possible number of individuals in all datasets tested and also, with similar effects on the allele frequency spectrum and Principal Component Analysis than PLINK and KING. NAToRA is freely available, both as a standalone tool that can be easily incorporated as part of a pipeline, and as a graphical web tool that allows visualization of the relatedness networks. NAToRA also accepts a variety of relationship metrics as input, which facilitates its use. We also release a genealogies simulator software used for different tests performed in this study.

1. Introduction

In omics research, we frequently apply methods that require independent observations. However, when these observations are individuals from a population, they may be relatives (i.e. not independent) (Supplementary Information: Section 1, SI:S1, Table S1). A common solution is to exclude all or part of relatives to reduce dependence, but more efficient solutions are needed to reduce dataset pruning. We present a relatedness-pruning method based on Complex Network Theory called NAToRA (Network Algorithm To Relatedness Analysis), which simultaneously minimizes the number of observations to be excluded from datasets, increasing their independence.

Specifically, NAToRA was inspired by a population genetics problem: the need to infer the genetic structure of a Brazilian population-based cohort that included relatives (i.e. the BAMBUÍ cohort study of Aging). When we inferred the population structure using the software ADMIXTURE (assuming K = 7 ancestry clusters, [1]), we found a putative biogeographic cluster exclusive of BAMBUÍ. Further investigation showed that this cluster was a set of related individuals that ADMIXTURE inferred to be a biogeographic cluster (Figure S1). This issue arose because ADMIXTURE assumes that individuals are unrelated (i.e. independent observations). For population genetics analyses that require independent observations, the strategies of pruning all related individuals or to randomly remove one or more individuals from groups of related individuals [2], [3], [4], [5], are hereafter called all-relatives pruning and random-pruning, respectively. These strategies can lead to unnecessary dataset loss.

In this paper we present the complete NAToRA algorithm that we preliminarily implemented for Kehdy et al. (2015) [6] to minimize the exclusion of related individuals from the BAMBUÍ cohort to perform ADMIXTURE analyses. Here, we formally present the algorithm with new options such as: (i) the optimal solution that guarantees the minimal sample loss, in addition to the heuristic solution, which approximates this minimal, (ii) the test to assess how the cut-off value used to define relatedness affects the number of individuals to be removed, and (iii) the inference of subsets of unrelated individuals without removing any individual from the original dataset. We used simulated and real data to compare NAToRA with other similar pruning methodologies. As companion products, we also release the freely available software to run NAToRA, which includes command line options to personalize execution and a web interface version, and a software to randomly generate simulated genealogies.

2. Theory

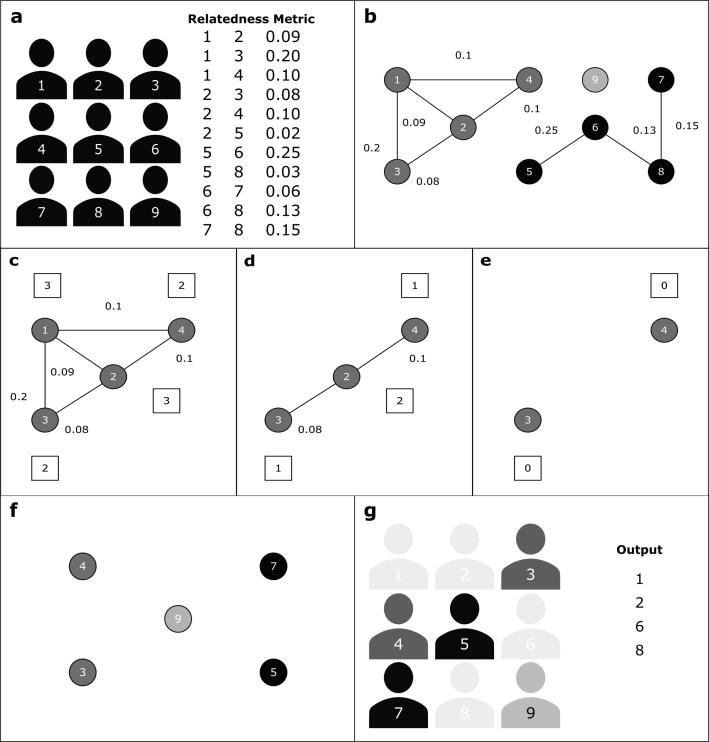
NAToRA is an algorithm that minimizes the number of individuals to be removed from a dataset. In the context of complex network theory, this is done by finding the maximum clique in the complement network (the NAToRA optimal solution). However, because this is an NP-Complete Problem [7], and it is frequently computationally infeasible, we developed a heuristic version of NAToRA that approximates the minimal reduction of the dataset. NAToRA models relatives as a network in which individuals (or more in general, observations) are nodes and relatedness coefficients between them are weights of their connections (or edges). In this network, genetically-related individuals called network families are sets of nodes that have at least one sequence of edges connecting all of them. Contrarily, unrelated individuals (or related below a specific relatedness cutoff value) are represented by disconnected nodes. An overview of the algorithm is shown in Fig. 1. The algorithm receives two mandatory inputs: (i) an adjacency list containing pairs of individuals and their relatedness coefficients for each pair (Fig. 1(a)), and (ii) a relatedness cutoff value indicating the maximum of the relatedness coefficient to be allowed after pruning (e.g., in this case corresponding to third-degree kinship and closer relatedness, Table S1). NAToRA creates a network containing only the individuals linked by relatedness coefficients greater than the cutoff value provided by the user (Fig. 1(b), illustrating a third-degree cutoff). From this network, the algorithm first detects and reports network families from the adjacency list coefficients. Then, for each detected family, the heuristic algorithm iteratively prunes individuals with more links than others, that is, with higher node degree centrality (NDC) [7] (Fig. 1(c)-(f)). NDC is a node metric based on its number of edges and it was chosen after comparisons with alternative metrics (SI: S2-S4). If there are individuals with equal NDC, NAToRA prunes those with the highest sum of its edges’ weights. If there is another tie, the algorithm removes one of them randomly. The main output of the algorithm is a list of individuals to be excluded from the original dataset (Fig. 1(g)). The Methods Section 6.1 and Figures S2 and S3 also detail and exemplify the implementation of the algorithm.

Fig. 1.

Overview of NAToRA’s (Network Algorithm To Relatedness Analysis) algorithm. (a) input file with relatedness metrics for pairs of individuals. (b) relatedness network modeled by NAToRA with minimum kinship cutoff of 0.07; grey-scale colours represent families of genetically-related individuals. (c), (d) and (e) show the node elimination process for the dark grey family network, in which individuals with the highest node degree centrality (NDC, denoted in white boxes) are iteratively removed (in this case the individuals 1 and 2 with NDC = 3). (f) relatedness-pruned network. (g) output file with a list of individuals to be removed from the dataset.

As mentioned in the previous paragraph, NAToRA’s heuristic algorithm uses the NDC node metric to determine which individuals to remove from the network. This metric was selected, among other network metrics, after extensive tests conducted during algorithm development to determine each metric's effect on sample reduction and relationship exclusion (SI: S2. Node Centrality Metrics to be tested). These tests were performed using pseudo-genealogies generated by a genealogy simulator that we developed (described in detail in SI: S3. Genealogy simulator, S4. NAToRA tests of different Centrality Metrics with simulated scenarios, Figures S4-S5, Tables S2-S5). The simulator aims to randomly create genealogies with reproductive behaviors similar to those observed in human populations, using parameters provided by the user that allow to create several different scenarios. After generating each genealogy, the simulator calculates the theoretical kinship coefficient (Table S1) among all pairs of related individuals [8].

3. Results

3.1. Genetic datasets

We tested the NAToRA pruning algorithm using relatedness matrices constructed from three genome-wide datasets including related individuals, different number of individual and kinship structure: (i) The BAMBUÍ Cohort Study of Aging (BAMBUÍ, n = 1,442 admixed Brazilians and 2,186,850 Single Nucleotide Variants (SNVs), Figure S6) [6], (ii) Matsiguenkas indigenous from the Peruvian Amazon Yunga (SHIMAA, n = 45 and 2,170,183 SNVs, Figure S7) [9], [10], (iii) GUZERÁ Bos indicus dairy cattle from the brazilian National Breeding Program (GUZERÁ, n = 1,036 and 32,195 segregating SNVs, Figure S8) [11]. This bovine dataset, being part of a Multiple Ovulation Embryo Transfer breeding program, includes top individuals from both sexes (but particularly bulls) and is composed by a large number of both maternal and paternal half-sibs, producing extremely complex, hard to disentangle pedigrees (SI: S5 Genetic Datasets to test and compare the NAToRA pruning algorithm). The study was approved by the Institutional Review Boards of the participating institutions.

3.2. Comparisons of NAToRA pruning algorithm with similar methods

To assess the performance of the different pruning methods we used four criteria: (i) the number of removed individuals, (ii) the number of relationships above the cutoff that remained in the dataset after the relatedness pruning process, (iii) changes in the Minor Allele Frequency (MAF) spectra (where the MAF is the allele with the second highest frequency for each locus), (iv) changes in the space defined by the first two Principal Components estimated from genotypes of the original dataset.

3.2.1. Effect of pruning on the number of individuals in the dataset and on the relatedness coefficient distributions

We compared NAToRA with the relatedness-pruning methods implemented in the genetic epidemiology software PLINK v1.90b6.9 [12] and KING 2.2.4 (Kinship-based INference for Genome-wide association studies) [13] (Methods Section 6.2; SI: S6 Description of other relatedness-pruning methods (PLINK, KING)) and with the all-relatives pruning strategy (that we assumed as the worst case scenario). Overall, NAToRA shows the best combination of effective relatedness-pruning by removing all unwanted relationships while keeping the largest possible number of individuals in all datasets (Table 1). Figures S9-S10 show how the distributions of the relatedness coefficients in the genetic datasets change with the pruning procedure, and how in none of the cases, the NAToRA algorithm allows for relatedness coefficients above the original cut-off value.

Table 1.

Comparison of relatedness-pruning results to generate datasets with only kinship relationships below second-degree. Methods are PLINK (--rel-cutoff), KING (--degree 2 --unrelated), NAToRA and the all-relatives pruning strategy. Cutoff values are 0.1768 for the relationship coefficient (calculated by PLINK, PI_HAT) and degree 2 for the kinship coefficient (calculated by KING). For NAToRA we let the algorithm select the method (heuristic or optimal). We compare NAToRA with PLINK and KING methods and the all-relatives pruning strategy.

Database	Relatedness estimated by	Number of individuals in the original dataset (number of relationships above the cutoff)	Pruning method (Parameters to exclude by method)	Unrelated Dataset Size: number of individuals	Number of relationships above the original cutoff after removing
BAMBUÍ	PLINK	1442(1572)	plink --rel-cutoff 0.1768	947	234
			all-relatives pruning	491	0
			NAToRA -c 0.1768	869	0
	KING	1442(9 2 0)	king --degree 2 --unrelated	880	1
			all-relatives pruning	602	0
			NAToRA --degree 2	950	0
SHIMAA	PLINK	45(95)	plink --rel-cutoff 0.1768	26	8
			all-relatives pruning	10	0
			NAToRA -c 0.1768	23	0
	KING	45(68)	king --degree 2 --unrelated	45	68
			all-relatives pruning	12	0
			NAToRA --degree 2	25	0
GUZERÁ	PLINK	1036(17875)	plink --rel-cutoff 0.1768	212	368
			all-relatives pruning	3	0
			NAToRA -c 0.1768	175	0
	KING	1036(12861)	king --degree 2 --unrelated	87	0
			all-relatives pruning	24	0
			NAToRA --degree 2	218	0

3.2.2. Effect of pruning on the dataset genetic diversity: Minor allele frequency spectra and Principal Component Analysis

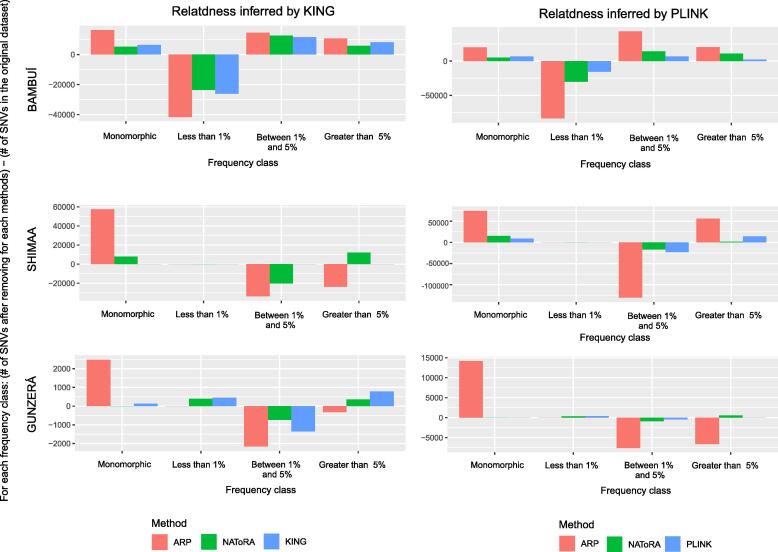
To assess the impact of pruning individuals to the overall dataset genetic diversity, we analyzed the allele frequency spectra (i.e. how alleles are distributed in frequency classes) and Principal Components of genotypes before and after the pruning procedure. We did that for each dataset, comparing the NAToRA methodology versus KING or PLINK methodologies and versus the all-relatives pruning strategy (assumed as the worst-case scenario). Analyses of the allele frequency spectra show that (Fig. 2): (i) in 11 from 18 comparisons of the original database vs. pruned database, we observed significant shifts of the allele frequency spectra in both directions (towards lower or higher frequencies, with P-values always < 0.002 for the two-sided Wilcoxon rank test [14] (Table S7 and Table S8). Non-significant shifts in the allele frequency spectra corresponded to the SHIMAA (characterized by a small number of individuals) and the GUZERÁ (characterized by very high levels of kinship); (ii) all methods produce different levels of loss of segregating SNVs, with the all-relative pruning strategy confirmed as the worst case scenario, as expected; (iii) in general, if the criteria for good performance is the absence of change in the allele frequency spectrum after pruning, we did not observe an overall better method among NAToRA, KING and PLINK, and method performances seem to depend on the specific dataset; finally (iv) from the 6 comparisons of NAToRA vs PLINK/KING pruned datasets, 3 correspond to significantly different allele frequency spectra and 3 do not (two-sided Wilcoxon rank test, P < 0.02), which means that in general, different pruning algorithms may produce datasets with different allele frequency spectra.

Fig. 2.

The impact of relatedness-pruning methods on Minor Allele Frequency (MAF) spectra. Bars represent the number of SNVs for each of the different relatedness-pruning methods (PLINK or KING, NAToRA and all-relatives pruning (ARP) minus the number of SNVs in the original dataset for each allele-frequency class. Positive values mean that there are more SNVs in that MAF interval on this specific dataset than in the original dataset. We divided the SNVs into four classes: Ultra rare (0 < MAF ≤ 0.01), rare (0.01 < MAF ≤ 5%), common (MAF > 5%) and monomorphic (MAF = 0). The monomorphic class includes the loss of SNVs due to the pruning procedure. For the SHIMAA, KING did not remove any individual, and therefore, there is no data for any frequency class.

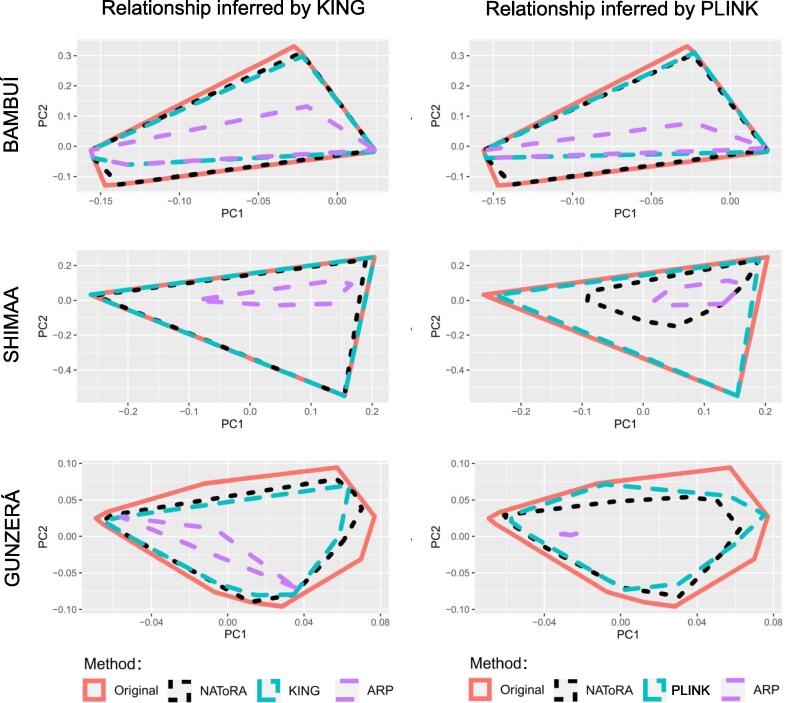
We also assessed the effect of pruning on the distribution of individuals in the space defined by the first two Principal Components (PCs) performed on the genotypes of the original dataset (Fig. 3, S11-S13). Again the all-relatives pruning strategy is confirmed as the worst-case scenario, showing a dramatic loss of the diversity (i.e. individuals) in the space defined by PC1 and P2. Overall, NAToRA, KING and PLINK pruning methods show a similar effect on the diversity in the PC1-PC2 space.

Fig. 3.

Convex hull polygons of the Principal Component Analysis (PCA) before and after pruning with different methods. Methods used were PLINK or KING, NAToRA and All-relatives pruning strategy (ARP). We show the first two Principal Components. The PCA was performed on the original dataset and then the pruned individuals were identified and mapped.

4. Discussion

NAToRA method of pruning relatives outperform KING and PLINK methods in eliminating most if not all the relatedness in the datasets, being parsimonious in the number of individuals to be removed from a dataset, showing comparable performance with KING and PLINK on its effect on allele frequency spectrum and on the distribution of individuals on the PC1-PC2 space.

NAToRA presents four advantages in comparison to KING and PLINK. First, it is flexible in accepting different similarity metrics for relatedness-pruning, while PLINK’s and KING’s pruning methods are tied to their own metrics of relatedness (Table 1). For example, NAToRA is also compatible with relatedness metrics calculated by the REAP method (Relatedness Estimation in Admixed Populations) [15] or SNPRelate [16], which are more appropriate for admixed populations than those calculated by PLINK and KING.

Second, although NAToRA provides an alternative to PLINK and KING’s relatedness-pruning methods, it can still be used in pipelines that include broader use of these software, such as genome-wide association testing. For example, one can use PLINK, KING, or other software to perform data quality control and to calculate relatedness metrics, and include NAToRA in the relatedness-pruning step (see NAToRA’s User Guide, SI:S7) to minimize dataset reduction.

Third, NAToRA also provides a function that partitions the original dataset in subsets of unrelated individuals, without excluding any individual from the total dataset. This function is useful for analyses that can be performed with subsets of independent data that can be later combined, as in population genetics with ADMIXTURE ancestry inferences in [17] (Figure S14). This approach identifies in the original dataset the set of all individuals without relatives called DU (Dataset Unrelated), while the individuals with relatives of the original dataset are redistributed in I subsets (each including DU) in a way that there are no relatives within each subset. For instance, we used this approach for genetic epidemiology studies on the cohort of BAMBUÍ that required fine-scale ancestry inferences as covariables [17]. We inferred fine-scale ancestry using ADMIXTURE [1], that is a method that requires unrelated individuals and that also requires the minimum loss of individuals for accurate ancestry inferences. In this case, we used NAToRA to create subsets of unrelated individuals that were analyzed with ADMIXTURE, and used the individuals from the DU set to check if the ancestry inferences matched across the different ADMIXTURE runs on the different subsets.

Fourth, NAToRA also provides a function called test (available on the command line version, with flag “--test”) that allows the user to check the estimated sample loss per relatedness cutoff applied, and whether or not the combination of the dataset size and relatedness cutoff allows the user to run the optimal version of the algorithm (SI: S8 Identifying feasible features for running the optimal algorithm). To use the test option, the user only informs a maximum value of relatedness/kinship together with the datasets’s adjacency list, and NAToRA calculates the estimated sample loss for 50 cutoffs ranging from a minimum until the maximum value informed by the user. This estimate is in the format of a graph with cutoff values in the x-axis and the estimated number of individuals to be eliminated in the y-axis (Figure S15).

Incidentally, we speculate that other applications of NAToRA rely on the identification of individuals with the highest centrality in a network. These individuals may be conceived as a reduced set of the most representative individuals of their families. This concept, for instance, may be applied in conservation genetics of small natural populations, to select individuals for reproduction. In the more general context of omics research, this application may allow the selection of representative individuals or observations for follow-up experiments.

5. Conclusion

Considering the importance of the number of individuals (observations) to gain statistical power, NAToRA provides both, a minimal reduction of sample size and an effective removal of undesired kinship relationships. NAToRA is freely available, both as a standalone tool that can be easily incorporated as part of an analysis pipeline, and as a graphical web tool that allows visualization of the relatedness networks.

6. Methods

6.1. Implementation of NAToRA

NAToRA was implemented as a greedy algorithm and is based on Graph Theory and Complex Network Theory. It was implemented in Python using the library NetworkX [18].

The input data is an adjacency list derived from a Genetic Relatedness Matrix (GRM) and a relatedness cutoff value that indicates the maximum kinship degree that should be accepted between the individuals in the matrix. The relatedness metric used in the GRM can be of any kind.

From the adjacency list, the algorithm creates a network N (Figure S2 (a)). In the context of Graph and Complex Network Theory, a network G (or graph) is a pair G=(V,E) consisting of a set of vertices V connected by a set of edges E [7], [19]. In our representation, the vertices are individuals and there is an edge between two individuals if the kinship coefficient is greater than zero. Since kinship is a bi-implication relationship (if a is relative of b then b is relative of a with the same degree), our network model is undirected and weighted by the values of GRM. In this work, all concepts of Complex Network and Graph Theory are for undirected networks [7].

In our methodology, we allow the user to select the minimum relatedness degree to be present in the dataset (the cutoff α). The network that only has edges with value above the cutoff value is called N_c (Network with cuts) (Figure S2 (b)). Using network $N_c$, the algorithm performs two analyses: (i) families detection and (ii) iterative pruning of individuals based on a node centrality metric.

To detect families, the algorithm identifies all connected components of Network $N_c$. A connected component is a set of nodes that has at least one path (sequence of edges which connect a sequence of nodes) between all of them. A connected network is a network that has a path between all nodes and it has only one connected component (Figure S2 (a)). On the other hand, a network is disconnected when there is at least one pair of vertices that are not connected by a path. This analysis is shown in Figure S2 (b) through the colors of the nodes, in which each color represents a different family. After identifying the families, the algorithm creates a file with this information that can be used, for example, as PLINK’s family ID (FID) or as a categorical co-variable in association studies.

The next step in the algorithm is to select the individuals to prune from network $N_c$ in order to have a network without edges (or an unrelated dataset). Finding the minimum number of nodes to be pruned in order to get a network without edges is analogous to the problem of finding the maximum clique in the complement network. In graph theory [7], a complement network H of a network G is a pair H=(V,B), where B is a set of edges that connect two nodes u and v if and only if there is not an edge connecting u and v in network G. So, in our network $N_c$, the complement network is the network of non-related individuals (Figure S16). A clique of a given network is a subnetwork in which for each pair of nodes (u,v) there is an edge between them (Figure S17). Finding the maximum clique, i.e., the clique that has the largest number of nodes, is an NP-Complete Problem [19]. In our model, to find the maximum clique in the complement network is to find the largest set of individuals which all are mutually unrelated. Because it is an NP-Complete problem, which can be computationally unfeasible depending on the network, we implement a heuristic that consists of iteratively pruning individuals based on a centrality metric.

The heuristic is implemented as follows, for each family identified by the algorithm: (i) it calculates the centrality metric for each individual and (ii) prunes the most central individual, storing its label. If there is a tie in the most central individual, we prune the individual that has the higher sum of the weights of the remaining edges. Steps (i) and (ii) are repeated until only individuals without edges or pairs of individuals linked by only one edge are kept in the dataset (Figure S2 (c-h)). When there are only pairs of individuals connected in the network, the node-pruning based on centrality metrics loses efficiency since both nodes will have the same centrality value. To solve this, we implemented a tiebreaker that consists of calculating the centrality of each individual in the pair using network N instead of network $N_c$. In network N, we select all edges with weights between an interval (i.e., min and max tiebreaker values, default values are 0.0 and the biggest relationship present on the original data), and then exclude the most central individual (Figure S2 (i-j)). In Figure S2 we present an example of how NAToRA works and all steps of NAToRA can be seen in Figure S3.

6.2. Comparison with existing pruning methods (KING and PLINK)

Although NAToRA accepts any relatedness metrics as input, it is not possible to directly compare PLINK’s and KING’s relatedness-pruning methods because they are tied to their relatedness estimates (PI_HAT for PLINK and its kinship coefficient estimates for KING). Thus, for each of the genetic datasets (BAMBUÍ, SHIMAA, GUZERÁ) we performed independent comparisons of NAToRA with PLINK and KING pruning methods, and in both cases, with the all-relatives pruning strategy.

For comparison with KING’s relatedness-pruning method, we set the network relatedness cutoff value to second degree (0.0884 according to the manual, which is the geometric mean between the second and third degree kinship theoretical values). For comparisons with PLINK’s relatedness-pruning method, we considered that its relatedness metric, PI_HAT = 2*kinship coefficient and set the cutoff value to 0.1768 [8].

We performed Principal Component Analysis using SNPRelate [16] and then identified and tagged the individuals that were pruned with the different methodologies. We compared pairs of Minor Allele Frequency spectra using the non-parametric two-sided Wicoxon rank tests [20].

6.3. Using NAToRA to create multiple sets of unrelated individuals

As seen in previous comparative results, our heuristic method is able to remove relationships from a dataset while keeping the number of individuals removed close to the minimum possible (optimal algorithm). Nevertheless, there are some analyses in which it is necessary to remove kinship without losing individuals, to avoid reducing the statistical power of the analysis. When we can divide the data into subsets without affecting the final result, we can use NAToRA to get I sets of unrelated individuals, in order to perform independent analysis on each of the I sets of unrelated individuals.

Starting with the complete Original Dataset (S₁), the first step to create the I sets of unrelated individuals is to identify in the $N_c$ network all individuals without relatives and store them as a list called DU (Dataset Unrelated). Each of the final I sets will include DU and an additional subset of unrelated individuals. After defining DU, we run NAToRA on the Original Dataset (S₁) and the algorithm will return a list of individuals to be removed (R₁). After removing these individuals from the Original Dataset S₁, we remain with a first set of unrelated individuals called AD1 (Analysis Dataset 1, that includes DU).

To create a second set of unrelated individuals, the algorithm removes from the Original Dataset (S₁) the individuals belonging to AD1 that are not part of DU, to create a new set of individuals called S₂, that will be the input for a further run of NAToRA with the same cut-off value. In other words, the new input file S₂ will be the union of DU and R₁ (the individuals removed in the previous run of NAToRA because showing high centrality in the network). The new run of NAToRA on S₁ will create a second set of individuals to be removed called R₂, and a second set of remaining unrelated individuals called AD2 (that again, includes DU). This process is repeated and the algorithm is finished when the output from NAToRA is empty. All steps are presented in Figure S14 and Figure S3.

Availability of supporting source code and requirements.

Project GitHub: https://github.com/ldgh/NAToRA_Public and

https://github.com/ldgh/NAToRASimulator.

Webtool address: https://www.ldgh.com.br/natora/.

Operating system(s): Platform independent.

Programming language: NAToRA was implemented in Python and the scripts that compose the NAToRA toolkit were implemented in Perl.

Other requirements: Python3 or higher and library NetworkX 2.0 or higher.

License: GNU.

Data Availability.

All the relationship estimates used on this work is freely available at https://github.com/ldgh/NAToRA_Public on Datasets folder.

CRediT authorship contribution statement

Thiago Peixoto Leal: Conceptualization, Investigation, Formal analysis, Software, Methodology, Writing – original draft. Vinicius C Furlan: Software, Writing – review & editing. Mateus Henrique Gouveia: Conceptualization, Methodology, Writing – original draft, Writing – review & editing. Julia Maria Saraiva Duarte: Formal analysis, Writing – review & editing. Pablo AS Fonseca: Resources, Writing – review & editing. Rafael Tou: Formal analysis, Writing – review & editing. Marilia de Oliveira Scliar: Methodology, Writing – original draft, Writing – review & editing. Gilderlanio Santana de Araujo: Methodology, Writing – original draft, Writing – review & editing. Lucas F. Costa: Formal analysis, Writing – review & editing. Camila Zolini: Supervision, Resources, Writing – review & editing. Maria Gabriela Campolina Diniz Peixoto: Resources, Writing – review & editing. Maria Raquel Santos Carvalho: Resources, Writing – review & editing. Maria Fernanda Lima-Costa: Resources, Writing – review & editing. Robert H Gilman: Resources, Writing – review & editing. Eduardo Tarazona-Santos: Supervision, Writing – original draft. Maíra Ribeiro Rodrigues: Supervision, Writing – original draft.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: