An extended multi-criteria group decision-making method with psychological factors and bidirectional influence relation for emergency medical supplier selection

Abstract

The COVID-19 pandemic outbreak spread rapidly worldwide, posing a severe threat to human life. Due to its unpredictability and destructiveness, the emergency has aroused great common in society. At the same time, the selection of emergency medical supplier is one of the critical links in emergency decision-making, so undertaking appropriate decision-making using scientific tools becomes the primary challenge when an emergency outbreak occurs. The multi criteria group decision-making (MCGDM) method is an applicable and common method for choosing supplier. Nevertheless, because emergency medical supplier selection should consider regarding many aspects, it is difficult for decision makers (DMs) to develop a comprehensive assessment method for emergency medical supplier. Therefore, few academics have focused on emergency situation research by the MCGDM method, and the existing MCGDM method has some areas for improvement. In view of this situation, in this study, we propose a new MCGDM method, which considers the bidirectional influence relation of the criteria, consensus and the psychological factors of DMs. It providers a good aid in emergency decision-making and it could apply to other types of MCGDM research. Firstly, DMs give their assessment in interval type-2 fuzzy sets (IT2FSs). Secondly, an extended IT2FSs assessment method and a novel ISM-BWM-Cosine Similarity-Max Deviation Method (IBCSMDM) are used for weighing all alternatives. The TODIM (an acronym for interactive and multi-criteria decision-making in Portuguese) can obtain the ranking results under different risk attenuation factors. Eventually, this extended IT2FSs-IBCSMDM-TODIM method is applied in a real case in Wuhan in the context of COVID-19 to illustrate the practicability and usefulness.

1. Introduction

In December 2019, the COVID-19 pandemic outbreak was first detected in Wuhan, China. Subsequently, it rapidly spread over 200 countries worldwide, with more than 160 million confirmed cases by the end of May 2021(Ahmad et al., 2021, Singh et al., 2020, Tirkolaee et al., 2021). This deadly pandemic greatly threatened world health (Ahmad et al., 2021, Tirkolaee et al., 2021). An emergency is considered an abnormal social event, and the COVID-19 pandemic is a typical emergency (Singh et al., 2020). It has the characteristics of suddenness, timeliness, universality and complexity, which can have a severe impact on the supply chain at the same time (Ivanov, 2020). For instance, according to the World Health Organization (WHO), after the COVID-19 outbreak occurred, global demand for medical supplies was expected to be about 100 times higher than usual1 . Therefore, it is critical to access emergency rescue services, timely and accurately (Ji & Zhu, 2012). If emergency medical supplies are not pre-positioned in advance, the emergency supplies will be far from the demand. For example, Hubei Province requested national emergency support two months after the outbreak of COVID-19 by allocating 40 million medical masks, 5 million sets of protective clothing, and 5,000 sets of infrared thermometers2 . Selecting appropriate supplier and signing agreements on preparing medical supplies in advance. By these methods effectively reduce the hazards due to delays in collecting emergency supplies (Hu and Dong, 2019, Mohammadi et al., 2016), because these measures provide a certain quantity and quality of emergency supplies in time (Hu & Dong, 2019). Hence, selecting and contracting with appropriate emergency medical supplier is critical in responding to emergencies.

In recent years, earthquakes, epidemics, mudslides, and other emergencies have occurred frequently, leading to severe impacts (Yáñez-Sandivari, Cortés, & Rey, 2021). When these emergencies arise, we need to propose a practical emergency decision-making approach through appropriate decision tools to minimize the impact and protect human life and property (Ahmad et al., 2021). Hence, many academic have carried out research on emergency decision-making, emergency supplier selection, emergency supply chain management, etc., and related research methods are also being developed. There are three main approaches to solve such problems, namely, quantitative analysis (Aghajani et al., 2020, Mohammadi et al., 2016, Vermuyten et al., 2018), qualitative analysis; Zhou, Xiu, Wang, & Yu, 2021), and a combination of quantitative and qualitative analysis (Ding and Liu, 2018, Ding et al., 2021). Among them, the MCGDM method considers simultaneously both quantitative and qualitative evaluation criteria in real-life applications, which is the typical and commonly method of the third type. In an emergency situation, many criteria are difficult to evaluate by quantitative description. Therefore, the MCGDM method may be mare convincing to some extent than other methods (Mohammadi et al., 2016, Wu et al., 2016, Yang et al., 2021). Besides, the MCGDM method is a common method for supplier selection, and many academics have proven the scientific and efficient characteristics of this method (Ding and Liu, 2018, Liu et al., 2019, Zhang et al., 2015), so has been applied to literature in many fields (Qin et al., 2017, Wu et al., 2019).

In recent years, a growing number of academics conducted research in emergencies by the MCGDM method (Fei et al., 2021, Ruan et al., 2016). However, due to factors such as high cost, long delay and low efficiency in emergency decision-making, it is difficult to ensure the timeliness, applicability and quality of relevant materials, which increases the complexity of the process of this method (Liu et al., 2019, Zhou and Guo, 2021). Meanwhile, scholars have seldom considered the complex relationship among these factors (Chen et al., 2021, Zhou and Guo, 2021). The current MCGDM method of supplier selection is not suitable for emergency situation. Further, DMs may have different risk appetites when making decisions, which present new challenges for academics to how to select emergency medical supplier (Liu et al., 2019, Mohammadi et al., 2016).

Through the literature review, we found that the existing studies by the MCGDM method may be difficult to accurately express the characteristics of emergency decision-making. Simultaneously, there is still sparse MCGDM research on the evaluation of emergency medical supplier, and current relative literature still has several limitations, divided into three types: (1) The existing emergency decision-making research did not take both psychological factors and bidirectional influence relationship into account. In realistic situations, there is often a complex causal relationship between elements. Meanwhile, DMs have different backgrounds, degrees of consensus, and psychological preferences. Therefore, it may be difficult for existing MCGDM methods to accurately express the incomplete rationality of DMs and the characteristics of the criteria in emergency medical supplier selection (Ding et al., 2021). (2) Few scholars have considered comprehensively how to weight assessment criteria in emergency decision-making, like subjective and objective aspects, weights of DMs and weights of criteria, etc. The single weighting method may cause the influence of several factors to be enhanced or weakened, affecting the accuracy of the results (Zhang et al., 2015). (3) Many existing MCGDM studies on decision-making are based on the type-1 fuzzy set, i.e., only utilizing the prime membership to represent assessment. This fuzzy set may have several limitations in the decision-making process,. and this limitation is even more pronounced in emergency medical supplier selection. For instance, it is insufficient to describe complex fuzzy evaluation information (Wan, Chen, & Dong, 2021), which leads to an imperfect evaluation process.

Therefore, to fill the research gap, our study proposes an extended MCGDM method based on IT2FSs that considers psychological factors and the bidirectional influence relationship. It is a new analysis framework based on correlation coefficients, an interpretation structure model, and the TODIM method for emergency medical supplier selection. Based on the idea of combining subjective and objective issues at the same time, we integrate deviation analysis and an extended Best-Worst Method (BWM) to get a novel weight. Further, a more scientific decision result is obtained by introducing type-2 fuzzy evaluation.

In addition, the main reasons why we propose the novel framework including comprehensive weight and TODIM, are as follows: (1) Both BWM and deviation analysis are commonly used for weighting in the MCGDM method. Wan et al. pointed out that BWM is a robust subjective weighting method, more in line with reality (Wan et al., 2021). At the same time, compared with the classical method such as Analytic Hierarchy Process (AHP), the BWM method requires fewer pairs of comparison. Hence it can reduce the workload and complexity of the decision-making process (Ahmad et al., 2021). Moreover, deviation analysis is a common objective weighting method (Ding et al., 2021, Wu et al., 2021). The maximum deviation method is one of development for deviation theory, which can express the difference between the evaluations more clearly (Lo & Guo, 2010). Further, it has been suggested that the weighting method is more scientific by combining subjective and objective aspects to complement each other (Liu, Chan, & Ran, 2016). Many scholars have proposed models with integrated weights (Cheng et al., 2017, Ding et al., 2021, Zhang et al., 2015). However, the first step of the BWM is to specify the best and worst indexes directly by DMs, which may have the problem of solid subjectivity; and the maximum deviation method does not consider the degree of consensus between DMs, which may cause the accuracy to be challenging to guarantee. Therefore, we extended these methods respectively and propose a comprehensive weight based on them. (2) The TODIM is one of the latest MCGDM methods to consider psychological factors. Tolga, Parlak, and Castillo (2020) applied TODIM to different scenarios, demonstrating the effectiveness of the TODIM approach. In addition, Wu et al. (2021) discussed TODIM in combination with other theories. As the emergency decision-making environment becomes increasingly complex and fuzzy, DMs often cannot express utterly rational preference information in many realistic situations (Ding et al., 2021). The TODIM is an appropriate way to solve this decision-making problem. (3) By describing membership with the prime and secondary membership, type-2 fuzzy sets retain the DMs' description information with more integrity. Type-2 fuzzy theory can be a good expression of uncertainty in the selection process of emergency medical supplier (Ding et al., 2021, Tolga et al., 2020). IT2FSs is one such type of assessment. It ensures the characteristics of type-2 fuzzy sets and avoids excessive computation (Wan et al., 2021). Hence, we extend the IT2FSs and try to evaluate emergency medical supplier more comprehensively.

There are three major contributions in this study: (1) To address the challenge of emergency medical supplier selection, we propose a decision-making framework considering psychological factors and bidirectional influence. Based on the limitations of existing studies and the advanced nature of psychological factors, an extended MCGDM method is proposed. This framework achieves the quantification of psychological factors and takes bidirectional influence relations among the criteria into account. It attempts to make for a more consummate approach is and closer to the real decision framework. (2) We present a novel quantifiable weighting approach and make the emergency decision-making process more scientific. Weighting is one of the necessary processes of the MCGDM method, so a novel quantifiable weight can effectively improve the scientific of decision-making process. Based on the consideration of psychological factors mentioned above, we propose a new weighting method for the decision-making framework. This method assigns weights both from DMs and criteria dimensions simultaneously, making the results more accurate. (3) In order to obtain more detailed evaluation information and more reasonable evaluation results, we use type-2 fuzzy sets for integrating data. The type-1 fuzzy set is a commonly MCGDM assessment methodology, however, this assessment approach is difficult to match the complexity of contingency scenarios. Compared to one type of assessment language, type -2 fuzzy sets can refine the assessment process. So, we used an extended type-2 fuzzy set approach to get more detailed assessment information, which could make the results more consistent with the substance of emergency medical supplier decisions. Further, we extend the theory of contingency decision-making assessment for research in IT2FSs based MCGDM method.

The rest of this article is arranged as follows. The second section introduces the research methods of the decision-making under emergencies, and reviews assessment methods, commonly used weights and ranking methods of the MCGDM method. The third section introduces the theoretical background of the assessment fuzzy sets and two ways for improvement of the traditional weights. The fourth section introduces 6 evaluation criteria for emergency medical supplier. The fifth section discusses the extended IT2FSs-IBCSMDM-TODIM method, which applies to emergency medical supplier. The sixth section applies the method mentioned in the previous section to a real case to get the ranking results, and discusses the ranking results and of this case study from two dimensions. The seventh section summarizes the research process and puts forward prospects for the future.

2. Literature review

2.1. Emergency medical supplier selection

In recent years, with the frequent occurrence of emergencies, such as earthquakes, epidemics, and mudslides, the preparation of emergency supplies is increasingly necessary. Through the WHO’s survey, we know that the demand for medical protective equipment has soared after the COVID-19 pandemic. For example, Jiangsu and Zhejiang Provinces of China, two provinces with relatively good economic development, health emergency supplies remain significantly constrained limited (Lo and Guo, 2010, Wan et al., 2021). It can be seen that the situation of emergency medical supplies in other parts of the China and even the world is profound. Hence, emergency supplies, especially emergency medical supplies, may not be available promptly in an emergency outbreak.

In 2010, Rawls and Turnquist (2010) proposed the pre-deployment of emergency supplies as a mechanism for improving natural disaster preparedness. Many scholars also discussed in detail how to preposition emergency supplies (Ji and Zhu, 2012, Yang et al., 2021). Choosing the appropriate emergency medical supplier to support the regular operation (Kaur & Singh, 2021), can reduce emergencies to some extent. Meanwhile, Rahimi-Ghahroodi, Al Hanbali, Zijm, and Timmer (2019) noted that organizations signing agreements with a supplier in advance is an effective way to respond to emergencies. This study pointed out that service providers can keep fewer local resources and occasionally turn to emergency supplier with sufficient spare parts and service engineering capacity to respond to maintenance requests. Therefore, the selection of emergency supplier is crucial for emergency decision-making. For example, Fei et al. (2021) discussed how to select medical providers after the outbreak of COVID-19. They also proposed a heterogeneous MCGDM frame based on the Dempster-Shafer theory. Many scholars have conducted research on emergency supplier and the perspective of providing supplier. For example, Ji and Zhu (2012) have expounded the connotation and characteristics of the emergency supplies supply chains, and they also analyzed the key factors of emergency management. Othman, Zgaya, Dotoli, and Hammadi (2017) proposed a scheduling plan for the emergence of the crisis. Yang et al. (2021) investigated how to select emergency medical supplier by preparing in advance. Based on the above analysis, research on emergencies supplier selection has become one of the mainstream trends in emergency research.

In the existing research on emergency supplier, many decision-making methods have beenadopted by scholars. Some academics have presented a comprehensive review of the recent literature on rescue operations in emergencies (Agarwal et al., 2020, Boujemaa et al., 2020, Yu et al., 2021). There are many methods of quantifiable mathematical models in the existing research. For example, Ruan et al. (2016) used a fuzzy clustering algorithm to optimize an emergency medical supplies scheduling algorithm. Several academics also analyze the order of emergency supplier. For instance, Zheng, Lin, Yuan, and Pan (2018) studied how the opportunity of emergency orders affected manufacturers, and determined under what conditions manufacturers could gain better profits when providing retailers with the chance of emergency orders. Yáñez-Sandivari et al. (2021) emphasized the importance of the development of such optimization models for disaster response. Overall, many scholars have analyzed the dispatch and other quantifiable themes of emergency decision-making (Nabeta et al., 2021, Zhao et al., 2021). In addition, some scholars have discussed emergency decision-making through purely qualitative methods. For example, Zhou et al. (2021) explored the transmission mechanism of misinformation about health emergencies by observing data. Liu, Liu, Tu, Li, and Li (2022) classified the risk of online public opinion on public health emergencies by empirical methods. However, the use of quantitative models alone for emergency medical supplier evaluation may have several limitations in application (Liu et al., 2013, Nassereddine et al., 2019), and a qualitative method alone may have a lower persuasive power compared to other methods (Budak et al., 2020, Zhou et al., 2021). Therefore, a combination of quantitative and qualitative analysis is more scientific and convincing (Song & Li, 2018). Several methods applied in emergency scenarios and relative decision researches are listed in Table 1 .

Table 1.

Representative Methods in Emergency and Relative Decision Researches.

References	Research Field	Research Objective	Method
(Chen et al., 2021)	Emergency Decision	Propose a novel MCGDM model to aid engineering emergency decisions.	MCGDM
(Ding et al., 2021)	Emergency Decision	Choose an appropriate emergency alternative.	MCGDM
(Agarwal et al., 2020)	Humanitarian Decision	Propose a solution to improve the implementation of humanitarian supply chain management.	MCGDM
(Boujemaa et al., 2020)	Emergency Medical Decision	Minimize dispatch costs for emergency medical services systems.	Stochastic programming model
(Budak et al., 2020)	Humanitarian Relief Decision	Choose an appropriate real-time location systems technology.	MCGDM
(Vermuyten et al., 2018)	Emergency Medical Decision	Addressing staffing issues in emergency medical services.	Algorithmic design
(Nassereddine et al., 2019)	Emergency Decision	Evaluate the emergency response system	MCGDM
(Song & Li, 2018)	Medical Decision	Determine the most suitable treatment program.	MCGDM
(Ruan et al., 2016)	Emergency Medical Decision	Optimize the dispatch of emergency medical supplies.	Clustering algorithm

The MCGDM method is a very important and commonly used selection method, which is suitable for emergency decision-making. Although few scholars have used the MCGDM method to select emergency medical supplier, it can be seen from Table 1 this method has become a new research trend for decision-making in emergency response and related fields. Therefore, there is an urgent need to select emergency medical supplier by MCGDM method.

A review of the extensive literature reveals that it’s necessary to select emergency medical supplier to ensure a timely supply of emergency items. Many existing decision method only use limited information to analyze quantifiable criteria (Liu et al., 2022). A more comprehensive analysis can be achieved by also considering non-quantifiable aspects. Hence, choosing a method that combines the qualitative and quantitative approaches is necessary in selecting emergency medical supplier. However, few scholars have used these methods, such as the MCGDM method, to evaluate emergency medical supplier. It is important to select emergency medical supplier by an appropriate and extended MCGDM method. In addition, most of the existing research on emergency supplier assessment evaluates the contract coordination, risk, reliability, agility, robustness, and other criteria of emergency supplier (Kaur & Singh, 2021). The evaluation criteria for selecting emergency supplier is also a worth debating dimension.

2.2. MCGDM method

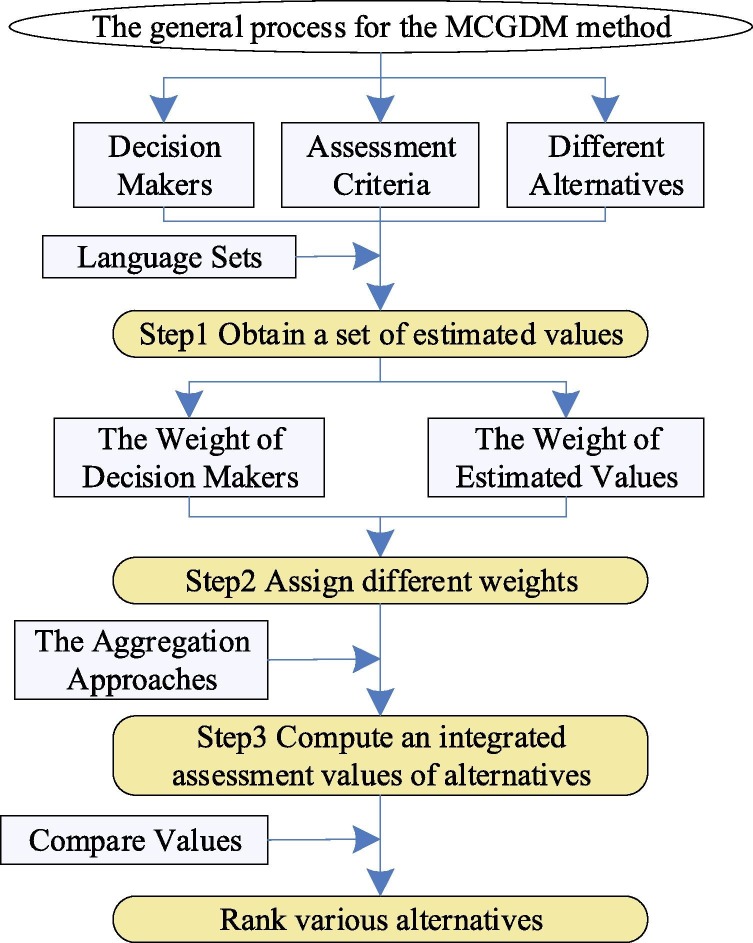
The MCGDM method combining effectively qualitative and quantitative characteristics, it is widely used in many kinds of supplier selection problems (Beikkhakhian et al., 2015, Qin et al., 2017, Wu et al., 2019). Overview to the MCGDM research areas, researchers often develop discussions in three steps. Firstly, DMs was evaluates different criteria of alternatives. Many academics low weighted evaluation criteria or DMs by different importance to make the evaluation process more realistic (Hwang & Yoon, 1981). Finally, the comprehensive score of each alternative is obtained by aggregation operators, and the ranking result of the alternatives is obtained. Fig. 1 shows the general process of the MCGDM Method.

Fig. 1.

General process for solving the MCGDM method.

There are both advantages and disadvantages of each sub-method in the MCGDM method. Scholars have explored the improvement or the combination of different methods, to achieve mutual complementation between methods. It can obtained a more reasonable and scientific result. Therefore, the research on MCGDM method usually focuses on three categories, which are also stick closely to the main three steps of this method, namely, language sets, weighting assignment, and aggregation operators. The follows provides a brief summary that current academics have explored for the MCGDM method in the field of emergencies.

Many scholars have analyzed which way to language sets is closer to reality of the situation. Zadeh (1965) first proposed the concept of the fuzzy set. Due to the uncertainty of objective conditions and the complexity of DMs' psychological factors, it is challenging to use precise numbers to fully determine DMs' assessment and preferences in the decision-making process (Guo, Yin, Zhang, Lin, & Li, 2020). Fuzzy numbers can be used to express uncertainty in the MCGDM method. With the continuous improvement is the appropriate these methods, DMs’ assessment can be expressed more rationally through different types of fuzzy sets, such as intuitionistic fuzzy sets (Atanassov, 1986), triangular fuzzy sets (Ding et al., 2021), hesitant fuzzy sets (Liao, Yang, & Xu, 2017), and triangular hesitant fuzzy sets (Cheng et al., 2017). Due to the increasing complexity of the decision-making environment, it is difficult for traditional fuzzy assessments to describe the decision-making environment accurately. Hence, Zadeh (1975) proposed the type-2 fuzzy sets, extending the conventional type-1 fuzzy set. It is characterized by the primary membership function (PMF) and the secondary membership function (SMF). Compared with IF1FSs, IT2FSs has more degrees of freedom and can describe uncertainty more effectively (Liu et al., 2013). Many scholars expanded the approach based on this premise. For instance, Mendel, John, and Liu (2006) simplified the calculation process, which could widen the scope of application in practical decision problems. Kahraman, Öztayşi, Uçal Sarı, and Turanoğlu (2014) took membership, height and fuzzy footprint area, as distance measures or profit and loss value functions. Meantime, several academics have discussed how to weight information in this fuzzy environment. For example, Baykasoğlu and Gölcük (2017) proposed a DEMATEL-TOPSIS (Technique for Order Performance by Similarity to an Ideal) Solution model based on type-2 fuzzy sets, which overcomes the assumption of preferred independence. In existing studies, many scholars have applied IT2FSs numbers to the ranking methods such as TOPSIS, AHP or Vlse Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method. For instance, Kahraman et al. (2014) discussed how type-2 fuzzy sets apply to AHP. Tolga et al. (2020) further extended the IT2FSs to the application of foreground theory or the TODIM method.

There are different levels of importance among assessments from DMs. Determining the weight is one of the critical aspects in multi-criteria decision-making, and a reasonable criteria weight should take the characteristics of DMs’ preference and decision data into account. Weighting methods can be divided into the objective weight and subjective weight. The entropy weight method is one of the classical objective weighting methods in the literature (Higgins et al., 2014, Liu et al., 2019, Zhou and Guo, 2021), and this method is used to determine the objective weight according to the dispersion degree of the alternative data. Based on the basic idea, there are extended methods of relative entropy and information entropy (Assaf, Charif, & Demir, 2021). Another objective weighting approach, the deviation maximization method, can maximize the total deviation of all evaluation indexes to all samples to be evaluated (Lo and Guo, 2010, Zhang et al., 2015). The difference of one alternative is more significant to all alternatives, the greater the alternative's evaluation effect. In addition, common subjective weighting methods include Decision Making Trial and Evaluation Laboratory (DEMATEL) (Ding et al., 2021, Zhou et al., 2011) and BWM (Ahmadi, Lo, Gupta, Kusi-Sarpong, & Liou, 2020). However, due to the limitations of purely objective or subjective weighting methods, Wu et al. (2019) achieved a weighted approach by combining the subjective preferences of DMs with objective information. In addition, several scholars also made more attempts on the weighting method. For instance, Ahmadi et al. (2020) considered the combination of preference information and BWM.

After weighing the criteria or DMs, the MCGDM method aggregates and sorts them by some integration Methods, such as, TOPSIS (Cheng et al., 2017), Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE) (Ahmadi et al., 2020), VIKOR (Liu et al., 2019), TODIM (Liu, Song, & Han, 2020). In addition, many methods used for integration and ranking have been applied in contingency scenarios, such as PROMETHEE (Nassereddine et al., 2019), VIKOR (Wu et al., 2019), and TODIM (Tolga et al., 2020). Among them, the TODIM method has been gradually extended to various assessments (Shishavan, Kutlu Gundogdu, Farrokhizadeh, Donyatalab, & Kahraman, 2020). It has become one of the leading research trends for ranking in the MCGDM method. Nevertheless, TODIM, the ordering method of MCGDM, has not been applied to selecting emergency medical supplier.

By analyzing the existing literature, we found that assessment by IT2FSs has become a new research trend. However, there are fewer related studies due to their abstractness and complexity. In addition, we found that the max deviation method, BWM, and TODIM, three commonly employed MCGDM methods, have been widely analyzed in existing research. Nevertheless, there is no research that discusses the integration of these methods for emergency decision-making. Meantime, few scholars have applied method which considers risk appetite or other factor in emergency decision-making, such as the TODIM method. Further, there are few studies on uncertainty, preference and psychological conditions in the actual situation, and there are some gaps in relevant fields.

2.3. Research Gaps

In recent years, emergencies have frequently occurred. According to the harmfulness and complexity of emergencies, it is necessary to undertake reasonable emergency decision-making research. In the existing theoretical investigations on disaster and emergency decision-making, there is little few research on how to select an emergency medical supplier. It is necessary to choose a method that combines qualitative and quantitative methods to make decisions. In light of the characteristics of the emergency relief medical supplier, it is sensible and appropriate to use a MCGDM method to evaluate the emergency supplier.

There are several limitations in the existing research on emergency decision-making by the MCGDM method. Table 2 lists several representative studies on the application field and the MCGDM method in emergencies and compares them with our study.

Table 2.

Representative Literatures of MCGDM Method in Emergencies.

Representative References	Application Field	MCGDM method
		Fuzzy sets		Weights		Aggregation Operators
		Type-2 Fuzzy	Other	Subjective Weight	Objective Weight
Wan et al. (2021)	Makeshift hospital selection	TrIT2 fuzzy	–	BWM	–	VIKOR
Tolga et al. (2020)	Medical device selection from three angles	Finite-interval-valued Type-2 Gaussian fuzzy	–	Directly given	–	TODIM
Ding et al. (2021)	Emergency alternative in GEDM	–	Hesitant triangular Fuzzy	Deviation minimum method	Entropy weight	TODIM
Nassereddine et al. (2019)	A new preference function is proposed to realize collaborative emergency response	–	Fuzzy	AHP	–	PROMETHEE
Higgins et al. (2014)	Prioritizing patients with COVID-19 and check the health of asymptomatic carriers	–	Fuzzy	–	Entropy	TOPSIS
Chen et al. (2021)	Propose a novel emergency decision model embedded with GRA algorithm	–	Heterogeneous	–	Relative Entropy	–
Ding and Liu (2018)	Identify critical factors for emergency management and make causal classifications	–	2DULVs	DEMATEL	–	–
Our study	Selection of Medical Emergency Supplier	IT2FSs	Extended BWM	Extended Max deviation method	TODIM

Abbreviations: MCGDM, Multi Criteria Group Decision-Making; GEDM, group emergency decision-making; GRA; grey relational analysis; TrIT2, Trapezoidal Interval Type-2; IT2FSs, Interval Type-2 Fuzzy Sets; 2DULVs, 2-Dimension Uncertain Linguistic Variables; BWM, Best-Worst Method; AHP, Analytic Hierarchy Process; DEMATEL, Decision Making Trial and Evaluation Laboratory; VIKOR, Vlse Kriterijumska Optimizacija I Kompromisno Resenje; TODIM, an acronym for interactive and multi-criteria decision-making in Portugese; PROMETHEE, Preference Ranking Organization Method for Enrichment Evaluation; TOPSIS, Technique for Order Performance by Similarity to an Ideal Solution.

Through the analysis above and in analyzing emergency decisions by MCGDM method in the Table 2, there is potential for limitation from three aspects: (1) In recent years, few scholars used psychological factors when selecting an emergency medical supplier. Nevertheless, several MCGDM approaches, such as prospect theory and TODIM approach, have taken the psychology of DMs into account (Zhou & Guo, 2021) and have become recent trends of humanitarian, disaster, and medical research. Moreover, in aggregating evaluation information using the traditional TODIM method in this field, the influence relationship between the criteria and DMs is rarely considered simultaneously. This process may neglect the mutual influence of factors, such as weak economic demand and the extremely high requirements for timeliness, in emergency decision-making resulting in inaccurate results. (2) Reviewing the existing weight of emergency criteria, many academics use a single weight. Among them, the objective weighting method mainly adopts the entropy weight method, which has limitations in some cases. Meantime, subjective weighting methods are especially directly given by DMs or determined by the DEMATEL method (Baykasoğlu and Gölcük, 2017, Zhou et al., 2011), which may have the problem of overly strong subjectivity leading to bias. (3) Existing assessment information in emergency decision situations are often described by type-1 fuzzy sets, such as triangular fuzzy sets, interval fuzzy sets, and probability fuzzy sets. However, due to the increasing complexity and uncertainty of the social and economic environment, processing imprecise information by type-1 fuzzy sets may lead to inaccurate decision results (Qin et al., 2017). Further, trapezoidal type-2 fuzzy numbers are too complicated and abstract (Baykasoğlu & Gölcük, 2017), and this would provide researchers with the opportunity to fill possible gaps in type-2 fuzzy sets.

3. Theoretical background

3.1. Interval Type-2 fuzzy sets

Because of the increasing complexity in the decision-making environment, Zadeh (1975) proposed a type-2 fuzzy set. IT2FSs is one of the type-2 fuzzy sets, and the relevant theory of IT2FSs is presented below.

Definition 1(Kahraman et al., 2014, Wu et al., 2019): Interval type-2 fuzzy sets.

For a domain of discourse$X$, an IT2FSs $\stackrel{\sim }{B}$ can be expressed as follows:

$$\stackrel{\sim }{B}=\left\{\left(\left(x,u\right),{\mu }_{\stackrel{\sim }{B}}\left(x,u\right)\right)\left|\forall x\in X,\right)\forall u\in J_x\subseteq \left[0,1\right]\right\}$$

In which $x$ is the domain of discourse of$\stackrel{\sim }{B}$, $u$ is the degree to which any element $x$ in the domain $X$ is a member of$\stackrel{\sim }{B}$;$u$ represents the major degree of membership, $s$ represents the degree of membership of$u$, it namely the secondary degree of membership. $\stackrel{\sim }{B}$ can also be expressed as $\stackrel{\sim }{B}={\int }_{x\in X}{\int }_{u\in J_x}{\mu }_{\stackrel{\sim }{A}}\left(x,u\right)/\left(x,u\right)$. If${\mu }_{\stackrel{\sim }{B}}\left(x,u\right)=1$, the type-2 fuzzy sets are IT2FSs:$\stackrel{\sim }{B}={\int }_{x\in X}{\int }_{u\in J_x}1/\left(x,u\right)$.

Definition 2 (Mendel et al., 2006) —

: Interval Trapezoidal Type-2 fuzzy sets.

The IT2FSs is a special form of trapezoidal type-2 fuzzy sets, which can be expressed as follows:$\stackrel{\sim }{A}\text{=}\left[\left({\underset{\_}{a}}_1,{\underset{\_}{a}}_2,{\underset{\_}{a}}_3,{\underset{\_}{a}}_4,\underset{\_}{h}\left(\stackrel{\sim }{A}\right)\right),\left({\overline{a}}_1,{\overline{a}}_2,{\overline{a}}_3,{\overline{a}}_4,\overline{h}\left(\stackrel{\sim }{A}\right)\right)\right]$, $\underset{\_}{h}\left(\stackrel{\sim }{A}\right)$ and $\overline{h}\left(\stackrel{\sim }{A}\right)$ represent the upper and lower membership functions respectively, both ${\underset{\_}{a}}_i$ and ${\overline{a}}_j$ represent the endpoint values of the IT2FSs, which meet these conditions:$i=\left\{1,2,3,4\right\}$,$j=\left\{1,2,3,4\right\}$,$0⩽{\overline{a}}_1⩽{\overline{a}}_2⩽{\overline{a}}_3⩽{\overline{a}}_4⩽1$,$0⩽\underset{\_}{h}\left(\stackrel{\sim }{A}\right)⩽\overline{h}\left(\stackrel{\sim }{A}\right)⩽1$,$\text{0}⩽{\underset{\_}{a}}_1⩽{\underset{\_}{a}}_2⩽{\underset{\_}{a}}_3⩽{\underset{\_}{a}}_4⩽1$,${\underset{\_}{a}}_i⩽{\overline{a}}_i$.

${\underset{\_}{u}}_i$ and ${\overline{u}}_i$ respectively represent the lower membership function and the upper membership function in the interval trapezoidal type-2 fuzzy sets, which can be expressed in the following:

$${\underset{\_}{u}}_i=\left\{\begin{array}{c}\underset{\_}{h}\left(\stackrel{\sim }{A}\right)·\left(x-{\underset{\_}{a}}_1\right)/\left({\underset{\_}{a}}_2-{\underset{\_}{a}}_1\right),{\underset{\_}{a}}_1⩽x<{\underset{\_}{\mathrm{a}}}_2\\ \underset{\_}{h}\left(\stackrel{\sim }{A}\right),{\underset{\_}{a}}_2⩽x<{\underset{\_}{\mathrm{a}}}_3\\ -\underset{\_}{h}\left(\stackrel{\sim }{A}\right)·\left(x-{\underset{\_}{a}}_3\right)/\left({\underset{\_}{a}}_4-{\underset{\_}{a}}_3\right),{\underset{\_}{a}}_3⩽x⩽{\underset{\_}{a}}_4\\ 0,otherwise\end{array}\right)$$

$${\overline{u}}_i=\left\{\begin{array}{c}\overline{h}\left(\stackrel{\sim }{A}\right)·\left(x-{\overline{a}}_1\right)/\left({\overline{a}}_2-{\overline{a}}_1\right),{\overline{a}}_1⩽x<{\overline{\mathrm{a}}}_2\\ \overline{h}\left(\stackrel{\sim }{A}\right),{\overline{a}}_2⩽x<{\overline{\mathrm{a}}}_3\\ -\overline{h}\left(\stackrel{\sim }{A}\right)·\left(x-{\overline{a}}_3\right)/\left({\overline{a}}_4-{\overline{a}}_3\right),{\overline{a}}_3⩽x⩽{\overline{a}}_4\\ 0,otherwise\end{array}\right)$$

The operation rules of trapezoidal IT2FSs are as follows:

• (1)
  $$\stackrel{\sim }{A_1}\oplus \stackrel{\sim }{A_2}=\left(\begin{array}{c}\left({\underset{\_}{a}}_{11}+{\underset{\_}{a}}_{21},{\underset{\_}{a}}_{12}+{\underset{\_}{a}}_{22},{\underset{\_}{a}}_{13}+{\underset{\_}{a}}_{23},{\underset{\_}{a}}_{14}+{\underset{\_}{a}}_{24};\min \left(\underset{\_}{h}\left({\stackrel{\sim }{A}}_1\right),\underset{\_}{h}\left({\stackrel{\sim }{A}}_2\right)\right)\right),\\ \left({\overline{a}}_{11}+{\overline{a}}_{21},{\overline{a}}_{12}+{\overline{a}}_{22},{\overline{a}}_{13}+{\overline{a}}_{23},{\overline{a}}_{14}+{\overline{a}}_{24};\min \left(\overline{h}\left({\stackrel{\sim }{A}}_1\right),\overline{h}\left({\stackrel{\sim }{A}}_2\right)\right)\right)\end{array}\right)$$
• (2)
  $$\stackrel{\sim }{A_1}\otimes \stackrel{\sim }{A_2}=\left(\begin{array}{c}\left({\underset{\_}{a}}_{11}{\underset{\_}{a}}_{21},{\underset{\_}{a}}_{12}{\underset{\_}{a}}_{22},{\underset{\_}{a}}_{13}{\underset{\_}{a}}_{23},{\underset{\_}{a}}_{14}{\underset{\_}{a}}_{24};\min \left(\underset{\_}{h}\left({\stackrel{\sim }{A}}_1\right),\underset{\_}{h}\left({\stackrel{\sim }{A}}_2\right)\right)\right),\\ \left({\overline{a}}_{11}{\overline{a}}_{21},{\overline{a}}_{12}{\overline{a}}_{22},{\overline{a}}_{13}{\overline{a}}_{23},{\overline{a}}_{14}{\overline{a}}_{24};\min \left(\overline{h}\left({\stackrel{\sim }{A}}_1\right),\overline{h}\left({\stackrel{\sim }{A}}_2\right)\right)\right)\end{array}\right)$$
• (3)
  $$\kappa \stackrel{\sim }{A_1}=\left(\left(\kappa {\underset{\_}{a}}_{11},\kappa {\underset{\_}{a}}_{12},\kappa {\underset{\_}{a}}_{13},\kappa {\underset{\_}{a}}_{14};\underset{\_}{h}\left({\stackrel{\sim }{A}}_1\right)\right),\left(\kappa {\overline{a}}_{11},\kappa {\overline{a}}_{12},\kappa {\overline{a}}_{13},\kappa {\overline{a}}_{14};\overline{h}\left({\stackrel{\sim }{A}}_1\right)\right)\right)$$
• (4)
  $$\begin{array}{c}{\left(\stackrel{\sim }{A_1}\right)}^{\kappa }=\\ \left(\left({\left({\underset{\_}{a}}_{11}\right)}^{\kappa },{\left({\underset{\_}{a}}_{1\text{2}}\right)}^{\kappa },{\left({\underset{\_}{a}}_{1\text{3}}\right)}^{\kappa },{\left({\underset{\_}{a}}_{1\text{4}}\right)}^{\kappa };\underset{\_}{h}\left({\stackrel{\sim }{A}}_1\right)\right),\left({\left({\overline{a}}_{11}\right)}^{\kappa },{\left({\overline{a}}_{12}\right)}^{\kappa },{\left({\overline{a}}_{13}\right)}^{\kappa },{\left({\overline{a}}_{14}\right)}^{\kappa };\overline{h}\left({\stackrel{\sim }{A}}_1\right)\right)\right)\end{array}$$

We give the arithmetic average ranking operator of interval trapezoidal fuzzy sets (Chen, 2013, Qin et al., 2017), which can be used to calculate each scenario:

$$R\left(\stackrel{\sim }{A_1}\right)=\left({\underset{\_}{a}}_1+{\underset{\_}{a}}_4/2+\underset{\_}{h}\left(\stackrel{\sim }{A}\right)+\overline{h}\left(\stackrel{\sim }{A}\right)/2\right)\times \sum _{i=1}^4\left({\underset{\_}{a}}_i\text{+}{\overline{a}}_i\right)/8$$ (1)

$$\begin{array}{c}\mathit{if}R\left(\stackrel{\sim }{A_1}\right)>\mathrm{R}\left(\stackrel{\sim }{{\mathrm{A}}_2}\right),\mathrm{then}\stackrel{\sim }{{\mathrm{A}}_1}\succ \stackrel{\sim }{{\mathrm{A}}_2}\\ ifR\left(\stackrel{\sim }{A_1}\right)=\mathrm{R}\left(\stackrel{\sim }{{\mathrm{A}}_2}\right),\mathrm{then}\stackrel{\sim }{{\mathrm{A}}_1}\sim \stackrel{\sim }{{\mathrm{A}}_2}\\ ifR\left(\stackrel{\sim }{A_1}\right)<\mathrm{R}\left(\stackrel{\sim }{{\mathrm{A}}_2}\right),\mathrm{then}\stackrel{\sim }{{\mathrm{A}}_1}\prec \stackrel{\sim }{{\mathrm{A}}_2}\end{array}$$

The distance between two alternatives A₁ and A₂ of interval trapezoidal fuzzy sets (Chen, 2013) is given:

$$\begin{array}{c}d\left(A_1,A_2\right)=1/8\times \text{|}\left({\overline{a}}_{21}-{\overline{a}}_{11}+{\overline{a}}_{22}-{\overline{a}}_{12}+{\overline{a}}_{23}-{\overline{a}}_{13}+{\overline{a}}_{24}-{\overline{a}}_{14}\right)+4\left({\underset{\_}{a}}_{11}-{\underset{\_}{a}}_{21}\right)\\ +2\left({\underset{\_}{a}}_{12}-{\underset{\_}{a}}_{22}\right)+2\left({\underset{\_}{a}}_{13}-{\underset{\_}{a}}_{23}\right)+4\left({\underset{\_}{a}}_{14}-{\underset{\_}{a}}_{24}\right)+3\left({\underset{\_}{a}}_{12}+{\underset{\_}{a}}_{13}-{\underset{\_}{a}}_{11}-{\underset{\_}{a}}_{14}\right)\times \overline{h}\left({\stackrel{\sim }{A}}_1\right)/\underset{\_}{h}\left({\stackrel{\sim }{A}}_1\right)\\ -3\left({\underset{\_}{a}}_{22}+{\underset{\_}{a}}_{23}-{\underset{\_}{a}}_{21}-{\underset{\_}{a}}_{24}\right)\times \overline{h}\left({\stackrel{\sim }{A}}_2\right)/\underset{\_}{h}\left({\stackrel{\sim }{A}}_2\right)\end{array}$$ (2)

Definition 3 (Chen, 2013; Mendel et al., 2006; Wu et al., 2019) —

: Comprehensive Score Function.

Combined with the characteristics of equations (1) ∼ (2), the mixing distance between alternatives A₁ and A₂ for each criterion is obtained, where β is the threshold of the comprehensive score function:

$$\text{Z}\left({\stackrel{\sim }{A}}_{m_1{m}_2}^{n_1}\right)=\left(\beta /M\right)\times \left|\text{R}\left({\stackrel{\sim }{A}}_{m_1{n}_1}\right)\text{- R}\left({\stackrel{\sim }{A}}_{m_2{n}_1}\right)\right|+\left(1-\beta \right)/M\times d\left({\stackrel{\sim }{A}}_{m_1{m}_2}^{n_1}\right)$$ (3)

Taking the score function of the alternative evaluation value itself and the symbolic distance between the two alternatives into consideration, combined with equation (3), we calculate the comprehensive score function of each alternative of IT2FSs as follows:

$$\overline{\text{Z}}\left({\stackrel{\sim }{A}}_{n_1}\right)=\sum _{m_1=1}^M\sum _{m_2=1}^M\text{Z}\left({\stackrel{\sim }{A}}_{m_1{m}_2}^{n_1}\right)$$ (4)

3.2. Interpretation structure model

The interpretation structure model (ISM) analyzes the relationships between metrics by decomposing them into different levels (Kannan, Pokharel, & Sasi Kumar, 2009). Through a series of matrix operations to obtain the hierarchy of the criteria, we analyze the DMs to assess whether there is influence among the criteria (Beikkhakhian et al., 2015). For the criteria interaction matrix $E=\left(\begin{array}{cccc}{E}_{11}& E_{12}& \cdots & E_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ E_{n1}& E_{n2}& \cdots & E_{\mathit{nn}}\end{array}\right)$, ${\text{E}}_{n_1{n}_2}\in \left\{O,D,I\right\}$, D indicates that there is a direct effect for alternative n₁ on the alternative n₂, I indicates that there is an indirect effect for alternative n₁ on the alternative n₂, O indicates that there is not a direct or indirect effect for alternative n₁ on the alternative n₂.

Definition 4 (Kannan et al., 2009) —

: Adjacency Matrix.

DMs, whose amount is P, jointly judge whether there is influence among N criteria in obtaining the criteria interaction matrix E, and then the adjacency matrix Y is given, where ${\text{y}}_{n_1{n}_2}\in \left\{0,1\right\}$:

$$Y=\left(\begin{array}{cccc}{y}_{11}& y_{12}& \cdots & y_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ y_{n1}& y_{n2}& \cdots & y_{\mathit{nn}}\end{array}\right)$$

$$\begin{array}{c}{\text{if E}}_{n_1{n}_2}\in \left\{D,I\right\},\text{then}{y}_{n_1{n}_2}=1\\ i{\text{f E}}_{n_1{n}_2}=O,\text{then}{y}_{n_1{n}_2}=0\end{array}$$

If ${\text{y}}_{n_1{n}_2}=0$, there is no obvious effect on N₂ for N₁. Otherwise, there is an obvious effect on N₂ to a certain extent for N₁. The reachable matrix is calculated in light of the Boolean algebraic rule: ${\left(Y+I\right)}^2=I+Y+Y^2$. Then, through the same calculation procedure we can obtain the equation ${\left(Y+I\right)}^k=I+Y+Y^2+\dots +Y^k$, where I represent the identity matrix.

Definition 5 (Kannan et al., 2009) —

: Reachable Matrix.

When equation (5) is satisfied, the reachable matrix V is obtained, where$v_{\mathit{ij}}\in \left\{0,1\right\}$.

$$V=\left(\begin{array}{cccc}{v}_{11}& v_{12}& \cdots & v_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ v_{n1}& v_{n2}& \cdots & v_{\mathit{nn}}\end{array}\right)$$

$${\left(Y+I\right)}^{k\text{- 1}}\ne {\left(Y+I\right)}^k\text{=}{\left(Y+I\right)}^{k+\text{1}}=V$$ (5)

In the reachable matrix, starting from alternative N₁, the set composed of reachable criteria is the reachable set of alternative N₁. The set composed of criteria that can correspond to reach alternative N₁ is the antecedent set of genus N₁, and the reachable set and antecedent set of each criterion is obtained respectively. The intersection of the reachable set and antecedent set is the joint set. If the joint set and reachable set are consistent, this alternative is determined as the first level. Then remove criteria of this level from the original matrix, with the same comparison get the second level alternative, until all the criteria are divided into different levels. The connection diagram represents the interaction relationship between the criteria.

3.3. Cosine Similarity

The initial assessment in the MCGDM method needs to be weighted by a suitable weighting method. Hence, we use a cosine similarity model to weigh the model to consider consensus among DMs. Existing similarity measures include Dice's measure, Jaccard's measure, cosine similarity, Pearson's correlation coefficient (Chiclana, Tapia García, del Moral, & Herrera-Viedma, 2013).

The greater the consensus and the deeper the interaction among DMs, the closer their perceptions of things and the more similar the evaluation information is (Shishavan et al., 2020). Few scholars have applied the cosine similarity method to the IT2FSs. We use cosine similarity to determine the weight of DMs, and the resemblance is used to modify the objective weight of the criteria.

Definition 6 (Simon, 1976) —

: Cosine Similarity.

DMs, whose quantity is P, evaluation N criteria of M alternatives, and Cosine Similarity is expressed as follows:

$$\text{Cos}\left({\stackrel{\sim }{A}}_{\mathit{lmn}},{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right)={\stackrel{\sim }{A}}_{\mathit{lmn}}·{\stackrel{\sim }{A}}_{\mathit{Lmn}}/\left(\left|{\stackrel{\sim }{A}}_{\mathit{lmn}}\right|·\left|{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right|\right)$$ (6)

where $1⩽l⩽P$ ,$1⩽L⩽P$,${\stackrel{\sim }{A}}_l=\left[\left({\underset{\_}{a}}_{1l},{\underset{\_}{a}}_{2l},{\underset{\_}{a}}_{3l},{\underset{\_}{a}}_{4l},\underset{\_}{h}\left(\stackrel{\sim }{A_l}\right)\right),\left({\overline{a}}_{1l},{\overline{a}}_{2l},{\overline{a}}_{3l},{\overline{a}}_{4l},\overline{h}\left(\stackrel{\sim }{A_l}\right)\right)\right]$, and ${\stackrel{\sim }{A}}_L=\left[\left({\underset{\_}{a}}_{1L},{\underset{\_}{a}}_{2L},{\underset{\_}{a}}_{3L},{\underset{\_}{a}}_{4L},\underset{\_}{h}\left(\stackrel{\sim }{A_L}\right)\right),\left({\overline{a}}_{1L},{\overline{a}}_{2L},{\overline{a}}_{3L},{\overline{a}}_{4L},\overline{h}\left(\stackrel{\sim }{A_L}\right)\right)\right]$ represents the scores of DM l and DM L on the alternative m and the criteria n respectively, and they satisfy the following equations:

$${\stackrel{\sim }{A}}_l·{\stackrel{\sim }{A}}_L=\left(\underset{\_}{h}\left({\stackrel{\sim }{A}}_l\right)·\underset{\_}{h}\left({\stackrel{\sim }{A}}_L\right)+\overline{h}\left({\stackrel{\sim }{A}}_l\right)·\overline{h}\left({\stackrel{\sim }{A}}_L\right)\right)\times \left(\sum _{i=1}^4{\underset{\_}{a}}_{\mathit{il}}·{\underset{\_}{a}}_{\mathit{iL}}+\sum _{i=1}^4{\overline{a}}_{\mathit{il}}·{\overline{a}}_{\mathit{iL}}\right)$$ (7)

$$\left|{\stackrel{\sim }{A}}_l\right|=\sqrt{\left({\left(\underset{\_}{h}\left({\stackrel{\sim }{A}}_l\right)\right)}^2+{\left(\overline{h}\left({\stackrel{\sim }{A}}_l\right)\right)}^2\right)\times \left(\sum _{i=1}^4{\left({\underset{\_}{a}}_{\mathit{il}}\right)}^2+\sum _{i=1}^4{\left({\overline{a}}_{\mathit{il}}\right)}^2\right)}$$ (8)

$$\left|{\stackrel{\sim }{A}}_L\right|=\sqrt{\left({\left(\underset{\_}{h}\left({\stackrel{\sim }{A}}_L\right)\right)}^2+{\left(\overline{h}\left({\stackrel{\sim }{A}}_L\right)\right)}^2\right)\times \left(\sum _{i=1}^4{\left({\underset{\_}{a}}_{\mathit{iL}}\right)}^2+\sum _{i=1}^4{\left({\overline{a}}_{\mathit{iL}}\right)}^2\right)}$$ (9)

Cosine Similarity between DM l and DM L is calculated according to the following equation, which is calculated by equations (6) ∼ (9):

$$\sum _{m=1}^M\sum _{n=1}^N\text{Cos}\left({\stackrel{\sim }{A}}_{\mathit{lmn}},{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right)=\sum _{m=1}^M\sum _{n=1}^N{\stackrel{\sim }{A}}_{\mathit{lmn}}·{\stackrel{\sim }{A}}_{\mathit{Lmn}}/\left(\left|{\stackrel{\sim }{A}}_{\mathit{lmn}}\right|·\left|{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right|\right)$$ (10)

Cosine Similarity of DM l relative to other $\left(P-1\right)$ DMs is calculated as follows:

$$\sum _{L=1}^P\sum _{m=1}^M\sum _{n=1}^N\text{Cos}\left({\stackrel{\sim }{A}}_{\mathit{lmn}},{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right)=\sum _{\text{L = 1}}^P\sum _{m=1}^M\sum _{n=1}^N{\stackrel{\sim }{A}}_{\mathit{lmn}}·{\stackrel{\sim }{A}}_{\mathit{Lmn}}/\left(\left|{\stackrel{\sim }{A}}_{\mathit{lmn}}\right|·\left|{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right|\right)$$ (11)

If the correlation between a DM and others is higher, the relative importance of this DM is greater. Therefore, the weight of DM l is calculated as follows:

$${\omega }_l=\sum _{L=1}^P\sum _{m=1}^M\sum _{n=1}^N\text{Cos}\left({\stackrel{\sim }{A}}_{\mathit{lmn}},{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right)/\sum _{l=1}^P\sum _{L=1}^P\sum _{m=1}^M\sum _{n=1}^N\text{Cos}\left({\stackrel{\sim }{A}}_{\mathit{lmn}},{\stackrel{\sim }{A}}_{\mathit{Lmn}}\right)$$ (12)

4. The evaluation criteria of emergency medical supplier

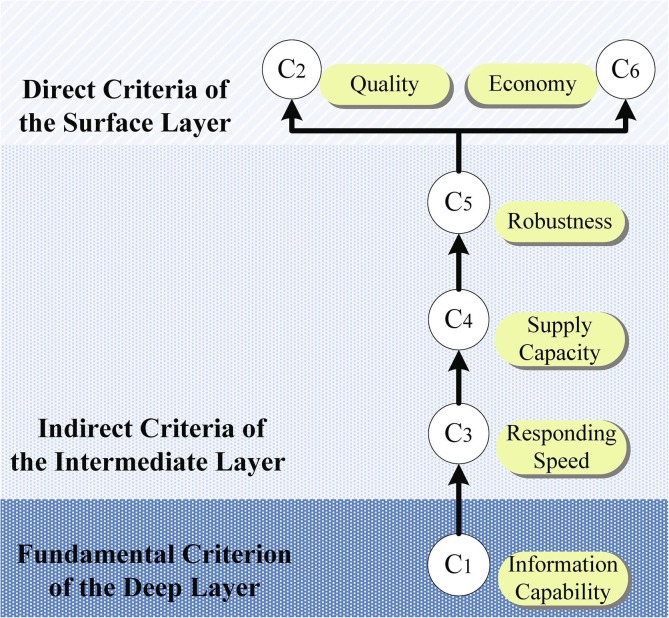
We analyze the selection of emergency medical supplier by six criteria, which are information capability (C₁), quality (C₂), response speed (C₃), supply capacity (C₄), robustness (C₅), and economy (C₆). Note that these criteria are all efficiency criteria, in which the higher the evaluation value, the better the alternative.

4.1. Information capabilities

Information capability is a highly aggregated criterion that includes the number of information platforms available to providers and their combined data processing capabilities. Information technology can be used to improve diagnostic accuracy, better ensure the safety of healthcare providers, reduce workload, save time and costs, and develop medical supplies (Tversky, 1979). Asadzadeh, Pakkhoo, Saeidabad, Khezri, and Ferdousi (2020) noted that information capabilities are expect to play an essential role in the recovery phase of COVID-19. In addition, several IT tools can save large numbers of staff, target emergency medical providers for rapid action, and conduct risk assessments (Chen et al., 2021).

The existence of information processing information capability allows better development of production options, emergency response options, information integration, and collaboration with other partners in the supply chain. In the era of big data, information capability is certainly one of the critical evaluation criteria for emergency medical supplier.

4.2. Quality

Quality is a fundamental requirement for supplies and is one of the necessary criteria for judging supplier. Vermuyten et al. (2018) examined in detail the importance of quality in emergency solution selection. For achieving emergency response efficiency, it is important to ensure adequate and even higher quality (Higgins et al., 2014). Several scholars also pointed out (Chen, 2013, Rawls and Turnquist, 2010, Zhou and Olsen, 2017) that when analyzing the quality criteria of emergency rescue medical supplier, there are mainly two aspects: the quality of production facilities and the quality of materials.

4.3. Response speed

Due to the devastating and unpredictable nature of an emergency, timely responses can effectively reduce adverse impacts and other economic losses (Aghajani et al., 2020, Zhou and Olsen, 2017). Supplier with emergency response experience tend to be able to expedite production and prepare accordingly promptly. If an emergency response supplier has sufficient emergency response experience, they can often respond better (Chen et al., 2021). Hence, response speed is one of the essential evaluation criteria, and it is influenced to some extent by emergency experience.

In a review of the available literature, the response speed is often difficult to determine because it is influenced by emergency experience, geographic location, production capacity, and storage capacity. Therefore, a subjective evaluation by DMs in different fields is necessary.

4.4. Supply capacity

Supply capacity includes production capacity and inventory capacity. High production capacity and inventory capacity can help supplier provide goods quickly in an emergency. The response speed is also an aspect to reflect supply capacity, which is also affected by production capacity and inventory capacity to a certain extent (Higgins et al., 2014). Supply capacity is a partially quantifiable criterion (Rawls and Turnquist, 2010, Xiang, 2020). However, relative supply capacity is more valuable than absolute supply capacity. For instance, several supplier have large production capacity, but their inventory capacity is insufficient, or they need to supply to multiple locations simultaneously. Then the relative supply capacity is less than the average level to some extent.

4.5. Robustness

Robustness means being solid and strong, that the ability of the system to survive in abnormal and dangerous situations (Lu, Shi, & Huang, 2018). It is a dimension that must be involved in analyzing emergencies, and is determined by the nature of the emergencies. Ji and Zhu (2012) pointed out that it is necessary to make pre-positioning decisions before the occurrence of disasters under the condition of high uncertainty and limited distribution information. Similarly, only by pre-deploying emergency supplies in advance can we achieve better stability and robustness.

The higher the robustness of a supplier, the greater the degree to which it can reduce the level of disruption caused by unexpected events and maintains daily production operations (Kaur & Singh, 2021).

4.6. Economy

The economic dimension is a highly complex criterion that can be evaluated with a high degree of variability by DMs in different fields. While the focus of analysis for contingent supplier differs from that of traditional retail supplier, it is also necessary to analyze costs. Production costs, transportation costs, and inventory management costs affect the price of materials and the overall decision (Zhou et al., 2011). Meanwhile, we need to be aware of the cost of any agreement. Since emergencies are usually unforeseen, having a contract with a supplier can help DMs to react faster. Further, transaction costs involve economic criteria (Ahmad et al., 2021). In addition, the quantity of inventory, the percentage of subsequent supplies, and the timeliness of collection all affect the economy’s effectiveness.

Economic criteria include quantifiable data, but they involve many aspects and are difficult to analyze from a complete perspective. Therefore, a comprehensive analysis of the relationship between actual economic effects and theoretical economic impacts can restore the essential economic utility of each alternative to some extent.

5. The proposed methodology

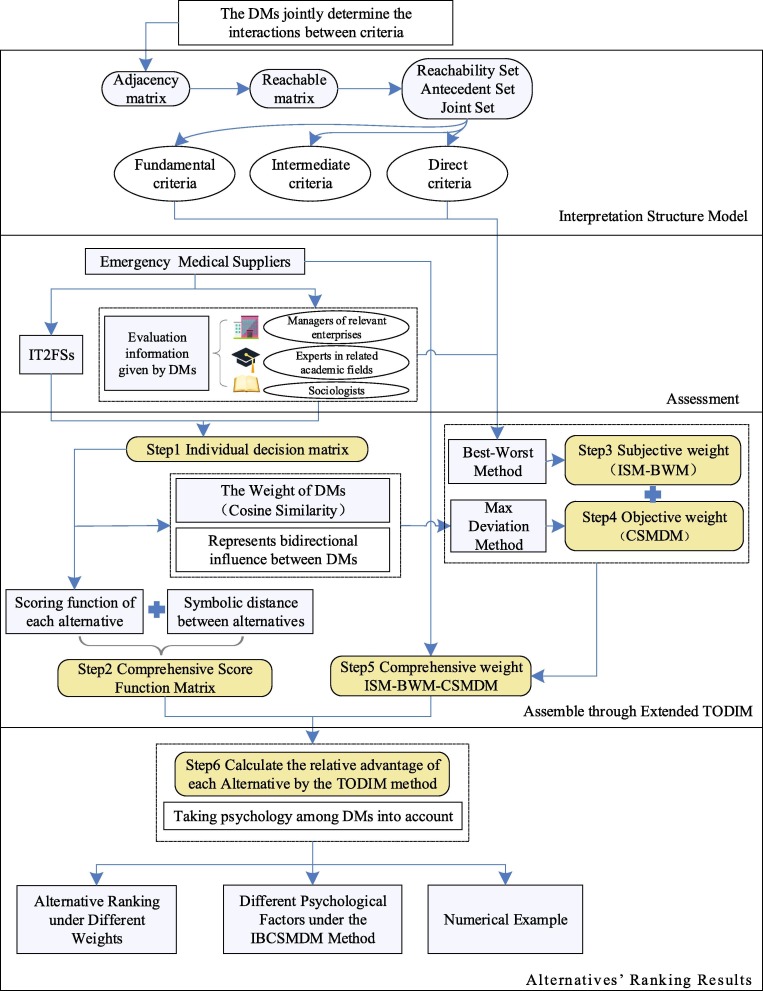
As shows in Table 1 and Table 2, no research has used fuzzy-2 sets and TODIM for supplier selection in the emergency medical field. Moreover, many new methods such as BWM have unique characteristics, which have attracted the attention of many researchers in recent years (Ahmad et al., 2021). We seriously consider some new methods and new theories, trying to solve classical and important emergency problems with new combinatorial methods. Differing from the traditional type-1fuzzy sets, the fuzzy sets in this paper consider the primary affiliation and the secondary affiliation. Uncertain information can be described more comprehensively by re-describing the fuzzy degree of membership or fuzzing the membership degree. However, the type-2 fuzzy set is too abstract and complex, and the excessive amount of computation limits its specific application in practical situations. Therefore, several scholars proposed the concept of IT2FSs. The secondary membership function is defined as the number 1. It considers the complexity of the decision environment and also dramatically reduces the complexity of fuzzy calculation. Considering that there are many criteria to be considered in the actual decision-making environment and there are complex interaction relations among the criteria, we describe the DMs’ assessment with the IT2FSs number. For emergency relief medical supplier, the assessment by the three types of DMs, managers in relevant enterprises, DMs in relative academic fields and sociologists, is converted into the corresponding IT2FSs number. After the fuzzy number is obtained, we aggregate the IT2FSss in light of the different weights of DMs and criteria to get the comprehensive score function.

The conceptual framework of the proposed methodology is shown in Fig. 2 :

Fig. 2.

Conceptual Framework of the Research Methodology.

The notations utilized in this paper are listed in Table 3 .

Table 3.

Definitions of the Notations in This Paper.

Notations	Definitions
$x$	The universe of values of $\stackrel{\sim }{A}$ set
$u$	On the degree to which any element $x$ on the domain $X$ belongs to the $\stackrel{\sim }{A}$ set
$\alpha$	The threshold for the combination of subjective weight and objective weight
$\beta$	Threshold combining score function and symbol distance threshold
${\mu }_{\stackrel{\sim }{A}}\left(x,u\right)$	Membership of $u$ set
$P$	Number of decisions
$M$	Number of alternatives
$N$	Number of criteria
$D$	Criteria have a direct effect on another criterion
$I$	Criteria have an indirect effect on another criterion
$O$	The criteria have no direct or indirect influence on another criterion
$\stackrel{\sim }{B}$	Type-2 fuzzy sets
$\stackrel{\sim }{A}$	IT2FSs Assessment
$A_B$	The weight matrix of other criteria relative to the optimal criteria
$A_W$	Weight matrix of other criteria relative to the worst criteria
$E$	Criteria interaction matrix
$Y$	Adjacency Matrix
$V$	Reachable matrix
$\underset{\_}{R}$	Decision Matrix
$\overline{R}$	The score function is calculated to get the matrix
$\overline{\overline{R}}$	The score function and sign distance are calculated to get a matrix
$R\left(A_i\right)$	Average sort function
$d$	Symbol distance
$Z$	Comprehensive distance between the two solutions
$\overline{Z}$	Comprehensive score function of the criteria
${\omega }_l$	weight of DMs
${\omega }^B$	The best subjective weight set determined by the BWM method
$\mathit{CR}$	Consistency test value of subjective weight
${\omega }^{\mathit{IB}}$	The best subjective weight set determined by the ISM-BWM method
${\omega }_D$	Weights determined by the maximum deviation method
${\omega }_{\mathit{nr}}$	The relative weight of alternative n to alternative r
${\zeta }_m$	The total value of alternative m
${\varphi }_{\mathit{me}}^n$	The relative dominance of alternative m to alternative e on the nth criteria
${\phi }_{\mathit{me}}$	Relative dominance of alternative m over alternative e
${\omega }^D$	Weights determined by the maximum deviation method
${\omega }^o$	Objective weight determined by CSMDM
${\omega }_n$	Comprehensive weight of the nth criteria
$\xi$	Consistency test number in BWM method

5.1. Establishing the individual decision matrix base on IT2FSs

We determine the individual decision matrix ${\underset{\_}{R}}^l$ to P DMs' inflected terms, where $l\in \left\{1,2,\dots ,P\right\}$, M represents the number of alternatives, N represents the number of criteria, and P represents the number of DMs.

$${\underset{\_}{R}}^l=\left(\begin{array}{cccc}{\stackrel{\sim }{A}}_{11}& {\stackrel{\sim }{A}}_{12}& \cdots & {\stackrel{\sim }{A}}_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{A}}_{m1}& {\stackrel{\sim }{A}}_{m2}& \cdots & {\stackrel{\sim }{A}}_{\mathit{mn}}\end{array}\right)$$

5.2. Determining the comprehensive score matrix

According to equation (1) and definition 1 ∼ 2, ${\underset{\_}{R}}^l$ is calculated to obtain the score matrix of P IT2FSs. The score matrix of the DM l is as follows:

$${\overline{R}}^l=\left(\begin{array}{cccc}R\left({\stackrel{\sim }{A}}_{11}\right)& R\left({\stackrel{\sim }{A}}_{12}\right)& \cdots & R\left({\stackrel{\sim }{A}}_{1n}\right)\\ ⋮& ⋮& \ddots & ⋮\\ R\left({\stackrel{\sim }{A}}_{m1}\right)& R\left({\stackrel{\sim }{A}}_{m2}\right)& \cdots & R\left({\stackrel{\sim }{A}}_{\mathit{mn}}\right)\end{array}\right)$$

Then according to Eqs. (2), (3) and definition 3, combined with the symbolic distance, the comprehensive score matrix ${\overline{\overline{R}}}^l$ of all DMs is obtained by the novel aggregation method:

$${\overline{\overline{R}}}^l=\left(\begin{array}{cccc}\text{Z}\left({\stackrel{\sim }{A}}_{11}\right)& Z\left({\stackrel{\sim }{A}}_{12}\right)& \cdots & Z\left({\stackrel{\sim }{A}}_{1n}\right)\\ ⋮& ⋮& \ddots & ⋮\\ Z\left({\stackrel{\sim }{A}}_{m1}\right)& Z\left({\stackrel{\sim }{A}}_{m2}\right)& \cdots & Z\left({\stackrel{\sim }{A}}_{\mathit{mn}}\right)\end{array}\right)$$

5.3. Determine the criteria weights with the IBCSMDM method

Step1: Determine the subjective weight through the ISM-BWM.

The BWM method makes a pairwise comparison between the selected optimal alternative and other criteria, and indicates the importance degree of the optimal alternative relative to other criteria, with numbers from 1 to 9 (Liu et al., 2020). For the traditional BWM method, the DM directly defines the optimal alternative and the worst alternative and constructs two sets of comparison vectors, one of which is used to represent the importance degree of the optimal alternative relative to other criteria, to obtain the weight matrix AB: $A_B=\left(a_{B1},a_{B2},\cdots ,a_{\mathit{BN}}\right)$. Similarly, the weight matrix of other criteria relative to the worst criteria is obtained AW: $A_W={\left(a_{1W},a_{2W},\cdots ,a_{\mathit{NW}}\right)}^T$.

The optimal alternative weight set satisfies the minimization of the maximum absolute difference: $\left\{\left|{\omega }_B-a_{\mathit{Bn}}{\omega }_n\right|,\left|{\omega }_n-a_{\mathit{nW}}{\omega }_W\right|\right\}$, the sum of weights is 1, and the ownership weight is non-negative, which is calculated as follows:

$$\begin{array}{c}\min \xi \\ s.t.\left|{\omega }_n{a}_{\mathit{Bn}}-{\omega }_B\right|⩽\xi \\ \left|{\omega }_n{a}_{\mathit{nW}}-{\omega }_W\right|⩽\xi \\ \sum _{n=1}^N{\omega }_n=1\\ {\omega }_n⩾0\end{array}$$ (13)

The optimal set of subjective weights ${\omega }^B=\left({\omega }_1^B,{\omega }_2^B,\cdots {\omega }_N^B\right)$ is obtained. After the subjective weight is obtained, a consistency test is carried out via the following equation:

$$\mathit{CR}=\xi /\mathit{CI}$$ (14)

The relation between the value of CI in the equation (14) and the number of criteria is as in Table 4 :

Table 4.

CI-Value.

Number Criteria	1	2	3	4	5	6	7	8	9
CI	0.00	0.44	1.00	1.63	2.30	3.00	3.73	4.47	5.23

However, in the first step of the traditional BWM method, the best and worst criteria are directly specified by the DM, leading to serious subjectivity. Therefore, an extended subjective weighting method that consideres the bidirectional influence relation among criteria is presented in our paper.

In the existing literature, the ISM model is usually regarded as the first stage of the two-stage model, which is difficult to be well associated with alternative sequencing (Tseng, Lim, & Wu, 2019); we use the ISM method to modify the BWM method, to reduce the deviation caused by subjective scoring. The fundamental and surface criteria obtained from the alternative hierarchy of the ISM model are the most important and least important criteria of the traditional BWM method. Suppose there are multiple fundamental or surface criteria, then, the DMs can choose the criteria at the same level in light of the specific situation and select only the optimal and the worst criteria.

DMs jointly determine the alternative interaction matrix, and stratify the evaluation criteria according to equations (13) ∼ (14) to get the best and worst criteria. Subjective weights are determined through equations (5), (13) ∼ (14):${\omega }^{\mathit{IB}}\text{=}\left({\omega }_1^{\mathit{IB}},{\omega }_2^{\mathit{IB}},\cdots {\omega }_N^{\mathit{IB}}\right)$.

Step2: Determine the objective weight through CSMDM.

Through equations (6) ∼ (12), combined with the characteristics of IT2FSs assessment, the objective weight ${\omega }_n$ of IT2FSs-Max Deviation Method are obtained (Wu et al., 2021):

$${\omega }_{n_1}=\text{Z}\left({\stackrel{\sim }{A}}_{n_1}\right)/\sum _{n_1\text{=}1}^N\text{Z}\left({\stackrel{\sim }{A}}_{n_1}\right)$$ (15)

The DM's weight is used to modify the maximum deviation method to obtain the objective weight. This weighting method takes the interrelationship among DMs and also reduces the excessive subjectivity of the weight into account as far as possible.

The evaluation value of the alternative has little difference among all the alternatives, and the alternative only plays a small role in the selection and comparison of the alternatives, so the evaluation alternative should be given a small weight. The fundamental idea of the maximum deviation method is introduced above. On the contrary, the greater the deviation of the alternative criteria values, the greater the weight. Weight is determined by the degree of difference, which can be used as the objective weight to weigh the alternative more reasonably. For M alternatives and N evaluation criteria, the difference between alternative M₁ and other samples is the deviation of M₁, where n represents the criteria n, where$m_1,m_2\in \left\{1,2,\dots ,M\right\}$,$n\in \left\{1,2,\dots ,N\right\}$, ${\omega }_D$ represents the weight determined by the maximum deviation method, and can be determined by the following equation:

$$f_{m_{1}n}\left({\omega }_D\right)=\sum _{n=1}^N\left|X_{m_{1}n}-X_{m_{2}n}\right|$$ (16)

The sum of deviation between the samples and other samples is expressed as follows:

$$f_n\left({\omega }_{\text{D}}\right)=\sum _{m_1=1}^M\sum _{m_2=1}^M\left|X_{m_{1}n}-X_{m_{2}n}\right|$$ (17)

The maximum total deviation can be obtained by calculating the maximum value as follows:

$$\begin{array}{c}\max \sum _{n=1}^N{f}_n\left({\omega }_D\right)=\sum _{n=1}^N\sum _{m_1=1}^M\sum _{m_1=1}^M\left|X_{m_{1}n}{X}_{m_{2}n}\right|\\ s.t.\sum _{n=1}^N{\omega }_{\mathit{Dn}}=1,n⩾0\left(n=1,2,\dots ,N\right)\end{array}$$ (18)

According to equations (16) ∼ (18), the following ${\omega }_n$ can be obtained, and then the optimal solution of weight can be obtained:

$${\omega }_D=\sum _{m_1=1}^M\sum _{m_2=1}^M\left|X_{m_{1}n}{X}_{m_{2}n}\right|/\sum _{n=1}^N\sum _{m_1=1}^M\sum _{m_2=1}^M\left|X_{m_{1}n}{X}_{m_{2}n}\right|$$ (19)

The degree of consensus between DMs is calculated through equation (12), and then cosine similarity (CS) is calculated, and the DMs are weighted. Since the subjective weight has already considered the interaction between criteria, the DM weight only modifies the objective weight to reduce the adverse effects of excessive interaction. The traditional maximum deviation method is modified by the CS of equations (16) ∼ (19).

The Objective weight ${\omega }^O\text{=}\left({\omega }_1^O,{\omega }_2^O,\cdots {\omega }_N^O\right)$ of the maximum deviation method modified by CS is calculated by the following equation:

$${\omega }_n^o={\omega }_l·{\text{Z}}^l\left({\stackrel{\sim }{A}}_n\right)/\sum _{n=1}^N\left({\omega }_l·{\text{Z}}^l\left({\stackrel{\sim }{A}}_n\right)\right)$$ (20)

The maximum deviation method is modified by cosine similarity and is determined by equations (6) ∼ (12), (16) ∼ (19).

Step3: Determine the comprehensive weight.

The subjective weight ${\omega }^{\mathit{IB}}\text{=}\left({\omega }_1^{\mathit{IB}},{\omega }_2^{\mathit{IB}},\cdots {\omega }_N^{\mathit{IB}}\right)$ and objective weight: ${\omega }^O\text{=}\left({\omega }_1^O,{\omega }_2^O,\cdots {\omega }_N^O\right)$ are obtained through equations (15), (20). Hence, the comprehensive weight can be calculated by the following equation:

$${\omega }_n=\alpha {\omega }_n^{\mathit{IB}}+\left(1-\alpha \right){\omega }_n^o$$ (21)

5.4. Ranking the alternatives based on the TODIM method

In the decision-making process, it is gradually noticed that the DMs are not fully rational, but have the characteristics of limited rationality (Simon, 1976), where different judgments can be made based on different psychological states and the degree of risk avoidance. Based on this, Tversky (1979) proposed the prospect theory. Subsequently, Gomes and Lima proposed the TODIM method (Gomes & Lima, 1992), which directly takes other alternatives as the evaluation reference point and simplifies and extends the prospect theory by calculating the perceived superiority of alternatives relative to other alternatives. Scholars have applied the TODIM method in the selection of emergency supplier (Tolga et al., 2020), which is based on prospect theory. This method introduces the attenuation factor θ of the loss, which indicates the psychological behavior of the DMs soon to obtain an equally accurate decision result (Chen, 2013, Qin et al., 2017).

Step1: According to equation (1) and definitions 1 ∼ 2, the score matrix of the IT2FSs evaluation matrix $\overline{R}={\left[x_{\mathit{mn}}\right]}_{M\times N}$ is obtained.

Step2: According to the weight ${\omega }_n$ of N indices, the relative weight ${\omega }_{\mathit{nr}}$ of alternative $C_n$ to $C_r$ is obtained, where${\omega }_{\mathit{nr}}={\omega }_n/{\omega }_r$,${\omega }_r=\max \left\{{\omega }_n\left|n=1,\cdots ,N\right)\right\}$.

Step3: The relative dominance degree ${\varphi }_{\mathit{me}}^n$ of alternative $A_m$ relative to $A_e$ on criterion n is calculated by the following equations:

$${\varphi }_{\mathit{me}}^n=\left\{\begin{array}{c}\sqrt{{\omega }_{\mathit{nr}}\left({\overline{x}}_{\mathit{mn}}-{\overline{x}}_{\mathit{en}}\right)/\sum _{n=1}^N{\omega }_{\mathit{nr}}},{\overline{x}}_{\mathit{mn}}>{\overline{\mathrm{x}}}_{\mathrm{en}}\\ 0{\overline{x}}_{\mathit{mn}}\text{=}{\overline{x}}_{\mathit{en}}\\ -\frac{1}{\theta }\sqrt{\sum _{n=1}^N{\omega }_{\mathit{nr}}\left({\overline{x}}_{\mathit{en}}-{\overline{x}}_{\mathit{mn}}\right)/{\omega }_{\mathit{nr}}},{\overline{x}}_{\mathit{mn}}<{\overline{\mathrm{x}}}_{\mathrm{en}}\end{array}\right)$$ (22)

$${\omega }_{\mathit{nr}}={\omega }_n/{\omega }_r$$ (23)

In light of equations (22) ∼ (23), the relative advantage degree ${\phi }_{\mathit{me}}$ of $A_m$ in equation (24) relative to $A_e$ is calculated, where$m,e\in \left\{1,2,\dots ,M\right\}$,${\omega }_r=\max \left\{{\omega }_n\left|n=1,\cdots ,N\right)\right\}$.

$${\phi }_{\mathit{me}}=\sum _{n=1}^N{\varphi }_{\mathit{me}}^n$$ (24)

where, θ is the attenuation factor of the loss$\left(\theta >0\right)$, which indicates the preference degree of DM to avoid loss. Different values of θ can lead to different value functions. The higher the θ value means the lower the degree of risk avoidance in the decision-making process.

Step4: Calculate the total value of alternative$A_m$.

$${\zeta }_m=\left(\sum _{e=1}^M{\phi }_{\mathit{me}}-{\min }_m\left\{\sum _{e=1}^M{\phi }_{\mathit{me}}\right\}\right)/\left({\max }_m\left\{\sum _{e=1}^M{\phi }_{\mathit{me}}\right\}-{\min }_m\left\{\sum _{e=1}^M{\phi }_{\mathit{me}}\right\}\right)$$ (25)

where $m=1,2,\cdots ,M$.

Step5: Rank each alternative in descending order according to the value of${\zeta }_m$.

The relative dominance degree of alternative n under IT2FSs is obtained, where$\theta >0$,$n,r\in \left\{1,2,\dots ,N\right\}$,${\omega }_r=\max \left\{{\omega }_n\left|n=1,\cdots ,N\right)\right\}$.

$${\varphi }_{\mathit{me}}^n=\left\{\begin{array}{c}\sqrt{{\omega }_{\mathit{nr}}·\overline{\text{Z}}\left({\stackrel{\sim }{A}}_{\mathit{me}}^{n_1}\right)/\sum _{n=1}^N{\omega }_{\mathit{nr}}},{\stackrel{\sim }{A}}_m^n\succ {\stackrel{\sim }{A}}_e^n\\ 0,{\stackrel{\sim }{A}}_m^n\sim {\stackrel{\sim }{A}}_e^n\\ -\frac{1}{\theta }\sqrt{\sum _{n=1}^N{\omega }_{\mathit{nr}}·\overline{\text{Z}}\left({\stackrel{\sim }{A}}_{\mathit{em}}^{n_1}\right)/{\omega }_{\mathit{nr}}},{\stackrel{\sim }{A}}_m^n\prec {\stackrel{\sim }{A}}_e^n\end{array}\right)$$ (26)

Then, the relative advantage ${\zeta }_m$ of IT2FSs is calculated in light of equation (26), and M alternatives are sorted in descending order according to the relative advantage ${\zeta }_m$.

According to DMs' different psychological factors, the ranking of different alternatives is analyzed by changing the risk attenuation factor θ.

5.5. The key procedures of the proposed approach

Step 1: Determine the Individual decision matrix ${\underset{\_}{R}}^1$ from the DMs.

Step 2: Determine the comprehensive score matrix $\overline{\overline{R}}$ by definition 3 and equations (2) ∼ (4).

Step 3: Determine the subjective weight ${\omega }^{\mathit{IB}}$ through the ISM-BWM method by definitions 4 ∼ 6 and equations (13) ∼ (14).

Step 4: Determine the objective weight ${\omega }^o$ through the CSMDM method and equation (15).

Step 5: Determine the combined weight $\omega$ by equation (21).

Step 6: Calculate the relative advantage $\zeta$ of each alternative by equations (22) ∼ (26).

6. A real case study and discussion

6.1. Case description

According to the characteristics of H district in Wuhan, Hubei Province, the extended MCGDM method proposed in this paper is applied to select three major emergency medical supplier in this area. By the end of May 2021, more than 60,000 cases had been confirmed in Hubei province, accounting for about two-thirds of the total number in China. With the increase in the outbreak of established patients in this area, there was a serious shortage of emergency medical supplies (Lo and Guo, 2010, Wan et al., 2021). There are three official emergency medical supplier in the H district regional center, A₁, A₂, and A₃, and cooperation with supply chain partners was proposed to provide rapid emergency response, and played a sizeable cooperative role for many emergency supplier. The cost of A₃ was about 80 percent of the average for the region at this time. A₁, the most extensive emergency supplier, located in the suburbs, provided a large number of emergency supplies, more than 25 percent of the total quantity in this region.

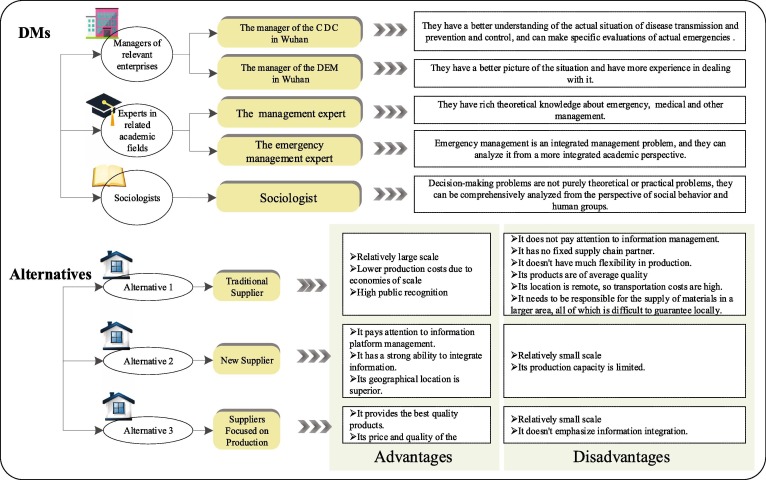
Due to the sudden and devastating nature of the emergency, the CDC needed to select one of the three providers in the region as the emergency medical provider, signing a long-term agreement to provide a certain percentage of emergency medical supplies in case of an outbreak of an emergency. The main advantages, disadvantages, and characteristics of these three supplier show in Fig. 3 .

Fig. 3.

Characteristic of the DMs and Alternatives.

The characteristics of the DMs and their contributions to this analysis process are shown in Fig. 3. These alternatives were sorted in light of the extended TODIM method of the IT2FSs-IBCSMDM method.

In the process of the evaluation and selection of emergency supplier, five DMs, the manager of the Control Disease Center (CDC) in Wuhan, the manager of the Department of Emergency Management (DEM) in Wuhan, the management expert, the expert in emergency management and a sociologist, were invited to evaluate the basic situation of the three emergency supplier and to score the six criteria. Among them, the managers like the CDC and DEM in Wuhan of relevant state enterprises. In contrast, the expert in management and emergency management belong to appropriate academic fields. Together with the sociologist, they could assess with different considerations.

6.2. Calculate the case by IT2FSs-IBCSMDM-TODIM method

In the design of IT2FSs, the following considerations are made: the DMs’ scores generally conform to a normal distribution; however, because the comprehensive ability of alternative alternatives is often better than the regional average, there is a certain degree of negative skewness. Therefore, the subjective definition conditions are as follows:

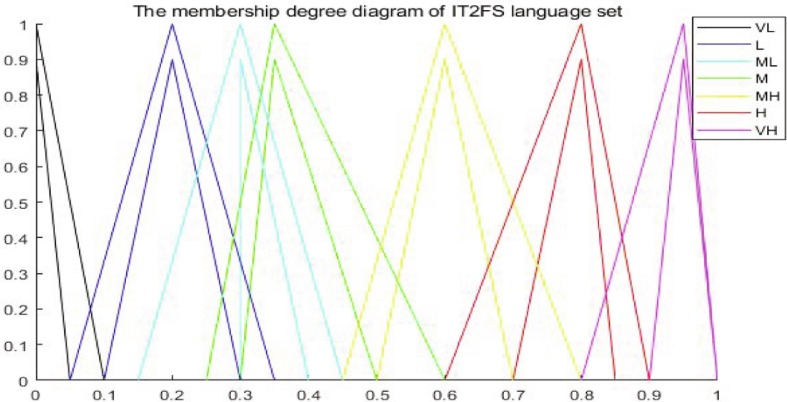
$\forall a\in \left\{{\underset{\_}{a}}_{1L},{\underset{\_}{a}}_{2L},{\underset{\_}{a}}_{3L},{\overline{a}}_{1L},{\overline{a}}_{2L},{\overline{a}}_{3L}\right\}<0.5$, where$\text{L}\in \left\{\mathit{VL},L,ML,M\right\}$. If it is close to the extreme values of the membership degree 0 and 1, the distance between the value endpoints is small. The reasons are as follows: in order to enhance the degree of difference between the evaluation values, while considering the extreme values; if a specific evaluation value is too low, it may bring a more significant adverse impact to the emergency response than the average seven-point point. On the contrary, an extremely high evaluation value can play a more decisive role. Combined with psychological factors such as people's tendency to use the median value in subjective rating and the characteristics of IT2FSs assessments in the existing literature (Ghorabaee, 2016, Kahraman et al., 2014, Qin et al., 2017), the linguistic terms and the corresponding IT2FSs needs are shown in Table 5:

Table 5.

Relation between Linguistic Terms and the Corresponding IT2FSs.

Linguistic Terms		IT2FSs
VL	Very Low	((0,0,0,0.1;1),(0,0,0,0.05;0.9))
L	Low	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))
ML	Medium Low	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))
M	Medium	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))
MH	Medium High	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))
H	High	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))
VH	Very High	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))

The values of the endpoints of the IT2FSs and its membership values are shown in Fig. 4 :

Fig. 4.

Value Endpoints and Degree of Membership of IT2FSs.

The specific steps for the DMs to evaluate each criterion and finally obtain the ranking of alternatives are as follows.

[Step 1] Five DMs' evaluations are proposed for all criteria of 3 alternatives, the evaluation linguistic terms as shown in Table 6 .

Table 6.

Evaluation of Linguistic Terms by Five DMs.

Assessment Information was given by DMs	Alternatives	Criteria
		C1	C2	C3	C4	C5	C6
DM1	A1	L	ML	M	L	H	H
	A2	VH	M	H	M	M	ML
	A3	VL	VH	VH	MH	M	MH
DM2	A1	L	M	ML	ML	H	VH
	A2	H	H	MH	M	MH	M
	A3	M	H	MH	MH	M	M
DM3	A1	L	MH	MH	MH	ML	ML
	A2	VH	MH	VH	M	VH	VH
	A3	MH	H	M	ML	L	H
DM4	A1	M	M	ML	M	MH	MH
	A2	VH	MH	VH	M	ML	M
	A3	ML	VH	L	ML	M	M
DM5	A1	M	ML	VH	VH	MH	M
	A2	MH	H	M	L	M	ML
	A3	M	VH	M	H	M	VH

In light of Table 7 , five individual decision matrices ${\underset{\_}{R}}^l$ are obtained by transforming into the corresponding IT2FSs, as shown in Table 7:

Table 7.

Individual Decision Matrix.

Individual Decision Matrix	Alternatives	Criteria
		C1	C2	C3	C4	C5	C6
${\underset{\_}{R}}^{\text{1}}$	A1	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))
	A2	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))
	A3	((0,0,0,0.1;1),(0,0,0,0.05;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))
${\underset{\_}{R}}^{\text{2}}$	A1	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))
	A2	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))
	A3	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))
${\underset{\_}{R}}^{\text{3}}$	A1	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))
	A2	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))
	A3	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))
${\underset{\_}{R}}^{\text{4}}$	A1	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))
	A2	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))
	A3	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))
${\underset{\_}{R}}^{\text{5}}$	A1	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))
	A2	((0.45,0.6,0.6,0.8;1),(0.5,0.6,0.6,0.7;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.05,0.2,0.2,0.35;1),(0.1,0.2,0.2,0.3;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.15,0.3,0.3,0.45;1),(0.2,0.3,0.3,0.4;0.9))
	A3	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.6,0.8,0.8,0.9;1),(0.7,0.8,0.8,0.85;0.9))	((0.25,0.35,0.35,0.6;1),(0.3,0.35,0.35,0.5;0.9))	((0.8,0.95,0.95,1;1),(0.9,0.95,0.95,1;0.9))

[Step 2] The matrix $\overline{R}$ is calculated according to equation (1). According to equations (2) ∼ (4), the threshold $\beta =0.5$ is taken to calculate and obtain the comprehensive score function matrix${\overline{\overline{R}}}^l$, and the specific values are shown in Table 8 :

Table 8.

Comprehensive Scores Function of Five DMs.

Comprehensive Scores	Alternatives	Criteria
		C1	C2	C3	C4	C5	C6
${\overline{\overline{R}}}^1$	A1	1.19	0.995	1.338	0.833	1.101	0.808
	A2	2.196	0.891	0.787	0.615	0.551	1.155
	A3	1.375	1.679	1.024	1.012	0.551	0.654
${\overline{\overline{R}}}^2$	A1	0.986	1.101	1.001	0.605	0.704	1.575
	A2	1.319	0.551	0.501	0.501	0.551	0.787
	A3	0.768	0.551	0.501	0.898	0.947	0.787
${\overline{\overline{R}}}^3$	A1	1.62	0.154	0.787	0.898	1.005	1.546
	A2	1.396	0.154	1.178	0.501	1.897	1.128
	A3	1.005	0.307	1.184	0.605	1.119	0.891
${\overline{\overline{R}}}^4$	A1	0.891	1.184	1.005	0.104	0.898	0.794
	A2	1.679	0.787	1.897	0.104	0.605	0.397
	A3	0.995	1.178	1.119	0.208	0.501	0.397
${\overline{\overline{R}}}^5$	A1	0.397	1.546	1.575	1.242	0.794	0.891
	A2	0.794	0.891	0.787	1.774	0.397	0.995
	A3	0.397	1.128	0.787	1.005	0.397	1.679

[Step 3] The subjective weight is calculated through the ISM-BWM method. In this evaluation process, like five DMs made group decisions, which can prevent an individual DM from paying too much attention on the characteristics of the relevant field. They also discussed whether there was any influence among the six criteria and gave a consistent conclusion. In light of definitions 4 ∼ 6 and the description of the criteria interaction matrix, the following results were obtained through discussion by the five DMs. A criteria interaction matrix is shown in Table 9 :

Table 9.

Criteria Interaction Matrix.

Criteria	C1	C2	C3	C4	C5	C6
C1	D	D	I	I	D	I
C2	O	D	O	O	O	D
C3	O	O	D	I	D	O
C4	O	I	O	D	I	I
C5	O	I	O	O	D	O
C6	O	O	O	D	O	D

In Table 9, if the relationship between two criteria is expressed as D or I, then the corresponding value in the adjacency matrix is 1. If the corresponding relation is O, then the corresponding value in the adjacency matrix is 0, and Table 10 is obtained:

Table 10.

Adjacency Matrix.

Criteria	C1	C2	C3	C4	C5	C6
C1	1	1	1	1	1	1
C2	0	1	0	0	0	1
C3	0	0	1	1	1	0
C4	0	1	0	1	1	1
C5	0	1	0	0	1	0
C6	0	0	0	1	0	1

In light of equation (5) and definitions 4 ∼ 5, the reachable matrix is obtained, as shown in Table 11 :

Table 11.

Reachable Matrix.

Criteria	C1	C2	C3	C4	C5	C6
C1	1	1	1	1	1	1
C2	0	1	0	1	0	1
C3	0	1	1	1	1	1
C4	0	1	0	1	1	1
C5	0	1	0	0	1	1
C6	0	1	0	1	1	1

According to the Table 11, C2 and C6 can be used as the first-level criteria, and the second-level criteria C₅ can be obtained after the removal of C₂ and C₆. Similarly, a total of five level-level criteria can be obtained, and their directed connection graph is shown in Fig. 5 :

Fig. 5.

Directed Connection Graph of Criteria Obtained by ISM Model.

As can be seen from the ISM model, C₁ is the only deep-level criteria in the first level, so Information Capability is taken as the optimal criteria. The direct criteria of the surface layer include two criteria, C₂ quality and C₆ economy. In selecting emergency supplier, the C₄ economy tends to have much less influence than traditional retail supplier, and the selection criteria pay more attention to timeliness, stability, and other characteristics. Quality is essential for all supplier and needs to be assured during emergency relief operations. So the policymakers settled on the C₆ economy as the worst-case criteria.

The importance of the optimal alternative relative to other criteria and the importance of other criteria relative to the worst alternative were assigned by the DMs. The importance of the best criterion in relation to itself is 1, and the importance of the worst criterion with itself is also 1. The following two matrices are given based on the opinions of all the management, DMs and scholars involved in the evaluation:$A_B=\left(1,4,3,5,2,8\right)$,$A_W={\left(8,3,3,6,7,1\right)}^T$.

Subjective weights ${\omega }^{\mathit{IB}}$ and $\xi$ were obtained according to equation (10). Conformance testing was carried out in light of equation (11). The results are shown in Table 12 .

Table 12.

Subjective Weigh and Consistency Check.

Criteria	${\omega }^{\mathit{IB}}$	ξ	Consistency Check
C1	0.366	0.1031	CR = 0.1031/3 = 0.03 < 0.1
C2	0.117
C3	0.156
C4	0.094
C5	0.234
C6	0.033

The result conforms to the consistency test because of$\mathit{CR}<0.1$.

[Step 4] After the assessment was given by the five DMs, the weight of the DMs was obtained according to the extended IT2FSs-IBCSMDM-TODIM method. Cosine similarity between the two DMs is shown in Table 13 :

Table 13.

Cosine Similarity between Two DMs.

	DM1	DM2	DM3	DM4	DM5
DM1	–	0.947	0.883	0.948	0.886
DM2	–	–	0.909	0.913	0.841
DM3	–	–	–	0.871	0.799
DM4	–	–	–	–	0.844
DM5	–	–	–	–	–

The cosine Similarity of each DM is calculated in light of equation (8), and the result is shown in Table 14 :

Table 14.

Cosine Similarity of Each DM.

DM1	DM2	DM3	DM4	DM5
3.664	3.610	3.462	3.575	3.371

The more relevant the DM is to other DMs, the greater is the importance. Therefore, the weights of all the calculated DMs can be calculated in the light of equations (9) ∼ (14), as shown in Table 15 :

Table 15.

Weights of Each DM.

ωD1	ωD2	ωD3	ωD4	ωD5
0.207	0.204	0.195	0.203	0.191

The objective weight was determined jointly from the evaluation characteristics of DMs and the contribution degree of criteria, or the interaction relationship between DMs was considered while analyzing the different degrees of criteria. The objective weights were calculated according to the Extended IT2FSs-IBCSMDM-TODIM method, as shown in Table 16 , where$n=1,2,\dots ,\text{6}$:

Table 16.

Objective Weights.

ωo1	ωo2	ωo3	ωo4	ωo5	ωo6
0.206	0.158	0.186	0.13	0.145	0.174

[Step 5] The comprehensive weight ${\omega }_n$ was determined, as shown in Table 17 , where$n=1,2,\dots ,\text{6}$, with the threshold taken$\alpha \text{=}0.5$:

Table 17.

Comprehensive Weights.

ω1	ω2	ω3	ω4	ω5	ω6
0.286	0.138	0.172	0.113	0.188	0.103

The subjective weight of the extended IT2FSs-IBCSMDM-TODIM method determines the influence relationship between the criteria. The larger the subjective weight, the higher the driving force of the alternative, making it easier to influence other criteria. The objective weight is considered from the contribution of these criteria to the evaluation of specific alternatives. Both subjective and objective weights consider the interaction relationship, but the specific perspectives are different and complementary to each other.

[Step 6] Calculate the relative advantage $\zeta$ taking the attenuation factor$\theta =1$ , ranking three emergency medical supplier, as shown in Table 18 .

Table 18.

Order of three alternatives if$\theta =1$.

Alternative	A1	A2	A3
$\zeta$	1	0.130	0
Order	1	2	3

It can be seen from Table 18 that there is a bigger advantage for A₁ than for A₂, while there is a slight advantage for A₂ than for A₃ when$\theta =1$.

There is a high information integration level for alternative A₂ and high material quality for alternative A₃, both having good location advantages. However, as can be seen from the ranking in Table 18, alternative A₁ is significantly better than alternatives A₂ and A₃. Alternative A₁ has a relatively large scale of operation and production, and the scale effect is noticeable. Nevertheless, it’s necessary to provide emergency medical supplies to large areas on time when an emergency occurs. Meanwhile, the distance between the city center and A₁, that maintains stability, and its relatively long operational experience, so it has certain comprehensive advantages in responding to emergencies. A₂ has a solid ability to integrate information and can make up the supply chain partners' resources and information to achieve synergy. Hence it has a higher comprehensive score than A₃, which focuses on production.

6.3. Discussion

• (1)Analysis of Different Weights or Different Psychological Factors.
• ✓Analysis of Alternative Ranking under Different Weights.

This paper considers the bidirectional influence relation of DMs, and differences among alternatives are considered a regard to the objective weights. The bidirectional influence relation of the criteria is deemed to be determined subjective weight. The difference between the criteria weights obtained using only objective weights or subjective weights and the comprehensive weighting method in this paper is shown in Fig. 6 :

Fig. 6.

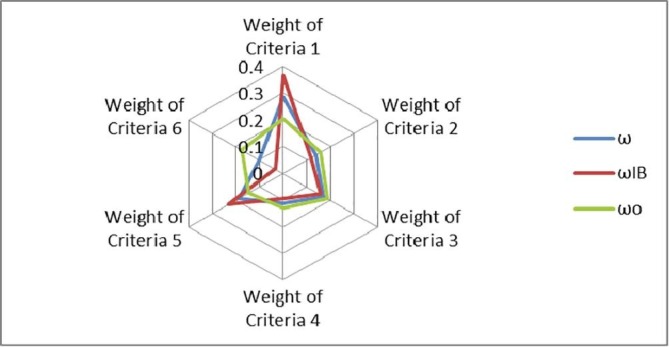
Alternative Weights for Three Type Weight Calculations.

As shown in Fig. 6, although criterion C₁ is more important than other criteria and can fundamentally influence different criteria, the following important criterion is C₅. The change of the evaluation value of criteria C₆ can barely affect other criteria, followed by C₄. The evaluation values of criteria C₁ and C₆ have significant and minimum differences, respectively, when considering the interactivity characteristics of the evaluators. Therefore, it can be seen from the figures that criterion C₁ has the most significant influence on ranking, while criterion C₆ has a minor effect. However, since criterion C₄ has the lowest degree of variation, its combined impact value is not significantly different from that of criterion C₆. Criteria similar to C₁ with a high driving force, high importance, and high difference are worthy of research and attention.

In addition, if only considering subjective weight, it can lead to excessive weight differences between criteria. At this time, only the objective influence relationship between the criteria was considered, but the contribution of the criteria to the specific alternative and the characteristics of DMs were not considered. On the contrary, if only its objective weights are considered, the weight differences between criteria are too small. Several criteria tend to directly or indirectly impact on other criteria, giving them higher weights may obtain more reasonable results.

• ✓Analysis of Different Psychological Factors under the IBCSMDM Method.

A significant feature of the TODIM method is the introduction of a risk attenuation factor θ. In light of the DMs' different psychological factors, the ranking of different alternatives can be analyzed by changing the risk attenuation factor θ.

The sensitivity analysis results show in Table 19 :

Table 19.

Relative Advantage and Ranking of Different θ-value.

Risk factor	θ = 0.01		θ = 1		θ = 2		θ = 5		θ = 20		θ = 100
Alternative	ζ	order	ζ	order	ζ	order	ζ	order	ζ	order	ζ	order
A1	1	1	1	1	1	1	1	1	1	1	1	1
A2	0	3	0.130	2	0.219	2	0.365	2	0.543	2	0.623	2
A3	0.01	2	0	3	0	3	0	3	0	3	0	3

When$1⩽\theta ⩽100$, it can be seen from Table 19 the alternative ranking is$A_1>{\mathrm{A}}_2>{\mathrm{A}}_3$, and it is more sensible for the CDC in H district of Wuhan to sign a long-term agreement with the emergency supplier A₁. At the same time, the increase of θ, which represents a lower degree of loss or risk avoidance of DMs, ${\zeta }_2$ keeps increasing.

Based on the above analysis, there is a characteristic that needs to consider information integration capability: a region with a more significant proportion of medical supplies in reserve or a larger number of supplier has a lower priority, which results in a much lower than average impact from emergencies in that region. This situation may lead to a low degree of risk aversion among DMs, in which case A₂ may become the top choice. In addition, through an advanced big data platform, A₂ can work with supply chain partners to adjust the type and quantity of products to be produced. When θ is extremely low, A₁ is preferred, followed by A₃ and A₂. Large-scale emergency supplier are still the best choice, but high-quality products and location advantages slightly outweigh information advantages.

• ✓Combined Analysis of Different Weights and Different Psychological Factors

Without considering the small and high-risk attenuation factors, ${\zeta }_m$ values of the three alternatives of IT2FSs-ISM-BWM extended TODIM method and IT2FSs-CSMDM extended TODIM method were calculated for the five attenuation factors:$\theta \in \left\{1,2,5,20,100\right\}$. The differences in the different θ values and weighting methods are shown in Fig. 7 :

Fig. 7.

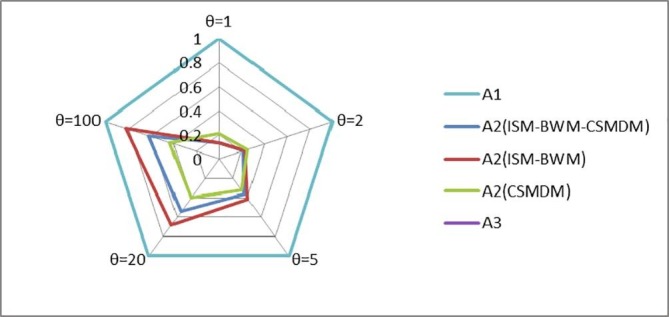
Relative Advantage of the three weights in the five θ-value cases.

As can be seen from Fig. 7, if only considering a subjective weight, the evaluation result is prone to be changed by the psychological factors of the DMs. Therefore, the results are susceptible to DMs' bias, and there is a high possibility of decision-making errors. If only from an objective weight, it isn't easy to take advantage of the main features of the TODIM method to help in decision-making. The hybrid weighting method of IBCSMDM, combined with the characteristics of IT2FSs, can better modify the TODIM method to help DMs make decisions.

• (2)Compared with Other Approaches.
• ✓Compared with Several Classical Approaches.

In current research, there are many classical MAGDM methods, which can be roughly divided into three categories: (1) Weighting methods, such as DEMATEL, BWM, entropy, information entropy, and relative entropy; (2) Ranking methods, such as TOPSIS, VIKOR, TODIM, Elimination and Choice Expressing Reality (ELECTRE) and PROMETHEE; (3) Comprehensive methods, such as AHP. Several common approaches are not covered in this article's synthesis list in Table 20 .

Table 20.

Other Classical Approaches and their Effects.

Effect	Other Classical Approaches									Our Study
	DEMATEL	Entropy	Information Entropy	Relative Entropy	AHP	TOPSIS	VIKOR	ELECTRE	PROMETHEE
Weighting of criteria	√	√	√	√	√	√	–	–	–	√
Weighting of DMs	–	√	√	√	–	–	–	–	–	√
Ranking	–	–	–	–	√	√	√	√	√	√

Among the nine other traditional approaches listed in Table 20, the entropy weight method is the most common among several methods to determine the weight. In addition, the basic ideas of AHP, which score the importance of each criterion with the weight obtained according to the characteristics of the matrix, are significantly different from other methods. Therefore, the method presented in this paper compares with some traditional methods: The assessment and rating information remain the same. In contrast, entropy was selected for weighting, and four ranking methods except AHP in Table 20 are specified for ranking.

IT2FSs were used to evaluate alternatives, and the classical entropy weight method was used for the standard individual decision matrix. Next, the IT2FSs assessment method in this paper was used to get the comprehensive scoring function, and then TOPSIS, VIKOR, ELECTRE, and PROMETHEE were used for sorting. The analysis results and shown in Table 21 .

Table 21.

Ranking Results of Different MCGDM Methods.

Ranking Method	Numerical Type	A1	A2	A3	Ranking
TOPSIS	${\pi }_1-Value$	0.429	0.424	0.369	$A_1>{\mathrm{A}}_2>{\mathrm{A}}_3$
VIKOR	$R-Value$	0.197	0.214	0.220	$A_1>{\mathrm{A}}_2>{\mathrm{A}}_3$
	$S-Value$	2.967	3.204	3.473	$A_1>{\mathrm{A}}_2>{\mathrm{A}}_3$
	$Q-Value$	0.000	0.603	1.000	$A_1>{\mathrm{A}}_2>{\mathrm{A}}_3$
ELECTRE	${\pi }_2-Value$	−0.036	−0.069	0.105	$A_{\text{3}}>{\mathrm{A}}_{\text{1}}>{\mathrm{A}}_{\text{2}}$
PROMETHEE	${\pi }_3-Value$	0.282	−0.167	−0.115	$A_1>{\mathrm{A}}_3>{\mathrm{A}}_2$

The rank results obtained by TOPSIS and VIKOR are consistent with the extended IT2FSs-IBCSMDM-TODIM method in$1⩽\theta ⩽100$; If DMs consider high levels of risk avoidance, the resulting calculation by the compatible TODIM method is consistent with the PROMETHEE. In addition, it can be seen that there is little difference between the four alternatives of the TOPSIS method, and the extension of TODIM can improve the accuracy of decision-making. For group utility maximization and individual regret minimization, the VIKOR method can adapt to sort according to the particular regret value R, group utility value S, and compromise value Q (The coefficient of the decision-making mechanism is 0.5), and the ranking is not changed.

In conducting Spearman-correlation coefficient analysis for the ranking results of several methods, it can be seen in Fig. 8 that only one ranking had a negative correlation coefficient. From the above analysis, the difference ${\pi }_3-Value$ between the alternatives of this method was minimal, while the Correlation Coefficient of the other four ranking methods and the extended TODIM method in this paper all had a value of 1.

Fig. 8.

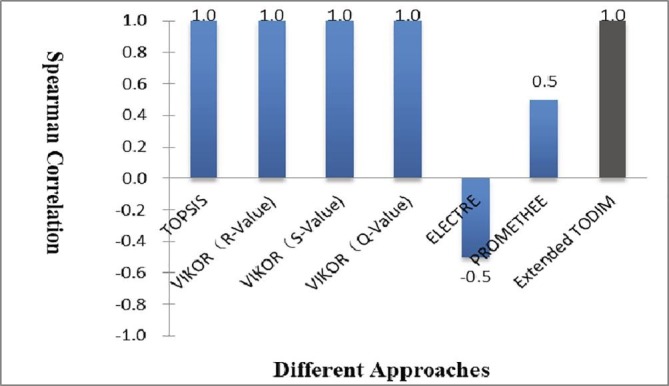
Spearman Correlation Coefficient of several ranking methods.

It can be seen from Fig. 8 that the extended TODIM method can take the psychological factors of the bounded rationality hypothesis of DMs into account and can also better analyze the increasingly complex situations in reality. It can be seen from Table 21 that the ranking calculated by ELECTRE, taking the consistency and conflict of the alternatives as to the central perspective, alternative A₃ is the best choice, followed by alternative A₁. Nevertheless, the difference in net dominance among the three alternatives is slight. The ranking is inconsistent with other methods, so it is less convincing than the extended TODIM method in this paper. However, traditional methods often ignore the weights of indicators or decision-makers, or think that they are directly given by decision-makers. Therefore, this paper is compared with other extended multiple index group decision making methods to verify the effectiveness and superiority of the extended method.

• ✓Compared with Other Extended Approaches.

In addition to the above analysis on classical methods, in recent years, scholars have begun to integrate the classical methods and proposed new extended methods. The extension aspects can be fundamentally divided into two categories: (1) Assessments processed by considering some complex situations, which can be close to the reality of the situation; (2) Weighting evaluation values by the mixed method. Nevertheless, through the above analysis, type-1 assessments sometimes have certain limitations, while type-2 assessments usually only consider the scores of a single index. In addition, the absolute subjective and objective weighting methods may lead to irrationality in the decision results. To some extent, the adoption of a complementary correction method can reduce the degree of irrationality. The hybrid weighting method for different scenarios has become research hotspot and challenge in recent years.

The main differences between our method and the classic methods are as follows: firstly, The evaluation is carried out by using interval type TWO fuzzy sets considering secondary membership degree. Secondly, the method in this paper considers both the criteria weight and DMs’ weight. Meantime, the weight of the criteria is not a simple arithmetic average of the subjective weight and objective weight. The characteristics of the index itself and the relationship between the indexes are considered. Therefore, the extension method obtained through the relevant modification method has certain superiority. Table 22 shows the main differences between our approach and the other two related approaches.

Table 22.

Difference between Approach in This Paper and Other Two Related Methods.

Characteristics	Fuzzy assessment	Comprehensive weights	Our study
Representative References	Baykasoğlu and Gölcük, 2017, Qin et al., 2017, Ghorabaee, 2016	Ding et al., 2021, Tseng et al., 2019
Decision information	IT2FSs which consider only one type of scoring function	IT1FSs	IT2FSs which consider comprehensive scoring function
Weight of criteria	Directly given, obtained from objective decision matrix and obtained from subjective preferences of DMs	The weight of subjective and objective decision information is considered comprehensively	The subjective and objective combination weighting method considering the importance of decision maker and index simultaneously

7. Conclusions

Emergencies such as the COVID-19 pandemic have generated a great deal of social concern. Emergencies are characterized by sudden and massive destructiveness, which leads to a rapid increase in demand for emergency supplies, especially emergency medical supplies. Hence, DMs and managers must make decisions about emergency medical supplier to provide adequate supplies promptly.

In this situation, an extended MCGDM approach and an evaluation framework for emergency medical supplier are proposed. We identify six evaluation criteria for emergency medical providers, assessment evaluation for six criteria by IT2FSs. Then, we weighted the assessment with an IBCSMDM approach that considered bidirectional relationships and consensus. Next, these evaluations were integrated by a novel IT2FSs model, and these alternatives were sorted by the TODIM method. At the same time, this approach also applies to other scenarios that require consideration of psychological factors and complex influence relationships between criteria and DMs.

Nevertheless, there are several limitations in this paper. Firstly, the universality of applications of type-2 fuzzy sets in various scenarios is yet to be tested. In the future, we will apply this fuzzy assessment and its extension method to other scenarios. Secondly, we mainly focus on innovation weights for DMs and criteria, and more efficient aggregation operators can be considered in future studies. In addition, because the characteristics are often more complex than assumed in our study, dynamicity and incompleteness might be explored in future research on emergency medical supplier.

Funding

This work was supported by the Natural Science Foundation of China [grant numbers 71862035]; The Yunnan Fundamental Research Project [grant numbers 2019FB085]; The 21th Yunnan Young and Middle-aged Academic and Technical Leaders Reserve Personnel Training Program [grant numbers 2019HB030]; The Yunnan Provincial Education Department Scientific Research Fund Project [grant numbers 2021Y556].

CRediT authorship contribution statement

Sen Liu: Conceptualization, Supervision, Investigation, Methodology, Writing – review & editing. Xiaojun He: Investigation, Validation, Software, Methodology, Writing – original draft. Felix T.S. Chan: Supervision, Formal analysis, Methodology. Zhiyong Wang: Supervision, Formal analysis, Methodology.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Biographies

Sen Liu received a Ph.D. degree in management science and engineering from Zhejiang University, Hangzhou, China, in 2014. He is currently a professor at School of Logistics, Yunnan University of Finance and Economics, Kunming, China. He has published many research papers in refereed journals such as Expert Systems with Applications, Industrial Management & Data Systems, etc. He also regularly tutors, advises and provides consulting support to firms with respect to their logistics and supply chain management strategy. His research areas include the logistics and supply chain management, information systems research and group decision making problems, etc.

Xiaojun He is currently pursuing a master's degree in management with the Yunnan University of Finance and Economics. She has won the National Scholarship and is running a scientific research fund project funded by the Education Department of Yunnan Province. Her main research direction is logistics and supply chain management.

Prof. Felix T.S Chan received his BSc Degree in Mechanical Engineering from Brighton University, UK, and obtained his MSc and PhD in Manufacturing Engineering from the Imperial College of Science and Technology, University of London, UK. He is currently a professor at Department of Decision Sciences, Macau University of Science and Technology. His current research interests are Logistics and Supply Chain Management, Operations Research, Production and Operations Management etc. To date, Prof. Chan has published over 16 book chapters, over 370 SCI refereed international journal papers and 310 peer reviewed international conference papers. Based on the recent compilations (2020) and (2021) from a research group of Stanford about the impact of scientists Prof. Felix Chan is categorized in the field of Operations Research, ranked 10 out of over 23,450 scientists worldwide, i.e., Top 0.04% worldwide, for TWO consecutive years (2020 and 2021).

Zhiyong Wang is a PhD in management and professor at the Yunnan University of Finance and Economics. He is currently a member of CPPCC of Yunnan Province, the Standing Committee of the Yunnan Provincial Committee of Democratic Revolution, and the director of the academic Affairs Office of the Yunnan University of Finance and Economics. He is also responsible for Yunnan provincial excellent course “International Financial Management”, chief expert member of Yunnan Provincial Philosophy and Social Science Research Base “Yunnan External Finance Research Base”, etc. His main research direction is international finance. Prof. Wang has published over 30 papers and 3 books.