Modeling multi-scale data via a network of networks

Abstract

Motivation

Prediction of node and graph labels are prominent network science tasks. Data analyzed in these tasks are sometimes related: entities represented by nodes in a higher-level (higher scale) network can themselves be modeled as networks at a lower level. We argue that systems involving such entities should be integrated with a ‘network of networks’ (NoNs) representation. Then, we ask whether entity label prediction using multi-level NoN data via our proposed approaches is more accurate than using each of single-level node and graph data alone, i.e. than traditional node label prediction on the higher-level network and graph label prediction on the lower-level networks. To obtain data, we develop the first synthetic NoN generator and construct a real biological NoN. We evaluate accuracy of considered approaches when predicting artificial labels from the synthetic NoNs and proteins’ functions from the biological NoN.

Results

For the synthetic NoNs, our NoN approaches outperform or are as good as node- and network-level ones depending on the NoN properties. For the biological NoN, our NoN approaches outperform the single-level approaches for just under half of the protein functions, and for 30% of the functions, only our NoN approaches make meaningful predictions, while node- and network-level ones achieve random accuracy. So, NoN-based data integration is important.

Availability and implementation

The software and data are available at https://nd.edu/~cone/NoNs.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Networks can be used in many domains to model entities and the complex systems involving them. For example, in biological networks, nodes are biological entities (such as genes or their protein products, tissues etc.) and edges are interactions between them; in social networks, nodes are generally individuals and edges are social interactions between them; and more. By modeling systems as networks, the important relationships can be studied, which can lead to deeper insights compared with analyzing each entity on its own.

Two important tasks in network science are node label prediction (Bhagat et al., 2011) and graph label prediction (Nikolentzos et al., 2017). In the former, given a single network, the goal is to predict labels of its nodes. In the latter, given multiple networks, the goal is to predict labels of those networks. For example, the former can be applied to a protein–protein interaction (PPI) network (PPIN), where nodes are proteins and edges are PPIs, to predict proteins’ functions; to a social network to uncover individuals’ demographics, hobbies and more. The latter can be applied to multiple proteins’ structure networks (PSNs), where nodes are amino acids and edges join those that are close in the 3D crystal structure, also to predict proteins’ functions; to multiple chemicals’ molecule networks, where nodes are atoms and edges are bonds, to predict their properties; and more. Note that both of these tasks fall under the umbrella of a more general problem of entity label prediction, where given entities of interest, the goal is to predict labels of the entities.

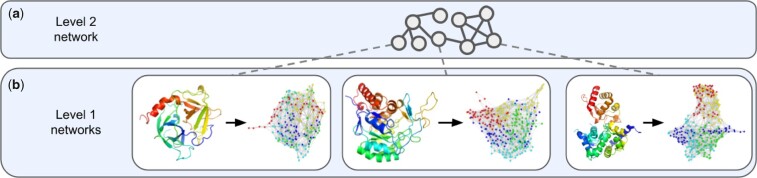
So, sometimes the entities (e.g. proteins) that are represented by nodes in a network (e.g. a PPIN) can themselves be modeled as networks (e.g. PSNs). We argue that the systems involving such entities should be integrated into a ‘network of networks’ (NoNs), where nodes in a network at a higher level (i.e. higher scale) are themselves networks at a lower level (Fig. 1). More specifically, we refer to the higher level of the NoN as the Level 2 network (Fig. 1a), which contains Level 2 nodes and Level 2 edges. Each Level 2 node has a corresponding Level 1 network at the lower level of the NoN (Fig. 1b), which contains Level 1 nodes and Level 1 edges. We number levels in this way with the idea that lower-level networks are the building blocks of higher-level networks. However, we tend to discuss Level 2 networks first, as doing so is often more convenient for developing intuition. Even though we analyze two-level NoNs in this study, NoNs can encompass more: proteins interact with each other to carry out cellular functioning, cells interact with each other to form tissues and so on, up the levels of biological organization. We hope to extend our work to encompass more than two levels in the future.

Fig. 1.

Illustration of a two-level biological NoN. (a) The Level 2 network is a PPIN, in which nodes are proteins. A dotted line joins each Level 2 node, i.e. each protein, to its corresponding (b) Level 1 network, i.e. its PSN. Only three Level 1 networks are shown for simplicity, but generally every Level 2 node can have a corresponding Level 1 network. Nodes in the PSNs are colored based on their corresponding amino acids in the ribbon diagram and are not indicative of node labels

Given the definition of an NoN, we can now characterize the task of entity label prediction in the context of our study. Specifically, since the entities of interest are represented by Level 2 nodes and, correspondingly, modeled as Level 1 networks, entity label prediction can refer to (i) using only the Level 2 network (Fig. 1a) to predict Level 2 nodes’ labels, corresponding to the task of node label prediction in the Level 2 network, (ii) using only Level 1 networks (Fig. 1b) to predict Level 1 networks’ labels, corresponding to the task of graph label prediction using the Level 1 networks and (iii) using the entire NoN to predict entities’ labels. In this study, the primary question we aim to answer is whether (iii) is more accurate than (i) and (ii), i.e. if NoN-based entity label prediction is more accurate than each of single-level node label prediction and graph label prediction alone.

In tackling this question, we make the following novel contributions: we construct and provide two new sources of NoN data, we develop novel approaches for NoN label prediction, and, most importantly, we are the first to test whether using NoN data in label prediction is more accurate than using only a single level. Next, we discuss each of these contributions.

Since to our knowledge labeled NoNs are limited, we provide two new sources of such data. First, we develop an NoN generator that can create a variety of synthetic NoNs (Section 2.3.1). Intuitively, given any set of single-level random graph generators, such as geometric (GEO; Penrose, 2003) or scale-free (SF; Barabási and Albert, 1999), our NoN generator combines random graphs created from these single-level generators at each level. In this way, we can label each entity (Level 2 node and its Level 1 network) based on which combination of single-level random graph generators it is involved in at the two levels. Our generator can control a variety of network structural parameters (Section 2.3.1), thus allowing for the mimicking of a variety of real-world systems. Second, we construct a biological NoN, consisting of a PPIN from BioGRID (Stark et al., 2006) at the second level and PSNs for proteins from Protein Data Bank (PDB; Berman et al., 2000) at the first level. Proteins are labeled based on their functions via gene ontology (GO) annotation data (Ashburner et al., 2000; Section 2.3.2). For each of the 131 GO terms considered, the goal is to predict whether or not each protein is annotated by that GO term. While computational protein functional prediction is relatively well-studied, the problem is still very relevant, as the accuracy of existing methods for this purpose is typically low. The continued importance of computational annotation of protein function (Gaudet et al., 2017) is a major motivator of our study. We expect the NoN data resulting from our study to become a useful resource for future research in both network science and computational biology, including for the problem of protein function prediction.

We also develop novel approaches for NoN label prediction. In general, label prediction approaches extract features of the entities and then perform supervised classification, i.e. prediction of the entities’ labels based on their features. So, for our study, there are three types of approaches to consider: (i) those that extract node-level features (i.e. features of nodes in the Level 2 network only), (ii) those that extract network-level features (i.e. features of Level 1 networks only) or (iii) those that extract NoN features (i.e. integrated Level 2 and Level 1 features). To our knowledge, approaches of type (iii) do not exist yet, so we create NoN features in two ways: by combining existing node- and network-level features and by applying the novel graph neural network (GNN) approach that we propose for analyzing NoNs.

Then, we aim to evaluate whether approaches of type (iii) outperform those of types (i) and (ii). If so, this would provide evidence that NoN-based data integration is useful for label prediction. To determine which approach types are the best, we evaluate them in terms of accuracy for synthetic NoNs, as class sizes are balanced, and in terms of the area under the precision recall curve (AUPR), precision, recall and F-score for the biological NoN, as class sizes are unbalanced.

For synthetic NoNs, we find that our NoN approaches outperform single-level node and network ones for those NoNs where the majority of nodes are not densely interconnected (i.e. where nodes do not tend to group into densely connected modules). For NoNs where there are groups of densely interconnected nodes (i.e. where there is clustering structure), an existing single-level approach performs as well as NoN approaches. For the biological NoN, we find that our NoN approaches outperform the single-level ones in a little under half of the GO terms considered. Furthermore, for 30% of the GO terms considered, only our NoN approaches make meaningful predictions, while node- and network-level ones achieve random accuracy. Also, while deep learning does not perform the best overall, it seems to be useful for otherwise difficult-to-predict protein functions. As such, NoN-based data integration is an important and exciting direction for future research.

Finally, it is important to discuss a few related topics. Given that we study a biological NoN, we must point out that existing studies have combined protein structural data with PPI data (Peng et al., 2014; Zhang et al., 2019) for various tasks. However, they generally do so by incorporating more basic non-network structural properties, such as proteins’ domains and families, with PPI data. On the other hand, our approaches combine PSN representations of detailed 3D protein structural properties with PPIN data through the NoN representation. Importantly, PSN-based models of protein structures have already been shown to outperform non-network-based (i.e. traditional sequence and ‘direct’ 3D structural) models in tasks such as protein structural comparison/classification (Faisal et al., 2017; Newaz et al., 2020) and protein functional prediction (Berenberg et al., 2021; Gligorijević et al., 2021). Thus, we hypothesize that incorporating state-of-the-art, i.e. PSN-based (rather than traditional sequence or ‘direct’ 3D structural), representations of protein structures with PPIN data into an NoN will be effective. Regardless, the goal of our study is to investigate network-based data integration by evaluating whether NoN label prediction is actually more accurate than each of node- and network-level alone. A comparison with other, non-network-based data integration schemes is outside the scope of this study and the subject of future work.

Some other network models of higher-order data exist as well. These include: multiplex, multimodal, multilevel and interdependent networks (Chen et al., 2019; Dong et al., 2020; Li et al., 2018; Morone et al., 2017; Perich and Rajan, 2020; Roth et al., 2017), which are sometimes used interchangeably and sometimes also referred to as ‘networks of networks’; hierarchical networks (Clauset et al., 2008); higher-order networks (Xu et al., 2016); hypergraphs (Berge, 1973); and simplicial complexes (Munkres, 2018). However, these all model different types of data compared with NoNs as we define them, so we cannot consider these other network types in our study.

There are also studies that do model data as NoNs. However, they differ from our proposed work in terms of data analyzed, application domain and/or network science task. With respect to data, besides synthetic NoNs, we analyze a PPIN-PSN biological NoN. However, these other studies analyze NoNs where the Level 2 network is a disease–disease similarity network and the Level 1 networks are disease-specific PPINs (Ni et al., 2016), where the Level 2 network is a social network and the Level 1 networks are individuals’ brain networks (Bassett and Mattar, 2017; Falk and Bassett, 2017; Parkinson et al., 2018), or where the Level 2 network is a chemical–chemical interaction network and Level 1 networks are molecule networks (Wang et al., 2020). With respect to application domain, while we aim to predict protein function, these other studies aim to identify disease causing genes (Ni et al., 2016), answer sociologically motivated questions like whether similarities between friends mean they have similar ways of thinking (Parkinson et al., 2018), or predict new chemical–chemical interactions (Wang et al., 2020). With respect to network science task, while we aim to predict entities’ labels, these other studies aim to identify important entities (Level 1 nodes; Ni et al., 2016), predict links between entities (Level 2 nodes; Wang et al., 2020) or embed multiple networks at the same level into a common low-dimensional space, using an NoN as an intermediate step (Du and Tong, 2019). While it might be possible to extend some of these existing studies to ours or vice versa, doing so could require considerable effort, as it would mean developing new methods, and code is not publicly available for all of the existing methods. All of this makes any potential extensions hard. As such, we cannot compare against these existing NoN-like methods.

2 Materials and methods

2.1 NoN definition

We define an NoN with l levels as follows. Let, $G^{(l)}=(V^{(l)},E^{(l)})$ be the level l network with node set $V^{(l)}$ and edge set $E^{(l)}\subseteq V^{(l)}\times V^{(l)}$. Each ‘level l node’ $v_i^{(l)}\in V^{(l)}$ itself corresponds to a ‘level l−1 network’ $G_i^{(l-1)}=(V_i^{(l-1)},E_i^{(l-1)})$. In other words, $V^{(l)}$ and $\{G_1^{(l-1)},\dots ,G_{\left|V^{(l)}\right|}^{(l-1)}\}$ are different notations that represent the same underlying concept—the set of entities that are represented by nodes in a level l network and correspondingly modeled as level l−1 networks. Note that we allow each level l−1 network to contain no nodes (and thus no edges). That is, $G_i^{(l-1)}$ can be an order-zero graph, signifying that $v_i^{(l)}$ has no corresponding level l−1 network. We assume that nodes from different level l−1 networks do not overlap—e.g. amino acids (nodes) from different PSNs do not represent the same physical entities, even if the types of the amino acids are the same. That is, $V_1^{(l-1)}\cap \dots \cap V_{\left|V^{(l)}\right|}^{(l-1)}=\varnothing$. Each level l−1 node $v_{i_j}^{(l-1)}\in V_i^{(l-1)}$ in each level l−1 network $G_i^{(l-1)}\in V^{(l)}$ itself corresponds to a level l−2 network $G_{i_j}^{(l-2)}=(V_{i_j}^{(l-2)},E_{i_j}^{(l-2)})$. This recursion continues until Level 1. We illustrate a two-level NoN in Figure 1.

2.2 Problem statement

Given an NoN $\{G^{(2)}=(V^{(2)},E^{(2)})$ and $\{G_1^{(1)},\dots ,G_{\left|V^{(2)}\right|}^{(1)}\}\}$, its label set $Y=y_1,\dots ,y_c$, and a function that maps entities (i.e. Level 2 nodes and thus their corresponding Level 1 networks) to their labels $f_{\text{true}}:V^{(2)}\to Y$, the goal is to learn a predictive function $f_{\text{pred}}:V^{(2)}\to Y$ through supervised classification.

In our study, this predictive function can be learned in three ways: for each Level 2 node $v_i^{(2)}$, using features based only on $G^{(2)}$, i.e. node-level features; for each Level 2 node’s corresponding Level 1 network $G_i^{(1)}$, using features based only on $G_i^{(1)}$, i.e. network-level features; and for each entity, using features based on both levels, i.e. NoN features. We aim to show that the predictive performance of f_pred when trained on NoN features is higher than those when using node- and network-level features alone, thereby indicating that NoN-based entity label prediction is more accurate than each of node label prediction and graph label prediction alone. A more formal description of the evaluation, including the training, validation and testing split; the loss function; and the performance measures, can be found in Section 2.5.

2.3 Data

2.3.1 Our synthetic NoN generator

We develop a generator that can create synthetic NoNs with a variety of parameters and multiple levels. In this study, we focus on two levels. While analyzing NoNs of three or more levels would be interesting, doing so would be difficult in the context of our study, especially since available real-world NoN data of so many levels is scarce. Namely, our main goal is to test whether NoN-based integration is worth it. With two levels, there exist very clearly defined and fairly comparable tasks: NoN versus node-level versus graph-level label prediction. With more levels, this is no longer the case. So, we leave such investigation of NoNs with more than two levels for future work.

We want our generator to create a two-level NoN with labeled entities (i.e. Level 2 nodes, and equivalently, Level 1 networks) such that only an approach using information from both levels should be able to attain high entity label prediction accuracy. To accomplish this, it is first useful to understand single-level random graph models and how they generate random graphs with various properties. In particular, we consider the GEO (Penrose, 2003) and SF (Barabási and Albert, 1999) models. An instance of GEO (i.e. a random geometric network) is created by placing nodes randomly in Euclidean space and adding an edge between those that are spatially close to each other, resulting in a network with Poisson-like degree distribution and high clustering coefficient. An instance of SF (i.e. a random SF network) is created using the concept of preferential attachment to join nodes—as the network is grown, nodes with high degree are more likely to gain edges (i.e. neighbors) compared with nodes with low degree, resulting in a network with a power-law degree distribution and low clustering coefficient. So, due to the different construction schemes, GEO and SF networks are topologically distinct. As such, node label prediction approaches can easily distinguish between nodes whose network neighborhoods are GEO-like and nodes whose network neighborhoods are SF-like; we can label nodes of the former as ‘GEO’ and nodes of the latter as ‘SF’. Similarly, graph label prediction approaches can easily distinguish between instances of GEO and instances of SF; we can label networks of the former as ‘GEO’ and networks of the latter as ‘SF’.

So, to generate an NoN, we combine GEO and SF at the two levels. In particular, let (m₁, m₂) denote an NoN where the Level 2 network is generated using random graph model m₂ and each Level 2 node’s Level 1 network is generated using random graph model m₁. Given such an NoN, we label its entities (Level 2 nodes and corresponding Level 1 networks) based on the (m₁, m₂) combination, just as we label single-level nodes/networks based on which of GEO or SF they are generated with. Now suppose we generate NoNs for each $(m_1,m_2)\in \{(\mathit{GEO},\mathit{GEO}),(\mathit{GEO},SF),(SF,\mathit{GEO}),(SF,SF)\}$, i.e. all four possible combinations of GEO and SF at the two levels. An entity label prediction approach would have to incorporate information from both levels in order to accurately predict each of the four labels: if an approach only used Level 1 information, it would fail to distinguish between (GEO, GEO) and (GEO, SF) since both are of type GEO at Level 1, and it would fail to distinguish between (SF, GEO) and (SF, SF) since both are of type SF at Level 1; Level 2 information would be needed. Similarly, if an approach only used Level 2 information, it would fail to distinguish between (GEO, GEO) and (SF, GEO) since both are of type GEO at Level 2, and it would fail to distinguish between (GEO, SF) and (SF, SF) since both are of type SF at Level 2; Level 1 information would be needed. These four combinations of GEO and SF are helpful initial constructions for ultimately generating an NoN that requires information from both levels to accurately make predictions for.

In this previous example, each of (GEO, GEO), (GEO, SF), (SF, GEO) and (SF, SF) is its own ‘isolated NoN’, disconnected from others. So, to more accurately model a real-world system, our generator joins each isolated NoN at the second level to form a connected NoN with multiple regions; this joining process is described below. We refer to the set of Level 2 nodes that originated from an isolated NoN as a ‘Level 2 node group’. We generate these isolated NoNs, each with a fixed number of Level 1 and Level 2 nodes and edges, such that when combined into a single connected NoN, the resulting NoN’s Level 2 network has 15 000 nodes and 300 000 edges to approximate the size of the human PPIN, and so that each Level 1 network has 200 nodes and 800 edges to approximate the average size of the PSNs. The entities (Level 2 nodes and corresponding Level 1 networks) of the resulting NoN have four labels, with an equal number of entities having each label, so balanced multiclass classification is performed. We visualize a toy NoN in Figure 2.

Fig. 2.

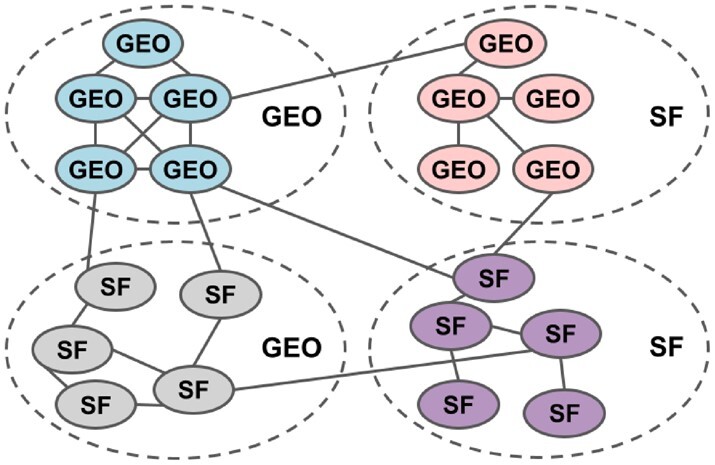
A toy synthetic NoN generated from two random graph models. Large dotted circles represent Level 2 node groups (originating from isolated NoNs) whose Level 2 nodes are connected in a random GEO- or SF-like fashion. Small solid circles represent Level 2 nodes whose Level 1 networks are of the random graph type indicated. Level 1 nodes and edges are not shown. Level 2 nodes are colored based on their label, i.e. their combination of Level 1 and Level 2 network topology {[(GEO, GEO), (GEO, SF), (SF, GEO) and (SF, SF)]}

Our generator joins isolated NoNs by randomly removing edges within Level 2 node groups and randomly adding the same number of edges across Level 2 nodes groups (across-edge amount). That is, we repeat the following process $a\%\times$ 300 000 times: (i) randomly select a Level 2 node group, (ii) randomly select an edge in that node group, (iii) delete that edge, (iv) randomly select two Level 2 nodes from different node groups and (v) add an edge between the selected nodes. We start with a = 5 to retain most of the Level 2 node groups’ originally generated GEO- and SF-like network topologies, and we systematically vary a to be 25, 50, 75 and 95 to test the effect of breaking the network topologies down. This also means that at a = 5 there is significant clustering (each Level 2 node group consists of densely interconnected nodes), whereas at a = 95 there is very little clustering.

We also introduce random rewiring to test each approach’s robustness to data noise (rewire-noise amount). Specifically, for $r\%$ rewire-noise, for each Level 1 network and each Level 2 node group, we randomly remove $r\%$ of the total edges and randomly add the same number of edges back. We vary r to be 0 (no noise), 10, 25, 50, 75 and 100 (completely random). Combining the a and r parameters, we generate a total of 5 × 6 = 30 synthetic NoNs. For a formal description of the NoN generation process and the parameters we vary (see Supplementary Section S1.1.1).

In our study, we report results for two-model NoNs, i.e. for {GEO, SF}. Note that we also analyzed three-model NoNs, adding the Erdős-Rényi (ER) model (Erdős and Rényi, 1960), i.e. for {GEO, SF, ER}. Because results are qualitatively and quantitatively similar, we do not discuss this analysis in the paper due to space constraints.

2.3.2 Biological NoN

We also investigate whether integration is useful in the applied task of protein functional prediction. We construct a biological NoN using the human PPIN and the proteins’ associated PSNs (see also Supplementary Section S1.1.2). We construct a PPIN using human PPI data from BioGrid (Stark et al., 2006) version 4.1.190; this PPIN has 18 708 nodes and 434 527 edges. Then, we map each protein ID to its corresponding PDB chain, resulting in 4776 PDB chains. Finally, we construct PSNs from these chains using an established process: nodes represent amino acids and edges join two amino acids if the distance between any of their heavy atoms (carbon, nitrogen, oxygen or sulfur) is within 6 Å (Faisal et al., 2017). The obtained biological NoN has 18 708 proteins at Level 2, of which 4776 have PSNs at Level 1.

To obtain label information, we rely on protein-GO term annotation data (accessed in October 2020; Ashburner et al., 2000). Of all protein-GO term annotations, we focus on biological process (BP) GO terms in which the annotations were experimentally inferred (EXP, IDA, IPI, IMP, IGI and IEP). From those, we keep only GO terms annotating the 4776 proteins that have PSNs, which results in 131 unique GO terms, i.e. classification labels. For each label g, proteins annotated by g constitute positive data instances. While we could consider negative data instances to be all proteins not annotated by g, this could add bias for proteins that are not annotated by g but are by GO terms related to g and would also create an extreme positive/negative imbalance. Instead, we define negative data instances to be proteins that are not currently annotated by any BP GO term, reducing the bias and resulting in more balanced classes. Ultimately, each label has between 20 and 277 positive data instances and 61 negative data instances; as there are 131 labels total, we perform binary classification 131 times (Section 2.5). Note that not all proteins have labels. Regardless, when extracting information from the Level 2 network, we consider all 18 708 nodes and 434 527 edges. However, for each label, we only perform classification on the positive and negative data instances.

2.4 Approaches for label prediction

We consider graph-theoretic approaches that are based on graphlets (Milenković and Pržulj, 2008), and graph learning approaches, namely, SIGN (Rossi et al., 2020) and DiffPool (Ying et al., 2018).

Graphlets are small subgraphs (a path, triangle, square etc.) that can be considered the building blocks of networks, and they can be used to extract features of both nodes and networks (Supplementary Section S1.2). The graphlet-based feature of a node in a general network is called its graphlet degree vector (GDV). GDVs of all nodes in a network can be collected into the network’s GDV matrix (GDVM) feature. One drawback of GDVM is that its dimensions depend on the size of the network—if performing graph label prediction of different sized networks using GDVM features, issues can arise. Thus, we also consider a transformation of GDVM, the graphlet correlation matrix (GCM; Yaveroğlu et al., 2014).

Given these definitions of graphlet features for nodes in a general network or for the entire general network itself, we now explain which features we use for nodes in a Level 2 network and which features we use for Level 1 networks. For the former, we extract each Level 2 node’s GDV (L2 GDV). For the latter, we extract each Level 1 network’s GDVM and GCM (L1 GDVM and L1 GCM). We use L1 GDVM when analyzing synthetic NoNs since we found that it outperformed L1 GCM. For the biological NoN, L1 GCM is the only viable feature since Level 1 networks (PSNs) have different numbers of nodes (amino acids).

Then, to obtain NoN graphlet features, we concatenate Level 2 nodes’ L2 GDVs with their networks’ L1 GDVMs or L1 GCMs. This results in five graphlet-based features: those for Level 1 networks (L1 GDVM and L1 GCM) that are used for graph label prediction, those for nodes in a Level 2 network (L2 GDV) that are used for node label prediction, and those for the entire NoN (L1 GDVM + L2 GDV and L1 GCM + L2 GDV) that are used for entity label prediction. As graphlet-based feature extraction is an unsupervised task, in order to perform classification, for each graphlet-based feature, we train a logistic regression classifier (Supplementary Section S1.4). So for example, when we say L2 GDV, we mean the L2 GDV feature under logistic regression.

SIGN aims to perform node label prediction (Supplementary Section S1.4). It first computes features of nodes based on various adjacency matrices, these variants including the square of the adjacency matrix and the adjacency matrix where each edge is weighed by the number of triangles it participates in. Then, it uses them in a neural network classifier. Mathematically, SIGN can be thought of as an ensemble of shallow graph convolutional network (GCN) classifiers, which is why it is a graph learning approach. In this study, when we say L2 SIGN, we mean its adjacency matrix-based features paired with its own classifier for node label prediction using only a Level 2 network.

DiffPool aims to perform graph label prediction (Supplementary Section S1.2). For each input network, DiffPool’s GNN summarizes nodes’ initial features into a hidden feature for the entire network. Then, given hidden features corresponding to the input networks, the GNN is trained on these hidden features to perform graph label prediction. When we say L1 DiffPool, we mean its GNN with the initial features chosen (Supplementary Section S1.4), for graph label prediction using only Level 1 networks.

As SIGN and DiffPool are single-level graph learning approaches, we also combine them into an NoN graph learning approach. Given each Level 2 node’s SIGN feature, we concatenate it with the Level 2 node’s corresponding Level 1 network’s hidden feature computed by DiffPool’s GNN. The GNN is then trained on these concatenated features to perform classification (any general purpose feature can be incorporated into DiffPool like this). When we say L1 DiffPool + L2 SIGN, we mean entity label prediction using the process described above, incorporating SIGN’s feature into DiffPool’s GNN. So, we use three graph learning-based approaches: L1 DiffPool, L2 SIGN and L1 DiffPool + L2 SIGN.

We also combine L1 GDVM + L2 GDV or L1 GCM + L2 GDV with L1 DiffPool + L2 SIGN to test whether integrating information across the graph theoretic and graph learning domains improves upon either alone. Graphlet-based features can be incorporated into DiffPool using the process described previously.

In summary, thus far, we have described five single-level approaches and five NoN approaches that we use (Table 1). Note that when discussing synthetic NoNs, ‘Combined all’ refers to L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN, but when discussing the biological NoN, ‘Combined all’ refers to L1 GCM + L2 GDV + L1 DiffPool + L2 SIGN.

Table 1.

Existing approaches that we consider and their generalized NoN counterparts

Single-level approaches		NoN approaches
Level 1	Level 2	Level 1 + Level 2
L1 GDVM (73$n_{L1}$)	L2 GDV (73)	L1 GDVM + L2 GDV
L1 GCM (121)	L2 GDV (73)	L1 GCM + L2 GDV
L1 DiffPool (64)	L2 SIGN ($n_{L2}$)	L1 DiffPool + L2 SIGN
		Combined all1
		Combined all2

Note: The value in parentheses next to each Level 1 approach indicates the size of each Level 1 network’s feature. For features that are matrices, the rows are concatenated to form a 1D feature. $n_{L1}$ is the size of the Level 1 network for which the feature is being computed. The value in parentheses next to each Level 2 approach indicates the size of each Level 2 node’s feature. $n_{L2}$ is the number of nodes in the Level 2 network. Sizes of NoN features (not shown) are sums of their corresponding single-level approaches, as the NoN features are formed via concatenation. ‘Combined all¹’ refers to L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN, which is used for synthetic NoNs ‘Combined all²’ refers to L1 GCM + L2 GDV + L1 DiffPool + L2 SIGN, which is used for the biological NoN.

Next, we describe our integrative GCN-based approach. We focus on GCNs for two reasons: (i) recent work has suggested that other GNN architectures do not offer very much benefit over GCNs (Rossi et al., 2020; Shchur et al., 2018; Wu et al., 2019), making such methods more complex for little gain and (ii) the extension of GCNs to NoNs is intuitive. Note that GCNs (and thus our extension of GCNs to NoNs) are often considered to be performing semi-supervised learning (Kipf and Welling, 2016), as they make use of the entire network structure, including unlabeled nodes, to infer network features of nodes. But because we make predictions only for labeled nodes (rather than for both labeled and unlabeled nodes), and for simplicity, we continue to refer to our considered task of entity label prediction as supervised in our study.

The basic unit of a GCN is a graph convolutional layer. Graph convolution layers allow each node to see information about its neighbors. So, we generalize graph convolution layers to NoNs so that each node receives information not only from its neighbors (in the same level), but also from its corresponding network at a lower level or from the network it is a part of at a higher level. This would be in line with intuition that, e.g. the feature of a protein should contain information about how it interacts with other proteins (i.e. its topology in the Level 2 network) and structural properties of the protein itself that allow for such interactions (topology of Level 1 nodes in its Level 1 network). Then, we can stack multiple NoN graph convolutional layers (with intermediate layers in between) to form an NoN-GCN (Supplementary Section S1.3). We refer to an NoN-GCN approach using λ layers as ‘GCN-λ’.

2.5 Evaluation

For a given NoN $\{G^{(2)}=(V^{(2)},E^{(2)})$ and $\{G_1^{(1)},\dots ,G_{\left|V^{(2)}\right|}^{(1)}\}\}$, its label set $Y=y_1,\dots ,y_c$, and a function that maps Level 2 nodes (and thus their corresponding Level 1 networks) to their labels $f_{\text{true}}:V^{(2)}\to Y$, the goal is to learn a predictive function $f_{\text{pred}}:V^{(2)}\to Y$. We do this by first splitting the data into three disjoint sets: training ($V_{\text{tr}}^{(2)}$), validation ($V_{\text{val}}^{(2)}$) and testing ($V_{\text{te}}^{(2)}$). Then, we train a classifier on the training set that aims to minimize the cross-entropy loss between $f_{\text{true}}(V_{\text{tr}}^{(2)})$ and $f_{\text{pred}}(V_{\text{tr}}^{(2)})$. We use $V_{\text{val}}^{(2)}$ to optimize hyperparameters and finally report the classifier’s performance on $V_{\text{te}}^{(2)}$, an independent set never seen in the training process and not used for determining hyperparameters. As typically done (Cai et al., 2020; Hu et al., 2020; Kulmanov et al., 2018), we form these disjoint sets using stratified sampling, repeating multiple times and averaging the results to reduce bias from the randomness of the sampling. For details on hyperparameter optimization and sampling (see Supplementary Section S1.4).

Regarding how we measure classification performance of an approach, for synthetic NoNs, we report classification accuracy (Supplementary Section S1.4) since class sizes are balanced. For the real-world NoNs, we report AUPR, precision@k, recall@k and F-score@k (Supplementary Section S1.4), since class sizes are not balanced. As commonly done, we also perform statistical tests to see whether each approach’s performance is significantly better than random, i.e. is ‘significant’ (Supplementary Section S1.4).

3 Results and discussion

3.1 Synthetic NoNs

We expect NoN approaches to outperform single-level ones. We find that at least one NoN approach (L1 GDVM + L2 GDV, L1 DiffPool + L2 SIGN, L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN, GCN-2 or GCN-3) outperforms or ties (is within 1% of) all single-level approaches (L1 GDVM, L2 GDV, L1 DiffPool and L2 SIGN) for 30 out of the 30 synthetic NoNs (Fig. 3 and Supplementary Figs S2–S6). Specifically, at least one NoN approach outperforms all single-level approaches for 9 out of the 30 NoNs, and at least one NoN approach is tied with L2 SIGN for 21 out of the 30 NoNs. L2 SIGN is the only single-level approach that ties NoN approaches. However, before we discuss why L2 SIGN performs as well as NoN approaches, we need to understand the effects of both across-edge amount and rewire-noise amount.

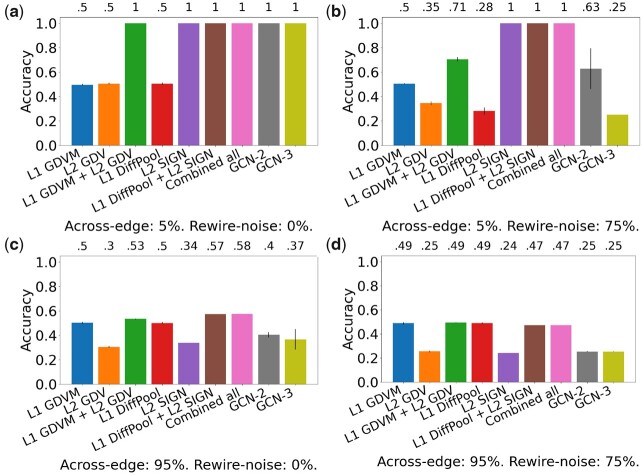
Fig. 3.

Comparison of the nine considered approaches in the task of label prediction for synthetic NoNs with the following parameters: (a) 5% across-edge and 0% rewire-noise amount, (b) 5% across-edge and 75% rewire-noise amount, (c) 95% across-edge and 0% rewire-noise amount and (d) 95% across-edge and 75% rewire-noise amount. ‘Combined all’ refers to L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN. Accuracy is shown above the bars. SDs are indicated at the top of each bar; some have very small values and are thus not visible. Recall from text that we expect an approach that only uses a single level to have around $\frac{\text{No}. \text{of\hspace{0.5em}models}}{\text{No}. \text{of\hspace{0.5em}labels}}$, or 0.5, accuracy when both across-edge and rewire-noise amount are low. However, L2 SIGN is likely able to achieve an accuracy of 1 in (a) and (b) since it captures clustering structure present in the Level 2 network. Results for other parameter combinations are shown in Supplementary Figures S2–S6

Recall that when we increase across-edge amount, Level 2 node groups’ original GEO- and SF-like network topologies are increasingly broken down and eventually become entirely random. When across-edge amount is high, most edges will exist across Level 2 node groups, not within (and there will be very little, if any, clustering structure in the Level 2 network). Thus, approaches using only Level 2 information (L2 GDV and L2 SIGN) will be making predictions on random data, and approaches that combine Level 1 and Level 2 information (all NoN approaches) will be making predictions on partially random data (Level 1 networks are unaffected by across-edge amount). So, for both types of approaches, when across-edge amount increases, we expect prediction accuracy to decrease (see also Scenarios 3 and 4 below). Indeed, we observe drops in accuracy for all approaches (Fig. 3c, d and Supplementary Figs S2–S6).

Recall that we increase rewire-noise amount to investigate approaches’ robustness to increasing data noise. When rewire-noise amount is high, both the Level 2 node groups’ and Level 1 networks’ original GEO- and SF-like network topologies will now be random (note, however, that clustering structure will not be affected since rewire-noise occurs within node groups, not across). So, all types of approaches will be making predictions on random data. As such, we expect that as rewire-noise amount increases, prediction accuracy will decrease (see also Scenarios 2 and 4 below). We observe these drops in accuracy for all approaches except L2 SIGN (Fig. 3b, d and Supplementary Figs S2–S6), which we discuss below.

We believe that it is helpful to understand what happens when each of across-edge amount and rewire-noise amount is minimized versus maximized. The following four scenarios outline the four possible combinations.

1. When both across-edge and rewire-noise amount are minimized (Fig. 3a and Supplementary Fig. S2a), the Level 2 node groups will exhibit the GEO- or SF-like network topology they were generated with, the Level 2 node groups will have high clustering structure, and the Level 1 networks will exhibit the GEO- or SF-like network topology they were generated with. As such, we expect NoN approaches to achieve accuracy of 1, as they will be able to capture the combination of network topologies at the two levels. Also, we expect single-level approaches to achieve an accuracy of 0.5 $\left(\frac{\text{No}. \text{of\hspace{0.5em}models}}{\text{No}. \text{of\hspace{0.5em}classes}}\right)$, as they will only be able to capture the difference between GEO and SF at a single level, which only accounts for half of the entities.

2. When across-edge amount is minimized and rewire-noise amount is maximized (Fig. 3b and Supplementary Fig. S2f), the Level 2 node groups will no longer have the GEO- or SF-like network topology they were generated with, as their topology will have been randomized. However, the Level 2 node groups will still exhibit clustering structure, as rewire-noise amount does not affect clustering structure (only across-edge amount does). The Level 1 networks will no longer exhibit the GEO- or SF-like network topology they were generated with, as they will have been randomized. As such, we expect NoN approaches to achieve an accuracy of 0.25 ($\frac{1}{\text{No}. \text{of\hspace{0.5em}classes}}$ for balanced class sizes), as the topologies of both the Level 2 node groups and the Level 1 networks are random, meaning there will be no topological signal at either level. Similarly, we expect single-level approaches to achieve an accuracy of 0.25.

3. When across-edge amount is maximized and rewire noise amount is minimized (Fig. 3c and Supplementary Fig. S6a), the Level 2 node groups will no longer have the GEO- or SF-like network topology they were generated with, as most edges will now exist across Level 2 node groups, not within them. As such, the Level 2 node groups will also no longer exhibit clustering structure. The Level 1 networks will be unaffected, still retaining their GEO- or SF-like topology. So, we expect NoN approaches to achieve an accuracy of 0.5, as they will only be able to distinguish between GEO and SF at Level 1, accounting for half the entities. We expect Level 2 approaches to achieve accuracy slightly higher than the 0.25 expected by random, since there will still be a small amount of topological signal. Namely, since 95% is the maximum across-edge amount, Level 2 node groups retain 5% of the edges they were initially generated with. We expect Level 1 approaches to achieve 0.5 accuracy, as they will capture the meaningful topological information in the Level 1 networks.

4. When across-edge amount is maximized and rewire-noise amount is maximized (Fig. 3d and Supplementary Fig. S6f), the Level 2 node groups will no longer have the GEO- or SF-like network topology they were generated with, as most edges will now exist between Level 2 node groups, not within them. As such, the Level 2 node groups will also no longer exhibit clustering structure. The Level 1 networks will no longer exhibit the GEO- or SF-like network topology they were generated with, as they will have been randomized. So, we expect NoN approaches to achieve an accuracy of 0.25, as the topologies of both the Level 2 node groups and the Level 1 networks will be random, meaning there will be no topological signal at either level. Similarly, we expect single-level approaches to achieve an accuracy of 0.25.

So, while we expect L2 SIGN to achieve an accuracy of 0.5 in the first scenario, we unexpectedly see that it achieves an accuracy of 1 (Fig. 3a). This surprising result warranted further investigation, which involved systematically increasing each of the across-edge and rewire-noise up to the amounts in the scenarios outlined in Points 2–4 above. From these analyses, we believe that L2 SIGN achieves higher than expected performance by capturing clustering structure in the Level 2 network. Namely, L2 SIGN performs better than expected when there is clustering structure in the networks, regardless of whether the network topologies are random (Scenarios 1 and 2, Fig. 3a and b), but it performs as expected when there is no clustering structure in general (Scenarios 3 and 4, Fig. 3c and d). This also makes sense given the kinds of adjacency matrix variants that L2 SIGN’s features are based on: the square of the adjacency matrix and the adjacency matrix where each edge is weighed based on the number of triangles it participates in. The former contains counts of the number of paths of length 2 and the latter contains counts of triangles, both of which are expected to be common in network regions with high clustering structure.

To summarize, L2 SIGN is able to perform as well as NoN approaches for 21 out of the 30 NoNs simply because there exists clustering structure in the Level 2 networks of those 21 NoNs. L2 SIGN’s ability to capture clustering structure is also likely why at low across-edge amounts, regardless of rewire-noise amount, NoN approaches incorporating L2 SIGN perform as well as they do. This also suggests that when one expects clustering structure in the data, incorporating SIGN could help.

Above, we analyze single-level approaches versus NoN approaches as well as trends regarding across-edge amount and rewire-noise amount. However, recall that the approaches we consider come from either the graph theoretic or graph learning domain. So, we also compare the two domains. For simplicity, we focus on the NoN approaches, i.e. L1 GDVM + L2 GDV from the graph theoretic domain and L1 DiffPool + L2 SIGN from the graph learning domain, as we already know that they outperform or tie single-level approaches. We find that L1 DiffPool + L2 SIGN outperforms L1 GDVM + L2 GDV for 20 out of the 30 NoNs, is tied for 9 out of the 30 NoNs, and is worse for 1 out of the 30 NoNs. However, as discussed above, for NoNs where across-edge amount is low and rewire-noise amount is high, L1 DiffPool + L2 SIGN’s performance likely comes from L2 SIGN. We also investigate whether combining research knowledge from the graph theoretic and graph learning domains improves upon each domain individually. This does not appear to be the case on the synthetic data, as L1 DiffPool + L2 SIGN is as good as L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN for 29 out of the 30 NoNs and is worse for only one NoN (Fig. 3 and Supplementary Figs S2–6).

Finally, recall that our extensions of existing node/graph label prediction approaches to their NoN counterparts (L1 GDVM + L2 GDV, L1 DiffPool + L2 SIGN, L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN) are concatenation-based, which is why we developed integrative NoN-GCN approaches (GCN-2 and GCN-3) as well. Regarding the NoN-GCN approaches themselves, we expect that GCN-3 will outperform GCN-2, as the former is a deeper model. However, this is not the case, as GCN-3 only outperforms GCN-2 for 2 out of the 30 NoNs, ties for 21 out of the 30, and is worse for 7 out of the 30 (Fig. 3 and Supplementary Figs S2–S6). This, combined with the fact that GCN-3 takes more time than GCN-2 (Section 3.3), is why we did not consider GCN-3 for the biological NoN. Still, we expect that the integrative NoN-GCN approaches will outperform the concatenation-based ones. We find that while the NoN-GCN approaches do perform well for low across-edge amounts and low rewire-noise amounts, they are not as robust to changes in those parameters compared with the concatenation-based ones. Specifically, NoN-GCN approaches perform as well as concatenation-based ones for 7 out of the 30 NoNs and are worse for 23 out of the 30 NoNs (Fig. 3 and Supplementary Figs S2–S6). These findings suggest that deep learning might not offer an advantage on this kind of synthetic data, or that more complex models are needed.

3.2 Biological NoN

Again, we expect NoN approaches to improve upon single-level ones. Since we consider 131 GO terms and parsing raw results for every single one would be difficult, we instead present summarized results over the 131. Specifically, given the eight considered approaches (L1 GCM, L2 GDV, L1 GCM + L2 GDV, L1 DiffPool, L2 SIGN, L1 DiffPool + L2 SIGN, L1 GCM + L2 GDV + L1 DiffPool + L2 SIGN and GCN-2), for each of AUPR, precision, recall and F-score, for each GO term, we do the following. We rank each of the eight approaches that are significant (Section 2.5) from first best (Rank 1) to eighth best (Rank 8), considering any approaches within 1% of each other to be tied. Then, for each approach, we count how many times (i.e. for how many GO terms) it has Ranks 1, 2 etc. We find that NoN approaches have Rank 1 for 49 out of the 131 GO terms with respect to AUPR, 37 out of 131 for precision, 35 out of 131 for recall, 33 out of 131 for F-score and 69 out of 131 for at least one of the four evaluation measures (Fig. 4 and Supplementary Fig. S7). We examine in more detail why NoN approaches work better than single-level approaches for some but not all GO terms, as follows.

Fig. 4.

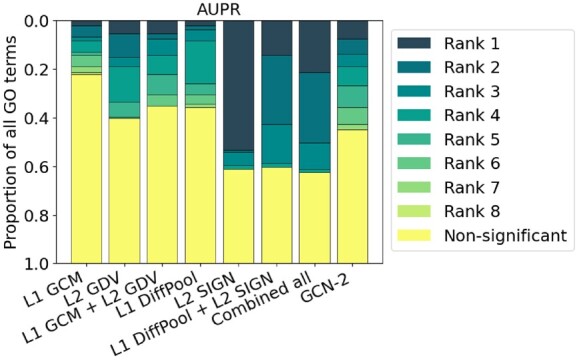
Summarized results of the eight considered approaches (as GCN-3 is not used for the biological NoN) in the task of protein functional prediction in terms of AUPR. For each GO term (out of the 131 total), we rank the eight approaches’ from best (Rank 1) to worst (Rank 8). Then, we calculate the proportion of GO terms each approach achieves each rank. ‘Combined all’ refers to L1 GCM + L2 GDV + L1 DiffPool + L2 SIGN. Results for other evaluation measures are shown in Supplementary Figure S7

First, we investigate whether the GO terms for which NoN approaches have Rank 1 are different than the GO terms for which L2 SIGN, the best approach overall, has Rank 1. If not, then NoN approaches would be redundant to L2 SIGN. To do so, for each NoN approach, we measure the overlap between the set of GO terms for which the given NoN approach has Rank 1 and the set of GO terms for which L2 SIGN has Rank 1. We find that NoN approaches have Rank 1 for mostly different GO terms compared with L2 SIGN, with a maximum overlap of around 6% (Supplementary Fig. S8). This suggests that NoN approaches are not redundant to L2 SIGN.

So, it makes sense to continue analyzing NoN approaches in comparison to single-level approaches. To better understand for which kinds of GO terms NoN approaches have Rank 1 versus for which kinds of GO terms single-level approaches have Rank 1, we do the following. For each evaluation measure, we split the 131 GO terms into six groups based on how single-level approaches perform in relation to NoN approaches, with ‘S’ referring to single-level approaches and ‘C’ referring to combined-level (i.e. NoN) approaches, as outlined in Table 2. As an example, for AUPR, ‘S < C’ indicates that the performance of single-level approaches (‘S’) is worse than (‘<’) the performance of NoN approaches (‘C’). In other words, the group ‘S < C’ contains all GO terms for which at least one NoN approach has Rank 1 (multiple NoN approaches can be tied with each other for Rank 1), and all single-level approaches have Rank 2 or worse, with respect to AUPR. Note that for a GO term in the above scenario, if no single-level approaches are significant, that GO term would be in the ‘C only’ group instead, corresponding to those GO terms for which only NoN approaches are significant.

Table 2.

Description of the six GO term groups based on how single-level (S) and combined-level (C), i.e. NoN, approaches perform

S only	At least one ‘S’ approach is significant;
	no ‘C’ approaches are significant.
S > C	At least one ‘S’ approach is significant and has Rank 1;
	at least one ‘C’ approach is significant but none have Rank 1.
S = C	At least one ‘S’ approach is significant and has Rank 1;
	at least one ‘C’ approach is significant and has Rank 1.
S < C	At least one ‘S’ approach is significant but none have Rank 1;
	at least one ‘C’ approach is significant and has Rank 1.
C only	No ‘S’ approaches are significant;
	at least one ‘C’ approach is significant.
No sig.	No approaches are significant.

Note: Rows with blue backgrounds correspond to the groups where NoN approaches are the best.

Given these groups, we investigate whether there are any GO terms where NoN approaches are necessary if one wants to make accurate predictions. We do so by looking at the number of GO terms for which at least one NoN approach has Rank 1 and all single-level approaches are strictly worse, i.e. not tied for Rank 1. This corresponds to the number of GO terms in the groups ‘S < C’ and ‘C only’. We find that NoN approaches have Rank 1 and are untied with any single-level approach for around 20–30% of all GO terms, depending on evaluation measure (Table 3). Taking the union over all evaluation measures, we find that there are 33 (25% of) GO terms in ‘S < C’ and 38 (29% of) in ‘C only’, i.e. a total of 60 (46% of) GO term across the two groups. That is to say, there are 33 GO terms where NoN approaches outperform single-level approaches (but single-level approaches are still significant) for at least one evaluation measure and, importantly, 38 GO terms where only NoN approaches are able to perform significantly better than random for at least one evaluation measure. In other words, for those 38 GO terms, only NoN approaches make meaningful protein functional predictions, while single-level ones achieve random accuracy. Taking the groups together, we find that there are 60 GO terms where NoN approaches have Rank 1 and single-level approaches are strictly worse for at least one evaluation measure. These results suggest that NoN approaches are necessary, especially if one wants to make predictions for certain GO terms.

Table 3.

Number of GO terms in each of the six groups for AUPR, precision, recall and F-score

	Number of GO terms in each group for
	AUPR		Precision		Recall		F-score		Union
S only	12	9%	20	15%	33	25%	31	24%	46
S > C	63	48%	45	35%	22	17%	30	23%	75
S = C	8	6%	8	6%	6	5%	4	3%	18
S < C	27	21%	8	6%	8	6%	9	7%	33
C only	14	11%	21	16%	21	16%	20	15%	38
No significance	7	5%	29	22%	41	31%	37	28%	43

Note: For example, for AUPR, there are 14 GO terms in the group ‘C only’. We also report the union of GO terms in a given group over all measures (Union). For example, there are 38 GO terms in the union of ‘C only’ over all evaluation measures. Rows with blue backgrounds correspond to the groups where NoN approaches are the best. The IDs and names of GO terms in each group for each measure can be found in Supplementary Tables S1–S4.

Since we now know that NoN approaches are important, we investigate which of them are the best. Here, we comment on results for AUPR (Supplementary Fig. S9a), only noting that results are qualitatively similar for other measures (Supplementary Figs S9–S13). For ‘S < C’, L1 GCM + L2 GDV + L1 DiffPool + L2 SIGN, i.e. the combination of graph theoretic and graph learning approaches, is the best overall NoN approach. It has Rank 1 for 19 GO terms, while all other NoN approaches have Rank 1 for fewer than 19 GO terms (Supplementary Fig. S9a). This suggests that integrating knowledge across domains is somewhat useful. For ‘C only’, GCN-2 has Rank 1 for nine GO terms, while all other NoN approaches have Rank 1 for fewer than nine GO terms (Supplementary Fig. S9b). In fact, for seven out of the nine GO terms, GCN-2 is the only approach that is significant (Supplementary Fig. S10). This suggests that deep learning could be useful for otherwise difficult-to-predict GO terms.

Finally, note that we did analyze the properties of GO terms in each of the six GO term groups, in order to see whether different GO term groups contain different kinds of GO terms. Specifically, for each group, we computed the distribution of the depths of the GO terms in the GO tree and the distribution of class sizes (number of proteins annotated by each GO term, which ranges from 20 to 277), and compared groups’ distributions to each other. We found that ‘S < C’ and ‘C only’ contain GO terms whose classes sizes are among the smallest, suggesting that NoN approaches may have some potential to make predictions for GO terms with limited training data. And while one might expect that GO terms with small class sizes correspond to those that are deep in the GO tree, we find that there is no significant difference between the six GO term groups with respect to GO term tree depth.

3.3 Running times

Last, we analyze approaches’ running times for the synthetic NoN with 5% across-edge and 0% rewire-noise amount as a representative; we choose a single NoN for two reasons. The first is that GCN-3 was only run on synthetic NoNs (Section 3.1), so they are the only NoNs where we can analyze the tradeoff between performance (Fig. 3) and running time. The second is simplicity: trends are qualitatively similar across all synthetic NoNs. For each approach, we record the time to extract all necessary features and the time for one epoch of training the associated classifier. For hardware details (see Supplementary Section S2.3).

First, GCN-3, which we found does not have a clear advantage over GCN-2 in terms of accuracy (Section 3.1), takes 4.25× longer to train. This poor tradeoff between accuracy and running time is why we did not consider GCN-3 for the biological NoN.

Second, recall that L1 DiffPool + L2 SIGN and L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN, the best approaches overall, are as good as each other in terms of accuracy, with the former being worse in only 1 out of the 30 NoNs. Thus, because L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN has longer feature extraction and training time than L1 DiffPool + L2 SIGN (Supplementary Table S5), L1 DiffPool + L2 SIGN would likely be the better approach to use for a general NoN when considering the tradeoff between accuracy and running time. Also recall that L2 SIGN performs as well as L1 DiffPool + L2 SIGN and L1 GDVM + L2 GDV + L1 DiffPool + L2 SIGN for 21 out of the 30 NoNs, in those NoNs where there is significant clustering structure in the Level 2 network. Thus, if one expects significant clustering structure in the Level 2 network of a general NoN, L2 SIGN should be considered, as its feature extraction time is around 77× faster and its training time is around 1.5× faster than those of L1 DiffPool + L2 SIGN (Supplementary Table S5).

4 Conclusion

We present a comprehensive framework to test whether integrating network information into an NoN leads to more accurate label predictions than using information from a single level alone. We also develop the first synthetic NoN generator that can create NoNs with a variety of parameters for study, construct a biological NoN from PPIN and PSN data and propose a novel GCN-based model for label prediction on NoNs. We have shown that on synthetic data, NoN approaches are among the best, and that on a real-world biological NoN, NoN approaches are necessary to make predictions about certain protein functions. As such, research into NoN-based data integration is promising, and likely could be applied to a variety of other tasks, especially as such NoN data becomes readily available.

To our knowledge, our study is the first to investigate data integration for label prediction using NoNs. As such, it is ‘just’ a proof of concept. Many opportunities exist for further advancement of our work. As an example, recall that studies have combined protein sequence and protein structural data with PPI data (Peng et al., 2014; Zhang et al., 2009, 2019). So, an important future direction is the comparison between different data integration schemes for various tasks.

As another example, an NoN as we define it might have a limitation when trying to model certain systems. Namely, an interaction between two entities at the higher level may actually be due to a number of interactions occurring at the lower level. For example, an interaction between two proteins occurs due to interactions between subsets of their amino acids. Unfortunately, with current biotechnologies, large-scale data on interactions between proteins are captured at the protein level rather than at amino acid level. So, these fine-grained, amino acid-level interactions cannot be captured by our current NoN model. Advancements to account for them will be necessary once such detailed data become available. This is especially important since even our current, simpler NoN model already leads to improvements compared with current methods. Therefore, a more advanced version should only improve further (for applicable systems). However, our current NoN model does have advantages. Namely, not all systems that can be modeled as complex networks of networks benefit from the more detailed representation. For example, as discussed in Section 1, Parkinson et al. (2018) study an NoN where an interaction between two Level 2 nodes (individuals in a social network) is based on the individuals’ friendships. This could not be represented by interactions between subsets of Level 1 nodes (neurons of the individuals’ brain networks). As our current NoN model would be favorable for such systems, further development of the coarse-grained, and the fine-grained, NoN models are both important directions.

As another example, while our integrative NoN-GCN approach is not significantly better than just combining features from the two levels overall, there are some protein functions for which it is the only approach to make non-random predictions. This indicates that the strength of our NoN model is not just from the availability of more features for prediction (i.e. two levels instead of one), but rather also from the actual integration of the two levels that the model provides. Importantly, this also means that research into more sophisticated, scalable and integrative deep learning models for NoNs, perhaps taking inspiration from SIGN’s pre-computable neighborhood aggregators, is worth pursuing.

As a final example, we only analyze a two-level NoN in our study, so expanding in scale is an important future direction.