Abstract
Motivation
Cancer survival prediction can greatly assist clinicians in planning patient treatments and improving their life quality. Recent evidence suggests the fusion of multimodal data, such as genomic data and pathological images, is crucial for understanding cancer heterogeneity and enhancing survival prediction. As a powerful multimodal fusion technique, Kronecker product has shown its superiority in predicting survival. However, this technique introduces a large number of parameters that may lead to high computational cost and a risk of overfitting, thus limiting its applicability and improvement in performance. Another limitation of existing approaches using Kronecker product is that they only mine relations for one single time to learn multimodal representation and therefore face significant challenges in deeply mining rich information from multimodal data for accurate survival prediction.
Results
To address the above limitations, we present a novel hierarchical multimodal fusion approach named HFBSurv by employing factorized bilinear model to fuse genomic and image features step by step. Specifically, with a multiple fusion strategy HFBSurv decomposes the fusion problem into different levels and each of them integrates and passes information progressively from the low level to the high level, thus leading to the more specialized fusion procedure and expressive multimodal representation. In this hierarchical framework, both modality-specific and cross-modality attentional factorized bilinear modules are designed to not only capture and quantify complex relations from multimodal data, but also dramatically reduce computational complexity. Extensive experiments demonstrate that our method performs an effective hierarchical fusion of multimodal data and achieves consistently better performance than other methods for survival prediction.
Availability and implementation
HFBSurv is freely available at https://github.com/Liruiqing-ustc/HFBSurv.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
As an aggressive disease, cancer has become the leading cause of death in the world. According to the latest global cancer report, the cancer burden is estimated 19.3 million new cases and almost 10.0 million deaths worldwide in 2020, among which breast cancer has become the most common cancer type (Sung et al., 2021). Given the fact that cancer is a complex and intrinsically heterogeneous disease, dramatic discrepancy in molecular and clinical characteristics can be observed across patients with the same cancer type (Beck, 2015), which in consequence significantly affects the clinical outcome and prognosis. Therefore, an urgent need exists for the development of efficient methods to accurately predict the survival of cancer patients, which can greatly assist clinicians in planning patient treatments and improving their life quality (Huang et al., 2020).
From a computational perspective, survival prediction is usually modeled to regress patients’ survival time (Ching et al., 2018). One standard method for survival prediction is the Cox proportional hazards (CoxPH) model, in which a linear combination of covariates contributes to the log-partial hazard of a patient. Furthermore, various extensions to CoxPH model, such as LASSO regularization (Tibshirani, 1997) and deep neural network supervised by Cox partial likelihood loss (Ching et al., 2018; Mobadersany et al., 2018), have been successfully proposed and demonstrate promising performance. Prior works (Chaudhary et al., 2018; Gevaert et al., 2006; Katzman et al., 2018) have tried to solve the problem of survival prediction based on genomic data obtained from high-throughput platforms. For example, gene expression data of breast cancer demonstrates great potential for identifying prognostic factors and brings good performance in predicting survival (Xu et al., 2012). In addition, copy number alteration (CNA) represents an important component of genetic variation and is also found to be useful for predicting survival (Shao et al., 2020; Sun et al., 2018; Wang et al., 2020). Although molecular data can reveal information valuable for survival of cancer patients, there is still scope for improving survival prediction performance by considering more cancer-related data.
Besides genomic data, pathological image can provide insight into morphological attributes of cells that are closely associated with the survival of cancer patients (Shao et al., 2020). With the emergence of digital whole-slide images, computing methods for analyzing pathological images have demonstrated promising capability to improve efficiency, accuracy and consistency (Cheng et al., 2017). Accordingly, several image-based methods (Cheng et al., 2018; Xu et al., 2016; Yu et al., 2016) have been developed for predicting survival. In this way, a number of features can be extracted from pathological images to characterize the size, shape, distribution and texture of nuclei. These predictive features have been reported to have a strong association with cancer patients’ survival, thus providing exciting opportunities for further study.
With the impact of genomic data or histopathological images in cancer study, the integration of above data types, in essence multimodal data, is crucial for our understanding of cancer heterogeneity and complexity. Accordingly, the rapid development of survival prediction models (Cheng et al., 2017; Ning et al., 2020; Yuan et al., 2012) using multimodal data suggests the effectiveness of fusing complementary information from different modalities to enhance predictive performance. Over the past years, multimodal fusion via deep learning has been emerged as an interdisciplinary field for solving challenging prediction tasks (Guo et al., 2019). Accordingly, several deep learning-based fusion methods for multimodal data are successfully proposed for cancer survival prediction (Cheerla and Gevaert, 2019; Mobadersany et al., 2018; Wang et al., 2020), which are highly flexible and can combine disparate heterogeneous data modalities in a non-linear manner.
In addition to the aforementioned multimodal fusion methods, the technique using Kronecker product shows its superiority in cancer survival prediction. Specifically, Kronecker product considers pairwise interactions of two input feature vectors by producing a high-dimensional feature of quadratic expansion (Kim et al., 2017). For example, as a pioneered work, Chen et al. (2020) present deep-learning-based framework named Pathomic Fusion for predicting survival outcome by fusing histology and genomic multimodal data, in which Kronecker product is taken to model pairwise feature interactions across modalities. To integrate gene expression data and pathological image, we previously propose a method named GPDBN (Wang et al., 2021) that adopts Kronecker product to model inter-modality and intra-modality relations for cancer prognosis prediction. Despite of promising results, using Kronecker product in multimodal fusion may introduce a large number of parameters that may lead to high computational cost and a risk of overfitting (Kim et al., 2017; Liu et al., 2018), thus limiting its applicability and improvement in performance. Another limitation of above approaches is that they only mine relations for one single time (i.e. single fusion) to learn multimodal representation. However, due to the complexity of multimodal data, such single fusion strategy still faces significant challenges in deeply mining the rich information from genomic data and pathological images for accurate survival prediction.
Considering the limitations mentioned above, in this work, we present a novel multimodal approach named hierarchical factorized bilinear fusion for cancer survival prediction (HFBSurv), which employs factorized bilinear models (Kim et al., 2017; Yu et al., 2017) to fuse genomic and image features step by step. Specifically, with a multiple fusion strategy HFBSurv decomposes the fusion problem into different levels and each of them integrates and passes the fused information progressively from the low level to the high level. In low-level fusion, instead of directly applying Kronecker product, we introduce a modality-specific attentional factorized bilinear module (MAFB) with significantly reduced training parameters and computational complexity to capture modality-specific relations and quantify their importance. In addition, we leverage a cross-modality attentional factorized bilinear module (CAFB) for high-level fusion, which allows relations across modality to be fully explored and enables different importance for them. We argue the proposed approach can capture diverse modality-specific and cross-modality relations among different modalities and fuse the features extracted from multiple modalities in a specialized, effective way. For verifying the effectiveness of our proposed approach, experiments are conducted on the breast cancer dataset from the Cancer Genome Atlas (TCGA) and the results demonstrate that HFBsurv achieves consistently better performance than other methods for survival prediction.
2 Materials and methods
2.1 Data preprocessing
In this work, the proposed method is tested on the breast invasive carcinoma cohort obtained from TCGA (Zhu et al., 2014). In detail, only patient samples with matched multimodal data including H&E-stained whole-slide images, gene expression, CNA and clinical information are selected for further study. In addition, by following previous study (Cheng et al., 2017) we exclude patients with missing or excessively short follow-up (i.e. shorter than 30 days). Finally, 1015 patients with the corresponding survival status and survival time are enrolled in this study. To comprehensively evaluate our survival prediction method, we adopt repeated holdout cross-validation by following Ching et al. (2018). In particular, the dataset is randomly partitioned into 80% training set and 20% testing set. To ensure the robustness of our results, the random partitioning process is repeated 10 times to generate 10 training/testing set pairs. After that, we train a prediction model using each training set and evaluate C-index and AUC of these models on the paired testing sets. Finally, we report the mean value and standard deviation of these 10 performance measurements.
In our study, the processing procedure of genomic data including gene expression and CNA is as follows. First, similar to prior works (Dhillon and Singh, 2020; Ding et al., 2016), for each data type the missing values over 10% of the patients are removed, and the other missing values are estimated by the weighted nearest neighbors algorithm. Second, according to previous study (Gevaert et al., 2006), we normalize the gene expression data and discretize them to three categories: overexpressed (1), baseline (0) and underexpressed (-1). Meanwhile the linear copy number values are normalized using z-score. After that, the gene expression and CNA data consists of 19 006 and 24 776 genes, respectively. Finally, a commonly used R package randomForestSRC (Yu et al., 2019) for survival analysis is adopted to select features, by which the top 80 gene expression and CNA features are chosen respectively for further study. It is of note that we only apply feature selection to the training set and a prediction model is built on the selected features to rigorously evaluate performance with the untouched paired testing set.
For pathological images, we extract quantitative image features by following previous study (Yu et al., 2016). Specifically, all images captured at 40× magnification are first divided into tiles of 1000 by 1000 pixels with bftools in an open microscopy environment. Next, we select 10 tiles with the highest image density defined as the summation of red, green and blue values (Sun et al., 2018). Then, a total of 2343 quantitative features are extracted from pathological images using CellProfiler (Carpenter et al., 2006), including the shape, size, texture as well as pixel intensity distribution of cells and nuclei. Finally, the feature selection procedure described above is performed to yield pathological image features with the same dimensionality as genomic features.
2.2 HFBSurv
2.2.1 Model architecture
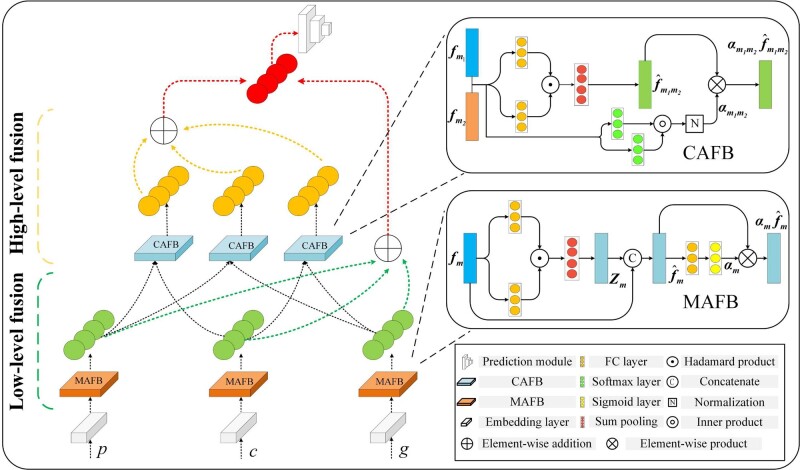
The hierarchical architecture of our proposed HFBSurv is presented in Figure 1, where three modalities are included as input: pathological image, CNA and gene expression , with being the dimensionality of and so on. For pre-processed feature from each modality, a fully connected (FC) embedding layer is adopted to map feature into similar embedding space for alleviating the statistical property differences between modalities (Gu et al., 2017). Specifically, each embedding layer has 80 and 50 neurons respectively and encodes the embedding as. After that, embedding of each modality is first used as input of MAFB (details are described in Section 2.2.2) to generate modality-specific representation capturing correlations and dependencies within each modality, as well as the weight representing the corresponding modality-specific importance. Then the feature vector of low-level fusion is calculated as the weighted average of all modality-specific representations and is formulated as . Intuitively, can efficiently focus on modality-specific fusion by taking into account intrinsic relations within each modality.
Fig. 1.
Illustration of the proposed HFBSurv architecture
Moreover, the low level also delivers representations of all modalities to the high level where the information is further fused to form representations between different modalities. We hypothesize that compared with the direct use of that may be noisy, using effective derived from the low level is more appropriate in generating useful cross-modality representations in the high level. In detail, modality-specific representations are fused two in two by CAFB (as revealed in the Section 2.2.3) to yield cross-modality representations and , as well as the weight representing the corresponding cross-modality importance. Note that can provide sufficient information regarding to the complex relations between modalities. Afterwards, the feature vector of high-level fusion is calculated as and , which could fully learn relations across modalities owing to the effectiveness of cross-modality representations .
Finally, we are therefore able to obtain two kinds of feature vectors i.e. and respectively. To make full use of them, HFBSurv concatenates and to obtain the final comprehensive multimodal representation by leveraging the complementary information from these intermediate feature vectors. To make survival prediction, is passed through a prediction module including two tanh activated FC layers containing 256 and 64 nodes, respectively, each followed by dropout layer with rate 0.25 to prevent overfitting. Then a final Cox layer is adopted to make survival prediction by performing Cox proportional hazards regression (Hao et al., 2018; Huang et al., 2019).
2.2.2 MAFB in low-level fusion
The exploitation of relations within each modality has been successfully introduced in cancer prognosis via bilinear model (Wang et al., 2021) or graph-based model (Subramanian et al., 2021). In this study, we focus on bilinear model since it can provide rich representations by exploiting the relations within each modality. Specifically, given -dimensional input vectors derived from a single modality such as gene expression, a full bilinear model is defined by:
| (1) |
where represents a projection matrix and denotes the output of the bilinear model. In practice, a bilinear model in Equation (1) can be implemented using Kronecker product followed by a linear mapping to project the representations into a h-dimensional output bilinear vector. Although the full bilinear model is valuable in capturing pairwise feature interactions, it also introduces a large number of parameters potentially leading to high computational cost and the overfitting risk (Liu et al., 2018; Mai et al., 2020a)
Motivated by recent advance in factorized bilinear model (Kim et al., 2017; Yu et al., 2017), in this study we develop MAFB to capture relations within each modality with the aim of facilitating low-level fusion in HFBSurv, which enjoy the dual benefits of much fewer parameters and robust expressive capacity of full bilinear model. As shown in Figure 1, MAFB takes the embedding of each modality as input and factorizes the projection matrix in Equation (1) into two low-rank matrices according to matrix factorization:
| (2) |
where is the latent dimensionality of the factorized matrices and , is the Hadamard product of two feature vectors, and is an all-one vector. By this means, the computational burden for learning a bilinear model will be dramatically reduced. For the purpose of obtaining output feature by Equation (2), the weights and to be learned are two three-order tensors. According to Yu et al. (2017), Equation (2) can be rewritten as follows:
| (3) |
where function performs sum pooling over by using a 1-D non-overlapped window with the size k, and are 2-D matrices reshaped from and , respectively. Finally, the modality-specific representation is obtained as shown below:
| (4) |
where denotes vector concatenation.
To obtain more discriminative features for multimodal representation and benefit downstream fusion, in MAFB we also introduce an unimodal attention to adaptively assign the weight for each modality-specific representation to quantify its importance. In detail, a sigmoid activated FC layer is adopted to process each modality-specific representation and outputs the corresponding importance, as defined below:
| (5) |
where and refer to parameter matrix and bias item of FC layer, respectively. By fully capturing intrinsic relations within each modality, provides a plausible way to generate appropriate modality-specific importance. Therefore, the output of MAFB for each modality is denoted as.
2.2.3 CAFB in high-level fusion
Performing fusion for mining complementary information across modalities plays an important role in multimodal fusion. In HFBSurv, CAFB is introduced to fuse diverse information of different modalities for explicitly exploring complex relations across modalities and assign different importance for them. Specifically, after receiving the modality-specific representations as well as the corresponding importance from the low level, the s-dimensional cross-modality representation can begenerated similar to Equation (2):
| (6) |
where factorized matrices and represent learnable weights to obtain the output feature. Equation (6) can be further rewritten as follows:
| (7) |
where and are 2-D matrices reshaped from and, respectively.
In addition, we specifically leverage a bimodal attention to identify the importance of the cross-modality representation. In detail, the similarity of and is first estimated as follows:
| (8) |
where the computed similarity is in the range of 0 to 1. We argue that using the weighted modality-specific representation in Equation (8) rather than the original embeddings as adopted in previous study (Mai et al., 2020b) renders a better indication of the degree of similarity between the two modalities. Then, the cross-modality importance is obtained by:
| (9) |
where represents a pre-defined term controlling the relative contribution of similarity and modality-specific importance, and here is set to 0.5. Therefore, the output of CAFB is the weighted cross-modality representation and .
2.3 Training
In this study, we use the Cox partial likelihood loss (Cheerla and Gevaert, 2019) with regularization to train the model end-to-end for survival prediction, which is defined as:
| (10) |
where the values , and for each patient represent the survival status, the survival time and the data, respectively, and is the neural network model trained for predicting the risk of survival, is a regularization hyperparameter to avoid overfitting.
HFBSurv follows a modern deep learning design and is implemented by PyTorch platform. In this study, l, h and s, i.e. the dimensionality of , and , are set to 50, 20 and 20, respectively. And the latent dimensionality k of the factorized matrices is set to 20. The learning rate and the λ are tunable hyper-parameters in our model. We train the model with Adam optimizer that is a widely used stochastic gradient descent algorithm. For each training/testing set pair, we first empirically preset learning rate to 1.2e-4 as a starting point for a grid search during training. After that, by following Ching et al. (2018), an optimal learning rate is determined through 5-fold cross-validation on the training set, using C-index as the performance metric. Finally, the model is trained on all of the training set using the optimal learning rate and then evaluated on the testing set. To determine an optimal value for , we check a few of different values via a simple grid search and settle on 3e-3 throughout the experiments. The server used for training is equipped with Intel Xeon 4110 @ 2.10 GHz CPU and NVIDIA GeForce RTX 2080Ti GPU.
2.4 Evaluation metrics
In this study, the Concordance Index (i.e. C-index) and AUC are served as our evaluation metrics by following previous study (Shao et al., 2020). Here, the C-index is calculated for quantifying the quality of the ranking at the patient level as below:
| (11) |
where represents number of comparable pairs of patients, denotes the patient’s actually observed survival and refers to the function of the indicator. The AUC measures the ranking quality at event-time level and can be computed as follows:
| (12) |
where and refer to the cumulative number of comparable pairs computed across all event times and the set of all possible event times in the dataset, respectively. With values of C-index and AUC ranging from 0 to 1, a higher value of C-index and AUC indicates better model prediction performance and vice versa.
3 Results
3.1 Evaluation of HFBSurv
In this study, extensive experiments are conducted to evaluate the performance of HFBSurv in repeated holdout cross-validation. To demonstrate that the hierarchical fusion strategy is indeed effective, we introduce four typical single-fusion methods to compare with HFBSurv: (i) Direct combination: concatenation from multimodal embeddings; (ii) Element-wise addition: element-wise addition from multimodal embeddings; (iii) Decision fusion: decision voting on the output of single modality network; (iv) Tensor fusion: Kronecker product from multimodal embeddings. For fair comparison, survival prediction using aforementioned fusion methods is performed by the same prediction module as described in Section 2.2.1.
Table 1 shows the C-index and AUC values of different methods, and some important observations are made as follows. We can see that HFBSurv achieves the best performance and shows remarkable improvement over single-fusion methods. Specifically, HFBSurv outperforms the Direct combination, Element-wise addition, Decision fusion and Tensor fusion by about 9.3%, 9.0%, 9.9% and 8.5%, respectively. These results suggest that by adopting multiple fusion strategy in a hierarchical way, the proposed HFBSurv can effectively capture diverse relations within and across modalities. Moreover, it is of note that compared with other single-fusion methods, Tensor fusion shows relatively higher C-index value, but the improvement in performance is limited probably due to the large number of parameters introduced by Kronecker product. Meanwhile, we can also infer from Table 1 that HFBSurv brings significant improvement on AUC compared to single fusion methods, demonstrating its superiority in generating more comprehensive multimodal representation for predicting patient survival.
Table 1.
Evaluation of HFBSurv using C-index and AUC values
| Fusion strategy | Method | C-index | AUC |
|---|---|---|---|
| Single | Direct combination | 0.673±0.039 | 0.706±0.041 |
| Element-wise addition | 0.676±0.040 | 0.711±0.048 | |
| Decision fusion | 0.667±0.083 | 0.707±0.087 | |
| Tensor fusion | 0.681±0.042 | 0.727±0.050 | |
| Hierarchical | Low | 0.702±0.026 | 0.734±0.033 |
| LowAtt | 0.719±0.024 | 0.756±0.028 | |
| High* | 0.748±0.029 | 0.788±0.033 | |
| HFBSurv | 0.766±0.024 | 0.806±0.025 |
Furthermore, we adopt four different configurations of HFBSurv to evaluate each component of the proposed method: (i) Low: only low-level fusion by incorporating MAFB without unimodal attention; (ii) LowAtt: only low-level fusion by incorporating full MAFB (i.e. with unimodal attention); (iii) High*: hierarchical (both low- and high-level) fusion by incorporating full MAFB and CAFB without bimodal attention; (iv) HFBSurv: our proposed hierarchical (both low- and high-level) fusion by incorporating full MAFB and full CAFB (i.e. with bimodal attention). Also, to compare fairly the same prediction module is adopted to predict survival.
As shown in Table 1, we can find that both Low and LowAtt achieve better performance than single fusion methods, which demonstrates the power of MAFB in capturing intrinsic relations within each modality. More importantly, High* and HFBSurv consistently yield remarkable improvements on C-index and AUC. For example, HFBSurv outperforms Low and LowAtt with 6.4% and 4.7% improvements on C-index, respectively. These results clearly highlight the benefit of conducting hierarchical fusion and the effectiveness of CAFB by exploring relations across modalities. In addition, we find the attention mechanism is a good technical choice for multimodal fusion in predicting survival. For example, after adding unimodal and bimodal attention, LowAtt and HFBSurv successfully improve the C-index by 1.7% and 1.8%, respectively. To conclude from the aforementioned analysis, the hierarchical fusion strategy and attentional factorized bilinear model are two crucial factors leading to the remarkable improvement of HFBSurv.
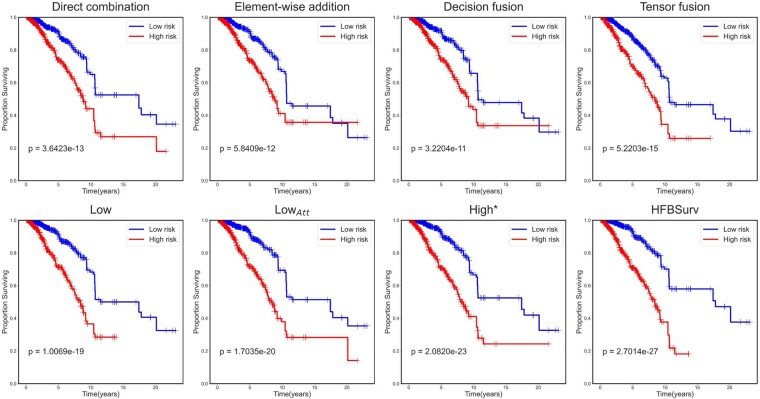
To further understand the improvement made by HFBSurv, Kaplan-Meier curves of the above approaches are plotted and displayed in Figure 2. In practice, we concatenate predicted risks from all of the test sets in the repeated holdout cross-validation and plot them against their survival time by following Chen et al. (2020). We can observe that HFBSurv enables easy separation of patients into low and high risk groups with remarkably better stratification (P-value = 2.7014e-27) in comparison to the best single fusion method Tensor fusion (P-value = 5.2203e-15). In addition, it is noteworthy that the HFBSurv can also provide a more favorable prognostic prediction as compared with High* (P-value = 2.0820e-23), LowAtt (P-value = 1.7035e-20) and Low (P-value = 1.0069e-19). All of these results clearly demonstrate the superiority of our method for multimodal fusion in survival prediction.
Fig. 2.
Performance evaluation of HFBSurv using Kaplan–Meier curve
3.2 Performance comparison with existing methods
HFBSurv is further assessed by comparing the performance with recent deep learning-based survival prediction methods MDNNMD (Sun et al., 2019), DeepSurv (Katzman et al., 2018), GPDBN(Wang et al., 2021) and Pathomic Fusion (Chen et al., 2020), as well as traditional methods RSF (Ishwaran et al., 2008), En-Cox (Yang and Zou, 2013) and LASSO-Cox (Tibshirani, 1997). For fair comparison, all aforementioned prediction models use exactly same multimodal features for performance evaluation throughout the experiment. From the experimental results listed in Table 2, it is obvious that all these methods have satisfying performance by incorporating multimodal information. Meanwhile, deep learning-based approaches generally exhibit better performance than traditional methods. For example, compared with LASSO-Cox, Pathomic Fusion boosts the C-index and AUC by 4.0% and 5.2%, respectively. More importantly, our proposed HFBSurv reaches a superior C-index of 0.766, which outperforms all other methods including Kronecker product-based GPDBN and Pathomic Fusion by a large margin. In addition to C-index, HFBSurv also achieves the best AUC value of 0.806 and consistently surpasses other investigated methods. These results suggest that our method performs an effective and specialized hierarchical fusion of multimodal data for survival prediction.
Table 2.
Performance comparison of HFBSurv and other methods using C-index and AUC values
| Method | C-index | AUC | |
|---|---|---|---|
| Traditional | RSF | 0.663±0.051 | 0.700±0.058 |
| En-Cox | 0.682±0.040 | 0.711±0.043 | |
| LASSO-Cox | 0.673±0.045 | 0.703±0.051 | |
| Deep-learning | DeepSurv | 0.705±0.051 | 0.745±0.060 |
| MDNNMD | 0.708±0.050 | 0.747±0.064 | |
| GPDBN | 0.721±0.063 | 0.763±0.067 | |
| Pathomic fusion | 0.713±0.035 | 0.755±0.042 | |
| HFBSurv | 0.766±0.024 | 0.806±0.025 |
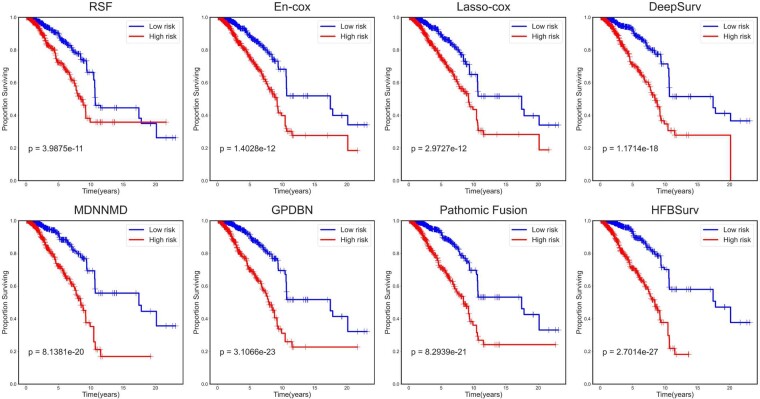
To further evaluate the performance of HFBSurv, we plot Kaplan–Meier curves of all investigated methods in Figure 3. It can be observed that for traditional methods, En-cox provides slightly better prognostic prediction with a P-value of 1.4028e-12 than RSF (P-value = 3.9875e-11) and LASSO-Cox (P-value = 2.9727e-12). Of all deep learning-based methods, GPDBN and Pathomic Fusion show competitive P-value of 3.1066e-23 and 8.2939e-21, respectively by adopting Kronecker product to capture pairwise feature interactions. In comparison, HFBSurv gives the most significant P-value of 2.7014e-27, which again confirms the effectiveness of the proposed method in predicting survival.
Fig.3.
Performance comparison of HFBSurv and other methods using Kaplan–Meier curve
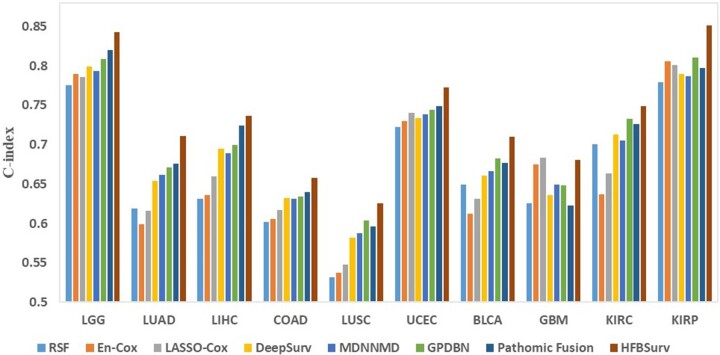
In addition, as a general framework HFBSurv can be applied to different cancer types. To validate our method on other cancers, we download and process 10 more publicly available cancer datasets from TCGA including brain lower grade glioma (LGG), lung adeno-carcinoma (LUAD), liver hepatocellular carcinoma (LIHC), colon adenocarcinoma (COAD), lung squamous cell carcinoma (LUSC), uterine corpus endometrial carcinoma (UCEC), bladder urothelial carcinoma (BLCA), glioblastoma multiforme (GBM), kidney renal clear cell carcinoma (KIRC) and kidney renal papillary cell carcinoma (KIRP). After that, we perform more comprehensive experiments to further investigate the performance improvements of our proposed method over other approaches. As can be seen from Figure 4 and Supplementary Table S1–S10, our method compares favorably against other existing methods in terms of both C-index and AUC. Taken together, these results clearly demonstrate the advantage of HFBSurv as a general framework for predicting survival of different cancer patients.
Fig.4.
Performance comparison of different methods on other TCGA datasets
3.3 Complexity comparison
One significant concern with deep learning is the computational cost of training and testing models. In this experiment, we compare HFBSurv with Pathomic Fusion and GPDBN since they have similar consideration to our method. Specifically, all models with original implementation are run in the equivalent environment as described in Section 2.4 and GPDPN is extended to handle the case of more than two modalities. We use the amount of trainable parameters as a proxy for the space complexity. As illustrated in Table 3, HFBSurv has 0.150M trainable parameters, which is approximately 12.5% and 13.2% of the number of parameters of Pathomic Fusion and GPDBN, respectively. To assess the time complexity of HFBSurv and the competitive methods, we calculate floating-point operations per second (FLOPS) of each method in testing. The results in Table 3 show that HFBSurv needs 0.206G FLOPS during testing, compared with 1.201G and 1.114G FLOPS in Pathomic Fusion and GPDBN, respectively. The main reason for fewer trainable parameters and number of FLOPS lies in that HFBSurv performs multimodal fusion using factorized bilinear model, and can significantly reduce the computational complexity and meanwhile obtain more favorable performance.
Table 3.
Comparison of model complexity
| Methods | Number of parameters | FLOPS |
|---|---|---|
| Pathomic Fusion | 1.201M | 1.219G |
| GPDBN | 1.114M | 1.130G |
| HFBSurv | 0.150M | 0.206G |
3.4 Univariate and multivariate Cox proportional hazards analysis
With the aim of evaluating the independent prognostic power of risk predicted by HFBSurv, we perform univariate and multivariate Cox proportional hazards analysis of HFBSurv risk and other standard clinicopathologic variables in breast cancer prognosis (Yu et al., 2019), including age at diagnosis, histologic grade, tumor size (T stage), lymph node invasion (N stage) and metastatic spread (M stage). As presented in Table 4, HFBSurv risk is significantly associated with survival by univariate Cox proportional hazards analysis (P-value = 2.84e-14). Moreover, multivariate Cox proportional hazards analysis identifies HFBSurv risk as a major prognostic factor when correcting for other clinicopathologic variables. At the same time, it is observed that age is also marginally significant in multivariate Cox proportional hazards analysis, but other clinicopathologic variables are not. Taken together, the above analysis demonstrates that our method shows substantial predictive power and HFBSurv risk is an independent prognostic factor (P-value = 2.71e-13, Hazard ratio =5.125, 95% CI, 2.98–6.96).
Table 4.
Hazard ratios for univariate and multivariate Cox proportional hazards analysis
| Univariate |
Multivariate |
||||||
|---|---|---|---|---|---|---|---|
| Variable | C-index | Hazard ratio | 95% CI | P value | Hazard ratio | 95% CI | P value |
| HFBSurv | 0.766 | 5.396 | 3.50–8.33 | 2.84e–14 | 5.125 | 2.98–6.96 | 2.71e–13 |
| Age | 0.631 | 1.626 | 1.10–2.41 | 0.015 | 1.510 | 1.01–2.25 | 0.043 |
| Grade | 0.649 | 2.373 | 1.67–3.38 | 2.00e–6 | 1.625 | 0.85–3.12 | 0.145 |
| T stage | 0.580 | 1.578 | 1.06–2.34 | 0.024 | 0.999 | 0.60–1.67 | 0.998 |
| N stage | 0.599 | 2.309 | 1.56–3.42 | 3.00e–5 | 1.442 | 0.78–2.66 | 0.241 |
| M stage | 0.538 | 1.812 | 1.14–2.89 | 0.013 | 1.487 | 0.91–2.43 | 0.112 |
4 Discussion
In this study, we propose a novel cancer survival prediction method HFBSurv via hierarchical factorized bilinear fusion. To obtain comprehensive multimodal representation for predicting survival of cancer patients, HFBSurv is carefully developed to deeply mine the rich information from multimodal data by conducting low- and high-level fusion step by step, which is distinct from the commonly adopted single fusion strategy. In this hierarchical fusion framework, MAFB and CAFB with much fewer training parameters are designed to capture complex modality-specific and cross-modality relations, respectively. The experiment results demonstrate that HFBSurv achieves remarkable improvement in performance over existing methods with dramatically reduced computational complexity. Furthermore, analysis of Kaplan–Meier curves and Cox proportional hazards are conducted to confirm the effectiveness of HFBSurv in cancer survival prediction.
Although HFBSurv has obtained promising predictive performance, there is still large room for improvement. Firstly, the performance of our method is still limited by available multimodal cancer data, which can be improved by expanding our study to include more patients. Meanwhile, despite that the performance advantage of HFBSurv over other existing methods is generally robust to smaller dataset size, it is worth noting that for GBM multimodal dataset with only 145 patients, Lasso-cox shows slightly better results than HFBSurv and meanwhile largely outperforms other deep learning-based methods, highlighting the potential usefulness of conventional methods on extremely small cancer datasets. Secondly, given that other genomic data (e.g. gene methylation, miRNA expression) are also valuable for cancer survival prediction, our method can be further enhanced by incorporating these different data types. Finally, we intend to explore a deep learning-based survival prediction method with improved interpretability in future work. In conclusion, we present a novel hierarchical multimodal fusion method for cancer survival prediction, which could be useful in a number of prediction tasks by integrating multimodal data and serve as a reliable and helpful tool for further studies.
Funding
This work was supported by the National Natural Science Foundation of China [61871361, 61971393, 61571414, 61471331].
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Ruiqing Li, School of Information Science and Technology, University of Science and Technology of China, Hefei AH230027, China.
Xingqi Wu, School of Information Science and Technology, University of Science and Technology of China, Hefei AH230027, China.
Ao Li, School of Information Science and Technology, University of Science and Technology of China, Hefei AH230027, China.
Minghui Wang, School of Information Science and Technology, University of Science and Technology of China, Hefei AH230027, China.
References
- Beck A.H. (2015) Open access to large scale datasets is needed to translate knowledge of cancer heterogeneity into better patient outcomes. PLoS Med., 12, e1001794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter A.E. et al. (2006) CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol., 7, R100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhary K. et al. (2018) Deep learning-based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res., 24, 1248–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheerla A., Gevaert O. (2019) Deep learning with multimodal representation for pancancer prognosis prediction. Bioinformatics, 35, i446–i454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R.J. et al. (2020) Pathomic fusion: an integrated framework for fusing histopathology and genomic features for cancer diagnosis and prognosis. IEEE Trans. Med. Imaging, 1. doi: 10.1109/TMI.2020.3021387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J. et al. (2017) Integrative analysis of histopathological images and genomic data predicts clear cell renal cell carcinoma prognosis. Cancer Res., 77, e91–e100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J. et al. (2018) Identification of topological features in renal tumor microenvironment associated with patient survival. Bioinformatics, 34, 1024–1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ching T. et al. (2018) Cox-nnet: an artificial neural network method for prognosis prediction of high-throughput omics data. PLoS Comput. Biol., 14, e1006076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhillon A., Singh A. (2020) eBreCaP: extreme learning-based model for breast cancer survival prediction. IET Syst. Biol., 14, 160–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Z. et al. (2016) Evaluating the molecule-based prediction of clinical drug responses in cancer. Bioinformatics, 32, 2891–2895. [DOI] [PubMed] [Google Scholar]
- Gevaert O. et al. (2006) Predicting the prognosis of breast cancer by integrating clinical and microarray data with Bayesian networks. Bioinformatics, 22, e184–e190. [DOI] [PubMed] [Google Scholar]
- Gu Z. et al. (2017) Learning joint multimodal representation based on multi-fusion deep neural networks. In: International Conference on Neural Information Processing. Guangzhou, China, pp. 276–285.
- Guo W. et al. (2019) Deep multimodal representation learning: a survey. IEEE Access, 7, 63373–63394. [Google Scholar]
- Hao J. et al. (2018) Cox-PASNet: pathway-based sparse deep neural network for survival snalysis. In: 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). Madrid, Spain, pp. 381–386.
- Huang Z. et al. (2019) SALMON: survival analysis learning with multi-omics neural networks on breast cancer. Front. Genet., 10, 166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S. et al. (2020) Artificial intelligence in cancer diagnosis and prognosis: opportunities and challenges. Cancer Lett., 471, 61–71. [DOI] [PubMed] [Google Scholar]
- Ishwaran H. et al. (2008) Random survival forests. Ann. Appl. Stat., 2, 841–860. [Google Scholar]
- Katzman J.L. et al. (2018) DeepSurv: personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol., 18, 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J.H. et al. (2017) Hadamard product for low-rank bilinear pooling. In: 5th International Conference on Learning Representations, ICLR 2017 – Conference Track Proceedings. Toulon, France, pp. 1–14.
- Liu Z. et al. (2018) Efficient low-rank multimodal fusion with modality-specific factors. In: Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics. Melbourne, Australia, pp. 2247–2256.
- Mai S. et al. (2020a) Locally confined modality fusion network with a global perspective for multimodal human affective computing. IEEE Trans. Multimed., 22, 122–137. [Google Scholar]
- Mai,S. et al. (2020) Modality to Modality Translation: An Adversarial Representation Learning and Graph Fusion Network for Multimodal Fusion. In: Proceedings of the AAAI Conference on Artificial Intelligence. New York, USA, pp. 164–172. [Google Scholar]
- Mobadersany P. et al. (2018) Predicting cancer outcomes from histology and genomics using convolutional networks. Proc. Natl. Acad. Sci. USA, 115, 2970–2979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ning Z. et al. (2020) Integrative analysis of cross-modal features for the prognosis prediction of clear cell renal cell carcinoma. Bioinformatics, 36, 2888–2895. [DOI] [PubMed] [Google Scholar]
- Shao W. et al. (2020) Integrative analysis of pathological images and multi-dimensional genomic data for early-stage cancer prognosis. IEEE Trans. Med. Imaging, 39, 99–110. [DOI] [PubMed] [Google Scholar]
- Subramanian V. et al. (2021) Multimodal fusion using sparse CCA for breast cancer survival prediction. In: 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI). Nice, France, pp. 1429–1432.
- Sun D. et al. (2018) Integrating genomic data and pathological images to effectively predict breast cancer clinical outcome. Comput. Methods Programs Biomed., 161, 45–53. [DOI] [PubMed] [Google Scholar]
- Sun D. et al. (2019) A multimodal deep neural network for human breast cancer prognosis prediction by integrating multi-dimensional data. IEEE/ACM Trans. Comput. Biol. Bioinf., 16, 841–850. [DOI] [PubMed] [Google Scholar]
- Sung H. et al. (2021) Global cancer statistics 2020: globocan estimates of incidence and mortality worldwide for 36 cancers in 185 countries. Cancer J. Clin., 71, 209–249. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. (1997) The lasso method for variable selection in the Cox model. Stat. Med., 16, 385–395. [DOI] [PubMed] [Google Scholar]
- Wang C. et al. (2020) A cancer survival prediction method based on graph convolutional network. IEEE Trans. Nanobiosci., 19, 117–126. [DOI] [PubMed] [Google Scholar]
- Wang Z. et al. (2021) GPDBN: deep bilinear network integrating both genomic data and pathological images for breast cancer prognosis prediction. Bioinformatics, 37, 2963–2970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu X. et al. (2012) A gene signature for breast cancer prognosis using support vector machine. In: 2012 5th International Conference on BioMedical Engineering and Informatics. Chongqing, China, pp. 928–931.
- Xu J. et al. (2016) Stacked sparse autoencoder (SSAE) for nuclei detection on breast cancer histopathology images. IEEE Trans. Med. Imaging, 35, 119–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y., Zou H. (2013) A cocktail algorithm for solving the elastic net penalized Cox’s regression in high dimensions. Stat. Interface, 6, 167–173. [Google Scholar]
- Yu K.-H. et al. (2016) Predicting non-small cell lung cancer prognosis by fully automated microscopic pathology image features. Nat. Commun., 7, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Z. et al. (2017) Multi-modal factorized bilinear pooling with co-attention learning for visual question answering. In: 2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy, pp. 1839–1848.
- Yu F. et al. (2019) Breast cancer prognosis signature: linking risk stratification to disease subtypes. Brief. Bioinf., 20, 2130–2140. [DOI] [PubMed] [Google Scholar]
- Yuan Y. et al. (2012) Quantitative image analysis of cellular heterogeneity in breast tumors complements genomic profiling. Sci. Transl. Med., 4, 157ra143. [DOI] [PubMed] [Google Scholar]
- Zhu Y. et al. (2014) TCGA-assembler: open-source software for retrieving and processing TCGA data. Nat. Methods, 11, 599–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.