Abstract
Three adamantane-1,3,4-thiadiazole hybrid derivatives namely; N-ethyl-5-(adamantan-1-yl)-1,3,4-thiadiazole-2-amine I, N-(4-fluorophenyl)-5-(adamantan-1-yl)-1,3,4-thiadiazole-2-amine II and (4-bromophenyl)-5-(adamantan-1-yl)-N-1,3,4-thiadiazole-2-amine III, have been synthesized and crystal structures have been determined at low temperature. The structures revealed that the orientation of the amino group is different in non-halogenated structures. Intra- and intermolecular interactions were characterized on the basis of the quantum theory of atoms-in-molecules (QTAIM) approach. Intermolecular interaction energies for different molecular pairs have been obtained using the PIXEL method. Hirshfeld surface analysis and 2D-fingerprint plots revealed that the relative contributions of different non-covalent interactions are comparable in compounds with halogen (Br and F) substitutions. Crystal structures of II and III show isostructural behaviour with 1D supramolecular constructs. In all three structures, the N–H⋯N hydrogen bond was found to be stronger among other noncovalent interactions. The H–H bonding showed a closed shell in nature and played significant roles in the stabilization of these crystal structures.
The nature and strength of various noncovalent interactions in three adamantane derivatives are characterized using QTAIM approach.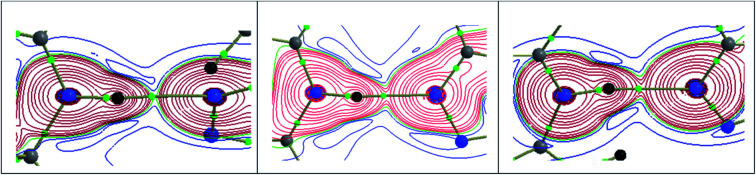
Introduction
1,3,4-Thiadiazole derivatives have long been known for their diverse applications in the medical, agricultural and material science fields.1 In the medical field, the 1,3,4-thiadiazole nucleus represents the essential pharmacophore of several marketed drugs or new drug candidates under clinical investigation. The major pharmacological activities of 1,3,4-thiadiazole-based drugs include carbonic anhydrase inhibitory activity,2 antibacterial,3 antifungal,4 anticancer,5 antiviral,6 trypanosomicidal,7 and anti-leishmanial activities.8 On the other hand, adamantane-based derivatives are currently used as efficient therapies for the treatment of various pathological disorders.9 In almost all cases, the incorporation of an adamantyl moiety into several molecules results in compounds with relatively high lipophilicity, which in turn modulate the bioavailability of these molecules.10
In continuation of our interest in the structural and pharmacological properties of adamantane-based derivatives,11 we present herein the crystal structures of three N-substituted-5-(adamantan-1-yl)-1,3,4-thiadiazole-2-amine derivatives. To delineate the effect of substituents and to have a qualitative picture of intermolecular interactions present in these compounds, we performed Hirshfeld surface and 2D-fingerprint plots.12 The lattice energies of these crystals and intermolecular interactions strengths of different molecular pairs observed in these structures were further quantified by the PIXEL method.13 Furthermore, the topological parameters for noncovalent interactions at their bond critical points (BCPs) were computed based on Bader's quantum theory of atoms in molecules (QTAIM) framework.14 The noncovalent bonding nature and character (HB and van der Waals interactions) were assessed by first four criteria of Koch–Popelier.15
These four criteria are (i) topology (BCP), (ii) electron density ρ(r) at the BCP (iii) Laplacian of the electron density ∇2ρ(r) and (iv) mutual penetration of the H and the acceptor atom. The fourth criterion of KP (hereafter KP-4) compares the bonding (rD and rA) and non-bonding radii of donor (r0D) and acceptor atoms (r0A). The bonding radii are taken as length from the BCP to the nuclei, whereas non-bonding radii of hydrogen and the acceptor atoms are taken as the gas phase van der Waals radii.16 The strong and weak intermolecular interactions in different molecules have been quantitatively analyzed using the first four criteria of KP successfully.17 The strength of various noncovalent interactions at their BCPs in these three structures was quantified using an empirical scheme [De = −0.5 × V(r)] proposed by EML18 and the total electronic energy density H(r) [H(r) = V(r) + G(r); where V(r) and G(r) represent potential energy density and kinetic energy density] proposed by Cremer & Kraka.19 In the bromo derivative, we observed a homo-halogen (Br⋯Br) contact and found to be important for stabilization. We report herein a detailed CSD (Cambridge Structural Database) analysis of Br⋯Br interaction to know its geometrical preferences.
Experimental
Synthesis and crystallization
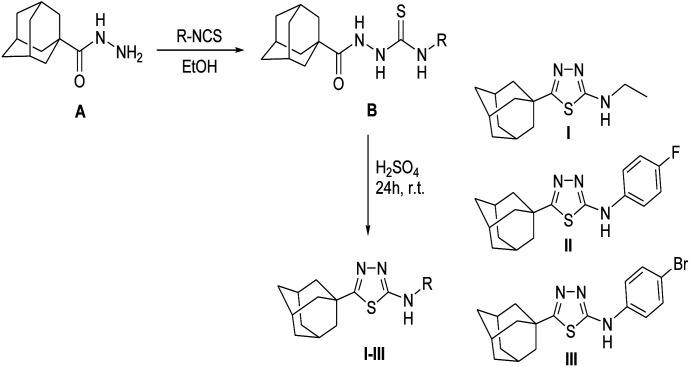
The title N-substituted-5-(adamantan-1-yl)-1,3,4-thiadiazole-2-amines I, II and III were synthesized starting with adamantane-1-carbohydrazide Avia treatment with the appropriate isothiocyanate to yield the corresponding 1-[(1-adamantan-1-yl)carbonyl]-4-substituted thiosemicarbazides B, which were cyclized to their 1,3,4-thiadiazole analogues I–III using sulphuric acid at room temperature for 24 hours (Scheme 1).20 Pure single crystals for X-ray analysis were obtained by slow evaporation of CHCl3 : EtOH (1 : 1) solution at room temperature. A detailed synthesis procedure and 1H NMR spectral data for compounds I–III are given in ESI.†
Scheme 1. The synthetic pathway for the target compounds I–III.
Single crystal X-ray structure determination
The selected suitable single crystals of compounds I–III were mounted using polybutene oil on a flexible loop fixed on a goniometer head and immediately transferred to the diffractometer. Single crystal X-ray diffraction data were collected on a Rigaku OD XtaLAB Synergy, Dualflex Pilatus 200 K diffractometer using a single wavelength X-ray source (Cu Kα radiation: λ = 1.54184 Å) (Rigaku Oxford Diffraction, 2015) from a micro-focus sealed X-ray tube and an Oxford liquid-nitrogen Cryostream cooler. Pre-experiment, data collection, data reduction and analytical absorption correction21 were performed with the program suite CrysAlisPro (CrysAlisPro (Version 1.171.40.16c), Rigaku Oxford Diffraction, 2018) using Olex2, a complete structure solution, refinement and analysis program.22 The structures were solved with the SHELXT small molecule structure solution program.23 All non-hydrogen atoms were refined with the SHELXL 2018/3 program package by full-matrix least-squares minimization on F2.24 The position of amine H atom was located from a difference Fourier map and freely refined. In compound I, the methyl H were constrained to an ideal geometry with C–H = 0.98 Å and Uiso(H) = 1.5Ueq(C), but were allowed to rotate freely about the C–C bond. The remaining H atoms were placed in calculated geometrical positions with C–H = 0.93–1.00 Å and Uiso(H) = 1.2Ueq(C).
Hirshfeld surface analysis
The Hirshfeld surface analysis has been performed with CrystalExplorer-17.5 program using the X-ray geometries after normalizing the H involving distances with N–H = 1.009 and C–H = 1.083 Å.25 The interatomic contacts were visualized on the Hirshfeld surface using three different colour (red-white-blue) scales. The red-white-blue colour schemes were used to identify the interatomic contact distances are shorter than vdW separation (red), equal to vdW separation (white) and longer than vdW separation (blue) from the Hirshfeld surface that was mapped over the function of dnorm. 2D-fingerprint plots were obtained from the Hirshfeld surface analysis in order to compute the relative contributions of different intermolecular interactions exist in the crystal structures.
PIXEL energy calculation
Intermolecular interaction energies for different dimers in the crystal structures of I–III and lattice energies for these compounds were calculated using the PIXELC module of CLP program.13 The intermolecular interaction energy (Etot) is the sum of the coulombic (Ecoul), polarization (Epol), dispersion (Edisp) and repulsion (Erep) energy terms. The X-ray geometries were used after the normalizing the H involving bond lengths as mentioned above. For the PIXEL calculation, the electron density of the molecules of I–III has been calculated at MP2/6-31G** level of theory using Gaussian program.26
DFT computation and QTAIM analysis
All the quantum chemical calculations were performed with the program Gaussian 09 program.26 In order to gain more insights into nature of intermolecular interactions found within different molecular dimers identified from PIXEL energy analysis, the topological analysis was performed with the AIMALL package.27 For this, the wave functions were generated from the single point energy calculation (at crystal structure geometry with the normalized H involving distances to their typical neutron values) at the M06-2X-D3/cc-pVTZ level of theory.28,29 Further, to understand the preference of N–H group orientation, we performed rigid potential energy surface scan for the torsion angle S1–C3–N1–C2 in compound I using Jaguar program30 with B3LYP functional,31 and 6-31G(d) basis set. The molecular electrostatic potentials were also computed with WFA-SAS program32 to identify the electrostatic complementary regions within the molecule.
Results and discussion
In the present study, we explored the role of various non-covalent interactions in three adamantane derivatives using different theoretical approaches. Two of the structures (II and III) contain halogen atoms (F and Br). Crystal data, data collection details and refinement statistics for all three compounds are presented in Table 1.
Crystal data and refinement parameters for compounds I–III.
| I | II | III | |
|---|---|---|---|
| Crystal data | |||
| Chemical formula | C14H21N3S | C18H20FN3S | C18H20BrN3S |
| M r | 263.40 | 329.43 | 390.34 |
| Crystal system, space group | Monoclinic, P21/c | Triclinic, P1 | Triclinic, P1 |
| Temperature (K) | 160 (2) | 160 (2) | 160 (2) |
| a, b, c (Å) | 9.8339 (2), 15.8974 (2), 9.4749 (2) | 6.7254 (7), 10.9787 (5), 11.9955 (10) | 6.7648 (2), 11.4551 (2), 11.4985 (2) |
| α, β, γ (°) | 90, 114.464 (2), 90 | 116.607 (6), 94.587 (8), 90.941 (6) | 110.417 (2), 95.240 (2), 93.613 (2) |
| V (Å3) | 1348.26 (5) | 788.01 (12) | 827.26 (3) |
| Z | 4 | 2 | 2 |
| Radiation type | Cu Kα | Cu Kα | Cu Kα |
| μ (mm−1) | 2.01 | 1.93 | 4.57 |
| Crystal size | 0.16 × 0.14 × 0.05 | 0.14 × 0.05 × 0.02 | 0.28 × 0.11 × 0.08 |
| Data collection | |||
| Diffractometer | XtalLab Synergy, Dualflex, Pilatus 200 K | XtalLab Synergy, Dualflex, Pilatus 200 K | XtalLab Synergy, Dualflex, Pilatus 200 K |
| Absorption correction | Analytical | Analytical | Analytical |
| T min, Tmax | 0.795, 0.902 | 0.851, 0.972 | 0.461, 0.767 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 15 881, 2920, 2798 | 12 473, 3183, 2735 | 14 178, 3385, 3269 |
| R int | 0.022 | 0.063 | 0.021 |
| (sin θ/λ)max (Å−1) | 0.637 | 0.625 | 0.625 |
| Refinement | |||
| R[F2 > 2σ(F2)], wR(F2), S | 0.032, 0.084, 1.06 | 0.065, 0.203, 1.06 | 0.023, 0.061, 1.05 |
| No. of reflections | 2920 | 3183 | 3385 |
| No. of parameters | 168 | 212 | 212 |
| H-atom treatment | H-atom treated by a mixture of independent and constrained refinement | H-atom treated by a mixture of independent and constrained refinement | H-atom treated by a mixture of independent and constrained refinement |
| Δρmax, Δρmin (e Å−3) | 0.30, −0.31 | 0.40, −0.34 | 0.27, −0.51 |
| CCDC no. | 1977639 | 1977750 | 1977643 |
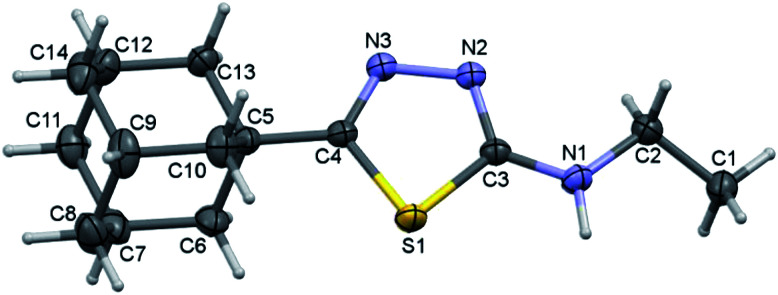
Crystal structure of I
Compound I crystallizes in the monoclinic system with the space group of P21/c and its asymmetric unit comprises of one molecule (Fig. 1). Four fused cyclohexane rings constitute the adamantane moiety and each of these six-membered rings is in chair conformation as evident from the Cremer and Pople puckering parameters.33 The orientation of the N–H group is in syn conformation with respect to the orientation of the S atom. Similar orientation has been observed in a closely related structure of methylamine derivative.34
Fig. 1. Thermal ellipsoidal plot of compound I. The ellipsoids are drawn at the 50% probability level.
In order to understand the preference of syn conformation of amine group in the solid state, we performed a rigid potential energy surface scan (PES). The results suggest that the syn conformation (S1–C3–N1–C2 = 5°) is found to be minimum energy conformer and the energy difference between syn and anti-conformations (180°) is being as small as 0.68 kcal mol−1. The PES diagram for compound I is given in ESI (Fig. S1†).
The adamantane core and the 1,3,4-thiadiazole ring are positioned nearly co-planar (6.98°) as evident from the dihedral angle formed between the mean planes of the respective units. The ethylamine moiety makes a dihedral angle of 21.51° with respect to the mean plane of the 1,3,4-thiadiazole ring. The topological analysis for the molecule of I (X-ray geometry) reveals that there is no intramolecular non-covalent interaction formed.
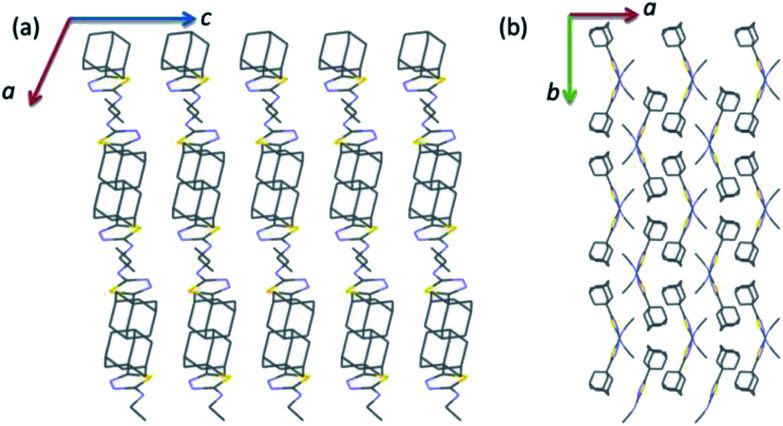
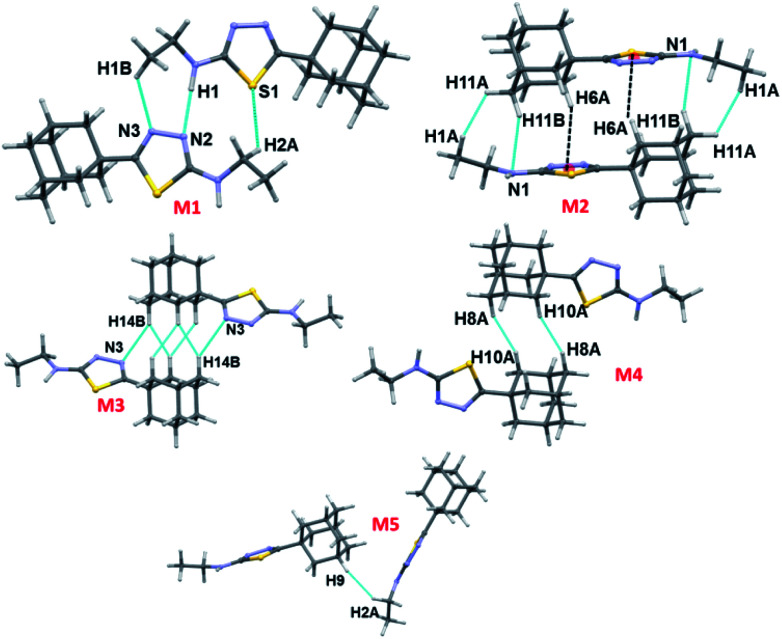
As illustrated in Fig. 2, the crystal structure of I can be described as layers in which adamantane moieties from adjacent layers are positioned closer to each other. This closer arrangement is stabilized by weak and short intermolecular Csp3–H⋯H–Csp3 type of interactions. As mentioned in the experimental section, the PIXEL energy analysis was carried out to identify the energetically significant molecular dimer in the crystalline state. In I, there are five molecular pairs (M1–5) identified from the PIXEL energy analysis and intermolecular interaction energies (Etot) for these dimers along with their partitioned energies are presented (Table 2 and Fig. 3). It should be emphasized that the energetically least dimers (M4–5) are purely stabilized by short intermolecular Csp3–H⋯H–Csp3 contacts. Similar adamantane–adamantane interactions (motif M4) mediated by Csp3–H⋯H–Csp3 bonding has been reported earlier.11 This interaction is named as H–H bonding and non-electrostatic nature of this closed-shell interaction have been discussed in detail.35
Fig. 2. Wireframe showing the crystal structure of I projected onto different planes (a) ac plane and (b) ab plane. All the H atoms have been omitted for clarity.
Intermolecular interaction energies (in kcal mol−1) obtained by the PIXEL method for various molecular pairs observed in the crystal structures of I–III.
| Motif | CD | Symmetry | Important interactions | Geometrya (H⋯A, ∠D–H⋯A) | E coul | E pol | E pol | E rep | E tot |
|---|---|---|---|---|---|---|---|---|---|
| Compound I | |||||||||
| M1 | 7.915 | x, −y + 3/2, z − 1/2 | N1–H1⋯N2 | 1.98, 176 | −11.4 | −5.4 | −5.4 | 12.5 | −11.5 |
| C1–H1B⋯N3 | 2.68, 136 | ||||||||
| C2–H2A⋯S1 | 3.11, 131 | ||||||||
| M2 | 4.755 | −x + 1, −y + 1, −z + 1 | C11–H11B⋯N1 | 2.63, 141 | −5.0 | −2.9 | −2.9 | 14.1 | −10.5 |
| H11A⋯H1A | 2.22, 119 | ||||||||
| C6–H6A⋯Cg1 | 2.77, 152 | ||||||||
| M3 | 6.831 | −x + 2, −y + 1, −z + 2 | C14–H14B⋯N3 | 2.72, 140 | −2.4 | −2.0 | −2.0 | 7.5 | −5.4 |
| H14B⋯H13A | 2.14, 149 | ||||||||
| H10B⋯H13A | 2.33, 142 | ||||||||
| M4 | 6.638 | −x + 2, −y + 1, −z + 1 | H10A⋯H8A | 2.20, 152 | −2.0 | −1.3 | −1.3 | 7.0 | −4.1 |
| M5 | 9.139 | −x + 2, y − 1/2, −z + 3/2 | H9⋯H2A | 2.37, 165 | −0.7 | −0.4 | −0.4 | 1.7 | −3.2 |
| Compound II | |||||||||
| M6 | 7.831 | −x + 2, −y + 1, −z + 1 | N1–H1⋯N2 | 1.91, 175 | −26.5 | −12.1 | −9.4 | 26.4 | −21.7 |
| M7 | 4.947 | −x + 1, −y + 1, −z + 1 | Cg1⋯Cg1 | 3.712 (4) | −3.6 | −2.6 | −15.7 | 10.0 | −11.8 |
| C17–H17B⋯C4 | 2.70, 172 | ||||||||
| C17–H17B⋯C3 | 2.74, 157 | ||||||||
| M8 | 6.725 | x − 1, y, z | C10–H10A⋯N2 | 2.72, 137 | −1.7 | −1.3 | −10.3 | 6.4 | −6.9 |
| C11–H11⋯C8 | 2.86, 142 | ||||||||
| H11⋯H14B | 2.37, 120 | ||||||||
| M9 | 8.488 | −x + 1, −y, −z + 1 | C10–H10B⋯F1 | 2.39, 168 | −2.3 | −0.8 | −6.0 | 3.8 | −5.3 |
| M10 | 7.520 | −x + 1, −y + 1, −z + 2 | H14A⋯H14A | 2.38, 123 | −1.2 | −0.7 | −6.8 | 4.2 | −4.6 |
| M11 | 10.551 | −x + 2, −y, −z + 1 | Cg2⋯Cg2 | 3.848 (4) | −0.9 | −0.4 | −5.7 | 3.4 | −3.6 |
| M12 | 11.492 | −x + 1, −y + 2, −z + 2 | H16⋯H17A | 2.34, 123 | −1.7 | −0.8 | −5.9 | 5.4 | −2.9 |
| H16⋯H18B | 2.38, 123 | ||||||||
| M13 | 14.388 | x − 1, y + 1, z + 1 | H18A⋯H6 | 2.21, 145 | −0.5 | −0.4 | −2.8 | 2.0 | −1.8 |
| Compound III | |||||||||
| M14 | 7.626 | −x, −y + 2, −z + 1 | N1–H1⋯N2 | 1.93, 169 | −28.0 | −13.3 | −10.6 | 28.5 | −23.4 |
| C5–H5⋯N3 | 2.59, 149 | ||||||||
| M15 | 5.201 | −x + 1, −y + 2, −z + 1 | Cg1⋯Cg1 | 3.687 (1) | −2.3 | −2.5 | −19.0 | 14.2 | −9.6 |
| H6⋯H14B | 2.27, 118 | ||||||||
| M16 | 8.088 | −x, −y + 1, −z + 1 | H10A⋯H10A | 1.93, 145 | −2.8 | −1.9 | −10.6 | 7.6 | −7.7 |
| C15–H15A⋯S1 | 3.06, 159 | ||||||||
| M17 | 6.765 | x − 1, y, z | C5–H5⋯Br1 | 3.02, 125 | −2.1 | −1.0 | −7.2 | 3.2 | −7.1 |
| M18 | 6.639 | −x + 1, −y + 1, −z + 1 | H2⋯H15B | 2.38, 135 | −2.7 | −2.0 | −11.8 | 9.6 | −6.9 |
| H2⋯H11 | 2.33, 106 | ||||||||
| H3⋯H11 | 2.18, 111 | ||||||||
| M19 | 11.498 | x, y, z − 1 | C13–H13⋯Br1 | 3.11, 138 | −1.1 | −0.4 | −4.7 | 2.5 | −3.6 |
| M20 | 13.867 | −x + 1, −y + 2, −z | C6–H6⋯Br1 | 2.92, 150 | −2.1 | −0.8 | −3.9 | 3.3 | −3.4 |
| M21 | 16.453 | −x, −y + 1, −z + 2 | H18A⋯H16 | 2.36, 147 | −0.8 | −0.4 | −4.3 | 2.7 | −2.9 |
| M22 | 13.863 | x − 1, y, z + 1 | C17–H17B⋯Br1 | 2.90, 145 | −0.5 | −0.4 | −2.7 | 1.9 | −1.8 |
| M23 | 16.338 | −x + 2, −y + 2, −z | C1–Br1⋯Br1 | 3.706 (1), 148.1 (1) | −0.6 | −0.2 | −1.5 | 1.5 | −0.8 |
Neutron values are given for all D–H⋯A interactions. CD: centroid-to-centroid distance of the molecular pair. Cg1 and Cg2 are the centroids of the thiadiazole and phenyl rings, respectively.
Fig. 3. Different dimeric motifs observed in crystal structure of I.
Three intermolecular interactions (N1–H1⋯N2, C1–H1B⋯N3 and C2–H2A⋯S1) stabilize the molecular dimer M1 (Etot: −11.5 kcal mol−1 with 70% contribution of electrostatic energy towards stabilization). The hydrogen bonding geometry favours for the N1–H1⋯N3 interaction (H1⋯N3 = 2.40 Å and ∠N1–H1⋯N3 = 143°). We note that the H2A⋯S1 interaction is established by slightly longer (by 0.12 Å) than the sum of the vdW radii of H and S atoms. The NCI plot and topological analysis reveals that the N1–H1⋯N3 interaction is not existing and only directional intermolecular N1–H1⋯N2 hydrogen bonding along with C1–H1B⋯N3 and C2–H2A⋯S1 interactions are formed (Fig. S2, ESI†). The second strongest molecular pair (M2; Etot: −10.5 kcal mol−1) forms through three intermolecular C–H⋯N (involving H11B and N1), C–H⋯Cg1(π) (involving H6A and centroid of the five-membered ring) and a short Csp3–H⋯H–Csp3 type (involving H atoms of adamantane and terminal methyl groups) H–H bonding interactions. The dispersion energy contributes 66–78% towards the stabilization of this and the subsequent dimers (M3–5) observed in I.
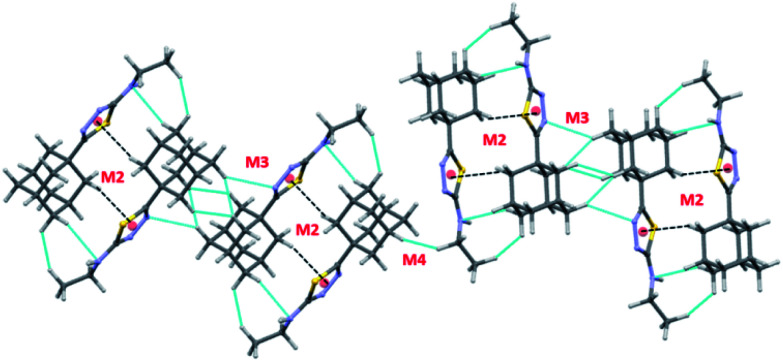
Molecules of I which are related by center of inversion that generate a molecular dimer M3 (Etot: −5.4 kcal mol−1). This dimer is stabilized by an intermolecular C–H⋯N (involving H14B and N3) interaction and two short H⋯H contacts (2.14 and 2.33 Å) involving H atoms of adjacent adamantane moieties. Dimers M4 (Etot: −4.1 kcal mol−1) and M5 (Etot: −3.2 kcal mol−1) are generated via short intermolecular Csp3–H⋯H–Csp3 type H–H bonding interactions. Adjacent adamantane moieties are interacting in M4, while adamantane and ethyl groups are interacting in M5. It is noted that the adjacent dimers of M2 are interconnected by motif M3 and this arrangement generate a sequence of motifs M2–M3–M2. The adjacent M2–M3–M2 sequences are further interlinked by motif M4 as shown in Fig. 4.
Fig. 4. Supramolecular association mediated by Csp3–H⋯H–Csp3 type H–H bonding interactions (motifs M3 and M4) in I. Small spheres represent the centroid of the five-membered ring.
Crystal structure of the fluoro derivative II
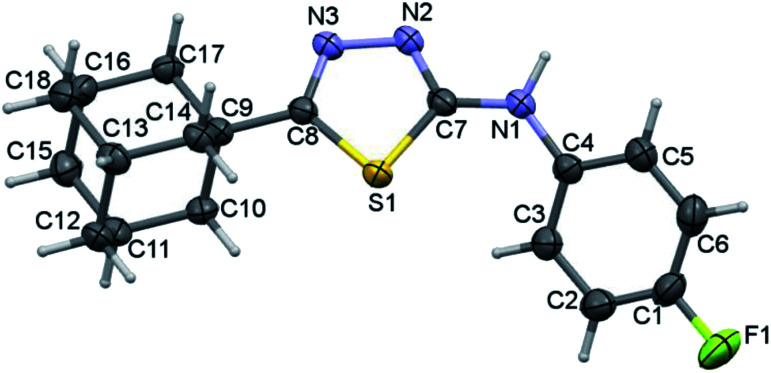
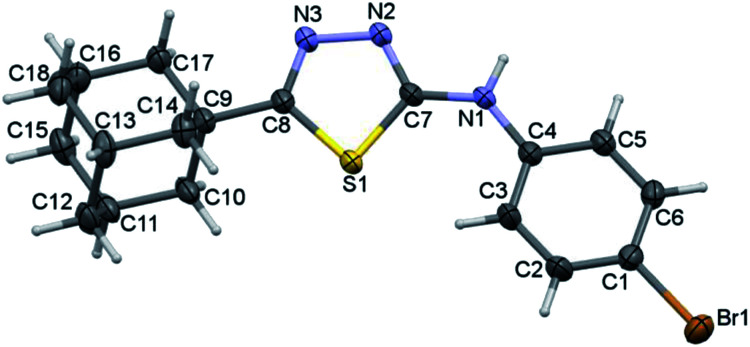
The fluoro derivative II crystallizes in the triclinic system with the centrosymmetric P1̄ space group and one molecule in the asymmetric unit (Fig. 5). The fused cyclohexane rings of the adamantane core exhibit chair conformation as observed in I. The orientation of the N–H group is in anti-conformation with respect to the orientation of S atom. This feature is completely different in the crystal structure of I and its closely related structure.34 The fluoro phenyl ring makes a dihedral angle of 36.59° with the plane of the five-membered ring.
Fig. 5. Thermal ellipsoidal plot of compound II. The ellipsoids are drawn at the 50% probability level.
Topological analysis has been performed for X-ray geometry of II to identify possible intramolecular noncovalent interactions. The topological parameters and molecular graphs are presented in ESI (Table S1 and Fig. S3†). An intramolecular C–H⋯S (involving H3 and S1) interaction is existed in the molecule of II. The dissociation energy (De) for this interaction was calculated to be 2.87 kcal mol−1 with the Rij value of 2.599 Å.
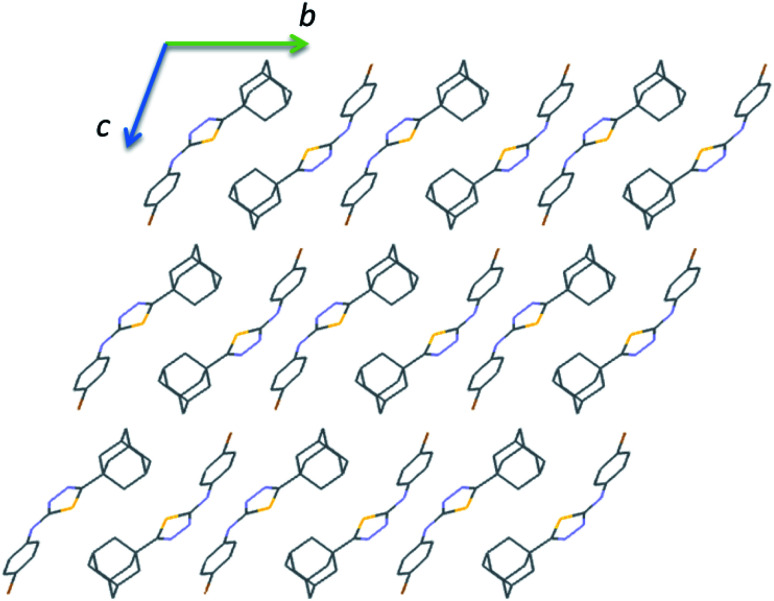
The crystal packing of II is completely different as compared to the crystal structure of I. The crystal packing can be described as hydrogen-bonded dimer mediated by N–H⋯N interaction and dimeric units packed as columnar manner along the crystallographic b axis (Fig. 6). In each column, the adjacent N–H⋯N mediated dimeric pairs are interlinked by intermolecular C–H⋯F interaction and π-stacking interaction between adjacent fluorophenyl rings. Further, the adamantane moiety of II in one column interacts with the adamantane moieties of the adjacent column via short intermolecular Csp3–H⋯H–Csp3 type H–H bonding interactions.
Fig. 6. Ball and stick diagram showing the crystal structure of II viewed down the a axis and all the H atoms have been omitted for clarity.
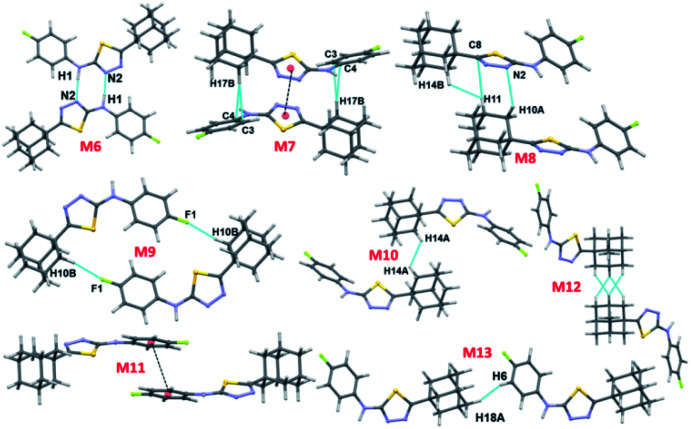
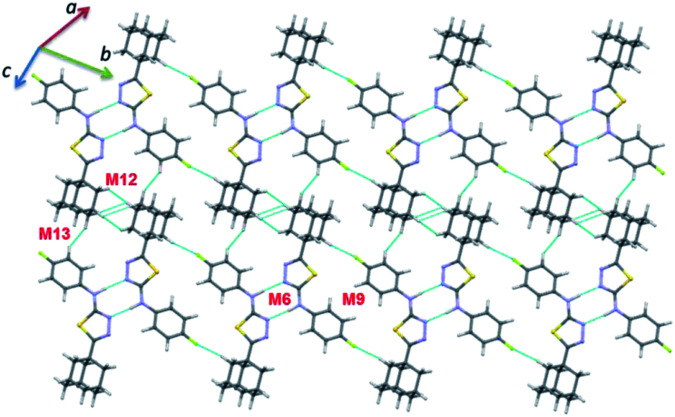
In compound II, eight energetically significant molecular pairs (motifs M6–M13; see Table 2 and Fig. 7) were revealed by the PIXEL energy analysis. The intermolecular interaction energies for these molecular pairs are ranging from −21.7 to −1.8 kcal mol−1. These molecular dimers are stabilized by different types of non-covalent interactions such as a strong N–H⋯N, several weak C–H⋯C(π), C–H⋯N, C–H⋯F, π-stacking interaction and short Csp3–H⋯H–Csp3 type H–H bonding interactions.
Fig. 7. Molecular pairs formed by different intermolecular interactions in II.
The strongest dimer (M6; Etot: −21.7 kcal mol−1) in this structure is formed by an intermolecular N–H⋯N interaction involving amine H atom and one of the N atoms of the thiadiazole ring with R22(8) synthon.36 This dimer is predominantly electrostatic in nature with 80% contribution towards the stabilization. The other dimers (M7–M13) found in this structure are dispersive in nature with the contribution of 66–81% towards stabilization. Dimer M7 (Etot: −11.8 kcal mol−1) forms by centrosymmetrically related molecules and stabilized by π-stacking interaction between adjacent five-membered rings and supported by a bifurcated intermolecular C–H⋯C(π) interactions (involving H13B and C3/C4).
Dimer M8 (Etot: −6.9 kcal mol−1) is featured with three intermolecular interactions such as C–H⋯N (involving H10A and N2), C–H⋯C(π) (involving H11 and C8) and a short Csp3–H⋯H–Csp3 (involving H11 and H14B) type H–H bonding interactions. A highly directional intermolecular C–H⋯F interaction generates a molecular dimer M9 (Etot: −5.3 kcal mol−1). We note that the dispersion energy is nearly contributing 2 fold excess that of electrostatic energy towards the stabilization of this dimer.
In M10 dimer (Etot: −4.6 kcal mol−1), adjacent adamantane moieties interconnected through Csp3–H⋯H–Csp3 H–H bonding interaction. This motif helps to link the adjacent dimers formed by motif M7. The combination of motifs M7 and M10 generate a molecular ribbon which runs along the crystallographic c axis (Fig. S4, ESI†). The fluorophenyl rings are stacked against each other with the centroid-to-centroid distance of 3.848 Å in M11 (Etot: −3.6 kcal mol−1). This stacking interaction is emanated from two adjacent dimers of M1.
Dimer M12 (Etot: −2.9 kcal mol−1) stabilizes by short and three centered Csp3–H⋯H–Csp3 (involving H16 and H17A/H18B) H–H bonding interactions in which two adjacent adamantane moieties are participated. Further, the neighbouring dimers formed by M9 interlinked by motif M12 as shown in Fig. 7. The least dimer M13 (Etot: −1.8 kcal mol−1) in II also stabilizes with H–H bonding interaction (involving H18A and H6) with Csp3–H⋯H–Csp2 type. It is of interest to note that the motifs M6, M9, M12 and M13 generate a molecular sheet as shown in Fig. 8.
Fig. 8. Supramolecular sheet constructed by motifs M6, M9, M12 and M13 in II.
Crystal structure of the bromo derivative III
The bromo derivative III crystallizes in the triclinic system with the centrosymmetric P1̄ space group and one molecule in the asymmetric unit (Fig. 9). The conformation of the fused cyclohexane rings and the orientation of the N–H group are very similar to that of the structure of II. The bromophenyl ring is less twisted as compared to fluorophenyl ring in II with respect to the mean plane of the five-membered ring. The dihedral angle between bromophenyl and five-membered ring is being 11.13°.
Fig. 9. Thermal ellipsoidal plot of compound III. The ellipsoids are drawn at the 50% probability level.
The QTAIM analysis reveals that the conformation of molecule III is stabilized by an intramolecular C–H⋯S interaction. Moreover, the bond path distance (2.439 Å) is quite shorter for an intramolecular C–H⋯S interaction as compared to II. The dissociation energy (De) for this interaction was computed to be 3.63 kcal mol−1. The molecular graph and topological parameters are presented in ESI (Table S2 and Fig. S5†).
The crystal structure of the bromo derivative is stabilized by intermolecular N–H⋯N, C–H⋯N, C–H⋯Br, C–H⋯S, π-stacking, short Csp2–H⋯H–Csp3 and Csp3–H⋯H–Csp3 types of H–H bonding and a Br⋯Br contact. The crystal packing of III is somewhat similar to that of II. The basic motif can be described as a hydrogen-bonded dimer formed by N–H⋯N and C–H⋯N interactions and this motif arranged as columnar fashion along the crystallographic b axis (Fig. 10).
Fig. 10. Crystal packing of III viewed down the a axis. All the H atoms have been omitted for clarity.
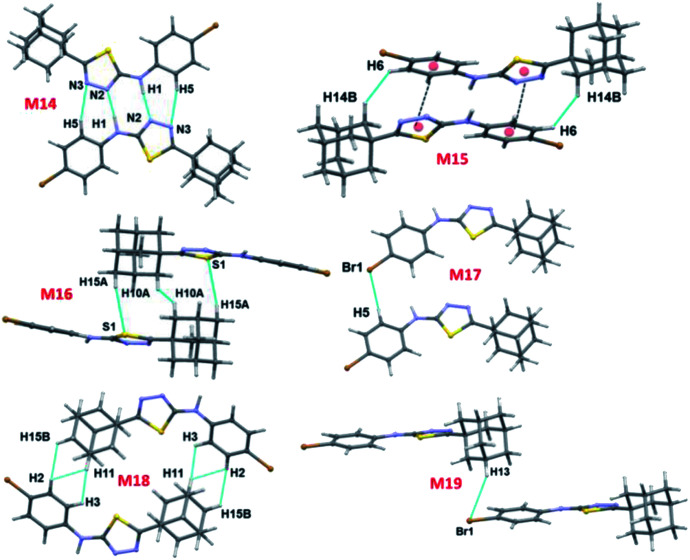
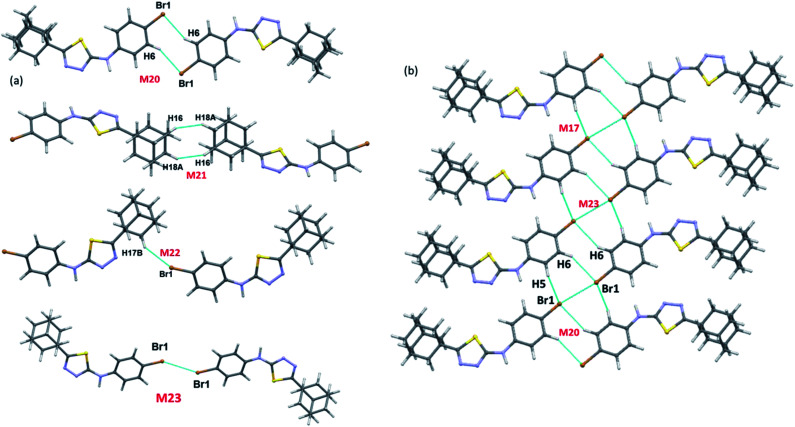
There are ten molecular dimers (M14–M23; see Fig. 11 and 12) brought out from the crystal structure with the PIXEL energy analysis. The intermolecular interaction energies (Etot) for these dimers range from −23.4 to −0.8 kcal mol−1. The strongest dimer is formed by intermolecular N–H⋯N (involving H1 and N2) and C–H⋯N (involving H5 and N3) interactions (motif M14, Etot: −23.4 kcal mol−1). This strong dimer is electrostatic in nature with the electrostatic energy contribution of 80%. The other dimers in this structure except dimer M20 are dispersive in nature with the dispersion contribution ranging from 65–80% towards the stabilization of these dimers. In the case of dimer M20 stabilization, the contribution of electrostatic and dispersion energies are 43 and 57%, respectively. We note that the way adjacent M14 dimers are interconnected is different as compared to the structure of II. The adjacent M14 dimers are associated via Csp2–H⋯H–Csp3 type of H–H bonding interactions (motif M18; Fig. S6, ESI†). In motif M18, the H atoms of phenyl and adamantane moieties are involved in the H–H bonding interactions with the separation of H⋯H atoms are ranging from 2.18 to 2.36 Å.
Fig. 11. Molecular pairs formed by different intermolecular interactions in III.
Fig. 12. (a) Molecular pairs formed by different intermolecular interactions and (b) molecular sheet formed by intermolecular C–H⋯Br and Csp2–Br⋯Br–Csp2 interactions in III.
Molecules related by center of inversion form a molecular stacking (motif M15, Etot: −9.6 kcal mol−1) in which five-membered ring stacking against bromophenyl ring. The molecular π-stacking arrangement is further supported by intermolecular H–H bonding with a short distance of 2.27 Å. The adjacent M15 dimers are interlinked via intermolecular H–H bonding interactions in which the neighbouring adamantane moieties are involved (motif M21).
In motif M16 (Etot: −7.7 kcal mol−1), adamantane moiety of one molecule interacts with the adamantane moiety of the centrosymmetrically related molecule via Csp3–H⋯H–Csp3 type of H–H bonding interaction with a very short contact distance of 1.93 Å. This dimer is further supported by a weak intermolecular C–H⋯S interaction (involving H15A and S1). It should be noted that the H⋯S distance is slightly longer than (by 0.07 Å) the sum of the van der Waals radii of the interacting atoms.
Four intermolecular C–H⋯Br interactions (motifs M17, M19, M20 and M22) observed in the crystal structure of bromo derivative. The intermolecular interaction energies for these dimers are as strong as −7.1 kcal mol−1 and as weak as −1.8 kcal mol−1. The phenyl protons are acting as donors for two of the C–H⋯Br interactions and the protons of the adamantane moiety acts as donors for the other two interactions. We note that the H⋯Br contact in motif M19 is slightly longer (by 0.06 Å) than the sum of vdW radii of interacting atoms and the corresponding contacts in other motifs are formed less than the sum of vdW. The least dimeric motif (M23, Etot: −0.8 kcal mol−1) forms by intermolecular Csp2–Br⋯Br–Csp2 contact and this interaction is classified as type I (trans-geometry) contact.37 As shown in Fig. 12(b), supramolecular sheet forms by Csp2–Br⋯Br–Csp2 and two C–H⋯Br interactions.
To grasp the geometrical choices of homo-halogen contact (Br⋯Br), we carried out a CSD search (CSD version 5.40, November 2018) with conditions along with the inter-contact between Br atoms is less than the sum of van der Waals radii (3.7 Å).38 This search yielded 947 hits with 1147 contacts and the minimum and average Br⋯Br distance are found to be 3.241 and 3.575 Å, respectively. Further analysis suggests that 39% of the contacts show type I [C–Br⋯Br (θ1); Br⋯Br–C (θ2) and θ1 = θ2] geometry and these contacts are located on the diagonal. It should be noted that 51% of the contacts display quasi type I geometry (|θ1 − θ2| < 20°). The remaining contacts (10%) belong to type II geometry (θ1 ≅ 90; θ2 ≅ 180 or θ1 ≅ 180; θ2 ≅ 90). The scatterplots of Br⋯Br distance and two angles (θ1 and θ2) are given in ESI (Fig. S7†). This is undoubtedly revealed that the Br⋯Br contact has more tendency to adopt type I geometry as observed in III.
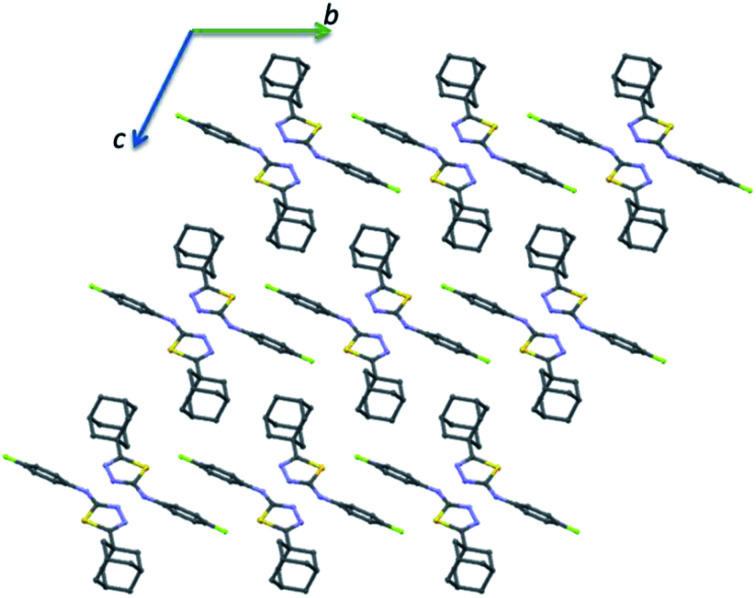
It is noted that the unit cell dimensions are comparable for structures II and III. To delineate the isostructurality between II and III, we calculated the isostructurality index (Π) for these structures as described by Fábián and Kálmán39 and the Π value is found to be zero. This value suggests that they are isostructural. To gain more information on the degree of packing similarity, we utilized XPac program.40 The XPac analysis reveals that these two structures display 1D supramolecular construct (row of molecules match) as shown in ESI (Fig. S8†). The dissimilarity index (x) was calculated to be 11.2 and this parameter quantifies the deviation between these structures from perfect geometrical similarity. The stretch parameter (D) gives information on the change in the intermolecular distance between two structures. This value is calculated to be 0.42 Å for these structures.
Molecular electrostatic potential surface map
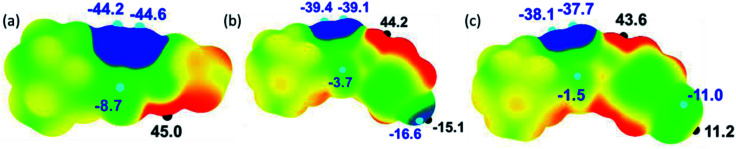
The molecular electrostatic potential surface map (MESP) has been extensively used to analyze noncovalent interactions and to identify electrophilic/nucleophilic sites on the molecule.41 The electrostatic potential mapped over the electronic density isosurface of the molecule at 0.001 au. The most positive (Vs,max) and negative potentials (Vs,min) are highlighted with small hemispheres along with values (Fig. 13). In all three structures, the amine H shows the most positive potentials in the range 42–45 kcal mol−1 and this feature indicating that the amine proton has best donating tendencies as compared to other protons in the molecule. Similarly, the most negative potentials are observed for N atoms of the thiadiazole ring. The Vs,min values for these atoms are slightly higher in I as compared to II and III. We also note that the accepting tendency for S atom is in the order of I > II > III.
Fig. 13. Molecular electrostatic potential surfaces of the structures (a) I, (b) II and (c) III mapped over the electronic density at 0.001 au contour. Colour ranges (in kcal mol−1): red: greater than 15; yellow: between 15 and 0; green: between 0 and −15 and blue: greater than −15. Important Vs,max and Vs,min values are given along with small hemispheres.
The fluoro and bromo derivatives show interesting features as can be seen from the Fig. 13. In the fluoro derivative, there is a σ-hole along C1–F1 bond in which the outermost region of its surface,42 with the Vs,max value of −15.1 kcal mol−1 and the unshared electrons on the F atom form negative potentials around its central portion with the Vs,min value of −16.6 kcal mol−1. A strong Vs,max value on the outermost region of C–F bond facilitates a directional non-covalent bonding. In contrast, the outermost portion of the C–Br surface has a positive potential with Vs,max value of 11.2 kcal mol−1. The central part of this bond constitutes negative potentials with the Vs,min value of −11.0 kcal mol−1. The negative potential corresponds to the lone-pair electrons of Br atom. The MESP and PIXEL energy analysis collectively suggest that the Br atom is preferred to interact with both electrophilic (positive site) and nucleophilic (negative site) sites.
Qualitative analysis of intermolecular interactions with Hirshfeld surface (HS) and 2D fingerprint plots (2D-FP)
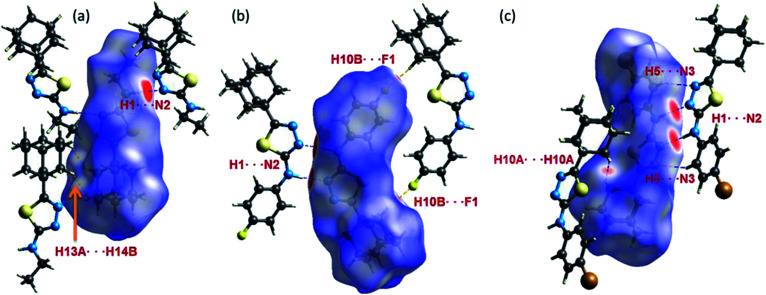
As can be seen from the HS diagram (Fig. 14), the intermolecular H1⋯N2 contact (motif M1) is shown as intense and wide red spots on the HS, whereas a small red spots appeared for intermolecular H13A⋯H14B contact (motif M3) in I. In II, three intermolecular short contacts (H1⋯N2, H10B⋯F1 and H7A⋯C3/C4) are visible on the HS. In III, the motif M13, comprises two intermolecular contacts (involving H1 and N2 and H5 and N3) is visible on the HS. The former contact is very short and shown as bright red areas, while the latter is shown as a paint red spots. It should be noted that intermolecular Csp3–H10A⋯H10A–Csp3 (motif M15) type H–H bonding is also identified on the HS with red spots.
Fig. 14. Hirshfeld surfaces highlight the close inter-contacts observed in structures (a) I, (b) II and (c) III.
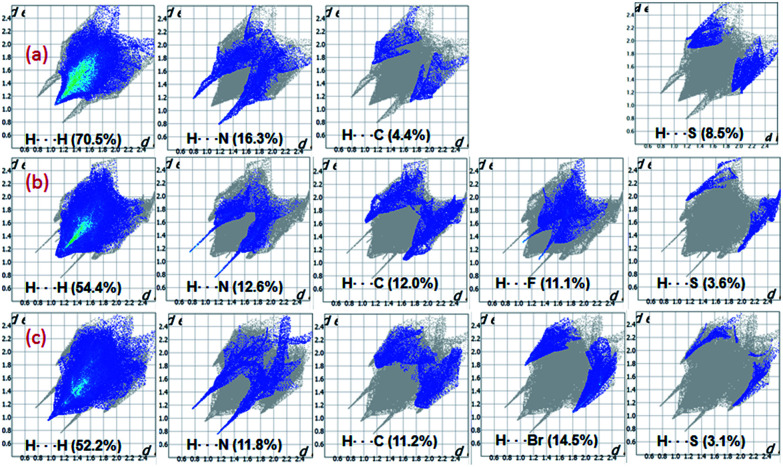
The fingerprint plots are used to delineate the relative contribution of different intermolecular contacts (Fig. 15). In all three structures, the H⋯H contacts constitute significant amount of interactions of the total HS area ranging from 52.2 to 70.5%. The shortest intermolecular H⋯N contacts are located near 2.0 Å with double spikes in all three structures. Further, there is a reduction in the relative contribution of H⋯C/C⋯H contacts which represent intermolecular C–H⋯C(π) interaction and a slight increase of H⋯S interaction in I as compared to II and III. The feature of H⋯S interaction is in good agreement with the MESP. Moreover, the reduction of H⋯C contacts is largely compensated by intermolecular H⋯H interactions.
Fig. 15. 2D-fingerprint plots for structures (a) I (b) II and (c) III. The percentage relative contributions of different intermolecular contacts are given.
The relative contributions of different intermolecular contacts are comparable in the bromo and fluoro derivatives. However, a noticeable difference is observed for the distribution of these contacts on the fingerprint plots. For instance, the H⋯H contacts are appeared as a sharp spike with the shortest distance is located around 1.9 Å in III, while the corresponding contacts are showed blunt end towards the shortest contacting region which is closer to 2.2 Å in II. Another remarkable difference is noticed for H⋯X (X = Br and F) contacts and the shortest H⋯F and H⋯Br contacts are located near 2.4 and 2.9 Å, respectively. The relative contribution of H⋯Br is slightly higher (3.4%) as compared to the contribution of H⋯F. According to the PIXEL energy analysis, the Br atom is involved as an acceptor in four different motifs, whereas the F atom is involved in only motif. Overall, the shortest distances of H⋯X contacts and their relative contributions in the respective structure are in good agreement with the PIXEL energy analysis. The intermolecular C⋯C contacts contribute only 2% to the total HS area in II and III, no such contact is observed in I. We observe that the Br⋯Br contact contributes only about 0.9% to the total HS area.
QTAIM analysis
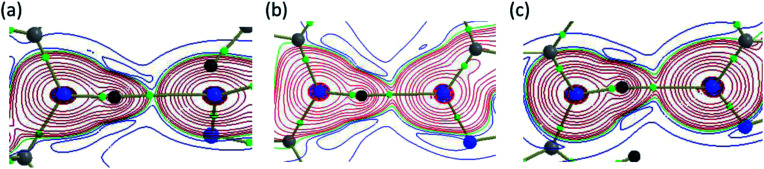
The topological parameters are computed for different noncovalent interactions at their point critical points (BCPs) in selected dimeric pairs of I–III to evaluate their nature and strength (Tables 3–5). The molecular graphs of selected molecular dimers featuring various noncovalent interactions at the bond critical points are given in ESI (Fig. S9–S11†). For the evaluation of intermolecular interactions, the first four criteria [(i) bond critical point (ii) electron density ρ(r), (iii) the Laplacian of electron density ∇2ρ(r) and mutual penetration of the H and the acceptor atom] of KP are used.43 It is worthy to note that the H–H bonding is characterized using the first 3 criteria of KP.
Topological parameters for intermolecular interactions in selected molecular pairs of I [ρ(r): electron density (e Å−3), ∇2ρ(r): Laplacian of electron density (e Å−5); V(r): potential energy density, G(r): kinetic energy density; H(r): total energy density; Rij: bond path (Å), De = −0.5 × V(r) in kcal mol−1 and the values of V(r), G(r) and H(r) are expressed in kJ mol−1 bohr−3].
| Interaction | R ij | ΔrD − ΔrA | ΔrD + ΔrA | ρ(r) | ∇2ρ(r) | V(r) | G(r) | H(r) | D e |
|---|---|---|---|---|---|---|---|---|---|
| M1 | |||||||||
| N1–H1⋯N2 | 2.010 | 0.243 | 0.769 | 0.173 | 1.949 | −55.1 | 54.1 | −1.0 | 6.6 |
| C1–H1B⋯N3 | 2.712 | 0.157 | 0.065 | 0.049 | 0.555 | −9.4 | 12.3 | 2.9 | 1.1 |
| C2–H2A⋯S1 | 3.142 | 0.108 | −0.116 | 0.034 | 0.364 | −5.6 | 7.8 | 2.2 | 0.7 |
| M2 | |||||||||
| C11–H11B⋯N1 | 2.643 | 0.172 | 0.124 | 0.060 | 0.695 | −12.6 | 15.8 | 3.2 | 1.5 |
| H11A⋯H1A | 2.291 | 0.052 | 0.590 | −10.6 | −13.3 | 2.7 | 1.3 | ||
| M3 | |||||||||
| C14–H14B⋯N3 | 2.741 | 0.154 | 0.034 | 0.046 | 0.512 | −8.7 | 11.3 | 2.6 | 1.0 |
| H14B⋯H13A | 2.171 | 0.053 | 0.568 | −10.8 | 13.2 | 2.3 | 1.3 | ||
| H10B⋯H13A | 2.368 | 0.038 | 0.393 | −7.2 | 8.9 | 1.8 | 0.9 | ||
| M4 | |||||||||
| H10A⋯H8A | 2.229 | 0.048 | 0.500 | −9.4 | 11.5 | 2.1 | 1.1 | ||
| M5 | |||||||||
| H9⋯H2A | 2.410 | 0.032 | 0.359 | −6.3 | 8.0 | 1.8 | 0.7 | ||
Topological parameters for intermolecular interactions in selected molecular pairs of II [ρ(r): electron density (e Å−3), ∇2ρ(r): Laplacian of electron density (e Å−5); V(r): potential energy density, G(r): kinetic energy density; H(r): total energy density; Rij: bond path (Å), De = −0.5 × V(r) in kcal mol−1 and the values of V(r), G(r) and H(r) are expressed in kJ mol−1 bohr−3].
| Interaction | R ij | ΔrD − ΔrA | ΔrD + ΔrA | ρ(r) | ∇2ρ(r) | V(r) | G(r) | H(r) | D e |
|---|---|---|---|---|---|---|---|---|---|
| M6 | |||||||||
| N1–H1⋯N2 | 1.943 | 0.274 | 0.832 | 0.220 | 1.922 | −70.3 | 61.3 | −9.0 | 8.4 |
| M7 | |||||||||
| C17–H17B⋯C4 | 3.133 | 0.125 | 0.151 | 0.053 | 0.611 | −10.5 | 13.6 | 3.1 | 1.3 |
| M8 | |||||||||
| C10–H10A⋯N2 | 2.753 | 0.157 | 0.021 | 0.047 | 0.532 | −9.1 | 11.8 | 2.7 | 1.1 |
| C11–H11⋯C8 | 2.912 | 0.031 | 0.031 | 0.040 | 0.450 | −8.2 | 10.2 | 2.0 | 1.0 |
| H11⋯H14B | 2.429 | 0.041 | 0.453 | −8.2 | 10.3 | 2.1 | 1.0 | ||
| M9 | |||||||||
| C10–H10B⋯F1 | 2.406 | 0.069 | 0.281 | 0.052 | 0.811 | −13.8 | 17.9 | 4.1 | 1.6 |
| M10 | |||||||||
| H14A⋯H14A | 2.427 | 0.040 | 0.437 | −8.0 | 10.0 | 2.0 | 1.0 | ||
| M12 | |||||||||
| H16⋯H17A | 2.405 | 0.040 | 0.433 | −8.0 | 9.9 | 1.9 | 1.0 | ||
| H16⋯H18B | 2.441 | 0.038 | 0.412 | −7.5 | 9.4 | 1.8 | 0.9 | ||
| M13 | |||||||||
| H18A⋯H6 | 2.279 | 0.051 | 0.563 | −10.2 | 12.8 | 2.6 | 1.2 | ||
Topological parameters for intermolecular interactions in selected molecular pairs of III [ρ(r): electron density (e Å−3), ∇2ρ(r): Laplacian of electron density (e Å−5); V(r): potential energy density, G(r): kinetic energy density; H(r): total energy density; Rij: bond path (Å), De = −0.5 × V(r) in kcal mol−1 and the values of V(r), G(r) and H(r) are expressed in kJ mol−1 bohr−3].
| Interaction | R ij | ΔrD − ΔrA | ΔrD + ΔrA | ρ(r) | ∇2ρ(r) | V(r) | G(r) | H(r) | D e |
|---|---|---|---|---|---|---|---|---|---|
| M14 | |||||||||
| N1–H1⋯N2 | 1.953 | 0.275 | 0.821 | 0.217 | 1.912 | −68.6 | 60.4 | −8.3 | 8.2 |
| C5–H5⋯N3 | 2.620 | 0.172 | 0.156 | 0.051 | 0.650 | −10.6 | 14.2 | 3.6 | 1.3 |
| M15 | |||||||||
| H6⋯H14B | 2.383 | 0.048 | 0.543 | −9.4 | 12.1 | 2.7 | 1.1 | ||
| M16 | |||||||||
| H10A⋯H10A | 1.963 | 0.082 | 0.920 | −17.9 | 21.5 | 3.6 | 2.1 | ||
| C15–H15A⋯S1 | 3.078 | 0.149 | −0.061 | 0.039 | 0.391 | −6.6 | 8.6 | 2.0 | 0.8 |
| M17 | |||||||||
| C5–H5⋯Br1 | 3.064 | 0.119 | 0.023 | 0.049 | 0.520 | −9.0 | 11.6 | 2.6 | 1.1 |
| M18 | |||||||||
| H3⋯H11 | 2.316 | 0.056 | 0.659 | −12.2 | 15.1 | 2.9 | 1.5 | ||
| H2⋯H11 | 2.530 | 0.049 | 0.608 | −10.7 | 13.6 | 2.9 | 1.3 | ||
| H2⋯H15B | 2.487 | 0.038 | 0.452 | −7.7 | 10.0 | 2.3 | 0.9 | ||
| M19 | |||||||||
| C13–H13⋯Br1 | 3.128 | 0.119 | −0.059 | 0.039 | 0.430 | −7.4 | 9.6 | 2.1 | 0.9 |
| M20 | |||||||||
| C6–H6⋯Br1 | 2.942 | 0.185 | 0.125 | 0.053 | 0.552 | −9.9 | 12.5 | 2.6 | 1.2 |
| M21 | |||||||||
| H18A⋯H16 | 2.400 | 0.037 | 0.395 | −7.2 | 9.0 | 1.8 | 0.9 | ||
| M22 | |||||||||
| C17–H17B⋯Br1 | 2.926 | 0.073 | 0.145 | 0.050 | 0.555 | −9.9 | 12.5 | 2.6 | 1.2 |
In I, one N–H⋯N and three C–H⋯N, one C–H⋯S, one C–H⋯C and five Csp3–H⋯H–Csp3 type H–H bonding interactions were observed. The bond critical points (BCPs) are clearly detected and confirmed the existence of these interactions except C–H⋯C(π) interaction. The ρ(r) values for these interactions lie in the range 0.032–0.173 e Å−3 and these values satisfy the KP limit [0.013 < ρ(r) e Å−3 < 0.236] for hydrogen bonds. It is interesting to convey that only three intermolecular interactions (N1–H1⋯N2, C11–H11B⋯N1 and Csp3–H11A⋯H1A–Csp3 type H–H bonding) are in agreement with the suggested values [0.580 < ∇2ρ(r) e Å−5 < 3.355] of KP. The KP-4 rule is found to be extremely important to differentiate the classical hydrogen bonds from van der Waals interactions. As shown in Table 3, all the classical intermolecular interactions showing hydrogen bonding character except C–H⋯S interaction.
The dissociation energies for these interactions are in the range of 0.7 to 6.6 kcal mol−1. Among these interactions, the intermolecular N1–H1⋯N2 (motif M1) hydrogen bond has a negative total electronic density H(r) value of −1.0 kJ mol−1 b−3. The positive value of Laplacian and H(r) < 0 indicate that the N–H⋯N interaction shows the intermediate bonding character between shared and closed shell interaction.44 The remaining interactions including H–H bonding are closed shell in nature as they obey the positive value of Laplacian and H(r) > 0. The results clearly demonstrate that the H–H bonding interactions also play significant roles in the crystalline state of I.
In II, the dissociation energies for intermolecular interactions are in the range of 0.9–8.4 kcal mol−1 (Table 4). The De value for Csp3–H⋯H–Csp3 and Csp3–H⋯H–Csp2 interactions are found to be 0.9–1.2 kcal mol−1. The ρ(r) values for intermolecular interactions noted in II fulfil the KP limit. However, only three intermolecular interactions (N1–H1⋯N2, C17–H17B⋯C4 and C10–H10B⋯F1) are obeyed the proposed KP limit for the Laplacian of the electron density. The positive value of Laplacian, H(r) > 0 and 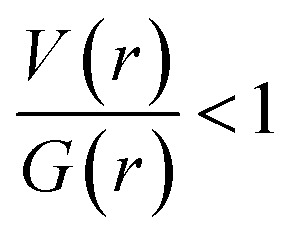 for the H–H bonding suggest that they are closed shell in nature. The remaining interactions are classified as hydrogen bond on the basis of KP-4 rule. It should be noted that the positive value of the Laplacian of electron density, H(r) < 0 and
for the H–H bonding suggest that they are closed shell in nature. The remaining interactions are classified as hydrogen bond on the basis of KP-4 rule. It should be noted that the positive value of the Laplacian of electron density, H(r) < 0 and 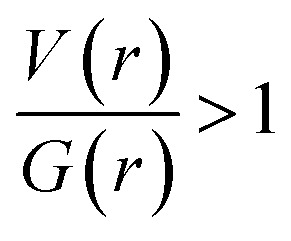 reveal that intermolecular N1–H1⋯N2 interaction is found to be intermediate bonding nature between shared and closed shell interaction as similar to the motif I. We note that the intermolecular C–H⋯F and C–H⋯C(π) interactions are found to be stronger after N–H⋯N hydrogen bond based on the H(r) values.
reveal that intermolecular N1–H1⋯N2 interaction is found to be intermediate bonding nature between shared and closed shell interaction as similar to the motif I. We note that the intermolecular C–H⋯F and C–H⋯C(π) interactions are found to be stronger after N–H⋯N hydrogen bond based on the H(r) values.
In III, the Laplacian of the electron density values for intermolecular N–H⋯N and C–H⋯N interactions comply with the proposed values for hydrogen bonds. The KP-4 rule suggests that N–H⋯N, C–H⋯N and three C–H⋯Br (out of four) interactions are showing hydrogen bonding character. The H–H bonding interactions in this structure are closed shell in nature. The distribution of total electronic energy density H(r) is shown in Fig. 16 for intermolecular N–H⋯N hydrogen bond in all three structures. From this figure one can see the transit region (between shared and closed shell nature) for N–H⋯N hydrogen bond in II and III. In III, the stronger interaction is found to be N–H⋯N followed by C–H⋯N, H–H bonding and C–H⋯Br interactions in regard to the H(r) values. The analysis of topological properties for these interactions apparently supports the importance of weak nature of non-classical H–H bonding interactions.
Fig. 16. Total electronic density distribution H(r) showing the formation of strong intermolecular N–H⋯N hydrogen bonds in (a) I, (b) II and (c) III. All the plots are drawn in the plane comprising the atoms involved in the hydrogen bond and small green spheres represent the bond critical points.
Conclusions
In the present investigation, three pharmaceutically promising adamantane–thiadiazole hybrid derivatives have been synthesized and their crystal structures at low temperature have been determined. The orientation of the amino group was completely different between halophenylamino and ethylamino derivatives. This feature was not favoured for the formation of a R22(8) synthon in I. Crystal structures of II and III showed isostructural behaviour with 1D supramolecular construct. Further, different theoretical tools were used to characterize the noncovalent interactions present in these compounds. Hirshfeld surface analysis revealed that the halogenated compounds showed similar relative contributions of different intermolecular interactions, whereas ethylamino derivative showed variations in the relative contributions of H⋯H and H⋯C and H⋯S contacts as compared to halogenated derivatives. Topological analysis was performed for selected dimeric pairs of these compounds. The first four criteria of KP have been used to characterize the nature and strength of noncovalent interactions. The results indicate that there was a strong N–H⋯N hydrogen bond formed between amino group and one of the N atoms of the thiadiazole ring. The strength of this interaction was found to be relatively weaker in I as compared to II and III. The molecular electrostatic potential surface map suggested that the S atom showed weaker accepting tendencies in varying degrees and participated in van der Waals interactions. The intermolecular C–H⋯N, C–H⋯F and C–H⋯Br and C–H⋯C(π) showed hydrogen bonding character and H–H bonding interactions displayed weak and closed shell in nature.
Conflicts of interest
The authors declare that they have no competing interests.
Supplementary Material
Acknowledgments
This work was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University through the Research Group Program (Grant No. RGP-1438-0010). ST thanks the DST-SERB (SB/YS/LS-19/2014) for financial support. ST and MJP would like to thank Laboratorio Nacional de Supercomputo del Sureste (LNS-BUAP) for computational resource.
Electronic supplementary information (ESI) available: Potential energy surface scan, topological parameters for intra- and intermolecular interactions, molecular graphs for intra- and intermolecular interactions. CCDC 1977639, 1977643 and 1977750. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra00733a
References
- (a) Hu Y. Li C.-Y. Wang X.-M. Yang Y.-H. Zhu H.-L. Chem. Rev. 2014;114:5572–5610. doi: 10.1021/cr400131u. [DOI] [PubMed] [Google Scholar]; (b) Jain A. K. Sharma S. Vaidya A. Ravichandran V. Agrawal R. K. Chem. Biol. Drug Des. 2013;81:557–576. doi: 10.1111/cbdd.12125. [DOI] [PubMed] [Google Scholar]
- Supuran C. T. Nat. Rev. Drug Discovery. 2008;7:168–181. doi: 10.1038/nrd2467. [DOI] [PubMed] [Google Scholar]
- (a) Kadi A. A. Al-Abdullah E. S. Shehata I. A. Habib E. E. Ibrahim T. M. El-Emam A. A. Eur. J. Med. Chem. 2010;45:5006–5011. doi: 10.1016/j.ejmech.2010.08.007. [DOI] [PubMed] [Google Scholar]; (b) Fosbinder R. J. Walter L. A. J. Am. Chem. Soc. 1939;61:2032–2033. doi: 10.1021/ja01877a024. [DOI] [Google Scholar]; (c) Li P. Shi L. Gao M.-N. Yang X. Xue W. Jin L.-H. Hu D.-Y. Song B.-A. Bioorg. Med. Chem. Lett. 2015;25:481–484. doi: 10.1016/j.bmcl.2014.12.038. [DOI] [PubMed] [Google Scholar]; (d) Zhou P. Mo X. Wang W. Chen X. Lou Y. Int. J. Mol. Sci. 2018;19:1271. doi: 10.3390/ijms19051271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (a) Cui Z.-N. Li Y.-S. Hu D.-K. Tian H. Jiang J.-Z. Wang Y. Yan X.-J. Sci. Rep. 2016;6:20204. doi: 10.1038/srep20204. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Li Y. Geng J. Liu Y. Yu S. Zhao G. ChemMedChem. 2013;8:27–41. doi: 10.1002/cmdc.201200355. [DOI] [PubMed] [Google Scholar]
- (a) Khoury H. J. Garcia-Manero G. Borthakur G. Kadia T. Foudray M. C. Arellano M. Langston A. Bethelmie-Bryan B. Rush S. Litwiler K. Karan S. Simmons H. Marcus A. I. Ptaszynski M. Kantarjian H. Cancer. 2012;118:3556–3564. doi: 10.1002/cncr.26664. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Altıntop D. M. Ciftci I. H. Radwan O. M. Sever B. Kaplancıklı A. Z. Ali F. S. T. Koga R. Fujita M. Otsuka M. Özdemir A. Molecules. 2018;23:59. doi: 10.3390/molecules23010059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gan X. Hu D. Chen Z. Wang Y. Song B. Bioorg. Med. Chem. Lett. 2017;27:4298–4301. doi: 10.1016/j.bmcl.2017.08.038. [DOI] [PubMed] [Google Scholar]
- Salomão K. de Souza E. M. Carvalho S. A. da Silva E. F. Fraga C. A. M. Barbosa H. S. de Castro S. L. Antimicrob. Agents Chemother. 2010;54:2023–2031. doi: 10.1128/AAC.01241-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serban G. Molecules. 2019;24:1557. doi: 10.3390/molecules24081557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (a) Liu J. Obando D. Liao V. Lifa T. Codd R. Eur. J. Med. Chem. 2011;46:1949–1963. doi: 10.1016/j.ejmech.2011.01.047. [DOI] [PubMed] [Google Scholar]; (b) Guy L. Graciela A. Curr. Med. Chem. 2010;17:2967–2978. doi: 10.2174/092986710792065027. [DOI] [PubMed] [Google Scholar]
- Wanka L. Iqbal K. Schreiner P. R. Chem. Rev. 2013;113:3516–3604. doi: 10.1021/cr100264t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (a) Al-Wahaibi L. H. Sujay S. Muthu G. G. El-Emam A. A. Venkataramanan N. S. Al-Omary F. A. M. Ghabbour H. A. Percino J. Thamotharan S. J. Mol. Struct. 2018;1159:233–245. doi: 10.1016/j.molstruc.2018.01.064. [DOI] [Google Scholar]; (b) Al-Wahaibi H. L. Hassan M. H. Abo-Kamar M. A. Ghabbour A. H. El-Emam A. A. Molecules. 2017;22:710. doi: 10.3390/molecules22050710. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Al-Wahaibi L. H. Joubert J. Blacque O. Al-Shaalan N. H. El-Emam A. A. Sci. Rep. 2019;9:19745. doi: 10.1038/s41598-019-56331-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spackman M. A. Jayatilaka D. CrystEngComm. 2009;11:19–32. doi: 10.1039/B818330A. [DOI] [Google Scholar]
- (a) Gavezzotti A. J. Phys. Chem. B. 2003;107:2344–2353. doi: 10.1021/jp022288f. [DOI] [Google Scholar]; (b) Gavezzotti A. Mol. Phys. 2008;106:1473–1485. doi: 10.1080/00268970802060674. [DOI] [Google Scholar]; (c) Gavezzotti A. New J. Chem. 2011;35:1360–1368. doi: 10.1039/C0NJ00982B. [DOI] [Google Scholar]; (d) Gavezzotti A. J. Phys. Chem. B. 2002;106:4145–4154. doi: 10.1021/jp0144202. [DOI] [Google Scholar]
- Bader R., Atoms in Molecules: A Quantum Theory, Oxford University Press, USA, 1994 [Google Scholar]
- Koch U. Popelier P. L. A. J. Phys. Chem. B. 1995;99:9747–9754. doi: 10.1021/j100024a016. [DOI] [Google Scholar]
- (a) Bondi A. J. Phys. Chem. 1964;68:441–451. doi: 10.1021/j100785a001. [DOI] [Google Scholar]; (b) Nyburg S. C. Faerman C. H. Acta Crystallogr., Sect. B: Struct. Sci. 1985;41:274–279. doi: 10.1107/S0108768185002129. [DOI] [Google Scholar]
- (a) Munshi P. Guru Row T. N. Cryst. Growth Des. 2006;6:708–718. doi: 10.1021/cg050484g. [DOI] [Google Scholar]; (b) Munshi P. Jelsch C. Hathwar V. R. Guru Row T. N. Cryst. Growth Des. 2010;10:1516–1526. doi: 10.1021/cg900649m. [DOI] [Google Scholar]
- Espinosa E. Molins E. Lecomte C. Chem. Phys. Lett. 1998;285:170–173. doi: 10.1016/S0009-2614(98)00036-0. [DOI] [Google Scholar]
- Cremer D. Kraka E. Angew. Chem., Int. Ed. 1984;23:627–628. doi: 10.1002/anie.198406271. [DOI] [Google Scholar]
- El-Emam A. A. Lehmann J. Monatsh. Chem. 1994;125:587–591. doi: 10.1007/BF00811852. [DOI] [Google Scholar]
- Clark R. C. Reid J. S. Acta Crystallogr., Sect. A: Found. Crystallogr. 1995;51:887–897. doi: 10.1107/S0108767395007367. [DOI] [Google Scholar]
- Dolomanov O. V. Bourhis L. J. Gildea R. J. Howard J. A. K. Puschmann H. J. Appl. Crystallogr. 2009;42:339–341. doi: 10.1107/S0021889808042726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheldrick G. Acta Crystallogr., Sect. A: Found. Adv. 2015;71:3–8. doi: 10.1107/S2053273314026370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheldrick G. Acta Crystallogr., Sect. C: Struct. Chem. 2015;71:3–8. doi: 10.1107/S2053229614024218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner M. J., McKinnon J. J., Wolff S. K., Grimwood D. J., Spackman P. R., Jayatilaka D. and Spackman M. A., CrystalExplorer17, University of Western Australia, 2017 [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery Jr J. A., Peralta J. E., Ogliaro F., Bearpark M. J., Heyd J., Brothers E. N., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A. P., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam N. J., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas Ö., Foresman J. B., Ortiz J. V., Cioslowski J. and Fox D. J., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013 [Google Scholar]
- Todd A. K., AIMALL version 19.02.13, TK Gristmill Software, Overland Park KS, USA, 2019 [Google Scholar]
- Zhao Y. Truhlar D. G. Theor. Chem. Acc. 2008;120:215–241. [Google Scholar]
- Grimme S. Antony J. Ehrlich S. Krieg H. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Bochevarov A. D. Harder E. Hughes T. F. Greenwood J. R. Braden D. A. Philipp D. M. Rinaldo D. Halls M. D. Zhang J. Friesner R. A. Int. J. Quantum Chem. 2013;113:2110–2142. doi: 10.1002/qua.24481. [DOI] [Google Scholar]
- (a) Becke A. D. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]; (b) Lee C. Yang W. Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]; (c) Vosko S. H. Wilk L. Nusair M. Can. J. Phys. 1980;58:1200–1211. doi: 10.1139/p80-159. [DOI] [Google Scholar]; (d) Stephens P. J. Devlin F. J. Chabalowski C. F. Frisch M. J. J. Phys. Chem. 1994;98:11623–11627. doi: 10.1021/j100096a001. [DOI] [Google Scholar]
- Bulat F. A. Toro-Labbé A. Brinck T. Murray J. S. Politzer P. J. Mol. Model. 2010;16:1679–1691. doi: 10.1007/s00894-010-0692-x. [DOI] [PubMed] [Google Scholar]
- Cremer D. Pople J. A. J. Am. Chem. Soc. 1975;97:1354–1358. doi: 10.1021/ja00839a011. [DOI] [Google Scholar]
- Al-Tamimi A.-M. S. Alafeefy A. M. El-Emam A. A. Ng S. W. Tiekink E. R. T. Acta Crystallogr., Sect. E: Struct. Rep. Online. 2013;69:o683. doi: 10.1107/S1600536813009033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (a) Matta C. F. Hernándex-Trujillo J. Tang T. H. Bader R. F. W. Chem.–Eur. J. 2003;9:1940–1951. doi: 10.1002/chem.200204626. [DOI] [PubMed] [Google Scholar]; (b) Matta C. F., in Hydrogen Bonding-New Insights, ed. S. Grabowski, Springer, 2006, ch. 9, pp. 337–375 [Google Scholar]; (c) Cukrowski I. Matta C. Chem. Phys. Lett. 2010;499:66–69. doi: 10.1016/j.cplett.2010.09.013. [DOI] [Google Scholar]
- Bernstein J. Davis R. E. Shimoni L. Chang N.-L. Angew. Chem., Int. Ed. 1995;34:1555–1573. doi: 10.1002/anie.199515551. [DOI] [Google Scholar]
- Al-Wahaibi L. H. Kumar N. S. El-Emam A. A. Venkataramanan N. S. Ghabbour H. A. Al-Tamimi A.-M. S. Percino J. Thamotharan S. J. Mol. Struct. 2018;1175:230–240. doi: 10.1016/j.molstruc.2018.07.102. [DOI] [Google Scholar]
- CSD search criteria: (i) 3D coordinates determined (ii) R-factor ≤ 0.05 (iii) not disordered (iv) no errors (v) not polymeric (vi) no ions (vii) no powder structures and (viii) only organic compounds
- Fábián L. Kálmán A. Acta Crystallogr., Sect. B: Struct. Sci. 1999;55:1099–1108. doi: 10.1107/S0108768199009325. [DOI] [PubMed] [Google Scholar]
- (a) Gelbrich T. Hursthouse M. B. CrystEngComm. 2005;7:324–336. doi: 10.1039/B502484F. [DOI] [Google Scholar]; (b) Gelbrich T. Hursthouse M. B. CrystEngComm. 2006;8:448–460. doi: 10.1039/B600753H. [DOI] [Google Scholar]; (c) Gelbrich T. Threlfall T. L. Hursthouse M. B. CrystEngComm. 2012;14:5454–5464. doi: 10.1039/C2CE25508A. [DOI] [Google Scholar]
- Politzer P. Murray J. S. Cryst. Growth Des. 2015;15:3767–3774. doi: 10.1021/acs.cgd.5b00419. [DOI] [Google Scholar]
- (a) Politzer P. Murray J. S. Clark T. Phys. Chem. Chem. Phys. 2013;15:11178–11189. doi: 10.1039/C3CP00054K. [DOI] [PubMed] [Google Scholar]; (b) Clark T. Hennemann M. Murray J. S. Politzer P. J. Mol. Model. 2007;13:291–296. doi: 10.1007/s00894-006-0130-2. [DOI] [PubMed] [Google Scholar]
- Popelier P. L. A. J. Phys. Chem. A. 1998;102:1873–1878. doi: 10.1021/jp9805048. [DOI] [Google Scholar]
- Espinosa E. Alkorta I. Elguero J. Molins E. J. Chem. Phys. 2002;117:5529–5542. doi: 10.1063/1.1501133. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.