Abstract
Isocyanurates are cyclic trimers of isocyanate molecules. They are generally known as highly thermostable compounds. However, it is interesting how the thermal stabilities of the isocyanurate molecules will be altered depending on the substituents of their three nitrogen atoms. We performed computational investigations on the thermochemical behaviors of isocyanurate molecules with various alkyl and phenyl substituents. The cyclotrimerization processes of isocyanates are highly exothermic. Our best estimate of the enthalpy change for the cyclotrimerization of methyl isocyanate into trimethyl isocyanurate was −66.4 kcal mol−1. Additional negative cyclotrimerization enthalpy changes were observed for n-alkyl-substituted isocyanates. This trend was enhanced with an extension of n-alkyl chains. Conversely, low negative cyclotrimerization enthalpy changes were shown for secondary and tertiary alkyl-substituted isocyanates. The n-alkyl-substituted isocyanurates were shown to be stabilized due to attractive dispersion interactions between the substituents. Meanwhile, the branched alkyl-substituted isocyanurates were destabilized due to the deformation of their isocyanurate rings. For various alkyl-substituted isocyanates, the sum of the deformation energy of the isocyanurate ring and the intramolecular inter-substituent nonbonding interaction energies was found to be linearly correlated with their cyclotrimerization energies. The cyclotrimerization energy for phenyl isocyanate was shown to have significantly deviated from the linear relationship observed for the alkyl-substituted isocyanurates. This is probably attributable to a remarkable change in the orbital resonance interactions during the cyclotrimerization of phenyl isocyanate to triphenyl isocyanurate.
Computational investigations on how the thermochemical stabilities of isocyanurate molecules depend on the substituents on the nitrogen atoms in the isocyanurate ring have been described.
1. Introduction
Isocyanurates are known as highly thermally and mechanically stable frameworks. By incorporating isocyanurate frameworks into polymer networks, the physical properties of the polymers will be improved. Thus, isocyanurate frameworks are the key components in rigid polyurethane foams, which are used in a variety of industrial applications, such as elastomers, sealants, coatings, and insulation boards.1–3 Furthermore, isocyanurates have diverse range of applications, such as medicines,4,5 selective anion binding,6,7 functional microporous materials,8,9 and coating materials.10
Cyclotrimerization of three isocyanate molecules is the most rapid, economical, and atom-efficient route to isocyanurates.3,11 A variety of catalysts have been developed for the cyclotrimerization processes. For example, amines,12 phosphines,13–17 N-heterocyclic carbenes,18 various anions,19,20 transition metal complexes,21,22 main-group metal complexes,3,23 hexamethyldisilazane,24 and N-heterocyclic olefins25 have been utilized as the catalysts for the cyclotrimerization of isocyanates. The mechanisms of these catalytic processes have been investigated using density functional theory (DFT) methods.3,16,17,20,21,26 All the DFT results suggest that the isocyanate cyclotrimerization processes are highly exothermic, which demonstrates that isocyanurates are quite thermodynamically stabilized molecules.
However, various substituents can be introduced on the nitrogen atoms of isocyanurate molecules. Kordomenos et al. synthesized two types of model block copolymers consisting of isocyanurate frameworks and investigated their thermal decomposition processes.2 Based on the experimentally determined decomposition temperature and rates, they concluded that the thermodynamic stability of the isocyanurate ring would be affected by the adjacent substituents. Furthermore, the conformational space of the isocyanurate molecules should increase rapidly as the substituents on the ring become larger and more flexible. However, it has not been well elucidated how the structural changes of the substituents alter the thermochemical stabilities and the conformational behaviors of the isocyanurate molecules (Scheme 1).
Scheme 1. Isocyanurate framework resulting from the cyclotrimerization of isocyanate molecules.
In the present study, we focused on the thermochemical stabilities and the conformational behaviors of isocyanurate molecules with different sorts of substituents on their nitrogen atoms. Previous DFT investigations explored the catalytic cyclotrimerization paths for computational model isocyanates such as methyl isocyanate,3,16,20,21,26 ethyl isocyanate,17 or phenyl isocyanate.16 Meanwhile, we investigated variously substituted isocyanurate molecules, such as primary, secondary, and tertiary alkyl-substituted trialkyl isocyanurates. However, we limited our research to isocyanurates with three identical substituents on the nitrogen atoms. In addition to DFT methods, we applied the post Hartree–Fock techniques (MP2 and CCSD(T)) for energy evaluations. The energy change that occurs as the three isocyanate molecules are converted into an isocyanurate molecule via cyclotrimerization is referred to as cyclotrimerization energy. This energy change is closely related to the thermochemical stability of the isocyanurate molecule. Hence, the cyclotrimerization energy was considered an indicator of the thermochemical stability of the isocyanurate molecule. Furthermore, to understand the conformational behaviors, the conformational spaces of the isocyanurate molecules were explored extensively. For comparison with the alkyl-substituted derivatives, the cyclotrimerization energy of phenyl isocyanate was also calculated.
This paper will describe our results in the following order. First, the computational results on the cyclotrimerization energy of methyl isocyanate are shown. Several selected computational levels were applied, and their reliabilities were verified by comparing their computational results with each other. Second, the results of the investigations on the conformational behaviors of the isocyanurate molecules with various alkyl and phenyl groups are described. Third, the factors closely related to the thermochemical stability of the isocyanurate molecule are presented. Namely, the degree of deformation of the six-membered isocyanurate rings was assessed. In addition, the magnitude of the intramolecular nonbonding interaction energies between the substituents on the ring was estimated. Finally, the calculated values for the cyclotrimerization energies of isocyanates possessing various substituents are shown. The relationships between the cyclotrimerization energies and the structural characteristics will be discussed.
2. Computational methods
We performed all the electronic state calculations using the Gaussian 09 program package.27 The B3LYP (Becke 3-parameter, Lee–Yang–Parr),28–30 MP2 (second-order Møller–Plesset perturbation),31,32 and CCSD(T) (coupled-cluster single, double, and perturbative triple)33 level calculations were employed. The frozen-core approximation was applied to the MP2 and CCSD(T) level computations. The intramolecular dispersion interactions were found to be essential for energy evaluations of the isocyanurate molecules. Hence, in addition to the B3LYP calculations, the dispersion-corrected B3LYP calculations (B3LYP-GD3 (ref. 34) and B3LYP-GD3BJ35) were performed. For the B3LYP DFT calculations, the “superfinegrid” was utilized. Dunning's correlation-consistent basis sets, cc-pVXZ and aug-cc-pVXZ (X = D, T, Q),36,37 were employed. Unless otherwise noted, geometry optimizations were carried out at the B3LYP-GD3/cc-pVTZ level. The scaling factors, 0.9854 and 0.9970, were used for the enthalpy corrections of the B3LYP and MP2-optimized geometries, respectively.38 The optimized structures of the isocyanurate molecules are shown in Fig. 1, 2, and S1,† and those of the isocyanate molecules are shown in Fig. S2.† The conformational analysis of the isocyanurate molecules was conducted using the CONFLEX program39 with the MMFF94S force field.40,41
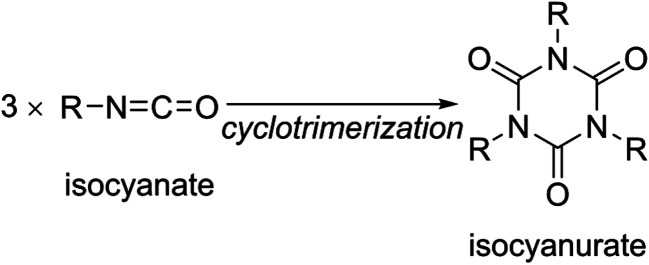
Fig. 1. Structures of tri-n-alkyl isocyanurates (see also Fig. S1†).
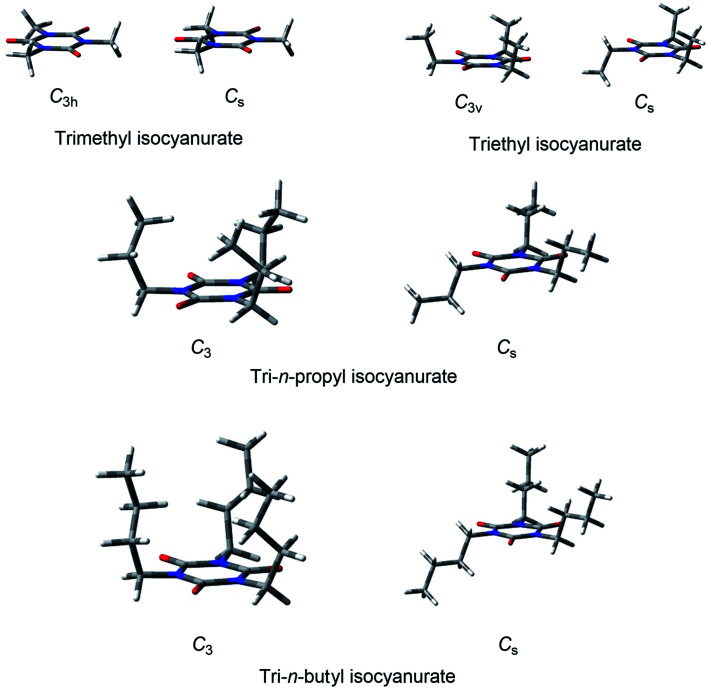
Fig. 2. Structures of the secondary and tertiary alkyl-substituted isocyanurates and triphenyl isocyanurate.
3. Results and discussion
3.1. Estimation of the cyclotrimerization energy of methyl isocyanate
The cyclotrimerization energy of methyl isocyanate was evaluated using several computational methods (Table 1). The global potential energy minimum structures of trimethyl isocyanurate and methyl isocyanate were confirmed to have C3h and Cs symmetries, respectively.
Calculated values of the electronic energy change for the cyclotrimerization of methyl isocyanatea.
| Energy evaluation method | Geometry optimization method | ||
|---|---|---|---|
| B3LYP/cc-pVTZ | B3LYP-GD3/cc-pVTZ | MP2/cc-pVTZ | |
| B3LYP/cc-pVTZ | −49.6 | −49.6 | −50.2 |
| B3LYP-GD3/cc-pVTZ | −58.1 | −58.1 | −58.6 |
| B3LYP-GD3BJ/cc-pVTZ | −61.7 | ||
| HF/cc-pVTZ | −56.4 | −56.4 | −59.4 |
| MP2/cc-pVTZ | −67.3 | −67.2 | −66.8 |
| CCSD(T)/cc-pVTZ | −70.2 | ||
| HF/aug-cc-pVTZ | −55.0 | −55.1 | −58.1 |
| MP2/aug-cc-pVTZ | −68.4 | −68.3 | −67.8 |
The energy value is provided in kcal mol−1. The cyclotrimerization enthalpy at 298 K can be calculated by adding the enthalpy correction term to the electronic energy changes provided in the Table. The enthalpy correction terms are +5.1, +5.1, and +5.2 kcal mol−1, respectively, for the B3LYP/cc-pVTZ, B3LYP-GD3/cc-pVTZ, and MP2/cc-pVTZ optimized geometries.
The calculated cyclotrimerization energies remained almost unchanged when the computational level utilized for the geometry optimizations was changed. However, they were quite sensitive to the computational level employed for energy evaluations. The calculated electronic energy changes for the cyclotrimerization were scattered in the range from −50 to −70 kcal mol−1. The CCSD(T) and B3LYP calculated values were the most and the least negative, respectively, and were at both ends of the calculated cyclotrimerization energy values. The values calculated with the dispersion-corrected B3LYP methods were more negative than the B3LYP values by about 10 kcal mol−1. A comparable amount of energy difference was observed between the MP2 and the Hartree–Fock (HF) values, and the former was more negative than the latter. In addition, the CCSD(T)-calculated value was more negative than the corresponding MP2 value by about 3 kcal mol−1.
We applied the two-layer ONIOM methods42 to the cyclotrimerization energy calculations of methyl isocyanate. For the trimethyl isocyanurate molecule, the isocyanurate ring moiety was assigned as the high computational level layer in our ONIOM calculations. Meanwhile, the three methyl substituents on the nitrogen atoms were assigned as the low computational level layer. The corresponding two-layer assignment was made for the methyl isocyanate molecule. The CCSD(T) energy evaluation was applied to the high computational level layer, whereas the MP2 or B3LYP-GD3 energy evaluation was applied to the low computational level layer. The ONIOM-calculated cyclotrimerization energies of methyl isocyanate are shown in Table 2.
ONIOM calculation results for the electronic energy change for the cyclotrimerization of methyl isocyanatea.
| Computational levelb | ΔEec |
|---|---|
| B3LYP/cc-pVTZ | −61.3 |
| B3LYP-GD3/cc-pVTZ | −65.5 |
| B3LYP-GD3BJ/cc-pVTZ | −65.7 |
| MP2/aug-cc-pVDZ | −71.3 |
| MP2/cc-pVTZ | −70.5 |
| MP2/aug-cc-pVTZ | −71.0 |
| MP2/aug-cc-pVQZ | −70.5 |
Energy values are provided in kcal mol−1. Geometry optimizations were carried out at the B3LYP-GD3/cc-pVTZ level.
The computational levels that were applied to the outer layer in the ONIOM calculation are presented. The CCSD(T)/cc-pVTZ computational level was commonly applied to the inner layer.
The cyclotrimerization enthalpy at 298 K can be calculated by adding the enthalpy correction term to the electronic energy changes provided in the Table. The enthalpy correction term is +5.1 kcal mol−1.
In pursuit of a very accurate and reliable value, we estimated the basis set limit value of the cyclotrimerization energy of methyl isocyanate at the CCSD(T) level. MP2 and CCSD(T) single-point energy evaluations were performed with the correlation-consistent basis sets (aug-cc-pVTZ, X = D, T, Q).36,37 The single-point energies were extrapolated to the basis set limit according to the procedures prescribed by Halkier et al.43,44 and Helgaker et al.45 Our estimate of the basis set limit value at the CCSD(T) level was −71.6 kcal mol−1. We consider this value our best estimate for the electronic energy change upon cyclotrimerization of methyl isocyanate. After consideration of the enthalpy corrections, the cyclotrimerization enthalpy change of methyl isocyanate at 298 K, ΔHR, was estimated to be −66.4 kcal mol−1 (see Table S5†).
The non-dispersion-corrected B3LYP values in Table 1 are considerably less negative compared to our best estimate value. The dispersion-corrected B3LYP values are similar to our best estimate value, but there are still significant differences from the best estimate value. Meanwhile, the ONIOM calculated cyclotrimerization values were more similar to our best estimate value than those obtained via the directly applied dispersion-corrected DFT or MP2 methods (Tables 1 and 2). In particular, the ONIOM calculations for which the MP2 method was applied to the low computational level outer layer suggested cyclotrimerization energies of −70.5 to −71.3 kcal mol−1. These values are in satisfactory agreement with our best estimate value. The ONIOM-calculated values were relatively insensitive to the basis set employed in the MP2 calculations for the outer layer. Replacing the MP2 method with the dispersion-corrected B3LYP or non-dispersion-corrected B3LYP method resulted in a worse agreement between the calculated cyclotrimerization energy values and our best estimate value.46
Previously calculated DFT ΔHR values for the cyclotrimerization of methyl isocyanate are as follows. Paul et al.21 reported B3PW91-level-calculated value of −63.9 kcal mol−1, which is rather close to our value. Meanwhile, the B3LYP value of −57.5 kcal mol−1 reported by Heift et al.20 is significantly less negative as compared to our value. In addition, Helberg et al.17 reported B2PLYP-level-calculated ΔHR value of −51.0 kcal mol−1 for cyclotrimerization of ethyl isocyanate.
3.2. Conformational behaviors of tri-primary-alkyl-substituted isocyanurates
Isocyanurate molecules substituted with long n-alkyl groups have conformational freedom (gauche/trans) within the n-alkyl chains. The conformational degrees of freedom in the n-alkyl chain increase exponentially as the substituent chain lengths extend. Thus, long n-alkyl substituents will allow a large number of possible conformers for isocyanurate molecules. For example, 22 possible conformers were found for tri-n-propyl isocyanurate through the conformational analysis using the MMFF94S force field, but the number of possible conformers increased to 465 for tri-n-butyl isocyanurate.47
We explored the conformational spaces of the isocyanurates substituted with n-propyl groups or n-alkyl groups longer than n-propyl group. The energy of each conformer was evaluated using the MMFF94S force field calculations and the B3LYP calculations. However, the results of the conformational energy evaluations through these two calculation methods were in contrast. The MMFF94S force field calculations showed a tendency to suggest low energies for the conformers in which three n-alkyl substituents are located close to each other. Meanwhile, the B3LYP calculations showed a tendency to suggest low energies for the extended-form conformers in which the three n-alkyl substituents are located apart from each other. The reason for this contradiction was speculated to be whether or not the intramolecular dispersion interactions were considered. The MMFF94S force field is not fully satisfactory, but the parameters to account for the dispersion interactions are incorporated in it.48,49 Meanwhile, in the B3LYP calculations, the dispersion interactions are ignored.
Previously, Tsuzuki et al. reported on the results of high-level ab initio investigations conducted on the intermolecular interactions of n-alkane dimers.50,51 They confirmed that attractive interactions exist due to the dispersion force between two n-alkane molecules. At appropriate distances, the stabilizing attractive dispersion interaction is larger than the repulsive steric interaction. As a result, the n-alkane dimer has potential energy minimum structures with energy lower than that of the two isolated molecular states. In addition, they found that the attractive dispersion intermolecular interaction between the two n-alkane chains increases as the chains elongate. The addition of one methylene unit increases the attractive interaction energy by about −0.9 kcal mol−1. According to their computations, the depths of the potential energy minima of n-butane and n-octane dimers are −2.97 kcal mol−1 and −6.68 kcal mol−1, respectively.
In recent papers, several groups have also reported that considering dispersion interactions will be important in assessing the thermochemistries of molecules in various cases. It has been demonstrated that the agreement between theories and experiments for various thermochemistries of molecules can be improved by appending the empirical dispersion corrections to DFT functionals.52–57 Furthermore, calculations including electron correlation have been shown to be indispensable for reproducing experimental observations that branching alkanes are more stable than their linear isomers (alkane branching effect).58,59 This result suggests the existence of attractive dispersion (van der Waals) interactions within the branched molecules.59 The intramolecular dispersion interactions are shown to be also related with the E/Z preference in some cases.60 Experimentally determined thermochemical stabilities of highly sterically crowded molecules suggest intramolecular attractive dispersion interactions.61
Considering these results, the dispersion interactions between the n-alkyl substituents of the isocyanurate molecules are expected to have non-negligible effects on their conformational energies. We, thus, evaluated the energy of each conformation using the dispersion-corrected B3LYP-GD3 method. Expectedly, the B3LYP-GD3 calculation suggested that the conformers in which the three substituents are in close proximity to each other are energetically favorable. The B3LYP-GD3 conformational energy evaluations led us to the conclusion that the conformers with the C3 symmetry are global energy minimum structures for a series of tri-n-alkyl isocyanurates. The C3 axis passes through the center of the isocyanurate ring, and the three substituents are around the C3 axis on the same side of the ring. In this structure, three n-alkyl substituents occupy the positions nearest to each other (Fig. 1 and S1†). Conversely, the most unstable conformation with the highest energy was found to be a mirror-symmetric structure with the Cs symmetry. The substituent on the Cs mirror plane is apart from the other two substituents and located on the opposite side of the isocyanurate ring. In this conformation, the three substituents are located as far apart as possible from each other (Fig. 1 and S1†). The attractive dispersion interactions and the steric repulsive interactions between the substituents will both be maximized in the C3 conformation. Conversely, both of these interactions will be minimal in the Cs conformation. The B3LYP-GD3 conformational energy evaluations indicate that the effects of the dispersion interactions are more predominant than those of the steric repulsive interactions.62
Table 3 shows the calculated energy differences between the two extreme conformers described above for isocyanurates substituted with primary alkyl groups. The positive values indicate that the energies of the C3 axis conformers were calculated to be lower than those of the Cs symmetric conformers. Negative values indicate that the calculation results suggested the reversed energy relationships between them. The “dispersion-blind” B3LYP and HF calculations suggested lower energies for the Cs conformers than for the C3 conformers. This indicates that the destabilization due to the steric repulsion between the n-alkyl substituents is greater in the C3 symmetric conformation than in the Cs conformation.
Calculated energy differences between the extreme conformers of tri-n-alkyl isocyanuratesa.
| R | Computational level | ||||||
|---|---|---|---|---|---|---|---|
| B3LYPb | HFb | B3LYP-GD3b | B3LYP-GD3BJb | MP2b | ONIOM (1)c | ONIOM (2)d | |
| Me (Cs–C3h) | 0.04 | 0.04 | 0.05 | 0.04 | 0.05 | 0.05 | 0.05 |
| Et (Cs–C3v) | −0.06 | −0.04 | 0.07 | 0.04 | 0.07 | 0.07 | 0.07 |
| n-Pr (Cs–C3) | −3.74 | −4.57 | 0.10 | −0.01 | 0.61 | 0.09 | 0.62 |
| n-Bu (Cs–C3) | −4.37 | −5.29 | 0.68 | 0.53 | 1.42 | 0.68 | 1.43 |
| n-Hex (Cs–C3) | −9.81 | −12.51 | 5.78 | 5.13 | 6.42 | 5.82 | 6.45 |
| n-Oct (Cs–C3) | −10.84 | 9.85 | 8.95 | 9.87 | |||
The energy differences between the conformers calculated without taking the BSSEs into account are provided in kcal mol−1. Positive values indicate that the conformers possessing the C3 axis are lower in energy than the Cs isomers. The geometries of the conformers were optimized at the B3LYP-GD3/cc-pVTZ level. The BSSE-corrected energy differences between the conformers are provided in Table S6 (see ESI), but almost identical results were obtained whether or not the BSSEs were taken into account.
The cc-pVTZ basis set was utilized.
ONIOM(CCSD(T)/cc-pVTZ:B3LYP-GD3/cc-pVTZ).
ONIOM(CCSD(T)/cc-pVTZ:MP2/cc-pVTZ).
Meanwhile, the dispersion interactions are considered not only by the B3LYP-GD3 calculations but also by the MP2 calculations. In addition, in our ONIOM schemes, the dispersion energies were evaluated at both the high and low computation level layers. The CCSD(T) method was employed for the high computational level layer in our ONIOM calculations. The B3LYP-GD3 and MP2 methods were applied to the low computational level layer in the ONIOM (1) and ONIOM (2) calculations, respectively (Table 3). These dispersion-considering calculations suggested that the energies of the C3 conformers were lower than those of the Cs conformers without exception.63 Furthermore, our calculations suggested that the stability of the C3 conformation relative to the Cs conformation increased as the substituent chain length increased. Evidently, the differences in inter-substituent nonbonding dispersion interactions are essential factors in considering the energy differences between these two conformations.
For the triethyl isocyanurate, the two possible conformers were found to have the C3v and Cs symmetries. In the C3v conformation, three ethyl groups were located on the same side of the isocyanurate ring. Conversely, in the Cs conformation, one ethyl group was located on the opposite side of the ring from the other two ethyl groups (see Fig. 1). The calculated energy differences between the C3v and Cs conformers were quite small (<0.1 kcal mol−1). However, the calculated energies of these conformers were reversed depending on whether or not the dispersion interactions were considered (Table 3). This trend is considered exactly equivalent to that seen with n-propyl or longer n-alkyl substituted isocyanurates. Thus, the C3v and Cs conformers of triethyl isocyanurate can be considered as analogous to the C3 and Cs conformers of n-propyl or relatively long n-alkyl-substituted isocyanurates, respectively.
Two stable conformers of trimethyl isocyanurate were found to have the C3h and Cs symmetries (see Fig. 1). These two conformers differ solely from each other in the orientation of the methyl groups, and the steric crowdedness of the C3h and Cs conformers is considered almost identical. Accordingly, the calculated energy differences between these two conformers were very small, less than 0.1 kcal mol−1. All the computational levels suggested that the C3h conformer is lower in energy than the Cs conformer.
3.3. Conformational analysis for isocyanurates with secondary and tertiary alkyl groups and phenyl groups
For the secondary and tertiary alkyl-substituted isocyanurates, the conformational degrees of freedom are limited compared to those of the primary alkyl-substituted derivatives. In addition to the conformers listed below (Fig. 2), no conformers with characteristic structures were found.
For tri-i-propyl isocyanurate, two stable conformers with the C3h and Cs symmetries were found. Both were mirror-symmetric with respect to the isocyanurate ring (Fig. 2). The energy difference between these two conformers was found to be less than 1 kcal mol−1. The global energy minimum structure of tri-cyclohexyl isocyanurate was found to have the C3h symmetry. For tri-t-butyl isocyanurate, we located two stable conformers with Cs and C3v symmetries. Both conformers were found to have a highly deformed isocyanurate ring. Our calculations indicated that the Cs symmetry conformer is lower in energy than the C3v isomer by about 1 kcal mol−1. For triphenyl isocyanurate, we located a stable structure with D3 symmetry. The angle formed by the phenyl group and the isocyanurate ring was about 73.6°, and the planarity of the phenyl ring and that of the isocyanurate ring were both found to be maintained.
3.4. Factors closely related to the thermochemical stabilities of isocyanurates
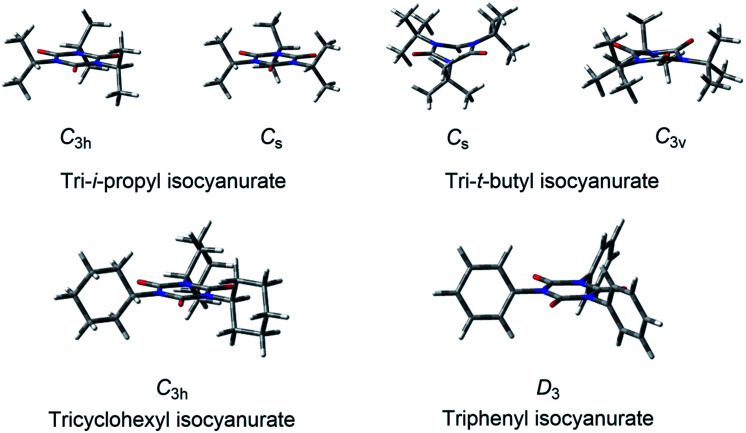
Among the various factors that may affect the thermochemical stability of isocyanurate molecules, we considered that the following two factors would be particularly important. The first one is the degree of deformation of the six-membered isocyanurate ring in the isocyanurate molecule. The second one is the magnitude of the intramolecular nonbonding interaction energy between the substituents on the nitrogen atoms. The importance of the latter is already suggested by the calculation results for the n-alkyl-substituted isocyanurates (Section 3.2). To assess these two factors separately, we divided the isocyanurate molecule into two portions. Namely, the C–N bonds between the substituents and the isocyanurate ring were cleaved. By capping each cleavage end with a hydrogen atom, we obtained an isolated unsubstituted isocyanurate ring and a trimer of an alkane or benzene molecule (Fig. 3).
Fig. 3. The C–N bond cleavages between the substituents and the isocyanurate ring in the isocyanurate molecule produce an alkane trimer and an unsubstituted isocyanurate ring. The above is shown for the C3 conformer of tri-n-octyl isocyanurate.
The ring deformation energies in the isocyanurate molecules were evaluated with the single-point CCSD(T) energies of the unsubstituted isocyanurate rings. The isocyanurate ring in the trimethyl isocyanurate molecule was found to display the smallest deformation among those in the trialkyl isocyanurate molecules. Hence, we adopted the trimethyl isocyanurate molecule as a reference for the deformation energy evaluations. Meanwhile, the inter-substituent interaction energies in the isocyanurate molecules were approximated with the intermolecular interaction energies of the alkane or benzene trimers described above. To correct the basis set superposition errors (BSSEs), the counterpoise correction64 was applied to the calculated interaction energies of the trimers. The estimates for the deformation energies of the isocyanurate rings and the inter-substituent interaction energies are listed in Tables 4 and 5, respectively. The positive and negative values indicate that the isocyanurate molecules will be destabilized and stabilized, respectively.
Calculated deformation energies of the isocyanurate rings in the isocyanurate moleculesa.
| R | Symmetry | |
|---|---|---|
| Primary alkyl-substituted isocyanurates | ||
| C 3 conformer | ||
| Me | C 3h | 0.0 |
| Et | C 3v | 0.5 |
| n-Pr | C 3 | 0.6 |
| n-Bu | C 3 | 0.8 |
| n-Hex | C 3 | 1.5 |
| n-Oct | C 3 | 1.2 |
| C s conformer | ||
| Me | C s | 0.0 |
| Et | C s | 0.5 |
| n-Pr | C s | 0.4 |
| n-Bu | C s | 0.4 |
| n-Hex | C s | 0.4 |
| n-Oct | C s | 0.4 |
| Secondary alkyl-substituted isocyanurates | ||
| i-Pr | C 3h | 2.7 |
| i-Pr | C s | 2.7 |
| Cy | C 3h | 2.4 |
| Tri-t-butyl isocyanurate | ||
| t-Bu | C s | 23.4 |
| t-Bu | C 3v | 22.3 |
| Triphenyl isocyanurate | ||
| Ph | D 3 | −0.8 |
Deformation energies were calculated at the CCSD(T)/cc-pVTZ level (see the text), and the calculated values are provided in kcal mol−1.
Intermolecular interaction energies of the alkane and benzene trimers derived from the isocyanurate moleculesa.
| R | Sym. | Computational methodb | |||
|---|---|---|---|---|---|
| B3LYP | B3LYP-GD3 | B3LYP-GD3BJ | MP2 | ||
| Primary alkyl-substituted isocyanurates | |||||
| C 3 conformer | |||||
| Me | C 3h | 0.3 | −0.5 | −0.5 | −0.4 |
| Et | C 3v | 0.3 | −0.9 | −0.9 | −0.7 |
| n-Pr | C 3 | 0.5 | −1.9 | −1.8 | −1.6 |
| n-Bu | C 3 | 0.6 | −2.6 | −2.5 | −2.3 |
| n-Hex | C 3 | 3.5 | −9.5 | −8.7 | −7.3 |
| n-Oct | C 3 | 5.1 | −13.0 | −12.0 | |
| C s conformer | |||||
| Me | C s | 0.3 | −0.5 | −0.5 | −0.4 |
| Et | C s | 0.3 | −0.9 | −0.8 | −0.7 |
| n-Pr | C s | 0.3 | −1.0 | −0.9 | −0.8 |
| n-Bu | C s | 0.3 | −1.0 | −1.0 | −0.9 |
| n-Hex | C s | 0.3 | −1.0 | −1.0 | −0.9 |
| n-Oct | C s | 0.3 | −1.1 | −1.0 | |
| Secondary alkyl-substituted isocyanurates | |||||
| i-Pr | C 3h | 0.3 | −1.3 | −1.2 | −1.1 |
| i-Pr | C s | 0.3 | −1.3 | −1.2 | −1.1 |
| Cy | C 3h | 0.3 | −1.5 | −1.5 | −1.4 |
| Tri-t-butyl isocyanurate | |||||
| t-Bu | C s | 0.6 | −2.3 | −2.2 | −1.9 |
| t-Bu | C 3v | 0.6 | −2.2 | −2.1 | −1.9 |
| Triphenyl isocyanurate | |||||
| Ph | D 3 | 0.6 | −1.0 | −1.0 | −1.0 |
The intermolecular interaction energies were calculated with taking the corrections for the BSSEs into account. The calculated energy values are provided in kcal mol−1.
The basis set cc-pVTZ was employed.
For the n-alkyl-substituted Cs conformers, the deformation energies were calculated to be 0.4–0.5 kcal mol−1 (Table 4). Their deformation energies were almost constant regardless of the alkyl chain length. Contrarily, for the n-alkyl-substituted C3 conformation, the deformation energy gradually increased as the n-alkyl chain elongated. The deformation energy of the n-propyl derivative was calculated to be 0.6 kcal mol−1, whereas it reached 1.5 and 1.2 kcal mol−1 for the n-hexyl and n-octyl derivatives, respectively. For the secondary alkyl-substituted isocyanurate molecules, the deformation energy of the isocyanurate ring slightly increased. The isocyanurate ring deformation energies for tri-i-propyl and tricyclohexyl isocyanurate were calculated to be 2.4–2.7 kcal mol−1. The ring deformation energy for the tertiary alkyl-substituted derivative, i.e., tri-t-butyl isocyanurate, further increased significantly to 22–23 kcal mol−1. Conversely, slightly negative deformation energy was shown for the triphenyl derivative, indicating almost no deformation of its isocyanurate ring.
The intermolecular interaction energies of the alkane/benzene molecule trimers are shown in Table 5. The “dispersion-blind” B3LYP calculations suggested repulsive intermolecular interactions for all the trimers. These repulsive interaction energies are considered to reflect the steric crowdedness between the substituents in the isocyanurate molecules. For the C3 conformer of the n-alkyl-substituted derivative, the inter-substituent repulsive interactions were suggested to have increased as the n-alkyl chains elongated. The B3LYP calculated interaction energy of the n-alkane trimer varied from 0.3 to 5.1 kcal mol−1 from the trimethyl derivative to the tri-n-octyl derivative of the C3 conformer. The repulsive interaction energies calculated for the t-butane trimer derived from tri-t-butyl isocyanurate were about 0.6 kcal mol−1. For the other isocyanurate derivatives, the inter-substituent repulsive interactions were estimated to be rather small. In relation to these isocyanurate derivatives, the B3LYP intermolecular interaction energies of the trimers were about 0.3 kcal mol−1.
Contrary to the non-dispersion-corrected B3LYP method, the dispersion-considering calculations showed attractive intermolecular interactions of the trimers without exceptions (Table 5). Hence, the attractive interactions must be primarily due to the dispersion force. The isocyanurate molecules should be stabilized by the intramolecular dispersion interactions between the substituents on the nitrogen atoms. However, the results in Table 5 imply that the degree of stabilization varies, depending on the type of substituent. Our calculations suggest that, due to the intramolecular inter-substituent dispersion interactions, the degree of stabilization of the isocyanurate molecules increases in the following order: phenyl-substituted derivative < secondary alkyl-substituted derivative < tertiary alkyl-substituted derivative. The intermolecular attractive interaction energies of the trimers derived from these isocyanurate molecules varied from −1.0 to −2.3 kcal mol−1.
For n-alkane trimers obtained from n-alkyl-substituted isocyanurate molecules, the attractive interactions were shown to have increased with the elongation of the n-alkane chains. The dependence of the attractive interaction energies on the n-alkane chain length was particularly remarkable in the trimers obtained from the C3 conformers. The B3LYP-GD3 interaction energy varied from −0.5 kcal mol−1 for methane trimer to −13.0 kcal mol−1 for the n-octane trimer derived from the C3 conformation (Table 5). Conversely, the dependence of the interaction energies on the substituent's chain length was less remarkable for the n-alkane trimers obtained from the Cs conformers. In addition, their attractive interactions were found to be relatively small. Noticeably, these differences between the alkane trimers derived from the C3 and Cs conformers are due to the differences in the distances between the n-alkane chains and in their orientations. These results regarding the trimers derived from n-alkyl-substituted isocyanurates are understandable in light of the findings on n-alkane dimers reported by Tsuzuki et al.50,51 The results in Tables 3 and 5 suggest that the stability differences between the C3 and Cs conformers are closely related to the magnitude of the inter-substituent interaction energies.
3.5. Cyclotrimerization energies of isocyanates
Table 6 shows the calculation results of the cyclotrimerization energies of isocyanate molecules with various substituents. The calculations employed the dispersion-corrected B3LYP-GD3 method and the two-layer ONIOM methods. The cc-pVTZ basis function was used for all the calculations. The assignment of the high and low computational layers in the ONIOM calculations was the same as that employed in Section 3.1. In this study, we carried out two types of ONIOM calculations, namely ONIOM (1) and ONIOM (2) (see Section 3.2).
Calculated values for the cyclotrimerization energies upon converting isocyanates into the corresponding isocyanuratesa.
| R | Sym. | Computational method | |||||
|---|---|---|---|---|---|---|---|
| B3LYP-GD3/cc-pVTZ | ONIOM (1)b | ONIOM (2)c | |||||
| Primary alkyl-substituted isocyanurates | |||||||
| C 3 conformer | |||||||
| Me | C 3h | −58.1 | (−53.0) | −65.5 | (−60.3) | −70.5 | (−65.3) |
| Et | C 3v | −60.2 | (−54.8) | −67.5 | (−62.1) | −73.3 | (−67.9) |
| n-Pr | C 3 | −59.3 | (−54.0) | −66.6 | (−61.3) | −72.6 | (−67.3) |
| n-Bu | C 3 | −60.0 | (−54.7) | −67.4 | (−62.1) | −73.6 | (−68.3) |
| n-Hex | C 3 | −65.1 | (−59.4) | −72.4 | (−66.7) | −78.5 | (−72.8) |
| n-Oct | C 3 | −69.1 | (−63.2) | −76.5 | (−70.6) | ||
| C s conformer | |||||||
| Me | C s | −58.1 | (−53.0) | −65.4 | (−60.2) | −70.4 | (−65.3) |
| Et | C s | −60.1 | (−54.7) | −67.5 | (−62.1) | −73.3 | (−67.9) |
| n-Pr | C s | −59.2 | (−53.9) | −66.5 | (−61.2) | −72.0 | (−66.8) |
| n-Bu | C s | −59.3 | (−54.0) | −66.7 | (−61.4) | −72.2 | (−66.9) |
| n-Hex | C s | −59.2 | (−54.0) | −66.6 | (−61.3) | −72.1 | (−66.8) |
| n-Oct | C s | −59.3 | (−54.0) | −66.6 | (−61.3) | ||
| Secondary-alkyl isocyanurates | |||||||
| i-Pr | C 3h | −51.0 | (−45.7) | −58.2 | (−52.9) | −63.3 | (−58.0) |
| i-Pr | C s | −51.0 | (−45.7) | −58.2 | (−52.9) | −63.2 | (−57.9) |
| Cy | C 3h | −50.6 | (−45.2) | −57.8 | (−52.4) | −63.5 | (−58.0) |
| Tri-t-butyl isocyanurate | |||||||
| t-Bu | C s | −23.4 | (−18.5) | −31.4 | (−26.5) | −37.2 | (−32.3) |
| t-Bu | C 3v | −22.6 | (−17.6) | −30.1 | (−25.1) | −36.5 | (−31.6) |
| Triphenyl isocyanurate | |||||||
| Ph | D 3 | −34.7 | (−30.5) | −41.8 | (−37.6) | −51.7 | (−47.4) |
The electronic energy changes and the enthalpy changes at 298 K (in the parentheses) for the cyclotrimerization are given in kcal mol−1.
ONIOM(CCSD(T)/cc-pVTZ:B3LYP-GD3/cc-pVTZ).
ONIOM(CCSD(T)/cc-pVTZ:MP2/cc-pVTZ).
Compared to the cyclotrimerization energies calculated with the ONIOM (2) method, those obtained with the B3LYP-GD3 and the ONIOM (1) methods were significantly less negative. Considering the results described in Section 3.1, the ONIOM (2) calculation is considered to be the most accurate and reliable among the three calculation methods listed in Table 6. Nevertheless, on changing the substituents, the three calculation methods showed similar trends regarding the increase or decrease in the cyclotrimerization energy. Thus, the effects of the substituents on the cyclotrimerization energies are considered to be reflected, at least qualitatively, in the results of all of the calculations in Table 6.
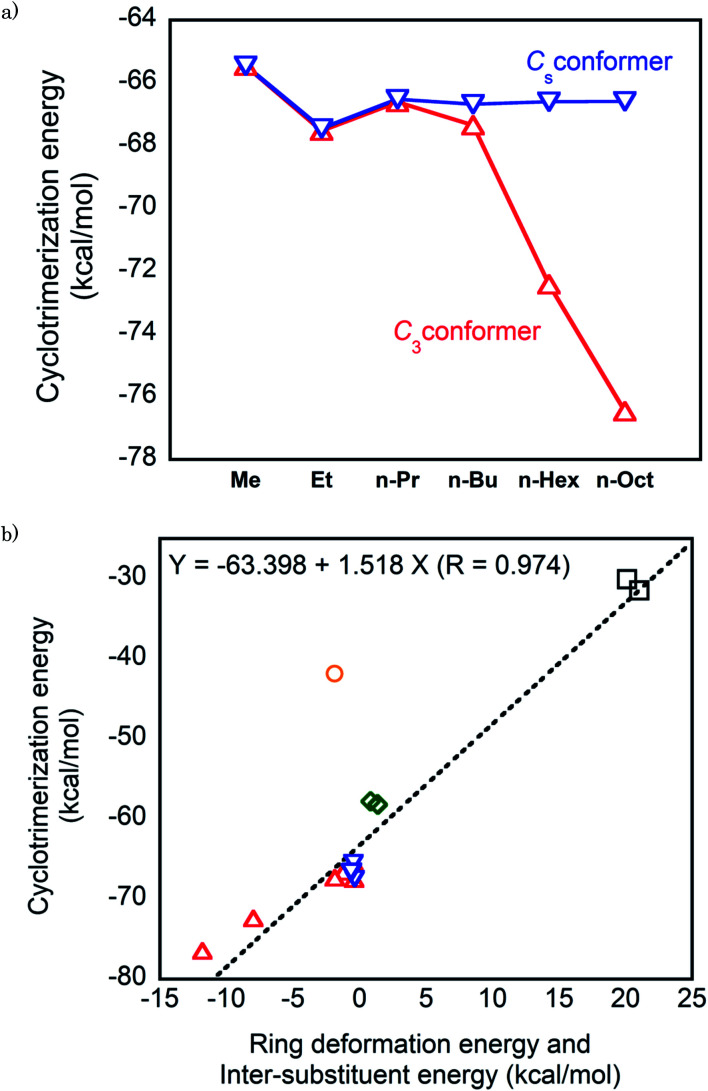
First, we consider the cyclotrimerization energies of n-alkyl-substituted isocyanates regarding the C3 and Cs conformations for the isocyanurate molecules obtained from cyclotrimerization. Fig. 4a shows the plots of the calculated cyclotrimerization energies against the substituent. For the C3 conformer generating processes, the cyclotrimerization energies change noticeably in the negative direction as the substituent n-alkyl is lengthened. The ONIOM (1) calculated value of the cyclotrimerization energy for methyl isocyanate was −65.5 kcal mol−1, whereas the corresponding values for n-hexyl and n-octyl derivatives shifted to −72.4 and −76.5 kcal mol−1, respectively. Meanwhile, the calculated cyclotrimerization energies for the Cs conformer generating processes are relatively insensitive when the substituent changes from methyl to n-octyl.
Fig. 4. (a) Plots of the cyclotrimerization energies against the substituents for the n-alkyl-substituted isocyanates. (b) Plots of the cyclotrimerization energies against the sum of the deformation energy of the isocyanurate ring and the intramolecular inter-substituent interaction energy in the isocyanate molecules. Red open triangle: C3 conformation of the n-alkyl-substituted isocyanurate, blue inverted triangles: Cs conformation of the n-alkyl-substituted isocyanurate, green opened diamond: secondary alkyl-substituted isocyanurates, black opened square: tri-t-butyl isocyanurate, and purple opened circle: triphenyl isocyanurate. The numerical values of the cyclotrimerization energies, the deformation energies of the isocyanurate rings, and the inter-substituent interaction energies are provided in Tables 6 (ONIOM (1)), 4, and 3, respectively.
As described in Section 3.2, the C3 and Cs conformers were confirmed to be the lowest and the highest energy conformers of the tri-n-alkyl isocyanurates, respectively. Hence, the cyclotrimerization energies for generating various conformers of n-alkyl-substituted isocyanurate are expected to be within the range between those for the C3 and Cs conformer generating processes. Thus, the overall cyclotrimerization energy of the n-alkyl-substituted isocyanate is expected to gradually change in the negative direction as the length of the substituent increases.
In addition to the length of the n-alkyl substituent chains, the type of alkyl substituents is responsible for altering the cyclotrimerization energies of the isocyanates. Compared with the cyclotrimerization energies of the n-alkyl substituted isocyanates, those of the secondary alkyl-substituted isocyanates are less negative by about 10 kcal mol−1. The calculation values of the cyclotrimerization energies for t-butyl isocyanate further shifted in the least negative direction. The differences in the cyclotrimerization energies of the alkyl isocyanates appear to be reflected, at least partially, in the reactivity differences for the cyclotrimerization reactions observed experimentally. For example, amine catalyst,12 as well as Mn(ii) and Fe(ii) complexes,22 was shown to efficiently catalyze the cyclotrimerization of primary isocyanates. However, these catalysts showed almost no catalytic activity toward the cyclotrimerization of secondary and tertiary isocyanates. In addition, it was reported that aluminium-complex-catalyzed cyclotrimerization of t-butyl isocyanate required slightly higher temperature as compared to that of primary alkyl isocyanates.3
These changes in the cyclotrimerization energies of the alkyl-substituted isocyanates can be interpreted considering the two factors described in Section 3.4. Namely, the deformation energies of the isocyanurate rings and the intramolecular inter-substituent nonbonding interaction energies in the isocyanurate molecules were considered. The relationship of the sum of these two energy components and the calculated values of the cyclotrimerization energies are shown in Fig. 4b. The calculated cyclotrimerization energy values for the isocyanates vary over a wide range from −30 to −75 kcal mol−1 when their substituents change. Nevertheless, the data points for the alkyl-substituted isocyanurates shown in Fig. 4b are almost on a straight line. The isocyanurate ring deformation and the inter-substituent interaction in the isocyanurate molecules are both directly related to the relative thermochemical stabilities of the isocyanurate molecules. Thus, the cyclotrimerization energy of a series of alkyl-substituted isocyanates is considered more closely related to the relative thermodynamic stabilities of isocyanurate molecules than to those of isocyanate molecules.
Meanwhile, the data point for the phenyl derivative in Fig. 4b has significantly deviated from the linear relationship observed for the alkyl analogs. Noticeably, there should be another factor affecting the cyclotrimerization energy of the phenyl derivative. This is probably attributable to a remarkable change in the resonance interactions during the cyclotrimerization of phenyl isocyanate to triphenyl isocyanurate. The global energy minimum structure of phenyl isocyanate is in the Cs symmetry (Fig. S2†). Thus, the π- and π*-orbitals of the phenyl ring in the phenyl isocyanate molecule are well overlapped with the π- and π*-orbitals of the N C double bond of the NCO moiety. This orbital overlap should induce significant resonance stabilization. In the triphenyl isocyanurate molecule, the angle between the phenyl ring and the isocyanurate ring is 73.6°. Thus, the π- and π*-orbitals of the phenyl ring almost hardly overlap with the π-orbitals of the isocyanurate ring. The resonance stabilization is expected to be significantly smaller in the triphenyl isocyanurate molecule than in the phenyl isocyanate molecule. The resonance stabilization caused by the orbital interactions between the NCO moiety and the phenyl group will be lost upon cyclotrimerization of phenyl isocyanate. For the alkyl derivatives, such a remarkable change in resonance stabilization does not occur during the cyclotrimerization (see the ESI† for the details).
Therefore, there are differences in terms of the orbital mixing between alkyl and aromatic derivatives. These differences might be related to the differences in the reactivity between alkyl and aromatic isocyanates toward the cyclotrimerization catalysts. Not a few of the reported catalysts are applicable to only either alkyl isocyanates or aromatic isocyanates. For example, proazaphosphatrane catalysts,15 Pd(0) complexes,21 and tin tetrasulfido complexes23 were reported to be efficient catalysts exclusively applicable for cyclotrimerization of aromatic isocyanates. Meanwhile, Mn(ii) or Fe(ii) complexes were reported to catalyze merely primary aliphatic isocyanates.22 Furthermore, N-heterocyclic olefins were shown to exhibit higher activity towards the cyclotrimerization of aromatic isocyanates than that of aliphatic isocyanates.25
4. Conclusions
In this study, we computationally investigated how the thermodynamic behaviors of isocyanurate molecules depend on the substituents on the nitrogen atoms in the isocyanurate ring. In particular, we focused on the intramolecular nonbonding dispersion interactions between the substituents and the deformation of the isocyanurate rings caused by the introduction of the substituents. Our calculations suggest that attractive interactions between n-alkyl substituents are quite significant. For example, the tri-n-octyl isocyanurate molecule is estimated to undergo stabilization of −13 kcal mol−1 due to the attractive dispersion interactions between the three n-octyl substituents. Due to such attractive interactions, tri-n-alkyl isocyanurates adopt the conformation in which the three n-alkyl substituents are closely located to each other in their global energy minima. Conversely, conformers in which the n-alkyl substituents are located far from each other exhibit relatively high energies. Meanwhile, the introduction of bulky substituents onto the nitrogen atoms induces the deformation of the isocyanurate ring. In particular, the isocyanurate ring in the tri-t-butyl isocyanurate molecule is shown to be highly deformed, and its deformation energy is estimated to be 22–23 kcal mol−1.
Isocyanurates are produced via cyclotrimerization of isocyanate molecules, and this process is generally highly exothermic. Our best estimate of the enthalpy change for the cyclotrimerization of methyl isocyanate into trimethyl isocyanurate is −66.4 kcal mol−1. Compared to this value, the cyclotrimerization processes for n-alkyl isocyanates, which generate tri-n-alkyl isocyanurates, are shown to be more exothermic. Conversely, the exothermicity for the cyclotrimerization processes of secondary or tertiary alkyl-substituted isocyanates is suggested to be reduced. Noticeably, these changes in exothermicity for the cyclotrimerization processes are related to the attractive dispersion interactions between the substituents and the deformation of the isocyanurate rings. The cyclotrimerization energies of the alkyl isocyanates are shown to correlate linearly with the sum of the interaction energy between the substituents and the deformation energy of the isocyanurate ring. The differences in the cyclotrimerization energies are considered to be closely related to those in the thermal stabilities of the isocyanurate molecules.
In summary, our results suggest two essential factors controlling the thermochemical stabilities and the conformational behaviors of trialkyl-substituted isocyanurate molecules. The first one is the degree of deformation of the isocyanurate ring accompanied with introduction of the substituents on the nitrogen atoms. The second one is the inter-substituent attractive dispersion interactions. Isocyanurate molecules will be thermodynamically destabilized due to the ring deformation accompanied with the introduction of sterically bulky alkyl substituents. Conversely, isocyanurate molecules can undergo non-negligible thermodynamic stabilization due to attractive dispersive interactions acting between alkyl substituents. In particular, our results suggest that long primary alkyl chains have been shown to generate quite large (>10 kcal mol−1) dispersion stabilization, and that the stabilization will be larger as the length of the alkyl chain is extended. Meanwhile, considering the plots shown in Fig. 4b, the thermochemical trend of the aromatic isocyanurate molecules can possibly be somewhat different from that of the alkyl derivatives.
Conflicts of interest
The authors declare no conflicts of interest.
Supplementary Material
Acknowledgments
This work was financially supported by the internal funds of AIST.
Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02463e
Notes and references
- Kordomenos P. I. Kresta J. E. Macromolecules. 1981;14:1434–1437. doi: 10.1021/ma50006a056. [DOI] [Google Scholar]
- Kordomenos P. I. Kresta J. E. Frisch K. C. Macromolecules. 1987;20:2077–2083. doi: 10.1021/ma00175a006. [DOI] [Google Scholar]
- Bahili M. A. Stokes E. C. Amesbury R. C. Ould D. M. C. Christo B. Horne R. J. Kariuki B. M. Stewart J. A. Taypor R. L. Williams P. A. Jones M. D. Harris K. D. M. Ward B. D. Chem. Commun. 2019;55:7679–7682. doi: 10.1039/C9CC03339D. [DOI] [PubMed] [Google Scholar]
- Ghosh M. Miller M. J. J. Org. Chem. 1994;59:1020–1026. doi: 10.1021/jo00084a018. [DOI] [Google Scholar]
- Murray A. P. Miller M. J. J. Org. Chem. 2003;68:191–194. doi: 10.1021/jo026391c. [DOI] [PubMed] [Google Scholar]
- Mascal M. Angew. Chem., Int. Ed. 2006;45:2890–2893. doi: 10.1002/anie.200504417. [DOI] [PubMed] [Google Scholar]
- Mascal M. Yakovlev I. Nikitin E. B. Fettinger J. C. Angew. Chem., Int. Ed. 2007;46:8782–8784. doi: 10.1002/anie.200704005. [DOI] [PubMed] [Google Scholar]
- Zhang Y. Riduan S. N. Ying J. Y. Chem.–Eur. J. 2009;15:1077–1081. doi: 10.1002/chem.200801570. [DOI] [PubMed] [Google Scholar]
- Preis E. Schindler N. Adrian S. Scherf U. ACS Macro Lett. 2015;4:1268–1272. doi: 10.1021/acsmacrolett.5b00726. [DOI] [PubMed] [Google Scholar]
- Ni H. Skaja A. D. Sailer R. A. Soucek M. D. Macromol. Chem. Phys. 2000;201:722–732. doi: 10.1002/(SICI)1521-3935(20000301)201:6<722::AID-MACP722>3.0.CO;2-D. [DOI] [Google Scholar]
- Fukui K. Tanimoto F. Kitano H. Bull. Chem. Soc. Jpn. 1965;38:1586–1589. doi: 10.1246/bcsj.38.1586. [DOI] [Google Scholar]
- Taguchi Y. Shibuya I. Yasumoto M. Tsuchiya T. Yonemoto K. Bull. Chem. Soc. Jpn. 1990;63:3486–3489. doi: 10.1246/bcsj.63.3486. [DOI] [Google Scholar]
- Verkade J. G. Acc. Chem. Res. 1993;26:483–489. doi: 10.1021/ar00033a005. [DOI] [Google Scholar]
- Pusztai Z. Vlád G. Bodor A. Horváth I. T. Laas H. J. Halpaap R. Richter F. U. Angew. Chem., Int. Ed. 2006;45:107–110. doi: 10.1002/anie.200502415. [DOI] [PubMed] [Google Scholar]
- Raders S. M. Verkade J. G. J. Org. Chem. 2010;75:5308–5311. doi: 10.1021/jo9023396. [DOI] [PubMed] [Google Scholar]
- Gibb J. N. Goodman J. M. Org. Biomol. Chem. 2013;11:90–97. doi: 10.1039/C2OB26547H. [DOI] [PubMed] [Google Scholar]
- Helberg J. Oe Y. Zipse H. Chem.–Eur. J. 2018;24:14387–14391. doi: 10.1002/chem.201804016. [DOI] [PubMed] [Google Scholar]
- Duong H. A. Cross M. J. Louie J. Org. Lett. 2004;6:4679–4681. doi: 10.1021/ol048211m. [DOI] [PubMed] [Google Scholar]
- Nambu Y. Endo T. J. Org. Chem. 1993;58:1932–1934. doi: 10.1021/jo00059a055. [DOI] [Google Scholar]
- Heift D. Benkő Z. Grützmacher H. Jupp A. R. Goicoechea J. M. Chem. Sci. 2015;6:4017–4024. doi: 10.1039/C5SC00963D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul F. Moulin S. Piechaczyk O. Le Floch P. Osborn J. A. J. Am. Chem. Soc. 2007;129:7294–7304. doi: 10.1021/ja068291k. [DOI] [PubMed] [Google Scholar]
- Sharpe H. R. Geer A. M. Williams H. E. L. Blundell T. J. Lewis W. Blake A. J. Kays D. L. Chem. Commun. 2017;53:937–940. doi: 10.1039/C6CC07243G. [DOI] [PubMed] [Google Scholar]
- Foley S. R. Yap G. P. A. Richeson D. S. Organometallics. 1999;18:4700–4705. doi: 10.1021/om990405w. [DOI] [Google Scholar]
- Roman M. Andrioletti B. Lemarie M. Bernard J.-M. Schwartz J. Barbeau P. Tetrahedron. 2011;67:1506–1510. doi: 10.1016/j.tet.2010.12.013. [DOI] [Google Scholar]
- Li C. Zhao W. He J. Zhang Y. Chem. Commun. 2019;55:12563–12565. doi: 10.1039/C9CC06402H. [DOI] [PubMed] [Google Scholar]
- Okumoto S. Yamabe S. J. Comput. Chem. 2001;22:316–326. doi: 10.1002/1096-987X(200102)22:3<316::AID-JCC1004>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Petersson G. A., Nakatsuji H., Li X., Caricato M., Marenich A., Bloino J., Janesko B. G., Gomperts R., Mennucci B., Hratchian H. P., Ortiz J. V., Izmaylov A. F., Sonnenberg J. L., Williams-Young D., Ding F., Lipparini F., Egidi F., Goings J., Peng B., Petrone A., Henderson T., Ranasinghe D., Zakrzewski V. G., Gao J., Rega N., Zheng G., Liang W., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Throssell K., Montgomery Jr J. A., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Keith T., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Millam J. M., Klene M., Adamo C., Cammi R., Ochterski J. W., Martin R. L., Morokuma K., Farkas O., Foresman J. B. and Fox D. J., GAUSSIAN 09 (Revision D.01), Gaussian Inc., Wallingford, CT, 2016 [Google Scholar]
- Becke A. D. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
- Lee C. Yang W. Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Miehlich B. Savin A. Stoll H. Preuss H. Chem. Phys. Lett. 1989;157:200–206. doi: 10.1016/0009-2614(89)87234-3. [DOI] [Google Scholar]
- Møller C. Plesset M. Phys. Rev. 1934;46:618–622. doi: 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
- Head-Gordon M. Pople J. A. Frisch M. J. Chem. Phys. Lett. 1988;153:5968–5975. doi: 10.1016/0009-2614(88)85250-3. [DOI] [Google Scholar]
- Pople J. A. Head-Gordon M. Raghavachari K. J. Chem. Phys. 1987;87:5968–5975. doi: 10.1063/1.453520. [DOI] [Google Scholar]
- Grimme S. Antony J. Ehrich S. Krieg H. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S. Ehrlich S. Goerigk L. J. Comput. Chem. 2011;32:1456–1465. doi: 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Dunning Jr T. H. J. Chem. Phys. 1989;90:1007–1023. doi: 10.1063/1.456153. [DOI] [Google Scholar]
- Kendall R. A. Dunning Jr T. H. Harrison R. J. J. Chem. Phys. 1992;96:6796–6806. doi: 10.1063/1.462569. [DOI] [Google Scholar]
- Sinha P. Boesch S. E. Gu C. Wheeler R. A. Wilson A. K. J. Phys. Chem. A. 2004;108:9213–9217. doi: 10.1021/jp048233q. [DOI] [Google Scholar]
- (a) Goto H. Osawa E. J. Am. Chem. Soc. 1989;111:8950–8951. doi: 10.1021/ja00206a046. [DOI] [Google Scholar]; (b) Goto H. Osawa E. J. Chem. Soc., Perkin Trans. 2. 1993:187–198. doi: 10.1039/P29930000187. [DOI] [Google Scholar]; (c) Goto H., Obata S., Nakayama N. and Ohta K., CONFLEX 8, CONFLEX Corporation, Tokyo, Japan, 2012 [Google Scholar]
- Halgren T. A. J. Comput. Chem. 1999;20:720–729. doi: 10.1002/(SICI)1096-987X(199905)20:7<720::AID-JCC7>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- Halgren T. A. J. Comput. Chem. 1999;20:730–748. doi: 10.1002/(SICI)1096-987X(199905)20:7<730::AID-JCC8>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- Dapprich S. Komaromi I. Byun K. S. Morokuma K. Frisch M. J. J. Mol. Struct.: THEOCHEM. 1999;461–462:1–21. doi: 10.1016/S0166-1280(98)00475-8. [DOI] [Google Scholar]
- Halkier A. Helgaker T. Jørgensen P. Klopper W. Olsen J. Chem. Phys. Lett. 1999;302:437–446. doi: 10.1016/S0009-2614(99)00179-7. [DOI] [Google Scholar]
- Curtiss L. A. Redfern P. C. Ravhavachari K. J. Chem. Phys. 2007;126:084108. doi: 10.1063/1.2436888. [DOI] [PubMed] [Google Scholar]
- Helgaker T. Klopper W. Koch H. Noga J. J. Chem. Phys. 1997;106:9639–9646. doi: 10.1063/1.473863. [DOI] [Google Scholar]
- We also made an estimation of the cyclotrimerization energy of methyl isocyanate using the thermochemical data known in the literature. The obtained estimate of the enthalpy change for the cyclotrimerization showed relatively wide uncertainty range from −62 to −70 kcal mol−1 (see the ESI for the details, Tables S1–S4†). However, our best estimate of −66.4 kcal mol−1 is within this uncertainty range
- The conformational analysis was carried out on the CONFLEX program24 using the MMFF94S force field with the search energy limit = 3.0 kcal mol−1
- Kaminski G. Jørgensen W. L. J. Phys. Chem. 1996;100:18010–18013. doi: 10.1021/jp9624257. [DOI] [Google Scholar]
- Chen B. Martin M. G. Siepmann J. I. J. Phys. Chem. 1998;102:2578–2586. doi: 10.1021/jp9801065. [DOI] [Google Scholar]
- Tsuzuki S. Uchimaru T. Mikami M. Tanabe K. J. Phys. Chem. A. 2002;106:3867–3872. doi: 10.1021/jp013985v. [DOI] [Google Scholar]
- Tsuzuki S. Honda K. Uchimaru T. Mikami M. J. Chem. Phys. 2006;124:114304. doi: 10.1063/1.2178795. [DOI] [PubMed] [Google Scholar]
- Karton A. Gruzman D. Martin J. M. L. J. Phys. Chem. A. 2009;113:8434–8447. doi: 10.1021/jp904369h. [DOI] [PubMed] [Google Scholar]
- Gruzman D. Karton A. Martin J. M. L. J. Phys. Chem. A. 2009;113:11974–11983. doi: 10.1021/jp903640h. [DOI] [PubMed] [Google Scholar]
- Zhou Y. Wu J. Xu X. Theor. Chem. Acc. 2016;135:44. [Google Scholar]
- Seebach D. Grošelj U. Schweizer W. B. Grimme S. Mück-Lichtenfeld C. Helv. Chim. Acta. 2010;93:1–16. doi: 10.1002/hlca.200900376. [DOI] [Google Scholar]
- Kohls E. Stein M. New J. Chem. 2017;41:7347–7355. doi: 10.1039/C7NJ01396E. [DOI] [Google Scholar]
- Grimme S. Huenerbein R. Ehtlich S. ChemPhysChem. 2011;12:1258–1261. doi: 10.1002/cphc.201100127. [DOI] [PubMed] [Google Scholar]
- Grimme S. Angew. Chem., Int. Ed. 2006;45:4460–4464. doi: 10.1002/anie.200600448. [DOI] [PubMed] [Google Scholar]
- McKee W. C. Schleyer P. v. R. J. Am. Chem. Soc. 2013;135:13008–13014. doi: 10.1021/ja403934s. [DOI] [PubMed] [Google Scholar]
- Wiberg K. B. Wang Y.-g. Petersson G. A. Bailey W. F. J. Chem. Theory Comput. 2009;5:1033–1037. doi: 10.1021/ct900059e. [DOI] [PubMed] [Google Scholar]
- Schreiner P. R. Chernish L. V. Gunchenko P. A. Tikhonchuk E. Y. Hausmann H. Serafin M. Schlecht S. Dahl J. E. P. Carson R. M. K. Fokin A. A. Nature. 2011;477:308–312. doi: 10.1038/nature10367. [DOI] [PubMed] [Google Scholar]
- Tsuzuki et al.50,51 evaluated the contribution of each energy term in the intermolecular interactions of the n-alkane dimers. The contributions of the electrostatic and induction energies were shown to be significantly small compared to the dispersion and the steric interaction energies
- One exceptional case was observed in the B3LYP-GD3BJ calculations for the n-propyl derivative. In spite of the dispersion correction implemented to the B3LYP-GD3 method, the Cs conformer of the n-propyl derivative was calculated to be slightly lower in energy than its C3 isomer. Not surprisingly, however, the calculated energy difference between the C3 and Cs conformers was almost negligible (around 0.01 kcal mol−1)
- Boys S. Bernardi F. Mol. Phys. 1970;19:553–566. doi: 10.1080/00268977000101561. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.