Neonatal encephalopathy prediction of poor outcome with diffusion-weighted imaging connectome and fixel-based analysis

Abstract

Background:

Better biomarkers of eventual outcome are needed for neonatal encephalopathy. To identify the most potent neonatal imaging marker associated with 2-year outcomes, we retrospectively performed diffusion-weighted imaging connectome (DWIC) and fixel-based analysis (FBA) on MRI obtained in the first four weeks of life in term neonatal encephalopathy newborns.

Methods:

Diffusion tractography was available in 15 out of 24 babies with MRI, 5 each with normal, abnormal motor outcome, or death. All fifteen except one underwent hypothermia as initial treatment. In abnormal motor and death groups, DWIC found 19 white matter pathways with severely disrupted fiber orientation distributions.

Results:

Using random forest classification, these disruptions predicted the follow-up outcomes with 89%−99% accuracy. These pathways showed reduced integrity in abnormal motor and death vs. normal tone groups (p < 10⁻⁶). Using ranked supervised multi-view canonical correlation and depicting just 3 of the 5 dimensions of the analysis, the abnormal motor and death were clearly differentiated from each other and the normal tone group.

Conclusion:

This study suggests that a machine-learning model for prediction using early DWIC and FBA could be a possible way of developing biomarkers in large MRI datasets having clinical outcomes.

Introduction

In term newborn infants with hypoxic-ischemic encephalopathy (HIE) who underwent cooling, neurodevelopmental performance was predicted by MRI determination of fractional anisotropy (FA) decrease in the white matter on early diffusion tensor imaging (DTI) (1). Basal ganglia and thalamic lesions associated with the severity of motor impairment and abnormal posterior limb of internal capsule signal intensity predicted the inability to walk independently by two years (2). Recent technical improvements in high-field MRI have made abnormalities more detectable. In current clinical practice, MRI interpretations are made by radiologists who may differ in their opinion of what constitutes critical brain injury. Furthermore, the state of art on prognostication based on MRI findings is still in its early stages. We may need a paradigm shift in achieving prognostication which is not based on the subjective opinion of a radiologist.

The present study is part of an evaluation of postnatal MRI dependent upon ‘intelligent data mining’. We have recently formed a Big Data group to analyze clinical MRIs in the neonatal period to discover new biomarkers for eventual neurobehavioral outcomes. Indeed, it is of clinical importance to ascertain which aspects of early brain development are predominantly related to the long-term consequences in order to improve early therapeutic interventions for newborn infants with HIE. Our immediate hypothesis was to determine whether the network analysis of the whole-brain connectome provides an accurate prediction for two-year outcomes such as normal tone, abnormal tone, and death.

In this study, we propose the use of clinical diffusion-weighted imaging (DWI) to investigate novel imaging markers at two anatomical levels, 1) axonal pathways using DWI connectome (DWIC) (3, 4) and 2) subcortical clusters using fixel-based analysis (FBA) (5). The advantage of such powerful imaging tools is to gauge atypical changes in fiber orientation distribution of DWI tractography data reflecting the severity of white matter injury due to severe perinatal hypoxia-ischemia. DWIC and FBA have been used to estimate macroscopic changes in white matter morphology by measuring the count of the streamline tract that connects every pair of cortical regions and the intra-axonal volume measured at individual fiber bundles within every voxel (called ‘fixel’). This is a feasibility study to use these methods on existing MRI data to identify efficient markers of perinatal white matter injury for accurate prediction of long-term motor outcome.

The objective of the present study is to mine the most effective DWIC-FBA marker of postnatal DWI that accurately predicts three long-term outcomes: death, normal, and abnormal motor (hypertonia) at two years follow-up of individual newborn. Our working hypothesis is that interrogation of the cerebral white matter tracts can serve as a biomarker for abnormal neurodevelopment. The streamline tract count can be a questionable marker of neurological connectivity due to the limited spatial resolution of DWI (e.g., ~2 mm) and low sensitivity of current tractography method to estimate fiber orientation distribution (FOD) function from clinically acquired DWI tractography data (6–8). The innovation of this study is that we utilize these limitations to derive a feasible and physiologically meaningful measure in the streamline tract count that quantifies the degree of atypically developed white mature structure in the HIE-affected brain. We then explore in a blinded fashion whether white matter pathways show atypical patterns of the streamline count in subpopulations with different outcomes (in abnormal and death groups compared to normal outcomes), how the atypical patterns in streamline counts are associated with other diffusivity measures, and which subcortical clusters show atypical changes in FBA metrics using a state-of-the-art machine learning technique.

Methods

Subjects

We performed a retrospective study of 24 term newborns of HIE whose neurobehavioral outcome was known on a follow-up visit to the Developmental Assessment Clinic of Children’s Hospital of Michigan. Clinical examination by a neonatologist data was available from electronic medical records. Out of the 24 with MRI, we found that DWI tractography scan was included in 15 newborns (gestation age = 39.2 ± 0.9 weeks and postconceptional age at MRI = 40.7 ± 1.3 weeks, Table 1). These 15 newborns were divided into three groups:

Table 1.

Perinatal characteristics of the study group.

No	Outcome	GA	Cooling	Sex	LOS	Age	PMA of MRI	Intensity change and involvement on MRI													NICHD Classification
								T1-w	T2-w	Ventricle Enlarged	Subdural Hematoma	Midline Shift	Cystic changes	Frontal Lobe	Parietal Lobe	Occipital Lobe	Cerebellar	Thalamus	Basal ganglia	Brainstem
1	N	39.3	1	F	18	1	40.3	↑	↓	0	1	0	0	1	1	1	0	0	0	0	1A
2	N	38.9	1	F	24	2.4	41.3	↑	0	0	0	0	0	1	0	0	0	0	0	0	1A
3	N	38.7	1	M	10	1.6	40.3	0	↑	0	0	0	0	0	0	0	0	0	1	0	n/a
4	N	38.0	1	M	14	1.1	39.1	↑	0	0	0	0	0	1	0	0	0	1	1	0	2B
5	N	40.0	1	F	9	1.3	41.3	↑	0	0	0	0	0	0	0	0	0	1	1	0	2A
6	A	39.5	0	M	11	1.3	41.3	↓	↑	1	0	0	0	0	1	1	0	0	1	0	n/a
7	A	39.7	1	M	39	3.7	43.4	↑	0	1	1	0	0	1	1	1	0	0	0	0	n/a
8	A	38.0	1	M	10	1.1	39.1	↑	↑	0	0	1	0	0	0	0	0	1	1	0	n/a
9	A	38.3	1	F	49	1	39.3	↑	↑	0	0	0	0	0	0	0	0	1	1	1	n/a
10	A	39.3	1	M	1	0.1	39.4	↑	↑	0	0	0	0	1	1	1	0	0	0	0	n/a
11	D	38.9	1	F	20	2.4	41.3	0	↑	1	0	0	1	1	1	1	1	1	1	0	n/a
12	D	41.7	1	F	10	0.9	42.6	0	↑	0	0	0	0	0	1	1	0	1	1	0	3
13	D	39.1	1	F	7	0.9	40.0	0	↑	0	0	0	0	1	1	1	0	1	1	0	3
14	D	39.0	1	M	16	1.3	40.3	0	↑	0	0	0	0	1	1	1	1	1	1	0	3
15	D	40.3	1	M	15	1.3	41.6	0	0	0	0	0	0	1	1	1	1	1	1	1	n/a

N: normal tone, A: abnormal tone, D: death, M: male, F: female. 1: Yes, 0: No, Gestation age (GA), Length of stay in hospital (LOS, in days), Age after birth for MRI (weeks), and Postmenstrual age (PMA) of MRI (weeks). MRI readings provided in a tabular form on right. ↑: hyper-intensity, ↓: hypo-intensity, National Institute of Child Health and Human Development (NICHD) classification of MRI injury.

1. any death postnatal

2. normal neurological examination at 2 years, especially normal tone, based on neontologist examination at the developmental follow-up clinic, and

3. any abnormal tone findings with hypertonia on the neurological exam at 2 years.

The ‘n’ was 5 per group. The present study was approved by the Wayne State University’s Institutional Review Board, and a waiver of written informed consent was obtained to perform the analysis of existing data in our clinical archive.

MRI acquisition

All neonatal MRI scans were performed on a 3T GE-Signa scanner (General Electric Healthcare Technologies, Milwaukee, WI) equipped with an 8-channel head coil and ASSET. MRI protocol followed guidelines for routine clinical imaging of DWI, DWI tractography, T₁-weighted image, and T₂-weighted image. DWI scan was acquired via echo-planer imaging (EPI) sequence in the axial plane, with respiratory gating at TR/TE = 4286/84 msec, FOV = 24 cm, 128×128 acquisition matrix (nominal resolution = 1.89 mm), contiguous 3 mm thickness to cover entire axial slices of the whole brain. Two b-values (0, 700 sec/mm²) were applied with number of excitations (NEX) = 2. DWI tractography scan was acquired using a double refocusing pulse sequence to reduce eddy current artifacts at TR = 12,500 ms, TE = 88.7 ms, FOV = 24 cm, 128×128 acquisition matrix, contiguous 3 mm thickness to cover entire axial slices of whole brain using 33 isotropic gradient directions with b = 800 s/mm², 1 b = 0 acquisition, and NEX = 1. For morphological analysis, a three-dimensional fast spoiled gradient echo sequence (FSPGR) was acquired for the T₁-weighted sagittal image of each participant at TR/TE/TI of 9.12/3.66/400 ms, slice thickness of 1.2 mm, and planar resolution of 0.78×0.78 mm². Axial T₂-weighted image was acquired with a fast spin-echo (FSE) sequence, with respiratory gating, at TR/TE of 9231/104 msec (effective) with 5 mm slice thickness, 0 mm gap, FOV = 20 cm, matrix size = 512×512, and NEX = 2.

A multidisciplinary team (nurse, neonatal nurse practitioner, MRI technicians) worked to minimize motion artifacts by a bundle-and-feed protocol, improve the quality of the image acquisition, and allow longer scan time for multiple trials. To minimize the potential confound from motion artifact, the present study excluded patients with unsuccessful MRI showing head motion ≥ 2 mm in DWI encoding data (i.e., voxel size of DWI image), which was evaluated by NIH TORTOISE DWI motion artifact correction package (https://tortoise.nibib.nih.gov/).

Advantages of extraction and evaluation of DWI connectome marker

Before performing the tractography analysis, we utilized the NIH TORTOISE DIFF_PREP package (9) to correct motion, noise, physiological artifacts, susceptibility-induced distortion, and eddy current-induced distortion. Fiber orientation distribution (FOD) function (10, 11) was estimated at every voxel of DWI b0 image by using constrained spherical deconvolution (CSD) method (12) that seeks the optimal combinations of multiple fiber compartments in directions and magnitudes of multiple crossing lobe pairs. In contrast to DTI, CSD can model multiple crossing fiber compartments at every single voxel. One hundred dynamically randomized seeding points and angular deviation ≤ 70° were applied at every voxel of the whole brain to reconstruct continuous fiber tract streamlines using the MRtrix3 package (http://www.mrtrix.org/) where the second-order integration over fiber orientation distributions (iFOD2) tractography (13) was applied to reconstruct the fiber tract streamlines continuously connecting the most probable neighborhood peak of FOD lobes at every voxel (14). The advantages of using FOD lobes (Fig. 1A) were principally three-fold. Immediately, one could obtain an idea of the directionality and magnitude of crossing fibers involved in a particular fiber tract (Fig. 1A). Secondly, we made an a priori assumption that brain injury will cause the FOD lobes to deviate from the values in normal regions found in the framework of the conventional tractography method, and result in more spurious streamlines. These deviations can then be used as a potential biomarker (Fig. 1 B). Thirdly, when the injury occurs to the fiber tract, the magnitude of the insult can be gauged by estimating abnormal FOD functions and reconstructing the directionality and magnitude of crossing fibers at the HIE-affected region (Fig. 1C).

Figure 1. Fiber orientation distribution (FOD) function as a potential biomarker of white matter injury.

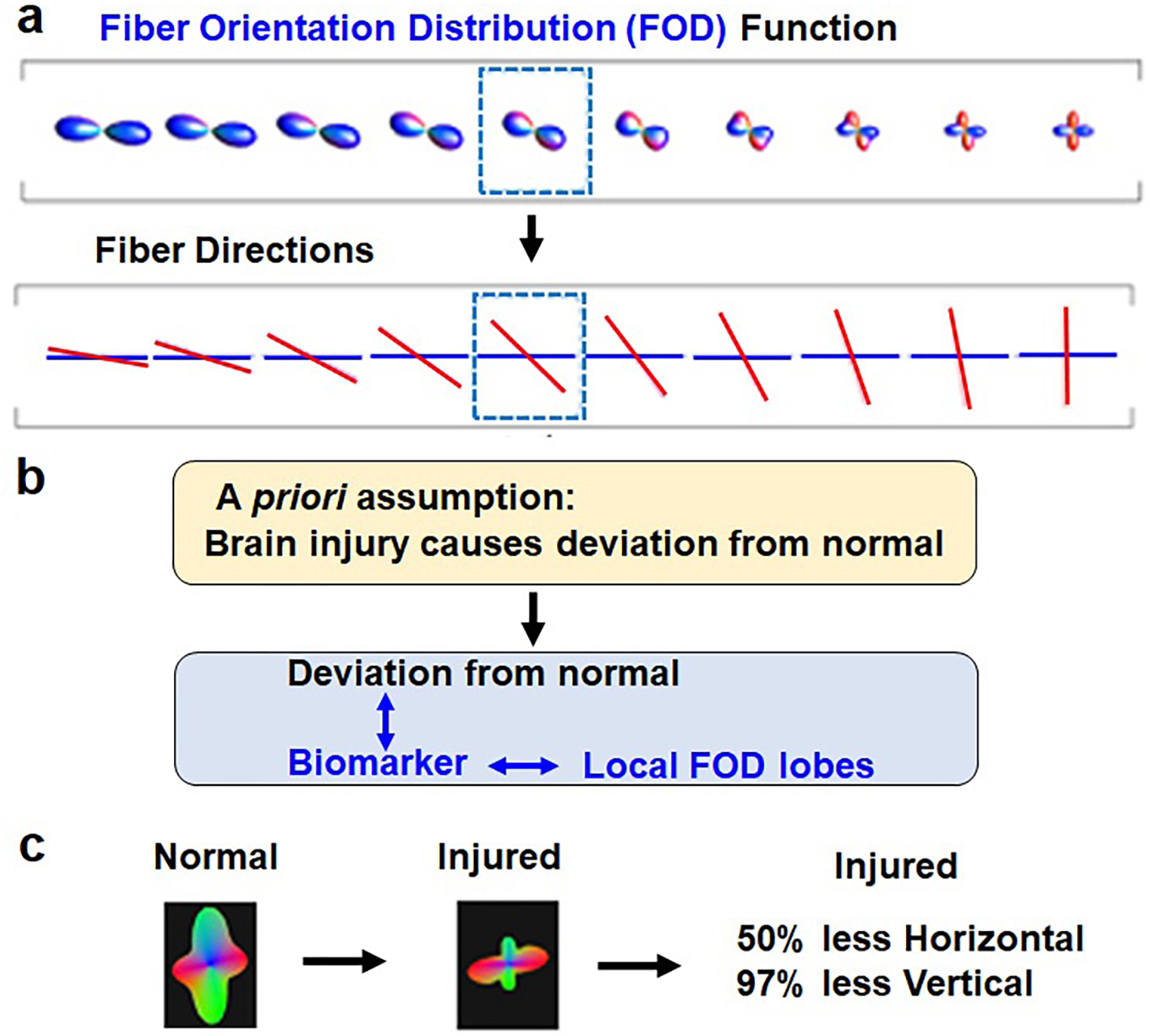
a Advantage of using fiber orientation distribution (FOD) function is that the crossing fiber compartments simulated in fiber directions can be depicted in the FOD lobe to reflect the contribution of the crossing fibers to the orientation distribution function. b A priori assumption of the present study using the local FOD lobes as a potential biomarker. c The magnitude of the injury can be depicted in the magnitudes of an example comparing a normal and injured FOD function lobe.

Whole-brain tracts of individual newborns were characterized by using automated anatomical labeling (AAL) parcellation of UNC neonate atlas (15) that consists of a set of 90 nodes, Ω_i=j=1–90, (Fig. 2 and supplementary table 1), resulting in whole-brain connectome, G = (Ω, S) where the elements of edges S(i,j) quantify the pair-wise connectivity strengths between Ω_i and Ω_j (i.e., the number of fiber streamlines scaled by the total volume of two nodes to stabilize inter-subject variability by correcting for intracranial volume). Three separate Wilcoxon rank-sum tests: 1) normal vs. abnormal motor, 2) normal motor vs. death and 3) abnormal motor vs. death at p < 0.05 after Šidák correction for multiple comparisons (16) were then combined to select pair-wise connection edges, S(i,j) of which log-strengths are significantly altered in three different groups, yielding a marker of log(S(i,j)) that can quantify significant changes in multiple edge strengths in the whole brain.

Figure 2. Schematic of the DWIC analysis to construct the connectome graph, G = (Ω, S) of an individual infant.

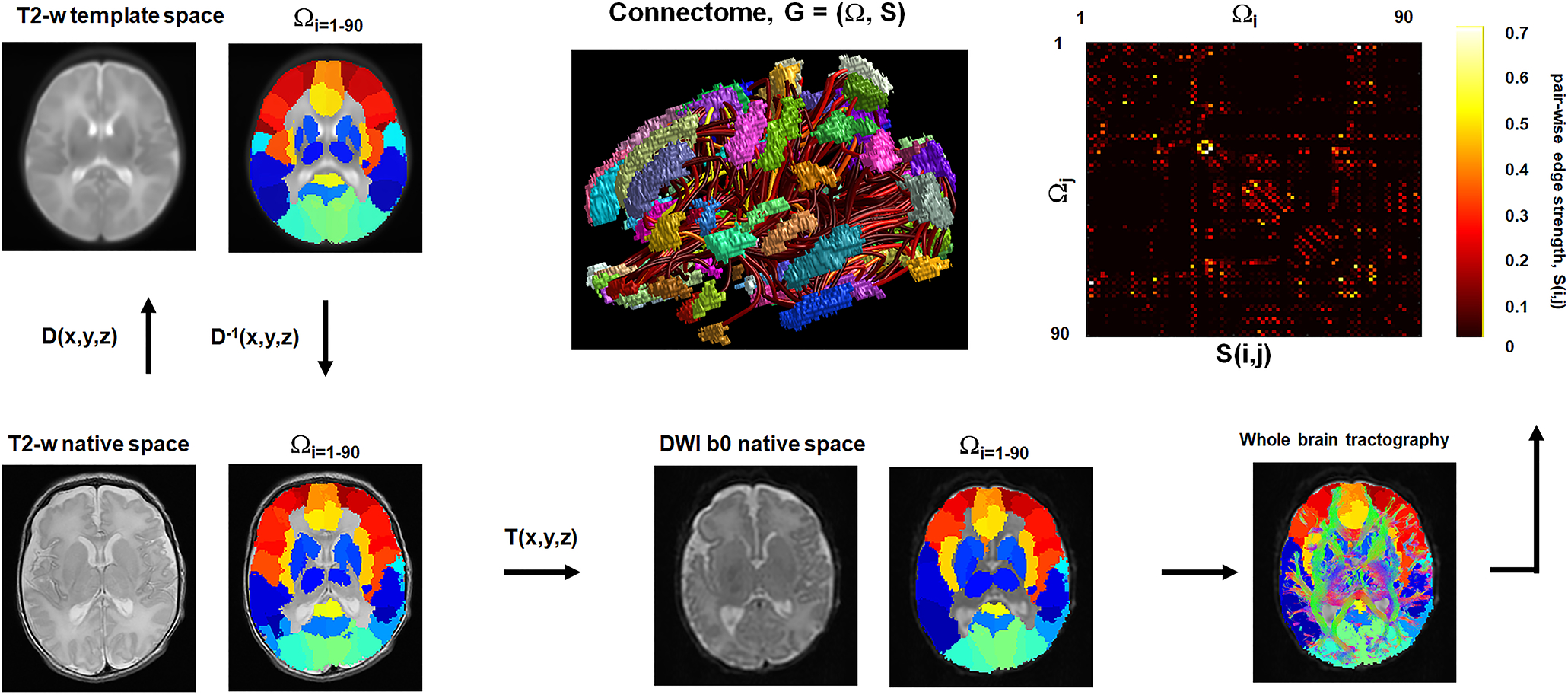
. Advanced normalization tools (ANTs, https://github.com/ANTsX/ANTs) was used to find a 3-D deformation field, D(x,y,z) that warps T2-w native image into the UNC neonatal T2-w template image (https://www.med.unc.edu/bric/ideagroup/free-softwares/unc-infant-0-1-2-atlases/). The inverse of D(x,y,z), D⁻¹(x,y,z) was then used to place the UNC neonatal AAL parcellation atlas of 90 cortical nodes, Ω_i=1–90 from T2-w template brain space to T2-w native brain space. Finally, the resulting AAL atlas was placed to native b0 space via non-linear warping of the ANTs, T(x,y,z) between T2-w native image and DWI b0 image and used to sort out whole brain tracts, leading to an adjacent matrix S(i,j) of which elements consist of connectivity edge strengths (i.e., the number of fiber streamlines scaled by the total volume of two nodes to stabilize inter-subject variability by correcting for intracranial volume). In an example of 3-D visualization (ID #1), colored patches and streamline tubes indicate Ω_i and S(i,j) in the given graph, G.

In addition to the marker of log (S(i,j)), four different markers were created by averaging four diffusivity measures (17): apparent diffusion coefficient (ADC, the degree of isotropic water diffusion), fractional anisotropy (FA, the degree of white matter integrity), axial diffusivity (AD) and radial diffusivity (RD) at individual streamline tracts included in each edge of log(S(i,j)) (i.e., streamline tracts connecting Ω_i and Ω_j). Combinations of axonal loss and myelin changes may affect combinations of AD and RD although these may not be precise reflections (18). We define a dimension as the total range of values obtained in each DWIC edge that has been deemed significant by a priori statistical criteria mentioned above.

Extraction and evaluation of FBA marker

FBA has been used to obtain more comprehensive markers reflecting the total number of white matter axons within a voxel (19–21). Most white matter voxels contain contributions from multiple fiber populations (often referred to as crossing fibers). Therefore, voxel averaged quantitative markers (e.g., FA, AD, RD, ADC, etc.) are not fiber-specific and have poor interpretability. Due to this limitation, fiber density (FD) (5) was estimated as a measure of intra-axonal volume at individual bundles of crossing fibers within every voxel (called “fixels”) by constructing the representative fiber bundle elements at the group level.

The detailed architecture of FBA has been presented elsewhere (5, 22). This study utilized a pipeline of FBA implemented in the MRtrix3 package (http://www.mrtrix.org/). Briefly, a group average response function was estimated after performing global intensity normalization across patients and used to reconstruct the FOD functions from 33-direction diffusion data of individual subjects. All FOD images were registered towards a study-specific group-average FOD template (n = 15 patients). Each FOD in the template was segmented into individual fixels by applying a fixel mask at the peak threshold of 0.1, thus defining the position and orientation of all fixels of interest across patients. Warps estimated from registration were applied to deform FOD images to the template space. Warping was done to ensure orientation information remained anatomically consistent across voxels (22). Each FOD in the warped images was segmented to determine a measure of FD (i.e., FOD lobe integral) per fixel. The estimated FD was compared between groups using fixel-based statistics called threshold-free cluster enhancement (TFCE) (23).

To identify the fixels of which FD values are the most effective in differentiating normal from abnormal motor and death groups, we performed two different TCFE analyses, 1) normal vs. abnormal motor and 2) normal vs. death. The fixel clusters of which FD values differ in two comparisons were obtained at the corrected p of TFCE < 0.05. FD values of each cluster were averaged, providing a marker that can quantify overall intra-axonal volume changes at the cluster level of the whole brain. We extracted other two FBA measures: fiber-bundle cross-section (FC), as an estimate of the difference in fiber bundle cross-section due to the non-linear warping that transforms FOD functions (or fixels) from subject to template space, and a combined measure of fiber density and cross-section (FDC), as the multiplication of fiber density (FD) by FC from the same clusters. These are used as additional markers quantifying overall changes in fiber-bundle cross-sectional area and fiber density-weighted by the difference in the cross-sectional extent of the tract, respectively.

Classification of DWIC and FBA markers for prediction of long-term outcome

It should be noted that this study was originally aimed to investigate whether novel imaging markers underlying the atypically developed brain abnormalities at two anatomical levels, 1) axonal pathways using DWIC and 2) subcortical clusters using FBA, can provide an accurate prediction for two-year outcomes. Thus, a set of multiple pathways (or clusters) consists of a multi-dimensional marker in the feature space. For each marker of DWIC and FBA, an in-house built random forest classification with 100 bagged ensemble of regression trees was used to evaluate individual marker performance in the framework of supervised multi-view canonical correlation (SMVCCA) (24, 25). The SMVCCA is an iterative process to reduce data dimensionality by fusing or integrating the high multi-dimensional data into a more amenable data representation for disease classification. It iteratively projects the original data into a given number of eigen vectors of their covariance matrix. In other words, the SMVCCA fuses (or integrates) the multi-dimensional marker values into lower-dimensional representation to improve separation between clinical outcomes. We defined a ‘fused dimension’ as the given number of eigen vectors and ‘fused marker’ as the projection of the original multi-dimensional marker values on the given number of eigen vectors, respectively. The steps of SMVCCA are given below:

Step 1. Iterative data reduction and classification using SMVCCA and Random forest algorithm X: data matrix, X∈ $R^{N\times M}$, i∈{1,…,N}, j∈{1,…,M}, N: number of subjects, M: number of multi-dimensional features; Y: class label vector, Y∈ $R^{N\times 1}$, Y_i=1 for normal motor, 2 for abnormal motor, 3 for death class

1. We calculated an optimal weight matrix $\widehat{W}$= [W_x W_Y] to maximize feature-feature correlation and class label-feature correlation

   $$\underset{W_X,W_Y}{\mathrm{argmax}}trace\left({\widehat{W}}^T\widehat{C}\widehat{W}\right)s.t.{\widehat{W}}^T{\widehat{C}}_d\widehat{W}=I$$

2. The solution of i) is ${\widehat{C}}_d^{-1}\widehat{C}\widehat{W}=\widehat{W}$ Λ that can be solved by [Λ, D]= eig(${\widehat{C}}_d,\widehat{C})$, eig: singular value decomposition.

   where Λ and D are the eigen vector matrix and eigen value matrix of ${\widehat{C}}_{d}and\widehat{C}$, respectively.

   $$\widehat{C}=\left[\overline{C}{\text{X}}^{\text{T}}\text{Y};{\text{Y}}^{\text{T}}\text{X}\text{zeros}\left(\mathrm{size}\left({\text{Y}}^{\text{T}}\text{X},1\right),\mathrm{size}\left({\text{X}}^{\text{T}}\text{Y},2\right)\right)\right];$$

   $${\widehat{C}}_d=\left[{\overline{C}}_d\text{zeros(size}\left({\overline{C}}_d,1\right),\mathrm{size}\left({\text{Y}}^{\text{T}}\text{Y},2\right)\right);\mathrm{zeros}\left(\mathrm{size}\left({\text{Y}}^{\text{T}}\text{Y},1\right),\mathrm{size}\left({\overline{C}}_d,2\right)\right){\text{Y}}^{\text{T}}\text{Y}];$$

   $${\overline{C}}_d=\mathrm{zeros}(\mathrm{size}(\text{C}));{\overline{C}}_d(1:(\mathrm{size}(\text{C},1)+1):\text{end})={\text{C}}_{\text{d}};\overline{C}=\text{C}-{\overline{C}}_d;$$

   C = covariance matrix of X

3. Iterative SMVCCA-based data reduction to fuse high dimensional feature vectors into a low dimensional feature vector, f and evaluate its classification accuracy in the random forest algorithm:

   for j = 1: M

   1. We next created a fused vector, f(j) with the dimension of j by using a subset of eigen vectors with the largest eigen values in Λ(j) = [Λ₁,.., Λ_j], Λ_j = j^th column vector of Λ, W(j) = Λ(j)

      f(j) = X*Λ(j)

   2. Then performed the supervised random forest algorithm to classify the fused feature vector, f(j) into three target classes, normal motor, abnormal motor, and death.

   3. Evaluated the classification accuracy of the fused feature vector, f(j) accuracy(j) = (True positive + True negative)/(True positive + False positive +True negative + False negative)

      end

Step 2. The optimal dimension of the fused feature vector, $\widehat{j}$ maximizing the classification accuracy is determined,

$$\widehat{j}=\underset{j}{\max }accuracy\left(j\right)$$

Step 3. The optimal fused feature vector, $\widehat{f}$ for outcome prediction then becomes,

$$\widehat{f}=X\mathrm{*}\Lambda \left(\widehat{j}\right)$$

Using two-fold cross-validation, training data instances (X and Y of train set samples) were first used to identify $\left(\widehat{j}\right)$ via Step 1 – 3. The identified $\left(\widehat{j}\right)$ was applied to test data instances (X and Y of train set samples) in order to assess the performance metrics of SMVCCA for outcome prediction (i.e., accuracy, sensitivity, specificity). This study repeated the above cross-validation 100 times. Mean and standard deviation of the performance metrics over these repetitions were reported in Table 3.

Table 3.

Mean and standard deviation of classification accuracy (Ac), sensitivity (Se), and specificity (Sp) obtained from the random forest algorithm of the multi-dimensional marker and patient metavariable. () indicates the dimension providing the highest accuracy for each multi-dimensional marker—bold shows that log(S(i,j)) has the highest accuracy value in each classification. Clinical and radiological variables of Table 1 were classified using the same classification algorithm for the comparison.

Modality	Marker	Without SMVCCA	With SMVCCA	With ranked SMVCCA
DWIC	log(S(i,j)) Ac	0.894±0.158 (19)	0.923±0.117 (4)	0.987±0.058 (5)
	Se	1.000±0.000 (19)	1.000±0.000 (4)	0.997±0.033 (5)
	Sp	0.888±0.222 (19)	0.942±0.158 (4)	1.000±0.000 (5)
	FA	0.476±0.132 (19)	0.570±0.197 (3)	0.444±0.146 (1)
		0.718±0.215 (19)	0.748±0.269 (3)	0.661±0.279 (1)
		0.163±0.239 (19)	0.423±0.337 (3)	0.198±0.223 (1)
	AD	0.411±0.156 (19)	0.563±0.158 (5)	0.437±0.153 (3)
		0.523±0.236 (19)	0.667±0.271 (5)	0.606±0.271 (3)
		0.119±0.208 (19)	0.746±0.322 (5)	0.283±0.345 (3)
	RD	0.393±0.172 (19)	0.483±0.154 (5)	0.360±0.153 (7)
		0.468±0.275 (19)	0.532±0.247 (5)	0.626±0.337 (7)
		0.357±0.369 (19)	0.605±0.388 (5)	0.323±0.356 (7)
	ADC	0.361±0.147 (19)	0.477±0.145 (6)	0.376±0.166 (6)
		0.454±0.271 (19)	0.535±0.241 (6)	0.590±0.364 (6)
		0.186±0.259 (19)	0.607±0.377 (6)	0.449±0.441 (6)
FBA	FD	0.641±0.172 (3)	0.628±0.166 (3)	0.650±0.174 (3)
		0.881±0.184 (3)	0.844±0.206 (3)	0.871±0.205 (3)
		0.442±0.362 (3)	0.436±0.386 (3)	0.443±0.388 (3)
	FC	0.327±0.164 (3)	0.351±0.150 (2)	0.300±0.148 (3)
		0.447±0.342 (3)	0.474±0.355 (2)	0.263±0.238 (3)
		0.599±0.397 (3)	0.272±0.327 (2)	0.510±0.355 (3)
	FDC	0.601±0.156 (3)	0.517±0.153 (3)	0.477±0.160 (3)
		0.853±0.196 (3)	0.845±0.202 (3)	0.843±0.219 (3)
		0.404±0.375 (3)	0.283±0.339 (3)	0.223±0.326 (3)
Clinical variable	Sex, GA, LOS	0.179±0.112 (3)	0.183±0.127 (2)	0.333±0.156 (2)
		0.059±0.127 (3)	0.040±0.093 (2)	0.378±0.284 (2)
		0.208±0.298 (3)	0.130±0.195 (2)	0.354±0.358 (2)
Radiological variable	Intensity change and involvement on MRI	0.520±0.143 (13)	0.160±0.263 (3)	0.641±0.153 (2)
		0.111±0.274 (13)	0.147±0.307 (3)	0.630±0.315 (2)
		0.285±0.284 (13)	0.082±0.180 (3)	0.736±0.280 (2)

In other words, two-fold cross-validation was applied to split the fused markers of entire study cohort into training and test sets. For each split, the bagged ensemble of the regression tree (forest) was optimized to yield maximal accuracy of correct classification at the training set (the first fold, n = 8). The optimized forest was then applied to predict the class memberships of the test set (the second fold, n = 7). One hundred random splits of the 15 samples into training and test sets were repeated to evaluate the overall accuracy of correct classification for the fused marker. As for the explorative comparison, each element value of the original multi-dimension marker was ranked according to its magnitude (e.g., 1 – 15 from the highest to the lowest). The resulting ranked multi-dimensional marker was then fused by the SMVCCA process, and finally re-classified with the forest algorithm using the two-fold cross-validation.

Results

To demonstrate the feasibility of the iFOD2 method using the second integral of FOD function in our dataset, we estimated the FOD functions at two regions of interest, i.e., the lateral part of the precentral gyrus and superior temporal gyrus, which are the core regions of the primary somatosensory motor system (Fig. 3). In both ROIs, shape and morphological features of FOD functions including magnitude (FOD lobe size), orientation (lobe direction), and the total number of lobes were atypically altered in abnormal motor and death subjects. Lower magnitudes, heterogeneous orientations, more spurious peaks were found in the two groups compared with normal subjects, implicating injured myelination and disrupted maturation of perinatal white matter in abnormal and death subjects, respectively. In the framework of subsequent probabilistic tractography, these atypical alterations inevitably increased spurious fiber streamlines (i.e., false-positive tracts that do not anatomically exist), leading to paradoxically increased strength of DWIC edge, S(i,j) in both the abnormal motor and death groups.

Figure 3. To the naked eye, three groups of 2-year outcomes can be differentiated by comparing the shapes of FOD functions in the somatosensory motor system.

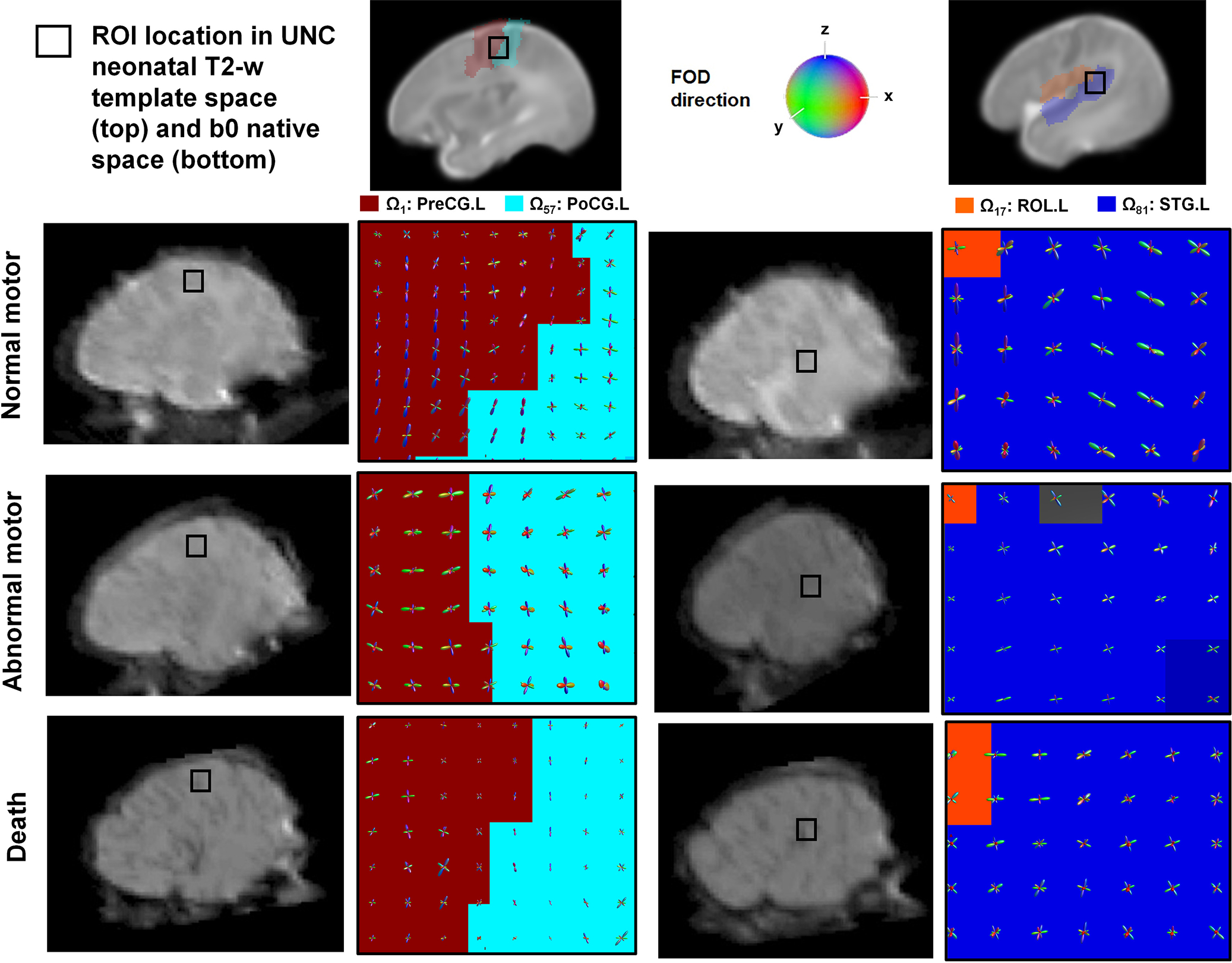
Representative examples of fiber orientation distribution (FOD) functions estimated from two regions of interest (ROI) by referring to the UNC neonatal T2-w template images, left lateral portion of the central sulcus and left superior temporal gyrus of three postmenstrual MRI age-matched subjects, normal, abnormal motor and death (all at 1.3 weeks). Left column: FOD functions located in the lateral portion of left central sulcus consisting of two AAL nodes, Ω₁: left precentral gyrus (PreCG.L) and Ω₅₇: left postcentral gyrus (PoCG.L). Right column: FOD functions located in the lateral portion of left superior temporal gyrus consisting of two AAL nodes, Ω₁₇: left Rolandic operculum (ROL.L) and Ω₈₁: left superior temporal gyrus (STG.L). Collectively, the total number of lobes, lobe orientation, and lobe size of each FOD function appear to be higher, more inconsistent, and smaller in abnormal motor and death groups, compared with normal group. A cautionary note is that this phenomenon inevitably increases more spurious fiber streamlines in the framework of probabilistic tractography. Random seeding per voxel continuously reproduces false-positive tracts by tracking false streamlines within a fixed constraint of angular deviation (e.g., ≤ 70°).

Figure 4 presents the results of the proposed DWIC markers determined by Wilcoxon rank-sum tests between three long-term outcome groups. Total 19 pair-wise edges, S(i,j) (Fig. 4A and Table 2) showed significant difference of group median in their log-strengths, log(S(i,j)) at the corrected p < 0.05, yielding a 19-dimensional DWIC marker of log(S(i,j)). Because of the overlap in observation in groups and multiple comparisons, caution has to be exercised about the biological importance of the statistical significance. Another way to look at the biological significance is to examine how much the Z score is beyond the value of ±1.96. Compared with normal group, pair-wise edge strength, log(S(i,j)), was significantly reduced in each of 19 pair-wise pathways in both abnormal tone and death groups with average Z-statistic value = −2.552/−2.507, p = 0.018/0.012 for abnormal tone and death respectively. The overall one-way ANOVAs for log(S(i,j)) were highly significant even after Šidák correction (a priori α = 0.0034) for multiple comparisons (p < 10⁻⁶ for normal vs. abnormal, normal vs. death, and abnormal vs. death), indicating the presence of significant differences between groups in the overall dataset. In the comparison of abnormal tone and death groups, we found that compared with abnormal group, death group has significantly lower strength in each of these 19 edges, with average Z-statistic value = −2.298, p = 0.026, which may not be as striking. The group variations of five 19-dimensional DWIC markers, log(S(i,j)), FA, AD, RD, and ADC, are shown in Fig. 4B where each 19-dimensional marker of individual patient was concatenated per group for two group comparisons in the box-and-whisker plots. FA showed significant differences in normal vs. abnormal (p < 10⁻⁶), normal vs. death (p < 10⁻⁶) and abnormal vs. death (p < 10⁻⁶). AD showed less striking but still significant differences in normal vs. death (p = 0.002). No significant difference was found in AD between in normal vs. abnormal (p = 0.016), and abnormal and death groups (p = 0.320). RD showed significant differences in normal vs. abnormal (p < 10⁻⁶), normal vs. death (p < 10⁻⁶) but not in abnormal vs. death (p = 0.026). ADC showed significant differences in normal vs. abnormal (p < 0.001), normal vs. death (p < 10⁻⁶). No significant difference was found in ADC between abnormal and death groups (p = 0.152).

Figure 4. Trend for differentiating three groups of 2-year outcomes by comparing five DWIC markers that were measured from neural pathways of interest.

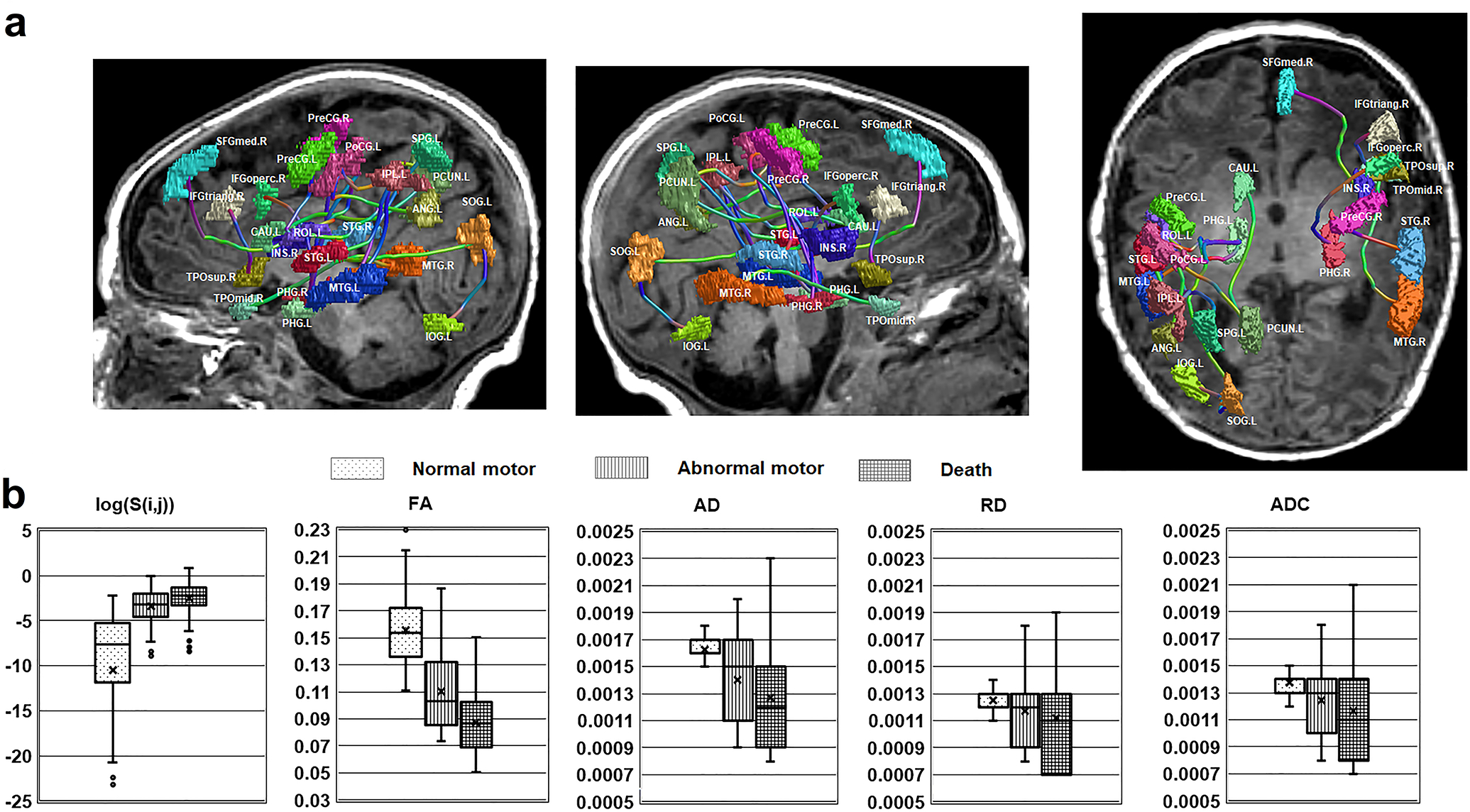
a Total 19 pair-wise connection edges, S(i,j) satisfying significant group difference in by Wilcoxon rank-sum tests for three comparisons: (1) normal vs. abnormal motor, (2) normal vs. death, and (3) abnormal motor vs. death (α < 0.05). Colored patch and streamline tube indicate AAL node, Ω_i and exemplar pathway of S(i,j) connecting two patches, Ω_i and Ω_j. Anatomical labels of 90 AAL nodes and two nodes of 19 edges are available in Supplementary Table 1 and Table 2. b Each diffusivity measure was averaged in all tracts of 19 pair-wise connection edges to define a 19-dimensional marker. Box and whisker plots, showing five DWIC markers: log(S(i,j)), significantly different for all three comparisons (Šidák correction α = 0.0034 for multiple comparisons); FA, significantly different in all three comparisons; AD, only significant in comparison 2 (normal vs death); RD and ADC, in first two comparisons (normal vs abnormal and vs death).

Table 2.

19 pair-wise connection edges, S(i,j) used to evaluate DWIC markers.

Edge	Ωi	Label	Anatomy	Ωj	Label	Anatomy
S(1,17)	1	PreCG.L	Precentral gyrus left	17	ROL.L	Rolandic operculum left
S(2,82)	2	PreCG.R	Precentral gyrus right	82	STG.R	Superior temporal gyrus right
S(10,42)	10	ORBmid.R	Orbitofrontal cortex (middle) right	42	AMYG.R	Amygdala right
S(12,40)	12	IFGoperc.R	Inferior frontal gyrus (opercular) right	40	PHG.R	ParaHippocampal gyrus right
S(14,84)	14	IFGtriang.R	Inferior frontal gyrus (triangular) right	84	TPOsup.R	Temporal pole (superior) right
S(17,39)	17	ROL.L	Rolandic operculum left	39	PHG.L	ParaHippocampal gyrus left
S(17,61)	17	ROL.L	Rolandic operculum left	61	IPL.L	Inferior parietal lobule left
S(24,30)	24	SFGmed.R	Superior frontal gyrus (medial) right	30	INS.R	Insula right
S(39,57)	39	PHG.L	ParaHippocampal gyrus left	57	PoCG.L	Postcentral gyrus left
S(39,85)	39	PHG.L	ParaHippocampal gyrus left	85	MTG.L	Middle temporal gyrus left
S(49,53)	49	SOG.L	Superior occipital gyrus left	53	IOG.L	Inferior occipital gyrus left
S(49,57)	49	SOG.L	Superior occipital gyrus left	57	PoCG.L	Postcentral gyrus left
S(57,65)	57	PoCG.L	Postcentral gyrus left	65	ANG.L	Angular gyrus left
S(57,67)	57	PoCG.L	Postcentral gyrus left	67	PCUN.L	Precuneus left
S(59,85)	59	SPG.L	Superior parietal gyrus left	85	MTG.L	Middle temporal gyrus left
S(61,81)	61	IPL.L	Inferior parietal lobule left	81	STG.L	Superior temporal gyrus left
S(61,85)	61	IPL.L	Inferior parietal lobule left	85	MTG.L	Middle temporal gyrus left
S(67,71)	67	PCUN.L	Precuneus left	71	CAU.L	Caudate left
S(86,88)	86	MTG.R	Middle temporal gyrus right	88	TPOmid.R	Temporal pole (middle) right

TFCE evaluations of FD (Fig. 5A) found three fixel clusters of interest in thalamus, posterior limb of internal capsule, and cerebellar peduncle, yielding a 3-dimensional FD marker for an individual subject. In all three clusters, FOD functions of abnormal and death groups had lower amplitudes leading to lower FD, compared with normal group. Each element of the 3-dimensional FD marker (left boxplot of Fig. 5B) suggests a group difference between normal and abnormal (p < 0.013). Similarly, each concatenation of the 3-dimensional FDC marker samples (right boxplot of Fig. 5B) suggests a group difference between normal and abnormal (p < 0.016), with no other differences with α < 0.05 found. These are suggestive findings, because if we use a correction for multiple comparisons, the α becomes non-significant.

Figure 5. Using α < 0.05, significant alterations of FOD functions underlying early hypoxic injuries were found in subcortical regions of abnormal motor and death groups including thalamus, posterior limb of internal capsule, and cerebellar peduncle.

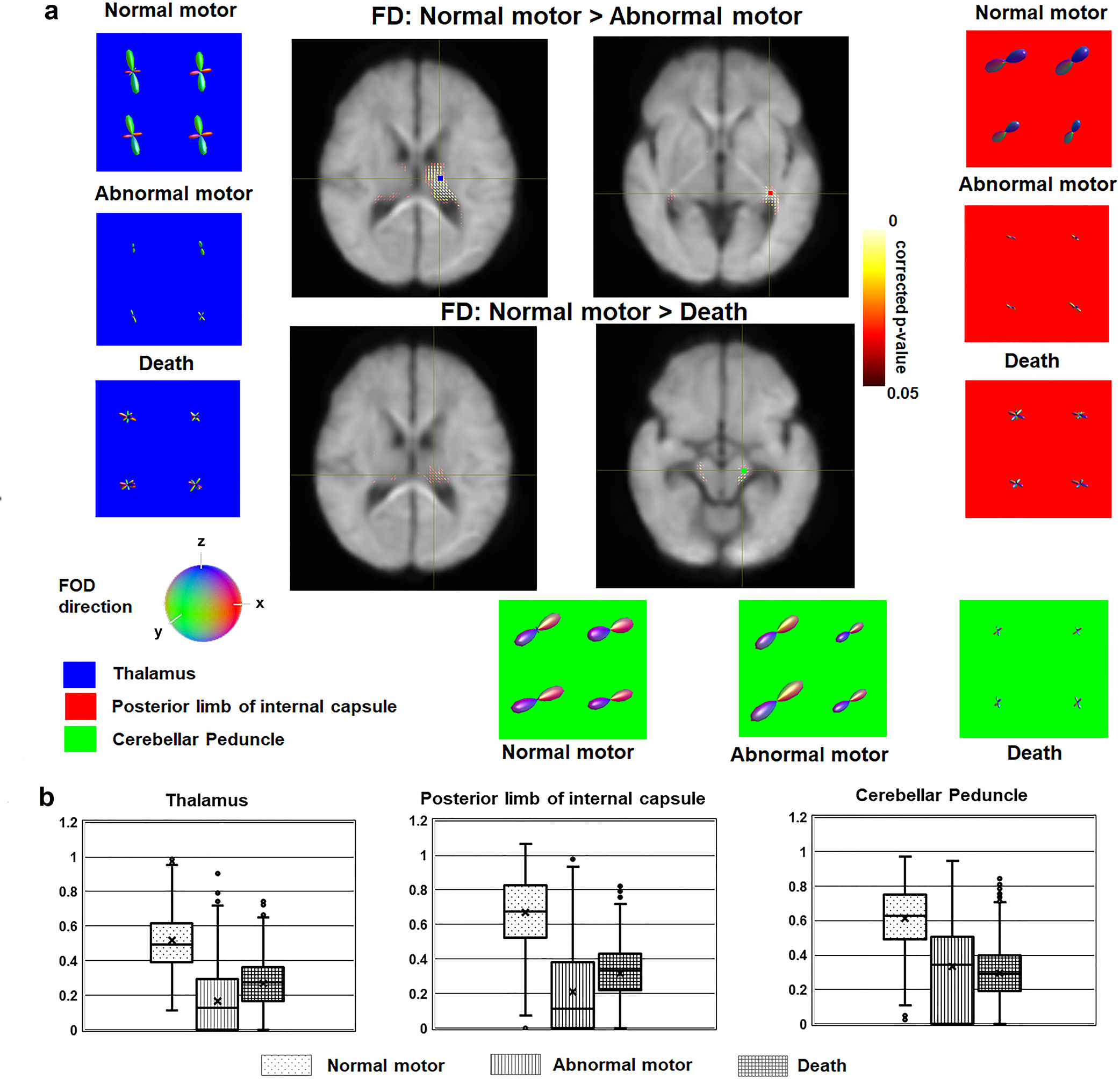
a Two TCFE analyses of FD maps, 1) normal vs. abnormal motor and 2) normal vs. death, were performed to identify fixel clusters of interest showing significant deviations from normal tone group at corrected p < 0.05. Four clusters were found in two regions of right thalamus (blue square box), posterior limb of internal capsule (red square box), and cerebellar peduncle (green square box). In each cluster, abnormal and death groups showed more FOD changes with lobes being narrower and weaker compared with those of normal tone group, leading to smaller FD values in abnormal motor and death groups. b Box-and-whisker plots of FD marker obtained from the voxels of three clusters. Each box indicates the sample range of 25th and 75th percentiles of each group. These are suggestive findings, because if we use a correction for multiple comparisons, the α becomes non-significant.

The subsequent random forest classification revealed that compared with other markers including clinical and radiological variables such as sex, gender, gestation age, length of stay in hospital, intensity change and involvement on MRI, a DWIC marker of log(S(i,j)) could achieve the highest accuracy to correctly classify the follow-up motor outcomes, up to 89% without SMVCCA, 92% with SMVCCA and 99% with ranked SMVCCA (Table 3). Of note, other markers had relatively lower accuracy compared with log(S(i,j)), indicating the outperformance of DWIC tract counts to differentiate malformed FOD functions affected by perinatal white matter injuries and immaturities. The log(S(i,j)) provided the most substantial separation between abnormal tone and death groups. The major finding of this study shows that we fused the 19-dimensional data and got 5 eigen vectors as the final ‘fused dimensions’ using ranked SMVCCA. We could depict just 3 of the 5 ‘fused dimensions’ of the analysis (it is impossible to depict 4- or 5-dimensions), and one can visually identify high risk populations from an MRI study of the eventual outcome (Fig. 6). As denoted by each colored ellipse representing the upper limit of the 3 fused-dimensional features to predict each group at the confidence level of 99% (i.e., Z-score = 2.58 under the assumption of normal distribution), no spatial overlap of the upper limit was found between every pair of three groups at the confidence level of 99%, indicating complete separation of the individual feature to predict three groups in the proposed feature space. This suggests that the combined 3 fused-dimensional statistic becomes more powerful biomarker showing high significance than individual DWIC outcomes which may not reach statistical significance due to multiple comparisons.

Figure 6. Prediction of the eventual outcome made easier by ranked SMVCCA showing a figure plotting 3 of the 5 fused dimensions which provided the most significant discrimination for three groups (Fig. 4 a).

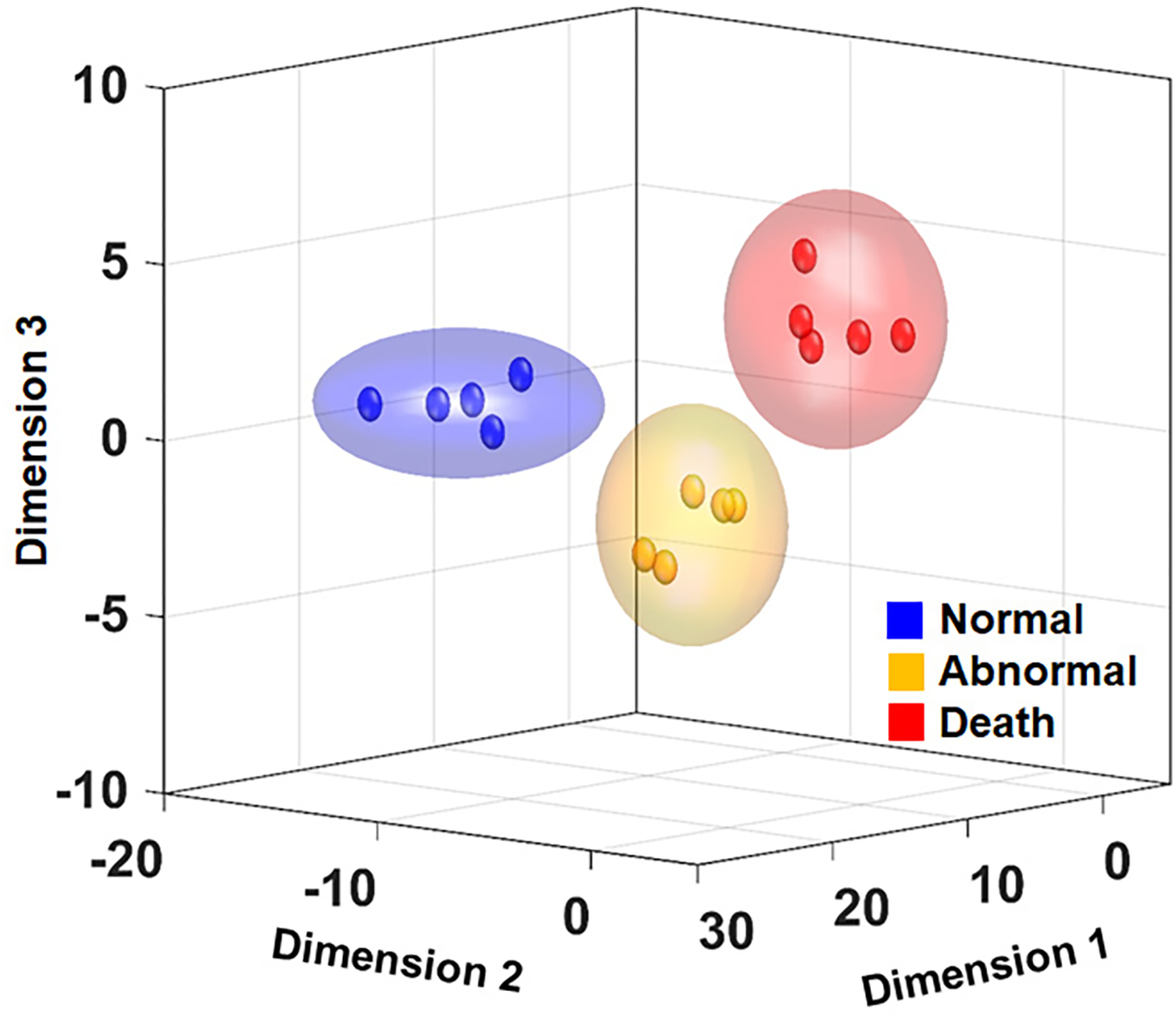
Each colored sphere indicates the three fused-dimensional feature of individual group subject. Each colored ellipse represents the upper limit of the three fused-dimensional features to predict each group at the confidence level of 99%.

Discussion

The major finding of this study is that a method using supervised multi-view canonical correlation can provide a predictive MRI of the possible eventual outcome, in our case, the ranked SMVCCA. The other findings of the present study are paradoxically increased edge strengths (log(S(i,j)), reduced white matter integrity (FA), increased radial diffusivity (RD), and reduced axonal density (FD) of the multiple white matter pathways in abnormal tone and death groups compared to the control group with normal tone. In the present study, DWIC and FBA of the same dataset were compared to extract the most potent marker for accurate prediction of long-term motor outcomes: normal tone, abnormal tone, and death. We showed perinatal white matter injuries and immaturities in forms of connectivity strength and FD that were altered in the thalamocortical network, including thalamus, posterior limb of internal capsule, and cerebellar peduncle. This work is the first to look at white matter abnormalities at different formulations of DWI features (i.e., pair-wise connection and fiber-specific bundle) that can further improve long-term prediction in the framework of conventional machine learning classification. The altered connectivity strength underlying the presence of FOD functions with noisy fiber tract peaks having low lobe amplitudes was confirmed by a significant reduction in white matter integrity (FA), myelination (RD), and axonal volume (FD) measured in the same dataset. The FOD functions with low lobe amplitudes may also reflect inadequate myelination or a state resulting from inadequate crosstalk between axons and oligodendroglia. Our neonatal marker log(S(i,j)) was gradually increased in abnormal and death groups, yielding a promising accuracy of the correct classification in the framework of conventional machine learning technique (e.g., 89%−99% for the test set which was not included to train the bagged ensemble of the regression tree). None of the other markers or their combinations, including clinical and radiological variables, differentiated between normal and abnormal tone and death. Please note that the superior performance of log (S(i,j)) might be explained by the fact that other diffusivity markers were evaluated from streamline tracts of S(i,j). A strategy to use other diffusivity measures to preselect streamline tracts of interest (in this study we used streamline count) may not necessarily be better in differentiating between clinical outcomes. Only when combining the various elements of individual marker using ranked SMVCCA, we found what could be considered a useful biomarker. Our reasoning is that even with these small numbers, we could clearly differentiate between the three subpopulations.

The present study supports that the advanced DWI method using DWIC and FBA has a strong potential to improve our ability for early identification of heterogeneous imaging abnormalities underlying white matter injuries and disrupted maturation processes across different motor outcomes. Previous works (25–28) have investigated age-related white matter development in infants, mainly focusing on the voxel-wise measure of white matter maturation reporting the effects of myelination and brain water on increasing FA and decreasing mean diffusivity. The efficacy of neonatal DWIC analysis to investigate the developmental trajectory of whole-brain using different network topology (more clustered pair-wise connection) has been used at 45 weeks post-conceptional age (29). The topological locality of structural brain networks has been used to help predict neurobehavioral outcomes such as Bayley-III cognitive and motor scores for preterm infants (predictive correlation = 0.19 and 0.31 for cognitive and motor score) (30). Preterm infants when imaged at 38.6–47.1 weeks and utilizing FBA found a relationship between fixel-based measures (FD, FC, FDC) with clinical risk factors in preterm, such as positive correlation with gestational age and negative correlation with days on requiring ventilation with FD, FC and FDC (29). This study also used a similar warping technique as ours. The warping of FOD may yield different results by causing a local shear and reduce number of fixels. Despite this limitation, when warping is used without bias, it could still be useful in the methodology in developing an objective biomarker. In a similar population as ours, using diffusion MRI at six months of age, there was only a trend to declining brain network integration and segregation with increasing neuromotor deficits following neonatal encephalopathy (31). DTI and functional MRI using a passive motor task at 40 to 48 weeks’ postconceptional age following perinatal brain injury showed FA and functional connectivity from the right supplemental motor area to be predictive of cerebral palsy at two years of age (32). The Neonatal Research Network MRI pattern of neonatal brain injury was reported as a robust biomarker of neurodevelopmental outcome at 6–7 years of age (33). A recent large cohort study (34) also reported that infants with better neurodevelopmental outcomes at the one and two-year follow-up showed higher FD, FC, and FDC in the corticospinal tract, midbrain, and corpus callosum, that suggests better information transfer capacity facilitated by increased number of neurons, increased myelination, thicker bundles, and/or combinations.

Even though our study was retrospective in design, our MRI analysis was done in a blinded fashion to the groups. We are fully aware of the limitations of low statistical powered studies and the bias to overestimated effect sizes (35, 36) and the need for more ‘n’ for machine learning. We were not expecting the clear differentiation between the three populations with difference between bounds of 99% confidence intervals in Fig. 6. More studies and replication in more significant numbers of samples are needed to further establish whether these predictive prognostic markers will remain differentiated between our patient groups. Using Big Data approaches, we can now feed more data into this methodology. Also, another limitation is that despite the exceptional potential of clinical DWI data, it remains controversial whether current DWI tractography techniques can accurately reconstruct macroscopic structures of FOD functions and effectively remove false-positive tracts at the low angular acquisition of water diffusion (37, 38). Also, CSD and FBA are problematic with our DWI data with b-value = 800 s/mm². Ideally, the b-value should be high (e.g., around 2500 – 3000 s/mm²) to reconstruct the FOD functions using CSD (12) and measure intra-axonal volume related to apparent fiber density (5, 39). When considering this practical problem, the proposed log(S(i,j)) marker might be limited in its ability to investigate the detailed mechanism about its biological origin. For instance, our preliminary data of abnormal motor and death groups showed a paradoxical increase in edge strength that may be related to the current pitfall of DWI tractography and our data quality, more likely tracking the wrong direction of the nearest fiber bundle at low spatial resolution. Nonetheless, we presumed that this spurious tracking would generate an exploratory marker that inevitably increases false-positive tracts in constructing the edge of DWIC when the FOD functions of neighboring bundles have more spurious peaks with weak amplitudes as the ones from infants in the abnormal motor and death groups.

In conclusion, continued and systematic investigation using machine learning techniques with clinical DWIC and FBA markers may improve early prediction of neonatal motor outcomes. It may also allow identification of distinct patterns of white matter injuries, allowing more rapid and targeted intervention for improving long-term outcomes in term infants as a series of DWI-based studies (40–42) was consistently suggested to predict behavioral profiles, cognitive abilities, and language functions at 1–2 years old.

Impact:

• Early connectome and fixel-based analysis of clinically acquired diffusion weighted imaging provide a new non-invasive imaging tool to predict the long-term motor outcomes after birth, based on the severity of white matter injury.

• Disrupted white matter connectivity as a novel neonatal marker achieves high accuracy of 89–99% to predict 2-year motor outcomes using conventional machine learning classification.

• The proposed neonatal marker may allow better prognostication that is important to elucidate neural repair mechanisms and evaluate treatment modalities in neonatal encephalopathy.