Noninvasive Arterial Compliance Estimation

Summary

Arterial compliance is an important cardiovascular parameter characterizing mechanical and structural properties of arteries and significantly influencing ventricular-arterial coupling. Decreased arterial compliance is associated with several physiological states and pathological processes. Furthermore, arterial compliance is influenced by other cardiovascular parameters even at short time scales. Today, there are numerous noninvasive methods of estimation arterial compliance in vivo introducing some level of confusion about selection of the best method for particular application and measurement setting. In this review, the most common noninvasive methods of arterial compliance estimation are summarized, discussed and categorized. Finally, interpretation of estimated arterial compliance in the context of other possible confounders is discussed.

Introduction

Arterial compliance (AC) is an important cardiovascular parameter characterizing mechanical properties of arteries. AC is significantly influenced by arterial structure and markedly influences cardiac load (Klabunde 2012, Westerhof et al. 2019). It is defined by the slope of pressure-volume relationship – a change in the arterial volume in relation to a given change in arterial pressure (Eq. 1):

$$C=\frac{\mathit{\Delta }V}{\mathit{\Delta }P}$$ (1)

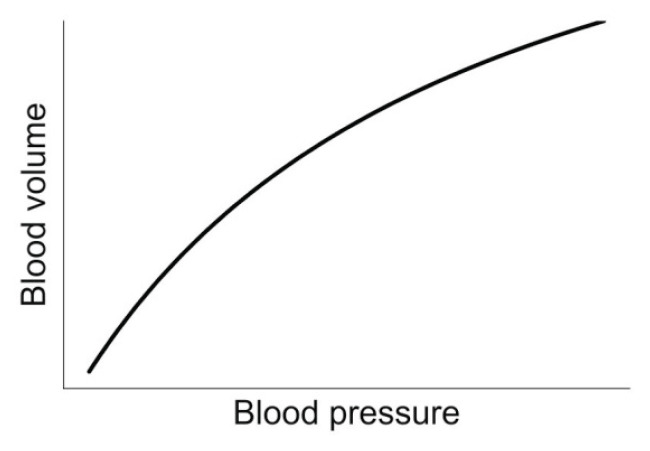
where V is arterial volume and P is intraarterial pressure. This relationship is nonlinear due to complex structure of arterial wall. Therefore, the value of measured AC (slope of pressure-volume relation) will be different when measured around different points of the nonlinear pressure-volume relationship (Chirinos 2012) (Fig. 1). Furthermore, AC is not only influenced by arterial wall composition, but also by arterial size, wall thickness and smooth muscle activity (Bank et al. 1995, Chirinos 2012).

Fig. 1.

Nonlinear relationship between intraarterial blood volume and blood pressure. The slope of the relationship defines AC.

Decreased value of AC (or increased arterial stiffness – AS) is associated with numerous physiological states and pathological processes. During aging, resting value of AC can reduce by half due to different mechanisms, many still poorly understood, which result in elastin fragmentation, collagen cross-linking and dysfunction of the endothelial lining and vascular smooth muscle cells (Butlin et al. 2020, O’Rourke and Hashimoto 2007).

Besides providing a conduit for blood, large arteries AC has also an important function in accommodating the blood ejected from the ventricles during each ejection without imposing an excessive afterload (Cavalcante et al. 2011, Chirinos 2012, Franklin 2006). In case of decreased AC, this function might be insufficient and blood pressure pulsatility may promote increased target organ damage through excessive penetration of pulsatility into peripheral target organs such as kidney or brain (Chirinos 2012, O’Rourke and Safar 2005). Furthermore, increased pulsatile stress can contribute to endothelial dysfunction, increased coronary atherosclerosis, rupture of unstable atherosclerotic plaques and acute coronary heart syndromes (Franklin 2006, Lyle and Raaz 2017). It is in accordance with a recent study founding an association between increased arterial stiffness and higher prevalence of carotid atherosclerosis (Selwaness et al. 2014). Additionally, a value of carotid-femoral pulse wave velocity (cfPWV), reflecting systemic AC, was found to be an independent predictor of coronary heart disease and stroke in healthy subjects and an independent predictor of mortality in the general population (Cavalcante et al. 2011, Mattace-Raso et al. 2006). Besides of these pathological relations with a decreased AC, diabetes, impaired renal function and untreated or poorly treated hypertension may lead to premature arterial stiffening (Franklin 2006).

AC is central in the pathogenesis of isolated systolic hypertension being considerably associated with increasing mortality (Chirinos 2012, Cohen and Townsend 2011, Franklin 2006). Epidemiological studies showed that an increase in AS measured by increased aortic pulse wave velocity (PWV) by 1 m/s raises cardiovascular risk by more than 10 % (Cavalcante et al. 2011, Vlachopoulos et al. 2010). Therefore, it is not surprising, that the estimation of AC has for a long time interested clinicians and cardiovascular physiologist and there is an increasing interest in incorporating the assessment of AC into routine cardiovascular examination.

In order to estimate AC or AS, numerous indexes and methods were proposed (Chirinos 2012, Hallock and Benson 1937, Levenson et al. 1981, Stergiopulos et al. 1995) and there are currently many approaches to the assessment of AC, ranging from imaging and ultrasound techniques to application of different mathematical models deriving AC from noninvasive measurement of arterial pressure and flow (Haluska et al. 2010) and PWV measurement. This introductory paper reviews and categorizes the most often used methods of AC estimation to better clarify their applicability, necessary requirements and limitations. Moreover, possible confounders of AC measurement are discussed.

Methods of AC estimation

Methods of AC estimation can be grouped into direct and indirect approaches. All direct methods are invasive. These methods measure mechanical properties of arteries after direct application of various mechanical stress.

On the other hand, indirect methods of AC estimation are based on analysis of blood pressure, distension and flow changes. These methods can be further separated into three groups – local and systemic AC estimation, and specific subgroup of indirect methods – surrogate indexes of AC. The major difference between local and systemic AC methods is in the fact that local indexes describe elastic properties only of the selected part of artery, whereas systemic indexes describe mechanical properties of the whole arterial tree. Surrogate indexes represent parameters influenced by changes in AC and therefore can be used to estimate changes in AC. All categories are illustrated in Fig. 2. In the next section, we introduce above mentioned groups of methods in more details.

Fig. 2.

Classification of AC estimation methods

Direct methods of AC estimation

In 1881, the relationship between pressure and volume was observed for the first time in isolated aorta from animal (Roy 1881). In this study, the aortas were gradually filled up with oil, which led to progressive increase in intra-aortic pressure from 0 to 300 mmHg (depending on the animal species). This procedure took 20 to 30 minutes, while the observer was recording intra-aortic pressure and volume in aorta. This work laid the foundations of the methodology of direct measurement of vascular mechanical properties.

In later experiments, human aortas extracted post mortem were measured (Hallock and Benson 1937). In this paper, authors were observing changes of volume in isolated thoracic aortas during gradual increase of intra-aortic pressure to the value of 230 mmHg. They found that AS is increasing not only with increasing pressure but also with age.

With gradual improvement of measurement technique the methodology was improving as well. Langewouters et al. (1984) observed change of diameter in isolated human aortas caused by increased intra-aortic pressure in a setting more corresponding to in vivo conditions including filling and immersing aortas into solution with physiologic blood concentration of O₂, CO₂, temperature and pH. The results led to the discovery of relationship between AC and pressure within 0 – 200 mmHg range and its estimated mathematical function:

$$AC(p)=\frac{A_m/\pi p_1}{1+{\left(\frac{p-p_{{}_0}}{p_1}\right)}^2}$$ (2)

where p is current value of blood pressure, Am, p₀ and p₁ are independent parameters specific for each sample of aorta. It was found that parameters p₀ and p₁ are closely related to age and sex whereas parameter A_m is only related to sex. Afterwards, Eq. 2 was applied by Wesseling et al. (1993) and together with three element Windkessel model they created a method enabling to predict blood flow curve for each heart beat from blood pressure curve, age and sex of the measured subject.

Indirect methods of AC estimation

Indirect methods of AC estimation can be divided into three groups – local and systemic AC estimation methods and surrogate indexes of AC (Fig. 2). In order to compute AC using an indirect method, it is required to record at least one of these signals – blood pressure, blood flow and changes of arterial diameter or cross-sectional area. Most of the methods require to simultaneously record two signals determined at the same site. However, this condition is not always possible to be satisfied using only noninvasive approaches. All signals can be measured invasively. However, this review focuses mostly on noninvasive methods of AC estimation and therefore in the next sections, only noninvasive ways of these signals acquisition and processing are discussed.

Local AC estimation

Assessment of local AC indexes is based on these approximations:

$$AC=\frac{\mathit{\Delta }V}{\mathit{\Delta }P}\approx \frac{\mathit{\Delta }D}{PP}$$ (3)

where ΔD represents changes of measured artery distension. It can be measured either by changes of diameter or cross-sectional. PP represents pulse pressure (difference between systolic blood pressure – SBP, and diastolic blood pressure – DBP). Necessary condition arising from these equations is to simultaneously and continuously measure at least two signals of the following at the same site – blood pressure, flow and distension changes.

Regarding blood pressure signal, it is possible to noninvasively and continuously measure it only in superficially located arteries using volume-clamp photoplethysmography method (Penaz 1973) or applanation tonometry (Kim and Braam 2013, Sato et al. 1993). The major limitation of these method is that they are only applicable to specific peripheral arteries enabling to measure peripheral blood pressure only. However, peripheral blood pressure curve differs from central blood pressure curve – i.e. measured in aorta – introducing a distortion in peripheral blood pressure curve due to pulse wave reflections (Kroeker and Wood 1955). Because aorta contributes by up to 65 % to the AC central blood pressure is more appropriate for determination of AC (Stergiopulos et al. 1995). This issue, at least partially, solves application of transfer function transforming peripheral blood pressure curve to central blood pressure curve.

Regarding continuous and noninvasive measurement of blood flow, two methods are commonly used – doppler ultrasonography and impedance cardiography. Doppler ultrasonography allows to measure blood flow velocity and together with measured diameter of monitored artery, it is possible to estimate blood flow in given artery (Drummond and Murphy 2012). Impedance cardiography is based on measurement of thoracic impedance. It cyclically changes in relation to cardiac cycle – with increasing volume of blood in the thoracic cavity, thoracic impedance decreases (Cybulski 2011, Drummond and Murphy 2012).

Finally, ultrasound wall-tracking, tissue Doppler imaging and magnetic resonance imaging (MRI) are capable of continuous and noninvasive estimation of diameter or cross-sectional area changes in given part of arterial tree (Chirinos 2012, Jackson et al. 2009, Meinders and Hoeks 2004, Vermeersch et al. 2008). Ultrasonography is accurate when applied on superficial arteries, whereas MRI is also applicable to deeply located arteries, including aorta.

Systemic AC estimation

The systemic AC indexes describes elastic properties of the whole arterial tree. The methods based on the Windkessel model create the largest group of methods estimating systemic AC indexes. These methods are further separated into analytical and numerical approaches. Analytical methods estimate AC by single calculation, whereas numerical methods need more iterations of calculation to progressively estimate AC value.

The model helps to understand how the arterial system works and it can be used to predict blood pressure and flow waveforms or to estimate arterial parameters. This review is focused only on estimation of AC therefore only methods related to its estimation are further discussed in next sections.

Windkessel model is a simplified model of arterial tree. The model was popularized for the first time by Frank at 1899 (Frank 1899). In this work, the heart and vascular system comprise closed hydraulic circuit. According to this analogy, the circuit contains the pump (analogy of the heart) with its outflow part connected to the container (analogy of the aorta) with free air space – so called Windkessel. When water is pumped from the reservoir (analogy to venous part of circulation) to the container, the air within is pressed which results in higher air pressure in the upper part of the container. During the inactive time of pump, the water is pushed out of the container by the pressed air which leads to the continuous outflow of water from the container to circuit (analogy to arterial tree).

There are several Windkessel models and the most commonly used include two-element Windkessel model (2WK) and three-element Windkessel model (3WK). 2WK model is described by two parameters – AC and total peripheral resistance (TPR), whereas 3WK is described by three parameters – AC, TPR and characteristic (aortal) impedance (Z_c).

There are several methods employing 2WK model for AC estimation: time decay method, area method (Liu et al. 1986, Randall et al. 1976), two-area method (Self et al. 1994) and pulse pressure method (Stergiopulos et al. 1994).

Using time decay method, AC can be estimated using this equation:

$$AC=\frac{\tau }{TPR}$$ (4)

where τ is a time constant. According to 2WK model (Liu et al. 1986), time constant τ governs the rate of aortic blood pressure exponential decay during diastolic phase (Fig. 3). The value of time constant τ represents a time needed to ~63% decrease of blood pressure from the beginning of the diastolic phase. Lower values of τ represent the faster rate of blood pressure decrease and vice versa. To calculate AC using time decay method, it is required to estimate the value of time constant τ and TPR. Time constant τ can be quantified from the aortal blood pressure wave during diastolic phase after transformation into semilogarithmic scale – it is expected that then blood pressure decay follows straight line with negative slope. Afterwards, reciprocal value of this slope, disregarding the sign, equals estimated value of the time constant τ.

Fig. 3.

Illustration of parameters derived from blood pressure curve required by 2WK model based methods. Time-decay method: exponential decay of blood pressure during diastolic phase governed by time constant τ is illustrated with red-dots. Area method: area under the blood pressure curve indicated by C and blood pressure values at the beginning and end of this part of blood pressure curve are measured. Two-area method: A area and the sum of B and C areas enter the calculation procedure introduced in the text.

The major problem of time constant τ estimation is in the noninvasive recording of central blood pressure wave. In several studies, authors decided to use peripheral blood pressure wave instead of central blood pressure wave (Levenson et al. 1981, Simon et al. 1983). However, this approach might lead to distorted τ value due to modification of exponential decay. It results from the superimposed reflected blood pressure wave when blood pressure curve is measured at peripheral artery hampering precise determination of the diastolic phase beginning. A method proposed by Arai et al. (2011) solves this issue by estimating time constant τ using – instead of whole peripheral blood pressure wave – only parameters which are minimally distorted by reflected pressure waves, i.e. DBP, cardiac cycle duration, time interval from the onset of systole to the systolic peak and mean blood pressure (MBP).

For estimation of AC from diastolic blood pressure decay, TPR should be also estimated using formula:

$$TPR=\frac{MBP}{CO}$$ (5)

where CO is cardiac output. However, this equation is only valid if hemodynamic parameters are stable.

The time decay method has one more drawback – the exponential decay of blood pressure during diastolic phase is not necessarily uniform. It means that time constant τ may differ according to the selected phase of blood pressure wave for determination of τ. To solve this drawback, area and two-area method were introduced – they use area under the blood pressure wave instead of exponential decay. Area method is based on time decay method, but it calculates time constant τ from the ratio of area under the diastolic phase and the difference between start and end pressure of this phase (Fig. 3). Similarly, two-area method uses area under blood pressure curve similarly to area method, but it estimates both AC and TPR without time constant τ estimation and utilizes two phases (systolic and diastolic phase) instead of one (diastolic) in area method:

$${\int }_{t_1}^{t_2}Q(t)dt=AC·(P_2-P_1)+\frac{1}{TPR}{\int }_{t_1}^{t_2}P(t)dt$$ (6)

where indexes 1 and 2 (t₁, t₂, P₁, P₂) specify time and pressure at the beginning and the end of the specific phase. Q(t) is blood flow function of time. The equation is applied during part of the systole (from the beginning of the blood pressure upstroke to the peak corresponding to systolic blood pressure) and the rest of the cardiac cycle (from the systolic peak to the end of the diastolic phase) (Fig. 3). Using this method, a set of two equation (for two parts) with two unknown parameters (AC and TPR) are obtained enabling to estimate both TPR and AC values even in unstable hemodynamic conditions.

Another 2WK method, pulse pressure method, estimates AC numerically whereas previously mentioned 2WK methods estimates AC analytically (Stergiopulos et al. 1994). The method estimates AC from both blood pressure and blood flow curves. At the beginning, the method estimates AC and TPR (Eq. 5) values and together using 2WK model and blood flow curve, the blood pressure curve is predicted by calculation. A new value of PP is extracted from predicted blood pressure curve and it is in the next step compared to measured value of PP. If these values are equal (or the difference between them is lower than given threshold) the computation of method is terminated and estimated value of AC is accepted. Otherwise, the value of AC is modified and the prediction of blood pressure curve is repeated (new iteration of calculation). The process is repeated until the predicted PP is within given tolerance close enough to measured PP value (Fig. 4). This method allows to compute AC also from peripheral blood pressure and blood flow curve instead of previous method requiring to measure central blood pressure and blood flow curves.

Fig. 4.

Workflow of numeric pulse pressure method of AC estimation based on 2WK model. At the beginning, blood flow and blood pressure recordings are taken (blue boxes). Afterwards, TPR is estimated using Eq. 5 and AC is selected randomly or estimated by another method. Using blood flow, TPR and AC, new blood pressure curve is predicted and PP is calculated from it (PPp). Similarly, PP is estimated from measured blood pressure curve (PPm). Both values of PP, measured and predicted, are compared (yellow box). If they are equal (or close enough within given tolerance), AC was estimated correctly (green box) and AC value is accepted as its estimate. Otherwise, AC has to be modified and new predicted blood pressure curve is calculated.

2WK model is an oversimplification of the cardiovascular system inevitably introducing potential errors. An important hemodynamic measure – arterial input impedance (Z_in) – reflecting the overall load (Chirinos 2012) can be estimated in frequency domain calculating the ratio of blood pressure and blood flow. After continuous blood flow measurement became available resulting in determination of Z_in, the short-comings of the 2WK methods became clear (Westerhof et al. 2019). Z_in predicted by 2WK was correct for low frequencies but it differed from real values for high frequencies. Due to these inconsistencies, Westerhof et al. (1971) proposed a new Windkessel model – 3WK. It extends traditional 2WK model by Z_c resulting in more realistic prediction of Z_in at high frequencies. From hemodynamic point of view, Z_c includes both inertia of blood and AC of the aorta at high frequencies:

$$Z_c=\sqrt{\frac{L}{{AC}_a}}$$ (7)

where L is inertia of blood and AC_a represents arterial compliance of the aorta. The value of Z_c is possible to be estimated from simultaneous measurement of blood pressure and blood flow curves in time or frequency domain (Qureshi et al. 2018). In time domain, Z_c is estimated from the slope of blood pressure-flow relationship at the beginning of the systolic ejection. In frequency domain, it is estimated from the ratio of blood pressure and blood flow employing Fourier transform (Dujardin and Stone 1981, Lucas et al. 1988, Nichols et al. 1977).

Several 3WK methods are suitable for AC assessment. The most commonly applied include: numerical 3WK method (suitable for unstable hemodynamic conditions) (Toorop et al. 1987), integral method (Shim et al. 1994) and low-frequency impedance method (Laskey et al. 1990). Surprisingly, none of these methods outperformed 2WK methods in an estimation of AC (Stergiopulos et al. 1995). However, the ability to better model Z_in of 3WK model was used for better prediction of blood flow curve from blood pressure curve (Wesseling et al. 1993). After integration of Z_c into 2WK models, estimated Z_in at higher frequencies is closer to real values. On the other hand, in low frequency band, the difference between estimated and real values of arterial input impedance is bigger than in 2WK models. Regarding estimation of AC, the values of Z_in at lower frequencies are more important and it explains why 2WK models are more reliable in AC assessment compared to more computationally cumbersome 3WK models.

Besides methods of systemic AC estimation based on Windkessel model, there is one rather old method – estimation of the AC as a ratio of stroke volume (SV) and PP (Remington and Noback 1948). This method suffers from one important limitation: the method assumes that SV is ejected into elastic arteries (mainly aorta) without considering simultaneously occurring continuous blood outflow to the periphery resulting in an overestimation of AC (Westerhof et al. 2019).

Surrogate indexes

The last group of indirect AC estimation methods is represented by surrogate indexes. These indexes are directly influenced by changes of AC. The most commonly used measures within this groups of methods include PWV and augmentation index (AI).

Currently, PWV is considered to be a gold standard method for noninvasive and easily reproducible arterial stiffness estimation (Laurent et al. 2006). The heart generates several types of sphygmic waves which propagate down the arterial system to the periphery and are manifested by changes in pressure, flow, velocity and distension of arterial wall (Korpas et al. 2009). The velocity of the sphygmic wave propagation within a selected arterial segment can be measured by recording of changes related to sphygmic wave at two locations in arterial tree. After measurement of the time delay of two corresponding parts (most commonly the beginning of the wave upstroke) of arterial waveform recorded on two different points of arterial tree, the ratio of distance between these two points and time delay provides averaged PWV within the measured segment. The major problem in PWV estimation refers to the lack of knowledge on exact distance between two measurement points potentially introducing an error into the calculation (Chirinos 2012). PWV is influenced by the length of the artery and elastic properties of the arterial wall within analyzed arterial segment. With increasing AC, the PWV gets slower and vice versa. Aortic PWV is commonly estimated over the carotid-femoral portion of arterial tree (carotid-femoreal PWV – cfPWV) (Chirinos 2012, Svačinová et al. 2020). Vardoulis et al. (2012) found an inverse relationship between AC and cfPWV when they were simulating propagation of pulse waves on computer model of arterial system:

$$AC=k·\frac{1}{cf{PWV}^2}$$ (8)

where k represents the influence of the measured arterial segment geometry. The value of k=37 was empirically estimated for the segment between carotid and femoral artery.

Another surrogate index of AC, augmentation index – AI, quantifies a change of blood pressure curve due to magnitude and timing of wave reflections. With increasing arterial stiffness, PWV is increasing as well resulting in faster propagation of reflected waves. Faster propagation of reflected waves back towards heart may coincide with forward waves resulting in SBP augmentation. If this summation of forward and backward reflected waves occurs within duration of systolic phase of cardiac cycle, it leads to increased SBP and afterload. On the contrary, with increased AC, PWV is slower and reflected waves are summed with forward waves during diastole supporting blood perfusion. AI is estimated as the ratio of augmented pressure and PP, where augmented pressure is defined as the difference between SBP and the pressure at the inflexion point of blood pressure – i.e. at the point where the second derivative of blood pressure curve equals 0 (Segers et al. 2007). Considering this definition, AI is not only influenced by PWV and thus indirectly by AC, but also by the magnitude of reflected wave. Since this magnitude is not straightforwardly related to AC, it introduces distortion in using AI as an indirect estimator of AC (Vlachopoulos et al. 2006, Westerhof et al. 2019).

Requirements of mentioned methods

This review focuses only on the most common methods of noninvasive estimation of AC. To summarize, an overview of necessary requirements for input parameters for all discussed indirect methods is presented in Table 1.

Table 1.

Estimation of AC – summary of necessary requirements of indirect methods for input parameters

Method	P(t)	PP	Q(t)	SV	Zc	Aorta	D(t)	ΔD	Stable conditions
Local AC estimation:ΔD/ΔP	−	+	−	−	−	−	−	+	−
Time decay method 1 (2WK)	+	−	−	+	−	−	−	−	+
Area method (2WK)	+	−	−	+	−	+	−	−	+
Two-area method (2WK)	+	−	+	−	−	−	−	−	−
Numerical pulse pressure method (2WK)	+	−	+	−	−	−	−	−	+
Numerical method (3WK)	+	−	+	−	−	−	−	−	−
Integral method (3WK)	+	−	+	−	+	+	−	−	+
Low frequency impedance method (3WK)	+	−	+	−	+	−	−	−	+
SV/PP 2	−	+	−	+	−	−	−	−	−
PWV 3	+	−	+	−	−	−	+	−	−
AI	+	−	−	−	−	+	−	−	−

+ necessary, − not necessary, P(t) – blood pressure curve, PP – pulse pressure, Q(t) – blood flow curve, SV – stroke volume, Z_c – characteristic impedance of the aorta, column „Aorta” – necessary to record signal in the aorta, D(t) – distension curve (changes of diameter or cross-sectional area), ΔD – difference between diameter during one cardiac cycle, AC – arterial compliance, 2WK – two-element Windkessel model, 3WK – three-element Windkessel model, PWV – pulse wave velocity, AI – augmentation index.

¹when using method proposed by Arai et al. (2011), it is not necessary to measure central blood pressure curve,

²in case of applying TF on peripheral blood pressure curve, it is not necessary to measure PP in the aorta,

³to measure PWV, only one of the indicated curves is necessary to be recorded but on two separate places.

AC estimation in the context of other parameters

In order to interpret estimated value of AC as an index of structural changes in arteries (e.g. related to atherosclerotic process), it is required to consider also changes of other parameters which are potential confounders of AC. These parameters often markedly change on a short time scales and therefore should be carefully considered during AC assessment in relation to various pathological states. Blood pressure is one of the most well-known parameters related to changes in AC. Results of early invasive studies implies a strong relationship between blood pressure and AC (Hallock and Benson 1937, Langewouters et al. 1984, Roy 1881). However, not only intra-arterial blood pressure influences AC value but AC also varies with changes of transmural pressure (Chang et al. 2009).

Furthermore, vasomotion – i.e. vasoconstriction and vasodilation – has an important influence on AC. Previous studies found a shift in relationship between AC and blood pressure to lower values of AC after evoking of vasoconstriction and vasodilation was accompanied by a shift to higher values of AC (Bank et al. 1995, Pagani et al. 1979). In accordance with this concept, an increase of PWV was observed after application of mild orthostatic stress evoked by lower-body negative pressure without a change in blood pressure, heart rate or TPR (Nardone et al. 2018).

In another study, Czippelova et al. (2019) observed a relationship between CAVI (index of PWV independent of blood pressure) and TPR. They found that young obese patients have lower CAVI values (increased AC) together with lower TPR values and lower sympathetic activity than control group. These results indicate an influence of sympathetic activity on AC. Furthermore, it was found that AC decreased during mental and orthostatic stress (Cohen et al. 2020, Hasegawa and Rodbard 1979, Huijben et al. 2012, Matsumura et al. 2019, Vlachopoulos et al. 2006) when higher sympathetic activity is assumed. Therefore, it is also important to standardize physiological state of the subject at a time of examination.

Changes of AC were also observed with changes of heart rate. Tan et al. (2016) found that PWV increased (AC decreased) with increasing heart rate as well independent of blood pressure changes. The mechanism behind this influence is still unknown. However, it is assumed that viscoelasticity of arteries might be involved in this mechanism – during tachycardia, the time available for recoil is shortened and the arteries remain stiff (Lantelme et al. 2002).

Conclusions

Arterial compliance is an important cardiovascular parameter influencing ventricular-arterial coupling. Decreased arterial compliance is associated with several physiological and pathological processes and states. Therefore, it is not surprising that numerous noninvasive direct or indirect methods of estimation were developed. However, with so many methods, it is difficult to decide which method is the best for particular clinical or research setting, which parameters or signals are necessary to be recorded to apply the selected method and how to interpret the results. In this review, the most commonly used noninvasive methods are discussed and categorized. Afterwards, summary table of methods requirements and conditions is presented. At the end, possible confounders are discussed. Although there are many noninvasive methods of AC estimation, most of them require to measure central blood pressure and/or blood flow. However, both signals are difficult to be obtained and new methods should be developed to establish a new gold standard of AC estimation with a more direct AC measurement and with a special attention put on a potential influence of confounding variables.