Thermodynamics of unfolding mechanisms of mouse mammary tumor virus pseudoknot from a coarse-grained loop-entropy model

Abstract

Pseudoknotted RNA molecules play important biological roles that depend on their folded structure. To understand the underlying principles that determine their thermodynamics and folding/unfolding mechanisms, we carried out a study on a variant of the mouse mammary tumor virus pseudoknotted RNA (VPK), a widely studied model system for RNA pseudoknots. Our method is based on a coarse-grained discrete-state model and the algorithm of PK3D (pseudoknot structure predictor in three-dimensional space), with RNA loops explicitly constructed and their conformational entropic effects incorporated. Our loop entropy calculations are validated by accurately capturing previously measured melting temperatures of RNA hairpins with varying loop lengths. For each of the hairpins that constitutes the VPK, we identified alternative conformations that are more stable than the hairpin structures at low temperatures and predicted their populations at different temperatures. Our predictions were validated by thermodynamic experiments on these hairpins. We further computed the heat capacity profiles of VPK, which are in excellent agreement with available experimental data. Notably, our model provides detailed information on the unfolding mechanisms of pseudoknotted RNA. Analysis of the distribution of base-pairing probability of VPK reveals a cooperative unfolding mechanism instead of a simple sequential unfolding of first one stem and then the other. Specifically, we find a simultaneous “loosening” of both stems as the temperature is raised, whereby both stems become partially melted and co-exist during the unfolding process.

Supplementary information

The online version contains supplementary material available at 10.1007/s10867-022-09602-2.

Introduction

Pseudoknotted RNA is one of the most prevalent RNA structures [1]. It has been found in nearly all organisms and is part of the functional domains of ribozymes, viral genomes, self-splicing introns and other biological systems [1–3]. First recognized in the turnip yellow mosaic virus in early 1980s [4], pseudoknots have at least two stem-loop structures, in which half of one stem is intercalated between the two halves of another stem [1, 5–7] (see Fig. 1). They provide a way for a single RNA strand to fold onto itself to form a globular structure capable of performing important biological functions, including ribosomal frameshifting [2, 8–11], catalysis of various ribozymes [12], metabolite-sensing riboswitches [13] and telomerase activity [3, 14–16]. Their contributions to ribosomal frameshifting are required for the replication and proliferation of all retroviruses, making pseudoknotted RNA molecules an attractive class of targets for the development of antiviral drugs.

Fig. 1.

The structure of MMTV VPK. (a) Illustration of nested and non-nested RNA secondary structures. In a nested structure, one arc representing base-pair interactions in a stem is completely embedded within the arc of another stem. In a non-nested structure, the two arcs cross each other but neither arc is completely embedded within the other. (b) The secondary structure of VPK. (c) The 3D structure of VPK (PDB ID: 1rnk)

Ribosomal frameshifting, metabolite sensing riboswitches and other biological functions of pseudoknotted RNA molecules are directly related to their structures, folding stability and conformational fluctuations [2, 3, 8, 9, 12, 13]. Therefore, knowledge of the three-dimensional structures of RNAs and their underlying free energy landscapes can help gain understanding of their functions. Due to substantial costs required for obtaining structures of RNAs using X-ray crystallography or NMR spectroscopy [17], the structures of a majority of RNA molecules are currently unsolved [18]. Computational prediction of secondary structures of non-pseudoknotted RNAs has been very successful [7, 19–26]. Among these prediction methods, Mfold [22], RNAstructure [23] and Vienna Packages [26] are based on dynamic programming and well-established Turner’s energy rules to generate a structure with the lowest free energy, with the condition that the RNA secondary structures are nested [20]. However, the requirement of the nested structure is violated in RNA pseudoknots (see Fig. 1a for an illustration), which makes the investigation of secondary structures of pseudoknotted RNAs far more challenging than non-pseudoknotted RNAs. Furthermore, information of secondary structures alone is not sufficient for accurate assessment of the stability and accessible conformations of pseudoknotted RNA molecules. A well-recognized challenge is to accurately account for the free energy of the loops, for which analysis of the ensemble of different spatial loop configurations is required [27–31]. Inadequacy in quantifying free energies of pseudoknotted loops posed a limit on what these earlier methods could achieve.

The folding of pseudoknotted RNA has received considerable attention [3, 9, 32–40]. Experiments using a variety of techniques revealed insights into the thermodynamics and kinetics of pseudoknotted RNA folding [3, 9, 38, 41–44]. Computational studies of RNA thermodynamics also helped in gaining better understanding of the inherent sequence-dependent variations and ionic dependency in RNA folding [35, 36, 40, 45]. Among well-studied pseudoknotted RNAs, a variant of Mouse Mammary Tumor Virus Pseudoknot (MMTV) provides an excellent model system for understanding the thermodynamics of hairpin type (H-type) pseudoknotted RNA molecules. Much of the available experimental data on MMTV are based on studies of this variant, called VPK (Fig. 1b, c) [9, 38, 42, 46].

One proposed folding mechanism of VPK is based on the observation that there are two unfolding transitions in its melting profile, which were thought to correspond to the sequential unfolding of the two stems, with no other intermediates significantly populated [9, 46]. Simulation studies based on three-dimensional structure using the coarse-grained three-interaction-sites (TIS) model successfully captured the salient features of the thermodynamics and kinetics of H-type pseudoknots, including structural transitions and the effects of salt on RNA stability, and further predicted that the pseudoknots could fold via parallel pathways [36, 39, 40]. However, as studies based on simulations are constrained by conformations that are accessible through trajectory sampling, a comprehensive picture of how VPK spontaneously folds is still lacking, and the specifics of folding and unfolding mechanisms are yet to be investigated in their full complexity. To gain in-depth understanding of these processes, it is necessary to consider a diverse ensemble of conformations that are thermodynamically relevant, including native structures, native-like structures and misfolded intermediates.

Here we studied thermodynamic properties of the pseudoknotted RNA molecule VPK using the PK3D (pseudoknot structure predictor in three-dimensional space) algorithm [29]. We generated spatial arrangements of structural elements of the RNA molecule and estimated their free energy. In addition, we incorporated conformational entropy of loops, which is essential for understanding the thermodynamics of pseudoknot folding. With this approach, we are able to predict (1) the melting temperatures of RNA hairpins with varying loop lengths and (2) the heat capacity versus temperature profiles of VPK. The predictions are in excellent agreement with previous experimental data. To further test our model, we analyzed the thermodynamics of the constituent hairpins of VPK and uncovered alternative conformations that are found to be more stable than the hairpin structures at low temperatures. These predictions were verified with new experiments that also show deviations from a simple two-state description of the hairpin unfolding transitions. Finally, through analysis of the distribution of base-pairing probabilities, our modeling results provide details of the unfolding mechanisms of VPK. In contrast to the previously held notion of sequential unfolding of first one stem and then the other, albeit via multiple pathways, our results demonstrate a cooperative unfolding mechanism, with simultaneous loosening of both stems, and an ensemble of structures with partially “frayed” stems that co-exist through most of the unfolding transition.

Materials and methods

Generation of candidate secondary structures

We first generated all possible stems for a RNA sequence. For a given RNA sequence s, we used the Smith-Waterman dynamic programming algorithm for local alignment to align s with its reverse sequence $s^{\prime }$, with the same nucleotides (nts) ordered from $3^{\prime }$ to $5^{\prime }$. Both Watson-Crick and $G-U$ wobble base pairings were considered matches. The scores of match, mismatch and gap were set to $+1$, $-50$ and $-100$, respectively. In addition, we required that the stem length be $\ge 2$ nt, i.e., a stem must contain at least one stack. The number of possible secondary structures increases dramatically if more stems are considered due to the combinatorial nature of the complexity in enumerating all possible combinations of stems. We therefore limited the number of stems to be $\le 4$. All possible secondary structures with $\le 4$ non-conflicting stems were generated, each of those that were feasible without conflicts (e.g., same nt(s) cannot belong to multiple stems) was considered as a conformational state.

Generation of 3D RNA conformations without loops

Three-dimensional structures were generated using the PK3D method. Below we give a brief description of this method, details of which can be found in Ref. [29]. With a set of feasible secondary structures containing non-conflicting stems, we constructed the 3D structures of the coarse-grained discrete state model of the RNA molecule. This is achieved by sequentially enumerating all possible conformations of the stems based on a pre-computed look-up table of the starting and ending positions according to the loop lengths, as well as the relative orientation between a loop and its connecting stems. The look-up table was calculated using a six-state discrete model [28], with the connected stems spatially arranged in all six possible orientations. The look-up table is for loops with lengths up to 7. For loops with length $>7$, we approximated them as loops of length 7.

Once a candidate conformation with given positions of stem regions was obtained, the shortest loop and its two corresponding stems were taken as one building block. We continued by adding the next shortest loop and its connected stems to the blocks until all loops were added. All blocks were then merged to form a full conformation. During this process, whenever a new stem was added to a partial conformation, and whenever two partial components were united, we examined and ensured that steric collisions did not occur and the lengths of loops connecting this new stem to stems already added were sufficiently long to accommodate them spatially.

Construction of $C_4$ and P atoms of RNA loops

For the loop regions of RNA conformations, we constructed all loop structures using the coarse-grained virtual bond model [27, 47, 48] and a chain-growth method. We considered only two effective virtual bonds that connect atoms P – $C_4$ and atoms $C_4$ – P, as well as their torsion angles $\theta$ and $\eta$. Nucleotides in RNA loop regions are represented only by the P and the $C_4$ atoms [27–29, 48]. In the virtual bond model, the virtual bond length was fixed at 3.9 Å and the bond angle at P and $C_4$ atoms were fixed to the values of 105${}^{\circ }$ and 95${}^{\circ }$, respectively. Coordinates of P and $C_4$ atoms were determined by the corresponding torsion angles. For loops of n torsion angles, the first $(n-6)$ torsion angles were sampled using a six-state discrete coarse-grained model following Ref. [28, 49]. The states of six torsion angle pairs were obtained from the 2,480 pairs of torsion angles for 156 structures in RNA05 database [50], followed by a k-means clustering process as described in Ref. [28]. The values of these six ($\theta$ , $\eta$) pairs are shown in Table 1.

Table 1.

The values of ($\theta$ , $\eta$) pairs of torsion angles in degree (${}^{\circ }$) for RNA

$\theta$	215.0	254.0	96.5	338.3	330.3	134.0
$\eta$	169.9	332.4	162.4	189.5	57.1	348.4

These values are taken from the RNA loop entropy study of Ref. [28]

For the last 6 torsion angles, we applied a modified CSJD analytical closure method to generate coordinates of the remaining backbone atoms [51]. The CSJD method is one of the most successful protein loop closure algorithm. It determines the loop conformations of the last six torsion angles by finding the real roots of a 16th-degree polynomial in one variable based on the kinematics of the equivalent rotator linkages [51]. It has been used in many protein loop studies [49, 52–54]. Different from the tri-peptide problem in protein loop modeling, here the 6 torsion angles are related to the coordinates of P and $C_4$ atoms of the last 5 nucleotides shown in Fig. 2. We have modified the CSJD algorithm for modeling loops in RNA molecules [49, 53].

Fig. 2.

The last 6 torsion angles for RNA loop closure. For the RNA loop ends with nucleotide ($n-1$), the coordinates of $P_{n-3}$, $C{4}_{n-3}$, $C{4}_n$ and $P_{n+1}$ are used as anchor atoms for loop closure

Thermodynamic model of RNA molecules

The basis interaction free energy $\mathrm{\Delta }{G}_B(x)$ of each RNA conformation $x$ was calculated as

$$\begin{array}{c}\hfill \mathrm{\Delta }{G}_B(x)=\mathrm{\Delta }H(x)-T\mathrm{\Delta }S(x).\end{array}$$ 1

Here $\mathrm{\Delta }H(x)$ and $\mathrm{\Delta }S(x)$ are the enthalpy and the configurational entropy, respectively, of a conformation $x$. The enthalpy $\mathrm{\Delta }H(x)$ comes from the contributions of the stacks: $\mathrm{\Delta }H(x)={\sum }_i\mathrm{\Delta }{H}_{\mathrm{stack}(\mathrm{i})}$, where $\mathrm{\Delta }{H}_{\mathrm{stack}(\mathrm{i})}$ is the enthalpy of a particular stack i.

For the stem, hairpin, bulge and short internal loops with $\le 4$ nts, the free energy values for each of the substructures were calculated using the Turner energy rules [20]. For loops with length $>4$ nts, including the longer internal loops, multi-branch loops and pseudoknotted loops, we used our calculated values of the loop configuration entropy when computing the free energies. Physically, the loop configuration entropy is determined by the end-to-end distance and the spatial interference from nearby loops or stems [55]. In our simplified model, the loop entropy is assumed to be determined only by its length and the end-to-end distance, which is determined by the positions of the stems that are connected by this loop. Following Ref. [28, 29], a pre-built table of loop entropy with each entry indexed by a loop length and an end-to-end distance was constructed by estimating the fraction of the number of conformations of the closed loop over the number of conformations of the random coil of the same length using a six-state discrete RNA chain model through sequential Monte Carlo sampling [28].

$\mathrm{\Delta }{G}_B(x)$ is computed as the basis free energy at salt conditions of 1M NaCl, where the Turner parameters are determined. To account for the effect of salt concentrations different from 1M NaCl, we computed the electrostatic free energy $\mathrm{\Delta }{G}_E(x)$ using the model of Denesyuk et al. [40]. This model combines the Debye-Hückel approximation with the effects of counterion condensation [56]:

$$\begin{array}{c}\hfill \mathrm{\Delta }{G}_E(x)=\frac{{\alpha }^2{e}^2}{2ϵ}\sum _{i,j}\frac{e^{-({\mathbf{r}}_i-{\mathbf{r}}_j)/\lambda }}{\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert },\end{array}$$ 2

where e is the proton charge, $ϵ$ is the dielectric constant of water and $\alpha$ is the counterion condensation coefficient, which takes into account that the effective charge of each phosphate group decreases from $-e$ to $-\alpha e$ when counterions are attracted by the highly negatively charged RNA. $\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert$ is the distance between two phosphates i and j located at ${\mathbf{r}}_i$ and ${\mathbf{r}}_j$. These distances are known since the coordinates of all phosphates of an RNA structure $x$ are available upon construction of the stems and loops. $\lambda$ is the Debye-Hückel screening length determined by salt concentration, which is obtained from the equation $\lambda ={(\frac{4\pi }{ϵk_{b}T}{\sum }_n{q}_n^2{\rho }_n)}^{-\frac{1}{2}}$ [40]. For an ion of type n, $q_n$ is the charge and ${\rho }_n$ is its number density in the solution, with ${\rho }_n\propto c$, where c is the molar concentration of the ion. This model has been shown to accurately describe salt dependencies of RNA structural elements such as stems, loops and pseudoknots [40, 42]. Overall, the interaction free energy $\mathrm{\Delta }{G}_I(x)$ of a RNA structure $x$ is:

$$\begin{array}{c}\hfill \mathrm{\Delta }{G}_I(x)=\mathrm{\Delta }{G}_B(x)+\mathrm{\Delta }{G}_E(x).\end{array}$$ 3

Calculation of base-pairing probability

Using the interaction free energy of each conformation $x$ evaluated as described above, the conditional coarse-grained partition function $Z_{i,j}(T)$ for the ensemble of conformations with base pair (i, j) formed can be calculated by summing over all possible conformations $\{x\}$ containing base pair (i, j)

$$\begin{array}{c}\hfill Z_{i,j}(T)=\sum _{\begin{array}{c}\exists (i,j)\\ \in x\end{array}}{e}^{\frac{-\mathrm{\Delta }{G}_I(x)}{k_{B}T}}.\end{array}$$ 4

The base-pairing probability $p_{i,j}(T)$ of the $(i,j)$ pair at temperature T can then be calculated as

$$\begin{array}{c}\hfill p_{i,j}(T)=\frac{Z_{i,j}(T)}{Z(T)}.\end{array}$$ 5

Here Z(T) is the partition function of our coarse-grained model, calculated for a given RNA sequence over the set of major conformations, with all $\le 4$ stems identified through dynamic programming connected by loops in spatially compatible configurations.

The probability distribution of base pairs can reveal the structural basis of the thermal stability and can shed light on the folding/unfolding pathways, as one can identify the stable base pairs and structures at a given temperature T [27].

Experimental studies on RNA hairpins

Experimental measurements of folding/unfolding thermodynamics were performed on RNA constructs that form the constituent hairpins of VPK. The constructs, denoted as HP1-2AP and HP2-2AP (Table 2), had a fluorescent nucleotide analog 2-aminopurine (2AP) incorporated within the sequences. HP1-2AP corresponds to nucleotides 1-21 in the VPK pseudoknot, with 2AP replacing an adenine at position 14 of the sequence. HP2-2AP corresponds to nucleotides 8-34 of VPK, with 2AP substituting an adenine at position 20 (13 in the HP2-2AP sequence). RNA samples were purchased from TriLink Biotechnologies, CA, and prepared for measurements as described in the Supplement. All measurements were performed in 10 mM MOPS pH 7, 50 mM KCl buffer.

Table 2.

RNA sequences for experimental studies

Sample	Sequence
HP1-2AP	5’-GGCGCAGUGGGCUXGCGCCAC-3’
HP2-2AP	5’-UGGGCUAGCGCCXCUCAAAAGGCCCAU-3’

X denotes the position of 2-aminopurine (2AP)

Equilibrium melting profiles were obtained using both absorbance and fluorescence measurements on HP1-2AP and HP2-2AP. The melting profiles for each RNA hairpin were described in terms of an empirical thermodynamic model consisting of three states: hairpin (H), alternate conformation (A) and unfolded (single-stranded) RNA (U). The absorbance and fluorescence melting profiles were fitted simultaneously in terms of the temperature-dependent populations of the three states, computed from the thermodynamic fit parameters, and their characteristic absorbance or fluorescence levels, also parameterized to be temperature dependent, as described in the Supplement. The best fit parameters of the model were obtained using a simulated annealing fitting procedure [57, 58]. The populations of each of these states thus obtained as a function of temperature were compared with corresponding populations obtained from the Pk3D modeling. The experimental and analysis details are provided in the Supplement.

Results

Loop entropy contribution to RNA hairpin stability

It is well known that single-stranded DNA (ssDNA) and RNA hairpin stability depends on the length and composition of the stem as well as the length of the loop [59–61]. Previous experimental studies on the stability of ssDNA and RNA hairpins with varying loop lengths showed that hairpins with smaller loops were much more stable than expected from considerations of loop entropy alone, with these effects more pronounced in the presence of monovalent ions in comparison with divalent ions [60, 61].

Here we tested our PK3D model against one such experimental study, by Kuznetsov et al. [60], where the hairpin stabilities of a series of RNA hairpin sequences 5’-CGAUCUU($U_i$)CCGAUCG-3’ with identical stems and varying loop lengths were measured in the presence of 2.5 mM MgCl${}_2$. The loop region in these hairpins is $UU(U_i)CC$, and the number of nucleotides in the loop is 4, 9 and 19 when i = 0, 5 and 15, respectively. Our predictions of the melting temperatures of these RNA hairpins are in close agreement with the experimentally measured values, as summarized in Table 3, indicating that our model accurately captures loop entropy contributions to hairpin stability under ionic conditions of 2.5 mM MgCl${}_2$. These results also demonstrate that PK3D can successfully describe RNA thermodynamics at salt conditions different from the typical 1 M NaCl used in most folding algorithms.

Table 3.

Melting temperatures of RNA hairpins with varying loop lengths

Loop Size	Experiment $T_m$ (${}^{\circ }$C)	PK3D $T_m$ (${}^{\circ }$C)
4	58	62
9	55	57
19	41	42

The melting temperatures ($T_m$) are for the sequence 5’-CGAUCUU($U_i$)CCGAUCG-3’ in 2.5 mM MgCl${}_2$. The loop size is 4, 9 and 19 when i = 0, 5 and 15, respectively. The experimental values are from Table 1 of Ref. [60] and have an uncertainty of $\pm 1^{\circ }$C

Unfolding thermodynamics of the constituent hairpins of VPK, measured in 50 mM KCl

To test how well our model can capture the thermodynamics of VPK pseudoknot, we first examined its two subsequences corresponding to the constituent hairpins that make up the pseudoknot. Sequence HP1 (G1-C19 of VPK) contains Stem 1 and Loop 1, with the $5^{\prime }$-end intact. Sequence HP2 (U8-U34 of VPK) contains Stem 2 and Loop 2, with the $3^{\prime }$-end intact. For each sequence, we computed its populations of conformations at different temperatures using PK3D and compared them with populations obtained from modeling of experimental melting data. The salt conditions used here in PK3D were 50 mM KCl, identical to the conditions of the experimental studies on these sequences.

HP1 forms an alternate structure that is more stable at low temperatures

The PK3D model predicts three major conformations populated in HP1 with varying fractions at different temperatures: a stem-loop structure which is referred to as the hairpin (Fig. 3a), an alternative secondary structure (Fig. 3b) and the ensemble of unfolded (single-stranded) conformations. The alternative structure has two more consecutive base pairs A6-U13 and G7-C12 forming an additional stack in the stem, with a single-nucleotide bulge, and a loop of only 4 nucleotides compared to 9 nucleotides in the loop of the hairpin structure. It is therefore predicted to be more stable at low temperatures than the hairpin, as it has a lower enthalpy and a lower entropic cost for loop formation compared with the hairpin structure. The model further predicts how the populations of the three major conformations change with temperature (Fig. 3c).

Fig. 3.

Comparison of experiment and computation for the folding thermodynamics of HP1. (a) The secondary structure of the hairpin conformation of HP1. (b) The secondary structure of an alternative conformation of HP1 predicted using PK3D. The adenine at position 14 (HP1-2AP) is in red circle in panels (a) and (b). (c) The relative populations of the three states of HP1 at different temperatures, computed from PK3D; hairpin (red), alternate (cyan), unfolded (yellow). (d) Corresponding relative populations of the three states, obtained from thermodynamic modeling of the experimental melting profiles. The color scheme in panel (d) is the same as in panel (c). The spread in populations (shown as shaded region) reflects the error in the thermodynamic parameters, obtained as described in the Supplement. The continuous lines represent the weighted average over this spread and the dashed lines represent the populations for the best fit parameters. The salt concentration was 50 mM KCl for both experiments and modeling

To monitor experimentally the melting of HP1 sequence, we replaced the adenine at position 14 with fluorescent nucleotide analog 2AP (HP1-2AP) and monitored the unfolding behavior of the labeled hairpin by measuring its absorbance and fluorescence as a function of temperature. Absorbance measurements primarily report on the overall changes in the extent of base pairing and base stacking as a function of temperature, while fluorescence measurements report on local changes in the vicinity of the 2AP probe. In HP1-2AP, the fluorescent nucleotide is expected to be part of the loop, adjacent to the stem, in the hairpin conformation (Fig. 3a) but is expected to bulge out in the alternative structure (Fig. 3b). Therefore, we anticipated a detectable decrease in 2AP fluorescence with increase in temperature when the population shifts from the alternative to the hairpin structure, and a smaller change in 2AP fluorescence upon complete unfolding of the hairpin. In contrast, we anticipated a smaller change in absorbance in the first transition and a more significant change when the hairpin unfolds.

The melting profiles (Fig. 4a and b) are consistent with what we anticipated and in qualitative agreement with the computational predictions, whereby the first transition observed in the temperature range below $\sim$60${}^{\circ }$C is attributed to the loss of the additional stack and the bulge in the alternate structure to form the hairpin structure (as reported by a relatively modest increase in absorbance and a significant decrease in 2AP fluorescence), while the second transition observed above $\sim$ 70${}^{\circ }$C is attributed to the loss of the hairpin structure (as reported by a sharp increase in absorbance from the loss of the stem).

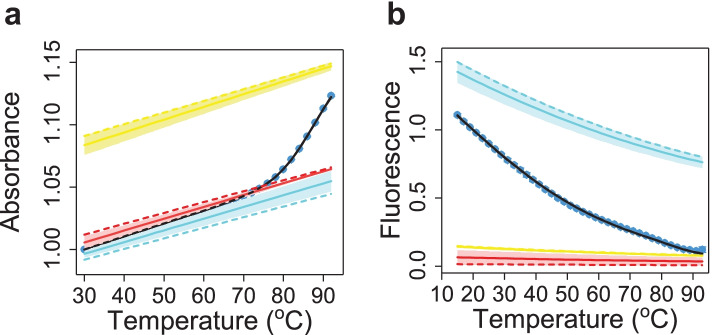
Fig. 4.

Three-state fit to the melting profiles of HP1-2AP. (a) Absorbance and (b) fluorescence melting profiles are shown. The data points (blue symbols) are the average of three independent sets of measurements, averaged after each measured profile was normalized to be 1 at 30 ${}^{\circ }$C for the absorbance data and at 20 ${}^{\circ }$C for the fluorescence data. The error bars are the standard error of the mean (s.e.m.) computed for the normalized data. The black lines are the best fits to the three-state thermodynamic model as described in the text. The absorbance and fluorescence levels (baselines) for each of the three states: hairpin (blue), alternate (red) and unfolded (yellow), obtained from the fit, are plotted as a function of temperature. The average baselines (continuous lines) and the spread (shaded region) are shown together with the baselines corresponding to the best fit parameters (dashed lines)

For a quantitative comparison between experiments and computation, we examined the absorbance and fluorescence melting profiles in terms of the thermodynamics of three states: hairpin (H), alternative (A) and unfolded (U) conformations, as described in the Supplement. The results from this modeling are discussed below. We note here that previous studies on these VPK constituent hairpins showed that the melting profiles could be described in terms of a two-state system [38, 42]. These studies relied on data that were measured using a single spectroscopic probe, either absorbance only [38] or fluorescence only [42], with the 2AP probe in the latter study placed at a position where it was insensitive to the alternate structure. Our results here highlight that measurements with multiple probes placed judiciously are needed to detect otherwise hidden alternative conformations.

The fits to the HP1-2AP melting profiles (Fig. 4a and b) yielded the populations of the three states as a function of temperature (Fig. 3d) for direct comparison with the computational results. The spread in the fits and the populations were computed as described in the Supplement and are largely from the uncertainties in the absorbance and fluorescence levels of the different states and their temperature dependencies that are not known a priori and, hence, are free parameters in the fits.

Two melting temperatures are identified in this three-state model: the first ($T_{\mathrm{m},\mathrm{A}\iff \mathrm{H}}$) is the temperature at which the alternative and hairpin conformations are equally populated, and the second ($T_{\mathrm{m},\mathrm{H}\iff \mathrm{U}}$) is the temperature at which the hairpin and the unfolded conformations are equally populated (Table 4). Results from PK3D calculation indicate that the first transition, from the melting of the two additional stacked base pairs in the alternative conformation to form the hairpin structure, occurs at $73$ ${}^{\circ }$C, while the unfolding of the hairpin occurs in the second transition, at 85 ${}^{\circ }$C. The fits to the experimental melting profiles reveal that the two transitions occur at 41.3 ± 1.1 ${}^{\circ }$C and $87.0\pm$ 0.3 ${}^{\circ }$C, respectively. The populations and melting temperatures predicted from the computations show good agreement with the results obtained from the fits to the experiments. In particular, the high-temperature hairpin-to-unfolded transition is captured remarkably well by the simulations. The discrepancy in the low-temperature alternative-to-hairpin transition could be from difficulties in accurate modeling of the single-nucleotide bulge conformation, which merits further investigation. Nonetheless, the extent of agreement between experiment and theory is noteworthy, especially considering that there were no adjustable parameters in the computations. These results also show that our model can unambiguously identify the nature of the intermediate or alternative structures that experiments alone cannot.

Table 4.

Melting transitions of HP1 and HP2 from experiments and computations

	HP1-2AP	HP1-PK3D	HP2-2AP	HP2-PK3D
$T_{\mathrm{m},\mathrm{A}\iff \mathrm{H}}$	41.3 ± 1.1 (40.4)	73	57.8 ± 2.0 (56.8)	5
$T_{\mathrm{m},\mathrm{H}\iff \mathrm{U}}$	87.0 ± 0.3 (87.1)	85	75.7 ± 2.6 (75.6)	75

The average values of the melting temperatures (in °C) obtained from fits to the experimental melting profiles of HP1-2AP and HP2-2AP and the corresponding errors, computed as described in the Supplement, are tabulated together with the best-fit parameters (in parenthesis). Corresponding values from simulations are denoted as HP1-PK3D and HP2-PK3D

HP2 also forms an alternative structure in addition to the hairpin

Similar to HP1, PK3D predicts the existence of three major populations of conformations for HP2, corresponding to a hairpin (Fig. 5a), an alternative structure (Fig. 5b) and the unfolded (single-stranded) ensemble. Compared to the hairpin structure, the predicted alternate structure has two more consecutive base pairs, A7-U15 and G8-C14, forming an additional stack, and a 5-nucleotide bulge. At low temperatures, this alternate conformation is predicted to be only slightly more stable than the hairpin conformation, with $T_{m,A\iff \mathrm{H}}$ predicted to be at $\sim$5 ${}^{\circ }$C, above which the hairpin conformation starts to be more populated (Fig. 5c). The second transition, corresponding to the melting of the hairpin conformation to the unfolded ensemble, is predicted to be at $T_{\mathrm{m},\mathrm{H}\iff \mathrm{U}}\sim$ 75 ${}^{\circ }$C.

Fig. 5.

Comparison of experimentally measured and computationally modeled folding thermodynamics of HP2. (a) The secondary structure of the hairpin conformation of HP2. (b) The secondary structure of an alternative conformation of HP2 predicted using PK3D. The adenine at position 13 (HP2-2AP) is in red circle in panels (a) and (b). (c) The relative populations of the three states of HP2 at different temperatures, computed from PK3D; hairpin (red), alternate (cyan), unfolded (yellow). (d) Corresponding relative populations of the three states, obtained from thermodynamic modeling of the experimental melting profiles. The color scheme in panel (d) is the same as in panel (c). The spread in populations (shown as shaded region) reflects the error in the thermodynamic parameters, obtained as described in the Supplement. The continuous lines represent the weighted average over this spread and the dashed lines represent the populations for the best fit parameters. The salt concentration was 50 mM KCl for both experiments and calculation

To experimentally monitor the unfolding of HP2, we again used a 2AP-labeled construct (HP2-2AP) in which an adenine at position 13 of the HP2 sequence was replaced with 2AP. This position is adjacent to the additional base pairs predicted to be formed in the alternate structure (Fig. 5b). Similar to HP1-2AP, the absorbance and fluorescence melting profiles of HP2-2AP are consistent with a three-state description of the folding thermodynamics (Fig. 6a and b). The absorbance measurements clearly reveal two distinct melting transitions, with a small increase in the absorbance at the low temperature transition and a larger increase in absorbance at the higher temperature transition (Fig. 6a). These transitions could be attributed to first the transition from the alternate structure to the hairpin structure, with loss of the additional stack, followed by the loss of the hairpin stem at high temperatures. The fluorescence melting profile detects a significant decrease in 2AP fluorescence that is coincident with the low temperature transition of the absorbance measurements, but with no further change in fluorescence at the high temperature transition (Fig. 6b). This sharp decrease in 2AP fluorescence is attributed to changes in the extent of 2AP stacking when the additional base pairs of the alternate structure adjacent to 2AP melt, similar to the trend observed in HP1-2AP in its hairpin-to-unfolded transition. In the hairpin structure of HP2-2AP, the 2AP probe is in the loop and far enough away from the stem, so that melting of the stem at the higher temperature goes undetected by 2AP.

Fig. 6.

Three-state fit to the melting profiles of HP2-2AP. (a) Absorbance and (b) fluorescence melting profiles are shown. The data points (blue symbols) are the average of three independent sets of measurements, averaged after each measured profile was normalized to be 1 at 30 ${}^{\circ }$C for the absorbance data and at 20 ${}^{\circ }$C for the fluorescence data. The error bars are the standard error of the mean (s.e.m.) computed for the normalized data. The black lines are the best fits to the three-state thermodynamic model as described in the text. The absorbance and fluorescence levels (baselines) for each of the three states: hairpin (blue), alternate (red) and unfolded (yellow), obtained from the fit, are plotted as a function of temperature. The average baselines (continuous lines) and the spread (shaded region) are shown together with the baselines corresponding to the best fit parameters (dashed lines)

As before, we examined the absorbance and fluorescence melting profiles simultaneously in terms of a three-state model and obtained the populations of the three states as a function of temperature (Figs. 5d and 6). For HP2-2AP, the low temperature transition, assigned to the interconversion between the alternate and hairpin conformations, occurred at $57.8\pm 2.0$ ${}^{\circ }$C, and the higher temperature transition, assigned to the melting of the hairpin, occurred at $75.7\pm 2.6$ ${}^{\circ }$C (Table 4). The higher temperature transition is in excellent agreement with the computational prediction; however, the low temperature transition deviates significantly from the prediction (58 ${}^{\circ }$C vs 5 ${}^{\circ }$C). The experiments indicate that the alternate structure is much more stable at low temperatures than predicted by PK3D.

One plausible explanation for this discrepancy is that at low monovalent salt conditions, such as the 50 mM KCl used in these measurements, smaller loops are in fact much more stable than predicted from entropic considerations alone, as pointed out by Kuznetsov et al in their study of ssDNA and RNA hairpins at different ionic conditions [60, 61]. This extra stability could come from intraloop stacking interactions that are not included in our model. A simple way to empirically account for this additional stability is to include a correction factor $\alpha$ multiplied to the loop entropy term $\mathrm{\Delta }{S}^{\prime }=\alpha \mathrm{\Delta }S$, such that the new $\mathrm{\Delta }{G}_B^{\prime }(x)$ is lower when $\alpha >1$. For example, when $\alpha$ is 1.25, the computed population curves of HP2 are in much better agreement with the experimentally determined population curves compared to that of $\alpha$ = 1 (Fig. 7a and b). The melting temperature of the early transition is now 40 ${}^{\circ }$C, which is closer to the experimental value of 58 ${}^{\circ }$C. This result suggests that an improved model of the loop entropy accounting for possible intraloop stacking effects will improve the accuracy of the computed thermodynamics and folding stability of RNA molecules.

Fig. 7.

The populations of the three main conformations of HP2 are plotted as a function of temperature for the hairpin (red), the alternate (cyan) and the unfolded (yellow), from (a) PK3D model computation with the correction factor $\alpha$ set to 1.25 and from (b) experiments

Heat capacity profiles of VPK

Next we compared the heat capacity profiles of the fully intact VPK pseudoknot measured previously [9] with the heat capacity computed using our method, as well as with other computational methods, including the Vienna Packages [26] and the original three interaction site (TIS) model as reported in [40]. The experimental salt condition is 1 M NaCl, which is the same as was used in the measurement of the Turner stacking enthalpy and entropy and therefore used unadjusted in our model.

The experimental data show that there are two distinct peaks in the heat capacity profiles of VPK, reflecting the loss of the tertiary structure first (at $T_{\mathrm{m}1}\sim$ 73 ${}^{\circ }$C) followed by the unfolding of any residual hairpin structures (at $T_{\mathrm{m}2}\sim 95$ ${}^{\circ }$C, Fig. 8).

Fig. 8.

Comparison of the experimentally measured (solid black) and modeled melting curves of VPK pseudoknot. The computed melting curves using TIS, ViennaRNA Package and PK3D are plotted as green dashed, blue dotted and red dot-dash lines, respectively. The salt concentration is 1 M NaCl

Results from the Vienna Package, TIS and PK3D all exhibit two peaks in the melting curves. However, the melting curve generated by our PK3D method has the best agreement with the experimental result (Fig. 8). Vienna Package fails to predict the correct melting temperatures of VPK: $T_{\mathrm{m}1}$ is incorrectly computed by Vienna Package to be 23 ${}^{\circ }$C, which is about 50 ${}^{\circ }$C lower than the experimental value. In addition, $T_{\mathrm{m}2}$, predicted to be 87 ${}^{\circ }$C, also deviates from the experimental value. TIS has much better prediction of $T_{\mathrm{m}1}$, but the $T_{\mathrm{m}2}$ value, predicted to be 89 ${}^{\circ }$C, is 6 ${}^{\circ }$C lower than the experimental result, such that the two peaks are not as clearly separated from each other as in the experiment. Furthermore, the overall shape of the melting curve is quite different from that measured in experiments, with the heat capacity value predicted at $T_{\mathrm{m}1}$ much higher than what is measured in experiment. Similar results were reported in a more recent TIS study (Fig. S15 of [42]).

In contrast, PK3D correctly describes the overall shape of the melting curve, including the locations and heights of the two peaks. $T_{\mathrm{m}1}$ in PK3D is calculated to be 73 ${}^{\circ }$C, which is the same as the experimental value. $T_{m2}$ is 92 ${}^{\circ }$C, which is only 3 ${}^{\circ }$C lower than the experimental value. The two peaks are clearly separated by $\mathrm{\Delta }{T}_m=19$ ${}^{\circ }$C. Furthermore, the heat capacity values at the two melting temperatures are similar to experimental values, in contrast to those obtained from the Vienna Package and the TIS study (Fig. 8).

Temperature dependent base-pairing probability of mouse mammary tumor virus (MMTV/VPK)

The two unfolding transitions of VPK can be easily identified by the two different transition temperatures $T_{\mathrm{m}1}$ and $T_{\mathrm{m}2}$. Course-grained (TIS) simulation studies on VPK attributed the lower temperature transition, $T_{\mathrm{m}1}$, to the loss of tertiary interactions and simultaneous unfolding of Stem 2, with the residual hairpin-loop structure containing Stem 1 unfolding at a higher temperature of $T_{\mathrm{m}2}$ [36]. The rationale was that Stem 1 in VPK is more stable, since it contains 5 C–G base pairs versus 4 in Stem 2, despite the fact that Stem 2 is longer (Fig. 1). Thus, these studies concluded that VPK folds by a hierarchical mechanism, albeit via parallel pathways [36], with the partitioning between the two pathways modulated by ionic strength changes [42]. Here, we take a more nuanced look at the unfolding thermodynamics, as discussed below.

Detailed inference about the unfolding mechanism can be drawn from the distribution of base-pairing probability obtained in our study (Fig. 9). Specifically, we found that two base pairs (8U-33A and 13U-28G) in the two ends of Stem 2 start to unfold at a low temperature of $\sim$30 ${}^{\circ }$C. As the temperature increases, Stem 1 becomes partially unfolded at about $T=55$ ${}^{\circ }$C. Three base pairs (1G-19C, 2G-18C and 3C-17G) in Stem 1 melt before unfolding of the remaining part of Stem 2. These three base pairs unfold before the other two base pairs in Stem 1. These conclusions are consistent with the fact that 3G-17C pair in the wild type MMTV is replaced by the 3C-17G pair in VPK. The disruption of the G-rich tracks in the wild type sequence makes Stem 1 in VPK not as stable as the wild type MMTV [62]. At $T=73$ ${}^{\circ }$C, the remaining four G-C and C-G base pairs in Stem 2 are also disrupted, which corresponds to the first transition peak at $T_{\mathrm{m}1}$. Stem 2 is not yet fully unfolded prior to the breaking of Stem 1. Both stems become partially melted and co-exist during the unfolding process. As the temperature increases further, Stem 1 eventually becomes fully disrupted, with the two base pairs 4G-16C and 5C-15G melted at $T_{\mathrm{m}2}$, which is the transition temperature observed in the experiment. The whole pseudoknot become fully unfolded when the temperature is higher than 105 ${}^{\circ }$C.

Fig. 9.

The plot for the pairing probabilities of base pairs of the VPK pseudoknot at different temperatures. Each curve represents a base pair, e.g. 1-19 stands for the base pair formed by first nucleotide 1G and the 19th nucleotide 19C. The structural changes of VPK at increasing temperature are shown as schematic diagrams. The melting base pairs at different temperatures are circled sequentially with increasing temperature

3D structures of mouse mammary tumor virus (MMTV/VPK)

PK3D correctly predicts the secondary structure of the lowest energy conformation of VPK. Furthermore, it is capable of generating three-dimensional native-like conformations, which are very similar to the experimentally solved structure. The root-mean-square deviation (RMSD) of all atoms of the non-loop regions is 3.9 Å upon superposition to the pdb structure (1rnk) (Fig. 10a). The spatial arrangement of stems and loops is overall similar to that of the native structure. PK3D also explicitly modeled the loops of RNA molecules in a coarse-grained fashion, where nucleotides in the loop region are represented by the P and the C${}_4$ atoms. The predicted structure with loops of VPK is shown in Fig. 10b. As the loops are represented by P and C${}_4$ atoms, only C${}_4$ atoms are used for calculating the RMSD of predicted structure to the native structure with loops. The RMSD of C${}_4$ atoms is 5.6 Å. This coarse-grained three-dimensional conformation of VPK can serve as a good starting point for further structural refinement.

Fig. 10.

Predicted 3D structure of VPK. (a) Predicted 3D structure of VPK stems without loops. (b) Predicted 3D structure of VPK with loops. The lowest energy conformation predicted by PK3D (cyan) is superimposed on the native structure (pdb 1rnk) colored in purple. The predicted P and C4 atoms in loops are shown in space-filling spheres

Discussion

In this paper, we studied the thermodynamic properties of pseudoknotted RNA molecule VPK and its constituent hairpins by generating spatial arrangements of structural elements of the RNA molecules. In addition, we incorporated conformational entropy of loops, which is essential for investigating folding thermodynamics of pseudoknotted RNAs [28, 34]. The RNA loops are explicitly constructed using a six-state discrete model and a variant of loop closure method CSJD [49, 51, 52]. With this approach, we uncovered alternative conformations accessible to even the simple hairpin structures for the subsequences of VPK, with these alternate structures more stable at low temperatures. We further accurately predicted the thermodynamics of hairpin unfolding, with our predictions validated by quantitative agreement with experiments performed on these hairpins.

Importantly, our approach enabled us to also predict the heat capacity profiles of VPK pseudoknot. The predicted thermodynamics of VPK is in excellent agreement with available experimental data. Our method provides a significant improvement in the prediction of VPK thermodynamics compared with results obtained using other methods.

We also made predictions on the unfolding mechanisms of pseudoknots by analyzing the distribution of base pairing probability. The results reveal cooperative unfolding instead of a simple sequential unfolding mechanism. Specifically, while Stem 1 is generally more stable than Stem 2, Stem 2 is not fully unfolded prior to the breaking of Stem 1. Both stems become partially melted and co-exist during the thermal unfolding process. Overall, these results give us a better understanding of how RNA molecules fold and help to illustrate the principles of sequence dependent folding mechanisms for pseudoknotted RNA molecules. As our methodology is general, we expect this method can be applied to study thermodynamics of more complex pseudoknotted RNAs.

PK3D can also generate three-dimensional conformations of RNA pseudoknots with explicitly modeled loop regions. The nucleotides in loop regions are represented by P and C${}_4$ atoms in a coarse-grained fashion. The arrangement of stems and loops in three-dimensional space is generally similar to that of the native structure. This coarse-grained three-dimensional model provides a close-to-native physical structure, which is useful as a starting point for further structural refinement.

There are limitations with our method. While our loop entropy calculation worked well for the VPK pseudoknot, there were discrepancies in modeling the low temperature alternative-to-hairpin transitions for both HP1 and HP2 subsequences. In the case of HP2, a correction in the loop entropy computation helped bridge this discrepancy in part. As it is difficult to determine a priori which type of correction to loop entropy needs to be applied, a better way to improve the estimation of the loop configurational entropy than an ad-hoc adjustment is to calculate the loop entropy of a specific problem based on explicitly modeled ensembles of loop conformations with the surrounding environment, with additional consideration of intra-loop interactions. As the P and $C_4$ atoms in the loop region are explicitly considered in our method, it is possible to calculate loop entropy and predict thermodynamics of RNA molecules with more accuracy.

Another challenge is the difficulty in modeling base triple tertiary interactions accurately using the current method for complex RNA structures. Accurate prediction for the base triple interactions requires an atomistic description of the RNA structure. Therefore, this model needs to be improved, e.g., by including more complete atomic coordinates for the regions of the structure involved in the tertiary interaction. Yet another limitation of the current method is the finite size constraint of long sequences, since the computation time is determined by the sizes of the RNA molecules, especially the total length of loops. However, this issue may be resolved by dividing the secondary structures link graph into several smaller segments or domains. With this simplification, the algorithm can be applied to larger and more complex RNA pseudoknots.

Supplementary information

Below is the link to the electronic supplementary material.

Funding Information

This work was supported by grants from the National Institutes of Health (R35 GM127084) to J.L. and National Science Foundation (MCB-1158217 and MCB-1715649) to A.A.

Declarations

Conflict of interest statement

None declared.