Unifying Coarse-grained Force Fields for Folded and Disordered Proteins

Abstract

Liquid-liquid phase separation drives the formation of biological condensates that play essential roles in transcriptional regulation and signal sensing. Computational modeling could provide high-resolution structural characterizations of these condensates and help uncover physicochemical interactions that dictate their stability. However, many protein molecules involved in phase separation often contain multiple ordered domains connected with flexible, structureless linkers. Simulating such proteins necessitates force fields with consistent accuracy for both folded and disordered proteins. We provide a critical review of existing coarse-grained force fields for disordered proteins and highlight the challenges in their application to folded proteins. After discussing existing algorithms for force field parameterization, we propose an optimization strategy that should lead to computer models with improved transferability across protein types.

Introduction

Proteins perform the majority of tasks within the cell. Their proper functions were believed to depend crucially on maintaining unique and stable three-dimensional (3D) structures. The structure-function relationship has led to significant efforts in studying the protein folding problem. Yet, recent studies suggest that a considerable fraction of eukaryotic proteomes is disordered [1, 2]. These intrinsically disordered proteins (IDPs) challenge traditional concepts of the structure-function relationship since their native states do not correspond to unique structures, but consist of an ensemble of heterogeneous conformations [3, 4]. The structural heterogeneity and disorderness could be of functional importance. They may be advantageous for multivalent interactions and mediating the formation of biological condensates through liquid-liquid phase separation [5–7].

The lack of well-defined 3D conformations for IDPs has made their structural characterization difficult. Techniques such as Förster resonance energy transfer (FRET), and small-angle X-ray scattering (SAXS), while offering valuable insights into the conformational ensemble, could not resolve the structural heterogeneity with atomic resolution. The experimental challenges in describing IDPs make computational modeling an attractive alternative. However, many existing force fields were optimized for ordered proteins and struggle to capture the size and flexibility of IDPs [8, 9]. As such, numerous groups have revised existing force fields or created new ones to ensure their accuracy in modeling IDPs [10–16].

Despite the progress in force field development, state-of-the-art computer models still face challenges describing folded and disordered proteins with consistent accuracy. As the same 20 amino acids encode both protein types, it should be possible, in principle, to create a unified force field for their modeling. Such a force field will enjoy a wide variety of applications. It would allow more accurate characterization of the stability of folded and misfolded structures to study disordered proteins that fold upon binding to a partner. In addition, it will enable simulations of proteins that include ordered regions separated by flexible, disordered linkers, a feature commonly seen in those that drive the formation of membraneless organelles.

In this review, we track the progress toward developing force fields applicable to both folded and disordered proteins. We review existing force fields for simulating IDPs, with a focus on coarse-grained models. We highlight the inherent difficulty for applying force fields optimized for IDPs to study folded proteins or vice versa due to their distinct compositional bias. Force field parameterization algorithms, including both top-down and bottom-up approaches, are then discussed in the context of their applicability for ensuring consistent performance for both protein types. Finally, we discuss an optimization strategy that emphasizes the inclusion of folded and disordered proteins in training set to help improve force field transferability.

Coarse-grained Force Fields for Disordered Proteins

All-atom force fields have been rather successful at studying protein folding and predicting protein structures. Improvements made in the torsion potentials and nonbonded interactions further allowed their application to disordered proteins, as discussed in several recent reviews [14–16]. However, conformational sampling, which is crucial for disordered proteins, can be computationally challenging for single proteins and may become prohibitively costly for studying the aggregation of multiple proteins. Therefore, there is broad interest in developing coarse-grained force fields for simulating IDPs.

Coarse-grained explicit solvent models could strike a good balance between accuracy and efficiency. The MARTINI force field follows a four-to-one mapping strategy to represent four heavy atoms with a single coarse-grained bead and has been used to study the phase behavior of IDPs [17–20]. However, achieving quantitative accuracy often requires further fine-tuning the force field [18–20], including strengthening protein-water interactions or weakening protein-protein interactions. A similarly coarse-grained force field, SIRAH, was introduced by Pantano and coworkers [21]. Unlike MARTINI, SIRAH avoids using artificial constraints to fix secondary structures and could, in principle, predict protein structures de novo. Its well-balanced secondary structure potentials succeed in stabilizing the crystal structure of folded proteins [21] and reproducing the conformational flexibility of IDPs [22].

Numerous groups have also made progress in developing coarse-grained implicit solvent models, which are highly efficient and ideal for large-scale aggregation and phase separation simulations. AWSEM-IDP [23] utilizes the framework from the Associative Memory, Water Mediated, Structure, and Energy Model (AWSEM) introduced by Wolynes and coworkers [24]. To model IDPs, Wu et al. reduced the strength of secondary structure terms and introduced biasing potentials on the radius of gyration (R_g), the value of which can be obtained from SAXS experiments or all-atom simulations. Baul et al. [25] introduced the self-organized polymer (SOP) coarse-grained model for IDPs by weakening the interaction potential among amino acids from the original SOP model [26]. SOP-IDP succeeded at resolving the sequence-specific heterogeneity between Aβ40 and Aβ42 [27]. Mioduszewski et al. [28] introduced a pseudo-improper dihedral potential to capture backbone and side-chain interactions in a one-bead-per-residue model for IDPs.

The hydrophobicity scale (HPS) model describes the interactions among amino acids with a simplified treatment of electrostatic energy and a short-range contact potential parameterized based on amino acid hydrophobicity [29]. It has been successfully applied to study the liquid-liquid phase separation of low complexity domains [30]. This model has been improved recently to capture temperature-dependent effects on solvent-mediated interactions [31], to account for cation-π interactions [32], and to better reproduce IDP radius of gyrations [33–35]. Latham and Zhang parameterized MOFF-IDP by introducing correctional contact potentials derived from SAXS data to the HPS model [36]. They showed that MOFF-IDP can reproduce R_g for a set of IDPs and succeed at de novo predictions, including the conformational change upon phosphorylation [37].

The various implicit solvent models differ in their resolutions and efficiency, and are suited for investigating different problems. For example, AWSEM-IDP brings along all the benefits of the original model, which uses three beads to represent each amino acid. In particular, AWSEM adopts a sophisticated energy function with many-body potentials and was shown to predict protein structures [24] and protein-protein binding interfaces [38] well. On the other hand, AWSEM-IDP is also computationally more expensive than HPS and related models using only one bead per amino acid. The difference in efficiency can be substantial when simulating large systems, rendering HPS and related models more appealing for phase separation studies.

Inconsistency between Folded and Disordered Protein Force Fields

It’s worth noting that the coarse-grained IDP force fields, in general, are not applicable to globular proteins. Many of the force fields were introduced for studying large-scale simulations of liquid-liquid phase separation and used somewhat simplified representations, with only one or two beads for the amino acids. The models were not expected to predict tertiary structures of folded proteins with high accuracy at this resolution. However, many of the force fields also over-predict the radius of gyration for globular proteins, indicating too weakened interactions among amino acids (Figure 1A). Similar effects are seen in force fields parameterized for folded proteins, which are often not transferable to IDPs and tend to predict overly collapsed structures (Figure 1B).

Figure 1:

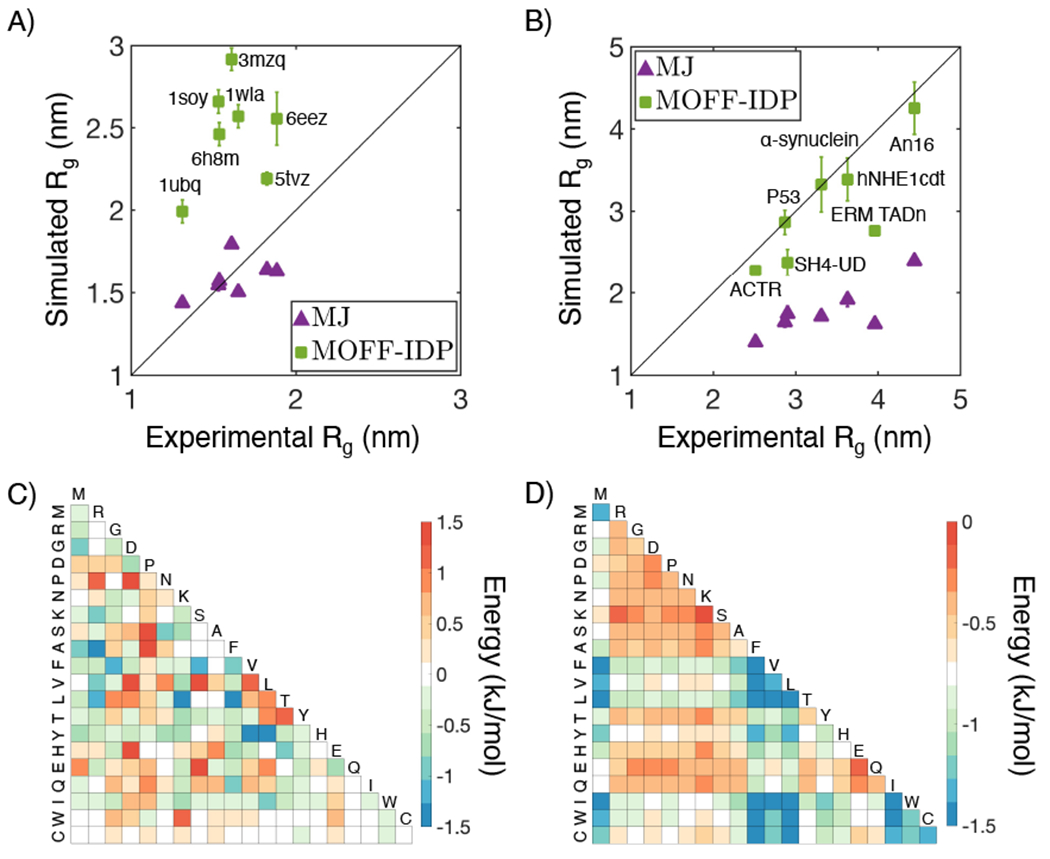
Existing coarse-grained protein force fields are often limited to either folded or disordered proteins, but not both. For example, MJ performs well on folded (A) but not disordered (B) proteins. The opposite trend can be seen for MOFF-IDP, an IDP force field introduced in Ref. [36]. The interaction matrices between amino acids for the two force fields are shown in parts C (MOFF-IDP) and D (MJ). The energy function for MJ can be found in Ref. [39], and interactions among amino acids are based on a scaled Miyazawa-Jernigan (MJ) potential by a factor of 0.6.

The inconsistency between force fields for folded and disordered proteins is not unique to coarse-grained models. All-atom force fields suffer similar issues. Significant efforts have been devoted to reparameterize the existing force fields to improve their accuracy at modeling disordered proteins [14–16]. However, as pointed out by Shaw and coworkers [40], many atomistic force fields still struggle at achieving consistent accuracy for modeling the size and secondary structure propensities for disordered proteins and the tertiary structures of folded proteins.

The difficulty in parameterizing force fields with consistent accuracy for both protein types can be partly attributed to their distinct sequence composition. Many IDPs are depleted of hydrophobic residues, which promote collapse and folding of globular proteins [41]. Instead, they favor stretches of polar, uncharged residues. Such motifs prevent secondary structure formation but may still drive protein compaction into structureless globules due to the favorable self-solvation [42]. Alternatively, some IDPs possess a higher frequency of charged amino acids and leverage the overall charge composition and patterning for their structural features [43]. Because of the lack of overlap in the sequence space, there is no guarantee that force fields parameterized primarily on one type of protein will be transferable to the other.

Algorithms for Coarse-grained Force Field Parameterization

Could one live with two sets of force fields for folded and disordered proteins, respectively? While intellectually less satisfying, such a solution could still be of practical use. The answer is, unfortunately, no. A survey on human proteins has revealed that a considerable amount of residues (30%) were found to be disordered for a significant fraction (24%) of proteins [42]. Therefore, many proteins contain a mixture of domains with distinct structural features and cannot be classified into the binary category of folded or disordered. To study such proteins, force fields that provide consistent treatment for both protein types must be introduced. Algorithms developed for optimizing force fields of globular proteins [8, 9], which we group into top-down and bottom-up approaches, offer inspirations on how one might achieve such consistency.

Top-down approaches rely on experimental data for force field parameterization. For ordered proteins, the large set of high-resolution structures resolved by X-ray crystallography provide a valuable resource. In addition, the energy landscape theory for protein folding [44–46] offers critical insight into the interactions among amino acids. For a protein to fold reliably into the native state or the crystal structure, the contacts found in the native state must be stronger than the ones found in unfolded or non-native conformations. This constraint is often described as the folding temperature (T _f) to be higher than the glass transition temperature (T_g), or pictorially, the funneled energy landscape [47]. Numerous algorithms have been introduced to parameterize coarse-grained force fields that satisfy constraints from the energy landscape theory, including optimization of the ratio T_f/T_g [48], Z-score optimization [49], maximizing the energy gap between the native and non-native conformation [50], etc.

Bottom-up approaches typically start with an ensemble of structures collected from all-atom simulations, and differ in the specific properties of the ensemble used for force field parameterization. For example, iterative Boltzmann inversion (IBI) [51], and inverse Monte Carlo [52] approaches attempt to match radial distribution functions (RDF) between pairs of particles computed from coarse-grained and atomistic simulations. We note that the ideal target property to be reproduced should be the probability distribution of the coarse-grained structural ensemble. The RDF corresponds to a lower-dimensional projection of this distribution. Due to the loss of information upon projection, even a perfect reproduction of RDF does not guarantee an accurate approximation of the original, high-dimensional conformational distribution [53]. The force matching method [54–56] aims to reproduce the forces acting on coarse-grained sites estimated from the atomistic structural ensemble. Shell introduced the relative entropy algorithm to minimize entropy loss upon coarse-graining [57]. Both methods strive to improve the agreement between conformation distributions estimated from coarse-grained and all-atom models.

Machine learning based methods have gained popularity in recent years [58]. In particular, neural networks provide flexible fitting of complex functions and are ideal for parameterizing high dimensional free energy surfaces and probability distributions from mean forces [59, 60]. Recently, Wang et al. introduced the CGnets method to directly parameterize coarse-grained models [61, 62]. CGnets was shown to out-perform traditional force matching methods in reproducing crucial features of the free energy surface. Alternatively, the free energy surface can be accurately represented by deep generative models, as shown by Noé et al. [63] and others [64–66]. Deep generative models do not require mean forces, and directly parameterize the probability distributions using conformations collected from MD simulations via maximum likelihood optimization. We note that current studies on machine learning based methods have mainly focused on parameterizing system-specific models. Additional work is needed to demonstrate their usefulness for deriving transferable force fields.

Strategy for Deriving Unified Force Fields with Consistent Accuracy

The use of experimental data to benchmark force fields as in top-down approaches could help ensure their transferability. Vitalis and Pappu introduced ABSINTH, an atomistic implicit solvent model that describes the solvation free energy using a combination of a direct mean-field interaction (DMFI) and the screening of polar interactions [67]. Parameters of ABSINTH were chosen to stabilize the folded states of two small proteins and reproduce NMR coupling constants and the polymeric properties of intrinsically disordered peptides. More recently, the force field has been updated with improved dihedral angles [68] and used to study proteins that undergo liquid-liquid phase separation [69]. Ferrie and Petersson introduced a reweighting scheme to switch fragment memory libraries between the two sets that reproduce secondary structure propensities for folded and disordered proteins, respectively [70]. When implemented into Rosetta Modeling Suite, the authors showed that the platform now performs well for predicting the structures for a list of folded and disordered proteins.

Since modern force fields often consist of a large set of parameters, a manual, systematic search of the entire parameter space can be challenging and even infeasible for a large set of experimental data. In that regard, bottom-up methods mentioned in the previous section are advantageous to enable near-autonomous force field optimization. Using a similar functional form as in ABSINTH for the solvation free energy, Bottaro et al. carried out systematic optimizations of parameters in the potential to match explicit solvent simulation data for an α–helical peptide and the GB1 hairpin [71]. They found that the resulting force field, EEF1-SB, performs well for unstructured proteins with an increased sampling of expanded conformations while maintaining the native structure of several folded proteins.

Combining top-down and bottom-up approaches may lead to new force field optimization strategies that are particularly helpful at ensuring the consistency between folded and disordered proteins (Figure 2). For example, as in bottom-up approaches, the coarse-grained force field could be parameterized using data collected from all-atom simulations. As all-atom force fields themselves have not yet achieved the desired accuracy, it is crucial to curate the simulated structural ensemble with experimental data, for example, via maximum entropy optimization [72–78]. Since the dataset would inevitably be finite, it is helpful to enforce constraints based on the energy landscape theory for ordered proteins as in top-down approaches to reduce the parameter space further and improve the robustness of force field optimization.

Figure 2:

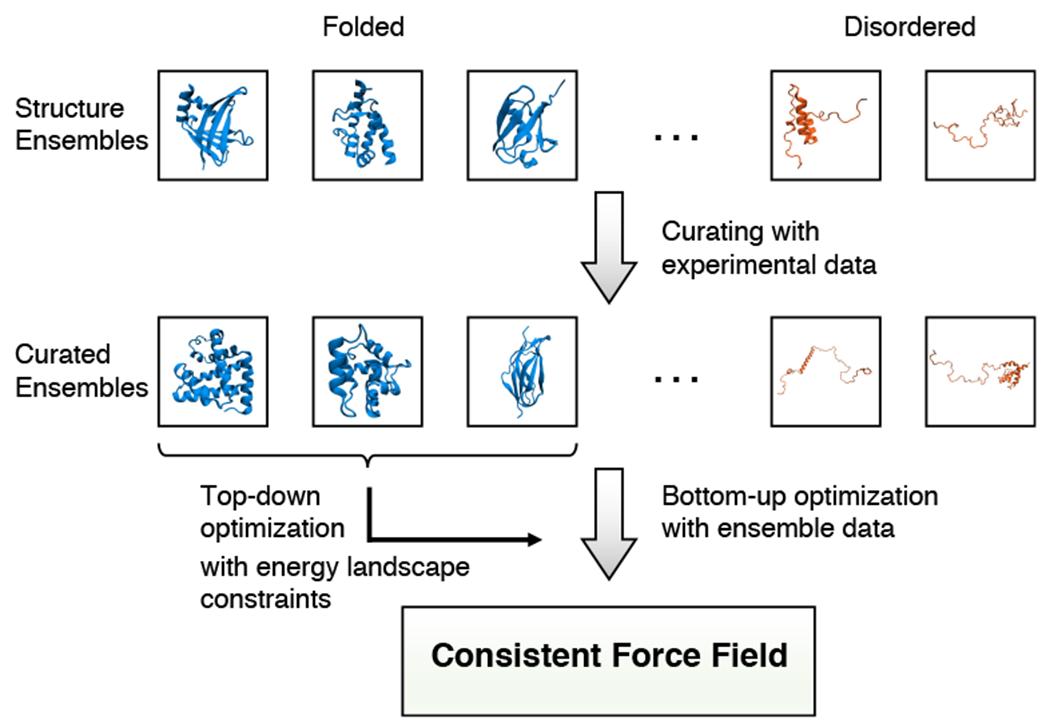
Illustration of the optimization strategy that combines top-down and bottom-up approaches to derive force fields with consistent accuracy. The training data used for parameter optimization consist of structure ensembles collected for a list of folded and disordered proteins. Ideally, the ensembles should be generated from atomistic simulations and further curated with experimental data. Bottom-up approaches such as energy matching or relative entropy minimization can be used to derive coarse-grained force field parameters that best approximate the conformational distribution of each protein. Importantly, top-down approaches can be introduced as additional constraints to enforce lower energy of the native state for folded proteins.

The optimization strategy introduced by Latham and Zhang offers some hints on how to combine different approaches in practice [39]. They constructed the reference structural ensembles using a coarse-grained model parameterized with the Miyazawa-Jernigan (MJ) potential. The ensembles, which included seven folded and sixteen disordered proteins, were corrected with SAXS data to ensure that the simulated R_g of different proteins match experimental values. Force field parameters were then tuned to reproduce the relative energy, and therefore, the probability density of individual conformations. The particular energy matching scheme introduced by the authors allowed them to ensure that the native states of folded proteins are lower in energy than the unfolded configurations. The resulting force field, termed MOFF, was shown to be transferable across folded and disordered proteins in predicting protein sizes (Figure 3). In favorable cases, the model succeeded in folding globular proteins to their native states.

Figure 3:

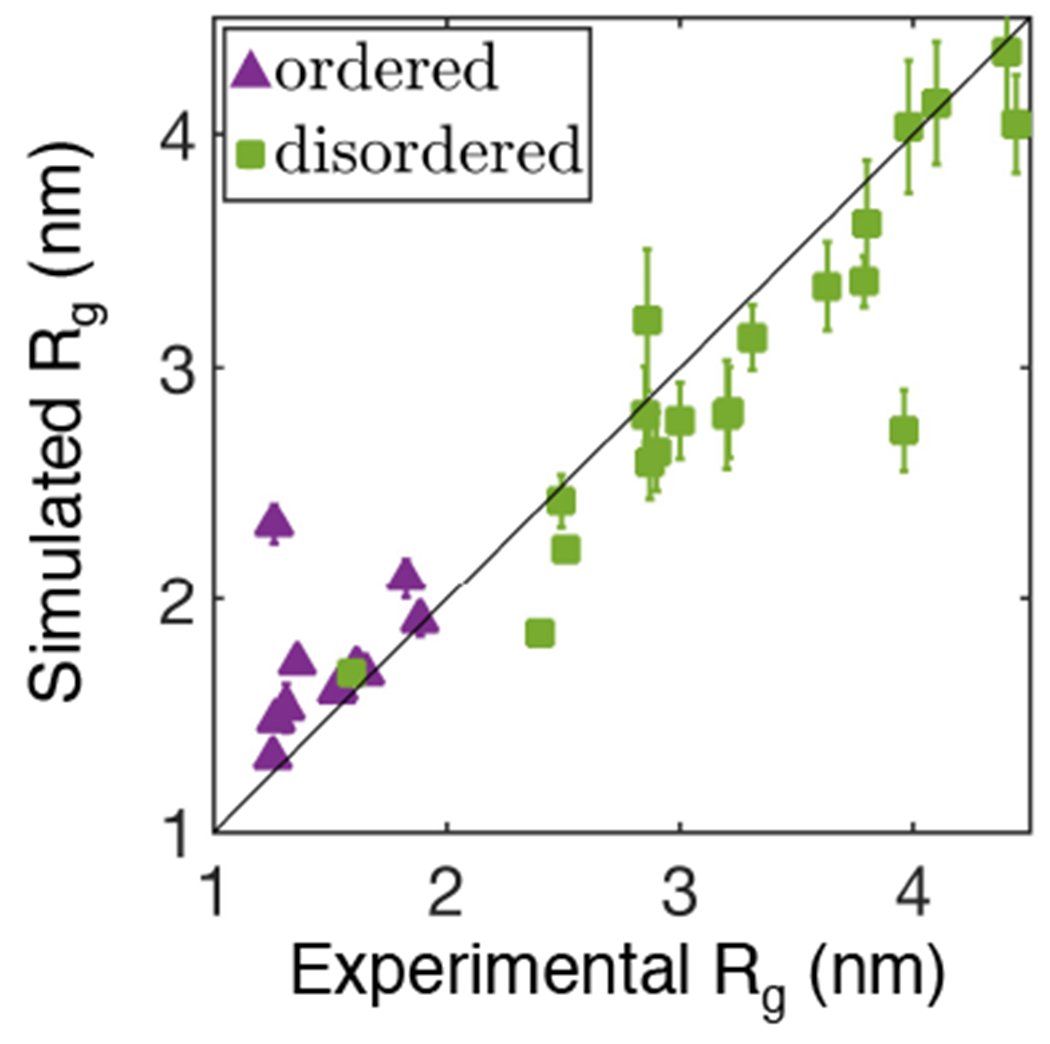
The force field introduced by Latham and Zhang in Ref. [39], MOFF, achieves consistent accuracy in predicting the size of both ordered (purple) and disordered (green) proteins.

Generalizing the Latham and Zhang strategy to structural ensembles built from all-atom simulations requires additional research. In particular, since the free energies of protein structures from all-atom simulations are unknown, their energy-matching approach cannot be directly applied. One can, in principle, use the relative entropy minimization approach to derive coarse-grained force fields. However, its computational overhead may become too costly, especially when a large list of proteins is included in building structural ensembles.