Cortical control of striatal fast-spiking interneuron synchrony

Abstract

Inhibitory fast-spiking interneurons in the dorsal striatum regulate actions and action strategies, including habits. Fast-spiking interneurons are widely believed to synchronize their firing due to the electrical synapses formed between these neurons. However, neuronal modeling data suggest convergent cortical input may also drive synchrony in fast-spiking interneuron networks. To better understand how fast-spiking interneuron synchrony arises, we performed dual whole-cell patch clamp electrophysiology experiments to inform a simple Bayesian network modeling cortico-fast-spiking interneuron circuitry. Dual whole-cell patch clamp electrophysiology revealed that while responsivity to corticostriatal input activation was high in fast-spiking interneurons, few of these neurons exhibited electrical coupling in adult mice. In simulations of a cortico-fast-spiking interneuron network informed by these data, the degree of glutamatergic cortical convergence onto fast-spiking interneurons significantly increased fast-spiking interneuron synchronization while manipulations of electrical coupling between these neurons exerted relatively little impact. These results suggest that the primary source of functional coordination of fast-spiking interneuron activity in adulthood arises from convergent corticostriatal input activation.

Graphical Abstract

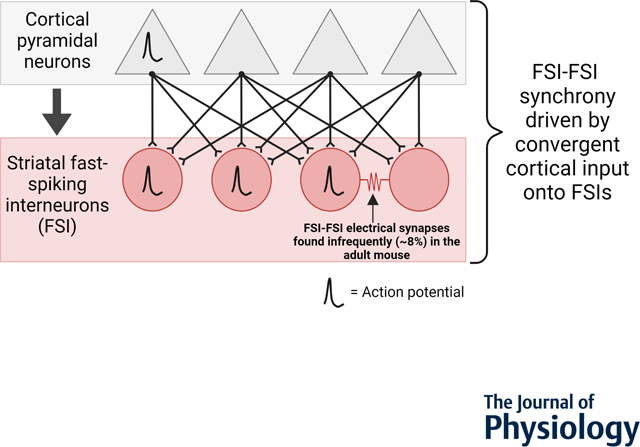
Dual whole-cell patch clamp recordings of dorsal striatal fast-spiking interneurons (FSIs; red circles) rarely (8 percentage) form electrical synapses with other FSIs in adult mouse. In a two-layer in silico model of cortical pyramidal neuron (gray triangles) input to FSIs using empirically defined cortico-FSI synaptic weights, synchronous FSI-FSI activity (in the absence of abundant electrical synapses) is achievable by convergent cortical pyramidal excitation of FSIs.

Introduction

The dorsal striatum is the entry point for the processing of cortical information by the basal ganglia, which regulates action learning and control (Gerfen and Surmeier, 2011; Klaus et al. 2019). The dorsolateral region of the striatum (DLS) is required for automatizing actions (Yin and Knowlton, 2006). Drugs of abuse, including alcohol, target the DLS to facilitate habit learning (Hopf et al., 2010; Lesscher et al., 2010; Corbit et al., 2012; Depoy et al., 2013) and the extent of habitual decision making predicts relapse in alcohol-dependent individuals (Sebold et al., 2014; Duka, 2017; Sebold et al. 2017). This underscores the role of the DLS (putamen in humans) in addiction. Given that alcohol modulates excitatory input to the striatum from the cortex (Cui et al., 2011; Depoy et al., 2013; Ma et al., 2018; Munoz et al., 2018), understanding how the DLS processes excitatory cortical input is critical for devising strategies to curb compulsive alcohol use.

A defining feature of the DLS is the enrichment of GABAergic, parvalbumin expressing fast-spiking interneurons (FSIs; Kita et al., 1990; Kawaguchi, 1993). While FSIs represent only ∼1% of the total striatal neuronal population (Luk and Sadicot, 2001), they are targeted by alcohol and other psychoactive drugs (Wiltschko et al., 2010; Blomeley et al., 2011; Patton et al., 2016), causally linked to habitual responding for sucrose (O’Hare et al., 2017), and required for compulsive ethanol consumption (Patton et al., 2020). FSIs are driven to fire action potentials primarily by cortical glutamatergic input (Gittis et al., 2010). Upon cortical activation, FSIs provide potent inhibitory, GABAergic control over neighboring medium spiny projection neurons (MSNs), thus forming a feedforward inhibitory microcircuit governing striatal output (Kita et al., 1990; Bennett and Bolam, 1994; Koos and Tepper, 1999; Tepper et al., 2004; Mallet et al., 2005).

FSIs functionally organize as ensembles in adult animals (Roberts et al., 2019). The ability of FSIs to co-activate enhances their modulation of striatal output through temporal summation, and is largely thought to be enabled by FSI-FSI electrical coupling (Koos and Tepper, 1999; Lau et al., 2010; Zhang et al., 2014). Dual electrophysiological recordings of FSIs in juvenile acute brain slices show that the electrical synapse connection rate between FSIs is roughly 30% (Koos and Tepper, 1999). Removal of electrical synapses between FSIs in a striatal network model assuming a similar electrical synaptic connectivity rate significantly alters the balanced firing of MSN subpopulations, providing in silico evidence for a functional role of FSI-FSI connectivity (Damodaran et al., 2014). However, connexin-36, the pore forming protein enabling electrical coupling between FSIs (Cummings et al., 2008), declines in expression throughout development into adulthood (Bruzzone et al., 1996; Belluardo et al., 2000). This suggests that electrical coupling concomitantly declines into adulthood. Yet, exploration of FSI-FSI electrical coupling and other regulators of FSI-FSI synchrony in adulthood is lacking.

Computational network modeling - using adolescent FSI-FSI electrical coupling rates - suggests that FSI-FSI coupling may actually decrease FSI firing, but this effect is abolished under conditions of coincident cortical input onto electrically coupled FSIs (Hjorth et al., 2009). This would suggest that FSIs are sensitive detectors to synchronized input from the cortex. Considering the anatomical findings that demonstrate broad areas of cortex converge onto FSIs, while focal areas of cortex synapse onto MSNs (Ramanathan et al., 2002), we herein further explore in silico how convergent cortical input onto FSIs contributes to FSI synchrony using adult mouse cortico-FSI chemical and FSI-FSI electrical synaptic properties derived experimentally ex vivo. We find that FSIs exhibit high responsivity to cortical input and rarely electrically couple in adult mouse brain slices. Applying these data to a computational model, we provide evidence that increasing the convergence of cortical input onto FSIs drives FSI-FSI synchrony more reliably than FSI-FSI electrical synapses. This provides a possible means by which FSIs synchronize in the face of decreasing FSI-FSI electrical coupling in adulthood.

Methods

Ethical Approval.

All procedures were performed in accordance with the United States Public Health Service Guide on Humane Care and Use of Laboratory Animals and were approved by the Institutional Animal Care and Use Committee at the University of Maryland School of Medicine. All animal procedures used in this study are compliant with the ethical principles of the Journal of Physiology.

Animals.

Mice were housed with littermates (2–5 per cage) under a 12-hr light/dark cycle (lights on at 0700 hours, off at 1900 hours) with ad libitum access to food and water. To enable visualization of parvalbumin-expressing FSIs for electrophysiological recordings, Pvalb-cre (Tanahira et al., 2009) mice were crossed with tdTomato reporter mice (Ai9(RCL-tdT); The Jackson Laboratory) to generate “Pv-tdT” mice. This allowed for selective expression of tdTomato fluorophore in cre-recombinase-expressing neurons (Pvalb-cre x floxedTdTomato; “Pv-tdT”; Madisen et al., 2010). Both male and female Pv-tdT mice were on a C57BL/6 background and aged 6–36 weeks old at the time of surgery.

Stereotaxic surgery and viral vectors.

At the time of surgery, mice were continuously anesthetized with isoflurane (induction 5%; maintenance 1–2%) and placed into a stereotaxic frame (David Kopf Instruments). A heating pad was used to maintain body temperature and mineral oil was applied to the eyes. Carprofen (5 mg/kg) was injected subcutaneously for analgesia. Breathing rate of the mice was monitored and toe pinches were delivered throughout the duration of the surgical procedure to ensure mice were properly anesthetized. To target cortical afferents into the striatum for optogenetic stimulation in acute slices, 250 nL of viral construct expressing channelrhodopsin and enhanced yellow fluorophore protein under the human synapsin 1 gene promoter (AAV5-hSyn-ChR2-eYFP; UPenn) was pressure injected into the primary (+1.78 mm AP, ±1.2 mm ML from bregma, −0.8 mm DV from brain surface) and secondary motor cortices (+1.18 mm AP, ±1.25 mm ML from bregma, −0.75 mm DV from brain surface) of Pv-tdT mice using a 0.5 µL Hamilton syringe. Following bilateral viral injections, the scalps were sutured with aliphatic polymers monofilament Blue nonabsorbable suture and the mice were singly housed in cages for 3 days of recovery. During the first day of recovery, lidocaine was applied to the head wound and carprofen (5 mg/kg) was administered subcutaneously. Carprofen (5 mg/kg) was administered for another two days of recovery before mice were rehoused with their cagemates.

Acute slice preparation for whole-cell patch-clamp electrophysiology.

Following >6 weeks post viral transfection surgery, Pv-tdT mice expressing ChR2 in the primary and secondary motor cortices were deeply anesthetized with isoflurane (vaporized, 5%). Their heads were decapitated and their brains were immediately extracted and submerged in 95% oxygen, 5% carbon dioxide (carbogen)-bubbled ice cold cutting solution (in mM: 194  sucrose, 30  NaCl, 4.5  KCl, 1  MgCl₂, 26  NaHCO₃, 1.2  NaH₂PO₄, and 10  D-glucose). Extracted brains were sliced at 250 μm with a vibratome (Leica VT 1200) and transferred to carbogen-bubbled artificial cerebrospinal fluid (aCSF; in mM: 124 NaCl, 4.5 KCl, 2 CaCl₂, 1 MgCl₂, 26 NaHCO₃, 1.2 NaH₂PO₄, and 10 D-glucose). No GABAA receptor blockers were included in the aCSF. Brain slices containing the DLS were incubated at 32.4 °C for 30 min before they were removed and stored at room temperature until recordings were performed. For mice over four months old, a modified critical protective recovery slicing protocol was used (Ting et al., 2014; Ting et al., 2018): following deep anesthesia with isoflurane (vaporized, 5%), mice were transcardially perfused with a high N-methyl-D-glucamine (NMDG) aCSF solution (in mM: 92 NMDG, 2.5 KCl, 1.25 NaH₂PO₄, 30 NaHCO₃, 20 HEPES, 25 glucose, 0.5 CaCl₂, 10 MgCl₂, pH=7.2–7.4, 300–310 mOsm). Following rapid decapitation, brains were removed and then sliced at 250 μm in this NMDG-containing aCSF and incubated at 33 °C for 12 minutes before being transferred to a 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES)-containing aCSF solution for the remainder of the day (in mM: 92 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 30 NaHCO₃, 20 HEPES, 25 glucose, 2 CaCl₂, 2 MgCl₂, pH 7.2–7.4, 300–310 mOsm).

To record, brain slices were hemisected, and transferred to a recording bath where they were perfused throughout recording with carbogen-bubbled aCSF (29–31 °C) via gravity perfusion. tdT-positive FSIs in the dorsal striatum were visualized and targeted for whole cell current clamp recordings through the epifluorescent light path illuminated by a mercury bulb lamp (X-Cite series 120Q). All whole-cell experiments were recorded using borosilicate glass pipettes (resistances ranging from 2–5MΩ) filled with a potassium-based internal solution (in mM: 126 K-Gluconate, 4 KCl, 10 HEPES, 4 ATP-Mg, 0.3 GTP-Na, and 10 Phosphocreatine; osmolarity ranging from 290–295 mOsm; pH 7.3). Cells were voltage (−60 mV) or current clamped using a MultiClamp 700B amplifier (Molecular Devices) and Clampex 10.4.1.4 software (Molecular Devices) was used for data acquisition. All recordings were filtered at 2 kHz and digitized at 10 kHz.

Electrical coupling between FSIs was determined by injecting current steps into one of a pair of FSIs and observing whether the FSI not receiving a current injection depolarized. FSI and MSN maximum firing rate was determined by increasing current step injections into the cells. Resting membrane potentials were recorded after correcting for the liquid junction potential (15.7 mV) as per the Nernst-Planck equation (Barry, 1994; Marino et al. 2014). Action potential thresholds were determined by injecting a gradual ramp of current into cells and recording the voltage at which they first detonated an action potential. The probability “P” of an FSI or MSN firing in response to cortical input was calculated at a variety of frequencies (1, 10, 20 Hz) by averaging the number of FSI or MSN action potentials elicited by 10 pulses of blue light (4 ms pulse width, 470 nm) over the course of 10 sweeps. To control for viral expression differences between animals, action potential firing fraction values were averaged across animals and statistical significance between cell types was determined by an unpaired t test. For all experimental groups, n is defined as individual neurons recorded from multiple in vitro brain slices from at least 4 mice.

Drugs.

All reagents for slice electrophysiology cutting and recording solutions were purchased from Sigma-Aldrich. All drugs were purchased from Tocris Bioscience.

Computational Model:

The model consists of two basic parameters. The first parameter is the number of FSI neurons in the circuit, which is manually defined by n. Each FSI received the same number of inputs, which is defined by the number of FSIs, (i.e. if there are 10 FSIs, each FSI received input from 10 cortical neurons). The second parameter is the value of “convergence”. Convergence was defined as the number of independent cortical neurons that target a given FSI. We quantified the percent of convergence as:

$$C\mathrm{\%}=\frac{(n^2-c)}{n(n-1)}$$ (1)

Where n is the number of FSIs in the circuit and c is the number of cortical neurons in the circuit. Cortical connectivity was determined randomly for simulations where the percent convergence ranged between 0% and 100%, but controlled so that no FSI received multiple inputs from the same cortical neuron. Following determination of the percent convergence and cortico-FSI connectivity, we then determined the number of lateral, electrical synaptic connections shared between FSIs. This was defined by the equation:

$$\lambda =\frac{x}{n^2-n}$$ (2)

Where λ is the rate of lateral connections, x is the total number of lateral connections, and n is the number of FSIs in the circuit. Determination of which FSIs shared lateral connections was random, and each connection was treated as bidirectional.

In the cortical layer, cortical neurons possessed an action potential firing probability of 0.005, which was kept homogeneous across all neurons to maintain a low baseline firing rate of roughly 5 Hz. The likelihood of an FSI firing an action potential was defined by the following equation:

$$p\left(FS{I}_n\right)\left(i, t\right)=\frac{p_{max}- p_0}{n}i+ \frac{p\left(FS{I}_n\right)\left(i, \left(t-1\right)\right)}{\tau }+\Sigma cc*p{\left(FS{I}_{gap}\right)}_n$$ (3)

Where $p_{max}$ is the likelihood of an FSI to fire given all inputs are active; this was determined experimentally to be 0.7 from slice electrophysiology data (see Results). $p_0$ is defined as the likelihood an FSI fires an action potential given no synaptic input onto the FSI, which is equivalent to the baseline firing rate. i is the number of cortical neurons that fired onto an individual FSI. This generated a linear tuning curve in response to increasing cortical stimulation. We approximated FSI dependence on cortical input as a line based off slice electrophysiology findings (see Results). $p\left({FSI}_n\right)\left(i, \left(t-1\right)\right)$ is the probability of firing in the previous time bin, decayed by a rate of $\tau$, which was modelled based off the average $\tau$ for FSIs from our electrophysiology findings (see Results). cc is the coupling coefficient, or the strength of lateral electrical synaptic connections, between FSIs. This was determined experimentally to be 0.03 on average (see Results). Lastly, ${p\left(FS{I}_{gap}\right)}_n$ is the firing probability of the n^th FSI connected to the FSI of interest. This term when multiplied by the coupling coefficient and summed across all FSIs that are electrically connected with the FSI of interest defines how electrically connected FSIs influence one another during the time interval. This equation was also kept uniform across FSIs, and each parameter was kept constant. Both cortical neurons and FSIs had an absolute refractory period of 1 ms.

Each simulation consisted of a 1s trial with each sampling bin size being 1ms. Individual trials either received synchronous input or did not, depending on the experiment. For simulations with synchronous input, we increased the probability of cortical neuron firing to approximately 1 at a frequency of 10Hz. Thus, at 50ms, 150ms, 250ms, 350ms, 450ms, 550ms, 650ms, 750ms, 850ms, and 950ms the probability of a cortical neuron to fire became 1, thereby generating synchronous input onto the FSIs. We deem this an approximation as in some instances these time intervals were timed with a cortical neuron’s refractory period.

To assess the network for synchrony, we calculated the cross correlation for each neuron and then averaged this across the population. This was repeated 20 times with a new network, where any random parameters were redrawn. To control for changes in neural firing, neural spike trains were shuffled and the cross-correlation of the shuffled spike trains was subtracted out (Damadoran et al., 2014). Additionally, to confirm that values chosen for these simulations were not biasing our interpretation we performed several parameter scans of relevant parameters that would influence FSI firing. Parameter scans were done by simulating a single network structure, where all connectivity had been determined and kept the same across simulations, then relevant parameters were varied. Following the simulations cross-correlations were calculated and values at 0s lag, when synchrony will be at its maximum were plotted.

Results

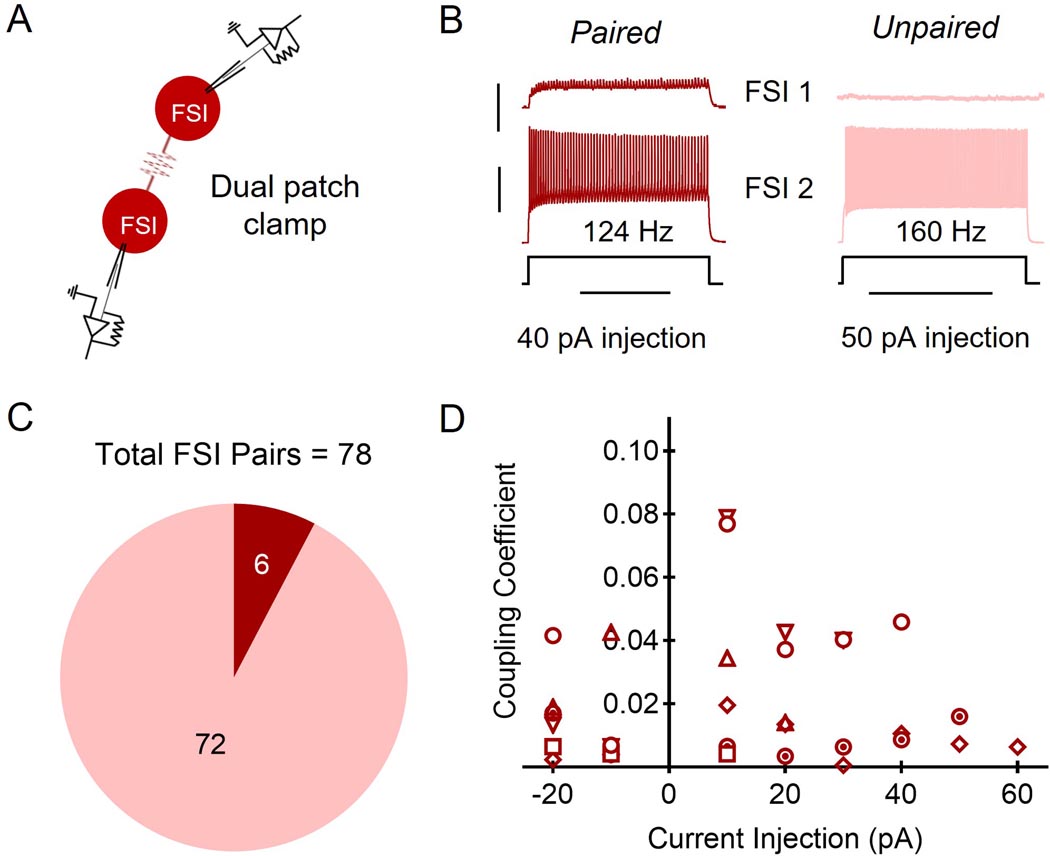
We performed dual current-clamp recordings of FSIs expressing a fluorescent reporter that were no more than 200 µm apart from n = 78 pairs and found that only ∼8% (n = 6) of FSI pairs exhibited electrical coupling (Fig. 1a, b, and c). The strength of these connections as measured by their coupling coefficients ranged from 0.0006 to 0.0789 (Fig. 1d). The highest value for current injection per cell pair varied depending on when the maximum firing rate was achieved. We did not observe any evidence of chemical synaptic transmission between FSIs.

Figure 1. Fast-spiking interneuron (FSI) electrical coupling.

A: Schematic of dual FSI recordings. B: Representative traces of paired and unpaired FSI paired recording responses to current injection into one FSI (FSI 2 in schematic). Current injection magnitude listed per FSI pair refers to last injection before FSI 2 was too depolarized to elicit an action potential. Scale bars: 5 mV (red trace)/30 mV (black trace), 1 s. C: 6 of 78 FSI pairs were electrically coupled (red) while 72 of 78 pairs were detectably un-paired (pink). D: Coupling coefficients for each FSI pair in the scatterplot. Each symbol is representative of a pair of FSIs (six symbols for six pairs).

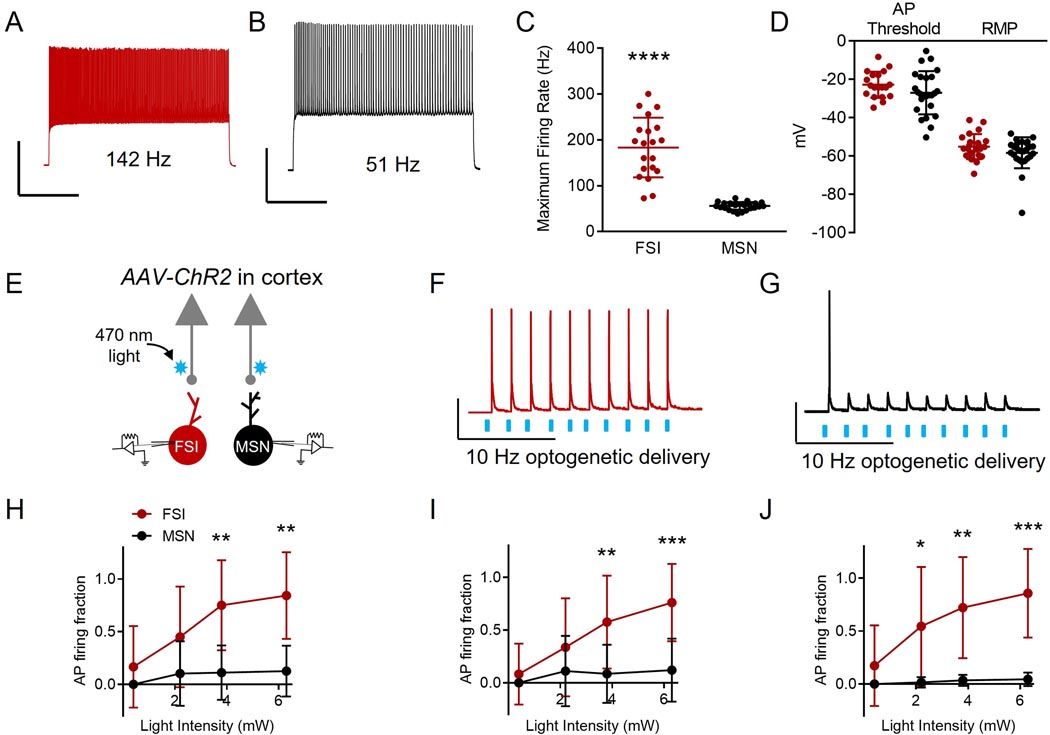
Next, we gathered empirical corticostriatal synaptic data in order to inform our subsequent network modeling methodology. Because we sought to understand whether increasing the frequency of convergent cortical input onto FSIs may drive their coordinated firing, we calculated the probability “P” of an FSI firing in response to cortical input at a variety of frequencies (1, 10, 20 Hz) across 10 sweeps. Primary and secondary motor cortices (M1 and M2, respectively) directly innervate both FSIs and MSNs (Ramanathan et al., 2002). FSIs are thought to synchronize their activity in vivo, while MSNs are not (O’Hare et al., 2017). Thus, we compared cortical input onto FSIs versus MSNs. To do this, we performed dual whole cell patch clamp recordings of FSIs and MSNs while activating M1/M2 input optogenetically. To distinguish between FSIs and MSNs, we utilized maximum firing rate as a measure (Fig. 2a and b). Consistent with known differences between the cell types, FSIs demonstrated a higher firing rate compared to MSNs (Fig. 2c; maximum firing rate in Hz for MSNs: 55.95 ± 8.372, for FSIs: 183.30 ± 65.01; n= 20 MSNs, n = 24 FSIs; t = 9.53, p < 0.0001; unpaired t test). To ensure healthy cellular recordings for both FSIs and MSNs, we measured resting membrane potentials (RMPs; Fig 2d; in mV for MSNs: −51.480 ± 29.2, for FSIs: −55.14 ± 6.521; n= 26 MSNs, n = 23 FSIs; t = 0.587, p = 0.560; unpaired t test) and action potential (AP) thresholds (Fig 2d; in mV for MSNs: −27.10 ± 11.27, for FSIs: −22.84 ± 6.806; n = 25 MSNs and n = 20 FSIs; t = 1.454, p = 0.153; unpaired t test), with a correction of 15.7 mV for liquid junction potential, and found that neither of which were statistically different. We found that FSI AP discharge followed an M1/M2 cortical afferent optogenetic 10 Hz light pulse train more faithfully than MSN AP firing across several light intensities (Fig. 2e - h; AP firing fraction for MSNs at 0.4 mW: 0.0 ± 0.0, for FSIs: 0.17 ± 0.39, n = 13 MSNs, n = 12 FSIs, p > 0.999; AP firing fraction for MSNs at 2.2 mW: 0.10 ± 0.31, for FSIs: 0.45 ± 0.15, n = 9 MSNs, n = 10 FSIs, p = 0.142; AP firing fraction for MSNs at 3.8 mW: 0.13 ± 0.24, for FSIs: 0.84 ± 0.41, n = 13 MSNs, n = 12 FSIs, p = 0.005; AP firing fraction for MSNs at 6.3 mW: 0.13 ± 0.24, for FSIs: 0.84 ± 0.41, n = 13 MSNs, n = 12 FSIs, p = 0.002; Kruskal-Wallis ANOVA). This effect was also observed with other light pulse frequencies, including 1 Hz (Fig. 2i; AP firing fraction of MSNs at 0.4 mW: 0.0 ± 0.0, for FSIs: 0.08 ± 0.29, n = 13 MSNs, n = 12 FSIs, p > 0.999; AP firing fraction for MSNs at 2.2 mW: 0.11 ± 0.33, for FSIs: 0.34 ± 0.47, n = 9 MSNs, n = 12 FSIs, p = 0.202; AP firing fraction for MSNs at 3.8 mW: 0.09 ± 0.28, for FSIs: 0.58 ± 0.44, n = 13 MSNs, n = 12 FSIs, p = 0.009; AP firing fraction for MSNs at 6.3 mW: 0.12 ± 0.30, for FSIs: 0.76 ± 0.37, n = 13 MSNs, n = 12 FSIs, p = 0.001; Kruskal-Wallis ANOVA) and 20 Hz (Fig. 2j; AP firing fraction of MSNs at 0.4 mW: 0.0 ± 0.0, for FSIs: 0.17 ± 0.38, n = 13 MSNs, n = 12 FSIs, p = 0.678; AP firing fraction for MSNs at 2.2 mW: 0.02 ± 0.05, for FSIs: 0.55 ± 0.56, n = 9 MSNs, n = 10 FSIs, p = 0.018; AP firing fraction for MSNs at 3.8 mW: 0.04 ± 0.05, for FSIs: 0.72 ± 0.48, n = 13 MSNs, n = 12 FSIs, p = 0.006; AP firing fraction for MSNs at 6.3 mW: 0.05 ± 0.06, for FSIs: 0.86 ± 0.42, n = 13 MSNs, n = 12 FSIs, p = 0.001; Kruskal-Wallis ANOVA).

Figure 2. FSI and medium spiny projection neuron (MSN) action potential (AP) firing in response to corticostriatal activation.

A: Representative trace of the firing rate of an FSI (red) in response to a current injection of 40 pA. Scale bars: 40 mV, 500 ms. B: Representative trace of the firing rate of an MSN (black) in response to a current injection of 40 pA. Scale bars: 40 mV, 500 ms. C: FSIs (n = 24) demonstrate a faster maximum firing rate compared to MSNs (n = 20 cells). **** p < 0.0001, as per unpaired t test. All data represented as mean + SD. D: Action potential (AP) thresholds and resting membrane potentials (RMP) are not significantly different for MSNs (AP threshold n = 25 cells; RMP n = 26 cells) and FSIs (AP threshold n = 20 cells, RMP n = 23 cells). Voltage values are corrected for liquid junction potential (15.7 mV). AP threshold p = 0.153 and RMP p = 0.560, as per unpaired t test. Data are represented as mean + SD. E: Schematic of dual FSI and MSN recordings while optogenetically activating corticostriatal inputs. F: Representative trace of dual current clamp recordings from FSIs in response to 470 nm 10 Hz optogenetic stimulation (AAV-ChR2) of cortical inputs. Scale bars: 30 mV, 10 ms. G: Representative trace of dual current clamp recordings from MSNs in response to 470 nm 10 Hz optogenetic stimulation (AAV-ChR2) of cortical inputs. Scale bars: 30 mv, 10 ms. H: The fraction of 470 nm 10 Hz light pulses that elicited APs for FSIs is not significantly greater than for MSNs at light intensities of 0.4 (n = 13 MSNs, n = 12 FSIs; p > 0.999) or 2.2 mW (n = 9 MSNs, n = 10 FSIs; p = 0.142), but is significantly greater for FSIs than for MSNs at light intensities of 3.8 (n = 13 MSNs, n = 12 FSIs; **p = 0.005) and 6.3 mW (n = 13 MSNs, n = 12 FSIs; **p = 0.002). Statistical values were determined using Kruskal-Wallis ANOVA. Data represented as mean + SD. I: The AP firing fraction of FSIs in response to 1 Hz 470 nm light pulses is not significantly greater than MSNs at 0.4 (n = 13 MSNs, n = 12 FSIs; p > 0.999) or 2.2 mW (n = 9 MSNs, n = 10 FSIs; p = 0.202), but is significantly greater for FSIs than for MSNs at 3.8 (n = 13 MSNs, n = 12 FSIs; **p = 0.009) and 6.3 mW (n = 13 MSNs, n = 12 FSIs; ***p = 0.001) light intensities. Statistical values were determined using Kruskal-Wallis ANOVA. Data represented as mean + SD. J: The fraction of 20 Hz 470 nm light pulses that elicited APs in FSIs is not significantly higher than for MSNs at 0.4 mW (n = 13 MSNs, n = 12 FSIs; p = 0.678), but is significantly higher for FSIs than for MSNs at 2.2 (n = 9 MSNs, n = 10 FSIs; *p = 0.018), 3.8 (n = 13 MSNs, n = 12 FSIs; **p = 0.006) and 6.3 mW (n = 13 MSNs, n = 12 FSIs; ***p = 0.001) intensities. Statistical values were determined using Kruskal-Wallis ANOVA. Data represented as mean + SD.

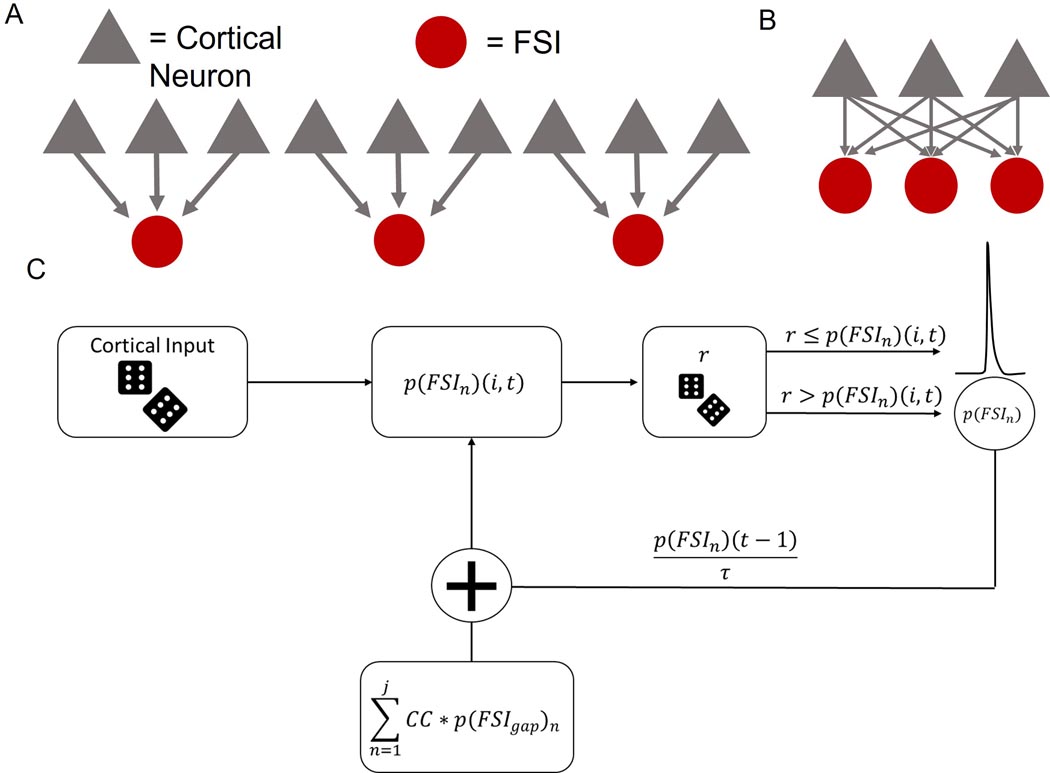
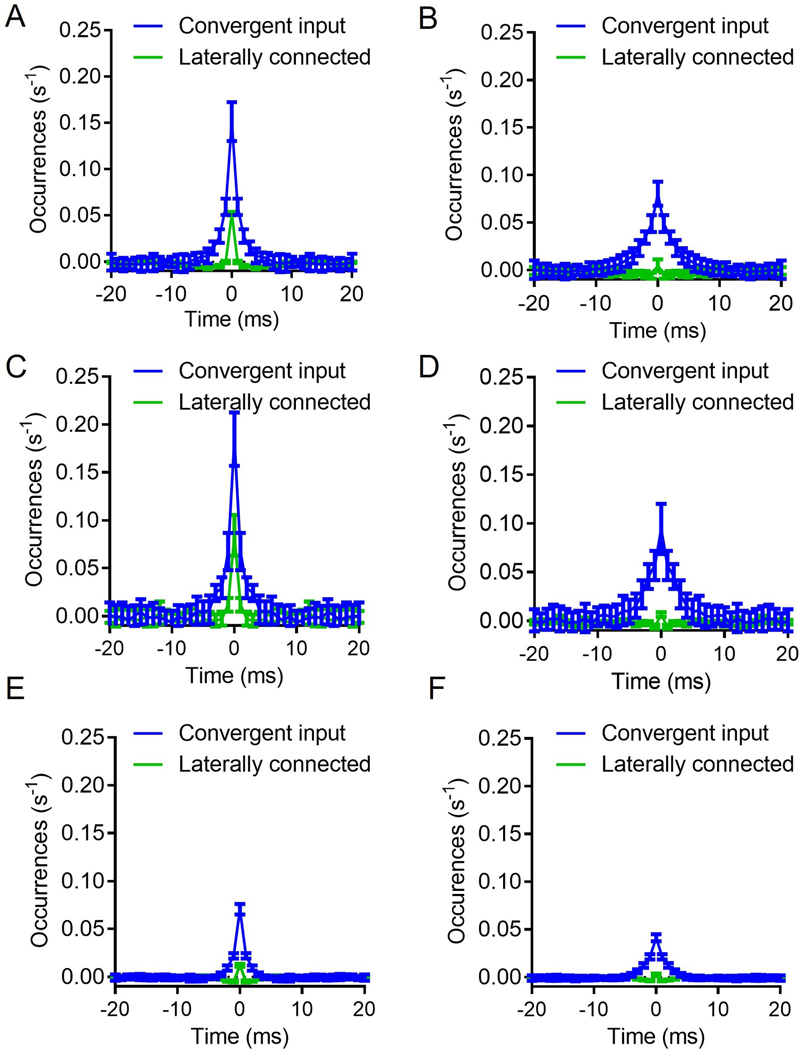
To further investigate the role of FSI-FSI electrical synapse connectivity on FSI synchrony using our experimentally-derived empirical data, we generated a simple probabilistic neural circuit with two layers: (i) an independent cortical layer and (ii) a layer of FSI neurons dependent on cortical and FSI input (Fig. 3; see Methods for details). Fig. 3a and b display the two extremes for an example case of 3 FSIs, whereby Fig. 3a shows 0% convergence, and Fig. 3b depicts 100% convergence. Simulations of this model, depicted in the flow diagram represented in Fig. 3c, show that FSIs exhibit more synchronous activity under the cortically convergent model than the FSI-FSI laterally electrical synapse connected model whether cortical input is synchronous or asynchronous (Fig. 4). With an n = 10 FSIs, the convergent model shows increased synchrony as assessed by the number of coincidently detected FSI-FSI action potential firing occurrences compared to the laterally connected model, regardless of whether cortical input was synchronous (Fig. 4a) or asynchronous (Fig. 4b). However, peak occurrences were higher in FSIs in the convergent model with synchronous input compared to asynchronous input. We repeated this for n = 5 (Fig. 4c and d) and n = 50 (Fig. 4e and f). When input was synchronous, FSIs exhibited lower occurrences in the lateral model compared to the convergent model (Fig. 4a, c, and e). When input was asynchronous, FSIs again exhibited lower occurrences in the laterally connected model compared to the convergent model (Fig. 4b, d, and f). In the simulations with synchronous input, both the convergent model and the laterally connected model exhibited peak occurences in the cross correlegram at 0 ms. This effect has been observed in previous models and is an artifact when the input is itself synchronous (Damadoran et al., 2014). Although the parameters used for these simulations were informed from our experimental results, we performed a series of parameter scans calculating the synchrony at the 0s lag, to explore whether or not parameter values varied the interpretation of our results (fig 5). Across each of the parameters tested, we found no cases in which the laterally connected model had larger synchrony than the convergent model. In figures 5B and 5D as we approach 0 the synchrony appears to approach infinity, this is due to the low firing of FSIs during these conditions and MATLABs xcorr function will disproportionately weigh them as more synchronous.

Figure 3. Model architecture and simulation flow.

A. A completely independent network has a number of cortical neurons (gray triangles) equal to the number of FSIs (red circles) squared. B. A completely convergent network has as many cortical neurons as FSI neurons. C. Cortical activity is drawn independently and randomly on each time bin. Then, the downstream FSI integrated the number of inputs it received to determine the likelihood to fire an action potential. To simulate neural variability, random noise is added by drawing a number from a distribution to determine if the neuron fired an action potential or it did not. If the neuron did fire, it then entered a refractory period. If the neuron did not fire an action potential, the probability to fire is stored and decayed by the time constant (τ) for the next iteration.

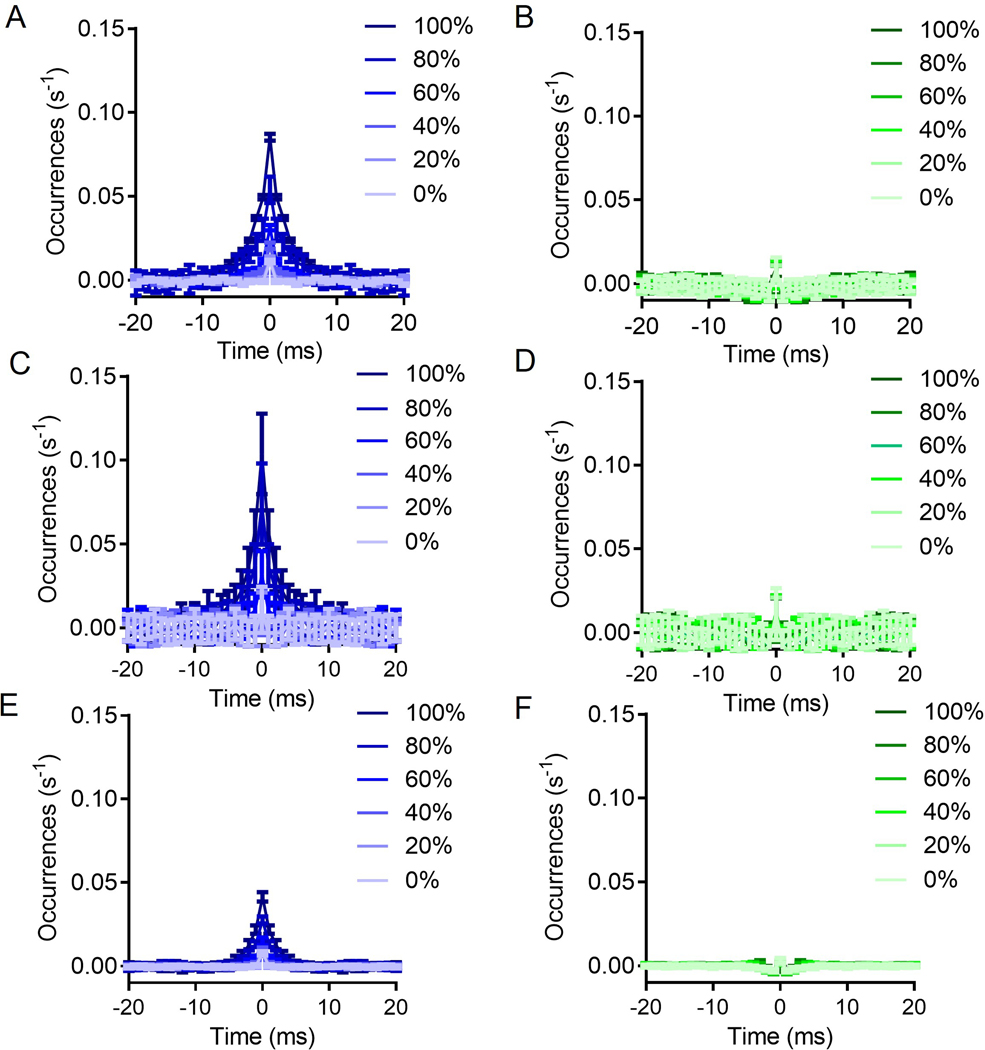
Figure 4: Simulations reveal that convergent cortical input induces higher levels of FSI-FSI synchrony compared to electrical synapse FSI-FSI connections.

A. Convergent input shows higher FSI synchrony in the presence of synchronous input, n =10 FSIs. B. Convergent input generates synchrony among FSIs in the absence of synchronous input, n =10 FSIs. C and D. Same as A and B, but instead n = 5. E and F. Same as A and B, but instead n = 50. Each condition was simulated 20 times. Data represented as mean +/− SD.

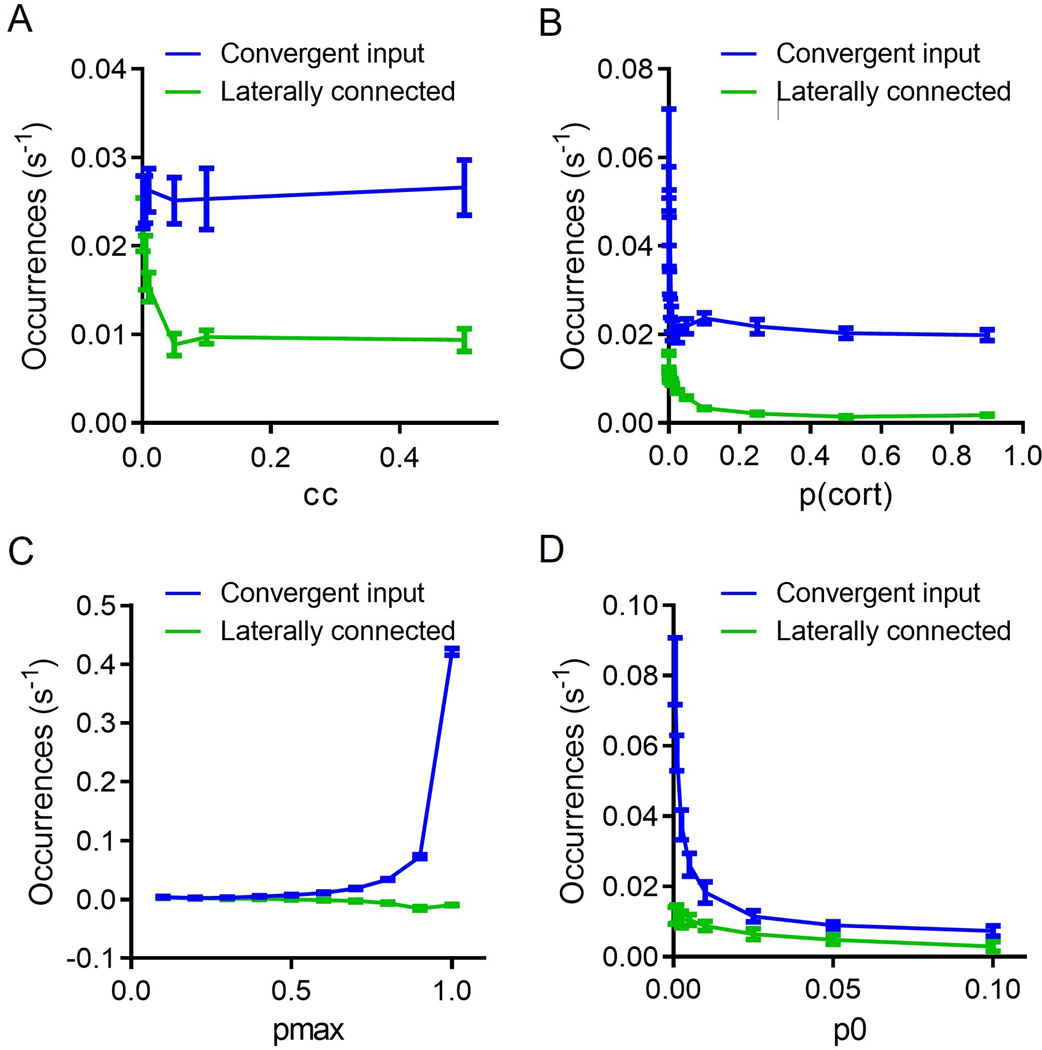
Figure 5: Parameter scans show larger synchrony in a convergent input than laterally connected.

A) Changing the coupling coefficient (CC) results in a decline in synchrony for the laterally connected model. B) Changing the probability of cortical neurons to fire (p_cort) shows a decline in synchrony with increasing cortical firing. C) Increasing the probability to fire if all inputs have been activated (pmax), results in increasing synchrony for the convergent model but not changes to the laterally connected model. D) Increasing the baseline probability of an action potential (p0) results in decrease synchrony across the two models. In each of the simulations the variables were kept constant unless otherwise stated as cc = 0.03, pmax = 0.7, p0 = 0.005. Additionally, these simulations were done under the spontaneous input conditions with n = 10 FSIs. 20 trials were run for each condition. Data represented as mean +/− SD.

To further assess the role of convergent input versus FSI-FSI lateral electrical synaptic connectivity contributions to FSI synchrony (as depicted in Fig. 3b), we varied the percentage of convergence and lateral connections independently of one another and observed whether this affected FSI-FSI action potential firing event occurence (Fig. 6). Increasing the percentage of cortical convergence in the absence of any lateral connections increased observed occurences for a network of 10 FSIs (Fig. 6a). However, increasing the percentage of lateral connections between FSIs in a network that had no cortical input convergence resulted in no significant change in occurrences (Fig. 6b). We repeated these simulations with n = 5 FSIs (Fig. 6c and d) and n = 50 FSIs (Fig. 6e and 6f). These modeling data - informed by empirically derived cortico-FSI synaptic properties - suggest that convergent cortical input influences FSI synchrony to a greater extent than lateral FSI-FSI connectivity.

Figure 6. Increasing convergent cortical input increases FSI synchrony, but increasing FSI-FSI electrical synaptic connections does not.

A. Increasing the percent of cortical input convergence directly increases FSI synchrony, n = 10 FSIs B. Increasing the percent of FSI-FSI electrical synaptic connections does not increase FSI-FSI synchrony, n = 10 FSIs. C and D: Same as A and B, but instead n = 5. E and F: Same as A and B, but instead n = 50. Each condition was simulated 20 times. Data represented as mean +/− SD.

Discussion

We found that FSI-FSI electrical coupling in adult mice occurred at ∼8% of assayed pairs and that FSIs fired with greater fidelity under cortical afferent stimulation than MSNs. Using these empirical FSI-FSI connectivity and cortico-FSI synaptic strength findings to inform our neural simulations of variant cortico-FSI networks, we showed that a major source of FSI-FSI synchrony may derive from convergent cortical input, while FSI-FSI electrical synapses may provide minor contributions to bulk FSI synchrony.

Strong evidence exists for electrical synapses to promote synchronous neuronal firing in the striatum, hippocampus, cortex, neocortex, and cerebellum (Galarreta and Hestrin, 1999; Mann-Metzer and Yarom, 1999; Beierlein et al., 2000; Hormuzdi, et al., 2001; Traub et al., 2001; LeBeau et al., 2003; Pfeuty et al., 2003; Zhang et al., 2017). In cortical FSIs, however, genetic deletion of connexin-36 does not abolish synchrony among this interneuron population (Salkoff et al., 2015). This is consistent with our computational findings, which suggest that the observed sparser electrical coupling between FSIs in adulthood, as compared to adolescence, may only fine-tune synchronous FSI responses to excitatory drive from the cortex. However, in the absence of coincident cortical excitation, electrical coupling between FSIs may actually shunt current and possibly suppress FSI firing (Hjorth et al., 2009). Taken together with the findings of Hjorth and colleagues (2009), these data suggest that the ability of electrical synapses to promote FSI-FSI synchrony may not only diminish with age, but also may only do so when FSIs are receiving coincident glutamatergic barrage from convergent cortical inputs.

There are important caveats to consider with the present modeling data. First, because our model is based on the number of action potentials in response to cortical afferent activation, it does not account for the possible lateral chemical synaptic inhibition from neighboring FSIs or inhibitory input from the globus pallidus (Bevan et al., 1998; Mallet et al., 2012). Also, while cortical input into striatum is the largest source of excitatory input onto FSIs, our model does not consider excitatory inputs from other areas such as thalamic nuclei (Sciamanna et al., 2015; Klug et al., 2018; Assous and Tepper, 2019; Assous and Tepper, 2019) and the pedunculopontine nucleus (Assous et al., 2019). Second, the model assumes homogeneity of FSI morphology and response properties. This assumption was made to simplify the model for simulations to directly target the role of electrical synapses. However, FSIs may vary in their presynaptic inputs and weight distributions (Assous and Tepper, 2019). Introducing heterogeneity in cortico-FSI synaptic weights could shift the results toward heterogeneous populations of synchronized FSIs, potentially reflecting functional FSI ensembles (Roberts et al., 2019). Lastly, the simulations presented here range from 5–50 FSIs in a circuit, while it is unknown exactly how many FSIs form functional ensembles, the model is limited in how many FSIs can be included to generate interpretable results. This is due to the nature of increasing lateral electrical synapses in network models, which results in increased firing rates (Damadoran et al., 2014). That is, if the model exceeds 100 FSIs in a network the firing rates reach non-physiological firing rates (∼1000 Hz).

Electrical synapse diminishment from development to adulthood is observed elsewhere in the mammalian central nervous system (Belluardo et al., 2000; Condorelli et al., 2000). The functional significance of this is unclear. Because development is a period in which rapid, extensive action learning occurs (Watanabe et al., 2007; DePasque and Galvan, 2017), perhaps electrical synapses between striatal FSIs aid in de novo action acquisition. Interestingly, alcohol inhibits connexin 36-containing electrical synapses in adulthood (Mustonen et al., 2004; Wentlandt et al., 2004; Mustonen et al., 2005), yet facilitates habit learning (Corbit et al., 2012). The impact of decreased connexin-36 and electrical synapse numbers between FSIs on the consolidation of actions and habits into adulthood requires further exploration.

In conclusion, we find that FSI electrical synapses weakly contribute to the synchrony of striatal FSIs in adult mice while convergent, and coincident, cortical excitation significantly drives FSI-FSI synchrony. These empirical data-informed modeling results support extant modeling data (Hjorth et al., 2009) and provide further insight into the origins of FSI functional ensemble behavior, which ultimately shape MSN output (Damodaran et al., 2014; Owen et al., 2018). These findings advance our current understanding of how the DLS processes excitatory input to promote automatized action (Diaz-Hernandez et al., 2018; Kim et al., 2019; Klaus et al., 2019). Given that FSIs regulate different, specific action subcomponents by firing in ensembles (Roberts et al., 2019), it is possible that different areas of cortex converge onto specific FSI ensembles to modulate the speed, and therefore timing (Kim et al., 2019), of the specific action subcomponents they encode. This mechanism could also drive specific FSI ensembles to fire during reward learning in order to distinguish between cues (Bakhurin et al., 2016; Lee et al., 2017). Considering that FSIs are causally linked to habitual responding (O’Hare et al., 2017) and are necessary for the development of compulsive ethanol consumption (Patton et al., 2020), the present data also implicate the cortico-FSI synapse as a possible viable target for therapeutic intervention in compulsive drug and alcohol consumption.

Key Points

• Electrical synapses between striatal fast-spiking interneurons in adult mice occur in ∼8% of assayed pairs.

• Coincident, convergent cortical input onto fast-spiking interneurons significantly contributes to fast-spiking interneuron synchrony

• Electrical synapses between fast-spiking interneurons provide only minor enhancement of fast-spiking interneuron synchrony.

• These results suggest a mechanism by which adult mouse fast-spiking interneurons of the striatum synchronize in the face of declining expression of the electrical synapse-forming connexin-36 protein.

Biography