Acoustic holograms for bilateral blood-brain barrier opening in a mouse model

Abstract

Transcranial focused ultrasound (FUS) in conjunction with circulating microbubbles injection is the sole non-invasive technique that temporally and locally opens the blood-brain barrier (BBB), allowing targeted drug delivery into the central nervous system (CNS). However, single-element FUS technologies do not allow the simultaneous targeting of several brain structures with high-resolution, and multi-element devices are required to compensate the aberrations introduced by the skull. In this work, we present the first preclinical application of acoustic holograms to perform a bilateral BBB opening in two mirrored regions in mice. The system consisted of a single-element focused transducer working at 1.68 MHz, coupled to a 3D-printed acoustic hologram designed to produce two symmetric foci in anesthetized mice in vivo and, simultaneously, compensate the aberrations of the wavefront caused by the skull bones. T1-weighed MR images showed gadolinium extravasation at two symmetric quasi-spherical focal spots. By encoding time-reversed fields, holograms are capable of focusing acoustic energy with a resolution near the diffraction limit at multiple spots inside the skull of small preclinical animals. This work demonstrates the feasibility of hologram-assisted BBB opening for low-cost and highly-localized targeted drug delivery in the CNS in symmetric regions of separate hemispheres.

I. INTRODUCTION

The blood-brain barrier (BBB) restricts the perfusion of therapeutic agents into the central nervous system (CNS), limiting most treatments and the development of novel therapeutical drugs for brain diseases. Microbubble-enhanced transcranial focused ultrasound (FUS) allows the non-invasive, localized, transient and safe BBB opening, and has been demonstrated in rodents [1]–[5], non-human primates [6]–[14] and humans [15], [16], showing a high potential for the treatment of neurological diseases.

The current technology for BBB opening using ultrasound relies on small implantable intracranial transducers, single-element FUS transducers or phased-array FUS transducers. However, these conventional methods consist of targeting only at a single location at a time (single-element transducers), or are generally used to target multiple locations sequentially within a small region (phased-arrays), not being able to target a set of distant locations simultaneously at both brain hemispheres. Target structures involved in brain disorders, such as hippocampus, caudate nucleus, or putamen, are symmetric, and therefore, a simultaneous bilateral BBB opening would allow the drug to be delivered into the mirrored part of the interest brain structure as well. On the one hand, the existing methods using a single-element transducer in small animals consist of a reduced MRI-compatible mechanism which mechanically moves the transducer achieving the conventional multi-focal targeting inside the brain of the rodent [17]–[24]. This mechanical movement is a limitation because the microbubbles are rapidly diluted into the bloodstream and filtered out from the lungs and liver, therefore several injections are required to sonicate multiple distant brain regions. Furthermore, a dedicated control MRI scan is carried out for each target location ensuring that the ultrasound is focused at the desired brain region considering the skull aberration effect. Equivalently, this bilateral focusing could also be done by using two fixed single-element FUS transducers, or even a linear array by subgrouping the elements and time-delaying. However, these conventional focused beams cover large volumes relative to the size of mice brain structures. Consequently, off-target structures are covered as well, thus providing a low-resolution, non-localized procedure. Besides, the approach of using neuronavigation systems for the controlled targeting in non-human primates [13], [14] requires several injections of microbubbles as well, in case of a multi-focal or large-volume BBB opening procedure, because the mechanical movement of the transducer is a time-limiting factor. On the other hand, MRI-guided phased-array systems used in clinical trials [15], [16] have shown the ability to electronically and independently control the magnitude and phase of each piezoelectric element in order to change the focal spot location, keeping the transducer fixed in the same position during the whole sonication procedure. Despite allowing targeting of multiple locations close to each other using a unique injection of microbubbles, this high-cost technology makes it not affordable for a wide clinical use. Moreover, this aforementioned equipment is limited by the steering angle with respect to its geometric focus due to the appearance of side lobes. In addition, its controller takes time to reach the target pressure, and by then the microbubbles may have been significantly reduced in number. Nevertheless, a recent study for small animal experiments [25] demonstrates the use of a high-frequency phased-array system targeting at high-resolution focal spots separated up to 4.5 mm, while keeping a reduced grating lobe formation. Note that the more elements included, the more complex the manufacturing procedure and the higher the cost.

Recently, acoustic holograms have been proposed for FUS to overcome these cost and time limitations [26]. An acoustic hologram is a material designed to spatially modulate the phase and, in some cases, the magnitude of a transmitted wavefront to synthesize a complex acoustic field [27]–[32]. These structures allow the synthesis of acoustic images, i.e., areas where the acoustic energy is high, combined with areas were the media is at rest. The technique of coupling an acoustic holographic lens to a single-element ultrasound transducer allows the generation of pressure fields of arbitrary shape, from simple focused beams [33], [34] to multi-focal spots or acoustic images matching the focal volume with the geometry of specific CNS structures [26] or complex distributions [35]–[37], self-bending beams [26], acoustic vortex beams [38], [39] or, recently, complex cavitation patterns [40]. Moreover, acoustic holographic lenses can be designed to compensate the strong phase aberrations of the wavefront produced by the refraction and attenuation of the skull [26], [33], [39], [41]. Multi-focal acoustic holograms are a low-cost alternative to avoid the time-inefficient mechanical movement of a single-element transducer [13] or single-spot lenses [34], while providing a high-localized focusing within the brain.

Acoustic holograms have been tested in water tanks, in phantoms or using ex vivo human skulls, but to date they have not been applied in vivo to produce a therapeutic effect. In this work, we demonstrate for the first time the capability of multi-focal acoustic holographic lenses performing a high-localized bilateral BBB opening in mice (a set of n = 3 mice are tested). The proposed method consists of a bifocal acoustic hologram coupled to a single-element FUS transducer, as sketched in Fig. 1, designed to simultaneously target both hemispheres in the brain of a mouse. A passive cavitation detector was introduced to monitor the therapy. In addition to focusing simultaneously at different, distant brain areas, this lens corrects the aberrations due to the skull, the brain, the coupling system, the central hole for the imaging transducer, and takes into account the reverberation and reflections inside the head of the animal, which consequently leads to a high-resolution targeting. Using this low-cost instrumentation we demonstrate the capability, feasibility and efficiency to produce a therapeutic effect in a preclinical animal model.

Fig. 1:

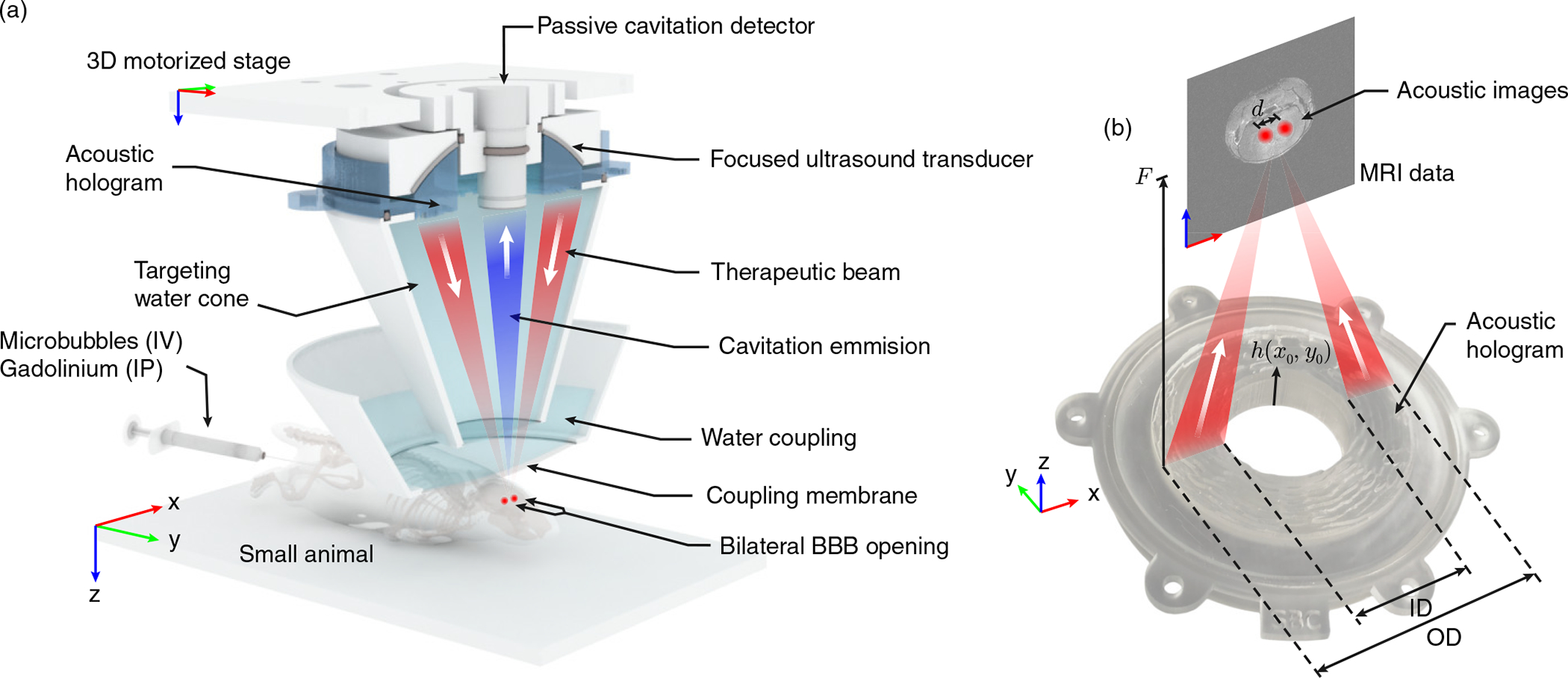
(a) Scheme of the preclinical therapeutic device using a bifocal acoustic hologram. Microbubbles were injected intravenously (IV) for the FUS delivery, while the gadolinium was injected intraperitoneally (IP) post-FUS delivery for the MRI procedure. (b) Photograph of the hologram manufactured by stereo-lithographic 3D-printing techniques using translucent resin, and geometrical parameters of the study. The thickness profile of the hologram is given by the function h(x₀, y₀).

II. METHODS

The procedure of BBB opening using a holographic lens is divided in five steps. First, we extract the geometry and acoustic properties of a separate mouse skull from X-ray μCT images, and we identify the target locations using MRI scans. Second, a plastic cone for the water coupling between the transducer and the head of the rodent is designed and 3D-printed. Third, a simulation is performed to calculate the acoustic field back-propagated from the targets to the holographic surface. This simulation includes the multiple-reflections and phase changes due to both the skull bones and the coupling cone. Fourth, the holographic acoustic lens is designed using the phase-conjugation of the back-propagated field, manufactured by using stereo-lithographic 3D-printing, and attached to a single-element FUS transducer, as shown in Fig. 1 (a–b). Fifth, microbubbles are injected to the mouse and, then, ultrasound is delivered to the mouse head while the treatment is monitored by measuring cavitation activity using a single-element passive-cavitation detector. Finally, MRI scans are carried out to assess the BBB opening.

A. Numerical simulation

We use a full-wave pseudo-spectral simulation method with k-space dispersion correction to numerically integrate the linearized constitutive relations of acoustics [42], [43]. This method is selected as it provides low numerical dispersion as compared with finite-differences methods [44]. We use an isotropic numerical grid with a spatial step of Δh = 176 μm, which corresponds to a spatial sampling of 5 grid points per wavelength in water for a frequency of 1.68 MHz, leading to simulations of more than 300-million grid points. The numerical temporal step Δt is set to 5.1 ns and 13.7 ns for the simulations with and without the head of the animal (particularly skull and brain media), respectively, leading to a Courant-Friedrichs-Lewy number of 0.2 in both configurations.

B. Mouse skull acquisition for simulation

Animal protocol AC-AAAS7407 was reviewed and initially approved on May 6th, 2017, by the Columbia University Institutional Animal Care and Use Committee (IACUC). The geometry and properties of the skull were acquired by μCT-scans (R_mCT2, Rigaku, Tokyo, Japan) from a single mouse (mass: 24 g, age: 8 weeks, sex: male, C57BL/6, Harlan, Indianapolis, IN, USA) with isotropic spatial resolution of 80×80×80 μm, extrapolated to 17 μm isotropic for the numerical simulation. It is assumed that the holographic acoustic lens designed from this single μCT-scan is capable of correcting the skull aberrations of different but similar individuals (n = 3 mice). Thereby, we can assess the reproducibility of a single lens design for several mice, as well as speed up the BBB opening procedure for all mice. The heterogeneous acoustical properties of the skull are derived converting the apparent density data, in Hounsfield units, to density and sound speed distributions using the linear-piecewise polynomials proposed in Refs. [45], [46]. The absorption of the mouse skull is assumed to be homogeneous [47]–[49] and it has been set to 28.3 dB/cm at 1.68 MHz [50] with a frequency-power law exponent of γ = 1. Afterwards, the brain volume is segmented from the cavity in the μCT-scan using the ITK-SNAP software [51]. Acoustical properties of the mouse brain are also included in the simulations, using ρ_brain = 1000 kg/m³, c_brain = 1600 m/s and an absorption coefficient of 0.7 dB/cm at 1.68 MHz [1] with γ = 1.

C. Lens design and manufacturing

The lens was designed to produce a time-reversed version of the wavefront diverging from the two target points, following the procedure described in Ref. [26] for flat transducers, modified here to be used in a focused ultrasound source. The single-element FUS transducer used was the Sonic Concepts H-204 (central frequency of 1.68 MHz, aperture of OD = 84.2 mm, internal hole diameter of ID = 43.6 mm, and radius of curvature of F₀ = 61.65 mm). First, the two targeted regions inside the brain of the mouse were transversely identified following the procedure described in Refs. [2], [3], [52], corresponding to two symmetric targets placed one in each brain hemisphere generally used for small animal models. The beam covered parts of the hippocampus, thalamus, and hypothalamus of both hemispheres. Furthermore, to demonstrate the focusing capabilities of the hologram, we selected a focusing depth for the hologram (F = 100 mm) different than the natural radius of curvature of the source (F > F₀). Then, we located a virtual monopole source in the simulation method at the center of each target. As we were using a spherically-focused transducer, the lens had to compensate the natural curvature of the wavefront. In addition, the central hole, the passive cavitation detector (PCD) used for monitoring the cavitation activity, and the plastic coupling cone would generate reflections that can be compensated by the hologram [53]. Therefore, the complete holographic information to design the lens is calculated by

$$H_L(x,y)=H_T^{*}(x,y)H_F^{*}(x,y),$$ (1)

where $H_T^{*}(x,y)$ is the complex conjugate of the recorded wavefront at the holographic surface due to the effects of the two virtual target sources, the plastic coupling cone, the skull and the brain, $H_F^{*}(x,y)$ is the complex conjugate of the recorded wavefront at the holographic surface generated by the FUS transducer, including its diffraction at the border and at the central hole where the PCD is located, (·)^∗ denotes complex conjugation, and x and y are the transversal coordinates along the holographic plane.

Then, a phase-only lens was designed using the phase of the total complex holographic information. By changing the height of the hologram h(x, y), as shown in Fig. 1 (b), the phase of the transmitted waves T(x, y) vary from 0 to 2π. The transmission at each surface point of the lens [54] is given by

$$T(x,y)=\frac{2Z_n\exp \left(-ik\left(d_0-h\right)\right)}{2Z_n\cos \left(k_{L}h\right)+i\left(Z_n^2+1\right)\sin \left(k_{L}h\right)},$$ (2)

where d₀ is the distance from the bottom of the lens (h = 0) to the holographic surface, the normalized impedance is given by Z_n = Z_L/Z₀, and Z₀ = ρ₀c₀ is the impedance of water and Z_L = ρ_Lc_L, k_L = ω/c_L, ρ_L and c_L, are the impedance, wave number, density, and sound speed of the lens material. As Eq. (2) cannot be inverted, we used an interpolation method to obtain the values of h(x, y) that produce arg(T) = arg(H_L), i.e., fitting the phase of the transmitted waves to the phase of the target hologram. As a result, we obtained the surface of the hologram for the focused ultrasound source. Both, the hologram and the coupling cone were 3D-printed using Clear-Resin, a photosensitive polymer for stereolithography using a Form 2 printer (FormLabs, Somerville, MA, USA), with a resolution of 50 μm and 100 μm in lateral and axial directions, respectively. For this material, we experimentally measured in a cylinder test piece, using pulse-echo techniques, a sound speed of c_L = 2580 m/s, a density of ρ_L = 1171 kg/m³ and an absorption of α = 4.6 dB/cm at 1.68 MHz, in agreement with the values reported in the literature [26], [27].

D. Guiding and monitoring system

The focused ultrasound transducer and the lens were confocally mounted with the Olympus V312-SU ultrasound imaging transducer (central frequency of 10 MHz, aperture of OD=6 mm, flat active element), as shown in Fig. 1 (a). This imaging device was used in pulse-echo mode to align the system at the beginning of the procedure. A metallic grid placed on top of the lambdoid suture of the skull was used as a reference, the system was aligned and, then, the grid was removed. The imaging transducer was driven by a pulser-receiver system (Panametrics, Waltham, MA, USA), which was connected to a digitizer (Gage Applied Technologies, Inc., Lachine, QC, CAN) integrated into a personal computer (PC, Dell Inc., TX, USA). The same imaging transducer was used in reception mode as a PCD during treatment to detect the cavitation activity of the microbubbles under the action of the therapeutic ultrasound field. Acoustic cavitation emissions were processed offline in MATLAB^© (The MathWorks, Natick, MA, USA).

Assuming that the PCD presents a linear response between the pressure at its surface, p(t), and the recorded voltage, V (t), the acoustic energy density, W, detected by the probe is proportional to

$$W\approx \frac{1}{T}{\int }_0^T\frac{p^2}{{\rho }_0{c}_0^2}dt~\frac{1}{T}{\int }_0^T{V}^{2}dt\approx \frac{1}{T}\sum _{t=0}^T{V}^2\mathrm{\Delta }t,$$ (3)

where V (t) is the voltage measured at each time point in Volts and Δt was the sampling period equal to 10 ns [55]. Then, frequency analysis was conducted to identify the cavitation dose at each sonication [13], [56].

E. Sonication and post-MRI procedure

For the in vivo experiment, 1 μl/g Definity (Lantheus Medical) microbubbles were injected intravenously and FUS was applied for a total of 2 minutes using a 1.68-MHz sinusoidal pulsed burst of 400 kPa peak-negative pressure (PNP), a pulse repetition frequency (PRF) of 5 Hz, and a pulse length of 1 ms. Then, 0.2 ml of gadolinium tracer was injected intraperitoneally and post-treatment in vivo BBBO was assessed using T1-weighted MRI. Mice were transferred to the MRI scanner, anesthetized with 1–2% isoflurane, placed in a 3-cm birdcage coil and scanned with a small-animal 9.4T MRI system (Bruker, Billerica, MA, USA). A contrast-enhanced T1-weighted 2D FLASH scan (TR/TE of 230/3.3 ms, flip angle of 70°, number of excitations of 18, in-plane resolution of 85 μm × 85 μm, slice thickness of 500 μm and receiver bandwidth of 50 kHz) was acquired ~30–45 min after FUS exposure, along both axial and coronal planes.

F. Cavitation signal processing

Time domain signals recorded by the PCD were used to estimate the energy and cavitation dose for each pulsed-burst sonication during the entire procedure. First, a Fast Fourier Transform (FFT) of each recorded waveform was performed. Second, three spectral areas were filtered and analyzed independently. The first region corresponds to the spectra around the n-th harmonic, given by the frequency bands nf_c −Δf ≤ f_h ≤ nf_c+Δf, where f_c = 1.68 MHz is the center frequency of the FUS transducer, n = 2, 3, …, 10 is the harmonic number and the narrow bandwidth around each harmonic component is set to Δf = 10 kHz. The fundamental frequency is ignored, due to the superposition of back-scattering and microbubble emission at this band. The second region corresponds to the spectra around the n-th ultra-harmonic, given by the frequency bands (n+1/2)f_c−Δf ≤ f_u ≤ (n+1/2)f_c +Δf. Note that the sub-harmonic (f_c/2) was not included in the calculation due to the limited bandwidth of the PCD. And the third spectral area corresponds to the broadband regions, given by the frequency band f_b, with f_h,n + Δf < f_b < f_u,n − Δf and f_u,n + Δf < f_b < f_h,n+1 − Δf. Third, cavitation doses were calculated as described before [13], [56], based on the root-mean-square voltage detected in the respective spectral areas. Harmonic stable (SCD_h), ultraharmonic stable (SCD_u) and inertial (ICD) cavitation doses were defined as

$${\text{CD}}_i=\frac{1}{N-1}\sum _{n=2}^N\sqrt{{\langle |\mathcal{F}(V){|}_{f_i}^2\rangle }_n},$$ (4)

where the index i indicates harmonic (h), ultra-harmonic (u), and broadband regions (b), to estimate SCD_h, SCD_u, and ICD, respectively, $\mathcal{F}(V)$ is the fast Fourier transform of the voltage signals V, and 〈·〉 is the average over the bands given by f_i. N = 10 bands were included. These doses were calculated for each acoustic pulse for in vivo experiments.

G. BBB opening volume quantification

Quantification was performed on the axial MRI slices for the n = 3 mice. First, the region of interest (ROI) was defined in the front left part of the brain to calculate the reference intensity for each mice and hemisphere. The threshold intensity I₀ to define BBB opening was set as the average intensity within the control ROI plus 3 standard deviations. Every axial slice was loaded sequentially, and a manual ROI was drawn within the entire hemisphere. All pixels having intensity higher than the threshold were counted to derive the BBB opening surface area in each slice. The total BBB opening volume (BBBOV, in mm³) per mouse and hemisphere was calculated by summing the BBB opening surface areas across all hemisphere slices and then multiplying by the slice thickness. Finally, the contrast enhancement (CE, in %) was calculated by dividing the mean intensity within the BBB opening areas by the mean intensity of the control ROI. To statistically compare the BBBOV and CE between right and left brain hemispheres, we used the Wilcoxon rank sum test [57], [58], where statistical significance was assumed at p < 0.05. BBBOV and CE results are presented as mean ± standard deviation, unless otherwise stated.

III. RESULTS

The results of this study are divided in two stages. First, we performed a calibration of the system designing a bifocal hologram in water. The pressure-field distribution was experimentally measured (see Appendix I) and compared to simulations. In this way, we assessed the accuracy of the method without biological tissues and we obtained the input electrical signal parameters to achieve 400 kPa-PNP at the two foci in water. Second, we designed a new lens to compensate the aberrations due to the coupling cone, skull and brain. We simulated the sonication through the head of the mouse to assess the focusing quality and to estimate the attenuation of the ultrasound beam. Thus, by amplifying the input electrical signal accordingly, we proceeded to the sonication of the anesthetized animal and, finally, the BBB opening was evaluated using T1-weighted magnetic resonance imaging.

A. System calibration

A bifocal hologram was firstly designed for calibration in water. This lens splits the single focus of the FUS transducer into two foci, in addition to shifting the focal distance from 61 mm to 100 mm. Fig. 2 shows the simulated pressure-field distribution compared to the acoustic measurements in the water tank. The pressure-field distribution results are shown as PNP normalized to p_PNP, the maximum rarefaction amplitude detected within the focal region. The elements forming the setup, i.e., the FUS transducer, lens and coupling cone, are shown in Fig. 2 (a) as continuous-white line contours. The energy is concentrated on the focal distance 100 mm, where two spots are visible in the simulations and measurements. Experimental axial pressure-field distribution is in agreement with simulation (see Fig. 2 (a), insets). Experimental transverse patterns, shown in Fig. 2 (c), also are in agreement with numerical predictions, shown in Fig. 2 (b). The experimental result shows a slightly higher amplitude at secondary lobes, located at y ≈ − 4.5, −1.5, 1.5 and 4.5 mm, as shown in Fig. 2 (e). The experimental lobes show a mean normalized amplitude of 0.46 (0.38 in simulation) with a root-mean square error of ϵ_RMSE = 0.087. We observe another secondary lobe at y = 0 mm with a normalized amplitude of 0.74 in experiment (0.60 in simulation, ϵ_RMSE = 0.087), emerging due to the mirror symmetry of the hologram.

Fig. 2:

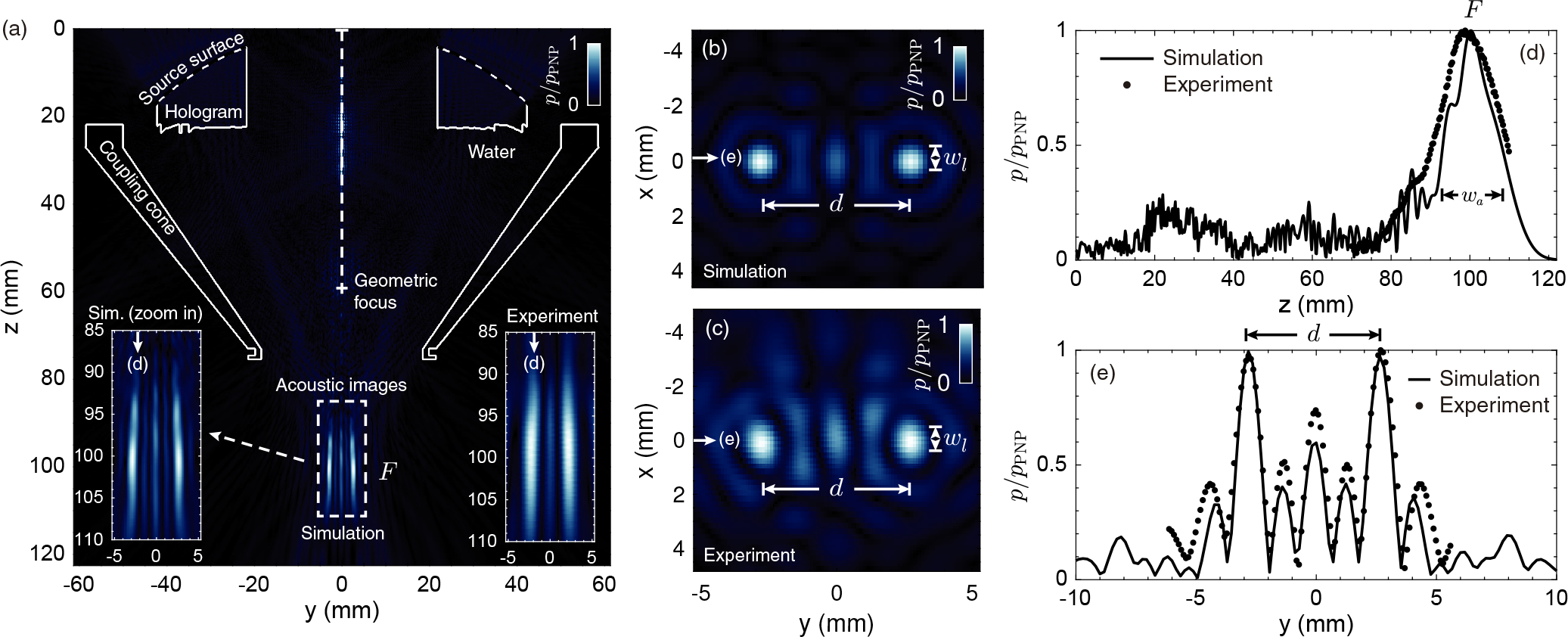
Pressure field distribution (normalized PNP) obtained in the calibration of the holographic acoustic lens. (a) Simulated axial plane at x = 0 mm showing in the insets both a zoom of the simulated field and the experimental measurement at the focal region. The contours of the lens and cone are shown in a continuous-white line. (b,c) Simulated and experimental transversal planes at z = 100 mm, respectively, showing the two focused spots separated a distance d. (d) Axial cross-section of the simulated (continuous-black line) and experimental (dotted-black line) pressure-field at y = 2.6 mm and x = 0 mm. (e) Transversal cross-section of the simulated (continuous-black line) and experimental (dotted-black line) pressure-field at z = 100 mm and x = 0 mm.

The cross-section of the acoustic field measured at x = 0 mm and y = 2.6 mm, i.e., axially along the right focus, is shown in Fig. 2 (d). The maximum of the PNP is observed at z = 98.8 mm (± 0.3 mm of measurement resolution) in the experiments, compared to z = 100.2 mm in simulation (± 0.18 mm of grid resolution). The experimental focal spot shows a depth-of-field of 19.2 mm, about 4 mm longer than the 15 mm of the simulated field. The overall amplitude envelope follows the shape of the simulated field, even far away from the focal spot. Finally, Fig. 2 (e) shows the transversal cross-section at z = 100 mm and x = 0 mm, i.e., transversely to both foci. The two symmetric focal spots appear at y = −2.6 mm and y = 2.6 mm (± 0.18 mm numerically, ± 0.1 mm experimentally), respectively, in both simulation and experimental calibration. The full-width at half-maximum (FWHM) in the transverse direction is 1.10 mm (± 0.18 mm of grid resolution) along both x and y directions for the simulation, compared to 1.1 mm (± 0.1 mm of measurement resolution) along y direction and 1.6 mm (± 0.1 mm of measurement resolution) along x direction for the calibration.

Overall, the bilateral focal spots and secondary lobes obtained numerically agree with the measured ones, thus demonstrating the high accuracy of the holographic approach.

Then, the hydrophone was positioned at the center of one focus (x = 0, y = −2.6 mm and z = 98.8 mm), and we performed acoustic measurements by changing the output voltage of the function generator, from 20 mV to 280 mV (peak) in steps of 20 mV. Using these data, we estimated the output voltage amplitude of the function generator ensuring 400 kPa-PNP at the focus in water. To produce 400 kPa-PNP in water at the center of the foci, we calculated that the output voltage is 190 mV (± 20 mV). Note that this value was enhanced at the treatment stage compensating for the attenuation produced by the head of the mouse and the efficiency of the transcranial hologram, as explained below.

B. Bilateral BBB opening

Once the lens was successfully calibrated in water, a transcranial simulation was performed to design a new lens, which would take into account the aberrations of the skull and the brain of the mouse, in addition to the effects due to the coupling cone. This transcranial simulation initially indicated that there was a pressure loss at the focus of ≈36 % due to the attenuation of the skull and brain of the mouse, and due to the efficiency of the new lens. Note that this new lens provides an enhanced efficiency for the transcranial focusing compared with the lens designed for the calibration used transcranially, as the new design includes the compensation for the aberrations of the coupling cone, skull, and brain of the animal. The output voltage of the function generator was increased accordingly to 297 mV obtaining 400 kPa-PNP to safely open the BBB [4], [5], [59], [60]. Two test mice were sonicated using these input parameters, and we detected gadolinium perfusion in T1-MRI images throughout almost the whole brain. The output voltage of the function generator was then reduced to 280 mV (the experimental loss was ≈32 % instead of the ≈36 % predicted) leading to a sharp bilateral BBB opening, indicating that the initial attenuation value was slightly overestimated by the simulation including the rodent tissues by a factor of ≈4 %. Three mice were treated at the chosen parameters to investigate feasibility across multiple animals.

A comparison between the simulated pressure-field distribution inside the head of the mouse, the calibration, and the resulting BBB openings analyzing the post-sonication T1-MRI acquisitions is shown in Fig. 3 for one of the mice. First, Fig. 3 (a) shows the simulated coronal pressure-field distribution at x = 0 mm where continuous-white lines show the contours of surface of the transducer, the hologram, the coupling cone, and the mouse skull. The pressure-field distribution shown here is normalized to p_PNP, which represents the PNP at the focal region inside the brain. A closer view of the coronal pressure-field distribution at the focal region is shown in Fig. 3 (c1), where the two symmetrical focal spots are marked by the two red arrows. The transverse (axial) cross-section of the simulated acoustic field at z = 100 mm is shown in Fig. 3 (b1), where two clear circular spots are observed, as indicated by red arrows.

Fig. 3:

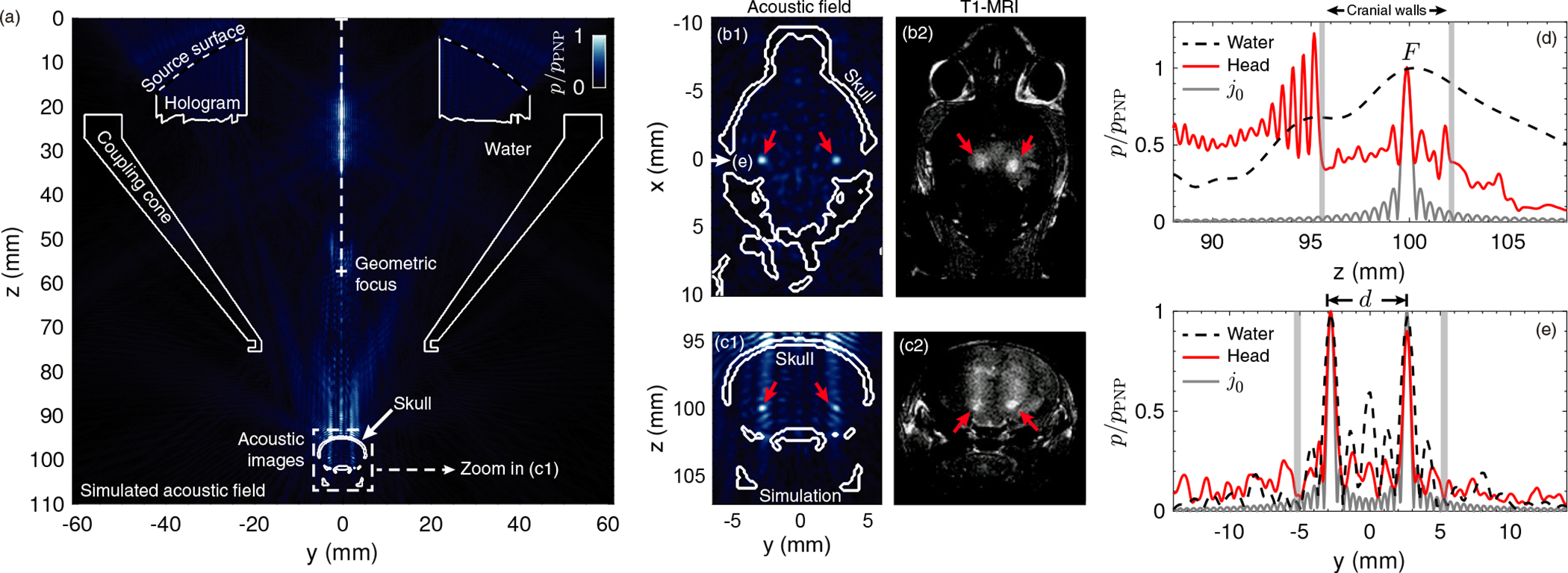
Pressure field distribution (normalized PNP) simulation compared to the BBB opening regions. (a) Simulated axial pressure-field distribution plane at x = 0 mm. The contours of the lens, cone and skull are shown in a continuous-white line. (b1,c1) Simulated transversal (at z = 100 mm) and axial (zoom in of (a) at x = 0 mm) pressure-field distribution planes, respectively, showing the two focused spots by red arrows. (b2,c2) Experimental transversal and axial T1-MRI planes, respectively, showing the two BBB openings, in light color, by red arrows. (d) Simulated axial cross-section of the calibration case (dashed-black line) and the transcranial case (continuous-red line) showing the pressure-field distribution at y = 2.6 mm and x = 0 mm. A spherical Bessel function of the first kind and zero-th order centered at the focal spot is shown in a continuous-gray line. (e) Simulated transversal cross-section of the calibration case (dashed-black line) and the transcranial case (continuous-red line) showing the pressure-field distribution at z = 100 mm and x = 0 mm. A spherical Bessel function of the first kind and zero-th order centered at the two focal spots is shown in a continuous-gray line.

In vivo tests were performed as described in Methods section on n = 3 mice. T1-MRI showed gadolinium extravasation at two symmetric focal spots in the axial and in the coronal plane, as shown in Figs. 3 (b2,c2), respectively. A bilateral BBB opening was achieved as indicated by the two red arrows.

On the one hand, we can observe that the two experimental BBB openings are separated 3.2 ± 1.0 mm (n = 3 mice, see detailed analysis in Table I) compared to 5.3 mm in simulation. The discrepancy is likely due to the differences between the skull scanned with μCT for manufacturing the lens and the skulls of the treated mice, or small misalignment of the system. Note that a sharp bifocal targeting was achieved for each mouse, as the separation distance d is large enough compared with the reduced radius R of the quasi-spherical spots.

TABLE I:

Comparison between the separation distance d and the mean size R of the bilateral BBBO across the three treated mice. Note that d corresponds to the distance between the center of mass of both BBBO spots, and R is the mean radius of the quasi-spherical BBBO regions.

Specimen number	BBBO separation d (mm)	BBBO size R (mm)
1	2.5	0.4
2	2.7	0.6
3	4.3	0.6

Average BBBOV was significantly different comparing both left and right hemispheres (p = 0.01, n = 3 mice). The average BBBOV calculated was 17.7 ± 6.8 mm³ and 34.9 ± 9.6 mm³ for the left and right hemispheres, respectively. The right hemisphere showed a higher BBBOV, as observed in Fig. 3 (b2,c2), where the two BBB opening spots appear slightly displaced to the right hemisphere, observing how the right BBB opening spot is brighter than the left one, and consequently off-target regions are also slightly brighter. This can be caused due to a misalignment of the transducer respect to the mouse skull. The predicted focal volume was defined at the decay of p_PNP/2, and the diameter of the resulting quasi-spherical spot was ≈0.55 mm, which corresponds to a focal volume of ≈0.1 mm³ per brain hemisphere. However, the diffusion of gadolinium agent within the brain tissue led to a larger size opening at the focal regions. Moreover, the experimental BBBOV includes small-size target regions where the BBB was clearly opened [see high-contrast quasi-spherical regions indicated by red arrows at z=100 mm in Fig. 3 (c2)], as well as large-size, off-target regions where the BBB was also opened but in a smaller degree [see medium-contrast elongated regions from z=97 to 99 mm in Fig. 3 (c2)]. Nevertheless, in terms of CE, the average value was marginally different between hemispheres (p = 0.04, n = 3 mice). The calculated CE was 17.6 ± 3.8 % and 25.3 ± 7.3 % for the left and right hemispheres, respectively.

On the other hand, acoustic holograms showed a particular advantage compared with conventional approaches generating transcranial bilaterally focused beams within the brain: the depth of field, i.e., the size of the focal spot in the z direction, can be reduced as compared with a progressive, conventional focused beam. This is clearly observed in the numerical results, see Fig. 3 (d), where the field along the z direction is shown for the hologram designed for the mouse and the one designed for water. Evaluating the axial cross-section, the depth of field of the focal spot for the transcranial case [continuous-red line in Fig. 3 (d)] is ≈0.5 mm (the wavelength at 1.68 MHz in brain tissue is 0.95 mm) compared to the 15 mm for the calibration case [dashed-black line in Fig. 3 (d)]. Furthermore, the full-width at half-maximum in the transversal direction is ≈0.6 mm for the transcranial case [continuous-red line in Fig. 3 (e)] compared to ≈1 mm for the calibration [dashed-black line in Fig. 3 (e)]. This enhancement of the focusing performance is associated with the ability of acoustic holograms to encode time-reversed wavefronts including the multiple reflections produced inside the mouse head, in analogy with other time-reversal systems [61]–[63]. Holograms encode waves in multiple directions by generating converging wavefronts to the focal spots and, simultaneously, secondary waves that are reflected on the walls of a leaky cavity, i.e., the skull and the walls of the coupling cone. Therefore, the angular spectrum of the resulting focused field by the hologram is enhanced as compared to the angular spectrum of a progressive focused beam. In this way, using holograms for FUS, the focal spot, that typically presents an elongated shape for a focused transducer, converges to a spot of quasi-spherical shape. As a reference, the limiting case of a spherically converging wave, given by a spherical Bessel function of the first kind and zero-th order, j₀(kr), where k is the wavenumber in the brain at the source frequency and r the radial distance centered at the focal spot, is plotted in Figs. 3 (d,e). We can see that the field produced by the hologram in the simulation is close to the theoretical diffraction limit, with the focal width being close to the half-wavelength limit. The corresponding focal spots are also visible in the experiments [see Figs. 3 (b2,c2)], corroborating the bilateral BBB opening and the ability of holograms to improve the focusing capabilities of conventional FUS systems. They present a spherical shape, but as the gadolinium exhibits diffusion through the brain tissue, the experimental focal spots in the T1-weighted MRI are slightly bigger, showing a diameter size of 1.0 ± 0.3 mm.

C. Cavitation analysis

The FFT corresponding to a single therapeutic pulse showing the range of the harmonics n = 1, 2, …, 8 is shown in Fig. 4 (a). The spectrogram for the whole experiment is represented in Fig. 4 (b), showing the stability on the microbubble emissions during the entire 2-min treatment, highlighting the prevalence of the harmonic frequencies n = 2, 3, 4. At the top of Figs. 4 (a,b) we indicate the three analyzed spectral regions used to assess the cavitation doses. The total energy calculated for each pulsed-burst during the whole treatment is represented in Fig. 4 (c). The energy shows variations between pulses, due to the different acoustic cavitation and the variations of microbubble concentration due to blood flow. However, the mean energy at the beginning and at the end of the treatment is similar. Harmonic stable (SCD_h), ultraharmonic stable (SCD_u) and inertial (ICD) cavitation doses are shown in Fig. 4 (d). First, SCD_u remains high and constant during the whole procedure. In contrast, SCD_u and ICD are two orders of magnitude lower than SCD_u, as it can also be visually identified in the spectrogram in Fig. 4 (b), confirming the absence of violent cavitation events which would compromise safety. This fact, in addition to the successful observed BBB openings shown previously, indicates that cavitation activity was likely occurring during sonication in a stable and repeatable way.

Fig. 4:

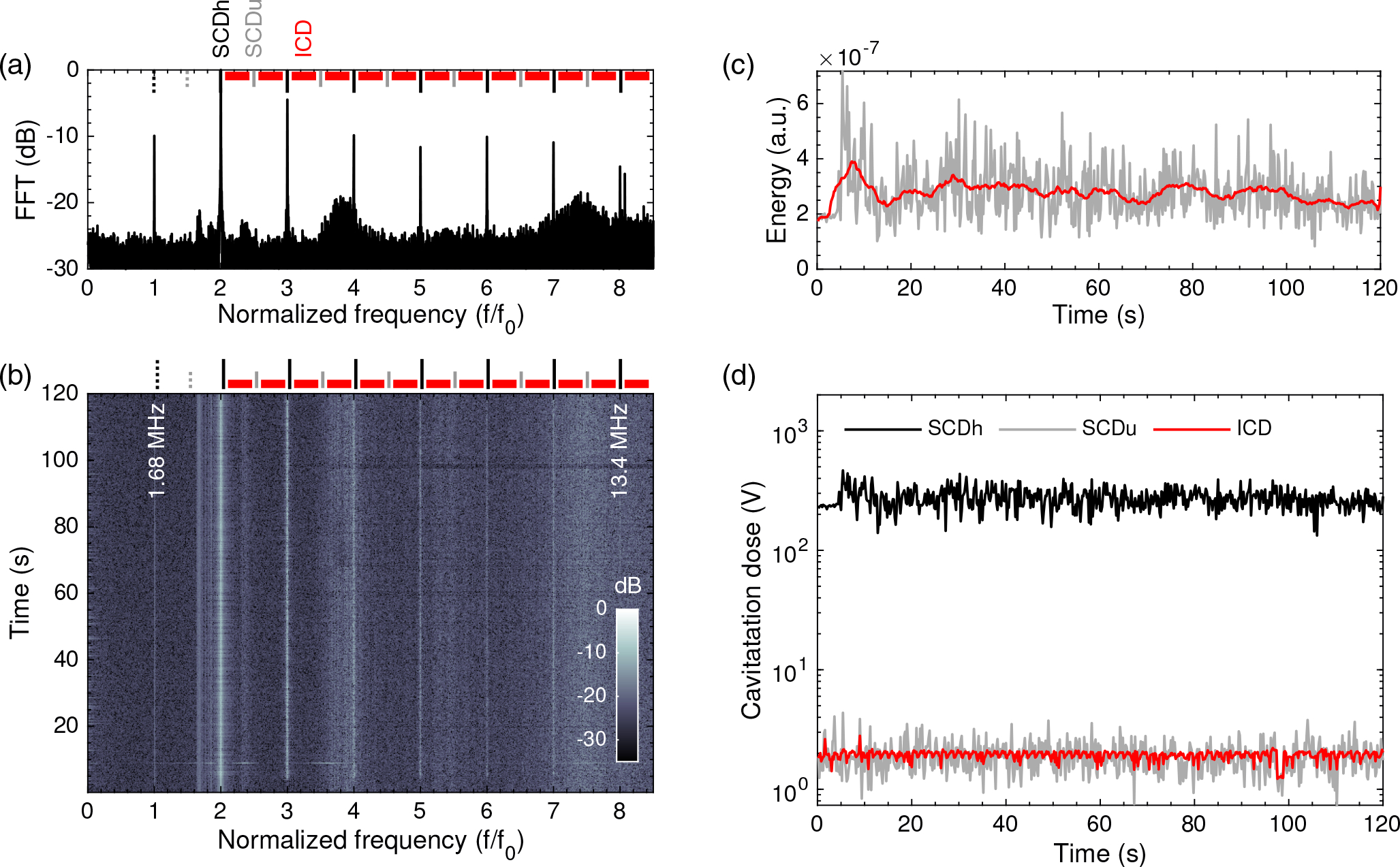
In vivo microbubble emission analysis over sonication time. (a) Normalized amplitude of the Fast Fourier Transform (FFT) performed over the cavitation emissions produced by a single pulse. (b) Spectrogram showing the evolution of the harmonics n = 1, 2, 3, 4, 5, 6, 7. (c) Energy evolution during the entire treatment (gray) and energy using a 5-second moving average filter. (d) Stable harmonic (black), stable ultraharmonic (gray), and inertial (red) cavitation doses.

IV. DISCUSSION

The proposed approach presents several limitations which must be discussed and understood to accurately control the technique.

On the one hand, the prediction of the location for the foci within the brain of the mice was not accurate. The separation distance d was 5.3 mm for the calibration in both simulation and experiment in the water tank. However, the experimental BBBO spots were separated d=3.2 ± 1.0 mm (see Table I for details) which is about 2 mm shorter than predicted in simulation (d=5.3 mm as in the calibration setup). Despite the same type, age, sex… of the mouse from which the μCT-scan was acquired compared to the three treated mice, the existing differences in the skull morphology across specimens were relevant, and an accurate foci prediction could not be performed. Using the μCT scan of the treated subjects would lead to a better ultrasound location prediction for each mouse. Therefore, a specimen-specific lens is needed, designed from the particular skull geometry and acoustic properties of each specimen, to provide a more accurate focusing prediction. Furthermore, other effects as imperfect coupling or small air pockets trapped within the lens surface may have contributed to the field distortion. Regarding clinical trials, the presented lenses are non-reconfigurable, therefore a personalized lens is ideally needed for each patient and treatment target. A new lens design is recommended to have an accurate beam control for each new focusing configuration, which consequently would result in a time-inefficiency procedure for the same patient, due to the removing and placing of the lenses for the different configurations. In this way, reconfigurable holograms, e.g., as those based on spatial sound modulators [31], are of great interest to transcranial ultrasound therapy. However, note that it has been previously proven that aberrations are still corrected despite a small misalignment, intentionally or not, in the transducer position [33]. These results showed the capabilities of using the same lens and apply a small displacement to the transducer in order to move the focal spot, covering even a larger volume, while still correcting the skull aberrations for the same specimen, but the lens behavior was not assessed across different skulls.

On the other hand, note that for clinical BBB opening applications, the central frequency (usually below 650 kHz) is lower than in preclinical applications (usually above 1 MHz in mice). The thickness of the hologram, i.e., the height of each pixel, is proportional to the wavelength in the material of the lens, therefore, holograms for preclinical applications require a higher resolution 3D-printing techniques and small printing errors could be detrimental in the focal shape generation.

Aside from this limitations, the proposed approach would provide additional advantages as compared with therapeutic phased-array systems regarding the number of active elements, e.g., up to 2048 in a phased-array device. Typically, therapeutic phased-arrays are built following a hemispherical geometry, where their active piezoelectric elements are commonly separated by a distance greater than half-wavelength and, therefore, their steering capability is limited by the emergence of strong grating lobes. However, the study reported in Ref. [25] provided a degree of steering similar to ours while keeping a reduced grating lobe effect, but the focal depth-of-field was ≈5 times larger than our result. In contrast, acoustic holograms allow encoding wavefronts with a higher spatial resolution, in this work up to 131784 elements, resulting in an enhanced focal resolution and steering capability, where no grating lobes were generated transcranially, but in the water calibration, as the constructive interference observed in the central axis was due to the symmetry of the reconstructed acoustic pattern, not to the steering capabilities). In addition, these lenses allow synthesizing not only the progressive focused waves towards the targets, but also the multiple-scattered waves inside a leaky cavity of irregular shape such as the skull. The design process takes into account the time-reversed (or phase-conjugated) version of the back-propagated wave traveling from the target structure, through the aberrating media, towards the holographic plane [26]. Therefore, in addition to compensating the phase aberrations introduced by the skull and the brain tissue, these acoustic lenses can replicate the reflections inside the head of the animal. This results in an enhancement of the angular spectrum of the synthesized waves and, thus, the hologram can ideally reconstruct a sharp acoustic image close to the diffraction limit [Figs. 3 (d,e)]. In practice, the depth-of-field of the focal spot, typically elongated for a focused ultrasound source, is greatly reduced in the axial direction: in this paper, a quasi-spherical focal spot was obtained. Since the targeted structure is always enclosed in the cranial cavity for the treatment of brain disease, holographic acoustic lenses show a great potential to enhance spatial resolution, becoming a safe, low-cost and highly-localized technique to target brain structures at the CNS in preclinical animal models.

V. CONCLUSION

In this work, we have demonstrated the first in vivo high-localized, simultaneous multi-focal BBB opening in mice using a 3D-printed acoustic hologram. Holographic lenses were effectively designed using a simulation including the skull of a mouse obtained from μCT-scan, from where its heterogeneous properties were acquired. The manufactured acoustic hologram shows the ability of simultaneously focusing at two mirrored targets in each hemisphere with a considerable reduced depth-of-field, allowing thus a high-localized, cost- and time-efficient BBB opening procedure for preclinical animal models. Only one sonication and, consequently, one administration of microbubbles, were sufficient to open simultaneously the BBB at different distant brain regions. Moreover, the finite-aperture lens showed the capability of producing a high-resolution focusing, where quasi-spherical blood-brain barrier opening regions were observed, due to the accurate control of the reverberation and reflections inside the cranial cavity. In this way, single-element systems based on acoustic holograms define a low-cost alternative to conventional techniques for producing bilaterally focused beams.

This study shows the feasibility, capability and efficiency of acoustic holograms for high resolution multi-focal blood-brain barrier opening. Moreover, the benefits of this approach can be widely useful in other applications such as neuromodulation, high-intensity focused ultrasound, ultrasound hyperthermia, transcranial imaging or drug and gene delivery, defining a promising solution to the complex requirements of these biomedical ultrasound applications.

APPENDIX I. ACOUSTIC CALIBRATION SETUP

A calibration lens was designed and manufactured to test the splitting of the single focus into two in a water tank, and to assess the input electrical signal parameters providing 400 kPa-PNP at the focal spots.

Acoustic pressure-field measurements were conducted using an Onda HGL-0200 hydrophone (Sensitivity of 0.19 mV/kPa at 1.68 MHz) placed at the bottom of a degassed and distilled water tank in a fixed position using a mechanical arm.

A custom coupling cone was designed and 3D-printed to fix the lens to the transducer and to hold the coupling water. The entire system was attached to a computer-controlled, three-dimensional positioning system (Velmex Inc., Lachine, QC, CAN). The FUS transducer was driven by a function generator (Agilent, Palo Alto, CA, USA) and a 50-dB power amplifier (325LA, ENI Inc., Rochester, NY, USA). For the x−y planes, the field was scanned from −5.3 mm to 5.3 mm in the x direction and from −4.85 mm to 4.85 mm in the y direction using a resolution of 0.1 mm (9 points per wavelength). For the x − z planes, the field was measured from −5.3 mm to 5.3 mm in the x direction and from 85 mm to 110 mm in the z direction using a resolution of 0.176 mm (5 points per wavelength).