Correlated Motions in Structural Biology

Abstract

Correlated motions in proteins arising from the collective movements of residues have long been proposed to have fundamental importance to key properties of proteins, from allostery and catalysis to evolvability. Recent breakthroughs in structural biology have made it possible to capture proteins undergoing complex conformational changes, yet intrinsic correlated motions within a conformation remain one of the least understood facets of protein structure. For many decades, the analysis of total X-ray scattering held the promise of animating crystal structures with correlated motions. With recent advances in both X-ray detectors and data interpretation methods, this long-held promise can now be met. In this perspective, we will introduce how correlated motions are captured in total scattering and provide guidelines on data collection, interpretation, and validation. As structural biology continues to push the boundaries, we see an opportunity for gaining atomistic insight into correlated motions using total scattering as bridge between theory and experiment.

Graphical Abstract

Introduction

The past decade has seen remarkable developments in structural biology that were once simply unimaginable. A confluence of hardware and software advances in cryo-electron microscopy (cryo-EM) has now made it possible to determine structures that were previously considered unattainable¹. In the X-ray field, the emergence of 4th generation light sources^2,3 has led to a renaissance of room-temperature studies at both X-ray free electron lasers (XFELs)⁴ and synchrotrons⁵. The past year also witnessed a breakthrough in the accuracy of protein structure prediction by machine learning algorithms⁶. On all fronts, structural biology techniques have reached a new level of sophistication. We are arguably experiencing the second major watershed since the “Big Bang”⁷ of protein X-ray crystallography.

The goal of structural biology has always been to relate structure to function. Yet since the beginning, it has been known that protein function can be better deduced by visualizing a change in structure. The seminal structures of hemoglobin in different states were critical in revealing how conformational change can be interpreted as inter-subunit allostery and explain cooperative oxygen binding⁸. Likewise, comparisons of lysozyme structures with and without inhibitor bound were the first example in which the active site of an enzyme and its interactions with a ligand were deduced with minimal prior knowledge^9,10. These foundational studies laid out an extremely successful template for structural biology – if multiple structures of a protein can be solved, we can deduce much about its specific function by careful inspection of the changes. Today, the development of novel approaches to visualize proteins in action is at the forefront of structural biology. In crystallography, there has been a concerted effort to probe room-temperature dynamics either kinetically in response to a perturbation^11–13 or at equilibrium by modeling multiple conformers^14–16. In cryo-EM, we have seen the development of techniques not only aimed at classification of single particles in different conformations^17,18 but also in the estimation of a continuous manifold that describes a protein’s structure^18–21. We expect these recent advances, especially in cryo-EM, to revolutionize structural analyses of large-scale conformational changes, such as domain motions.

What remains to be done? Although much can be learned from observing changes in structure, there are collective structural fluctuations within a single conformation, known as correlated motions, that are difficult to visualize but are important to understand. In the context of allostery, subtle correlated motions are implicated in sensing local changes, such as ligand binding, and propagating a signal through the protein to alter its activity. For many proteins, like hemoglobin, the outcome of signal propagation is a large-scale conformational change that can be interpreted to explain changes in activity²². However, even when high-resolution structures of different allosteric states are known, the mechanism by which small-scale changes generate a global change is not readily apparent. Moreover, there is a phenomenon known as “dynamic allostery” or “fluctuation-induced allostery” which does not invoke any conformational change. First described by Cooper and Dryden²³, it was argued from statistical mechanics that allosteric signaling can occur solely through different movement patterns within a protein without any discernible changes to the average structure. To date, various instances of dynamic allostery have been identified experimentally, such as inter-subunit communication in catabolite activator protein (CAP)²⁴ and tuning of ligand-binding affinity by a peripheral alpha helix in PDZ domains²⁵.

Furthermore, the potential roles of subtle protein motions in catalysis has been one of the greatest debates in modern enzymology^26–32. For the structural biologist, it is useful to consider how motions may contribute to different parts of the rate constant as described by transition-state theory²⁶. In this framework, the reactant and transition state are in a quasi-equilibrium, such that the rate constant is proportional to a Boltzmann distribution that has an exponential dependence on the activation free energy. The pre-exponential factor in the rate constant includes the transmission coefficient, which can account for phenomena such as quantum mechanical tunneling in reactions that involve the transfer of light particles. This factor is thought to be sensitive to fluctuations in the donor-acceptor distances³⁰. For the best-studied system of dihydrofolate reductase (DHFR), a diverse set of experimental and theoretical tools has been applied that suggest that a network of residues undergo sub-angstrom to angstrom-scale correlated motions that are relevant to catalysis^33–37 and that this network is preserved throughout evolution^33,38,39. Yet it has also been argued that the dominant contribution to enzymatic rate enhancements comes from the structure itself, i.e. that the polar environment of the active site is pre-organized in a way that water molecules are not⁴⁰.

To achieve a physical understanding of the unique properties of proteins, it is clear that correlated motions must be investigated in addition to structure (Fig. 1). Thus far, a number of computational approaches have been developed to predict networks of residues that may display correlated motion²². These include sequence-based methods that infer the coevolution between residues from multiple sequence alignments (MSA)⁴¹, as well as the physical modeling of structural dynamics by elastic network models (ENM)^42–44 or molecular dynamics (MD) simulations⁴⁵ and graph-theory analysis based on proximity and bonding between residues in protein structures^46,47. Direct measurements of correlated motions, on the other hand, are challenging, and thus far, largely limited to nuclear magnetic resonance (NMR) spectroscopy, where different methods can be applied to cover a wide range of time scales from ps to s⁴⁸.

Figure 1.

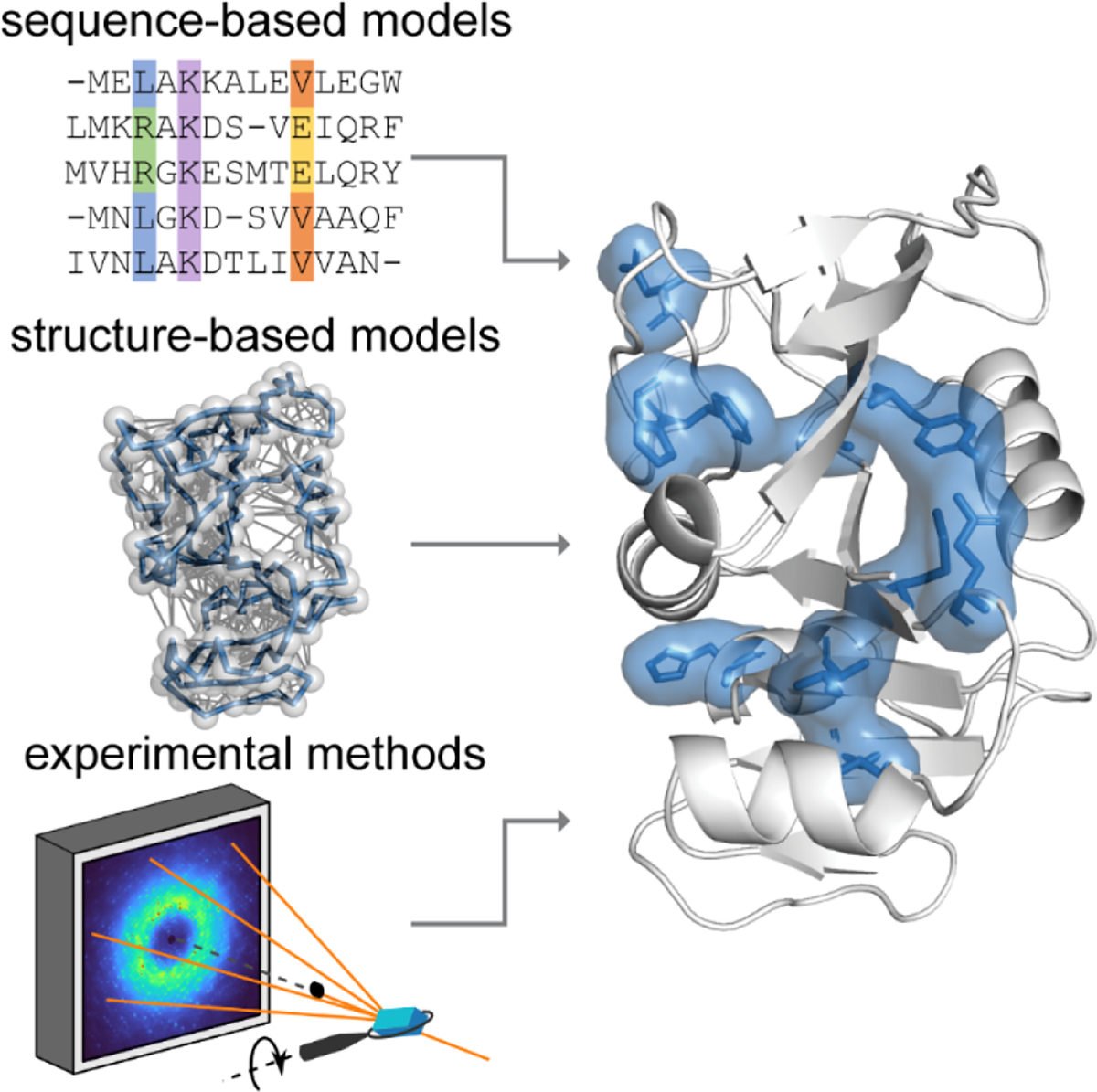
Combining theoretical and experimental approaches to determine how motions are correlated in proteins. Theoretical models include those based on sequence (represented by an MSA) and structure (represented by an ENM). Among experimental methods, total X-ray scattering from crystals stands out for its ability to measure high-resolution structure and correlated motions simultaneously. Shown on the right is a set of residues that was predicted to coevolve in DHFR (PDB: 1RX2) by statistical coupling analysis⁴¹ (shown in blue).

In this perspective, we will focus on a new approach to X-ray crystallography that provides a direct measure of correlated motions: the analysis of total scattering from protein crystals. The total scattering signal contains both Bragg diffraction and diffuse scattering, from which both atomic detail and correlated motions can be obtained⁴⁹. The measurement is unique in that data for both the average structure and its fluctuations can be collected in a single experiment on the same sample, and thus, the two can be compared directly in a self-consistent manner. Furthermore, the total scattering signal provides a powerful restraint for bridging the gap between experiment and theory. Here, we will begin with a brief introduction on how atomic displacements are represented in protein crystallography (B-factors) in order to explain how information on correlated displacements is contained in diffuse scattering. We will then provide guidelines on data collection, processing, and interpretation. Finally, we will discuss grand challenges and opportunities, particularly in emerging areas of interest, such as relating correlated motions to sequence and evolution.

Understanding conformational disorder in terms of correlated motions

In crystallography, structure determination relies on the integrated intensities of the Bragg reflections – the bright spots that are captured in diffraction images (Fig. 2A). This dataset, which we call “Bragg diffraction,” reports on the mean electron density of the unit cell of the crystal, where the average is over time and space. Although the lattice imposes more orderliness on proteins than if they were completely free in solution, the inside of a protein crystal is a crowded but watery environment with non-covalent contacts between neighboring molecules. As a result, individual molecules in a protein crystal sample a conformational ensemble that share similarities with the ensemble in solution⁵⁰. Often, evidence for distinct conformations can be seen in the mean electron density and modeled by accounting for their partial occupancies⁵¹. In addition, apparent fluctuations in atomic positions result in a local blurring of the electron density. This blurring is quantified during structure refinement by fitting atomic B-factors that specify the width of a Gaussian probability distribution for each atom’s displacement from the average position⁵².

Figure 2.

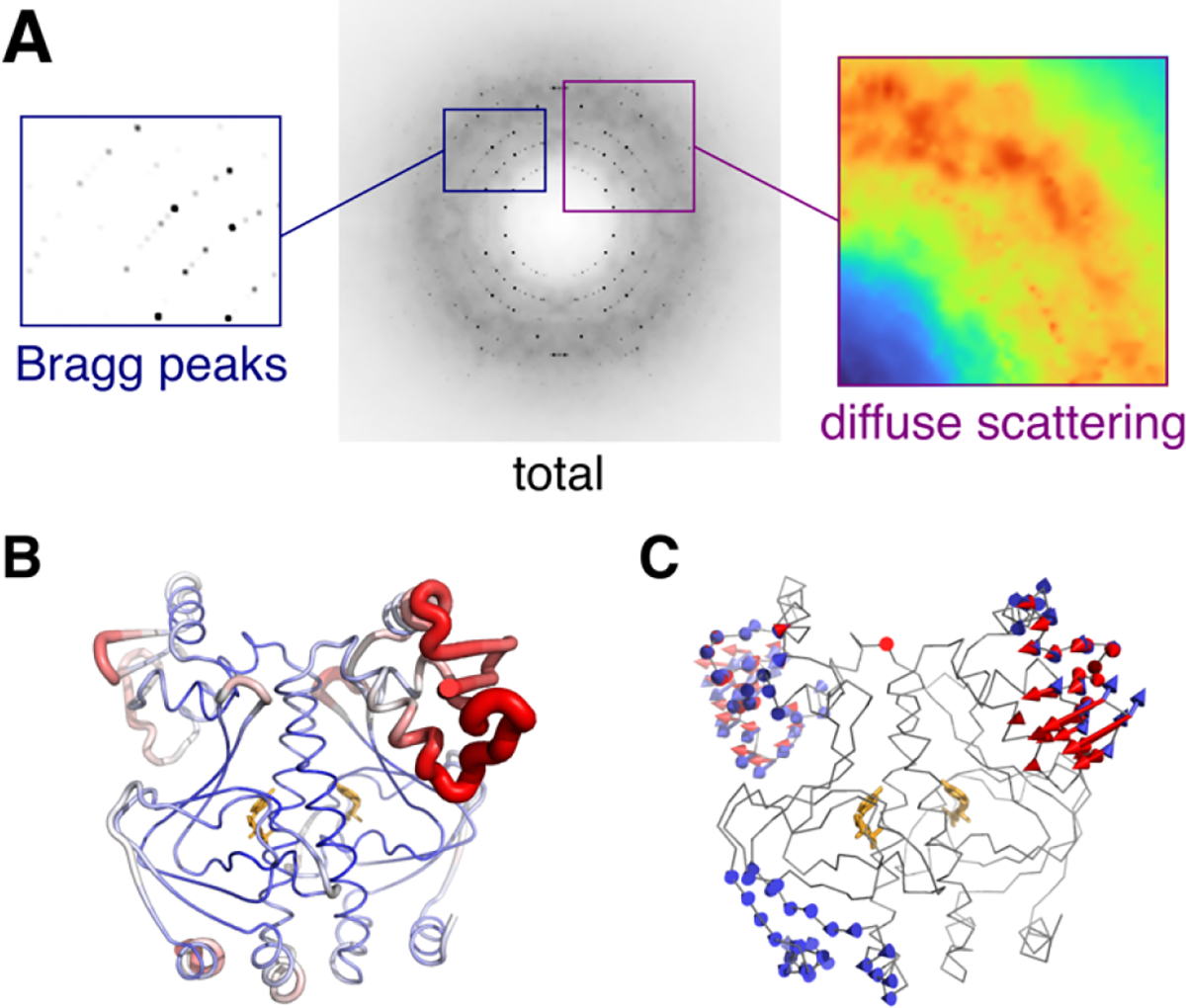
Components of total scattering illustrated using the experimental X-ray structure of CAP (PDB: 1g6n⁵³) with dynamics added using ENM simulations⁵⁴ of one unit cell. (A) The simulated diffraction image contains two signals: Bragg peaks (left) that depend on the average structure, and diffuse scattering (right) that arises from correlated atomic displacements (in this case, vibrations of the ENM). (B) B-factors refined to experimental Bragg data vary along the polypeptide chain (blue to red). (C) Normal modes of the ENM seem to explain regions of high experimental B-factor. The reality of such collective motions can be verified by diffuse scattering analysis.

Crystallographic B-factors often display a distinct pattern along a polypeptide chain that, for a given protein crystal, is largely reproducible from experiment to experiment (Fig. 2B). Thus, although Bragg data contain no information about displacement correlations, B-factors can help identify potential regions of flexibility and mobility in a protein^55,56. In addition, motions may be inferred from more sophisticated disorder models applied during crystallographic structure refinement, including normal mode⁵⁷, TLS⁵⁸, and multi-conformer¹⁴ approaches. In computational studies of allostery and correlated motions, B-factors are often used for experimental validation⁵⁹. B-factors are particularly relevant to ENMs, whose normal modes naturally predict Gaussian-distributed fluctuations that can be compared directly with experiment^60–62 (Fig. 2C). B-factors are also commonly compared with mean-squared fluctuations in MD simulations, both for validation and for benchmarking force fields⁶³.

However, there are two major limitations to B-factors. First, although B-factors are used to restrain dynamical models, they are not a particularly powerful restraint. In fact, very different models can account for B-factors equally well, making interpretation ambiguous. For example, it has been questioned whether the correlation between B-factors and ENM displacements is physically meaningful, or if it merely reflects the tendency for greater disorder on the surface of a protein compared with the core⁶⁴. Second, B-factors contain contributions from multiple sources of disorder, and thus, without accounting for these other sources, they overestimate the atomic motions arising from protein motions. As we will describe below, the contribution of non-protein dynamics cannot be treated as a constant, and thus, the use of so-called normalized B-factor⁵⁵ is insufficient.

Fortunately, diffraction images contain a second signal called “diffuse scattering” (Fig. 2A). This signal is a direct consequence of disorder: photons lost from the high-resolution Bragg reflections are scattered instead, leaving a faint pattern everywhere in the diffraction image, between and underneath Bragg peaks. As a result, diffuse scattering is directly related to B-factors, but the information content differs. While B-factors come from the average electron density, diffuse scattering depends intimately on how atomic displacements are correlated with each other⁴⁹. The two are thus complementary. By analyzing the diffuse scattering and Bragg diffraction simultaneously (total scattering analysis), a more complete view of the structural fluctuations in a crystal can be gained⁵⁴.

Historically, protein diffuse scattering was difficult to measure accurately, especially in the vicinity of intense Bragg peaks⁶⁵. The use of a direct detector recently enabled the first clear measurement of the three-dimensional diffuse scattering from a protein crystal, allowing for a detailed analysis of the various contributions to the signal (further described below and in Fig. 3)⁵⁴. Importantly, intense near-Bragg features were resolved for the first time, which revealed that the crystals contained phonon-like displacement waves extending over hundreds of angstroms. A key take-away is that lattice disorder resulting from displacement waves accounted for the bulk of the B-factors in the most-ordered atoms in the protein. Thus, it was necessary to subtract this lattice contribution from the B-factors to reveal the true contribution from protein motions.

Figure 3.

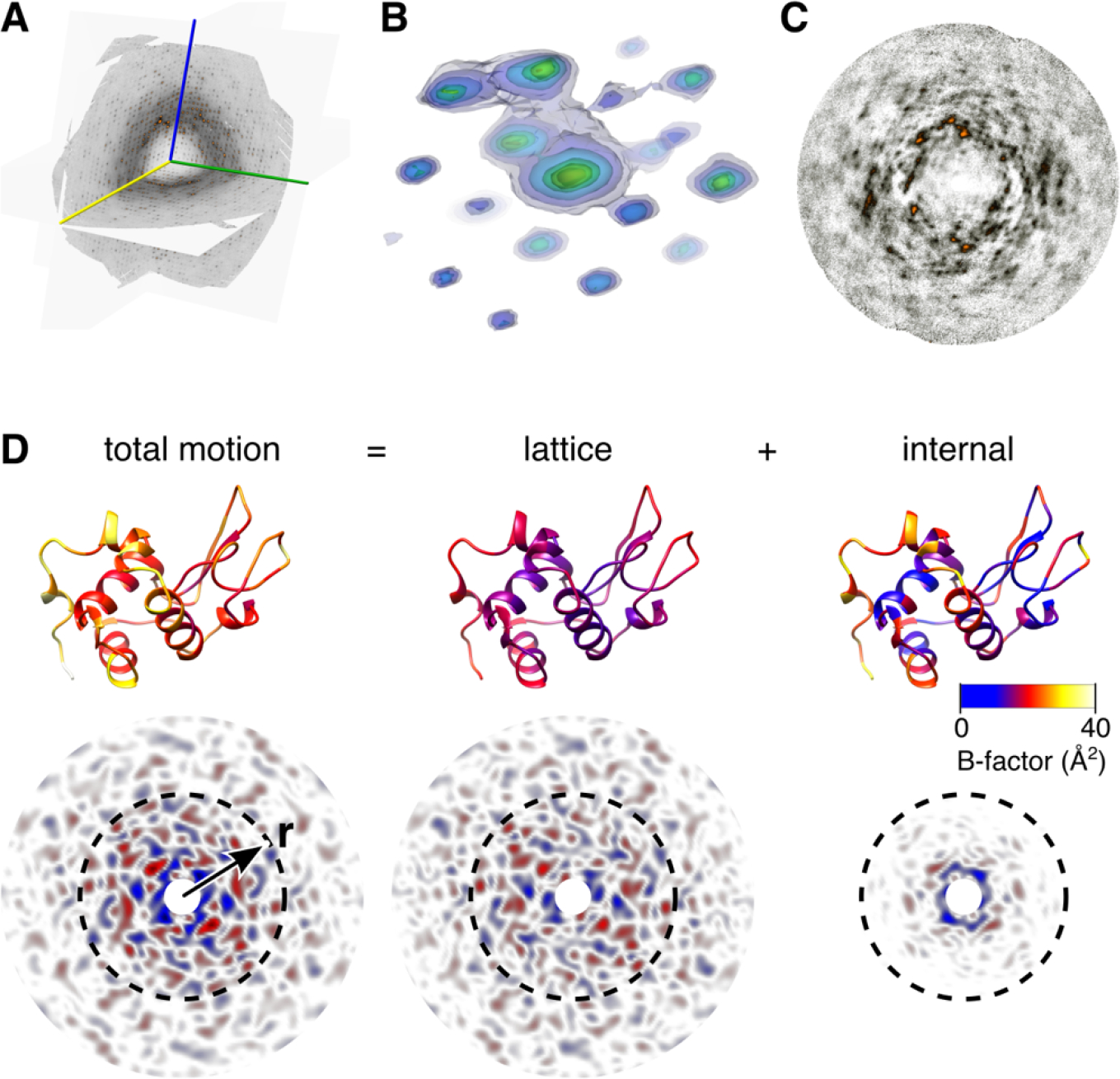
Total scattering analysis separates motion into lattice and internal components⁵⁴. (A) Three-dimensional map of diffuse scattering from triclinic lysozyme shown as intersecting central slices. A movie showing this volume from multiple perspectives is available online. The scattering includes an intense isotropic ring that may be subtracted to better visualize the halo and cloudy features. (B) Around Bragg peaks are three-dimensional halos (shown here as transparent contours, blue to yellow) attributed to thermally excited lattice vibrations. (C) Cloudy features due to short-ranged correlated motion are most visible in sections mid-way between Bragg planes. (D) Total motion and correlations are quantified using B-factor (top, PDB 6o2h⁵⁴) and diffuse Patterson maps (bottom), which report electron density fluctuations vs. inter-atomic vector, r. A lattice dynamics model fit to diffuse halos accounts for most of the B-factor for well-ordered atoms (total vs. lattice, top) and the correlated motions at large distances (total vs. lattice, bottom), but underestimates those at short distance (r < 10 Å, dashed circles). An ENM describing protein dynamics was fit to the residual B-factors (top right). The simulated diffuse Patterson of the protein dynamics model (bottom right) explains the remaining short-ranged correlations.

Now that historical limitations have largely been overcome, we expect biological applications of total scattering to become increasingly common. Thus, it will be important to establish guidelines and best practices to ensure data quality and robust interpretations, as occurred with crystallography, small-angle X-ray scattering, and cryo-EM. In the following, we outline the issues based on our experience so far, both to guide design of future experiments and to help evaluate published results.

How to measure total scattering

With modern detectors, total scattering experiments can be measured in much the same way as conventional, single-crystal diffraction. It may even be possible to extract diffuse scattering patterns from conventional diffraction images deposited in public databases^66,67. However, without optimizing the experiment, the kind of quantitative, total scattering analysis we describe here will be difficult. One reason is that proper treatment of background is extremely important for diffuse scattering as it competes with the signal of interest. Unlike in conventional diffraction experiments, total scattering measurements require a separate measurement of the background or its effective elimination. Furthermore, most diffraction data are currently collected at temperatures of 100 K to mitigate radiation damage. Although cryo-cooled crystals also exhibit diffuse scattering^66,68, room temperature is preferred for dynamic studies as the conformational ensembles best resemble the physiological state¹⁵. Additionally, the cryo-cooling process may add strain to the crystal lattice^69–71, which increases mosaicity and constitutes an additional perturbation to be accounted for. As we detail here, high-quality data can be obtained without cryocooling if extra care is taken in sample selection and experimental setup.

The first and most obvious consideration is signal-to-noise ratio. In terms of the number of photons recorded, diffuse scattering is actually comparable to Bragg diffraction⁶⁵. However, the diffuse signal is much weaker because those photons are spread over the entire detector, while Bragg diffraction is concentrated in sharp peaks. Moreover, much of the diffuse signal is isotropic and relatively featureless, with the more informative signal present as small rapidly varying features. Crystal scattering also competes with background from other sources that can be a challenge to eliminate, such as air in the beam path, liquid on the crystal surface, and other mounting materials like loops and capillaries. Finally, if the data are collected at room temperature, the total exposure budget is severely limited by susceptibility to radiation damage^72,73. For all of these reasons, it helps considerably if the crystals are large by current standards. While excellent Bragg data may be collected from small (< 50 μm) crystals using cryo- or serial crystallography, room-temperature diffuse scattering practically requires larger crystals (smallest dimension > 100 μm). The possibility of using XFELs for total scattering from microcrystals is revisited in the final section.

The second consideration is diffraction quality. It is sometimes assumed that diffuse scattering requires poorly diffracting crystals. While the diffuse signal is most obvious when Bragg peaks are weak⁷⁴, the evidence so far is that all protein crystals produce strong diffuse scattering⁴⁹, even those that diffract to exceptionally high resolution⁵⁴. Poor diffraction quality often results from high mosaicity, a kind of macroscopic disorder often described in terms of distortions and misalignment of so-called mosaic blocks⁷⁰, as opposed to the microscopic lattice disorder measured by diffuse scattering. Mosaicity broadens both Bragg peaks and diffuse scattering features, setting a fundamental limit on how finely the diffuse map can be sampled. Thus, although a mosaicity of 1° is sometimes tolerable for Bragg datasets, it would be problematic for diffuse scattering. The highly detailed diffuse maps from triclinic lysozyme⁵⁴ benefited from the low apparent mosaicity of ~0.02°. In a similar vein, X-ray sources optimized for high flux often have high energy bandwidth and beam divergence and therefore produce a similar broadening effect⁷⁵.

The final consideration is data collection strategy. The diffuse map results from merging individual diffraction images, which represent slices through the 3D reciprocal space in different orientations. The merging process is an opportunity to estimate and correct for uncontrolled variables in the measurement, such as the volume of the crystal in the X-ray beam and variations in response across the detector. As in anomalous diffraction experiments, the best collection strategy is to aim for high redundancy⁷⁶, so that regions of reciprocal space are observed multiple times independently. Collecting from several different crystals or tilting the spindle axis also helps fill in blind spots in reciprocal space caused by Ewald sphere curvature and physical gaps between detector panels. The background scattering from the diffraction instrument should also be measured and subtracted from each image. It may be necessary to collect backgrounds as a function of spindle angle if the mounting materials cast a shadow on the detector⁵⁴. Some background scattering can also be removed computationally during merging, as long as it is isotropic and present in only some rotation angles⁵⁴.

The internal consistency of the data (i.e. 3D diffuse map) can be assessed using metrics commonly in use for Bragg data such as CC1_/2, the correlation coefficient between random half-datasets binned by resolution shell⁷⁷. The map quality sets an upper limit on model-data agreement, and this can be calculated from CC1_/2 using the CC* estimate^54,77. Note that statistics such as CC1_/2 depend on how finely the map is sampled, which is not an issue for Bragg data, so care must be taken to always specify the sampling and to compare datasets sampled on the same grid.

How to interpret total scattering

As described above, one set of diffraction images produces two datasets: the integrated Bragg intensities and the 3D diffuse map. For total scattering analysis, the datasets first need to be placed on the same intensity scale relative to each other. Both datasets can then be placed on an absolute intensity scale of electron units^16,54. The inelastic scattering component, which contains no structural information, can then be subtracted from the diffuse map, leaving the elastic scattering for the remainder of the analyses (Fig. 3A).

The resulting diffuse map can be further divided into different components. The most noticeable feature is a broad ring-shaped background at ~3 Å resolution (Fig. 3A), which arises from both the disordered solvent and from the protein⁷⁸. Although it is potentially informative and useful for evaluating dynamical models, it can be subtracted for visualization purposes. Once the background is “turned off,” the fine features become visible. The most intense are typically found close to the Bragg peaks and are associated with lattice disorder. With sufficient sampling, halos with distinctive three-dimensional shapes can be observed (Fig. 3B). Different physical processes produce distinct intensity profiles⁴⁹. For example, if the intensity decays away from the Bragg peak with a power-law exponent of −2, then acoustic phonon-like vibrations are a likely source⁵⁴. Far from the Bragg peaks, it is common to see a cloudy pattern (Fig. 3C), which includes the scattering from collective motions of the protein⁷⁹. After these initial inspections, the diffuse map can be interpreted by rigorous comparison with the simulated scattering from atomistic simulations.

Building an accurate model of the lattice disorder is the key to total scattering interpretation. The reasons are twofold. First, it allows for the lattice component of the B-factors to be estimated and subtracted (Fig. 3D, top). Because lattice dynamics involve rotations (not just translations) of molecules⁸⁰, its contribution to the B-factors cannot be assumed to be a constant value. Second, it allows the short-ranged correlations associated with lattice motion to be accounted for when analyzing the cloudy pattern. Thankfully, lattice vibration models have relatively few degrees of freedom that can be fit using even just a subset of intense three-dimensional halos⁵⁴. In contrast to previous methods, which relied on cloudy scattering exclusively^49,68, refining the lattice model to the halos allows for unambiguous separation of lattice motion from internal motion.

Once the lattice disorder is understood in detail, we can focus on the continuous cloudy pattern, which extends throughout reciprocal space and is associated with the correlated motions of atoms within the unit cell. Separating the contributions from lattice and internal motion to the cloudy pattern in reciprocal space is difficult. However, by calculating the Fourier transform of the diffuse scattering intensities, i.e. the “diffuse Patterson map”⁵⁴, the data are transformed into a readily interpretable form (Fig. 3D, bottom left). The diffuse Patterson represents electron density fluctuations as a function of pairwise distance between atoms. The part of this map near the origin (e.g. smaller than the size of the protein) is affected by correlations that are short-ranged, while further from the origin, the correlations between unit cells predominate. To reveal the correlations from protein dynamics, one option is to simulate the diffuse Patterson from the lattice dynamics model (Fig. 3D, bottom center) and subtract it from the experimental Patterson. However, this must be done very carefully, as any errors in the model could produce spurious signals. A safer approach is to simulate internal motions riding on top of lattice motions (Fig. 3D, bottom right) and to check whether adding internal motions improves agreement in this central region of the Patterson. Importantly, model-data agreement should be checked with both datasets, Bragg and diffuse. Thus, the combination of internal and lattice motions should agree with the B-factors.

Fitting a dynamical model to diffuse scattering and B-factors simultaneously is a long-standing goal of this field⁸¹ that has yet to be realized in a robust way. However, it is generally possible to derive several realistic candidate models of protein dynamics from the B-factors corrected for lattice disorder and rank them according to agreement with the diffuse Patterson. Such an approach has the additional advantage of illustrating how well the data discriminate between candidates. Although there is not yet an unbiased indicator to prevent overfitting that is comparable to R_work/R_free in conventional crystallographic refinement, we can employ the dynamical equivalent of the omit map by testing whether model refinement with certain motions of interest suppressed worsens the model-data agreement⁵⁴.

As in conventional crystallography, multiple metrics should be used for assessing model accuracy. In using model-data correlations (CCs), it is important to note that the intense halos will dominate the statistics. One way to put lattice and internal motion on a more equal footing is to focus on the central part of the Patterson only for computing CCs⁵⁴. Although CCs are useful, they are normalized by the variance in each resolution shell, and thus it is important to verify that the model correctly predicts the signal strength (variance) vs. resolution⁶⁸. It should be noted that diffuse scattering patterns tend to correlate with the molecular transform, and therefore even a very crude model can easily obtain CCs of ~0.5⁴⁹. Substantially better agreement is needed to establish the accuracy of a model.

Challenges and Opportunities for the Future

Over the past several decades, the importance of correlated motions in protein function has become increasingly apparent. However, as with all areas of protein science, the information we can obtain by examining the properties of one specific protein sequence is limited. In truth, all proteins have evolutionarily related counterparts, which may display similar yet divergent behaviors. Thus, an emerging trend is to use evolution as an additional dimension to understand protein functions by comparing sequences that share the same evolutionary origin^82,83. In the context of enzyme catalysis, the utility of this approach is exemplified by studies on DHFR, where coupled networks of residues were identified by mixed quantum/classical MD simulations of the hydride transfer reaction and correlated with sequence conservation across multiple organisms³³. In a later study³⁹, a curated MSA of DHFR was constructed in order to identify rare events that demark changes from one invariant sequence motif to another. The dynamic pattern of the active-site Met20 loop from one species was engineered into that of another by substituting divergent sites with evolutionary significance identified in this way³⁹. Statistical coupling analysis (SCA)³⁸ of an MSA of DHFR also revealed coevolving residues that form a contiguous network in the structure and show strong correlation with residues identified by NMR to be involved in millisecond dynamics during the catalytic cycle³⁵.

In addition to comparing extant sequences from different organisms, sequences resurrected by ancestral sequence reconstruction can be compared with extant homologs to track the evolutionary trajectory of correlated motions and their role in protein function⁸⁴. For example, Zou et al.⁸⁵ utilized MD simulations to compare the dynamics of a β-lactamase specific for penicillin degradation with its ancestral counterparts, which show promiscuity but no substantial structural differences. They were able to identify regions with altered dynamics and key residues that contribute to the difference, signifying the importance of dynamics in the tradeoff between activity and specificity in the evolution of β-lactamase.

Conformational dynamics are also thought to be a key contributor to protein evolvability^86,87, defined as the ability of proteins to adopt new functions through mutations. According to this view, protein fluctuations sample minor conformations that serve as precursors for new functions. To test such intriguing proposals, directed evolution of novel enzymes is of particular interest, where sequences from different iterations may be compared to elucidate the relationship between correlated motions and changes in traits^83,88,89. As an example, variants of artificial retro-aldolases that were produced by directed evolution⁹⁰ were later examined by MD⁸⁹, and a population shift toward catalytically competent arrangement of active-site residues was observed along the evolutionary pathway, which interestingly, also included distal mutations. With a novel algorithm, residues exhibiting correlated motions were also inferred from the MD trajectory which further rationalized the conformational conversion. Recently, directed evolution of a bifunctional ancestor enzyme was demonstrated using a library of mutants with altered backbone dynamics generated by transposon-based random insertions or deletions (indels)⁹¹.

As evident from the examples above, the emerging interest in evolution of correlated motions relies heavily on the synergy between computational and experimental methods. We see several opportunities for advancing these studies with total scattering analysis. Perhaps the most critical area is in improving the accuracy of MD. With the recent advance in measurement, it has become clear that all-atom MD is not yet able to accurately predict correlated motions implied by diffuse scattering⁵⁴. A major contributor to this discrepancy is the fact that the predictive ability of MD (RMSD of ~0.4 Å for triclinic lysozyme⁹²) cannot match the coordinate precision of Bragg diffraction (~0.03 Å for PDB 6o2h⁹³), which has a cascading effect on the ability of MD to predict the diffuse signal⁵⁴. In the future, methods to restrain or otherwise improve MD using total scattering data will be of great importance, both for the accuracy of the simulation itself and for gaining atomistic insight into correlated networks in proteins. Integration of multiple experimental methods will also lead to a deeper understanding of the information contained in different types of data. Of particular interest is combining total scattering analysis with solid-state NMR, which can both be performed on protein crystals⁹⁴. Finally, the quest to understand the link between evolutionary sequence correlations and functional dynamics represents a grand challenge in molecular biophysics (Fig. 4). From sequence analysis, it is clear that selection pressure drives certain groups of residues to coevolve and that these groups can highlight areas of functional importance in a structure⁹⁵. In the case of the PDZ domain, a deep double-mutational library of multiple homologs was experimentally characterized to show that the SCA matrix couplings can have thermodynamic interpretation⁹⁵. However, a general connection between co-evolving residues and motion has not been established. Thus, direct comparisons between theory and dynamic experiments will play a crucial role in in gaining a precise understanding of how correlated motions can be predicted from sequence.

Figure 4.

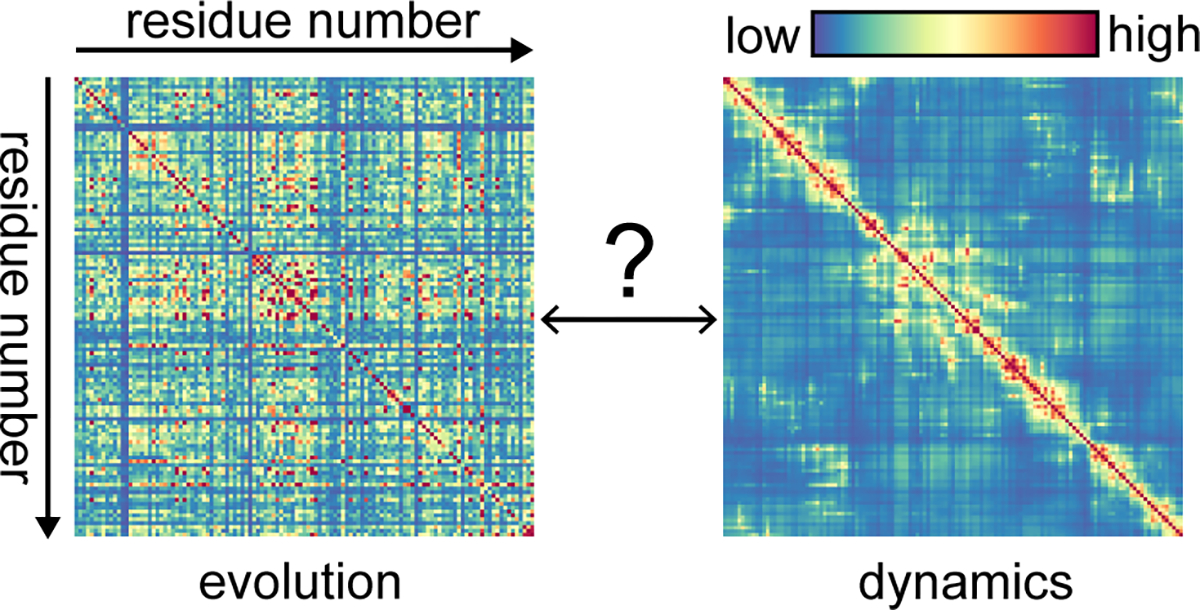
Evolutionary and dynamic perspectives on residue-residue correlations. (Left) Evolutionary correlation according to SCA⁴¹ applied to an MSA of a hydrolase family that contains lysozyme (Pfam PF00062). (Right) Displacement correlations⁹⁶ in lysozyme according to an ENM derived from total scattering analysis (Fig. 3). Establishing the connection between these two perspectives is necessary to fully understand protein function and allostery.

To bring total scattering analysis to a wider audience, several areas of development are of high priority. The first is to get around the issue of crystal size for room-temperature studies. Although we recommend maximizing signal to noise with large (>100 μm) crystals, inevitably, we will need to work with smaller ones in a serial fashion, i.e. by collecting one or a few frames of images from many crystals. We see no fundamental reason why such experiments cannot be done at synchrotrons or X-FELs today, however accurate measurement of total scattering has special requirements for the X-ray detector, properties of the beam such as divergence and energy bandwidth, and sample environment. The primary requirements for a detector are that photons are detected directly (i.e. via a semiconductor), that dynamic range is sufficient to measure Bragg peaks and diffuse scattering simultaneously, and that any variability in pixel response is well-characterized. We must also consider how to minimize background scattering and computationally correct for sources that can’t be eliminated. One promising experimental approach is to eschew X-ray windows and instead use humidified helium gas to prevent crystal dehydration⁹⁷. Second is the issue of data processing software. As with all structural techniques, the availability of user-friendly software packages will be important for bringing total scattering analysis to a wide audience. This is contingent on standardization in the field, and we hope that our recommendations for data collection, processing, and validation will accelerate this process. Finally, we foresee a potential for machine-learning methods in the future, either in data processing or in interpretation of total scattering data⁹⁸. For example, it would be of great interest to use machine-learning to classify signals that are from different types of motion. Towards such a goal, we as a community must first produce the learning data, namely, a collection of total scattering datasets that are fully understood.

These are exciting times to be a structural biologist. With technical breakthroughs in cryo-EM and X-ray diffraction experiments, we have an unprecedented array of tools to address virtually any structural question. But perhaps more importantly, these methods give a new window into the correlated motions of proteins. We anticipate that in the coming decade, total scattering will provide a much-needed bridge between dynamics on short time scales from NMR and MD with highly precise structural measurements required for insight into chemical mechanism. Especially when combined with bioinformatic approaches to evolution, structural biology may finally answer the question that started the field: how does allostery work?

ABBREVIATIONS

EM

electron microscopy

XFEL

X-ray free electron laser

MSA

multiple sequence alignment

ENM

elastic network model

MD

molecular dynamics

CAP

catabolite activator protein

DHFR

dihydrofolate reductase

NMR

nuclear magnetic resonance

TLS

translation libration screw-axis

CC

correlation coefficient

PDB

Protein Data Bank

RMSD

root mean squared distance

SCA

statistical coupling analysis