Abstract
Paclitaxel (PTX) is a major chemotherapeutic drug that is effective against a wide variety of cancers, particularly breast, ovarian and lung cancer. For a weakly basic chemotherapeutic drug such as PTX, the development of the acidic tumor microenvironment (Warburg effect) has a remarkable impact on therapeutic resistance. The present approach takes advantage of the acidic tumor microenvironment by incorporating lansoprazole (LAN), a proton pump inhibitor (PPI), with PTX as a potent therapeutic combination that is capable of reversing PTX resistance. To deliver optimal amounts of the drugs to neoplastic cells, a nano drug delivery system was selected. To design the nanoformulation process in a limited framework, typical formulation parameters were optimized and validated by the application of response surface methodology (RSM) using Box–Behnken design (BBD). On the basis of critical quality aspects, the experimental design helped to determine the optimal particle size (243.7 nm), zeta potential (−9.14 mV) and encapsulation efficiencies (88.91% and 80.35% for PTX and LAN respectively). The optimized formulation (PTX–LAN–PLGA-NPs) exhibited sustained in vitro release profiles over 384 hours for both the encapsulated drugs. The Korsmeyer–Peppas model was found to be the best fitted model for the release kinetics, where the release mechanism follows Fickian diffusion. In in vitro anti-tumor efficacy experiments using Michigan Cancer Foundation-7 (MCF-7) breast cancer cells, the PTX–LAN–PLGA-NPs exhibited a steep decrease in cell viability compared to the pure drugs. Taken together, the results strongly support that incorporation of PTX and LAN in nanoparticles (NPs) is a promising approach for cancer chemotherapy.
Development of statistically optimized, paclitaxel–lansoprazole, dual drug loaded PLGA nanoparticles as a promising tumor acidic microenvironment targeted chemotherapeutic approach.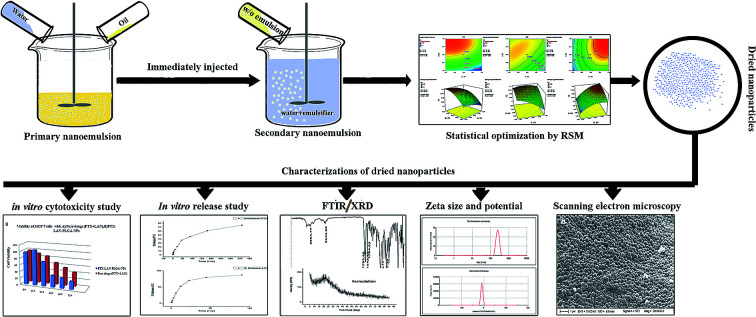
1. Introduction
Pharmaceutical ‘quality by design’ (qbd) is a scientific approach based on understanding the influences of process parameters through quality risk management. It involves the identification of independent variables or factors that affect the product or process, followed by studying their effects on a dependent variable or response. In contrast to conventional design, each process parameter is varied keeping other factors are kept constant. This approach has gained popularity since its recent promotion by regulatory agencies, including the United States Food and Drug Administration (USFDA), the European Medicines Agency (EMEA), and the Medicines and Health Products Regulatory Agency (MHRA). In the literature, various experimental designs are available; however, in the present study, Box–Behnken design (BBD) was found to be highly suitable to fabricate optimized products with a minimum number of experiments.1–3
Paclitaxel (PTX) is a well-known member of the anti-neoplastic family; it is popular due to its broad spectrum of activity with a unique mechanism of action. PTX acts as a microtubule-stabilizing agent that selectively disrupts microtubule dynamics, which leads to mitotic arrest and finally results in cell death. It has been found to be effective in treating various forms of advanced and refractory cancers, including colon, bladder, Kaposi's sarcoma, and lung cancer, and is considered to be the best treatment option for ovarian and breast cancer.4–6 Researchers at the Johns Hopkins Oncology Center reported 30% and 56% PTX response rates in patients with advanced ovarian cancer and metastatic breast cancer, respectively.7 The National Cancer Institute (NCI) considers this drug to represent the most significant advancement in chemotherapy in the past 15 to 20 years.6
Despite having a remarkable anti-tumor activity, resistance remains a major issue that limits the therapeutic efficacy of paclitaxel. Among the contributing factors, the acidic tumor microenvironment is a well-known factor in developing chemoresistance, which weakens and overcomes antitumor efficacy. The “Warburg effect,” consisting of hypoxia and altered glycolysis, creates a hostile acidic environment, where the cells upregulate several classes of proton exchangers that extrude H+ ions outside the intracellular environment as a survival mechanism. This process enables cells with aggravating malignant features to proliferate.8,9
Various studies have shown that among proton pumps, V-ATPases are associated with multidrug resistance,10 which can be reversed simply by using proton pump inhibitors.8 As prodrugs, they utilize acidic pH and protons for their activation;11,12 therefore, they can selectively target cancer cells in the acidic microenvironment and act as irreversible blockers of hydrogen/potassium adenosine triphosphatase (ATPase).13 The auxiliary effects of proton pump inhibitors (PPIs) against different cancers were previously demonstrated in both pre-clinical and clinical studies, with very few side effects. PPIs can target major malignant properties of a cancer cell, such as invasiveness, migration, proliferation and drug resistance, by decreasing tumor acidity.8,14,15 These drugs can also act as chemosensitizers or provide direct effects as antitumor agents.10,16 Among the members of its family, lansoprazole (LAN) exhibits the greatest effectiveness against tumor cells, even at lower concentrations.15,17 Hence, in this regard, a combination of PTX–LAN should be advantageous due to the synergistic effects of the drugs and the suppression of drug resistance.
However, the selection of an effective drug delivery system (DDS) that delivers optimal amounts of drugs to the targeted neoplastic cells, enhances drug efficacy and decreases adverse effects while leaving healthy tissues untouched, is highly difficult.18,19 Recent developments in the field of nanotechnology have opened several arenas of controlled and targeted delivery for combination chemotherapeutics. Nanocarrier-mediated combination chemotherapy offers the advantages of a low toxicity profile, passive targeting by enhanced permeability and retention (EPR) effects, and potential inhibition of drug resistance by influencing intracellular endocytic uptake.20 In contrast with APIs administered separately, when drugs are combined in a single nanocarrier system, the exposure of each drug in the body can be controlled more precisely, which may translate into synergistic action.21
Hence, the main goal of this work was to develop a statistically optimized polymeric nano drug delivery system that combines PTX with LAN. The nanocarrier system addressed the major physicochemical hindrances of the drugs, such as the poor water solubility of PTX and the instability of LAN in heat, light and acidic media. The determinant factors of the dual drug (PTX–LAN)-loaded nanocarrier system were optimized using Box–Behnken design to determine the formulation with the most appropriate physicochemical properties for prolonged therapeutic response. PLGA was used in this study because it demonstrates biocompatibility and biodegradation and thus is a suitable candidate for our intended response.22
2. Materials and methods
2.1. Materials
Paclitaxel and lansoprazole samples were received as gifts from Fresenius Kabi Oncology Ltd., Kolkata, West Bengal and Aurobindo Pharma, Hyderabad, respectively. Acid-terminated poly d,l-lactide-co-glycolide (PLGA, 50 : 50, M.W. 38 000–54 000, Resomer® RG 504H) and polyvinyl alcohol (PVA, M.W. 31 000 to 50 000 and 98% to 99% hydrolyzed) were purchased from Sigma-Aldrich (Germany). Reagents such as dichloromethane (DCM) and sodium bicarbonate were of analytical grade and were obtained from Merck Life Science Private Limited, Mumbai, India. Ethanol was purchased from Merck KGaA, Germany. The dialysis bag (i.d. 14.3 mm, molecular weight cutoff 12 000 to 14 000 Da) was obtained from Hi Media, Mumbai, India. Deionized water was acquired from a Milli-Q system (Merck Millipore) at the Bioequivalence Study Centre, Jadavpur University, Kolkata-32, West Bengal. Human breast cancer cells (MCF-7) were obtained from the National Centre for Cell Science (Pune, Maharashtra, India).
2.2. Methods
2.2.1. Preparation of paclitaxel and lansoprazole dual drug-loaded nanoparticles (PTX–LAN–PLGA-NPs)
Dual drug-loaded NPs were prepared by a double emulsion solvent evaporation method using PTX and LAN in combination. The process involved a series of nanoformulations that were designed to limit the major drawbacks associated with the delivery of the concerned drugs. Major process parameters, such as the concentration of PVA in the primary emulsion, the amount of PLGA and the stirring speed of the homogenizer, were varied at 3 levels (Table 1). The aqueous phase contained PVA solution, whereas the oil phase contained drugs and polymer dissolved in a solvent mixture of DCM and ethanol (7 : 3, 3 mL). The primary emulsion was produced by dropwise addition of the aqueous phase to the organic solution under high speed (25 000 rpm) homogenization (IKA T10 basic Turrax Ultra homogenizer) for 2 minutes. Further, the prepared w/o emulsion was added gently to the PVA solution (60 mL, 2%) and re-emulsified by homogenization for 4 minutes. The final w/o/w emulsion was stirred (at 180 rpm) for 6 hours using a magnetic stirrer for complete removal of organic solvent. A few drops of ammonia solution (2.5% v/v) were added to the secondary emulsion in order to maintain a pH of 8 during the solidification process of the NPs. To fabricate NPs free from excess surfactant (PVA) and unloaded drugs, the resulting solution was centrifuged (3K30, Sigma) at a speed of 16 000 rpm for 30 minutes and the NPs were collected and washed thrice with deionized Milli-Q water. The obtained PTX–LAN–PLGA-NPs were freeze dried at −60 °C and maintained for further analysis.
Experimental domain of the 33 Box–Behnken design approach and determined responses.
| Independent Variables | Levels | Dependent Variables | ||
|---|---|---|---|---|
| −1 | 0 | +1 | ||
| PVA concentration in % w/v (X1) | 1 | 2 | 3 | Particle size in nm (Y1) |
| Amount of polymer (PLGA) in mg (X2) | 50 | 100 | 150 | Zeta potential in mV (Y2) |
| Homogenizing speed in rpm (X3) | 10 000 | 20 000 | 30 000 | Encapsulation efficiency in % (Y3 for PTX and Y4 for LAN) |
| Run | Factor X1 PVA (%) | Factor X2 PLGA (mg) | Factor X3 speed (min−1) | Response Y1 Particle size (nm) | Response Y2 ZP (mV) | Response Y3 EE (%) | Response Y4 EE (%) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 0 | 258.92 | 1.7 | 34 | 41 |
| 2 | 0 | 1 | 1 | 264.49 | 9.4 | 85 | 77 |
| 3 | 0 | 0 | 0 | 302.73 | 7.8 | 61 | 54 |
| 4 | −1 | −1 | 0 | 327.71 | 3.9 | 21 | 15 |
| 5 | 0 | 0 | 0 | 294.26 | 6.9 | 58 | 53 |
| 6 | 1 | 0 | 1 | 240.57 | 6.8 | 68 | 60 |
| 7 | 0 | 0 | 0 | 308.51 | 7.5 | 56 | 48 |
| 8 | 0 | −1 | −1 | 341.31 | 2.4 | 29 | 26 |
| 9 | 1 | 0 | −1 | 379.32 | 3.2 | 45 | 42 |
| 10 | −1 | 1 | 0 | 373.94 | 8.7 | 47 | 44 |
| 11 | 0 | −1 | 1 | 252.67 | 3.1 | 41 | 35 |
| 12 | 0 | 0 | 0 | 298.51 | 7.8 | 59 | 57 |
| 13 | 1 | 1 | 0 | 283.19 | 6.8 | 82 | 74 |
| 14 | 0 | 0 | 0 | 295.21 | 7.6 | 66 | 57 |
| 15 | −1 | 0 | 1 | 357.67 | 6.9 | 38 | 29 |
| 16 | −1 | 0 | −1 | 428.92 | 7.2 | 30 | 25 |
| 17 | 0 | 1 | −1 | 406.95 | 5.8 | 54 | 45 |
2.2.2. Experimental design
According to the results obtained in preliminary trials, the PVA concentration in the primary emulsion (% w/v) (X1), amount of PLGA (mg) (X2) and homogenizing speed (rpm) (X3) were found to be the major dominant independent variables strongly influencing the responses, including particle size (nm) (Y1), ZP (mV) (Y2) and EE (%) (Y3 and Y4), for the PTX–LAN–PLGA-NPs. In the present study, BBD was selected because of its suitability to explore different response surfaces together with the construction of rotatable or nearly rotatable second-order polynomial designs23,24 with slightly better efficacy in comparison with other methods (central composite, Doehlert matrix and three-level full factorial design).3,25 BBD contains fewer design points and is less expensive than central composite design while possessing the same number of factors.1,2
In the experimental section, the design consisted of 17 combinations of independent variables whose coded levels were developed using Design Expert Trial version 7 software (State-Ease Inc, Minneapolis, MN, USA) (Table 1). In accordance with the combinations, the experiments were performed for three factors at three levels to study the effect of each independent variable on the dependent variables (response variables). The combinations indicate the coordinates at the mid-point of each edge (eight), the center point of each surface of the cube (six) and the three replicated center points of the cube. The experiments were continued further with feeding of the response data into the concerned response surface quadratic design, and the responses were analyzed by ANOVA to select the model that fitted best to the data. The study utilized ANOVA tests along with regression analysis performed in each trial, where the response (Yi) was measured by the formula given below.
| Yi = b0 + b1X1 + b2X2 + b3X3 + b4X1X2 + b5X1X3 + b6X2X3 + b7X12 + b8X22 + b9X32 | 1 |
where Yi = measured response; b0 = intercept of the polynomial equation; b1–b9 = regression coefficients regarding respective independent variables, including the main effects (X1, X2, and X3), interacting effects (X1X2, X1X3 and X2X3) and quadratic effects (X12, X22, and X32).26,27
Acceptance of the model was considered on the basis of p values <0.05 and reasonable agreement between the predicted and adjusted correlation coefficients. A significant model was established with suitable values of b-coefficients, p-values, and F-values with all other statistical parameters, including multiple correlation coefficients (R2), adjusted multiple correlation coefficients (adjusted R2), predicted multiple correlation coefficients (predicted R2) and lack of fit.
2.2.3. Optimization and validation of the model
A multi-criteria methodology is applied when various responses must be considered at the same time and it is necessary to determine optimal compromises between the total numbers of the responses taken into account. The desirability function, which is a geometric mean of all transformed responses, is the most important and most currently used multi-criteria methodology for optimization.28 In the present study, we utilized a desirability function to create the best fitted values of the operating variables to obtain desirable responses in compliance with the selected criteria.24,29 In the optimization section, a few suggestions were obtained by the software based on the desired outputs of particle size (minimum), ZP (maximum) and EE (maximum) of the nanoformulation. Among these solutions, three were randomly chosen as checkpoint combinations to perform experiments. The error percentages were calculated by comparing the values obtained from the predicted and experimental formulations. The validation of the present statistical experimental design was associated with the performance of these random checkpoint formulations.3,30,31 Moreover, the optimized formulation was selected from the checkpoint list in view of the maximum value of desirability and the minimum percentage of errors and was further utilized for nanoformulation batch preparation and characterization.
2.2.4. Characterization
2.2.4.1. Fourier transform infrared (FTIR) spectroscopy
FTIR (Nicolet iS10, Thermo Fisher Scientific, USA) studies were performed to analyze the integrity of the components used in the formulation. The FTIR spectra of PTX, LAN, PLGA, the PTX–LAN–PLGA physical mixture and the PTX–LAN–PLGA-NPs were recorded in the solid state over the scanning range of 400 cm−1 to 4000 cm−1.
2.2.4.2. Differential scanning calorimetry (DSC)
Differential scanning calorimetry was performed to identify the final states of the encapsulated drugs and to investigate possible interactions between the drugs and the polymer. Typical phase transitions such as glass transitions and endothermic transitions were compared among the raw drugs (PTX, LAN), their physical mixture (PTX–LAN–PLGA), blank PLGA-NPs and PTX–LAN–PLGA-NPs using a DSC (Perkin Elmer Pyris Diamond DSC, Central research facility, IIT, Kharagpur) instrument. The test samples were sealed in an aluminum pan and analyzed from 5 °C to 350 °C at a heating rate of 10 °C per minute under a constant flow of nitrogen (40 mL per minute).
2.2.4.3. X-ray diffractometry
X-ray diffractometry (XRD) analysis was performed to diagnose the physical states (crystalline or amorphous) of the entrapped drugs embedded within the NPs. The XRD patterns of PTX, LAN, PLGA, the physical mixture, blank PLGA NPs and the PTX–LAN–PLGA-NPs were acquired using an Ultima-III instrument (Rigaku; Met. & Mat. Engg. Dept., Jadavpur University), in which the samples were exposed to X-radiation emitted from a Cu source with a Kβ filter. The system was operated in continuous mode at a voltage of 40 kV and a current of 30 mA. In the solid state, all the samples were analyzed directly in a 2θ scanning range of 5° to 90° at a rate of 2° per minute with a stepwise increment of 0.05°.
2.2.4.4. Surface morphology
The surface morphology of the formulated PTX–LAN–PLGA NPs was studied by scanning electron microscopy (EVO 18, Special Edition, ZEISS). A tiny amount of sample was mounted on a receiver plate fitted with carbon adhesive tapes, and excess sample was removed by a hand blower. Then, the receiver plates were exposed for gold coating (Quorum Q150T ES) and analyzed directly by the scanning electron microscope to study the morphology of the optimized nanoformulation. In the scanning electron microscope, the data were captured at two different magnification levels (10 000× and 20 000×).
2.2.4.5. Particle size and zeta potential measurements
For the particle size measurements, pre-weighed (0.1%) PTX–LAN–PLGA-NPs were properly diluted in deionized water and sonicated for 5 minutes to form a uniform dispersion before placing the sample suspension in a quartz cuvette.23 Finally, the resulting suspension was used for the determination of the average particle size and ZP of the prepared NPs using a Zetasizer Nano ZS90 instrument (Malvern Instruments, United Kingdom).
2.2.5. Drug encapsulation efficiency
The EE was analyzed by quantifying the drugs entrapped within the PTX–LAN–PLGA-NPs using the LC-MS/MS system (API2000, Absciex). NPs (10 mg) were dissolved in dichloromethane to extract PTX and LAN from the polymer matrix. Then, the dissolved samples were precipitated with methanol (1.3 mL) and mixed in a vortex mixer for 5 minutes. After that, the samples were centrifuged at 12 000 rpm at 4 °C for 10 minutes to collect the supernatant. The clear solution (supernatant) was kept under a constant nitrogen flow at a temperature of 25 °C for complete evaporation of the solvents. The dried sample was further reconstituted with a combination of methanol and water (1 : 1, 100 μL) and assayed directly by injecting it into the LC-MS/MS system. The instrumental run was carried out with a validated LC-MS/MS method using a C18 column and a mobile phase combination of ACN and 2 mM ammonium acetate (70 : 30). Later, the EE (%) and drug loading (DL%) values were calculated using the equations below.28,30
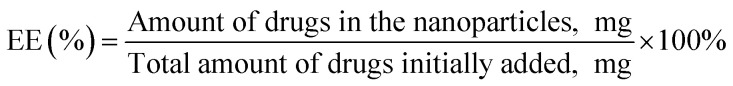 |
2 |
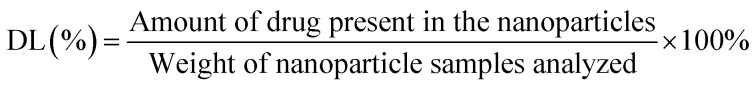 |
3 |
2.2.6. In vitro release and drug release kinetics studies
The in vitro release study was carried out in medium containing phosphate buffer saline (PBS) at pH 7.4 under sink conditions.32,33 A pre-weighted (10 mg) sample of the optimized PTX–LAN–PLGA-NPs was suspended in 5 mL of buffer solution containing 1% Tween 80 and packed in an end-sealed dialysis membrane bag. The packed bags were maintained in a water bath shaker containing 100 mL of buffer solution containing Tween 80. The study was carried out at 37 ± 0.5 °C under the influence of continuous shaking at 100 rpm.32 The total amount of NPs was that where the total amount of drugs inside the particles was less than 10% of their solubility limit in PBS, which ensures perfect in vitro release conditions of a hydrophobic drug. The samples were withdrawn at 0 hour, 1 hour, 2 hours, 4 hours, 6 hours, 12 hours, 24 hours, 48 hours, 96 hours, 192 hours and 384 hours.33,34 At each time point, samples (500 μL) were collected and replaced with the same volume of PBS to maintain equilibrium. The samples obtained at different time points were centrifuged at 12 000 rpm for 5 minutes and the supernatant was collected. The DCM present in the supernatant solution was allowed to evaporate completely, and the residue was reconstituted with a combination of methanol and water (1 : 1, 100 μL). The drug content in each withdrawn sample was measured by the previously validated LC-MS/MS method.
The kinetics of PTX and LAN release from the optimized nanoformulation were determined by fitting the obtained data to various kinetic models,35–40 including the zero order release model (eqn (4)), first order release model (eqn (5)), Higuchi model (eqn (6)) and Korsmeyer–Peppas model (eqn (7)):21,31
| Qt = k0t | 4 |
| log Q0 − log Qt = k1t/2.303 | 5 |
| Qt=kH√t | 6 |
| Qt = kKPtn | 7 |
where, t = time, Qt = amount of drug released at time t, Q0 = initial amount of drug in the nanoparticles, k0 = zero-order rate constant, k1 = first order rate constant, kH = Higuchi constant, kKP = rate constant in the Korsmeyer–Peppas model equation, n = release exponent.
2.2.7. In vitro cytotoxicity study
The in vitro cytotoxicity of the PTX–LAN–PLGA-NPs was determined in MCF-7 cells using the MTT assay method. This assay is based on the reduction of a yellow tetrazolium salt, 3-[4,5-dimethylthiazol-2-yl]-3,5-diphenyltetrazolium bromide dye (MTT), to a purple formazan product based on the metabolic capacity of cellular mitochondrial succinate dehydrogenase. In this study, the cells were cultured in Eagle's Minimum Essential Medium (MEM; Hi-media), supplemented with fetal bovine serum (10% v/v, Hi-media) and penicillin–streptomycin (1%, Gibco), in a CO2 incubator (Heraeus, BB 15, Function Line, Thermo Fisher Scientific) at 37 °C with 5% CO2 and 95% relative humidity. After reaching confluence of 1 × 104 cells per well, the cells were seeded in 96-well flat-bottom plates and allowed to adhere for a period of 24 hours in an incubator under the same conditions described above. PTX–LAN–PLGA-NPs and a raw drug mixture (PTX and LAN, concentrations 25 μg mL−1 each) were added to separate wells after separate dilution in culture medium (100 μL) and were incubated for 24 hours, 48 hours, 60 hours and 72 hours. At each time point, MTT (Sigma-Aldrich Co.) solution (100 μL, 5 mg mL−1 in PBS) was added and incubated at 37 °C for 4 hours. To dissolve formazan crystals, DMSO (100 μL) was added, followed by incubation for 30 minutes. The same procedure was performed with MCF 10A mammary gland breast cells to determine the cytotoxicity of the PTX–LAN–PLGA-NPs. The absorbance of each well was measured at 570 nm using a microplate reader (multimode plate reader, SpectraMax M5; Molecular Devices, CA, USA). The cell viability was calculated by the following equation using untreated cells as the negative control indicating 100% viability.41,42
 |
8 |
where Abstest cells = the amount of formazan determined for cells treated with each different formulation, Abscontrol cells = the amount of formazan determined for the control cells.4
3. Results and discussion
3.1. Preparation of nanoparticles
The preparation of dual drug-loaded NPs was the major challenge in this work. Therefore, the formulation was carried out in a controlled environment based on the typical demands of the drugs encapsulated into the polymeric matrix. PTX exhibits a common delivery problem in that it tends to aggregate as crystals very readily in a formulation.43 On the other hand, inclusion of LAN may create another critical hurdle due to its instability to heat, light, and acidic environments44 if adequate measures are not taken. An effective method was successfully developed by carefully controlling these parameters with the aid of statistical optimization. One of the prime features of the dual drug-loaded nanoformulation (PTX and LAN) was the solubilization of the drug based on a co-solvent approach. Due to the structural complexity of its diterpenoid ring system substituted with hydrophobic units, PTX is a highly lipophilic drug45 with a high log P value (∼4) and low aqueous solubility (<0.01 mg mL−1).7 Due to the absence of ionizable functional groups in the structure, the common methods to increase water solubility, including alteration of pH, salt formation and addition of charged complexing agents, are not suitable for PTX.6,45 Increase of water solubility can be a contributing factor that decreases the dosage and toxicity of PTX.46 Additionally, the drug loading in nanocarriers is influenced by the relative distribution of the drug between the polymeric phase and the aqueous phase, which depends largely on the solid-state solubility of the drug in the nanocarrier matrix. A mixed solvent system of DCM: ethanol (7 : 3) was found to be extremely effective to dissolve both the drugs and polymer; it offered substantial stability to the drugs in the nanoemulsion system with a high EE. On the other hand, the instability of LAN in organic solvents due to the development of acidic pH, which probably arises due to the carboxylic groups of the polymer (PLGA 50 : 50),32 was addressed by carefully maintaining the pH at 8. Because it is a lipophilic weak base with a pKa of 4, LAN appears to be especially sensitive compared to other members of the PPI family.44 The pH of the nanoemulsion was maintained by mixing sodium bicarbonate in the aqueous phase during preparation of the primary and secondary emulsions. Further, the sensitivity associated with heat was minimized by controlling the temperature at 20 °C during the process of emulsification. The solvent evaporation process was carried out for 12 hours in a dark room to limit light-catalyzed degradation reactions.
3.2. Statistical optimization
Optimization refers to improving the performance of a system, a process, or a product in order to obtain the maximum benefit from it. In this work, BBD was utilized to prepare PTX–LAN–PLGA-NPs according to the desired particle size (small), ZP (high) and EE (high). It was applied to decrease variation in the process and optimize the nanoformulation to obtain desirable properties. Unlike the traditional one-variable-at-a-time method, BBD includes the interactive effects of the variables; therefore, it exhibits the complete effects of the independent parameters on the response. It contains fewer design points and decreases the number of experiments necessary to conduct the study, which saves time and expense as well as consumption of reagents and materials.28 In the selected range of independent variables, responses were shown to vary at its maximum extends. The parameter levels were expressed in codes (−1, 0, +1); a positive sign represented a synergistic effect, while a negative sign indicated an antagonistic effect.23 Data were analyzed using Stat-Ease Design Expert software to obtain analysis of variance (ANOVA), regression coefficients and regression equations. Mathematical relationships were generated using multiple linear regression analysis; these equations represented the quantitative effects of the independent parameters on the response variables. The coefficients with more than one factor term and with higher order terms exhibited interaction terms and a quadratic relationship, respectively.24 BBD was used to optimize and evaluate the main effects, interaction effects and quadratic effects of the independent variables on the particle size, ZP and EE. The experimentally measured responses of the optimal batch of the nanoformulation were close to the predicted responses generated by the design. Each of the dependent variables is discussed below with respect to the independent variables.
3.3. Evaluation of particle size
Particle size and size distribution (PDI) are two major characteristics of NPs that have significant impacts for its prospective application. For an anticancer nanoformulation, size plays a major role in invading the leaky vasculatures of cancer cells for execution of therapy.47 In 17 consecutive runs, the present quadratic model represented a wide variation of particle sizes (240.57 nm to 428.92 nm) (Table 1). Based on its F-value of 183.97, this model is significant, with only 0.01% chance that this value could occur due to noise. Furthermore, the “Lack of Fit F-value” of 0.66 implied that this value is not significant relative to the pure error. There is a 61.89% chance that this value could occur due to noise. Considering their p values < 0.05, the model terms X1, X2, X3, X1X3, X2X3, X12, X22 and X32 were found to be significant (Table 2). The predicted coefficient value of 0.9733 showed a good correlation with the adjusted coefficient value of 0.9904. Additionally, the “Adeq Precision” value of 46.11 is a sufficient indicator that this model can be used to navigate the design space. The following polynomial equation represents the best description of the particle size after eliminating insignificant terms (p > 0.05).
| Y1 = 299.84 − 40.78X1 + 18.49X2 − 55.14X3 − 16.88X1X3 − 13.45X2X3 + 23.18X12 − 12.08X22 + 28.60X32 | 9 |
ANOVA for the mean particle size (Y1), zeta potential (Y2), encapsulation efficiency for paclitaxel (Y3) and encapsulation efficiency for lansoprazole (Y4).
| Source | Particle size | ZP | EE for PTX | EE for LAN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SS | F value | P > F value | SS | F value | P > F value | SS | F value | P > F value | SS | F value | P > F value | |
| Model | 48 720.49 | 183.97 | <0.0001 | 85.82 | 98.45 | <0.0001 | 5229.87 | 50.69 | <0.0001 | 4449.95 | 32.03 | <0.0001 |
| X 1 | 13 304.07 | 452.13 | <0.0001 | 8.41 | 86.78 | <0.0001 | 1081.13 | 94.30 | <0.0001 | 1352 | 87.59 | <0.0001 |
| X 2 | 2736.52 | 92.99 | <0.0001 | 48.02 | 495.78 | <0.0001 | 2556.13 | 222.96 | <0.0001 | 1891.13 | 122.52 | <0.0001 |
| X 3 | 24 321.15 | 826.54 | <0.0001 | 7.22 | 74.54 | <0.0001 | 684.5 | 59.71 | 0.0001 | 496.13 | 32.14 | 0.0008 |
| X 1 X 2 | 120.56 | 4.09 | 0.0826 | 0.02 | 0.23 | 0.6445 | 121 | 10.56 | 0.0141 | 4 | 0.26 | 0.6264 |
| X 1 X 3 | 1139.06 | 38.71 | 0.0004 | 3.80 | 39.26 | 0.0004 | 56.25 | 4.91 | 0.0623 | 49 | 3.17 | 0.1180 |
| X 2 X 3 | 724.15 | 24.61 | 0.0016 | 2.10 | 21.71 | 0.0023 | 90.25 | 7.87 | 0.0263 | 132.25 | 8.57 | 0.0221 |
| X 1 2 | 2262.47 | 76.89 | <0.0001 | 2.05 | 21.15 | 0.0025 | 464.21 | 40.49 | 0.0004 | 306.00 | 19.82 | 0.0030 |
| X 2 2 | 614.89 | 20.89 | 0.0026 | 10.08 | 104.10 | <0.0001 | 51.58 | 4.49 | 0.0716 | 13.27 | 0.86 | 0.3847 |
| X 3 2 | 3442.96 | 117.01 | <0.0001 | 2.68 | 27.65 | 0.0012 | 76.05 | 6.63 | 0.0367 | 165.79 | 10.74 | 0.0135 |
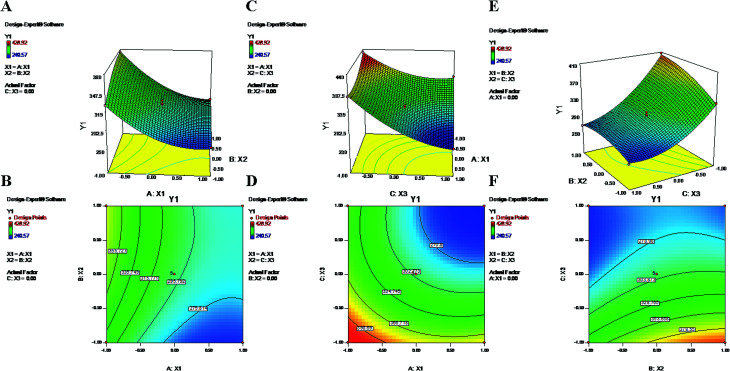
During the process of primary emulsification, a high concentration of PVA emulsifies the aqueous and oil phases by lowering the interfacial tension. Later, for the process of secondary emulsion, it is utilized in a larger volume (aqueous phase) at a low concentration to stabilize the particles of the final w/o/w double emulsion. The equation and contour plots (Fig. 1) show a decrease in particle size (Y1) with increasing value of the PVA concentration (X1) (Table 2). The higher concentration of PVA easily connected the biphasic layers by developing a protective layer around the droplets, which restricted the droplets to coalescence into large droplets.48 Additionally, high speed homogenization (X3) was applied to generate high shear stress, which breaks the droplets into smaller pieces.49 Therefore, a large volume of aqueous phase in the secondary emulsion stabilizes the system and provides sufficient space for retention of small droplets. As a result, a stable nanoformulation with small, discrete particles and a low polydispersity index (PDI) was obtained (Formulation no. 6).5,50 On the other hand, an inadequate concentration of PVA may result in agglomeration and increased particle size23,51 (Formulation no. 16) (Fig. 1). The plots (Fig. 1) highlight the inverse relationship of the homogenizing speed (X3) with Y1. Furthermore, it is evident from previous studies and the abovementioned equation that X2 (PLGA content) has a direct relationship with Y1 (Fig. 1). A higher content of PLGA (50 : 50) can increase the viscosity of the organic phase, resulting in a breakdown of droplets and, thereby, the development of larger, fused, semiformed particles during the process of emulsification49 (Formulation no. 17). A higher concentration may favor polymer–polymer interactions, causing more polymer chains to become associated during diffusion into the aqueous medium.52 The interaction terms X1X3 and X2X3 caused a decrease of Y1 at both lower and higher levels of X1, X2 and X3, whereas it increased at centre level.
Fig. 1. 2-D isoresponse contour plots (B, D and F) and 3-D response surface plots (A, C and E) of Y1 (particle size).
3.4. Evaluation of zeta potential
The zeta (ξ) potential is the electrostatic potential that exists at the shear plane of a particle. It is a key factor that denotes the stability of a nanoformulation.53 In a colloidal dispersion, the magnitude of the ZP indicates the degree of electrostatic repulsion between similarly charged particles. In general, a nanoformulation is considered stable if it has a high potential (>+30 mV or <−30 mV);54,55 however, for particles intended to be in systemic circulation, a near-neutral ZP is preferred to avoid interactions with in vivo plasma components. Furthermore, a positive potential causes toxicity due to the excessive binding affinity of the particles for cellular components.23 In the present study, the model represents ZP values in a range of −1.7 mV to −9.4 mV for 17 suggested runs (Table 1). The obtained ‘F-value’ of 98.45 signifies that in the model, there is only a 0.01% chance that this value could occur due to noise. Furthermore, the Prob > F value of 0.05 fitted well with the criteria; thus, the model is significant. The “Adjusted R-Square” value of 0.9821 showed reasonable agreement with the “Predicted R-Square” value of 0.9661. Additionally, the “Lack of Fit F-value” of 0.32 was not significant, with only an 81.42% possibility that this value could be due to noise. The “Adeq Precision” ratio of 31.735 indicated an adequate signal which is sufficient for the model to navigate the design space. The polynomial equation for ZP is shown below with the significant (Table 2) (p < 0.05) model terms (X1, X2, X3, X1X3, X2X3, X12, X22 and X32):
| Y2 = 7.52 − 1.03X1 + 2.45X2 + 0.95X3 + 0.97X1X3 + 0.73X2X3 − 0.70X12 − 1.55X22 − 0.80X32 | 10 |
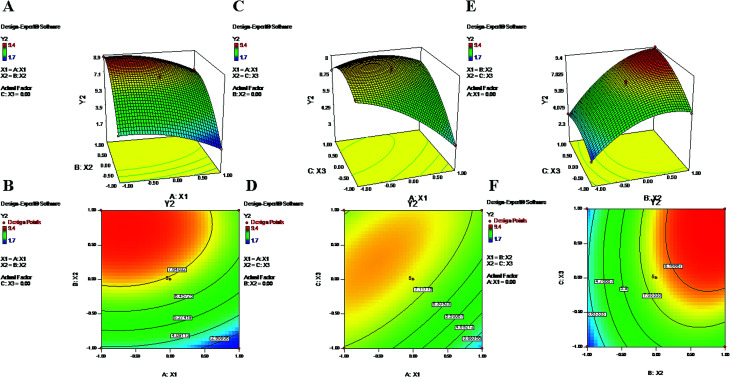
The above-mentioned polynomial equation represents a quadratic model which shows a direct relationship between the PLGA content (X2) and ZP (Y2). It shows that a higher concentration of X2 can partially enhance the value of ZP (Y2) (Fig. 2). The terminal carboxylic acid group of PLGA may influence the development of this potential difference between two surfaces of the dispersion medium. According to the literature, in the absence of PVA, the surface charge of PLGA NPs is approximately −45 mV; this is attributed to the carboxylic end groups of the polymer.52 Regarding X2, the obtained positive coefficient further supports the phenomenon (eqn (9)). On the other hand, the equation provides a picture of the reciprocal relationship of Y2 with PVA% (X1), which exhibited an increase of the negative potential with decreasing values of X1.39 As mentioned in previous studies, PVA has a tendency to coexist on the surface of NPs even after repetitive washing. Hence, it is possible that an increased concentration of X1 tends to decrease the value of electronegativity of the ZP.52 The contour plots (Fig. 2) and the negative coefficient represented by the polynomial equation coincide with the abovementioned fact. Additionally, PVA, as a non-ionic surfactant, tends to form a film around the NPs. This residual content may be responsible for shielding surface charges, thereby causing the decrease of the ZP.23,52 Furthermore, from eqn (9), higher values of Y2 can be attributed to increased speed of homogenization (X3) (Fig. 2). The application of high-speed homogenization produces smaller particles with larger surface areas, which generates a high ZP.22 In the contour plots (Fig. 2), the effects of two variables on Y2 were visually evident when a third parameter was fixed at center level. The parameters X2 and X3 both increased the ZP when the level was increased from −1 to 1 (Formulation no. 2.), whereas X1 caused a reverse effect on Y2 (Formulation no. 1). The interaction terms X1X2 and X2X3 increased the value of ZP as their levels increased. The quadratic terms X12, X22 and X32 were expressed with negative coefficients in the model; they caused decreases of Y2 at low and high levels and an increase of Y2 at center level.
Fig. 2. 2-D isoresponse contour plots (B, D and F) and 3-D response surface plots (A, C and E) of Y2 (zeta potential).
3.5. Evaluation of encapsulation efficiency
The encapsulation of drugs directly correlates with their therapeutic potential; hence, this factor is of utmost importance in terms of effective chemotherapy.56 The EE values for 17 suggestive runs were found to be in ranges of 21% to 85% and 15% to 77% for PTX and LAN, respectively (Table 1), where the lower values are attributed to losses of drugs and polymer during the secondary emulsification process. Determination of the response ‘EE’ (Y3 and Y4) is important because it has a relationship with the therapeutic efficacy of a drug delivery system. The statistical quadratic model showed significant F values of 50.69 and 32.03 for the EEs of PTX and LAN, respectively. The “Lack of Fit F-values” of 0.51 (PTX) and 1.3 (LAN) indicated that the model was not significant relative to the pure error. The “Pred R-Square” and “Adj R-Square” values were in good correlation with each other for both drugs. Furthermore, the “Adeq Precision” ratios of 23.923 (PTX) and 19.456 (LAN) expressed adequate signals that are useful for the model to navigate the design space. The significant model terms (p < 0.05) were considered (Table 2) for PTX (eqn (6)) and LAN (eqn (7)) to construct polynomial equations, shown below:
| Y3 = 60 + 11.63X1 + 17.88X2 + 9.25X3 + 5.50X1X2 + 4.75X2X3 − 10.50X12 − 4.25X32 | 11 |
| Y4 = 53.80 + 13.00X1 + 15.38X2 + 7.88X3 + 5.75X2X3 − 8.52X12 − 6.27X32 | 12 |
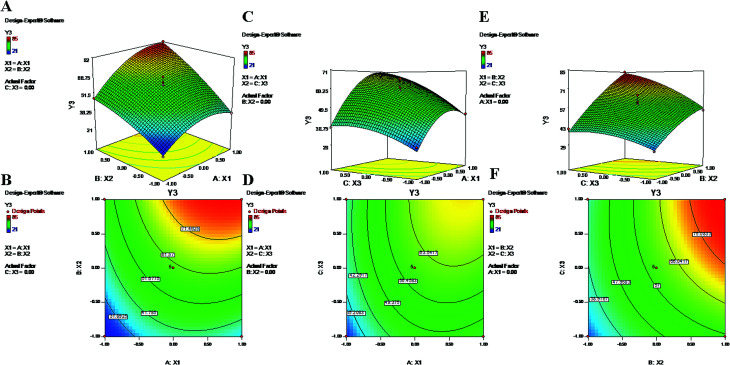
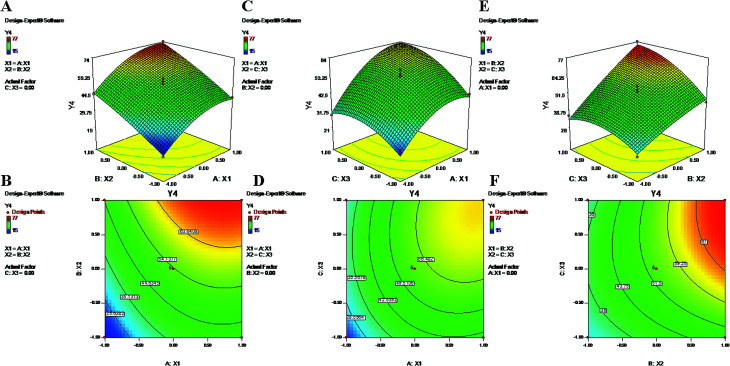
The polynomial equations clearly indicate direct relationships of the EE with all three independent variables, viz. PVA%, PLGA content and homogenizing speed (Fig. 3 and 4). According to the response surface plots (Fig. 3 and 4), PLGA was found to have a maximum effect on EE (Y3 and Y4). Sathyamoorthy et al. also supported this phenomenon for hydrophobic drugs such as PTX and LAN, which exhibit greater miscibility and interactions with polymeric solutions. A higher concentration of PVA (X1) (1% to 3%) is used during primary emulsion (w/o) to obtain uniform droplets. The surfactant concentration in the primary emulsion (X1) lowers the surface tension so that the organic and aqueous layers become miscible; as a result, uniformly stable nanodroplets are produced that hold the drugs in the polymer matrix (Fig. 3 and 4). A higher amount of PVA offers a greater surface area, which stabilizes the nanoformulation along with small particles and low PDI.5,50 Additionally, PVA with 87% to 89% hydroxylation causes a significant increment in EE because the hydroxyl groups of PVA can be adsorbed on the NP surfaces, forming a thick film via stronger intra- or inter-molecular interactions57 that resist drug diffusion. On the other hand, a higher PLGA content (X2) results in a higher EE (Formulation no. 2), probably based on the miscibility of the drugs in the organic solution and drug–polymer interactions.22 Higher amounts of polymer produce more viscous organic solutions, which can hinder drug diffusion from the organic phase into the aqueous phase; this may result in a higher drug EE.52,57 An increase in homogenizing speed (X3) was also found to be responsible for a slight increase of the EE (Formulation no. 2). The reason may be that increased homogenization speed results in smaller, uniformly sized particles, which in turn generate a larger surface area for the polymer to facilitate accommodation of a greater number of drug molecules; this may lead to higher values of EE (Fig. 3 and 4).52 The contour plots of Y3 and Y4 exhibit the effects of two factors on Y3 and Y4 separately while keeping the third factor constant at center level. These figures visually illustrated that the effects are very similar for both drugs. With increasing levels of the individual factors (X1, X2 and X3), the EE was found to increase (Fig. 3 and 4). The interaction terms X1X2 and X2X3 increase the value of Y4 as their levels increase, as with their effects on Y3. The quadratic terms X12 and X32 were expressed with negative coefficients in the model; they caused decreases of Y3 at lower and higher levels. Similar quadratic effects were observed in the case of Y4.
Fig. 3. 2-D isoresponse contour plots (B, D and F) and 3-D response surface plots (A, C and E) of Y3 (encapsulation efficiency of PTX).
Fig. 4. 2-D isoresponse contour plots (B, D and F) and 3-D response surface plots (A, C and E) of Y4 encapsulation efficiency of LAN.
3.6. Validation of the developed models
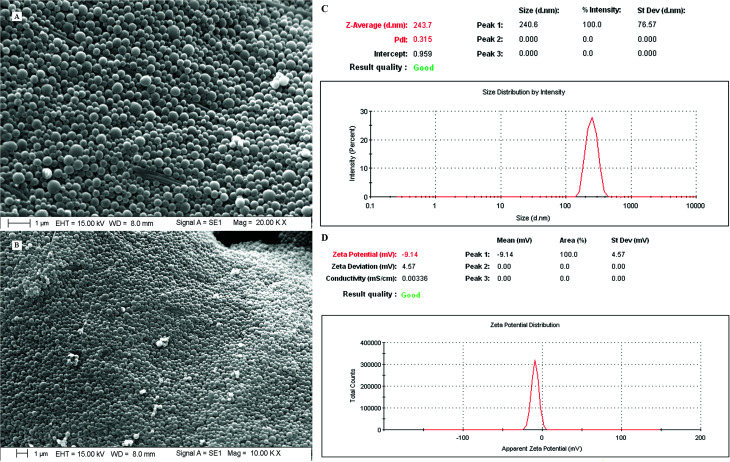
The requisites of an optimum formulation were restricted to ‘minimum’ for the particle size (nm) and ‘maximum’ for the ZP (mV) and EE (%) of both the drugs. Design Expert software and ANOVA were utilized successfully to draw the statistical significance for each effect associated with dependent parameters by comparing the mean square against an estimated experimental error. Using the desirability function approach, a numerical optimization technique was applied to generate the optimum settings and suitable levels of constraints to achieve desired responses of the nanoformulation. Among the solutions predicted by the software, three random checkpoint formulations (Table 3) were performed with the calculation of error (%) between the observed and predicted values. The final optimal PTX–LAN-NPs were obtained with a combination of the coded values 0.5 for PVA, 0.99 for PLGA, and 1 for homogenizing speed; these exhibited a particle size of 243.7 nm (Fig. 8), a ZP of −9.14 mV (Fig. 8) and EEs of 88.91% for PTX and 80.35% for LAN, respectively, with a desirability function value of 0.99 (Table 3). The experimental values of DL of the optimized nanoformulation were found to be 47.58% and 43% for PTX and LAN, respectively.
Optimized nanoformulation and release kinetics of the optimized PTX–LAN–PLGA nanoparticles in different models.
| Composition | Response variable | Predicted value | Experimental value | % Error | |||
|---|---|---|---|---|---|---|---|
| X 1 | X 2 | X 3 | |||||
| Optimized formulation | 0.5 | 0.99 | 1 | Y 1 | 240.56 | 243.7 | −1.30 |
| Y 2 | 9.13 | 9.14 | −0.11 | ||||
| Y 3 | 91.79 | 88.91 | +3.13 | ||||
| Y 4 | 81.22 | 80.35 | +1.07 | ||||
| Zero order model | First order model | Higuchi model | Korsmeyer–Peppas model | ||||
|---|---|---|---|---|---|---|---|
| R 2 | R 2 | R 2 | R 2 | ||||
| PTX | LAN | PTX | LAN | PTX | LAN | PTX | LAN |
| 0.733 | 0.674 | 0.412 | 0.416 | 0.591 | 0.550 | 0.902 | 0.890 |
Fig. 8. SEM images (A, magnification 20× and B, magnification 10×), particle sizes and polydispersity index (C) and zeta potential (D) of the optimized nanoformulation (PTX–LAN–PLGA-NPs).
3.7. Solid state characterization of the nanoparticles
3.7.1. FTIR spectroscopy
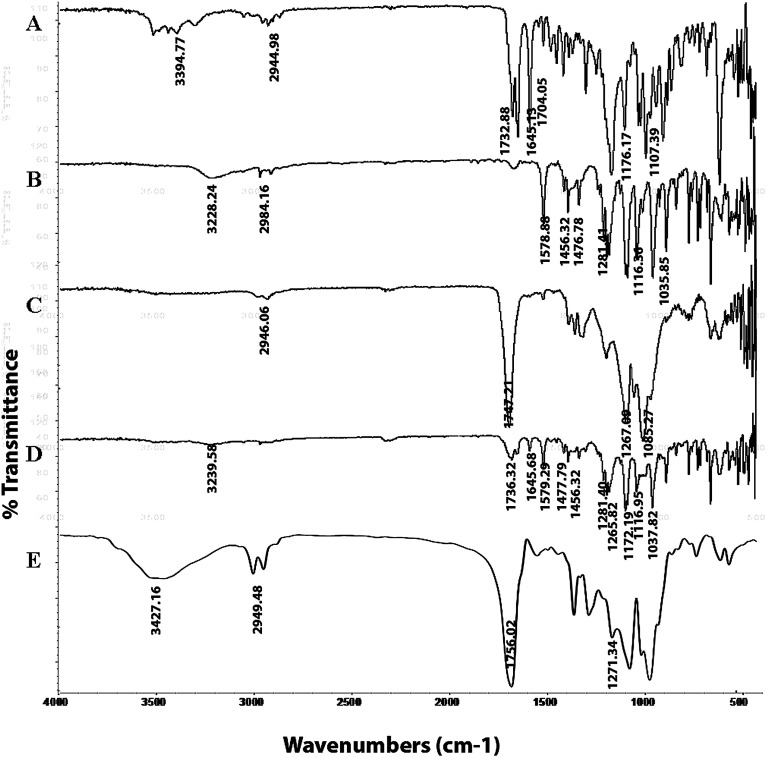
The FTIR spectra of PTX, LAN, PLGA, the PTX–LAN–PLGA physical mixture and the PTX–LAN–PLGA-NPs are depicted in Fig. 5. The characteristic absorption peaks of PTX regarding the C–H stretching vibrations, ester C O stretching vibrations, amide stretching vibrations, C O stretching vibrations from ketone groups, C–O stretching of C–ONH, C–O–C asymmetric stretching vibration of esters and C–O–H stretching vibration of secondary alcohols were observed at 2944.98 cm−1, 1732.88 cm−1, 1645.13 cm−1, 1704.05 cm−1, 3394.77 cm−1, 1176.17 cm−1 and 1107.39 cm−1, respectively. The peaks for LAN sulfinyl (S O), C–N on the pyridyl ring, ether bonds, amine-NH, –CH2–, and aromatic ring vibrations appeared at 1035.85 cm−1, 1281.41 cm−1, 1116.36 cm−1, 3228.24 cm−1, 1476.78 cm−1 and 1456.23 cm−1, respectively. The characteristic peaks for PLGA were found at 3358.18 cm−1 for O–H stretching, 2946.06 cm−1 for C–H stretching, 1747.21 cm−1 for stretching of carbonyl groups and at 1267.09 cm−1 for stretching of C–O groups. Absorption spectral peaks of PTX, LAN and PLGA were also observed in the physical mixture of PTX–LAN–PLGA, with no significant shifts in their wave numbers. The spectrum of the dual drug-loaded NPs depicted typical peaks of PLGA; the absence of some characteristic peaks of PTX and LAN was noted, which may be due to the higher fraction of polymer in comparison to those of the drugs. This did not indicate any chemical instability of drugs within the NPs. These results reveal that there were no chemical interactions between the drugs and excipients used in the formulation.56–58
Fig. 5. FTIR spectra of the pure drugs PTX (A) and LAN (B), PLGA (C), the physical mixture (D) and the dual drug-loaded nanoformulation (E).
3.7.2. Differential scanning calorimetry
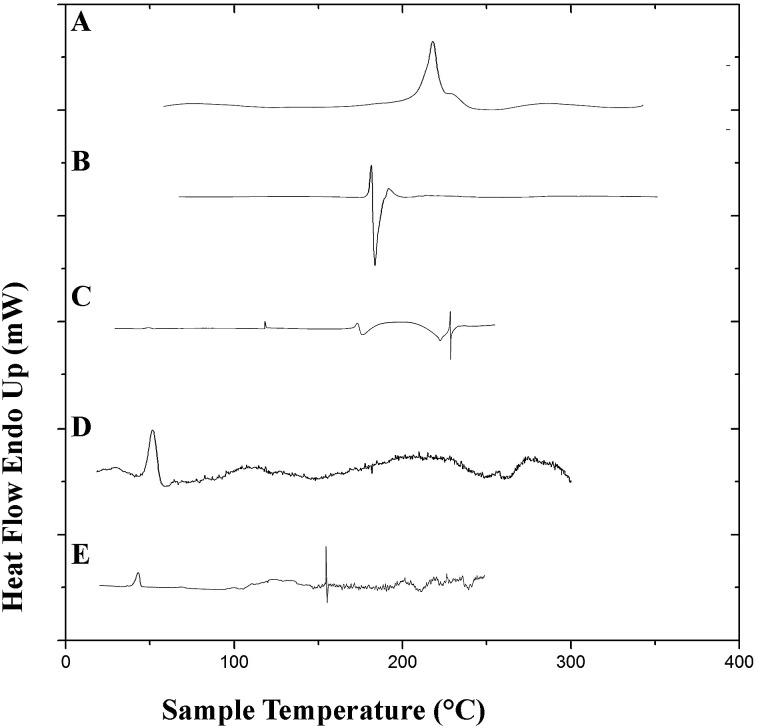
Differential scanning calorimetry studies were performed to observe the integrity of the encapsulated drugs and polymer. DSC thermograms of the pure drugs (PTX, LAN), the physical mixture of PTX–LAN–PLGA, blank PLGA NPs and dual drug-loaded NPs are shown in Fig. 6. In the thermogram of pure PTX, the endothermic peak at 220 °C corresponds to its characteristic melting point. Pure LSP also showed a peak at its melting point, namely a sharp endothermic peak at 181.6 °C. The sharp endothermic peaks for pure PTX and LAN at 220 °C and 181.6 °C, respectively, indicate their crystalline natures. The nanoformulation depicted no distinctive crystalline peaks of the drugs in its DSC profile, suggesting decreased crystallinity of the drugs or the existence of the drugs as a solid mixture within the polymer matrix.23 The DSC studies confirmed that PTX, LAN and PLGA are compatible with each other.
Fig. 6. DSC plots of the pure drugs PTX (A) and LAN (B), the physical mixture (C), blank PLGA nanoparticles (D) and the dual drug-loaded nanoformulation (E).
3.7.3. X-ray diffraction analysis (XRD)
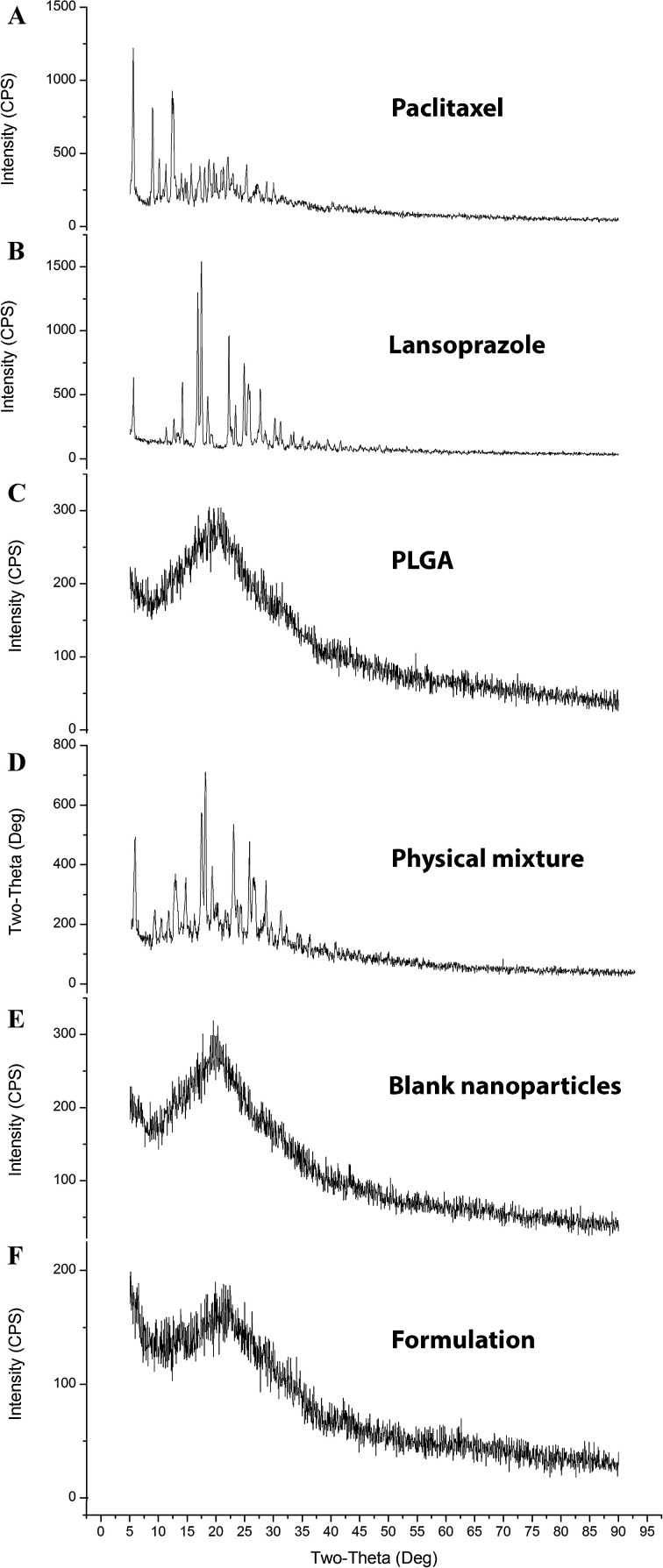
The diffractograms (Fig. 7) exhibited several sharp and high-intensity diffraction peaks for both pure PTX and LAN. In all these respective peaks, both the drugs showed sharp peaks, specifying typical crystalline natures. There was no remarkable difference between the XRD patterns of the blank NPs and PTX–LAN–PLGA-NPs. The absence of characteristic peaks of the drugs in the NPs can be attributed to dominance of the amorphous nature of the polymer over the drugs and embedding of the drug molecules well below the polymer layer. Moreover, the drug molecules were molecularly dispersed within the matrix; the drugs may have been transformed to amorphous states from their crystalline states after encapsulation into the NPs. This amorphous property of the drugs may enhance their aqueous solubility due to high molecular motion and greater internal energy.59
Fig. 7. XRD plots of the pure drugs PTX (A) and LAN (B), PLGA (C), the PTX–LAN–PLGA physical mixture (D), the blank nanoformulation (E) and the dual drug-loaded nanoformulation (F).
3.7.4. Surface morphology
The dual drug-loaded PLGA NPs exhibited smooth, spherical, discrete, homogeneous particles <250 nm in size (Fig. 8). The optimized final formulation showed a particle size of 243.7 nm and a polydispersity index of 0.315 (Fig. 8).
3.8. In vitro drug release studies
The experiments were carried out under neutral conditions (blood physiological environment). The study revealed initial rapid release for both PTX and LAN. This may be due to the release of drugs adhered to the surface of the NPs.21 Steady and controlled release of the drugs occurred by diffusion of the drugs from the polymeric core of the NPs due to the gradual disintegration of the polymeric matrix via the thin layers of liquid surrounding the particles.60 Due to the presence of free carboxyl groups, acid-terminated PLGA (PLGA 50 : 50) provided more swelling due to water uptake compared to the more hydrophobic ester-terminated PLGA.34,61 Sustained release of both drugs was obtained up to 384 hours after the initial rapid release, as presented in Fig. 9. The cumulative% drug releases over 384 hours were found to be 94% and 81% for PTX and LAN, respectively. Because both drugs present low water solubility, the release kinetics of the drugs from the NPs can be linked to self-erosion of the polymeric matrix rather than diffusion.34 The erupted release may be due to the large surface-to-volume ratio of the NPs.21 According to the literature, PLGA (50 : 50) has a long degradation period of 102 days.62
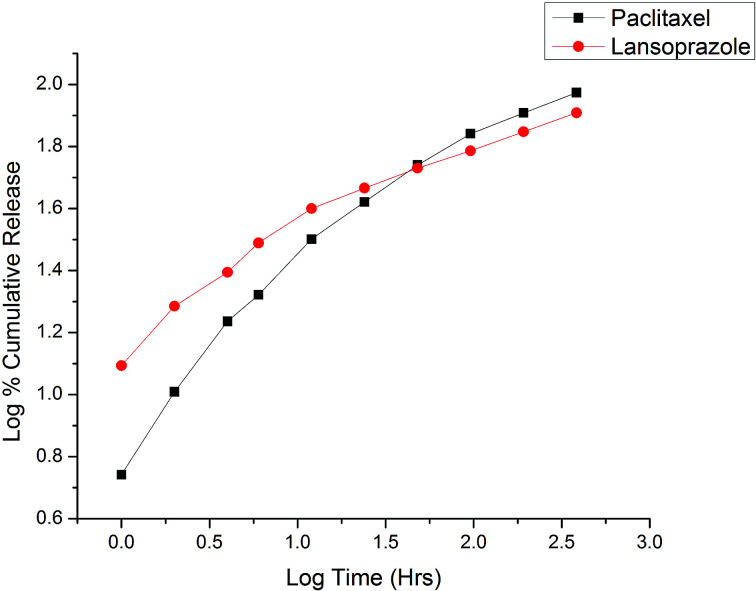
Fig. 9. Korsmeyer–Peppas release kinetics of the optimized nanoformulation.
The in vitro release kinetics of both drugs were studied by fitting the cumulative release data in various models, including the zero order kinetic model (% cumulative drug release vs. time plot); the first order kinetic model (log % cumulative release vs. time); the Higuchi model (% cumulative release vs. square root of time); and the Korsmeyer–Peppas model (log % cumulative release vs. log time). On the basis of the highest correlation (R2) coefficient values (R2 = 0.902 for PTX and R2 = 0.890 for LAN, Table 3), it can be concluded that the Korsmeyer–Peppas model (Fig. 9) is the best fitted model for the release kinetics of the optimized nanoformulation. The magnitudes of the release exponent ‘n’ (n = 0.5 for PTX and n = 0.345 for LAN) indicate that the release mechanism follows Fickian diffusion.39
3.9. In vitro cytotoxicity
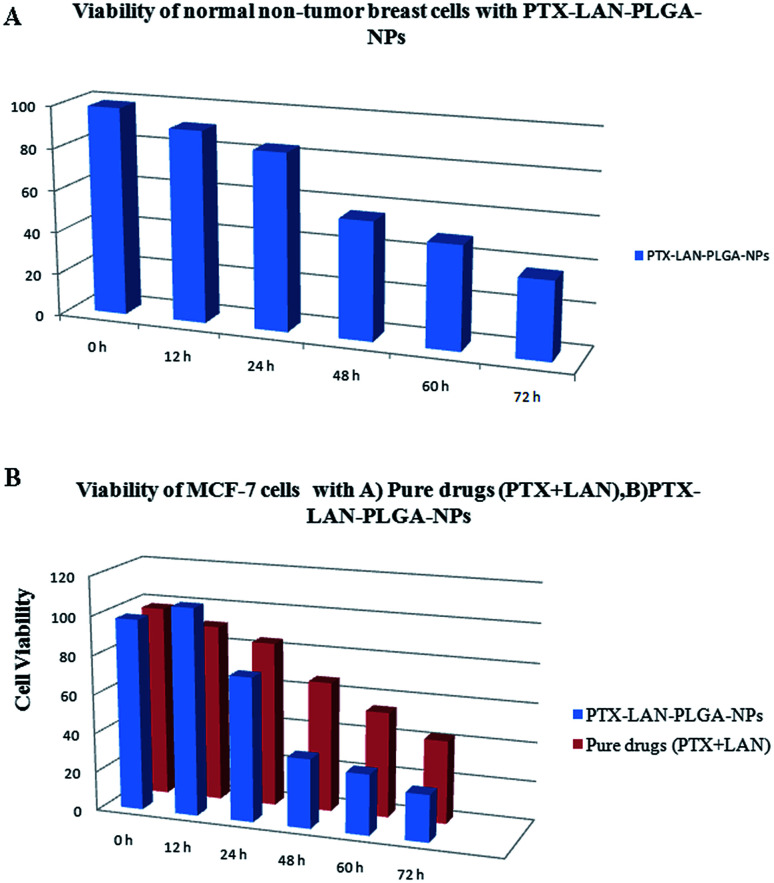
In this study, the cytotoxicity of the PTX–LAN–PLGA-NPs was compared with that of a combination of pure PTX and LAN (Fig. 10B). The experiment was performed with a 25 μg mL−1 drug concentration because this corresponds to the maximum concentration of PTX achievable in human plasma.4 The results exhibited a more substantial time-dependent decrease of cell viability with the nanoformulation compared to the combined pure drugs (25 μg mL−1 each). With prolonged incubation, a large number of cells entered the G2 and M phases of the cell cycle, where PTX is highly active.42 The PTX–LAN–PLGA-NPs showed a marked decrease (35.54%) of viability at 48 h and showed maximum inhibition (23.99%) at 72 h, whereas the pure drugs were found to exhibit much different effects. The reason for the enhanced cytotoxicity may be the combined treatment of PTX and LAN, in addition with the facile uptake of the NPs, which resulted in high intracellular concentrations and controlled release of the drugs from the polymer matrix.63 Compared to MCF-7 cells, PTX–LAN–PLGA-NPs showed less cytotoxicity to non-tumor breast cells (Fig. 10A). This may be due to the absence of a naturally developed extracellular acidic microenvironment in non-tumor breast cells, which was utilized as a trigger for the activation of LAN in order to exert synergistic action with PTX in the PTX–LAN–PLGA-NPs for MCF-7 cells.
Fig. 10. Viability of MCF-10A breast cellsd with PTX–LAN–PLGA-NPs (A) and MCF-7 cells with pure drugs (PTX + LAN) and PTX–LAN–PLGA-NPs (B).
4. Conclusion
The novelty of this study is the development of a dual drug-loaded nanoformulation utilizing a common PPI that selectively targets the tumor microenvironment. To the best of our knowledge, a developmental study of nanoformulations containing PTX and LAN together has not been reported earlier. The dosage form, loaded in a biodegradable PLGA carrier matrix, exhibited sustained release of both drugs for a prolonged period; this may help overcome the obstacles to PTX chemotherapy in the acidic environment of cancer cells. The tunable properties of the double emulsion solvent evaporation method were explored in detail to prepare a nanoformulation with a high encapsulation efficiency, low average particle size and high zeta potential. Box–Behnken design was utilized to optimize the results statistically and develop a precise polymeric drug delivery system with a minimum number of experiments. The validation of the model by performing additional checkpoint experiments ensured the integrity of the results in the field of pharmaceutical drug delivery systems. Additionally, the PTX–LAN–PLGA-NPs exhibited promising antitumor efficacy compared to the raw drugs. In conclusion, the scientific investigation involving optimization through Box–Behnken design may result in promising candidate for the fight against cancer.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
The authors express sincere gratitude to the Bioequivalence Study Centre and Department of Pharmaceutical Technology, Jadavpur University, for providing enormous support to undertake this research. Furthermore, for the commencement of some experiments, the help provided by Indian Institute of Technology, Kharagpur; Centre for Research in Nanoscience and Nanotechnology, Kolkata; and Metallurgical & Material Engineering Department, Jadavpur University is worth mentioning.
References
- Maleki Dizaj S. Lotfipour F. Barzegar-Jalali M. Zarrintan M.-H. Adibkia K. J. Drug Delivery Sci. Technol. 2015;29:125–131. doi: 10.1016/j.jddst.2015.06.015. [DOI] [PubMed] [Google Scholar]
- Aqil M. Kamran M. Ahad A. Imam S. S. J. Mol. Liq. 2016;214:238–248. doi: 10.1016/j.molliq.2015.12.077. [DOI] [Google Scholar]
- Shaikh M. V. Kala M. Nivsarkar M. Eur. J. Pharm. Sci. 2017;100:262–272. doi: 10.1016/j.ejps.2017.01.026. [DOI] [PubMed] [Google Scholar]
- Fonseca C. Simões S. Gaspar R. J. Controlled Release. 2002;83:273–286. doi: 10.1016/S0168-3659(02)00212-2. [DOI] [PubMed] [Google Scholar]
- Cerqueira B. B. S. Lasham A. Shelling A. N. Al-Kassas R. Mater. Sci. Eng., C. 2017;76:593–600. doi: 10.1016/j.msec.2017.03.121. [DOI] [PubMed] [Google Scholar]
- Singla A. K. Garg A. Aggarwal D. Int. J. Pharm. 2002;235:179–192. doi: 10.1016/S0378-5173(01)00986-3. [DOI] [PubMed] [Google Scholar]
- Surapaneni M. S. Das S. K. Das N. G. ISRN Pharmacol. 2012;2012:15. doi: 10.5402/2012/623139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh M. Fais S. Spugnini E. P. Harguindey S. Abu Izneid T. Scacco L. Williams P. Allegrucci C. Rauch C. Omran Z. J. Exp. Clin. Cancer Res. 2015;34:93. doi: 10.1186/s13046-015-0204-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fais S. J. Transl. Med. 2015;13:368. doi: 10.1186/s12967-015-0735-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spugnini E. Fais S. Semin. Cancer Biol. 2017;43:111–118. doi: 10.1016/j.semcancer.2017.01.003. [DOI] [PubMed] [Google Scholar]
- Shin J. M. Kim N. J. Neurogastroenterol. Motil. 2013;19:25–35. doi: 10.5056/jnm.2013.19.1.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin J. M. Sachs G. Curr. Gastroenterol. Rep. 2008;10:528–534. doi: 10.1007/s11894-008-0098-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Numico G. Fusco V. Franco P. Roila F. Crit. Rev. Oncol. Hematol. 2017;111:144–151. doi: 10.1016/j.critrevonc.2017.01.014. [DOI] [PubMed] [Google Scholar]
- Taylor S. Spugnini E. P. Assaraf Y. G. Azzarito T. Rauch C. Fais S. Drug Resist. Updates. 2015;23:69–78. doi: 10.1016/j.drup.2015.08.004. [DOI] [PubMed] [Google Scholar]
- Canitano A. Iessi E. Spugnini E. P. Federici C. Fais S. Cancer Lett. 2016;376:278–283. doi: 10.1016/j.canlet.2016.04.015. [DOI] [PubMed] [Google Scholar]
- Chen M. Zou X. Luo H. Cao J. Zhang X. Zhang B. Liu W. Cell Biol. Int. 2009;33:1008–1019. doi: 10.1016/j.cellbi.2009.05.004. [DOI] [PubMed] [Google Scholar]
- Azzarito T. Venturi G. Cesolini A. Fais S. Cancer Lett. 2015;356:697–703. doi: 10.1016/j.canlet.2014.10.017. [DOI] [PubMed] [Google Scholar]
- Tsuchida K., in Encyclopedia of Cancer, ed. M. Schwab, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, pp. 1160–1162, 10.1007/978-3-642-16483-5_1734 [DOI] [Google Scholar]
- Bazak R. Houri M. Achy S. E. Hussein W. Refaat T. Mol. Clin. Oncol. 2014;2:904–908. doi: 10.3892/mco.2014.356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi J. Y. Thapa R. K. Yong C. S. Kim J. O. J. Pharm. Invest. 2016;46:325–339. doi: 10.1007/s40005-016-0252-1. [DOI] [Google Scholar]
- Khuroo T. Verma D. Khuroo A. Ali A. Iqbal Z. J. Mol. Liq. 2018;257:52–68. doi: 10.1016/j.molliq.2018.02.091. [DOI] [Google Scholar]
- Narayanan K. Subrahmanyam V. M. Venkata Rao J. Enzyme Res. 2014;2014:162962. doi: 10.1155/2014/162962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sathyamoorthy N. Magharla D. Chintamaneni P. Vankayalu S. Beni-Suef Univ. J. Basic Appl. Sci. 2017;6(4):362–373. doi: 10.1016/j.bjbas.2017.06.002. [DOI] [Google Scholar]
- Venugopal V. Kumar K. J. Muralidharan S. Parasuraman S. Raj P. V. Kumar K. V. OpenNano. 2016;1:1–15. doi: 10.1016/j.onano.2016.03.002. [DOI] [Google Scholar]
- Ferreira S. L. C. Bruns R. E. Ferreira H. S. Matos G. D. David J. M. Brandão G. C. da Silva E. G. P. Portugal L. A. dos Reis P. S. Souza A. S. dos Santos W. N. L. Anal. Chim. Acta. 2007;597:179–186. doi: 10.1016/j.aca.2007.07.011. [DOI] [PubMed] [Google Scholar]
- Das S. K. Yuvaraja K. Khanam J. Nanda A. Chem. Eng. Res. Des. 2015;96:1–14. doi: 10.1016/j.cherd.2015.01.014. [DOI] [Google Scholar]
- Mahajan H. S. Tatiya B. V. Nerkar P. P. Powder Technol. 2012;221:168–176. doi: 10.1016/j.powtec.2011.12.063. [DOI] [Google Scholar]
- Bezerra M. A. Santelli R. E. Oliveira E. P. Villar L. S. Escaleira L. A. Talanta. 2008;76:965–977. doi: 10.1016/j.talanta.2008.05.019. [DOI] [PubMed] [Google Scholar]
- Vera Candioti L. De Zan M. M. Cámara M. S. Goicoechea H. C. Talanta. 2014;124:123–138. doi: 10.1016/j.talanta.2014.01.034. [DOI] [PubMed] [Google Scholar]
- Akl M. A. Kartal-Hodzic A. Oksanen T. Ismael H. R. Afouna M. M. Yliperttula M. Samy A. M. Viitala T. J. Drug Delivery Sci. Technol. 2016;32:10–20. doi: 10.1016/j.jddst.2016.01.007. [DOI] [Google Scholar]
- Chourasiya V. Bohrey S. Pandey A. Materials Discovery. 2016;5:1–13. doi: 10.1016/j.md.2016.12.002. [DOI] [Google Scholar]
- Alai M. Lin W. J. Int. J. Nanomed. 2015;10:4029–4041. doi: 10.2147/IJN.S82366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panyam J. Williams D. Dash A. Leslie-Pelecky D. Labhasetwar V. J. Pharm. Sci. 2004;93:1804–1814. doi: 10.1002/jps.20094. [DOI] [PubMed] [Google Scholar]
- Yerlikaya F. Ozgen A. Vural I. Guven O. Karaagaoglu E. Khan M. A. Capan Y. J. Pharm. Sci. 2013;102:3748–3761. doi: 10.1002/jps.23686. [DOI] [PubMed] [Google Scholar]
- Varelas C. G. Dixon D. G. Steiner C. A. J. Controlled Release. 1995;34:185–192. doi: 10.1016/0168-3659(94)00085-9. [DOI] [Google Scholar]
- Gibaldi M. Feldman S. J. Pharm. Sci. 1967;56:1238–1242. doi: 10.1002/jps.2600561005. [DOI] [PubMed] [Google Scholar]
- Higuchi T. J. Pharm. Sci. 1961;50:874–875. doi: 10.1002/jps.2600501018. [DOI] [PubMed] [Google Scholar]
- Higuchi T. J. Pharm. Sci. 1963;52:1145–1149. doi: 10.1002/jps.2600521210. [DOI] [PubMed] [Google Scholar]
- Korsmeyer R. W. Gurny R. Doelker E. Buri P. Peppas N. A. Int. J. Pharm. 1983;15:25–35. doi: 10.1016/0378-5173(83)90064-9. [DOI] [PubMed] [Google Scholar]
- Peppas N. A. Sahlin J. J. Int. J. Pharm. 1989;57:169–172. doi: 10.1016/0378-5173(89)90306-2. [DOI] [Google Scholar]
- Dhamecha D. Jalalpure S. Jadhav K. Jagwani S. Chavan R. Pharmacol. Res. 2016;113:547–556. doi: 10.1016/j.phrs.2016.09.037. [DOI] [PubMed] [Google Scholar]
- Danhier F. Lecouturier N. Vroman B. Jérôme C. Marchand-Brynaert J. Feron O. Préat V. J. Controlled Release. 2009;133:11–17. doi: 10.1016/j.jconrel.2008.09.086. [DOI] [PubMed] [Google Scholar]
- Ma P. Mumper R. J. J. Nanomed. Nanotechnol. 2013;4:1000164. doi: 10.4172/2157-7439.1000164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He W. Yang M. Fan J. H. Feng C. X. Zhang S. J. Wang J. X. Guan P. P. Wu W. AAPS PharmSciTech. 2010;11:1287–1293. doi: 10.1208/s12249-010-9493-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meerum Terwogt J. M. Nuijen B. Ten Bokkel Huinink W. W. Beijnen J. H. Cancer Treat. Rev. 1997;23:87–95. doi: 10.1016/S0305-7372(97)90022-0. [DOI] [PubMed] [Google Scholar]
- Lin J. Cai Q. Tang Y. Xu Y. Wang Q. Li T. Xu H. Wang S. Fan K. Liu Z. Jin Y. Lin D. Int. J. Pharm. 2018;536:272–282. doi: 10.1016/j.ijpharm.2017.10.043. [DOI] [PubMed] [Google Scholar]
- Fahmy T. M. Fong P. M. Goyal A. Saltzman W. M. Mater. Today. 2005;8:18–26. doi: 10.1016/S1369-7021(05)71033-6. [DOI] [Google Scholar]
- Zhao H. Gagnon J. Häfeli U. O. Biomagn. Res. Technol. 2007;5:2. doi: 10.1186/1477-044X-5-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma N. Madan P. Lin S. Asian J. Pharm. Sci. 2016;11:404–416. doi: 10.1016/j.ajps.2015.09.004. [DOI] [Google Scholar]
- Afrooz H. Ahmadi F. Fallahzadeh F. Mousavi-Fard S. H. Alipour S. J. Drug Delivery Sci. Technol. 2017;41:174–181. doi: 10.1016/j.jddst.2017.06.020. [DOI] [Google Scholar]
- Feczkó T. Tóth J. Dósa G. Gyenis J. Chem. Eng. Process. 2011;50:846–853. doi: 10.1016/j.cep.2011.05.006. [DOI] [Google Scholar]
- Tefas L. R. TomuŢĂ I. Achim M. Vlase L. Clujul Med. 2015;88:214–223. doi: 10.15386/cjmed-418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. Yang M. Portney N. G. Cui D. Budak G. Ozbay E. Ozkan M. Ozkan C. S. Biomed. Microdevices. 2008;10:321–328. doi: 10.1007/s10544-007-9139-2. [DOI] [PubMed] [Google Scholar]
- Dhas N. L. Ige P. P. Kudarha R. R. Powder Technol. 2015;283:234–245. doi: 10.1016/j.powtec.2015.04.053. [DOI] [Google Scholar]
- Clogston J. D. and Patri A. K., in Characterization of Nanoparticles Intended for Drug Delivery, ed. S. E. McNeil, Humana Press, Totowa, NJ, 2011, pp. 63–70, 10.1007/978-1-60327-198-1_6 [DOI] [Google Scholar]
- Kumari A. Singla R. Guliani A. Yadav S. K. EXCLI J. 2014;13:265–286. [PMC free article] [PubMed] [Google Scholar]
- Song X. Zhao Y. Wu W. Bi Y. Cai Z. Chen Q. Li Y. Hou S. Int. J. Pharm. 2008;350:320–329. doi: 10.1016/j.ijpharm.2007.08.034. [DOI] [PubMed] [Google Scholar]
- Ning Y., Interpretation of Infrared Spectra, in Interpretation of Organic Spectra, ed. Y. Ning, 2011, 10.1002/9780470825181.ch5 [DOI] [Google Scholar]
- Mendiratta C. Kadam V. Pokharkar V. J. Chem. Pharm. Res. 2011;3(6):536–543. [Google Scholar]
- Sahana B. Santra K. Basu S. Mukherjee B. Int. J. Nanomed. 2010;5:621–630. doi: 10.2147/IJN.S9962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentile P. Chiono V. Carmagnola I. Hatton P. V. Int. J. Mol. Sci. 2014;15:3640–3659. doi: 10.3390/ijms15033640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussein A. S. Abdullah N. Ahmadun F. R. IET Nanobiotechnol. 2013;7:33–41. doi: 10.1049/iet-nbt.2012.0012. [DOI] [PubMed] [Google Scholar]
- Wang B. Yu X.-C. Xu S.-F. Xu M. J. Nanobiotechnol. 2015;13:22. doi: 10.1186/s12951-015-0086-4. [DOI] [PMC free article] [PubMed] [Google Scholar]