Dental microfracture detection using wavelet features and machine learning

Abstract

Microfractures (cracks) are the third most common cause of tooth loss in industrialized countries. If they are not detected early, they continue to progress until the tooth is lost. Cone beam computed tomography (CBCT) has been used to detect microfractures, but has had very limited success. We propose an algorithm to detect cracked teeth that pairs high resolution (hr) CBCT scans with advanced image analysis and machine learning. First, microfractures were simulated in extracted human teeth (n=22). hr-CBCT and microCT scans of the fractured and control teeth (n=14) were obtained. Wavelet pyramid construction was used to generate a phase image of the Fourier transformed scan which were fed to a U-Net deep learning architecture that localizes the orientation and extent of the crack which yields slice-wise probability maps that indicate the presence of microfractures. We then examine the ratio of high-probability voxels to total tooth volume to determine the likelihood of cracks per tooth. In microCT and hr-CBCT scans, fractured teeth have higher numbers of such voxels compared to control teeth. The proposed analytical framework provides a novel way to quantify the structural breakdown of teeth, that was not possible before. Future work will expand our machine learning framework to 3D volumes, improve our feature extraction in hr-CBCT and clinically validate this model. Early detection of microfractures will lead to more appropriate treatment and longer tooth retention.

1. INTRODUCTION

Epidemiologic studies report that cracked teeth are the third most common cause for tooth loss in industrialized countries, after caries and periodontal disease.¹ This trend is expected to continue to increase as the US population ages² and retain their teeth longer. Recently reported data also shows that cracked teeth are more common in under-served populations.³ Histological studies demonstrate that all cracks are colonized by bacteria, which can cause pulpal and periapical disease,^4,5 both of which cause intense pain which is the most common reason why patients seek emergency dental care.^6,7 If left undetected, cracks continue to progress and ultimately result in tooth loss.

Cracked teeth are extremely hard to detect. The clinical symptoms, such as pain upon biting and sensitivity,^8,9 are often discontinuous with periods of remission. 2D intraoral radiographs and CBCT scans are imaging tools used to detect cracks but also have significant limitations. Radiographs are often insufficient to detect non-displaced cracked teeth because (1) when cracks are not aligned with the x-ray beam they do not result in feature contrast and (2) superimposition of overlying structures and the 3D nature of the cracks limits contrast and hampers interpretation. CBCT adds the advantage of capturing 3D structures but is subject to partial volume effects. Even with the recent developments that offer small Field of View (FOV), high resolution modes for endodontic use in CBCT, challenges still exist for the detection of cracks such as those arising from qualitative and subjective human evaluation.^10,11

These motivations drove the development of the work presented here, in which we invented an algorithm to provide an enhanced detection and visualization approach by coupling hr-CBCT with advanced image analysis methods and machine learning. Early detection and localization of cracks in a non-invasive, data-driven, quantitative way is of utmost importance in ensuring appropriate treatment and in preventing tooth loss.¹²

2. DATA

2.1. Fracture simulation

Our ex-vivo sample consists of 36 extracted human premolars, first molars and second molars. We simulated stress microfractures in a subsample of the total (n=22), while the other sound teeth were used as controls (n=14). In order to simulate microfractures, the teeth were placed in resin trays and stabilized using dental wax to simulate the periodontal ligament (figure 1.a.).

Figure 1.

Simulation of fractures in ex-vivo teeth: (left) Preparation of extracted teeth in resin trays; (center) Instron machine and custom insert that simulates intraoral occlusal forces; (right) Confirmation of superficial cracks via transillumination

A customized compression insert was fit into the central grooves of the teeth to evenly distribute forces onto the occlusal surfaces just as would happen in the mouth (1.b.). A continuous force (⩽ 400N) was exerted on the grooves using an INSTRON E3000 Electropuls. All the teeth were then examined with and without transillumination by two masked investigators (1.c.). The presence/absence of superficial micro cracks, their location, extent and orientation was recorded. Before image analysis, we confirmed that our standardized method induces cracks in extracted teeth in a reliable manner (p=0.017) via Chi square. From that superficial evaluation, cracks are mesio-distally oriented and propagate from the crown towards the root of the tooth, which mimics the common clinical presentations of stress induced dental cracks.

2. Micro CT

All teeth were scanned using a desktop microCT imaging system (Bruker Skyscan 1172, Belgium) at a pixel size of 11.97 μm, with an exposure set at 1500 ms and voltage at 60 kV, 167 μA, equipped with a 0.5mm Al filter. Scan settings were set at a 0.30 rotation step with a frame averaging value of 8. Reconstruction was performed with a minimum compressed-sensing (CS) value of 0.00000 and maximum CS value of 0.142390.

2.3. High-resolution CBCT

To increase the similarities with its clinical presentation, the teeth were placed in a human jaw and stabilized with wax(figure 2.a). The teeth were randomly arranged so that each jaw contained 2 molars and 1 premolar, and each set of teeth had 2 fractures and 1 control. The jaws were placed in water to mimic soft tissue (figure 2.b). All hr-CBCT volumes were acquired with the Planmeca ProMax 3D Mid ProFace, located at the Oral and Maxillofacial Radiology Clinic at the University of Texas Health San Antonio with acquisition parameters FOV 40 × 50 mm, 90 kV, 12.5 mA, 15 s, endodontic resolution mode, 75 μm voxels.

Figure 2.

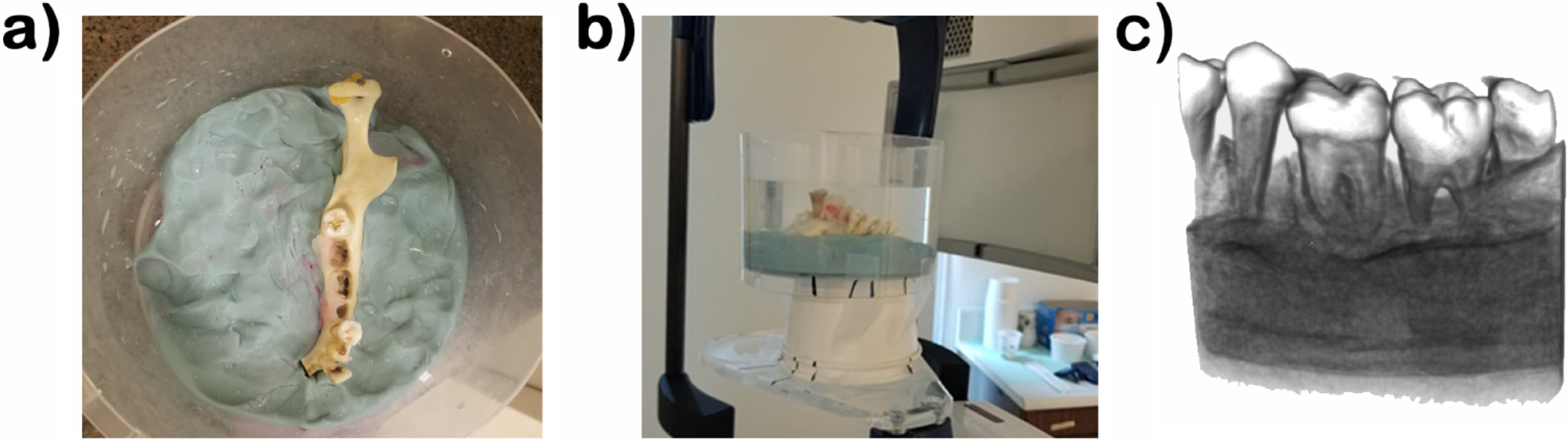
High-resolution CBCT acquisition of our ex-vivo simulated data. a) Dry mandible without teeth placement; b) Acquisition set up; c) Volume rendering of present geometry in scan.

3. METHODS

Our method computes imaging features specific to tooth microfractures based on advanced image processing methods and 3D wavelets. These features are then used to train and run a U-Net to enhance the detection of those lesions in teeth.

3.1. Registration and Segmentation of ex-vivo sample

In order to facilitate the detection of fractures in CBCT, we registered the microCT volumes to the CBCT data using the external geometry of the tooth. First, the microCT tooth was segmented using Otsu thresholding¹³ followed by an opening operation and a fill holes filter to segment the whole tooth (pulp, dentin and enamel). The geometry in the CBCT was obtained from a fixed threshold (see figure 2.c). The microCT (figure 3.d) was first aligned to the CBCT by a known transform that is custom for the pre, first or second molar locations and then refined using iterative closest point¹⁴ to register the microCT volume and segmentation into the CBCT space (see figure 3.a).

Figure 3.

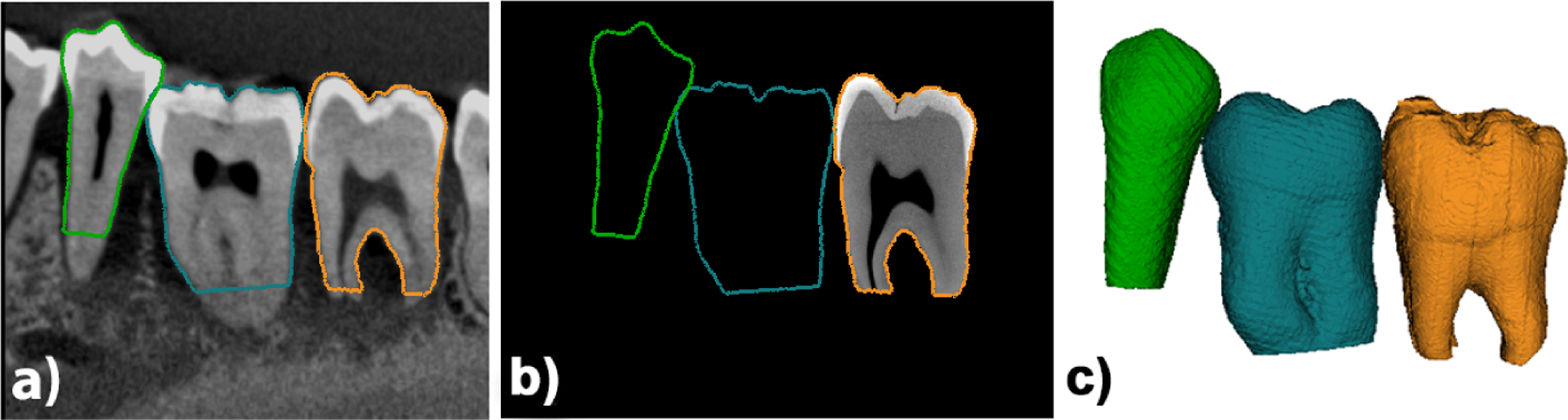
Imaging modalities for ex-vivo data. a) hr-CBCT; b) registered microCT ; c) registered microCT geometry.

3.2. Feature computation

Our feature extraction pipeline (figure 4.a) includes the following steps: image pre-processing, computation of wavelet pyramid based on the signal present in the input image, monogenic signal generation, phase analysis, and inverse wavelet pyramid construction (spatial reconstruction).

Figure 4.

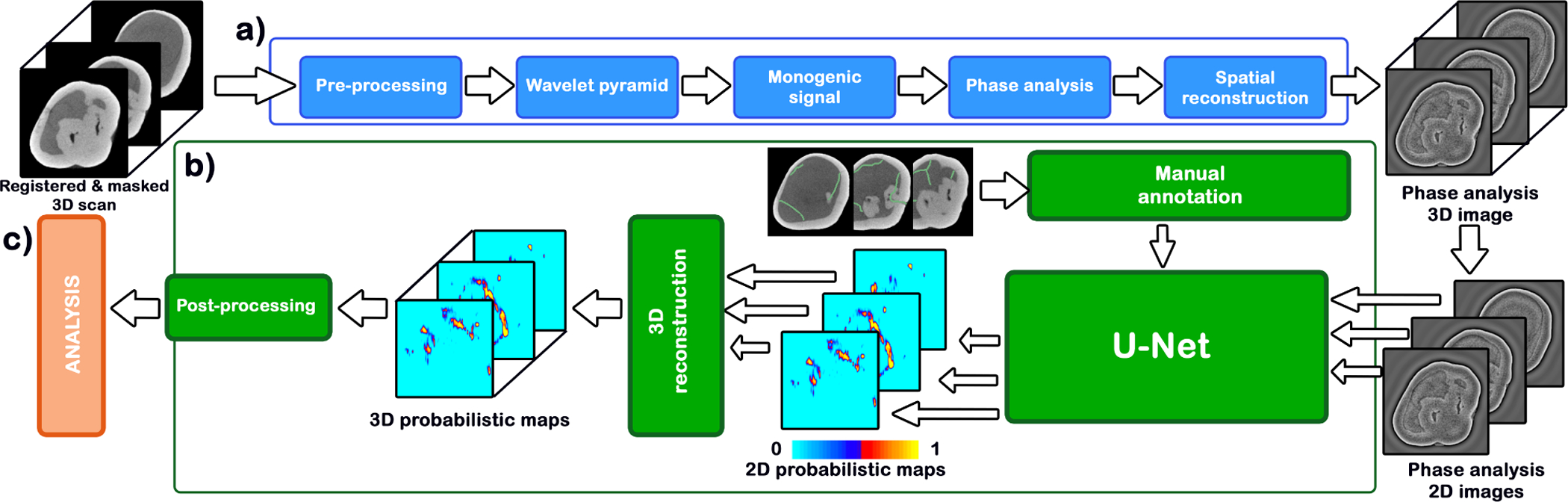
Algorithm workflow. (a) Feature computation, in blue (b) Fracture detection, in green (c) Analytical assessment, in red.

3.2.1. Image pre-processing

Each tooth is cropped from the scan by computing the smallest bounding box that includes the whole tooth geometry. This volume is then padded until all dimensions are multiples of 256 in order to facilitate the wavelet decomposition so different spatial bands do not overlap.

3.2.2. 3D Isotropic Wavelets

Wavelets provide a signal decomposition framework that allows for good localization in both the spatial and frequency domains. There is an abundant amount of theoretical work in this field^15–17 that has been applied to research in areas such as theoretical physics, seismology and image processing. Wavelets are similar to a windowed Fourier Transform, but with the advantage that the spatial resolution can be modulated, localizing imaging features based on both their frequency and location in space.

Wavelet decomposition

Consider the following wavelet decomposition for a signal $f,\forall f\in L_2\left({ℝ}^d\right)$, where s represents the number of levels and l represents the number of high-pass bands.

$$f(x)=\sum _{s\in \mathbb{Z}}\sum _{l\in {\mathbb{Z}}^d}\langle f,{\psi }_{s,l}\rangle {\psi }_{s,l}(x)$$ (1)

The family of functions {ψ_s,l} is a wavelet frame (equation 2), constructed by means of translations and dilations of the mother wavelet function ψ.

$${\psi }_{s,l}(x)=a^{-d\cdot s/2}\psi \left(a^{s}x-l\right)$$ (2)

Each dilation, defined by the dilation matrix A, squeezes or stretches the mother wavelet, acting as a change of scale. In equation (2) we consider A = aI_d to be a diagonal matrix with the same dilation factor a in all dimensions. The translation operator l moves and centers the location of the mother wavelet ψ, which must have finite energy $\psi \in L_2\left({ℝ}^d\right)$, i.e ${\int }_{-\infty }^{\infty }\psi {(x)}^{2}dx<\infty$.

Wavelet pyramid

In image processing, the practical implementation of the wavelet transform is called wavelet pyramid construction.^18–20 This involves passing an image through successive levels of filters where at each level the image is down-sampled and multiple non-overlapping band-pass filters are applied to capture different ranges of frequency components of the input image. Figure 5.a shows the model of the wavelet pyramid construction process. By changing the number of high-pass bands, we can capture wide range of frequencies responsible for smooth and sharp edges. By changing the number of levels, we can generate multi-scale versions of an image, where certain scales can capture specific imaging features better than others. The ultimate result of the wavelet pyramid is a set of wavelet coefficients (in figure 5, see d_s,h, where s ∈ {1,…,Levels}, and h ∈ {1,…,HighPassSubBands}).

Figure 5.

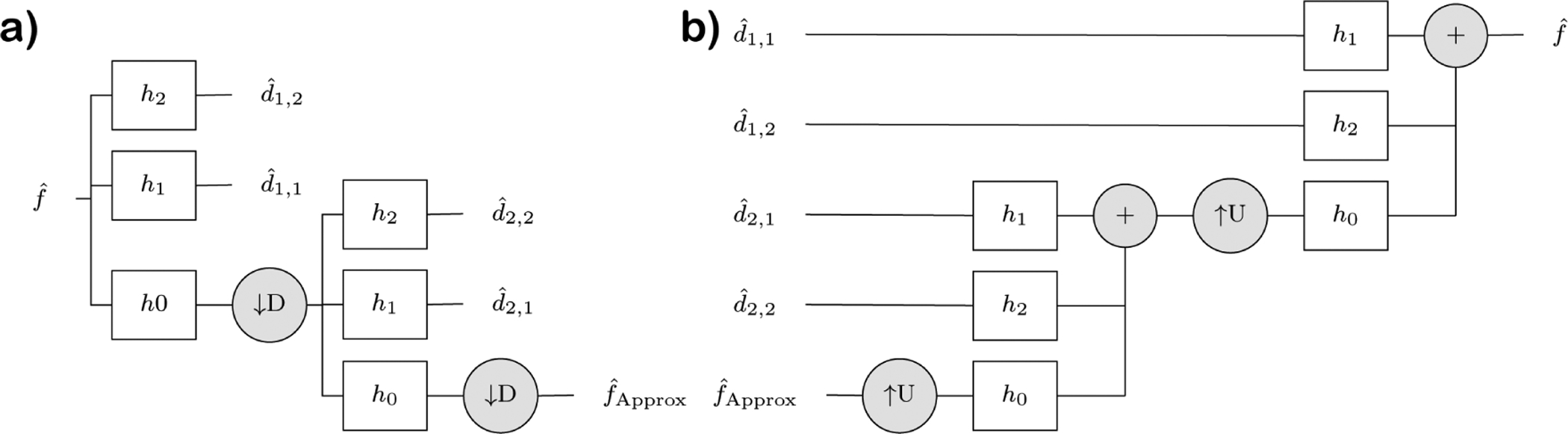
Example of wavelet pyramid for two-level pyramid with two high pass sub-bands. (a) Forward transform: The wavelet coefficients d are the result of applying high-frequency band-pass filters (HP) to the input image in the frequency domain. The process is recursive for the desired number of scales after applying a low-pass frequency filter and a down-sampling operator (D). (b) Inverse transform (spatial reconstruction)

The forward wavelet pyramid outputs a set of wavelet coefficients with information about each scale. A steerable filter^18,20,21 can be applied to select the orientation where the feature of interest is maximum. We use the Simoncelli steerable filter with 3 scales and 3 high-pass filters.

Monogenic signal and Phase analysis

The monogenic wavelet²² is an n-D generalization of the 1-D analytical wavelet signal.²³ Instead of using the Hilbert transform to convolve the wavelet coefficients, it uses the Riesz transform to generalize the computation to higher dimensions and thus it is well suited for image analysis. The monogenic signal allows for the decomposition of multidimensional signals $f\in L_2\left({ℝ}^d\right)$ into phase and amplitude. We can define the monogenic signal as the d + 1 dimensional vector

$$f_m(x)=\left(f(x),R_{1}f(x),\dots ,R_{d}f(x)\right)$$ (3)

Where R_i denotes the Riesz transform to the dimension i. The phase of the monogenic signal is defined as

$${\alpha }_f=\mathit{\text{arctan}}\frac{\sqrt{\left(R_1{f}^2\right)+\dots \left(R_d{f}^2\right)}}{f}$$ (4)

This phase contains information about the signal structure and it is resistant to local image changes in brightness due to artifacts.

Spatial reconstruction

Finally we compute the inverse wavelet pyramid to reconstruct the phase images into the spatial domain (see Figure 5.b). Reconstructing the multiscale coefficients from the phase provides a feature image that enhances microfractures and filaments.

3.3. Fracture detection

The next step consists of using the phase images for the detection of microfractures (figure 4.b) using machine learning. To do this, we use a standard U-Net architecture²⁴ taking 128×128 images as input with 7 convolutional layers and 7 up-sampling layers. The network is trained using a selection of axial slices from 9 each microCT images of teeth with cracks manually annotated.

Because the cracks are so small in volume relative to the size of the image, we start training by dilating the annotations and using a cross entropy loss which is heavily weighted toward reducing false negatives at the expense of the false positive rate. As the network is trained, the annotation dilation is reduced from 7 to 4 to 0 pixels and the cross entropy weighting is moved from weighing false negatives 100× more importantly to weighing them evenly.

The output of the U-Net is an image where each pixel is the probability that a crack is present. For a new 3D volume, we run each axial slice through the network individually and reconstruct a full probability volume. We then threshold this volume at 0.5 and look at connected components (CC) remaining in the volume image. In this image, cracks tend to show up as long, thin connected components in the axial slices. Images that have no cracks have fewer, smaller connected components relative to those that have cracks present.

4. RESULTS

The probabilistic maps obtained from our machine learning algorithm, described in section 3.3, were first thresholded at 0.5 from a range of [0,1]. The number of CC per tooth varied from 315 to 1000. Cracked teeth have a broader spread of number of CC (between 315 and 1000) than control teeth (between 408 and 751). In addition, the range of the largest CC in cracked teeth (range from 125 to 1336 voxels) is also a little broader than that of control teeth (range from 149 to 1210 voxels), suggesting a higher variability in cracked teeth samples. In microCT images, cracks tend to show up as long, thin connected components. Images that have no cracks have fewer, smaller connected components relative to those that have cracks present.

In order to detect cracks in teeth, we chose distance-weighted discrimination (DWD)²⁵ as our detection method and validated the results with direction-projection-permutation (DiProPerm)²⁶ hypothesis tests. DWD was developed as an improved version of support vector machines (SVM) for linear classification.²⁵ DiProPerm is a permutation-based hypothesis test that assesses the chance that the observed degree of separation happened as a result of expected random variation. It was developed with DWD in mind as an area of application, but it represents a general framework of nonparametric hypothesis testing built to discern visually discovered typical and atypical behavior in high-dimensional settings.

Figure 6.a and b show the results of classifying the CC elements found in the 14 control (blue dots) and 31 cracked (red dots) teeth imaged with microCT, illustrated by projecting each tooth in the DWD and its orthogonal principal component directions (OPC1).²⁷ Kernel density estimates of the data projected onto the DWD separating hyperplane show no clear separation between control and cracked teeth. Thus, DiProPerm confirms no significance separation between the two groups (see Figure 6.b p = 0.74). Further analysis into hr-CBCT images suggests that this lack of separation seems to be caused by more limited detection ability that results from many more false positives despite the elevated component numbers.

Figure 6.

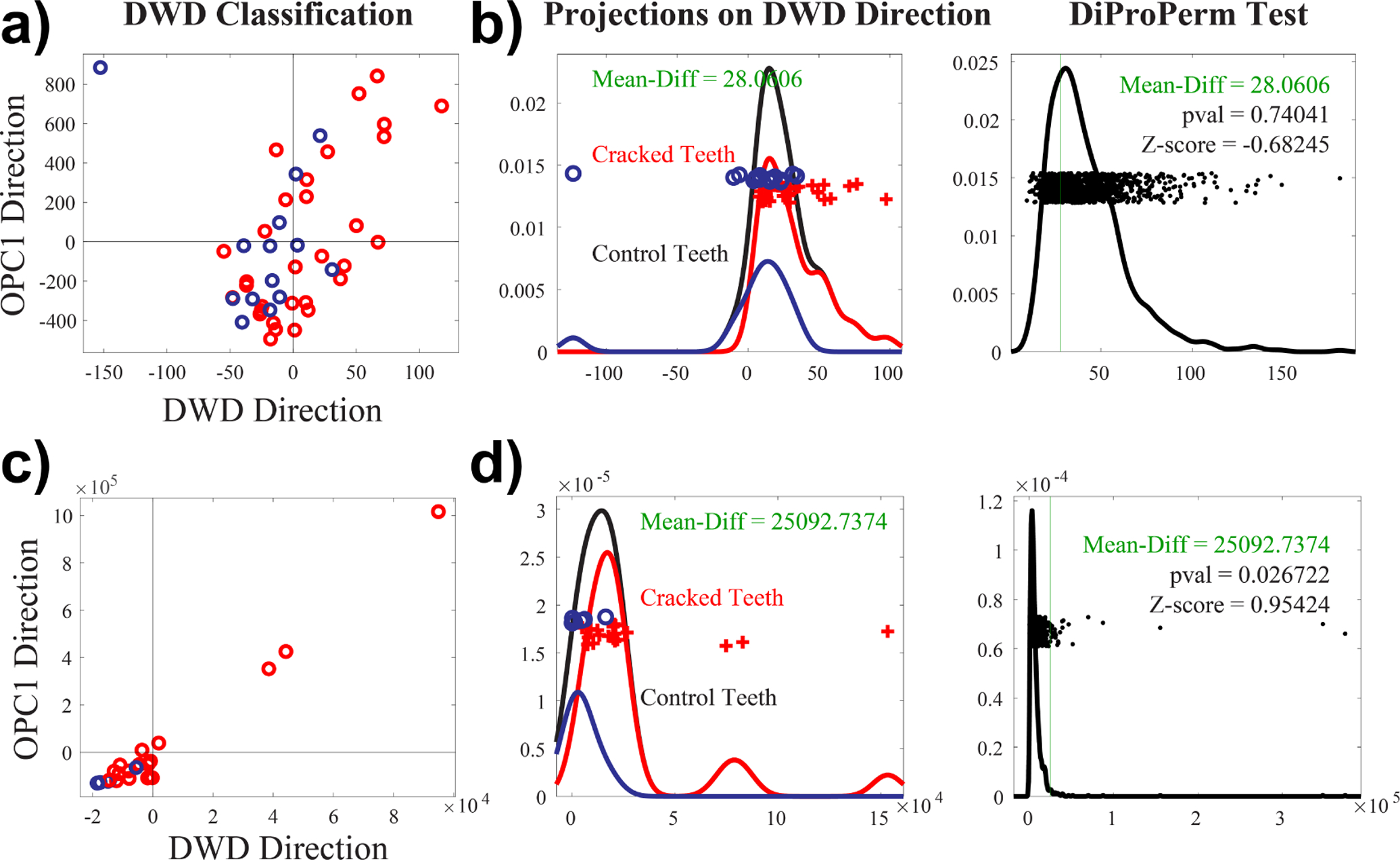
DWD classification of connected component analysis obtained from our machine learning algorithm for a) microCT and for c) synthetically generated hr-CBCT. Each data sample is projected onto the DWD direction as well as the orthogonal principle component 1 (OPC1) direction. Kernel density estimates of the data projections onto the DWD separating hyperplane and permutation tests using DiProPerm for b) microCT and for d) synthetically generated hr-CBCT. Demonstrates a significant separation of the two groups using synthetic hr-CBCT but not microCT.

Detailed analysis into the acquisition parameters of the hr-CBCT revealed that the endodontic mode often uses smoothing filters intended to provide visually appealing images without the presence of artifacts. These filters are useful to better perceive the gross tooth structure and generate 3D reconstructions but can destroy fine features like microfractures. To validate this finding, we tested our algorithm on a previously published dataset of synthetically generated cracks in hr-CBCT.²⁸

Figure 6.c and d show the results of classifying the CC elements found in the 19 synthetically cracked (red dots) and 6 control (blue dots) hr-CBCT images, showing appropriate separation of CC obtained from control and cracked teeth using a similar plane projection. DiProPerm also showed a significant separation result (see Figure 6.d p = 0.026) even for this small sample size. Results with this data suggest that our approach can be applied to hr-CBCT (clinically) when the images are not over-processed. In future stages of this project all images will be acquired without additional filters moving forward.

It is important to mention that thresholding for the presence of large connected components has the added benefit of flagging potential cracks. This provides the clinician with the ability to visually inspect the images and determine if the highlighted area is a crack or not. Figure 7 shows an example of how the probability maps can guide the physician to the crack. The probability maps also give an opportunity to the physician to evaluate the severity of the crack, as illustrated in 8

Figure 7.

Axial slices of a) a microCT tooth scan with a crack in the lower right and the resulting probability map that highlights the crack; b) a CBCT tooth scan with a spurious detection that can be dismissed due to appearance in the image.

Figure 8.

a) Original tooth volume with two arrows indicating a subtle crack (right) and a strong crack (left). B) Probability map overlay, with values interpolating from 0 (red) to 1 (purple). The larger crack is shown in purple indicating a strong probability (value = 1), while the subtle crack is shown in green (value = 0.6).

5. DISCUSSION

We have proposed a method that can enhance the diagnostic accuracy of dental professionals by using the phase images resulting from wavelet analysis to train a deep learning classifier that creates probabilistic maps for microfractures. The proposed wavelet framework presents a superior flexibility and computational performance compared to other methods used for filament-like feature detection, such as Frangi’s vessel enhancement algorithm.²⁹ This is possible due to the combination of a highly customizable isotropic wavelet backbone that can be configured to be sensitive to features in any orientation and scale.

We are aware that the hr-CBCT currently yields very limited detection ability and does not demonstrate the advantage of using wavelet analysis for this task. Detailed analysis into the acquisition parameters of the hr-CBCT revealed that the endodontic mode often uses smoothing filters intended to provide nice looking images without the presence of artifacts. These filters are useful to better perceive the gross tooth structure and generate 3D reconstructions but can destroy fine features like microfractures. To validate this finding, we tested our algorithm on a previously published dataset of synthetically generated fractures in hr-CBCT.²⁸ We were able to correctly detect all but one fracture in this data, showing that our approach can be applied to CBCT when the images are not over-processed.

Future work will focus on validating the ability of the algorithm to localize the fracture, studying the effectiveness of different types of wavelets and classifiers to detect different microfracture types, changing the orientation of the Reisz transform, and validate the algorithm in clinical hr-CBCT images.