Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2019 Jan 22;9(6):3128–3139. doi: 10.1039/c8ra08770a

Understanding thermal decomposition kinetics of flame-retardant thermoset polylactic acid

Yihan Li 1, Zhe Qiang 2, Xie Chen 1, Jie Ren 1,✉
PMCID: PMC9059930  PMID: 35518982

Abstract

The Flynn–Wall–Ozawa method was applied to study the local activation energy of flame retardant thermoset PLA, and the results showed that with an increase of conversion of thermal degradation, the local activation energy was increased slowly. When the conversion of thermal degradation was under 15%, the activation energy of flame retardant thermoset PLA was lower than that of thermoset PLA, attributed to the low bond energy of P–C bond. When the conversion of thermal degradation exceeded 15%, the dehydration charcoal effect of phosphorous compound slowed down the process of thermal degradation, and the activation energy of flame retardant thermoset PLA was higher than that of thermoset PLA, indicating that the addition of 9,10-dihydro-9-oxa-10-phosphaphenanthrene-10-oxide (DOPO) enhances the thermal stability of thermoset PLA. The Coats–Redfern method and invariant kinetic parameters method were used to understand kinetics details about this process including the activation energy and apparent pre-exponential factor, and estimated contribution ratios for the 18 kinetic functions. The results showed that the addition of DOPO didn't impact the most important mechanism of thermal degradation but changed the contribution ratios of the 18 kinetic functions. According to the functional relationship between decomposition rate with temperature and quality conversion rate, three-dimension surface plots were made to understand the change regulation of decomposition rate. We found that the addition of DOPO reduced the decomposition rate of thermoset PLA, attributing to the dehydration charcoal effect of phosphorous compound which restrained the interesterification of PLA, and thus enhancing the thermal stability of thermoset PLA.

The Flynn–Wall–Ozawa method was applied to study the local activation energy of flame retardant thermoset PLA, and the results showed that with an increase of conversion of thermal degradation, the local activation energy was increased slowly.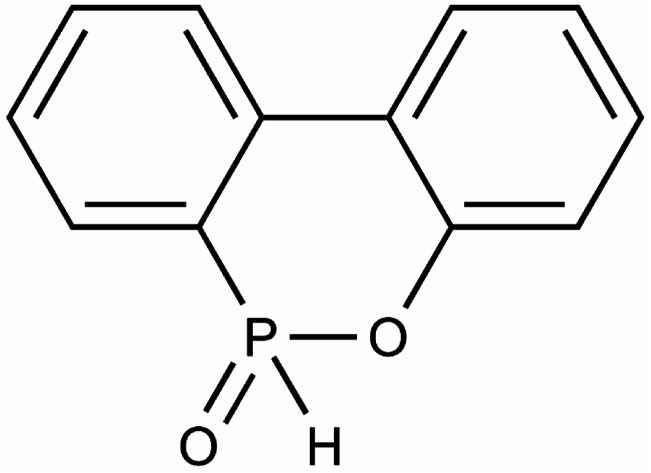graphic file with name c8ra08770a-ga.jpg

1. Introduction

Thermal stability of polymers is one of the greatest considerations for their potential applications including packaging, auto interiors, aerospace and flame-retardant coatings,1–3 especially when these polymeric materials need to perform under intermediate or even high temperature conditions. Thermal degradation of polymers is usually from overheating, which leads to molecular bond breakage, and thus influencing the material properties. Generally, three different polymer thermo-degradation mechanisms exist: thermal decomposition from the effect of temperature, thermo-oxidative degradation from elevated temperatures with the presence of oxygen and thermo-mechanical degradation when any mechanical stress is involved.4 As the pyrolysis process of polymers is primarily kinetically dependent,5 many factors can affect the thermal degradation kinetics such as temperature, polymer molecular weight, and their macromolecular architecture.6 For thermoset polymer composites, this kinetics process can also be influenced by the type of additive, crosslinking density and how good a dispersion of nanofillers is in the matrix. Understanding the thermal degradation behavior of polymer is important to analyse its flame retardancy properties and charcoal mechanism under either inert or oxidizing environment.7 Many researchers applied numerical analysis method to simulate the thermal degradation process and establish a dynamic model to describe various degradation mechanisms8–10 with using many approximation theories such as asymptotic expansion, Doyle's approximation, etc.11–13

Poly(lactic acid) (PLA), as a biodegradable polyester, has received significant attention for industrial applications due to its unique properties of high strength, high modulus, biocompatibility and easy processability.14 It has been reported that the greenhouse gas emission rate of PLA is approximately 1600 kg CO2 per metric ton, while that of polypropylene (PE), polystyrene (PS), polyethylene terephthalate (PET), and nylon are 1850, 2740, 4140, and 7150 kg CO2 per metric ton, respectively.15 PLA is a type of thermally degradable material that burns at a relatively rapid heat release rate (HRR), negligible chars.16 The thermal degradation of PLA is caused by random chain scission or specific chain-end scission because its repeated aliphatic ester structure is relatively easy to hydrolyse and break down.17 Thermoset polylactic acid (TSPLA) is a kind of polymer material which can improve its heat-resistant and weatherability and mechanical properties by introducing highly crosslinked molecular structure in polylactic acid to make the movement of molecular chain greatly limited.18 The prepolymer was synthesized on the basis of ring open polymerization or direct condensation.19 The prepolymer was modified by the end group, with unsaturated double bonds or other reactive end groups, adding initiator or catalyst, combined with heating, illumination and irradiation to induce functional terminal crosslinking and synthesis of thermoset poly(lactic acid). Introduction of crosslinking can significantly reduce the degradation rate of PLA compared to its linear analogous. Since the chemical structure of its backbone has not changed greatly,18 it is still degradable and contains the advantages for green environment. Crosslinking turns out to be beneficial for enhancing the heat stability and mechanical properties of linear PLA. Improved thermal stability could be obtained by synthesizing thermoset PLA.20 The thermoset polylactic acid prepared by crosslinking makes up the poor durability and low strength of the polylactic acid itself, but the crosslinking also leads to the increase of brittleness, which limits its application. Since PLA has been widely used for many biodegrading purposes, research on the stability of polylactic acid (PLA) has also aroused the interest of many scholars. In order to better control thermal decomposition to achieve the goal of producing desired products or handling waste disposal, the reaction mechanisms of PLA thermal decomposition should be understood.21 In the degradation process, PLA are first decomposed to low molecular weight products due to the environmental effects such as heat, sunlight, etc. and then they are decomposed by microorganisms as carbon source.22 However, it presents considerable processing issues due to its sensitivity to stocking and processing conditions.22 Several groups have reported the thermal degradation mechanisms of PLA, and no radicals were produced in the various pyrolysis reactions.23,24 Research efforts have been focused on the enhancement of PLA thermal stability in order to allow it to be used under severe operation conditions.25 In order to improve the thermal stability of polylactic acid, the most common method is to add nanoscale or micron-scale layered silicates (such as montmorillonite) in the polylactic acid matrix composites.26–28 The greatest characteristics of this method not only improve the thermal stability of the composite, but also improve the mechanical properties, and reduce the cost.29,30

However, there are very limited studies about thermoset poly(lactic acid) thermal stability.31 Therefore, this paper focuses on the thermal degradation kinetics of thermoset poly(lactic acid) and discusses the effect of flame retardant DOPO on the thermal degradation behavior of thermoset poly(lactic acid).

The organophosphorus flame retardant 9,10-dihydro-9-oxa-10-phosphaphenanthrene-10-oxide (DOPO), is a white flaky or powdery green phosphorus containing flame retardant. It is an effective reactive flame retardant for polylactic acid, which is smokeless and non-toxic, halogen-free,32 and has excellent antioxidant and water resistance. Because of the biphenyl and phenanthrene ring structure in the molecular structure, the thermal stability and flame retardancy of DOPO are improved compared the ordinary non-cyclic organophosphates. Meanwhile, the DOPO molecule has a P–H bond, which can react with unsaturated bonds, carbonyl groups and epoxy bonds.33 It can be used not only as an addition type flame retardant, but also as a reactive flame retardant, which is embedded in the molecular chain of the polymer by reaction, and is combined with the polymer chain in the form of covalent bond.

Here, a thermoset polylactic acid (TSPLA) and its flame-retardant composites with DOPO (TSPLA–5%DOPO) were studied. Based on the application of Flynn–Wall–Ozawa method, Coats–Redfern method is used to calculate the thermal degradation kinetic parameters. In addition, the kinetic model of thermal degradation was established by the constant dynamic parameter method, and the effect of the addition of DOPO on the thermal degradation behavior of TSPLA was discussed and analysed.

2. Experimental

2.1. Experimental section

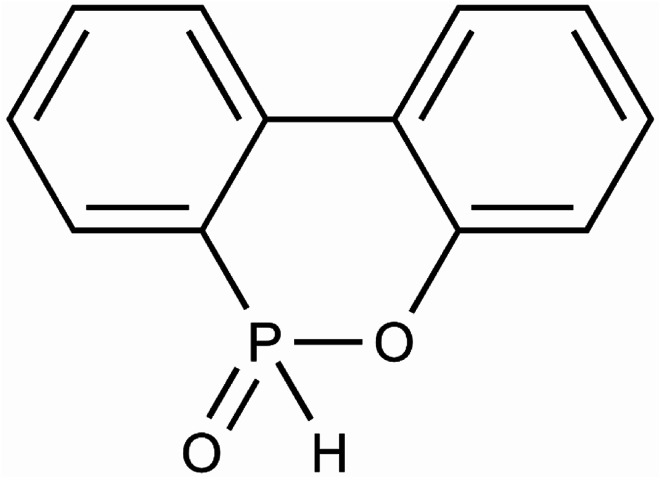
The thermal degradation process was determined by DSC equipment (the Q100 type test instrument of TA company in the United States). The thermal degradation process of the sample was carried out in the Al2O3 crucible. The weight of the experimental samples required was 5–10 mg per test. Nitrogen was chosen as inert gas during the experiment, and the flow rate was 50 ml min−1. The reference material in the DSC device was an empty Al2O3 crucible. The heating rates were 10 K min−1, 20 K min−1, 30 K min−1 and 40 K min−1, respectively, and started heating at room temperature until the material was completely decomposed. Based on the experimental data of thermogravimetric analysis, the thermal degradation behavior of TSPLA was studied by the classical thermal degradation kinetics method, and the effect of DOPO addition on the thermal stability of TSPLA was discussed. The structure of DOPO was shown in Fig. 1. In addition, the dynamic model and degradation mechanism of TSPLA during thermal degradation were determined by the constant dynamic parameter method. Finally, a three-dimensional surface map of thermal degradation rate and thermal degradation temperature was drawn, and the thermal degradation behavior of TSPLA was directly reflected.

Fig. 1. Structure of DOPO.

Fig. 1

Open in a new tab

2.2. Theoretical basis of thermal degradation kinetics

Equal conversion analysis method was selected to determine the activation energy for the thermos-decomposition reaction, which can be described as aA(s) → bB(s) + cC(s) and follows the Arrhenius rule when the thermal decomposition temperature is linearly increased at a certain heating rate.34

The degradation rate of thermoset PLA during thermal degradation is expressed by the following formula:

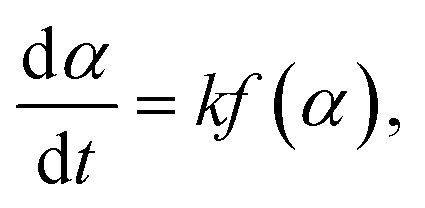2.2. 1

in which α represents the conversion (decomposition) rate of PLA and k is the Arrhenius (Arrhenius) rate constant, which can be described as:

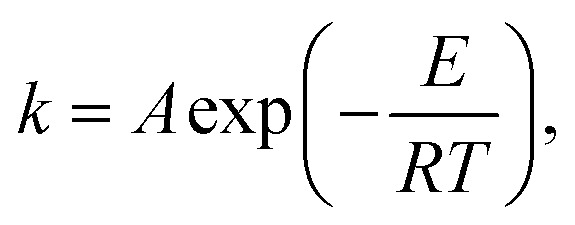2.2. 2

where A is the former factor, R is the gas constant (8.314 J mol), T is the temperature, and E indicates the activation energy for the reaction. By combining the formula (1) and (2), the kinetics of decomposition can be described as follows:

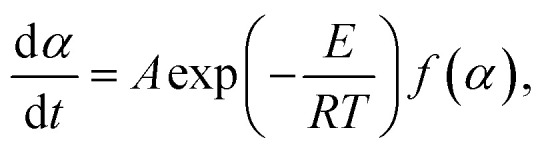2.2. 3

For the non-isothermal thermal decomposition test of thermoset polylactic acid, the heating rate is another important parameter, and the expression is as follows:

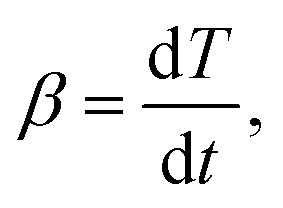2.2. 4

Therefore, the expression (2) and (3) can be further expressed as:

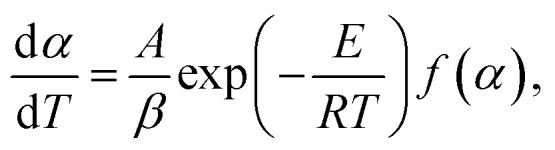2.2. 5

Based on this theory, the thermal degradation kinetics of thermoset poly(lactic acid) was studied and discussed in combination with Flynn–Wall–Ozawa, Coats–Redfern and invariant kinetic parameters.

3. Result and discussion

3.1. Determination of thermogravimetric curves of thermoset polylactic acid

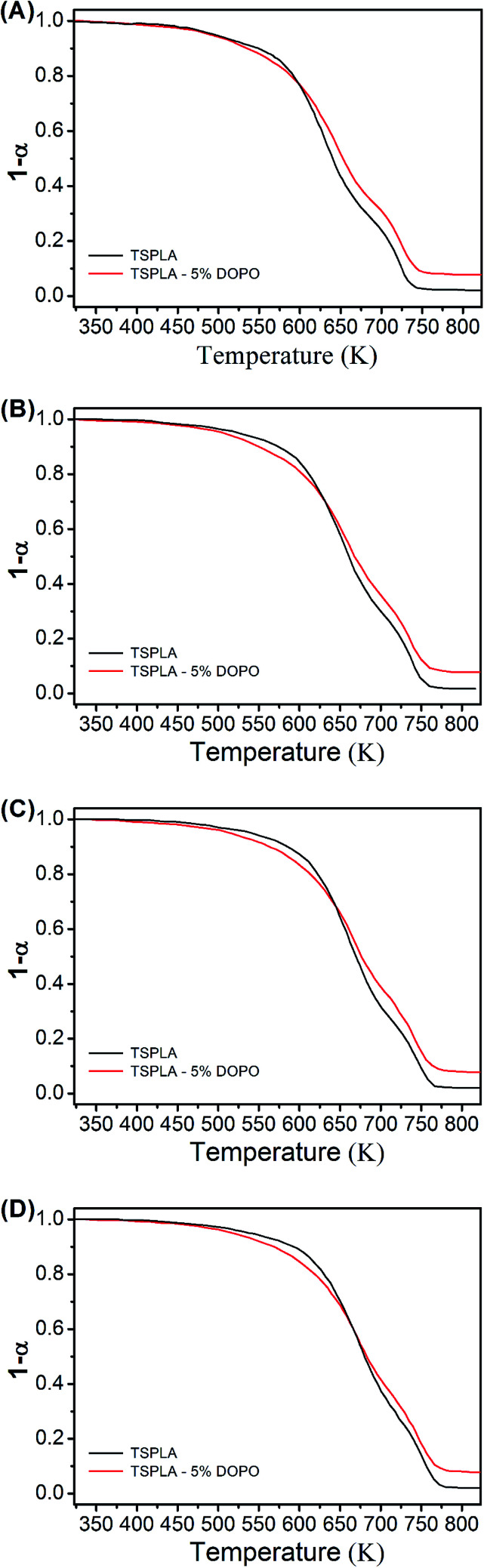
Fig. 2 is the thermal degradation curves of TSPLA and TSPLA–5%DOPO at different heating rates, which shows the addition of flame retardant DOPO reduced the decomposition temperature of TSPLA at the early stage of thermal degradation. Fig. 2A, B, C and D are the thermal degradation curves of TSPLA and TSPLA–5%DOPO at 10 K min−1; 20 K min−1; 30 K min−1; 40 K min−1, respectively. The bond energy of the DOPO P–C bond is lower and the thermal decomposition is easy to break. Therefore, the initial decomposition of the polymer was advanced, and its thermal stability was reduced. When the conversion rate was 50%, the decomposition temperature of TSPLA–5%DOPO was higher than that of TSPLA, which was because the dehydration of phosphorus compounds to carbon increased the thermal stability of the polymer.

Fig. 2. The thermogravimetric curves of TSPLA and TSPLA–5%DOPO at different heating rates. (A) 10 K min−1; (B) 20 K min−1; (C) 30 K min−1; (D) 40 K min−1.

Fig. 2

Open in a new tab

3.2. Determination of flame retardancy

Limit oxygen index (LOI), also known as critical oxygen concentration, is the lowest oxygen concentration required for material combustion under experimental conditions. Limit oxygen index (LOI) of flame retardant thermoset polylactic acid (PLA) with different DOPO content was tested, and the lowest oxygen concentration was obtained, which could directly evaluate the flame retardancy of PLA. With higher the limiting oxygen index, the material is to more difficult to be burned, that is, the better the flame retardancy.

The Limited Oxygen Index (LOI) test was conducted according to GB/T 2406-2009, ‘Determination of Combustion Behavior of Plastics by Oxygen Index Method’. The pre-pressed composite plate was cut into 120 mm wide rectangular splines with 10 mm width. Fifteen standard splines were prepared for each group, and each spline was marked 50 mm away from the ignition end. The specific testing process is as follows: equipment should be calibrated before testing; the spline was fixed vertically in the centre of the combustion cylinder; the top of the sample was ignited by the igniter, and the igniter was removed immediately after ignition so that the flame action time did not exceed 30 seconds; the ratio of oxygen to nitrogen should be adjusted to record combustion time and distance; when the spline burning time exceeded 3 minutes or the flame front exceeded 50 mm, the oxygen concentration should be lowered. If the spline burning time was less than 3 minutes or the flame front exceeds 50 mm, the oxygen concentration should be increased. After repeating the steps mentioned above, the oxygen content of the material when burning for 3 minutes or about 50 mm was recorded, which was the oxygen index of the material.

The oxygen index test results of flame-retardant thermoset poly(lactic acid) with different DOPO content was shown in Table 1. The oxygen index of nonflame-retardant thermoset poly(lactic acid) is 22.9%. When the DOPO content was 5%, the oxygen index was 25.3%. With the increase of DOPO content, the oxygen index increased and the increase was small. And when the addition of DOPO was 5%, the LOI result of the material has increased, at the same time, the thermal stability of the sample has also been improved. It can be seen that the addition of DOPO can improve the flame retardancy of thermoset poly(lactic acid).

Oxygen index of flame retardant thermoset polylactic acid with different DOPO content.

Sample DOPO (wt%) P content (wt%) LOI (%)
TSPLA 0 0 22.9
TSPLA–DOPO5 5 0.72 25.3
Open in a new tab

3.3. Thermal degradation kinetics of thermoset polylactic acid

3.3.1. Flynn–Wall–Ozawa method

The Friedman method is one of the most commonly used differential methods in the method of equal conversion thermal analysis,35 which is the most direct way to get the activation energy. The equal conversion integral method is also called the Flynn–Wall–Ozawa method (FWO method).36,37

The Flynn–Wall–Ozawa method is based on the Arrhenius law, and the approximate theory of Doyle is applied.38 The specific expression is as follows:

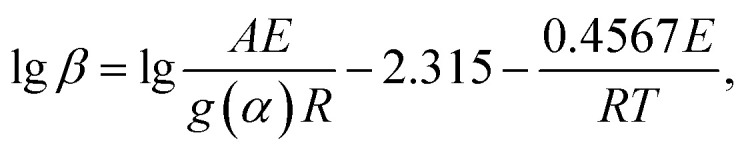3.3.1. 6

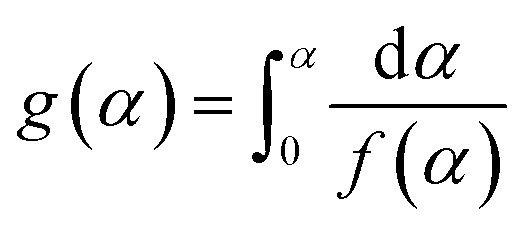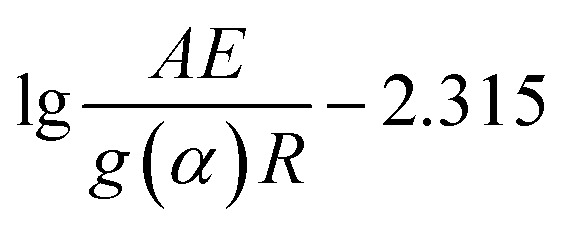In the formula, g(α) is the integral form of the thermal degradation mechanism of the material: Inline graphic. The Inline graphic part in the formula (6) is obviously a definite value for a given degradation conversion rate of α. Therefore, by fitting the linear relationship between lg β and 1/T (considering the unit transformation, fitting lg β vs. 1000/T actually), the slope k value of the linear relation combined with formula (6) can get the corresponding activation energy E. It could be seen that the activation energy calculated by the FWO method is independent of the mechanism function f(α). Especially, when the degradation mechanism function is uncertain, the method can also calculate the thermal degradation activation energy of the material.

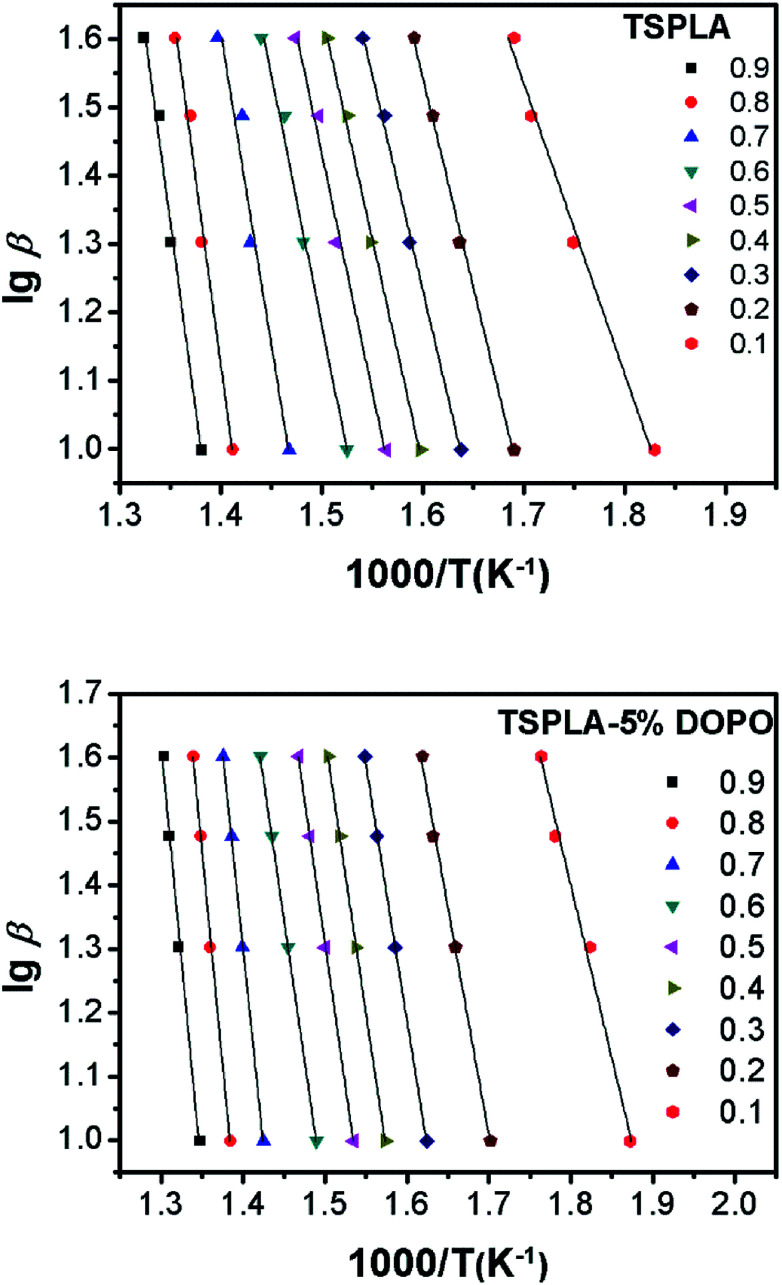
Fig. 3 shows the lg β vs. 1/T fitting line for TSPLA and TSPLA–5%DOPO at different conversion rates (10–90%). The correlation coefficients of the fitted lines in the graph are all higher than 95%, as shown in Table 2. Since the better parallelism is maintained between the fitted lines, the Flynn–Wall–Ozawa method is suitable for the thermal degradation kinetics analysis of the material system. From Table 2, we find that the addition of 5% flame retardant DOPO increases the activation energy of TSPLA thermal degradation from 137.002 kJ mol−1 to 171.392 kJ mol−1, indicating that DOPO helps to improve the thermal stability of TSPLA.

Fig. 3. Linear lines of lg beta and 1/T of TSPLA and TSPLA–5%DOPO under different degradation rates.

Fig. 3

Open in a new tab
The fitting slope, correlation coefficient and activation energy of different degradation rates.
α TSPLA TSPLA–5%DOPO
k R E (kJ mol−1) k R E (kJ mol−1)
0.1 −4.229 0.983 76.9869 −5.368 0.987 97.727
0.2 −5.890 0.997 107.225 −7.243 0.998 131.861
0.3 −6.220 0.998 113.232 −8.049 0.999 146.536
0.4 −6.489 0.996 118.129 −8.507 0.999 154.869
0.5 −6.703 0.993 122.025 −9.008 0.999 163.981
0.6 −7.133 0.985 129.853 −8.918 0.998 162.355
0.7 −8.538 0.954 155.43 −12.132 0.999 220.860
0.8 −10.67 0.977 194.242 −13.638 0.999 248.272
0.9 −10.72 0.996 195.152 −13.008 0.987 236.811
AVG −7.525 0.987 137.002 −9.415 0.996 171.392
Open in a new tab

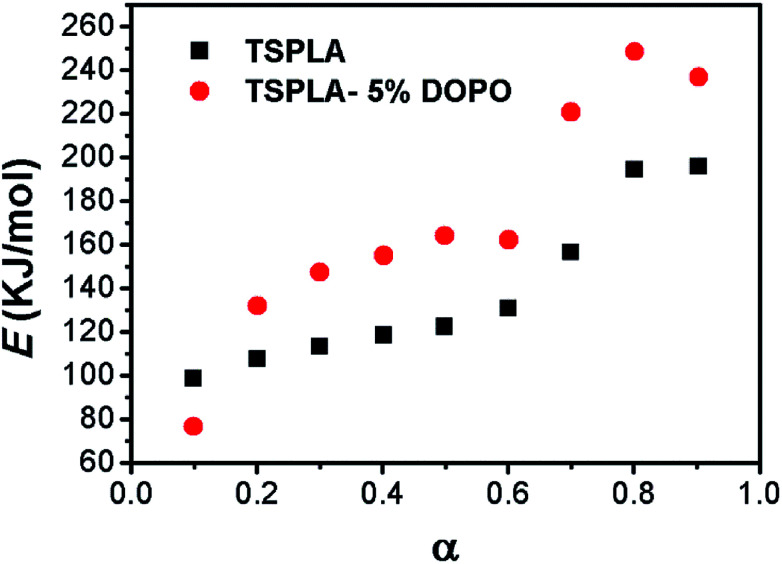
Fig. 4 demonstrates the change in the thermal degradation activation energy of TSPLA and TSPLA–5%DOPO under different degradation rates. With the process of thermal degradation, the activation energy of the thermal degradation of the polymer showed a slow rising trend. When the conversion rate of thermal degradation is 10%, the activation energy of thermal degradation of TSPLA–5%DOPO was less than TSPLA. However, when the conversion rate of thermal degradation exceeded 15%, the activation energy of thermal degradation of TSPLA–5%DOPO was obviously higher than that of TSPLA. Compared with other factors, the bond energy of the P–C bond is lower,39 so DOPO affected the initial thermal degradation stage of TSPLA, and the activation energy of thermal degradation could be reduced. However, with the thermal decomposition temperature continuing to rise, dehydration charring effect of the phosphide improved the thermal degradation activation energy.

Fig. 4. Degradation activation energy of TSPLA and TSPLA–5%DOPO under different degradation rates.

Fig. 4

Open in a new tab

3.3.2. Constant dynamic parameter method

Based on the related compensation effect, for further study on the thermal degradation kinetics, this paper adopted invariant kinetic parameter method (constant kinetic parameters method, IKP method), which was proposed by Lesnikovich and Levchik.40,41 The thermal degradation mechanism of thermoset polylactic acid was discussed in this paper and thermal degradation of materials is very complicated. In the perspective of theoretical simulation, many mechanisms needed to be used to describe the actual process. Different mechanism of thermal degradation corresponded to the different mechanism function f(α), and each mechanism function could be associated with the thermal degradation mechanism of the material by the dynamic parameters and the compensation effect.42 For a certain mechanism function fj(α) (j = 1, 2, 3…), there is the following relational expression:

ln Ajv = Bv + IvEjv, 7

Ajv and Ejv are the apparent pre-exponential and activation energies of the mechanism function f(α) corresponding to the different heating rate βv (v = 1, 2, 3…).

For a certain mechanism function f(α), it could be easily obtained by the formula (3):

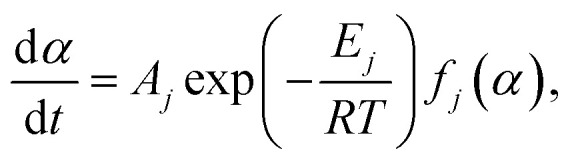3.3.2. 8

When the heating rate is βv, the formula (8) can be deformed as follows:

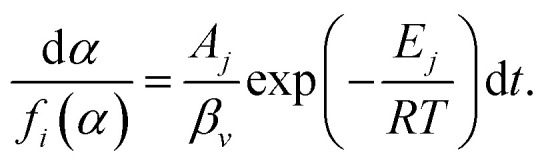3.3.2. 9

In the process of thermal degradation of solids, many gaseous products were produced, and the degradation process was complex. Therefore, it also involved various mechanisms (such as random nucleation mechanism, phase boundary reaction mechanism, diffusion mechanism, etc.), and theoretical analysis required multiple mechanism functions f(α) as well. The IKP method also applies to the thermal degradation process which was not defined by thermal degradation mechanism or mechanism function. By using the related theory of IKP method, the invariable kinetic parameters and the occurrence probability of each degradation mechanism could be obtained from the thermogravimetric curve. In the study of constant dynamic parameters, the degradation mechanism and its mechanism function are classified into 18 categories in the process of thermal degradation,43 which was shown in Table 2.

The Coats–Redfern method45 can be used to obtain the activation energy and the apparent pre-index factors which are required by the IKP analysis method. The Coats–Redfern method is also an integral method, which is often applied to the thermal degradation of materials.46,47 The formula (5) is integrated on both sides and replaced by the progressive value:

ln[gj(α)/T2iv] = ln(AjvR/βvEjv) − Ejv/RTiv 10

In the formula above, i represents the number of data points, and j is the number of the mechanism function in Table 3. The ln[gj(α)/Tiv2] vs. 1/Tiv is proposed to synthesize a straight line, and the activation energy E can be obtained by the slope calculation of the line, and the apparent pre-exponential factor A is obtained by the intercept. In addition, the Bv and Iv in formula (6) and (7) are the compensation parameters of the mechanism function f(α) at the heating rate βv, which can be obtained from the fitting line of ln Ajvvs. Ejv with its slope and intercept.

18 dynamic models used in the IKP method.44.
Kinetic models f j (α) g j (α)
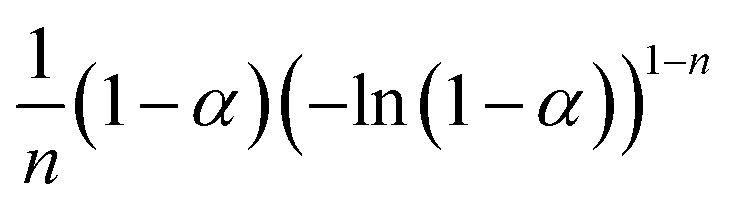
Nucleation and nucleus growing graphic file with name c8ra08770a-t20.jpg (−ln(1 − α))n S1, n = 1/4
S2, n = 1/3
S3, n = 1/2
S4, n = 2/3
S5, n = 1
Phase boundary reaction (1 − α)n 1 − (1 − α) S6, plane symmetry
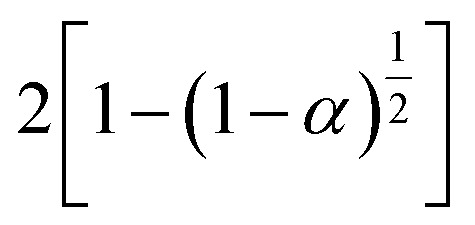
graphic file with name c8ra08770a-t21.jpg S7, cylindrical symmetry
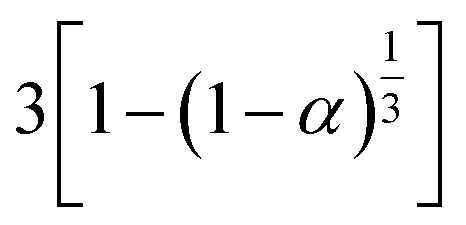
graphic file with name c8ra08770a-t22.jpg S8, spherical symmetry
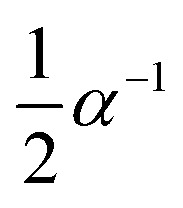
Diffusion graphic file with name c8ra08770a-t23.jpg α 2 S9, plane symmetry
[−ln(1 − α)]−1 α + (1 − α)ln(1 − α) S10, cylindrical symmetry
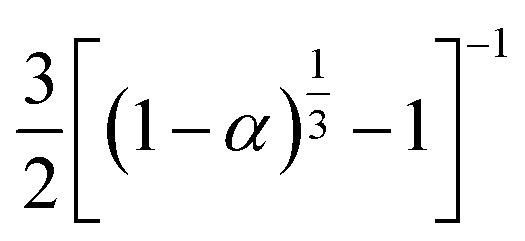
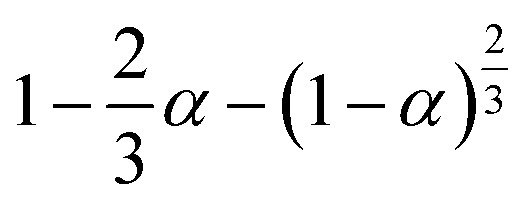
graphic file with name c8ra08770a-t24.jpg graphic file with name c8ra08770a-t25.jpg S11, spherical symmetry
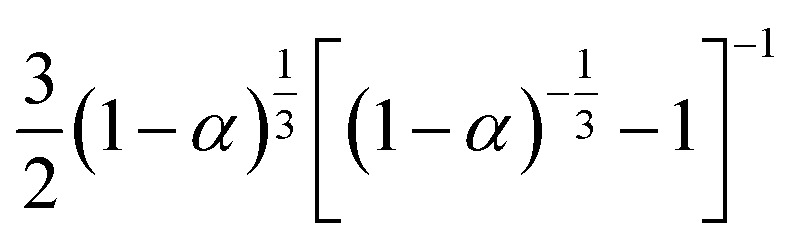
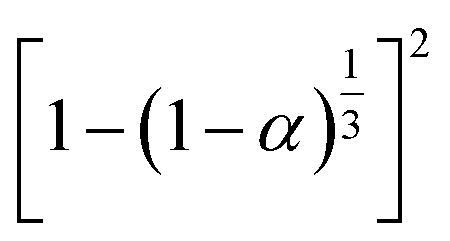
graphic file with name c8ra08770a-t26.jpg graphic file with name c8ra08770a-t27.jpg S18, Jander's type
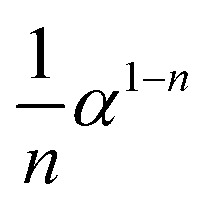
Potential law graphic file with name c8ra08770a-t28.jpg α n (0 < n < 2) S12, n = 1/4
S13, n = 1/3
S14, n = 1/2
S17, n = 2/3
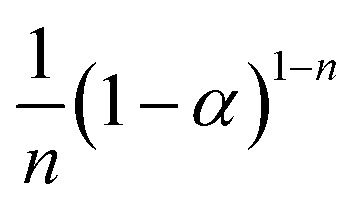
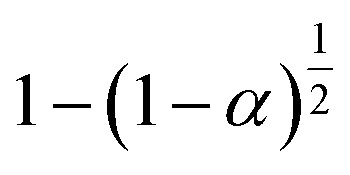
Reaction order graphic file with name c8ra08770a-t29.jpg graphic file with name c8ra08770a-t30.jpg S15, n = 1/2
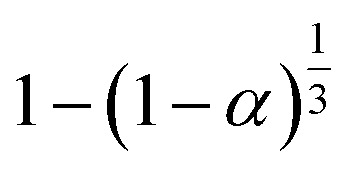
graphic file with name c8ra08770a-t31.jpg S16, n = 1/3
Open in a new tab

Lesnikovich et al.48 studied the physical meaning of the parameters Bv and Iv of each temperature rise rate, βv. And it is can be obtained:

Bv = ln(kv), 11
Iv = 1/RTv. 12

In the formula, kv is the Arrhenius rate constant of the heating rate under the βv. We can replace the expression (11) and (12) into (7) and get the following:

Bv = ln(Ainv) − IvEinv, 13

The Ainv, Einv, which is obtained by this formula, is a constant dynamic parameter.

The TG curves of TSPLA and TSPLA–5%DOPO at different heating rates were processed and calculated by Coats–Redfern method. The values of activation energy and pre-exponential factors corresponding to the 18 mechanism functions were summarized in Tables 4 and 5. In the case of unclear degradation mechanism, the probability of each dynamic function can be calculated by IKP method, which is specific to the content of 3.3 Section.

Activation energy and pre-finger factor of TSPLA obtained by Coats–Redfern method.
β 1 = 10 K min−1 β 2 = 20 K min−1 β 3 = 30 K min−1 β 4 = 40 K min−1
g(α) E 1 (kJ mol−1) ln A1 (s−1) E 2 (kJ mol−1) ln A2 (s−1) E 3 (kJ mol−1) ln A3 (s−1) E 4 (kJ mol−1) ln A4 (s−1)
S1 3.93 −10.75 5.24 −9.61 6.40 −8.84 6.32 −8.59
S2 8.73 −9.09 10.64 −7.95 12.14 −7.20 12.14 −6.93
S3 18.33 −6.62 21.45 −5.37 23.78 −4.52 23.78 −0.50
S4 27.94 −4.47 32.18 −3.08 35.33 −2.12 35.42 −1.92
S5 47.14 −0.48 53.63 1.20 58.53 2.40 58.70 2.56
S6 31.09 −4.32 35.58 −2.91 38.91 −1.92 39.24 −1.70
S7 38.24 −2.57 43.73 −1.03 47.72 0.053 47.97 0.25
S8 41.08 −1.91 46.89 −0.32 51.12 0.79 51.38 0.98
S9 72.66 3.48 82.06 5.54 88.88 7.03 89.62 7.21
S10 81.39 4.52 91.95 6.70 99.52 8.61 100.27 8.75
S11 85.05 4.52 96.11 6.79 104.01 8.45 104.76 8.58
S12 1.83 −11.99 4.36 −10.01 1.50 −11.28 4.49 −9.35
S13 6.90 −9.75 8.73 −8.58 10.23 −7.80 9.56 −7.76
S14 10.31 −8.90 12.39 −7.77 13.97 −7.01 14.05 −6.76
S15 38.33 −3.26 43.73 −1.72 47.72 −0.64 48.05 −0.44
S16 41.07 −3.01 46.89 −1.42 51.13 −0.30 51.38 −0.12
S17 17.21 −7.23 20.12 −6.01 22.28 −5.19 22.45 −4.95
S18 92.62 5.80 104.51 8.20 113.24 9.96 113.82 10.06
Open in a new tab
Activation energy and pre-finger factor of TSPLA–5%DOPO obtained by Coats–Redfern method.
β 1 = 10 K min−1 β 2 = 20 K min−1 β 3 = 30 K min−1 β 4 = 40 K min−1
g(α) E 1 (kJ mol−1) ln(A1) (s−1) E 2 (kJ mol−1) ln(A2) (s−1) E 3 (kJ mol−1) ln(A3) (s−1) E 4 (kJ mol−1) ln(A4) (s−1)
S1 3.83 1.88 22.45 5.09 2.83 3.91 7.99 4.52
S2 5.94 3.78 6.65 4.57 7.48 5.70 8.31 6.34
S3 14.13 6.09 14.97 6.88 16.63 7.99 16.63 8.63
S4 22.45 8.00 24.11 8.86 25.77 10.03 26.60 10.75
S5 39.08 11.50 41.57 12.41 44.06 13.70 44.90 14.35
S6 25.77 8.13 26.60 9.06 29.10 10.25 29.93 10.85
S7 31.59 9.66 33.26 10.58 35.75 11.90 36.58 12.45
S8 34.09 10.20 35.75 11.15 38.24 12.40 39.08 13.05
S9 61.52 14.80 64.85 15.85 69.01 17.70 70.67 18.05
S10 68.17 15.80 72.33 16.96 77.32 18.50 78.98 18.15
S11 71.50 15.50 75.66 16.60 80.65 18.20 82.31 18.95
S12 1.16 1.24 1.66 2.29 1.00 2.46 8.83 3.74
S13 3.33 2.59 1.83 2.38 4.41 4.47 9.99 5.23
S14 9.98 4.78 10.81 5.56 9.15 5.90 9.39 6.56
S15 31.59 8.94 33.26 9.88 35.75 11.20 36.58 11.85
S16 34.09 9.11 35.75 10.05 38.24 11.30 39.08 11.95
S17 13.30 5.57 24.11 5.76 15.80 7.54 16.63 8.13
S18 80.15 16.5 82.31 17.59 88.13 18.40 91.45 20.05
Open in a new tab

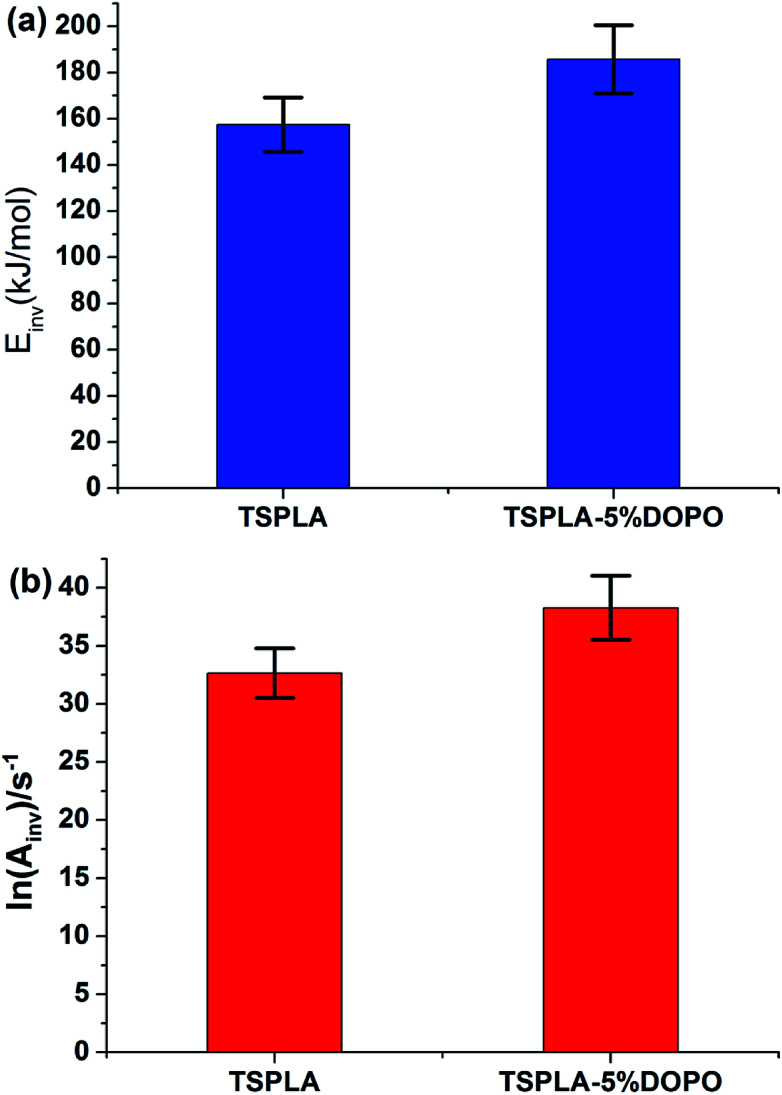
For four different heating rates, the corresponding kinetic parameters can be calculated according to the formula (13). On the basis of Tables 4 and 5, we applied formula (7) to line fitting the ln A vs. E at different heating rates, and get the compensation parameters Bv and Iv, as shown in Table 6. Next, the Bvvs. Iv was fitted linearly with the formula (13), and then the invariant dynamic parameters Einv and Ainv were obtained. From Fig. 5, the activation energy of TSPLA and TSPLA–5%DOPO obtained by IKP method was 157.422 and 185.744 kJ mol−1, respectively. The results were in good agreement with the results obtained by the FWO method.

Compensation parameters and fitting correlation coefficients of TSPLA and TSPLA–5%DOPO.
β (K min−1) B v I v R
TSPLA 10 2.748 0.190 0.994
20 4.098 0.181 0.986
30 4.396 0.179 0.984
40 4.589 0.179 0.986
TSPLA–5%DOPO 10 2.703 0.191 0.962
20 3.104 0.190 0.943
30 4.383 0.182 0.961
40 4.726 0.181 0.947
Open in a new tab
Fig. 5. Constant dynamic parameters of TSPLA and TSPLA–5%DOPO.

Fig. 5

Open in a new tab

3.3.3. Study on kinetic function of thermal degradation

The thermal degradation process of polymer materials is of certain complexity, and many dynamic functions need to be analysed theoretically. IKP theory can be applied to calculate the occurrence probability of the kinetic mechanism of materials in the process of thermal degradation, and finally get the function expression which can accurately describe the process of thermal degradation.

The constant dynamic parameters Einv and Ainv obtained in the last section play a decisive role in determining the dynamic function. In order to get the specific form of the dynamic function, it is also necessary to do statistical processing of the data obtained.49 For a certain mechanism function fj(α), there is an expression under a given heating rate βv:

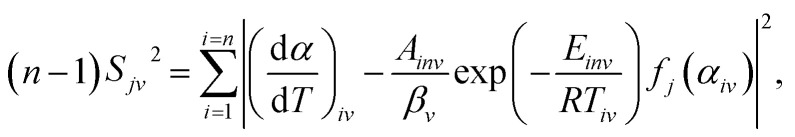3.3.3. 14

The most probable mechanism function, whose corresponding value 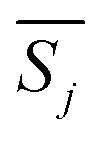Inline graphic is minimum, 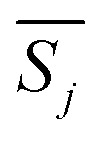Inline graphic is expressed as:

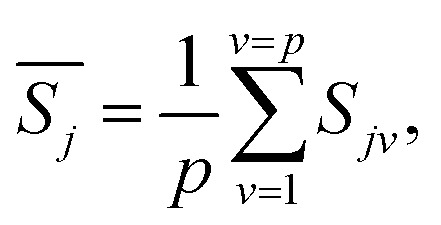3.3.3. 15

Among them, p represents the number of heating rates selected. The occurrence probability of each mechanism function fj(α) is closely related to the following expression:

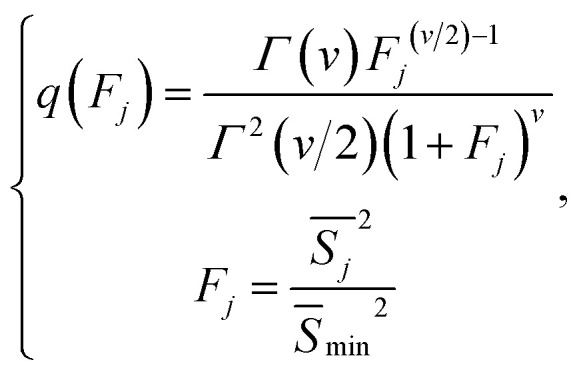3.3.3. 16

In the formula, Γ is the Γ function for statistics, the expression is 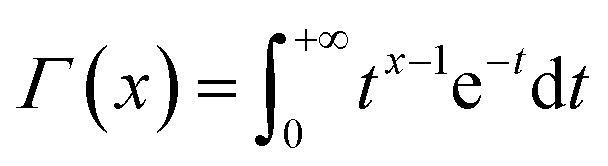Inline graphic. v is a discrete-time value of freedom, which is equal to the number of temperature rising rates of p.50 The precondition of the probability of every mechanism function calculated by the IKP method is that the events of L dynamic functions are independent of each other:

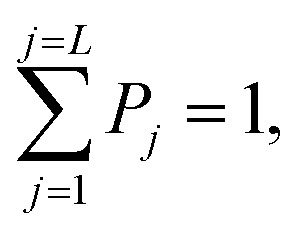3.3.3. 17

P j is defined as:

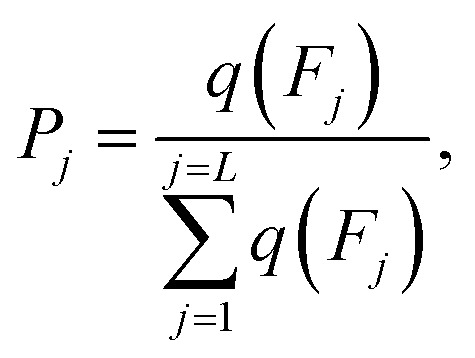3.3.3. 18

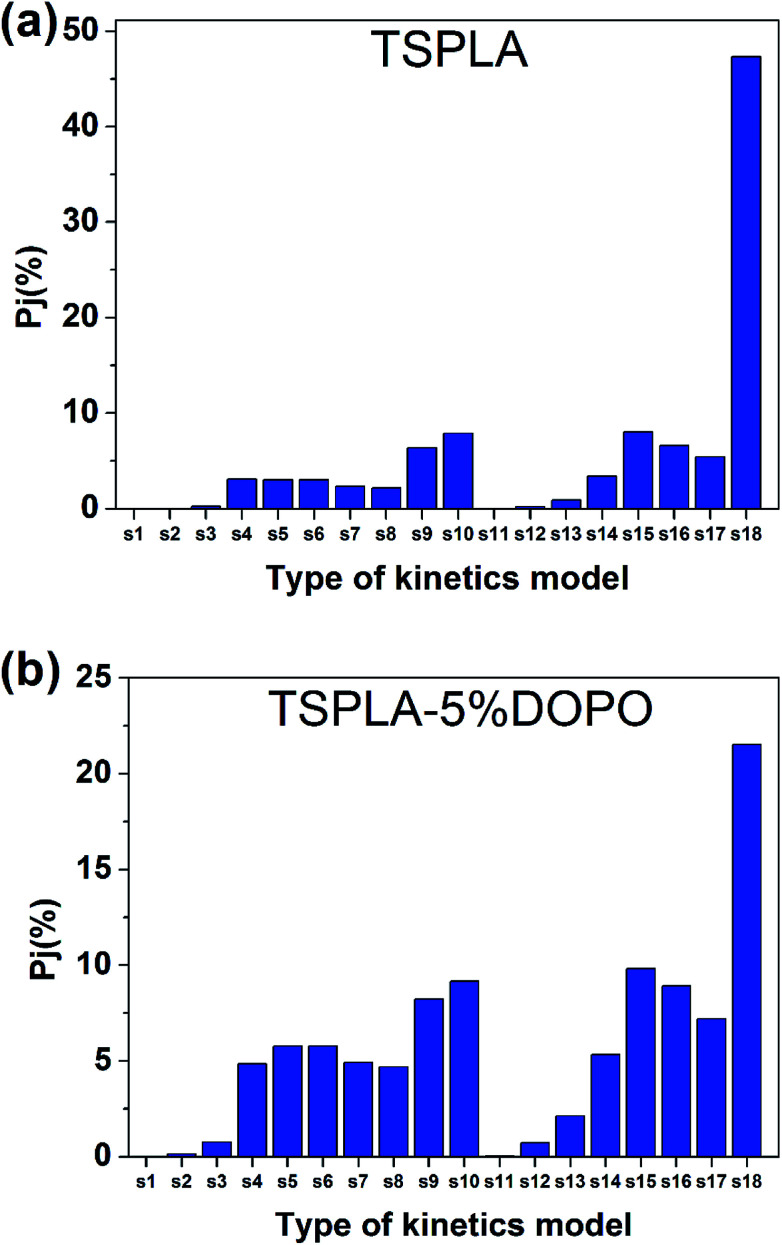
For the L dynamic functions selected in this article, please refer to Table 4. The probability of the occurrence of a dynamic function is calculated by using the above formula, as shown in Fig. 6, and the specific data is shown in Table 7.

Fig. 6. Probability distribution graph of dynamic functions of TSPLA (a) and TSPLA–5%DOPO (b).

Fig. 6

Open in a new tab
Probability of the occurrence of TSPLA and TSPLA–5%DOPO dynamic functions.
TSPLA TSPLA–5%DOPO
Type of kinetics model P j (%) Type of kinetics model P j (%)
S1 0.00% S1 0.02%
S2 0.03% S2 0.14%
S3 0.26% S3 0.76%
S4 3.08% S4 4.84%
S5 3.02% S5 5.78%
S6 3.02% S6 5.78%
S7 2.32% S7 4.91%
S8 2.15% S8 4.69%
S9 6.36% S9 8.22%
S10 7.90% S10 9.17%
S11 0.01% S11 0.06%
S12 0.21% S12 0.72%
S13 0.88% S13 2.13%
S14 3.41% S14 5.33%
S15 8.01% S15 9.82%
S16 6.60% S16 8.92%
S17 5.42% S17 7.20%
S18 47.32% S18 21.53%
Open in a new tab

The thermal degradation of polymers could not be simply described and explained by a single degradation mechanism, on account of including a variety of forms and processes.51 As shown in Fig. 6 and Table 7, the 18 kinetic models listed in Table 4 had different degrees of contribution to the thermal degradation process of TSPLA and TSPLA–5%DOPO. For the thermal degradation process of TSPLA, the highest contribution rate of S18 thermal degradation kinetic model was about 47.3%, which means that the diffusion mechanism played a core role in the thermal degradation process of TSPLA. In addition, S9, S10, S15 and S16 also played a significant role, and their contribution rates were about 6.4%, 7.9%, 8% and 6.6%, respectively. Therefore, in addition to the diffusion mechanism, the reaction series mechanism was also an important mechanism for the thermal degradation of TSPLA. The addition of 5% DOPO changed the value of the contribution rate of the kinetic models to the thermal degradation process, but it did not change the core mechanism of thermal degradation. For the thermal degradation process of TSPLA–5%DOPO, S18 was still the dynamic model with the largest contribution ratio. Its contribution rate was about 21.5%, and the contribution rate of S9, S10, S15 and S16 were up to 1.3–2.3%. These probability fluctuations may be attributed to the dehydration of phosphorus compounds to carbonization, which slowed the transfer of heat and the volatilization of thermal decomposition products.52 Therefore, the main stage of thermal degradation of PLA/DOPO can be explained by S18 degradation model, i.e. diffusion degradation mode.

In the process of thermal degradation of polymer materials, the relationship between thermal degradation rate and mass transformation percentage and decomposition temperature could be established, as shown in formula (19).

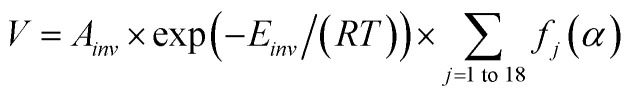3.3.3. 19

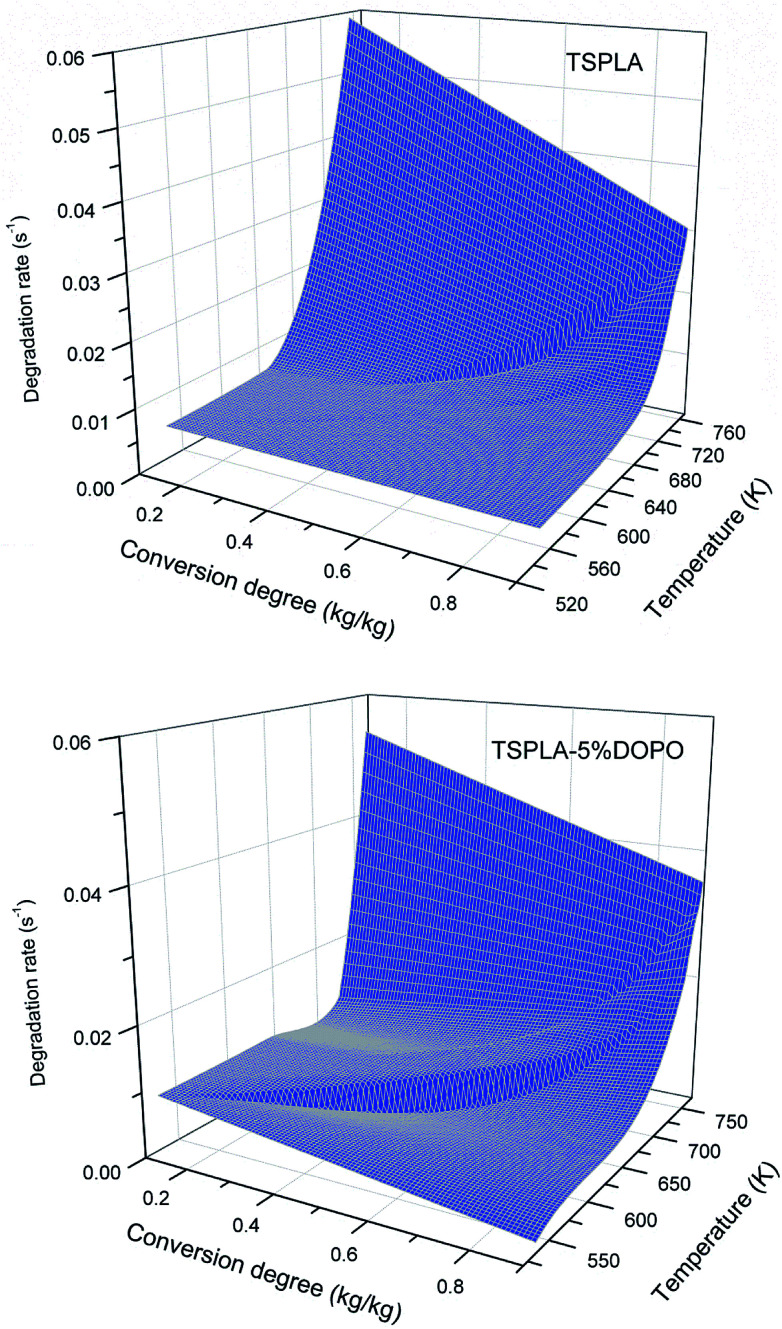
On the basis of formula (19), combined with interpolation method in numerical analysis, we could get two three-dimensional maps shown in Fig. 7, which could intuitively show the change rule of thermal degradation rate of TSPLA and TSPLA–5%DOPO with mass percentage and thermal degradation temperature. Overall, the addition of 5%DOPO reduced the thermal degradation rate of TSPLA, but did not change the mechanistic law of the change of thermal degradation rate. Polylactic acid has a complicated thermal decomposition process, and its main mechanism is intramolecular or intermolecular transesterification.53 At the same time, the dehydration of phosphorus containing compounds to a certain extent inhibits the transesterification of polylactic acid and improves the thermal stability of the polymer.54 With the rising of thermal degradation temperature, the thermal degradation rate of the two materials increased slowly. While the thermal degradation rate increased rapidly, when the thermal degradation temperature reached 700 K (about 427 degrees). In the high temperature degradation area, the fast decomposition products under high temperature could slow down the thermal degradation process to some extent, and protected the materials. Therefore, with the increase of conversion percentage, the decomposition rate had an obvious downward trend.55

Fig. 7. Thermal degradation rate diagram of TSPLA and TSPLA–5%DOPO.

Fig. 7

Open in a new tab

4. Conclusion

Under the protection of nitrogen, using DSC test method to obtain the TG curves under different heating rates of TSPLA and TSPLA–5%DOPO in the process of thermal degradation process. Based on the application of Flynn–Wall–Ozawa method, Coats–Redfern method is used to calculate the thermal degradation kinetic parameters. In addition, the kinetic model of thermal degradation was established by the constant dynamic parameter method, and the effect of the addition of DOPO on the thermal degradation behavior of TSPLA was discussed and analysed. The specific analysis is as follows:

(1) According to the Flynn–Wall–Ozawa method, for a given thermal degradation conversion rate, the linear relationship between lg beta and 1/T is fitted, and the slope activation energy can be converted into the corresponding activation energy of the thermal degradation conversion rate. From the experimental data, the average thermal degradation activation energy of TSPLA was 137.002 kJ mol−1, and the average thermal degradation activation energy of TSPLA–5%DOPO was 171.392 kJ mol−1. This indicates that the addition of DOPO increases the thermal stability of TSPLA, which is attributed to the dehydration of phosphorus compounds to carbonization slowing down the process of thermal degradation. With the rising of the conversion rate of thermal degradation α, the activation energy of thermal degradation tended to increase slowly. When the conversion rate of thermal degradation α is less than 15%, the thermal degradation activation energy of TSPLA–5%DOPO is smaller than that of TSPLA, which is caused by the lower bond energy of the P–C bond. When the conversion rate of thermal degradation α is greater than 15%, the activation energy of thermal degradation of TSPLA–5%DOPO is obviously higher than that of TSPLA.

(2) Using the Coats–Redfern method, the activation energy values and the apparent pre-index factors corresponding to the 18 dynamic functions were calculated. On this basis, the constant dynamic parameters of the two kinds of materials were obtained by the compensation effect and the constant dynamic parameter method. Among them, the apparent activation energy of TSPLA was Einv = 157.422 kJ mol−1, and the apparent activation energy of TSPLA–5%DOPO was Einv = 185.744 kJ mol−1, which was consistent with the conclusion obtained by FWO method.

(3) The parameter Ainv and Einv obtained by the constant kinetic parameter method were used to evaluate the contribution rate of 18 kinetic functions to the thermal degradation of two materials. The results showed that the addition of DOPO changed the contribution rate of each kinetic model to the thermal degradation process, but did not change the core mechanism of thermal degradation. S18 kinetic model is the most important degradation mechanism of the two materials in the process of thermal degradation.

(4) A three-dimensional surface map of the thermal degradation rate of TSPLA and TSPLA–5%DOPO was drawn by the function of decomposition rate, decomposition temperature and mass conversion rate. Compared with TSPLA, the thermal degradation rate of TSPLA–5%DOPO decreased to a certain extent. This is mainly because the dehydration of phosphorus containing compounds inhibited the transesterification of polylactic acid to a certain extent and improved the thermal stability of the polymer.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

Acknowledgments

This study was financially supported by the Shanghai Automotive Industry Science and Technology Development Foundation (Grant No. 1006), the National High-Tech R&D Program of China (No. 2013AA032202), the National Natural Science Foundation of China (No. 51203118), the Fundamental Research Funds for the Central Universities and the Open Funds for Characterization of Tongji University.

References

  1. Gupta B. Revagade N. Hilborn J. et al., Poly(lactic acid) fiber: An overview. Prog. Polym. Sci. 2007;32(4):455–482. doi: 10.1016/j.progpolymsci.2007.01.005. [DOI] [Google Scholar]
  2. Lu F. Yu H. Yan C. et al., Polylactic acid nanocomposite films with spherical nanocelluloses as efficient nucleation agents: effects on crystallization, mechanical and thermal properties. RSC Adv. 2016;6(51):46008–46018. doi: 10.1039/C6RA02768G. [DOI] [Google Scholar]
  3. Cao Y. Ju Y. Liao F. et al., Improving the flame retardancy and mechanical properties of poly (lactic acid) with a novel nanorod-shaped hybrid flame retardant. RSC Adv. 2016;6(18):14852–14858. doi: 10.1039/C5RA25112E. [DOI] [Google Scholar]
  4. Cuadri A. A. Martín-Alfonso J. E. Thermal, thermo-oxidative and thermomechanical degradation of PLA: A comparative study based on rheological, chemical and thermal properties. Polym. Degrad. Stab. 2018;150:37–45. doi: 10.1016/j.polymdegradstab.2018.02.011. [DOI] [Google Scholar]
  5. Das P. Tiwari P. Thermal degradation kinetics of plastics and model selection. Thermochim. Acta. 2017;654:191–202. doi: 10.1016/j.tca.2017.06.001. [DOI] [Google Scholar]
  6. Low H. Y. Ishida H. Mechanistic study on the thermal decomposition of polybenzoxazines: effects of aliphatic amines. J. Polym. Sci., Part B: Polym. Phys. 1998;36(11):1935–1946. doi: 10.1002/(SICI)1099-0488(199808)36:11&#x0003c;1935::AID-POLB15&#x0003e;3.0.CO;2-8. [DOI] [Google Scholar]
  7. Steffen R. Meir M. Rekstad J. et al., Kinetics of degradation-induced polymer luminescence: A polyphenylene sulfide/elastomer blend under dry heat exposure. Polymer. 2018;136:71–83. doi: 10.1016/j.polymer.2017.12.045. [DOI] [Google Scholar]
  8. Wang X. S. Li X. G. Yan D. Thermal decomposition kinetics of poly (trimethylene terephthalate) Polym. Degrad. Stab. 2000;69(3):361–372. doi: 10.1016/S0141-3910(00)00083-5. [DOI] [Google Scholar]
  9. Bilbao R. Mastral J. F. Ceamanos J. et al., Kinetics of the thermal decomposition of polyurethane foams in nitrogen and air atmospheres. J. Anal. Appl. Pyrolysis. 1996;37(1):69–82. doi: 10.1016/0165-2370(96)00936-9. [DOI] [Google Scholar]
  10. Carrasco F. Pagès P. Gámez-Pérez J. et al., Kinetics of the thermal decomposition of processed poly (lactic acid) Polym. Degrad. Stab. 2010;95(12):2508–2514. doi: 10.1016/j.polymdegradstab.2010.07.039. [DOI] [Google Scholar]
  11. Ekmekyapar A. Basar C. A. Yuceer M. Nonisothermal Dehydration Kinetics of Tincalconite by Thermal Analysis Data. J. Chem. Eng. Jpn. 2009;42(7):478–484. doi: 10.1252/jcej.07we288. [DOI] [Google Scholar]
  12. Mehmet Y. Roche R. S. A study of the thermal degradation of polystyrene by thermal volatilization analysis. J. Appl. Polym. Sci. 1976;20(7):1955–1965. doi: 10.1002/app.1976.070200722. [DOI] [Google Scholar]
  13. Carrasco F. The evaluation of kinetic parameters from thermogravimetric data: comparison between established methods and the general analytical equation. Thermochim. Acta. 1993;213:115–134. doi: 10.1016/0040-6031(93)80010-8. [DOI] [Google Scholar]
  14. Dhar P. Katiyar V. Thermal degradation kinetics of polylactic acid/acid fabricated cellulose nanocrystal based bionanocomposites. Int. J. Biol. Macromol. 2017;104:827–836. doi: 10.1016/j.ijbiomac.2017.06.039. [DOI] [PubMed] [Google Scholar]
  15. Liu L. Zachariah M. R. Stoliarov S. I. et al., Enhanced thermal decomposition kinetics of poly (lactic acid) sacrificial polymer catalyzed by metal oxide nanoparticles. RSC Adv. 2015;5(123):101745–101750. doi: 10.1039/C5RA19303F. [DOI] [Google Scholar]
  16. Jing J. Zhang Y. Tang X. et al., Synthesis of a highly efficient phosphorus-containing flame retardant utilizing plant-derived diphenolic acids and its application in polylactic acid. RSC Adv. 2016;6(54):49019–49027. doi: 10.1039/C6RA06742E. [DOI] [Google Scholar]
  17. Zeng C. Zhang N. W. Feng S. Q. et al., Thermal stability of copolymer derived from L-lactic acid and poly(tetramethylene) glycol through direct polycondensation. J. Therm. Anal. Calorim. 2013;111:633–646. doi: 10.1007/s10973-012-2542-9. [DOI] [Google Scholar]
  18. Chang S. K. Zeng C. Li J. et al., Synthesis of polylactide-based thermoset resin and its curing kinetics. Polym. Int. 2012;61(10):1492–1502. doi: 10.1002/pi.4233. [DOI] [Google Scholar]
  19. Åkesson D. Skrifvars M. Seppälä J. et al., Synthesis and characterization of a lactic acid-based thermoset resin suitable for structural composites and coatings. J. Appl. Polym. Sci. 2010;115(1):480–486. doi: 10.1002/app.30800. [DOI] [Google Scholar]
  20. Chen X. Zhang N. Gu S. et al., Preparation and properties of ramie fabric-reinforced thermoset poly lactic acid composites. J. Reinf. Plast. Compos. 2014;33(10):953–963. doi: 10.1177/0731684413520264. [DOI] [Google Scholar]
  21. Ye Q. Q. Huang Z. Hao Y. et al., Kinetic study of thermal degradation of poly(L-lactide) filled with β-zeolite. J. Therm. Anal. Calorim. 2016;124:1471–1484. doi: 10.1007/s10973-016-5314-0. [DOI] [Google Scholar]
  22. Mandal D. K. Bhunia H. Bajpai P. K. et al., Thermal degradation kinetics and estimation of lifetime of radiation grafted polypropylene films. Radiat. Phys. Chem. 2017;136:1–8. doi: 10.1016/j.radphyschem.2017.03.036. [DOI] [Google Scholar]
  23. Speranza V. De Meo A. Pantani R. Thermal and hydrolytic degradation kinetics of PLA in the molten state. Polym. Degrad. Stab. 2014;100:37–41. doi: 10.1016/j.polymdegradstab.2013.12.031. [DOI] [Google Scholar]
  24. Cheon J. Y. Park W. H. Enhanced thermal stabilization of polymer nanofibrous web using self-polymerized 3, 4-dihydroxy-L-phenylalanine. Polymer. 2017;125:126–133. doi: 10.1016/j.polymer.2017.08.005. [DOI] [Google Scholar]
  25. Zhou Q. Xanthos M. Nanosize and microsize clay effects on the kinetics of the thermal degradation of polylactides. Polym. Degrad. Stab. 2009;94(3):327–338. doi: 10.1016/j.polymdegradstab.2008.12.009. [DOI] [Google Scholar]
  26. Pluta M. Galeski A. Alexandre M. et al., Polylactide/montmorillonite nanocomposites and microcomposites prepared by melt blending: structure and some physical properties. J. Appl. Polym. Sci. 2002;86(6):1497–1506. doi: 10.1002/app.11309. [DOI] [Google Scholar]
  27. Paul M. A. Alexandre M. Degée P. et al., New nanocomposite materials based on plasticized poly (L-lactide) and organo-modified montmorillonites: thermal and morphological study. Polymer. 2003;44(2):443–450. doi: 10.1016/S0032-3861(02)00778-4. [DOI] [Google Scholar]
  28. Jin X. Chen X. Cheng Q. et al., Non-isothermal crystallization kinetics of ramie fiber-reinforced polylactic acid biocomposite. RSC Adv. 2017;7(73):46014–46021. doi: 10.1039/C7RA09418C. [DOI] [Google Scholar]
  29. Marras S. I. Zuburtikudis I. Panayiotou C. Nanostructure vs. microstructure: morphological and thermomechanical characterization of poly (L-lactic acid)/layered silicate hybrids. Eur. Polym. J. 2007;43(6):2191–2206. doi: 10.1016/j.eurpolymj.2007.03.013. [DOI] [Google Scholar]
  30. Chen G. X. Yoon J. S. Morphology and thermal properties of poly (L-lactide)/poly (butylene succinate-co-butylene adipate) compounded with twice functionalized clay. J. Polym. Sci., Part B: Polym. Phys. 2005;43(5):478–487. doi: 10.1002/polb.20345. [DOI] [Google Scholar]
  31. Iniguez-Franco F. Auras R. Burgess G. et al., Concurrent solvent induced crystallization and hydrolytic degradation of PLA by water-ethanol solutions. Polymer. 2016;99:315–323. doi: 10.1016/j.polymer.2016.07.018. [DOI] [Google Scholar]
  32. Hu J. Shan J. Wen D. et al., Flame retardant, mechanical properties and curing kinetics of DOPO-based epoxy resins. Polym. Degrad. Stab. 2014;109:218–225. doi: 10.1016/j.polymdegradstab.2014.07.026. [DOI] [Google Scholar]
  33. Salmeia K. A. Gaan S. An overview of some recent advances in DOPO-derivatives: chemistry and flame retardant applications. Polym. Degrad. Stab. 2015;113:119–134. doi: 10.1016/j.polymdegradstab.2014.12.014. [DOI] [Google Scholar]
  34. Venkatesh M. Ravi P. Tewari S. P. Isoconversional kinetic analysis of decomposition of nitroimidazoles: Friedman method vs. Flynn–Wall–Ozawa method. J. Phys. Chem. A. 2013;117(40):10162–10169. doi: 10.1021/jp407526r. [DOI] [PubMed] [Google Scholar]
  35. Ahmad N. Alam M. Al-Otaibi M. A. N. Thermal decomposition and kinetic studies of solid riboflavin using model-free methods. Prog. React. Kinet. Mech. 2015;40(1):86–94. [Google Scholar]
  36. Flynn J. H. Wall L. A. A quick, direct method for the determination of activation energy from thermogravimetric data. J. Polym. Sci., Part B: Polym. Lett. 1966;4(5):323–328. doi: 10.1002/pol.1966.110040504. [DOI] [Google Scholar]
  37. Ozawa T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965;38(11):1881–1886. doi: 10.1246/bcsj.38.1881. [DOI] [Google Scholar]
  38. Doyle C. D. Estimating isothermal life from thermogravimetric data. J. Appl. Polym. Sci. 1962;6(24):639–642. doi: 10.1002/app.1962.070062406. [DOI] [Google Scholar]
  39. Camino G. Grassie N. McNeill I. C. Influence of the fire retardant, ammonium polyphosphate, on the thermal degradation of poly (methyl methacrylate) J. Polym. Sci., Polym. Chem. Ed. 1978;16(1):95–106. doi: 10.1002/pol.1978.170160110. [DOI] [Google Scholar]
  40. Lesnikovich A. Levchik S. A method of finding invariant values of kinetic parameters. J. Therm. Anal. Calorim. 1983;27(1):89–93. doi: 10.1007/BF01907324. [DOI] [Google Scholar]
  41. Lesnikovich A. L. Levchik S. Isoparametric kinetic relations for chemical transformations in condensed substances (analytical survey). II. Reactions involving the participation of solid substances. J. Therm. Anal. Calorim. 1985;30(3):677–702. doi: 10.1007/BF01913614. [DOI] [Google Scholar]
  42. Nikolaev A. V. Logvinenko V. A. Gorbatchev V. M. Special features of the compensation effect in non-isothermal kinetics of solid-phase reactions. J. Therm. Anal. Calorim. 1974;6(4):473–477. doi: 10.1007/BF01914927. [DOI] [Google Scholar]
  43. Yang M. H. On the thermal degradation of poly (styrene sulfones). VII. Evaluations of poly (styrene sulfone) thermal stability using invariant kinetic parameters. J. Appl. Polym. Sci. 2002;85(8):1698–1705. doi: 10.1002/app.10809. [DOI] [Google Scholar]
  44. Richard-Campisi L. Bourbigot S. Le Bras M. et al., Thermal behaviour of cotton-modacrylic fibre blends: kinetic study using the invariant kinetic parameters method. Thermochim. Acta. 1996;275(1):37–49. doi: 10.1016/0040-6031(95)02729-7. [DOI] [Google Scholar]
  45. Coats A. W. Redfern J. P. Kinetic parameters from thermogravimetric data. Nature. 1964;201(4914):68. doi: 10.1038/201068a0. [DOI] [Google Scholar]
  46. Doğan F. Kaya İ. Bilici A. Non-isothermal degradation kinetics of poly (2, 2′-dihydroxybiphenyl) Polym. Bull. 2009;63(2):267–282. doi: 10.1007/s00289-009-0084-5. [DOI] [Google Scholar]
  47. Albano C. Rodríguez B. Karam A. et al., Nitrile rubber–bentonite composites: a thermal degradation study. Polym. Bull. 2012;68(7):1935–1950. doi: 10.1007/s00289-011-0680-z. [DOI] [Google Scholar]
  48. Lesnikovich A. I. Levchik S. V. Guslev V. G. Thermolysis of potassium tetraperoxochromate (V). II. Linear heating. Thermochim. Acta. 1984;77(1–3):357–365. doi: 10.1016/0040-6031(84)87074-4. [DOI] [Google Scholar]
  49. Cataño L., Albano C. and Karam A., et al., Thermal Stability Evaluation of PA6/LLDPE/SEBS-g-DEM Blends, Macromolecular Symposia, Weinheim, WILEY-VCH Verlag, 2007, vol. 257, (1), pp. 147–157 [Google Scholar]
  50. Albano C. Cataño L. Perera R. et al., Thermodegradative and morphological behavior of composites of HDPE with surface-treated hydroxyapatite. Polym. Bull. 2010;64(1):67–79. doi: 10.1007/s00289-009-0140-1. [DOI] [Google Scholar]
  51. Albano C. Rodríguez B. Karam A. et al., Nitrile rubber–bentonite composites: a thermal degradation study. Polym. Bull. 2012;68(7):1935–1950. doi: 10.1007/s00289-011-0680-z. [DOI] [Google Scholar]
  52. Fan Y. Nishida H. Hoshihara S. et al., Pyrolysis kinetics of poly (L-lactide) with carboxyl and calcium salt end structures. Polym. Degrad. Stab. 2003;79(3):547–562. doi: 10.1016/S0141-3910(02)00374-9. [DOI] [Google Scholar]
  53. McNeill I. C. Leiper H. A. Degradation studies of some polyesters and polycarbonates—2. Polylactide: degradation under isothermal conditions, thermal degradation mechanism and photolysis of the polymer. Polym. Degrad. Stab. 1985;11(4):309–326. doi: 10.1016/0141-3910(85)90035-7. [DOI] [Google Scholar]
  54. Kuljanin-Jakovljević J. Marinović-Cincović M. Stojanović Z. et al., Thermal degradation kinetics of polystyrene/cadmium sulfide composites. Polym. Degrad. Stab. 2009;94(6):891–897. doi: 10.1016/j.polymdegradstab.2009.03.004. [DOI] [Google Scholar]
  55. Almeras X. Dabrowski F. Le Bras M. et al., Using polyamide 6 as charring agent in intumescent polypropylene formulations II. Thermal degradation. Polym. Degrad. Stab. 2002;77(2):315–323. doi: 10.1016/S0141-3910(02)00066-6. [DOI] [Google Scholar]

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES