Abstract
The thermodynamic values of the four surfactants, anionic surfactants, nonionic surfactants, zwitterion surfactants and gemini surfactants, were calculated by molecular dynamics simulation. The calculated results of thermodynamic parameters showed that the four surfactant can form micelles spontaneously. The mainly force for micellization process is entropy-driven, and as the temperature increases, the entropy-driven contribution is gradually reduced. There are linear enthalpy–entropy compensation phenomena for the four surfactants. Among the studied four surfactants, the gemini surfactant is the easiest to form micelles and has good stability, the zwitterion surfactant is the second, and the anionic surfactant is the least stable.
The thermodynamic values of the four surfactants, anionic surfactants, nonionic surfactants, zwitterion surfactants and gemini surfactants, were calculated by molecular dynamics simulation.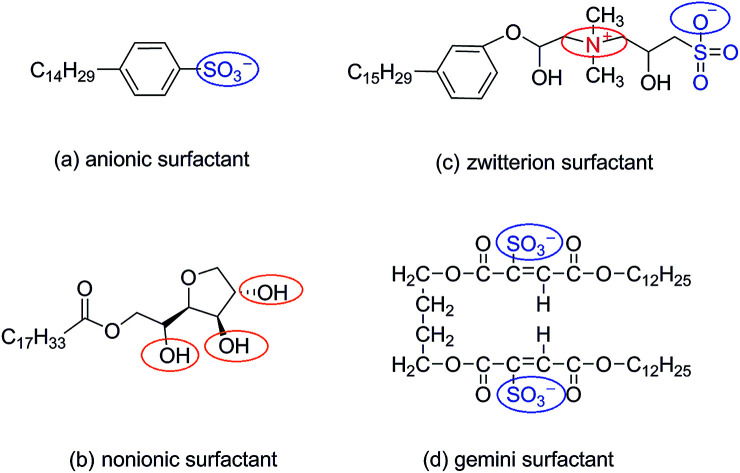
1. Introduction
Surfactants are amphiphilic molecules which contains both a hydrophilic polar head group and a hydrophobic hydrocarbon chain known as tail group.1 Surfactants include nonionic, anionic, cationic, and zwitterionic in nature, it will self-assemble and may form a variety of structures that includes micelles, vesicles, liposomes, microtubules, and bilayers.2 Surfactants have turned into a subject of research on account of their properties and have been used in pharmaceutical, chemical industry or environmental applications. People have gotten extensive consideration of uses in cosmetics, paints, dyestuffs, pharmaceuticals, agrochemicals, fibers or plastics.3–5 When the surfactant is dissolved in water, the surfactant molecules aggregate into micelles whose hydrophilic heads are exposed to water at the surface and their hydrophobic tails are shielded inside. The driven force of self-assembly have hydrophobic, van der Waals forces, hydrogen bonding and electrostatic interactions in addition to the interaction of the head groups. Ben-Naim A. Y.6 clarified the concept of hydrophobic interactions and discussed in detail about temperature and pressure dependence of the hydrophobic interactions and the impact on thermodynamics. These studies by the author lay the foundation for the hydrophobic interaction theory of aqueous solution. The performance of self-assembling spontaneously of surfactants makes them convincing used in colloidal system. The surfactants are mixed with other substances has a wide range of applications, including microemulsions for enhancing oil recovery (EOR).7
Although it is clear that surfactant micelle formation has many meaningful applications, but we should pay more attention to how micelle formation process, what is important is how the molecular structure of the surfactant and its physicochemical properties in solution affect the micellization behavior.8 Aniansson and Wall9,10 described the surfactant micellization process, which includes only the insertion/extraction of a single unimers.11 In the first step of micellization, the aggregation of micelles is redistributed while the number of micelles remains unchanged. In the next step, the number of micelles changes through the formation and decomposition process, and the micellization process approaches equilibrium. The theory has been widely accepted. Bai12 measured thermodynamic values of gemini cationic surfactants were determined by microcalorimetry, which monitoring and recording the calorimetric curve of a change process by microcalorimeter, one can find that the micellization process for C12C12C12Br2 is driven jointly by enthalpy and entropy, and the contribution of the enthalpy to ΔGmic is about 61%. However, the micellization process for C12C6DAB is driven mainly by entropy, and the contribution of ΔHmic to ΔGmic is just about 3.4%.
Molecular simulation plays an increasingly important role in providing detailed information on the self-assembly of surfactants in aqueous solutions. Micelle formation process can be simulated at atomic level; Stephenson13 evaluate the free-energy change associated with changing micelle composition. Through the comparison between the two models, indicted that the selection of the thermodynamic integration free-energy method was justified and predicted which model was closer to the experimental data. Alessandra and Mark14 studied solvent water analogs of 18 of the 20 naturally amino acids. The estimation of solvation free energy in cyclohexane solution and chloroform solution was based on the calculation of thermodynamic integral free energy using molecular dynamics simulation. Calculation results showed force field reproducible experimental solvation free energy of non-polar analogs with reasonable accuracy. The existence of enthalpy–entropy compensation in surfactant systems has been reported by many scholars,15–21 but its formation process and causes have different opinions.22–24 Liu25,26 investigated enthalpy–entropy compensation for simulating sulfobetaine-type zwitterionic gemini surfactants and ionic liquid surfactants, free energy data at different temperatures were obtained. The results show that the micellization of surfactant in aqueous solution is an entropy-driven processes, a longer hydrophobic chain length will enhance the stability of the micelles of growth of surfactants. These show that free-energy calculations have emerged as a powerful tool that can play a predictive role in micellization. However, these studies only deals with the same series of gemini surfactants. It remains to be verified whether this method is suitable for other types of surfactant systems. Therefore, for the first time, this paper attempts to explain the micellization of different types of surfactants from a microscopic perspective, which will be an interesting and valuable study.
In the previous work,27,28 we systematically discussed the behavior of four different types of surfactants at the oil/water interface and the salt resistance. It was found that the system formed by the gemini surfactant is the most stable and the effect of reducing the interfacial tension is the highest, while the surface activity of the gemini surfactant and the zwitterion surfactant showed good salt resistance. This paper supplements the research of four surfactant systems, focusing on the micellization ability and thermodynamic properties of different kinds of surfactants, and discuss the thermodynamic parameters such as enthalpy and entropy. It can explain the mechanism of surfactant formation of micelles from microscopic phenomena and provide theoretical guidance for the application of surfactants.
2. Simulation details
2.1. Molecular models
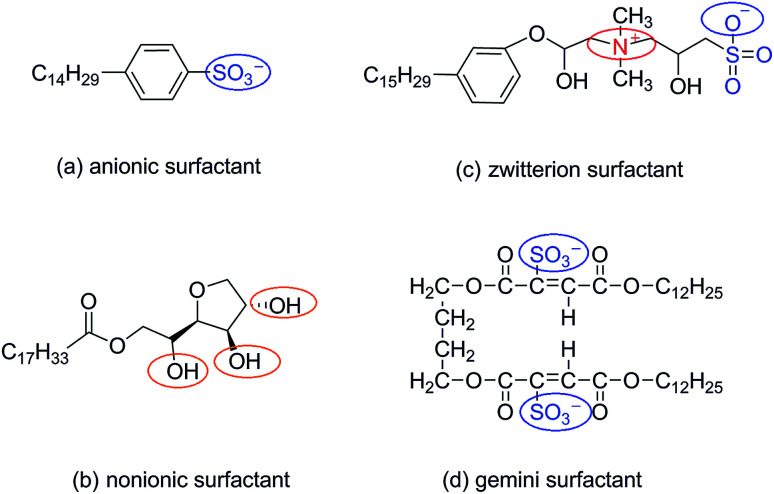
The four types of surfactants made in this article are anionic surfactants, nonionic surfactants, zwitterion surfactants and gemini surfactants, respectively. The molecular structures of anionic, zwitterion, nonionic, and gemini surfactants are shown in Fig. 1. The initial structure of the four types of surfactants was drawn by ChemDraw, then the molecules were optimized using the B3LYP/6-31+g(d) basis set in GAMESS (US)29,30 software, and the charge distribution was calculated using the Kollman–Singh31 method. All simulations were carried out by GROMACS (5.1.2),32–35 and we use GROMOCS 53a6 force field to describe and constrain atoms in simulation. Force field parameters in the database were corrected through the Automated Topology Builder (ATB).36 ATB cannot be directly calculated for molecules with more than 40 atoms. For this reason, we cut the surfactant molecules into fewer than 40 fragments, redistribute the charge and bond parameters, and finally merge the fragments to form force field parameters. The water molecule adopted for the simple point charge SPC/E model.37
Fig. 1. Molecular structure of four surfactants.
The simulation calculation uses the SD frog hopping algorithm. Firstly, the steepest descent method and the conjugate gradient method are used to minimize the energy of the system in the vacuum configuration. After the 5 ns equilibrium simulation is completed, the equilibrium state of each configuration in the extraction vacuum is placed in a 3 × 3 × 3 nm box and then solvated the entire system, last subjected to a 10 ns molecular dynamics simulation, and then changed the λ value to run 20 times, each 10 ns simulation operation. In this process, one surfactant molecule and 856 water molecules are optimized. The integral steps in vacuum and aqueous solution are 0.5 fs and 2 fs, respectively, and NVT and NPT are selected. The pressure is 1 atm, the temperature is set to 300, 310, 320, 330, 340 K, the temperature coupling uses the Langevin piston method, the van der Waals truncation radius in the solution is 1.2 nm, and the long-range electrostatic interaction uses PME38 Method calculation.
2.2. Free energy calculations
Free Energy Perturbation (FEP) theory is a method based on statistical mechanics that is used in computational chemistry for computing free energy differences from molecular dynamics. Its specific theory has been reported by many scholars.39–41 In the explanation of the principle from state A to state B. The change in free energy can be calculated by the formula.42
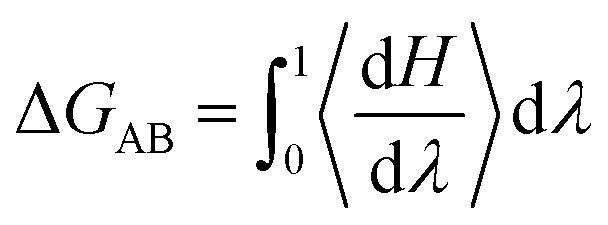 |
1 |
In this approach the Hamiltonian H is made a function of a coupling parameter, λ. The λ dependence of the Hamiltonian defines a pathway that connects states A and B. In this simulation λ is calculated by the fixed-length window growth method at states A (λ = 0) to states B (λ = 1), and the average is divided into 20 equal parts. For every λ-point system value is simulated using the method described in 2.1. The averages of the derivatives, ∂H(λ)/∂λ at each of the λ-points [eqn (1)] were then obtain ΔGAB.
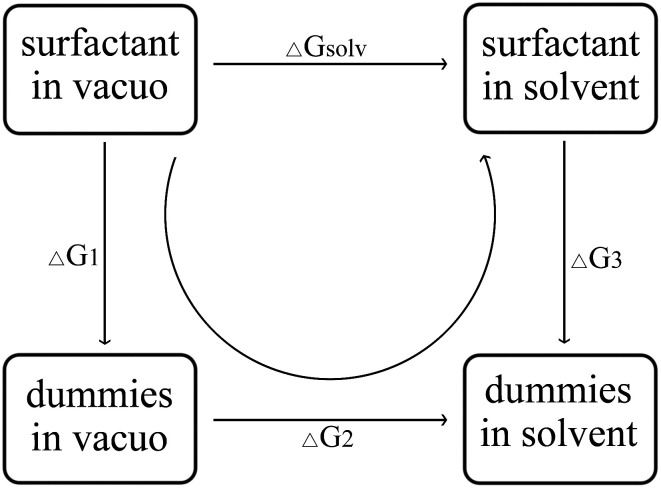
The hydration free energy of the surfactant, that is, the change in the free energy of a surfactant molecule from a vacuum to an aqueous solution, the hydration free energy can be calculated by the thermodynamic cycle of Fig. 2. ΔGsolv called solvation free energy, is the work required to transfer a molecule from the gas phase into solution. In Fig. 2, ΔG1 is the work required to remove all internal non-bonding interactions in the compound in a vacuum. ΔG2 refers to the work required to transfer the dummy solute from the vacuum to the solvate phase. ΔG3 refers to the work required to remove solute–solvent and solute intramolecular interactions. This is accomplished by gradually mutating all atoms in a given compound (state A) to “virtual” atoms (state B).
Fig. 2. Thermodynamic cycle diagram.
3. Results and discussion
3.1. Hydration free energy of four types of surfactant
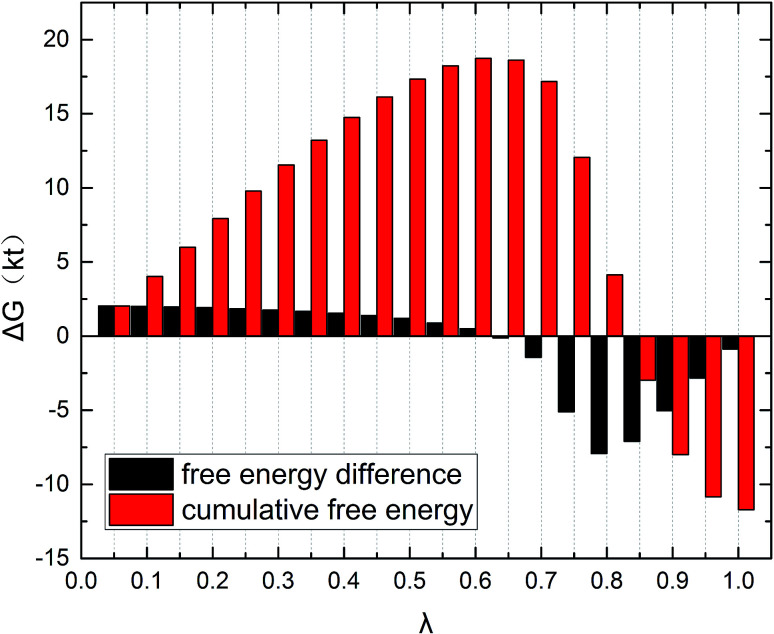
The gmx bar module of the GROMACS was used to analyze the data, and the Bennett Acceptance Ratio (BAR) was used to calculate the free energy difference.43 Take the simulation of zwitterion surfactant as an example, Fig. 3 shows free energy corresponding to different λ. The relative free energy difference and the cumulative free energy of each λ interval of the surfactants are added, and it can be seen that the displayed data overlap significantly, which can achieve the purpose of sufficient sampling. From the data in Table 1, the calculated free energy difference fluctuates less and the error is within 5%. And the four surfactants  are negative in the simulated temperature range under investigation, indicating that the micellization process of the four types of surfactant in aqueous solution is spontaneous, and the micelle solution formed is a thermodynamic stable system. This is consistent with some of the thermodynamic parameters measured by traditional experimental methods, which shows that the molecular simulation method can better explain the formation mechanism of surfactant aqueous micelle.44,45
are negative in the simulated temperature range under investigation, indicating that the micellization process of the four types of surfactant in aqueous solution is spontaneous, and the micelle solution formed is a thermodynamic stable system. This is consistent with some of the thermodynamic parameters measured by traditional experimental methods, which shows that the molecular simulation method can better explain the formation mechanism of surfactant aqueous micelle.44,45
Fig. 3. Free energy corresponding to different λ.
Gibbs free energies of four different types of surfactant at different temperatures.
| T/K |
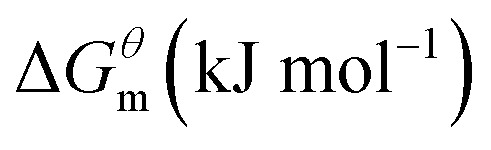
|
|||
|---|---|---|---|---|
| Anionic | Nonionic | Zwitterion | Gemini | |
| 300 | −18.59 ± 0.67 | −18.67 ± 0.45 | −26.06 ± 0.75 | −24.62 ± 0.67 |
| 310 | −19.28 ± 0.75 | −19.97 ± 0.92 | −28.76 ± 1.11 | −26.84 ± 0.85 |
| 320 | −20.09 ± 0.54 | −21.86 ± 0.51 | −31.56 ± 0.68 | −41.78 ± 0.94 |
| 330 | −21.54 ± 0.83 | −25.11 ± 0.62 | −32.49 ± 1.11 | −45.59 ± 1.89 |
| 340 | −22.47 ± 0.48 | −27.25 ± 0.69 | −33.10 ± 0.40 | −46.05 ± 0.40 |
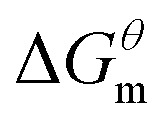 reduced as the temperature rises, this is mainly because the association of the hydrophobic chains strengthened of the surfactant molecules with temperature rises, which is conducive to the formation of molecular aggregates. The process of forming micelles is dehydration and the rise of the temperature destroys the hydrogen bonding between the water molecules and the oxygen atoms in the head group, that is, reduces the hydration of the head group and promotes micelle formation. Comparing different types of surfactants, it can be found that the gemini surfactant is most likely to form micelles with increasing temperature, followed by zwitterion surfactant, and the most difficult to form micelles are anionic surfactant. Analysis of the reason may be the double-tailed chain of gemini surfactant has a strong hydrophobic effect.
reduced as the temperature rises, this is mainly because the association of the hydrophobic chains strengthened of the surfactant molecules with temperature rises, which is conducive to the formation of molecular aggregates. The process of forming micelles is dehydration and the rise of the temperature destroys the hydrogen bonding between the water molecules and the oxygen atoms in the head group, that is, reduces the hydration of the head group and promotes micelle formation. Comparing different types of surfactants, it can be found that the gemini surfactant is most likely to form micelles with increasing temperature, followed by zwitterion surfactant, and the most difficult to form micelles are anionic surfactant. Analysis of the reason may be the double-tailed chain of gemini surfactant has a strong hydrophobic effect.
3.2. Prediction of thermodynamics parameters
Based on the calculated 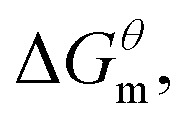 we can calculate and derive the thermodynamic parameters of the micellization process using the following formula.46,47
we can calculate and derive the thermodynamic parameters of the micellization process using the following formula.46,47
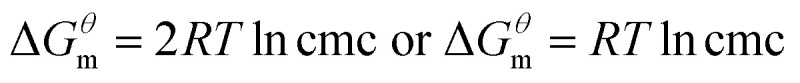 |
2 |
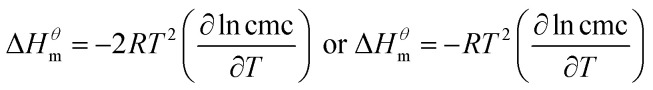 |
3 |
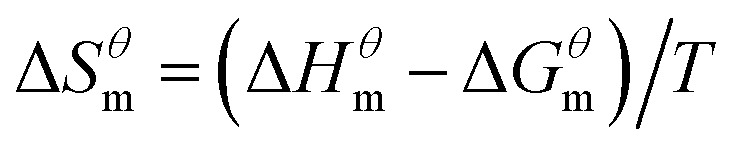 |
4 |
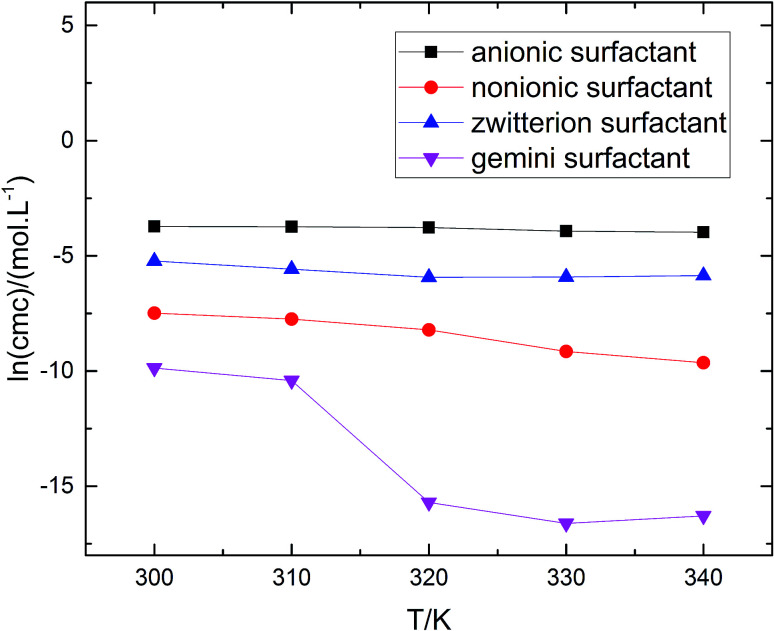
where R is the molar gas constant, T is the thermodynamic temperature, and cmc is the critical micelle concentration. There are different calculation formulas in formula (2) and (3), mainly for different treatment methods for ionic surfactants and nonionic surfactants. The data of Table 1 is substituted into the mass action model of the micellization process (eg, formula (2)–(4)), ln(cmc) at different temperatures can be calculated by the formula (2). As shown in Fig. 4, using the curve of ln(cmc) and T, the slope (bias) of each point can be obtained, and then the thermodynamic parameters such as standard molar enthalpy changes and entropy change in the micellization process can be obtained by formula (3) and (4). The final results are shown in the Table 2. It can be seen from Table 2 that the influence of four different types of surfactant from  to
to 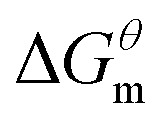 is more obvious than
is more obvious than 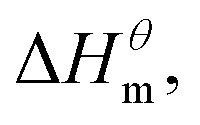 indicating that entropy driving contributes a lot in the process of micellization. As the temperature increases,
indicating that entropy driving contributes a lot in the process of micellization. As the temperature increases,  has a decrease first and then increasing,
has a decrease first and then increasing, 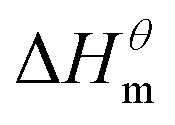 and
and 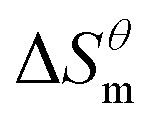 have the opposite trend, which indicates that the entropy drive is dominant in the micellization process, with increasing temperature, its dominant role gradually diminished. When the temperature is low, it is absolutely dominant. As the temperature rises to a certain extent, this contribution shows a downward trend, and the driving force of enthalpy is opposite to this effect, and the contribution is gradually increased.
have the opposite trend, which indicates that the entropy drive is dominant in the micellization process, with increasing temperature, its dominant role gradually diminished. When the temperature is low, it is absolutely dominant. As the temperature rises to a certain extent, this contribution shows a downward trend, and the driving force of enthalpy is opposite to this effect, and the contribution is gradually increased.
Fig. 4. ln(cmc)–T plots of four different types of surfactant.
Thermodynamics parameters of the micellization of four different types of surfactant in aqueous solutions.
| Sample | T/K |
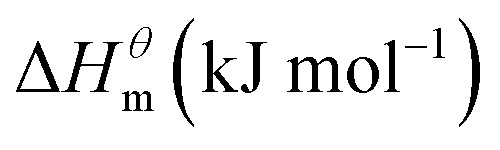
|
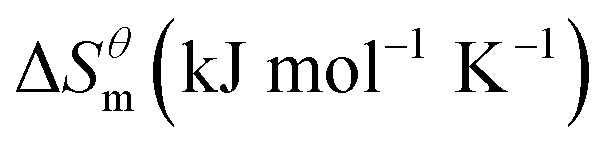
|
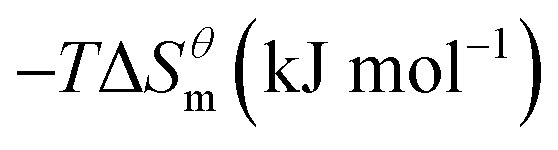
|
|---|---|---|---|---|
| Anionic | 300 | 2.04 | 0.07 | −20.63 |
| 310 | 3.92 | 0.07 | −23.20 | |
| 320 | 15.77 | 0.11 | −35.86 | |
| 330 | 18.00 | 0.12 | −39.54 | |
| 340 | 9.42 | 0.09 | −31.89 | |
| Nonionic | 300 | 19.67 | 0.13 | −38.34 |
| 310 | 29.21 | 0.16 | −49.18 | |
| 320 | 59.76 | 0.26 | −81.62 | |
| 330 | 64.44 | 0.27 | −89.55 | |
| 340 | 46.89 | 0.22 | −74.14 | |
| Zwitterion | 300 | 53.20 | 0.26 | −79.23 |
| 310 | 56.50 | 0.28 | −85.26 | |
| 320 | 29.08 | 0.19 | −60.64 | |
| 330 | −6.94 | 0.08 | −25.55 | |
| 340 | −12.72 | 0.06 | −20.38 | |
| Gemini | 300 | 40.62 | 0.22 | −65.24 |
| 310 | 233.02 | 0.84 | −259.86 | |
| 320 | 264.04 | 0.96 | −305.82 | |
| 330 | 26.56 | 0.22 | −72.15 | |
| 340 | −31.33 | 0.04 | −14.72 |
In particular, when the temperature of zwitterion surfactants and gemini surfactants reached 330 K and 340 K respectively, their enthalpy value was negative, and the micellation process turned into the exothermic process. From the temperature of 300–340 K, the micellation of anions and nonionic surfactants is an endothermic process.
At present, the mechanism of micelle formation of single-head chain in aqueous solution has been recognized by most people, that is, the main reason is the hydrophobic interaction of alkane chains.48,49 Tanford48 pointed out that liquid water mainly consists of two forms, the first, it is a structured icy water molecule (iceberg structure) formed by hydrogen bonding, and the second is a non-hydrogen bonded free water molecule. When the surfactant molecule is dissolved in water, it promotes the formation of ice-like water molecular structure. An iceberg structure is formed around the alkane chain, resulting in a decrease in the water entropy value. The water system discharges the hydrophobic alkane portion of the surfactant molecule as much as possible to destroy the iceberg structure and increase the entropy of the system. The final result is that the hydrophobic alkane chains aggregate to form a micelle. But the reason for the increase in entropy value Lee49 deemed that the disintegration of the iceberg structure increases the degree of disorder of water, thereby promoting the formation of micelles. Sequencing also increases the entropy of the system. From the data we simulated, the main driving force for the formation of micelles in different types of surfactant aqueous solutions is derived from the entropy effect. Since the gemini has two hydrophobic tail chains, the entropy change is much larger than the other three surfactants. The positive and negative values of enthalpy are mainly compared with the two forces of orderly polymerization of surfactant monomer and destruction of iceberg effect. When the energy required to destroy the iceberg effect is greater than the monomer aggregation, it mainly reflects the endothermic, 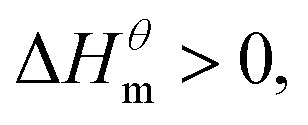 and the energy required to destroy the iceberg effect is less than the energy released by the polymerization of the monomer to form the micelle, the process is exothermic
and the energy required to destroy the iceberg effect is less than the energy released by the polymerization of the monomer to form the micelle, the process is exothermic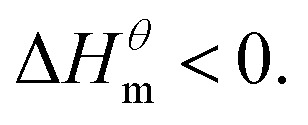 Nusselder and Engberts50 believed that negative
Nusselder and Engberts50 believed that negative 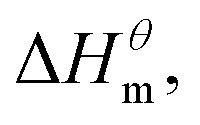 dispersion forces play an important role in micelle formation, surfactant and solvent interactions leads to the observed exotherm. From the point of view of the above, zwitterionic and gemini surfactants contribute more to Gibbs free energy and are more likely to form micelles, especially at high temperatures.
dispersion forces play an important role in micelle formation, surfactant and solvent interactions leads to the observed exotherm. From the point of view of the above, zwitterionic and gemini surfactants contribute more to Gibbs free energy and are more likely to form micelles, especially at high temperatures.
3.3. The enthalpy–entropy compensation of micelles
There is a clear linear relationship between the enthalpy change and the entropy change in the host–guest interaction solution system, in the solution reaction system and in some thermal decomposition reaction systems, this phenomenon is called enthalpy–entropy compensation.15 In fact, a large number of enthalpy–entropy compensation phenomena have been reported in surface adsorption, micelle formation, and related research.16–21 The enthalpy–entropy compensation of the same type of surfactant has a linear relationship and the temperature concentration is around 307 K, which has been confirmed by Lai,22 but whether the different types of surfactants follow the linear relationship, there are few reports. According to Lumry23 on the study of enthalpy–entropy compensation phenomenon, the micellization process is mainly divided into two processes. One is the “desolvation” part, i.e., the dehydration of the hydrocarbon tail of surfactant molecules. Second is the aggregation of the hydrocarbon tails of surfactant molecules to form a micelle while the micellization process is dominated by entropy driving, but in this process, the entropy changes, the initial contribution is larger, and the later stage is relatively small, but it is still the main driving force compared with enthalpy. In combination with the above two processes, the mutual enthalpy change 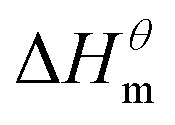 and entropy change
and entropy change 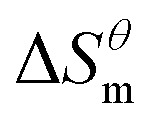 of the surfactant micellization process can be described by the formula (5).
of the surfactant micellization process can be described by the formula (5).
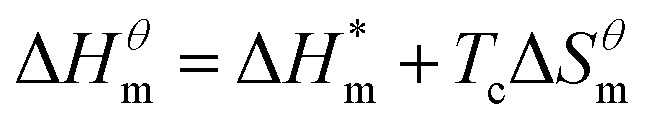 |
5 |
It can be seen from eqn (5) that when 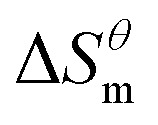 is 0 (a hypothetical limit condition), the value of enthalpy is equal to
is 0 (a hypothetical limit condition), the value of enthalpy is equal to 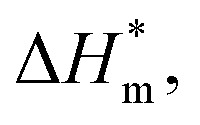 which reflecting the interaction between the solute and the solute, ignoring the influence of the solvent, it is a phenomenon on the molecular alkane chain aggregation process. Here the smaller
which reflecting the interaction between the solute and the solute, ignoring the influence of the solvent, it is a phenomenon on the molecular alkane chain aggregation process. Here the smaller 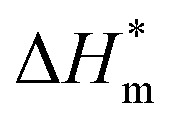 value, the more stable of the formed micelle system. Similarly, in another limit condition, when
value, the more stable of the formed micelle system. Similarly, in another limit condition, when 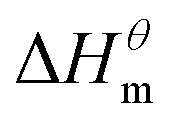 is 0, the micelle formation process is mainly entropy-driven, and the obtained entropy is
is 0, the micelle formation process is mainly entropy-driven, and the obtained entropy is 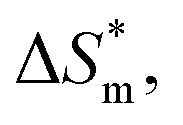 the larger
the larger 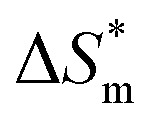 value is, the more stable the micelle system is. The slope of Tc called the compensation temperature, can be explained as the characteristic of the solute–solute and solute–solvent interactions in the above two extreme condition.
value is, the more stable the micelle system is. The slope of Tc called the compensation temperature, can be explained as the characteristic of the solute–solute and solute–solvent interactions in the above two extreme condition.
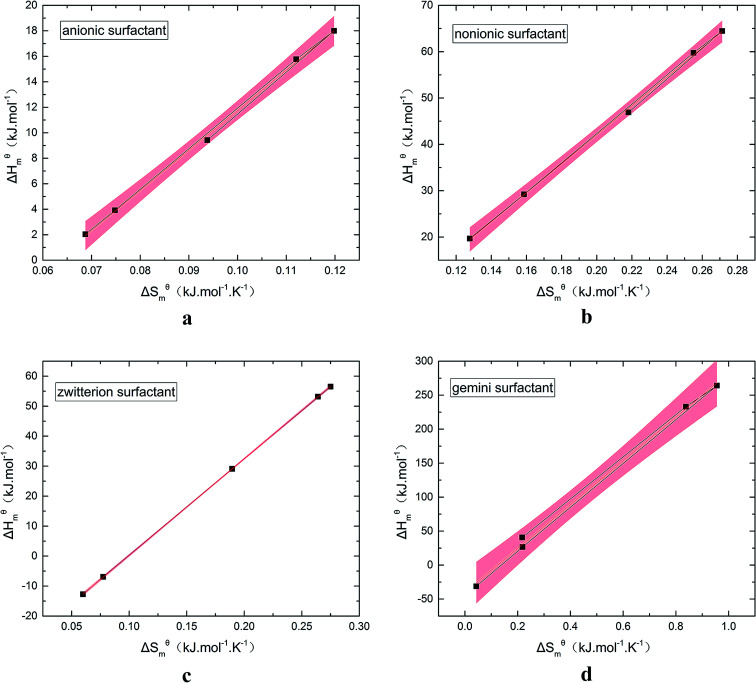
Fig. 5 is a 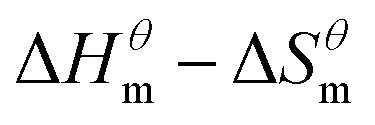 graph of four different types of surfactant in the micellization process of aqueous solution. From our simulation study, one can find that four different types of surfactant show a good linear relationship between enthalpy–entropy compensation. However, the compensation temperature is slightly different. According to Lai22 research, if the compensation is due to temperature change, the compensation temperature gives the information of energy transfer, whether the compensation temperature is the same can be used to infer whether the micellization process follows the same mechanism. If it is not temperature disturbance, compensation temperature on the process mechanism is not indicative.
graph of four different types of surfactant in the micellization process of aqueous solution. From our simulation study, one can find that four different types of surfactant show a good linear relationship between enthalpy–entropy compensation. However, the compensation temperature is slightly different. According to Lai22 research, if the compensation is due to temperature change, the compensation temperature gives the information of energy transfer, whether the compensation temperature is the same can be used to infer whether the micellization process follows the same mechanism. If it is not temperature disturbance, compensation temperature on the process mechanism is not indicative.
Fig. 5.
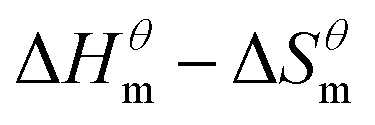 plots of four different types of surfactant.
plots of four different types of surfactant.
Ranatunga24 also believes that the compensation temperature only indicates that the relative contributions of entropy and enthalpy to free energy are equal and cannot be used as evidence that the process follows the same mechanism. The mechanism in this aspect needs to be further explored. It can be seen from Fig. 5 in this work that the anion and nonionic surfactant compensation temperatures are 314 K and 312 K, respectively, while the zwitterion surfactant and the gemini surfactant have a compensation temperature of 321 K. The difference of temperature is small, indicating that the dehydration effects of different surfactant molecules may be similar.
Table 3 shows the calculation results of the curve 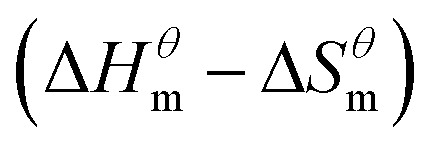 fitting into a linear equation and the sum about
fitting into a linear equation and the sum about 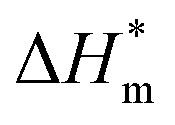 and
and 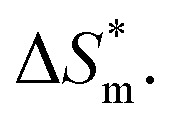 . From the data in the table, one knows that the order of the values is anionic > nonionic > zwitterion > gemini surfactant, and the value of
. From the data in the table, one knows that the order of the values is anionic > nonionic > zwitterion > gemini surfactant, and the value of  is exactly the opposite. Gemini surfactant have the strongest ability and stability to form micelles, followed by zwitterion surfactant, and the worst is anionic surfactant, mainly because of the higher number of hydrophobic chains of the zwitterion and nonionic surfactant. Therefore, the micelle formation is tighter and the stability is high. Nonionic surfactant has a double bond structure in the hydrophobic chains, which leads to an increase in the degree of branching of the hydrophobic group and an increase in the volume of the space, thereby weakening the hydrophobic effect, resulting the tight in the micelles formed by the surfactant being inferior to the zwitterion and gemini surfactant.
is exactly the opposite. Gemini surfactant have the strongest ability and stability to form micelles, followed by zwitterion surfactant, and the worst is anionic surfactant, mainly because of the higher number of hydrophobic chains of the zwitterion and nonionic surfactant. Therefore, the micelle formation is tighter and the stability is high. Nonionic surfactant has a double bond structure in the hydrophobic chains, which leads to an increase in the degree of branching of the hydrophobic group and an increase in the volume of the space, thereby weakening the hydrophobic effect, resulting the tight in the micelles formed by the surfactant being inferior to the zwitterion and gemini surfactant.
Results of fitted equation of 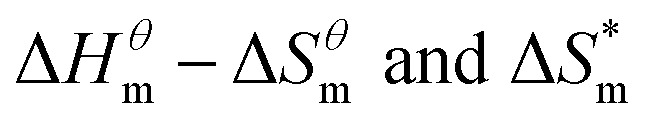 .
.
| Sample | R (%) | T c/K |
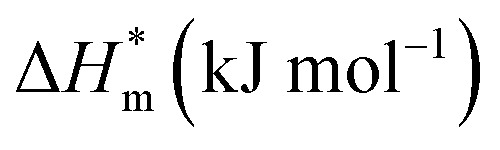
|
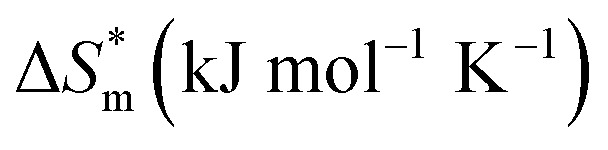
|
|---|---|---|---|---|
| Anionic | 99.95 | 314 | −19.69 | 0.06 |
| Nonionic | 99.97 | 312 | −20.58 | 0.06 |
| Zwitterion | 99.99 | 321 | −31.93 | 0.10 |
| Gemini | 99.90 | 321 | −39.63 | 0.12 |
4. Conclusions
In this paper, FEP calculation was used to study surfactant polymerization mechanism in aqueous solution, this process is achieved by molecular dynamics simulation. The main conclusion is listed below:
(1) We calculate the Gibbs free energy of four surfactants at different temperatures. The smaller the values of the solvating free energy change, the better the stability of the surfactant molecules. The same type of surfactant is easier to form micelles with increasing temperature. At the same temperature, gemini surfactant > zwitterion surfactant > nonionic surfactant > anionic surfactant.
(2) From the 20 systems of the four surfactants at different temperatures, it can be found that the micelles formed by each system are spontaneous, entropy plays a leading role, but as the temperature increases, the dominant role of entropy decreases gradually, the contribution of enthalpy to it gradually increases. At the same time, we also found that the temperature of the different types of surfactants during the micellization process will have different degrees of influence on the enthalpy. The micellarization process between anionic and nonionic surfactants at 300–340 K is an endothermic process. The amphoteric and gemini surfactants changed from an endothermic process to an exothermic process at 330 K and 340 K, meaning that the thermodynamic properties of micellization changed at this temperature.
(3) There are enthalpy–entropy compensation phenomena in the micelle formation process of different types of surfactant in aqueous solution, and the compensation temperatures are 314, 312, 321, 321 K, respectively. And it can be seen from the values of 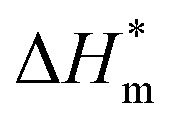 and
and 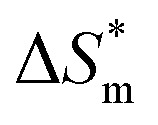 that the gemini and zwitterion surfactant have strong ability to form micelles and have good stability.
that the gemini and zwitterion surfactant have strong ability to form micelles and have good stability.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This work is supported by the National Basic Research Program of China (2012CB723308), the National Natural Science Foundation of China (51337002, 21201059, and 50977019), the Natural Science Foundation of Heilongjiang province (E2018041).
Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09670h
References
- Fletcher K. A. Pandey S. Surfactant aggregation within room-temperature ionic liquid 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide. Langmuir. 2004;20:33–36. doi: 10.1021/la035596t. [DOI] [PubMed] [Google Scholar]
- Evans D. F. Self-organization of amphiphiles. Langmuir. 1988;4(1):3–12. doi: 10.1021/la00079a002. [DOI] [Google Scholar]
- Moroi Y., Micelles: theoretical and applied aspects, Springer Science & Business Media, 1992 [Google Scholar]
- Finean J. B., Membrane mimetic chemistry-characterization and applications of micelles, microemulsions, monolayers, bilayers, vesicles, host-guest systems, and polyions, Wiley, 1982 [Google Scholar]
- Holmberg K., Bo J., Kronberg B. and Lindman B., Physicochemical Properties of Surfactants and Polymers Containing Oxyethylene Groups, John Wiley & Sons, Ltd, 2003, ch. 4 [Google Scholar]
- Ben-Naim A. Y., Hydrophobic interactions, Springer Science and Business Media, 2012 [Google Scholar]
- Vladimir A. Manrique E. Enhanced Oil Recovery: An Update Review. Energies. 2010;3(9):1529–1575. doi: 10.3390/en3091529. [DOI] [Google Scholar]
- Rosen M. J., Characteristic Features of Surfactants, John Wiley & Sons, Inc., 2004 [Google Scholar]
- Aniansson E. A. G. Wall S. N. Kinetics of step-wise micelle association. Correction and improvement. J. Phys. Chem. 1975;79(8):857–858. doi: 10.1021/j100575a019. [DOI] [Google Scholar]
- Aniansson E. A. G. Wall S. N. Almgren M. Hoffmann H. Kielmann I. Ulbricht W. Zana R. Lang J. Tondre C. Theory of the kinetics of micellar equilibria and quantitative interpretation of chemical relaxation studies of micellar solutions of ionic surfactants. J. Phys. Chem. 1976;80(9):905–922. doi: 10.1021/j100550a001. [DOI] [Google Scholar]
- Honda C. Hasegawa Y. Hirunuma R. Nose T. Micellization Kinetics of Block Copolymers in Selective Solvent. Macromolecules. 1994;27(26):7660–7668. doi: 10.1021/ma00104a022. [DOI] [Google Scholar]
- Bai G. Wang Y. Yan H. Thomas R. K. Enthalpies of Micellization of Double Chain and Gemini Cationic Surfactants. J. Colloid Interface Sci. 2001;240:375–377. doi: 10.1006/jcis.2001.7642. [DOI] [PubMed] [Google Scholar]
- Stephenson B. C. Stafford K. A. Beers K. J. Blankschtein D. Application of Computer Simulation Free-Energy Methods to Compute the Free Energy of Micellization as a Function of Micelle Composition. 1, Theory. J. Phys. Chem. B. 2008;112(6):1634–1640. doi: 10.1021/jp0727603. [DOI] [PubMed] [Google Scholar]
- Villa A. Mark A. E. Calculation of the free energy of solvation for neutral analogs of amino acid side chains. J. Comput. Chem. 2002;23(5):548–553. doi: 10.1002/jcc.10052. [DOI] [PubMed] [Google Scholar]
- Inoue Y. Hakushi T. Liu Y. Tong L. Shen B. Jin D. Thermodynamics of molecular recognition by cyclodextrins. 1. Calorimetric titration of inclusion complexation of naphthalenesulfonates with .alpha.-, .beta.-, and .gamma. -cyclodextrins: enthalpy-entropy compensation. J. Am. Chem. Soc. 1993;115(2):475–481. doi: 10.1021/ja00055a017. [DOI] [Google Scholar]
- Balcan M. Anghel D. F. Voicu A. Balcan D. C. Determination of thermodynamic parameters of ethoxylated nonionic surfactants by means of reversed-phase high-performance liquid chromatography. Colloids Surf., A. 2002;204(1–3):141–151. doi: 10.1016/S0927-7757(02)00007-9. [DOI] [Google Scholar]
- Kim H. U. Lim K. H. A model on the temperature dependence of critical micelle concentration. Colloids Surf., A. 2004;235(1–3):121–128. doi: 10.1016/j.colsurfa.2003.12.019. [DOI] [Google Scholar]
- Alizadeh N. Ranjbar B. Mahmodian M. Electrochemical study of thermodynamics of interaction of lysozyme with sodium dodecyl sulfate in binary ethanol-water mixtures. Colloids Surf., A. 2003;212(2–3):211–218. doi: 10.1016/S0927-7757(02)00310-2. [DOI] [Google Scholar]
- Gonzalez-Perez A. Del Castillo J. L. Czapkiewicz J. Rodriguez J. R. Thermodynamics of micellization of decyldimethylbenzylammonium bromide in aqueous solution. Colloids Surf., A. 2004;232(2–3):183–189. doi: 10.1016/j.colsurfa.2003.10.018. [DOI] [Google Scholar]
- Zhu Y. P. Masuyama A. Kirito Y. I. Okahara M. Preparation and properties of double-or triple-chain surfactants with two sulfonate groups derived from N-acyldie-thanolamines. J. Am. Oil Chem. Soc. 1991;68(7):539–543. doi: 10.1007/BF02663831. [DOI] [Google Scholar]
- Bedö Z. Berecz E. Lakatos I. Enthalpy-entropy compensation of micellization of ethoxylated nonyl-phenols. Colloid Polym. Sci. 1992;270(8):799–805. doi: 10.1007/BF00776152. [DOI] [Google Scholar]
- Lai G. Zhou R. Han X. Zheng X. Thermodynamic Interpretation of Enthalpy-Entropy Compensation. Chemistry. 2005;68(12):928–934. [Google Scholar]
- Lumry R. Rajender S. Enthalpy-entropy compensation phenomena in water solutions of proteins and small molecules: a ubiquitous property of water. Biopolymers. 1970;9(10):1125–1227. doi: 10.1002/bip.1970.360091002. [DOI] [PubMed] [Google Scholar]
- Ranatunga R. Vitha M. F. Carr P. W. Mechanistic implications of the equality of compensation temperatures in chromatography. J. Chromatogr. A. 2002;946(1–2):47–49. doi: 10.1016/S0021-9673(01)01539-4. [DOI] [PubMed] [Google Scholar]
- Liu G. Gu D. Liu H. Ding W. Li Z. Enthalpy-entropy compensation of ionic liquid-type gemini imidazolium surfactants in aqueous solutions: a free energy perturbation study. J. Colloid Interface Sci. 2011;358:521–526. doi: 10.1016/j.jcis.2011.03.064. [DOI] [PubMed] [Google Scholar]
- Liu G. Gu D. Liu H. Wei D. Luan H. Lou Y. Thermodynamic properties of micellization of sulfobetaine-type zwitterionic gemini surfactants in aqueous solutions-a free energy perturbation study. J. Colloid Interface Sci. 2012;375:148–153. doi: 10.1016/j.jcis.2012.02.027. [DOI] [PubMed] [Google Scholar]
- Shi P. Zhang H. Lin L. Song C. Chen Q. Li Z. Molecular dynamics simulation of four typical surfactants at oil/water interface. J. Dispersion Sci. Technol. 2018;39:1258–1265. doi: 10.1080/01932691.2017.1392319. [DOI] [Google Scholar]
- Shi P. Zhang H. Lin L. Song C. Chen Q. Li Z. Molecular dynamics study of the effect of inorganic salts on the monolayer of four surfactants at the oil/water interface. J. Dispersion Sci. Technol. 2018:1–9. [Google Scholar]
- Schmidt M. W. Baldridge K. K. Boatz J. A. Elbert S. T. Gordon M. S. Jensen J. H. Koseki S. Matsunaga N. Nguyen K. A. Su S. General atomic and molecular electronic structure system. J. Comput. Chem. 1993;14(11):1347–1363. doi: 10.1002/jcc.540141112. [DOI] [Google Scholar]
- Dykstra C., Frenking G., Kim K. and Scuseria G., Theory and Applications of Computational Chemistry: The First Forty Years, Elsevier, 2011 [Google Scholar]
- Singh U. C. Kollman P. A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984;5(2):129–145. doi: 10.1002/jcc.540050204. [DOI] [Google Scholar]
- Scott W. R. P. Hünenberger P. H. Tironi I. G. Mark A. E. Billeter S. R. Fennen J. Torda A. E. Huber T. Peter Krüger A. Gunsteren W. F. V. The GROMOS Biomolecular Simulation Program Package. J. Phys. Chem. A. 1999;103(19):3596–3607. doi: 10.1021/jp984217f. [DOI] [Google Scholar]
- van Gunsteren W. F., Billeter S. R., Eising A. A., Hünenberger P. H., Krüger P., Mark A. E., Scott W. R. and Tironi I. G., Biomolecular simulation: the {GROMOS96} manual and user guide, 1996 [Google Scholar]
- Kutzner C. Van Der Spoel D. Fechner M. Lindahl E. Schmitt U. W. De Groot B. L. Grubmüller H. Speeding up parallel GROMACS on high-latency networks. J. Comput. Chem. 2007;28(12):2075–2084. doi: 10.1002/jcc.20703. [DOI] [PubMed] [Google Scholar]
- Hess B. Kutzner C. Van Der Spoel D. Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008;4(3):435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- Malde A. K. Zuo L. Breeze M. Stroet M. Poger D. Nair P. C. Oostenbrink C. Mark A. E. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J. Chem. Theory Comput. 2011;7(12):4026–4037. doi: 10.1021/ct200196m. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C., Postma J. P. M., Gunsteren W. F. V. and Hermans J., Interaction Models for Water in Relation to Protein Hydration, Intermolecular Forces, Springer, Dordrecht, 1981, pp. 331–342 [Google Scholar]
- Essmann U. Perera L. Berkowitz M. L. A smooth particle mesh Ewald method. J. Chem. Phys. 1998;103(19):8577–8593. doi: 10.1063/1.470117. [DOI] [Google Scholar]
- Whittaker M. Floyd C. D. Brown P. Gearing A. J. H. Design and therapeutic application of matrix metalloproteinase inhibitors. Chem. Rev. 1999;99(9):2735–2776. doi: 10.1021/cr9804543. [DOI] [PubMed] [Google Scholar]
- Pohorille A. Jarzynski C. Chipot C. Good practices in free-energy calculations. J. Phys. Chem. B. 2010;114(32):10235–10253. doi: 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
- Christ C. D. Mark A. E. Van Gunsteren W. F. Basic ingredients of free energy calculations: a review. J. Comput. Chem. 2010;31(8):1569–1582. doi: 10.1002/jcc.21450. [DOI] [PubMed] [Google Scholar]
- Mark A. E., Free Energy Perturbation Calculations, John Wiley & Sons, Ltd, 2002 [Google Scholar]
- Bennett C. H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976;22(2):245–268. doi: 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
- Yu T. Li Z. Ding W. Luo S. Q. Luan H. X. Tong W. Cheng J. C. Enthalpy-entropy compensation of micellization of alkyl aryl sulfonates in aqueous solutions. Acta Phys.-Chim. Sin. 2010;26(3):638–642. [Google Scholar]
- Wu W. X. Luan H. X. Ding W. Yu T. Qu G. M. Thermodynamics for Micellization of Anionic-Nonionic Gemini Surfactants. Petrochem. Technol. 2013;42:39–45. [Google Scholar]
- Geng F. Liu J. Zheng L. Yu L. Li Z. Li G. Tung C. Micelle Formation of Long-Chain Imidazolium Ionic Liquids in Aqueous Solution Measured by Isothermal Titration Microcalorimetry. J. Chem. Eng. Data. 2010;55(1):147–151. doi: 10.1021/je900290w. [DOI] [Google Scholar]
- Smirnova N. A. Vanin A. A. Safonova E. A. Pukinsky I. B. Anufrikov Y. A. Makarov A. L. Self-assembly in aqueous solutions of imidazolium ionic liquids and their mixtures with an anionic surfactant. J. Colloid Interface Sci. 2009;336(2):793–802. doi: 10.1016/j.jcis.2009.04.004. [DOI] [PubMed] [Google Scholar]
- Tanford C., The Hydrophobic Effect: Formation of Micelles and Biological Membranes, J. Wiley, 2nd edn, 1980 [Google Scholar]
- Lee D. J. Huang W. H. Enthalpy-entropy compensation in micellization of sodium dodecyl sulphate in water/methanol, water/ethylene glycol and water/glycerol binary mixtures. Colloid Polym. Sci. 1996;274(2):160–165. doi: 10.1007/BF00663448. [DOI] [Google Scholar]
- Nusselder J. J. H. Engberts J. B. F. N. Toward a better understanding of the driving force for micelle formation and micellar growth. J. Colloid Interface Sci. 1992;148(2):353–361. doi: 10.1016/0021-9797(92)90174-K. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.