Do soft anions promote protein denaturation through binding interactions? A case study using ribonuclease A

Abstract

It has long been known that large soft anions like bromide, iodide and thiocyanate are protein denaturing agents, but their mechanism of action is still unclear. In this work we have investigated the protein denaturing properties of these anions using Ribonuclease A (RNase A) as a model protein system. Salt-induced perturbations to the protein folding free energy were determined using differential scanning calorimetry and the results demonstrate that the addition of sodium iodide and sodium thiocyanate significantly decreases the melting temperature of the protein. In order to account for this reduction in protein stability, we show that the introduction of salts that contain soft anions to the aqueous solvent perturbs the protein unfolding free energy through three mechanisms: (a) screening Coulomb interactions that exist between charged protein residues, (b) Hofmeister effects, and (c) specific anion binding to CH and CH₂ moieties in the protein polypeptide backbone. Using the micellization of 1,2-hexanediol as a ruler for hydrophobicity, we have devised a practical methodology that separates the Coulomb and Hofmeister contributions of salts to the protein unfolding free energy. This allowing us to isolate the contribution of soft anion binding interactions to the unfolding process. The analysis shows that binding contributions have the largest magnitude, confirming that it is the binding of soft anions to the polypeptide backbone that is the main promoter of protein unfolding.

Soft anions promote protein folding through binding backbone CH and CH₂ groups.

Introduction

It has long been known that the addition of the salts of large soft anions to aqueous solutions of proteins significantly influences their stability and dynamics.^1–6 However, applying classical electrostatic theory to proteins has one major limitation: in classical electrostatic theory the only differences between the ions are those of charge and size,⁷ while a large body of experimental observations have clearly shown that different salts influence the stability of the native state of proteins in an ion-specific manner that cannot be solely the result of charge and size differences. Examples of these ion-specific effects have been observed in the thermodynamic and kinetic parameters of the protein folding process,^8–15 in protein solubility (salting-out and salting-in),^16–19 loop and domain motions,^20,21 protein aggregation and oligomerization,²² and enzymatic activity.^23–25

A large number of theoretical and experimental studies have been dedicated to understanding ion-specific phenomena at the molecular level.^26–28 In this regard, perhaps the most informative example of ion-specificity explains how different ions interact with the air–water interface.^29,30 The general consensus is that weakly polarizable hard ions that have high charge density and strongly interact with their hydration shell, are excluded from the air–water interface and cause an increase in the surface tension of water; in contrast, highly polarizable soft ions that have low charge density and weakly interact with their hydration shell are preferentially solvated at the water interface and lead to a decrease in surface tension.³¹ Surface-specific techniques have confirmed that a measurable excess of polarizable soft anions exist at the air–water interface and that the degree of this partitioning follows the Hofmeister series, while hard cations are excluded from the interface.³² This is consistent with the idea that unlike strongly hydrated ions, weakly hydrated ions can readily discard their hydration shell water molecules and associate with the interface.³¹ Biophysical ion-specific effects have often been analyzed by treating the protein–water interface as if it were a surface analogous to the air–water interface.^9,33–39 Based on this analogy, the ion-specific thermodynamic effects that are observed in protein systems have often been interpreted in terms of tendencies of the ions to partition into or to avoid the protein–water interface:^36,37 Ions that partition into the protein–water interface favor protein states that have larger surface areas (e.g., the unfolded state or non-aggregated forms), while ions that are excluded from the interface favor protein states that have smaller surface areas (e.g., the folded state or aggregated forms). Although this ion partitioning paradigm provides a useful thermodynamic framework for understanding ion specific effects on biopolymer processes it presents a challenge, namely that it is difficult to pinpoint the general mechanism by which ions interact with the heterogeneous protein–water interface. This notwithstanding, it has been shown that coarsely decomposing the protein surface into three distinct chemical types (aliphatic hydrocarbon, aromatic hydrocarbon and polar amide) and analyzing the salt-induced changes in protein folding in terms of ion interactions with these three surface types, can provide a useful semi-quantitative interpretation of the observed ion specificities in protein folding.^9,33,40

Measurements of protein stability have shown that the soft anions thiocyanate, iodide and bromide significantly destabilize the folded state of protein.^9,41–45 At a first glance, it may seem logical to interpret the effects of these soft ions in terms of their interaction with aliphatic hydrocarbon, aromatic hydrocarbon and polar amide surfaces; however, a series of elegant studies on model polypeptides that combined thermodynamic, spectroscopic and theoretical approaches call this interpretation into question.^46–49 These studies have clearly shown that: (a) thiocyanate, iodide and bromide can bind directly to CH and CH₂ groups that are adjacent to electron-withdrawing moieties (e.g., alpha carbons on the polypeptide backbone),^46,48 suggesting that the partitioning of these ions in the near vicinity of these groups should be different from what is observed elsewhere on the hydrophobic surface; (b) these binding interactions are strong enough to measurably inhibit the thermally induced aggregation of these model polypeptides. From a protein folding standpoint, it is therefore reasonable to expect that these binding interactions with soft anions will significantly affect protein thermodynamics. However, the magnitude of these binding effects on the protein folding thermodynamics is unknown.

In this work, we have investigated how the soft anions thiocyanate, iodide and bromide influence the unfolding of a model protein (ribonuclease A) using DSC (differential scanning calorimetry). Ribonuclease A (RNase A) was chosen because its folding thermodynamics has the following attractive features. First, its folding mechanism is well known and it has been established that at pH values equal or less than 4 values it unfolds via a two-state mechanism.⁵⁰ Second, it is one of the few proteins that thermally unfolds in a reversible manner, simplifying the DSC analysis of its folding thermodynamics.⁵⁰ Third, it maintains its structure/function integrity within a large pH range.⁵¹ We have quantified salt effects on the RNase A folding free energy by measuring how the addition of salt changes the melting point temperature of the protein. We have also developed a new methodology to isolate the contribution of soft anion binding interactions to RNase A folding thermodynamics. Our results demonstrate that the denaturant properties of soft anions is mostly due to the strength of their interaction with moieties in the polypeptide backbone, rather than general interactions between these anions and the hydrophobic portions of the protein–water interface.

Materials and methods

Materials

Sodium chloride, sodium bromide, sodium iodide, sodium thiosulfate, sodium acetate, lithium chloride, potassium chloride, cesium chloride and ammonium chloride were purchased from Fisher Scientific; 1,2-hexanediol, pyrene, benzoylacetone and ANS (8-anilinonaphthalene-1-sulfonic acid) were purchased from Sigma Aldrich; lyophilized Ribonuclease A (RNase A) prepared from bovine pancreas and RNA from yeast were purchased from Worthington Biochemical Corporation.

Differential scanning calorimetry (DSC) measurements

RNase A was dialyzed to remove aggregates resulting from lyophilization during the purification process. 4–5 mL protein samples containing RNase A in 10 mM acetate buffer at pH 4 were dialyzed overnight at 4 °C in 1.0 L of buffer (10 mM acetate buffer at pH 4) using commercial Spectra/Por 7 pre-treated dialysis membrane with 2 kDa pore size (Spectrum Labs). Buffer dialysate was removed the following day and replaced with fresh buffer of the same composition and dialyzed for an additional 1–2 hours. The dialysate buffer was used as the reference solution, so that the presence of enzyme accounts for the only difference between enzyme and reference solutions. The final protein concentration was determined by measuring absorbance of protein at 278 nm using a Thermo Scientific Helios Zeta double-beam UV/VIS spectrophotometer (RNase A has an extinction coefficient of 8640 cm⁻¹ M⁻¹ provided by the manufacturer). The activity of the dialyzed enzyme was checked using the method of Kalnitsky et al.⁵² DSC experiments were performed using a Nano DSC (TA Instruments) with 0.3 mL capillary cell volume. Samples were equilibrated at 20 °C and then heated to 85 °C with a scan rate of 1 °C per minute and at 3 atm. Samples were degassed for 10 min before loading cells and pressurized at 3 atm to avoid bubble formation data were analyzed using NanoAnalyze (TA Instruments), and the baseline subtracted heat rate was fit to a two-state scaled model for the transition. The melting temperature (T_m) is the peak of the melting curve.

Critical micelle concentration (CMC) determination

The use of pyrene for determining the CMC of surfactants is well known and the methodology of Aguiar et al.⁵³ was followed for all samples except those containing CsCl and NaI. All samples were made from a 4.23 M stock solution of 1,2-hexanediol. For each set of measurements a fresh stock of pyrene was prepared in ethanol and its concentration was determined by UV/vis spectroscopy (extinction coefficient of 54 000 cm⁻¹ M⁻¹ at 335 nm).⁵⁴ The final concentration of pyrene in all samples was 1 μM. The samples were prepared and after overnight incubation, data were collected on the next day. To prepare 1.5 mL of sample, aliquots from the 1,2-hexanediol stock, the concentrated salt solution of interest and the pyrene stock were delivered to a microfuge tube and diluted with distilled water to a total volume of 1.5 mL to yield the required surfactant and salt concentrations. All 1.5 mL samples were prepared in a triplicate and all measurements were conducted at room temperature (22 °C). Fluorescence spectra were measured on a Fluorolog-3 Horiba Jobin Yvon spectrofluorometer. The pyrene emission spectra were recorded from 365 to 450 nm using an excitation wavelength of 334 nm; excitation and emission slits were set to 1 nm band pass resolution. The ratio of fluorescence intensities at wavelengths 373 and 384 nm were plotted as a function of surfactant concentration. The inflection point of the resulting plot yields the CMC. In the case of the NaI samples, we have determined the CMC using the method of Bocchini et al.⁵⁵ The samples were prepared as above and the final concentration of ANS in each sample was 10 μM. The ANS emission spectra were recorded from 420 to 600 nm using an excitation wavelength of 370 nm; excitation and emission slits were set to 5 nm band pass resolution. The increase in the intensity at 521 nm was monitored and plotted against the surfactant concentrations and the CMC was determined from the inflection point. The CMC concentrations of the CsCl samples were determined using the absorbance of benzoylacetone using the method of Shoji et al.⁵⁶ The samples were prepared as above and the final concentration of benzoylacetone was set to 50 μM. The absorbance spectra of the samples were measured on a Thermo Scientific Helios Zeta UV/VIS spectrophotometer and recorded from 200 to 380 nm. The ratio between the absorbance values measured at 250 nm and 312 nm was plotted against the surfactant concentration. The inflection point of the resulting plot is the measured CMC. All fluorescence and absorbance measurements were done in semi-micro quartz cuvettes with a 10 × 3 mm geometry.

Results

Specific salt effects on the melting temperature of RNase A

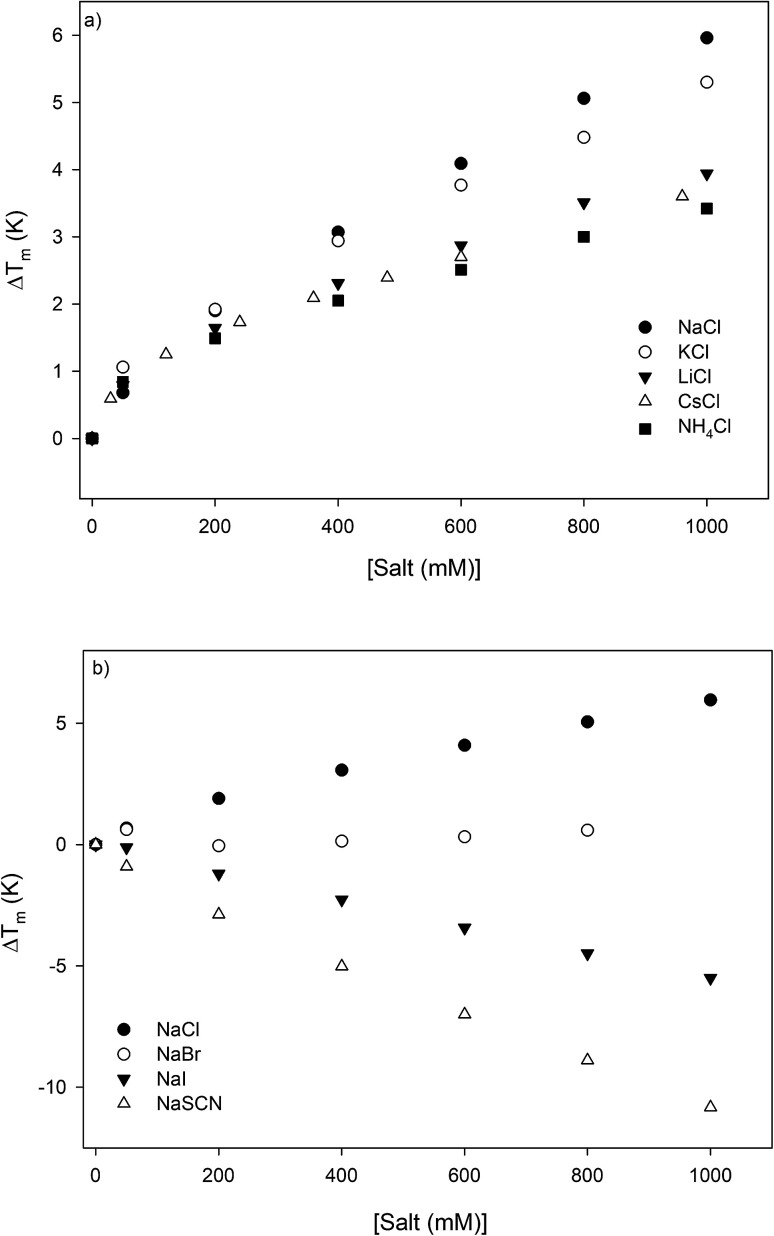
The thermodynamic consequences of adding a series of monovalent salts to a solution of RNase A are shown in Fig. 1 and Table 1. Fig. 1a shows that adding chloride salts increases the melting temperature of RNase A. The data in Fig. 1a demonstrate that although the addition of these salts increases the stability of RNase A, this effect is cation specific and yields the following rank order:

NaCl > KCl > LiCl > CsCl > NH₄Cl 1

Fig. 1. The salt concentration dependence observed in the melting temperature of RNase A as measured by DSC for a series of: (a) chloride salts and (b) sodium salts. The average uncertainty of 0.6 K has not been shown. In the absence of salt, the melting temperature of RNase A has been determined to be 53.7 ± 0.6 °C.

Salt-induced effects on the melting temperature ΔT_m and melting enthalpy ΔH_m as determined by DSC measurements performed at pH 4, the uncertainties are determined from repeating the measurements on triplicate samples. The values of these thermodynamic parameters at low salt concentration are: T_m = 326.8 ± 0.6 K and ΔH_m = 392 ± 7 kJ mol⁻¹.

	ΔTm (K)	ΔHm (kJ M−1)		ΔTm (K)	ΔHm (kJ M−1)		ΔTm (K)	ΔHm (kJ M−1)
[NaCl] (mM)			[KCl] (mM)			[LiCl] (mM)
50	0.7 ± 0.6	414 ± 7	50	1.1 ± 0.6	406 ± 7	50	0.8 ± 0.6	393 ± 7
200	1.9 ± 0.6	413 ± 7	200	1.9 ± 0.6	407 ± 7	200	1.6 ± 0.6	404 ± 7
400	3.1 ± 0.6	404 ± 7	400	2.9 ± 0.6	406 ± 7	400	2.3 ± 0.6	396 ± 7
600	4.1 ± 0.6	402 ± 7	600	3.8 ± 0.6	420 ± 7	600	2.9 ± 0.6	404 ± 7
800	5.1 ± 0.6	406 ± 7	800	4.5 ± 0.6	411 ± 7	800	3.5 ± 0.6	408 ± 7
1000	6.0 ± 0.6	416 ± 7	1000	5.3 ± 0.6	409 ± 7	1000	3.9 ± 0.6	404 ± 7

[NH4Cl] (mM)			[NaSCN] (mM)			[NaI] (mM)
50	0.8 ± 0.6	413 ± 7	50	−0.9 ± 0.6	397 ± 7	50	−0.1 ± 0.6	407 ± 7
200	1.5 ± 0.6	412 ± 7	200	−2.9 ± 0.6	387 ± 7	200	−1.5 ± 0.6	387 ± 7
400	2.1 ± 0.6	409 ± 7	400	−5.0 ± 0.6	362 ± 7	400	−2.8 ± 0.6	379 ± 7
600	2.5 ± 0.6	395 ± 7	600	−7.0 ± 0.6	355 ± 7	600	−4.2 ± 0.6	363 ± 7
800	3.0 ± 0.6	405 ± 7	800	−8.9 ± 0.6	319 ± 7	800	−5.5 ± 0.6	352 ± 7
1000	3.4 ± 0.6	413 ± 7	1000	−10.8 ± 0.6	323 ± 7	1000	−6.7 ± 0.6	341 ± 7

[CsCl] (mM)			[NaBr] (mM)
30	0.6 ± 0.6	410 ± 7	50	0.6 ± 0.6	404 ± 7
120	1.2 ± 0.6	410 ± 7	200	−0.1 ± 0.6	408 ± 7
240	1.7 ± 0.6	403 ± 7	400	0.1 ± 0.6	403 ± 7
360	2.1 ± 0.6	409 ± 7	600	0.3 ± 0.6	393 ± 7
480	2.4 ± 0.6	410 ± 7	800	0.6 ± 0.6	395 ± 7
600	2.7 ± 0.6	408 ± 7
960	3.6 ± 0.6	408 ± 7

With the exception of NH₄Cl, the effect of the chlorides on RNase A stability roughly follows other cation Hofmeister series given in the literature;^2,57,58 and is also consistent with their effectiveness in stabilizing the folded states of proteins and decreasing hydrophobic solubility.^38,39 The effects of the sodium salts on RNase A thermodynamics as seen in Fig. 1b are much more diverse than those of the chlorides: the addition of NaCl stabilizes RNase A, the addition of NaBr has minimal effect, while the addition of NaI and NaSCN significantly destabilizes the protein. This anion specific effect on RNase A stability can be represented by the following:

NaCl > NaBr > NaI > NaSCN 2

which follows the traditional anion Hofmeister series in the literature.⁵⁹

Specific salt effects on the micellization of 1,2-hexanediol

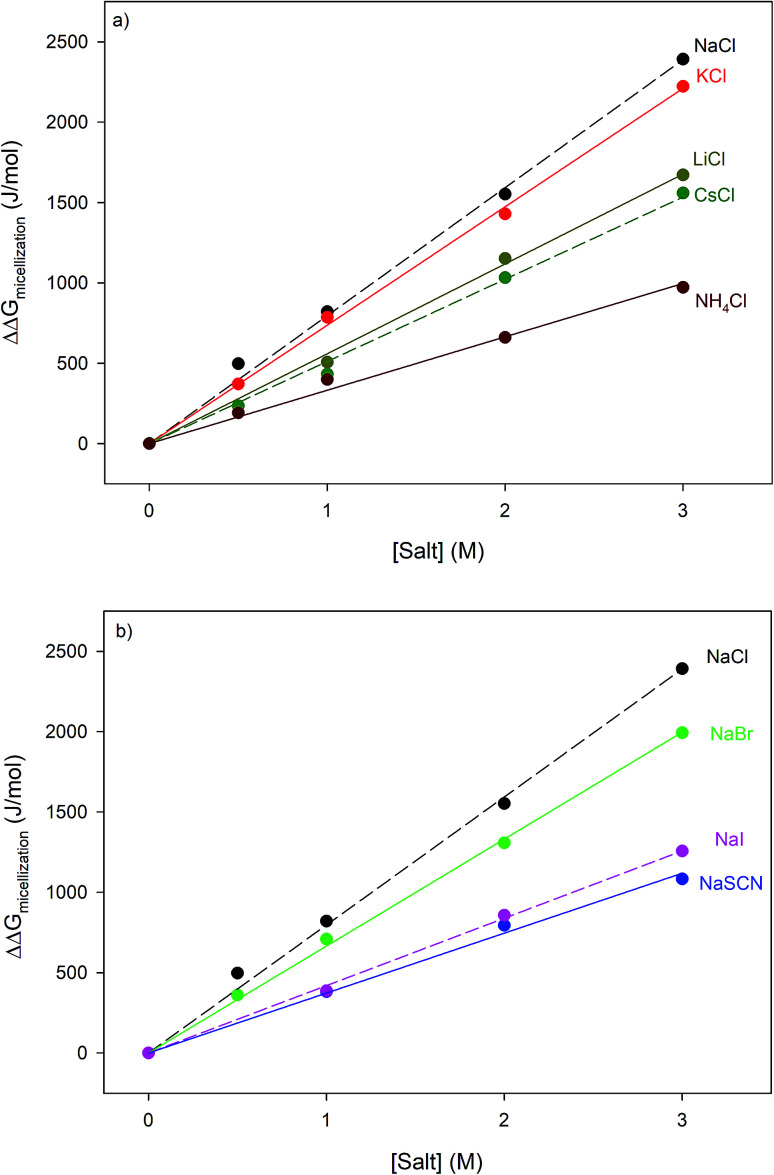
The effects of the same series of monovalent salts on the micellization of 1,2-hexanediol are shown in Table 2. It clear from this table that the addition of these salts causes a decrease in the CMC value of 1,2-hexanediol. The specific effect of each salt on the micelle formation can be characterized thermodynamically:⁶⁰

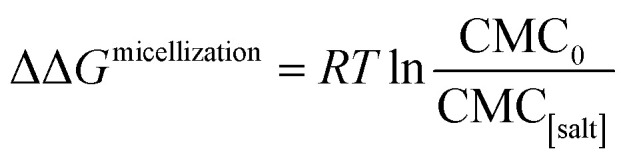3

where ΔΔG^{micellization} is the change in micellization Gibbs free energy due to the addition of salt, CMC₀ and CMC_[salt] are the critical micelle concentrations measured at low and the given salt concentrations. Fig. 2 plots ΔΔG^{micellization} as a function of salt concentration for all the CMC values tabulated in Table 2. It is clear from Fig. 2 that ΔΔG^{micellization} is linearly dependent on salt concentration and that the slope of this dependence is salt specific:

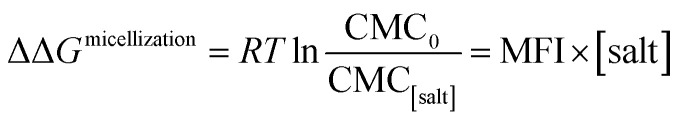3a

where MFI (Micelle Formation Increment) is a constant characterizing the efficiency of each salt in promoting micellization and these values are shown in Table 3. Although the addition of all salts promotes micelle formation, the efficiency of the chloride and sodium salts in promoting micelle formation follow these rankings:

MFI_NaCl > MFI_KCl > MFI_LiCl > MFI_CsCl > MFI_NH4Cl 4

MFI_NaCl > MFI_NaBr > MFI_NaI > MFI_NaSCN 5

Critical micelle concentrations of 1,2-hexanediol determined under different salt concentrations using the methodologies outlined in the Materials and methods section.

	0 M	0.5 M	1 M	2 M	3 M
LiCl	0.60 ± 0.02	—	0.49 ± 0.01	0.38 ± 0.01	0.31 ± 0.01
NaCl	0.60 ± 0.01	0.49 ± 0.01	0.44 ± 0.01	0.32 ± 0.01	0.23 ± 0.01
KCl	0.61 ± 0.01	0.53 ± 0.01	0.45 ± 0.01	0.34 ± 0.01	0.25 ± 0.01
CsCl	0.61 ± 0.05	0.56 ± 0.05	0.52 ± 0.04	0.40 ± 0.04	0.33 ± 0.03
NH4Cl	0.60 ± 0.01	0.52 ± 0.02	0.50 ± 0.01	0.45 ± 0.01	0.39 ± 0.01
NaBr	0.55 ± 0.01	0.47 ± 0.01	0.41 ± 0.01	0.32 ± 0.01	0.24 ± 0.01
NaI	0.64 ± 0.03	—	0.55 ± 0.03	0.45 ± 0.04	0.39 ± 0.02
NaSCN	0.59 ± 0.01	0.52 ± 0.01	0.51 ± 0.01	0.43 ± 0.01	0.39 ± 0.01

Fig. 2. Specific salt effects measured on the micellization thermodynamics of 1,2-hexanediol obtained by applying eqn (3) to the CMC values shown in Table 2; panel (a) represents chloride salts and panel (b) represents sodium salts. The straight lines represent the best linear fits correlating the data. The results of these fits are shown in Table 3.

Fitting parameters obtained from fitting the data in Fig. 2 to eqn (3a), MFI is the micellization free energy increment while R² is the coefficient of determination.

Salt	MFI	R 2
NaCl	796 ± 50	0.9966
KCl	736 ± 50	0.9986
LiCl	558 ± 50	0.9976
CsCl	511 ± 50	0.9954
NH4Cl	332 ± 50	0.9903
NaBr	665 ± 50	0.9987
NaI	419 ± 50	0.9985
NaSCN	373 ± 50	0.9945

These rankings are identical to those given in eqn (1) and (2).

Discussion

Thermodynamic analysis

As can be seen in Fig. 1, at pH 4 addition of the chloride salts causes the melting point of RNase A to increase, while adding NaI and NaSCN lowers the melting temperature of the protein. These changes in protein melting point can be related to the unfolding free energy change through the following formalism. In the absence of salt, the standard state folding free energy change of a protein at any temperature T is given by eqn (6a):^12,43,61

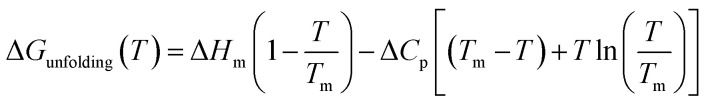6a

where ΔH_m and T_m are the protein melting enthalpy and protein melting temperatures determined under low-salt conditions. Based on this equation, at low salt concentrations ΔG_unfolding at T_m will be zero. The addition of salt will perturb the melting temperature from T_m to T_m + ΔT_m and the ΔH_m to 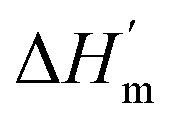, therefore at a given concentration [salt], the folding free energy change at T_m will be:

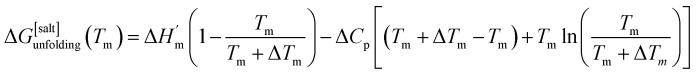6b

The salt-induced perturbation to the unfolding free energy change measured at the low-salt melting temperature T_m is defined as ΔΔG_unfolding = ΔG^[salt]_unfolding(T_m) − ΔG_unfolding(T_m). For small perturbations to the melting temperature the second term in eqn (6b) becomes negligible, yielding eqn (6c):⁶¹

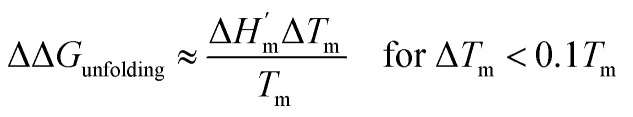6c

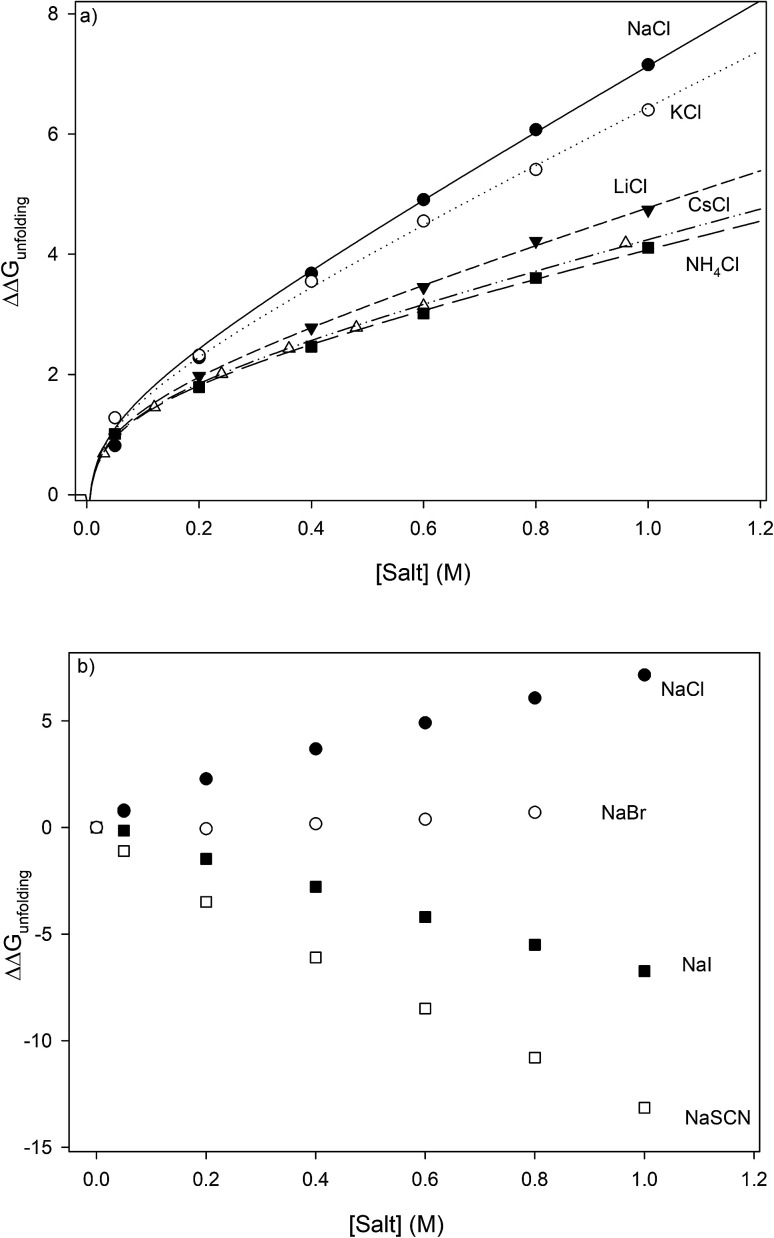
where 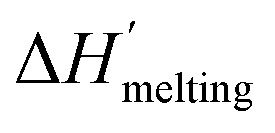is the protein melting enthalpy at a given saline solution as determined by DSC, T_m is the protein melting temperature measured at low salt concentration and ΔT_m is the difference between the melting temperature of a protein in a given saline solution and T_m. Applying eqn (6c) to the DSC data of Table 1, enables us to plot ΔΔG_unfolding as a function of salt concentration for the monochloride and monosodium salts in Fig. 3, clearly showing the salt specificity.

Fig. 3. Salt specific perturbations to the free energy of unfolding ΔΔG_unfolding of RNase A determined for a series of (a) chlorides and (b) sodium salts. The lines in part (a) represent the best global fits to eqn (23a) sharing parameter A and b.

Most systematic analyses of salt effects on proteins postulate that salt addition influences the stability of proteins through nonspecific Coulomb and ion-specific Hofmeister effects.^9,40,62 The formalism of Record et al.,^{9,33,36–40,62,63} quantifies Hofmeister effects on the protein folding process by “m-values”, the derivative of the free energy of unfolding with respect to salt concentration:†

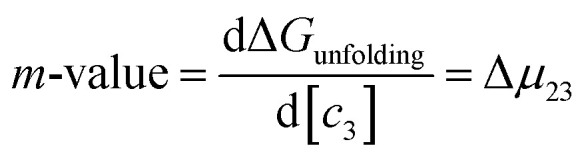7

where μ₂₃ is defined in terms of changes in the activity coefficient γ of the protein 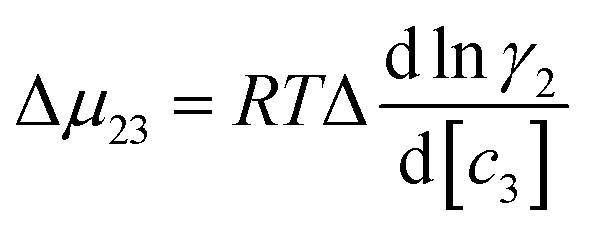; μ₂₃ is therefore closely related to the preferential interaction coefficient as defined by Timasheff (Γ_μ3),⁶⁴ that characterizes how well the salt (as a sum of its component ions) interacts with the protein surface compared to water molecules. In the case of the protein folding process, Δμ₂₃ can be expressed as a function of protein solubility:

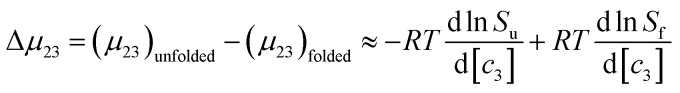8

In which S_u and S_f are the solubilities of the unfolded (u) and folded (f) forms of the protein. Although the protein surface is clearly heterogeneous, it can be coarsely decomposed into three distinct chemical surface types: aliphatic hydrocarbon, aromatic hydrocarbon and polar amide (the oxygen and nitrogen moieties).^9,33 The salt-induced changes in solubility can now be expressed as the sum of the contributions from these surfaces:

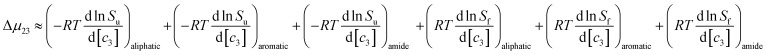9

this can be rewritten as:

Δμ₂₃ ≈ (μ^u₂₃)_aliphatic + (μ^u₂₃)_aromatic + (μ^u₂₃)_amide − (μ^f₂₃)_aliphatic − (μ^f₂₃)_aromatic − (μ^f₂₃)_amide 10

The contribution of each type of surface i to Δμ₂₃ is given in the following definition:

11

The fraction 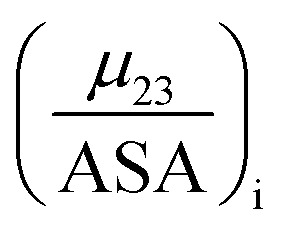is the solute interaction potential that quantifies the interaction of one unit area of surface type i with the salt of interest and (ASA)_i is the water accessible area of surface i. In the coarse decomposition, the assumption is that the nature of each type of surface in both the folded and unfolded states remains the same. Therefore, the interaction of a unit area of aliphatic (or arom atic/amide) surface with the salt does not change as the protein unfolds. The value of 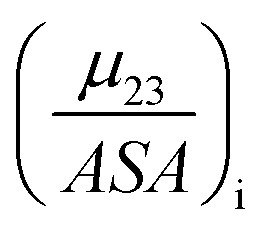remains is constant and the change it is the difference in the magnitude of solvent exposed surface area that changes that leads to differences in (μ₂₃)_i that exist between the folded and unfolded protein states. Substituting eqn (11) into eqn (10) yields:

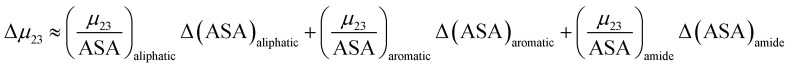12

In this equation Δ(ASA)_aliphatic is the change in protein aliphatic surface area between the unfolded and folded states, Δ(ASA)_aromatic is the change in protein aromatic surface area between the unfolded and folded states and Δ(ASA)_amide is the change in protein amide surface area between the unfolded and folded states. Therefore, in principle, if the values of the salt interaction potential are known for each kind of surface and the change in surface area is available from structural data, the effect of each salt on the protein folding process can be calculated.

The solute partitioning model (SPM),^36–38 provides a blueprint to calculate values of 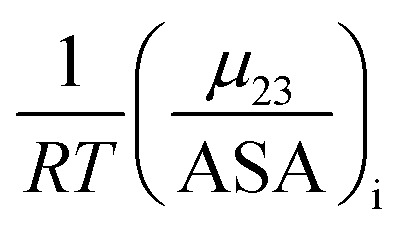for proteins from the salt concentration dependency of the solubility of model hydrocarbon and peptide compounds. The aliphatic portion of the protein surface is assumed to be very similar to that of a simple hydrocarbon like ethane. Applying SPM to ethane solubility data results in:

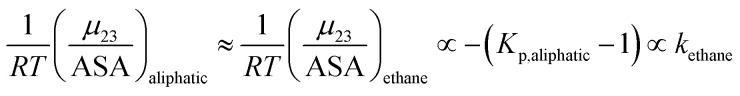13

K _p,aliphatic is a partition coefficient that quantifies exclusion or accumulation of salt near the aliphatic hydrocarbon surface and k_ethane is the ion specific Setschenow constant⁶⁵ of a simple hydrocarbon like ethane. The salt interaction potentials of the aromatic and polar amide surfaces can also be similarly defined:

14

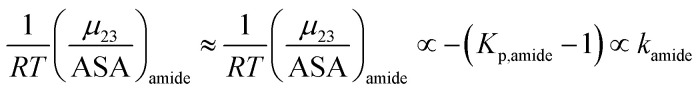15

The m-value for a protein unfolding can be re-written as:

m-value = aΔ(ASA)_aliphatick_ethane + a′Δ(ASA)_aromatick_benzene + a′′Δ(ASA)_amide{−(K_p,amide − 1)} 16

a, a′ and a′′ are the proportionality constants, which allows us to re-write eqn (16) as:

m-value = αk_ethane + βk_benzene + δ{−(K_p,amide − 1)} 16a

Although this compartmentalization of the m-value is useful, its use is limited because reliable and consistent experimental values of Setschenow constants for simple hydrocarbons are not easily obtained. However, the MFI parameter has a similar definition to the Setschenow constant and given that it is easy to measure, we now investigate the potential use of the MFI values of 1,2-hexanediol as an easily obtainable surrogate for hydrocarbon Setschenow constants.

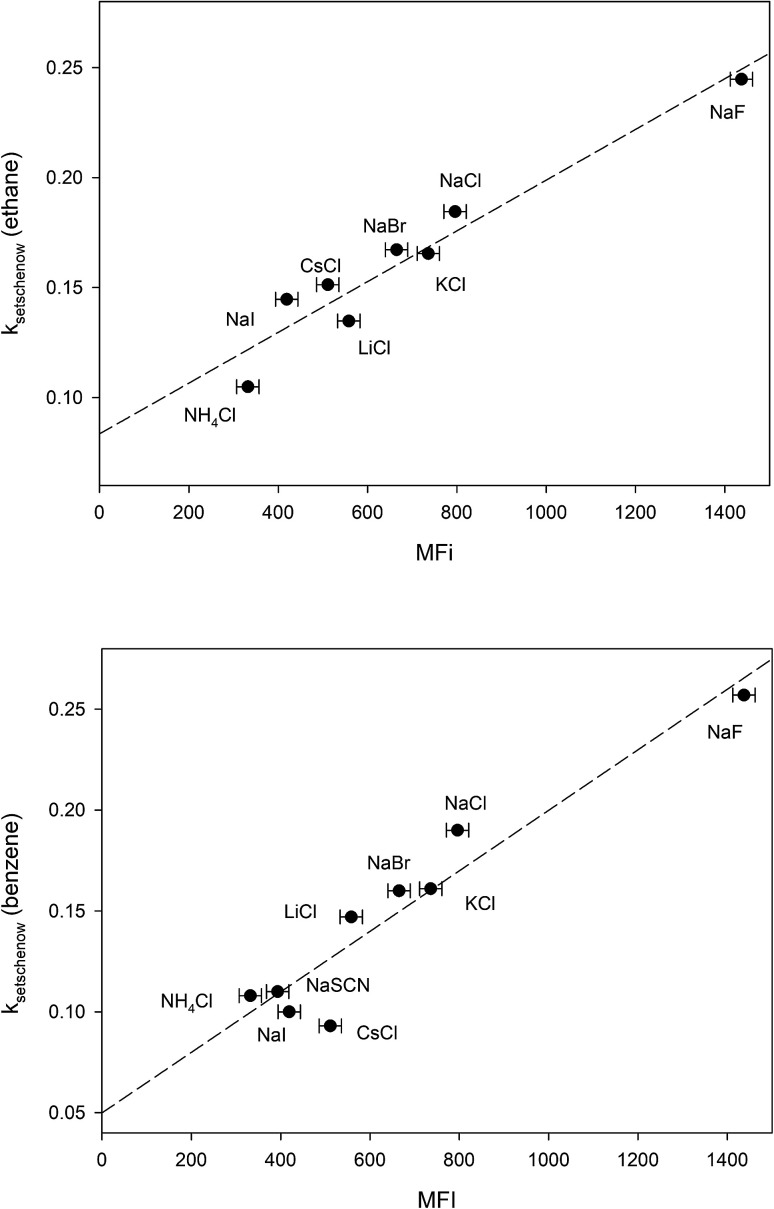
The free energy of micellization, ΔG_{micellization} is defined as the free energy of transferring one mole of monomer amphiphile from water to the micelle phase. For 1,2-hexanediol, this can be broken down into the sum of two transfer processes:⁶⁶ (a) transfer of the hydrocarbon tail from water to micelle, (b) transfer of the diol head from water to micelle. 1,2-Hexanediol micelles are small and not very compact,⁶⁷ therefore the micellization process may not cause a large change in the water accessible surface area for hydroxyl groups. In addition, studies done on cation–carbohydrate interactions indicate that lone hydroxyl groups do not displace cation hydration waters and a favorable steric arrangement of three hydroxyl groups is required for complex formation with cations.^68,69 More recent measurements performed in pure glycerol also demonstrate that the interaction between alkaline cations and glycerol is very weak.⁷⁰ This suggests that it is likely that salt-induced changes to the solubility of the hydrocarbon tail group is the major contributor to the differences between measured MFI values. In Fig. 4 we have plotted the Setschenow constants of ethane⁷¹ and benzene⁶⁵ as a function of MFI and the resulting linear correlations demonstrate that this is indeed the case:

k^ethane_Setschenow = (0.08 ± 0.01) + (0.00012 ± 0.00001)MFI r² = 0.93 17

k^benzene_Setschenow = (0.05 ± 0.02) + (0.00015 ± 0.00002)MFI r² = 0.90 18

Fig. 4. Plotting the ion-specific MFI values of Table 3 against the experimentally determined Setschenow constants obtained from ref. 65 and 71. The dashed line represents the best linear fit obtained from the data.

Substituting eqn (17) and (18) in (16a) yields:

m-value = MFI(0.00012α + 0.00015β) + 0.008α + 0.05β + δ{−(K_p,amide − 1)} 19

The amide surface contribution to the m-value is proportional to −(K_p,aliphatic − 1) and, with the exception of ammonium chloride, the values of K_p,amide of all the other salts in this study are very close to each other (all are within 7% of the mean value of 1.67).^36,37,62 Therefore, for all other salt species in this study except NH₄Cl, the amide surface contribution to the m-value can be assumed to be close to a constant value (m_amide).

m-value = MFI(0.00012α + 0.00015β) + 0.008α + 0.05β + m_amide 19a

Coulombic salt effects on protein stability are often predicted to scale with the Debye–Huckel limiting law, i.e., linearly depend on the square root of the solvent ionic strength.^72–76 It has however been shown that there is no real justification for this assumption⁷² and a more thorough analysis of salt-induced coulombic effects on protein folding free energy predicts that for the monovalent salts in this study they following functional form:^9,40

Salt-induced Coulomb effects = ΔΔG^unfolding_coulombic (1 M) + b ln[c₃] 20

ΔΔG^unfolding_coulombic (1 M) is the Coulomb contribution to the unfolding free energy at a salt concentration of 1 M and b is a constant; this contribution is not salt specific. Therefore, in the absence of any specific interactions between salt components and RNase A, the salt induced perturbations to the RNase A unfolding free energy in this study (except NH₄Cl) should follow eqn (21):

ΔΔG_unfolding = ΔΔG^unfolding_coulombic (1 M) + b ln[c₃] + {MFI(0.00012α + 0.00015β) + 0.008α + 0.05β + m_amide} × [c₃] = ΔΔG^unfolding_coulombic (1 M) + b ln[c₃] + {MFI × ψ + χ}[c₃] = ΔΔG^unfolding_coulombic (1 M) + b ln[c₃] + {m-value}[c₃] 21

b, ψ and χ are constants.

Analyzing the effects of the chloride salts on the folding free energy of RNase A

The effects of monochloride salts on the unfolding free energy of RNase A are shown in Fig. 3a. In order to apply eqn (21) to the unfolding data of the monochlorides we must check for the existence of any specific interactions that may exist between the cations and RNase A and assess their effects. Cations are known to interact significantly with carboxylate groups (the cation binding constant values are between 3–13 M⁻¹)⁷⁷ and their contribution to the unfolding process can be represented by:

ΔΔG^{carboxylate binding}_unfolding = −ΔnRT ln(1 + K_carb[c₃]) 22

where Δn is the difference in the number of carboxylate moieties available for the cations to interact with in the unfolded and folded states and K_carb is the cation–carboxylate binding constant. RNase A has a total of 10 carboxylate containing residues as well as the c-terminus, and the pK_a's of most of these residues is close to 4.⁷⁸ In order to simplify our analysis, we can expand eqn (22) as a Taylor series centered around 1 M concentration:

22a

Truncating the series at the third order gives a reasonable approximation for ln(1 + K_carb[c₃]) for c₃ concentrations between 1 and 0.2 M if K_carb values vary between 3 M⁻¹ and 13 M⁻¹. Adding eqn (22a) to (21) results in an algebraic relationship having the form:

ΔΔG_unfolding = A + b ln[c₃] + C[c₃] + D[c₃]² + E[c₃]³ 23

where the constants A, C (m-value), D and E are salt specific and the constant b is the same for all salts. We have globally fit the data of Fig. 3a to eqn (23) sharing the constant b in all fits. Comparing the goodness of the fits show that truncating the quadratic and cubic terms has minimal effect on the correlation quality, allowing us to simplify eqn (23) to:

ΔΔG_unfolding = A + b ln[c₃] + (m-value)[c₃] 23a

The results of fitting the data of Fig. 3a to eqn (23a) are shown in Table 4. They show that the value of the constant A is almost constant, staying within the range of 2.04 ± 0.20 kJ mol⁻¹. Eqn (22a) predicts that if K_carb varies from 3 to 13, for Δn = 1, A should also commensurately vary by approximately 2 kJ mol⁻¹. The fact that A is effectively constant and the cubic and quadratic terms make no significant contribution suggests that Δn must be more than an order of magnitude smaller than 1. In other words, unfolding the protein has little effect on the cation accessibility of the protein carboxylate moieties and A is effectively ΔΔG^unfolding_coulombic (1 M). This is to be expected because aspartate and glutamate residues of RNase A are not buried within the protein and are solvent accessible⁷⁹ and binding interactions between monovalent cations and carboxylate moieties would therefore have little effect on the protein folding thermodynamics.

The first three columns are the results of fitting the data of Fig. 3a to eqn (23a) and globally sharing a common parameter b = 0.41 ± 0.02. The fourth and fifth columns are the results of fitting the data of Fig. 3a to eqn (23a) and globally sharing A = 2.07 ± 0.09 and b = 0.41 ± 0.03.

Salt	A	m-Value	R 2	m-Value	R 2
NaCl	1.84 ± 0.07	5.38 ± 0.09	0.9994	5.1 ± 0.1	0.9962
KCl	2.23 ± 0.07	4.14 ± 0.09	0.9991	4.4 ± 0.1	0.9963
LiCl	2.05 ± 0.07	2.73 ± 0.09	0.9990	2.7 ± 0.1	0.9990
CsCl	2.04 ± 0.07	2.2 ± 0.1	0.9996	2.2 ± 0.1	0.9994
NH4Cl	2.07 ± 0.07	2.01 ± 0.09	0.9986	2.0 ± 0.1	0.9985

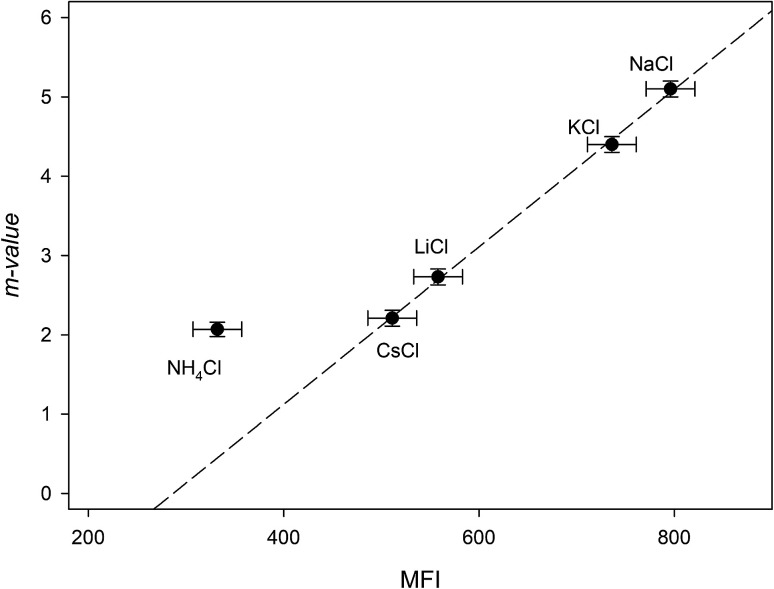
The addition of NaCl, KCl, LiCl, CsCl and NH₄Cl therefore, may affect the RNase A free energy through interacting with the aliphatic, aromatic and amide surfaces of the protein and through Coulomb interactions. Eqn (23a) can now be applied to the data in Fig. 3a and we have globally fit the data to this equation by sharing the parameters ΔΔG^unfolding_coulombic (1 M) and b between them. The results of these fits are shown in Table 4. We now investigate the dependence of the m-value parameter on MFI values for the monochlorides. As it can be seen in Fig. 5, the MFI values for each salt correlates linearly with their associated m-value, except as expected for ammonium chloride which has a significantly different K_p,amide than the others:

m-value = (−2.8 ± 0.2) + (0.0099 ± 0.0003)MFI r² = 0.999 24

Fig. 5. Plotting the “m-value” parameters from Table 4 against the salting-out efficiency as represented by the MFI values of Table 3. The dashed line represents the best linear fit obtained from passing the line through NaCl, KCl, LiCl and CsCl.

As a note, it can be observed that the experimental m-value for NH₄Cl (−2.0 kJ mol⁻²) is larger than the value predicted by eqn (24). This is consistent with our analysis if we compare the experimentally determined⁹K_p,amide value of 1.2 for NH₄Cl with the average K_p,amide value of 1.67: the smaller K_p,amide value would contribute less to the negative portion of eqn (16a), leading to a larger than expected m-value.

Therefore, if no specific interactions exist between the components of a salt and RNase A moieties and the salt that has a K_p,amide value close to 1.67, the effect of salt addition on the RNase A folding free energy can be described by:

25

Analyzing the effects of the sodium salts on the folding free energy of RNase A

Fig. 3b plots the effects of NaSCN, NaI and NaBr on the unfolding free energy of RNase A. It can be clearly seen that the effects of these salts on RNase A stability cannot be described by eqn (25). In other words, interactions other than generic changes in the solubility of the aliphatic, aromatic and amide surfaces of the protein are also contributing to the protein's destabilization. The salt-induced changes in the unfolding free energy can therefore be expressed as:

26

Because the K_p,amide values of NaI, NaSCN and NaBr are all close to 1.67, eqn (25) can be substituted in the equation above resulting in:

ΔΔG_unfolding = 2.07 + 0.41 ln[c₃] + {−2.8+(0.0099)MFI}[c₃] + ΔΔG_excess 27

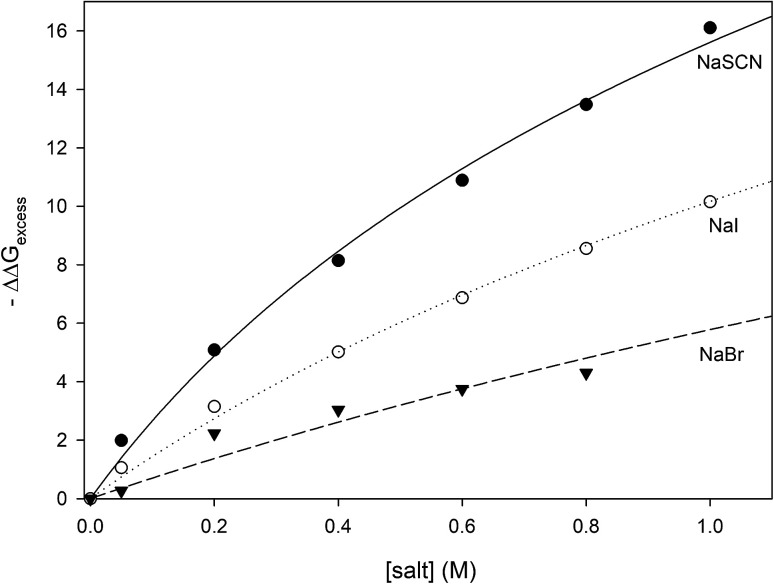
where the values of −ΔΔG_excess have been calculated for all measured concentrations of NaI, NaSCN and NaBr and are plotted in Fig. 6. It can be seen that the salt concentration dependence of −ΔΔG_excess saturates at high concentrations of salt suggestive of binding. This is to be expected because soft anions have been shown to bind to CH₂ and CH species that are adjacent to strongly electron withdrawing moieties such as carbonyl groups.⁴⁶ Unfolding the protein can expose more of these anion-binding “hotspots” to the solvent, thereby providing more binding sites for the anions. Consequently, the concentration dependence of −ΔΔG_excess should be expressed by eqn (28) which is similar to the denaturant binding model as developed by Schellman:⁸⁰

−ΔΔG_excess = RTΔn ln(1 + K[anion]) 28

Fig. 6. Plotting −ΔΔG_excess as a function of anion concentration. The lines represent the best fits obtained from correlating the data to eqn (28).

R and T are the gas constant and temperature respectively, Δn is difference between the number of anion binding sites in the folded and unfolded states, and K is the average binding constant of the anion to the protein. NMR studies have shown that iodide and thiocyanate bind to the same locations on the polypeptide backbone,^27,47,48 therefore we have correlated the data in Fig. 6 globally to eqn (28) sharing RTΔn between all fits, with the resulting fitting parameters are listed in Table 5. The binding constants follow the order:

K_thiocyanate > K_iodide > K_bromide 29

The results of fitting the data of Fig. 6 to eqn (13). All data are globally fit to eqn (13), sharing the parameter RTΔn, among all fits. The R² is the coefficient of determination for the global fit to each set of data.

Anion	Binding constant K sharing RTΔn = 13 ± 2(kJ mol−1)	Binding constant K of the anions to polypeptide backbone moieties as reported by Cremer and co-workers	R 2
SCN−	2.2 ± 0.5 (M)−1	4 (ref. 46) and 2.6 (ref. 47) (M)−1	0.996
I−	1.1 ± 0.2 (M)−1	1.5 (ref. 46) (M)−1	0.997
Br−	0.54 ± 0.09 (M)−1	Less than 1 (ref. 46) (M)−1	0.930

The thermodynamic data are well described by the anion binding model, suggesting that the anions of interest are promoting protein unfolding through increased binding interactions with the unfolded state. The values of the binding constants shown in Table 5 are very similar to those measured for anions binding to polypeptide backbone moieties as determined by NMR and turbidity measurements on model polypeptides^27,46,48,49 confirming that it is likely our analysis has successfully isolated the binding contribution of the soft anions to the unfolding free energy. One result that can be a bit surprising is the relatively small value of Δn (6 ± 1), the difference between the number of anion binding sites existing in the folded and unfolded forms of RNase A. If every alpha carbon in the unfolded state of RNase A corresponds to one available anion binding site, then a value of Δn = 6 ± 1 implies that RNase unfolding has only exposed approximately six more CH₂ or CH moieties to the aqueous solvent. It should be noted however that NMR studies on the binding of anions to a model capped triglycine peptide demonstrates that the three adjacent alpha carbons are not equally available for the anion binding;⁸¹ in fact, one of the alpha carbons of the triglycine does not exhibit any anion bonding. This strongly suggests that not all alpha carbons of the protein backbone are available for anion binding in our experiments. In this case, each residue represents a fraction of a backbone binding site as defined by eqn (28) and the number of alpha carbons getting exposed by RNase A unfolding would be significantly larger than six. It also must be noted that the ΔΔG_unfolding values that we report are calculated at T_m and at temperatures close to the melting point the protein structure is highly dynamic;⁸² at temperatures close to the protein melting point, the polypeptide backbone of the folded state of RNase A should also become more accessible to anions. This additional accessibility of the folded state to anions may also contribute to the small magnitude of Δn. In summary, our thermodynamic analysis demonstrates that soft anions stabilize the unfolded state of proteins through binding interactions, the most likely binding partner being the alpha carbons of the polypeptide chain.

Conclusions

In this study we have investigated the effects of monovalent cations and anions on the folding free energy of RNase A. In our analysis we have assumed that the addition of salts can affect the protein stability through three potential mechanisms:⁹ modulating Coulomb interactions, Hofmeister effects and specific binding interactions between ions and protein moieties. The effect of salt addition on Coulomb interactions are given by eqn (20) and this effect is independent of the nature of the salt. It should be noted that at pH 4 even though the protein retains its structure/functional integrity, it has a high excess of positive charge (11 lysine and 5 arginine residues, 5 aspartate and 5 glutamate residues; the carboxylate pK_a is on average close to 4).⁸³ Under these conditions, the addition of salt should screen electrostatic repulsion interactions and our experimental results show that at pH 4 and 1 M salt concentration, this contribution stabilizes the folded state of RNase A by ∼2.07 kJ mol⁻¹.

Hofmeister effects on protein folding processes are characterized by m-values, the salt specific derivative of the free energy of unfolding with respect to salt concentration. In order to quantify Hofmeister effects caused by the chloride salts we have adopted the Record formalism^33,37 and assumed that the protein surface can be coarsely divided into three distinct chemical surface types: aliphatic hydrocarbon, aromatic hydrocarbon and polar amide (the oxygen and nitrogen moieties). We have demonstrated that the contributions of the solvation of the hydrocarbon surfaces to the RNase A folding m-values are linearly dependent on the MFI values of 1,2-hexanediol measured in the same salt. We have also shown that under our experimental conditions, the folding free energy of RNase A is not affected by binding events involving cations and protein carboxylate groups. Therefore, in the absence of any specific interactions existing between protein moieties and salt components, and if the partition coefficient of a salt in the vicinity of the amide groups (K_p,amide) is close to 1.67, the effects of adding a monovalent salt to an RNase A solution at pH 4 is given by eqn (25). For the chloride salt species studied, Hofmeister effects stabilize the folded state of RNase A. The magnitude of this stabilization measured at pH 4 and 1 M salt concentration, varies from ∼5 kJ mol⁻¹ for NaCl to ∼2 kJ mol⁻¹ for NH₄Cl.

The effects of NaSCN, NaI and NaBr on the folding free energy of RNase A would also include contributions from specific binding interactions: anions of these salts can bind to CH or CH₂ moieties that are directly adjacent to electron-withdrawing substituents.⁴⁶ This complicates quantifying the Hofmeister contribution of these salts to RNase A stability because the carbons constituting the protein aliphatic surface should be divided into two populations: simple aliphatic carbons and those adjacent to electron withdrawing groups (anion binding hotspots). Applying the coarse decomposition of the protein surface as outlined above would only be valid if the change in surface area of the available anion binding hotspots associated with protein unfolding is small compared to the to the total change in aliphatic surface area that the protein experiences as it unfolds. In addition to the backbone alpha carbons, other potential anion binding hotspots may be located on the charged and polar lysine, arginine, asparagine, glutamine and proline residues. However, these sidechains are not often found buried in the protein interior,⁸⁴ therefore, it is mostly interactions between soft anions and backbone CH and CH₂ groups that contribute to the unfolding free energy. Calculations based on the structure and the heat capacity of RNase A show that approximately sixty percent of the nonpolar surface area of the protein is buried in the folded state.⁸⁵ The change of Δn = 6 ± 1 which is equivalent to a change of 6CH and/or CH₂ groups becoming exposed to solvent would thus represent a small change in the fraction of nonpolar surface area becoming exposed to solvent. Therefore, using eqn (25) to calculate the Coulomb and Hofmeister contributions to the unfolding free energies is an acceptable approximation and we have isolated the contribution of soft anion binding to the unfolding free energy. In the case of NaSCN, NaI and NaBr, anion binding destabilizes the folded state respectively by ∼16.1, 10.1 and 4.3 kJ mol⁻¹; in contrast, the stabilizing Hofmeister contribution of these salts are ∼0.8, 1.3 and 2.9 kJ mol⁻¹. Clearly, these anion–backbone interactions are the reason why these soft anions promote protein unfolding.

The methodology outlined in this paper presents a practical way to separate the contributions of Coulomb and Hofmeister effects on the folding free energy for any given protein as a monoprotic salt is added to the protein solvent, summarized in the following way. First, the effects of adding NaCl, KCl, LiCl, CsCl and NH₄Cl on the folding thermodynamics of the protein of interest must be determined. The effects of these salts on the protein unfolding free energy should be fitted to eqn (11) globally, sharing the same Coulomb contribution. If cation–carboxylate binding does not contribute significantly to the protein unfolding process, the data will be well-correlated with eqn (11) and the Coulomb contribution of salt addition to the protein folding process can be isolated. As we have demonstrated above, because NaCl, KCl, LiCl, CsCl have similar K_p,amide values, the m-values resulting from the fitting process above should be linearly dependent on the commensurate 1,2-hexanediol MFI values. Therefore, a linear least squares regression fit to these data will yield a correlation line similar to eqn (24) that can be used to estimate the Hofmeister contribution of salt addition to the protein folding process for any salt that has a K_p,amide that is close to 1.67.

As a final note, this work also can provide an explanation about variations observed in the position of ammonium in the cation Hofmeister series. Traditionally, ammonium has been considered to be a more efficient salting-out agent for proteins compared to other monovalent cations.^2,77 However, in this work as well as a number of other protein folding studies,^9,73,86 ammonium promotes protein folding to a much weaker extent than other monovalent cations. This apparent discrepancy can be explained if the mode of action of this cation is taken into account. Compared to other alkali cations, ammonium strongly binds to carboxylate groups. These groups are usually located on the protein surface, therefore ammonium-carboxylate binding can attenuate carboxylate–carboxylate repulsive forces between neighboring proteins and thus promote protein aggregation and salting out. In the case of protein folding thermodynamics, the unfolding process does not change the solvent accessibility of the surface carboxylates, which minimizes the role ammonium-carboxylate interactions can play in the protein folding process. This is why the ammonium cation can only have a much more modest effect on the protein folding processes compared to the alkali cations.

Conflicts of interest

There are no conflicts to declare.