Bulk and grain-scale minor sulfur isotope data reveal complexities in the dynamics of Earth’s oxygenation

Significance

The permanent disappearance of mass-independent sulfur isotope fractionation (S-MIF) from the sedimentary record has become a widely accepted proxy for atmospheric oxygenation. This framework, however, neglects inheritance from oxidative weathering of pre-existing S-MIF–bearing sedimentary sulfide minerals (i.e., crustal memory), which has recently been invoked to explain apparent discrepancies within the sulfur isotope record. Herein, we demonstrate that such a crustal memory effect does not confound the Carletonville S-isotope record; rather, the pronounced Δ³³S values identified within the Rooihoogte Formation represent the youngest known unequivocal oxygen-free photochemical products. Previously observed ³³S-enrichments within the succeeding Timeball Hill Formation, however, contrasts with our record, revealing kilometer-scale heterogeneities that highlight significant uncertainties in our understanding of the dynamics of Earth’s oxygenation.

Abstract

The disappearance of mass-independent sulfur isotope fractionation (S-MIF) within the c. 2.3-billion-year-old (Ga) Rooihoogte Formation has been heralded as a chemostratigraphic marker of permanent atmospheric oxygenation. Reports of younger S-MIF, however, question this narrative, leaving significant uncertainties surrounding the timing, tempo, and trajectory of Earth’s oxygenation. Leveraging a new bulk quadruple S-isotope record, we return to the South African Transvaal Basin in search of support for supposed oscillations in atmospheric oxygen beyond 2.3 Ga. Here, as expected, within the Rooihoogte Formation, our data capture a collapse in Δ^3×S values and a shift from Archean-like Δ³⁶S/Δ³³S slopes to their mass-dependent counterparts. Importantly, the interrogation of a Δ³³S-exotic grain reveals extreme spatial variability, whereby atypically large Δ³³S values are separated from more typical Paleoproterozoic values by a subtle grain-housed siderophile-enriched band. This isotopic juxtaposition signals the coexistence of two sulfur pools that were able to escape diagenetic homogenization. These large Δ³³S values require an active photochemical sulfur source, fingerprinting atmospheric S-MIF production after its documented cessation elsewhere at ∼2.4 Ga. By contrast, the Δ³³S monotony observed in overlying Timeball Hill Formation, with muted Δ³³S values (<0.3‰) and predominantly mass-dependent Δ³⁶S/Δ³³S systematics, remains in stark contrast to recent reports of pronounced S-MIF within proximal formational equivalents. If reflective of atmospheric processes, these observed kilometer-scale discrepancies disclose heterogenous S-MIF delivery to the Transvaal Basin and/or poorly resolved fleeting returns to S-MIF production. Rigorous bulk and grain-scale analytical campaigns remain paramount to refine our understanding of Earth’s oxygenation and substantiate claims of post-2.3 Ga oscillations in atmospheric oxygen.

The transition from an anoxic and biologically limited planet toward today’s familiar oxygenated world is thought to have occurred in a stepwise fashion, proceeding via two pronounced increases in pO₂ that bound the Proterozoic Eon (1–3). Of these, Earth’s initial oxygenation—commonly referred to as the Great Oxidation Event [GOE (4)]—represents perhaps the most fundamental transformation experienced by the Earth System, with deep-seated climatic and biogeochemical ramifications (5–8). Despite its undeniable geobiological importance, deciphering the intricacies of planetary oxygenation, and its broader consequences, has historically been hindered by a paucity of direct atmospheric proxies, leaving our understanding largely extrapolated from strictly surficial observations.

The recognition of mass-independent sulfur isotope anomalies (S-MIF; Δ³³S ≳ |0.4‰|, Eqs. 2 and 3, Methods) within the sedimentary minor sulfur isotope record, however, overcame this deadlock and, until recently (9), was regarded as the only direct means of tracking the evolution of atmospheric chemistry (10–13). Scrutiny of this now heavily populated record reveals that Δ^3×S* values carried by the majority of sulfur-bearing phases deposited prior to ∼2.3 billion years ago (Ga) are conspicuously pronounced (SI Appendix, Fig. S1), featuring Δ³⁶S/Δ³³S ratios (−1.5 to −0.9; 14, 15) that deviate significantly from those that characterize processes active on the contemporary planet^† (2, 16, 17). In detail, the generation and preservation of S-MIF approximating that entombed within the geological record is directly linked to low atmospheric oxygen in multiple ways: Firstly, there are only two experimentally verified mechanisms—SO₂ photolysis (10, 12, 18) and SO₂ photo(de)excitation (19–21)—capable of generating the large Δ³³S and Δ³⁶S values archived in the geological record (SI Appendix, Fig. S1). These candidate mechanisms rely on photons that are readily absorbed by oxygen and ozone, in turn, confining S-MIF genesis to atmospheric domains largely devoid of these ultraviolet-shielding gases (22, 23). More subtly, reduced atmospheres permit chemically discrete exit channels, presenting vectors that shuttle S-MIF to surficial settings that are otherwise homogenized when atmospheric oxygen exceeds 10⁻⁵ of the present atmospheric level [PAL (13)]. Finally, oxygen-impoverished oceans increase the preservation potential of S-MIF, ensuring the rapid burial of discrete sulfur phases before their isotopic composition is lost via homogenization (24, 25). Assimilating these links with vanishingly low oxygen availability, several authors have proposed that the geological loss of S-MIF can be used as a robust indicator of a rise in atmospheric oxygen above 10⁻⁵ PAL (13), thereby providing a convenient stratigraphic marker defining the GOE (10, 11, 26–31).

Despite its simple elegance, capturing the geological demise of S-MIF has proven surprisingly difficult and, rather than clarifying matters, emerging data have served to polarize the debate. For instance, after over a decade of searching (27, 30), the demise of S-MIF was finally captured in a continuous section within several proximal expressions of the Rooihoogte Formation cored within the South African Transvaal Basin (28) (Figs. 1 and 2). Here, the seemingly logical collapse of Δ^3×S values to near zero, coupled with the transition from Archean-like Δ³⁶S/Δ³³S slopes to their mass-dependent (S-MDF) counterparts, was used to conclude that planetary oxygenation occurred quickly (<10⁶ y), culminating in an oxygenated atmosphere by ∼2.33 Ga (28). This narrative, however, proved short-lived and has since been contested by reports of more-or-less continuous small-magnitude S-MIF extending beyond 2.31 Ga within the Western Australian Turee Creek Group (32, 33). Here, acknowledging the marked diachrony between the available minor sulfur isotope records, the persistence of S-MIF within the supposedly younger Kazput Formation (32, 34–37), was interpreted to reflect inheritance from a crustally adulterated seawater sulfate reservoir (i.e., S-MIF bearing) that was sustained by oxidative sulfide weathering in response to a much earlier rise in oxygen beginning at, or before, 2.45 Ga (32, 33). Taking a contrarian viewpoint, the recent identification of S-MIF within the Transvaal Basin in the overlying Timeball Hill and Boshoek formations has been interpreted to capture primary syndepositional atmospheric S-MIF genesis (8). Here, leveraging sporadic ³³S enrichments (Δ³³S values up to ∼3‰) associated with Archean-like Δ³⁶S/Δ³³S systematics, Poulton et al. envisage a protracted and climate-driven oscillatory atmospheric evolution, whereby permanent atmospheric oxygenation was delayed by up to 100 million years beyond the deposition of the Rooihoogte Formation (8).

Fig. 1.

Geographic and geologic maps locating core KEA-4 and the EBA cores (-1, -2, and -4) within the Carletonville area of the Transvaal Basin, South Africa. The geologic map, providing the broad spatial context, has been simplified from Coetzee et al. (51), while the precise locations of core KEA-4 (34) and cores EBA-1, -2, and -4 (8, 34) within the Eastern Boundary Area of the Kloof Goldfields mining district (gray shading) are taken from Sibanye Stillwater’s open access documentation. The redline within Lower Right signifies the less than 5 km of separation between core KEA-4 and EBA-1. The EBA cores themselves are conservatively separated by less than 500 m. Les., Es., and Mozamb. abbreviate Lesotho, Eswatini, and Mozambique, respectively.

Fig. 2.

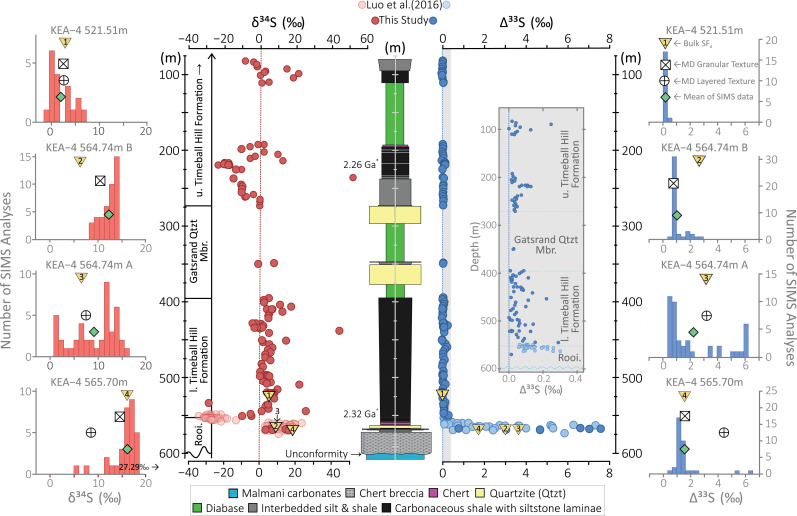
Bulk and grain-scale triple sulfur isotope data from core KEA-4. Here, the bulk SF₆-derived δ³⁴S (red) and Δ³³S (blue) data are plotted stratigraphically, while the intrasample δ³⁴S and Δ³³S ranges are illustrated as color-coded, sample-specific, histograms. The stratigraphic position of the samples studied by SIMS are located numerically as yellow triangles. For clarity, the gray Inset illustrates the stratigraphic spread in Δ³³S values between 0 and 0.4‰ that was otherwise obscured by the large Δ³³S values that typify the Rooihoogte Formation (Rooi). Within the stratigraphic plots, the majority of the data below 548.85 m have been published previously (34) and are separated from those reported herein via the use of lighter shaded datapoints. The δ³⁴S and Δ³³S histograms are constructed using respective 1 and 0.4‰ bin widths, each centered at 0‰. Superimposed on these histograms, the respective green and yellow symbols depict the average SIMS-derived values and their corresponding SF₆ bulk values. Ornamented open symbols reflect microdrilled (MD), texture-specific, SF₆-derived values (34). Where applicable, analytical uncertainties are encompassed by individual data points. Age constraints are provided by a Re–Os isochron obtained from diagenetic pyrites straddling the Rooihoogte–Timeball Hill formational boundary (2,316 ± 7 Ma) (33, 69) and upper-intercept ²⁰⁷Pb/²⁰⁶Pb SHRIMP ages of tuff-hosted zircons from the lower (2,310 ± 9 Ma) (63) and upper Timeball Hill Formation (2,256 ± 6 and 2,266 ± 4 Ma; 63). The lower (l.) and upper (u.) Timeball Hill formations are separated by the oolitic–ironstone-bearing Gatsrand Quartzite Member (Gatsrand Qtzt Mbr)/Klapperkop Member (51) (SI Appendix).

Conceptually, while not new, the influence of oxidative sedimentary recycling via the so-called crustal memory effect [CME (38, 39)] has remained firmly rooted within the theoretical domain owing to the lack of demonstrably coeval datasets necessary to validate its operation. Accordingly, the cratonic dichotomy emerging from the ever-growing Paleoproterozoic database (8, 28, 30–33, 35) has served to realize some of these theoretically grounded concerns, prompting some workers to question the overall significance of the geological departure of S-MIF (3, 32, 33, 40). Accepting that CME-induced inertia has the potential to mask atmospheric dynamics and their wider relationship with other geobiological/climatic events (3, 32, 39), there is now a pressing need to understand how, if at all, these weathering signals have permeated the minor sulfur isotope record and, ultimately, how we reconcile these conflicting signals to reconstruct the operation of the Earth system. Consequently, to simultaneously explore the existence, longevity, and influence of the CME within South Africa’s minor sulfur isotope record, while testing hypotheses surrounding a delayed and dynamic route to planetary oxygenation, we revisit the Rooihoogte–Timeball Hill sedimentary succession deposited in the Carletonville area of the Transvaal Basin (Figs. 1 and 2 and SI Appendix). Here, focusing on a proprietary diamond drill core, KEA-4, leveraging traditional fluorination dual-inlet gas-source isotope ratio mass spectrometry (GS-IRMS, Methods), we first extended the available bulk quadruple sulfur isotope chemostratigraphy through the majority of the Timeball Hill Formation. Pyrites from selected samples were then subjected to in situ isotopic analysis via secondary-ion mass spectrometry (SIMS; Methods) to reveal how the identified S-isotope variability became entrained within the geological record. Contextualizing these data within available intra- (8) and interbasinal datasets (31–33) hints toward a complex and dynamic route to planetary oxygenation that we are only beginning to resolve.

Results

Stratigraphic Quadruple Sulfur Isotope Variability within Core KEA-4.

Based on the stratigraphic evolution of Δ^3×S values and related changes in the Δ³⁶S/Δ³³S ratios carried by chemically isolated pyrites within three cores (EBA-2 , EBA-4, and KEA-4; Fig. 1 and Methods), the Carletonville sedimentary succession was subdivided into three distinct chemostratigraphic intervals (28). Subsequent work, albeit generally lacking Δ³⁶S data, has since broadly corroborated these observations, extending them to an additional core (EBA-1; Fig. 1) (8). Within this framework, the initial quadruple sulfur isotope data from the S-MIF interval (>563.68 m) of core KEA-4 documented Δ³³S values as high as 7.4‰ and Δ³⁶S/Δ³³S systematics that populated the Archean reference array (ARA; Fig. 3) (14, 15, 41). By contrast, pyrites from the S-MDF interval (<558.56 m) were found to possess near-zero Δ³³S values (|<0.3‰|) and Δ³⁶S/Δ³³S ratios that approximated mass-dependent expectations (∼−7; Fig. 3 (16). Separating these distinctive sulfur isotope systematics, the so-called transitional interval displayed variable, yet muted, Δ³³S values associated with atypically shallow Δ³⁶S/Δ³³S slopes (28).

Fig. 3.

Bulk-derived Δ³⁶S–Δ³³S systematics of chemically isolated sulfides from core KEA-4. (B, Inset) Expanded data condensed around the origin, conforming to the gray box in A. In both plots, color is used to separate samples from the Rooihoogte (black) and the lower (orange) and upper (blue) Timeball Hill formations, respectively. Filled symbols differentiate our data from those presented previously (34) (open symbols). Dashed lines in each plot correspond to the so-called Archean reference array (blue, Δ³⁶S/Δ³³S ≈−0.9 (14, 15, 47), the inferred mixing S-MIF–S-MDF array (green, Δ³⁶S/Δ³³S = −3.2) identified by Poulton et al. (8), and the much steeper slope resulting from biologically mediated mass-dependent processes (gray, Δ³⁶S/Δ³³S ≈−7 (14, 22). Common external 3σ uncertainties are shown for Δ³³S (±0.021‰) and Δ³⁶S (± 0.285‰). SI Appendix, Fig. S4 presents a lithostratigraphic dissection of Inset for clarity.

Although we focused most of our attention toward extending KEA-4’s bulk quadruple sulfur isotope record into the overlying Timeball Hill Formation, six additional samples were analyzed from the S-MIF interval within the Rooihoogte Formation (Figs. 2–4 and Dataset S1). Here, akin to the previously reported enveloping samples (28), these samples also display a large range of Δ³³S values (0.77 to 7.59‰) that, irrespective of their magnitude, conform to the ARA (Fig. 3) (14, 15, 41). By contrast, the newly presented bulk samples (n = 121) display a surprising lack of variability, with average (±1 SD, hereafter 1σ) Δ³³S and Δ³⁶S values of 0.04 ± 0.05 and −0.6 ± 0.33‰, respectively. These observations remain in stark contrast to stratigraphically isolated reports of elevated Δ³³S values (up to ∼3‰) within the Timeball Hill Formation captured by Poulton and colleagues’ lower resolution, and principally triple sulfur isotope, EBA dataset (8), which is separated from our own by perhaps 5 km (Fig. 1 and SI Appendix, Figs. S2–S4). Here, manifest principally as small positive Δ³³S values (<0.3‰), our data broadly resemble those previously reported from the lowermost few meters of the lower Timeball Hill Formation (8, 28). Within the context of the entire dataset, the Timeball Hill data clearly diverge from those from the Rooihoogte-housed S-MIF interval, clustering around the theoretically forecast S-MDF slope (Fig. 3) (16). Interestingly, however, an enlargement around the origin reveals a previously unrecognized spread (Fig. 3), with some samples plotting toward, or even upon, the ARA (Fig. 3B). Lithostratigraphic dissection of this data implies that the incidence of potentially post–Rooihoogte-aged mass-independent behavior decreases up section, with its disappearance prior to the deposition of the upper Timeball Hill Formation (Fig. 3B and SI Appendix, Fig. S2). Again, these observations conflict with the limited Archean-like quadruple sulfur isotope data (n = 5) presented from cores EBA-1 and -2 (8).

Fig. 4.

Bulk- and SIMS-derived Δ³³S–δ³⁴S systematics of sulfides from core KEA-4. (B, Inset) Expanded data condensed around the origin, conforming to the gray box in A. In both plots, bulk and spatially resolved data are differentiated by shape and color. Here, colored circles place the bulk GS-IRMS data within a lithostratigraphic context, while colored diamonds discriminate between samples targeted by SIMS analysis (see legend). The dashed line represents the positive relationship between Δ³³S and δ³⁴S (Δ³³S ≈ 0.9 × δ³⁴S) seen in Neoarchean sulfides, whose origin is thought by the majority^‡ to record mixing between atmospherically derived elemental sulfur (S₈) and sulfate (SO₄^2-) carrying positive and negative Δ³³S values, respectively (23, 47). Around this array, MSR causes lateral movement in δ³⁴S (arrows) via the preferential reduction, conversion, and precipitation of low-δ³⁴S pyrite, concurrently driving the δ³⁴S of seawater sulfate to higher values. The endmembers discussed in the text (ES1 and ES2) are approximately located in red. Precision varies by analytical approach, with larger uncertainties associated with SIMS analysis relative to more traditional GS-IRMS analysis. Adopting the larger of these uncertainties, only within Inset (B) do the SIMS Δ³³S uncertainties become resolvable beyond the datapoints (red vertical error bar).

The δ³⁴S data span a greater range (−29 to +54‰) than their published counterparts (28), capturing a range equivalent to that seen over Earth’s entire history (2). That said, within this dataset, given the general scarcity and stratigraphic isolation of δ³⁴S values exceeding +20‰ (n = 6), the samples that define the upper end of this range could be considered outliers that perhaps reflect a high-order variability that is not fully captured by our sampling resolution (Fig. 2). Stratigraphic consideration of these δ³⁴S data illustrates that the previously documented transition to low δ³⁴S values beginning within the transitional interval was geologically short-lived and, rather than reflecting a broadscale evolution of δ³⁴S values (28), captured the falling limb of a now broadly resolved large negative δ³⁴S excursion that recovers within the lowermost few meters of the Timeball Hill Formation. Excluding a stratigraphically isolated ³⁴S-depleted sample at 535.93 m and four ³⁴S-enriched samples at 548.23, 515.68, 453.30, and 441.20 m, compared to the remainder of the record, the lower Timeball Hill dataset features a relatively restricted range of δ³⁴S values. Here, δ³⁴S values hover around 0 to 10‰ until ∼440 m, whereafter they appear to define a 50-m-thick positive excursion and recovery, which is terminated by a diabase intrusion beneath the overlying Gatsrand Quartzite Member (Fig. 2). Immediately above the Gatsrand Quartzite Member, within the upper Timeball Hill Formation, δ³⁴S values descend from around 0 to −24‰ over ∼50 m, prior to making an ossilatory recovery, before, once again, being truncated by a diabase intrusion (Fig. 2). Thereafter, the δ³⁴S values waver between 0 and 20‰ ahead of a descent toward more negative values in the upper part of our record. Comparison of the δ³⁴S data between our record and those of EBA-1 and EBA-2 shows similar trends, with similarly centered bimodal distributions within the Rooihoogte and lower Timeball Hill formations ceding to an approximately unimodal distribution within the upper Timeball Hill Formation. Given this broad approximation in δ³⁴S data, it is surprising, therefore, that we record vastly discrepant Δ³³S systematics (SI Appendix, Fig. S3).

Core KEA-4 under the Microscope.

In situ sulfur isotope analysis typically reveals striking inter- and intragrain isotopic heterogeneities (24, 29, 32, 42) that are homogenized via conventional fluorination GS-IRMS approaches (28). Consequently, to understand how the atypically large Δ³³S values seen in the bulk SF₆ record are distributed at the microscale, samples were selected for SIMS analysis from two discrete depths (565.70 and 564.74 m) within the Rooihoogte Formation and a single depth (521.51 m) within the overlying lower Timeball Hill Formation (Fig. 2 and SI Appendix, Fig. S5). Discriminating texturally, sample KEA-4 564.74 m was subdivided for SIMS analysis, with subsamples A and B featuring visibly layered and granular pyrites, respectively (SI Appendix, Fig. S5).

Backscattered electron (BSE) images of these SIMS targets show that the pyrites can be loosely described as either euhedral or amorphous agglomerates; however, subtle contrast differences apparent within some of the BSE images hint toward more complex growth/recrystallization histories as should be expected in 2.3-billion-year-old rocks (Dataset S2). BSE images demonstrate that most pyrite grains, irrespective of their stratigraphic level, feature more inclusion-rich interiors and inclusion-poor exteriors, implying at least a common two-stage growth history throughout the succession (Dataset S2). Indeed, similar textures are apparent in core EBA-2 (8, 28), implying that analogous multistage growth histories may be common across the entire Carletonville area. Importantly, in certain instances, pyrites from core KEA-4 have been observed to disturb primary sedimentary laminae, signaling that these pyrites were precipitated, and subsequently overgrown, prior to compaction (28). Pyrite grain size variability was found to be independent of the host lithology (i.e., mudstone–fine siltstone), and the grain size of the examined pyrites (10s to 100s μm) universally exceeded those of the host matrix (28). Given that pyrite is more dense than most common rock-forming minerals, hydraulic equivalence should exclude detrital pyrites within normal offshore sedimentary régimes (28, 43, 44), leaving the pyrite inventory dominated by authigenic pyrites. This inference is reinforced by the absence of observable rounded and/or pitted pyrite grains (or cores) that would be indicative of prolonged transport (42, 44). Interestingly, however, we concede that a brecciated mudstone encountered at 213.7 m within the upper Timeball Hill Formation (Figs. 2–4 and SI Appendix, Fig. S6) presents a curious exception. Here, the entrainment of older pyrites within mudstone clasts provides a hypothetical mechanism whereby S-MIF–bearing pyrites could escape oxidative destruction via shielding during transport beneath an oxygenated atmosphere. In this instance, despite returning mass-dependent quadruple sulfur isotope systematics at the bulk scale (δ³⁴S = 12.45; Δ³³S = 0.04; Δ³⁶S = 0.34), it is important to stress that these data are sample specific, and, thus, the dominance of S-MDF shown in a 5-cm-thick sample taken at 213.7 m in core KEA-4 may not be representative of this widespread and often overlooked facies (45). Equally, as recently argued by Warke et al. (46), lithological control on S-MIF delivery may be more common in glaciogenic or high-energy lithotypes and, as such, may explain some of the large Δ³³S values seen in Rietfontein Member and its reworked equivalent found in the basal Boshoek Formation (8) (SI Appendix).

At a cursory glance, the SIMS dataset broadly echoes the main features identified from the bulk dataset whereby the large Δ³³S values that typify the S-MIF interval are lost in the overlying S-MDF interval as Δ³³S values collapse to 0‰ (0.02 ± 0.06‰, n = 18). Here, bulk SF₆, texture-specific SF₆, and average SIMS-derived Δ³³S values coalesce at 0‰, signaling a representative sampling strategy and, thus, true isotopic homogeneity in this part of the record (Fig. 2 and Dataset S3). Closer scrutiny of the SIMS data from the S-MIF interval (>563.68 m), however, reveals a startling heterogeneity, with SIMS-derived Δ³³S values spanning the full spectrum encompassed by the Carletonville succession (0.34 to 7.4‰). Importantly, each sample showcases different Δ³³S ranges and distributions. For example, each of the three samples from the S-MIF interval features a population of pyrites with Δ³³S values around 1 to 2‰, while only two samples exhibit an additional, less well-constrained population with Δ³³S values exceeding 6‰ (i.e., KEA-4 565.70 m and KEA-4 564.74 m A). When average GS-IRMS– and SIMS-derived values are compared, a varying degree of agreement is observed. For instance, while close agreement between analytical approaches is seen in sample KEA-4 565.70 m, the SIMS datasets from samples KEA-4 564.74 m A and B seem to be biased toward lower Δ³³S values. This analytical mismatch implies that the large Δ³³S values may be more common and volumetrically important than our SIMS data portrays; an analytical oversight particularly apparent in sample KEA-4 564.74 m B where Δ³³S values never exceed 4‰ (Fig. 2).

Grain-scale δ³⁴S analysis reveals large spatial variability throughout (Fig. 2). In the S-MDF interval, the δ³⁴S data are roughly centered on the relevant mean and texture-specific δ³⁴S values, defining a slightly positively skewed population with an average δ³⁴S value of 4.68 ± 2.17‰ (±1σ). In contrast, while δ³⁴S values are generally higher in the S-MIF interval, again, each sample displays different δ³⁴S ranges and distributions. For instance, sample KEA-4 564.74 m A features the most dispersed population, with a δ³⁴S range of 3.74 to 17.74‰ that forms a bi, or possibly tri, modal distribution. The remaining samples define tighter populations (i.e., less dispersed), albeit with outliers, with δ³⁴S values ranging from 10.85 to 16.50‰ in sample KEA-4 564.74 m B and 8.02 to 27.29‰ in sample KEA-4 565.70 m, respectively. Similar discrepancies between the SIMS- and GS-IRMS–derived datasets imply a bias toward higher δ³⁴S values and thus an undersampling of a pyrite phase carrying lower δ³⁴S values within the SIMS-derived dataset.

When the data are considered together in Δ³³S–δ³⁴S three-isotope space (Fig. 4 and SI Appendix, Fig. S3), the samples from the S-MIF interval define a steep array with a negative slope. This slope is defined by an endmember (ES1) with elevated Δ³³S values (∼7‰) and less positive δ³⁴S values (∼5‰) and another (ES2) with muted Δ³³S values (∼1‰) and more positive δ³⁴S values (∼17‰). While it is tempting to relate these systematics to morphology, in practice, this is not easy in core KEA-4, and no unifying model could be applied. Tantalizingly, in sample KEA-4 564.74m B, more euhedral pyrites seem to feature elevated δ³⁴S values (15.1 ± 0.92‰, n = 33) and more subdued Δ³³S values (0.8 ± 0.20‰, n = 33), whereas amorphous pyrites possess lower δ³⁴S values (11.9 ± 0.92‰, n = 9) and higher Δ³³S values (2.1 ± 0.74‰, n = 9). This relationship, however, is not as distinct in the remaining samples and, in fact, may be reversed (e.g., KEA-4 564.74 m A). Given that pyrite genesis is inherently governed by the immediate diagenetic realm, as we go on to discuss, there is no a priori reason why pyrite morphology should easily translate to intergrain sulfur isotope systematics. Perhaps there is no better example to illustrate this oversimplification than Grain 9 from sample KEA-4 564.74 m A (Fig. 5, SI Appendix, Fig. S7, and Dataset S2). Here, this amalgamation of three morphologically and chemically similar pyrite grains chronical a broadly analogous range of Δ³³S variability over 300 μm (Fig. 5 and SI Appendix, Fig. S7) as has been reported from rocks spanning the first two billion years of Earth's history (SI Appendix, Fig. S1)—morphology is clearly not the key discriminator here.

Fig. 5.

Elemental maps (Fe, As, Co, and Ni) of representative pyrite agglomerates selected from the S-MDF (KEA-4 521.51m, Domain no. 1a, Grain 1; A–D) and the S-MIF (KEA-4 564.74m A, Domain no. 4b, Grain 9; E–H) intervals. The pink circles locate the SIMS pits within each WDS map, with the resultant Δ³³S and δ³⁴S data disclosed as the numerator and denominator, respectively. The arrows in H emphasize the subtle siderophile-rich zone discussed within the text. See SI Appendix, Fig. S7 for an annotated interpretation of H.

To understand how such profound isotopic variability becomes transposed and incorporated into the geological record, the chemistry of Grain 9 and an additional control from the S-MDF interval (KEA-4 521.51 m, Domain no. 1a, Grain 1, Dataset S2) were mapped by wavelength-dispersive X-ray spectroscopy (WDS; Methods). Besides the core–rim textural differences revealed via SEM-derived BSE imagery (Dataset S2), the resulting WDS maps unveiled complex and important growth histories that would have otherwise remained opaque (Fig. 5 and SI Appendix, Fig. S7). Focusing on Grain 9 obtained from within the S-MIF interval, an irregular embayed growth zone enriched in Co and Ni, perhaps reflecting the partial dissolution of the earliest generation of pyrite, was found to separate two generations of chemically analogous and otherwise Co- and Ni-impoverished pyrites (Fig. 5 E–H and SI Appendix, Fig. S7). The recognition of this subtle Co- and Ni-rich aureole is of fundamental importance because it acts as an intragrain stratigraphic marker, providing temporal context for the observed subgrain sulfur isotope variability (Fig. 5E and SI Appendix, Fig. S7). In detail, the two SIMS analyses outside of the Co- and Ni-rich rim returned atypically large Δ³³S values centered around 7‰ (Domain 4b nos. 3 and 4, Dataset S2), while the three analyses appearing within the rim’s interior were associated with much lower magnitude Δ³³S values (Domain 4b nos. 1 and 2, 6, Δ³³S = 0.35 to 0.99‰; Dataset S2). A similar spatial separation is mirrored within the δ³⁴S data, with larger positive δ³⁴S values (∼16 to 17‰) confined to the inside of the Co- and Ni-rich rim, while lower δ³⁴S (∼4‰) values are confined to its exterior. The single analysis that appeared to straddle the siderophile-defined rim (Domain 4b no. 5, Dataset S2) features intermediate Δ³³S and δ³⁴S values that we attribute to roughly equal mixing between the pre- and post-rim endmembers (Fig. 5E and SI Appendix, Fig. S7). Excluding the analysis associated with intermediary sulfur isotope systematics as an analytically induced mixing artifact (42), we again identify two isotopically distinct end members: (ES1) pyrites located within, and therefore predating, the metal-rich rim that possess muted Δ³³S (<1‰) and more positive δ³⁴S values (∼17‰) and (ES2) pyrites postdating the Co- and Ni-rich rim that feature elevated Δ³³S (∼7‰) values coincident with less positive δ³⁴S values (∼4‰). Within the wider SIMS dataset from the S-MIF interval, it is these endmembers that define the steep negative Δ³³S–δ³⁴S arrays apparent in Fig. 4, thus verifying the extension of these observations to the wider dataset.

Discussion

Two Coexisting Isotopically Distinct Sulfur Pools Fingerprint Anoxic Photochemistry.

Grain 9, from 565.70-m core-depth within the S-MIF interval, shows unprecedented Δ³³S variability (Fig. 5), recording a similar spread in Δ³³S values as encountered over the entirety of Earth's history (SI Appendix, Fig. S1). Surprisingly, after mapping Grain 9, we noticed that analyses returning elevated Δ³³S values and more subdued δ³⁴S values (ES1) were separated from those with apposing sulfur isotope systematics (ES2) by a subtle embayed dissolution/growth zone enriched in Co and Ni (Figs. 4 and 5 and SI Appendix, Fig. S7). This observation implies that the elevated Δ³³S values were entombed within the pyrite record relatively late compared to the more inclusion-rich core.

Given that Δ^3×S values serve as quasi-conservative tracers with the Earth’s exogenic sulfur cycle (i.e., they cannot be created or destroyed, only diluted), the restriction of large magnitude Δ³³S values toward the periphery of Grain 9 can be hypothetically rationalized by the postdepositional ingress of photolytic sulfur remobilized from juxtaposed Archean-aged sediments. That said, it is imperative to note that fewer than 2% of minor sulfur isotope measurements made on appropriately aged materials return Δ³³S values that exceed those seen in the Rooihoogte Formation (i.e., 7.6‰; Fig. 2 and SI Appendix, Figs. S1, S4, S7 and S9), and, those that do, are separated from the Rooihoogte Formation by hundreds of kilometers and some 200 million years (24, 41). Consequently, invoking late-stage sulfur ingress not only requires a mechanism capable of selectively remobilizing sulfur sourced from the most extreme positive tail of the geological Δ³³S record (SI Appendix, Fig. S1) but, more locally, commands an unidentified source of sulfur with Δ³³S values of sufficient size to dominate the bulk data obtained from the S-MIF interval (Fig. 2). Even if we disregard these improbable corollaries, we consider an explanation reliant on late-stage sulfur ingress incongruous with the stratigraphic δ³⁴S, Δ^3×S, and Δ³⁶S/Δ³³S heterogeneity captured within the wider Carletonville minor sulfur isotope record (Figs. 2 and 3) (8, 28), which would presumably be diminished/erased via wholesale late-stage sulfur addition. This viewpoint is reinforced at the grain scale, in which SIMS analyses from the Rooihoogte Formation capture a remarkable range of Δ³³S values whose distributions appear to be highly sample specific yet disappear as the bulk Δ³³S values collapse to zero within the overlying Timeball Hill Formation (Fig. 2). Finally, besides the subtle intragrain siderophile-rich aureole, the trace element (As, Ni, and Co) systematics of the pre- and post-rim pyrites in Grain 9 are remarkably similar. This observation is in strong conflict with the injection of an externally sourced fluid, which, reasonably, would be expected to be chemically distinct, culminating in the growth of chemically distinct pyrites and metal monosulfides. Indeed, the infrequent detection of acid-volatile sulfide throughout the examined succession and, where measurable, its mass-dependent sulfur isotope systematics provide strong empirical evidence against hydrothermal sulfur remobilization and retention (Methods and Dataset S1). Moreover, the lack of any strong correlation between Δ³³S (or δ³⁴S) and WDS-derived trace-metal concentrations (SI Appendix, Fig. S8 and Dataset S4) bolster this stance and, when combined with the preceding arguments, effectively preclude postdepositional sulfur ingress as a viable explanation of the observed spatial sulfur isotope heterogeneity.

Eliminating postdepositional explanations, a syn-depositional model must be sought to explain the spatial Δ³³S variability observed within Grain 9 (Fig. 5E) and, via extrapolation, the entire SIMS dataset (Fig. 4). Here, drawing conceptually from the ideas developed by Farquhar et al. (24), we argue for the coexistence of two isotopically distinct diagenetically active sulfur pools. Although alternate views exist (25, 47–50), against an oxygen-free backdrop, most workers envisage the operation of two Archean atmospheric exit channels, supplying elemental sulfur (S₈) and sulfate (SO₄^2-) to the Earth’s surficial sulfur cycle with positive and negative Δ³³S values, respectively^‡ (12, 13, 41, 51). Indeed, it is the relative proportions of each of these sulfur sources that is thought to underpin the Δ³³S–δ³⁴S array that typifies Neoarchean-aged sulfides (Δ³³S ≈ 0.9 × δ³⁴S (47). Consequently, the divergence from these purely photochemical expectations toward a steep linear relationship constrained by ES1 (↑Δ³³S and↓ δ³⁴S) and ES2 (↓Δ³³S and ↑δ³⁴S; Fig. 4) within our dataset is curious and presents the opportunity to track pyrite formation 2.3 billion years ago.

The extreme isotopic heterogeneity juxtaposed at the micrometer scale (Fig. 5E) requires that the sulfur sources for ES1- and ES2-type pyrites were unable to undergo full isotopic exchange and managed to evade homogenization during early diagenesis. Pyrite formation is a complex process that can be conceptually reduced to two steps: namely, the conversion of aqueous sulfide to metastable iron monosulfides (FeS) and its conversion to pyrite (52, 53). While the latter involves numerous complex pathways, broadly speaking, the process is simplified within the literature to the H₂S and the polysulfide pathways (53, 54). Against an oxygen-free backdrop, polysulfides would have perhaps formed via the reaction between microbial sulfate reduction (MSR)-derived sulfide and atmospherically sourced S₈. Accordingly, the Δ³³S values of pyrites produced via the polysulfide pathway should reflect the relative proportion of sulfate-derived sulfur to S₈-derived sulfur (24).

Negative Δ³³S values are conspicuously absent from our dataset (Fig. 4), which would be typically invoked to fingerprint derivation from a photolytic sulfate source (17, 22, 24). Nonetheless, given the expectation that sulfate should be available within the porewaters during early diagenesis, we hypothesize that the initially formed ES2-type pyrites acquired the bulk of their sulfur via MSR of porewater sulfate, with a potentially small contribution from elemental sulfur resulting in the intermediate Δ³³S values we observe. By contrast, we propose the later-stage pyrites, featuring atypically large Δ³³S values, derived their sulfur principally from a photolytic S₈ source as MSR-derived sulfide became scarcer; a notion supported by the relatively restricted range of δ³⁴S values displayed by ES2 pyrites housed within these relatively total organic carbon- and Fe-replete rocks (8, 40) that, in turn, imply the operation of MSR under generally sulfate-limited conditions (Fig. 4). Indeed, similar rationalizations have been invoked to explain the small-scale Δ³³S variability in the 2.7-billion-year-old Joy Lake sequence (55) and the ∼2.65 to 2.5-billion-year-old Campbellrand–Malmani carbonate platform (24), demonstrating the existence of multiple diagenetically active and isotopically distinct sulfur pools is not a unique feature of our study area and ought to be considered more widely.

Searching for the CME.

The prevalence of muted Δ³³S values within the Paleoproterozoic minor sulfur isotope record (29–33, 42, 56) has been proposed to be a consequence of the oxidative weathering of continentally housed S-MIF–bearing sulfides fueled by a rise in atmospheric oxygen in proximity to the Archean–Proterozoic boundary (24–27). If true, such a memory effect serves to decouple the sedimentary S-MIF record from contemporaneous atmospheric chemistry (3, 32, 38, 49). On this basis, perhaps unjustly considering the magnitude of the Δ³³S values (Figs. 2 and 3), the atmospheric significance of the observations made by Luo et al. (28) were questioned via the recognition of sub-2‰ Δ^3×S values with Archean-like Δ³⁶S/Δ³³S ratios preserved within the Australian Kazput Formation, purportedly deposited well after 2.3 Ga (32, 33). This apparent diachronous disappearance of S-MIF was used to argue for regional-scale expressions of the CME, resulting from a rise in atmospheric oxygen before 2.45 Ga (32, 33). While we remain unconvinced that the clearly facies-controlled ephemeral decreases in δ³⁴S and Δ³³S values seen within the siltstones of the upper Boolgeeda Iron Formation record an important oxidation event (32), the existence of the CME outside of Western Australia remains largely a theoretical construct (39). As such, we look to our expanded bulk and grain-scale minor sulfur isotope records for evidence of such an effect within the Transvaal Basin (Figs. 2–5).

The complete disassociation of the Carletonville minor sulfur isotope record from atmospheric chemistry via the CME is contested by the recollection of the computational weathering experiments conducted by Reinhard and colleagues (39). Here, by applying geologically reasonable boundary conditions, Reinhard et al. placed an extreme upper limit of ∼3‰ on the weathering-derived Δ³³S signal that could be conveyed to a hypothetical global seawater sulfate inventory (SI Appendix, Fig. S1). Given that the S-MIF interval in the Carletonville area features Δ³³S values encroaching on 8‰ (Fig. 2) (28), we can effectively preclude crustal inheritance via a crustally adulterated seawater sulfate reservoir as the primary control on the bulk isotope systematics. In fact, our grain-scale fingerprinting of the S₈ photolytic endmember strongly argues for more direct photochemical modulation (28). Candidly, there is no known way of divorcing the high magnitude Δ^3×S values seen at the bulk, and now at the grain, scale within the Rooihoogte Formation from active photochemistry (Figs. 2 and 3). Accordingly, we stress that these data demand an oxygen-free atmosphere and should be considered a robust marker of such.

Moving forward, understanding how the Rooihoogte minor sulfur isotope record is dominated by photolytic sulfur (8, 28) while other successions have seemingly been compromised remains crucial to decoding the meaning and utility of the sedimentary S-MIF record. Forgoing the large magnitude Δ^3×S values seen in the S-MIF interval (Figs. 2–5), the CME remains a largely unexplored concern, obstructing the interpretation of the wider Paleoproterozoic minor sulfur isotope record (29, 30, 32, 46). Immediately above the proposed transitional interval, Δ^3×S values collapse to near-zero coincident with a transition toward steeper Δ³⁶S/Δ³³S slopes (28). Because of the restricted stratigraphic range of the quadruple sulfur isotope data presented by Luo et al. (28), compounded by the presence of large stratigraphic gaps separating the discrete cores analyzed by Philippot et al. (32), we consider it extremely unlikely that the original records (28, 32, 33) would have displayed much overlap. Consequently, to make a fair comparison and search for the CME above the loss of S-MIF in the Carletonville area, we extended the bulk SF₆ record into the upper Timeball Hill Formation (SI Appendix, Figs. S2–S4). Despite these efforts, however, we failed to capture any Δ³³S values outside of the conservative threshold of |0.3‰| that has been used to discriminate between S-MIF and S-MDF (8) (Figs. 2 and 3 and SI Appendix, Fig. S2). Grain-scale examination of a sample from 521.51 m is equally monotonous, with SIMS data defining a tight population of Δ³³S values centered at 0‰ (Figs. 2 and 5). Constrained by U–Pb ages of two closely spaced microtuffs from the upper Timeball Hill Formation (57), these data encompass upwards of 50 million years of sedimentation, extending the Carletonville quadruple sulfur isotope record to ∼2.26 Ga (57). Within this extended framework, the observed isotopic monotony demonstrates that, at least in core KEA-4, there is no strong evidence for the reappearance of S-MIF within the resolution of our dataset (Figs. 2–5 and SI Appendix, Figs. S2–S4). Instead, the apparent predominance of largely mass-dependent sulfur isotope behavior within core KEA-4 after 2.3 Ga (28) remains in stark contrast to the sulfur isotope systematics of the supposedly crustally influenced Australian Turee Creek succession (32, 33, 42) and, indeed, the computational forecasts of 10- to 100-million-year survival times of S-MIF within the Earth’s exogenic sulfur cycle from which these claims were grounded (39).

At the most simple level, the effectively instantaneous loss of S-MIF in the Carletonville area of the Transvaal Basin (Fig. 2) can be reconciled with its persistence within the Turee Creek Group by invoking either 1) basin-controlled heterogeneities in the Δ³³S values carried by seawater sulfate (32, 33, 36) or 2) that the ages linking the two records are misinterpreted (35, 37). The Turee Creek Group is linked to the studied succession by a Re–Os isochron age obtained from the glaciogenic Meteorite Bore Member (32) and supporting U–Pb detrital zircon ages (34). Rejecting the depositional significance of these ages, Bekker et al. (35, 37) recently presented a series of contested stratigraphic arguments (36, 37) concluding that the Turee Creek succession was much older (i.e., 2.45 to 2.42 Ga) than previously envisaged (i.e., 2.45–2.2 Ga) and hence predates the examined succession (Fig. 2 and SI Appendix, Fig. S9). While we concede that Bekker and colleagues’ (35) reinterpretation is more convenient, resulting in quadruple sulfur isotope systematics that are more reminiscent of those reported from older rocks (SI Appendix, Fig. S9), it is pertinent to recall the dichotomy we identify within proximal and indisputably age-equivalent records from within the same basin (SI Appendix, Figs. S2 and S3). While Archean-aged catchments apparently fail to yield nonzero Δ³³S values under contemporary boundary conditions (58), modern catchments do, in fact, yield sulfur isotope heterogeneities (59). Consequently, it remains plausible that heterogeneities might have been communicated to the presumably much smaller early Paleoproterozoic seawater sulfate reservoir (32, 33), culminating in basinal heterogeneities that were perhaps amplified within the Turee Creek Basin. Clearly, further geochronological constrains are needed to discriminate between these competing explanations (32, 33, 35–37); however, for now, we strongly caution against the use of sulfur isotope chemostratigraphy to construct, or test, hypothesized correlation schemes.

Returning to the Transvaal (Fig. 2), we see no evidence to support a long-lived and/or pronounced CME above the loss of S-MIF in the Carletonville quadruple sulfur isotope record. That said, within our record, the samples plotting between the expected S-MIF and S-MDF Δ³⁶S/Δ³³S arrays (SI Appendix, Fig. S4) may record subtle and short-lived expressions of crustal recycling. Furthermore, the muted Δ³³S values captured by ES2-type pyrites within our SIMS dataset may signal the influence of the CME beneath an anoxic atmosphere capable of S-MIF export. While the full exploration of these hypotheses awaits detailed isotopic and elemental grain-scale analyses, the notion of prolonged low-level sulfide oxidation is supported by recent pO₂ estimates derived from the Archean–Paleoproterozoic increase in shale-housed molybdenum abundances and δ^98/95Mo values (66).

A Dynamic Route to Atmospheric Oxygenation?

Concerning the timing and trajectory of planetary oxygenation and its role within the evolution of the climate system, contrasting opinions abound (5, 28, 30, 32, 33, 35). Initially, the term GOE was coined to describe the broad evolution from a reducing atmospheric state to a more oxidizing equivalent in which O₂ rose above ultra-trace levels, occurring on hundred-million-year timescales (4). Subsequently, however, perhaps incited by its unintended linguistic connotations, the GOE has been publicized by some as a singular event (27, 28, 30), while others perceive a multistage or dynamic transition occurring on a range of timescales (5, 8).

Alongside the blueprints of planetary oxygenation, early Paleoproterozoic sedimentary successions contain evidence for up to four glacial episodes between ∼2.45 and 2.22 Ga (5, 7, 11). Recording the oldest and perhaps best known of these, the Makganyene Formation, housed within the Griqualand West Basin, comprises a series of tropical glaciomarine diamictites that are interpreted to reflect the oldest known Snowball Earth event (7). Recent U–Pb dating of cross-cutting mafic volcanics genetically related to the Ongeluk Formation constrains this glacial episode to before 2.43 Ga, making it potentially correlative with glacial episodes preserved globally (5). Indeed, in Fennoscandia, Warke et al. (31) documented a loss of S-MIF prior to 2,434 ± 6.6 Ma, reporting negative Δ³³S values with Δ³⁶S/Δ³³S systematics that statistically resemble the ARA within the Seidorechka Sedimentary Formation that surrender to near-zero Δ³³S values that define a steep S-MDF–like Δ³⁶S/Δ³³S slope in the overlying volcanically influenced Polisarka Sedimentary Formation. Placing this Fennoscandian shift in quadruple sulfur isotope systematics within the relevant chronostratigraphic frameworks, these authors presented a case for one broadly synchronous S-MIF to S-MDF transition, arguing that the GOE preceded a Paleoproterozoic Snowball Earth glaciation (31). Although this is geochronologically permissible (31), numerous stratigraphic arguments invalidate the implied correlation between the Fennoscandian loss of S-MIF and its supposed equivalent within the Rooihoogte Formation (Figs. 2 to 5 and SI Appendix, Fig. S7) (5, 28, 35, 41, 61). Consequently, excluding an unrecognized volcanically derived overprint, these Fennoscandian data combined with those presented herein demand the diachronous loss of S-MIF. Put differently, these records require at least two discrete intervals whereby S-MIF production was terminated as atmospheric oxygen rose above 10⁻⁵ PAL (13). In turn, these observations imply a dynamic route to planetary oxygenation (5, 8), precluding conceptual models reliant on a unidirectional evolutionary driver of planetary oxygenation (i.e., the emergence of oxygenic photosynthesis) (62). Rather, the apparent oscillatory nature of atmospheric oxygen during the early Paleoproterozoic is better reconciled with an Earth system vulnerable to tipping points encountered through biological and/or tectonic feedbacks (5, 8).

Compiling available redox indicators from the Kaapvaal-housed Griqualand West and Transvaal basins, Gumsley et al. (5) envisaged at least three broad oscillations in atmospheric pO₂ (SI Appendix, Fig. S9). In their model, the authors foretold a short-lived rise in pO₂ in the wake of the ∼2.43 Ga Makganyene-aged Snowball Earth, which, following from the previous discussion, has since been substantiated by the apparent Fennoscandian loss of S-MIF in the prelude to the Paleoproterozoic’s first glacial episode (31). The second and third oxygenation episodes pictured by Gumsley et al. (5) are constrained by the loss of relatively high magnitude Δ^3×S values and the shift from Δ³⁶S/Δ³³S slopes that populate the ARA toward those that conform to theoretical MDF predictions within the lower portions of the Duitschland and Rooihoogte formations, respectively (27, 28, 30). While the paucity of high-precision age constraints currently precludes unequivocal distinction between the conflicting stratigraphic arguments (35, 45, 46, 61) that underpin the separation of these hypothesized oxygenation episodes, in their absence, we can confidently assert that the Rooihoogte-housed loss of S-MIF (Fig. 2 and SI Appendix, Figs. S2 and S3) represents the youngest texturally constrained evidence for an oxygen-free atmosphere some 2.3 billion years ago (63). Moreover, its separation from the apparent Fennoscandian loss of S-MIF by perhaps 100 million years supports a dynamic path toward a fully oxygenated atmosphere punctuated by rises and falls in atmospheric pO₂ above and below the 10⁻⁵ PAL (13) threshold necessary to attenuate atmospheric S-MIF export (5, 8).

More recently, Poulton and colleagues (8) have reported stratigraphically isolated Δ³³S values encroaching on 3‰, which they argue record repeated returns to a reduced atmospheric state capable of S-MIF production beyond 2.3 Ga. Within our quadruple sulfur isotope dataset, despite our higher sample resolution, we fail to capture this variability in a core separated by less than 5 km (Figs. 1–5 and SI Appendix, Figs. S2–S4). This kilometer-scale discrepancy has two provisional explanations: 1) the dichotomy between the records speaks to spatially variable S-MIF delivery within the Transvaal Basin or 2) extremely rapid atmospheric shifts that are not captured within our higher resolution record. Discrimination between these two competing explanations requires targeted grain-scale sulfur isotope analysis to texturally fingerprint the vector, and therefore significance, of these clearly rare ³³S enrichments seen beyond 2.3 Ga. For now, however, these imagined younger oscillations in atmospheric oxygen (8) appear to have operated at a higher temporal frequency than those envisaged by Gumsley et al. (5), implicating different drivers that are more difficult to reconcile with rapid and repeated relapses within the global climate system. Mechanistic uncertainties aside, the apparent oscillatory nature of S-MIF within the geological minor sulfur isotope record suggests that the disappearance of S-MIF would not make a definitive chemostratigraphic marker nor can it be readily employed to define the GOE itself (32), which, upon appropriate investigation, may be subdivisible into a series of oxygenation episodes.

Conclusions and Outlook.

In search of supporting evidence to substantiate claims of post-2.3 Ga oxygen dynamics, we produced a high-resolution quadruple sulfur isotope record extending up into the upper Timeball Hill Formation yet failed to capture Δ³³S values that exceed 0.3‰. By contrast, within the S-MIF interval of the Rooihoogte Formation, SIMS analyses disclose pronounced inter- and intrasample Δ³³S variability, featuring some of the most prominent Δ³³S values ever reported from the geological record. The preservation and differential stratigraphic distribution of these elevated Δ³³S values effectively precludes postdepositional overprinting while implicating complex incorporation of isotopically distinct sulfur pools into pyrite. Importantly, given the preponderance of small magnitude Δ³³S values within the geological minor sulfur isotope record, the larger magnitude Δ³³S values observed in the Rooihoogte Formation cannot be reconciled with inheritance from crustally adulterated seawater (39) and, instead, are most parsimoniously explained as primary atmospheric derivatives. The presence of large-magnitude Δ³³S values in association with Archean-like Δ³⁶S–Δ³³S slopes and their subsequent disappearance within the Rooihoogte Formation provide direct evidence for the accumulation of atmospheric oxygen above 10⁻⁵ PAL (13) by ∼2.3 Ga (63). Persistently low Δ³³S values coupled with generally mass-dependent Δ³⁶S/Δ³³S systematics within the Timeball Hill Formation deemphasize the wider significance of the CME within the Transvaal Basin as it was originally proposed (39). That said, a more muted influence may have been identified and awaits verification. Chronological and stratigraphic arguments (5, 35, 46, 61) separate the S-MIF to S-MDF transition documented herein from a supposed equivalent in the Imandra–Varzuga Greenstone Belt, northwest Russia (31), by in excess of 100 million years. This apparent repeated loss of S-MIF at ∼2.4 and ∼2.3 Ga lends credence to models that invoke feedback-driven dynamics in the prelude to irreversible atmospheric oxygenation (5). Discrepancies between the Transvaal-housed minor sulfur isotope records separated by a few kilometers, however, highlights difficulties in reconstructing the narrative of Earth’s oxygenation and, at present, offers little concrete support for inferred oxygen dynamics beyond 2.3 Ga.

Methods

Bulk quadruple sulfur isotope data were generated at the Massachusetts Institute of Technology via conventional chemical isolation, allowing the capture of sulfide-derived sulfur as Ag₂S (8, 28, 64) (SI Appendix). Here, fluorination and subsequent purification allow precise quadruple sulfur isotope determination by GS-IRMS, yielding respective 2σ δ³⁴S, Δ³³S, and Δ³⁶S uncertainties of 0.26, 0.014, and 0.19‰ (28). In situ triple sulfur isotope measurements were conducted using the CAMECA IMS 1280 housed at the Wisconsin Secondary Ion Mass Spectrometer Laboratory (WiscSIMS), University of Wisconsin–Madison. Detailed descriptions of the instrument and the employed measurement protocol are provided elsewhere (29, 42, 65–67) and are summarized within SI Appendix for completion. At WiscSIMS, calibration was achieved using UWPy-1, yielding an average 2σ reproducibility of 0.08 and 0.31‰ for Δ³³S and δ³⁴S, respectively. Irrespective of the approach, following convention (2, 17), both bulk and grain-scale sulfur isotope data are reported in delta (δ) notation, reflecting permil (‰) deviations of the least abundant isotope (^33,34,36S) normalized to its most abundant counterpart (³²S), relative to the same ratio in the international reference standard, Vienna Canyon Diablo Troilite:

$${\mathrm{\delta }}^{\mathrm{3X}}\mathrm{S=}\left[{\left({}^{\mathrm{3X}}\mathrm{S}{\mathrm{/}}^{\mathrm{32}}\mathrm{S}\right)}_{\mathrm{sample}}\mathrm{/}{\left({}^{\mathrm{3X}}\mathrm{S}{\mathrm{/}}^{\mathrm{32}}\mathrm{S}\right)}_{\mathrm{V-CDT}}\mathrm{–1}\right]*\mathrm{1000}.$$ [1]

Most processes fractionate S isotopes mass dependently, whereby δ³³S ≈0.515 × δ³⁴S and δ³⁶S ≈1.91 × δ³⁴S. Departure from this mass-dependent behavior, termed MIF, is expressed in capital-delta (Δ) notation in which

$${\mathrm{\Delta }}^{\mathrm{33}}\mathrm{S=1000}*\left[\ln \left({\mathrm{\delta }}^{\mathrm{33}}\mathrm{S/1000\hspace{0.17em}+\hspace{0.17em}1}\right)\mathrm{–0}\mathrm{.515}*\ln \left({\mathrm{\delta }}^{\mathrm{34}}\mathrm{S/1000\hspace{0.17em}+\hspace{0.17em}1}\right)\right],$$ [2]

and

$${\mathrm{\Delta }}^{\mathrm{36}}\mathrm{S=1000}*\left[\ln \left({\mathrm{\delta }}^{\mathrm{36}}\mathrm{S/1000\hspace{0.17em}+\hspace{0.17em}1}\right)\mathrm{–1}\mathrm{.91}*\ln \left({\mathrm{\delta }}^{\mathrm{34}}\mathrm{S/1000\hspace{0.17em}+\hspace{0.17em}1}\right)\right].$$ [3]

Finally, the in situ elemental composition of pyrites was determined using a JEOL JXA-8100 electron probe microanalyzer equipped with four wavelength-dispersive spectrometers (WDS) housed within the State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences. The respective 1σ precision associated with major (i.e., Fe and S) and trace (i.e., As, Cr, Co, and Ni) metal(oid) determinations was found to be better than 0.4 and 10% when elemental concentrations exceeded 1,000 ppm. As before, instrumental conditions and approaches are outlined within the SI Appendix.

Data Availability

All study data are included in the article and/or supporting information.