Significance
An influential idea in neuroscience is that neural circuits do not only passively process sensory information but rather actively compare them with predictions thereof. A core element of this comparison is prediction-error neurons, the activity of which only changes upon mismatches between actual and predicted sensory stimuli. While it has been shown that these prediction-error neurons come in different variants, it is largely unresolved how they are simultaneously formed and shaped by highly interconnected neural networks. By using a computational model, we study the circuit-level mechanisms that give rise to different variants of prediction-error neurons. Our results shed light on the formation, refinement, and robustness of prediction-error circuits, an important step toward a better understanding of predictive processing.
Keywords: predictive processing, inhibitory interneurons, prediction-error neurons, homeostatic plasticity, sensory coding
Abstract
Predictable sensory stimuli do not evoke significant responses in a subset of cortical excitatory neurons. Some of those neurons, however, change their activity upon mismatches between actual and predicted stimuli. Different variants of these prediction-error neurons exist, and they differ in their responses to unexpected sensory stimuli. However, it is unclear how these variants can develop and coexist in the same recurrent network and how they are simultaneously shaped by the astonishing diversity of inhibitory interneurons. Here, we study these questions in a computational network model with three types of inhibitory interneurons. We find that balancing excitation and inhibition in multiple pathways gives rise to heterogeneous prediction-error circuits. Dependent on the network’s initial connectivity and distribution of actual and predicted sensory inputs, these circuits can form different variants of prediction-error neurons that are robust to network perturbations and generalize to stimuli not seen during learning. These variants can be learned simultaneously via homeostatic inhibitory plasticity with low baseline firing rates. Finally, we demonstrate that prediction-error neurons can support biased perception, we illustrate a number of functional implications, and we discuss testable predictions.
The theory of predictive processing posits that neural networks strive to predict sensory inputs and use prediction errors (PEs) to constantly refine an inner model of the world (1–3). Neural hallmarks of PEs have been found widely. Dopaminergic neurons in the basal ganglia and striatum encode reward PEs (4). Some neurons in layer 2/3 of the rodent primary visual cortex (V1) (5, 6) or neurons in the telencephalic areas of adult zebrafish (7) are driven by mismatches between actual and predicted visual consequences of motor commands. Similarly, a subset of cortical neurons responds to auditory feedback perturbations during vocalization (8, 9), and some excitatory cells in mouse barrel cortex are sensitive to abrupt mismatches of tactile flow and the animal’s running speed (10). However, those neurons are embedded in complex circuits that exhibit a rich diversity of cell types interacting in many ways (11–15). It is mostly unresolved whether and how this diversity collaboratively shapes, processes, and refines PEs.
Mismatches may occur in two variants; sensory inputs can be overpredicted (OP) or underpredicted (UP), depending on whether the prediction is larger or smaller than the sensory stimulus, respectively. While dopaminergic neurons signal mismatches bidirectionally (4), this may be impossible for neurons with very low spontaneous firing rates as, for instance, cortical neurons in layer 2/3 of V1 (16, 17) because negative deviations would be bounded from below. Thus, it has been suggested that cortical PE neurons come in two flavors (1, 3); negative prediction-error (nPE) neurons only increase their activity relative to baseline (BL) when a sensory stimulus is smaller than predicted, while positive prediction-error (pPE) neurons only increase activity when a sensory stimulus is larger than predicted.
Computing PEs, no matter whether negative or positive mismatches, requires inhibition (3). Despite being outnumbered by excitatory neurons, inhibitory interneurons shape cortical computations in many ways (11, 14, 18–22). This rich repertoire of interneuron function is accompanied by great diversity in their morphology, physiology, connectivity patterns, and synaptic properties (11, 14). In a computational model of layer 2/3 of rodent V1, it has been shown that the presence of nPE neurons imposes constraints on the interneuron network in the form of a balance of excitation and inhibition (E/I balance) (23). However, it is not resolved whether the coexistence of nPE and pPE neurons imposes further requirements on the interneuron circuit they are embedded in. Moreover, the formation of mismatch neurons in layer 2/3 of V1 relies on normal visuomotor coupling during development (6). This suggests that PE neurons are experience-dependent, raising the question of how networks self-organize to give rise to them. While it has been shown that separate nPE and pPE circuits can be learned by means of homoestatic inhibitory plasticity (23), it is not resolved if and how this generalizes to networks with both nPE and pPE neurons.
To elucidate the circuit-level mechanisms that underlie the parallel formation of both PE neuron types, we design a rate-based computational model with excitatory neurons and three types of inhibitory neurons. We first show that in a simplified mean-field network, nPE and pPE neurons can coexist when an E/I balance is established. Moreover, the interneuron circuit must comprise two distinct sources of somatic inhibition. The dendritic inhibition must be driven by feed-forward bottom-up signals. We demonstrate that depending on the distribution of actual and predicted sensory inputs onto the interneurons, the mismatch response of PE neurons is either the result of an excess of excitation at the dendrites or the suppression of somatic inhibition. Once established, these PE neurons are robust to moderate network perturbations. We then simulate a heterogeneous network model and show that both nPE and pPE neurons can be learned simultaneously by inhibitory homeostatic plasticity when the network is exposed to predicted sensory stimuli and the excitatory neurons exhibit low BL firing rates. When synaptic plasticity establishes a balance of excitatory and inhibitory inputs, the PE neurons are robust and generalize to stimuli not seen during learning. Furthermore, we investigate how the ratio of nPE and pPE neurons depends on the predictability of sensory stimuli during learning, the distribution of actual and predicted sensory inputs, and the initial connectivity between neurons. Finally, we connect a heterogeneous PE circuit with an attractor network and show that PE neurons can support biased perception (24–29). By means of the example of a contraction bias, we illustrate a number of functional implications for PE neurons. We show that they can act as an internal cue switching the network between attractors, may underpin generalization across distinct stimuli statistics, and can support faster learning.
Results
Given that neural circuits contain an astonishing variety of neuron types and cell type–specific connections (11, 13, 14), we wondered under which constraints both nPE and pPE neurons can develop simultaneously in the same recurrent network. To address this question, we studied a rate-based network model with excitatory pyramidal cells (PCs) and inhibitory parvalbumin-expressing (PV), somatostatin-expressing (SOM), and vasoactive intestinal peptide–expressing (VIP) interneurons (Fig. 1A). The relative distribution of neuron types, their connection probabilities, and strengths are motivated by electrophysiological studies (e.g., refs. 12, 13, and 30–35) (SI Appendix has details). While all inhibitory neurons are modeled as point neurons (36), the excitatory neurons are simulated as two coupled point compartments, representing the soma and the dendrites, respectively.
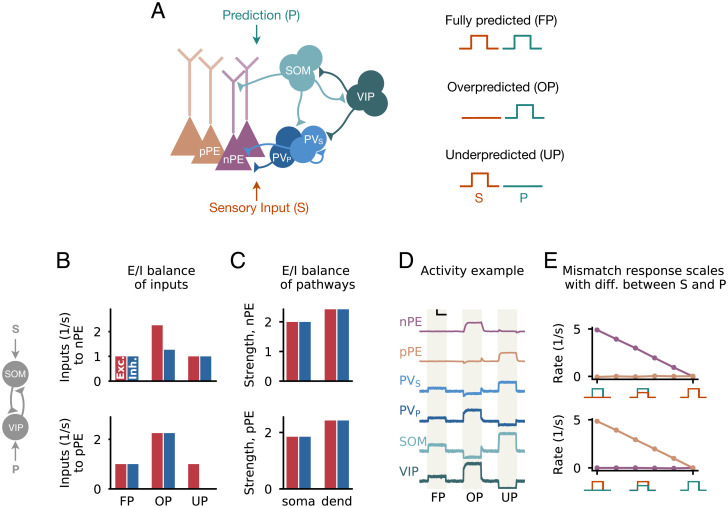
Fig. 1.
Multipathway E/I balance in nPE and pPE neurons. (A, Left) Network model with excitatory PCs and inhibitory PV, SOM, and VIP neurons. Connections from PCs are not shown for the sake of clarity. In a PE circuit, PCs act as either nPE or pPE neurons. The somatic compartment of PCs and half of the PV neurons (PV) receive the actual sensory input, while the dendritic compartment of PCs and the remaining PV neurons (PV) receive the predicted sensory input. SOM and VIP neurons receive either actual or predicted sensory input. (A, Right) Sensory stimuli can be FP, OP, or UP. (B–E) Mean-field network derived from A with the SOM neuron receiving the actual sensory input and the VIP neuron receiving the predicted sensory stimulus. (B) In a PE circuit, the excitatory (red) and inhibitory (blue) inputs are balanced for FP sensory stimuli for both nPE and pPE neurons. This balance is preserved for UP stimuli (nPE neurons; Upper) or OP stimuli (pPE neurons; Lower). Stimulus strength is . Shown are the inputs without the excitatory background input that defines the BL firing rate. (C) Both nPE (Upper) and pPE (Lower) neurons exhibit balanced pathways onto both soma and dendrites. (D) Example activity of all neuron types for FP as well as OP and UP stimuli for a network parameterized to establish an E/I balance in the pathways. The vertical black bar denotes ; the horizontal black bar denotes 500 ms. (E) Mismatch responses for nPE (Upper) and pPE (Lower) neurons scale with the difference between actual and predicted sensory inputs.
All neurons receive an excitatory background input to ensure reasonable BL firing rates in the absence of any sensory stimulation (“BL phase”). In addition, we stimulated the neurons with time-varying inputs that represent actual and predicted sensory stimuli. It is known that excitatory neurons receive feed forward, sensory inputs at their basal dendrites and perisomatic region and feedback projections from higher-order cortical areas at their apical dendrites (37, 38). These feedback projections are assumed to carry information about expectations, beliefs, or predictions (37, 39, 40) and mediate a broad range of functional roles (41, 42). While the distribution of feed-forward and feedback inputs among the compartments of PCs is well studied, the distribution among different types of cortical inhibitory interneurons is less certain and likely diverse (14, 38, 43, 44). To account for different input distributions and their effect on the formation of nPE and pPE neurons, the inputs onto inhibitory interneurons are varied in our simulations.
To identify nPE and pPE neurons, we modeled their responses to different combinations of actual and predicted sensory information. When the sensory input is fully predicted (FP; that is, both inputs are equal), the PE neurons remain at their BL. Mismatches can come in two flavors; either the predicted sensory input is larger than the actual sensory input (“overpredicted” in ref. 6; this phase is referred to as the “mismatch phase”) or smaller than the actual sensory input (“underpredicted” in ref. 6; this phase is referred to as the “playback phase”). While nPE neurons only increase their firing rate relative to BL when the sensory input is OP, pPE neurons increase their activity when the sensory input is UP.
A Multipathway E/I Balance in nPE and pPE Neurons.
To investigate the conditions under which both PE neuron types coexist, we first made use of a simplified mean-field analysis of the full neural network, for which the dynamics of each neuron type or compartment are represented by a linear equation.
We found that in a network with inhibitory PV, SOM, and VIP neurons, both nPE and pPE neurons can coexist when the interneuron network establishes an E/I balance (ref. 23 discusses homogeneous nPE circuits). An informative example of such a balance is a network in which SOM neurons receive sensory inputs and VIP neurons receive a prediction thereof (Fig. 1 B–E). Both PE neurons types receive at their soma the same amount of excitatory and inhibitory inputs when the network is stimulated with FP sensory stimuli. For nPE neurons, this balance is preserved for stimuli larger than predicted and temporarily broken in favor of excitation for stimuli smaller than predicted. In contrast, for pPE neurons, the E/I balance is preserved for stimuli smaller than predicted and temporarily broken for stimuli larger than predicted (Fig. 1B).
Importantly, our analysis shows that this E/I balance is a balance in not only the total inputs onto PE neurons but also, the pathways those inputs can take through the circuit (SI Appendix, Fig. S1 and SI Text have details). To show this, we computed the sum of all pathways that originate from a particular neuron type/compartment and ended either at the soma or at the dendrites of PE neurons. The contributions for all neuron types/compartments, separated into net excitatory and inhibitory pathways, reveal an E/I balance (Fig. 1C and SI Appendix, Fig. S2B). As a consequence of the balanced pathways, the ability of PE neurons to remain at their BL activity is independent of the particular stimulus strength, provided the neuronal input–output transfer functions are sufficiently linear.
A mean-field network with this compartment-specific E/I balance shows both nPE and pPE neurons (Fig. 1D). The activity of PV, SOM, and VIP neurons varies between the different phases, reflecting the underlying connectivity required to achieve a multipathway E/I balance and the different inputs onto the interneuron types. In line with mismatch neuron responses in the V1 (6), the simulated mismatch responses increase with the difference between actual and predicted sensory inputs (Fig. 1E).
Our analysis revealed that a circuit with only one source of somatic inhibition was not sufficient to give rise to both nPE and pPE neurons. This can be intuitively understood by the following reasoning. The dendrites are balanced or inhibited for one of the two mismatch phases (SI Appendix, Fig. S2) and hence, do not contribute to the somatic activity. As a result, any change of activity in PE neurons must be a consequence of changes in the somatic inputs. The PE neuron type increasing the activity during that mismatch phase requires the currents flowing through the interneuron circuit to be unbalanced. However, the PE neuron type that remains at its BL during that mismatch phase requires the currents flowing through the interneuron circuit to be balanced (derivations are in SI Appendix). These two conditions cannot be satisfied in an interneuron circuit in which the currents are directed through one soma-targeting interneuron population only. In our network, somatic inhibition is provided by PV neurons. To create two types of somatic inhibition, we, therefore, subdivided PV neurons into two groups, one receiving sensory inputs and the other one receiving a prediction thereof. Given the vast diversity of feed-forward and feedback inputs to PV neurons reported experimentally (38, 43, 44), this assumption is plausible for real biological systems. However, other than PV neurons, other soma-targeting interneurons (11) can contribute to establishing an E/I balance, so that the division of PV neurons into subpopulations is not a strict requirement.
The results are robust to the input distributions onto SOM and VIP neurons (SI Appendix, Fig. S2). Changing their inputs only affects the pathway strengths that are required to achieve an E/I balance. However, we find that for mismatch responses to develop, SOM neurons, VIP neurons, or both must receive the actual sensory input (SI Appendix, Fig. S2). The resulting PE circuits differ not only in terms of the interneuron connectivity but also, in the underlying mechanisms that give rise to the mismatch responses in nPE and pPE neurons. The responses of nPE neurons to OP stimuli and the responses of pPE neurons to UP stimuli are either the result of an excess of excitation at the dendrites or a withdrawal of somatic inhibition (SI Appendix, SI Text).
In summary, our analysis shows that in a simplified mean-field network, PE neurons with arbitrary BL activity require a multipathway E/I balance. Mismatch responses are the consequence of a temporary imbalance of excitation and inhibition caused either by an excess of dendritic excitation or by the suppression of somatic inhibition. Moreover, the coexistence of nPE and pPE neurons requires at least two distinct sources of somatic inhibition, as well as dendrite-targeting interneurons that are also driven by sensory inputs.
PE Neurons Are Robust to Network Manipulations.
Neurons are constantly bombarded with nonstationary local and long-range synaptic inputs and regulated by neuromodulators, like acetylcholine or dopamine. Moreover, the activity of both excitatory and inhibitory neurons is modulated by behavioral states and highly context dependent (45). This naturally leads to the question of whether PE neurons are robust to network perturbations. If nPE and pPE neurons were sensitive to small changes in the background inputs, they would need to be reconfigured constantly. To study the network’s ability to withstand perturbations, we individually injected additional inputs to the neurons of our PE circuits (Fig. 2A). In our analysis, we focused on moderate perturbation strengths to ensure that none of the neuron types are silenced.
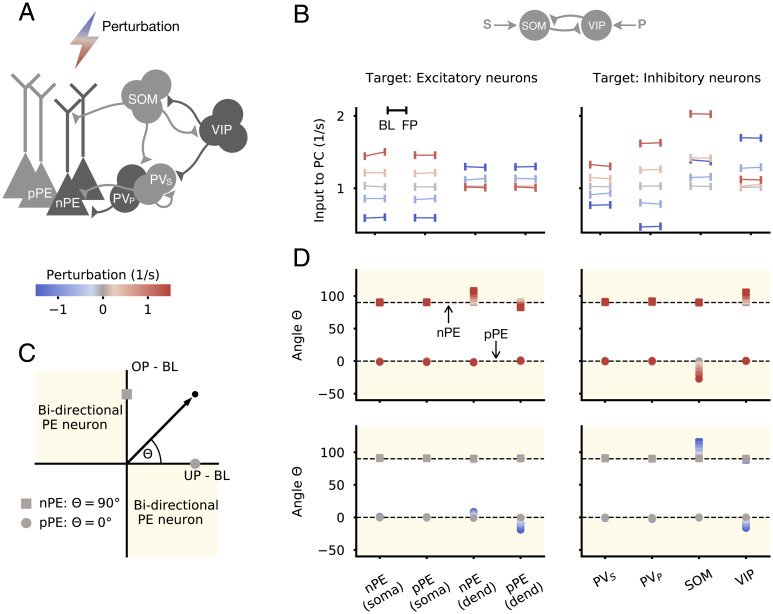
Fig. 2.
PE neurons are robust to moderate network perturbations. (A) Each neuron type/compartment of a mean-field network with nPE and pPE neurons is perturbed with an additional inhibitory or excitatory input. The same circuit as in Fig. 1 B–E is shown. SOM neurons receive the actual sensory input, while VIP neurons receive a prediction thereof. (B) Total input into PE neurons during the absence of sensory stimuli (BL) and for FP sensory stimuli (FP) for different perturbation strengths and different perturbation targets (Left shows compartments of PCs, and Right shows inhibitory neurons). Total inputs in both phases are almost equal as a result of the established E/I balance. Gray indicates no perturbation. (C) Illustration of nPE (square) and pPE (circle) neurons in the input space. Input space is defined by the total input to PCs for OP and UP sensory stimuli. nPE neurons lie on the positive part of the y axis, while pPE neurons lie on the positive part of the x axis. Beige areas denote bidirectional PE neurons. Θ defines the angle in the input space. (D) Θ for different perturbation strengths (Upper: excitatory; Lower: inhibitory) and different perturbation targets (Left: compartments of PCs; Right: inhibitory neurons). Perturbations have minor effects on nPE and pPE neurons, especially when BL firing rates of PCs are low.
A unifying hallmark of both nPE and pPE neurons is that they remain at their BL for FP stimuli. Hence, the total input to PE neurons for anticipated stimuli must be equal to the total input in the absence of sensory stimuli. Both excitatory and inhibitory network perturbations change the inputs to PE neurons in the BL phase (Fig. 2B and SI Appendix, Fig. S3). However, the total inputs for FP sensory stimuli change to the same extent (Fig. 2B and SI Appendix, Fig. S3), leading to no significant changes in activity relative to BL.
In the next step, we wondered how PE neurons change their responses to unexpected mismatches when these mismatches are accompanied by neuron-specific perturbations. For each perturbation target and strength, we plotted the total input for OP and UP sensory stimuli. In this depiction, nPE neurons lie on the positive part of the y axis, while pPE neurons lie on the positive part of the x axis (Fig. 2C). The second and fourth quadrants denote the range of bidirectional PE neurons that either increase activity for sensory inputs smaller than predicted and decrease activity for sensory inputs larger than predicted or vice versa. We quantify perturbation-induced changes of PE neuron activity by the angle Θ in this input space (Θ = 90: nPE neurons, Θ = 0: pPE neurons).
Perturbations that targeted the soma of nPE and pPE neurons, either directly or indirectly through PV neurons, have no or only comparatively small effects on the responses upon unexpected mismatches (Fig. 2D). Perturbations that targeted the dendrites, either directly or indirectly through SOM and VIP neurons, can have salient effects for some of the perturbation strengths tested. In those cases, unidirectional PE neurons mostly transition into bidirectional PE neurons. However, when excitatory neurons have very low (close to zero) BL activities, negative deviations from the BL are bounded from below and hence, are undetectable.
Altogether, these perturbation experiments show that once an E/I balance has been established and gives rise to nPE and pPE neurons, these neurons are robust to moderate network manipulations and hence, do not need to be reconfigured. Moreover, our simulations indicate that perturbations of either the dendrites of PCs or interneurons that target them can modulate the mismatch responses of PE neurons.
nPE and pPE Neurons Develop through Inhibitory Plasticity with a Low Homeostatic Target Rate.
It has been shown that mismatch neurons in the V1 are experience-dependent and require visuomotor coupling to develop normally (6). This suggests that PE neurons are formed through learning. In a model of rodent V1, nPE and pPE neurons were learned separately by means of local, homeostatic inhibitory plasticity (23). It is, however, not resolved how this can be generalized to learning nPE and pPE neurons in the same recurrent network simultaneously.
The homeostatic inhibitory plasticity used in ref. 23 establishes a target rate in the PCs for all inputs the network is exposed to during learning. A direct consequence is that nPE neurons may form when the network is exposed to stimuli that are smaller than or equal to the prediction. Likewise, pPE neurons may develop when the network is exposed to sensory stimuli that are larger than or equal to the prediction. The increase of activity in nPE neurons for OP stimuli and in pPE neurons for UP stimuli is, hence, a result of the network never experiencing the respective mismatch during training. This clearly shows a dilemma; to learn nPE and pPE neurons in the same network, it must be exposed to FP as well as OP and UP stimuli. The plasticity rule, however, will keep the excitatory neurons at a target rate throughout, so that neither nPE nor pPE neurons could emerge (SI Appendix, Fig. S4A).
We found that a simple solution is to train the network only with phases of FP sensory inputs and set the homeostatic target rate of PCs to zero so that any excess of somatic inhibition is not reflected in the firing rates because it is bounded from below. By using FP sensory inputs only, we assume that initially, predictions develop independently from and faster than PE neurons. Hence, we do not consider early phases of development in which sensory inputs most likely cannot be perfectly predicted. However, we will later show that both nPE and pPE neurons can still develop in the face of moderate noise, leading to OP and UP stimuli during learning.
To show that in this way, both nPE and pPE neurons can develop, we made a subset of inhibitory synapses subject to experience-dependent plasticity (Fig. 3A). While the synapses onto PCs follow an inhibitory plasticity rule akin to ref. 46, the inhibitory synapses onto PV neurons follow an approximation of the backpropagation of error rule (47). This distinction was necessary as all plastic synapses in the network must collectively change to accommodate the objective function: that is, minimizing the deviations from a target of the PCs. While this information is immediately available at synapses onto PCs, it must travel to all other synapses. To avoid biologically questionable error backpropagation through the connections from PV neurons onto the PCs, we assume that the deviations are carried through the connections from the PCs to the PV neurons. This rule can be interpreted such that synapses onto PV neurons change in proportion to the difference between the excitatory recurrent drive onto them and a homeostatic target (SI Appendix and refs. 23 and 48 have more details).
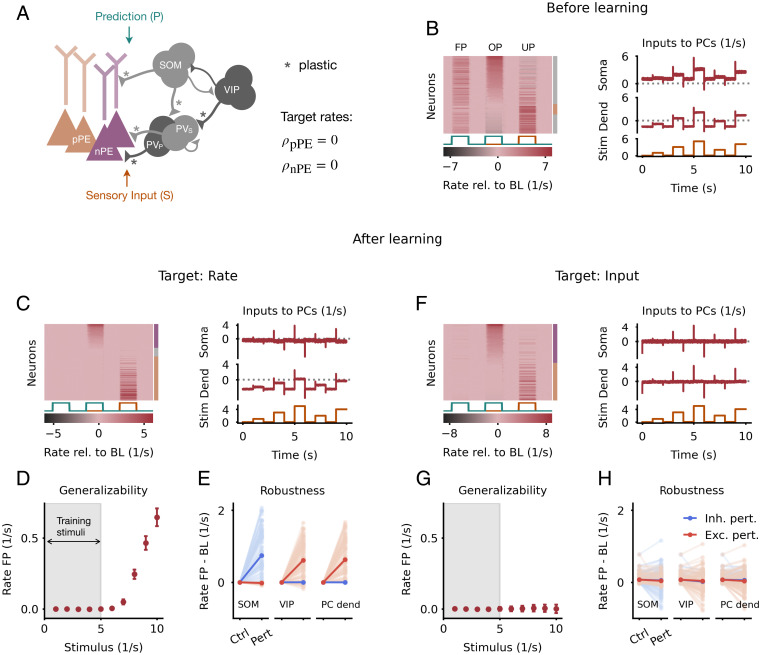
Fig. 3.
nPE and pPE neurons develop through inhibitory plasticity with a low homeostatic target rate. (A) Heterogeneous network model with excitatory PCs and inhibitory PV, SOM, and VIP neurons. All PCs receive actual sensory input at the somatic compartment and a prediction thereof at the dendritic compartment; 50% of the PV neurons, 70% of the SOM neurons, and 30% of the VIP neurons receive the sensory stimuli. The remaining cells receive the prediction. Connections marked with an asterisk undergo experience-dependent plasticity. Target rates for PCs are set to zero. (B) Responses of and inputs to PCs before learning. (B, Left) Responses relative to BL of all PCs for FP, OP, and UP stimuli sorted by amplitude of mismatch response in OP. Almost none of the PCs are classified as PE neurons summarized by the bar to the right (gray: no PE neuron; purple: nPE neuron; orange: pPE neuron). (B, Right) Mean input into both soma and dendrites of PCs for FP stimuli. Inputs are not balanced. (C) Same as in B but after learning with an inhibitory plasticity rule that establishes a zero target rate in PCs. (C, Left) Most of the PCs are either nPE (purple) or pPE (orange) neurons (indicated by the colored bar to the right). (C, Right) Mean inputs into both soma and dendrites of PCs for FP stimuli are not balanced. (D) Median and SEM of PC responses for FP sensory stimuli. The gray area indicates the range of stimuli used during learning. Sensory stimuli that are larger than the training stimuli evoke neuron responses. (E) Inhibitory (blue) and excitatory (red) perturbations can cause the PE neurons to deviate from their BL activity. Light colors denote single neurons, and dark colors denote the population average. (F–H) Same as C–E but with an inhibitory plasticity rule that establishes a target for the total input to PCs (target: zero). (F, Left) Most of the PCs are either nPE (purple) or pPE (orange) neurons (indicated by the colored bar to the right). (F, Right) Mean inputs into both soma and dendrites of PCs for FP stimuli are balanced. (G) Sensory stimuli that are larger than the training stimuli evoke only minor neuron responses. The PE neurons can generalize beyond the training stimuli. (H) PE neurons are robust to inhibitory and excitatory perturbations after learning. Ctrl, control; Pert, perturbation.
Before learning, the network was randomly initialized with a connectivity motivated by experimental studies (12, 13, 30–35), leading to PCs that show deviations from BL in all phases (Fig. 3 B, Left). The excitatory and inhibitory inputs at both soma and dendrites of PCs are unbalanced for FP stimuli (Fig. 3 B, Right). Only very few neurons could, therefore, be classified as PE neurons. The total inputs to PCs for OP and UP stimuli were negatively correlated and showed a near balance of top-down predictions and bottom-up sensory inputs (49) (SI Appendix, Fig. S5A). During learning, the inhibitory synapses collectively adjusted their efficacy to keep the PCs at their target rate for perfectly predicted sensory inputs (SI Appendix, Fig. S6A). At the end of learning, the majority of PCs showed response patterns akin to nPE or pPE neurons (Fig. 3 C, Left). The balance of top-down predictions and bottom-up sensory inputs was preserved after learning (SI Appendix, Fig. S5B). However, the excitatory and inhibitory inputs at both soma and dendrites of PCs are not perfectly balanced (Fig. 3 C, Right). That is a consequence of the target rate being equal to the neurons’ rectification threshold. The objective function () is already satisfied when the total input to PCs is less than or equal to zero for all stimuli presented during training. That is, the network does not necessarily strive for an E/I balance. While this does not hamper the formation of nPE and pPE neurons per se, it compromises some of the properties of PE neurons that emerge from this balance. On the one hand, the ability to generalize beyond the training stimuli does not hold (Fig. 3D). On the other hand, the network is less robust to perturbations (Fig. 3E), which means that PE neurons would have to be relearned continuously.
We, therefore, modified our plasticity rules by introducing a target for the total input to PCs, instead of a target for their firing rate. This allows the synaptic weights to adjust to both positive and negative deviations from the target and forces the network to establish an E/I balance. After learning, excitatory and inhibitory inputs to both soma and dendrites are balanced on a stimulus by stimulus basis (Fig. 3 F, Right). As before, almost all PCs developed into nPE or pPE neurons (Fig. 3 F, Left), and the balance of top-down predictions and bottom-up sensory inputs is preserved (SI Appendix, Fig. S5C). In addition, nPE and pPE neurons generalize beyond the training stimuli (Fig. 3G), and PE neurons are more robust to moderate network perturbations (Fig. 3H).
While we used inhibitory homeostatic plasticity, other forms of plasticity may be equally suited to learning nPE and pPE neurons. However, we note that plasticity rules that do not establish a homeostatic firing rate may not be sufficient. To show that, we trained a network in which the synapses onto the PCs followed a Hebbian plasticity rule as before, while the synapses onto the PV neurons followed an anti-Hebbian plasticity rule. When the network was trained with FP sensory inputs only, the PCs show strong activation for predicted as well as unpredicted sensory stimuli and hence, do not develop into nPE and pPE neurons (SI Appendix, Fig. S4B).
In summary, our results show that networks with inhibitory homeostatic plasticity can give rise to both nPE and pPE neurons when the homeostatic target rate is zero. Moreover, when the plasticity acts to establish a target for the total input to excitatory neurons, the PE neurons’ ability to withstand network perturbations and generalize is improved.
Mismatch Responses Are Determined by Initial Connectivity and Inputs onto the Interneurons.
Training a network solely with FP sensory inputs (Fig. 3) does not constrain the neuron responses to mismatches. Theoretically, the PC responses to OP and UP stimuli can be classified into four cases (SI Appendix, Fig. S7). When PCs are silent in the absence of sensory inputs, these neurons would be nPE neurons, pPE neurons, silent neurons, or neurons that indicate mismatches independent of the valence. We, therefore, wondered how network properties, like the connectivity before learning or the distribution of inputs to the interneurons, determine the ratio between nPE and pPE neurons.
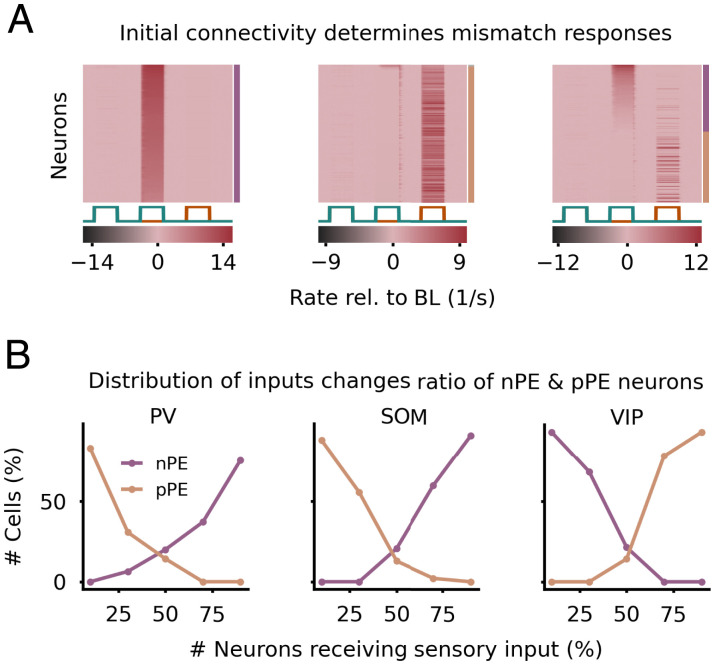
A homogeneous mean-field analysis reveals that the initial connectivity determines whether a PC develops into an nPE or pPE neuron. The different PE neuron types take up distinct parameter ranges in the weight space defining the interneuron connectivity (SI Appendix, Fig. S7). The size of each area is an approximation of the faction of cells that develop into nPE or pPE neurons and changes with the parameterization of the network (SI Appendix, Fig. S7). For a mean-field network in which SOM neurons receive the actual sensory input and VIP neurons receive a prediction thereof, nPE neurons require that PV neurons receive stronger inhibition from VIP neurons than from SOM neurons. This relationship is reversed for pPE neurons. The dependence on the initial connectivity is confirmed in our network simulations. When the initial connectivity is closer to the nPE manifold, PCs tend to develop into nPE neurons (Fig. 4 A, Left). Likewise, when the initial connectivity is closer to the pPE manifold, PCs tend to develop into pPE neurons (Fig. 4 A, Center). Hence, for networks to give rise to both types of PE neurons (Fig. 4 A, Right), the initial connectivity should comprise sufficiently large parameter spaces or regions close to both manifolds.
Fig. 4.
Initial connectivity and distribution of inputs onto interneurons determine mismatch responses of PE neurons. (A) For three different initial weight configurations, the network forms nPE neurons (Left), pPE neurons (Center), or both (Right). Mean initial weights: , and (Left); , and (Center); , and (Right). SOM neurons and 50% of the PV neurons receive the actual sensory input, while VIP neurons and the remaining PV neurons receive a prediction thereof. , weight from PV neurons onto soma of PCs; , recurrent inhibition between PV neurons; , weight from SOM neurons onto PV neurons; , weight from VIP neurons onto PV neurons. (B) The number of PV neurons (Left), SOM neurons (Center), or VIP neurons (Right) that receive the actual sensory input is varied. The ratio of nPE and pPE neurons changes with the distribution of actual and predicted sensory inputs onto the interneurons. For the neuron types for which the distribution of inputs was not varied, the fraction of neurons receiving the actual sensory input was set to 0.5.
The areas in the weight space defining the different PE neuron types change with the distribution of actual and predicted sensory inputs onto the interneurons (SI Appendix, Fig. S7). Our simplified mean-field analysis shows that nPE neurons are more likely to develop when SOM neurons receive the actual sensory input and VIP neurons receive a prediction thereof, while pPE neurons are more likely to emerge when the inputs onto SOM and VIP neurons are reversed. This is confirmed in our network simulations by changing the distribution of actual and predicted sensory inputs onto PV, SOM, and VIP neurons (Fig. 4B). When the majority of PV or SOM neurons receive the actual sensory input, PCs tend to develop into nPE neurons. Likewise, by increasing the number of VIP neurons that receive a prediction of the expected sensory input, most of the PCs become nPE neurons after training. If these ratios are inverted, the PE circuit is biased toward pPE neurons.
Finally, the predictability of sensory stimuli during training can bias the formation of PE neurons. Given that neuronal networks receive substantial noise due to, for instance, the random nature of synaptic transmission, synapse failures, or channel noise (50), sensory inputs and predictions thereof will rarely be perfectly equal. As a consequence, networks are exposed not only to perfectly predicted sensory stimuli but also, to small mismatches between them. When the transmission of the predicted sensory input becomes less reliable, the number of pPE neurons strongly decreases up to a point where no pPE neurons are formed during learning (SI Appendix, Fig. S8A). Similarly, when the transmission of the actual sensory input becomes less reliable, the number of nPE neurons strongly decreases up to a point where no nPE neurons are formed (SI Appendix, Fig. S8B). While both the numbers of nPE and pPE neurons decrease equally when the network is exposed to noisy stimuli, PE neurons can still form. This reflects the network’s ability to tolerate positive and negative deviations between actual and predicted sensory inputs when both phases are presented equally (SI Appendix, Fig. S8C).
Altogether, this shows that the initial connectivity, distribution of actual and predicted sensory inputs onto interneurons, and stimulus predictability during learning determine which PE neurons emerge and that the formation of nPE and pPE neurons is robust with respect to variations in these parameters.
PE Neurons Bias Unpredictable Percepts toward the Mean of the Stimulus Statistic.
Previous experiences shape perception and behavior. A salient example of experience-dependent biased perception is bias toward the mean (also known as contraction bias). A stimulus drawn from a random distribution is perceived larger when it is smaller than the mean of the stimulus distribution and perceived smaller when it is larger than the mean. This well-known phenomenon was described centuries ago (51, 52), has been reproduced many times in tasks that involve the reproduction of a perceived variable (24–29), and has been attributed to Bayesian computation in which a system integrates information about prior stimulus statistics (25, 26). We speculated that PE neurons can support biased perception.
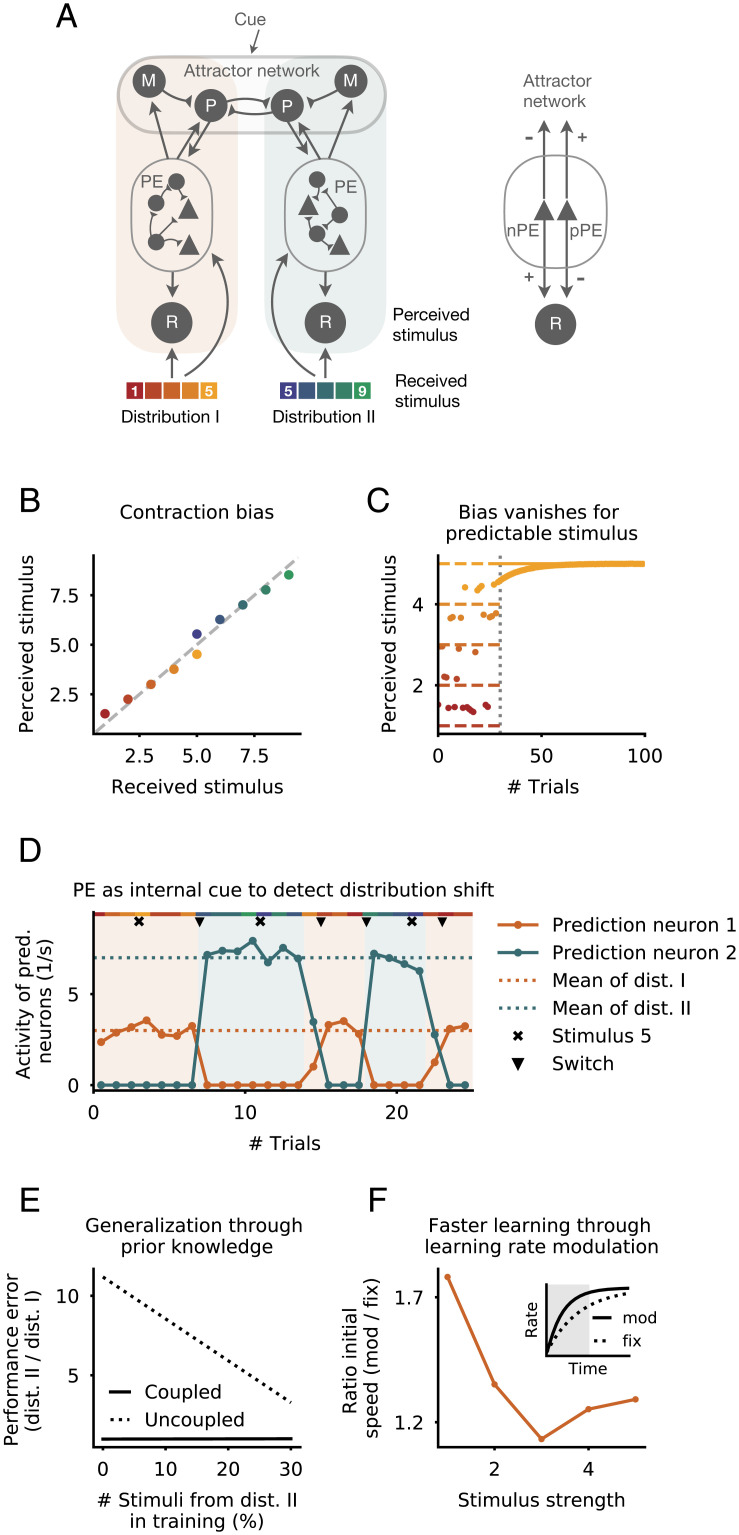
To this end, we simulated two connected subnetworks, the neurons of which are only responsive to a range of stimuli drawn from one of two uniform distributions. The strength of sensory stimuli ranges from 1/s to 5/s for the first distribution (associated with the first subnetwork) and from 5/s to 9/s for the second distribution (associated with the second subnetwork). Each subnetwork consists of a PE circuit as studied before connected with a representation neuron and an attractor network (Fig. 5A). The attractor network consists of two types of neurons termed the “memory neuron” and the “prediction neuron.” The memory neurons, modeled as perfect integrators (that is, line attractors), project onto the prediction neuron of their corresponding subnetwork. The prediction neurons are mutually connected via inhibitory synapses (53), hence forming two fixed points. In each trial, they receive a cue signal that indicates the distribution from which the stimulus is drawn. The attractor network thus dynamically generates the prediction that is forwarded to one of the two subnetworks. Neurons of the attractor network receive inputs from both nPE and pPE neurons. While nPE neurons inhibit the attractor neurons (for instance, through inhibitory interneurons not explicitly modeled here), pPE neurons excite them (motivated by ref. 3). The representation neurons, whose activity represents the perceived stimulus, not only receive the sensory stimulus itself but are also connected to both nPE and pPE neurons of their respective subnetwork, with reversed connectivity (Fig. 5A). For simplicity, we assume that during the presentation of random stimuli, the PE circuits are not updated significantly: for instance, because the learning rate is small compared with the changes in activity or simply because the effect of positive and negative mismatch phases is balanced (SI Appendix, Fig. S8C).
Fig. 5.
The role of PE neurons in biased perception. (A, Left) Attractor–memory network with PE neurons. The network consists of two subnetworks, the neurons of which are only responsive to a subset of stimuli. Each subnetwork comprises a representation neuron (R) and a PE circuit. Both R and PE neurons receive sensory stimuli of either of two uniform distributions. The PE circuit is connected to both the R and an attractor network that comprises memory neurons (M) and prediction neurons (P). The two prediction neurons are mutually connected via inhibitory synapses and receive excitatory input from the memory neuron of their respective subnetwork. (A, Right) nPE and pPE neurons connect to M, P, and R neurons with opposing sign. (B) The PE neurons establish a contraction bias for both distributions. A stimulus that is smaller than the distribution mean is perceived stronger, while a stimulus that is larger than the distribution mean is perceived weaker. (C) The response of the representation neuron becomes unbiased after the transition (dotted vertical line) from a uniform distribution to a binary distribution because the stimulus becomes predictable. (D) The network does not receive a cue signal indicating the distribution from which the stimuli are drawn. After an uncued switch from one distribution to another, the former inactive prediction neuron becomes active, and the former active prediction neuron becomes inactive (network switching is denoted by a triangle). This is the result of the PE neurons and the mutual inhibition between both prediction neurons. Stimulus present in both distributions does not evoke a switch (denoted by x). Shaded areas denote the distributions from which the stimuli are drawn. (E) Both distributions equally change from uniform to binary (to maximal values of former uniform distributions). A network in which the PE neurons are equally coupled to both memory neurons (solid line) shows the same performance error for both distributions independent of the training set composition. A network in which the PE neurons are only coupled to the memory neuron of their respective subnetwork (dashed line) shows a larger error for the distribution that is underrepresented during training. (F) Speed of learning (defined as the averaged change of activity in the first 50 ms; the gray area in Inset) is increased when PE neuron activity modulates the learning rate based on the degree of the stimulus’ unpredictability compared with a fixed learning rate (solid vs. dashed lines in Inset).
Contraction bias for unpredictable and predictable stimuli.
In each trial, only one of the two prediction neurons is active. This is a consequence of the mutual inhibition between them and a cue signal that inhibits the prediction neuron that is not selective for the stimulus shown. The activity of the prediction neuron is determined by the activity of the memory neuron and the PE neurons of their respective subnetwork. Because in our model, the memory neurons perfectly integrate the inputs from nPE neurons that inhibit them and from pPE neurons that excite them, the activity of the memory neuron approaches the mean of the distribution the subnetwork is exposed to. Hence, the active prediction neuron also approximately represents the mean of the past stimuli. When the sensory input is smaller than the activity of the prediction neuron, nPE neurons are active. Because nPE neurons excite the representation neuron, the perceived stimulus is larger than the received stimulus. In contrast, when the sensory input is larger than the activity of the prediction neuron, pPE neurons are active. Because we assume that the net effect of pPE neurons on representation neurons is negative, the perceived stimulus is smaller than the received stimulus. This effect is particularly pronounced for the stimulus present in both distributions (i.e., 5 ).
The preceding results suggest that the bias is a consequence of the unpredictability of the stimulus. Hence, when the sensory input becomes predictable, the bias should eventually vanish. To test this, after some trials with random stimuli, we always presented the same sensory input. The activity of the PE neurons slowly changes the memory neuron until it represents the actual stimulus. As a result, over time, the prediction neuron itself represents the sensory input, a consequence being that the PE neurons become silent. Hence, the bias vanishes, and the perceived stimulus equals the received stimulus (Fig. 5C).
PE neurons may act as an internal cue.
While the distribution from which the stimulus is drawn had been cued to the network so far, very often changes in the environment or underlying tasks occur spontaneously without clues. We figured that PE neurons may act as internal cues that support a switch between attractors when stimuli are suddenly drawn from the other distribution. Immediately after the network experiences an unexpected switch, the prediction neuron that had been active in the previous trials remains active. However, after some time, the PE neurons of that subnetwork suppress the activity of the prediction neuron. At the same time, the PE neurons of the other subnetwork excite the corresponding prediction neuron. Together with the mutual inhibition between prediction neurons, the wrong expectation is eventually corrected successfully (Fig. 5D). Importantly, stimuli that are present in both distributions are not sufficient to cause a switch (Fig. 5D, stimuli denoted by x). Altogether, this shows that PE neuron activity may underlie fast adaptation to unexpected situations by forcing the attractor network to switch between fixed points.
Generalization through prior knowledge.
PE neurons might also support generalization across environments or tasks by making use of prior knowledge encoded in the connectivity between the PE circuit and the attractor network. To illustrate this, let us assume that any change of one distribution will equally affect the other distribution. In our network, this can be implemented by cross-coupling the PE neurons of one subnetwork with the memory neuron of the other subnetwork. As a result, any changes in input statistics will equally affect both memory neurons, even when the network is only exposed to samples of one distribution. To confirm this, we changed both distributions from uniform to binary. We then trained the network briefly with the new input statistics. While networks without cross-coupling show larger performance errors for the distribution that was underrepresented during training, networks with cross-coupling show the same test error for both distributions independent of the training set composition (Fig. 5E). Hence, PE neurons can support generalization by modulating memory neurons of all subnetworks.
Faster learning through modulation of learning rates.
Finally, PE neurons could also facilitate learning by adjusting learning rates based on the degree of predictability of sensory stimuli. In such a scenario, unexpected stimuli would increase the learning rate, leading to faster adaptation of synaptic connections. On the neuronal level, this could be achieved by bottom-up sensory inputs arriving at the proximal locations of the basal dendrites, while PE neurons target the distal locations of basal dendrites. The distal synapses may then only elicit NMDA (N-methyl-D-aspartate) spikes that cause the proximal synapses to strengthen (54). To illustrate this, we repeatedly stimulate subnetwork 1 with the same stimulus and update the synaptic weight connecting the stimulus with the representation neuron. Over time, the activity of the representation neuron will approach the stimulus. However, this process is faster when PE neurons increase the learning rate. To quantify the speedup in learning, we compute the rate of change in the activity of the representation neuron at the beginning of training for both a learning rate that is fixed and one that is modulated by the activity of PE neurons (Fig. 5F). As expected, the speedup is larger for stimuli that deviate more from the distribution mean. This illustrates that modulating learning rates by the degree of unpredictability (or surprise) of an event can underpin fast learning.
Discussion
We showed that both nPE and pPE neurons require an E/I balance for FP sensory inputs. This balance is not only a balance in the inputs to the PCs but also a balance of pathways that the actual and predicted sensory inputs can take through the recurrent network. Moreover, when PCs exhibit an arbitrary BL firing rate, the E/I balance at the soma must be preserved for UP stimuli in nPE neurons and for OP stimuli in pPE neurons (Fig. 1 and SI Appendix, Figs. S1 and S2). While this has been shown in separate nPE and pPE circuits in which SOM and VIP neurons receive fixed inputs (23), we corroborate these findings in networks in which both PE neuron types coexist, and the inputs onto SOM and VIP neurons are flexible.
Importantly, nEP and pPE neurons can act in parallel in the same recurrent network without the need for segregated subcircuits. Based on our mathematical analysis, we showed that for both PE neurons to coexist, somatic inhibition must come in two distinct variants (SI Appendix). Moreover, we demonstrated that in such networks, SOM and VIP neurons can receive both actual and predicted sensory input, as long as at least one of them is driven by the actual sensory input (SI Appendix, Fig. S2). The resulting PE circuits differ in terms of the interneuron connectivity and the underlying mechanisms that give rise to the mismatch responses in nPE and pPE neurons. Their mismatch responses are either the result of an excess of excitation at the dendrites that are forwarded to the soma or the suppression of somatic inhibition (SI Appendix, SI Text).
While in the present study, we have focused on a canonical interneuron circuit with PV, SOM, and VIP interneurons (for instance, refs. 12, 13, and 32), our mathematical analysis can be straightforwardly extended to an arbitrary number of interneurons. In this motif, somatic inhibition is provided by PV neurons, while dendritic inhibition is provided by the SOM–VIP circuit. nPE and pPE neurons can also emerge without VIP neurons (discussion and appendix in ref. 23). However, VIP neurons in our network 1) contribute to amplifying mismatch responses (6, 22) and 2) allow SOM neurons to receive both the actual and the predicted sensory inputs, respectively (SI Appendix, Fig. S2), which is in line with studies showing that interneurons receive both feed-forward and feedback inputs (38, 43, 44).
We showed that PE neurons formed through an E/I balance are robust to moderate network perturbations (Fig. 2 and SI Appendix, Fig. S3). This is a desirable feature because it ensures that PE circuits do not need to be reconfigured constantly. In some cases, when the dendrites were perturbed directly or indirectly through SOM or VIP neurons, the former unidirectional PE neurons could transition into bidirectional PE neurons. This effect is a consequence of the dendrites not being in an E/I balance during the mismatch phases. To establish such a balance for OP or UP stimuli, more dendrite-targeting interneurons would be required. For example, neuron derived neurotrophic factor-expressing neurons that are mainly located in layer 1 have been shown to inhibit the apical dendrites located in the superficial layers (55) and are, hence, a promising candidate in establishing a target activity in the dendrites and shaping dendritic PEs.
While it has been shown that separate nPE and pPE neurons can be learned via inhibitory homeostatic plasticity (23), here we demonstrated that nPE and pPE neurons can simultaneously develop in the same recurrent network (Figs. 3 and 4) when additional assumptions are met. On the one hand, the network should mainly experience FP sensory inputs. Hence, we assumed that predictions have already been developed and that mismatches are rare. This is in line with an experimental study performed in layer 2/3 of rodent V1 (6) showing that the formation of nPE neurons relies on normal visuomotor coupling during development. On the other hand, the homeostatic firing rate of PCs must be close to zero. This assumption is in line with studies showing an astonishingly low spontaneous firing rate for neurons in some regions of the cortex (for instance, refs. 16 and 17). In fact, the existence of unidirectional PE neurons has been attributed to low BL firing rates (1, 3). If the PCs have a BL firing rate significantly larger than zero, nPE and pPE neurons in our network would be bidirectional. We speculate that learning nPE and pPE neurons with nonzero BL firing rates require different forms of plasticity (taking into account the type of PE neuron a PC should develop to) or gating signals that guide or restrict learning to a subset of input phases. For instance, it has been hypothesized that neuromodulators that are active during self-motion may support the formation of PE circuits (3).
Because we used a target firing rate equal to the neuron’s rectification threshold, the resulting PE neurons did not necessarily exhibit an E/I balance. We, therefore, modified the plasticity rule such that it establishes a target for the total input to PCs instead of a target rate. We showed that with this plasticity rule, the PE neurons generalize beyond the range of sensory stimuli seen during learning and are robust to network perturbations (Fig. 3). A similar result could theoretically be achieved by simply increasing the target rate slightly. However, we speculate that learning an E/I balance in such systems would be comparatively slow as negative deviations are still bounded from below. While we have employed a homeostatic plasticity rule that establishes a target for the total input, we assume that plasticity rules processing deviations from a target membrane potential (56, 57) can be equally used. While we did not investigate all forms of plasticity, we note that plasticity rules that do not establish a homeostatic firing rate in PCs may be inappropriate to learning nPE and pPE neurons (SI Appendix, Fig. S4B).
Furthermore, we showed that the ratio of nPE and pPE neurons is determined by the initial connectivity and the distribution of actual and predicted sensory inputs onto SOM and VIP neurons (Fig. 4 and SI Appendix, Fig. S7). While in networks in which SOM neurons receive the actual sensory input and VIP neurons receive a prediction thereof, PCs are more likely to develop into nPE neurons, PCs are more likely to develop into pPE neurons when the inputs onto the interneurons are reversed. However, both PE neuron types can develop for both input configurations as long as the initial connectivity covers sufficiently large parameter spaces or regions close to both nPE and pPE manifolds.
In our model, the connections onto the soma and the dendrite of PCs as well as the inhibitory connections from SOM and VIP neurons onto PV neurons underwent inhibitory plasticity. This choice was motivated by the observation that in layer 2/3 of V1, the excitatory neurons and PV neurons, but not SOM and VIP neurons, show experience-dependent activity (6). However, we do not expect the learning of PE neurons to be compromised when all inhibitory synapses are plastic. Recently, it has been shown that NMDA receptor–dependent plasticity in early development is crucial for the responses to unpredictable and predictable stimuli in V1 (58). This suggests that excitatory plasticity plays a pivotal role in the formation of PE neurons. While we kept all excitatory connections fixed during learning, we expect that in our network, PE neurons can develop with excitatory homeostatic plasticity, inhibitory homeostatic plasticity, or both.
Predictive processing requires at least two types of neurons: neurons that signal the mismatch between bottom-up and top-down inputs and neurons that encode predictions (3). On top of this, other functionally distinct neuron types may exist: for instance, neurons that only increase their activity when sensory inputs are FP. While a thorough investigation of the circuit-level mechanisms that give rise to these distinct neurons is beyond the scope of this work, it is intriguing to speculate on how they may develop simultaneously in the same recurrent network. In our networks, only PE neurons could develop. This suggests that for other neuron types to emerge, additional cellular mechanisms and/or plasticity rules are necessary. A mechanism that has long been associated with combining feed-forward and feedback information is BAC firing (backpropagation–activated calcium spike firing). In BAC firing, a back-propagating action potential from the soma—when coinciding with input at the distal dendrites—can cause calcium spikes that trigger a burst of action potentials (37, 59). It is conceivable that burst-dependent plasticity (60) acting on the synapses from top-down and bottom-up inputs onto PCs equipped with BAC firing, in combination with local inhibitory homeostatic plasticity mechanisms considered here, supports a richer diversity of neuron types. The type of PC responses to predicted and unpredicted stimuli after learning might then be a consequence of differences in cellular properties, the sensitivity to gating signals (e.g., neuromodulators), or the learning rates of the plasticity rules present in the same network.
Finally, we showed that an attractor–memory network with a PE circuit can reproduce the contraction bias for unpredictable stimuli (Fig. 5). We demonstrated, by means of the example of biased perception, that PE neurons can act as an internal cue that indicates unannounced switches between stimulus distributions. Moreover, we illustrated that PE neurons may underpin generalization across stimulus statistics and can support faster learning (Fig. 5). Other than the role of prior expectations in perceptual inference (for instance, refs. 1, 42, and 61), PEs may govern learning. In the rodent visual cortex, neuron responses to predicted and unpredicted sensory stimuli show systematic changes across days (62). Recently, it has been demonstrated that there is a close link between predictive coding and supervised learning, in which nonbiological weight changes by the backpropagation algorithm can be replaced with local Hebbian plasticity of connections in predictive coding networks (63–66). Furthermore, it has been shown that biologically plausible learning schemes can ease the temporal and structural credit assignment problem (67, 68). Moreover, the model in ref. 67 has recently received support from experimental data showing that PE neurons in anterior frontal–striatal networks could serve as feature-specific eligibility traces (69).
Our work makes a number of predictions that could be tested experimentally. 1) PE neurons arising from balanced pathways are robust to network perturbations: that is, they remain at BL for FP sensory inputs. 2) If PE neurons change upon perturbation, it mainly affects their responses to unpredicted stimuli. Those changes primarily occur for direct or indirect (through SOM and VIP neurons) perturbations of the dendrites and usually lead the former unidirectional PE neurons to act as bidirectional PE neurons. These predictions can be tested by optogenetically or pharmacogenetically manipulating neuron types/compartments. 3) Both nPE and pPE neurons are hidden bidirectional PE neurons because of their low BL firing rate. This can be directly tested by elevating their BL activity through external excitatory stimulation because additional input should not affect the PE neurons’ ability to remain at their BL activity for FP sensory stimuli (see above). 4) PE neurons generalize beyond the stimuli used during learning. By carefully designing experiments that restrict learning to a subset of stimuli, the developing PE neurons can be tested for their ability to generalize. 5) PE neurons underlie contraction bias. It means the observed bias should vanish for targeted silencing of PE neurons. Moreover, if only one of the two PE neuron types is silenced, the bias would only occur for one side of the stimulus distribution. Although still challenging, by employing recent technological advances [for instance, multiphoton holographic optogenetics (70) and neuron tagging based on activity-dependent promoters (71, 72)], targeted manipulation of nPE and pPE neurons may be in reach soon.
Expected sensory stimuli are recognized more swiftly (73, 74), giving an evolutionary advantage in a world where seconds can make the difference between life and death. Hence, continuous detection of deviations between expected and actual sensory inputs and the subsequent refinement of predictions may be a central task for neural networks. Our work sheds light on the formation and refinement of PE neurons in cortical circuits, an important step toward a better understanding of the brain’s ability to predict sensory stimuli.
Materials and Methods
Excitatory neurons in the PE circuit are simulated as two coupled point compartments, representing the soma and the dendrites. All other neurons are modeled as point neurons. The activity of each neuron/compartment ri is represented by a rectified, linear differential equation (36):
| [1] |
| [2] |
where τi denotes the time constant, the vector w contains the connection strengths, and Ii is the overall input comprising external background and actual or predicted sensory inputs.
In plastic PE circuits, a number of connections between neurons are subject to experience-dependent changes. The connections from PV and SOM neurons onto the soma and the apical dendrites, respectively, obey an inhibitory Hebbian plasticity rule (46). The connections from both SOM and VIP neurons onto PV neurons implement a local approximation of a backpropagation of error rule that relies on information forwarded to the PV neurons from the PCs (23, 48).
We define PCs as nPE neurons when their activity in BL and for FP, OP, and UP stimuli satisfies the following equations:
| [3] |
| [4] |
Similarly, we define PCs as pPE neurons when
| [5] |
| [6] |
In practice, we tolerate small deviations in phases in which the PE neurons are supposed to remain at BL as long as these deviations are smaller than 10% of the neuron’s maximal response.
Detailed methods and supporting analyses as well as values for neuron, network, plasticity, and simulation parameters can be found in SI Appendix.
Supplementary Material
Acknowledgments
We thank Vezha Boboeva, Douglas Feitosa Tomé, Júlia Gallinaro, and Klara Kaleb for comments on earlier versions of this manuscript, and we thank all members of the laboratory of C.C. for discussion and support. This work was supported by Biotechnology and Biological Sciences Research Council (BBSRC) Grants BB/N013956/1 and BB/N019008/1, Wellcome Trust Grant 200790/Z/16/Z, Simons Foundation Grant 564408, Engineering and Physical Sciences Research Council (EPSRC) Grant EP/R035806/1, and Deutsche Forschungsgemeinschaft (DFG) Grant 460088091.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2115699119/-/DCSupplemental.
Data Availability
Source code to reproduce the simulations, analyses, and figures are available in GitHub (https://github.com/lhertaeg/SourceCode_Hertaeg2021). All other data are included in the manuscript and/or SI Appendix.
References
- 1.Rao R. P., Ballard D. H., Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87 (1999). [DOI] [PubMed] [Google Scholar]
- 2.Friston K., A theory of cortical responses. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 815–836 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Keller G. B., Mrsic-Flogel T. D., Predictive processing: A canonical cortical computation. Neuron 100, 424–435 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schultz W., Dickinson A., Neuronal coding of prediction errors. Annu. Rev. Neurosci. 23, 473–500 (2000). [DOI] [PubMed] [Google Scholar]
- 5.Keller G. B., Bonhoeffer T., Hübener M., Sensorimotor mismatch signals in primary visual cortex of the behaving mouse. Neuron 74, 809–815 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Attinger A., Wang B., Keller G. B., Visuomotor coupling shapes the functional development of mouse visual cortex. Cell 169, 1291–1302.e14 (2017). [DOI] [PubMed] [Google Scholar]
- 7.Huang K.-H., et al., A virtual reality system to analyze neural activity and behavior in adult zebrafish. Nat. Methods 17, 343–351 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Eliades S. J., Wang X., Neural substrates of vocalization feedback monitoring in primate auditory cortex. Nature 453, 1102–1106 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Keller G. B., Hahnloser R. H., Neural processing of auditory feedback during vocal practice in a songbird. Nature 457, 187–190 (2009). [DOI] [PubMed] [Google Scholar]
- 10.Ayaz A., et al., Layer-specific integration of locomotion and sensory information in mouse barrel cortex. Nat. Commun. 10, 2585 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Markram H., et al., Interneurons of the neocortical inhibitory system. Nat. Rev. Neurosci. 5, 793–807 (2004). [DOI] [PubMed] [Google Scholar]
- 12.Pfeffer C. K., Xue M., He M., Huang Z. J., Scanziani M., Inhibition of inhibition in visual cortex: The logic of connections between molecularly distinct interneurons. Nat. Neurosci. 16, 1068–1076 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jiang X., et al., Principles of connectivity among morphologically defined cell types in adult neocortex. Science 350, aac9462 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tremblay R., Lee S., Rudy B., Gabaergic interneurons in the neocortex: From cellular properties to circuits. Neuron 91, 260–292 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wamsley B., Fishell G., Genetic and activity-dependent mechanisms underlying interneuron diversity. Nat. Rev. Neurosci. 18, 299–309 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Polack P.-O., Friedman J., Golshani P., Cellular mechanisms of brain state-dependent gain modulation in visual cortex. Nat. Neurosci. 16, 1331–1339 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xue M., Atallah B. V., Scanziani M., Equalizing excitation-inhibition ratios across visual cortical neurons. Nature 511, 596–600 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Isaacson J. S., Scanziani M., How inhibition shapes cortical activity. Neuron 72, 231–243 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Litwin-Kumar A., Rosenbaum R., Doiron B., Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes. J. Neurophysiol. 115, 1399–1409 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yang G. R., Murray J. D., Wang X.-J., A dendritic disinhibitory circuit mechanism for pathway-specific gating. Nat. Commun. 7, 12815 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wilmes K. A., Clopath C., Inhibitory microcircuits for top-down plasticity of sensory representations. Nat. Commun. 10, 5055 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hertäg L., Sprekeler H., Amplifying the redistribution of somato-dendritic inhibition by the interplay of three interneuron types. PLOS Comput. Biol. 15, e1006999 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hertäg L., Sprekeler H., Learning prediction error neurons in a canonical interneuron circuit. eLife 9, e57541 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jazayeri M., Shadlen M. N., Temporal context calibrates interval timing. Nat. Neurosci. 13, 1020–1026 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ashourian P., Loewenstein Y., Bayesian inference underlies the contraction bias in delayed comparison tasks. PLoS One 6, e19551 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Petzschner F. H., Glasauer S., Iterative Bayesian estimation as an explanation for range and regression effects: A study on human path integration. J. Neurosci. 31, 17220–17229 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Acerbi L., Wolpert D. M., Vijayakumar S., Internal representations of temporal statistics and feedback calibrate motor-sensory interval timing. PLOS Comput. Biol. 8, e1002771 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Akrami A., Kopec C. D., Diamond M. E., Brody C. D., Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 554, 368–372 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Meirhaeghe N., Sohn H., Jazayeri M., A precise and adaptive neural mechanism for predictive temporal processing in the frontal cortex. Neuron 109, 2995–3011.e5 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fino E., Yuste R., Dense inhibitory connectivity in neocortex. Neuron 69, 1188–1203 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Packer A. M., Yuste R., Dense, unspecific connectivity of neocortical parvalbumin-positive interneurons: A canonical microcircuit for inhibition? J. Neurosci. 31, 13260–13271 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lee S., Kruglikov I., Huang Z. J., Fishell G., Rudy B., A disinhibitory circuit mediates motor integration in the somatosensory cortex. Nat. Neurosci. 16, 1662–1670 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pi H.-J., et al., Cortical interneurons that specialize in disinhibitory control. Nature 503, 521–524 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jouhanneau J.-S., Kremkow J., Dorrn A. L., Poulet J. F., In vivo monosynaptic excitatory transmission between layer 2 cortical pyramidal neurons. Cell Rep. 13, 2098–2106 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pala A., Petersen C. C. H., In vivo measurement of cell-type-specific synaptic connectivity and synaptic transmission in layer 2/3 mouse barrel cortex. Neuron 85, 68–75 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wilson H. R., Cowan J. D., Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Larkum M., A cellular mechanism for cortical associations: An organizing principle for the cerebral cortex. Trends Neurosci. 36, 141–151 (2013). [DOI] [PubMed] [Google Scholar]
- 38.Harris K. D., Shepherd G. M., The neocortical circuit: Themes and variations. Nat. Neurosci. 18, 170–181 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mumford D., On the computational architecture of the neocortex. II. The role of cortico-cortical loops. Biol. Cybern. 66, 241–251 (1992). [DOI] [PubMed] [Google Scholar]
- 40.Friston K., Hierarchical models in the brain. PLoS Comput. Biol. 4, e1000211 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gilbert C. D., Li W., Top-down influences on visual processing. Nat. Rev. Neurosci. 14, 350–363 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Heeger D. J., Theory of cortical function. Proc. Natl. Acad. Sci. U.S.A. 114, 1773–1782 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sun Q., et al., A whole-brain map of long-range inputs to GABAergic interneurons in the mouse medial prefrontal cortex. Nat. Neurosci. 22, 1357–1370 (2019). [DOI] [PubMed] [Google Scholar]
- 44.Naskar S., Qi J., Pereira F., Gerfen C. R., Lee S., Cell-type-specific recruitment of GABAergic interneurons in the primary somatosensory cortex by long-range inputs. Cell Rep. 34, 108774 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pakan J. M., et al., Behavioral-state modulation of inhibition is context-dependent and cell type specific in mouse visual cortex. eLife 5, e14985 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Vogels T. P., Sprekeler H., Zenke F., Clopath C., Gerstner W., Inhibitory plasticity balances excitation and inhibition in sensory pathways and memory networks. Science 334, 1569–1573 (2011). [DOI] [PubMed] [Google Scholar]
- 47.Rumelhart D. E., Hinton G. E., Williams R. J., Learning representations by back-propagating errors. Nature 323, 533–536 (1986). [Google Scholar]
- 48.Mackwood O., Naumann L. B., Sprekeler H., Learning excitatory-inhibitory neuronal assemblies in recurrent networks. eLife 10, e59715 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jordan R., Keller G. B., Opposing influence of top-down and bottom-up input on excitatory layer 2/3 neurons in mouse primary visual cortex. Neuron 108, 1194–1206.e5 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Faisal A. A., Selen L. P., Wolpert D. M., Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Vierordt K., Der Zeitsinn Nach Versuchen (H. Laupp, 1868).
- 52.Hollingworth H. L., The central tendency of judgment. J. Philos. Psychol. Sci. Methods 7, 461–469 (1910). [Google Scholar]
- 53.Wong K.-F., Wang X.-J., A recurrent network mechanism of time integration in perceptual decisions. J. Neurosci. 26, 1314–1328 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bono J., Clopath C., Modeling somatic and dendritic spike mediated plasticity at the single neuron and network level. Nat. Commun. 8, 706 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Abs E., et al., Learning-related plasticity in dendrite-targeting layer 1 interneurons. Neuron 100, 684–699.e6 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Clopath C., Büsing L., Vasilaki E., Gerstner W., Connectivity reflects coding: A model of voltage-based STDP with homeostasis. Nat. Neurosci. 13, 344–352 (2010). [DOI] [PubMed] [Google Scholar]
- 57.Pedrosa V., Clopath C., Voltage-based inhibitory synaptic plasticity: Network regulation, diversity, and flexibility. bioRxiv [Preprint] (2020). https://www.biorxiv.org/content/10.1101/2020.12.08.416263v1 (Accessed 12 June 2021).
- 58.Widmer F. C., Keller G. B., Developmental plasticity in visual cortex is necessary for normal visuomotor integration and visuomotor skill learning. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.06.20.449148v1 (Accessed 21 June 2021).
- 59.Larkum M. E., Zhu J. J., Sakmann B., A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature 398, 338–341 (1999). [DOI] [PubMed] [Google Scholar]
- 60.Payeur A., Guerguiev J., Zenke F., Richards B. A., Naud R., Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits. Nat. Neurosci. 24, 1010–1019 (2021). [DOI] [PubMed] [Google Scholar]
- 61.Spratling M. W., Predictive coding as a model of response properties in cortical area V1. J. Neurosci. 30, 3531–3543 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gillon C. J., et al., Learning from unexpected events in the neocortical microcircuit. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.01.15.426915v2 (Accessed 29 March 2021).
- 63.Whittington J. C. R., Bogacz R., An approximation of the error backpropagation algorithm in a predictive coding network with local hebbian synaptic plasticity. Neural Comput. 29, 1229–1262 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sacramento J. a., Ponte Costa R., Bengio Y., Senn W., “Dendritic cortical microcircuits approximate the backpropagation algorithm” in Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Bengio S., et al., Eds. (Curran Associates, Inc., Red Hook, NY, 2018), vol. 31. [Google Scholar]
- 65.Millidge B., Tschantz A., Buckley C. L., Predictive coding approximates backprop along arbitrary computation graphs. arXiv [Preprint] (2020). https://arxiv.org/abs/2006.04182 (Accessed 10 August 2021). [DOI] [PubMed]
- 66.Rosenbaum R., On the relationship between predictive coding and backpropagation. arXiv [Preprint] (2021). https://arxiv.org/abs/2106.13082v3 (Accessed 10 August 2021). [DOI] [PMC free article] [PubMed]
- 67.Rombouts J. O., Bohte S. M., Roelfsema P. R., How attention can create synaptic tags for the learning of working memories in sequential tasks. PLoS Comput. Biol. 11, e1004060 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Bredenberg C., Lyo B., Simoncelli E., Savin C., “Impression learning: Online representation learning with synaptic plasticity” in Advances in Neural Information Processing Systems 34 Pre-Proceedings (NeurIPS 2021), Ranzato M., et al., Eds. (Curran Associates, Inc., Red Hook, NY, 2021), vol. 34. [Google Scholar]
- 69.Oemisch M., et al., Feature-specific prediction errors and surprise across macaque fronto-striatal circuits. Nat. Commun. 10, 176 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Adesnik H., Abdeladim L., Probing neural codes with two-photon holographic optogenetics. Nat. Neurosci. 24, 1356–1366 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Kawashima T., Okuno H., Bito H., A new era for functional labeling of neurons: Activity-dependent promoters have come of age. Front. Neural Circuits 8, 37 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.DeNardo L., Luo L., Genetic strategies to access activated neurons. Curr. Opin. Neurobiol. 45, 121–129 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Courville A. C., Daw N. D., Touretzky D. S., Bayesian theories of conditioning in a changing world. Trends Cogn. Sci. 10, 294–300 (2006). [DOI] [PubMed] [Google Scholar]
- 74.Mazzucato L., Camera G. La, Fontanini A., Expectation-induced modulation of metastable activity underlies faster coding of sensory stimuli. Nat. Neurosci. 22, 787–796 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source code to reproduce the simulations, analyses, and figures are available in GitHub (https://github.com/lhertaeg/SourceCode_Hertaeg2021). All other data are included in the manuscript and/or SI Appendix.