Abstract
The electron deficiency and strong bonding capacity of boron have created numerous species with unusual structural and electronic properties in the form of pure and hetero-atom doped boron clusters. Here we identified D9d-symmetry Na2B18 and Na2B18− tubular boron clusters as global minima, whose stability is significantly enhanced by two doped sodium atoms. The doped Na atoms trigger strong charge transfer from Na to the boron motifs, resulting in salt complexes (Na22+B182− and Na22+B183−). In particular, the optimal electrostatic interactions arising from the doping effect play a crucial role in stabilizing the tubular structure against the planar and quasi-planar preferences of the negatively charged boron clusters.
The optimal electrostatic interactions arising from the doping effect play a crucial role in stabilizing the tubular structure against the planar and quasi-planar preferences of the negatively charged boron clusters.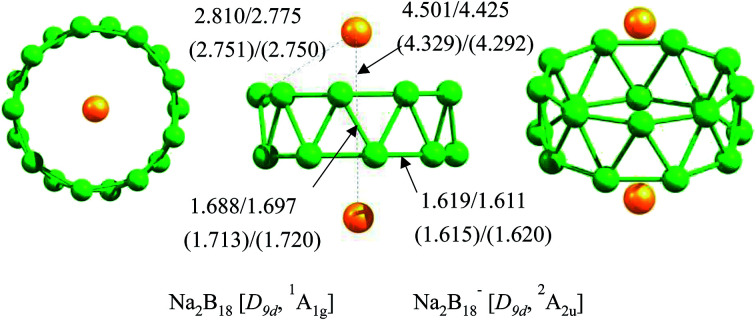
1. Introduction
Zero-dimensional boron clusters have received incessant attention from the aspects of their molecular shapes and multi-center bonding.1,2 In comparison with cage-like structured bulk boron,3 boron clusters Bn, from small size to an extended size range at least up to B38− (B16+), prefer to form planar or quasi-planar structures, which have been confirmed via experimental and high-level computational studies.4,5 Remarkably, over past decades, a set of pure and doped boron clusters have been systematically characterized, which constantly pushes our current understanding of the structural evolution of isolated boron clusters.6–8 Recently, the discovery of all-boron fullerenes,9,10 borophenes and boron sheets on metal surfaces,11–14 motivated by their carbon analogues, has overwhelmingly enriched studies of the chemistry of boron and may lead to new boron-based materials. On the other hand, studies of doped boron clusters with transition metals, such as metal-centered monocyclic rings,7 metalloborophenes,15 half-sandwich structures,16,17 and metal-centered tubular structures and cages,18–23 have created a series of clusters with novel structures and chemical bonding. All these doped-boron clusters have pushed the limits of recorded coordination numbers and structural chemistry.
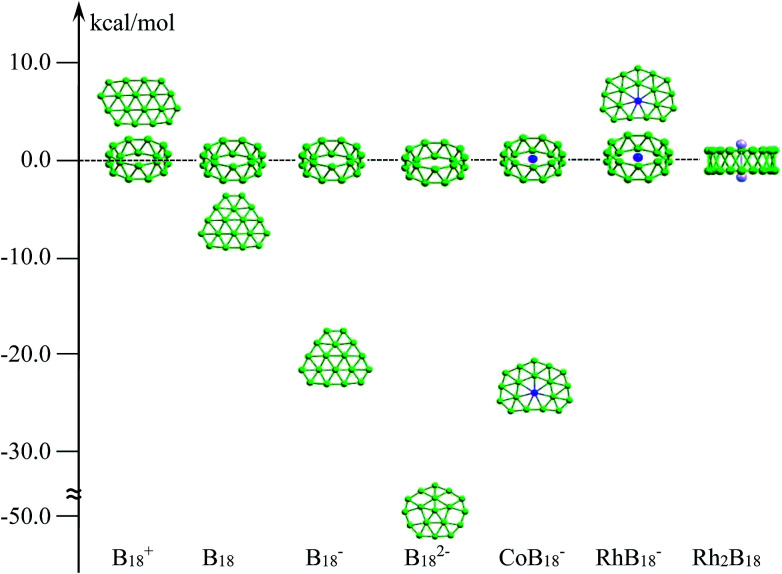
Tubular boron structures are a very special case in terms of isolated boron clusters. They have aroused widespread interest for many years because they can be considered not only as a key indicator of the 2D-to-3D (planar to three-dimensional form) structural transition of boron clusters, but also as embryos for boron nanotubes. The two-ring B20 tubular cluster is the first example and it is characterized as the global minimum on the basis of computational calculations, yet it has not been observed experimentally.24,25 Remarkably, cationic B2n+ (n = 9–10) tubular structures were clearly confirmed via joint ion mobility experiments combined with density functional theory (DFT) calculations.5 For anionic boron clusters, planar or quasi-planar boron (2D) forms remain critical competing alternatives that are more stable in energy than the tubular forms; this has been confirmed via photoelectron spectroscopy (PES) combined with theoretical investigations.26–28 The 2D preference of negatively charged boron clusters can be ascribed to the fact that electron addition tends to enhance the stability of the 2D form over the corresponding 3D isomer, irrespective of the available electrons.29 For instance, as shown in Scheme 1, the tubular structure of B18+ was suggested to be the global minimum, whereas the B18, B18− and B182− analogues were found to be high-energy isomers.5,30–32 Meanwhile, it is noted that the stability of a tubular structure deceases along with an increase in electrons, so it is difficult to stabilize doubly or more negatively charged boron tubular clusters. Interestingly, doped boron clusters with transition metals have led to the achievement of mono-metal-centered tubular boron clusters. Recently, tubular MB16− (M = Co, Mn), RhB18− and TaB20− have been characterized via PES combined with theoretical predictions.18,22,33,34 Clearly, the strong covalent interactions between the transition metal and tubular boron motifs significantly stabilize the tubular structures. Recent works have shown that the tubular-to-cage-like structural transition has started in large mono-metal-based boron clusters.21,35
Scheme 1. The relative energy differences in kcal mol−1 between tubular structures and low-lying planar forms at the DFT level.5,30–32.
Our recent work revealed that the thermodynamic stability of tubular boron clusters was significantly promoted in Li-doped boron species (LiB20 and LiB20−) in comparison with bare anionic B20 species.36 This is because the optimal electrostatic interactions arising from charge transfer significantly improve the stability of tubular boron clusters. In this work, we followed the same strategy and found that the effects from two doped Na atoms can tune the preference between 2D and tubular forms in the difficult case of negatively charged B18, where the tubular form is a high-energy isomer. Herein we report an investigation into di-alkali metal doped boron clusters in the form of Na2B18 and Na2B18− species. Surprisingly, rather than forming a half-sandwich structure with the quasi-planar structure of bare B18, B18− and B182−, the Na2B18 and Na2B18− clusters are predicted to have tubular structures, where the two Na atoms are located on the high-symmetry axis of the tubular structures and the two sides of the double-ring boron. Chemical bonding analysis has revealed that the tubular clusters are charge-transfer complexes formed by Na+ and B182− (B183−), where the optimal electrostatic interactions between Na and boron clusters are found.
2. Computational details
The structure search is performed using the PSO algorithm within the revolutionary scheme, as implemented via CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) code.37 Specifically, in the PSO search, the population size is set to 30, and the number of generations is maintained at 30. The best 60% of structures are selected through PSO to generate the next generation, while the other structures are generated randomly to guarantee structural diversity. The B3LYP/6-31G(d) level of theory was used to optimize the initial structure with a variety of spin states, and for the low-lying (<30 kcal mol−1 above the global minimum) isomers, we employed B3LYP/6-311+G(d) and TPSSh/6-311+G(d) for better geometrical and frequency predictions. The single-point calculations for the low-lying isomers were performed at the CCSD(T)/6-311+G(d)//TPSSh/6-311+G(d) level of theory. We found that T1 values are in the range of 0.01 to 0.03 for the low-lying isomers, indicating that the mono-determinantal method can be safely employed for our species. Electron detachment energies from the closed-shell ground state of Na2B18− and the low-lying isomers were computed at the TD-B3LYP/6-311+G(2df) level of theory based on B3LYP/6-311+G(d) geometry. The chemical bonding in Na2B18 and Na2B18− has been revealed via natural bonding orbital (NBO)38 and adaptive natural density partitioning (AdNDP) algorithm analysis.39 Total energies were corrected using the zero-point energies (ZPE). All calculations were carried out with the GAUSSIAN09 program package.40
3. Results and discussion
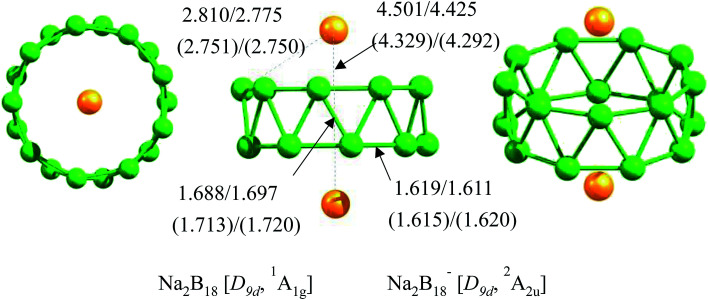
CALYPSO was performed to explore the potential energy surfaces of neutral Na2B18 and anionic Na2B18− clusters in low and high spin states. At the B3LYP/6-311+G(d) and TPSSh/6-311+G(d) levels of theory, the tubular structures of Na2B18 and Na2B18− were found to be local minima, with large lowest frequencies of above 100.0 cm−1 (see Table 1) and high D9d-symmetry, where the two Na atoms are located on the high-symmetry axis of the tubular structures (see Fig. 1). Furthermore, the tubular structures were predicted to be global minima at the B3LYP, TPSSh and single-point CCSD(T) levels of theory with the 6-311+G(d) basis set. In particular, they are 2.1 and 2.0 kcal mol−1 more stable than the second lowest isomers of the Na2B18 and Na2B18− species, respectively, at the single-point CCSD(T)/6-311+G(d)//TPSSh/6-311+G(d) level of theory. All low-lying isomers are provided in the ESI.† For the nearest competing isomers, the B18 motif possesses a quasi-planar structure that is similar to the low-lying isomers of bare anionic B182−, and the two Na atoms were located above or beside the quasi-plane of the boron clusters.
The smallest frequencies (Vmin, cm−1) of the tubular structures, NPA charges on Na and B (QNa and QB, |e|), bond properties (bond length (Å), Wiberg bond indices in parenthesis) and HOMO–LUMO gaps (gap, eV). All values have been computed at the B3LYP/6-311+G(d) level of theory.
| Species | V min (cm−1) | BNa–Na (Å) | BNa–B (Å) | BB–B (Å) | Q Na (|e|) | Q B (|e|) | Gap (eV) |
|---|---|---|---|---|---|---|---|
| Na2B18 | 131.3 | 4.501 (0.00) | 2.810 (0.01) | 1.688; 1.619 (0.71); (0.96) | 0.96 | −0.11 | 2.07 |
| Na2B18− | 176.1 | 4.329 (0.00) | 2.751 (0.01) | 1.713; 1.615 (0.65); (1.01) | 0.95 | −0.16 | 1.15 |
Fig. 1. Three views of the Na2B18 and Na2B18− species. The point group symmetries and spectroscopic states are shown in square brackets. All distances are in Å; the values shown in parentheses refer to the anionic Na2B18− system, the values before the backslash are obtained at the B3LYP/6-311+G(d) level of theory and the ones after the backslash are obtained at the TPSSh/6-311+G(d) level of theory.
The structural details of the tubular structures of Na2B18 and Na2B18− are tabulated in Table 1. The structures of the neutral and anionic forms are very similar, except for the significant difference in the Na–B and Na–Na interaction distances. Contrasting with neutral Na2B18, the Na–B and Na–Na interaction distances in the Na2B18− cluster were clearly reduced by 0.06 and 0.17 Å, respectively. The calculated natural atomic charge on the Na atom is about 0.95 |e| in the Na2B18 and Na2B18− species, indicating that Na serves as the donor of one electron to the B18 tubular motifs, forming typical charge-transfer Na22+B182− and Na22+B183− complexes. The calculated natural atomic charges on the B atoms are −0.11 and −0.16 |e| in the Na2B18 and Na2B18− species, respectively, resulting in stronger electrostatic interactions between Na+ and the anionic boron cluster in the Na2B18− system compared to the neutral analogue. This is the reason that shorter Na–B and Na–Na interaction distances were found in the anionic Na2B18− system. It is worth noting that the Na–B bond distances in both neutral and anionic Na2B18 are longer than a Na–B single bond (2.4 Å) obtained using the self-consistent covalent radii of Pyykko,41 which is consistent with the negligible Wiberg bond indices (WBIs) listed in Table 1. Clearly, the two kinds of B–B bonds, inter-ring and intra-ring, are found in both neutral and anionic tubular species. The inter-ring B–B bonds are responsible for holding two monocyclic B9 rings together, and are clearly longer (about 0.07 Å) than the intra-ring B–B bonds (1.62 Å). The WBIs of the two kinds of B–B bonds further confirm the assessment of bond distances. Moreover, their strength can be referenced to the value of a typical B–B single bond (1.70 Å). It is worthy of note that two such kinds of B–B bonds have been found in all the tubular structures of pure boron or hetero-doped boron clusters. Note that the formation of Na–B interactions in Na2B18 and Na2B18− species effectively removes the electronic charge of two Na atoms, which evidently promotes the electrostatic interactions between Na+ and the tubular boron motifs, giving rise to the eighteen optimal Na–B interactions and high thermodynamic stability of the tubular structures.
As discussed above, both Na2B18 and Na2B18− species are essentially charge-transfer complexes between Na+ and B182− (B183−). To discover how the further thermodynamic stability of tubular structures is gained, we investigated two kinds of dissociation pathways by means of: (i) Na2B18 → 2Na+ + B182− and (ii) Na2B18 → 2Na + B18; and (iii) Na2B18− → 2Na+ + B183− and (iv) Na2B18− → 2Na + B18− for the Na2B18 and Na2B18− species, where all these fragments are in their electronic ground states. At the TPSSh/6-311+G(d) level of theory, pathways (i) and (ii) for Na2B18 give dissociation energies of 283.1 and 121.7 kcal mol−1, respectively, and pathways (iii) and (iv) for Na2B18− give dissociation energies of 441.4 and 81.5 kcal mol−1, respectively. The high dissociation energies indicate the good stability against the dissociation of M and M+ for tubular motifs. Additionally, the degrees of Na+ and tubular boron interaction could be approximately estimated and compared. The interaction energies between Na+ and tubular boron are estimated to be 171.5 and 253.9 kcal mol−1, half of the total dissociation energies of pathways (i) and (iii), respectively, where the boron fragments are in ground electronic states with the framework of a tubular structure. Strong electrostatic interactions between Na+ and the tubular boron motifs provide a key driving force for stabilizing these charge-transfer complexes in the neutral and anionic states. The optimized structures of the bare tubular B182− and B183− clusters lie 59.8 and 64.3 kcal mol−1 higher in energy, respectively, than the quasi-planar minimum at the TPSSh/6-311+G(d) level of theory. The tubular structures of the anionic B182− and B183− species are significantly stabilized by means of doping two cationic Na+ ions, resulting in effective charge transfer in the tubular structures. Moreover, additional electrostatic stabilization occurred in Na2B18− compared to Na2B18via one more electron being only localized in the tubular boron motifs. Thus, only electrostatic interactions between Na and the B18 clusters make Na2B18 and Na2B18− highly thermodynamically stable species.
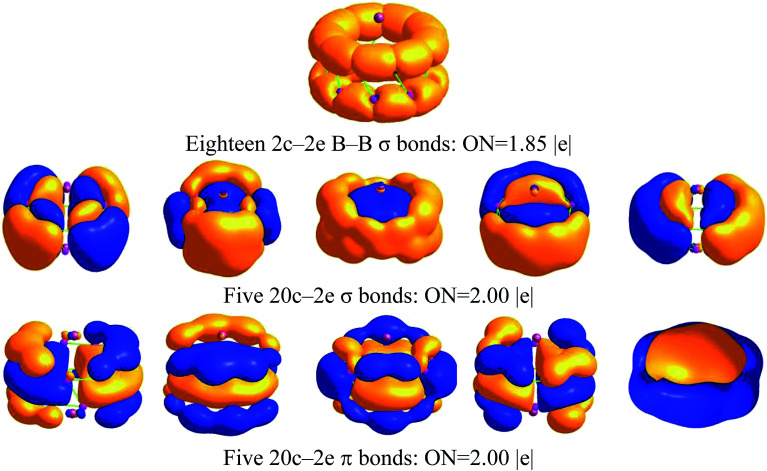
The molecular orbitals of Na2B18− are given in Fig. S2,† and one unpaired electron resides in a singly occupied molecular orbital (SOMO) instead of a closed-shell neutral one. To further understand the structure and stability of the tubular structure, we analyzed the chemical bonding of the Na2B18 system using the adaptive natural density partitioning (AdNDP) method at the B3LYP/6-311+G(d) level of theory. AdNDP analysis transformed the 28 canonical molecular orbitals of the Na2B18 system into localized and delocalized multi-center bonds, as shown in Fig. 2. There are three types of bond in the tubular boron cluster. The first row depicts eighteen two center-two electron (2c–2e) localized σ bonds with an occupation number (ON) of 1.85 |e|, which is very similar to the ON of a bare B18 cluster, as shown in the ESI.† The remaining AdNDP bonds can be considered as delocalized multi-center σ and π bonds between the two B9 rings. The second and third rows exhibit five delocalized σ and π bonds, respectively, representing strong bonding interactions between the five delocalized σ and π bonds in each B9 ring. The second and third row each describe an aromatic system, resulting in fairly stable D9d tubular Na2B18 clusters.
Fig. 2. AdNDP analysis of Na2B18 computed at the B3LYP/6-311+G(d) level of theory; ON stands for occupation number.
To facilitate the future experimental characterization of the anionic tubular Na2B18− system, we use time-dependent (TD)-B3LYP/6-311+G(2df) theory to calculate the vertical electron detachment energies (VDEs) for the three lowest energy isomers. Tubular Na2B18− is predicted to have an extremely low first VDE of 1.65 eV, originating from the detachment of the electron from the SOMO, which is significantly lower in energy than the other low-lying isomers by about 0.9 eV (see Table S1–S3†). The first adiabatic electron detachment energy (ADE) is calculated as the total energy difference between Na2B18− and Na2B18 using their respective optimized geometries. The ADE values are 1.63, 1.97 and 1.88 eV for the three low-lying isomers I, II and III. Overall, the tubular structure has a clear signal compared to the other low-lying isomers and this can be distinguished in experiments. The calculated infrared (IR) absorption spectrum of the neutral Na2B18 tubular structure is depicted in Fig. S5,† which should aid the forthcoming experimental characterization of the tubular structures.
Small boron clusters have been found to show planar and quasi-planar preferences and electron delocalization in both the σ and π frameworks has been shown to be the major driving force. A tubular structure was first shown to be viable for the neutral B20 cluster and was suggested to be the embryo for boron nanotubes.24 Ion mobility and DFT calculations suggested that cationic boron clusters (Bn+) prefer to take up tubular structures for n > 15.5 However, for anionic Bn− clusters, no tubular clusters have been observed up to n = 40.4 This trend results from the fact that electron addition tends to enhance the stability of 2D isomers over the corresponding 3D isomers, irrespective of the available electrons. Clearly, the strong metal–boron covalent interactions in CoB16−, MnB16− and RhB18− are critical in stabilizing tubular structures, and they require a perfect electronic and structural match between the metal and the boron cluster to justify the balance between M–B interactions in the tubular isomers and 2D electron delocalization.18,33,34 By means of a detailed analysis of the structural and electronic properties, the anionic tubular structures stabilized by doped alkali metals are found to be due to strong electrostatic interactions between Na+ and the anionic B18 motifs. Following this idea, we further extend this strategy to the other alkali metals (M = Li, K). The initial geometries were constructed by replacing Na with M atoms in term of the isomers of the Na-doped system, as shown in Fig. S1 and S2.† As shown in Fig. S6,† all the low-lying isomers are given for the M2B18 and M2B18− (M = Li, K) species. As predicted, the tubular boron clusters were the lowest-energy isomers for all species at the TPSSh/6-311+G(d) level of theory. In the case of tubular boron structures, two kinds of B–B bond show an insignificant change for all the M-doped systems (M = Li, Na, K), whereas the M–B and M–M interaction distances increase along with the size of the alkali metal (see Fig. S7†). This work suggests a new strategy where the electrostatic interactions can be used to clearly tune the boron arrangement preference, which is further useful for understanding the structural evolution of boron clusters.
4. Conclusions
In summary, we present a symmetric theoretical investigation into the viability of tubular structures in Na2B18 and Na2B18− clusters. We found that tubular structures with high D9d symmetry have been predicted to be global minima via high-level calculations. Chemical bonding analysis revealed that the tubular structures are charge-transfer complexes, where the two Na atoms are localized on the axis of the tubular structure, giving rise to optimal Na–B electrostatic interactions. The strong electrostatic interactions between Na+ atoms and tubular boron structures appear to be critical in stabilizing the tubular structure, which is an unfavorable configuration in comparison to the quasi-planar and planar arrangement of pure anionic boron species because of 2D electron delocalization. The Na2B18 and Na2B18− species represent a new class of metal-doped boron clusters, providing new insights into tubular boron species and further recommending boron clusters as a promising building block for new boron-based nanostructures.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This work was funded by the National Natural Science Foundation of China (No. 11874178, 21503088). Anita Das acknowledges SERB, India, for providing a National Post-Doctoral Fellowship (N-PDF application no. PDF/2017/000315). The partial calculations in this work were supported by the High Performance Computing Center of Jilin University, China.
Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra10123j
References
- Kondo T. Sci. Technol. Adv. Mater. 2017;18:780–804. doi: 10.1080/14686996.2017.1379856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L.-S. Int. Rev. Phys. Chem. 2016;35:69–142. [Google Scholar]
- Oganov A. R. Chen J. Gatti C. Ma Y. Ma Y. Glass C. W. Liu Z. Yu T. Kurakevych O. O. Solozhenko V. L. Nature. 2009;457:863–867. doi: 10.1038/nature07736. [DOI] [PubMed] [Google Scholar]
- Li W.-L. Chen X. Jian T. Chen T.-T. Li J. Wang L.-S. Nat. Rev. Chem. 2017;1:71. doi: 10.1038/s41570-017-0071. [DOI] [Google Scholar]
- Oger E. Crawford N. R. M. Kelting R. Weis P. Kappes M. M. Ahlrichs R. Angew. Chem., Int. Ed. 2007;46:8503–8506. doi: 10.1002/anie.200701915. [DOI] [PubMed] [Google Scholar]
- Sergeeva A. P. Popov I. A. Piazza Z. A. Li W.-L. Romanescu C. Wang L.-S. Boldyrev A. I. Acc. Chem. Res. 2014;47:1349–1358. doi: 10.1021/ar400310g. [DOI] [PubMed] [Google Scholar]
- Romanescu C. Galeev T. R. Li W.-L. Boldyrev A. I. Wang L.-S. Acc. Chem. Res. 2013;46:350–358. doi: 10.1021/ar300149a. [DOI] [PubMed] [Google Scholar]
- Alexandrova A. N. Boldyrev A. I. Zhai H. J. Wang L. S. Coord. Chem. Rev. 2006;250:2811–2866. doi: 10.1016/j.ccr.2006.03.032. [DOI] [Google Scholar]
- Zhai H.-J. Zhao Y.-F. Li W.-L. Chen Q. Bai H. Hu H.-S. Piazza Z. A. Tian W.-J. Lu H.-G. Wu Y.-B. Mu Y.-W. Wei G.-F. Liu Z.-P. Li J. Li S.-D. Wang L.-S. Nat. Chem. 2014;6:727–731. doi: 10.1038/nchem.1999. [DOI] [PubMed] [Google Scholar]
- Lv J. Wang Y. Zhu L. Ma Y. Nanoscale. 2014;6:11692–11696. doi: 10.1039/C4NR01846J. [DOI] [PubMed] [Google Scholar]
- Li W. L. Chen Q. Tian W. J. Bai H. Zhao Y. F. Hu H. S. Li J. Zhai H. J. Li S. D. Wang L. S. J. Am. Chem. Soc. 2014;136:12257–12260. doi: 10.1021/ja507235s. [DOI] [PubMed] [Google Scholar]
- Mannix A. J. Zhou X.-F. Kiraly B. Wood J. D. Alducin D. Myers B. D. Liu X. Fisher B. L. Santiago U. Guest J. R. Yacaman M. J. Ponce A. Oganov A. R. Hersam M. C. Guisinger N. P. Science. 2015;350:1513–1516. doi: 10.1126/science.aad1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng B. Zhang J. Zhong Q. Li W. Li S. Li H. Cheng P. Meng S. Chen L. Wu K. Nat. Chem. 2016;8:563–568. doi: 10.1038/nchem.2491. [DOI] [PubMed] [Google Scholar]
- Zhang Z. Yang Y. Penev E. S. Yakobson B. I. Adv. Funct. Mater. 2017;27:1605059. doi: 10.1002/adfm.201605059. [DOI] [Google Scholar]
- Li W.-L. Jian T. Chen X. Chen T.-T. Lopez G. V. Li J. Wang L.-S. Angew. Chem., Int. Ed. 2016;55:7358–7363. doi: 10.1002/anie.201601548. [DOI] [PubMed] [Google Scholar]
- Chen T.-T. Li W.-L. Jian T. Chen X. Li J. Wang L.-S. Angew. Chem., Int. Ed. 2017;56:6916–6920. doi: 10.1002/anie.201703111. [DOI] [PubMed] [Google Scholar]
- Popov I. A. Li W. Piazza Z. A. Boldyrev A. I. Wang L. J. Phys. Chem. A. 2014;118:8098–8105. doi: 10.1021/jp411867q. [DOI] [PubMed] [Google Scholar]
- a Popov I. Jian T. V Lopez G. Boldyrev A. I. Wang L.-S. Nat. Commun. 2015;6:8654. doi: 10.1038/ncomms9654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv J. Wang Y. Zhang L. Lin H. Zhao J. Ma Y. Nanoscale. 2015;7:10482–10489. doi: 10.1039/C5NR01659B. [DOI] [PubMed] [Google Scholar]
- Tam N. M. Pham H. T. Van Duong L. Pham-Ho M. P. Nguyen M. T. Phys. Chem. Chem. Phys. 2015;17:3000–3003. doi: 10.1039/C4CP04279D. [DOI] [PubMed] [Google Scholar]
- Li H.-R. Liu H. Tian X.-X. Zan W.-Y. Mu Y.-W. Lu H.-G. Li J. Wang Y.-K. Li S.-D. Phys. Chem. Chem. Phys. 2017;19:27025–27030. doi: 10.1039/C7CP05179D. [DOI] [PubMed] [Google Scholar]
- Li W.-L. Jian T. Chen X. Li H.-R. Chen T.-T. Luo X.-M. Li S.-D. Li J. Wang L.-S. Chem. Commun. 2017;53:1587–1590. doi: 10.1039/C6CC09570D. [DOI] [PubMed] [Google Scholar]
- Wang Y. Wu X. Zhao J. J. Cluster Sci. 2018;29:847–852. doi: 10.1007/s10876-018-1369-3. [DOI] [Google Scholar]
- Kiran B. Bulusu S. Zhai H.-J. Yoo S. Zeng X. C. Wang L.-S. Proc. Natl. Acad. Sci. U. S. A. 2005;102:961–964. doi: 10.1073/pnas.0408132102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romanescu C. Harding D. J. Fielicke A. Wang L.-S. J. Chem. Phys. 2012;137:14317. doi: 10.1063/1.4732308. [DOI] [PubMed] [Google Scholar]
- Sergeeva A. P. Piazza Z. A. Romanescu C. Li W. L. Boldyrev A. I. Wang L. S. J. Am. Chem. Soc. 2012;134:18065–18073. doi: 10.1021/ja307605t. [DOI] [PubMed] [Google Scholar]
- Popov I. A. Piazza Z. A. Li W.-L. Wang L.-S. Boldyrev A. I. J. Chem. Phys. 2013;139:144307. doi: 10.1063/1.4824156. [DOI] [PubMed] [Google Scholar]
- Luo X.-M. Jian T. Cheng L.-J. Li W.-L. Chen Q. Li R. Zhai H.-J. Li S.-D. Boldyrev A. I. Li J. Wang L.-S. Chem. Phys. Lett. 2017;683:336–341. doi: 10.1016/j.cplett.2016.12.051. [DOI] [Google Scholar]
- Pham H. T. Van Duong L. Pham B. Q. Nguyen M. T. Chem. Phys. Lett. 2013;577:32–37. doi: 10.1016/j.cplett.2013.05.041. [DOI] [Google Scholar]
- Sergeeva A. P. Averkiev B. B. Zhai H.-J. Boldyrev A. I. Wang L.-S. J. Chem. Phys. 2011;134:224304. doi: 10.1063/1.3599452. [DOI] [PubMed] [Google Scholar]
- Moreno D. Pan S. Zeonjuk L. L. Islas R. Osorio E. Martínez-Guajardo G. Chattaraj P. K. Heine T. Merino G. Chem. Commun. 2014;50:8140–8143. doi: 10.1039/C4CC02225D. [DOI] [PubMed] [Google Scholar]
- Tai T. B. Tam N. M. Nguyen M. T. Chem. Phys. Lett. 2012;530:71–76. doi: 10.1016/j.cplett.2012.01.039. [DOI] [Google Scholar]
- Jian T. Li W.-L. Popov I. A. Lopez G. V. Chen X. Boldyrev A. I. Li J. Wang L.-S. J. Chem. Phys. 2016;144:154310. doi: 10.1063/1.4946796. [DOI] [PubMed] [Google Scholar]
- Jian T. Li W.-L. Chen X. Chen T.-T. Lopez G. V. Li J. Wang L.-S. Chem. Sci. 2016;7:7020–7027. doi: 10.1039/C6SC02623K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H.-R. Liu H. Lu X.-Q. Zan W.-Y. Tian X.-X. Lu H.-G. Wu Y.-B. Mu Y.-W. Li S.-D. Nanoscale. 2018;10:7451–7456. doi: 10.1039/C8NR01087K. [DOI] [PubMed] [Google Scholar]
- Liang W. Das A. Dong X. Cui Z. Phys. Chem. Chem. Phys. 2018;20:16202–16208. doi: 10.1039/C8CP01376D. [DOI] [PubMed] [Google Scholar]
- Wang H. Wang Y. Lv J. Li Q. Zhang L. Ma Y. Comput. Mater. Sci. 2016;112:406–415. doi: 10.1016/j.commatsci.2015.09.037. [DOI] [Google Scholar]
- Reed A. E. Weinstock R. B. Weinhold F. J. Chem. Phys. 1985;83:735–746. doi: 10.1063/1.449486. [DOI] [Google Scholar]
- Zubarev D. Y. Boldyrev A. I. Phys. Chem. Chem. Phys. 2008;10:5207–5217. doi: 10.1039/B804083D. [DOI] [PubMed] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 [Google Scholar]
- Pyykko P. Atsumi M. Chem.–Eur. J. 2009;15:12770–12779. doi: 10.1002/chem.200901472. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.