Ionic association analysis of LiTDI, LiFSI and LiPF₆ in EC/DMC for better Li-ion battery performances

Abstract

New lithium salts such as lithium bis(fluorosulfonyl)imide (LiFSI) and lithium 4,5-dicyano-2-(trifluoromethyl)imidazole-1-ide (LiTDI) are now challenging lithium hexafluorophosphate (LiPF₆), the most used electrolyte salt in commercial Li-ion batteries. Thus it is now important to establish a comparison of these electrolyte components in a standard solvent mixture of ethylene carbonate and dimethyl carbonate (EC/DMC: 50/50 wt%). With this aim, transport properties, such as the ionic conductivity, viscosity and ⁷Li self-diffusion coefficient have been deeply investigated. Moreover, as these properties are directly linked to the nature of the interionic interactions and ion solvation, a better understanding of the structural properties of electrolytes can be obtained. The Li salt concentration has been varied over the range of 0.1 mol L⁻¹ to 2 mol L⁻¹ at 25 °C and the working temperature from 20 °C to 80 °C at the fixed concentration of 1 mol L⁻¹. Experimental results were used to investigate the temperature dependence of the salt ion-pair (IP) dissociation coefficient (α_D) with the help of the Walden rule and the Nernst–Einstein equation. The lithium cation effective solute radius (r_Li) has been determined using the Jones–Dole–Kaminsky equation coupled to the Einstein relation for the viscosity of hard spheres in solution and the Stokes–Einstein equation. From the variations of α_D and r_Li with the temperature, it is inferred that in EC/DMC LiFSI forms solvent-shared ion-pairs (SIP) and that, LiTDI and LiPF₆ are likely to form solvent separated ion-pairs (S₂IP) or a mixture of SIP and S₂IP. From the temperature dependence of α_D, thermodynamic parameters such as the standard Gibbs free energy, enthalpy and entropy for the ion-pair formation are obtained. Besides being in agreement with the information provided by the variations of α_D and r_Li, it is concluded that the ion-pair formation process is exergonic and endothermic for the three salts in EC/DMC.

Insight is given on the type of ion-pairs that could be formed in EC/DMC by Li-salts LiTDI, LiFSI and LiPF₆.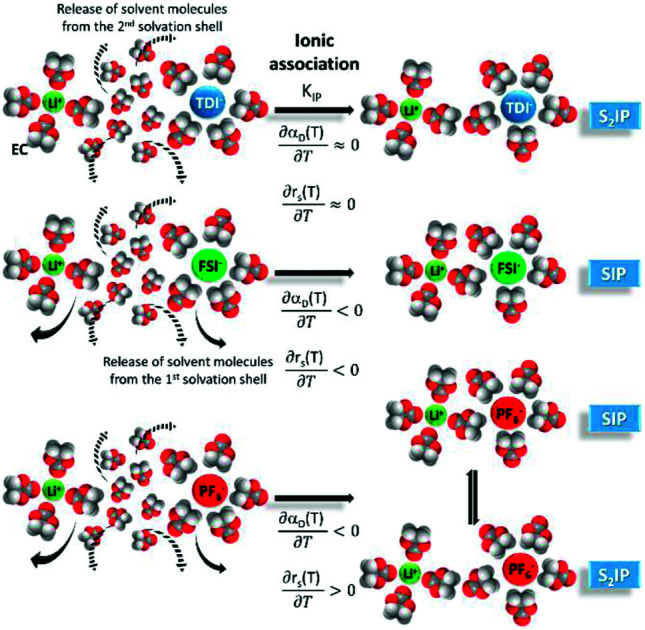

1. Introduction

The current desire to continuously increase the use of renewable and green energy in order to reduce the dependence on fossil fuel reserves comes with the necessity to multiply solar, tidal and wind power harvesting technologies. However, green energy is intermittent and depends on the weather. An energy shortage (at night, during windless and/or cloudless periods) has as much chance of happening as an energy surplus (summer days, storms). The use of technologies capable of storing energy directly where it is produced does not only solve the problem of the uncertainty of green energy delivery but also relieves the power grid and prevents its expansion. Indeed, the produced energy does not have to be transported over great distances as it is when coming from large-scale power plants, and the line-losses are reduced. Batteries are ideal candidates for such an application. Furthermore, stationary batteries can buffer voltage fluctuations to meet the power demands of consumers.

The lithium-ion battery (LiB) is the most popular rechargeable battery compared to other technologies due to its high energy density and its good cycle life.^1–6 Since the commercialization of its first generation by Sony in 1990 (ref. 7) LiBs have known an impressive increase in performance and a decrease in price.⁸ Today, LiBs can not only be found in all kinds of portable electronic devices such as smartphones, portable computers and digital cameras but also in larger systems such as electric vehicles.⁶ Thus, because of the increasing use of the LiB technology it is important for the future LiB generations to be even more performant and safe. To increase the energy density of LiBs higher-capacity materials are being explored. Oxygen-based and sulfur (Li₂S) positive electrodes are currently being studied^9,10 while silicon-alloys^11–13 show promising results as negative electrode material. Safety can be improved through a better choice of the battery components.

The electrolyte is one of the most important component of Li-ion batteries and represented a production of 103 kt and 1.4 B$ in revenues in 2016.¹⁴ Among all the Li salts that can be used as electrolyte salts, only lithium tetrafluoroborate (LiBF₄) and lithium hexafluorophosphate (LiPF₆) have been commercialized in current cells. Nevertheless, new salts like lithium bis(fluorosulfonyl)imide (LiFSI) and lithium 4,5-dicyano-2-(trifluoromethyl)imidazole-1-ide (LiTDI) are now challenging LiPF₆. Despite exhibiting many advantages over LiPF_6, the main limitation for their use in commercial batteries is their cost and availability. One of the objectives of this article is to establish a comparison between LiPF₆, LiTDI and LiFSI dissolved in a standard solvent: a mixture of ethylene carbonate and dimethyl carbonate (EC/DMC: 50/50 wt%). Beside security issues and interface stability with electrode materials, ion transport properties are the most important features for an electrolyte. Hence, in this work is presented an extended comparative study of the electrolyte transport properties, such as ion conductivity, electrolyte viscosity and self-diffusion coefficients. Moreover, from a deep study of these properties, are inferred other important parameters such as ion size, ion solvation and ion pairing, which can allow a better understanding of the behavior of lithium salts in solution.^15,16

2. Theory

2.1. Ion-pairing

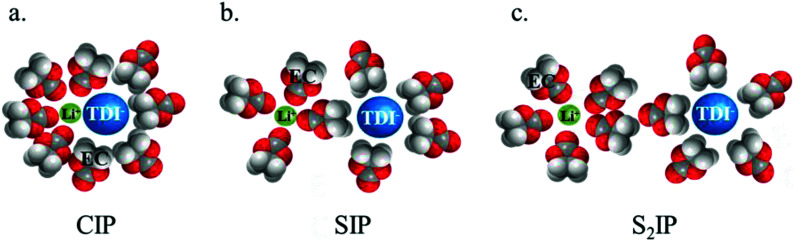
Electrolytes for Li-ion batteries generally contain 1 mol L⁻¹ of lithium salt dissolved in a mixture of alkylcarbonate solvents such as EC/DMC. In spite of the relatively high dielectric constant of EC, the formation of ion-pairs (IP) may occur. If M⁺, X⁻ and S stand respectively for the metallic cation, the anion and a solvent molecule then three kinds of ion-pairs are commonly described as illustrated in Fig. 1: (M⁺X⁻) the contact ion-pairs (CIP), (M⁺SX⁻) the solvent shared ion-pairs (SIP) and the (M⁺SSX⁻) solvent separated ion-pairs (S₂IP) when both ions retain their primary solvation shell. In low permittivity solvents higher ion-aggregates (AGG) may exist such as M⁺X⁻M⁺ triple ions, (M⁺X⁻)₂ ion-pair dimers, or even larger species.^17,18 Ion-pair population varies with ion size, solvent properties and temperature. The thermodynamic parameters describing ion association are the molar Gibbs free energy (ΔG_IP) for ion pairing and the related enthalpy (ΔH_IP) and entropy (ΔS_IP). These parameters are linked to each other and to the activity ratio (Q_r) and equilibrium constant (K_IP) of the chemical reaction describing the association, by the following equation.

ΔG_IP = ΔH_IP − TΔS_IP = RT ln(Q_r/K_IP) 1

Fig. 1. Schematic view of different types of ion-pairs, (a) contact ion-pair (CIP), (b) solvent-shared ion-pair (SIP) and (c) solvent separated ion-pair (S₂IP) in the case of the LiTDI salt dissolved in EC.

The ionic association process which leads to CIP or SIP is generally dominated by a positive ΔH_IP.

ΔH_IP = ΔH_el + ΔH_sol 2

where ΔH_el and ΔH_sol are the electric and solvation contributions to enthalpy.

The coulombic energy released when two oppositely charged ions are brought together, forming an ion pair, is an exothermic process (ΔH_el < 0 J mol⁻¹) but this contribution is overcompensated by the de-solvation contribution making the ion-pairing enthalpy ΔH_IP(T) positive. As a matter of fact, during association, the electric field becomes smaller around the ions that are now paired and consequently, an appreciable number of electrostricted solvent molecules are released to the bulk solvent. This phenomenon, being the inverse process of solvation, leads to a large endothermic solvation enthalpy contribution (ΔH_sol) which dominates the overall enthalpy ΔH_IP. The entropy variation ΔS_IP corresponding to the formation of an ion pair can also be expressed as the sum of two terms:

ΔS_IP = ΔS + ΔS_sol 3

where ΔS and ΔS_sol are respectively the ion pairing entropy variation under vacuum and the entropy variation resulting from the change in ion solvation in the considered solvent.

Ion association leads to a decrease in entropy ΔS < 0 J K⁻¹ mol⁻¹ as a solution containing un-associated ions is more disordered than a solution containing ion-pairs. Still, the displacement of solvent molecules from the solvation shell of the cation or the anion to the bulk solvent leads to a positive contribution (ΔS_sol > 0 J K⁻¹ mol⁻¹) to the global entropy. The sign of ΔS_IP depends on the magnitude of these two opposite contributions. Often the resulting ion pairing entropy is positive.

In the case of CIP and SIP, a large release of solvating molecules to the bulk occurs and hence ΔH_IP ≥ 0 J mol⁻¹ and ΔS_IP > 0 J K⁻¹ mol⁻¹. According to the Van't Hoff equation, any increase in temperature will favors ion pairing. On the contrary, in the case of S₂IP only solvent molecules belonging to the second solvation shell may be released during ion-pairing leading to a low and possibly negative association enthalpy and entropy. In consequence, any temperature increase will have no effect or favor ion-pair dissociation, depending on the magnitude of ΔH_IP.

2.2. Lithium effective ionic radius

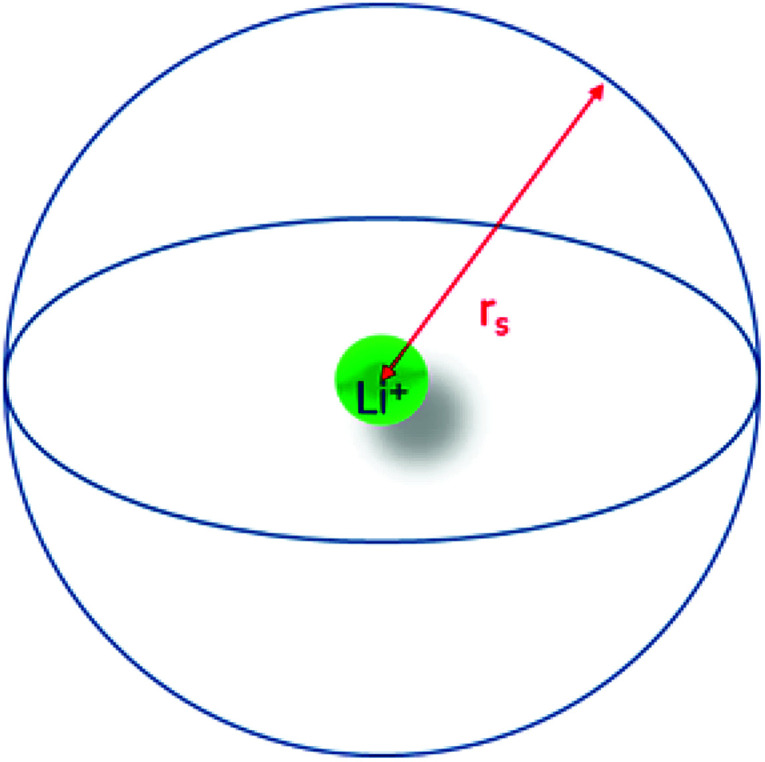
As presented in Fig. 2, the Li⁺ effective solute radius (r_s) represents the radius of the sphere englobing the species that participate in the first solvation layer of the lithium cation, its center.

Fig. 2. Schema presenting the lithium cation effective solute radius.

Two methods were used herein to estimate r_s. The first one makes use of the Stokes–Einstein equation applied to ⁷Li self-diffusion coefficients as:

D(Li) = kT/c 4

where c and k are the drag coefficient and the Boltzmann constant. For spherical entities, the drag coefficient is related to the effective radius r_s,stokes by applying the Stokes law:

c = 6πηr_s,stokes 5

where η is the viscosity of the electrolyte. Thus, from eqn (4) and (5) the effective Stokes radius can be deduced:

r_s,stokes = (kT)/(6πηD(Li)) 6

The second approach for determining r_s, is to use both the Einstein relation for the viscosity of a solution of hard spheres and its extension to spherical shaped suspensions (8)¹⁹ and the Jones–Dole–Kaminsky (JDK) eqn (7):^20–23

η_r = 1 + A√C + BC + DC² 7

In this equation, η_r is the relative viscosity of the solution (η_r = η/η°), C the salt concentration and A, B, D parameters describing respectively long-range ion–ion interactions, volume effects and short-range interactions. At concentrations higher than 0.1 mol L⁻¹ the A√C term is negligible.²⁴ The B parameter is closely linked to the molar volume of the solute as indicated by the Einstein relation (8). Finally, D remains an adjustable parameter as no equation has yet been found to calculate this term. At concentrations lower than 0.1 mol L⁻¹ the DC² term can be considered negligible compared to the other terms of the JDK equation but is predominant at higher concentrations.

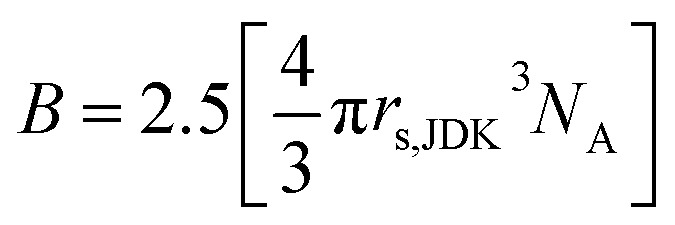8

where B is the JDK equation parameter, N_A the Avogadro number (6.022 × 10²³ mol⁻¹) and r_s,JDK the solute effective radius determined by using the JDK equation. Hence, its value is given by:

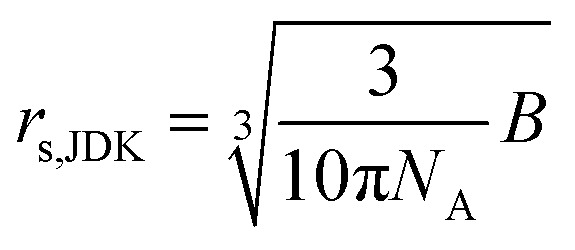9

2.3. Ion-pair dissociation coefficients

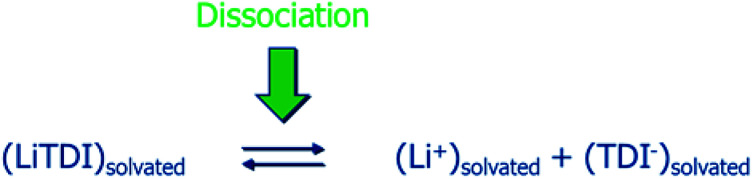
The dissociation coefficient (α_D) of the lithium salt, dissolved at the concentration C in the solvent mixture, is defined by the equilibrium described in Fig. 3.

Fig. 3. Schema defining the dissociation phenomena.

Determining α_D is not straightforward when the solute activity coefficient is difficult to determine and this is the case for the present electrolytes.

Nevertheless, two alternative methods can be used for this purpose. The first one makes use of the Walden rule (Method 1) and the second involves the use of the self-diffusion coefficients of the charged species (Method 2).

2.3.1. Method 1: the Walden rule

The classical Walden rule²⁵ is an empirical rule stating that the molar conductivity Λ (mS cm² mol⁻¹) times the viscosity η (mPa s) is constant for the same ionic species in different solvents. However, the Λη product independence to the solvent is only true at high dilution at which point ionic association is negligible and salt concentration does not affect viscosity.²⁶ This rule is relatively well adapted to the study of aqueous solutions and of a high number of organic solutions. Angell has extended the previous relation to other types of solutions by introducing the “fractional Walden rule”²⁷(10):

Λη^ν = constant 10

where ν is a constant 0 < ν < 1.^28–31

By plotting ln(Λ) vs. ln(η) for the present electrolytes, ν was found to be close to 1 as indicated by the values displayed in Table 1.

Values of the constant ν of the fractional Walden rule for LiTDI,³² LiPF₆ (ref. 32) and LiFSI.

	LiTDI	LiPF6	LiFSI
ν	1.0	0.9	0.8

The dissociation coefficients of LiTDI, LiPF₆ and LiFSI could then be estimated using eqn (11):^33–35

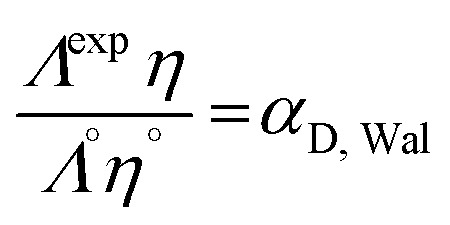11

where Λ^exp, Λ°(Τ) and η°(Τ) are the measured molar conductivity, the high dilution limiting molar conductivity (reported in Table 2) and the solvent viscosity, all three depending on the temperature.

Limiting molar conductivity Λ° values of LiTDI, LiFSI, and LiPF₆ in EC/DMC (50/50 wt%) at different temperatures.

		25 °C	50 °C	60 °C	80 °C
Λ° (10−4 × S m2 mol−1)	LiTDI	50.5	68.9	76.6	92.2
	LiFSI	43.5	59.2	65.5	78.8
	LiPF6	49.4	63.7	79.4	85.7

The limiting molar conductivity Λ° values were obtained by extrapolating at high dilution the variations of Λ vs. C^1/2 according to the Debye–Hückel–Onsager eqn (12):

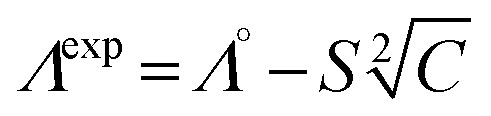12

where S is a constant.

2.3.2. Method 2: Nernst–Einstein equation

This method involves the knowledge of the self-diffusion coefficient values of the ionic species.³⁶ The ratio of the experimental molar conductivity Λ^exp to the molar conductivity (S m² mol⁻¹) calculated from the Nernst–Einstein equation (Λ^NE) represents the dissociation coefficient of the considered salt:

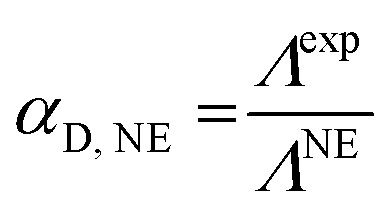13

Λ ^NE is calculated using eqn (14):

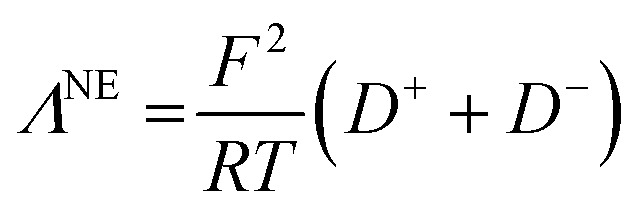14

where F is the Faraday constant, R the ideal gas constant, D⁺ and D⁻ the self-diffusion coefficients of the cation and the anion, and T the temperature. The measured self-diffusion coefficients of the lithiated species (D(⁷Li)) and of the fluorinated species (D(¹⁹F)) were considered close enough to D⁺ and D⁻ to consider that:

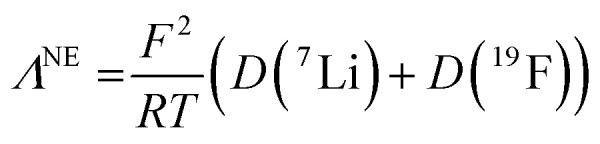15

Λ ^NE values are derived from the assumption that all of the diffusing lithiated and fluorinated species detected during the Pulse-Gradient Spin-Echo Nuclear Magnetic Resonance (PGSE-NMR) measurement contribute to the molar conductivity. Hence, the Nernst–Einstein equation gives the molar conductivity of the electrolyte as it should be if all ion-pairs were dissociated and/or if all charged species contribute to the bulk conductivity.

3. Experimental

3.1. Material and cell preparation

Highly pure (GC grade, molecular purity >99%) ethylene carbonate (EC) purchased from Fluka, and anhydrous dimethylcarbonate (DMC, molecular purity >99%) purchased from Sigma-Aldrich, were used as received. The alkyl-carbonate EC/DMC (50/50 wt%) mixture used was prepared using a Sartorius 1602 MP balance with a ±1 × 10⁻⁴ g accuracy in an argon filled MBraun glove box at 25 °C with less than 5 ppm of moister content. A GeneCust desiccant bag was placed in the mixture to reduce the water content to a minimal level.

The battery grade lithium hexafluorophosphate (LiPF₆) purchased from Fluorochem was kept and used under the dry atmosphere of the glove box.

The lithium 4,5-dicyano-2-(trifluoromethyl)imidazole-1-ide (LiTDI) and lithium bis(fluorosulfonyl)imide (LiFSI) were supplied by Arkema (Pierre-Bénite, France). Before use LiTDI was dried under vacuum at 120 °C and then placed under a dry atmosphere in the glove box and kept there. LiTDI, LiFSI and LiPF₆ were dissolved in EC/DMC (50/50 wt%) at concentrations going from 1 × 10⁻⁴ mol L⁻¹ to 2 mol L⁻¹ in the glove box and kept there until use.

Prior to any measurement, the water content of each electrolyte was measured using an 831 Karl-Fisher Coulometer (Metrohm). The water content of the LiPF₆ and LiFSI electrolytes was lower than 20 ± 1 ppm and that of the LiTDI electrolytes, lower than 100 ± 1 ppm as this salt is very hygroscopic.

3.2. Experimental methods

3.2.1. Conductivity measurements

Were performed using two different instruments. The first is a Crison (GLP 31) digital multi-frequencies (1000–5000 Hz) conductometer. The temperature (from 10 °C to 80 °C) was controlled by a JULABO thermostat bath with an accuracy of 0.2 °C. Before any measurement the conductometer cell was calibrated using standard KCl solutions at three different concentrations. The second instrument is a BioLogic Multichannel Conductivity Meter based on frequency Response Analyser (MCM 10) connected to a Peltier based temperature control unit with 10 slots (WTSH 10). The measurements where made using sealed cells with Pt parallel plate electrodes protecting the samples from air exposure.

3.2.2. Density and viscosity measurements

Were carried out from 10 °C to 60 °C using respectively an Anton Parr digital vibrating tube densitometer (model 60/602, Anton Parr, France) and an Anton Parr rolling-ball viscometer (Lovis 2000M/ME, Anton Parr, France). In both cases the cell temperature was regulated within ±0.02 °C. Dynamic viscosity values reported in this paper were calculated by taking into account the effect of the sample density and the buoyancy of the ball in each sample as a function of temperature. The densitometer was firstly calibrated at all temperatures with degassed water and dehumidified air at atmospheric pressure as recommended by the constructor while ultra-pure water was used to calibrate the viscometer. The uncertainty of the density and viscosity measurements were better than 5 × 10⁻⁵ g cm⁻³, and 1%, respectively.

3.2.3. Pulse-gradient spin-echo NMR (PGSE-NMR)

Experiments were performed on a Bruker DSX100 NMR spectrometer with a 2.35 T superconducting magnet, equipped with a 10 mm microimaging probe (Micro5 Bruker) without a lock system. The Larmor resonance frequencies are 39.91 MHz and 94.20 MHz for ⁷Li and ¹⁹F nuclei, respectively. All measurements were performed with the same NMR pulse sequence. In order to determine the activation energy for the diffusion process of each species, the NMR runs were carried out over a temperature range from 20 °C to 80 °C within an accuracy of ±1 °C and a step ΔT = 5 °C. The samples were prepared and placed in sealed glass tubes in a glove box. For NMR measurements, samples were thermally equilibrated at each temperature during 30 min before any acquisition in order to allow a good homogeneity of the set point temperature across the whole samples. Finally, all chemical shift references were set to a particular arbitrary value for convenience. Self-diffusion data concerning LiPF₆ and LiTDI in EC/DMC are taken from the literature.

4. Results and discussion

The transport properties of LiTDI, LiFSI and LiPF₆ in EC/DMC are investigated at fixed concentration (1 mol L⁻¹) over a large temperature range or at 25 °C as a function of the concentration in Li salt that ranges from 0 to 2 mol L⁻¹. From these results, the Li⁺ effective radius, the mean ion-pair dissociation coefficient and the thermodynamic parameters for ion-pair formation are determined. Finally, the most likely ion-pair structure for these salts is proposed.

4.1. Conductivity, viscosity and self-diffusion coefficients

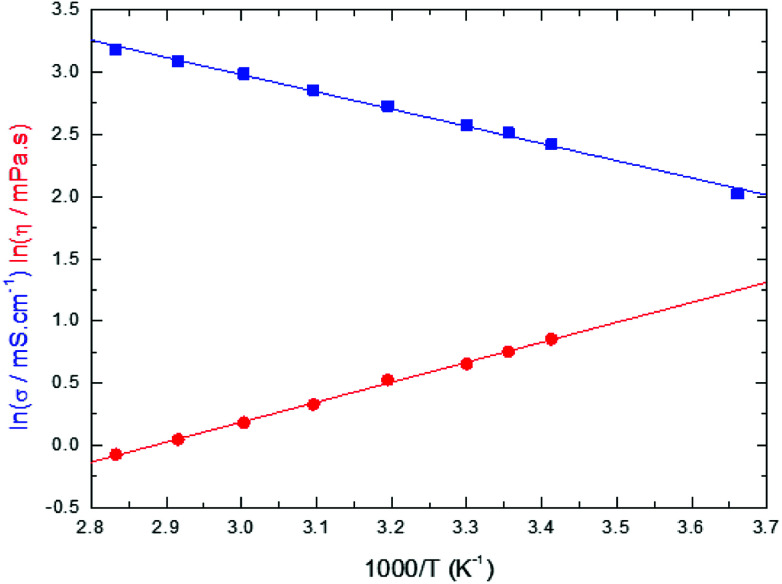
Conductivities and viscosities of the studied electrolytes are used here to calculate the ion-pair (IP) dissociation coefficient by using the Walden rule. With this aim, LiFSI conductivities and viscosities in EC/DMC have been measured as a function of the temperature and the results are presented in Fig. 4.

Fig. 4. Logarithmic plot of the conductivity (blue squares) and the viscosity (red discs) of LiFSI at 1 mol L⁻¹ in EC/DMC (50/50 wt%) as a function of 1/T.

The data plotted in Fig. 4 shows that the Arrhenius equations for the conductivity and the viscosity are verified:

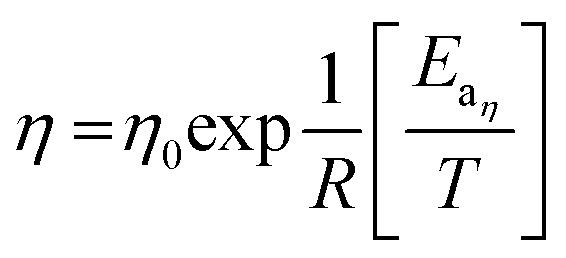16

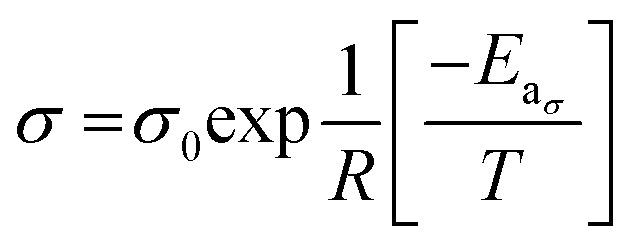17

In eqn (16) and (17), E_aη and E_aσ are the activation energies for the two processes and η₀ and σ₀ fitting parameters. The values of these parameters are reported in Table 3 together with those for LiTDI and LiPF₆ in EC/DMC. The R² correlation coefficient values, which are over 0.99, show that eqn (16) and (17) fit perfectly the experimental results obtained over the temperature range investigated.

Arrhenius fitting parameters for the conductivity and viscosity of the investigated 1 mol L⁻¹ LiX (X = TDI⁻, FSI⁻ or PF₆⁻) in EC/DMC (50/50 wt%) electrolytes with R² the correlation coefficient resulting from the fit procedure.

Conductivity	σ 0 (mS cm−1)	E aσ (kJ mol−1) ±0.5	R 2
LiTDI	1324	13.6	0.9948
LiFSI	1292	11.6	0.9965
LiPF6	1545	12.1	0.9986

Viscosity	η 0	E aη (kJ mol−1) ±0.5	R 2
LiTDI	0.017	14.1	0.9992
LiFSI	0.009	13.4	0.9979
LiPF6	0.011	14.1	0.9984

The E_aσ values are a slightly lower than that of E_aη but, by taking into account the uncertainty, it can be considered that E_aσ ≃ E_aη (especially for LiTDI). When E_aσ = E_aη the Walden product ση is strictly independent of the temperature and hence remains constant. Thus, this relation in only approximately verified.

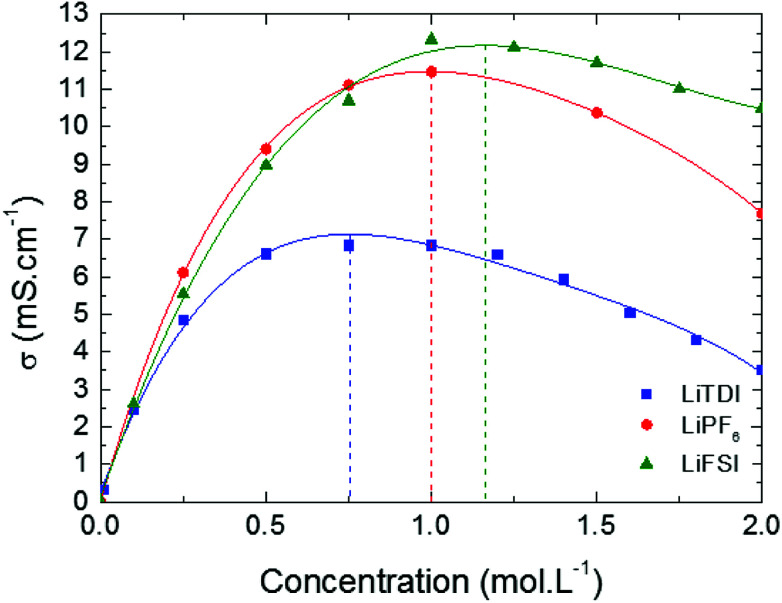
Conductivity variations at 25 °C of LiTDI, LiFSI and LiPF₆ in EC/DMC have been represented as a function of the salt concentration in Fig. 5. All curves present a maximum of conductivity, which depends on the nature of the anion: at 0.75 mol L⁻¹ for LiTDI, 1 mol L⁻¹ for LiPF₆ and 1.16 mol L⁻¹ for LiFSI. The maximum of conductivity σ_max for each electrolyte is reported in Table 4. In the case of LiTDI, σ_max is only of 6.8 mS cm⁻¹ owing to its lower dissociation coefficient³² in EC/DMC. This means that LiTDI starts forming ion-pairs at a lower concentration than LiFSI and LiPF₆. Once the maximum conductivity is reached, the conductivity drops more or less sharply owing to the increase in viscosity that depends on the salt anion.

Fig. 5. Conductivity of LiTDI, LiFSI and LiPF₆ in EC/DMC at 25 °C as a function of the salt concentration.

Maximum conductivity (σ_max) and concentration in salt at which it is obtained (C_m) in EC/DMC at 25 °C.

	LiTDI	LiFSI	LiPF6
σ max (mS cm−1)	6.8	12.3	11.4
C m (mol L−1)	0.75	1.16	1.00

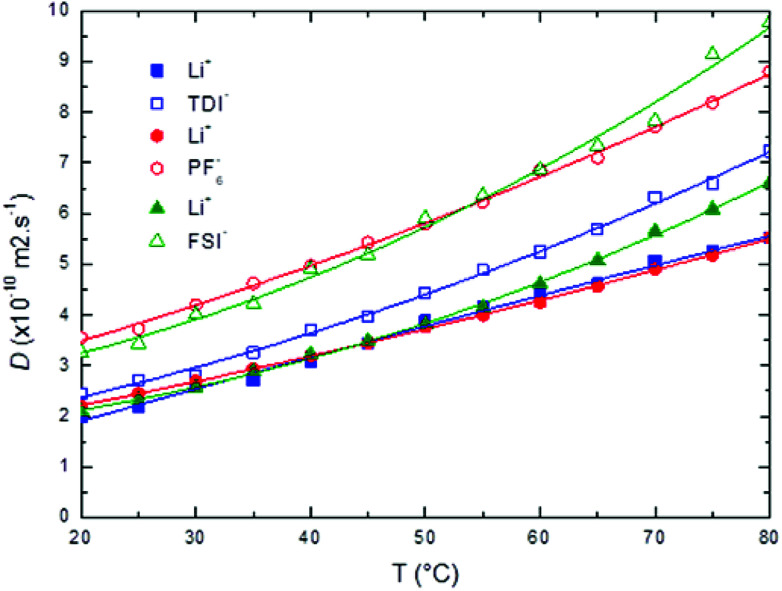
The ⁷Li and ¹⁹F self-diffusion coefficients (D(⁷Li) and D(¹⁹F)) of the LiTDI, LiPF₆ and LiFSI at 1 mol L⁻¹ in EC/DMC electrolytes were determined by PGSE-NMR as a function of the temperature. Results are reported in Fig. 6.

Fig. 6. ⁷Li and ¹⁹F self-diffusion coefficients (D(⁷Li) and D(¹⁹F)) of LiTDI (blue squares), LiPF₆ (red circles) and LiFSI (green triangles) at 1 mol L⁻¹ in EC/DMC as a function of the temperature.

It can be noticed that D(⁷Li), which corresponds to the self-diffusion of all species containing at least one ⁷Li nucleus, does not exhibit any significate change from one lithium salt to the other contrarily to D(¹⁹F), the self-diffusion of all species containing at least one ¹⁹F nucleus. D(¹⁹F) values are larger than D(⁷Li) and depends on the anion size with the following sequence:D(¹⁹F)_TDI < D(¹⁹F)_FSI ⋍ D(¹⁹F)_PF6

Hence, the species containing a smaller anion diffuse more rapidly.

4.2. Lithium effective ionic radius

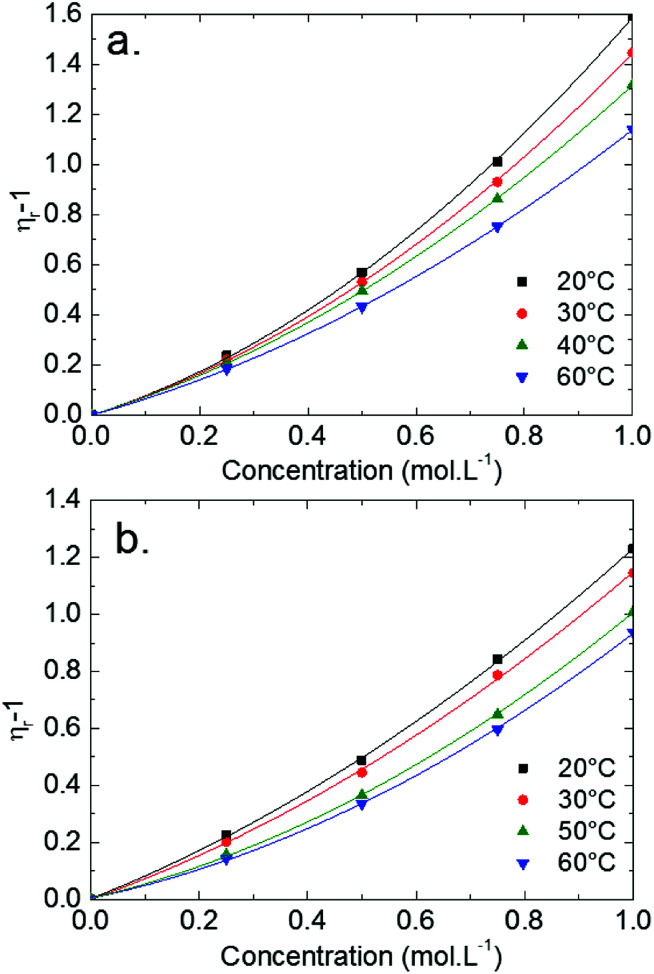
Relative viscosities of LiTDI and LiFSI in EC/DMC are plotted against the salt concentration in Fig. 7 at several temperatures. All curves have been fitted according to the JDK eqn (7). It can be noticed that the DC² term of this equation becomes predominant when the salt concentration is over 0.1 mol L⁻¹. The fitting curves exhibit a high correlation constant: R² = 0.99999, justifying the use of the JDK equation.

Fig. 7. Variations of the relative viscosity (η_r − 1) as a function of the concentration of LiTDI (a) and LiFSI (b) in EC/DMC at several temperatures.

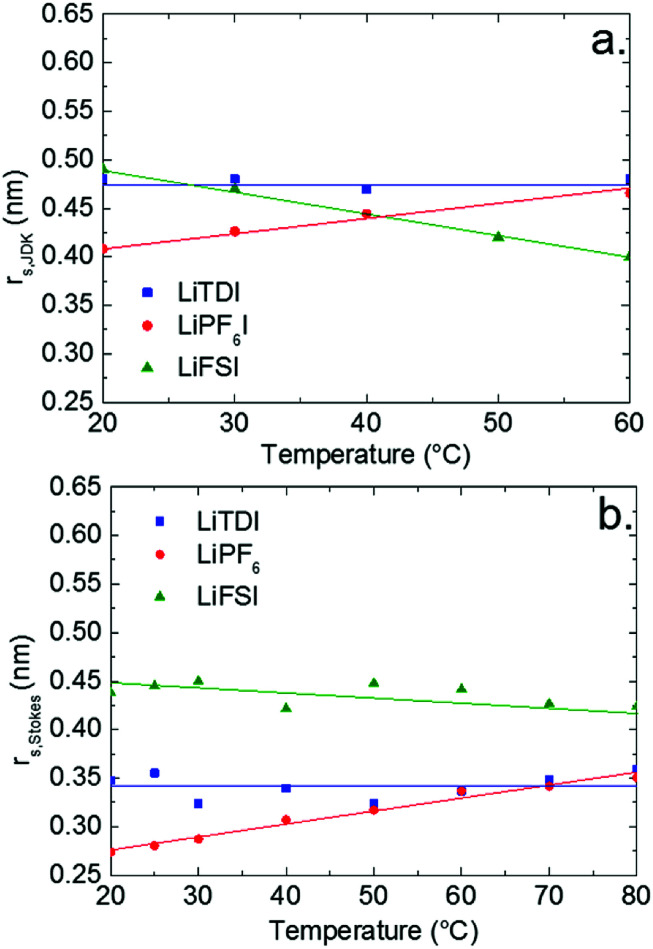
The JDK equation B parameter values and that of the r_s,JDK radii, deduced from eqn (9), for the LiTDI, LiFSI and LiPF₆ electrolytes are reported in Table 5. The Li⁺ effective solute radius, which has been obtained by using the JDK equation coupled to the Einstein relation and by applying the Stokes–Einstein equation, is plotted against the temperature in Fig. 8.

Values of B and of r_s,JDK obtained by coupling the Einstein relation and the JDK equation for LiTDI, LiFSI and LiPF₆ in EC/DMC.

	T (°C)	B (L mol−1)	r s,JDK (nm)
LiTDI	20	0.69	0.48
	30	0.68	0.48
	40	0.66	0.47
	60	0.66	0.48
LiFSI	20	0.75	0.49
	30	0.68	0.47
	50	0.45	0.42
	60	0.40	0.40
LiPF6	20	0.43	0.41
	30	0.49	0.43
	40	0.55	0.45
	60	0.64	0.47

Fig. 8. The effective Li⁺ solute radius calculated from the JDK equation (a) and the Stokes–Einstein equation (b) in the electrolytes containing 1 mol L⁻¹ of LiTDI, LiFSI or LiPF₆ in EC/DMC as a function of the temperature.

The graphs reported in Fig. 8 show that r_s,JDK values are systematically larger than r_s,Stokes. The reason for that is not clear but in the case of r_s,JDK, the ions or ion-pairs are submitted to a shear stress but not in the case of r_s,Stokes which is deduced from self-diffusion measurements. Hence, the transport conditions are not strictly equivalent and the number of solvating molecules could be different.

Regarding the variations of r_s,JDK and r_{s Stokes} with the temperature, the same trend is observed when the temperature is increased: r_s (Li⁺, LiTDI) does not vary significantly, r_s (Li⁺, LiPF₆) increases and r_s (Li⁺, LiFSI) decreases. This suggests that the three lithium salts form different types of ion-pairs which themselves exhibit a different behavior when the temperature is raised. This will be analyzed in the following paragraphs.

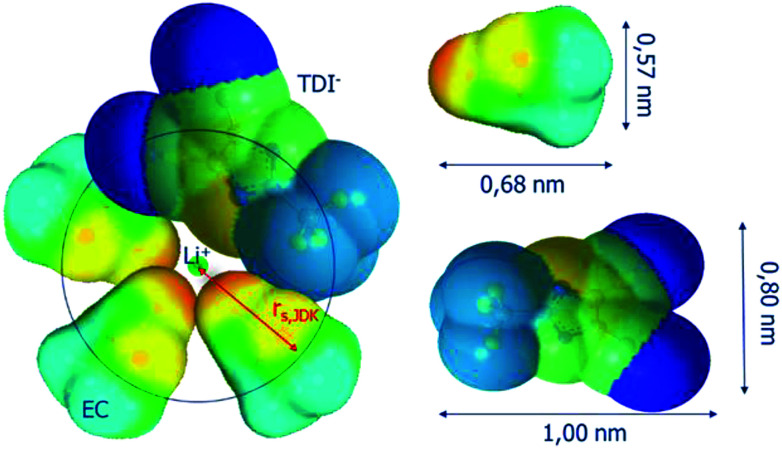
The first solvation layer of the lithium cation for LiTDI in EC/DMC has been modelized using the Conductor-Like Screening Model (COSMO) procedure. The results of this simulation are represented in Fig. 9. Three solvent molecules and one anion were arranged around the cation without considering polarization and deformation of the electron cloud.

Fig. 9. Representation of the first solvation sphere of Li⁺ in the case of LiTDI dissolved in EC/DMC.

The black circle having the lithium cation at its center corresponds to the section of the JDK solvation sphere (radius r_s,JDK). As the r_s,Stokes is even smaller, it appears clearly that the JDK equation allows a better estimation of the lithium effective solute radius. One possible reason for that is that the r_s,Stokes values are deduced from D(⁷Li), the self-diffusion coefficient of all species containing a lithium ion and not D⁺, that of free lithium ions only.

4.3. Ion-pair dissociation coefficients

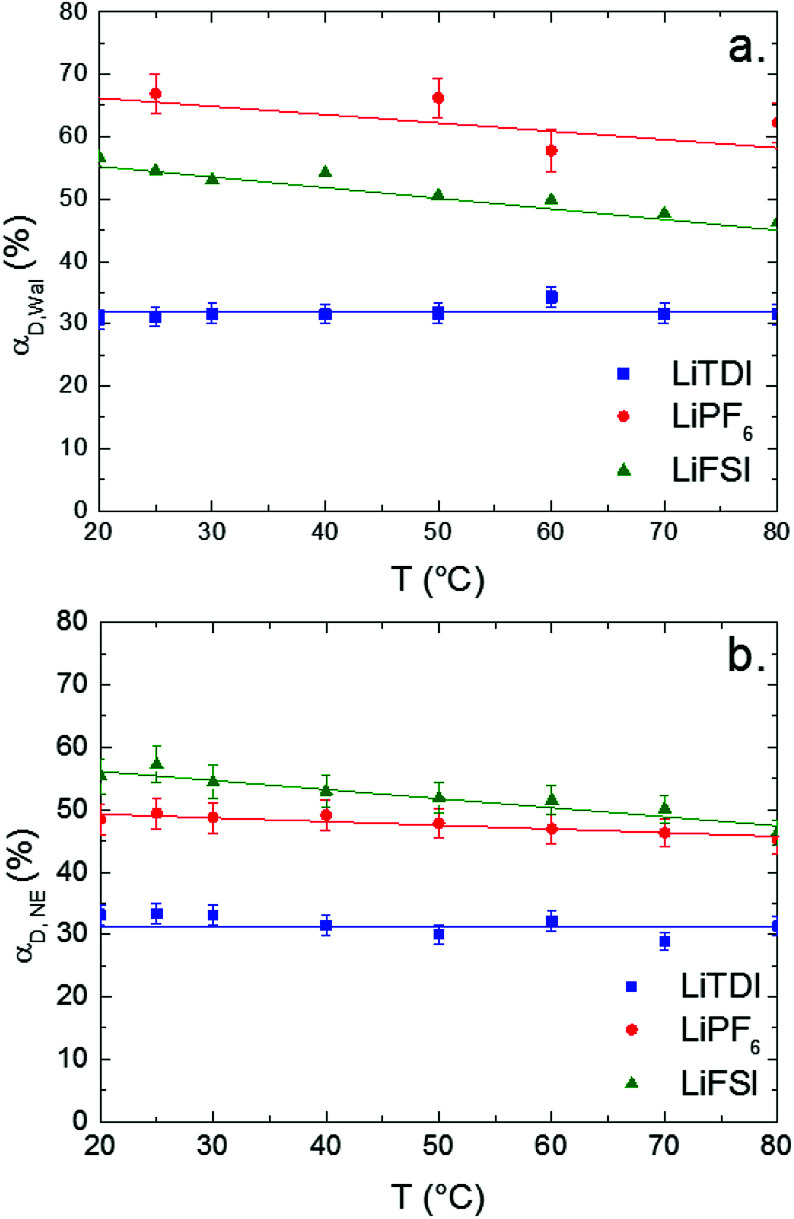
Variations of the ion-pair dissociation coefficients with the temperature which are obtained by using eqn (11) (α_D,Wal) or eqn (13) (α_D,NE) are plotted in Fig. 10.

Fig. 10. Dissociation coefficients of LiTDI, LiFSI and LiPF₆ in EC/DMC at 1 mol L⁻¹ measured using the Walden rule (a) and the Nernst–Einstein equation (b), as a function of the temperature.

As expected from its lower conductivity, LiTDI is the less dissociated salt of the three in EC/DMC even with TDI⁻, a large hückel anion with a highly delocalized negative charge.³⁷ The size of the anion and its delocalized charge should be in favor of poor coulombic interactions. It can be noticed that both methods lead to α_D values which are in fair agreement for LiTDI and LiFSI but not for LiPF₆ as the difference reaches 15%. As indicated by the graphs reported in Fig. 10, both methods agree on the variations of α_D with the temperature: α_D does not depend on the temperature in the case of the LiTDI based electrolyte, but on the contrary, decreases with the temperature in the case of LiPF₆ and LiFSI. These observations suggest that the ion pairs formed by each salt in EC/DMC do not have the same structure. It can also be noted that the temperature independence of α_D (LiTDI) is in agreement with the relation between the activation energies E_aη ≈ E_aσ which has been found experimentally for LiTDI. Thus, according to eqn (16) and (17), the Walden product does not depend on the temperature.

4.4. Gibbs free energy of association for LiTDI, LiPF6 and LiFSI in EC/DMC

The dissociation coefficient of LiTDI, LiFSI and LiPF₆ in EC/DMC, which is strictly below 1 at the selected concentration of 1 mol L⁻¹, is evidence of the existence of ion-pairs and/or larger aggregates within the electrolytes. The equilibrium constant K_IP for ion pair formation:Li⁺ + X⁻ → LiXcan be deduced from α_D values by:

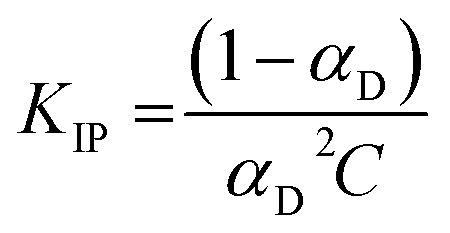18

The standard Gibbs free energy for ion pair formation, 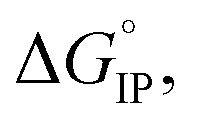can be calculated by:

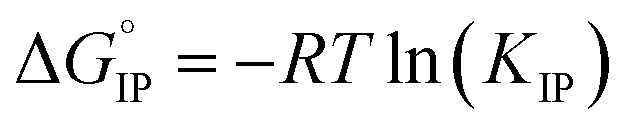19

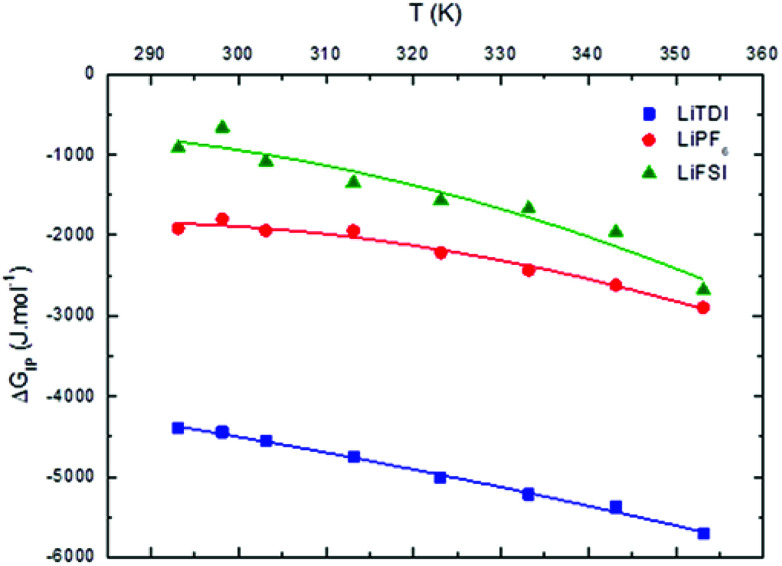
The temperature dependence of 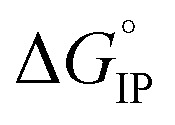is plotted in Fig. 11. 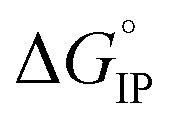values calculated with α_D,Wal and α_{D, NE} are close excepted in the case of LiPF₆. Because the LiFSI-EC/DMC electrolyte has a higher conductivity than LiPF₆-EC/DMC it is likely that LiFSI is in a less associated state in the present experiment conditions. Thus, the considered 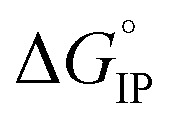(LiPF₆) was calculated using α_D,NE.

Fig. 11. Standard Gibbs free energy 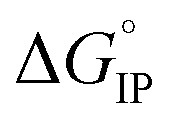for ion pair formation as a function of the temperature for LiTDI, LiPF₆ and LiFSI at 1 mol L⁻¹ in EC/DMC.

For LiPF₆ and LiFSI in EC/DMC, 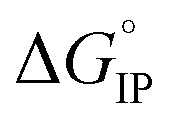values are negative. Thus, the entropy contribution to the free energy dominate the enthalpy contribution meaning that ion-pair formation here follows an exergonic process. 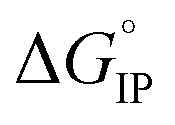decreases when the temperature rises owing to the weakening of ion–solvent interactions. That is also the case for LiTDI even though IP association was seen to be very weakly temperature dependent (Fig. 10). 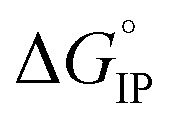variations can be fitted by the following polynomial equation:¹⁶

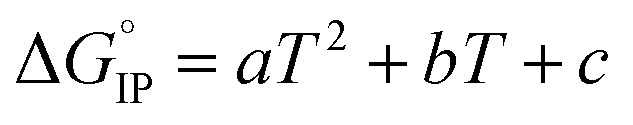20

Values of constants a, b and c are summarized in Table 6 along with the correlation coefficient R².

Values of the a, b and c constants in eqn (20) for LiTDI, LiPF₆ and LiFSI at 1 mol L⁻¹ in EC/DMC. R² is the correlation coefficient.

	a (J mol−1 K−2)	b (J mol−1 K−1)	c (J mol−1)	R 2
LiTDI	−0.06	17.02	−4193	0.994
LiPF6	−0.23	128.82	−20117	0.97
LiFSI	−0.25	135.16	−18685	0.92

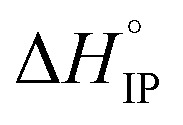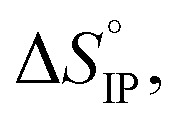and respectively the ion-pair formation standard enthalpy and entropy can be calculated by using eqn (21) and (22):

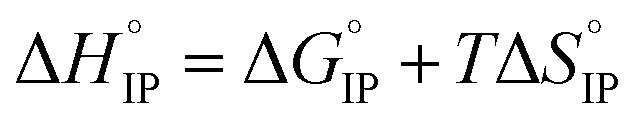21

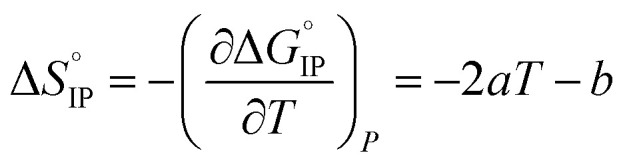22

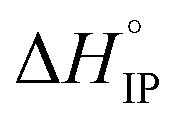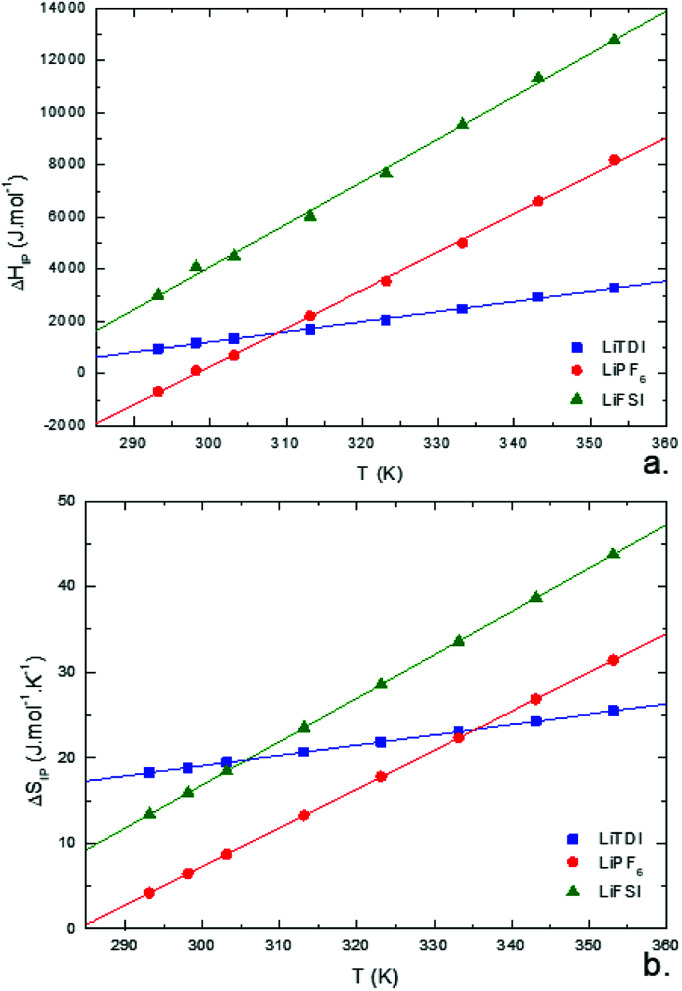
and 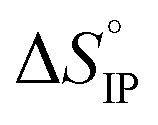variations with the temperature are presented in Fig. 12.

Fig. 12. Standard enthalpy 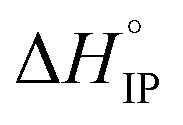(a) and entropy 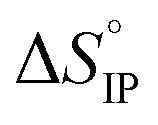(b) for ion-pair formation as a function of the temperature for LiTDI, LiPF₆ and LiFSI at 1 mol L⁻¹ in EC/DMC.

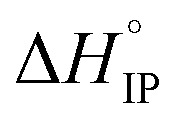and 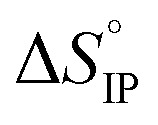values both increase with the temperature. 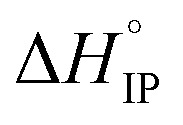is negative only for LiPF₆ below 300 K and 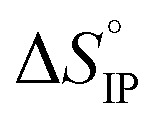is always positive. For these lithium salts in EC/DMC, ion-pairing is an endothermic process excepted for LiPF₆ at temperatures below 300 K.

Entropy can be taken as a measure of disorder resulting from the formation of ion-pairs. During the association process, the number of molecules is reduced from 2 to 1 which means that a change in ion solvation occurs: more than one solvent molecule is released and this number is likely to increase when the temperature is raised. However, increasing the electrolyte temperature has a low impact on the association entropy of the LiTDI-based electrolyte. This could be explained by considering that the kind of ion-pairs formed by LiTDI in EC/DMC are of the S₂IP type. Owing to weaker interactions between solvated ions in the ion-pairs, the ion pairing process will be less affected by temperature variations. Thus, fewer solvent molecules are released during the association process of LiTDI than during that of LiPF₆ and LiFSI.

4.5. Discussing the ion-pair structure of LiTDI, LiPF₆ and LiFSI in EC/DMC

Association of free ions into ion-pairs is an endothermic (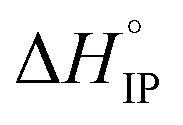 > 0) and an exergonic ( 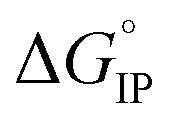< 0) phenomenon for LiTDI, LiFSI and LiPF₆ in EC/DMC. Due to the nature of EC, a strongly polar molecule with a high dielectric constant preferentially solvating Li⁺ in EC/DMC,³⁸ the formation of CIP is unlikely. This kind of ion-pairs are found in solvents of low dielectric constant like dioxanne, benzene or cyclohexane. A positive value for 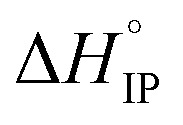indicates that the desolvation, which occurs during the formation of the ion-pairs, brings a predominant positive contribution (ΔH_sol) to the standard enthalpy over the negative contribution due to the released coulombic energy (ΔH_el). Thus, the formation of a SIP structure appears more likely for LiPF₆ and LiFSI. Concerning LiTDI, for which the 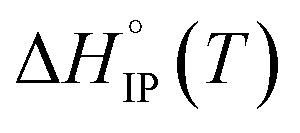slop is weaker than that of LiFSI and LiPF₆, the modulus of the two different contributions of the association enthalpy might be close enough to nearly compensate each other which is in fair agreement with a S₂IP type of ion-pairing as stated previously.

It was also noticed that the average Li⁺ effective solute radius, which takes into account free solvated lithium ions and those engaged in IP or larger aggregates, could vary with the temperature. A reduction of this radius after a rise in temperature (LiFSI) would suggest the formation of ion-pairs of the SIP type. On the contrary, an increase or no variation of the effective solute radius with the temperature (LiTDI) would more likely suggest the formation of S₂IP.

Finally, LiPF₆ presents a peculiar behavior. The Li⁺ effective solute radius increases with the temperature and, it is the only salt that exhibits a negative standard enthalpy at room temperature or below. As the number of free ions within the solution decreases when the temperature is raised, this phenomenon can be explained by the transformation of a number of SIP into S₂IP. This also explains the change in sign of 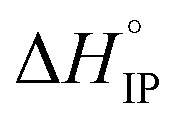for LiPF₆-based electrolyte in EC/DMC.

5. Conclusion

The conductivity and viscosity study of LiFSI, LiTDI and LiPF₆ solutions in EC/DMC show that these two transport processes are not strictly coupled as their activation energies differ by 1 to 2 kJ mol⁻¹. The reason for that could be the formation of ion-pairs when the concentration in salt in solution is increased to 1 mol L⁻¹. The best conductivity at room temperatures is obtained for LiFSI followed closely by LiPF₆, the reason for this being a lower dissociation coefficient for LiTDI. In addition, the maximum in conductivity is obtained in the case of LiFSI and LiPF₆ around 1 mol L⁻¹ but only 0.75 mol L⁻¹ for LiTDI.

The ion-pair dissociation coefficient (α_D) and the lithium cation effective solute radius (r_s) of the LiTDI, LiFSI and LiPF₆ salts in an EC/DMC binary solvent were investigated at temperatures ranging from 25 °C to 80 °C. The ion-pair structures of these salts, i.e. solvent-shared ion-pair (SIP) and solvent separated ion-pair (S₂IP), were deduced from the study of the variations of α_D and r_s. α_D was determined by using the Walden rule and also by using the self-diffusion coefficients values and the Nernst–Einstein equation. Both methods gave results in fair agreement for the variations of α_D with the temperature. In a similar way, r_s was calculated using the Jones–Dole–Kaminsky equation coupled with the Einstein relation and the Stokes–Einstein equation. Even though the first method leads to higher values for r_s than the other, there was a good agreement concerning the variations of r_s with the temperature. By analyzing the variations of α_D and r_s with the temperature, LiFSI and LiPF₆ ion-pairs could be characterized as SIP. However, in the case of LiPF₆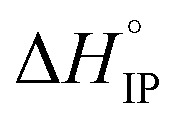 exhibits a sign change above room temperature meaning that SIP and S₂IP could co-exist at room temperature and that a number of SIP transform to S₂IP when the solution temperature is raised. In the case of the LiTDI-based electrolyte, α_D, r_s, 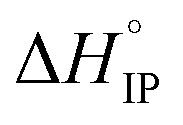and 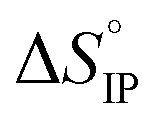are not temperature dependent. This has been assigned to the fact that LiTDI ion-pairs are of the S₂IP type.

The temperature dependence of the Gibbs free energy, enthalpy and entropy for the ion-association process thermodynamic parameters allowed us to confirm the selected ion-pair structure for each lithium salt. Moreover, the standard Gibbs free energy 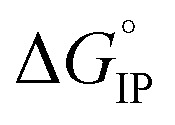for ion-pair formation is negative for all electrolytes meaning that this process is exergonic. 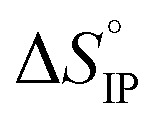is positive at all temperature investigated indicating that there is a net increase in the number of free solvent molecules during the ion association process. 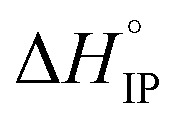is positive excepted for LiPF₆ at room temperature or below. It can be concluded that the desolvation process is more energetic than the coulombic contribution to the overall ion-pair formation. Future work will now be devoted to Raman spectroscopy in order to confirm the ion-pair structures.

Conflicts of interest

There are no conflicts to declare.