Isoquinoline gas-phase absorption spectrum in the vacuum ultraviolet between 3.7 and 10.7 eV. New valence and Rydberg electronic states

Abstract

VUV photons from a synchrotron source were used to record the gas-phase absorption spectrum of isoquinoline over the range 3.5 to 10.7 eV. The rich spectrum exhibits both broad and sharp features, of varying intensities, that are analyzed into eight valence and eight Rydberg transitions. Previous data on the valence transitions of isoquinoline were essentially limited to solution spectra up to 5.4 eV. Our study increases their number considerably. The features in the 3.96 eV region are discussed in terms of vibronic coupling between the nπ* 1¹A′′ and ππ* 2¹A′ valence electronic states. The intensities of some spectral features are augmented by collective π-electron modes considered to be of plasmon-type. Assignments of the valence transitions were facilitated by our DFT calculations and by earlier Pariser–Parr–Pople MO calculations. The calculation results are compared and their relative value is discussed. The DFT calculations reproduce very well a number of experimentally determined properties of the ground state of isoquinoline, in particular its bond distances and angles, rotational constants, vibrational frequencies and dipole moment. No Rydberg series of isoquinoline have previously been observed. Three of the newly observed Rydberg series converge to the D₀ electronic ground state of the ion, while two converge to the D₁ and three to the D₃ excited electronic states of the cation. Astrophysical applications of the VUV absorption spectrum of isoquinoline, in particular the measured absorption cross-sections, are briefly discussed. A comparison between the absorption spectra of isoquinoline and quinoline highlights their similarities and differences, related to their respective molecular orbitals.

VUV photons from a synchrotron source were used to record the gas-phase absorption spectrum of isoquinoline over the range 3.5 to 10.7 eV.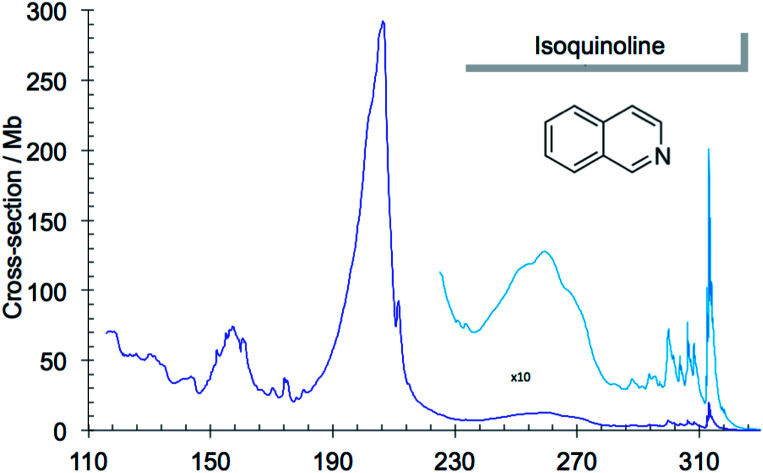

1. Introduction

The azaarenes quinoline and isoquinoline, in which a benzene ring is fused to pyridine, are nitrogen analogues of the polycyclic aromatic hydrocarbon (PAH) naphthalene. They can be considered as examples of PANHs, the term now used by astrophysicists for nitrogen analogues of PAHs. Their presence has been suggested, and in some cases observed, in a number of astrophysical sites: planetary atmospheres,¹ the interstellar medium^2–4 and in meteorites.^5,6 The gas-phase absorption spectra of these azaarenes are of use for furthering their astrophysical potential and their observation, in addition to astrochemical modelling studies of their photochemistry in planetary atmospheres, the ISM and circumstellar media. We note that recent laboratory studies^7,8 have shown that quinoline and isoquinoline can be synthesised under high temperature conditions representing circumstellar envelopes of carbon stars. There have been radiofrequency spectroscopic attempts to observe both C₉H₇N isomers quinoline and isoquinoline in the circumstellar envelopes of carbon-rich stars.⁸ Although no positive signals were observed, it has proved possible to derive upper limits on quinoline and isoquinoline column densities.

Since the photon absorption of isoquinoline extends in the VUV into energy regions where photoionization processes occur, the measurement of photoionization quantum yields as function of excitation energy will become necessary in order for the absorption cross-sections to be exploited in cosmochemical modeling, although some coarse grain information can be obtained using rule-of-thumb estimations of photon energy dependent ionization quantum yields.^10,11 This information is notably required in studies of photophysical and photochemical processes that involve superexcited electronic states of neutral molecules.¹²

The VUV absorption spectrum of gas-phase quinoline has recently been studied.¹³ The present work is a study of the VUV absorption spectrum of its isomer, gas-phase isoquinoline. A comparison between the results of the quinoline and isoquinoline spectral studies is given in a later section (Section 4) which includes a discussion on astrophysical applications. Previous studies of the absorption spectra of isoquinoline have been carried out mainly in solution or in matrices in the near-UV region. The fluorescence and phosphorescence spectra of isoquinoline have been studied in detail.¹⁴ Previous gas phase studies of the electronic transitions of isoquinoline^15–23 are limited to the 3.8–4.5 eV region. They are mainly concerned with the interaction of low-lying quasi-degenerate n–π* 1¹A′′ and π–π* 1¹A′ states and with related internal conversion and intersystem crossing behavior. Absorption spectra of isoquinoline in solution have an upper energy limit of 5.4 eV.^14,24,25

The synchrotron radiation source provided photons that enabled us to extend absorption spectra of gas phase isoquinoline up to 10.7 eV. Our spectral analysis identified new valence transitions, and assigned eight Rydberg series of bands converging to several electronic states of the cation. This study also provided data on the UV and VUV absorption cross sections of isoquinoline that are potentially of use of in modeling cosmochemical processes.

2. Experimental

2.1. Absorption spectra measurements

Absorption measurements on isoquinoline were performed on the AU-UV beamline stationed in the ASTRID2 synchrotron facility at Aarhus, Denmark. The beamline, its resolution possibilities, and procedure for determining absorption cross sections are described in detail elsewhere.^26,27 Isoquinoline was introduced at room temperature into a gas cell whose path length (l) is 15.5 cm. The entrance and exit windows of the gas cell are in MgF_2, VUV transparent to about 10.8 eV (115 nm). VUV radiation was made available at selected energies by the use of a toroidal dispersion grating. Wavelength scanning was achieved with step sizes mainly ranging from 0.05 to 0.2 nm that were chosen in accord with the degree of spectral feature structure in various regions of the spectrum. Some measurements were made over a limited spectral range with 0.02 nm steps. Photon resolution is 0.08 nm, which corresponds to 2 meV at the mid-point of the wavelength region measured. A UV-VUV sensitive photomultiplier (ET Enterprises 9406B) was used to measure the intensity of light transmitted through the gas (I_t). A small gap between the exit window of the gas cell and the recording photomultiplier is evacuated so as to maintain transparency at photon energies above 5.5 eV by preventing air contamination. For the energy range below 5.5 eV higher order radiation is avoided by letting air into the gap. The MgF₂ entrance window of the cell eliminates higher order radiation of energy above 11 eV. Measurement of the gas pressure is made by a heated capacitance manometer (Inficon CDG100D). The pressure used for the spectral measurements ranged from 0.025 to 0.075 mbar. The maximum vapour pressure of the sample at room temperature was indeed 0.075 mbar. The pressure was chosen so as to keep the average attenuation to within a small range around 50%, in order to avoid saturation effects. The intensity of the synchrotron beam current is measured during each wavelength scan, and the measured spectral intensity is normalised to the beam current. A background scan is recorded with an evacuated cell so as to provide the I₀ intensity. Wavelength calibration was carried out by comparison with well-known standard absorption spectra, as follows: nitrogen between 120 and 150 nm; two SO₂ bands in the mid (185–225 nm) and long wavelength range (275–315 nm).

The measured absorption cross sections are accurate to ± 5%. They were obtained by applying the Beer–Lambert law: I_t = I₀ exp(nσl). The highest purity commercially available (Sigma-Aldrich) isoquinoline sample underwent 4 freeze–pump–thaw cycles and received no further treatment before use.

2.2. Computations: methods and results

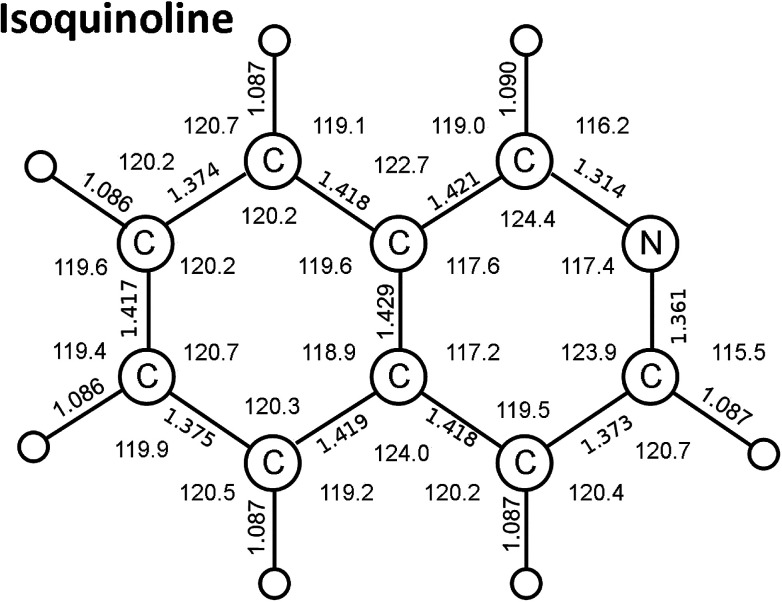
Calculations of the valence transitions of isoquinoline (C_s symmetry group structure, Fig. 1) were carried out to aid in spectral transition assignments, in particular of the π–π* transitions. Previous reported computations of these transitions are predominantly by Pariser–Parr–Pople (P–P–P) quantum mechanical methods. We carried out time-dependent DFT calculations of structural and spectroscopic properties of isoquinoline for comparison with previous theoretical studies. We note that the TD-DFT formalism, as derived from Kohn–Sham theory, is essentially an empirically corrected version of the random-phase approximation used in Hartree–Fock methods.^28,29

Fig. 1. Isoquinoline ground state bond distances (Å) and angles (degrees) calculated by a time-dependent DFT method. (see text).

We carried quantum chemical calculations with the GAUSSIAN 16 program, Revision A.03.³⁰ Geometry optimization of isoquinoline was performed using two different basis sets: the hybrid density functional B3LYP and 6-31+G(D,P) basis set (calculation A) and the B971/6-311 +G(D,P) combination (calculation B). Normal mode analysis confirmed that the final optimized geometries were true potential energy minima. The geometric centres of calculation A and calculation B isoquinoline molecules are the same. The average difference between calculations A and B in the coordinates of the atoms with respect to this center is 0.005 Å with a maximum of 0.007 Å. This suggests that there are no significant differences in the accuracies between the two calculation methods.

The calculation B structure was used to carry out TD-DFT calculations of electronic state energies and dipole transition oscillator strengths using the CAM-B3LYP hybrid density-functional³¹ along with 6-31+G (d,p) as basis-set.

2.2.1. Geometry and other structural properties

The geometry of isolated isoquinoline has not been measured directly. Our calculated bond distances and bond angles (Fig. 1) are in very reasonable agreement with other calculated values.^32,33 These bond distances and angles have, however, been measured for crystalline isoquinoline in an X-ray crystal structure study;³⁴ we note that the structure is complicated by an inversion symmetry in the crystal. The atom–atom bond distances obtained with the calculation A and calculation B functionals have an average deviation from the X-ray determined structures generally less than 0.01 Å, the calculation B values being slightly better than those of calculation A.

The calculated rotational constants, based on our calculated isoquinoline structures, are in quite good agreement with the experimental values (Table 1) determined by high-resolution microwave and/or optical spectroscopy measurements on ground state isoquinoline.^33,35–37 Another criterion of quality of our calculations is the dipole moment of isoquinoline. Our values agree well with the dipole moment determined by gas-phase polarization measurements,³⁸ although they are about 9% greater than Stark effect values (Table 1). Polarization measurements of the dipole moment in the gas phase necessitate measurement over a temperature range of at least 100 K, as achieved by Buckingham et al.³⁸ Stark effect measurements of gas-phase dipole moments are subject to uncertainties that are discussed by Kisiel et al.³³

Isoquinoline ground state rotational constants and dipole moment: calculated and experimental values.

A Rotational constants

(a) DFT calculated: (present study)

A = 3.1921294 GHz, B = 1.2330017 GHz, C = 0.8894428 GHz

(b) Microwave spectroscopy33

A = 3.19900020 GHz, B = 1.237931586 GHz, C = 0.892753595 GHz

(c) FIR spectroscopy36

Analysis based on ν30. A = 3.2003697 GHz, B = 1.2387657 GHz, C = 0.8937165 GHz

(d) FIR spectroscopy37

Analysis based on ν37. A = 3.1980719 GHz, B = 1.23780915 GHz, C = 0.8928502 GHz

B Dipole moment

(a) DFT calculated: 2.7536 Debye (present study)

(b) Polarisation measurement38: 2.73 ± 0.03 Debye

(c) Stark effect measurement33: 2.5277 Debye

2.2.2. Vibrational frequencies of the ground state

Table 2 presents the ground state harmonic and anharmonic vibrational frequencies of the thirty-one a′ and fourteen a′′ vibrational modes of isoquinoline calculated by our DFT method. A comparison is made with experimental values³⁹ and with those of other calculations. These provide comparative tests of the various calculation methods of vibrational frequencies. The experimental frequencies of Wait and McNerney³⁹ are from Raman and infra-red spectroscopic studies in either liquid or gas phase. To make their mode assignments, Wait and McNerney carried out a normal coordinate analysis using the Urey-Bradley Force-Field, including Kekulé modification, using force constants that were derived from naphthalene and s-triazine. More recently, other information, in particular on the frequencies of modes 28, 31, 40, 41, 43 and 45 of isoquinoline was obtained by Martin-Drumel et al.³⁵ in high resolution gas phase far-infrared spectroscopic studies using a Fourier transform instrument.

Isoquinoline vibrational frequencies (cm⁻¹): harmonic and anharmonic frequency calculation results compared with observed values.

Vibrational mode39	Observed39	DFT [A] harmon present study	DFT [B] harm present study	DFT harmon35	DFT [A] anharmon present study	DFT [B] anharmon present study	DFT anharmon35	Hartree–Fock32
1 a′	3089	3189	3187	3189	3066	3057	3051	3374
2 a′	3059	3179	3176	3177	3034	3031	3043	3372
3 a′	3055	3177	3175	3176	3070	3059	3048	3361
4 a′	3055	3166	3163	3164	3046	3048	3049	3352
5 a′	3024	3161	3158	3159	3027	3022	3022	3347
6 a′	3007	3158	3156	3155	2998	2999	3005	3340
7 a′	2994	3124	3122	3120	3003	2993	2996	3321
8 a′	1625	1664	1658	1662	1673	1617	1621	1846
9 a′	1587	1623	1617	1621	1586	1581	1585	1802
10 a′	1556	1605	1601	1604	1574	1569	1566	1785
11 a′	1497	1533	1528	1530	1499	1493	1495	1671
12 a′	1461	1489	1483	1484	1457	1456	1459	1625
13 a′	1432	1464	1457	1459	1433	1426	1429	1593
14 a′	1382	1410	1405	1406	1383	1378	1374	1525
15 a′	1377	1400	1396	1397	1364	1359	1367	1495
16 a′	1315	1364	1362	1363	1333	1331	1333	1471
17 a′	1273	1290	1283	1284	1262	1255	1256	1388
18 a′	1253	1278	1270	1270	1256	1250	1251	1378
19 a′	1178	1241	1238	1239	1219	1214	1217	1331
20 a′	1140	1205	1200	1201	1186	1181	1182	1293
21 a′	1119	1168	1163	1163	1150	1144	1145	1255
22 a′	1095	1160	1154	1155	1144	1138	1139	1192
23 a′	1034	1062	1059	1060	1045	1041	1041	1135
24 a′	1014	1036	1032	1033	1018	1015	1015	1081
25 a′	959	957	950	950	944	937	937	1030
26 a′	778	812	807	807	802	795	796	866
27 a′	765	790	786	787	779	775	776	851
28 a′	637/640 (ref. 35)	656	650	651	649	642	644	698
29 a′	522/521 (ref. 35)	530	527	527	525	521	522	566
30 a′	504/502 (ref. 35)	511	507	507	506	501	501	544
31 a′	381	362	358	358	360	355	355	386
32 a′′	984	1005	998	999	982	976	976	1127
33 a′′	971	993	987	988	977	974	972	1118
34 a′′	945	976	970	968	958	954	954	1096
35 a′′	930	946	940	947	938	936	931	1067
36 a′′	862	877	872	874	864	862	862	973
37 a′′	825	844	841	845	830	829	830	935
38 a′′	800	789	782	791	782	779	780	863
39 a′′	742	753	751	752	741	739	739	837
40 a′′	611/635 (ref. 35)	652	648	652	640	637	641	705
41 a′′	482/480 (ref. 35)	493	489	491	484	481	483	542
42 a′′	459/457 (ref. 35)	469	465	468	461	460	461	518
43 a′′	355/376 (ref. 35)	386	384	384	378	377	378	431
44 a′′	201/181 (ref. 35)	184	184	185	178	180	182	207
45 a′′	182/166 (ref. 35)	171	171	171	168	161	168	189
Slope		1.047 ± 0.004	1.048 ± 0.004	1.048 ± 0.004	0.994 ± 0.004	0.994 ± 0.004	0.994 ± 0.004	1.105 ± 0.005
Intercept		−21 ± 6	−27 ± 7	−26 ± 7	16 ± 7	9 ± 6	11 ± 6	3 ± 10
Correlation coefficient		0.99981	0.99980	0.99980	0.99975	0.99979	0.99980	0.99961

Included in Table 2 are the vibrational frequencies of isoquinoline calculated in a force-field study by Bandyopadhyay and Manogaran³² with a geometry obtained with Hartree–Fock theory using a 6-31G** basis set. To reconcile the ab initio values of the harmonic vibrational frequencies in the table with experimental values necessitates 0.7–1.0 scaling for the a′ vibrational modes and 0.5–1.0 for the a′′ modes. Scott and Radom⁴⁰ have compared a number of ab initio, semiempirical and DFT calculations of molecular harmonic vibrational frequencies so as to propose useful scaling values.

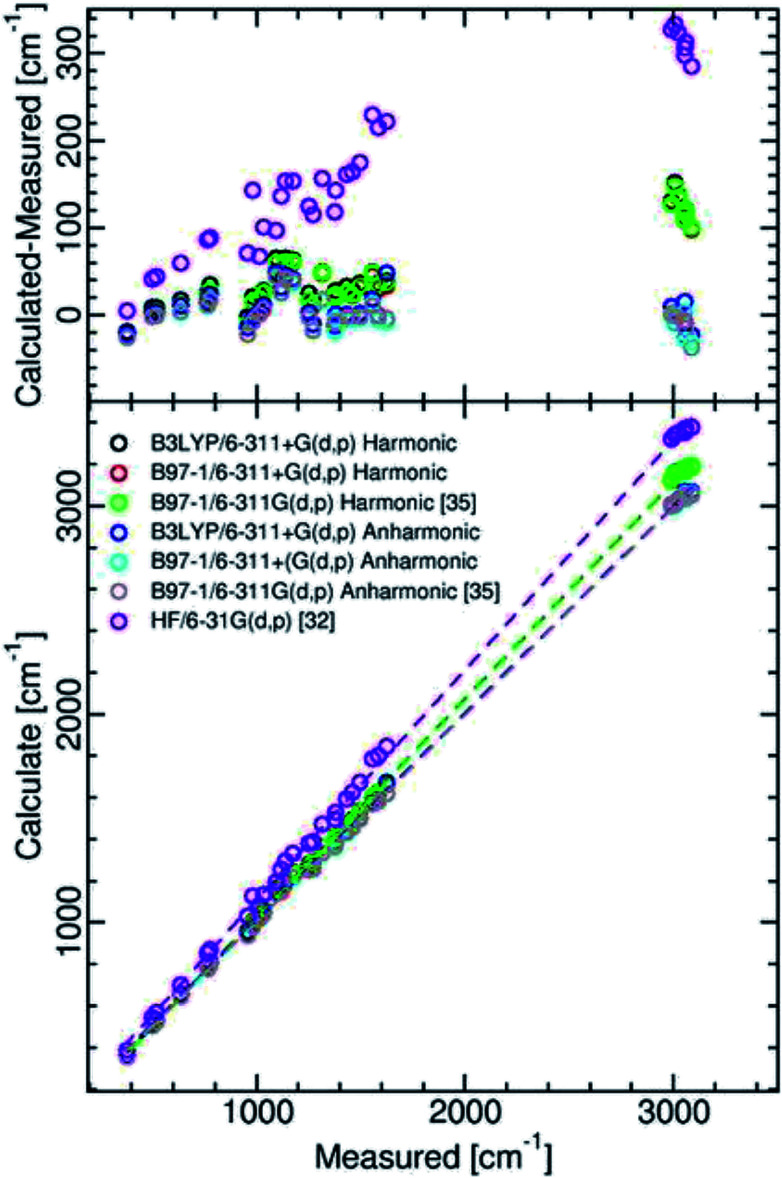
The results presented in Table 2 show that our calculation A and calculation B anharmonic frequencies, which were obtained using the second-order vibrational perturbation theory devised by Barone,⁴¹ in Gaussian 16, require little scaling. There is generally less than 2% deviation of the anharmonic frequencies from observed. They are mainly nearer in value than those calculated by Martin-Drumel et al.³⁵ with the hybrid B97-1 functional and the 6-311G(d,p) basis set. One can rationalize this as essentially resulting from the different characteristics of second-order vibrational perturbation theory used in the various used versions of Gaussian. A graphical comparison of the various calculation results is presented in Fig. 2, with the relevant statistics given in Table 2.

Fig. 2. Comparison between measured and calculated isoquinoline ground state vibrational frequencies.

Examination of Table 2 and Fig. 2 shows that, as compared with the Hartree–Fock calculation of Bandyopadhyay and Manogaran,³² the values of the DFT calculations necessitate far less scaling or refinement techniques to come into line with observed values. This is consistent with the conclusions of the comparative study of Scott and Radom.⁴⁰

2.2.3. Electronic state energies and transition oscillator strengths

The calculation B structure was used in the time-dependent DFT method²⁸ calculation of the transition energies and oscillator strengths involving 161 singlet electronic excited states of isoquinoline up to 11.457 eV (sixty-eight A′ states, eighty-one A′′ states). Since the eigenvalues depend critically on M.O. energy differences in time-dependent DFT calculations these may not provide reliable values for transition energies. The upper energy limit of our calculation was chosen to be greater than our observational limit of 10.7 eV in order to accommodate inaccuracies in the calculated energies. We stress, however, that the DFT calculations allow us to identify strong and weak electronic transitions, since oscillator strengths calculated by DFT methods depend little on the precision of calculated transition energies.^42,43 We note also that the true oscillator strengths can be modified if there exist plasmon-type interaction effects (see later). Table 3 lists the valence transition energies and oscillator strengths calculated by the DFT method. In the energy range up to 11.457 eV there are 33 allowed ¹A′ ← ¹A′ transitions whose oscillator strength is calculated to be greater than f = 0.01, but only six greater than f = 0.1.

Isoquinoline. DFT calculated singlet valence transition energies and oscillator strengths.

Transition	Transition energy eV	Oscillator strength f
2A′ ← 1A′	4.5447	0.0577
1A′′ ← 1A′	4.6945	0.0020
3A′ ← 1A′	4.8606	0.0340
2A′′ ← 1A′	5.5463	0.0012
4A′ ← 1A′	6.1018	0.6111
3A′′ ← 1A′	6.2021	0.0015
5A′ ← 1A′	6.2099	0.5681
6A′ ← 1A′	6.3992	0.1484
4A′′ ← 1A′	6.5418	0.0004
7A′ ← 1A′	6.5672	0.1306
8A′ ← 1A′	6.7328	0.0186
5A′′ ← 1A′	6.7512	0.0083
6A′′ ← 1A′	7.0696	0.0006
7A′′ ← 1A′	7.1185	0.0001
8A′′ ← 1A′	7.1486	0.0184
9A′ ← 1A′	7.1868	0.0143
9A′′ ← 1A′	7.2219	0.0000
10A′′ ← 1A′	7.3624	0.0055
11A′′ ← 1A′	7.4753	0.0079
10A′ ← 1A′	7.5549	0.0028
11A′ ← 1A′	7.6716	0.0063
12A′′ ← 1A′	7.6858	0.0002
12A′ ← 1A′	7.6967	0.0416
13A′′ ← 1A′	7.7432	0.0006
14A′′ ← 1A′	7.7956	0.0002
15A′′ ← 1A′	7.8639	0.0033
13A′ ← 1A′	7.9357	0.0106
14A′ ← 1A′	8.0364	0.0049
16A′′ ← 1A′	8.0528	0.0022
17A′′ ← 1A′	8.0896	0.0004
15A′ ← 1A′	8.1207	0.1941
16A′ ← 1A′	8.2507	0.0407
18A′′ ← 1A′	8.2673	0.0029
19A′′ ← 1A′	8.2980	0.0001
20A′′ ← 1A′	8.3500	0.0001
17A′ ← 1A′	8.3710	0.1121
18A′ ← 1A′	8.3833	0.0758
21A′′ ← 1A′	8.3974	0.0111
22A′′ ← 1A′	8.4080	0.0006
23A′′ ← 1A′	8.4796	0.0080
19A′ ← 1A′	8.4975	0.0037
20A′ ← 1A′	8.5112	0.0175
24A′′ ← 1A′	8.5320	0.0017
21A′ ← 1A′	8.5959	0.0091
25A′′ ← 1A′	8.6072	0.0015
26A′′ ← 1A′	8.7368	0.0176
22A′ ← 1A′	8.7702	0.0021
23A′ ← 1A′	8.8861	0.0006
27A′′ ← 1A′	8.9566	0.0027
28A′′ ← 1A′	8.9763	0.0001
24A′ ← 1A′	8.9992	0.0020
29A′′ ← 1A′	9.1004	0.0012
30A′′ ← 1A′	9.1170	0.0012
31A′′ ← 1A′	9.1334	0.0030
32A′′ ← 1A′	9.1717	0.0001
25A′ ← 1A′	9.1807	0.0032
33A′′ ← 1A′	9.2130	0.0001
26A′ ← 1A′	9.2295	0.0030
27A′ ← 1A′	9.2400	0.0523
34A′′ ← 1A′	9.2651	0.0020
35A′′ ← 1A′	9.3087	0.0006
36A′′ ← 1A′	9.3516	0.0004
28A′ ← 1A′	9.3675	0.0029
37A′′ ← 1A′	9.4244	0.0004
38A′′ ← 1A′	9.4312	0.0012
29A′ ← 1A′	9.4433	0.0031
39A′′ ← 1A′	9.4771	0.0000
30A′ ← 1A′	9.5055	0.0011
40A′′ ← 1A′	9.5516	0.0215
31A′ ← 1A′	9.5638	0.0018
32A′ ← 1A′	9.5778	0.0285
41A′′ ← 1A′	9.5983	0.0026
42A′′ ← 1A′	9.6323	0.0010
43A′′ ← 1A′	9.7502	0.0000
33A′ ← 1A′	9.7552	0.0535
44A′′ ← 1A′	9.7787	0.0007
34A′ ← 1A′	9.8038	0.0050
35A′ ← 1A′	9.8922	0.0818
36A′ ← 1A′	9.9224	0.0129
37A′ ← 1A′	10.0229	0.0233
38A′ ← 1A′	10.0304	0.0097
45A′′ ← 1A′	10.0402	0.0068
46A′′ ← 1A′	10.0562	0.0023
47A′′ ← 1A′	10.1134	0.0062
48A′′ ← 1A′	10.1212	0.0001
39A′ ← 1A′	10.1427	0.0005
49A′′ ← 1A′	10.1785	0.0101
40A′ ← 1A′	10.1865	0.0883
50A′′ ← 1A′	10.1957	0.0050
41A′ ← 1A′	10.2137	0.0029
42A′ ← 1A′	10.2549	0.0010
51A′′ ← 1A′	10.2709	0.0132
52A′′ ← 1A′	10.3008	0.0000
43A′ ← 1A′	10.3085	0.0195
53A′′ ← 1A′	10.3157	0.0000
54A′′ ← 1A′	10.3553	0.0035
44A′ ← 1A′	10.3684	0.0027
45A′ ← 1A′	10.4017	0.0010
55A′′ ← 1A′	10.4305	0.0432
46A′ ← 1A′	10.4367	0.0032
47A′ ← 1A′	10.4839	0.0072
56A′′ ← 1A′	10.4875	0.0017
57A′′ ← 1A′	10.4995	0.0040
48A′ ← 1A′	10.5298	0.0022
49A′ ← 1A′	10.5522	0.0003
58A′′ ← 1A′	10.5641	0.0000
59A′′ ← 1A′	10.57777	0.0010
60A′′ ← 1A′	10.6265	0.0071
50A′ ← 1A′	10.6501	0.0037
61A′′ ← 1A′	10.6599	0.0002
62A′′ ← 1A′	10.6975	0.0664
63A′′ ← 1A′	10.7133	0.0212
51A′ ← 1A′	10.7170	0.0308
64A′′ ← 1A′	10.7514	0.1542
52A′ ← 1A′	10.7570	0.0312
53A′ ← 1A′	10.7793	0.0376
54A′ ← 1A′	10.8408	0.0034
65A′′ ← 1A′	10.8593	0.0076
66A′′ ← 1A′	10.8945	0.0002
67A′′ ← 1A′	10.8989	0.0111
55A′ ← 1A′	10.9273	0.0102
68A′′ ← 1A′	10.9568	0.0013
56A′ ← 1A′	10.9718	0.0018
69A′′ ← 1A′	11.0181	0.0000
70A′′ ← 1A′	11.1184	0.0330
71A′′ ← 1A′	11.1220	0.0016
72A′′ ← 1A′	11.1720	0.0554
57A′ ← 1A′	11.1988	0.0954
58A′ ← 1A′	11.2224	0.0212
73A′′ ← 1A′	11.2283	0.0006
74A′′ ← 1A′	11.2480	0.0051
75A′′ ← 1A′	11.2679	0.0447
59A′ ← 1A′	11.2753	0.1237
76A′′ ← 1A′	11.2818	0.0161
60A′ ← 1A′	11.2968	0.0186
77A′′ ← 1A′	11.3149	0.0070
78A′′ ← 1A′	11.3382	0.0178
61A′ ← 1A′	11.3818	0.0123
79A′′ ← 1A′	11.3932	0.0427
80A′′ ← 1A′	11.4047	0.0027
62A′ ← 1A′	11.4178	0.0667
63A′ ← 1A′	11.4244	0.0267
81A′′ ← 1A′	11.4570	0.0003

3. Results and discussion

3.1. The absorption spectrum: general remarks

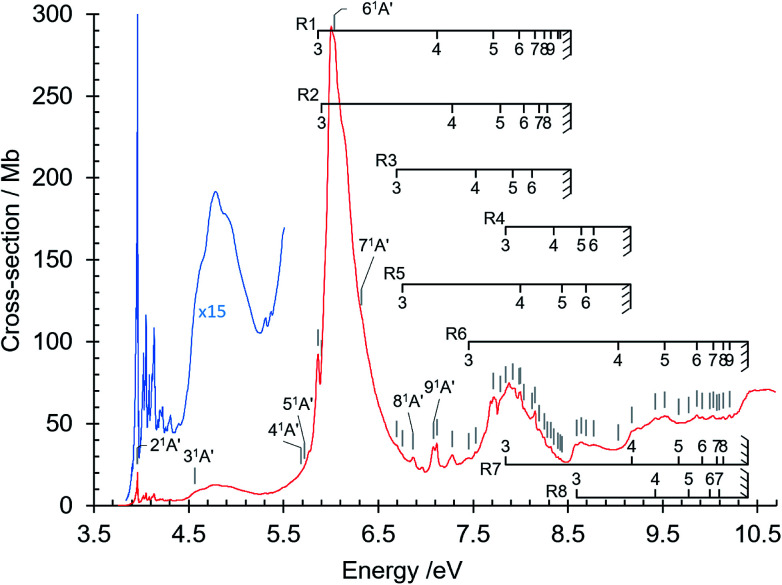
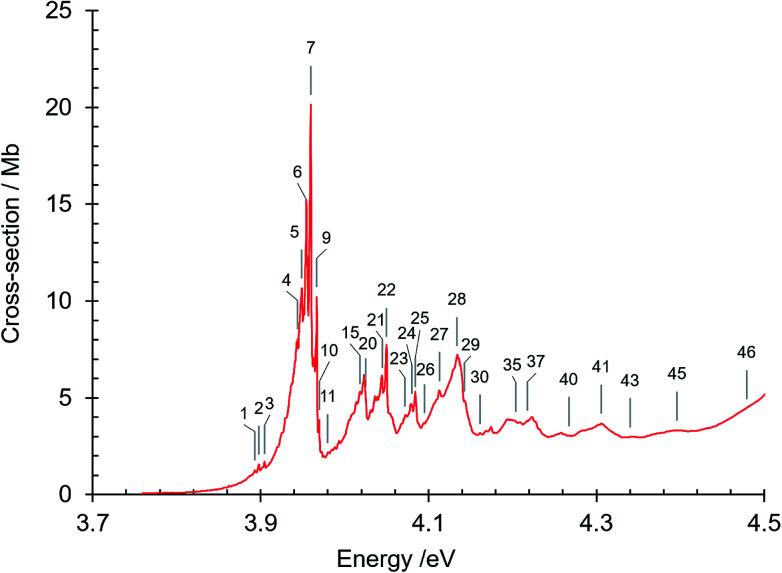
The absorption spectrum of gas phase isoquinoline between 3.6 and 10.7 eV, shown in Fig. 3, includes as an inset a 15× intensity magnification of the region between 3.8 and 5.6 eV. This spectrum contains a great number of features, of which many are small peaks that overlie diffuse continua. A few of the measured features are incompletely resolved shoulders in the peaks. The 161 measured features are seen in greater detail in intensity zooms of a number of parts of the absorption spectrum. We give typical examples that respectively show the spectral regions 3.7–4.5 eV (Fig. 4), 4.5–5.8 eV (Fig. 5), 5.5–6.6 eV (Fig. 6), 6.3–8.5 eV (Fig. 7) and 8.5–10.7 eV (Fig. 8). The band energies reported in Table 4 are recorded for clear peaks forming maxima in the recorded absorption cross-sections and, in the case of less well-resolved features, as gradient particularities in the absorption profile. The precision of peak energy pointing, between ±0.0006 eV and ±0.004 eV, is a function of the spectral energy range and the step size used in wavelength scanning. The measured features are listed in Table 4 as band numbers, band energies and band assignments. The assignments of the valence transitions have been made with the help of quantum mechanical calculations of electronic state energies and transition strengths, as discussed below.

Fig. 3. Absorption spectrum of isoquinoline between 3.6 and 10.8 eV. Rydberg series bands are marked. The origin bands O⁰₀ of the set of π–π* valence transitions 2¹A′ ←1¹A′ up to 9¹A′ ←1¹A′ (Table 4) are indicated as 2¹A′…. 9¹A′. Vibrational components of vibronic transitions listed in Table 4 are not denoted, for figure clarity.

Fig. 4. Absorption spectrum of isoquinoline between 3.7 and 4.5 eV. Band numbers are pinpointed.

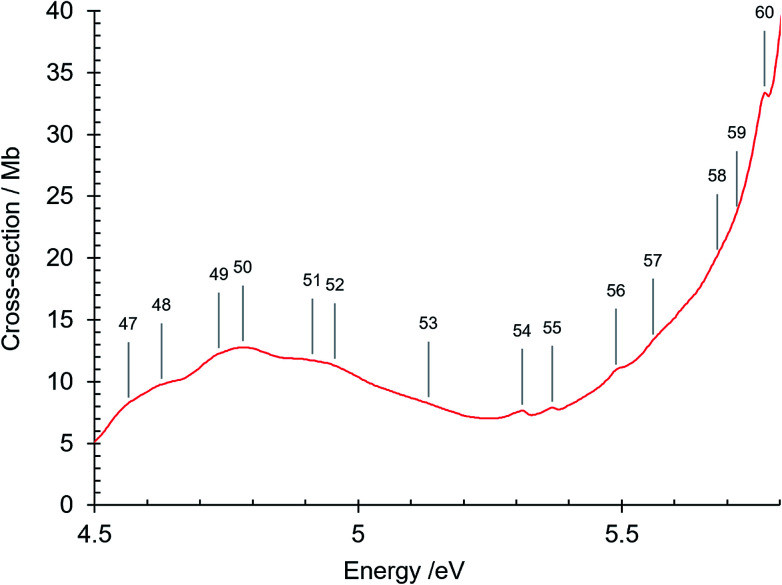
Fig. 5. Absorption spectrum of isoquinoline between 4.5 and 5.8 eV. Band numbers are pinpointed.

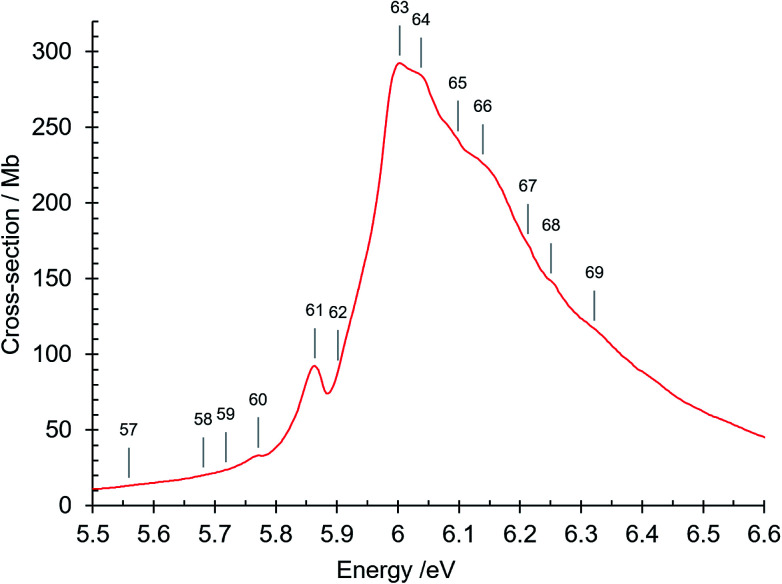
Fig. 6. Absorption spectrum of isoquinoline between 5.5 and 6.6 eV. Band numbers are indicated.

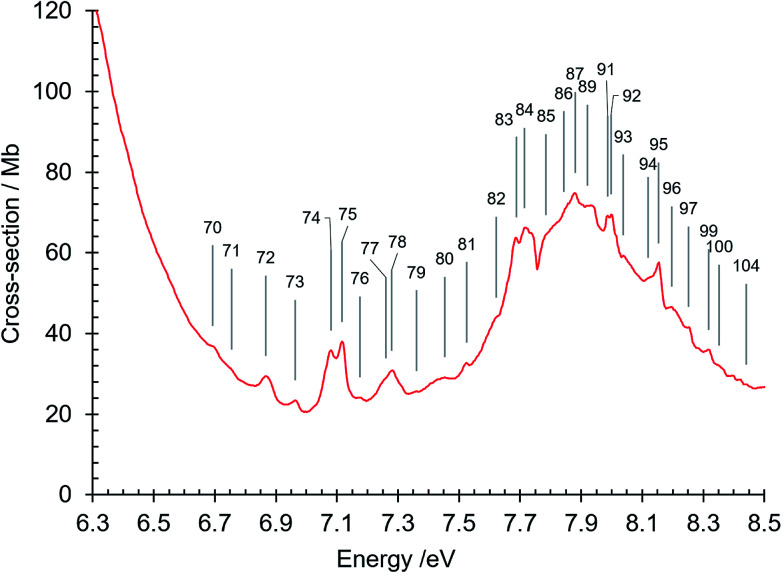
Fig. 7. Absorption spectrum of isoquinoline between 6.3 and 8.5 eV. Band numbers are pinpointed.

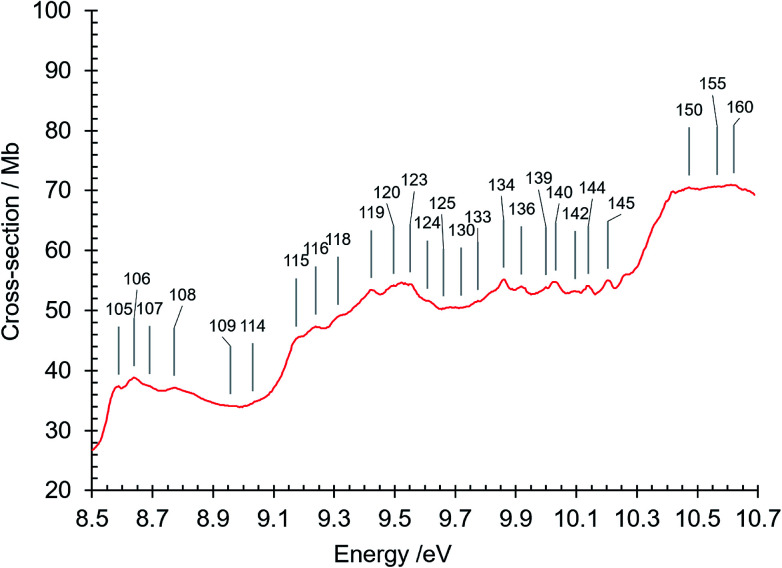
Fig. 8. Absorption spectrum of isoquinoline between 8.5 and 10.7 eV. Band numbers are pinpointed.

Isoquinoline gas-phase absorption spectrum: band energies and assignments.

Band no.	Energy/eV	Energy/cm−1	Assignment
1	3.893	31399	Hot band (see text)
2	3.898	31439	Hot band 500 cm−1 (see text)
3	3.905	31496	Hot band (see text)
4	3.944	31810	s33 (sequence, see text)
5	3.949	31851	s22 (sequence, see text)
6	3.954	31891	s11 (sequence, see text)
7	3.960	31939	π–π* 21A′ ← 11A′O00: 0+(ππ*) (principal component)
8	3.963	31964
9	3.967	31996	a10s11 (see text)
10	3.970	32020	0−: a10(nπ*) (principal component)
11	3.980	32101	0=: b10(nπ*) (principal component)
12	3.989	32173
13	3.994	32217	21A′ ← 11A′φ20
14	4.014	32375
15	4.018	32407
16	4.023	32448	21A′ ← 11A′α10
17	4.032	32520
18	4.036	32552
19	4.039	32577
20	4.025 (sh)	32464
21	4.045	32625
22	4.050	32665	21A′ ← 11A′β10
23	4.072	32843
24	4.080	32907
25	4.084	32940	21A′ ← 11A′α20
26	4.095	33028
27	4.113	33173	21A′ ← 11A′α10β10
28	4.134	33343	21A′ ← 11A′γ10
29	4.143	33415	21A′ ← 11A′α30
30	4.161	33561
31	4.168	33617
32	4.175	33673	21A′ ← 11A′α20β10
33	4.194	33827
34	4.197	33851	21A′ ← 11A′ γ10α10
35	4.204	33907
36	4.209	33948	21A′ ← 11A′γ10β10
37	4.218	34020
38	4.224	34069
39	4.258	34343	21A′ ← 11A′γ10α20
40	4.267	34415	21A′ ← 11A′α20β20
41	4.306	34730	21A′ ← 11A′γ20
42	4.336	34972
43	4.340	35004
44	4.345	35045
45	4.396	35456	21A′ ← 11A′γ20β10
46	4.479 (sh)	36125
47	4.564	36814	π–π* 31A′ ← 11A′O00
48	4.627	37316	31A′ ← 11A′α10
49	4.736	38204	31A′ ← 11A′γ10
50	4.781	38561
51	4.913	39626
52	4.956	39973
53	5.133	41400
54	5.311	42836
55	5.368	43296
56	5.489	44272
57	5.559	44836
58	5.681	45822	π–π* 41A′ ← 11A′O00
59	5.718	46120	π–π* 51A′ ← 11A′O00
60	5.771	46546	41A′ ← 11A′β10
61	5.864	47296	R1 (n = 3) O00, δ = 0.7409
62	5.902 (sh)	47603	R2 (n = 3) O00, δ = 0.724
63	6.003	48417
64	6.038	48699	π–π* 61A′ ← 11A′O00
65	6.098	49183
66	6.139	49514	61A′ ← 11A′β10
67	6.213	50111
68	6.251	50417
69	6.322	50990	π–π* 71A′ ← 11A′O00; R4 (n = 3) O00, δ = 0.8142
70	6.693	53982	R3 (n = 3) O00, δ = 0.28
71	6.755	54482	R5 (n = 3) O00, δ = 0.621
72	6.867	55386	π–π* 81A′ ← 11A′O00
73	6.963	56160	81A′ ← 11A′β10
74	7.081	57112	π–π* 91A′ ← 11A′O00
75	7.117	57402	R1 (n = 4) O00, δ = 0.8969
76	7.175	57870	91A′ ← 11A′β10
77	7.261	58564
78	7.280	58717	R1 (n = 4) z10; R2 (n = 4) O00, δ = 0.70
79	7.360	59362
80	7.453	60112	R6 (n = 3) O00, δ = 0.851
81	7.526	60701	R3 (n = 4) O00, δ = 0.32
82	7.622	61475
83	7.687	61999
84	7.715	62225	R1 (n = 5) O00, δ = 0.9141
85	7.785	62790	R2 (n = 5) O00, δ = 0.726
86	7.843	63258	R4 (n = 4) O00, δ = 0.8183; R7 (n = 3) O00, δ = 0.693
87	7.880	63556	R1 (n = 5) z10
88	7.904	63750
89	7.920	63879	R3 (n = 5) O00, δ = 0.28
90	7.930	63959
91	7.986	64411	R1 (n = 6) O00, δ = 0.9989
92	7.999	64516	R5 (n = 4) O00, δ = 0.577
93	8.038	64830	R2 (n = 6) O00, δ = 0.741
94	8.120	65492	R3 (n = 6) O00, δ = 0.24
95	8.154	65766	R1 (n = 7) O00, δ = 0.9845
96	8.197	66113	R2 (n = 7) O00, δ = 0.608
97	8.252	66557	R1 (n = 8) O00, δ = 1.004
98	8.281	66790	R2 (n = 8) O00, δ = 0.608
99	8.318	67089	R1 (n = 9) O00, δ = 0.9888
100	8.352	67364	R4 (n = 5) O00, δ = 0.8965
101	8.383	67613
102	8.397	67726	R1 (n = 11) O00, δ = 0.8856
103	8.420	67912	R1 (n = 12) O00, δ = 0.8784
104	8.440	68073	R5 (n = 5) O00, δ = 0.653
105	8.589	69275	R8 (n = 3) O00, δ = 0.259
106	8.640	69686	R4 (n = 6) O00, δ = 0.8848
107	8.690	70089	R5 (n = 6) O00, δ = 0.620
108	8.771	70743	R4 (n = 7) O00, δ = 1.0859
109	8.958	72251
110	8.965	72307
111	8.975	72388
112	8.991	72517
113	9.007	72646
114	9.031	72840	R6 (n = 4) O00, δ = 0.847
115	9.174	73993	R7 (n = 4) O00, δ = 0.669
116	9.239	74517
117	9.246	74574
118	9.312	75103
119	9.423	76004	R8 (n = 4) O00, δ = 0.268
120	9.497	76598
121	9.523	76808	R6 (n = 5) O00, δ = 1.061
122	9.534	76896
123	9.552	77042
124	9.607	77485
125	9.660	77913
126	9.667	77969	R7 (n = 5) O00, δ = 0.692
127	9.684	78106
128	9.701	78243
129	9.709	78308
130	9.720	78397
131	9.728	78461
132	9.736	78526
133	9.774	78832	R8 (n = 5) O00, δ = 0.338
134	9.860	79526	R6 (n = 6) O00, δ = 0.9804
135	9.887	79744
136	9.919	80002	R7 (n = 6) O00, δ = 0.68
137	9.959	80324
138	9.967	80389
139	9.999	80647	R8 (n = 6) O00, δ = 0.175
140	10.031	80905	R6 (n = 7) O00, δ = 0.9277
141	10.072	81236	R7 (n = 7) O00, δ = 0.559
142	10.096	81429	R8 (n = 7) O00, δ = 0.310
143	10.105	81502
144	10.140	81784	R6 (n = 8) O00, δ = 0.7937; R7 (n = 8) O00, δ = 0.766
145	10.204	82300	R6 unresolved n = 9, n = 10; R7 (n = 9) O00, δ = 0.668
146	10.264	82784	R6 unresolved n > 10 values
147	10.272	82849
148	10.397	83857
149	10.419	84034
150	10.472	84462
151	10.498	84672
152	10.538	84994
153	10.547	85067
154	10.556	85139
155	10.565	85212
156	10.574	85285
157	10.583	85357
158	10.597	85470
159	10.611	85583
160	10.620	85656
161	10.656	85946

A review by Innes et al.¹⁴ lists the triplet and singlet state energies and oscillator strengths of n–π* and π–π* transitions of isoquinoline, culled from experimental and theoretical studies available in 1988. Data on the π–π* transitions were published earlier by Baba and Yamzaki⁴⁴ in their Pariser–Parr–Pople SCF LCAO MO method calculation study of the absorption spectrum of isoquinoline. Their calculation yielded eight π–π* transitions up to 7.13 eV, as did the SCF MO calculations of Nishimoto,⁴⁵ who used a fixed core approximation. Eight calculated π–π* transitions are reported in this energy region by Tinland,⁴⁶ who used the P–P–P SCF LCAO MO method, and by Ridley and Zerner⁴⁷ whose SCF LCAO MO calculations employed a modified INDO method (Table 5).

Isoquinoline π–π* mA′ ← 1A′ electronic singlet state transition energies E (eV) and oscillator strengths (f). Observed and calculated SCF-LCAO-MO and DFT values.

Excited state mA′	a24	b49	c46	d45	e47	f48	g44 (Baba)	h DFT present study	i Obs. present study	h–i unsigned	g–i unsigned
2	4.500	3.876	4.004	3.97	4.03	4.11	4.06	4.5447	3.960	0.5847	0.100
	0.026	1Lb	0.040	0.051	0.09	0.01	0.118	0.0577
3	5.671	5.287	4.497	4.52	4.61	4.83	4.42	4.8606	4.564	0.2966	0.144
	0.189	1La	0.194	0.180	0.16	0.24	0.147	0.0340
4		6.250	5.527	5.31	5.55		5.34	6.1018	5.681	0.4208	0.331
		1Bb	0.207	0.059	0.12		0.020	0.6111
5			5.618	5.50	5.79	5.77	5.64	6.2099	5.718	0.4919	0.078
			0.831	1.132	0.89	0.02	0.489	0.5681
6			5.772	5.66	5.89		5.79	6.3992	6.038	0.3612	0.248
			0.836	0.257	0.81		0.382	0.1484
7			6.068	5.80	6.35		5.98	6.5672	6.322	0.2452	0.342
			0.070	0.475	0.52		1.151	0.1306
8			6.258	6.18	6.48		6.30	6.7326	6.867	0.1344	0.567
			0.519	0.568	0.08		0.540	0.0186
9			6.229	6.96	6.84		7.13	7.1868	7.081	0.1058	0.049
			0.149	0.001	0.01		0.001	0.0143
10								7.5549
								0.0028
11								7.6716
								0.0063
12								7.6967
								0.0416
13								7.9357
								0.0106
14								8.0364
								0.0049
15								8.1207
								0.1941
16								8.2507
								0.0407
17								8.3710
								0.1121
18								8.3833
								0.0758
19								8.4975
								0.0037
20								8.5112
								0.0175

Calculations that included configuration interactions were carried out in some studies.^44,47,48 On the other hand, as listed in Table 5, more limited π–π* transition calculations were done by Favini et al.,²⁴ by Mataga⁴⁹ and by Wagner et al.⁴⁸ Goodman and Harrell⁵⁰ made analogous calculations on the n–π* transitions of isoquinoline. Their results and those of our own DFT calculations (Table 5), have helped in assigning the valence transitions of isoquinoline in our gas phase spectrum. Rydberg transition bands of isoquinoline were observed for the first time in our study. There are no reported calculations on Rydberg transitions of isoquinoline.

Our analysis and discussion of the π–π* transitions of isoquinoline analysis are based substantially on the calculation results of Baba and Yamakazi.⁴⁴ We note that their transition energies and oscillator strengths agree well with those of Nishimoto⁴⁵ and are in satisfactory agreement with the values reported by Tinland⁴⁶ and by Ridley and Zerner.⁴⁷ We remark that the valence transition energies calculated by the DFT method are greater than those of the older, mainly P–P–P, calculations. Our DFT calculations indicate that only a few of the n–π* transitions (Table 3) have oscillator strengths (f ∼ 0.01) possibly of sufficient value to be observable in our spectra (see below).

3.1.1. Absorption 3.8–4.5 eV: 2¹A′ ← 1¹A′ π–π* transition origin band region. Vibronic coupling with the 1¹A′′ nπ* state

The spectral features in this energy region (Fig. 3 and 4) are sharp up to about 4.2 eV. They become more diffuse at higher energies. The maximum absorption cross-section between 3.7 and 5.2 eV is 15 Mb at about 4.8 eV. This region has previously been well studied in solution and in the vapor phase. It contains both n–π* and π–π* transitions. The gas-phase studies of Hiraya et al.,^15,16 assign a very weak n–π* transition, 1¹A′′ ← 1¹A′, that appears close to the initial π–π* spectral region. They report the origin band of the 1¹A′′ ← 1¹A′ transition to be at 30 821 cm⁻¹ (3.821 eV). This closeness in energy is consistent with our DFT calculations, whose calculated energy separation is 1208 cm⁻¹ (Table 3) as compared with the experimental value 1118 cm⁻¹ (see below), although the calculated order of the first n–π* and π–π* transition energies is reversed with respect to the experimental values (see below).

Our calculations give oscillator strengths of f = 0.0020 and 0.0577 respectively for the 1¹A′′ ← 1¹A′ n–π* and the 2¹A′ ← 1¹A′ π–π* transitions, consistent with their observed relative strengths.^15,16 The weakness of the n–π* transition origin band makes it unobservable in our absorption spectrum of isoquinoline. We note, however, that in the TD-DFT calculations (Table 3), of the 64 n–π* transitions calculated to occur up to 10.8 eV, only ten of them are calculated to have an oscillator strength greater than f = 0.01, (and only one greater than f = 0.1, the 64A′′ ← 1A′ transition at 10.7514 eV, f = 0.1542), are possibly adequate for observation in our spectra. However, these would occur at energies above 7 eV (Table 3) in spectral regions of intense valence π–π* transitions and Rydberg bands.

It is known that the order of the first n–π* and π–π* transition energies is reversed in mixed crystals with naphthalene or durene hosts (cited by Hassan and Hollas,⁵¹) and in solvents where H-bonded complexes can form.⁵² This reversed order is given in our DFT calculations on isoquinoline (Table 3). However, in the gas phase, the 1¹A′′ ← 1¹A′ n–π* transition origin is reported to lie at 30 821 cm⁻¹,^15,16 which is about 1118 cm⁻¹ below the strongest of a trio of close-lying features seen in the high resolution gas phase spectrum of isoquinoline.^15,16 These three spectral features, traditionally denoted as 0⁺, 0⁻ and 0⁼ respectively, are in the π–π* 2¹A′ ← 1¹A′ origin band region, and they correspond to features in the 3.960 eV band region in our study (Tables 4 and 6). They have been shown to be due to near-resonance vibronic coupling between the n–π* 1¹A′′ and π–π* 2¹A′ vibronic levels,^15,16,18 the coupling being induced by out-of-plane ν(a) and ν(b) vibrations of a′′ symmetry in the 1¹A′′ state.⁵¹

Isoquinoline absorption origin region.

Band no.	Absorption cross-section Mb × 10 [relative int.]	Energy/eV	Energy/cm−1 [ν – 31939]	Energy/cm−1 [relative int.] Fischer and Naaman18
1	12.70 [0.06]	3.893	31399 [541]	31384 (−14)
2	15.57 [0.08]	3.898	31439 [−500]	31426 (−13)
3	17.02 [0.08]	3.905	31496 [−443]	31481 (−15)
4	80.30 [0.40]	3.944	31810 [−129]	31797 (−13) [0.14]
5	106.71 [0.53]	3.949	31851 [−88]	31841 (−10) [0.27]
6	151.87 [0.75]	3.954	31891 [−48]	31885 (−6) [0.55]
7	201.41 [1.00]	3.960	31939 [0]	31925 (−14) [1.00]
8	70.48 [0.35]	3.963	31964 [+25]	31960 (−4) [0.27]
9	102.12 [0.51]	3.967	31996 [+57]	31983 (−13) [0.33]
10	38.52 [0.19]	3.970	32020 [+81]	32008 (−12) [0.05]
11	22.01 [0.11]	3.980	32101 [+162]	*
12	24.44 [0.12]	3.989	32173 [+234]	*
13	27.72 [0.14]	3.994	32214 [+275]	32203 (−11)

The relative proportion of the 2¹A′ state varies across the envelope of the origin band region measured by Hiraya et al,¹⁵ as can be seen in a more refined way in the rotational contour analysis of a high resolution gas phase spectrum of isoquinoline absorption in the 31 925 cm⁻¹ region.⁵¹ The assignments 0⁺(ππ*), 0⁻ a¹₀(nπ*) and 0⁼ b¹₀(nπ*) in Tables 4 and 6 refer to the principal zero-order vibronic components in the observed band (see below). The spectral effects of vibronic coupling between these non-degenerate but close-lying two states have been studied in detail by Fischer and co-workers.^18,19,53

We recall that the isoquinoline n–π* 1¹A′′ level is shifted to higher energies, above the π–π* 2¹A′ level, in an isoquinoline hydrogen-bonded complex with methyl alcohol in a supersonic jet.⁵² The π–π* transition origin band has a single feature, at 31 880 cm⁻¹ (3.953 eV) in this case, indicating that the π–π* 2¹A′ level is no longer perturbed by the n–π* 1¹A′′ state.

The features between 3.893 and 3.994 eV, severely marked by vibronic interactions, are also presented in Table 6, where we compare related gas-phase spectral observations of this complex spectral region. The data of Fischer and Naaman¹⁸ are from absorption spectra recorded on photographic plates. Their reported band energies, used without confirmation in other isoquinoline studies^19,54 are consistently about 10 cm⁻¹ smaller than our measurements. The reported relative intensities of the bands follow the relative trends of our absorption cross section measurements but there are some quantitative differences, due no doubt to the well-known difficulty of measuring band intensities on photographic plates. We remark that the relative intensities of the three main bands, denoted traditionally as 0⁺, 0⁻ and 0⁼, reported as 1.00 : 0.63 : 0.20 by Hiraya et al.,¹⁵ based on a jet-cooled multiphoton ionization photoelectron study, are in excellent agreement with those obtained by our absorption cross-section measurements, 1.00 : 0.51 : 0.19 (Table 6). These features have also been shown not to be hot bands.¹⁸

Following the assignments of Fischer and Naaman,¹⁸ bands numbered 1, 2 and 3 are true hot bands that are three members of a sequence progression with a sequence interval ν′ − ν′′ ≈ 40 cm⁻¹. Calculations indicate that in the 2 ¹A′ and 1¹A′′ states the sequence forming vibrations have frequencies 135.5 cm⁻¹ and ∼175.5 cm⁻¹,¹⁸ (139 cm⁻¹ and 182 cm⁻¹),¹⁹ respectively. The band number 13 at 3.994 eV can be assigned to excitation of two quanta of the sequence-forming mode ν′(φ) ∼139 cm⁻¹, a mode possibly related to ν′′(44) = 181 cm⁻¹ or ν′′(45) = 166 cm⁻¹ that are out-of-plane vibrations in ground state isoquinoline (Table 2).

Band number 7 is the most intense of the origin band group and is chiefly ¹ππ* in character.¹⁸ The assignments of bands numbered 7, 9 and 10, (respectively 0⁺, 0⁻ and 0⁼) are the principal components of the products of the resonance between the zero-order levels 0(¹ππ*), a(¹nπ*) and b(¹nπ*), where 0(¹ππ*) is the vibrationless level of the 2¹A′ ¹ππ* state and a and b refer to out-of-plane modes active in the 1¹A′′ ¹nπ* state. The ν(a) and ν(b) modes and their frequencies have not been identified^18,19 but their frequencies could be of the order of 1000 cm⁻¹.⁵¹ The coupling parameter via ν(a), 26 cm⁻¹, is bigger than through ν(b), 10 cm⁻¹,⁵¹ so that vibronic absorption band a¹₀ is stronger than band b¹₀, as evidenced in our spectra by band number 10 at 3.970 eV being about twice as intense as band number 11 at 3.980 eV (Tables 4 and 6).

Some other bands in this region have assignments involving mode s, involved in the sequence structure.^18,51 The relevant ground and excited state zero-order mode frequencies (before resonant level interactions) are 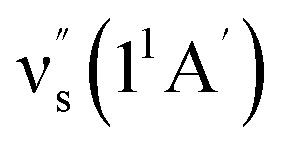= 181 cm⁻¹i.e. mode ν₄₄ (Table 2), 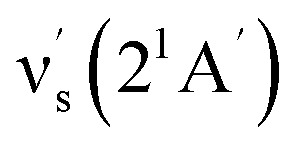= 135.5 cm⁻¹, 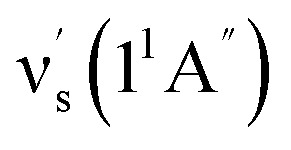= 175.5 cm⁻¹.

Bands numbered 4–45 (Table 4) are assigned to vibronic components of the π–π* 2¹A′ ← 1¹A′ transition. Four vibrational modes are considered to be active in the excited state: ν′(φ) = 139 cm⁻¹, a non-totally symmetric vibration, active in two quanta as discussed above, ν′(α) = 510 cm⁻¹, ν′(β) = 730 cm⁻¹ and ν(γ) ∼1400 cm⁻¹. Related frequencies in the ground state are ν′′(30) = 502 cm⁻¹, ν′′(26) = 778 cm⁻¹, ν′′(13) = 1432 cm⁻¹, ν′′(14) = 1382 cm⁻¹.

The strongest of the bands numbered 4–45 are present in the gas phase absorption spectra of Okajima and Lim⁵⁵ and of Keith-Jameson et al.²² but their energies were not reported. Our band frequencies are consistent with those reported up to 4.174 eV in a gas phase absorption spectrum by Fischer and Naaman.¹⁸

The diffuseness of the vibronic bands at energies above 4.05 eV in all reported gas phase absorption spectra of isoquinoline, was attributed by Fischer and Naaman¹⁸ to the fast relaxation processes of internal conversion between the lowest excited singlet ππ and nπ* electronic states, in addition to singlet-triplet intersystem crossing. On the other hand, Fischer and Knight¹⁹ emphasized the effects of spectral congestion in creating the broadness of the bands. It is probable that both internal conversion and spectral congestion are in play.^20,23 We note, for example, that the density of vibronic states in the 2¹A′ level at about 4.1 eV, ∼1130 cm⁻¹ above the 0⁺ level, can be estimated to be of the order of 1 per cm⁻¹. The density of quasi-degenerate vibronic levels in the 1¹A′′ state would be much higher at that energy, thus ensuring the possibility of much vibronic mixing between the n–π* and π–π* levels.

The vibronic bands of the 2¹A′ ← 1¹A′ transition are also observed in condensed phase absorption spectra^{24,25,56–58} but the spectral resolution is insufficient to investigate possible influences of solvent on isoquinoline vibronic level energies as well as to consider further aspects of mixed n–π* and π–π* levels in the absorption bands.

The structured features in the 3.8–4.4 eV region is followed by a broad diffuse band whose maximum is at ∼4.76 eV but which contains small features assigned to the 3¹A′ ← 1¹A′ π–π* transition, in particular band number 47 at 4.564 eV as the O⁰₀ origin band. Our DFT calculation places this transition at 4.86 eV, f = 0.034 (Table 3). Several P–P–P studies calculate this transition to be in the 4.4–4.6 eV region (Table 5). The two lowest singlet π–π* transitions, respectively 2¹A′ ← 1¹A′ and 3¹A′ ← 1¹A′, were listed by Baba and Yamazaki⁴⁴ to have been observed at 3.91 eV, f = 0.023 (calc 0.118) and 4.66 eV, f = 0.085 f (calc) = 0.147 respectively.

We remark that Wagner et al.,⁴⁸ who calculate the 3¹A′ ← 1¹A′ transition at 4.83 eV (f = 0.24), consider that the 3¹A′ electronic state corresponds to ¹L_a, using the designation of Platt which is based on a free electron model,⁶⁰ whereas Zimmerman and Joop⁵⁶ made an ¹L_b (long axis polarised) assignment as indicated by their measurements of fluorescence polarization.

We note also that Favini et al.²⁴ studied the absorption spectrum of isoquinoline up to about 5.4 eV in cyclohexane and methanol solutions, i.e. in the range 220–400 nm. The 270 nm (4.59 eV) broad band maximum shifts to higher energies in cyclohexane (268 nm, 4.63 eV in methanol and to 265 nm, 4.68 eV in cyclohexane), and the spectrum exhibits more structure in cyclohexane.

3.1.2. Valence transitions: 5.2–7.2 eV

This is also a structured region (Fig. 5–7). Bands numbered 58–60 are assigned to the 4¹A′ ← 1¹A′ and 5¹A′ ← 1¹A′ π–π* transitions. The oscillator strengths for these transitions differ strongly in their calculated values in Table 5, reflecting differences in the complexity of the electron correlations in the various theoretical methods. The absorption cross-section then rises to a single sharp band at 5.864 eV (band no. 61) and then to a maximum at 6.003 eV (band no. 63). The bands number 61 and 62 are Rydberg features, as described later (Section 3.1.4.1). The absorption cross section continues as a decreasingly intense broad band up to ∼6.8 eV but contains three shoulder features (i) at 6.038 eV (band no. 64) assigned to the π–π* 6¹A′ ← 1¹A′ O⁰₀ transition, (ii) at 6.139 eV (band no. 66), assigned to a vibronic component of the latter and (iii) at 6.322 eV (band no. 69) assigned to two overlapping transitions, the π–π* 7¹A′ ← 1¹A′ O⁰₀ band, and the R3 Rydberg n = 3 O⁰₀ transition whose Rydberg limit is the first excited ion state at 9.16 eV (see below). Two more π–π* transitions are assigned in the 6.8–7.1 eV region: 8¹A′ ← 1¹A′ and 9¹A′ ← 1¹A′ and their vibronic components (bands numbered 72–74 and 76).

The peak at 6.003 eV has an absorption cross section of 292 Mb. Its high intensity can be considered to be due to plasmon-type effects that result from the existence of collective modes of the π electrons.^61–65 These many-body effects are not considered in Hartree–Fock method single particle calculations. We note that naphthalene, which is closely related to isoquinoline, has a strong absorption peak at 5.89 eV (ref. 66) that is considered as being of plasmon-type,⁶⁵ resulting in an increased intensity of the ¹B_b π–π* valence transition.⁶⁷

3.1.3. Tests of valence transition energy calculations

The calculated and observed transition energies of isoquinoline are compared in Table 5. The tabulated values of UD, the unsigned difference between the DFT calculated energies and the eight assigned transition energies extend from 0.1058 to 0.5847 eV, with an average value of 0.3305 eV. There have been many time-dependent DFT benchmark test calculations of the electronic state energies of both diatomic and polyatomic molecules.^28,68–78 These calculations are principally of singlet valence excited states although there are a few that also include triplet states and Rydberg electronic states. These benchmark calculations provide comparisons of the efficiencies of various functionals, one of the best being among the hybrid density functional B3LYP, which contains 20% of Hartree–Fock exchange.⁷⁸ A typical criterion of the quality of TD-DFT calculation performance has been defined: when, in TD-DFT calculations of excited electronic states, the mean unsigned differences (MUD) between experimental and calculated energies are less than 0.36 eV the TD-DFT calculations are considered to be of value,⁷⁸ although it should be stated that in a typical set of benchmark molecules the actual UD values often have a large range, of up to or greater than 1 eV. Our TD-TFT calculation results on isoquinoline are thus consistent with the MUD < 0.36 eV criterion. There are other useful criteria to be considered, dependent on the degree of precision required. Examination of Table 5 shows that our calculated energies are far from so-called spectroscopic accuracy, and from the much less rigorous chemical accuracy of 0.05 eV. The calculated energies can be considered as “coarse-grained values”, yet are useful in spectral assignments.

It is of interest to consider what are the possible sources of errors in TD-DFT calculations. These are discussed by Burke et al.,⁴³ who mention the problem of adequately taking the exchange–correlation potential into account. In addition there is the possibility that the local adiabatic approximation no longer holds. This approximation is of importance in the case of frequency independent exchange–correlation functionals with which the exchange–correlation potential adjusts instantaneously to variations of the electron density. Prilj et al.⁷⁹ have discussed the origins of errors in TD-DFT calculations of the excited state energies of heteroaromatic molecules. They stress that L_b states are sensitive to correlation effects, and that L_a states have considerable double excitation characteristics.

Table 5 also lists the UD values cerning the π–π* excitation energies calculated by Baba and Yamazaki⁴⁴ by the P–P–P SCF LCAO method including configuration interaction. These are the lowest set of P–P–P calculation UD values of the studies listed in Table 5. The UD values of Baba and Yamazaki range from 0.049 to 0.567 eV, with an average value of 0.232 eV, which is 30% better than the average UD in our DFT calculation results. We note that the UD values decrease with increasing excitation energy in our DFT calculation, but increase in the P–P–P calculations of Baba and Yamazaki.

3.1.4. Rydberg and other transitions: 7.2–10.8 eV

The 7.2–10.8 eV spectral region exhibits strong π–π* transition continua underlying a number of relatively weak features many of which we assigned to Rydberg bands. There are no previous observations of Rydberg bands in isoquinoline spectra. The bands which we assign to Rydberg series are found to converge to the ground and also to excited electronic states of the ion, as discussed below.

The broad diffuse band in the 7.5–8.5 eV region has a maximum at 7.88 eV, where the absorption cross section is 75 Mb (Fig. 3 and 7). In the region from 7.7 eV to the maximum at 7.88 eV there is a unique feature, between bands number 84 and 85 (Fig. 3 and 7) exhibiting a sharp dip in intensity to a minimum absorption cross-section of 56.7 Mb at 7.754 eV. The intensity profile in this spectral region strongly resembles some absorption profiles in the 7.5 eV region of the naphthalene spectrum^{61,66,80–82} that have been interpreted as anti-resonance features resulting from interaction between Rydberg states and isoenergetic valence states that have a large density of vibronic states inhomogenously broadened by intramolecular vibrational redistribution.^81,82 The situation is that of the statistical limit case of radiationless transitions⁸³ in which here a Rydberg state interacts with an effective continuum formed by the broadened valence state. We suggest that the 7.7–7.85 eV absorption profile in isoquinoline is another example of such interference effects. We do not attempt to precisely identify the Rydberg and valence states concerned in this sharp antiresonance process but it is interesting to note that three close-lying singlet π–π* valence states, 10¹A′, 11¹A′ and 12¹A′, are calculated by our DFT calculation (Tables 3 and 5) to occur in the 7.5–7.7 eV region where several Rydberg bands are observed (Table 4).

Beyond 8.5 eV and up to the 10.8 eV limit, where the absorption cross section is also ∼77 Mb, there is a series of broad diffuse structures with superposed very small features, many of which have been assigned as Rydberg transition features. It is noteworthy that the absorption markedly increases at about 8.53 eV, 9.16 eV and 10.32 eV, corresponding to successive ionization energies of isoquinoline.^84,85 These inflexions of the absorption curve are very prominent and are discussed in more detail below. The origin of the background continua in isoquinoline requires further theoretical and experimental investigation, in particular concerning the possible existence, at the high energy end of the measured absorption spectrum, of transitions other than π–π* and n–π* transitions, since π–σ*, σ–π* and σ–σ* transitions could also exist in this spectral region.⁶² The latter are certainly among those transitions given by our DFT calculations of electronic state energies and transition oscillator strengths in the 8–11.4 eV region (Table 3), as can be seen in the various molecular orbital transition components associated with these high energy transitions (not reported).

3.1.4.1. Rydberg series converging to the ion ground electronic state at 8.53 eV

We identified three Rydberg series that converge on the D₀ doublet ground state of the isoquinoline cation. For our analysis we use the equation E(n) = IE − R/(n − δ)² for the energy E(n) of the nth Rydberg series member, where IE (isoquinoline) = 8.53 eV, the Rydberg constant R = 13.606 eV, and δ is the value of the quantum defect. The n = 3 first member of the R1 Rydberg series (Table 4, Fig. 3) is assigned to band number 61 (R1, n = 3, δ = 0.741). This band is observed in a spectral region notable for π–π* valence transitions. The n = 4, 5, 6, … (Table 4) members have greater values (δ = 1.0 ± 0.1) of their quantum defects. We can rationalize these higher δ values with respect to n = 3 by noting that the radius of the Rydberg orbital in the n = 3 Rydberg state is much the same as that of the ion core. This can result in coupling between Rydberg and π orbitals which would create departure from the hydrogen ion core based model formula used above to determine E(n) values. Naphthalene, a parent molecule of isoquinoline, exhibits an analogous difference between n = 3 and n ≥ 4 Rydberg level quantum defect values in its lowest Rydberg series where the n = 3 members have δ ∼0.68,⁸⁶ and n ≥ 4 Rydberg levels δ ∼0.85.⁶⁶

Rydberg bands of the R1 series have been observed up to n = 12, the latter being near ionization limit of 8.53 eV. Band resolution limitations are considered to be responsible for the range of quantum defect values around δ ∼0.88 found for the greatest values of n in this Rydberg series. We were unable to assign the n = 10 member, expected to occur at about 8.366 eV for δ = 0.9. This Rydberg level may have been displaced by interaction with a valence state such as the 18¹A′ valence state calculated to occur at 8.3833 eV (Table 3). The existence of a smaller δ values for the smaller n members of a Rydberg series can be due to a more marked effect of the core potential in comparison to the situation existing in higher n levels. The quantum defect values of the R1 Rydberg series bands lead us to assign R1 as an ns series in which an electron is ejected from the HOMO π⁻¹ orbital (Table 7).

Isoquinoline Rydberg series.

Rydberg series	Ion state energy limit of series	Observed members	Average quantum defect δ	Rydberg electronic transition
R1	D0 8.53 eV	n = 3–12	δ ∼ 0.90	11A′ → (HOMO)π−1ns
R2	D0 8.53 eV	n = 3–8	δ ∼ 0.68	11A′ → (HOMO)π−1np1
R3	D0 8.53 eV	n = 3–6	δ ∼ 0.28	11A′ → (HOMO)π−1np2
R4	D2 9.16 eV	n = 3–7	δ ∼ 0.85	11A′ → (HOMO−2)π−1ns
R5	D2 9.16 eV	n = 3–6	δ ∼ 0.62	11A′ → (HOMO−2)π−1np1
R6	D3 10.40 eV	n = 3–8	δ ∼ 0.90	11A′ → (HOMO−3)π−1ns
R7	D3 10.40 eV	n = 3–9	δ ∼ 0.68	11A′ → (HOMO−3)π−1np1
R8	D3 10.40 eV	n = 3–6	δ ∼ 0.27	11A′ → (HOMO−3)π−1np2

Some of the R1 series bands correspond to vibrational components of the Rydberg transitions (Table 4). The vibrational frequencies are ν(x) ∼1160 cm ⁻¹ and ν(z) ∼1320 cm ⁻¹. Galué et al. have measured an IRMPD spectrum of the ground state of the isoquinoline cation.⁸⁷ This spectrum exhibits a broad strong band at ∼750 cm⁻¹, two broad bands at about 1000 and 1100 cm⁻¹ respectively, and strong, but broad, bands at ∼1200 and ∼1450 cm⁻¹. The latter vibrational frequencies, close to those of the R1 Rydberg series vibrational components, probably correspond to carbon–carbon stretch modes.

A second group of Rydberg bands that converge to the D₀ ground state at 8.53 eV was assigned for the n = 3–8 levels, forming the R2 series. Their quantum defect values range from δ = 0.61 to 0.74 (Table 4, Fig. 3). The R2 series bands do not have any recognizable vibrational features. We consider this Rydberg series, assigned as an np₁ series (Table 7), to also be associated with the electron ejection from the HOMO π⁻¹ orbital. Another series of Rydberg bands, R3, whose six members, n = 3–8, converge to the ion ground state, with a quantum defects ∼0.28, is assigned as 1¹A′ → (HOMO)π⁻¹np₂.

The absorption spectrum in the 8 eV region exhibits a strong background π–π* transition continuum (Fig. 3 and 7). As mentioned above, the absorption intensity in this region reaches a maximum at 7.88 eV (σ_abs = 75 Mb), and is followed by a minimum at about 8.47 eV, close to IE(isoquinoline) = 8.53 eV. At higher energies there is a broad continuum whose intensity increases to a maximum at 8.64 eV (σ_abs = 38.8 Mb), drops to a minimum at 8.99 eV, and then rises to a maximum at 9.52 eV (σ_abs = 55 Mb). The minima correspond in energy to the onset of ionization channels, 8.47 eV reflecting the onset of the first ionization of isoquinoline, and 8.99 eV the onset of higher energy ionization channels mentioned previously. The cross section decreases to a minimum at 10.23 eV, just below the 10.40 eV ionization limit after which it rises to plateau beginning at about 10.4 eV where σ_abs ∼70 Mb.

3.1.4.2. Rydberg series converging to the ion excited electronic state at 9.16 eV

The HeI photoelectron spectrum of isoquinoline has been interpreted by Brogli et al.⁸⁵ as having two close-lying ion excited states, of π⁻¹ and n⁻¹ character, in the 9.16 eV region. In their diagram correlating molecular orbitals of naphthalene and isoquinoline they effectively assign the n⁻¹ state to be D₁ and the π⁻¹ state to be D₂, a classification that we follow. We assigned five bands to the R4 Rydberg series converging on the D₂ ion excited state, considered as π⁻¹, at 9.16 eV. This limit corresponds to a single clear onset in the absorption cross-section (Fig. 3, 7 and 8) and is also the ionization energy reported by Eland and Danby from their photoelectron spectroscopy study.⁸⁴ Brogli et al.⁸⁵ gave an uncertain value of 9.30 eV for this ionization energy from their HeI PES spectrum. We tried out both 9.16 and 9.3 eV as possible Rydberg limit values and found that 9.16 eV enabled us to assign five R4 bands, with consistent quantum defects whereas a R4 limit of 9.3 eV was far less satisfactory. The definitive identification of two separate π⁻¹ and n⁻¹ ion states in this energy region requires new high resolution optical and photoelectron spectroscopy studies.

The five assigned R4 features are bands number 69 ((n = 3) O⁰₀δ = 0.81), 86 ((n = 4) O⁰₀, δ = 0.82), 100 ((n = 5) O⁰₀δ = 0.90), 106 ((n = 6) O⁰₀, δ = 0.89) and 108 ((n = 7) O⁰₀, δ = 1.08) (Table 4). The Rydberg transition is 1¹A′ →(HOMO−2)π⁻¹ns.

A second Rydberg series of four members converging to the D₂ ion level was assigned: R5, n = 3–6, δ ∼0.62. The corresponding Rydberg transition is 1¹A′ →(HOMO−2)π⁻¹ np₁.

Attempts to find corresponding Rydberg series converging to the other electronic excited state of the ion in this energy region, considered as the 1¹A′ →(HOMO −2)n⁻¹ D₁ electronic state, were not successful.

3.1.4.3. Rydberg series converging to the ion excited electronic state at 10.40 eV

Six bands are assigned to the R6 Rydberg series converging to the ion D₃ excited state at 10.40 eV. Their principal quantum numbers are n = 3–8, with quantum defects of the order δ = 0.9 ± 0.1 (Table 4). Band number 145 at 10.204 eV may represent an unresolved overlap of the n = 9 and n = 10 Rydberg bands and band number 146 unresolved further members of this Rydberg series closer to the limit at 10.40 eV. It is interesting that the quantum defects of the n = 3 terms of the various ns Rydberg series increase with the Rydberg limit energy: δ = 0.74 (R1), δ = 0.81 (R4), δ = 0.85 (R6). This indicates that the n = 3 electron penetration to the nucleus is more effectively shielded as the ionization limit increases.

Two other Rydberg series converging to the D₃ excited state were assigned: R7, with seven components, n = 3–9, δ ∼0.68, considered as a 1¹A′ →(HOMO−3)π⁻¹np₁ series and the more limited R8 series whose four components, n = 3–6, have quantum defects δ ∼0.27 corresponding to a np₂ series.

We remark that the D₃ ← D₀ electronic transition spectrum of the cation of isoquinoline, observed by photodissociation spectroscopy,⁸⁸ exhibits vibrational components, in particular with frequencies assigned as ν₃₀ = 511 cm⁻¹, ν₂₇ = 795 cm⁻¹ and ν₁₃ = 1412 cm⁻¹. It is often the case that Rydberg vibrational components are similar to those observed in transitions to electronic states of a molecular ion achieved by direct photoionization of a neutral molecule. The vibrational modes excited can, however, be different than those excited in an electronic transition within a molecular ion, since the Franck–Condon factors are not necessarily the same in the two cases. Examination of the Rydberg series converging to the D₃ excited state of the isoquinoline cation failed to observed bands that would correspond to vibrational components of the D₃ ← D₀ cation transition seen in the photodissociation spectra of Dryza.⁸⁸ We then compared the cation spectra of isoquinoline⁸⁸ with bands occurring in direct photoionization to the D₃ excited states of the cation observed in HeI photoelectron spectra.^84,85 This showed that there is apparently a considerable difference in Franck–Condon factors in the two cases. We also examined the analogous spectra in naphthalene and came to the same conclusion as to a difference in Franck–Condon factors in these cases.^{66,84,85,88,89}

4. Comparison between quinoline and isoquinoline absorption spectra

It is of interest to compare the absorption spectra of quinoline¹³ and isoquinoline explored over the same energy region 3.5–10.7 eV. There are many similarities but also some interesting differences between the two spectra. Both C₉H₇N molecules have C_s symmetry and the same number of a′ and a′′ vibrational modes whose corresponding frequencies are of the same order of magnitude but with some differences according to whether the N atom is in the α (quinoline) or the β (isoquinoline) position. Quinoline and isoquinoline are isoelectronic with naphthalene, whose valence transitions are all π–π* but the azamolecules possess non-bonding electrons associated with the nitrogen atom that give rise, in addition, to n–π* transitions. A comparison between the calculated structures of quinoline (Fig. 1 in ref. 13) and isoquinoline (Fig. 1) indicates that changing the nitrogen atom from the α to the β position leads to substantial changes in bond lengths and ring angles in the ring containing the N atom but little modification of the other aromatic ring.

Molecular orbital correlations between naphthalene, quinoline and isoquinoline can be used to rationalise a number of spectral properties, here the valence and the Rydberg transitions of the azamolecules. We note that eight valence transitions m¹A′ ← 1¹A′ were observed in quinoline:¹³ the transitions m = 2, 3,…8, whose origin bands lie between 3.991 and 6.981 eV, and the m = 12 transition at 7.795 eV. Isoquinoline also has eight assigned m¹A′ ← 1¹A′ valence transitions: m = 2, 3, …9, between 3.960 and 7.081 eV. The energy of the 2¹A′ ← 1¹A′ transition in isoquinoline is 31 meV smaller than the corresponding transition in quinoline.¹³ On the other hand, the 3¹A′ ← 1¹A′ transition in isoquinoline at 4.564 eV is at a higher energy than in quinoline (4.441 eV). These differences can be rationalised on a Koopmans theorem⁹⁰ approximation approach, using ionization energies to assess molecular orbital energy differences and considering the optical transitions on a single configuration basis. From the known ionization energies of quinoline and isoquinoline we estimate that the energy of the 2¹A′ ← 1¹A′ transition in isoquinoline would lie 98 meV below that in quinoline as compared with the experimental value 31 meV, in agreement with the sign of the difference. A better quantitative agreement is not to be expected since this approach does not take into account effects of interaction between close-lying 2¹A′ππ* and 1¹A′′nπ* states, whose zero-order differences in energy differ significantly in quinoline and isoquinoline as discussed below.

With this approach we also calculate the energy difference between the 3¹A′ ← 1¹A′ and the 2¹A′ ← 1¹A′ transitions to be 552 meV in quinoline and 630 meV in isoquinoline; our experimental values, respectively 450 meV and 604 meV, are in good agreement with the calculated values. We remark that in this single configuration Koopmans theorem approach to molecular orbital energies we also neglect the effects of rapid orbital reorganisation that occurs on photoionization.⁹¹

Our DFT and the Baba and Yamazaki⁴⁴ P–P–P calculations of π–π* transition energies of both quinoline¹³ and isoquinoline gave similar levels of accuracy with respect to observed values, as measured by UD, the unsigned energy difference, the average DFT and P–P–P values being respectively UD = 260 and 340 meV in quinoline,¹³ and UD = 331 and 232 meV in isoquinoline. The UD values are of the same order of magnitude but the DFT calculations are overall more accurate than the P–P–P calculations in quinoline, the reverse being found in isoquinoline.

The 3.8–4.4 eV spectral region exhibits vibronic interaction effects between the 2¹A′ππ* and 1¹A′′nπ* electronic states in both quinoline and isoquinoline. The energy gap between the nπ* and ππ* origin levels is greater in quinoline (1804 cm⁻¹)¹⁶ than in isoquinoline (1118 cm⁻¹). This gives rise to very different vibronic structures in this energy region for the two azamolecules. These structures have been well analysed in isoquinoline (Tables 4 and 6) but more scantily in quinoline where the features are more complex.¹⁶

Both quinoline and isoquinoline have strong broad absorption peaks in the 6 eV region, with maxima at 6.218 eV, σ = 194 Mb in quinoline⁷ and 6.003 eV, σ = 292 Mb in isoquinoline. The high intensity is considered to be due in part to plasmon-type effects as discussed above. The larger peak cross-section in isoquinoline indicates a greater influence of the collective modes of the π electrons in this energy region. The difference in the peak energies and intensities marks the difference between the π electron structures in the α-N and β-N azamolecules.

Previous to our work on the VUV absorption spectra of quinoline¹³ and isoquinoline no Rydberg transitions had been reported for these two molecules. We observed eight Rydberg series in quinoline and eight in isoquinoline. In quinoline there are two series, ns and np₁, that converge to the D₀ level of the cation (HOMO)π⁻¹, three series, ns, np₁ and np₂, to the D₃ state (HOMO−3)π⁻¹ and three series to D₄ (HOMO−4)π⁻¹. Rydberg series were not observed converging to the D₁ state (HOMO−1)π⁻¹ or to the D₂ level (HOMO−2)n⁻¹. Rydberg series observed in isoquinoline (Table 7) converge to the D₀ (HOMO)π⁻¹, D₂(HOMO−2)π⁻¹ and D₃ (HOMO−3)π⁻¹ electronic states of the ion. A series converging to the D₁ level (HOMO−2)n⁻¹ was not observed. That there are differences between the Rydberg series observed for the two molecules can be considered as resulting, in part, from differences in the order of the π and the σ-type n orbitals as expressed in the M.O. correlation diagram.⁸⁵ We mention also that an antiresonance feature due to interaction between a Rydberg level and a quasi-continuum of π−π* transition character was observed in isoquinoline at about 7.75 eV; no similar feature was observed in the absorption spectrum of quinoline. Further experimental and theoretical studies on these rich absorption spectra are required to advance our understanding of the valence and Rydberg transitions in these azamolecules.

5. Conclusion

The gas-phase absorption spectrum of isoquinoline was measured over the photon energy range 3.6–10.7 eV using the ASTRID2 synchrotron radiation facility at Aarhus, Denmark as the photon source, as was previously done over the same energy range for quinoline.¹³ Previous absorption spectral studies on isoquinoline were mainly in solution, with an upper energy limit of 5.6 eV. Quantum-mechanical calculations, using time-dependent DFT methods, were carried out to determine properties of the ground state of isoquinoline such as geometry, rotational constants, vibrational frequencies and dipole moment. The results are in very satisfactory agreement with experimental data. Previously published results of Pariser–Parr–Pople (P–P–P) quantum mechanical calculations of electronic state energy levels and dipole transition strengths, as well as the results of our DFT calculations, enabled us to assign eight π–π* singlet m¹A′ ← 1¹A′ valence electronic transitions of isoquinoline. This considerably increases the number of electronic transitions previously known for isoquinoline. We discuss the relative quality and trends of the results of the P–P–P and DFT calculations. Although they are far from spectroscopic or chemical accuracy, these results have been of much use in assigning the valence transitions. No n–π* transitions of isoquinoline were observed, coherent with their low DFT- calculated oscillator strengths. Some of the broad spectral features, such as an intense broad band peaking at 6.003 eV, are suggested to have intensity contributions from plasmon-type collective π electron mode effects. A feature in the 7.7–7.8 eV region has an absorption profile reminiscent of an anti-resonance between Rydberg and valence levels.

Rydberg bands of isoquinoline were never previously reported. We observed and assigned eight Rydberg series, three of which, R1, R2 and R3 converge to the D₀ ion ground state. Two further Rydberg series, denoted respectively as R4 and R5, converge to the D₂ excited state of the cation at 9.16 eV, and three more, the R6, R7 and R8 series, converge to the D₃ excited state at 10.40 eV. There appears to be a trend to a lesser penetrability of the 3 s electron as the ionization limit increases with successive ion electronic states, reflected in the increase of the 3 s electron quantum defect.

There are 161 measured features in our absorption spectrum, of which we were unable to assign 80, mainly high-energy features. This is a region where we expect to find high energy valence transitions, as well as Rydberg bands converging to highly excited cation states, extending to or above the D₃ level energy.⁸⁵ In the lower energy region, vibronic interactions between n–π* and π–π* electronic states can cause apparent irregularities in band energies that require very high resolution spectroscopy and associated photophysical measurements to untangle, as has been done for the origin region presented in Table 6. Interesting new studies are thus called for.

The isoquinoline absorption cross-sections that we measured over an extended energy region that includes the VUV down to 10.7 eV represent new useful data for astrophysics, in particular for theoretical modeling of the photochemistry of isoquinoline in planetary atmospheres, the ISM and circumstellar media, as mentioned in the introduction where it is noted that quinoline and isoquinoline could be synthesised under high temperature conditions representing circumstellar envelopes of carbon stars.^7,8 Radiofrequency spectroscopic attempts to observe both C₉H₇N isomers quinoline and isoquinoline, in the circumstellar envelopes of carbon-rich stars have not been successful beyond providing upper limits on quinoline and isoquinoline column densities.⁹

Further modelling exploitation of the photon absorption spectra of quinoline and isoquinoline in the VUV will require information on photoionization quantum yields as function of excitation energy, in particular in energy regions involving superexcited electronic states of neutral molecules.¹² In the case of isoquinoline we have used a rule-of-thumb method¹⁰ to evaluate the photoionization quantum yield, γ_i (13.6 eV) = 0.55, at the 13.6 eV energy limit of the astrophysical HI region. Thus, at 13.6 eV, as in the analogous case of quinoline,¹³ about 45% of the absorbed photon energy is available for relaxation processes of the neutral molecule. Such processes include molecular dissociation. At 10.7 eV, the energy upper limit of our absorption spectrum, the rule-of-thumb method indicates that about 75% of the incident photon energy is dissipated in non-ionization photophysical processes.

A comparison of the absorption spectra of quinoline and isoquinoline over the same energy range is given in Section 4 in which various spectral aspects of these species are considered as being due, in part, to specific characteristics of the respective molecular orbitals in the two azamolecules. The many similarities, and some interesting differences, in the absorption spectra of these two isomers, can have a bearing on their respective photophysical properties and eventually on their role in astrophysical processes.

Conflicts of interest

There are no conflicts to declare.