Skip to main content
NCBI home page
Nature Communications logoLink to Nature Communications
. 2022 May 2;13:2364. doi: 10.1038/s41467-022-30074-4

Emergent multiferroism with magnetodielectric coupling in EuTiO3 created by a negative pressure control of strong spin-phonon coupling

Run Zhao 1,2,#, Chao Yang 3,4,#, Hongguang Wang 5,✉, Kai Jiang 6,✉, Hua Wu 7, Shipeng Shen 8, Le Wang 8,12, Young Sun 9, Kuijuan Jin 8, Ju Gao 2, Li Chen 10, Haiyan Wang 10, Judith L MacManus-Driscoll 11, Peter A van Aken 5, Jiawang Hong 3,✉, Weiwei Li 1,11,✉, Hao Yang 1,✉
PMCID: PMC9061821  PMID: 35501352

Abstract

Negative pressure has emerged as a powerful tool to tailor the physical properties of functional materials. However, a negative pressure control of spin-phonon coupling for engineering magnetism and multiferroicity has not been explored to date. Here, using uniform three-dimensional strain-induced negative pressure in nanocomposite films of (EuTiO3)0.5:(MgO)0.5, we demonstrate an emergent multiferroicity with magnetodielectric coupling in EuTiO3, matching exactly with density functional theory calculations. Density functional theory calculations are further used to explore the underlying physics of antiferromagnetic-paraelectric to ferromagnetic-ferroelectric phase transitions, the spin-phonon coupling, and its correlation with negative pressures. The observation of magnetodielectric coupling in the EuTiO3 reveals that an enhanced spin-phonon coupling originates from a negative pressure induced by uniform three-dimensional strain. Our work provides a route to creating multiferroicity and magnetoelectric coupling in single-phase oxides using a negative pressure approach.

Subject terms: Ferroelectrics and multiferroics, Ferroelectrics and multiferroics, Magnetic properties and materials

Negative pressure tailors the physical properties of functional oxide materials. Here, the authors demonstrate an emergent multiferroism with magnetodielectric coupling in EuTiO3 created by a negative pressure control of strong spin-phonon coupling.

Introduction

Owing to the interplay between the fundamental degrees of freedom1,2, namely, spin, charge, orbital, and lattice, perovskite oxides exhibit a variety of fascinating functionalities, such as superconductivity, magnetism, ferroelectricity, and multiferroicity. Recently, a negative pressure, due to an enlargement of lattice constants in three-dimensions (3D), has emerged as a powerful tool to tailor and enhance physical properties of known functional oxides, such as ferroelectricity3–6 and superconductivity7. Density functional theory (DFT) calculations have shown that a negative pressure can increase the tetragonality and the polarization in PbTiO33 and BaTiO38. Experimentally, Wang et al. demonstrated that a negative pressure can be induced in PbTiO3 nanowires through a radial density gradient, and enhanced ferroelectric and piezoelectric properties were observed4,5. To obtain a negative pressure, three-dimensional tensile stress needs to be realized in nanoscale regions of the films. However, in standard epitaxial oxide films only in-plane (IP) biaxial strain engineering is possible. A strategy to achieve a negative pressure in epitaxial oxide films involves the growth of self-assembled vertically aligned nanocomposites (VANs) which are composed of two phases9. By selecting appropriate two phases with different lattice constants and different elastic moduli, the phase with the stiffer materials can induce a few % tensile strain level at the vertical interfaces. By combining the vertical tensile strain with the horizontal strain induced by the substrate, it is possible to exert a negative pressure on the target phase in the VAN films for tailoring its physical functionalities10. Kursumovic et al. showed such negative pressure in BaTiO3:Sm2O3 VAN film11. This negative pressure led to the transverse piezoelectric coefficient in the BaTiO3 phase, d31, being positive at a value >200 pm/V and up to at least 250 °C. Zhang et al. utilized the negative pressure to realize a giant remanent polarization of 236.3 µC/cm2 in the PbTiO3 phase in the PbTiO3:PbO VAN film6. In YBa2Cu3O7-δ:BaZrO3 VAN film, a strong modification of superconducting properties in the YBa2Cu3O7-δ phase has been achieved by applying a negative pressure7. Nevertheless, previous theoretical and experimental works mainly focused on the negative pressure engineering of lattice and orbital degrees for tailoring and enhancing physical properties. The effects of a negative pressure associated with the creation or enhancement of magnetism and multiferroicity are still less explored using a combination of spin, phonon (lattice), and orbital degrees.

The strong cross-coupling of multiple degrees of freedom, such as spin–phonon (lattice) coupling, is a potential source of robust multiferroicity. Amongst perovskite oxides, EuTiO3 (ETO) is paraelectric (PE)12 and G-type antiferromagnetic (AFM)13 with strong spin–phonon coupling and has attracted intensive attention for achieving enhanced ferromagnetic (FM)-ferroelectric (FE) properties and magnetoelectric coupling. In terms of the magnetoelectric properties, DFT calculations have shown how the underlying physics leading to the observation of spin–phonon coupling can be utilized to control the ferroic ground states in ETO14. Subsequent experiments in epitaxial strained 22 nm ETO thin films (grown on DyScO3 substrates) have demonstrated an IP tensile strain-induced FM–FE phase15 and the suppression of the AFM order by an external electric field16, both of which are consistent with the theoretical predictions. However, the observed saturation magnetization (~3µB/Eu2+) is significantly smaller than the theoretical value (~7µB/Eu2+) because of an inhomogeneous magnetic state with the coexistence of FM and non-FM states formed in ETO thin film17. The macroscopic FE polarization and giant magnetoelectric effect have yet to be achieved largely due to the leakage issue in strained ETO thin film with a thickness <25 nm and a lack of high-quality substrates that would provide the necessary value of horizontal biaxial strain. In addition, the microscopic mechanism of magnetic phase transition under epitaxial biaxial strain and magnetoelectric effect induced by the spin–phonon coupling is still under debate14,18,19. Back to the spin–phonon coupling in ETO, the most effective path in realizing the magnetoelectric effect is still attributed to the displacement of B-site (Ti) ions along out-of-plane (OOP) direction16,20. However, the IP biaxial strain can only indirectly change the Ti displacement via the changed cell volume. Hence, ETO is a unique model system to study how a negative pressure control of strong spin–phonon coupling creates a multiferroicity and magnetoelectric coupling effect.

In this work, we have designed self-assemble VAN thin films composed of ETO and MgO fabricated by using pulsed laser deposition. The results of scanning transmission electron microscopy (STEM) and X-ray diffraction (XRD) show that a uniform 3D epitaxial strain has been implemented to induce a negative pressure in the ETO phase via the MgO phase. This results in a control of strong spin–phonon coupling for creating a FM phase with a Curie temperature (TC) of ~3.4 K and a FE phase with a TC of ~255 K. The interplay between spins and phonons was revealed by measuring the magnetodielectric effect and investigating how the magnetization affects the phonons. DFT calculations unravel how the negative pressure control of the competition of the nearest IP and OOP magnetic interactions and the movement of Ti ions induces ferroic phase transitions and further engineers the strong spin–phonon coupling in ETO. Overall, our work demonstrates a pathway to create a multiferroicity and magnetoelectric effect in single-phase oxides using a negative pressure approach.

Results

Structural investigations of an ETO:MgO VAN film by STEM and XRD

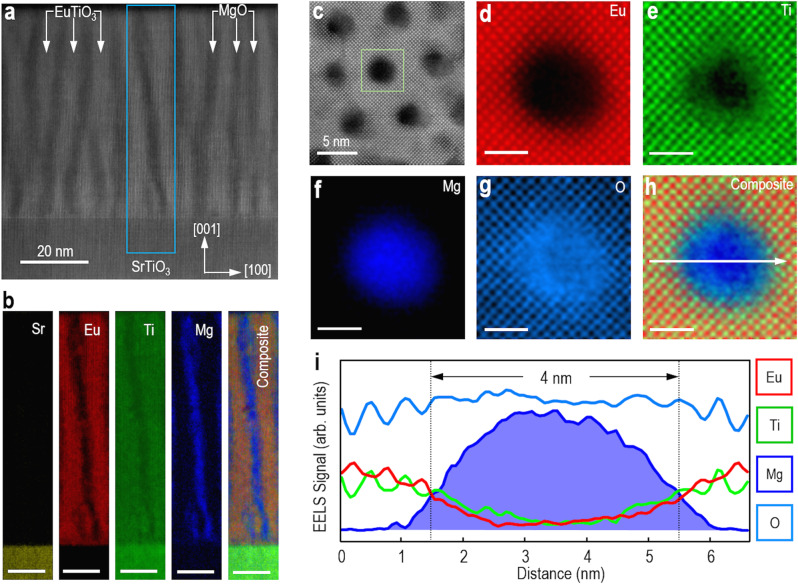
STEM images in the high-angle annular dark-field (HAADF) mode21,22, both in cross-section (Fig. 1a) and plan-view (Fig. 1c), as well as STEM electron energy-loss spectroscopy (EELS) maps (Fig. 1b, d–h) show a clear phase separation between high-quality epitaxial ETO and MgO. Vertically aligned interfaces between the two phases form throughout the thin film (Fig. 1a, c). The MgO nanopillars with an average diameter of ~4 nm are uniformly distributed and embedded in an ETO matrix (Fig. 1a, c, Supplementary Fig. 1, and Supplementary Fig. 2c–g). EELS maps in both the cross-section (Fig. 1b) and plan-view images (Fig. 1d–i) orientations show that the interface between the two phases in the VAN is very sharp, as expected, since the structure forms by self-assembly.

Fig. 1. STEM investigations of an ETO:MgO VAN film.

Fig. 1

Open in a new tab

a Z-contrast HAADF-STEM image of the VAN film in cross-sectional orientation, projected along the [010] zone axis. b Atomically resolved STEM-EELS elemental maps of a single nanopillar, corresponding to the rectangle region in (a). Scale bar: 10 nm. c HAADF-STEM image of the VAN film in plan-view orientation, showing MgO nanopillars embedded in an ETO matrix. d–h Atomically resolved STEM-EELS elemental maps of a single nanopillar, corresponding to the rectangle region in (c). Scale bar: 2 nm. i EELS signal intensity profiles across the ETO/MgO interfaces extracted along the white arrow direction in (h).

The epitaxial quality of ETO:MgO VAN films was further studied by XRD θ−2θ scans (Supplementary Fig. 2a). The films show sharp (00l) peaks of ETO and MgO, indicative of a preferential orientation of the two phases. The OOP lattice constant of ETO is calculated to be 4.01 ± 0.01 Å (Supplementary Table 1). Comparing with bulk ETO lattice constant of 3.905 Å, the corresponding vertical strain (along the c-axis) is calculated to be +2.56% for the ETO phase, which results from the large vertical interfacial area and the lattice mismatch between the two phases in the VAN film.

3D strain-induced negative pressure in an ETO:MgO VAN film

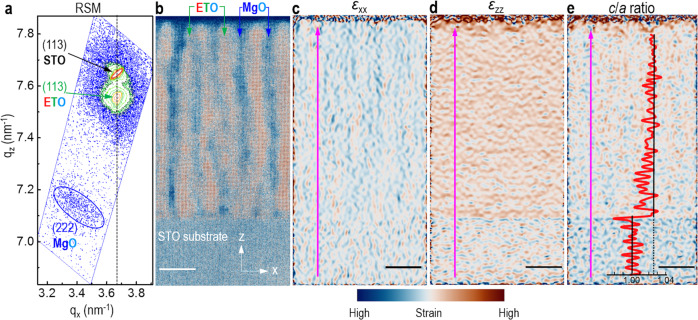
To understand more about how a negative pressure forms in the VAN film, the growth and lattice matching modes of the VAN film were revealed via the close-up STEM image of an individual MgO nanopillar (Supplementary Fig. 3). Owing to the structural misfit and thermal expansion effect in the nucleation stage, the isolated MgO (rock salt) islands wet the STO (perovskite) substrate and are embedded in the ETO film matrix (region 1 in Supplementary Fig. 3a). For a VAN film thickness above 5 nm, the MgO nanopillars developed and then the vertical interfaces between ETO and MgO were formed along the OOP direction (region 2 in Supplementary Fig. 3a). During the growth of the VAN film, the ETO phase experienced a volume expansion in three mutually perpendicular directions, which is induced by that the stiffer STO substrate and the MgO nanopillars impart a negative pressure on the ETO (C11-STO»C11-ETO and C44-MgO > C44-ETO)23,24. Under such negative pressure, the embedded MgO nanopillars exert a tensile force on the surrounding ETO phase along the OOP direction due to the lattice mismatch between ETO and MgO. The MgO nanopillars along the IP direction are not constrained by the substrate and it undergoes compression from the expanded ETO matrix upon cooling due to thermal expansion effects25. Misfit dislocations were formed at the vertical interfaces between the ETO and MgO phases for relaxing the misfit strain (Supplementary Fig. 4). Furthermore, a more detailed analysis of the crystal structure was undertaken by high-resolution asymmetric X-ray reciprocal space map (RSM) around the (113) and (103) reflections of STO. An enhanced OOP lattice constant in the ETO phase (4.01 ± 0.01 Å) indicates that the ETO phase is OOP tensed by the MgO phase (the bulk average lattice constant of ETO is 3.905 Å, and of MgO is 4.212 Å). As shown in Fig. 2a, the STO and ETO peaks share the same qx position, indicating that the ETO phase in the VAN film is coherently strained to the STO substrate. Hence, 3D strain is formed in the ETO phase. And IP lattice constant of the ETO phase is determined to be 3.90 ± 0.01 Å (Table S1). Based on the IP (a) and OOP (c) lattice constants of ETO, a c/a ratio of 1.03 is obtained. Considering that the elastic constant C44 of ETO phase is 116.3 GPa under zero pressure23, a negative pressure along the OOP direction (for the measured c/a = 1.03) is estimated to be around −2.98 GPa. In addition, there is no difference in the (103), (013), (−103), and (0–13) Bragg peak positions of the ETO phase (Supplementary Fig. 5), indicating that the ETO phase has a tetragonal structure. The angles between TiO6 octahedra in the ETO phase are further found to be around 180° along the IP and OOP directions (Supplementary Fig. 6 and Supplementary Fig. 7). Hence, according to the Glazer notation26, the space group of the ETO phase is determined to be tetragonal P4/mbm (a0a0c+ or a0a0c−)27.

Fig. 2. Strain analysis of an ETO:MgO VAN film.

Fig. 2

Open in a new tab

a Reciprocal space map of (113) Bragg reflection of ETO and STO, and (222) Bragg reflection of MgO. b Colored HAADF-STEM image of the VAN film in cross-section. Respective IP (εxx) (c) and OOP (εzz) (d) strain maps obtained from STEM-based GPA. The lattice of the STO substrate was taken as a reference for strain analysis. e The corresponding c/a map calculated with (c, d). The inset shows a profile of c/a ratio extracted along the arrow direction. Scale bar: 20 nm.

The distribution of 3D strain in the ETO phase was further visualized by conducting geometric phase analysis (GPA) from the HAADF-STEM image (Fig. 2b)28. The IP strain component (ɛxx) and OOP strain component (ɛzz) calculated relative to the STO substrate region are shown in Fig. 2c–e. These maps clearly demonstrate that the ETO phase in the VAN film has a very uniform 3D strain distribution. More importantly, a profile of c/a values is extracted along the arrow direction, as shown in Fig. 2d, and an average c/a ratio is around 1.03, agreeing very well with the value determined from XRD and RSM measurements.

Multiferroic properties of an ETO:MgO VAN film

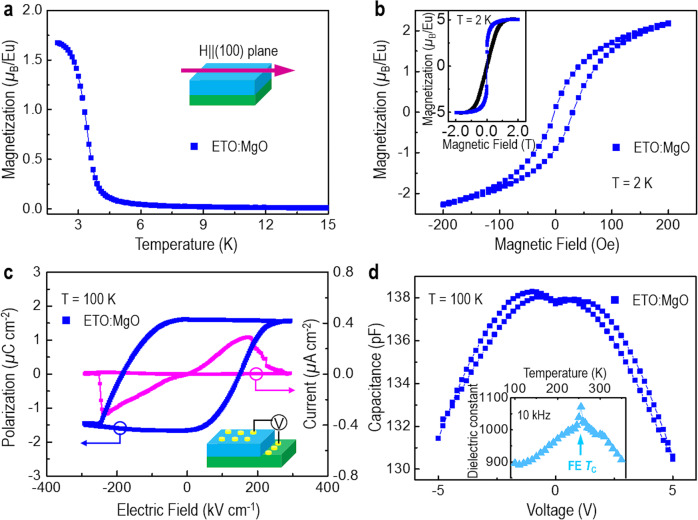
The magnetic properties of 300 nm thick VAN and 300 nm thick plain films are compared in magnetization versus temperature (M–T) and magnetic field (M–H) plots in Fig. 3a, b and Supplementary Fig. 8. The plain ETO film displays a distinct AFM transition around 5.1 K (Supplementary Fig. 8b), close to magnetic ordering temperature (TN ~ 5.3 K) for bulk ETO12,13. In contrast, the magnetization (M) of the VAN film increases monotonically with decreasing temperature and almost saturates at 2 K (Fig. 3a). Furthermore, a clear magnetic hysteresis loop with a coercivity (HC) of ∼18 Oe is observed in the VAN film. Hence, these results strongly suggest that the ETO phase is FM in the VAN film. The FM Curie temperature (TC,FM) is further determined to be ~3.4 K (Supplementary Fig. 8d). The saturation magnetization (MS) value measured at ± 2 T is around 5 µB/Eu2+, which is much higher than that of the strained 22 nm ETO thin film grown on the DyScO3 substrate (~3µB/Eu2+)13. As we show later, this can be attributed to the formation of a homogeneous magnetic state induced by uniform 3D strain in the VAN film.

Fig. 3. Multiferroic properties of an ETO:MgO VAN film.

Fig. 3

Open in a new tab

a Temperature and (b) magnetic field-dependent magnetization measured by applying a magnetic field along the IP direction. The inset of (b) shows the comparison of magnetic hysteresis loops measured by applying a magnetic field along the IP (blue) and OOP (black) directions. c Ferroelectric polarization hysteresis loop and switching current measured by PUND and at 1 kHz. d Capacitance–voltage curve measured at 100 K. The inset shows the temperature-dependent dielectric constant showing a FE TC of ∼255 K.

Strong ferroelectric (FE) properties were observed in the 300 nm-thick ETO:MgO VAN film (Fig. 3c, d). After subtracting the linear dielectric contribution, a polarization–electric field (P–E) hysteresis loop with a switched polarization (∆P) of value ~3.3 µC/cm2 and switching current were obtained at 100 K (Fig. 3c). Using the Berry phase methods29, the ferroelectric polarization was further calculated (Supplementary Fig. 9). Its value is of the same order of magnitude with the experimental value (Supplementary Fig. 10). This implies that the ETO phase is FE in the VAN film. A capacitance–voltage (C–V) hysteresis curve was also measured at 100 K (Fig. 3d). The observation of a butterfly-like characteristic shape of C–V hysteresis curve further confirms that the ETO phase is FE.

To determine the FE Curie temperature (TC,FE), the temperature-dependent dielectric constant was measured at a frequency of 10 kHz and is shown as an inset of Fig. 3c. The peak position of PE to FE is clearly visible at ~255 K, comparable to the previous work15. The peak position does not shift with frequency (Supplementary Fig. 11), indicating a normal, rather than a relaxed, FE transition formed in the ETO phase30. It should be pointed out that, due to the low dielectric constant of MgO, its contribution to the dielectric constant of the VAN film can be neglected31. Overall, the above results show that the ETO phase in the VAN film is transformed from PE in bulk ETO into FE to at least at 100 K, with a TC,FE of around 255 K.

Discussion

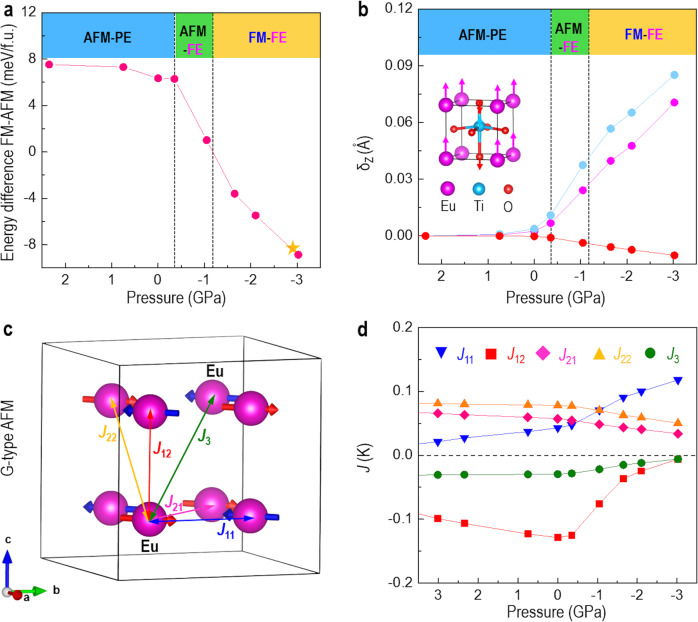
To gain further insights into the correlation between negative pressure and its link to the multiferroic properties and electronic structures in ETO, we performed the first-principles calculations. The simulated energy difference between FM and AFM configurations clearly shows a magnetic phase transition from AFM to FM at a negative pressure of ~−1.17 GPa (Fig. 4a). In addition, the extracted atom displacements (Fig. 4b) show that the oxygen atoms move downward, while the Eu and Ti atoms move upward along the OOP direction under a negative pressure. Overall, the ETO experiences three types of phase transitions with the increase of negative pressure along the OOP direction, i.e., AFM–PE ground phase, AFM–FE phase with a negative pressure larger than ~−0.35 GPa, and FM–FE phase with a negative pressure larger than ~−1.17 GPa. Since the movement of atoms affects the relative strength of the atomic orbital interactions, it is expected that magnetic exchange coupling (Fig. 4c) will be changed as well32–34. As shown in Fig. 4d, the nearest OOP AFM (J12) dominates the magnetic coupling and determines an AFM ground state at ambient pressure. With the increase of negative pressure, the exchange coefficients of J12, J21, J22, and J3 reduce sharply and J12 and J3 are close to zero at ~−3 GPa. In contrast, the nearest IP magnetic interaction J11 increases quickly and its absolute value becomes the largest one compared with the other magnetic interactions. Hence, the AFM to FM phase transition mainly originates from the competition between the AFM exchange interaction J12 and FM exchange interaction J11 under negative pressures, due to stronger interactions between Eu 4 f, O 2p, and Ti 3d orbitals (Supplementary Fig. 12). This is quite different from the AFM to FM phase transition in IP biaxial strained ETO, in which the competition between the AFM superexchange and the indirect FM exchange via Eu 5d states18, or the modification of the third nearest-neighbor Eu ion superexchange interaction mediated through the central Ti ion16.

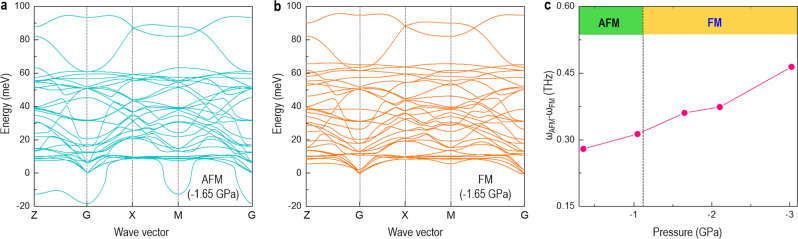
Fig. 4. Phase transitions and magnetic interactions in ETO under pressure, from DFT calculations.

Fig. 4

Open in a new tab

a The energy difference between FM and AFM showing a clear magnetic phase transition. The star represents the experimental negative pressure. b Atom displacement along z-direction (OOP direction) showing a clear ferroelectric phase transition. The inset shows a schematic diagram for the movement of atoms under pressure. c Schematic diagram with a G-type AFM magnetic configuration adopted for ETO, with different interactions. J1m (m = 1,2) refers to the nearest interactions, J2n (n = 1,2) refers to the next-nearest interactions, and J33 refers to the next-next-nearest interactions. d Calculated variation of magnetic exchange coefficients of ETO under different pressures.

It shows that the FM interactions dominate the magnetic coupling, when a negative pressure is larger than ~−1.17 GPa, agreeing well with the observation of FM in the ETO phase in VAN film under an experimental negative pressure of −2.98 GPa. Additionally, the magnetic exchange coefficient of J12 experiences an abrupt change at ~−0.35 GPa. This value is coincided with the critical pressure, where the PE-FE phase transition occurs. This indicates that the magnetic spins are coupled with phonons (lattice) in ETO. As further evidenced in Fig. 5a, the phonon dispersion of ETO with an AFM configuration possess large negative modes at Z, G, and M high symmetry points. In contrast, at the same negative pressure of −1.65 GPa, the calculated phonon dispersions of ETO with a FM configuration have no negative modes (Fig. 5b). Furthermore, upon applying a negative pressure, the largest frequency shift (Fig. 5c) is around 0.48 THz which is comparable to the reported values in other multiferroic materials35,36. It should be noticed that the ferroelectric phase transition also affects the soft mode. These results confirm that spin and phonons are strongly coupled, which can be tuned by a negative pressure simultaneously.

Fig. 5. Phonon dispersions in ETO under negative pressure, from DFT calculations.

Fig. 5

Open in a new tab

a Phonon dispersion in ETO with an AFM configuration and ideal crystal structure. b Phonon dispersion in ETO with a FM configuration and distorted FE crystal structure. c The change of soft phonon frequency (polar mode) of ETO with a distorted FE crystal structure under different negative pressures.

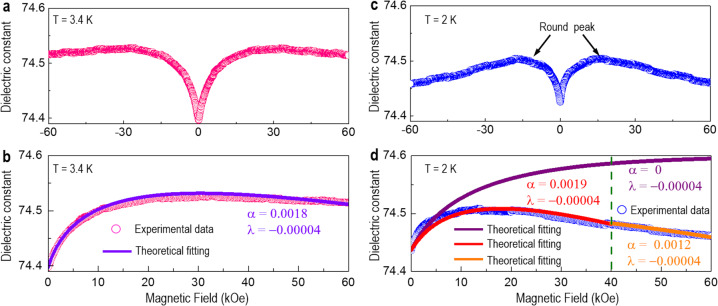
Owing to the spin–phonon coupling significantly modified by the negative pressure, magnetoelectric coupling was further achieved by performing the magnetodielectric measurements (Fig. 6a, c and Supplementary Fig. 13). When the temperature is 10 K, the ETO is in its PM-FE state (Supplementary Fig. 14). The magnetization increases with the magnetic field. Due to the spin–phonon interactions, the dielectric constant monotonically increases with magnetic field, following a behavior similar to that of the magnetization versus magnetic field12,20. Interestingly, with a further decrease of temperature to 3.4 K (Fig. 6a) and 2 K (Fig. 6c), as ETO transforms into its FM–FE state, the dielectric constant as a function of the magnetic field evidently deviates from the monotonically increasing trend, showing a round peak at ± 16 kOe (Fig. 6c).

Fig. 6. Magnetodielectric coupling of an ETO:MgO VAN film.

Fig. 6

Open in a new tab

Magnetic field-dependent dielectric constant measured at 3.4 K (a) and 2 K (c). Comparison of the theoretical results with the experimental data of the magnetic field-dependent dielectric constant at 3.4 K (b) and 2 K (d). The open circles represent the experimental data, while the solid lines represent the theoretical results with different parameters. λ is the biquadratic spin–phonon coupling coefficient and α is the corresponding coefficient to scale the strength of the tuning effect of the magnetic field on the lattice parameters.

In order to capture the underlying physics more clearly, we performed the Landau free energy expansion (Supplementary Discussion 1) to describe the coupling between the spin (magnetic ordering parameters) and phonon (lattice). When the temperature is at 3.4 K, the round peak in the magnetic field dielectric constant is negligible (Fig. 6a). The magnetic moments tend to be disordered at the magnetic phase transition temperature of TC,FM (3.4 K), so the magnetic field plays a more significant role in ordering magnetic moments. Consequently, this causes a more remarkable increase of the dielectric constant with an increasing magnetic field. Meanwhile, by fitting the experimental data (Fig. 6b), the coupling strength α between the magnetic field and the strain is found to decrease in comparison to 2 K. As a result, the effect arising from the magnetic field on the alignment of the magnetic spins and enhancement of the dielectric constant is strong enough to suppress the reduction of the dielectric constant that is caused by the magnetostriction37, leading to a disappearance of the round peak at 10 K (Supplementary Fig. 14).

As the temperature decreases to 2 K, the ETO is in a FM–FE state, i.e. both MS and PS are nonzero and these two order parameters are coupled to each other. Considering the magnetic field-induced magnetostriction, which contributes to the stabilization of the FE phase and reduces the dielectric susceptibility in the FE phase, the dielectric susceptibility gradually bends from its monotonic increasing trend as the magnetic field increases and shows a round peak (Fig. 6c). By fitting the experimental data with different types of theoretical models (Fig. 6d), we find that the competition between the two mechanisms, i.e. spin–phonon coupling and magnetostriction, causes the unusual behavior of dielectric constant with magnetic field. A spin–phonon coupling at a lower magnetic field and a magnetostriction at the middle range of a magnetic field can be obtained. Up to a higher magnetic field of 40 kOe, weakened magnetostriction arises from the crossover from a negative to a positive increased length (Supplementary Discussion 2).

In summary, in this study, epitaxial ETO:MgO VAN thin films were designed to explore a negative pressure control of strong spin–phonon coupling for creating multiferroicity and magnetoelectric coupling in the single-phase ETO. Vertical epitaxy along with the sharp MgO/ETO interfaces produces an enormous tetragonality (c/a = 1.03) in the ETO phase. The calculated negative pressure along the OOP direction yields −2.98 GPa. Consequently, this enables the transformation of the ETO phase from bulk AFM–PE into FM–FE with corresponding TCs of 3.4 K and 255 K, respectively. Due to the formation of a large negative pressure induced by uniform 3D strain, a pure PS value of 1.65 µC/cm2 with OOP polarization is achieved. DFT calculations reveal that under the negative pressures the magnetic phase transition is mainly due to the competition between the AFM exchange interaction J12 and FM exchange interaction J11 and the spins are strongly coupled with phonons. Furthermore, due to the strong spin–phonon coupling, the magnetoelectric coupling effect is achieved in the FM–FE state of ETO. This work presents a promising approach to negative-pressure-engineered single-phase 3d or 5d-based multiferroics38, originating from the unique structure and properties of the VAN films.

Methods

Thin film preparation

Self-assembled VAN thin films of (EuTiO3)0.5:(MgO)0.5 were grown on both (001) SrTiO3 (STO) and 0.5 wt.% Nb-doped SrTiO3 (Nb-STO) substrates by pulsed laser deposition. Film thicknesses of 70 nm and 300 nm were grown. As a reference, a plain EuTiO3 film of 300 nm thickness was grown on a LaAlO3 (LAO) substrate (Supplementary Fig. 15). All thin films were grown at a deposition temperature of 750 °C with an oxygen pressure of 5 × 10−3 Pa and then cooled down to room temperature under the same oxygen pressure. The laser pulse rate was 3 Hz and the laser fluence was 2 J/cm2.

XRD characterization

The phase and the crystalline quality of the thin films were investigated by X-ray diffraction (XRD) on a high-resolution X-ray diffractometer (Empyrean, PANalytical, The Netherlands) using Cu Kα radiation (λ = 1.5405 Å). To explore the 3D strain state, asymmetric RSM around (113) of STO was also measured. IP (a and b) lattice parameters were determined by RSM map using the epitaxy software package. The c lattice parameter was calculated from theta-2theta, was also cross-checked by the RSM map and was found to be the same within ±0.01 Å.

Ferroelectric, dielectric, magnetic and magnetodielectric characterizations

Ferroelectric hysteresis loops and switching current were collected from the current density–voltage (J–V) curves via the double-wave method in a physical properties measurement system (PPMS-9, Quantum Design)39,40. Dielectric measurements were carried out using an Impedance analyzer (E4990A). The temperature was controlled by a Linkam Scientific Instruments HFS600E-PB4 system. The magnetodielectric effects were measured using an Agilent 4980 A LCR meter in a cryogen-free superconducting magnet system (Oxford Instruments, TeslatronPT). For the ferroelectric, dielectric, and magnetodielectric measurements, Pt top electrodes with an area of 8 × 10−4 cm2 and the VAN films grown on Nb-STO substrates were used. The magnetic measurements were carried out using a PPMS-9 and a superconducting quantum interface device magnetometer (SQUID, Quantum Design).

Scanning transmission electron microscopy

STEM specimens in both cross-sectional and plan-view orientations were prepared by tripod polishing followed by argon-ion milling at liquid-N2 temperature41. STEM studies were conducted using a spherical aberration-corrected STEM (JEM-ARM200F, JEOL Co. Ltd.) equipped with a cold-field emission gun and a DCOR probe Cs-corrector (CEOS GmbH) operated at 200 kV. The STEM images were obtained by an ADF detector with a convergent semi-angle of 20.4 mrad and collection semi-angles of 70−300 mrad. In order to make precise measurements of lattice constants, ten serial frames were acquired with a short dwell time (2 μs/pixel), aligned, and added afterward to improve the signal-to-noise ratio (SNR) and to minimize the image distortion of HAADF images. Atomically resolved HAADF-STEM images have been analyzed using Geometric Phase Analysis (GPA) for strain analysis. EELS acquisition was performed by a Gatan GIF Quantum ERS imaging filter equipped with a Gatan K2 Summit camera with a convergent semi-angle of 20.4 mrad and a collection semi-angle of 111 mrad. EELS spectrum imaging was performed with a dispersion of 0.5 eV/channel and 456 eV drift tube energy with a 4000-pixel wide detector for the simultaneous acquisition of signals of Ti-L2,3, O-K, Eu-M4,5, Mg-K, and Sr-L2,3 edges. Energy-dispersive X-ray spectroscopy (EDS) was performed using a 100 mm2 JEOL Centurio SDD-EDX detector. The raw spectrum image data were denoised by applying a principal component analysis (PCA) with the multivariate statistical analysis (MSA) plugin (HREM Research Inc.) in Gatan DigitalMicrograph and then smoothed using a spatial filter in Gatan DigitalMicrograph. The analysis of the size distribution of MgO pillars was conducted using a built-in function in Gatan DigitalMicrograph. The coordinate positions of oxygen ions were determined by Gaussian fitting the oxygen columns in ABF images, and then used to calculate the angles between neighboring TiO6 octahedra42,43.

Density functional theory

We performed DFT calculations in the Vienna ab initio simulation package (VASP) with projector-augmented wave potentials in the GGA + U framework44,45. An on-site Coulomb parameter U = 5.7 eV and Hund’s exchange J = 1.0 eV were chosen for the strong electron correlation effects on the f shells of Eu atom, which were well tested in the work of Lee et al.15. The I4/mcm structure with the lowest total energy was chosen as the ground state, which was confirmed by previous experiment work46. The 6 × 6 × 6 k-point grid and a 500 eV plane-wave energy cutoff were used in our calculations. Geometric relaxations were done by keeping the IP lattice parameter fixed and relaxing the OOP lattice parameters. Residual force threshold was set to 0.001 eVÅ−1. Exchange parameters for an Ising model were fitted to total energy calculations in a 2 × 2 × 2 perovskite supercell that consists of 40 atoms and 8 different magnetic configurations. Different from the exchange constants for c/a ~ 1 structures35,36, a total of five magnetic exchange constants are considered in our calculations due to the experimental ratio of c/a ~ 1.03. The details of defined and calculated magnetic exchange constants can be found in Supplementary Discussion 3. We calculated the phonon frequency with the help of Phonopy package and the DFPT method implemented in the VASP code.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Supplementary information

Supplementary information (1.8MB, pdf)
Reporting Summary (1.3MB, pdf)
Lasing Reporting Summary (803.6KB, pdf)

Acknowledgements

This work was supported by the National Key Basic Research Program of China (Grant No. 2019YFA0308500) and the National Nature Science Foundation of China (Grant No. 92163102, 52172269, 11774172, 52172269, 92163102, 52102177, 51725104, 11721404, and 1217021241). W.-W.L. also acknowledges support from the National Natural Science Foundation of Jiangsu Province (Grant No. BK20210313), the Jiangsu Specially-Appointed Professor Program, and Top-notch Academic Programs Project of Jiangsu Higher Education Institutions (TAPP). C.Y. acknowledges supports from the Natural Science Fund Project of Hunan Province, China (Grant No. 2020JJ5453) and the Scientific Research Fund of Hunan Provincial Education Department, China (Grant No. 20B487). J.H. also acknowledges support from Beijing Natural Science Foundation (Grant No. Z190011) and the Technological Innovation Project of Beijing Institute of technology. Theoretical calculations were performed using resources of the National Supercomputer Centre in Guangzhou. H.W. acknowledges support from the Natural Science Foundation of Shanghai (21ZR1402400) H.W. acknowledges the support from the U.S. National Science Foundation for the TEM effort (DMR-2016453 and DMR-1565822). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 823717-ESTEEM3. W.-W.L. and J.L.M.-D. acknowledge support from EPSRC Grants EP/L011700/1, EP/N004272/1. J.L.M.-D. also acknowledges support from the Royal Academy of Engineering, Grant CiET1819_24.

Author contributions

Z.R. and C.Y. contributed equally. W.-W.L, J.H., and H.Y. conceived the project and directed the research. R.Z. and W.-W.L. did sample preparation, performed XRD and magnetic measurements with the help from J.K. and J.G. L.W. and K.J. performed ferroelectric measurements. S.S. and Y.S. carried out dielectric and magnetodielectric measurements. L.C. and H.W. conducted the TEM measurements. H.G.W. and P.A.v.A. conducted the STEM measurements and related data analysis. H.W. performed Landau calculations. C.Y. and J.H. performed DFT calculations. All authors contributed to the work and commented on the paper.

Peer review

Peer review information

Nature Communications thanks Claudio Cazorla and the other anonymous reviewer(s) for their contribution to the peer review of this work.

Data availability

All the experimental/calculation date that support the findings of this study are available from the corresponding authors upon reasonable request.

Code availability

All the codes used for this study are available from the corresponding authors upon reasonable request.

Competing interests

The authors declare no competing interests.

Footnotes

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

These authors contributed equally: Run Zhao, Chao Yang.

Contributor Information

Hongguang Wang, Email: hgwang@fkf.mpg.de.

Kai Jiang, Email: kjiang@ee.ecnu.edu.cn.

Jiawang Hong, Email: hongjw@bit.edu.cn.

Weiwei Li, Email: wl337@nuaa.edu.cn.

Hao Yang, Email: yanghao@nuaa.edu.cn.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-022-30074-4.

References

  • 1.Hwang HY, et al. Emergent phenomena at oxide interfaces. Nat. Mater. 2012;11:103–113. doi: 10.1038/nmat3223. [DOI] [PubMed] [Google Scholar]
  • 2.Li W, Shi J, Zhang KHL, MacManus-Driscoll JL. Defects in complex oxide thin films for electronics and energy applications: challenges and opportunities. Mater. Horiz. 2020;7:2832–2859. doi: 10.1039/D0MH00899K. [DOI] [Google Scholar]
  • 3.Tinte S, Rabe KM, Vanderbilt D. Anomalous enhancement of tetragonality in PbTiO3 induced by negative pressure. Phys. Rev. B. 2003;68:144105. doi: 10.1103/PhysRevB.68.144105. [DOI] [Google Scholar]
  • 4.Wang J, et al. Negative-pressure-induced enhancement in a freestanding ferroelectric. Nat. Mater. 2015;14:985–990. doi: 10.1038/nmat4365. [DOI] [PubMed] [Google Scholar]
  • 5.Kvasov A, et al. Piezoelectric enhancement under negative pressure. Nat. Commun. 2016;7:12136. doi: 10.1038/ncomms12136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Zhang L, et al. Giant polarization in super-tetragonal thin films through interphase strain. Science. 2018;361:494–497. doi: 10.1126/science.aan2433. [DOI] [PubMed] [Google Scholar]
  • 7.Zhao R, et al. Precise tuning of (YBa2Cu3O7-δ)1-x:(BaZrO3)x thin film nanocomposite structures. Adv. Funct. Mater. 2014;24:5240–5245. doi: 10.1002/adfm.201304302. [DOI] [Google Scholar]
  • 8.Moriwake H, Koyama Y, Matsunaga K, Hirayama T, Tanaka I. Isostructural phase transitions of tetragonal perovskite titanates under negative hydrostatic pressure. J. Phys.: Condens. Matter. 2008;20:345207. [Google Scholar]
  • 9.MacManus-Driscoll JL. Self-assembled heteroepitaxial oxide nanocomposite thin film structures: designing interface-induced functionality in electronic materials. Adv. Funct. Mater. 2010;20:2035–2045. doi: 10.1002/adfm.201000373. [DOI] [Google Scholar]
  • 10.Huang J, Li W, Yang H, MacManus-Driscoll JL. Tailoring physical functionalities of complex oxides by vertically aligned nanocomposite thin-film design. MRS Bull. 2021;46:159–167. doi: 10.1557/s43577-021-00028-0. [DOI] [Google Scholar]
  • 11.Kursumovic A, et al. A new material for high-temperature lead-free actuators. Adv. Funct. Mater. 2013;23:5881–5886. doi: 10.1002/adfm.201300899. [DOI] [Google Scholar]
  • 12.Katsufuji T, Takagi H. Coupling between magnetism and dielectric properties in quantum paraelectric EuTiO3. Phys. Rev. B. 2001;64:054415. doi: 10.1103/PhysRevB.64.054415. [DOI] [Google Scholar]
  • 13.Chien C-L, DeBenedetti S, Barros FDS. Magnetic properties of EuTiO3, Eu2TiO4, and Eu3Ti2O7. Phys. Rev. B. 1974;10:3913–3922. doi: 10.1103/PhysRevB.10.3913. [DOI] [Google Scholar]
  • 14.Fennie CJ, Rabe KM. Magnetic and electric phase control in epitaxial EuTiO3 from first principles. Phys. Rev. Lett. 2006;97:267602. doi: 10.1103/PhysRevLett.97.267602. [DOI] [PubMed] [Google Scholar]
  • 15.Lee JH, et al. A strong ferroelectric ferromagnet created by means of spin–lattice coupling. Nature. 2010;466:954–958. doi: 10.1038/nature09331. [DOI] [PubMed] [Google Scholar]
  • 16.Ryan PJ, et al. Reversible control of magnetic interactions by electric field in a single-phase material. Nat. Commun. 2013;4:1334. doi: 10.1038/ncomms2329. [DOI] [PubMed] [Google Scholar]
  • 17.Geng Y, Lee JH, Schlom DG, Freeland JW, Wu W. Magnetic inhomogeneity in a multiferroic EuTiO3 thin film. Phys. Rev. B. 2013;87:121109. doi: 10.1103/PhysRevB.87.121109. [DOI] [Google Scholar]
  • 18.Akamatsu H, et al. Antiferromagnetic superexchange via 3d states of titanium in EuTiO3 as seen from hybrid Hartree-Fock density functional calculations. Phys. Rev. B. 2011;83:214421. doi: 10.1103/PhysRevB.83.214421. [DOI] [Google Scholar]
  • 19.Akamatsu H, et al. Strong spin-lattice coupling through oxygen octahedral rotation in divalent europium perovskites. Adv. Funct. Mater. 2013;23:1864–1872. doi: 10.1002/adfm.201202477. [DOI] [Google Scholar]
  • 20.Kamba S, et al. Magnetodielectric effect and phonon properties of compressively strained EuTiO3 thin films deposited on (001)(LaAlO3)0.29-(SrAl1/2Ta1/2O3)0.71. Phys. Rev. B. 2012;85:094435. doi: 10.1103/PhysRevB.85.094435. [DOI] [Google Scholar]
  • 21.Li W, et al. Atomic-scale control of electronic structure and ferromagnetic insulating state in perovskite oxide superlattices by long-range tuning of BO6 octahedra. Adv. Funct. Mater. 2020;30:2001984. doi: 10.1002/adfm.202001984. [DOI] [Google Scholar]
  • 22.Li W, et al. Interface engineered room-temperature ferromagnetic insulating state in ultrathin manganite films. Adv. Sci. 2020;7:1901606. doi: 10.1002/advs.201901606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Li L, et al. Structural and magnetic phase transitions in EuTi1-xNbxO3. Phys. Rev. B. 2015;92:024109. doi: 10.1103/PhysRevB.92.024109. [DOI] [Google Scholar]
  • 24.Karki BB, et al. Structure and elasticity of MgO at high pressure. Am. Mineralogist. 1997;82:51–60. doi: 10.2138/am-1997-1-207. [DOI] [Google Scholar]
  • 25.MacManus-Driscoll J, et al. New strain states and radical property tuning of metal oxides using a nanocomposite thin film approach. APL Mater. 2015;3:062507. doi: 10.1063/1.4919059. [DOI] [Google Scholar]
  • 26.Glazer, A., Mabud, S. & Clarke, R. Powder profile refinement of lead zirconate-titanate at several temperatures I. PbTiO3. Acta Crystallogr. B: Struct. Crystallogr. Cryst. Chem.34, 1065 (1978).
  • 27.Yang Y, Ren W, Wang D, Bellaiche L. Understanding and revisiting properties of EuTiO3 bulk material and films from first principles. Phys. Rev. Lett. 2012;109:267602. doi: 10.1103/PhysRevLett.109.267602. [DOI] [PubMed] [Google Scholar]
  • 28.Hÿtch MJ, Snoeck E, Kilaas R. Quantitative measurement of displacement and strain fields from HREM micrographs. Ultramicroscopy. 1998;74:131–146. doi: 10.1016/S0304-3991(98)00035-7. [DOI] [Google Scholar]
  • 29.Menéndez C, Cazorla C. Giant thermal enhancement of the electric polarization in ferrimagnetic BiFe1-xCoxO3 solid solutions near room temperature. Phys. Rev. Lett. 2020;125:117601. doi: 10.1103/PhysRevLett.125.117601. [DOI] [PubMed] [Google Scholar]
  • 30.Kuwabara M, Goda K, Oshima K. Coexistence of normal and diffuse ferroelectric-paraelectric phase transitions in (Pb,La)TiO3 ceramics. Phys. Rev. B. 1990;42:10012–10015. doi: 10.1103/PhysRevB.42.10012. [DOI] [PubMed] [Google Scholar]
  • 31.Lee S, et al. Novel electroforming-free nanoscaffold memristor with very high uniformity, tunability, and density. Adv. Mater. 2014;26:6284–6289. doi: 10.1002/adma.201401917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Goodenough JB. Theory of the role of covalence in the perovskite-type manganites LaMnO3. Phys. Rev. 1955;100:564–573. doi: 10.1103/PhysRev.100.564. [DOI] [Google Scholar]
  • 33.Zhu M, et al. Ferromagnetic superexchange in insulating Cr2MoO6 by controlling orbital hybridization. Phys. Rev. B. 2015;92:094419. doi: 10.1103/PhysRevB.92.094419. [DOI] [Google Scholar]
  • 34.Kanamori J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids. 1959;10:87–98. doi: 10.1016/0022-3697(59)90061-7. [DOI] [Google Scholar]
  • 35.Cazorla C, Íñiguez J. Insights into the phase diagram of bismuth ferrite from quasiharmonic free-energy calculations. Phys. Rev. B. 2013;88:214430. doi: 10.1103/PhysRevB.88.214430. [DOI] [Google Scholar]
  • 36.Cazorla, C., Diéguez, O. & Íñiguez, J. Multiple structural transitions driven by spin-phonon couplings in a perovskite oxide. Sci. Adv.3, e1700288. [DOI] [PMC free article] [PubMed]
  • 37.Reuvekamp P, et al. Tiny cause with huge impact: polar instability through strong magneto-electric-elastic coupling in bulk EuTiO3. J. Phys.: Condens. Matter. 2015;27:262201. doi: 10.1088/0953-8984/27/26/262201. [DOI] [PubMed] [Google Scholar]
  • 38.Katayama T, et al. Ferroelectric and magnetic properties in room-temperature multiferroic GaxFe2-xO3 epitaxial thin films. Adv. Funct. Mater. 2018;28:1704789. doi: 10.1002/adfm.201704789. [DOI] [Google Scholar]
  • 39.Fukunaga M, Noda Y. New technique for measuring ferroelectric and antiferroelectric hysteresis loops. J. Phys. Soc. Jpn. 2008;77:064706–064706. doi: 10.1143/JPSJ.77.064706. [DOI] [Google Scholar]
  • 40.Liao W-Q, et al. A lead-halide perovskite molecular ferroelectric semiconductor. Nat. Commun. 2015;6:7338. doi: 10.1038/ncomms8338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Wang H, et al. An optimized TEM specimen preparation method of quantum nanostructures. Micron. 2021;140:102979. doi: 10.1016/j.micron.2020.102979. [DOI] [PubMed] [Google Scholar]
  • 42.Wang Y, Salzberger U, Sigle W, Eren Suyolcu Y, van Aken PA. Oxygen octahedra picker: a software tool to extract quantitative information from STEM images. Ultramicroscopy. 2016;168:46–52. doi: 10.1016/j.ultramic.2016.06.001. [DOI] [PubMed] [Google Scholar]
  • 43.Wang, H. et al. Tunable Magnetic Anisotropy in Patterned SrRuO3 Quantum Structures: Competition between Lattice Anisotropy and Oxygen Octahedral Rotation. Adv. Funct. Mater. 2108475 (2022).
  • 44.Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. 1993;47:558–561. doi: 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  • 45.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  • 46.Allieta M, et al. Role of intrinsic disorder in the structural phase transition of magnetoelectric EuTiO3. Phys. Rev. B. 2012;85:184107. doi: 10.1103/PhysRevB.85.184107. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary information (1.8MB, pdf)
Reporting Summary (1.3MB, pdf)
Lasing Reporting Summary (803.6KB, pdf)

Data Availability Statement

All the experimental/calculation date that support the findings of this study are available from the corresponding authors upon reasonable request.

All the codes used for this study are available from the corresponding authors upon reasonable request.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES