Contribution of hydrophobic interactions to protein mechanical stability

Graphical abstract

Abstract

The role of hydrophobic and polar interactions in providing thermodynamic stability to folded proteins has been intensively studied, but the relative contribution of these interactions to the mechanical stability is less explored. We used steered molecular dynamics simulations with constant-velocity pulling to generate force-extension curves of selected protein domains and monitor hydrophobic surface unravelling upon extension. Hydrophobic contribution was found to vary between one fifth and one third of the total force while the rest of the contribution is attributed primarily to hydrogen bonds. Moreover, hydrophobic force peaks were shifted towards larger protein extensions with respect to the force peaks attributed to hydrogen bonds. The higher importance of hydrogen bonds compared to hydrophobic interactions in providing mechanical resistance is in contrast with the relative importance of the hydrophobic interactions in providing thermodynamic stability of proteins. The different contributions of these interactions to the mechanical stability are explained by the steeper free energy dependence of hydrogen bonds compared to hydrophobic interactions on the relative positions of interacting atoms. Comparative analyses for several protein domains revealed that the variation of hydrophobic forces is modest, while the contribution of hydrogen bonds to the force peaks becomes increasingly important for mechanically resistant protein domains.

1. Introduction

Many soluble proteins adopt a folded state in functional form. Folding is associated with free-energy gain that is attributed to polar, directional interactions [1], [2] on one hand, and to the hydrophobic effect [3], [4] on the other hand. Polar interactions include hydrogen bonds, salt-bridges and interactions of higher order multipole moments of polar groups. The physical interpretation of hydrophobic interactions is less straightforward [5], [6]; however, it includes the tendency of non-polar groups to minimize their contact with polar water in favour of forming contacts among themselves, resulting in the burial of non-polar groups in the protein core. There are diverging estimations for the relative contribution of polar versus hydrophobic interactions to protein folding [7], [8], [9], [10]. While it is established that hydrophobic interactions supply a significant free-energy gain to protein folding, the role of polar interactions is more controversial as their formation typically includes the exchange of protein-water interactions for protein–protein and water-water interactions.

Polar and hydrophobic interactions not only provide thermodynamic stability, but they also determine the mechanical properties of proteins. Single-molecule force spectroscopy techniques like atomic force microscopy and optical tweezers are used primarily to explore the mechanical properties of biopolymers including proteins [11], [12], [13]. In addition, steered molecular dynamics (SMD) simulations beneficially complement these experiments by providing the molecular mechanisms and atomic level structural changes behind the experimentally observed response to the applied force [14]. Although the timescale of the computations is typically several orders of magnitude shorter than that of the experiments, owing to the limitations of the computational capacity, there are several pieces of evidence that the structural changes observed in computations are also relevant at experimental conditions. Notable examples include the SMD predicted sequence of strand detachments in the I91 (formerly I27) domain of titin [14], [15], [16] and the role of water molecules in the breaking of interstrand hydrogen bonds upon unfolding [17]. Similarly, experimental and computational evidence agree in the strain induced opening of titin’s C-terminal kinase domain before unfolding and also in the identification of critical residues in the titin kinase-ATP interactions [18], [19]. Computations and experiments also consistently observe unfolding intermediates in fibronectin type III₁ domains [20], [21] and in spectrin [22]. AFM experiments and SMD simulations jointly revealed the mechanism by which the complex of a pathogen adhesin and fibrinogen β resists to extreme forces [23] and a mutant of the SARS-CoV-2 spike protein strengthens its binding to the ACE2 receptor [24].

The large number of experimental and computational studies accumulated significant amounts of information on the relationship between structural features and mechanical properties of proteins. As a general trend, all β proteins are mechanically more resistant than α-helical or α/β proteins [25]. The arrangements of secondary structure elements and the direction of pulling force also affect mechanical stability [26], [27], [28], [29], [30], [31], [32]. The access of water molecules to the associated secondary structure elements is an important factor in the resistance to force [33] and in the mechanism of detachment of the elements [17].

Mechanical resistance to force is associated primarily with hydrogen bonds connecting secondary structure elements. It has been illustrated by SMD simulations of the force-induced unfolding of titin’s I91 domain that a force peak appears during the simultaneous burst of the hydrogen bonds between backbones of antiparallel β-strands [14], [34]. The mechanism of hydrogen bond breaking in producing the force peak was later elaborated by showing that water molecules contribute to the weakening and cleavage of the hydrogen bonds [17]. The role of hydrogen bond breaking in the formation of force peaks in the force induced unfolding of FnIII₁ domain has also been shown by SMD simulations [21].

Although hydrogen bonds connecting secondary structure elements contribute fundamentally to the mechanical resistance of proteins, there are several indications that hydrophobic effects also play a role. The unfolding force of the α/β protein GB1 was found to critically depend on hydrophobic mutations (F → L and Y → L) along the sheared surfaces within the hydrophobic core [35]. In another study, the hydrophobic core of the 10th fibronectin III (FnIII) domain of human fibronectin was replaced with that of the mechanically stronger tenascin FnIII domain and the unfolding force of the engineered protein exhibited a 20% increase, matching that of the tenascin FnIII [36]. Further indication of the importance of hydrophobic effect comes from the comparative study of protein L and ubiquitin, where higher mechanical stability was measured for the latter although the number of hydrogen bonds between the unfolding structural units does not differ; by contrast, the number of contacts between residues is higher in the mechanically more stable ubiquitin [37].

In the present contribution we report SMD simulations for various protein domains and systematically analyse the relationship between force peaks and hydrophobic interactions in the course of force-induced protein unfolding. Our objectives are to quantify the contribution of hydrophobic surface unravelling (see later for an explanation) to the observed force peaks and determine how this contribution varies with the structural features and physiological role of protein domains.

2. Methods

The coordinates of the protein domains were downloaded from the Protein Data Bank [38], except for polylysine that was built manually with Maestro [39]. Each domain was immersed in a TIP3P [40] water box using VMD [41]. The size of the water box was selected so that each atom was at least at a 10 Å separation from the edges of the box, and the length of the maximal extension was added in the pulling direction. Simulations were carried out with the CHARMM36 force field [42] using the NAMD 2.10 program [43]. Equilibration started with 10,000 steps of minimization of water molecules with fixed protein atoms followed by 10,000 steps of minimization without any constraint. The system was heated to 300 K by a stepwise increment of temperature in 30 ps. 500 ps volume equilibration completed the preparation of the system. Constant temperature was enforced using Langevin dynamics with a damping coefficient of 5 ps⁻¹. Constant pressure was enforced with a Nosé-Hoover-Langevin piston with a period of 100 fs and a damping time scale of 50 fs. The van der Waals interaction cutoff was set to 12 Å and long-range electrostatics was calculated using particle-mesh Ewald summation with a grid size of < 1 Å. The proteins were initially positioned so that the vector pointing from the N-terminal residue Cα atom to the C-terminal residue Cα atom is along the z-axis. Steered molecular dynamics (SMD) simulations were performed by constraining the position of the Cα atom of the N-terminal residue and exerting force on the Cα atom of the C-terminal residue along the z-axis. 1 Å∙ns⁻¹ constant velocity pulling with a spring constant of 7 kcal∙(mol∙Ų)^-1 was applied in all SMD simulations, except where otherwise noted. Snapshots were taken at regular intervals of the simulation trajectory, and hydrophobic surfaces were calculated with the NACCESS program [44] using default parameters (all atoms except N and O atoms were treated as non-polar, and their corresponding surface was considered as hydrophobic) to obtain hydrophobic surface as a function of extension. The NACCESS program calculates the atomic accessible surface by rolling a probe around the van der Waals surface according to the method of Lee and Richards [45]. The extension (E[t]) was evaluated as the difference between the actual (z[t]) and initial (z[0]) z-coordinates of the C-terminal Cα atom attached to the moving spring: E[t] = z[t]-z[0]. The hydrophobic surface – extension function was numerically differentiated to obtain the hydrophobic surface unravelling as a function of extension. For each system the SMD simulations were performed five times using different random numbers to generate the initial Maxwell distribution of velocities; averages and 90% confidence intervals are reported.

3. Results and discussions

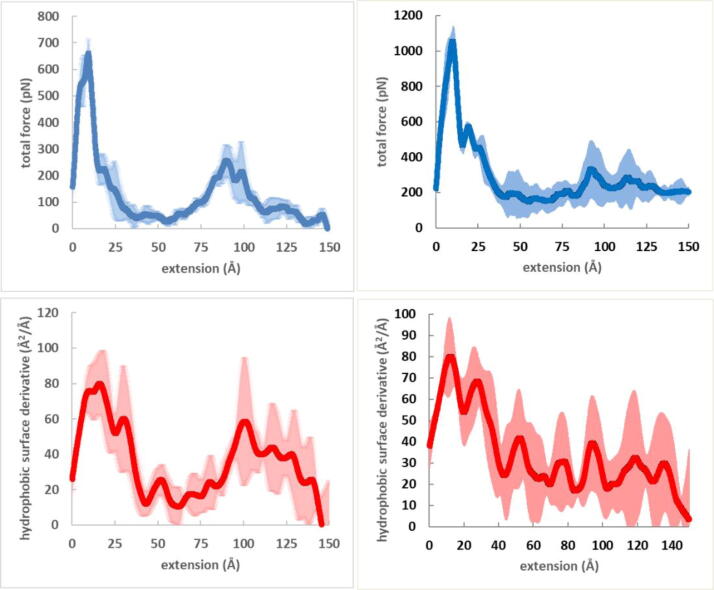
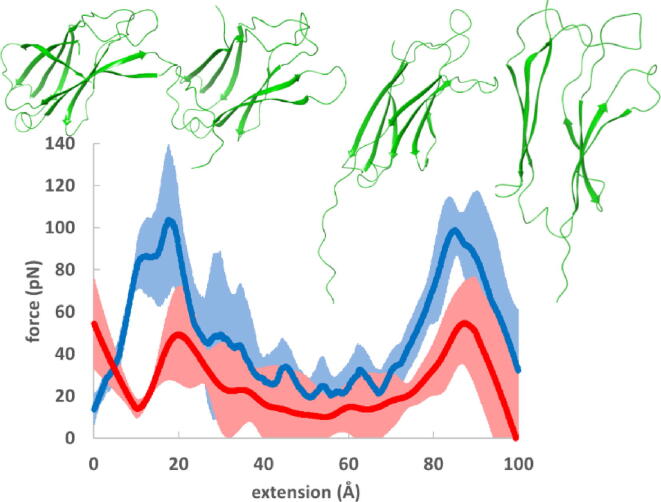
The SMD simulations provided us with force-extension curves and hydrophobic surface-extension curves as it is described in the Methods section. These latter curves give the magnitude of hydrophobic surface as a function of protein extension. A numerical differentiation of this function gives the change of the hydrophobic surface upon the extension of the protein and this function will be called hydrophobic surface unravelling function. As free energy change is associated with hydrophobic surface exposure (or burial), free-energy can be assigned to the magnitude of the hydrophobic surface, and this allows the conversion of the hydrophobic surface unravelling function to hydrophobic force-extension function. This latter function is attributed to the force arising from hydrophobic surface unravelling upon protein extension. The assignment of free energy to the hydrophobic surface will be discussed later. Here we show, in Fig. 1, the force versus extension, the hydrophobic surface versus extension and hydrophobic surface unravelling versus extension functions obtained from SMD simulation for the I91 immunoglobulin domain of titin (PDB 1WAA) [46] and for the fibronectin FnIII₁ domain (PDB 1OWW) [21]. These domains are well suited for our investigations as they both adopt β-sandwich structure, have characteristic force peaks and have been investigated both by experimental [11], [15], [20], [47] and computational [14], [16], [21], [48], [49] methods.

Fig. 1.

Force versus extension (left), hydrophobic surface versus extension (middle) and hydrophobic surface unravelling versus extension (right) functions obtained from SMD simulation for the I91 immunoglobulin domain of titin (top) and for the fibronectin III₁ domain (bottom). 90% confidence intervals are also shown.

The shapes of the force and hydrophobic surface unravelling curves display similarity, and this suggests that hydrophobic surface unravelling is related to the peaks of the force-extension function. It has to be noted that force peaks obtained with 1 Å/ns pulling velocity, as those presented in Fig. 1 are seriously overestimated with respect to the force peaks extrapolated to zero pulling speed [50]. Another point to be noted is that the hydrophobic surface change was not converted to force, rather it has a dimension of Ų/Å (surface/extension). Thus, the scales of the functions are not relevant and only their shapes are considered at this stage. It is noticeable that the force-extension curves in Fig. 1 have a peak at low extensions, and they also have a peak near 100 Å showing that these domains unfold via intermediate states. The existence of an intermediate under experimental conditions was indeed observed for FnIII₁, [20] however, it was not observed for I91. Since I91 has been investigated thoroughly and no intermediate corresponding to the extension around 100 Å has been reported, it can be concluded that the second peak appearing in the conditions of the SMD simulation is not present in the experimental conditions characterized by much lower pulling speeds. Nevertheless, the comparative analysis of the force and the hydrophobic surface unravelling curves is legitimate as far as they belong to the same unfolding events.

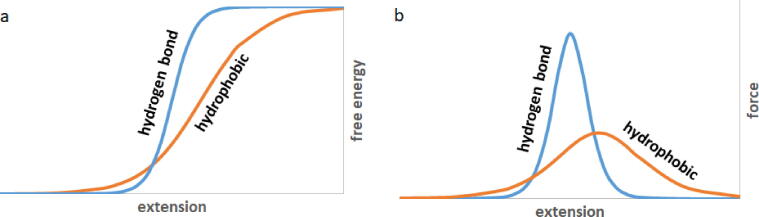
Despite the similarity in the shapes of the curves in Fig. 1, it is apparent that hydrophobic surface unravelling peaks tend to be shifted toward higher extensions compared to the total force peaks (Fig. S1). The positions of the hydrophobic surface unravelling peaks are at the right tails of the force peaks. This phenomenon can be explained by investigating the free energy versus extension function of the hydrogen bond interactions, on one hand, and that of the hydrophobic interactions, on the other hand. Strong hydrogen bonds have strict geometrical requirements both in terms of the donor–acceptor distance and the donor-H-acceptor angle. The free-energy gain of the hydrogen bond formation rapidly diminishes with increasing deviation from the optimal geometric parameters [51], [52]. This contrasts with the non-directional hydrophobic interactions where less steep dependence of the free energy on the geometric parameters can be assumed. Schematic comparisons of the extension dependence of both free-energy and force for hydrogen bond and hydrophobic interactions are shown in Fig. 2. The less steep increase of the free energy for hydrophobic interactions results in a force peak with lower maximum that is shifted towards higher extensions. Note that free-energy changes corresponding to hydrogen bond and to hydrophobic interaction are identical in Fig. 2. This equality is an approximation adopted in the lack of consensus on the relative contributions of hydrophobic and polar interactions to the stability of folded proteins [7], [8], [9]. The important point here is the distinction between thermodynamic stability associated with free energy differences and force resistance associated with the shape of the free energy versus extension curve.

Fig. 2.

Schematic representation of a) free energy vs. extension and b) force vs. extension for hydrogen bonding and for hydrophobic interactions.

The hydrophobic force peak in Fig. 2.b has a lower maximum that is positioned at the right tail of the hydrogen bond force peak. This situation resembles the relationship between the force peaks and the hydrophobic unravelling peaks in Fig. 1, suggesting that force peaks can primarily be attributed to hydrogen bond breaking, and hydrophobic surface unravelling supplies a smaller contribution mainly to the right tail of the force peak.

At this point, energy assignment to hydrophobic surface unravelling is required to convert the surface to free-energy and the surface change corresponding to unit extension to force. Indeed, the hydrophobic surface of proteins is typically buried in the hydrophobic core, and the formation of this hydrophobic core is considered to be a significant driving force of protein folding [7]. The reverse process, namely the exposure of the hydrophobic surface to water increases the free energy of the system primarily by decreasing the entropy that results from the rearrangement of water molecules around the hydrophobic surface. The magnitude of the free energy change corresponding to hydrophobic surface burying and exposure to water has been investigated from several aspects. It has to be pointed out, however, that although significant correlation between the area of non-polar surface solvated and the corresponding free energy change has been documented [10], [53], [54], the relationship is clearly approximate as it does not take into account the structural details of the interacting partners [55], [56], [57]. This is reflected in the varying estimation of the free energy change upon hydrophobic surface solvation. Selected values are shown in Table1. They span a range between 0.3 and 3.3 pN·Å⁻¹ (free energy/surface), the highest value exceeding more than ten times the lowest one.

Table 1.

Estimates of the free energy of solvation of a hydrophobic surface.

hydrophobic surface solvation free energy		System	Reference
J·mol−1·Å−2	pN·Å−1a
37	0.6	hydrophobic ligand–protein binding	[53]
75	1.2	protein hydrophobic solvation	[54]
111b	1.8	protein hydrophobic solvation	[58]
200	3.3	protein/hydrocarbon solvation	[10]
18–45c	0.3–0.7	protein unfolding	[59]

^aJ·mol⁻¹·Å⁻² is converted to pN·Å⁻¹ by the multiplying factor of 0.0166 obtained as a product of 10^–3/4.184 (J to kcal) and 69.5 (kcal·mol⁻¹·Å⁻¹ to pN).

^bcalculated as the ratio of 150kT work at 300 K and the associated 33 nm² hydrophobic surface area change.

^csum of enthalpic and entropic contributions at 60 °C.

In addition, the hydrophobic surface area versus extension function as calculated from molecular dynamics snapshots is inherently not smooth and therefore represents additional uncertainty in assigning force to hydrophobic surface unravelling. In the following discussion we will use a free energy value of 0.5 pN·Å⁻¹ which is at the lower end of available free-energy estimates. Hence the calculated free-energy and force are expected to be lower bounds to their actual values.

It is worth noting that while there is a quantitative relationship between hydrophobic surface unravelling and free energy change, the connection between polar surface unravelling and free energy change is less straightforward. Although protein folding and ligand–protein complex formation are accompanied with polar surface burial, its free energy consequence depends on the involvement of the polar atoms in hydrogen bond interactions and not only on the magnitude of the polar surface change [53], [60]. This is confirmed by finding no similarity between the force-extension and polar surface unravelling-extension curves as it is exemplified by the I91 and FnIII₁ domains in Fig. S2.

Our objective was to compare hydrophobic forces to the total forces. We first investigated the I91 domain of titin that has been thoroughly studied by both experimental and computational means. The magnitude of the force peak near 10 Å extension was calculated and measured at a wide range of pulling speeds [11], [14], [15], [16], [47], [48], [49]. The peak force value extrapolated to zero pulling speed was near 200 pN [50], [61]. The hydrophobic force peaks were calculated from hydrophobic surface unravelling. Although pulling speed may affect the unfolding route and thus hydrophobic surface unravelling, there are several examples where experimentally and computationally observed unfolding routes are similar despite the several order of magnitude difference in the applied pulling speeds [14], [15], [16], [17], [18], [19], [20], [21], [22]. The sensitivity of the total force peak and the insensitivity of the hydrophobic surface unravelling to the pulling velocity were confirmed by the two SMD simulations performed for the I91 domain with tenfold difference in pulling speed (Fig. 3). The force peaks obtained with 1 Å∙ns⁻¹ and 10 Å∙ns⁻¹ pulling velocities were ∼650 pN and ∼1050 pN, respectively, while the hydrophobic surface unravelling peaks were ∼80 Å²∙Å⁻¹ in both simulations. Note that the hydrophobic surface unravelling is calculated from the structural changes along the unfolding route that appears not to be very sensitive to the pulling velocity. In contrast, the magnitude of the force peak is significantly affected by the velocity dependent relaxation of the system.

Fig. 3.

Force peaks (top) and hydrophobic surface unravelling peaks (bottom) with 1 Å∙ns⁻¹ (left) and 10 Å∙ns⁻¹ (right) pulling velocities for the I91 immunoglobulin domain of titin. The pulling velocity has a more pronounced effect on the magnitude of the force peaks compared to the magnitude of the hydrophobic surface unravelling peaks.

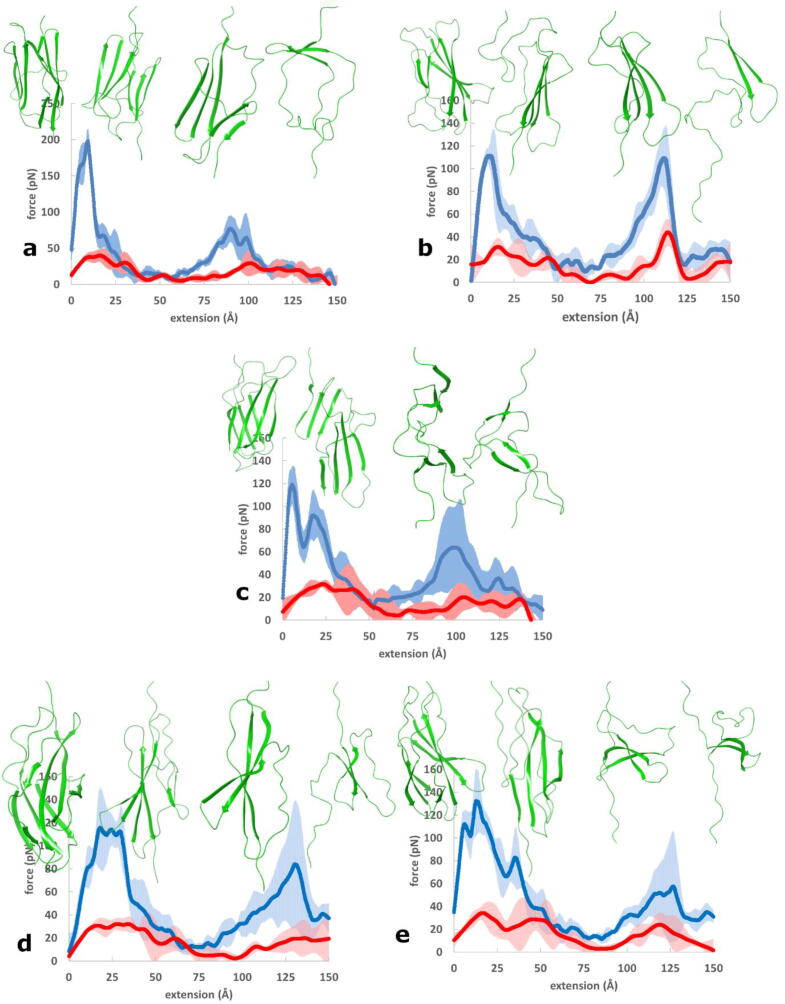
These data support that SMD force-extension curves scaled to low pulling velocities can be compared to hydrophobic surface unravelling curves. The force-extension curves obtained from SMD simulations with 1 Å∙ns⁻¹ pulling velocity were scaled by 200/650 = 0.3 based on 200 pN force peak of I91 extrapolated to zero pulling speed and the 650 pN force peak obtained from the simulations. These scaled forces were compared to the hydrophobic forces obtained from the hydrophobic surface unravelling (Ų·Å⁻¹) multiplied by 0.5 pN·Å⁻¹ as described above. The total and hydrophobic forces of five β-sandwich domains, namely the I91 immunoglobulin domain of titin (PDB 1WAA) [46], the fibronectin III₁ domain (PDB: 1OWW) [21], the fibronectin III₁₀ domain (PDB 1FNF) [62]. the fibronectin III (FnIII) type A77 and A78 domains of titin (PDB 3LPW) [63] are shown in Fig. 4. We note that the comparison of the scaled SMD forces and the hydrophobic forces with system- and extension-independent scaling factors is an approximation that does not take into account the domain-dependent relationship between pulling velocities and rupture forces [47] and the potentially extension-dependent relationship between simulated and experimentally measured forces. We apply these scaling factors only for β-sandwich domains assuming less variation of the factors for the similar structural motifs. By contrast, these factors will not be applied to other types of investigated domains (see later).

Fig. 4.

Total (blue) and hydrophobic (red) force-extension curves for a) the I91 immunoglobulin domain of titin (PDB 1WAA) [46], b) the fibronectin III₁ domain (PDB: 1OWW) [21], c) the fibronectin III₁₀ domain (PDB 1FNF) [62], d) the fibronectin III (FnIII) type A77 domain of titin (PDB 3LPW) [63] and e) the FnIII type A78 domain of titin (PDB 3LPW) [63]. 90% confidence intervals are also shown. Ribbon diagrams of the proteins before and after force peaks indicate structural changes (downward pulling direction). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The total force curves exhibit a maximum near 10 Å extension in each of the investigated domains. This force peak is the largest for the I91 domain, and it is smaller albeit similar in height for the other domains. The higher force peak of I91 compared to FnIII₁ and FnIII₁₀ is in line with reported experimental and computational studies [20]. We are not aware of either experimental or computational investigations of the mechanical stability of the A77 and A78 domains of titin. These domains are part of the A-band section of titin which is less extensible than titin's I-band section. The A-band section is assumed not to function as a molecular spring under physiological conditions [64]. Nevertheless, the A-band contains Ig and FnIII domains which are potentially resistant to mechanical stress. Furthermore, it is worth noting that the mechanosensor function associated with the kinase domain presumes a certain level of extensibility along titin's A-band section as well [19]. The A77 and A78 domains have force peaks that are similar to those of FnIII₁ and FnIII₁₀ domains of fibronectin, indicating a similar force resistance. Another force peak near or above 100 Å extension appears for each of the domains investigated. This peak points at the presence of an unfolding intermediate. This intermediate near 100 Å extension, however, has not been observed for the I91 domain. By contrast, such an intermediate was detected for the fibronectin FnIII₁ domain. Indeed, the two peaks of FnIII₁ have similar height of about 120 pN that is higher than the second peak of both the I91 and the other domains investigated. Although the second peak appears on the force-extension curves of FnIII₁₀, A77 and A78 domains, they are all considerably smaller and exhibit larger 90% confidence intervals. The intermediate is occasionally observed experimentally for FnIII₁₀ [65], [66], [67], [68] and, based on our calculations, it is not expected to be characteristic for the A77 and A78 domains.

The hydrophobic forces are considerably smaller than total forces for all investigated domains. Their contribution to the peaks is further reduced by their shift towards higher extensions (see also Fig. S1 focusing on the unfolding peaks). In this way, the tallest force peak of 200 pN of I91 includes approximately 40 pN hydrophobic contribution. The heights of the hydrophobic force peaks exhibit a modest variation for the β-sandwich domains investigated; they are around 40 pN for each domain. More important variation is seen in the shift of their position with respect to the total force peak. The most important relative contribution to the total force peak is seen for domains A77 and A78 (Fig. 4d and e, respectively), where about one fourth of the force can be assigned to the hydrophobic surface unravelling. The significantly higher total force peak of I91 compared to the other β-sandwich domains, and the similar hydrophobic force peaks of all these domains imply that the extra mechanical stability of the I91 domain does not come from hydrophobic interactions. SMD simulations showed that force peaks of the I91, FnIII₁ and FnIII₁₀ domains correspond to the simultaneous rupture of several inter-strand hydrogen bonds [17], [21], [66]. The differences between the total and hydrophobic forces shown for the I91 and FnIII₁ domains in Fig. S3 can be attributed to polar forces but they are not equal to the polar surface unravelling discussed above. Polar forces exhibit peaks at the locations of the total forces; thus, these peaks are assigned to the simultaneous breaking of several inter-strand hydrogen bonds. The most apparent differences between the total and polar force curves are at the right tail of the total peaks, where the effect of hydrophobic interactions is important. The important variations in the magnitude of the total force peaks and the similar magnitude of the hydrophobic force peaks suggest that forces emerging from surface unravelling gain importance in less force resistant proteins.

Considering now the force peak at extensions near or exceeding 100 Å, a well-defined hydrophobic force peak appears for the FnIII₁ domain (Fig. 4b). FnIII₁ is a domain for which the existence of the second peak is confirmed experimentally at low pulling velocities. The relative contribution of the hydrophobic force to this total force peak amounts to about one fourth, similarly to the first peak near 10 Å extension.

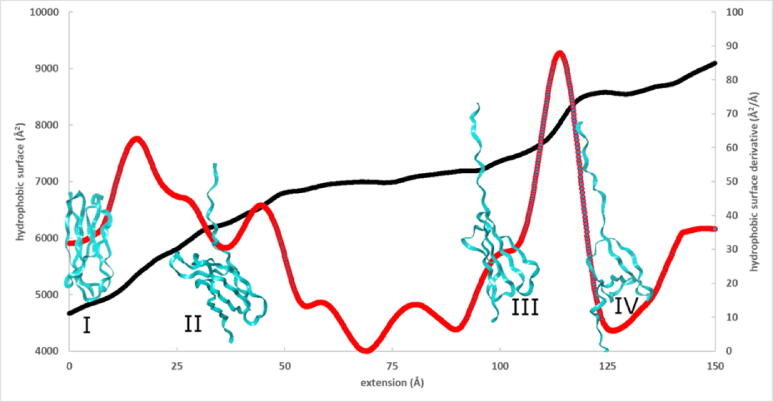
The structural changes associated with hydrophobic forces were analysed in greater detail. Fig. 5 shows the variation of the hydrophobic surface and hydrophobic surface unravelling as a function of extension for the FnIII₁ domain. The first force peak corresponds to the separation of strands from the β-barrel as it is indicated by the ribbon diagrams of FnIII₁ at 7 and 35 Å extensions in Fig. 5. This β-strand separation also results in an increase in the hydrophobic surface. Residues with the largest change in hydrophobic surface area are shown in Fig. 6.

Fig. 5.

Hydrophobic surface (black) and its derivative (red) as a function of extension for the FnIII₁ domain. Representative structures before and after force peaks are also shown. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

Residues with highest hydrophobic surface change before and after force peaks. Structures I and II correspond to the force peak between 7 and 35 Å, and structures III and IV correspond to the force peak between 100 and 125 Å extensions in Fig. 5.

The largest hydrophobic surface changes correspond to β-strands separated by extension. When making a transition from structure I to structure II, the residues with large hydrophobic surface exposures are Val4, Val6, Phe7, Ile8, Pro12, Phe89 and Thr90. No changes with similar magnitude were observed between structures II and III, where the already separated strands are drifting apart. By contrast, high exposure was found between structures III and IV for residues Ile30, Leu63, Tyr69, Ile74, Ile76, Phe87 and Phe89. These data show that β-barrel structures bury hydrophobic surfaces, and their unravelling upon unfolding results in the generation of force.

The systems examined so far are either immunoglobulin or fibronectin type III domains. They share a β-sandwich topology, and their functions are associated with mechanics. Interestingly, in β-strands the frequency of occurrence of amino acids with large side chains and aromatic rings versus charged amino acids is greater versus lower than average, respectively [69]. This is in line with the nature of amino acids giving the highest contribution to hydrophobic forces for FnIII₁ as identified above, and demonstrates that domains with β-sandwich topology are well optimized for enhanced mechanical stability not only because of the hydrogen bonding network but also because of the buried hydrophobic surfaces.

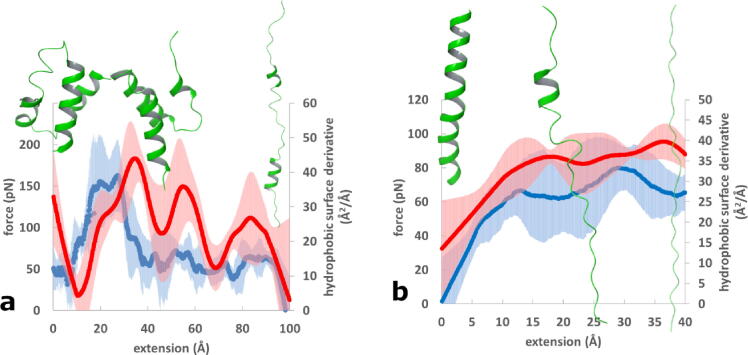
The role of hydrophobic interactions in the force-induced extension of three other protein domains with lower mechanical stabilities was also investigated. The first C2 domain of synaptotagmin I [70] (C2) is an eight-strand β-sandwich domain, and, in contrast to the seven-strand β-sandwich domains such as immunoglobulin and fibronectin type III, the two terminal strands point in the same direction. The staphylococcal protein A immunoglobulin-binding B domain [71] (FB) is a bundle of three α-helices. A polylysine peptide formed by 30 L-lysine residues (Lys₃₀) was also studied. Polylysine at high pH has been shown to have unprotonated sidechains and to adopt α-helical conformation [72], [73]. These domains are expected to have low mechanical stabilities with smaller or no forces peak in their force-extension curves. The C2 polyprotein has been studied with AFM at a pulling velocity of 0.6 nm·ms⁻¹, and the 60 pN force peaks were fitted with a single contour length increment [74]. By contrast, we are not aware of any experimental investigation of the mechanical stability of FB. Both the C2 and the FB domains were studied by SMD simulations, and it was found [34] that neither of them display force peaks at 0.5 Å·ps⁻¹ pulling speed. Our calculations, however, apply a much lower pulling speed of 1 Å·ns⁻¹ that may allow for the observation of force peaks obscured by the higher noise associated with a higher pulling speed. The mechanical stability of polylysine has been investigated by AFM [75], [76], [77]. The force–extension curve together with the hydrophobic force curve for the C2 is shown in Fig. 7. The force versus extension and hydrophobic surface derivative versus extension curves for FB and Lys₃₀ are shown in Fig. 8. Note that while the factors scaling SMD forces and transforming hydrophobic surface derivatives to forces were kept for the C2 domain structurally related to the other β-sandwich domains, they were not applied for FB and Lys₃₀ owing to the different structural and mechanical properties of the latter domains.

Fig. 7.

Total (blue) and hydrophobic (red) force-extension curves for the C2 domain of synaptotagmin I (PDB: 1RSY) [70] (C2). 90% confidence intervals are also shown. Ribbon diagrams of the proteins before and after force peaks indicate structural changes (downward pulling direction). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 8.

Force (blue) and hydrophobic surface derivative (red) versus extension curves for a) immunoglobulin binding domain (PDB: 1BDD) [71] (FB) b) polylysine (Lys₃₀). 90% confidence intervals are also shown. Ribbon diagrams of the proteins at characteristic points of the curves indicate structural changes (downward pulling direction). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The C2 domain exhibits a scaled force peak of ∼ 100 pN height near 20 Å extension. The height is comparable to the smaller force peaks obtained for the β-sandwich domains shown in Fig. 4. Another force peak above 80 Å extension with similar height points at the presence of an unfolding intermediate. The calculated hydrophobic force curve shows a shape similar to the SMD force curve. The height of the hydrophobic force peaks is ∼ 40 pN similarly to those observed for β-sandwich domains. The position of the first hydrophobic force peak is shifted compared to the total force, similarly to what was observed for the first peak of each domain investigated. By contrast, the shift in the positions of total and hydrophobic forces is small for the second peak (∼80 Å, Fig. 8b) resulting in an increased relative contribution of the hydrophobic force.

The FB domain exhibits a dominating (double) force peak at a low extension near 25 Å and, in this respect, it resembles the curves shown for β-sandwich domains in Fig. 4. However, the height of the peak is lower than any of the corresponding low-extension peaks in Fig. 4. (Note that the latter curves are scaled by a 0.3.) This observation makes it questionable whether this peak would appear in an experimental force-extension curve obtained at several orders of magnitude lower pulling speeds, since the peak may disappear owing to the opportunity of enhanced system relaxation. Nevertheless, it is interesting to see that the hydrophobic surface derivative also shows a well-defined peak shifted by a few Ångströms to the right. The height of this peak (∼40 Å²/Å) is lower than the corresponding peaks of β-sandwich domains (60–80 Å²/Å). The apparent difference between the mechanical properties of the FB and the β-sandwich domains stems from their different architecture. The FB domain is a short sequence of 48 amino-acids that adopts a structure with three α-helical segments and connecting loops [71].

The force of the helical Lys₃₀ peptide exhibit an initial rise and a plateau upon extension. This force plateau was observed for several small helical proteins both experimentally and in simulations. While the 60–80 pN magnitude of the force is somewhat higher than reported forces for small alpha helices with various sequences [78], [79], it is lower than the observed ∼200 pN force obtained for polylysine in the form of Cys₃Lys₃₀Cys [75], [77]. The hydrophobic surface derivative follows the force curve with a shift toward higher extensions and this is similar to what was observed for all other systems. The plateau of the hydrophobic surface derivative is at 35–40 Å²/Å and is lower than the peaks seen in the β-sandwich domains (cf. with Fig. S1).

While both forces and hydrophobic surface derivatives are smaller for the α-helical structures than for the β-sandwich domains, the hydrophobic forces have increased relative contribution as observed for the FB and Lys₃₀ domains. While the role of hydrogen bonds in the mechanical stability of force-resistant domains is well studied, the factors governing the mechanical properties of helical polypeptides are less understood. Contributing factors include the sequence that affects side-chain-dependent properties and interactions [79], [80], [81] and the dihedral potential that provides greater free energy barrier to extension than do intrahelical hydrogen bonds [82]. The mechanical stability of interacting helices also affects the elasticity of coiled-coils that show structural transitions at low forces [83], [84]. The role of various factors like hydrophobic interactions, hydrogen bonds and dihedral potentials have to be further investigated for a better understanding of the mechanical properties of helical domains.

Our analysis shows that hydrogen bonds have a dominating role in providing structural and mechanical stability to protein systems. This finding is in line with the interpretation of previous SMD simulations using constant-velocity pulling, where force peaks were associated with the breaking of hydrogen bonds [14], [16]. This view is also supported by molecular dynamics analysis of the forces among hydrophilic and hydrophobic groups. The former are higher and depend on the relative orientation of the interacting groups [85]. Hydrogen bonds appear to make an essential contribution also to the structural stability of ligand–protein complexes as it is shown by the success of the dynamic undocking method that supports the identification of protein ligands [86]. The forces arising from hydrophobic surface unravelling were found to be a fraction of the total force. Our estimate is one fifth for the I91 domain of titin and about one third for other, mechanically less resistant β-sandwich domains. This is in sharp contrast with the relative contribution of hydrogen bonding and hydrophobic interactions to the thermodynamic stability of folded proteins and ligand–protein complexes. It is well established that hydrophobic interactions are significant in providing thermodynamic stability to the folded state with respect to the unfolded state [4], [7], [10]. The importance of hydrophobic interactions in ligand–protein complexes increases with ligand size. While polar interactions are dominant in the complexes of fragment-sized ligands, hydrophobic interactions become the major source of binding free energy for protein complexes of larger ligands [87]. However, hydrophobic and polar interactions may not be totally uncoupled as it is exemplified by H-bonds in water-shielded cavities [88], [89]. There are varying estimations on the free-energy gain of hydrogen bonding, primarily because the formation of solute–solute and water-water hydrogen bonds upon protein binding are accompanied by the loss of solute-water hydrogen bonds [7], [9], [90], [91]. The apparent differences between the relative contributions of hydrogen bonding and hydrophobic interactions to the thermodynamic stability, on one hand, and to the mechanical resistance, on the other hand, are explained by the different dependence of these interactions on the relative positions of the interacting partners as shown in Fig. 2.

4. Conclusion

Steered molecular dynamics simulations of protein domains generate force-extension curves of the unfolding, and they can also be used to generate hydrophobic force-extension curves. The latter are obtained by i) recording hydrophobic surface area as a function of extension, ii) transforming hydrophobic surface area into free energy using estimated hydrophobic surface solvation free energy, and iii) differentiating the free energy numerically with extension. The quantitative comparison of total and hydrophobic forces was made by scaling the total SMD forces to force peaks extrapolated to zero pulling velocity. The estimated maximal magnitude of forces arising from hydrophobic surface unravelling are around 40 pN (with the assumption of 0.5 pN·Å free energy per Ų hydrophobic surface) that is a fraction of the highest force peaks observed for β-sandwich domains with low pulling speed (100–200 pN depending on the actual domain [11], [20], [50]). Moreover, since hydrophobic surface unravelling force peaks are shifted to larger extensions, their contribution to the highest force peaks is smaller than their maximal value. Consequently, force peaks observed in constant-velocity pulling experiments and SMD simulations are dominated by hydrogen bond breaking, while hydrophobic interactions contribute to the high-extension tail of the peaks.

We showed for several protein domains with varying secondary structure elements and varying mechanical stability that the hydrophobic surface unravelling force peaks are smaller and shifted to higher extension compared to total force peaks. The interpretation of this finding is based on the different free energy dependence of hydrogen bonding and hydrophobic interactions on the relative geometry of atoms involved. The steep dependence of the free energy on the relative geometry of the interacting partners in hydrogen bonds leads to high forces when the geometry distorts owing to the force induced extension of proteins. Free energy of hydrophobic interactions changes less steeply with the relative positions of the interacting partners, and this results in smaller force peaks that are shifted toward larger extensions. This explains why the relative contribution of hydrogen bonding and hydrophobic interactions to the mechanical stability of proteins is not parallel with their importance in providing thermodynamic stability to folded proteins where hydrophobic interactions is accepted to play a dominant role [10], [92].

The relative contribution of hydrophobic unravelling to the force peaks is more important for mechanically less stable domains and for unfolding intermediates. In particular, SMD simulations for fibronectin domains of titin and fibronectin predict force peaks significantly lower than those for I91, but a comparable contribution of the hydrophobic surface unravelling forces (∼40 pN peak height). Similarly, the first C2 domain of synaptotagmin I whose function is not associated with mechanical stress and adopts an 8-strand β-sandwich structure has a higher relative contribution of hydrophobic forces. The small immunoglobulin-binding B domain with α-helical structure exhibits small total force and hydrophobic surface derivative peaks, while Lys₃₀ with a single α-helix extends with a constant force and hydrophobic surface derivative in SMD simulations. The reduced mechanical resistance of α-helices compared to β-sandwich domains is accompanied with a shift in the relative importance of contributing interactions; the barrier to extension is not dominated by hydrogen bonds [82] and although hydrophobic surface unravelling forces are reduced their relative contribution is increased. These findings suggest that both hydrogen bonds and hydrophobic interactions contribute to the mechanical stability of most protein domains, but increased stability is achieved in folds where simultaneous hydrogen bond breaking is required for unfolding. These are exemplified by the immunoglobulin domains of titin, and to a lesser extent by the fibronectin domains of titin and fibronectin where the arrangement of hydrogen bonds in the β-sandwich structure assures added resistance to mechanical stress.

CRediT authorship contribution statement

György G. Ferenczy: Conceptualization, Investigation, Writing – original draft. Miklós Kellermayer: Conceptualization, Writing – review & editing, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: